
工科数学分析上机作业
说明:以下两道题均是使用Matlab 语言,且在Matlab 7.0中运行通过。
1.(两个重要极限)计算下列函数的函数值并画出图形,观察两个重要极限值。
(1)y=f(x)=; (2)y=f(x)=.
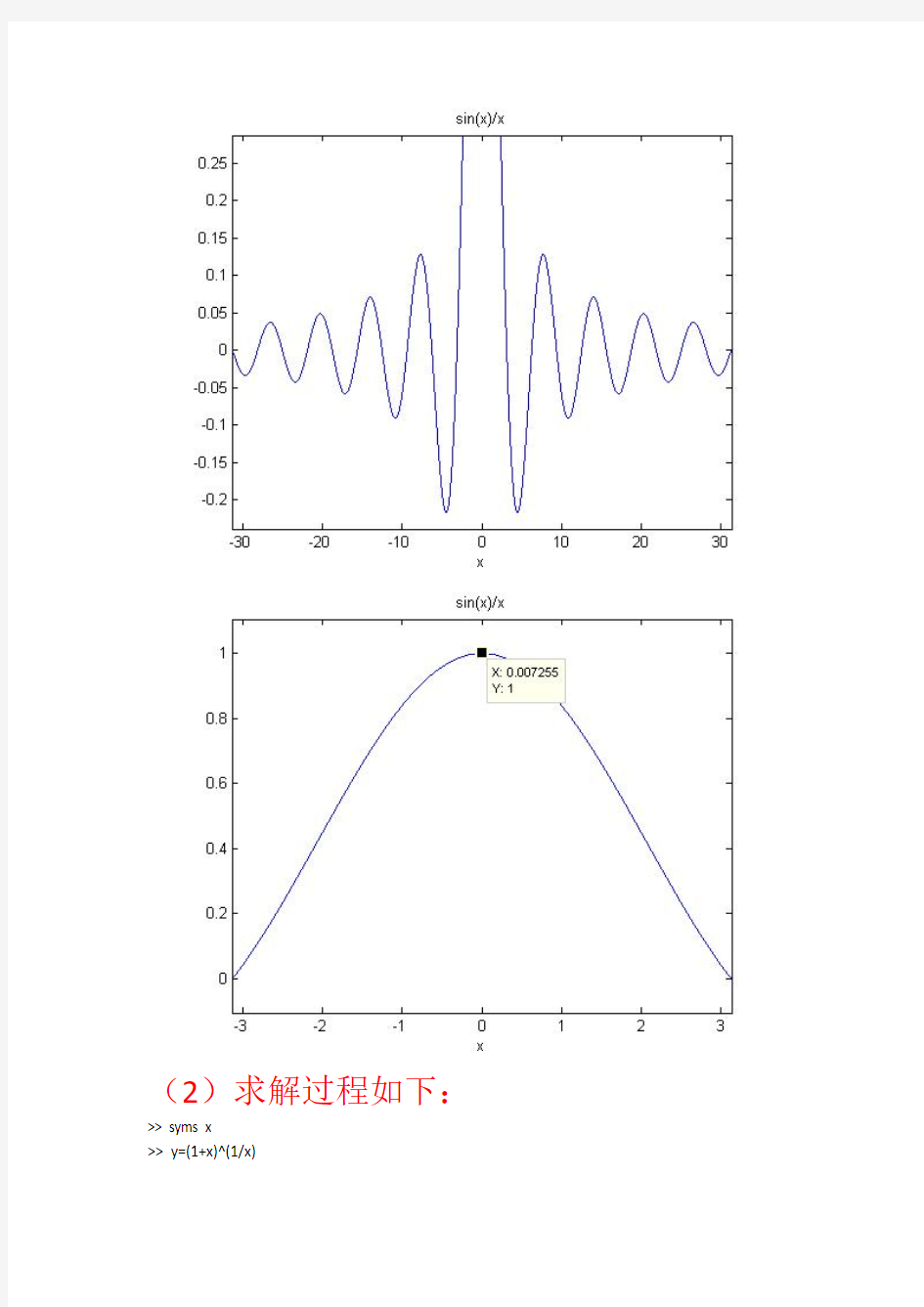
sin x x (1+x)1x 解:(1)求解过程如下:
>> syms x
>> y=limit(sin(x)/x)
y =
1
>> ezplot(sin(x)/x,[-10*pi,10*pi])
>> ezplot(sin(x)/x,[-1*pi,1*pi])
其图形如下:
(2)求解过程如下:>> syms x
>> y=(1+x)^(1/x)
y =
(1+x)^(1/x)
>> y=limit((1+x)^(1/x))
y =
exp(1)
>> ezplot((1+x)^(1/x),[-1000,1000]) >> ezplot((1+x)^(1/x),[-10,10]) >> ezplot((1+x)^(1/x),[-1,1])
其图像如下:
分析如下:(1)当x 取值为[-30,30]时,由该题的第一个图像可以看到,函数值在不断震荡,一会为正数,一会为负数。
而当x 取值为[-3,3]时,函数值始终大于0。当x 趋近于0时,由该题的第二个图像可以得到函数值为1。
另外,该结论也可以由夹逼法则证明,结果不变,当x 趋近于0时,函数值仍为1。
(2)由该题的三个图像可以知道,该函数在定义域内为单调递减函数。且由该题的第一和二个图像知道,当x 在
[0,10]区间内,函数递减趋势非常迅速。由该题的第三个图像知道,当x 趋于0 时,函数值为自然对数的底数 e ,即约为2.71828.
3.计算f(x)=,
12+1√2π
∫x 0e ?t 2/2dt 1?x ?3的函数值{f (0.1k );k=1,2,…,30}.计算结果取7位有效数字。
解:计算过程为:
>> f1= @(t) exp(-(t).^2/2)
f1 =
@(t) exp(-(t).^2/2)
>> for i=1:30
s(i,1)=1/2+1/sqrt(2*pi)*quad(f1,0,i*0.1); end
>> fprintf('%9.7g\n',s);
0.5398278
0.5792597
0.6179114
0.6554217
0.6914625
0.7257469
0.7580363
0.7881446
0.8159399
0.8413447
0.8643339
0.8849303
0.9031995
0.9192434
0.9331929
0.9452007
0.9554345
0.9640697
0.9712834
函数定义: % 目标函数 function f = fun(x) fm=0; for i=1:499 fmi = (1-x(i))^2 + 100*(x(i+1)-x(i)^2)^2; fm=fm+fmi; end f =fm; end % 梯度 function g = grad(x) g = zeros(500,1); g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); for i=2:499 g(i)=2*(x(i)-1)+400*x(i)*(x(i)^2-x(i+1))+200*(x(i)-x(i-1)^2); end g(500) = 200*(x(500)-x(499)^2); end % 二阶梯度
function g = grad2(x) g = zeros(500,500); g(1,1)=2+400*(3*x(1)^2-x(2)); g(1,2)=-400*x(1); for i=3:500 g(1,i)=0; end for i=1:498 g(500,i)=0; end g(500,499)=-400*x(499); g(500,500)=200; for i=2:499 for j=1:500 if j==i-1 g(i,j)= -400*x(i-1); elseif j==i g(i,j)= 2+400*(3*x(i)^2-x(i+1))+200; elseif j==i+1 g(i,j)= -400*x(i); else g(i,j)=0; end end end end 1.最速下降法 function x_star = steepest(x0,eps) gk = grad(x0); res = norm(gk); k = 0; while res > eps && k<=50000 dk = -gk;
抛物型方程有限差分法 1. 简单差分法 考虑一维模型热传导方程 (1.1) )(22x f x u a t u +??=??,T t ≤<0 其中a 为常数。)(x f 是给定的连续函数。(1.1)的定解问题分两类: 第一,初值问题(Cauchy 问题):求足够光滑的函数()t x u ,,满足方程(1.1)和初始条件: (1.2) ()()x x u ?=0,, ∞<<∞-x 第二,初边值问题(也称混合问题):求足够光滑的函数()t x u ,,满足方程(1.1)和初始条件: ()13.1 ()()x x u ?=0,, l x l <<- 及边值条件 ()23.1 ()()0,,0==t l u t u , T t ≤≤0 假定()x f 和()x ?在相应的区域光滑,并且于()0,0,()0,l 两点满足相容条件,则上述问题有唯一的充分光滑的解。
现在考虑边值问题(1.1),(1.3)的差分逼近 取 N l h = 为空间步长,M T = τ为时间步长,其中N ,M 是 自然数, jh x x j ==, ()N j ,,1,0Λ=; τ k y y k ==, ()M k ,,1,0Λ= 将矩形域G {}T t l x ≤≤≤≤=0;0分割成矩形网格。其中 ()j i y x ,表 示网格节点; h G 表示网格内点(位于开矩形G 中的网格节点)的集合; h G 表示位于闭矩形G 中的网格节点的集合; h Γ表示h G -h G 网格边界点的集合。 k j u 表示定义在网点()k i t x ,处的待求近似解,N j ≤≤0,M k ≤≤0。 注意到在节点()k i t x ,处的微商和差商之间的下列关系 ((,)k j k j u u x t t t ????≡ ? ????): ()() ()ττ O t u t x u t x u k j k j k j +??? ????=-+,,1 ()() ()2112,,ττ O t u t x u t x u k j k j k j +??? ????=--+ ()()()h O x u h t x u t x u k j k j k j +??? ????=-+,,1 ()() ()h O x u h t x u t x u k j k j k j +??? ????=--,,1 ()() ()2112,,h O x u h t x u t x u k j k j k j +??? ????=--+ ()()() ()2 222 11,,2,h O x u h t x u t x u t x u k j k j k j k j +???? ????=+--+ 可得到以下几种最简差分格式
大连理工大学2009年研究生入学考试数学分析试题 一、解答下列问题。 1、 判断下列数列是否收敛 222 111123n ++++…… 2、 设{}n a 1= 1= 3、 判断下列函数是否一致连续 ()1cos n f x e x ??= ??? ,(]0,1x ∈ 4、 设,y u f xy x ??= ???,求:22u x ??,2u x y ??? 5、 已知:()f a 存在,求()()lim x a xf a af x x a →-- 6、 设()f x 在[],a b 上可导,且()f a =()f b ,证明:存在(),a b ξ∈,使得 ()()()22f f a f ξξξ-= 7、 求极限()2lim ln n x x x →∞ 8、 求下列函数的Fourior 级数展开(),0,0x x f x x x ππππ+≤,使得 ()()0f x f x ≥,()00,x x x δδ∈-+,证明存在一个区域I 使得()f x 在I 上是一个常数。 二、设()f x 是[],a b 上具有连续的导数,()0a b <<,()()0f a f b ==,()2 1b a f x dx =?, 证明()()2 2'14b a x f x dx >? 三、给定函数列()()()2,3,n x x Inx f x n n α==…试问当α取何值时,(){}n f x 在[0,)+∞上
大连理工大学2001年硕士生入学考试 数学分析试题 一. 从以下的1到8题中选答6题 1. 证明:2 ()f x x =在区间[0,]M 内一致连续(M 为任意正数),但是在[0,)+∞不一致 连续 2. 证明:若()f x 在[,]a b 内连续,那么()f x 在[,]a b 内Riemann 可积. 3. 证明:若1α>,那么广义积分1 sin x dx α+∞ ? 收敛 4. 证明:若()f x ,()g x 为区间(,)a b 上的连续函数,对任意的(,)(,)a b αβ?有: ()()f x dx g x dx β β α α =??,那么, ()()f x g x ≡于(,)a b 5. 证明:若1 n n a ∞ =∑收敛,那么 1 nx n n a e ∞ -=∑在[0,)+∞一致收敛 6. 已知:2 ,0 ()0,0 x e x f x x -?≠?=?=??,求"(0)f 7. 已知:()() 1(,)()2 2x at x at x at x at u x t d a φφψαα+-++-= + ?. 其中, ψ和φ分别是可以求导一次和求导两次的已知函数,计算 22 222 (,)(,)u x t u x t a t x ??-?? 8. 计算,半径为R 的球的表面积 二. 从9到14题中选取6题 9.已知: lim '()0x f x →∞ =,求证: () lim 0x f x x →∞ =
10.证明: ()a f x dx +∞ ? 收敛,且lim ()x f x λ→+∞ =,那么0λ= 11.计算曲面积分: 333 S I x dydz y dzdx z dxdy = ++??, 其中S 为旋转椭球面222 2221x y z a b c ++=的外侧 12.设()[0,1]f x C ∈,(0)0f =,(1)1f =,0()1f x ≤<. 求证: ()()n n S x f x =对于任意小于1的正数δ,在区间(0,1]δ-一致收敛,但是不在(0,1)一致收敛 13.设()[0,1]f x C ∈,(0)0f =,(1)1f =,0()1f x ≤<. 求证: 1 0lim ()0n n f x dx →∞ =? 14.证明:若()[,]n u x C a b ∈,1,2,...,...n =且1 ()n n u b ∞ =∑发散,那么1 ()n n u x ∞ =∑不在[,)a b 一致收 敛
大连理工大学《工程抗震》大作业
题目1:底部剪力法。 钢筋混凝土5层框架经质量集中后计算简图如下图所示,各层高均为3m , 集中于各楼层的重力荷载代表值分别为: 1500kN G =,2550kN G =,3580kN G =,4600kN G =,5450kN G =。结构阻尼比0.05ξ=,自振周期为10.55s T =,Ⅰ1类 场地类别,设计地震分组为第一组,抗震设防烈度为8度(设计基本地震加速度为0.30g )。按底部剪力法计算结构在多遇地震时的水平地震作用及地震剪力。 3580kN =2550kN =1500kN =(a )计算简图 4600kN =5450kN = 解:查《建筑设计抗震规范》表5.1.4知,8度多遇地震,αmax=设计地震分组为第一组, Ι类场地,取Tg= Tg=<T1=<5Tg= α1=(Tg/T1)r η2αmax =()××=≈ 查《建筑设计抗震规范》表5.2.1知,T 1=>=×= 取δn=T1+=×+= 总水平地震作用标准值: F EK =α1Geq=×(500+550+580+600+450)×85%=
各楼层水平地震作用标准值: Fi=G i H i F EK (1-δn)/∑G j H j (i=1,2,3n) ∑G j H j =500×3 +550×6+580×9+600×12+450×15=23970KN ·m F 1=[500×3××]/23970= F 2=[550×6××]/23970= F 3=[580×9××]/23970= F 4=[600×12××]/23970= F 5=[450×15××]/23970= 计算各楼层的层间地震剪力 V 1= F 1+ F 2+ F 3+ F 4+ F 5=++++= V 2= F 2+ F 3+ F 4+ F 5=+++=152KN V 3= F 3+ F 4+ F 5=++= V 4= F 4+ F 5=+= V 5=F 5= 题目3:怎样判断土的液化如何确定土的液化严重程度,并简述抗液化措施。 答:饱和松散的砂土或粉土(不含黄土),地震时易发生液化现象,使地基承载力丧失或减弱,甚至喷水冒砂,这种现象一般称为砂土液化或地基土液化。其产生的机理为:地下水位以下的饱和砂土和粉土颗粒在地震作用下,土颗粒之间有变密的趋势。因空隙水不能及时排出,土颗粒就处于悬浮状态,形成如同液体一样的现象,即所谓的土的液化现象。地基土液化判别过程可以分为初步判断和标准贯入试验判别两大步骤。下面分别予以介绍。 1、初步判断 饱和的砂土或粉土(不含黄土)当符合下列条件之一时,可初步判别为不液化或不考虑液化影响: (1)地质年代为第四纪晚更新世(Q3)及其以前时且处于烈度7度或者8度地区时可判为不液化土。 (2)粉土的粘粒(粒径<0.005mm )含量百分率当烈度为7度时大于10%、当烈度为8度时大于13%、当烈度为9度时大于16%,可判为不液化土。 (3)浅埋天然地基,当地下水位深度和覆盖非液化土层厚度满足下式之一时,可不考虑液化影响。 03w b d d d >+- 02 u b d d d >+-
大连理工大学入学测试机考专升本高等数学模拟题1、题目Z1-2(2)() 标准答案:A 2、题目20-1:(2)() 标准答案:A 3、题目20-2:(2)() 标准答案:B 4、题目20-3:(2)() 标准答案:A 5、题目20-4:(2)() 标准答案:D 6、题目20-5:(2)() 标准答案:D
标准答案:A 8、题目20-7:(2)() 标准答案:D 9、题目20-8:(2)() 标准答案:C 10、题目11-1(2)() 标准答案:C 11、题目11-2(2)() 标准答案:B 12、题目11-3(2)() 标准答案:A 13、题目20-9:(2)() 标准答案:C
标准答案:D 15、题目11-5(2)() 标准答案:C 16、题目20-10:(2)() 标准答案:B 17、题目11-6(2)() 标准答案:B 18、题目11-7(2)() 标准答案:C 19、题目11-8(2)() 标准答案:C 20、题目11-9(2)() 标准答案:D 21、题目11-10(2)() 标准答案:B
标准答案:C 23、题目19-2:(2)() 标准答案:B 24、题目19-3:(2)() 标准答案:D 25、题目12-1(2)() 标准答案:D 26、题目12-2(2)() 标准答案:D 27、题目19-4:(2)() 标准答案:B 28、题目12-3(2)() 标准答案:B 29、题目12-4(2)() 标准答案:C
标准答案:A 31、题目19-5:(2)() 标准答案:C 32、题目12-6(2)() 标准答案:A 33、题目12-7(2)() 标准答案:B 34、题目19-6:(2)() 标准答案:B 35、题目12-8(2)() 标准答案:B
2010工科数学分析基础(微积分)试题 一、填空题 (每题6分,共30分) 1.函数?? ? ?? ??? ??-≥+=01 0)(2πx x e x bx a x f bx ,=- →)(lim 0x f x ,若函数)(x f 在0=x 点连续,则b a ,满足 。 2.=?? ? ??+∞→x x x x 1lim , =??? ??+++???++++++∞→n n n n n n n n n 2222211lim 。 3.曲线? ??==t e y t e x t t cos 2sin 在()1,0处的切线斜率为 ,切线方程为 。 4.1=-+xy e y x ,=dy ,='')0(y 。 5.若22 lim 2 21=-+++→x x b ax x x ,则=a ,=b 。 二、单项选择题 (每题4分,共20分) 1.当0→x 时,1132-+ax 与x cos 1-是等价无穷小,则( ) (A )32= a , (B )3=a , (C). 2 3 =a , (D )2=a 2.下列结论中不正确的是( ) (A )可导奇函数的导数一定是偶函数; (B )可导偶函数的导数一定是奇函数; (C). 可导周期函数的导数一定是周期函数; (D )可导单调增加函数的导数一定是单调增加函数; 3.设x x x x f πsin )(3-=,则其( ) (A )有无穷多个第一类间断点; (B )只有一个跳跃间断点; (C). 只有两个可去间断点; (D )有三个可去间断点; 4.设x x x x f 3 )(+=,则使)0() (n f 存在的最高阶数n 为( )。 (A )1 (B )2 (C) 3 (D )4 5.若0)(sin lim 30=+→x x xf x x , 则20) (1lim x x f x +→为( )。 (A )。 0 (B )6 1 , (C) 1 (D )∞
绝 密★启用前 大连理工大学网络教育学院 2010年9月份《高等数学》课程考试 模拟试卷答案 考试形式:闭卷 试卷类型:A 一、单项选择题(本大题共10小题,每小题2分,共20分) 1.B 2.C 3.A 4.C 5.D 6.C 7.D 8.A 9.A 10.B 二、填空题(本大题共10小题,每小题3分,共30分) 1.dx x 45 2.x e 3.0 4.5 5.C x x +-3 31 (不写常数C 扣1分) 6.0 7.)cos(2 2y x x 8.2ln 21 9.61 10.C x y +=22(不写常数C 扣1分) 三、计算题(本大题共5小题,每小题8分,共40分) 1.解:11lim )1)(1(1lim 1 1lim 1121+=+--=--→→→x x x x x x x x x (4分)21=(4分) 2.解:)(sin sin 1'= 'x x y (4分)x x cos sin 1=x cot =(4分) 3.解:??=x xd xdx 33sin 313sin (4分)C x +-=3cos 31(4分)(不写常数C 扣1分) 4.解法1:令x t =,则tdt dx t x 2,2== 当1=x 时,1=t ;4=x 时,2=t (4分) 于是???=?=212 14122dt e dt t t e dx x e t t x (2分) )(21222e e e t -==(2分) 解法2:x d e dx x e x x ??=41412(4分))(21422e e e x -==(4分) 5.解:t dt dx 4=(2分) t dt dy cos =(2分)
大连理工大学2005硕士研究生考试试题数学分析试题及解答 一、 计算题 1、 求极限:122 2 (i) ,lim n n n n a a na a a n →∞ →∞+++=其中 解: 1212222...(1)(1)lim lim lim ()(1)212 n n n n n n a a na n a n a a Stolz n n n n +→∞→∞→∞+++++===+-+利用公式 2、求极限:2 1lim (1)x x x e x -→∞ + 解: 22 2 222 1(1) 1lim (1)lim()1111(1)(1)(ln(1)) 1lim lim 11 1111(())21lim 121(1)112lim (1)lim( )lim()x x x x x x x x x x x x x x x x x x x x e x e e x x x x x x o e x x x x e x e e x x e x e e e -→∞→∞→∞→∞→∞-→∞→∞→∞++=+-++-+=--+- +==--+- ∴+=== 3、证明区间(0,1)和(0,+∞)具有相同的势。 证明:构造一一对应y=arctanx 。 4、计算积分2 1 D dxdy y x +?? ,其中D 是x=0,y=1,y=x 围成的区域 解:
1120220001 1 1011ln()|ln(1)ln [(1)ln(1)(1)ln ]|2ln 2 y y D dxdy dxdy x y dy y x y x y dy ydy y y y y y y ==+++=+-=++-+-+=?? ????? 5、计算第二类曲线积分:22 C ydx xdy I x y --=+?,22:21C x y +=方向为逆时针。 解 : 222222002222 2tan 2222 cos ,[0,2)1sin 211 sin cos 4cos 222113cos 22cos 22 13(2)(1)812arctan 421(2)(1)2 311421C x x y ydx xdy I d d x y x x x x d x dx x x x x ππθθ θπθθθθθθθθ +∞+∞=-∞-∞=?? ∈? =?? ---=???→=-+++-+-++?????→-=--+++ +=-?????换元万能公式代换22 6426212x dx d x x ππ+∞+∞-∞-∞+=-++??+ ??? ?? 6、设a>0,b>0,证明:1 11b b a a b b ++?? ?? ≥ ? ?+?? ?? 。 证明:
大工高等数学课程考试模 拟试卷A答案 Prepared on 24 November 2020
机密★启用前 大连理工大学网络教育学院 2015年3月份《高等数学》课程考试模拟试卷答案 考试形式:闭卷试卷类型:A 一、单项选择题(本大题共10小题,每小题2分,共20分)1、C 2、A 3、C 4、B 5、B 6、C 7、D 8、B 9、C 10、A 二、填空题(本大题共 10 小题,每小题 3 分,共 30 分) 1、2 1 -=x y 2、0 3、dx x x x x x x x ??? ? ??-+---22 22121)23(arccos 6 4、>(或写成“大于”) 5、C x x +-3sin 31 sin 6、13-=x y 7、x 2 sin 2ππ 8、C e x +--9、必要10、 2 2y x xy + 三、计算题(本大题共5小题,每小题8分,共40分) 1、解:所给极限为“ ”型,注意当0→x 时,x x ~)1ln(+(4分)。因此 211sin lim sin lim )1ln(sin lim 000=+=?? ? ??+=+=++→→→x x x x x x x x x x x x x (4分) 2、解:本题为第一类换元法计算不定积分 解法Ⅰ做变量代换,令,1 ,ln du dx x u x ==(4分) C x C u udu dx x x +=+==??ln sin sin cos ln cos (4分) 解法Ⅱ凑微分法,使用凑微分公式 3、解:依前述求定义域的原则,需有???>+-≥--01204222x y y x ,(4分)即???>+≤+x y y x 214 222(4分)
双曲型方程的有限差分法 线性双曲型方程定解问题: (a )一阶线性双曲型方程 ()0=??+??x u x a t u (b )一阶常系数线性双曲型方程组 0=??+??x t u A u 其中A ,s 阶常数方程方阵,u 为未知向量函数。 (c )二阶线性双曲型方程(波动方程) ()022=?? ? ??????-??x u x a x t u ()x a 为非负函数 (d )二维,三维空间变量的波动方程 0222222=???? ????+??-??y u x u t u 022222222=???? ????+??+??-??z u y u x u t u §1 波动方程的差分逼近 1.1 波动方程及其特征 线性双曲型偏微方程的最简单模型是一维波动方程: (1.1) 22 222x u a t u ??=?? 其中0>a 是常数。 (1.1)可表示为:022 222=??-??x u a t u ,进一步有
0=??? ????+?????? ????-?? u x a t x a t 由于 x a t ?? ±??当a dt dx ±=时为()t x u ,的全导数 (=dt du dt dx x u t u ???+??x u a t u ??±??=),故由此定出两个方向 (1.3) a dx dt 1 ±= 解常微分方程(1.3)得到两族直线 (1.4) 1C t a x =?+ 和 2C t a x =?- 称其为特征。 特征在研究波动方程的各种定解问题时,起着非常重要的作用。 比如,我们可通过特征给出(1.1)的通解。(行波法、特征线法) 将(1.4)视为),(t x 与),(21C C 之间的变量替换。由复合函数的微分法则 2 12211C u C u x C C u x C C u x u ??+??=?????+?????=?? x C C u C u C x C C u C u C x u ????? ? ????+????+?????? ????+????=??2 212121122 2221222122 12C u C C u C C u C u ??+???+???+??= 2 2 22122122C u C C u C u ??+???+??= 同理可得 a t t a t C -=??-=??1,a t C =??2 ???? ????-??=?????+?????=??21 2211C u C u a t C C u t C C u t u
绪论部分: 2、简述环境问题的分类?(10分) 答:环境问题是多方面的,但大致可分为两类:原生环境问题和次生环境问题。由自然力引起的为原生环境问题,也称为第一环境问题。由于人类生产和生活引起生态系统破坏和环境污染,反过来又危及人类自身和生存和发展的现象,为次生环境问题,也叫第二环境问题。原生环境问题和次生环境问题很难截然分开,它们之间常常存在着某种程度的因果关系和相互作用。 4、什么是环境化学,学习环境化学有什么意义?(10分) 答:环境化学是一门研究有害化学物质在环境介质中的存在、化学特性、行为和效应及其控制的化学原理和方法的科学。 意义:用来掌握污染来源,消除和控制污染,确定环境保护决策,以及提供科学依据诸方面都起着重要的作用。 5、简述环境化学的分支学科。(10分) 答:主要包括6类。 ①环境分析化学:是研究化学品的形态、价态、结构、样品前处理和痕量分析的学科。 ②环境污染化学:大气、水体和土壤环境化学,元素循环的化学过程。 ③污染控制化学:主要研究与污染控制有关的化学机制及工艺技术中化学基础性问题。 ④污染生态化学:是研究化学污染物在生态系统中产生生态效应的化学过程的学科。 ⑤环境计算化学:主要利用有效的数学近似以及电脑程序计算分子的性质。 ⑥环境生物化学:是研究环境化学品对生命影响的学科。 第一章: 1、地球环境主要由哪些圈层构成?英文单词?各之间有什么联系?各有哪些性 质?(10分) 答:地球环境主要由大气圈(atmosphere)、水圈(hydrosphere)、土壤圈(pedosphere)、岩石圈(lithosphere)和生物圈(biosphere)构成。 联系:大气圈、水圈、土壤圈和生物圈共同组成了地球环境系统,每个圈层都离不开
大连理工大学专升本高等 数学题库道 Last updated on the afternoon of January 3, 2021
Z题库建议搜索作业帮 [题型]单选题 [章节] [类别]模拟 [题干]题目编号01 [选项] [答案]D [解析] [难度]易 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号02 [选项] [答案]A [解析] [难度]易 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号03 [选项] [答案]A [解析] [难度]易 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号04 [选项]
[答案]A [解析] [难度]易 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号05 [选项] [答案]D [解析] [难度]易 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号06 [选项] [答案]D [解析] [难度]中 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号07 [选项] [答案]C [解析] [难度]易 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号08
[答案]B [解析] [难度]中 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号09 [选项] [答案]B [解析] [难度]中 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号10 [选项] [答案]A [解析] [难度]中 [分数]2 [题型]单选题 [章节] [类别]模拟 [题干]题目编号11 [选项] [答案]B [解析] [难度]中 [分数]2 [题型]单选题
2000年大连理工大学硕士生入学考试试题——数学分析 一、从以下的第一到第八题中选取6题解答,每题10分 1. 证明:1 ()f x x =于区间0(,1)δ(其中001δ<<)一致连续,但是于(0,1)内不一致连续 证明: 01212(1)0,()[1]2 (2)1||()|()()|f x x x f x f x δδδδεδδε<= =+=-∈-+≤<≠∈为无理数,对于,,取,显然这样的存在 当所以,在无理点连续 为有理数,。不难找到趋近于的收敛子列:无理数这样显然不连续。
机 密★启用前 大连理工大学网络教育学院 2018年春《高等数学》 期末考试复习题 ☆ 注意事项:本复习题满分共:400分。 一、单项选择题(本大题共60小题,每小题2分,共120分) 1、设x x x x f 2)(,)(2==?,则=)]([x f ?( ) A 、2 2x B 、x x 2 C 、x x 2 D 、x 22 答案:D 2、下列结论正确的是( ) A 、函数x y 5=与x y 5-=关于原点对称 B 、函数x y 5=与x y -=5关于x 轴对称 C 、函数x y 5=与x y 5-=关于y 轴对称 D 、函数x y 5=与x y 5log =关于直线y=x 对称 答案:D 3、设)(x f 在()+∞∞-,内定义,则下列函数中必为奇函数的是( ) A 、|)(|x f y = B 、|)(|x f y -= C 、c y = D 、)(2 x xf y = 答案:D 4、下列极限存在的有( ) A 、2 ) 1(lim x x x x +∞→ B 、1 21 lim 0-→x x C 、x x e 1 lim → D 、x x x 1 lim 2++∞ → 答案:A 5、当0→x 时,与x x --+11等价的无穷小量的是( ) A 、x B 、x 2 C 、2 x D 、2 2x 答案:A 6、当∞→n 时,为了使n 1sin 2 与k n 1 等价,k 应为( ) A 、 2 1 B 、1
C 、2 D 、3 答案:C 7、已知三次抛物线3x y =在点1M 和2M 处的切线斜率都等于3,则点1M 和2M 分别为( ) A 、(-1,-1)及(1,1) B 、(-1,1)及(1,1) C 、(1,-1)及(1,1) D 、(-1,-1)及(1,-1) 答案:A 8、根据函数在一点处连续和可导的关系,可知函数???? ???≥<<≤+=1,1 10,20,2)(2 x x x x x x x x f 的不可导点是( ) A 、1-=x B 、0=x C 、1=x D 、2=x 答案:C 9、设x x y 2 212--=,则='y ( ) A 、 ()2 22 214x x -- B 、 ()2 22 212x x +-- C 、 ()2 22 212x x -- D 、 ()2 22 214x x +- 答案:D 10、=)(arccos x d ( ) A 、xdx 2 sec B 、xdx 2 csc C 、 dx x 2 11- D 、dx x 2 11-- 答案:D 11、在区间[-1,1]上,下列函数中不满足罗尔定理的是( ) A 、1)(2 -=x e x f B 、)1ln()(2 x x f += C 、x x f =)( D 、2 11 )(x x f += 答案:C 12、下列极限中能使用罗必达法则的有( ) A 、x x x x sin 1sin lim 20 → B 、?? ? ??-+∞ →x x x arctan 2lim π C 、x x x x x sin sin lim +-∞→ D 、2 sin lim x x x x ∞ → 答案:B 13、下列函数对应的曲线在定义域内为凹的是( ) A 、x e y -= B 、)1ln(2 x y += C 、3 2x x y -= D 、x y sin = 答案:A 14、下列函数中原函数为)0(ln ≠k kx 的是( )
大连理工大学2000年数学分析真题 (2) 大连理工大学2001年数学分析真题 (4) 大连理工大学2002年数学分析真题 (6) 大连理工大学2003年数学分析真题 (8) 大连理工大学2004年数学分析真题 (10) 大连理工大学2005年数学分析真题 (12) 大连理工大学2006年数学分析真题 (14) 大连理工大学2008年数学分析真题 (16) 大连理工大学2009年数学分析真题 (18) 大连理工大学2010年数学分析真题 (20) 大连理工大学2011年数学分析真题 (22) 大连理工大学2013年数学分析真题 (24) 大连理工大学2014年数学分析真题 (25) 大连理工大学2015年数学分析真题 (28) 大连理工大学2016年数学分析真意 (30) 大连理工大学2017年数学分析真题 (32)
大连理工大学2000年数学分析真题 一.从以下的第一到第八题中选取6题解答,每题10分 1.证明: ()x x f 1 = 于区间()10,δ(其中0<0δ<1)一致连续,但是于(0,1)内不一致连续。 2.证明:若()x f 于[a ,b]单调,则()x f 于[a ,b]内Riemann 可积。 3.证明:Dirichlet 函数: ()()?? ???==有理数为无理数q p x q x x f ,1,0在所有无理点连续,在有理点间断。 4.证明:若()()b a C x f ,∈,(指(a ,b )上的连续函数,且任意()()b a ,,?βα, ()?=β α 0dx x f ,那么()()b a x x f ,0∈≡,。 5.证明:∑∞ =-1 n nx ne 于(0,+∞)不一致收敛,但是对于0>?δ,于[)+∞,δ一致收敛。 6.证明:()?? ???=≠=0,00 ,1sin 4 x x x x x f ,在0=x 处有连续的二阶导数。 7.利用重积分计算三个半长轴分别为a,b,c 的椭球体的体积。 8.计算第二类曲面积分:??∑ ++zdxdy ydzdx xdydz ,其中,∑是三角形 ()10,,=++>z y x z y x ,,法方向与z y x ,,轴成锐角为正。 9.假设∞ →=n n a a lim ,证明2 2lim 2 21a n na a a a n n n = +++∞ → 。 11.计算曲面积分?? ++=S dxdy z dzdx y dydz x I 3 3 3 ,S 为椭球面122 2222=++c z b y a x 的外侧。 12.设()[]()?-==-∈>1 1 ,,3,2,111,10 n dx x C x n n ,, ,φφφ,对于任意的c>0,()x n φ在[][] 1,,1,1c -上一致收敛于0。证明:对于任意()[]1,1-∈C x g ,()()()?-∞→=1 1 0lim g x x g n n φ 13.证明:一个严格递增函数的间断点只能是第一类间断点
i.常微分方程初值问题数值解法 常微分方程初值问题的真解可以看成是从给定初始点出发的一条连续曲线。差分法是常微分方程初值问题的主要数值解法,其目的是得到若干个离散点来逼近这条解曲线。有两个基本途径。一个是用离散点上的差商近似替代微商。另一个是先对微分方程积分得到积分方程,再利用离散点作数值积分。 i.1 常微分方程差分法 考虑常微分方程初值问题:求函数()u t 满足 (,), 0du f t u t T dt =<≤ (i.1a ) 0(0)u u = (i.1b) 其中(,)f t u 是定义在区域G : 0t T ≤≤, u <∞上的连续函数,0u 和T 是给定的常数。我们假设(,)f t u 对u 满足Lipschitz 条件,即存在常数L 使得 121212(,)(,), [0,]; ,(,)f t u f t u L u u t T u u -≤-?∈∈-∞∞ (i.2) 这一条件保证了(i.1)的解是适定的,即存在,唯一,而且连续依赖于初值0u 。 通常情况下,(i.1)的精确解不可能用简单的解析表达式给出,只能求近似解。本章讨论常微分方程最常用的近似数值解法-差分方法。先来讨论最简单的Euler 法。为此,首先将求解区域[0,]T 离散化为若干个离散点: 0110N N t t t t T -=<<<<= (i.3) 其中n t hn =,0h >称为步长。 在微积分课程中我们熟知,微商(即导数)是差商的极限。反过来,差商就是微商的近似。在0t t =处,在(i.1a )中用向前差商 10()()u t u t h -代替微商du dt ,便得 10000()()(,())u t u t hf t u t ε=++ 如果忽略误差项0ε,再换个记号,用i u 代替()i u t 便得到 1000(,)u u hf t u -= 一般地,我们有 1Euler (,), 0,1,,1n n n n u u hf t u n N +=+=- 方法: (i.4) 从(i.1b) 给出的初始值0u 出发,由上式可以依次算出1,,N t t 上的差分解1,,N u u 。
姓名:__________ 大 连 理 工 大 学 盘锦校区期中试题 学号:__________ 任课教师:________ 课 程 名 称: 高等数学A(1) 试卷: A 考试形式:闭卷 学院(系):_______ 授课院(系):基础教学部_ 考试日期:2016年11月19日 试卷共 6页 _____ 级_____ 班 装 一. 填空题(每题6分,共计30分) 1. 12011lim 1cos _____;lim ______.1x n x x n n x →∞→+???? -== ? ?-???? 2. )lim 0,_____,____._x ax b a b →-∞ -===则 3. 2,1; ()1____,____., 1. x x f x x a b ax b x ?≤====? +>?设在点处可导,则 224sin d 4.(),. sin cos d t x t y t y t t t x π==??=+?设为参数则=___________ 25.____,ln ,____. a y ax y x === 当时曲线和相切切点为 二. 选择题(每题4分,共计20分) 1 () ()()()0()()(). ()0,()()()0,()()1.()()0()0.lim(1()),f x x A f x g x x B f x g x C x f x g x D x g x f x f x g x x f x g x e →→=→→→≠+=和是时的等价无穷小. 当时是比是更高阶的无穷小.当时是比是更高阶的无穷小. 设函数和是时的无穷小量 且若则( ).
2013级工科硕士研究生 《矩阵与数值分析》课程数值实验报告 大连理工大学 Dalian University of Technology
一、设 6 2 2 10 1 N N j S j = = - ∑,分别编制从小到大和从大到小的顺序程序分别计算 100001000000 , S S 并指出两种方法计算结果的有效位数。 程序代码: 从小到大: function f=s(N); %定义函数s f=0; %初始值为0 for j=N:-1:3 %j从3到n循环(从小到大) ft=1000000/(j^2-1); %Sj f=f+ft; %SN end 从大到小: function f=s(N); %定义函数s f=0; %初始值为0 for j=N:-1:3 %j从3到n循环(从小到大) ft=1000000/(j^2-1); %Sj f=f+ft; %SN end 执行结果: 从小到大: s(10000) ans = 4.16566671666167e+05 s(1000000) ans =
4.166656666671731e+05 有效数字:16,16 从大到小: s(10000) ans = 4.165666716661668e+05 s(1000000) ans = 4.166656666671667e+05 有效数字:16,16 分析: 小数和大数相加时,按照从大到小的顺序和按照从小到大的顺序得出的结果不同,前者由 于舍入误差的影响而使结果不准确,所以应避免大数吃小数的现象。 二、解线性方程组 1.分别利用Jacobi 迭代法和Gauss-Seidel 迭代法求解线性方程组Ax b =,其中常向量为()21n -维随机生成的列向量,系数矩阵A 具有如下形式 1111 11 1122n n n n n n n n T I I I A I I T I --------+-?? ?- ?= ? - ? -+? ? , 其中1 211112n T --?? ? - ?= ?- ? -? ? 为1n -阶矩阵,1n I -为1n -阶单位矩阵,迭代法计算停止的条件为:10 12 10k k x x -+-<,给出10,100,1000n =时的不同迭代步数. 程序代码: