非平稳信号的广义小波分析及其工程应用报告
徐文豪
1.窗口傅里叶变换
1.1原理分析
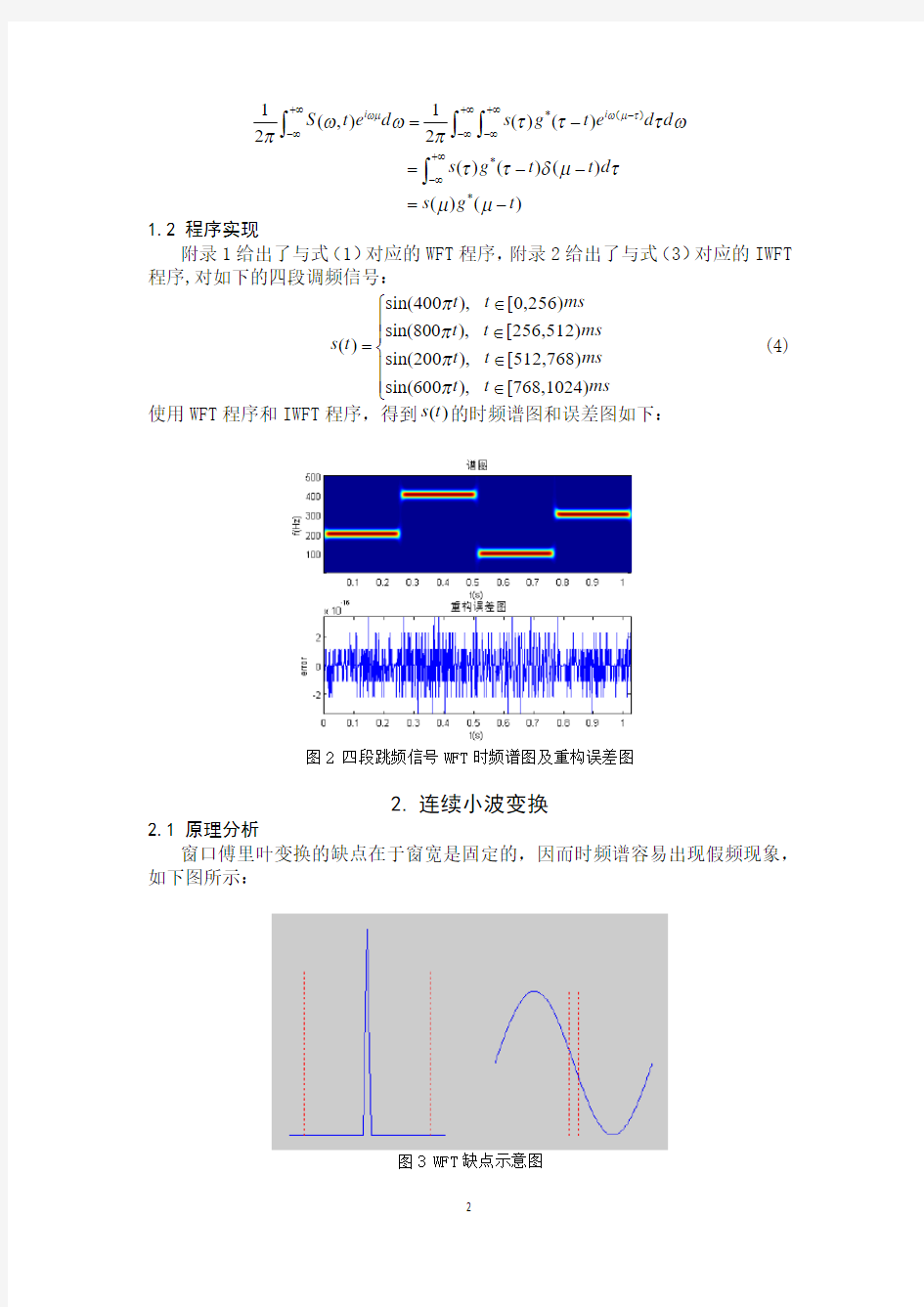
众所周知,傅里叶变换可以获取信号的全局频谱,但很多时候,我们需要的是信号的瞬时频谱,如机械故障检测、地震信号瞬时属性提取等。为了达到这个目的,一种很直观的思路就是截取信号的一小段做傅里叶变换,并将得到的频谱作为该小段中心位置的频谱。这种变换称之为窗口傅里叶变换(WFT),其示意图如下:
从数学上描述WFT应为:对平方可积信号()
s x和平方可积窗函数()
g x,定义窗口傅里叶变换如下:
+
(,)()()i x
S t s x g x t e dx
ω
ω∞-
-∞
=-
?(1) 值得强调的是,式(1)中窗函数()
g x的支撑大小对时频谱的有效性有着很大的影响,当窗宽过大或过小时都会使时频谱出现较严重的假象。作者在实际编程时发现,当信号的长度为L,取一个较小的正值ε作为值零阈值,则取窗宽点数半径为一般能达到较理想的效果。
将()()
s x g x t-视为整体,假设
2
g≠并通过逆傅里叶变换可得逆窗口傅里叶变换如下:
2
2
1
()(,)()
2
i x
s x S t g x t e d dt
g
ω
ωω
π
+∞+∞
-∞-∞
=-
??(2) 式(2)对推导WFT值域(,)
S t
ω的性质有着很重要的作用,如重建核方程等。但由于使用双重积分,其在实现时稍显繁琐,殷勤业的《时频分析及其在工程中的应用》讲义中给出了一个更简单的重构公式如下:
*
1
()(,)
2(0)
i t
s t S t e d
g
ω
ωω
π
+∞
-∞
=?(3) 其推导如下:
*()**11
(,)()()22()()()()()
i i S t e d s g t e d d s g t t d s g t ωμ
ωμτωωτττω
π
π
ττδμτμμ+∞
+∞+∞
--∞
-∞
-∞
+∞-∞
=
-=--=-?
??
?
1.2 程序实现
附录1给出了与式(1)对应的WFT 程序,附录2给出了与式(3)对应的IWFT 程序,对如下的四段调频信号:
sin(400),[0,256)sin(800),[256,512)()sin(200),[512,768)sin(600),[768,1024)t t ms t t ms s t t t ms t t ms
ππππ∈??∈?=?∈??∈? (4)
使用WFT 程序和IWFT 程序,得到()s t 的时频谱图和误差图如下:
图2 四段跳频信号WFT 时频谱图及重构误差图
2. 连续小波变换
2.1 原理分析
窗口傅里叶变换的缺点在于窗宽是固定的,因而时频谱容易出现假频现象, 如下图所示:
图3 WFT 缺点示意图
图3中,对快变信号采用大窗或对慢变信号采用小窗都必然会造成假频。解决这一问题的思路是使窗宽可变,这就是连续小波变换(CWT)的思路。在CWT 中我们一般把窗函数称为小波函数,其支撑如下所示:
图4 小波函数的支撑
从数学上描述CWT 应为:对平方可积信号()s x 和平方可积小波()x ψ,定义连续小波变换如下:
1(,)()(),0p x b
S a b s x dx p a a
ψ+∞-∞
-=>? (5) 其中系数1
p a
的引入是为了小波在平移伸缩之后1
p 范数不变,即
111
()()p
p
p
x b
x a
a
ψψ-=
(6)
对式(5)中的连续小波变换,常见的逆变换公式如下:
,23211
()(,)()()
a b p s t S a b t dadb a d ψψωωω
+∞+∞--∞-∞+∞-∞
=???
(7)
其中,1()()a b p
t b
t a
a
ψψ-=
称为时间尺度原子。 与WFT 类似,式(7)对推导CWT 值域(,)S a b 的性质有着很重要的作用,如重建核方程等,但其一般只能通过二重数值积分进行计算,速度慢且误差大。Holschneider 在《Wavelets: An Analysis Tool 》中给出了当范数变量1p =时的一个简单重构公式:
1
0(,)()S a t s t C da a ψ+∞-=?
(8) 0?()C d ψψωωω
+∞=? (9)
如果能求出C ψ的值,则可利用数值积分计算式(8)的值。遗憾的是式(9)是不一定收敛的,例如对常用的Morlet 小波
(2
()/2?ωσψω--(),式(9)在0处发散。
高老师的讲义中给出了当范数1/2p =时的一个简单逆变换公式,但其有效性我还没有搞懂,其计算过程如下:
1
Re (,)1()M
j S a t s t C
δ
==
(10)
1
Re (,0)M
j S a C δ==(11)
式(11)中(,0)j S a δ表示单位脉冲信号[]n δ在0时刻尺度为j a 处CWT 的值。
2.2 程序实现
附录3给出了与式(8)对应的CWT 程序,附录4给出了与式(10)对应的ICWT 程序,对地球物理中常用的Ricker 信号(取主频为50Hz),取Gauss 小波
(22
()/(2)?()2s ωμψω--=,参考刘乃豪师兄提供的资料)使用CWT 程序和ICWT 程序,并利用频率尺度转换关系,得到其时频谱和重构误差如下:
图5 50Hz 主频Ricker 信号CWT 时频谱图及重构误差图
从图5可以看出,对Ricker 信号,在选取与其相配的小波函数之后,不用考虑窗宽,连续小波变换就能得到很好的时频谱和重构精度。CWT 具有自适应性的优点可以从其Heisenberg 盒得到进一步验证:
图6 连续小波变换的Heisenberg 盒
从图6可以看出,CWT 既具有显微镜的功能,又具有望远镜的功能。
即当尺度a
较小时,有可能捕捉小范围的信号变化,而当尺度a 较大时,有可能捕捉大范围的信号变化。
然而,福兮祸之所倚,祸兮福之所伏,图6的Heisenberg 盒也反映出了CWT 的一大缺点,即低频可能看不见(频率分辨率过高,而离散尺度有限),高频可能看不清(频率分辨率过低),这种现象可以从式(4)的四段调频信号反应出来,同样取高斯小波,四段调频信号的CWT 时频谱和重构误差如下:
图7四段跳频信号CWT 时频谱图及重构误差图
从图7可以很明显的看出,在CWT 时频谱中,信号频率分辨率随着频率的增大而降低。这里需要指出的是,缓解这一问题的一个有效方法是二进制采样,其能够在低频部分采相对较多的点并在高频部分采相对较少的点。令一方面,图7也反应出图5的高重构精度并不适合所有信号,其原因可能有两个,一是Ricker 信号的变化较平缓而四段调频信号的变化较剧烈,二是高斯小波可能与四段调频信号不太匹配。
3. 最优对偶标架变换
3.1 原理分析
标架是指Hilbert 空间H 中的一个完备序列{}
i
h ,其满足对任意x H ∈,存在,0A B >,使得
2
2
2
,i
i
A x x h
B x ≤≤∑
(12)
其中x 为x 的由内积诱导的范数。A 和B 分别称为标架下界和标架上界,特别地,当A B C ==时,称这个标架为紧标架,并称C 为紧标架的冗余度。
已经证明对任意标架{}
i
h
,存在对偶标架{}i
γ ,使得对于任意x H ∈,有
,i i
i
x x h γ=∑ (13)
而当{}
i
h 为紧标架时,Daubechies 已证明其对偶标架为1i h C ??????
。 对采样间隔为dx ,长度为L 的周期离散信号[]s
k (将有限离散信号周期化可
以得到更好的边界重构精度),定义其对偶标架变换及逆变换如下:
001
,,,0
[]((1))L m n
m n m n k C s k k dx γ-==-∑ (14)
0011
,,,00
[]((1))M N m n m n m n m n s k C h k dx --===-∑∑
(15)
其中M 为时间采样点数,N 为波数采样点数,{}
00,,()m n m n x γ 为由分析函数()x γ 的平移调制生成的标架,{}
00
,,()m n m n h x 为由综合函数()h x 的平移调制生成的{}
00
,,()m n m n x γ
的对偶标架,00
,,()m n m n h x 的定义如下:
000
()0,,()(())i n n dN d x m n m n h x h x m m dM dx e ξ+?=-+? (16)
其中00,m n 分别为时间和波数初始采样点(引入这两个常量是为了在标架相空间中得到更多的空间波数信息),,dM dN 分别为时间和波数采样间隔点数且满足
dM M dN N L ?=?=,2d L dx
π
ξ=
?为波数离散采样间隔。 通过给定综合函数()h
x 的离散采样序列[]h k ,由式(14)和式(15)可推出分析函数()x γ 的离散采样序列[]k γ 所满足的方程组:
1
*0
[][][][]L pk M
k M h k qN W k p q N γδδ--?=?+=∑ (17)
其中0p M ≤
式(17)所对应方程组的系数矩阵H 是dM dN ?行L 列的,故若dM dN L
?=且系数矩阵满秩时可以解出唯一的*γ
,然而Daubechies 已经证明这种情况下重构公式是不稳定的,一般称这种情形下的采样为临界采样。钱世锷在著作《Joint Time –Frequency Analysis 》中提出取dM dN L ?<,并在方程组的解空间中寻找与
[]h
k 最接近的解*opt
γ ,令方程组的值向量为μ,并假设2
1h = 则可构造对应的优化问题如下:
*2
1
*
02
[]min []L opt H k k h k γ
μγγγ-===-∑
(18)
对式(18)进行简单推导得
*
*
1min 1opt H M N γμ
γγ=?????
=-
????
?
? (19)
式(19)意味着要在*H γμ= 的解空间中寻找模最小的解。由广义逆矩阵理论[21],可给出所需解的表达式如下:
*opt H γμ+=
(20)
其中H +表示矩阵H 的Moore-Penrose 逆。对于计算H +,钱世锷书中是通过判断H 是否行满秩并通过SVD 分解将行不满秩的情形转换为行满秩情形,这样不仅计算繁琐还会影响计算精度。实际上有直接计算矩阵MP 逆的快速算法,如Greville 递推法,而在matlab 中可直接调用库函数pinv 实现。
然而,式(20)只能处理规模相对较小的矩阵,且由于使用复数运算会影响计算精度。钱世锷书中在以上的基础上通过将大系数矩阵分解为多个小系数矩阵,将复数运算化为实数运算,给出了求解方程组的快速算法:
1
*0
1[][][]M l h k l M qN k l M q N γδ-=+?++?=∑ (21)
其中021q N ≤
对采样间隔为dx 的信号,一般取如下归一化的高斯函数作为综合函数:
2()1/422()(),x
dx h x e dM N ααπαπ-==
? (22)
其中α的取值是钱世锷书中给出的[]h k 和[]opt k γ 间取得最小误差的条件。必须注意到的是,[]h x 的支撑h L 不应也不必等于L ,否则当L 很大时,求解对偶标架将相对比较耗时。由殷勤业讲义3-4节的内容和作者编程时的经验,一般h L 取N 时
可以达到很好的效果,且若让[]h k 在0:1h L -的值为()h x 在(/2:/21)h h L L dx --?的值并在其它点处为0,则可以利用式(21)只计算长度为h L 的对偶函数向量。
对偶标架变换的重构误差精度与时频采样点数M N ?与信号长度L 之比有关,这可以被称为对偶标架采样冗余度C ,定义如下:
M N L
C L dM dN
?=
=? (23)
3.2 程序实现
附录5给出了与式(21)对应的快速计算最优对偶标架的程序,附录6给出了与式(14)对应的最优对偶标架变换的程序,附录7给出了与式(15)对应的逆最优对偶标架变换程序。同样对式(4)的四段跳频信号,取采样冗余度2C =,使用最优对偶标架变换程序和逆最优对偶标架变换程序得到时频谱和重构误差如下:
图8四段跳频信号最优对偶标架时频谱图及重构误差图从图8可以看出,最优对偶标架变换只用了WFT存储量的1/512,就得到了有效的谱图和非常高的重构精度,这暗示了最优对偶标架变换在处理较大数据的潜力。实际上,对长度为131072的音乐片段(许嵩《忧伤还是快乐》截取,音乐
C=的最优对偶标架变换得到时频图和重采样频率为44100Hz),使用冗余度64
构误差如下:
图9 音乐片段最优对偶标架变换时频谱图及重构误差图
考虑到该段音乐为钢琴片段,图9中的时频谱是比较合理的,且程序运行时间只有26.65s(其中有限支撑最优对偶标架的计算时间仅为0.004s),再加上非常高的重构精度,完全可以断言最优对偶标架变换具有处理实际数据的能力。
最优对偶标架变换另一个比较好的特点是,其自动选择了一个比较好的窗宽
C= (见式(22))。首先对变化较慢的频率为7.8125Hz的正弦信号,使用冗余度64的最优对偶标架变换得到时频谱图和重构误差图如下:
图10 慢变信号最优对偶标架变换时频谱图及重构误差图
其次,对变化剧烈的单位脉冲信号,仍使用冗余度64C =的最优对偶标架变换,得到其时频谱图和重构误差图如下:
图11 快变信号最优对偶标架变换时频谱图及重构误差图
从图10和图11可以看出,最优对偶标架自动选择的窗宽可以同时较好地处理慢变信号和快变信号,这给使用带来了较大的便利。
最后需要说明的是冗余度和重构精度的关系,事实上求解对偶标架的方程组式(17)的系数矩阵规模为M N L ???,而/()C L M N =??。因此C 越大,对偶标架满足的方程组就越欠定,所得的最优对偶标架就接近紧标架,因而有较高的重构精度(标架正反变换都线性有界(连续)的充要条件是其为紧标架)。而当C 达到一定程度,使得解空间中已经有很好的对偶标架时,重构精度就应当保持稳定了。上述讨论可以从最优对偶标架变换重构精度随冗余度的变化验证,对长度为1024的100Hz 正弦信号,结果如下表所示:
表1 最优对偶标架变换重构精度随冗余度变化表
C upperBound 1
3e-3 2 1e-15 4 1e-15 8 8e-16 16
8e-16
从表1中可以看出,当冗余度2C =时,解空间中应该就已经包含了很接近紧标架的对偶标架了。
4. Grossman 对偶标架变换
4.1 原理分析
不同于构造方程组,Grossman 给出了一个极其简单的构造性求解对偶标架的 方法。为便于该方法的叙述,称和为常数1的函数集为单位1的分割,定义平移
算子na T 为()()()na T f x f x na =-,定义调制算子mb M 为2()()()i mbx
mb M f x e f x π=,则
有:
定理1:设{:}n n a T n z φφ=∈是对单位1的分割,0n φ≥,任意选择[0,1]p ∈,如果令()[()]p g x x φ=,那么,{:,}m n mb na g M T g m n Z =∈定义了一个Gabor 分析标架,相应的综合标架可为,{:,}m n mb na M T m n Z γγ=∈,这里γ定义为1()[()]p x x γφ-=。 Gross 对偶标架变换实现的关键是单位1的分割,但实际上这可以直接通过将一个窗函数离散向量求和归一化实现。
4.2 程序实现
附录8给出了Grossman 对偶标架变换的实现(其需要调用附录6和附录7中 的程序),对主频为50Hz 的Ricker 信号,取采样冗余度64C =,使用Grossman 对偶标架变换程序得到其时频谱图和重构误差如下:
图12 50Hz 主频Ricker 信号Grossman 对偶标架变换时频图和重构误差图
相对于最优对偶标架变换,Grossman 对偶标架变换节省了求解最优对偶标架的时间,然而,当采样冗余度C 较小时,Grossman 对偶标架变换的重构误差精度较低,对长度为1024的100Hz 正弦信号,结果如下表所示:
表2 Grossman对偶标架变换重构精度随冗余度变化表
C upperBound
1 6e-1
2 3e-1
4 6e-2
8 3e-3
16 5e-6
32 2e-11
64 5e-16
128 5e-16
256 5e-16
C≤时,应选择对比表1和表2并结合计算量可得出结论,当采样冗余度32
C≥时,应选择Grossman对偶标架变换。最优对偶标架变换,当采样冗余度64
5.附录
附录1:WFT的matlab程序
%窗口傅里叶变换程序
%s为长度为N的离散信号,w为窗函数指针
%S为s的加窗变换,其分量S(i,j)(j<=N/2)表示(i-1)*dx位置在频率(j-1)*df的振幅function S=wft(s,w,dx)
N=length(s);
S=zeros(N);
x=(0:(N-1))*dx; %记录s中各点所在的位置
for n=1:N
xBar=(n-1)*dx;
tmp=s.*conj(w(x-xBar));
S(n,:)=fft(tmp);
end
S=S*dx;
End
附录2:IWFT的matlab程序
%逆窗口傅里叶变换程序
%s为离散信号,S为其窗口傅里叶变换,dx为采样间隔
%w为窗函数
%计算公式源于殷勤业《时频分析及其在工程中的应用》讲义P50
function s=iwft(S,w,dx)
N=size(S,1);
s=zeros(1,N);
ifftVec=diag(ifft(S,[],2));
for n=1:N
s(n)=1/(dx*conj(w(0)))*ifftVec(n);
end
end
附录3:CWT的matlab程序
%连续小波变换程序
%s为待分析信号,psiCaret为小波的频域表达式匿名函数
%scaleVec为尺度向量
%p指使时间尺度原子在1/p范数下保持不变的常量
function S=myCwt(s,dt,scaleVec,psiCaret,p)
N=length(s);
M=length(scaleVec);
dOmega=2*pi/(N*dt);
S=zeros(M,N);
sCaret=fftshift(fft(s));
unitImaginary=sqrt(-1);
coefMat=repmat(exp(-unitImaginary*(0:N-1)*pi),M,1)*dOmega/(2*pi); for j=1:M
a=scaleVec(j);
psiCaretVec=psiCaret(a*(-N/2:N/2-1)*dOmega);
S(j,:)=N/a^(p-1)*ifft(sCaret.*conj(psiCaretVec));
end
S=coefMat.*S;
End
附录4:ICWT的matlab程序
%这是针对p=1/2的连续小波(Morlet)变换的逆变换程序
%原理出于高老师的讲义
%S为小波变换结果,scaleVec为尺度向量
%alpha为Morlet小波频率分辨率
function s=myIcwt(S,scaleVec,alpha)
N=size(S,2);
cDelta=sqrt(alpha)*sum(1./scaleVec);
s=1/cDelta*sum(real(S)./repmat(sqrt(scaleVec'),1,N));
end
附录5:快速计算最优对偶标架的matlab程序
%快速计算最优对偶标架程序
%hTildeVec为综合函数离散向量(整个程序中变量命名基于殷勤业讲义)
%dM为对偶标架时间采样间隔点数
%dN为对偶标架频率采样间隔点数
%gammaTildeVec为最优对偶标架函数离散向量
function gammaTildeVec=fastCalcOptimalDualFrame(hTildeVec,dM,dN)
%判断输入的有效性
if fix(abs(dM))~=dM || fix(abs(dN))~=dN
error('dM和dN必须为正整数');
end
if mod(length(hTildeVec),dM)~=0 || mod(length(hTildeVec),dN)~=0 error('hTildeVec的长度必须为dM以及dN的整数倍');
end
if dM*dN>length(hTildeVec)
error('采样间隔过大,无法恢复信号!');
end
%计算所需常量
L=length(hTildeVec);
N=L/dN; %计算对偶标架频率采样点数
M=L/dM; %计算对偶标架时间采样点数
%初始化变量
gammaTildeVec=zeros(1,L);
hKMat=zeros(dN,M);
muKBarVec=zeros(dN,1);
muKBarVec(1)=1/N;
%循环k计算最优对偶标架函数
for k=0:dM-1
%构造dN行M列的系数矩阵
for q=0:dN-1
for l=0:M-1
hKMat(q+1,l+1)=hTildeVec(mod(k+l*dM+q*N,L)+1);
end
end
%利用MP逆求解能量最小的解
gammaKBarVec=(pinv(hKMat)*muKBarVec)'; %注意这里包含共轭了
gammaTildeVec(k+(0:M-1)*dM+1)=gammaKBarVec;
end
gammaTildeVec=real(gammaTildeVec);
end
附录6:对偶标架变换的matlab程序
%对偶标架变换程序
%sTilde为长度为L的离散信号变量命名基于殷勤业讲义
%gammaTildeVec为最优对偶标架函数离散向量
%dM为对偶标架时间采样间隔点数
%dN为对偶标架频率采样间隔点数
%m0为空间采样起点,要求其值为[0,dM-1]间的整数
%n0为波数采样起点,要求其值为[-L/2,-L/2+dN-1]间的整数
%cTildeMat为对偶标架系数矩阵
function cTildeMat=dualFrameTransform(sTilde,gammaTildeVec,dM,dN,m0,n0)
%判断输入的有效性
if length(sTilde)~=length(gammaTildeVec)
error('要求对偶标架离散向量和信号维数相同!');
end
if mod(length(sTilde),dM)~=0
error('dM必须为整数且能整除信号长度');
end
if mod(length(sTilde),dN)~=0
error('dN必须为整数且能整除信号长度');
end
if rem(m0,1)~=0 || m0<0 || m0>dM-1
error('m0必须为[0,dM-1-1]间的整数');
end
if rem(n0,1)~=0 || n0<-length(sTilde)/2 || n0>-length(sTilde)/2+dN-1
error('n0必须为[-L/2,-L/2+dN-1]间的整数');
end
%计算所需常量
L=length(sTilde);
M=L/dM; %计算对偶标架空间采样点数
N=L/dN; %计算对偶标架波数采样点数
%计算对偶标架系数矩阵cTildeMat
cTildeMat=zeros(M,N);
for m=0:M-1
cache=fft(sTilde.*conj(gammaTildeVec(mod((0:(L-1))-m0-m*dM,L)+1))); cTildeMat(m+1,:)=cache(mod(n0+(0:N-1)*dN,L)+1);
end
end
附录7:对偶标架逆变换的matlab程序
%逆对偶标架变换程序
%cTildeMat为对偶标架系数矩阵,变量命名基于殷勤业讲义
%hTildeVec为综合函数离散向量
%dM为对偶标架时间采样间隔点数
%m0为空间采样起点,要求其值为[0,dM-1]间的整数
%n0为波数采样起点,要求其值为[-L/2,-L/2+dN-1]间的整数
%sTilde0为对偶标架重构信号
function sTilde0=inverseDualFrameTransform(cTildeMat,hTildeVec,dM,dN,m0,n0)
%判断输入的有效性
if rem(m0,1)~=0 || m0<0 || m0>dM-1
error('m0必须为[0,dM-1-1]间的整数');
end
if rem(n0,1)~=0 || n0<-length(hTildeVec)/2 || n0>-length(hTildeVec)/2+dN-1
error('n0必须为[-L/2,-L/2+dN-1]间的整数');
end
%计算所需常量
[M,N]=size(cTildeMat);
L=length(hTildeVec);
unitImaginary=sqrt(-1);
%重构信号
sTilde0=zeros(1,L);
ifftCTildeMat=ifft(cTildeMat,[],2);
for m=0:M-1
sTilde0=sTilde0+hTildeVec(mod((0:L-1)-m0-m*dM,L)+1).*ifftCTildeMat(m+1,mod(0:L-
1,N)+1);
end
sTilde0=N*exp(unitImaginary*n0*(0:L-1)*2*pi/L).*sTilde0;
end
附录8:Grossman对偶标架变换的matlab程序
%主程序
clear;clc;
%初始化变量
dt=0.001;
L=2^10;
sTilde=sin(2*pi*100*((0:L-1)*dt).^1); %构造正弦信号
%sTilde=[sin(400*(0:L/4-1)*pi*dt),sin(800*(L/4:2*L/4-1)*pi*dt),sin(200*(2*L/4:3 *L/4-1)*pi*dt),sin(600*(3*L/4:L-1)*pi*dt)]; %构造四段跳频信号
%sTilde=(1-2*(pi*(50)*(-L/2:L/2-1)*dt).^2).*exp(-(pi*(50)*(-L/2:L/2-1)*dt).^2); %ricker信号;
%[sTilde,fs,~]=wavread('截取忧伤还是快乐.wav');sTilde=transpose(sTilde(:,1));sTilde=sTilde(1:L);dt=1/fs; %实际音频信号
%计算Grossman对偶标架
if fix(log2(length(sTilde)))~=log2(length(sTilde))
error('信号的长度必须为2的整数次方');
end
L=length(sTilde);
C1=256; %设置对偶标架变换的冗余度
dM=2^(ceil(log2(sqrt(L/C1))));
dN=L/(C1*dM); %模拟紧标架变换deltaX与deltaKsi间的关系
M=L/dM; %计算对偶标架时间采样点数
N=L/dN; %计算对偶标架频率采样点数
alpha=2*pi/(dM*N); %根据殷勤业讲义计算使综合向量和分析向量最接近的高斯函数待定参数
hTildeVec=1/sqrt(dt)*fftshift((alpha/pi)^(1/4)*exp(-alpha/2*(-L/2:L/2-1).^2)); %将综合函数的峰值放在中心处,与殷勤业讲义一致
phiVec=hTildeVec/sum(hTildeVec); %计算单位1分解的母函数
p=0.5; %设置Grossman对偶标架的指数参数
gVec=phiVec.^p;
gammaVec=phiVec.^(1-p)/C1; %对紧标架而言,对偶标架的幅度是原标架的幅度除以C1
%进行对偶标架变换
m0=0;
n0=-L/2;
cTildeMat=dualFrameTransform(sTilde,gammaVec,dM,dN,m0,n0);
%绘制重构误差图
subplot(212);
sTilde0=real(inverseDualFrameTransform(cTildeMat,gVec,dM,dN,m0,n0));
xIndex=(0:L-1)*dt+(-L/2)*dt;
plot(xIndex,sTilde-sTilde0);
axis tight;
xlabel('t(s)');ylabel('error');
title('重构误差图');
%绘制谱图
subplot(211);
cache=transpose(cTildeMat);
cache=cache(N/2+1:N,:);
xIndex=(0:M-1)*dM*dt+(-L/2)*dt;
yIndex=n0/(L*dt)+(N/2:N-1)*(dN/(L*dt));
plotMat(abs(cache).^2,xIndex,yIndex,2,'t(s)','f(Hz)','谱图');
E RDAS实验报告 图像融合实验 数据来源 采用Erdas中examples文件内的2000年Atlanta多光谱TM数据和高清全色Pan数据。两图为同一地区不同坐标影像,故使用前需预处理从而得到实验区域。 目的 多光谱TM数据分辨率较低但包含多波段色彩,而全色Pan数据只包含一层高清影像,为了得到研究区域的高清彩色影像,我们将TM和Pan数据在Erdas2014中进行融合以达到实验目的。 方法 在遥感领域运用较多的融合方法有主成分变换法、比值变换法、小波变换法和HIS变换法。本实验则运用HIS变换法。IHS属于色度空间变换,从多光谱彩色合成影像上分离出代表信息的明度(I)和代表光谱信息的色调(H)、饱和度(S)等3个分量,并采用相同区域的高分辨率全色波段数据代替明度(I)进行空间信息融合。 步骤 1.几何校正 因原始图像空间坐标不同,需选取控制点进行几何校正。本实验校正方法为多项式法,选取6个控制点进行校正,其校正叠加截图如下:
2.叠加剪切 由校正结果可知两图像只有部分区域重合,所以建立AOI对重合区域进行剪切,以得到研究区域,截图如下: 3.重采样 因多光谱图像分辨率较低,像元点较大,若要与全色图融合出高清影像需进行重采样来调整像元大小,以达到与高清图一致。 4.二次剪切 因图为栅格,统一像元后,边缘区必然会有一定的扩展(如下图),虽说扩展的范围较小,但在科研应用方面不符合要求,故须二次剪切。 5.RGB转HIS
TM图像选取前三层再分别赋予蓝、绿、红三色,转化为HIS格式,如下图: 6.直方图匹配 将高清图像直方图以标准图像的直方图为标准作变换,使全色光图和HIS图中I层两图像的直方图相同和近似,从而使两幅图像具有类似的色调和反差,以便作进一步的运算。 7.图像叠加 运用Layer stack功能将全色光高清图和H、S图层进行叠加即所谓的图像融合。它将多波段图层组合到了一起,从而得到新的包含多个有助于研究者使用的多波段影像。 8.IHS转RGB
1什么是小波函数?(或小波函数满足什么条件?) 答:设)()(2R L t ∈?,且其Fourier 变换)(ω? 满足可允许性(admissibility )条件 +∞
小波分析及其在通信中的应用 专业:电子信息工程 姓名:张天雷 学号:123408148 河南城建学院 2011年05月29日
小波分析及其在通信中的应用 摘要:小波分析是傅里叶分析的重大突破,是当今许多领域研究的热点。从小波分析的发展历程出发,介绍了小波在现代通信中的一些应用,并指出了未来的一些研究方向。 关键词:小波变换;傅里叶变换;小波应用;通信 小波(Wavelet)这一术语,顾名思义,“小波”就是小的波形。所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式。小波分波是自1986年以来由于Meyer、Mallat和Daubechies等的奠基工作而迅速发展起来的一门新兴学科,它是傅立叶分析划时代的发展结果。与Fourier 变换相比,小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier 变换的困难问题, 小波分析的目的是“既要看到森林(信号的概貌) ,又要看到树木(信号的细节) |”。因此,它被誉为“学显微镜”。 小波分析已经在图像处理、语音识别,声学,信号处理,神经生理学,磁性谐振成像,地震测量,机械故障诊断,生物医学,医疗卫生,以及一些纯数学应用如解决一些微分方程式等领域取得一系列重要应用。小波变换理论在通信中的应用研究在国际上日益受到重视。小波函数提供的一系列正交基非常适合通信系统中的信号波形设计,扩频特征波形设计,多载波传输系统的正交子信道划分等。 小波变换技术在通信系统中的信源编码、信道编码、调制、均衡、干扰抑制和多址等方面具有广阔的应用前景。 一、小波分析在通信系统中的研究动态 如何在各种信道环境下实现有效可靠的信息传输一直是通信领域关注的课
南京师范大学物理科学与技术学院 医用电子学论文 论文名称:基于小波变换的心电信号噪声消除 院系:物科院 专业:电路与系统 姓名:聂梦雅 学号: 121002043 指导教师:徐寅林
摘要 以小波变换的多分辨率分析为基础, 通过对体表心电信号(ECG) 及其噪声的分析, 对ECG信号中存在的基线漂移、工频干扰及肌电干扰等几种噪声, 设计了不同的小波消噪算法; 并利用MIT/BIH 国际标准数据库中的ECG 信号和程序模拟所产生的ECG 信号, 分别对算法进行了仿真与实验验证。结果表明, 算法能有效地滤除ECG 信号检测中串入的几类主要噪声, 失真度很小, 可满足临床分析与诊断对ECG 波形的要求。 关键词: ECG 信号, 小波变换, 基线漂移, 工频干扰, 肌电干扰
Abstract We apply the multi-resolution analysis (MRA ) of wavelet transform ( WT ) , which was proposed by Mallat [ 5 ] , to suppress the three main types of noises existing in electrocardiogram ( ECG ) signals : baseline wander, power line interference and electro my ographical interference. We apply Mallat algorithm [ 4 ] to suppress the baseline wander in ECG signals. We apply the sof t-thresholding algorithm, proposed by donohoetal on the basis of MRA of WT , to suppress power line interference in ECG signals. We apply Mallat algorithm and then the algorithm proposed by Donohoetal to suppress the electro my ographical interference in ECG signals ,who sefrequency range varies f rom 5Hz to 2kHz. We performed simulations ,using both ECG signals from MIT/BIH database, and ECG signals generated via computer simulation .The results show that the algorithm can suppress the main no isesexisting in ECG signals efficiently with very little distortion, and can satisfy the requirement s of clinical analysis and diagnosis on ECG waveforms. Key words: ECG (electro cardio gram ) signal, wavelet transform , baseline wander, power line interference , electro my ographical interference
信号分析与处理应用 数字信号处理是当代流行的一门技术,由于它方法灵活,实现简便,在振动、声学、地震、通讯、雷达、控制系统和生物医学工程等广泛的科学技术领域中发挥着至关重要的作用。以下便是我对信号处理技术在某些工程上的应用做的简要了解。 一.FFT算法在无功补偿控制器上的应用 在电力系统中,无功功率是影响电压稳定的一个重要因素,无功补偿是保证电力系统高效可靠运行的有效措施之一。采用快速傅里叶变换,对复杂的时域信号进行处理以得到较为清晰的频域信号,对电参量进行实时的检测和处理,以达到无功补偿的最佳效果。控制器同时采样三相电压、三相电流,利用FFT算法对电网中的电参数进行实时测量,只需3次FFT就可计算出三相电压、三相电流的FFT结果。这里以一相电压和电流的测量算法为例: 同时采样N点电压序列{u(n)}和电流序列{i(n)},二者构成一个复数离散时间序列: N 继续对u(n),i(n)进行DFT变换,由其复数共轭性质得到电压、电流的频谱。系统在处理数据的过程中,首先对式(2)进行FFT变换得到X(K),然后就可得到X*(N-K),继而利用DFT变换方法得到电压、电流的频谱,写出电压电流的K次谐波分量。这里不考虑直流分量,可导出此相各次(1≤K≤N/2-1)谐波电压、电流的有效值(UK,IK)和有功功率(PK)。并以此为依据,算出相电压有效值、电流有效值、有功功率P、视在功率S、无功功率Q,以及功率因数λ以及总谐波畸变率。利用电压、电流向量与其频谱的关系,可以得到电压初相角和电流初相角。这样,系统得到了此相的各项参数,同理可知三相功率即为各项参数之和。由以上数据处理过程可知,利用FFT算法将直流分量及交流分量的各次谐波分离出来以后,在数据处理过程中只考虑交流分量,也就消除了测试电路中直流漂移对测量精度的影响。 可见,采用DSP进行FFT运算,实现了跟踪测量输入信号的频率。根据实际频率计算采样周期的算法,在不增加硬件投资的条件下解决了同步采样的问题。这种软件锁相的改进方法,实现简便,实时性较高,计算工作量小。而基于交流采样和傅里叶算法的三相功率计算方法,能有效地消除了三相功率测量中,由于谐波引起的误差,提高测量精度。 二.采样定理在音频的数字化上的应用 音频信号的分析是语音通信、语音识别、语音合成、语音增强等技术的前提与基础。只有将语音信号分析成表示其特性的参数,才可能利用这些参数进行高效的语音通信,才可能建立用于语音合成的语音库和用于语音识别的模版或知识
《小波分析》试题 适用范围:硕士研究生 时 间:2013年6月 一、名词解释(30分) 1、线性空间与线性子空间 解释:线性空间是一个在标量域(实或复)F 上的非空矢量集合V ;设V1是数域K 上的线性空间V 的一个非空子集合,且对V 已有的线性运算满足以下条件 (1) 如果x 、y V1,则x +y V1; (2) 如果x V1,k K ,则kx V1, 则称V1是V 的一个线∈∈∈∈∈性子空间或子空间。2、基与坐标 解释:在 n 维线性空间 V 中,n 个线性无关的向量,称为 V 的一组n 21...εεε,,,基;设是中任一向量,于是 线性相关,因此可以被基αn 21...εεε,,,线性表出:,其中系数 αεεε,,,,n 21...n 21...εεε,,,n 2111an ...a a εεεα+++=是被向量和基唯一确定的,这组数就称为在基下的坐标,an ...a a 11,,,αn 21...εεε,,,记为 () 。an ...a a 11,,,3、内积 解释:内积也称为点积、点乘、数量积、标量积。,()T n x x x x ,...,,21= ,令,称为x 与y 的内积。 ()T n y y y y ,...,,21=[]n n y x y x y x y x +++=...,2211[]y x ,4、希尔伯特空间 解释:线性 完备的内积空间称为Hilbert 空间。线性(linearity ):对任意 f , g ∈H ,a ,b ∈R ,a*f+b*g 仍然∈H 。完备(completeness ):空间中的任何柯西序列都收敛在该空间之内。内积(inner product ):
第六章小波变换的几个典型应用 6.1 小波变换与信号处理 小波变换作为信号处理的一种手段,逐渐被越来越多领域的理论工作者和工程技术人员所重视和应用,并在许多应用中取得了显著的效果。同传统的处理方法相比,小波变换取得了质的飞跃,在信号处理方面具有更大的优势。比如小波变换可以用于电力负载信号的分析与处理,用于语音信号的分析、变换和综合,还可以检测噪声中的未知瞬态信号。本部分将举例说明。 6.1.1 小波变换在信号分析中的应用 [例6-1] 以含躁的三角波与正弦波的组合信号为例具体说如何利用小波分析来分析信号。已知信号的表达式为 应用db5小波对该信号进行7层分解。xiaobo0601.m 图6-1含躁的三角波与正弦波混合信号波形 分析: (1)在图6-2中,逼近信号a7是一个三角波。 (2)在图6-3中细节信号d1和d2是与噪声相关的,而d3(特别是d4)与正弦信号相关。 图6-2 小波分解后各层逼近信号 图6-3 小波分解后各层细节信号 6.1.2 小波变换在信号降躁和压缩中的应用 一、信号降躁 1.工程中,有用信号一般是一些比较平稳的信号,噪声通常表现为高频信号。2.消躁处理的方法:首先对信号进行小波分解,由于噪声信号多包含在具有较高频率的细节中,我们可以利用门限、阈值等形式对分解所得的小波系数进行处理,然后对信号进行小波重构即可达到对信号的消躁目的。 小波分析进行消躁处理的3种方法: (1)默认阈值消躁处理。该方法利用ddencmp生成信号的默认阈值,然后利用wdencmp函数进行消躁处理。 (2)给定阈值消躁处理。在实际的消躁处理过程中,阈值往往可通过经验公式获得,且这种阈值比默认阈值的可信度高。在进行阈值量化处理时可利用函数wthresh。 (3)强制消躁处理。该方法时将小波分解结构中的高频系数全部置为0,即滤掉所有高频部分,然后对信号进行小波重构。方法简单,消躁后信号比较平滑,但易丢失信号中的有用成分。 小波阈值去噪方法是目前应用最为广泛的小波去噪方法之一。 3.信号降噪的准则: 1.光滑性:在大部分情况下,降噪后的信号应该至少和原信号具有同等的光滑性。
小波分析复习题 1、简述傅里叶变换、短时傅里叶变换和以及小波变换之间的异同。 答:三者之间的异同见表 2、小波变换堪称“数学显微镜”,为什么? 答:这主要因为小波变换具有以下特点: 1)具有多分辨率,也叫多尺度的特点,可以由粗及精地逐步观察信号; 2)也可以看成用基本频率特性为)(ωψ的带通滤波器在不同尺度a 下对信号作滤波; 如果)(t ?的傅里叶变换是)(ωψ,则)(a t ?的傅里叶变换为)(||a a ω ψ,因此这组滤波 器具有品质因数恒定,即相对带宽(带宽与中心频率之比)恒定的特点。a 越大相当于频率越低。 3)适当的选择基本小波,使)(t ?在时域上位有限支撑,)(ωψ在频域上也比较集中,便可以使WT 在时、频两域都具有表征信号局部特征能力,因此有利于检测信号的瞬态或奇异点。 4)如)(t x 的CWT 是),(τa WT x ,则)(λt x 的CWT 是),( λ τ λλa WT x ;0>λ 此定理表明:当信号)(t x 作某一倍数伸缩时,其小波变换将在τ,a 两轴上作同一比例的 伸缩,但是不发生失真变形。 基于上述特性,小波变换被誉为分析信号的数学显微镜。 3、在小波变换的应用过程中,小波函数的选取是其应用成功与否的关键所在,请列举一些选择原则。 答:选择原则列举如下:(也即需满足的一些条件和特性) 1)容许条件
当?∞ +∞-∞<=ωω ωψ?d c 2 ) (时才能由小波变换),(τa WT x 反演原函数)(t x ,?c 便是对 )(t ?提出的容许条件,若∞→?c ,)(t x 不存在,由容许条件可以推论出:能用作基本小 波)(t ?的函数至少必须满足0)(0==ωωψ,也就是说)(ωψ必须具有带通性质,且基本小波 )(t ?必须是正负交替的振荡波形,使得其平均值为零。 2)能量的比例性 小波变换幅度平方的积分和信号的能量成正比。 3)正规性条件 为了在频域上有较好局域性,要求),(τa WT x 随a 的减小而迅速减小。这就要求)(t ?的 前n 阶原点矩为0,且n 值越大越好。也就是要求? =0)(dt t t p ?,n p ~1:,且n 值越大越好, 此要求的相应频域表示是:)(ωψ在0=ω处有高阶零点,且阶次越高越好(一阶零点就是容许条件),即)()(01 ωψω ωψ+=n ,0)(00≠=ωωψ,n 越大越好。 4)重建核和重建核方程 重建核方程说明小波变换的冗余性,即在τ-a 半平面上各点小波变换的值是相关的。 重建核方程:τττττ?? ?∞ +∞ ∞-=0 00200),,,(),(),(a a K a WT a da a WT x x ; 重建核:><== ?)(),(1)()(1),,,(0000* 00t t c dt t t c a a K a a a a ττ? ττ??????ττ 4、连续小波变换的计算机快速算法较常用的有基于调频Z 变换和基于梅林变换两种,请用 框图分别简述之,并说明分别适合于什么情况下应用。 答: 1)基于调频Z 变换 ),(2a j a n j e A e W ππ--== 运算说明: a .原始数据及初始化:原始数据是)(k ?(1~0-=N k )和a 值,初始化计算包括 a j e A π-=和a n j e W π2-=。 --- 1)(2N k r )2(am N π 12~2--N N 对应于:1~0-=N r
《医学图像处理》实验报告 实验十:小波变换 日期: 2014年05月06日 摘要 本次实验的实验目的及主要内容是: 一维小波变换和反变换 二维小波变换和反变换 二维小波细节置零、去噪
一、技术讨论 1.1实验原理 小波变换的原理:是指一组衰减震动的波形,其振幅正负相间变化为零,是具有一定的带宽和中心频率波组。小波变换是用伸缩和平移小波形成的小波基来分解(变换)或重构(反变换)时变信号的过程。不同的小波具有不同带宽和中心频率,同一小波集中的带宽与中心频率的比是不变的,小波变换是一系列的带通滤波响应。它的数学过程与傅立叶分析是相似的,只是在傅立叶分析中的基函数是单频的调和函数,而小波分析中的基函数是小波,是一可变带宽内调和函数的组合。 小波去噪的原理:利用小波变换把含噪信号分解到多尺度中,小波变换多采用二进型,然后在每一尺度下把属于噪声的小波系数去除,保留并增强属于信号的小波系数,最后重构出小波消噪后的信号。其中关键是用什么准则来去除属于噪声的小波系数,增强属于信号的部分。 1.2实验方法 1)dwt函数(实现1-D离散小波变换) [cA,cD]=dwt(X,’wname’)使用指定的小波基函数‘wname’对信号X进行分解,cA和cD分别是近似分量和细节分量; [cA,cD]=dwt(X,Lo_D,Hi_D)用指定的滤波器组Lo_D,Hi_D对信号进行分解 2)idwt函数(实现1-D离散小波反变换) X=idwt(cA,cD,’wname’) X=idwt(cA,cD,Lo_R,Hi_R) X=idwt(cA,cD,’wname’,L) X=idwt(cA,cD,Lo_R,Hi_R,L) 由近似分量cA和细节分量cD经过小波反变换,选择某小波函数或滤波器组,L为信号X中心附近的几个点 3)dwt2函数(实现2-D离散小波变换) [cA,cH,cV,cD]=dwt2(X,’wname’) [cA,cH,cV,cD]=dwt2(X,’wname’) cA近似分量,cH水平细节分量,cV垂直细节分量,cD对角细节分量 4)idwt2函数(实现2-D离散反小波变换) X=idwt2(cA,cH,cV,cD,’wname’) X=idwt2(cA,cH,cV,cD,Lo_R,Hi_R) X=idwt2(cA,cH,cV,cD,’wname’,S) X=idwt2(cA,cH,cV,cD,Lo_R,Hi_R,S)
1.单项选择题 1 . 用脉冲响应不变法进行IIR数字滤波器的设计,它的主要缺点是频谱的( )所产生的现象。B A. 干扰 B. 交叠 C. 冲击 D. 阶跃 2 . 用窗函数法设计FIR数字滤波器时,过渡带的宽度不但与窗的类型有关,还与窗的( )有关。得分: 5 A A. 采样点数 B. 采样频率 C. 采样范围 D. 采样周期 3 . 当采样频率不满足奈奎斯特采样定理时,就会发生频谱的( )。得分: 5 D A. 采样 B. 非采样 C. 不混叠 D. 混叠 4 . δ(n)的z变换是()。A A. 1 B. δ(w) C. 2πδ(w) D. 2π 5 . 无限长单位冲激响应(IIR)滤波器的结构是()型的。C A. 非递归 B. 反馈 C. 递归 D. 不确定 6 . 若数字滤波器的单位脉冲响应h(n)是对称的,长度为N,则它的对称中心是()。 B A. N/2 B. (N-1)/2 C. (N/2)-1 D. 不确定 7 . y(n)+0.3y(n-1) = x(n)与y(n) = -0.2x(n) + x(n-1)是( )。C A. 均为IIR B. 均为FIR C. 前者IIR,后者FIR D. 前者FIR, 后者IIR
8 . 对于序列的傅立叶变换而言,其信号的特点是()D A. 时域连续非周期,频域连续非周期 B. 时域离散周期,频域连续非周期 C. 时域离散非周期,频域连续非周期 D. 时域离散非周期,频域连续周期 9 . 实序列的傅里叶变换必是( )。A A. 共轭对称函数 B. 共轭反对称函数 C. 奇函数 D. 偶函数 10 . 若序列的长度为M,要能够由频域抽样信号X(k)恢复原序列,而不发生时域混叠现象,则频域抽样点数N需满足的条件是( )。A A. N≥M B. N≤M C. N≤2M D. N≥2M 2.判断题 1. y(n)=x2(n)+3所代表的系统是时不变系统。√ 2. 用窗函数法设计FIR数字滤波器时,改变窗函数的类型可以改变过渡带的宽度。√ 3. 有限长序列的N点DFT相当于该序列的z变换在单位圆上的N点等间隔取样。× 4. 一个线性时不变离散系统是因果系统的充分必要条件是:系统函数H(z)的极点在单位圆内。× 5. 对正弦信号进行采样得到的正弦序列必定是周期序列。√ 6. 在离散傅里叶变换中引起混迭效应的原因是因为为采样时没有满足采样定理。√ 7. 在A/D变化之前让信号通过一个低通滤波器,是为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。此滤波器亦称为“平滑”滤波器。× 8. 在D/A变换之后都要让信号通过一个低通滤波器,是为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故友称之为“抗折叠”滤波器。× 9. 如果采样频率过低,再DFT计算中再频域出现混迭线性,形成频谱失真;需提高采样频率来克服或减弱这种失真。√
一、叙述小波分析理论发展的历史和研究现状 答:傅立叶变换能够将信号的时域和特征和频域特征联系起来,能分别从信号的时域和频域观察,但不能把二者有机的结合起来。这是因为信号的时域波形中不包含任何频域信息,而其傅立叶谱是信号的统计特性,从其表达式中也可以看出,它是整个时间域内的积分,没有局部化分析信号的功能,完全不具备时域信息,也就是说,对于傅立叶谱中的某一频率,不能够知道这个频率是在什么时候产生的。这样在信号分析中就面临一对最基本的矛盾——时域和频域的局部化矛盾。 在实际的信号处理过程中,尤其是对非常平稳信号的处理中,信号在任一时刻附近的频域特征很重要。如柴油机缸盖表明的振动信号就是由撞击或冲击产生的,是一瞬变信号,单从时域或频域上来分析是不够的。这就促使人们去寻找一种新方法,能将时域和频域结合起来描述观察信号的时频联合特征,构成信号的时频谱,这就是所谓的时频分析,亦称为时频局部化方法。 为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并开发了一系列新的信号分析理论:短时傅立叶变换、时频分析、Gabor 变换、小波变换Randon-Wigner变换、分数阶傅立叶变换、线形调频小波变换、循环统计量理论和调幅—调频信号分析等。其中,短时傅立叶变换和小波变换也是因传统的傅立叶变换不能够满足信号处理的要求而产生的。 短时傅立叶变换分析的基本思想是:假定非平稳信号在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱。但从本质上讲,短时傅立叶变换是一种单一分辨率的信号分析方法,因为它使用一个固定的短时窗函数,因而短时傅立叶变换在信号分析上还是存在着不可逾越的缺陷。 小波变换是一种信号的时间—尺度(时间—频率)分析方法,具有多分辨
小波分析上机实验报告 院系:电气工程及自动化学院 学科:仪器科学与技术
实验一小波分析在信号压缩中的应用 一、试验目的 (1)进一步加深对小波分析进行信号压缩的理解; (2)学习Matlab中有关信号压缩的相关函数的用法。 二、相关知识复习 用一个给定的小波基对信号进行压缩后它意味着信号在小波阈的表示相对缺少了一些信息。之所以能对信号进行压缩是因为对于规则的信号可以用很少的低频系数在一个合适的小波层上和一部分高频系数来近似表示。 利用小波变换对信号进行压缩分为以下几个步骤来完成: (1)进行信号的小波分解; (2)将高频系数进行阈值量化处理。对从1 到N 的每一层高频系数都可以选择不同的阈值并且用硬阈值进行系数的量化; (3)对量化后的系数进行小波重构。 三、实验要求 (1)对于某一给定的信号(信号的文件名为leleccum.mat),利用小波分析对信号进行压缩处理。 (2)给出一个图像,即一个二维信号(文件名为wbarb.mat),利用二维小波分析对图像进行压缩。 四、实验结果及程序 (1)load leleccum %将信号装入Matlab工作环境 %设置变量名s和ls,在原始信号中,只取2600-3100个点 s = leleccum(2600:3100); ls = length(s); %用db3对信号进行3级小波分解 [c,l] = wavedec(s, 3, 'db3'); %选用全局阈值进行信号压缩 thr = 35; [xd,cxd,lxd,perf0,perfl2] = wdencmp('gbl',c,l,'db3',3,thr,'h',1); subplot(2,1,1);plot(s); title('原是信号s'); subplot(2,1,2);plot(xd); title('压缩后的信号xd');
题1:设{},j V j Z ∈是依尺度函数()x φ的多分辨率分析,101()0x x φ≤
11()3.k k h k p -=为高通分解滤波器,写出个双倍平移正交关系等式 题6:列出二维可分离小波的4个变换基。 题8:要得到“好”的小波,除要求滤波器0()h n 满足规范、双正交平移性、低通等最小条件外,还可以对0()h n 加消失矩条件来得到性能更优良的小波。 (1) 请写出小波函数()t ψ具有p 阶消失矩的定义条件: (2) 小波函数()t ψ具有p 阶消失矩,要求0()h n 满足等式: (3) 在长度为4的滤波器0()h n 设计中,将下面等式补充完整: 222200000000(0)(1)(2)(3)1 (0)(2)(1)(3)0 ,1 2h h h h h h h h n ?+++=???+==??? 规范性低通双平移正交阶消失矩
2005年研究生《小波理论及应用》复习题 1. 利用正交小波基建立的采样定理适合于:紧支集且有奇性(函数本身或其导数不连续)的函数(频谱无限的函数)。Shannon 采样定理适合于频谱有限的信号。 2. 信号的突变点在小波变换域常对于小波变换系数模极值点或过零点。并且信号奇异性大小同小波变换的极值随尺度的变化规律相对立。只有在适当尺度下各突变点引起的小波变化才能避免交迭干扰,可以用于信号的去噪、奇异性检测、图象也缘提取、数据压缩等。 3. 信号在一点的李氏指数表征了该点的奇异性大小,α越大,该点的光滑性越小,α越小,该点的奇异性越大。光滑点(可导)时,它的1≥α;如果是脉冲函数,1-=α;白噪声时0≤α。 4. 做出三级尺度下正交小波包变换的二进数图,小波包分解过程?说明小波基与小波包基的区别? 5. 最优小波包基的概念:给定一个序列的代价函数,然后在小波包基中寻找使代价函数最小的基――最优基。 6. 双通道多采样率滤波器组的传递函数为: ()()()()()()()()()()()()()z X z G z G z H z H z X z G z G z H z H z Y z Y z Y -??????-++??????+=+=∧∧∧∧212121请根据此式给出理想重建条件: 为了消除映象()z X -引起的混迭:()()()()0=-+-∧ ∧z G z G z H z H
为了使()z Y 成为()z X 的延迟,要求:()()()()k CZ z G z G z H z H -∧∧=+ (C,K 为任一常数) 7. 正交镜像对称滤波器()()n h n g ,的()jw e G 与()jw e H 以2π=w 为轴左右对称。如果知道QMF 的()n h ,能否确定()()()n h n g n g ∧ ∧,,? ()()()n h n g n 1-= ,()()()n g n h n 1--=∧ , ()()()n h n g n 1-=∧ 8. 试列出几种常用的连续的小波基函数 Morlet 小波,Marr 小波,Difference of Gaussian (DOG ),紧支集样条小波 9. 试简述海森堡测不准原理,说明应用意义? 10. 从连续小波变换到离散小波变换到离散小波框架-双正交小波变换-正交变换、紧支集正交小波变换,其最大的特点是追求变换系数的信息冗余小,含有的信息量越集中。 11. 解释紧支集、双正交、正交小波、紧支集正交小波、光滑性、奇异性。 12. 已知共轭正交滤波器组(CQF )()n h 请列出()()()n g n h n g ∧ ∧,,。 ()()() ()()()()()()???????-=--=-=---=∧∧n h n N g n g n N h n h n N h n g n n 11 13. 共轭正交滤波器()()n g n h ,的()jw e G 与()jw e H 的关系与QMF 情况
科技文献检索作业 卷 试 料 小波分析及其应用 测控技术1103 雷创新
小波分析及其应用 1.小波分析的概念和特点 1.1小波理论的发展概况 20世纪80年代逐渐发展和兴起的小波分析(wavelctanalysis)是20世纪 数学领域中研究的重要杰出成果之一。小波分析理论作为数学界中一种比较成熟的理论基础,应用到了各种领域的研究当中,推动了小波分析在各工程应用中的发展。它作为一种新的现代数字信号处理算法,汲取了现代分析学中诸如样条分析、傅立叶分析、数值分析和泛函分析等众数学多分支的精华部分,替代了工程界中一直应用的傅立叶变换,它是一种纯频域分析方法,不能在时频同时具有局部化特性。而小波分析中的多尺度分析思想,犹如一台变焦照相机,可以由粗及精逐步观察信号,在局部时频分析中具有很强的灵活性,因此有“数学显微镜”的美称。它能自动随着频率增加而调节成窄的“时窗”和宽的“频窗”,又随着频率降低而调节成宽的“时窗”和窄的“频窗”以适应实际分析需要。另外,小波变换在经过适当离散后可以够成标准正交基或正交系,这些在理论和应用上都具有十分重要的意义,因此,小波分析在各个领域得到了高度的重视并取得了许多重要的成果。 小波变换作为一种数学理论和现代数字信号处埋方法在科学技术界引起了越来越多专家学者的关注和重视。在数学家看来,基于小波变换的小波分析技术是当今数值分析、泛函分析、调和分析等半个多世纪以来发展最完美的结晶,是正在发展中的新的数学分支。在工程领域,特别是在信号处理、图像处理、机器视觉、模糊识别、语音识别、流体力学、量子物理、地震勘测、电磁学、CT成像、机械故障诊断与监控等领域,它被认为是近年来在工具及方法上的重大突破。然而,小波分析虽然在众多领域中已经取得了一定的成果,但是,有专家预言小波分析理论的真正高潮并没有到来。首先,小波分析尚需进一步完善,除一维小波分析理论比较成熟以外,向量小波和多维小波则需要进行更加深入的研究与讨论;其次,针对不同情况选择不同的小波基函数,实现的效果是有差别性的这一问题,对最优小波基函数的选取方法有待进一步研究。在今后数年中,小波理论将成为科技工作者经常使用的又一锐利数学工具,极大地促进科技进步及各个领域工程应用的新发展。 小波分析的概念最早是在1974年由法国地质物理学家 J.Morlet提出的,并通过物理直观和信号处理的实际经验建立了反
一、题目:一维Haar 小波2次分解 二、目的:编程实现信号的分解与重构 三、算法及其实现:离散小波变换 离散小波变换是对信号的时-频局部化分析,其定义为:/2200()(,)()(),()()j j Wf j k a f t a t k dt f t L R φ+∞---∞=-∈? 本实验实现对信号的分解与重构: (1)信号分解:用小波工具箱中的dwt 函数来实现离散小波变换,函数dwt 将信号分解为两部分,分别称为逼近系数和细节系数(也称为低频系数和高频系数),实验中分别记为cA1,cD1,它们的长度均为原始信号的一半,但dwt 只能实现原始信号的单级分解。在本实验中使用小波函数db1来实现单尺度小波分解,即: [cA1,cD1]=dwt(s,’db1’),其中s 是原信号;再通过[cA2,cD2]=dwt(cA1,’db1’)进行第二次分解,长度又为cA2的一半。 (2)信号重构:用小波工具箱中的upcoef 来实现,upcoef 是进行一维小波分解系数的直接重构,即: A1 = upcoef('a',cA1,'db1'); D1 = upcoef('a',cD1,'db1')。 四、实现工具:Matlab 五、程序代码: %装载leleccum 信号 load leleccum; s = leleccum(1:3920); %用小波函数db1对信号进行单尺度小波分解 [cA1,cD1]=dwt(s,'db1'); subplot(3,2,1); plot(s); title('leleccum 原始信号'); %单尺度低频系数cA1向上一步的重构信号 A1 = upcoef('a',cA1,'db1'); %单尺度高频系数cD1向上一步的重构信号 D1 = upcoef('a',cD1,'db1'); subplot(3,2,3); plot(A1); title('单尺度低频系数cA1向上一步的重构信号'); subplot(3,2,5); plot(D1); title('单尺度高频系数cD1向上一步的重构信号'); [cA1,cD1]=dwt(cA1,’db1'); subplot(3,2,2); plot(s); title('leleccum 第一次分解后的cA1信号'); %第二次分解单尺度低频系数cA2向上一步的重构信号 A2= upcoef('a',cA2,'db1',2); %第二次分解单尺度高频系数cD2向上一步的重构信号 D2 = upcoef('a',cD2,'db1',2); subplot(3,2,4); plot(A2);
北京工业大学 通信系统工程应用训练报告 专业:通信工程 学生姓名:刘莹莹 指导教师:席大林 完成时间:2016年4月29日
目录 训练十一 DFT性质研究 (1) 训练十二 DFT及抽样定理研究 (13) 训练十三数字滤波器制作 (20) 训练十四 IIR数字滤波器设计与实现 (25) 训练十五线性卷积计算 (46) 训练十六 FIR数字滤波器设计与实现 (55)
训练十一 DFT性质研究 验证dft函数正确性 设置原始输入信号为x[8]={{1,0},{2,0},{3,0},{4,0},{5,0},{6,0},{7,0},{8,0}},将输入信号x[8]进行DFT正变换,dft(X,x,8,1),输出保存在X[8],如下: 可以看到,输入信号x(n)已经变换到频域X(k),且仍为8位。再对X[8]进行DFT反变换,dft(x,X,8,-1),重新得到x[8],观察得到的输出与原始输入数据是否相同。 结果如下: 可以看到,输出的x[8]取值仍为 x[8]={{1,0},{2,0},{3,0},{4,0},{5,0},{6,0},{7,0},{8,0}},证明经过DFT正反变换后,
信号能够恢复原始信号。
根据帕塞瓦尔定理,应有时域、频域总能量相等:。经过计算,时域、频域能量和分别为,证明时域、频域能量和相同,符合帕塞瓦尔定理。 综上,证明DFT变换正确。 A、补0效应研究 原数组: x[8]={{1,0},{2,0},{3,0},{4,0},{5,0},{6,0},{7,},{8,0}} 示例程序中补0后数组为: x2[16]={{1,0},{2,0},{3,0},{4,0},{5,0},{6,0},{7,0},{8,0},{0,0},{0,0},{0,0},{0,0} ,{0,0},{0,0},{0,0},{0,0}} 补0方式 我使用的补0方式为: for(i=8;i<13;i++)x2[i]=COMPLEX(0,0); 补0后数组为: x2[13]={{1,0},{2,0},{3,0},{4,0},{5,0},{6,0},{7,0},{8,0},{0,0},{0,0},{0,0},{0,0} ,{0,0}} 结果分析与图 在时域中,信号长度增加,由于所增加的项均为零,波形仍与未补0时相同 未补零时的信号时域图
1、小波变换在图像处理中有着广泛的应用,请简述其在图像压缩中的应用原理? 答:一幅图像经过一次小波变换之后,概貌信息大多集中在低频部分,而其余部分只有微弱的细节信息。为此,如果只保留占总数数量1/4的低频部分,对其余三个部分的系数不存储或传输,在解压时,这三个子块的系数以0来代替,则就可以省略图像部分细节信息,而画面的效果跟原始图像差别不是很大。这样,就可以得到图像压缩的目的。 2、给出GPEG数据压缩的特点。 答:(1)一种有损基本编码系统,这个系统是以DCT为基础的并且足够应付大多数压缩方向应用。 (2)一种扩展的编码系统,这种系统面向的是更大规模的压缩,更高精确性或逐渐递增的重构应用系统。 (3)一种面向可逆压缩的无损独立编码系统。 3、设计雪花检测系统 答:1)获得彩色雪花图像。2)灰度雪花图像。3)图像的灰度拉伸,以增强对比度。4)阈值判断法二值化图像。5)图像的梯度锐化。6)对图像进行自定义模板中值滤波以去除噪声。7)用梯度算子对雪花区域的定位。8)利用hough变换截下雪花区域的图片。 9)雪花图片几何位置调整。 4、用图像处理的原理设计系统,分析木材的年轮结构。 答:1)获得彩色木材年轮图像。2)灰度木材年轮图像。3)灰度拉伸以增加对比度。4)阈值判定法二值化图像。5)图像的梯度锐化。6)对图像进行自定义模板中值滤波以去除噪声。7)用梯度算子对木材年轮圈进行定位。8)图片二值化。9)利用边界描述子对木材的年轮结构进行识别。 5、给出生猪的尺寸和形貌检测系统。 答:1)获得彩色生猪图像。2)灰度生猪图像。3)图像的灰度拉伸,以增强对比度。4)阈值判定法二值化图像。5)图像的梯度锐化。6)对图像进行自定义模板中值滤波以除去噪声。 7)用梯度算子对生猪区域的定位。8)利用hough变换截下生猪区域的图片。9)生猪图片几何位置调整。10)生猪图片二值化。11)利用边界描述子对生猪尺寸和形貌的识别。 第二种答案:(类似牌照检测系统) 1)第一步定位牌照 由图像采集部件采集生猪的外形图像并将图像存储在存储器中,其特征在于:数字处理器由存储器中读入并运行于生猪外形尺寸检测的动态检测软件、从存储器中依次读入两幅车辆外形图像数据、经过对生猪外形图像分析可得到生猪的高度,宽度和长度数据即生猪的外形尺寸。通过高通滤波,得到所有的边对边缘细化(但要保持连通关系),找出所有封闭的边缘,对封闭边缘求多边形逼近,在逼近后的所有四边形中,找出尺寸与牌照大小相同的四边形。生猪形貌被定位。 2)第二步识别 区域中的细化后的图形对象,计算傅里叶描述子,用预先定义好的决策函数,对描述子进行计算,判断到底是数字几。 6、常用的数字图像处理开发工具有哪些?各有什么特点? 答:目前图像处理系统开发的主流工具为Visual C++(面向对象可视化集成工具)和MATLAB的图像处理工具箱(lmage processing tool box)。两种开发工具各有所长且有相互间的软件接口。 微软公司的VC++是一种具有高度综合性能的面向对象可视化集成工具,用它开发出来