
直线的参数方程及应用
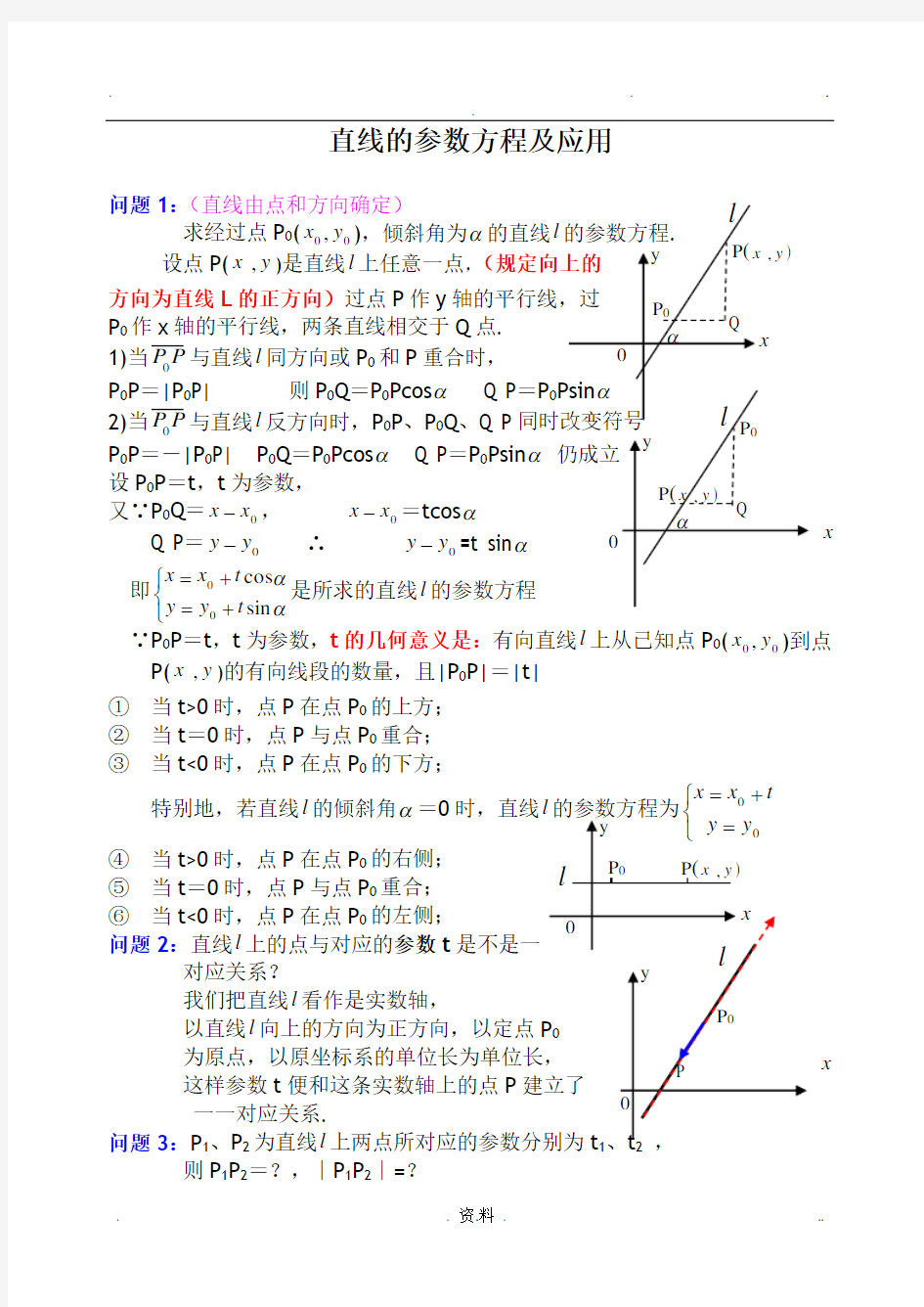
问题1:(直线由点和方向确定)
求经过点P 0(00,y x ),倾斜角为α的直线l
设点P(y x ,)是直线l 上任意一点,方向为直线L 的正方向)过点P 作y P 0作x 轴的平行线,两条直线相交于Q 点.
1)当P P 0与直线l 同方向或P 0和P 重合时,
P 0P =|P 0P| 则P 0Q =P 0Pcos α Q P =P 02)当P P 0与直线l 反方向时,P 0P 、P 0Q 、Q P P 0P =-|P 0P| P 0Q =P 0Pcos α Q P =P 0Psin α 设P 0P =t ,t 为参数,
又∵P 0Q =0x x -, 0x x -=tcos α
Q P =0y y - ∴ 0y y -=t sin α 即?
??+=+=ααsin cos 00t y y t x x 是所求的直线l 的参数方程 ∵P 0P =t ,t 为参数,t 的几何意义是:有向直线l 上从已知点P 0(00,y x )到点 P(y x ,)的有向线段的数量,且|P 0P|=|t|
① 当t>0时,点P 在点P 0的上方;
② 当t =0时,点P 与点P 0重合;
③ 当t<0时,点P 在点P 0的下方;
特别地,若直线l 的倾斜角α=0时,直线?+=0t x x ④ 当t>0时,点P 在点P 0的右侧; ⑤ 当t =0时,点P 与点P 0重合;
⑥ 当t<0时,点P 在点P 0的左侧; 问题2:直线l 上的点与对应的参数t 是不是一 对应关系?
我们把直线l 看作是实数轴, 以直线l 向上的方向为正方向,以定点 这样参数t 便和这条实数轴上的点P 一一对应关系.
问题3:P 1、P 2为直线l 则P 1P 2=?,∣P 1P 2∣=? x
x
P 1P 2=P 1P 0+P 0P 2=-t 1+t 2=t 2-t 1,∣P 1P
问题4:若P 0为直线l 上两点P 1、P 2的中点,P 1、P 2 参数分别为t 1、t 2 ,则t 1、t 2 根据直线l 参数方程t 的几何意义,
P 1P =t 1,P 2P =t 2,∵P 0为直线l 上两点P 1、P 2的中点,∴|P 1P|=|P 2P|
P 1P =-P 2P ,即t 1=-t 2, t 1t 2<0
一般地,若P 1、P 2、P 3是直线l 上的点, 所对应的参数分别为t 1、t 2、t 3,P 3为P 1、P 2 则t 3=221t t + (∵P 1P 3=-P 2P 3, 根据直线l 参数方程t 的几何意义,
∴P 1P 3= t 3-t 1, P 2P 3= t 3-t 2, ∴t 3-t 1=-(t 3-t 2,) )
总结:
1、 直线参数方程的标准式
(1)过点P 0(00,y x ),倾斜角为α的直线l 的参数方程是
???+=+=α
αsin cos 00t y y t x x (t 为参数)t 的几何意义:t 表示有向线段P P 0的数量,P(y x ,) P 0P=t ∣P 0P ∣=t 为直线上任意一点.
(2)若P 1、P 2是直线上两点,所对应的参数分别为t 1、t 2,
则P 1P 2=t 2-t 1 ∣P 1P 2∣=∣t 2-t 1∣
(3) 若P 1、P 2、P 3是直线上的点,所对应的参数分别为t 1、t 2、t 3
则P 1P 2中点P 3的参数为t 3=221t t +,∣P 0P 3∣=2
21t t + (4)若P 0为P 1P 2的中点,则t 1+t 2=0,t 1·t 2<0
2、 直线参数方程的一般式
过点P 0(00,y x ),斜率为a
b k =的直线的参数方程是 ???+=+=bt
y y at x x 00 (t 为参数) 例题:
1、参数方程与普通方程的互化
例1:化直线1l 的普通方程13-+y x =0为参数方程,并说明参数的几何意 义,说明∣t ∣的几何意义.
x
33 设倾斜角为α,tg α=-33,α= π65, cos α =-23, sin α=21 1l 的参数方程为???????=-=t y t x 21231 (t 为参数)
t 是直线1l 上定点M 0(1,0)到t 对应的点M(y x ,)的有向线段M M 0的数量.由???????=-=-(2) 21(1)
231t y t x (1)、(2)两式平方相加,得222)1(t y x =+-
∣t ∣=22)1(y x +-∣t ∣是定点M 0(1,0)到t 对应的点M(y x ,)的有向线段M M 0的长.
点拨:求直线的参数方程先确定定点,再求倾斜角,注意参数的几何意义.
例2:化直线2l 的参数方程???+=+-= t 313y t x (t 为参数)为普通方程,并求倾斜角,
说明∣t ∣的几何意义.
解:原方程组变形为???=-=+ (2) t 31
(1) 3y t x (1)代入(2)消去参数t ,
得)3(31+=-x y (点斜式) 可见k=3, tg α=3,倾斜角α=3
π 普通方程为 01333=++-y x (1)、(2)两式平方相加,得2
224)1()3(t y x =-++∴∣t ∣=2)1()3(22-++y x ∣t ∣是定点M 0(3,1)到t 对应的点M(y x ,)的有向线段M M 0的长的一半. 点拨:注意在例1、例2中,参数t 的几何意义是不同的,直线1l 的参数方程 为???????=-
=t y t x 21231即?????=+=ππ65sin 65cos 1t y t x 是直线方程的标准形式,(-23)2+(2
1)2=1, t 的几何意义是有向线段M M 0的数量.直线2l 的参数方程为?
??+=+-= t 313y t x 是非标准的形式,12+(3)2=4≠1,此时t 的几何意义是有向线段M M 0的数量的一半.
你会区分直线参数方程的标准形式吗?
例3:已知直线l 过点M 0(1,3),倾斜角为3π,判断方程???
????+=+=t y t x 233211(t 为参数)和方程???+=+= t
331y t x (t 为参数)是否为直线l 的参数方程?如果是直线l 的参数方程,指出方程中的参数t 是否具有标准形式中参数t 的几何意义.
解:由于以上两个参数方程消去参数后,均可以得到直线l 的的普通方程 0333=+--y x ,所以,以上两个方程都是直线l 的参数方程,其中
???????+=+=t y t x 233211 cos α =21, sin α=2
3,是标准形式,参数t 是有向线段M M 0的数量.,而方程?
??+=+= t 331y t x 是非标准形式,参数t 不具有上述的几何意义. 点拨:直线的参数方程不唯一,对于给定的参数方程能辨别其标准形式,会利用参数t 的几何意义解决有关问题.
问题5:直线的参数方程???+=+= t
331y t x 能否化为标准形式?
是可以的,只需作参数t 的代换.(构造勾股数,实现标准化)
???+=+= t 331y t x ????
????+++=+++=))3(1()3(13 3))3(1()3(11122222222t y t x 令t '=t 22)3(1+ 得到直线l 参数方程的标准形式???
????'+='+=t 233211y t x t '的几何意义是有向线段 M M 0的数量.
2、直线非标准参数方程的标准化
一般地,对于倾斜角为α、过点M 0(00,y x )直线l 参数方程的一般式为,.
???+=+=bt
y y at x x 00 (t 为参数), 斜率为a b tg k ==α (1)
当22b a +=1时,则t 的几何意义是有向线段M M 0的数量.
(2) 当22b a +≠1时,则t 不具有上述的几何意义.
???+=+=bt y y at x x 00可化为???
????+++=+++=)()(2222022220t b a b a b y y t b a b a a x x 令t '=t b a 22+ 则可得到标准式???
????'++='++=t b a b y y t b a a x x 220220 t '的几何意义是有向线段M M 0的数量. 例4:写出经过点M 0(-2,3),倾斜角为
43π的直线l 的标准参数方程,并且 求出直线l 上与点M 0相距为2的点的坐标. 解:直线l 的标准参数方程为?????+=+-=ππ43sin 343cos 2t y t x 即???
????+=--=t y t x 223222(t 为参数)(1) 设直线l 上与已知点M 0相距为2的点为M 点,且M 点对应的参数为t, 则| M 0M|=|t| =2, ∴t=±2 将t 的值代入(1)式
当t=2时,M 点在 M 0点的上方,其坐标为(-2-2,3+2); 当t=-2时,M 点在 M 0点的下方,其坐标为(-2+2,3-2).
点拨:若使用直线的普通方程利用两点间的距离公式求M 点的坐标较麻烦, 而使用直线的参数方程,充分利用参数t 的几何意义求M 点的坐标较 容易.
例5:直线?
??-=+=
20cos 420sin 3t y t x (t 为参数)的倾斜角 . 解法1:消参数t,的34--x y =-ctg20°=tg110°
解法2:化为标准形式: ???-+=-+= 110
sin )(4110cos )(3t y t t x (-t 为参数) ∴此直线的倾斜角为110°
基础知识测试1:
1、 求过点(6,7),倾斜角的余弦值是2
3的直线l 的标准参数方程. 2、 直线l 的方程:???+=-=
25
cos 225sin 1t y t x (t 为参数),那么直线l 的倾斜角( ) A 65° B 25° C 155° D 115°
3、 直线???
????+-=-=t y t x 521511(t 为参数)的斜率和倾斜角分别是( ) A) -2和arctg(-2) B) -2
1和arctg(-21) C) -2和π-arctg2 D) -2
1和π-arctg 21 4、 已知直线???+=+=α
αsin cos 00t y y t x x (t 为参数)上的点A 、B 所对应的参数分别为t 1,t 2,点
P 分线段BA 所成的比为λ(λ≠-1),则P 所对应的参数是 . 5、直线l 的方程: ??
?+=+=bt y y at x x 00 (t 为参数)A 、B 是直线l 上的两个点,分别对应参
数值t 1、t 2,那么|AB|等于( )
A ∣t 1-t 2∣
B 22b a +∣t 1-t 2∣ C
2221b a t t +- D ∣t 1∣+∣t 2∣ 6、 已知直线l :???+-=+= t 351y t
x (t 为参数)与直线m :032=--y x 交于P 点,求点
M(1,-5)到点P 的距离.
例6:已知直线l 过点P (2,0),斜率为3
4
和抛物线x y 22=相交于A 、B 两点,
设线段AB 的中点为M,求: (1)P 、M 两点间的距离|PM|; (2)M 点的坐标; (3)线段AB 的长|AB|
解:(1)∵直线l 过点P (2,0),斜率为34,3 cos α =53, sin α=54∴直线l 的标准参数方程为?????=+=t y t x 5453
2(t 为参数)* ∵直线l 和抛物线相交,将直线的参数方程代入抛物线方程x y 22=中, 整理得 8t 2-15t -50=0 Δ=152+4×8×50>0,设这个二次方程的两
个根为t 1、t 2,由韦达定理得 t 1+t 2=
815, t 1t 2=4
25- ,由M 为线段AB 的中点,根据t 的几何意义,得| PM|=221t t + =1615
∵中点M 所对应的参数为t M =16
15,将此值代入直线的标准参数方程*, M 点的坐标为?????=?==?+=4316155416411615532y x 即 M (1641,43)
(3) |AB|=∣t 2-t 1∣= 222114)(t t t t -+=738
5 点拨:利用直线l 的标准参数方程中参数t 的几何意义,在解决诸如直线l 上两点间的距离、直线l 上某两点的中点以及与此相关的一些问题时,比用直线l 的普通方程来解决显得比较灵活和简捷.
例7:已知直线l 经过点P (1,-33),倾斜角为3
π, (1)求直线l 与直线l ':32-=x y 的交点Q 与P 点的距离| PQ|;
(2)求直线l 和圆22y x +=16的两个交点A ,B 与P 点的距离之积.
解:(1)∵直线l 经过点P (1,-33),倾斜角为3
π,∴直线l 的标准参数方 程为?????+-=+=3sin 333cos 1ππt y t x ,即???????+-=+=t y t x 2333211(t 为参数)代入直线l ':
32-=x y 得032)2
333()211(=-+--+t t 整理,解得t=4+23 t=4+23即为直线l 与直线l '的交点Q 所对应的参数值,根据参数t 的几 何意义可知:|t|=| PQ|,∴| PQ|=4+23.
(2) 把直线l 的标准参数方程为???????+-=+=t y t x 2333211(t 为参数)代入圆的方程
22y x +=16,得16)2
333()211(22=+-++t t ,整理得:t 2-8t+12=0, Δ=82-4×12>0,设此二次方程的两个根为t 1、t 2 则t 1t 2=12
根据参数t 的几何意义,t 1、t 2 分别为直线和圆22y x +=16的两个交点
A, B 所对应的参数值,则|t 1|=| PA|,|t 2|=| PB|,
所以| PA|·| PB|=|t 1 t 2|=12
点拨:利用直线标准参数方程中的参数t 的几何意义解决距离问题、距离的乘积(或商)的问题,比使用直线的普通方程,与另一曲线方程联立先求得交点坐标再利用两点间的距离公式简便.
例8:设抛物线过两点A(-1,6)和B(-1,-2),对称轴与x 轴平行,开口向右,
解:由题意,得抛物线的对称轴方程为y=2.设抛物线顶点坐标为(a ,2) 方程为(y ―2)2=2P(x -a ) (P>0) ①
∵点B(-1,-2)在抛物线上,∴(―2―2)2=2P(-1-a )
a P=-8-P 代入① 得(y ―2)2=2P x +2P+16 ②
将直线方程y=2x +7化为标准的参数方程tg α=2, α为锐角,
cos α =51, sin α=52 得???
????+=+-=t y t x 525511(t 为参数) ③ ∵直线与抛物线相交于A ,B, ∴将③代入②并化简得:
75
212542--+t P t =0 ,由Δ=355)6(42+-P >0,可设方程的两根为t 1、t 2, 又∵|AB|=∣t 2-t 1∣=
222114)(t t t t -+=410 4
354]4)212(5[2?+-P =(410)2 化简,得(6-P)2=100 ∴ P=16 或P=-4(舍去) 所求的抛物线方程为(y ―2)2=32x +48
点拨:(1)(对称性) 由两点A(-1,6)和B(-1,-2)的对称性及抛物线的对称性质,设出抛物线的方程(含P 一个未知量,由弦长AB 的值求得P ).
(2)利用直线标准参数方程解决弦长问题.此题也可以运用直线的普通方程与抛物线方程联立后,求弦长。对于有些题使用直线的参数方程相对简便些.
例9:已知椭圆13
4)1(2
2=+-y x ,AB 是通过左焦点F 1的弦,F 2为右焦点, 求| F 2A|·| F 2B|的最大值.
解:由椭圆方程知a =2,b=3,c=1, F 1(0,0),F 2(2,0),设过的弦所在直线的
参数方程为?
??==ααsin cos t y t x (t 为参数) 代入椭圆方程整理得 (3+sin 2α)t 2-6 t cos α-9=0 ,Δ=36cos 2α+36(3+sin 2α)>0 此方程的解为t 1、t 2,分别为A 、B 两点
对应的参数,由韦达定理t 1+t 2=αα2sin 3cos 6+ t 1 t 2=α
2sin 39+- 根据参数t 的几何意义,t 1、t 2 分别为过点F 1的直线和椭圆的两个交点 A, B 所对应的参数值,| F 1A|=|t 1| |F 1B|=|t 2|
|AB|=∣t 2-t 1∣= 222114)(t t t t -+=α
2sin 312+