圆的综合复习

圆的综合复习

授课目的：会解证与角，线段相关的几何问题；会运用垂径定理，切线长定理，相交弦定理，切割线定理，割线定理计算、证明一类与圆相关的几何问题；会解与三角形，方程，函数等知识点结合，设计一类与圆有关的中考压轴题。

考点分析：（分析考试题型、所占分值、易错点）

圆在初中数学体系中处在核心地位，是中考的重头戏，占题量的16%--20%。题型主要有选择题，填空题，解答题，作图题（包括阅读理解题，开放探索题等）。

一、复习

二、新授（知识点与经典例题）

1．圆的定义：

(1)线段OA绕着它的一个端点O旋转一周，另一个端点A所形成的封闭曲线，叫做圆．

(2)圆是到定点的距离等于定长的点的集合．

2．与圆有关的角

(1)圆心角：顶点在圆心的角叫圆心角．

圆心角的性质：圆心角的度数等于它所对的弧的度数．

(2)圆周角：顶点在圆上，两边都和圆相交的角叫做圆周角．

圆周角的性质：

①圆周角等于它所对的弧所对的圆心角的一半．

②同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等．

③90°的圆周角所对的弦为直径；半圆或直径所对的圆周角为直角．

④如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形．

⑤圆内接四边形的对角互补；外角等于它的内对角．

(3)弦切角：顶点在圆上，一边和圆相交，另一边和圆相切的角叫弦切角．

弦切角的性质：弦切角等于它夹的弧所对的圆周角．

弦切角的度数等于它夹的弧的度数的一半．

【经典例题精讲】

例1 下列命题正确的是( )

A．相等的圆周角对的弧相等 B．等弧所对的弦相等

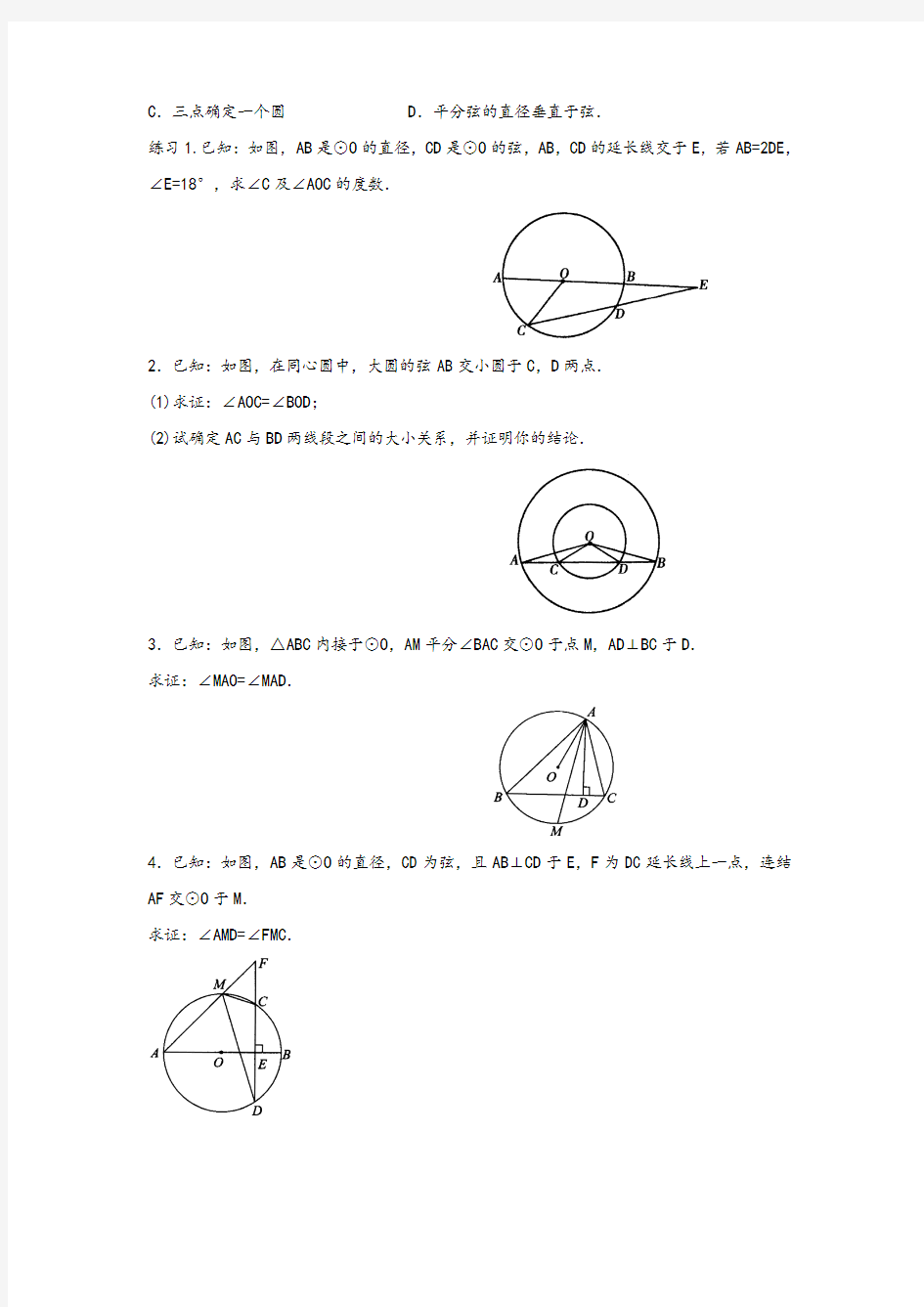
C．三点确定一个圆 D．平分弦的直径垂直于弦．

练习1.已知：如图，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于E，若AB=2DE，∠E=18°，求∠C及∠AOC的度数．

2．已知：如图，在同心圆中，大圆的弦AB交小圆于C，D两点．

(1)求证：∠AOC=∠BOD；

(2)试确定AC与BD两线段之间的大小关系，并证明你的结论．

3．已知：如图，△ABC内接于⊙O，AM平分∠BAC交⊙O于点M，AD⊥BC于D．

求证：∠MAO=∠MAD．

4．已知：如图，AB是⊙O的直径，CD为弦，且AB⊥CD于E，F为DC延长线上一点，连结AF交⊙O于M．

求证：∠AMD=∠FMC．

3．圆的性质：

(1)旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；圆是中心对称图形，对称中心是圆心．

在同圆或等圆中，两个圆心角，两条弧，两条弦，两条弦心距，这四组量中的任意一组相等，那么它所对应的其他各组分别相等．

(2)轴对称：圆是轴对称图形，经过圆心的任一直线都是它的对称轴．

4垂径定理及推论：

(1)垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．

(2)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．

(3)弦的垂直平分线过圆心，且平分弦对的两条弧．

(4)平分一条弦所对的两条弧的直线过圆心，且垂直平分此弦．

(5)平行弦夹的弧相等．

【经典例题精讲】

1已知：如图，AB是⊙O的直径，弦CD交AB于E点，BE=1，AE=5，∠AEC=30°，求CD的长．

2．已知：如图，A，B是半圆O上的两点，CD是⊙O的直径，∠AOD=80°，B是的中点．

(1)在CD上求作一点P，使得AP＋PB最短；

(2)若CD=4cm，求AP＋PB的最小值．

3.如图，有一圆弧形的拱桥，桥下水面宽度为7.2m，拱顶高出水面2.4m，现有一竹排运送一货箱从桥下经过，已知货箱长10m，宽3m，高2m(竹排与水面持平)．问：该货箱能否顺利通过该桥?

5．三角形的内心、外心、重心、垂心

(1)三角形的内心：是三角形三个角平分线的交点，它是三角形内切圆的圆心，在三角形内部，它到三角形三边的距离相等，通常用“I”表示．

(2)三角形的外心：是三角形三边中垂线的交点，它是三角形外接圆的圆心，锐角三角形外心在三角形内部，直角三角形的外心是斜边中点，钝角三角形外心在三角形外部，三角形外心到三角形三个顶点的距离相等，通常用O表示．

(3)三角形重心：是三角形三边中线的交点，在三角形内部；它到顶点的距离是到对边中点距离的2倍，通常用G表示．

(4)垂心：是三角形三边高线的交点．

6．圆内接四边形和外切四边形

(1)四个点都在圆上的四边形叫圆的内接四边形，圆内接四边形对角互补，外角等于内对角．

(2)各边都和圆相切的四边形叫圆外切四边形，圆外切四边形对边之和相等．

【经典例题精讲】

1. 四边形ABCD内接于⊙O，∠A︰∠B︰∠C＝1︰2︰3，求∠D．

7．判定一个点P是否在⊙O上．

设⊙O的半径为R，OP＝d，则有

d>r点P在⊙O 外；

d＝r点P在⊙O 上；

d

8．直线和圆的位置关系：

设⊙O 半径为R，点O到直线l的距离为d．

(1)直线和圆没有公共点直线和圆相离d>R．

(2)直线和⊙O有唯一公共点直线l和⊙O相切d＝R．

(3)直线l和⊙O 有两个公共点直线l和⊙O 相交d

9．切线的判定、性质：

(1)切线的判定：

①经过半径的外端并且垂直于这条半径的直线是圆的切线．

②到圆心的距离d等于圆的半径的直线是圆的切线．

(2)切线的性质：

①圆的切线垂直于过切点的半径．

②经过圆心作圆的切线的垂线经过切点．

③经过切点作切线的垂线经过圆心．

(3)切线长：从圆外一点作圆的切线，这一点和切点之间的线段的长度叫做切线长．

(4)切线长定理：从圆外一点作圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．

【经典例题精讲】

如图，D是⊙O的直径CA延长线上一点，点 B在⊙O上，

且AB＝AD＝AO．

（1）求证：BD是⊙O的切线；

已知：如图，PA，PB，DC分别切⊙O于A，B，E点．

(1)若∠P=40°，求∠COD；

若PA=10cm，求△PCD的周长．

(2)

如图，⊙O内切于△ABC，∠BOC=105°，∠ACB=90°，

（2011丰台二模20题）. 已知：如图，在Rt△ABC中，∠C=90°，点E在斜边AB上，以Array AE为直径的⊙O与BC边相切于点D，联结AD.

（1）求证：AD是∠BAC的平分线；

B

B

（2011石景山二模20题）．已知：如图，ABC AF 为△的角平分线，以BC 为直径的圆与边AB 交于点,D E 点为弧BD 的中点，联结CE 交AB 于H ，AC AH =． （1）求证：AC 与⊙O 相切；

（2）若6=AC ，10=AB ，求EC 的长．

10．圆和圆的位置关系：

11．两圆的性质：

(1)两个圆是一个轴对称图形，对称轴是两圆连心线．

(2)相交两圆的连心线垂直平分公共弦，相切两圆的连心线经过切点．

【经典例题精讲】

已知相交于A、B两点，的半径是10，的半径是17，公共弦AB＝16，求两圆的圆心距．

12．圆中有关计算：

圆的面积公式：，周长C＝2πR．

圆心角为n°、半径为R的弧长．

圆心角为n°，半径为R，弧长为l的扇形的面积．

弓形的面积要转化为扇形和三角形的面积和、差来计算．

圆柱的侧面图是一个矩形，底面半径为R，母线长为l的圆柱的体积为，侧面积为2πRl，全面积为．

圆锥的侧面展开图为扇形，底面半径为R，母线长为l，高为h的圆锥的侧面积为πRl ，全面积为，母线长、圆锥高、底面圆的半径之间有．

【经典例题精讲】

1．若圆锥的底面半径为2cm，母线长为3cm，则它的侧面积为( )．

A．2cm2 B．3cm2 C．6cm2 D．12cm2

2．若圆锥的底面积为16cm2，母线长为12cm，则它的侧面展开图的圆心角为( )．A．240°B．120°C．180°D．90°

3．底面直径为6cm的圆锥的侧面展开图的圆心角为216°，则这个圆锥的高为( )．

A ．5cm

B ．3cm

C ．8cm

D ．4cm

4．若一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图扇形的圆心角为( )． A ．120°

B ．1 80°

C ．240° D. 300°

5.已知：如图，在边长为a 的正△ABC 中，分别以A ，B ，C 点为圆心，a 21长为半径作

，

，

，求阴影部分的面积．

6．已知：如图，Rt △ABC 中，∠C=90°，∠B=30°，,34 BC 以A 点为圆心，AC 长为半径作

，求∠B 与

围成的阴影部分的面积．

三、相关定理： 1.相交弦定理

圆内的两条相交弦，被交点分成的两条线段长的积相等。（经过圆内一点引两条线，各弦被这点所分成的两段的积相等）

说明：几何语言： 若弦AB 、CD 交于点P ，则PA ·PB=PC ·PD （相交弦定理）

例1． 已知P 为⊙O 内一点，，⊙O 半径为

，过P 任作一弦AB ，

设，

，则

关于的函数关系式为 。

例2． 已知PT 切⊙O 于T ，PBA 为割线，交OC 于D ，CT 为直径，若OC=BD=4cm ，AD=3cm ，求PB 长。

四、辅助线总结

1.圆中常见的辅助线

1）．作半径，利用同圆或等圆的半径相等．

2）．作弦心距，利用垂径定理进行证明或计算，或利用“圆心、弧、弦、弦心距”间的关系进行证明．

3）．作半径和弦心距，构造由“半径、半弦和弦心距”组成的直角三角形进行计算．4）．作弦构造同弧或等弧所对的圆周角．

5)．作弦、直径等构造直径所对的圆周角——直角．

6)．遇到切线，作过切点的弦，构造弦切角．

7)．遇到切线，作过切点的半径，构造直角．

8)．欲证直线为圆的切线时，分两种情况：(1)若知道直线和圆有公共点时，常连结公共点和圆心证明直线垂直；(2)不知道直线和圆有公共点时，常过圆心向直线作垂线，证明垂线段的长等于圆的半径．

9)．遇到三角形的外心常连结外心和三角形的各顶点．

10)．遇到三角形的内心，常作：(1)内心到三边的垂线；(2)连结内心和三角形的顶点．

11)．遇相交两圆，常作：(1)公共弦；(2)连心线．

12)．遇两圆相切，常过切点作两圆的公切线．

13)．求公切线时常过小圆圆心向大圆半径作垂线，将公切线平移成直角三角形的一条直角边．

2、圆中较特殊的辅助线

1)．过圆外一点或圆上一点作圆的切线．

2)．将割线、相交弦补充完整．

3)．作辅助圆．

【中考热点】

近年来，在中考中圆的应用方面考查较多，与一元二次方程、函数、三角函数、实际问题、作图等是中考中的热点，也是难点．

三、梳理错题

1有下列结论：（1）平分弦的直径垂直于弦；（2）圆周角的度数等于圆心角的一半；（3）等弧所对的圆周角相等；（4）经过三点一定可以作一个圆；（5）三角形的外心到三边的距离相等；（6）等腰梯形一定有一个外接圆；（7）垂直于半径的直线是圆的切线．其中正确的个数为（）

A、1个

B、2个

C、3个

D、4个

易错点：对弧、弦、圆周角等概念理解不深刻，特别是弦所对的圆周角有两种情况要特别注意，两条弦之间的距离也要考虑两种情况.

2思考下列命题：

（1）等腰三角形一腰上的高线等于腰长的一半，则顶角为75度；

（2）两圆圆心距小于两圆半径之和，则两圆相交；

（3）在反比例函数y=中，如果函数值y＜1时，那么自变量x＞2；

（4）圆的两条不平行弦的垂直平分线的交点一定是圆心；

（5）三角形的重心是三条中线的交点，而且一定在这个三角形三角形的内部；其中正确命题的有几个（）A、1B、2C、3D、4

对垂径定理的理解不够，不会正确添加辅助线运用勾股定理进行解题

2015中考数学分类汇编圆综合题学生版

2015中考数学真题分类汇编圆综合题 一．解答题（共30小题） 1．（2015?大连）如图，AB是⊙O的直径，点C，D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于点E，与AB的延长线相交于点F． （1）求证：EF与⊙O相切； （2）若AB=6，AD=4，求EF的长． 2．（2015?潍坊）如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE． （1）求证：直线DF与⊙O相切； （2）若AE=7，BC=6，求AC的长． 3．（2015?枣庄）如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE． （1）判断DE与⊙O的位置关系，并说明理由； （2）求证：BC2=CD?2OE； （3）若cos∠BAD=，BE=6，求OE的长． 4．（2015?西宁）如图，已知BC为⊙O的直径，BA平分∠FBC交⊙O于点A，D是射线BF上的一点，且满足=，过点O作OM⊥AC于点E，交⊙O于点M，连接BM， AM． （1）求证：AD是⊙O的切线；

（2）若sin∠ABM=，AM=6，求⊙O的半径． 5．（2015?广元）如图，AB是⊙O的弦，D为半径OA的中点，过D作CD⊥OA交弦于点E，交⊙O于点F，且CE=CB． （1）求证：BC是⊙O的切线； （2）连接AF、BF，求∠ABF的度数； （3）如果CD=15，BE=10，sinA=，求⊙O的半径． 6．（2015?北海）如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C． （1）求证：PE是⊙O的切线； （2）求证：ED平分∠BEP； （3）若⊙O的半径为5，CF=2EF，求PD的长． 7．（2015?莆田）如图，在四边形ABCD中，AB=AD，对角线AC，BD交于点E，点O 在线段AE上，⊙O过B，D两点，若OC=5，OB=3，且cos∠BOE=．求证：CB是⊙O的切线．

初中九年级数学《圆的综合应用》适应性训练试卷及解析

《圆的综合应用》适应性训练试卷 1．如图，△ABC内接于⊙O，BD是⊙O的直径，∠A=120°，CD=?2cm，?求扇形BOC的面积． 1题图 2.已知AB是⊙O的直径，C点在⊙O上，F是AC的中点，OF的延长线交⊙O于点D，点E在AB的延长线上， ∠A＝∠BCE． （1）求证：CE是⊙O的切线； （2）若BC＝BE，判定四边形OBCD的形状，并说明理由． 2题图 4

4 3. 如图，AB 为⊙O 的直径，点C 、D 都在⊙O 上，且CD 平分∠ACB ，交AB 于点E ． （1）求证：∠ABD ＝∠BCD ； （2）若DE ＝13，AE ＝17，求⊙O 的半径； （3）DF ⊥AC 于点F ，试探究线段AF 、DF 、BC 之间的数量关系，并说明理由． 3题图 参考答案 1. 解：∵∠A =120°，∴BDC 所对的圆心角=240°， ∴∠BOC = 120 °，∴∠COD =60°， ∵OC=OD ，∴△COD 是等边三角形， ∵CD =2cm ，∴OC=OD =2cm ， ∴S 扇形BOC =2120π24π3603 cm 2 ． 2. （1）证明：∵AB 是⊙O 的直径， ∴∠ACB ＝90°，∴∠ACO +∠BCO ＝90°， ∵OC ＝OA ，∴∠A ＝∠ ACO ， ∴∠A +∠BCO ＝90°，

∵∠A＝∠BCE，∴∠BCE+∠BCO＝90°， ∴∠OCE＝90°，∴CE是⊙O的切线； （2）解：四边形OBCD是菱形， 理由：∵BC＝BE，∴∠E＝∠ECB， ∵∠BCO+∠BCE＝∠COB+∠E＝90°， ∴∠BCO＝∠BOC，∴BC＝OB， ∴△BCO是等边三角形，∴∠AOC＝120°， ∵F是AC的中点，∴AF＝CF， ∵OA＝OC，∴∠AOD＝∠COD＝60°， ∵OD＝OC，∴△COD是等边三角形， ∴CD＝OD＝OB＝BC， ∴四边形OBCD是菱形． 3. （1）证明：∵CD平分∠ACB， ∴∠ACD＝∠BCD， ∵∠ACD＝∠ABD，∴∠ABD＝∠BCD； （2）解：如图1，过点E作EM⊥AD于点M， ∵AB为⊙O的直径，∴∠ACB＝90°，∠ADB＝90°，∴∠DAB＝∠BCD＝45°， 4

中考数学专题复习圆的综合的综合题

一、圆的综合真题与模拟题分类汇编（难题易错题） 1．如图，点P在⊙O的直径AB的延长线上，PC为⊙O的切线，点C为切点，连接AC，过点A作PC的垂线，点D为垂足，AD交⊙O于点E． (1)如图1，求证：∠DAC=∠PAC； (2)如图2，点F（与点C位于直径AB两侧）在⊙O上，BF FA =，连接EF，过点F作AD 的平行线交PC于点G，求证：FG=DE+DG； (3)在(2)的条件下，如图3，若AE=2 3 DG，PO=5，求EF的长． 【答案】（1）证明见解析；（2）证明见解析；（3）EF=32． 【解析】 【分析】 （1）连接OC，求出OC∥AD，求出OC⊥PC，根据切线的判定推出即可； （2）连接BE交GF于H，连接OH，求出四边形HGDE是矩形，求出DE=HG，FH=EH，即可得出答案； （3）设OC交HE于M，连接OE、OF，求出∠FHO=∠EHO=45°，根据矩形的性质得出 EH∥DG，求出OM=1 2 AE，设OM=a，则HM=a，AE=2a，AE= 2 3 DG，DG=3a， 求出ME=CD=2a，BM=2a，解直角三角形得出tan∠MBO＝ 1 2 MO BM =，tanP= 1 2 CO PO =,设 OC=k，则PC=2k，根据OP=5k=5求出k=5，根据勾股定理求出a，即可求出答案．【详解】 （1）证明：连接OC， ∵PC为⊙O的切线，

∴OC⊥PC， ∵AD⊥PC， ∴OC∥AD， ∴∠OCA=∠DAC， ∵OC=OA， ∴∠PAC=∠OCA， ∴∠DAC=∠PAC； （2）证明：连接BE交GF于H，连接OH， ∵FG∥AD， ∴∠FGD+∠D=180°， ∵∠D=90°， ∴∠FGD=90°， ∵AB为⊙O的直径， ∴∠BEA=90°， ∴∠BED=90°， ∴∠D=∠HGD=∠BED=90°， ∴四边形HGDE是矩形， ∴DE=GH，DG=HE，∠GHE=90°， ∵BF AF =， ∴∠HEF=∠FEA=1 2 ∠BEA=190 2 o ?=45°， ∴∠HFE=90°﹣∠HEF=45°， ∴∠HEF=∠HFE， ∴FH=EH， ∴FG=FH+GH=DE+DG； （3）解：设OC交HE于M，连接OE、OF， ∵EH=HF，OE=OF，HO=HO， ∴△FHO≌△EHO， ∴∠FHO=∠EHO=45°，

中考数学专题：圆.(学生版)

中考数学试题专题复习：圆 【学生版】 一、选择题 1. （天津3分）已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是 (A) 相交 (B) 相离 (C) 内切 (D) 外切 2.（内蒙古包头3分）已知两圆的直径分别是2厘米与4厘米，圆心距是3厘米，则这两个圆的位置关系是 A 、相交 B 、外切 C 、外离 D 、内含 3,（内蒙古包头3分）已知AB 是⊙O 的直径，点P 是AB 延长线上的一个动点， 过P 作⊙O 的切线，切点为C ，∠APC 的平分线交AC 于点D ，则∠CDP 等于 A 、30° B 、60° C 、45° D 、50° 4.（内蒙古呼和浩特3分）如图所示，四边形ABCD 中，DC∥AB，BC=1， AB=AC=AD=2．则BD 的长为 A. 14 B. 15 C. 32 D. 23 5.（内蒙古呼伦贝尔3分）⊙O 1的半径是cm 2，⊙2的半径是cm 5，圆心距是cm 4，则两圆的位置关系为 A. 相交 B. 外切 C.外离 D. 内切 6.（内蒙古呼伦贝尔3分）如图，⊙O 的半径为5，弦AB 的长为8，M 是弦AB 上的动点, 则线段OM 长的最小值为. A. 5 B. 4 C. .3 D. 2 7.（内蒙古呼伦贝尔3分）如图，AB 是⊙O 的直径，点C 、D 在⊙O 上 ，∠BOD=110°， AC∥OD，则∠AOC 的度数 A. 70° B. 60° C. 50° D. 40° 8.（内蒙古乌兰察布3分）如图， AB 为 ⊙ O 的直径， CD 为弦， AB ⊥ CD ， 如果∠BOC = 700 ，那么∠A 的度数为 A 70 0 B. 350 C. 300 D . 200 17．填空题 1.（天津3分）如图，AD ，AC 分别是⊙O 的直径和弦．且∠CAD=30°．OB⊥AD，交AC 于点B ．若OB=5，则BC 的长等于 ▲ 。

圆的知识综合应用A

一、填空题： 1.圆是（ ）图形，它有（ ）条对称轴。（ ）确定圆的位置，（ ）确定圆的大小。 2.圆周长和直径的比值叫做（ ），用字母（ ）表示，它是一个（ ）小数。 3.甲圆的半径是乙圆的直径，甲圆和乙圆的直径比是（ ），乙圆的面积是甲圆的（ ）。 4.如果要画一个周长是37.68厘米的圆，那么圆规两脚间的距离是（ ）。 5.在一个边长是6厘米的正方形内画一个最大的圆，这个圆的周长是（ ）厘米。 6.在一个长8厘米，宽4厘米的长方形内画一个最大的圆，这个圆的面积是（ ）平方厘米。 7.如果圆的半径扩大a 倍，则圆的直径扩大（ ）倍，周长扩大（ ）倍，面积扩大（ ）倍。 8.两个圆的直径比是2:5，这两个圆的周长比是（ ），面积比是（ ）。 9.小圆的直径是大圆的12 ，则大圆的周长是小圆的（ ）倍，小圆的面积是大圆的（ ）。 10.一个圆的半径是6厘米，这个圆内的最大正方形的面积是（ ）平方厘米。 二、综合应用： 1.地球赤道的半径约是0.64万千米，绕赤道5周大约有多少万千米？ 2.一辆自行车的轮胎的外直径是1.2米，每分钟转30周，这辆自行车每分钟行驶多少米？ 3.一个挂钟的分针长20厘米，这个挂钟的分针转动1小时后，它扫过的面积是多少？ 4.一棵大树横截面的周长约是3.14米，这棵大树的横截面的面积是多少平方米？ 5.一个圆形花圃的直径是12米，花圃的外面筑了一条宽4米的环形小路，这条小路的面积是多少？ 6. 一辆自行车轮胎的外直径约是60厘米，若每分钟转200圈，通过一座长2000米的桥，大约需要多 少分钟？（得数保留整数） 六上数学练习题——圆的知识

圆中综合题复习专题

圆中综合题复习专题 第一组 1.若集合A ＝{(x ，y)|x 2＋y 2≤16}，B ＝{(x ，y)|x 2＋(y －2)2≤a －1}且A ∩B ＝B ，则a 的取值范围是________． 解：由题意知B ?A.当a<1时，B ＝?，满足题意；当a ＝1时，B ＝{(0，2)}，满足题意；当a>1时，则集合A ，B 分别表示圆面x 2＋y 2≤16与圆面x 2＋(y －2)2 ≤a －1，由题意得B 内含于A ，从而4－a －1≥2，解得a ≤5.综上，a ≤5. 2.已知两点A (1,2)，B (5,5)到直线l 的距离分别是3和2，则满足条件的直线共有_____条. 解以A (1,2)为圆心，3为半径的圆A ：(x －1)2＋(y －2)2＝9，以B (5,5)为圆心，2为半径的圆B ：(x －5) 2＋(y －5)2＝4，根据题意所要满足的条件，则l 是圆A 与圆B 的公切线，因为A (1,2)，B (5,5)两点间的距离d ＝5，即d ＝r 1＋r 2，所以圆A 与圆B 相外切，所以有3条公切线. 3.过点(3，1)作圆()1122=+-y x 的两条切线，切点分别为A ，B ，则直线AB 的方程为________． 解：点P (3，1)与圆心C (1，0)PA 2,则以P (3，1)为圆心，以2为半径的圆P 方程为(x －3)2＋(y －1)2 ＝4,则两圆的交点即为A ，B ，两圆相减可得AB 的方程为2x ＋y －3＝0． 4.在平面直角坐标系xOy 中，已知圆1C ： ()()22481x y -+-=，圆2C ：()()22 669x y -++=．若圆心在x 轴上的圆C 同时平分圆1C 和圆2C 的圆周，则圆C 的方程是_______________________． 解：由题意，圆C 与圆C 1和圆C 2的公共弦分别为圆C 1和圆C 2的直径，设C (a ，0），则(a ﹣4)2+(0﹣8)2+1=(a ﹣6)2+(0+6)2+9，∴a =0，∴圆C 的方程是x 2+y 2=81． 5.圆x 2＋y 2＝1与圆(x ＋4)2＋(y －a )2＝25相切，则实数a 的值为________． 15+，解得a =± 51=-，得0a =.综上 a =±0． 6.在平面直角坐标系xOy 中，若与点A(2，2)的距离为1且与点B(m ，0)的距离为3的直线恰有两条，则实数m 的取值范围是________． 解:由题意知以A(2，2)为圆心，1为半径的圆与以B(m ，0)为圆心，3为半径的圆相交，所以4<(m －2)2＋ 4<16，所以－23＋2

圆轨迹的综合运用

2017 年青年教师赛课教案 张堃 【上课课题】 点的运动路径与相关最值问题 【授课班级】 初三1班 【教材分析】 本节课综合了初二相似与初三圆的内容，介绍了三种产生特殊直线的构造方法与2种产生圆的构造方法.在中考处于A卷20题、B卷填空题、与B卷28题的位置. 【学情分析】 在近段时间周练与周测陆续出现了一些涉及到动点的最值问题，孩子没有形成对点的运动路径进行研究的意识，对常见的描述运动路径的方式不熟悉，在老师的指导下解决了一些问题，但没有系统的进行归纳.没有先画图猜想，再进行证明的意识.学习有畏难情绪，需要引导孩子找到分析问题的方式，并能独立解决相关问题，增强自信. 【教学目标】 1.理解3种构造直线的方式，与2种构造圆的方式； 2.能从具体问题识别路径的构造方式，从运动路径直观理解如何取到最值； 3.引导学生独立解决问题，增强信心. 【1+X 问题群设置】 1.主问题 如何确定点的运动路径？ 2.问题群（任务群） 设问1：已知△ADC，若△BCD的面积与△ADC的面积相等.那么 满足条件的B点的运动路径是什么？ 追问：实质是什么？ 设问2：在不知道的情况下，如何猜想路径（引导作图） 设问3：A为直线外一定点，B为直线上一动点，当B在直线上沿一方 向运动到C点时.AB中点M运动的路径为什么图形？ 追问：为什么？ 设问4：考试时遇到复杂图形常不能直观观察得到点运动的路径，此 时可以通过什么方式去猜想？

设问5：若一点定点A 到线段BC 两端点距离AB=AC ，则点A 的运动路径是什么？ 设问6：D 定Q 动，若求DQ 最小值，我们需研究什么？ 追问：对于PB 两个定点，我们发现QP=QB ，那么Q 点的运动路径是什么？ 设问7：线段BC 上所有的点是否都绕圆心O 旋转？ 画图后追问：所有的这些圆共同组成了一个什么图形？ 追问：若要确定这个圆，我们只需找到什么就可以了？ 设问8：若圆外有一定点P 到BC 线段上一点H 的最大距离与最小距离怎么求？（强调研究动点轨迹在最值问题重的作用） 设问9：H 是定点，G 是动点，按照前面的经验，我们只需要研究G 点运动的什么就可以了？ 设问10：在折叠过程中有那些相等的线段？ 追问：M 是定点，QM=AM ，说明什么？ 设问11：一定能把C 点折到我想要的位置吗？ 追问：为什么？ 【教学过程】 教学环节 教学内容 教师活动 学生活动 信息技术运用 引入 课题 介绍本节 课主题 介绍课题在中考中的地位，明确本节课将总常见的结产生轨迹的方式 明确本节课的目的，进入学习状态 知识 讲解 请学生讲 解基本模 型1，并介绍在例题1种的应用. 请学生直接讲轨迹，及原理 设问1：已知△ADC ，若△BCD 的面积与△ADC 的面积相等.那么满足条件的B 先听学生讲解 几何画板展示作图及运动过程

中考数学综合题专题复习【圆】专题解析

中考数学综合题专题复习【圆】专题解析 一．教学内容: １．圆的内容包括:圆的有关概念和基本性质,直线和圆的位置关系，圆和圆的位置关系，正多边形和圆。 2. 主要定理: (1)垂径定理及其推论。 (２）圆心角、弧、弦、弦心距之间的关系定理。 (3)圆周角定理、弦切角定理及其推论。 （4)圆内接四边形的性质定理及其推论。 （5）切线的性质及判定。 （6)切线长定理。 (7)相交弦、切割线、割线定理。 (8)两圆连心线的性质，两圆的公切线性质。 (9）圆周长、弧长；圆、扇形，弓形面积。 （10）圆柱、圆锥侧面展开图及面积计算。 (11)正n边形的有关计算。 二. 中考聚焦: 圆这一章知识在中考试题中所占的分数比例大约如下表： 圆的知识在中考中所占的比例大,题型多，常见的有填空题、选择题、计算题或证明题，近年还出现了一些圆的应用题及开放型问题、设计型问题,中考的压轴题都综合了圆的知识。 三. 知识框图： 圆 圆的有关性质 直线和圆的位置关系圆和圆的位置关系正多边形和圆 ? ? ? ? ? ? ?

圆的有关性质 圆的定义 点和圆的位置关系（这是重点） 不在同一直线上的三点确定一个圆 圆的有关性质 轴对称性—垂径定理（这是重点） 旋转不变性 圆心角、弧、弦、弦心距间的关系 圆心角定理 圆周角定理（这是重点） 圆内接四边形（这是重点） ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 直线和圆的位置关系 相离 相交 相切 切线的性质（这是重点） 切线的判定（这是重点） 弦切角（这是重点） 和圆有关的比例线段（这是重点难点） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圆和圆的位置关系 外离 内含 相交 相切 内切（这是重点） 外切（这是重点）两圆的公切线 ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? 正多边形和圆 正多边形和圆 正多边形定义 正多边形和圆 正多边形的判定及性质 正多边形的有关计算（这是重点）圆的有关计算 圆周长、弧长（这是重点） 圆、扇形、弓形面积（这是重点） 圆柱、圆锥侧面展开图（这是重点） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 【典型例题】 【例1】. 爆破时,导火索燃烧的速度是每秒0.9cm，点导火索的人需要跑到离爆破点１２０m以外的安全区域。这个导火索的长度为１8cm,那么点导火索的人每秒钟跑6.5m是否安全? 分析:爆破时的安全区域是以爆破点为圆心,以1２０m为半径的圆的外部，如图所示:

圆的方程练习题(学生版)

圆的方程练习题（学生版） 1．求过点()()1,1,1,1A B --，且圆心在直线20x y +-=上的圆的方程. 2．若圆过A （2，0），B （4，0），C （0，2）三点，求这个圆的方程． 3．已知圆经过()()2,5,2,1-两点，并且圆心在直线1 2 y x =上。 (1)求圆的方程； (2)求圆上的点到直线34230x y -+=的最小距离。 4．已知圆C 同时满足下列三个条件：①与y 轴相切；②在直线y x =上截得弦长为③圆心在直线30x y -=上.求圆C 的方程. 5．求圆心在直线3x+y-5=0上，并且经过原点和点（4，0）的圆的方程 6．求圆心为（1，1）并且与直线4=+y x 相切的圆的方程。

7．求与圆x 2+y 2?2x =0外切且与直线x + 3y =0相切于点M (3,? 3)的圆的方程. 8．求圆心在直线 40x y --=上，并且过圆22640x y x ++-=与圆 226280x y y ++-=的交点的圆的方程. 9．已知圆心为C 的圆经过三个点O (0,0)、A (?2,4)、B (1,1)． (1)求圆C 的方程； (2)若直线l 的斜率为?4 3，在y 轴上的截距为?1，且与圆C 相交于P 、Q 两点，求△O P Q 的面积． 10．已知圆C ：x 2+y 2+10x+10y+34=0。 （I ）试写出圆C 的圆心坐标和半径； （II ）若圆D 的圆心在直线x=-5上，且与圆C 相外切，被x 轴截得的弦长为10，求圆D 的方程。 11．已知圆C 的圆心在直线y =1 2x 上，且过圆C 上一点M (1,3)的切线方程为y =3x . （Ⅰ）求圆C 的方程； （Ⅱ）设过点M 的直线l 与圆交于另一点N ，以M N 为直径的圆过原点，求直线l 的方程.

中考数学专题复习 圆的综合应用(原卷版+解析)

专题10 圆的综合运用 一选择题 1.（南通市崇川区启秀中学一模）一个圆锥的侧面展开图形是半径为8cm，圆心角为120°的扇形，则此 圆锥的底面半径为() A. 8 3cm B. 16 3 cm C. 3cm D. 4 3 cm 2.(无锡市四校联考一模)如图，AB是⊙O的直径，DB、DE别切⊙O于 点B、C，若∠ACE=25°，则∠D的度数是() A. 50° B. 55° C. 60° D. 65° 3.(绍兴市一模)如图，AB为⊙O的切线，切点为A．连结AO，BO，BO与⊙O交于点C，延长BO与⊙O 交于点D，连结AD．若∠ABC＝36°，则∠ADC的度数为（） A．27°B．32°C．36° D．54° 4.（唐山市遵化市一模）如图，一个边长为4cm的等边三角形ABC的高 与⊙O的直径相等．⊙O与BC相切于点C，与AC相交于点E，则CE 的长为() A. 4cm B. 3cm C. 2cm D. 1.5cm 5.（广东省北江实验学校一模）如图，AB是⊙O的直径，且经过弦CD的中点H， 已知cos∠CDB＝4 5 ，BD＝5，则OH的长度为( ) A.2 3B.5 6 C.1 D.7 6

6.(上海市杨浦区一模)如图，AB 是⊙O 的直径，点C 和点D 是⊙O 上位于直径AB 两侧的点，连接AC ，AD ，BD ，CD ，若⊙O 的半径是13，BD ＝24，则sin ∠ACD 的值是（ ） A ． B ． C ． D ． 7. （合肥168中一模）如图，以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点，交直角边AC 于点E ，B 、E 是半圆弧的三等分点，弧BE 的长为2 3π，则图中阴影部分的面积为( ) A. π 9 B. √3π9 C. 3√32 ?3π2 D. 3√32 ?2π3 8.(无锡市四校联考一模)已知直线y =?x +7a +1与直线y =2x ?2a +4同时经过点P ，点Q 是以M(0,?1)为圆心，MO 为半径的圆上的一个动点，则线段PQ 的最小值为( ) A. 10 3 B. 16 3 C. 8 5 D. 185 二 填空题 9.(无锡市四校联考一模)圆锥的底面半径为14cm ，母线长为21cm ，则该圆锥的侧面展开图的圆心角为______度． 10.(绍兴市一模)如图所示，在Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8，若以点C 为圆心，r 为半径的圆与边AB 所在直线有公共点，则r 的取值范围为 ． 11.（合肥市天鹅湖教育集团一模）如图，在Rt ABC ?中，90ACB ∠=?，3BC =，2AB =，以点A 为圆心，以AC 为半径画弧，交AB 于D ，则扇形CAD 的周长是_____________（结果保留π）．

2019中考真题圆综合题

1.（2019江苏扬州）（本题满分10分）如图，AB 是⊙O 的弦，过点O 作OC ⊥OA ，OC 交于AB 于P ，且CP=CB 。 （1）求证：BC 是⊙O 的切线； （2）已知∠BAO=25°，点Q 是弧A m B 上的一点。 ①求∠AQB 的度数； ②若OA=18，求弧A m B 的长。 【考点】：直线与圆的位置关系，扇形的弧长，圆心角于圆周角关系， 等腰三角形 【解析】： 解（1）连接OB ∵CP=CB ∴∠CPB=∠CBP ∵OA ⊥OC ∴∠AOC=90° ∵OA=OB ∴∠OAB=∠OBA ∵∠PAO+∠APO=90° ∴∠ABO+∠CBP=90° ∴∠OBC=90° ∴BC 是⊙O 的切线 （2）①∵∠BAO=25° OA=OB ∴∠BAO=∠OBA=25° ∴∠AOB=130°∴∠AQB=65° ②∵∠AOB=130° OB=18 ∴l 弧AmB=（360°-130°）π×18÷180=23π 2.（江苏泰州）如图，四边形ABCD 内接于⊙O ，AC 为⊙O 的直径，D 为弧AC 的中点，过点D 作DE ∥AC ,交BC 的延长线于点E. （1）判断DE 与⊙O 的位置关系，并说明理由； （2）若⊙O 的半径为5，AB=8，求CE 的长.

3.（2019山东济宁）（8分）如图，AB是⊙O的直径，C是⊙O上一点，D是的中点，E 为OD延长线上一点，且∠CAE＝2∠C，AC与BD交于点H，与OE交于点F． （1）求证：AE是⊙O的切线； （2）若DH＝9，tan C＝，求直径AB的长． 【分析】（1）根据垂径定理得到OE⊥AC，求得∠AFE＝90°，求得∠EAO＝90°，于是得到结论； （2）根据等腰三角形的性质和圆周角定理得到∠ODB＝∠C，求得tan C＝tan∠ODB＝＝，设HF＝3x，DF＝4x，根据勾股定理得到DF＝，HF＝，根据相似三角形的性质得到CF＝＝，求得AF＝CF＝，设OA＝OD＝x，根据勾股定理即可得到结论． 【解答】解：（1）∵D是的中点， ∴OE⊥AC， ∴∠AFE＝90°， ∴∠E+∠EAF＝90°， ∵∠AOE＝2∠C，∠CAE＝2∠C， ∴∠CAE＝∠AOE， ∴∠E+∠AOE＝90°， ∴∠EAO＝90°， ∴AE是⊙O的切线； （2）∵∠C＝∠B， ∵OD＝OB，

(完整版)2017中考数学圆的综合题试题

圆的综合题 1. 如图，AB 是⊙O 的弦，AB ＝4，过圆心O 的直线垂直AB 于点D ，交⊙O 于点C 和点E ，连接AC 、BC 、OB ，cos ∠ACB ＝1 3 ，延长OE 到点F ，使EF ＝2OE . (1)求证：∠BOE ＝∠ACB ; (2)求⊙O 的半径； (3)求证：BF 是⊙O 的切线． 2. 如图，AB 为⊙O 的直径，点C 为圆外一点，连接AC 、 BC ，分别与⊙O 相交于 点D 、点E ，且? ?AD DE ，过点D 作DF ⊥BC 于点F ，连接BD 、DE 、AE . (1)求证：DF 是⊙O 的切线； (2)试判断△DEC 的形状，并说明理由； (3)若⊙O 的半径为5，AC ＝12，求sin ∠EAB 的值． 3. (2016长沙9分)如图，四边形ABCD 内接于⊙O ，对角线AC 为⊙O

的直径，过点C作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF. (1)求∠CDE的度数； (2)求证：DF是⊙O的切线； (3)若AC＝25DE，求tan∠ABD的值． 4. (2016德州10分)如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC 于点D，过点E作直线l∥BC. (1)判断直线l与⊙O的位置关系，并说明理由； (2)若∠ABC的平分线BF交AD于点F，求证：BE＝EF; (3)在(2)的条件下，若DE＝4，DF＝3，求AF的长． 5. (2015永州)如图，已知△ABC内接于⊙O，且AB＝AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD.

(1)求证：BE ＝CE ； (2)试判断四边形BFCD 的形状，并说明理由； (3)若BC ＝8，AD ＝10，求CD 的长． 6 (2017 原创)如图，AB 切⊙O 于点B ，AD 交⊙O 于点C 和点D ，点E 为 ?DC 的中点，连接OE 交CD 于点F ，连接BE 交CD 于点G . (1) 求证：AB ＝AG ； (2) (2)若DG ＝DE ，求证：GB 2 ＝GC ·GA ； (3)在(2)的条件下，若tan D ＝3 4 ，EG ＝10，求⊙O 的半径． 7.(2015达州)在△ABC 的外接圆⊙O 中，△ABC 的外角平 分线CD 交⊙O 于点D ，F 为? AD 上一点，且??AF BC ，连接DF ，并延长DF 交BA 的延

圆的综合练习题及答案

圆的综合练习题答案 1.如图，已知AB 为⊙O 的弦，C 为⊙O 上一点，∠C =∠BAD ，且BD ⊥AB 于B . （1）求证：AD 是⊙O 的切线； （2）若⊙O 的半径为3，AB =4，求AD 的长. （1）证明: 如图, 连接AO 并延长交⊙O 于点E , 连接BE , 则∠ABE =90°. ∴ ∠EAB +∠E =90°. ……………………1分 ∵ ∠E =∠C , ∠C =∠BAD ， ∴ ∠EAB +∠BAD =90°. ∴ AD 是⊙O 的切线. ……………………2分 （2）解：由（1）可知∠ABE =90°. ∵ AE =2AO =6, AB =4, ∴ 5222=-= AB AE BE . …………………………………………………3分 ∵ ∠E=∠C =∠BAD , BD ⊥AB , ∴ .cos cos E BAD ∠=∠ …………………………………………………4分 ∴ .AE BE AD AB = .6 524=AD 即 ∴ 5 5 12= AD . …………………………………………………5分 2.已知：在⊙O 中，AB 是直径，AC 是弦，OE ⊥AC 于点E ，过点C 作直线FC ，使∠FCA ＝∠AOE ，交 AB 的延长线于点D. （1）求证：FD 是⊙O 的切线； （2）设OC 与BE 相交于点G ，若OG ＝2，求⊙O 半径的长； 证明：（1）连接OC （如图①）， ∵OA ＝OC ，∴∠1＝∠A. ∵OE ⊥AC ，∴∠A ＋∠AOE ＝90°. ∴∠1＋∠AOE ＝90°. 又∠FCA ＝∠AOE ， 图① ∴∠1＋∠FCA ＝90°. 即∠OCF ＝90°. ∴FD 是⊙O 的切线. ……………………………………………………2分 （2）连接BC （如图②）， ∵OE ⊥AC ，∴AE ＝EC. 又AO ＝OB ， ∴OE ∥BC 且BC OE 2 1 = .……………3分 ∴△OEG ∽△CBG. 图②

2020-2021中考数学专题复习分类练习 圆的综合综合解答题附答案解析

2020-2021中考数学专题复习分类练习 圆的综合综合解答题附答案解析 一、圆的综合 1．如图，△ABC 是⊙O 的内接三角形，点D 在BC uuu r 上，点E 在弦AB 上（E 不与A 重 合），且四边形BDCE 为菱形． （1）求证：AC=CE ； （2）求证：BC 2﹣AC 2=AB?AC ； （3）已知⊙O 的半径为3． ①若AB AC =5 3 ，求BC 的长； ②当 AB AC 为何值时，AB?AC 的值最大？ 【答案】（1）证明见解析；（2）证明见解析；（3）2；②32 【解析】 分析：（1）由菱形知∠D=∠BEC ，由∠A+∠D=∠BEC+∠AEC=180°可得∠A=∠AEC ，据此得证； （2）以点C 为圆心，CE 长为半径作⊙C ，与BC 交于点F ，于BC 延长线交于点G ，则CF=CG=AC=CE=CD ，证△BEF ∽△BGA 得BE BG BF BA =，即BF?BG=BE?AB ，将BF=BC-CF=BC-AC 、BG=BC+CG=BC+AC 代入可得； （3）①设AB=5k 、AC=3k ，由BC 2-AC 2=AB?AC 知6k ，连接ED 交BC 于点M ，Rt △DMC 中由DC=AC=3k 、MC= 1 2 6k 求得22CD CM -3，可知OM=OD-3，在Rt △COM 中，由OM 2+MC 2=OC 2可得答案．②设OM=d ，则MD=3-d ，MC 2=OC 2-OM 2=9-d 2，继而知BC 2=（2MC ）2=36-4d 2、AC 2=DC 2=DM 2+CM 2=（3-d ）2+9-d 2，由（2）得AB?AC=BC 2-AC 2，据此得出关于d 的二次函数，利用二次函数的性质可得答案． 详解：（1）∵四边形EBDC 为菱形， ∴∠D=∠BEC ， ∵四边形ABDC 是圆的内接四边形， ∴∠A+∠D=180°， 又∠BEC+∠AEC=180°， ∴∠A=∠AEC ，

相似三角形与圆的综合应用

个性化辅导讲义

1在厶ABC 中,AB = AC, / A = 36° , / ABC 的平分线 BD 与AC 交于D,求证: 知识概括、方法总结与易错点分析 相似三 角形的概念与判定 （一） 定义：对应角相等，对应边成比例的两个三角形叫相似三角形。 相似三角形的对应边的比叫做相似比（也叫相似系数）。 （二） 判定： ① 平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形 相似。 ② 两边对应成比例且夹角相等的两个三角形相似。 ③ 有两个角对应相等的两个三角形相似。 ④ 三条边对应成比例的两个三角形相似。 ⑤ 一条直角边和斜边对应成比例的两个直角三角形相似。 ⑥ 直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似。 相似三角形的性质 2.两个相似三角形对应中线之比是 3:7，周长之和为30cm,贝陀们的周长分别是 AB BC 3 ?如图，已知AD = DE AC 求证：△ ABM A ACE 4. 在 Rt △ ABC 中，/ ACB=90 , CD! AB 于 D,贝U BD ： AD 等于( (A ) a : b (B ) a 2 : b 2 (C ) a ： . b ( D )不能确定 5. 如图，在△ ABC 中，/ ACB= 90°, CD! AB 于 D, DEI AC 于 E , DE = 1 求BC 的值。 (1) BC = BD (2)

1. 相似比：相似三角形对应边的比值 2. 相似三角形各组对应角相等 3. 相似三角形各组对应边的比值相等 4. 相似三角形对应高线的比，对应中线的比和对应角平分线的比都等于相似比 5. 相似三角形周长的比等于相似比 6. 相似三角形面积的比等于相似比的平方 7. 直角三角形中，斜边上的高线是两条直角边在斜边上的射影的比例中项 针对性练习 1 .两个相似三角形的对应角平分线的长分别为10cm和20cm,若它们的周长的差是60cm,则较大的三角形的周长是--—--，若它们的面积之和为260cnf,则较小的三角形的面积为--—-- cm2 2. 如图，PLMh为矩形，AD丄BC于D, PL : LM=5： 9,且BC=36cm AD=12cm 求矩形PLMlN勺周长 A 3. 如图，在Rt△ ABD中，/ ADB=90 ,CD丄AB于C, AC=20cm,BC=9cm求AB及BD的长 B

圆的综合练习题及答案完整版

圆的综合练习题及答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】

圆的综合练习题答案 1.如图，已知AB 为⊙O 的弦，C 为⊙O 上一点，∠C =∠BAD ，且BD ⊥AB 于B . （1）求证：AD 是⊙O 的切线； （2）若⊙O 的半径为3，AB =4，求AD 的长. （1）证明: 如图, 连接AO 并延长交⊙O 于点E , 连接BE , 则∠ABE =90°. ∴ ∠EAB +∠E =90°. …………………… ∵ ∠E =∠C , ∠C =∠BAD ， ∴ ∠EAB +∠BAD =90°. ∴ AD 是⊙O 的切线. ……………………（2）解：由（1）可知∠ABE =90°. ∵ AE =2AO =6, AB =4, ∴ 5222=-=AB AE BE . …………………………………………………3分 ∵ ∠E=∠C =∠BAD , BD ⊥AB , ∴ .cos cos E BAD ∠=∠ …………………………………………………4分 ∴ . AE BE AD AB = ∴ 5 512=AD . …………………………………………………5分 2.已知：在⊙O 中，AB 是直径，AC 是弦，OE⊥AC 于点E ，过点C 作直线FC ，使∠FCA＝∠AOE，交 AB 的延长线于点D. （1）求证：FD 是⊙O 的切线； （2）设OC 与BE 相交于点G ，若OG ＝2，求⊙O 半径的长； 证明：（1）连接OC （如图①）， ∵O A ＝OC ，∴∠1＝∠A. ∵OE ⊥AC ，∴∠A ＋∠AOE ＝90°. ∴∠1＋∠AOE ＝90°. 又∠FCA ＝∠AOE ， 图① ∴∠1＋∠FCA ＝90°. 即∠OCF ＝90°. ∴FD 是⊙O 的切线. (2) 分 （2）连接BC （如图②）， ∵OE ⊥AC ，∴AE ＝EC. 又AO ＝OB ， ∴OE ∥B C 且BC OE 2 1 = (3)

圆的综合运用

圆的综合 （一）、知识要点 1、所给条件为特殊角或者普通角的三角函数时； (1)特殊角问题或者锐角三角函数问题，必须有直角三角形才行，如果题目条件中给的特殊角并没有放入直角三角形中时，需要构造直角三角形。 构造圆中的直角三角形，主要有以下四种类型： ①利用垂径定理； ②直接作垂线构造直角三角形； 半径相等圆周角=圆周角圆心角=2圆周角 弦切角=圆周角 射影定理模型 综合利用各种方法 2、所给条件为线段长度、或者线段的倍分关系时； (1)因为圆中能产生很多直角三角形，所以可以考虑利用勾股定理来计算线段长度，在利用勾股定理来

计算线段长度时，特别是在求半径时，经常会利用半径来表示其他线段的长度，常见情形如下； (2)圆中能产生很多相似三角形，所以经常也会利用相似三角形对应边成比例来计算线段长度，常见的圆中相似情形如下： △ADE ∽△ACB E D C B A △ADE ∽△BCE E D C B A △ABD ∽△CAD ∽△ CBA △ABC ∽△ADB ∽△BDC A △ABO ∽△ADB ∽△BDO △ABC ∽△OBD 二、典型例题 能力提升类 例1 如图，⊙O 的直径AB 与弦EF 相交于点P ，交角为45°，若2 2 8PE PF +=，求直径AB 。

评析：解答此题需注意应用数形结合的思想，熟练运用勾股定理和完全平方公式。 例2如图，正方形ABCD内接于⊙O，点P在劣弧AB上，连结DP，交AC于点Q．若QP QO ， 求QC QA 的值。 评析：本题考查了相交弦定理，即“圆内两弦相交于圆内一点，各弦被该点所分得的两线段的长的乘积相等”。熟记并灵活应用定理是解答本题的关键。 综合运用类 例3如图，已知直径与等边三角形ABC的高相等的圆与三角形的AB边和BC边相切于点D和E，与AC边相交于点F和G，求∠DEF的度数。 例4已知△ABC中，∠ACB＝90°，AB边上的高线CH与△ABC的两条内角平分线AM、BN 分别交于P、Q两点，PM、QN的中点分别为E、F。 求证：EF∥AB

(完整版)2017年中考真题圆综合大题

2017 年圆综合大题 8.（2011年苏州市?第26题8分）如图，已知AB 是⊙ O的弦，OB＝2，∠B＝30°，C是弦AB 上的任意一点（不与点 A 、B重合），连接CO并延长CO交于⊙ O于点D，连接AD．（1）弦长AB 等于▲ （结果保留根号）； （2）当∠ D＝20°时，求∠ BOD 的度数； （3）当AC 的长度为多少时，以 A 、C、D 为顶点的三角形与以B、C、O 为顶点的三角形相似？请写出解答过程． 9．（2012年苏州市第27题满分8分）如图，已知半径为2的⊙O与直线l相切于点A，点P 是直径AB左侧半圆上的动点，过点P作直线l 的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC 的长为x（2

11．（2014?苏州第27题8分）如图，已知⊙ O上依次有A、B、C、D四个点，= ，连 接AB、AD、BD，弦AB不经过圆心O，延长AB到E，使BE=AB，连接EC，F是EC的中点，连接BF ． （1）若⊙ O 的半径为3，∠ DAB =120°，求劣弧的长； 2）求证：BD； （3）设G 是BD 的中点，探索：在⊙ O 上是否存在点P（不同于点B），使得PG=PF ？并说明PB 与AE 的位置关系．江南汇教育网 12．（2015年苏州第26题满分10分）如图，已知AD 是△ABC的角平分线，△O经过A、B、D三点，过点B作BE△AD，交△O于点E，连接ED． （1）求证：ED△AC； 2 （2）若BD=2CD，设△EBD 的面积为S1，△ADC 的面积为S2，且S1216S2 4 0，求△ABC 的面积． 13．（2016年苏州第26 题10 分）如图，AB 是△O 的直径，D、E 为△O 上位于AB 异侧的两点，连接BD 并延长至点C，使得CD=BD，连接AC 交△O 于点F，连接AE 、DE 、DF ． （1）证明：△E= △C； （2）若△E=55 °，求△BDF 的度数； （3）设DE 交AB 于点G，若DF =4，cosB = ，E 是的中点，求EG?ED 的值．

中考专题复习圆的综合题(含答案)

中考专题复习圆的综合题 1．如图，△ABC 中，以BC 为直径的圆交AB 于点D ，∠ACD =∠ABC ． （1）求证：CA 是圆的切线； （2）若点E 是BC 上一点，已知BE =6，tan ∠ABC =3 2，tan ∠AEC =35 ，求圆的直径． 2. 如图右，已知直线PA 交⊙0于A 、B 两点，AE 是⊙0的直径．点 C 为⊙0上一点，且AC 平分∠PAE ，过C 作C D ⊥PA ，垂足为D 。 (1)求证：CD 为⊙0的切线； (2)若DC+DA=6，⊙0的直径为l0，求AB 的长度.

3．（已知四边形ABCD 是边长为4的正方形，以AB 为直径在正方形内作半圆，P 是半圆上的动点（不与点 A 、 B 重合），连接PA 、PB 、P C 、P D ． (1)如图①，当PA 的长度等于 ▲ 时，∠PAB ＝60°； 当PA 的长度等于 ▲ 时，△PAD 是等腰三角形； (2)如图②，以AB 边所在直线为x 轴、AD 边所在直线为y 轴， 建立如图所示的直角坐标系（点A 即为原点O ），把△PAD 、 △PAB 、△PBC 的面积分别记为S 1、S 2、S 3．坐标为（a ，b ）， 试求2 S 1 S 3－S 22的最大值，并求出此时a ，b 的值． 4、

5．如图，BD是⊙O的直径，OA⊥OB，M是劣弧AB ⌒上一点，过点M点作⊙O的切线MP交OA的延长线于P点，MD与OA交于N点． （1）求证：PM＝PN； （2）若BD＝4，PA＝3 2 AO，过点B作BC∥MP交⊙O于C点，求BC的长． 6．（如图，点P为△ABC的内心，延长AP交△ABC的外接圆于D，在AC延长线上有一点E，满足AD2＝AB·AE，求证：DE是⊙O的切线.