2014-2015五年级美国大联盟

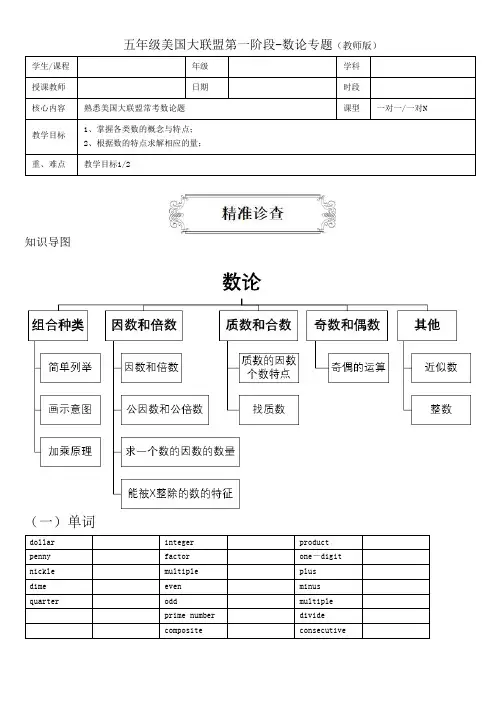
五年级美国大联盟第一阶段-数论专题（教师版）学生/课程年级学科授课教师日期时段核心内容熟悉美国大联盟常考数论题课型一对一/一对N教学目标1、掌握各类数的概念与特点；2、根据数的特点求解相应的量；重、难点教学目标1/2知识导图（一）单词dollar integer product penny factor one－digit nickle multiple plusdime even minus quarter odd multipleprime number dividecomposite consecutive（二）词组square root at least a millionpositive integers greatest common factor least common multiple two －digit multiples be divisible by the sum of【参考答案】square root 平方根 at least 至少 a million一百万 positive integers 正整数 greatest common factor 最大公因数 least common multiple 最小公倍数 two －digit multiples 两位数的倍数 be divisible by 被……整除 the sum of总和dollar 美元 integer 整数 product 积 penny 1美分 factor 因数 one －digit 一位数 nickle 5美分 multiple 倍数 plus 加 dime 10美分 even 偶数 minus 减 quarter25美分odd奇数 multiple 乘 prime number 质数 divide 除composite合数consecutive连续的导学一：组合种类知识点讲解1、简单列举有些题目，因其所求的答案有多种，用算式不容易表示，需要采用一一列举的方法解决。

装订线内不准答题小学2014～2015学年度第二学期 五年级英语竞赛考试题（卷） 得分 _________ 一、写出下列字母的左邻右舍，注意大小写一致。

（10分） b G j D r 二、选出下列单词中一种与众不同的一项。

（共10分 ） （ ）1. Ａ．lunch Ｂ．breakfast Ｃ.dinner Ｄ．paper （ ）2. Ａ．eat Ｂ．have Ｃ.does Ｄ．play （ ）3. Ａ．red Ｂ．clever Ｃ.tall Ｄ. train （ ）4. Ａ．with Ｂ．usually Ｃ.sometimes Ｄ．often （ ）5. Ａ．his Ｂ．me Ｃ.her Ｄ．your 三、根据答语，用特殊疑问词填空。

（共10分） 1. -- do you eat zongzi? -- We eat zongzi on Dragon Boat Day. 2. -- do you go shopping?-- I often go shopping on the weekend. 3. -- do you live ?-- I live on an island. 4. -- season do you like best?-- I like spring best. 5. -- do ou like winter?-- Because I can make a snowman.四、句子配对（从B 栏中选出A 栏的正确答语）。

（共10分）<A>( ) 1.When is Dragon Boat Day ？( ) 2.Why da you like summer best? ( ) 3.What do you do on Saturdays?( ) 4.What’s the weather like in summer?( ) 5.When do you get up?<B>A. It’s very hot.B. It’s usually in June.C. At 6 in the morning.D. I oftenclean my room.E. Because I like summer vacation .五、根据中文提示，用适当的单词填空。

2013-2014年度美国“数学大联盟杯赛”(中国赛区)初赛答案(三、四年级)一、选择题1. A.Since 0 is a factor, 2 × 0 × 1 × 4 = 0.A) 0B) 7C) 8D) 20142. B.If 2 years ago I was 3 years old, I am now 3 + 2 = 5.A) 4B) 5C) 6D) 233. D.8 + (60 ÷ 4) = 8 + (15) = 23.A) 15B) 17C) 22D) 234. B.(1 + 7) + (2 + 6) + (3 + 5) = 3 × 8 = 24 = 4 + 20.A) 4B) 20C) 24D) 285. C.The prime numbers less than 10 are 2, 3, 5, and 7.A) 2B) 3C) 4D) 56. B.Caleb the dog dreams he has 12 dozen bones. Since 12 dozen = 12 × 12 = 144, there are 144 ÷ 2 = 72 pairs. Caleb will have to dig 72 holes.A) 24B) 72C) 144D) 2887. C.From 9:45 PM to 10:45 PM is 60 mins. From 10:45 PM to 11 PM is 15 mins. From 11 PM to 11:10 PM is 10 mins. That’s (60 + 15 + 10) mins.A) 65B) 75C) 85D) 958. D.From January 1st to January 31st, there are 16 odd-numbered dates. From February 1st to February 21st, there are 11 odd-numbered dates. That’s 27 × $2 = $54.A) $48B) $50C) $52D) $549. C.9 × 9 + 9 × 8 + 9 × 7 + 9 × 6 = 9 × (9 + 8 + 7 + 6).A) 20B) 24C) 30D) 3610.D.Manny weighs three times as much as Murray. Manny also weighs 8000 kg more than Murray, so 8000 kg is twice Murray’s weight. Thus Murray weighs 4000 kg and Manny weighs 12 000 kg.D) 12 00011.B.I have twice as many shirts as hats, and four times as many hats as scarves. If I have 24 shirts, I have 24÷ 2 = 12 hats and 12 ÷ 4 = 3 scarves.A) 2B) 3C) 6D) 1212.C.My coins have a total value of $6.20. If I have 1 of each coin, I have (1 + 5 + 10 + 25)¢ = 41¢. Subtract 41¢ from $6.20 repeatedly until there is 5¢ left. After 15 subtractions, there is 5¢ left. I have 15 + 5 or20 pennies.A) 10B) 15C) 20D) 2513.D.The diagrams demonstrate choices A, B, and C.A) 14 kmB) 10 kmC) 8 kmD) 1 km14.C.(2014 −1014) + (3014 − 2014) = 1000 + 1000 = 2000.A) 0B) 1000C) 2000D) 201415.A.10 + (9 ×8) − (7 × 6) = 10 + 72 − 42 = 40.A) 40B) 110The prime factorization of 72 is 2 × 2 × 2 × 3 × 3. The largest prime is 3.A) 3B) 7C) 36D) 7217.D.6 × 4 = 24 = 96 ÷ 4.A) 6B) 12C) 24D) 9618.C.If 6 cans contain 96 teaspoons of sugar, 1 can contains 96 ÷ 6 = 16 teaspoons of sugar. Thus 15 cans contain 16 × 15 = 240 teaspoons of sugar.A) 192B) 208C) 240D) 28819.C.The largest possible such sum is 98 + 99 = 197.A) 21B) 99C) 197D) 19820.B.Ann sent Wilson hearts with odd numbers with odd tens digits. The number on each heart he received must be two digits with both digits odd. There are 5 possible tens digits and 5 possible ones digits.That’s a total of 5 × 5 = 25 hearts.A) 23B) 25C) 30D) 4521.B.Since Rich ate his favorite sandwich 8 days ago, today is the 9th day of the month. Since the shortest month has 28 days, it is at least 28 − 9 = 19 days until the last day of the month. He must wait 1 more day.A) 1922.D.The factors of 49 are 1, 7, and 49. Since 49 has 3 factors, it has a prime number of factors.A) 6B) 12C) 36D) 4923.D.Dividing a certain two-digit number by 10 leaves a remainder of 9, so it is 19, 29, 39, 49, 59, 69, 79, 89, or 99. The only number listed with remainder 8 when divided by 9 is 89, so the number is 89 and 8 + 9 = 17.A) 7B) 9C) 13D) 1724.A.The whole numbers less than 1000 that can be written as such a product are 0 × 1 × 2, 1 × 2 × 3, 2 × 3 ×4, 3 × 4 × 5, 4 × 5 × 6, 5 × 6 × 7, 6 × 7 × 8, 7 × 8 × 9, 8 × 9 × 10, and 9 × 10 ×11. In all, that’s 10.A) 10B) 11C) 15D) 2125.B.The only such numbers are 5432, 5431, 5430, 5421, 5420, 5410, 5321, 5320, 5310, and 5210. In all, there are 10 such numbers.A) 3B) 10C) 69D) 12026.C.2014 × 400 = 805 600; the hundreds digit is 6.A) 0B) 5C) 6D) 827.B.Greta was 110 cm tall 2 years ago, when she was 10 cm taller than her brother. Her brother was 100 cmB) 130C) 140D) 15028.B.The number 789 678 567 456 is added to the number 987 876 765 654. Since we carry a 1 when adding the left-most digits, the sum has 12 + 1 digits.A) 12B) 13C) 24D) 2529.D.We must find which number among the choices is two more than a multiple of 5. Divide each choice by5 (or recogniz e that any number that ends in “2”or “7” is 2 more than a multiple of 5).A) 4351B) 5215C) 5616D) 646230.C.Of every 11 people, there are 2 adults and 9 children. Since 99 ÷ 11 = 9, there are 9 groups of 11 people.Of these, 9 × 2 = 18 are adults.A) 9B) 11C) 18D) 22二、填空题31.5.32.22.33.4.34.1.35.617.36.21.37.499.38.765.39.69.40.10.。

⼀⽂读懂美国数学⼤联盟，你想知道的都在这⾥！The Math League美国数学⼤联盟杯赛由两位美国著名的数学教育家Mr. Steven R. Conrad和Mr. Daniel Flegler创办，于1977年成功举办第⼀届，如今不仅在美国及北美地区影响⼒巨⼤，更是在国际上拥有全球影响⼒的数学赛事。

两位数学家的初衷是希望可以通过竞赛促进学⽣享受数学，启发学⽣学会利⽤数学解决实际⽣活中遇到的问题，提升创造性思维和批判性思维，更是考察学⽣听说读写综合英语能⼒。

每年有超过100万名中⼩学⽣参加。

相⽐中国现有数学竞赛的形式，Math League更灵活⽣动，更容易激发学⽣对数学的兴趣，从⽽理解数学、欣赏数学，⽽不是看见数学就害怕。

不仅如此，参加Math League更能在未来申请上添砖加⽡。

Math League竞赛流程与规则美国“数学⼤联盟杯赛”分为中国区初赛、中国区复赛和美国决赛三个阶段：中国区初赛：竞赛详情：以下为按不同年级组区分的竞赛详情，获奖证书上也根据以下表格仅标明年级组：年级组考试时考试时⽐赛形式：笔试竞赛详情：⽐赛形式：间题型题⽬总分备注三年级90分钟选择题40道英⽂题200分答题卡四年级90分钟选择题40道英⽂题200分答题卡五年级90分间题型题⽬总分备注钟选择题40道英⽂题200分答题卡六年级90分钟选择题40道英⽂题200分答题卡七年级（初⼀）90分钟选择题40道英⽂题200分答题卡⼋、九年级组（初⼆、初三）90分钟选择题40道英⽂题200分答题卡⾼中（⾼⼀、⾼⼆、⾼三）90分钟填空题30道英⽂题300分笔试请考⽣准备好2B铅笔、签字笔、橡⽪等考试⼯具，禁⽌使⽤修正液、涂改带、计算器等。

考试时组委会给每个学⽣提供数学常⽤词汇表竞赛结果：初赛结束后每位选⼿均会受到以下初赛成绩统计与分析及禁⽌携带任何形式的字典、词典、计算器、及任何资料竞赛结果：查缺补漏试题：全国初赛成绩统计：成绩正态分布图、平均分、标准差、区分度等。

2014-2015年度美国”数学大联盟杯赛“（中国赛区）初赛（十、十一、十二年级）一、选择题（每小题10分，答对加10分，答错不扣分，共100分，请将正确答案A 、B 、C 或者D 写在每题后面的圆括号内。

）正确答案填写示例如下：=-⨯⨯20522 ？ （A ）A)5 B)15 C)25 D)301. Meg loves her megaphone! The large circular end has a circumference that is the reciprocal of its diameter. What is the area of the circle? ( )A)π14 B) π12 C) 14 D) 122. How many solutions does the equation x x +=233 have? ( )A)0 B)1 C)2 D)43. If y x =-1, which of the following is always true for any value of x ? ( )A) ()()x y -=-2211B) ()()x x y y -=-222211 C) ()()x x y y --=-222211 D) ()()()()x x y y -+=-+22221111 4. Lee the crow ate a grams of feed that was 1% seed, b grams of feed that was 2% seed, and c grams of feed that was 3% seed. If combined, all the feed he ate was 1.5% seed. What is a in terms of b and c ?( )A)b c +3B)b c +3 C)b c +23 D)b c +32 5. If <x 0 and <.x 2001, then x -1 must be ( )A)less than -10B)between-0.1 and 0 C)between 0and 0.1 D) greater than 106. At 9:00 A.M., the ratio of red to black cars in a parking lot was 1 to 5. An hour later the number of red cars had increased by 2, the number of black cars had decreased by 5, and the ratio of red to black cars was 1 to 4. How many black cars were in the lot at 10:00 A.M.? ( )A)13 B)15 C)60 D)657. If x ≠1and x ≠-1, then ()()()x x x x x --++-32241111=( ) A)x -21 B) x +21 C) x -241 D) x -341 8. The Camps are driving at a constant rate. At noon they had driven 300 km.At 3:30 P.M. they had driven 50% further than they had driven by 1:30 P.M.What is their constant rate in km/hr? ( )A)150 B)120 C)100 D)909. The letters in DIGITS can be arranged in how many orders without adjacent I ’s? ( )A)240 B)355 C)600 D)71510. Al, Bea, and Cal each paint at constant rates, and together they are painting a house. Al and Bea togethercould do the job in 12 hours; Al and Cal could to it in 15, and Bea and Cal could do it in 20. How many hours will it take all three working together to paint the house?( )A)8.5 B)9 C)10 D)10.5二、填空题（每小题10分，答对加10分，答错不扣分，共200分）11. What is the sum of the degree-measures of the angles at the outer points ,,,A B C D and E of a five-pointed star, as shown? Answer: . 12. What is the ordered pair of positive integers (,k b ), with the least value of k , which satisfiesk b ⋅⋅=34234?Answer: .13. A face-down stack of 8 playing cards consisted of 4 Aces (A ’s) and 4 Kings (K ’s).After I revealed and then removed the top card, I moved the new top card to thebottom of the stack without revealing the card. I repeated this procedure until thestack without revealing the card. I repeated this procedure until the stack was leftwith only 1 card, which I then revealed. The cards revealed were AKAKAKAK ,in that order. If my original stack of 8 cards had simply been revealed one card at atime, from top to bottom (without ever moving cards to the bottom of the stack),in what order would they have been revealed?Answer: .14. For what value of a is one root of ()x a x a -+++=222120 twice the other root?Answer: .15. Each time I withdrew $32 from my magical bank account, the account ’sremaining balance doubled. No other account activity was permitted. My fifth$32 withdrawal caused my account ’s balance to become $0. With how manydollars did I open that account?Answer: .16. In how many ways can I select six of the first 20 positive integers, disregarding the order in which these sixintegers are selected, so that no two of the selected integers are consecutive integers?Answer: .17. If, for all real ,()()xx f x f x =-21, what is the numerical value of f (3)?Answer: .18. How many pairs of positive integers (without regard to order) have a least common multiple of 540?Answer: .19. If the square of the smaller of consecutive positive integers is x , what is the square of the larger of thesetwo integers, in terms of x ?Answer: .20. A pair of salt and pepper shakers comes in two types: identical and fraternal.Identical pairs are always the same color. Fraternal pairs are the same colorhalf the time. The probability that a pair of shakers is fraternal is p andthat a pair is identical is .q p =-1 If a pair of shakers is of the same color, AE DCBword 格式-可编辑-感谢下载支持 determine, in terms of the variable q alone, the probability that the pair is identical. Answer: .21. As shown, one angle of a triangle is divided into four smaller congruentangles. If the lengths of the sides of this triangle are 84, 98, and 112, as shown,how long is the segment marked x ?Answer: .22. How long is the longer diagonal of a rhombus whose perimeter is 60, if threeof its vertices lie on a circle whose diameter is 25, as shown?Answer: .23. The 14 cabins of the Titanic Mail Boat are numbered consecutively from1 through 14, as are the 14 room keys. In how many different ways canthe 14 room keys be placed in the 14 rooms, 1 per room, so that, for everyroom, the sum of that room ’s number and the number of the key placed inthat room is a multiple of 3?Answer: .24. For some constant b , if the minimum value of ()x x b f x x x b -+=++2222is 12, what is the maximum value of ()f x ? Answer: .25. If the lengths of two sides of a triangle are 60cos A and 25sin A , what is the greatest possible integer-length of the third side?Answer: .26. {}n a is a geometric sequence in which each term is a positive number. If a a =5627, what is the value oflog log log ?a a a +++3132310Answer: . 27. What is the greatest possible value of ()=sin cos ?f x x x ++3412Answer: .28. Let C be a cube. Triangle T is formed by connecting the midpoints of three edges of cube C . What is the greatest possible measure of an angle of triangle T ?Answer: .29. Let a and b be two real numbers. ()sin f x a x b x =++34 and (lg log )f =3105. What is the value of (lg lg )f 3?Answer: .30. Mike likes to gamble. He always bets all his chips whenever the number of chips he has is <=5. He always bets n （10-）chips whenever the number of chips he has is greater than 5 and less than 10. He continues betting until either he has no chips or he has more than 9 chips. For every round, if he bets n chips. The probability that he wins or loses in each round is 50%. If Mike begins with 4 chips, what is the probability that he loses all his chips?Answer: .1129884xword格式-可编辑-感谢下载支持。

2018-2019年度美国“大联盟”(Math League)思维探索活动第一阶段(五年级)(活动日期：2018年11月25日，答题时间：90分钟，总分：200分)学生诚信协议：答题期间，我确定没有就所涉及的问题或结论，与任何人、用任何方式交流或讨论， 我确定我所填写的答案均为我个人独立完成的成果，否则愿接受本次成绩无效的处罚。

请在装订线内签名表示你同意遵守以上规定。

考前注意事项：1. 本试卷是五年级试卷，请确保和你的参赛年级一致；2. 本试卷共4页(正反面都有试题)，请检查是否有空白页，页数是否齐全；3. 请确保你已经拿到以下材料：本试卷(共4页，正反面都有试题)、答题卡、答题卡使用说明、英文词汇手册、 草稿纸。

试卷、答题卡、答题卡使用说明、草稿纸均不能带走，请留在原地。

4. 本试卷题目很多也很难，期待一名学生所有题目全部答对是不现实的，能够答对一半题目的学生就应该受到表扬和鼓励。

选择题：每小题5分，答对加5分，答错不扣分，共200分，答案请填涂在答题卡上。

1. 2018 + 2019 = 20 + 18 + 20 + 19 + ?A) 0B) 2000C) 3960D) 40002. If 1/3 of my hats are red, and 36 are not red, I have ? hats.A) 18B) 54C) 72D) 1083. The sum of the measures of the 2 smallest angles of a triangle could beA) 151 degrees B) 135 degrees C) 121 degreesD) 61 degrees4. 2018 = 20 × ? + 18 × 1A) 1B) 10C) 18D) 1005. Every English letter appears in my 2018-letter password at least once. The letter A appears at most ? times.A) 77B) 78C) 1992D) 19936. Which of the following is the product of 2 consecutive integers?A) 182B) 195C) 208D) 2217. The least integer with a prime number of different prime factors isA) 6B) 8C) 12D) 158. I have 5 coins consisting of pennies, nickels, and dimes. If I have at least 1 of each type of coin, the least possible value of my 5 coins isA) 5¢B) 15¢C) 16¢D) 18¢9. Exactly ? different 3-digit area codes can be made using only 2s and 3s, with at leastone 2 and one 3 in each area code.A) 4B) 6C) 9D) 1210. How many multiples of 10 are factors of 102?A) 1B) 2C) 3D) 411. My team had to win a certain number of games to make it to the finals, and we won every 6th game we played. If my team qualified for the finals after our 96th game, how many wins did we need?A) 12 B) 16 C) 18D) 9012. What is the greatest common factor of 1 × 3 × 5 × 7 × 9 and 2 × 4 × 6 × 8 × 10?A) 1B) 3C) 5D) 1513. The expression 2400 is the product of exactly ? sixteens.A) 25B) 50C) 100D) 20014. The 2nd act of a 3-act play is 1/3 the length of the entire play. If the 1st act is twice as long as the 3rd, what fraction of the play is the 3rd act?A) 1/9 B) 2/9 C) 3/9 D) 4/9 15. If I double my speed of 12 000 m/hr., my new speed will beA) 200 m/min. B) 400 m/min. C) 600 m/min.D) 2400 m/min.16. Which of the following could be the perimeter of an equilateral triangle with integralside-lengths?A) 2017B) 2018C) 2019D) 202017. The greatest of 10 consecutive positive integers is a prime number. What is the least possible sum of these integers?A) 65B) 77C) 127D) 12918. One-fourth of Ed’s balloons popped, with 2 balloons popping every3 minutes for an hour. How many balloons did not pop?A) 40 B) 80 C) 120 D) 160 19. What is the greatest common factor of 68 and 86?A) 22B) 44C) 66D) 8820. The expression 1002018 can be written as the product of exactly ? prime numbers.A) 5 × 2018B) 4 × 2018C) 2 × 2018D) 201821. How many integers have a square root greater than 15 and less than 16?A) 0B) 1C) 29D) 3022.=A) 0B) 54C) 90D) 14423. Each day for a month, Sully wakes up 5 minutes earlier than he did the day before. IfSully woke up at 6:50 a.m. on a Monday, on what day did he wake up at 6:20 a.m.?A) Sunday B) Monday C) TuesdayD) Wednesday24. The product of all factors of 21 equals 21 × ? .A) 1B) 2C) 3D) 2125. (1234 + 0 + 1234 + 1 + 1234 + 2 + 1234 + 3 + 1234 + 4) ÷ 5 =A) 1234B) 1234 + 1C) 1234 + 2D) 1234 + 326. On a number line, two different integers are each the same distance from my favorite integer and have a sum of 144. What is my favorite integer?A) 31B) 36C) 48D) 7227. Last year I spent $180 for 80 pairs of shades. This year I spent $180for 5 fewer pairs of the same shades. How much did the price per pair increase since I bought them last year?A) 15¢B) 72¢C) 96¢D) 120¢28. I drove at a constant speed of 60 km/hr. without stopping. At exactly 5:00 p.m. I had traveled 318 km. At what time did I start driving?A) 10:42 a.m. B) 11:42 a.m. C) 12:42 p.m.D) 1:42 p.m.29. I added 3 of the numbers 11111, 22222, 33333, 44444, 55555, 66666, 77777, 88888, and 99999. My sum was one of these 9 numbers. When my sum was divided by 11, the remainder could not have beenA) 5B) 6C) 7D) 830. I wrote the 101 integers from 1 to 101 in order on paper. If I wrote 101 digits per line, what was the sum of the last 4 digits on the first line?A) 11B) 17C) 19D) 2131. The product of all the factors of an integer greater than 1 equals the cube of that integer.What is the least integer for which this is true?A) 24B) 18C) 12D) 832. On our last history test, at least one student scored each of the grades A, B, C, D, and F. If 8 got an A, 15 got a C or higher, 10 got a B or lower, and only one student got a D, how many students got an F?A) 1B) 2 C) 3 D) 5 33. (22 × 24 × 26 × … × 298 × 2100) ÷ (21 × 23 × 25 × … × 297 × 299) =A) 2B) 249C) 250D) 210034. Starting at 1:00 p.m., a ball was rolled in each of two lanes. A ballwas rolled once every 15 seconds in one lane and once every 18 seconds in the other. By 1:44 p.m., how many times had balls been rolled at the same time in both lanes?A) 29B) 30C) 40D) 4435. I counted backwards out loud from 2018 by ones. When I said my 50th multiple of 8, howmany numbers had I counted?A) 252B) 395C) 400D) 161836. If 30% of a number is 42, the 50% of the number is?A) 60B) 70C) 84D) 10837. The perimeter of a square is 12. The area of the square is?A) 3B) 6C) 9D) 1238. A year is called a lucky year if the sum of its digits is 18. For example, 1917 is alucky year since 1 + 9 + 1 + 7 = 18. How many lucky years are there between 2018 and 2108? A) 2B) 3C) 4D) 539. I ran 1 km in 6.0 minutes. Rabbit ran 50% faster and finished inA) 3.0 minutes B) 4.0 minutes C) 4.5 minutesD) 9.0 minutes40. If the pattern of the first 5 letters of ABCDEABCDEABCDE … continues to the right, the 2018th letter in the pattern would beA) A B) BC) CD) D or E。