储层流体高压物性参数计算方法
- 格式:ppt
- 大小:660.00 KB
- 文档页数:56

气相参数求解(一)潜热的计算: 按文献上的公式计算 (二)比热容的计算:(1)由于考虑的是低压下的蒸发状态,以理想气体状态计算'23p c A BT CT DT =+++ (1) 式中,, , , A B C D 可以从有关资料附录查到。
(2)混合气体比热容 液滴蒸汽质量比:,/vapvap o air vap airM m M Y M M =+- (3),vap f m =0 (4)液滴蒸汽摩尔比:,0,00/vap vap y p p = (5),0,,0,0//(1)/vap vapvap vap vap vap airm M y m M m M ∞=+- (6)蒸汽摩尔比:,0,()/2vap vap vap y y y ∞=+ (7)介质气体摩尔比:1air vap y y =- (8)混合气体比热容:''',,p p vap vap p air air c c y c y =+ /cal mol K ⋅ (9)(三)混合气体粘度计算 (1)动力粘度1/30.809c V σ= (10)式中,σ为硬球直径,单位为0A 。
//1.2593c k T ε= (11)式中,κ为Boltzmann 常数,ε为特征能量。
*/TT εκ=(12) **exp(*)exp()V B A C E FT T DT Ω=++ (13) 式中, 1.16145, 0.14874, =0.52487, 0.77320, 2.16178, 2.43787A B C D E F =====Vμ= (14) 式中,M 是蒸汽分子量,μ为粘度,单位P μ(微泊),7110a P P s μ-=⋅估算*T 为约化温度(3)对于二元混合气体的粘度,C.R.Wilke 应用了Sutherland 的动力模型理论得到:112212122121m y y y y y y μμμφφ=+++ (16)式中,1/21/421212121/212[1(/)(/)]|8[1(/)]|M M M M μμφ+=+ 11211222M M μφφμ= 12,μμ分别是双元混合气体中两种气体的粘度 ,12,y y 分别是双原混合气体中两种气体的摩尔比。

石油储层岩石物性参数测定方法研究石油是当今世界最重要的能源之一,其储层岩石的物性参数对石油勘探和开发具有至关重要的影响。
物性参数的准确测定对于评估石油储层的储量、渗透率和产能等具有重要意义。
因此,研究和发展石油储层岩石物性参数的测定方法是当前石油领域中重要的课题。
一、岩心采集与样品制备岩心是从地下石油储层中获取的一种岩石样品,对于岩石物性参数的测定具有重要意义。
岩心采集过程应当注意保持其在地下储层中的原位应力和孔隙结构,避免损坏其物性。
采集后的岩心样品应当进行特定大小的切割和研磨,以获得待测参数所需的试样。
二、孔隙度测定方法孔隙度是指储层岩石中的孔隙空间所占的百分比。
测定孔隙度的常用方法包括压汞法、氮气吸附法和浸泡法等。
其中,压汞法是一种常用且精确的方法。
它基于压力平衡原理,测量在不同压力下岩石孔隙内的汞体积,进而计算出孔隙度。
三、渗透率测定方法渗透率是指岩石对流体流动的能力,是评估石油储层导流性能的重要指标。
常用的渗透率测定方法有恒压法和恒流法。
恒压法是通过施加一定压力差,测量流体在岩石样品中的渗流速度,从而计算渗透率。
恒流法则是通过施加一定的流量,测量岩石内部的压力变化,进而求得渗透率。
四、饱和度测定方法饱和度是指储层岩石中的孔隙空间被流体填充的程度。
常见的饱和度测定方法有重力法、浸泡法和放射性同位素法等。
其中,重力法是一种简单而常用的方法,通过称量岩石样品在干态和浸泡后的质量差异来计算饱和度。
五、岩石密度测定方法岩石密度是指岩石单位体积的质量,对于评估岩石物理性质和石油储层的勘探具有重要影响。
测定岩石密度的方法主要有质量法、回声法和核磁共振法等。
其中,质量法是最常见的一种方法,通过称重岩石样品在空气中和水中的质量差异来计算岩石密度。
综上所述,石油储层岩石物性参数的准确测定对于石油勘探和开发具有重要意义。
岩心采集与样品制备、孔隙度、渗透率、饱和度以及岩石密度的测定方法是目前研究的关键点。
通过不断深入研究和创新,我们可以更准确地评估储层的储量、渗透率和产能,为石油储层开发提供可靠的理论依据和技术支持。


第三章储层流体的物理特性所谓储层流体,这里指的是储存于地下的石油、天然气和地层水。
其特点是处于地下的高压、高温下,特别是其中的石油溶解有大量的气体,从而使处于地下的油气藏流体的物理性质与其在地面的性质有着很大的差别。
例如,当储层流体从储层流至井底,再从井底流至地面的过程中,流体压力、温度都会不断降低,此时会引起一系列的变化—原油脱气、体积收缩、原油析蜡;气体体积膨胀、气体凝析出油;油田水析盐—即离析和相态转化过程,而这一系列变化过程对于油藏动态分析、油井管理、提高采收率等都有重要的影响。
又如,进行油田开发设计和数值模拟时,必须掌握有关地下流体的动、静态物理参数,如石油和天然气的体积系数、溶解系数、压缩系数、粘度等;在进行油气田科学预测方面,如在开采初期及开采过程中,油田有无气顶、气体是否会在地层中凝析等,都需要对油气的物理化学特性及相态变化有深刻的认识,才能作出判断。
因此可以毫不夸张地说,不了解石油、天然气和水的性质及其问的相互关系,不掌握它们的高压物性参数,那么,科学地进行油田开发、采油及油气藏数值模拟等便无从讲起。
第一节油气藏烃类的相态特征石油和天然气是多种烃类和非烃类所组成的混合物。
在实际油田开发过程中,常常可以发现:在同一油气藏构造的不同部位或不同油气藏构造上同一高度打井时,其产出物各不相同,有的只产纯气,有的则油气同产。
在油气藏条件下,有的烃是气相,而成为纯气藏;有的是单一液相的纯油藏;也有的油气两相共存,以带气顶的油藏形式出现。
在原油从地下到地面的采出过程中,还伴随有气体从原油中分离和溶解的相态转化等现象。
那么,油藏开采前烃类究竟处于什么相态,为什么会发生一系列相态的变化,其主要原因是什么?用什么方式来描述烃类的相态变化?按照内因是事物变化的根据,外因则是事物变化的条件,可以发现油藏烃类的化学组成是构成相态转化的内因,压力和温度的变化是产生相态转化的外部条件。
因此,我们从研究油藏烃类的化学组成人手,然后再进一步研究压力温度变化时对相态变化的影响。





砂岩储层物性统计分析及预测方法砂岩储层是石油勘探开发中常见的储层类型,因其储集孔隙率高、流动性能好而备受关注。
而在砂岩储层的开发中,物性统计分析与预测方法起着至关重要的作用。
本文将对砂岩储层的物性统计分析及预测方法进行探讨。
一、砂岩储层的物性类型及影响因素砂岩储层的物性主要包括孔、隙、渗透率和饱和度等。
而这些物性又受到岩性、厚度、成分、孔隙类型、胶结物的类型、含油度和地质时代等因素的影响。
因此,对砂岩储层物性的分析和认识对于石油勘探开发具有重要意义。
二、砂岩储层的物性统计分析方法对砂岩储层的物性进行统计分析,可以发现它们之间的相互关系。
通过对不同自然条件下的储层性质的测量和统计,可得到其统计分布规律,比如,渗透率的大多数数据也是服从正态分布的。
(一)孔隙大小分布分析孔隙大小分布是砂岩储层的重要物性之一,也是储层物性统计分析的基础。
对孔隙大小分布的分析有助于确定储层的孔隙结构特征,以及孔隙连接性和渗透率等物性。
常用的分析方法有:自动孔径分析仪、气体吸附法、水蒸气吸附法等。
(二)渗透率分析渗透率是砂岩储层中最重要的物性之一,它影响储层的有效性和开发潜力。
常用的统计分析方法包括:直接测渗法、氩气渗透法、压汞法等。
(三)饱和度分析饱和度是指储层中的水、油等流体占孔隙空间的百分比,它是储层中流体分布和渗流特性的重要参数。
常用的方法有动态水压层测试、伽玛射线测井法等。
三、砂岩储层的物性预测方法砂岩储层物性的预测能力直接影响油气勘探的成功率和开发潜力,因此砂岩储层物性的合理预测对于油气勘探开发至关重要。
(一)基于统计学模型的物性预测通过对样本数据进行统计分析,建立数学模型,以此预测砂岩储层的物性。
常用的方法有多元线性回归分析、主成分分析、人工神经网络等。
(二)基于地质模型的物性预测基于地质模型的物性预测是一种常用的物性预测方法。
该方法依据储层的地质特征和物性参数的空间变化规律,建立三维地质模型,并根据地质模型的不同参数来进行储层物性预测。

第一部分 储层流体性质1 储层气体性质1.1天然气组成换算天然气是混合气,其组成有三种表示方法,即体积分数、摩尔分数和质量分数。
对理想气体,体积分数和摩尔分数等值。
从质量分数换算为体积或摩尔分数)/()/(i i i i i M W M W y ∑=(1-1)反之,从体积或摩尔分数换算为质量分数:)()(i i i i i M y M y W ∑=(1-2)式中:i M —天然气中组分i 的分子量;i y 、i W —分别表示天然气中组分i 的摩尔分数(或体积分数)和质量分数。
1.2真沸点馏分特征化气体分析报告中的真沸点馏分(例如庚烷以上的组分,用符号C 7+表示),属于不确定组分,其临界压力、临界温度、分子量和偏心因子等物性参数,不能像确定组分(例如甲烷、乙烷)那样,可以直接从有关书籍或手册中查出。
通过实验方法可以测得真沸点馏分的密度(或相对密度)和沸点,则其临界压力、临界温度等另外一些物性参数,常用一些相关公式计算。
下面介绍几个。
1.2.1Lee-Kesler 公式(1976)T C =[341.7+811.1γ+(0.4244+0.1174γ)(1.8T b )+(0.4669-3.2623γ)105/(1.8T b )]/1.8 (1-3) ln(p c )=3.3865-0.0566/γ-(0.24244+2.2898/γ+0.11857/γ2)10-3×(1.8T b )+(1.4685+3.648/γ0.47227/γ2)10-7×(1.8T b )2 –(0.42019+1.6977/γ2)10-10×(1.8T b )3 (1-4) M=-12272.6+9486.4γ+(4.6523-3.3287γ)(1.8T b )+[(1-0.77084γ-0.02058γ2)(1.3437-720.79/1.8T b )]107/(1.8T b )+[(1-0.80882γ+0.02226γ2)(1.8828-181.98/1.8T b )]1012/(1.8T b )3 (1-5) 当ϕ>0.8时,ω=-7.904+0.1352K-0.007465K 2+8.359ϕ+(1.408-0.01063K)/ϕ (1-6) 当ϕ<0.8时,ω =[-ln(9.869p c )-5.92714+6.09648/ϕ+1.28862 ln ϕ-0.169347ϕ6]/[15.2518-15.6875/ϕ-13.4721 ln ϕ+0.43577ϕ6] (1-7) 式中 T c ————真沸点馏分临界温度, K ; p c ————真沸点馏分临界压力, MPa ; T b ————真沸点馏分沸点, K ;γ——真沸点馏分相对密度;M ——真沸点馏分平均分子量;ω——真沸点馏分偏心因子;K ——Watson 特性因子;γ/)8.1(31b T K =ϕ ——对比沸点。
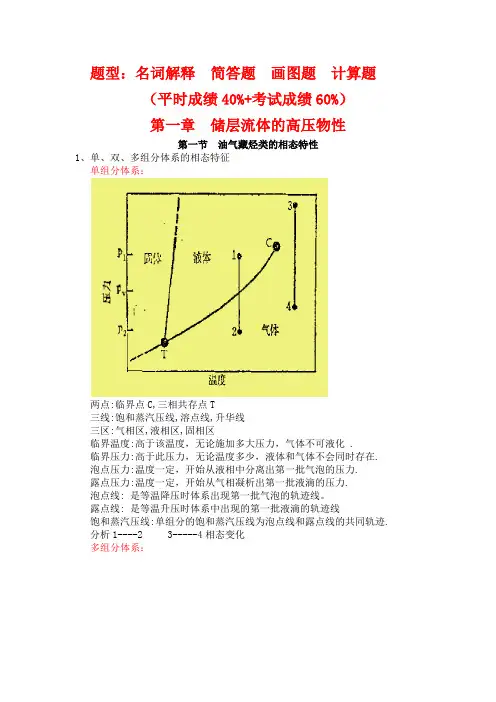
题型:名词解释简答题画图题计算题(平时成绩40%+考试成绩60%)第一章储层流体的高压物性第一节油气藏烃类的相态特性1、单、双、多组分体系的相态特征单组分体系:两点:临界点C,三相共存点T三线:饱和蒸汽压线,溶点线,升华线三区:气相区,液相区,固相区临界温度:高于该温度,无论施加多大压力,气体不可液化 .临界压力:高于此压力,无论温度多少,液体和气体不会同时存在.泡点压力:温度一定,开始从液相中分离出第一批气泡的压力.露点压力:温度一定,开始从气相凝析出第一批液滴的压力.泡点线: 是等温降压时体系出现第一批气泡的轨迹线。
露点线: 是等温升压时体系中出现的第一批液滴的轨迹线饱和蒸汽压线:单组分的饱和蒸汽压线为泡点线和露点线的共同轨迹.分析1----2 3-----4相态变化多组分体系:(1)双组分体系的相图不再是一条单调曲线,而是一开口的环形曲线.(2)双组分体系的临界点不再是两相共存的最高压力和温度点, 而是泡点线和露点线的对接点.(3)双组分体系的两相区介于两纯组分的饱和蒸汽压曲线之间, 且临界压力高于各组分的临界压力,但临界温度确界于两组分的临界温度之间.(4)两组分中哪个组分的含量占优势,露点线或泡点线就靠近哪一组分的饱和蒸汽压线。
(5)两组分的浓度越接近则两相区的面积越大,两组分的组成有一组分的含量占绝对优势,两相区就越窄长.(6)两组分系统中,组成系统的物质不同其临界点也不同,而且分子结构越相近的两组分,其临界点轨迹曲线越扁平。
如果两组的挥发性和分子量差别愈大时,临界点轨迹所包围的面积愈大,临界凝析压力也愈高.2、等温反凝析现象的解释当体系处于A点时体系为单一气相。
当压力降至B点时,由于压力下降,烃分子距离加大,因而分子引力下降,这时被气态轻烃分子吸引的(或分散到轻烃分子中的)液态重烃分子离析出来,因而产生了第一批液滴。
而当压力进一步下降到D点时,由于气态轻烃分子的距离进一步增大,分子引力进一步减弱,因而就把液态重烃分子全部离析出来,这时在体系中就凝析出最多的液态烃而形成凝析油。