锁相环仿真(基于MATLAB)
- 格式:doc
- 大小:214.50 KB
- 文档页数:10

Matlab与通信仿真课程设计报告Matlab与通信仿真课程设计报告班级:12通信(1)班姓名:诸葛媛学号:Xb12680129实验⼀S-函数&锁相环建模仿真⼀、实验⽬的1.了解S函数和锁相环的⼯作原理2.掌握⽤S函数建模过程,锁相环载波提取仿真⼆、实验内容1、⽤S函数编写Similink基本模块(1)信源模块实现⼀个正弦波信号源,要求其幅度、频率和初始相位参数可以由外部设置,并将这个信号源进⾏封装。
(2)信宿和信号显⽰模块实现⼀个⽰波器⽊块,要求能够设定⽰波器显⽰的扫描周期,并⽤这个⽰波器观察(1)的信源模块(3)信号传输模块实现调幅功能,输⼊⽤(1)信源模块,输出⽤(2)信宿模块;基带信号频率1KHz,幅度1V;载波频率10KHz,幅度5V实现⼀个压控正弦振荡器,输⼊电压u(t)的范围为[v1,v2]V,输出正弦波的中⼼频率为f0Hz,正弦波的瞬时频率f随控制电压线性变化,控制灵敏度为kHz/V。
输⼊⽤(1)信源模块,输出⽤(2)信宿模块2、锁相环载波提取的仿真(1)利⽤压控振荡器模块产⽣⼀个受10Hz正弦波控制的,中⼼频率为100Hz,频偏范围为50Hz到150Hz的振荡信号,并⽤⽰波器模块和频谱仪模块观察输出信号的波形和频谱。
(2)构建⼀个抑制载波的双边带调制解调系统。
载波频率为10KHz,被调信号为1KHz正弦波,试⽤平⽅环恢复载波并进⾏解调。
(3)构建⼀个抑制载波的双边带调制解调系统。
载波频率为10KHz,被调信号为1KHz正弦波,试⽤科斯塔斯环恢复载波并进⾏解调。
(4)设参考频率源的频率为100Hz,要求设计并仿真⼀个频率合成器,其输出频率为300Hz。
并说明模型设计上与实例3.26的主要区别三、实验结果分析1、⽤S函数编写Similink基本模块(3)为了使S函数中输⼊信号包含多个,需要将其输⼊变量u初始为制定维数或⾃适应维数,⽽在S函数模块外部采⽤Simulink基本库中的复⽤器(Mux)将3⾏的信号矩阵。


基于matlab环境下FSK的调制与解调的分析王涛(学号:200412110)(物理与电子信息学院 04级电子信息工程班,内蒙古呼和浩特 010022)指导教师:刘美玲摘要:本文是基于matlab环境下对信号的调制与解调和误码率的分析,以及硬件实验与理论仿真实验的比较。
方法是通过matlab软件进行数学建模软件编程使模拟仿真成功,而硬件实验是利用现有实验设备进行实验分析。
根据二者在各个方面不同的特点,取长补短应用于教学之中。
关键词: Matlab;环境;调制;解调;分析中图分类号: TN91 文献标识码: B1引言MATLAB是由MATH WORKS公司于1984年推出的一种面向科学与工程的计算软件,通过MATLAB和相关工具箱,工程师、科研人员、数学家和教育工作者可以在统一的平台下完成相应的科学计算工作。
MATLAB 本身包含了 600 余个用于数学计算、统计和工程处理的函数,这样,就可以迅速完成科学计算任务而不必进行额外的开发。
业内领先的工具箱算法极大的扩展了MATLAB 的应用领域,所以MATLAB自推出以来就受到广泛的关注。
MATLAB特点: 一,数值计算功能,在MATLAB中,每个数值元素都视为复数,而且只有双精度(64位)一种数据格式,省去多种的设置,虽然在运行速度和内存消耗方面付出了代价,却使MATLAB的编程大大简化。
MATLAB的数值计算基本功能包括:矩阵运算、多项式和有理分式计算、数据统计分析以及数值分析等。
二,符号计算功能,在实际应用中,除了数值计算外,还需要得到方程的解析解,简化和展开多项式和函数表达,求解函数值等,所有这些均属于符号计算的领域。
三,便栈式的编程语言,与Fortran和C等高级语言相比,MATLAB的语法规则更简单,更贴近人的思维方式和表达习惯,使得编写程序就像在便栈上列写公式和演算一样。
四,强大而简易的作图功能,能根据输入数据自动确定坐标绘图。
五,高智能化,绘图时自动选择最佳坐标,大大方便了用户。

电网不平衡下三相锁相环研究1. 本文概述随着现代电力系统的快速发展,三相电力系统的不平衡现象日益凸显,对电力系统的稳定性和电能质量产生了严重影响。
为了解决这一问题,三相锁相环(ThreePhase PhaseLocked Loop, 3PPLL)作为一种有效的电力系统同步技术,受到了广泛关注。
本文旨在深入探讨电网不平衡条件下三相锁相环的工作原理、性能评估及优化策略,为提高三相电力系统的运行效率和稳定性提供理论依据和技术支持。
本文首先介绍了三相锁相环的基本原理,包括其数学模型和锁相机制。
随后,详细分析了电网不平衡对三相锁相环性能的影响,包括相位误差、频率偏移和稳态误差等方面。
在此基础上,本文提出了一种改进的三相锁相环结构,通过引入先进的控制策略和滤波技术,有效提高了锁相环在电网不平衡条件下的性能。
本文还通过仿真和实验验证了所提改进三相锁相环的有效性和优越性。
仿真结果表明,在电网不平衡条件下,所提锁相环具有更快的动态响应、更高的稳态精度和更强的鲁棒性。
实验结果进一步验证了仿真分析的结论,证明了所提改进三相锁相环在实际电力系统中的应用潜力。
本文对电网不平衡下的三相锁相环进行了全面研究,不仅分析了电网不平衡对锁相环性能的影响,还提出了一种有效的改进策略,并通过仿真和实验验证了其性能。
研究结果为三相电力系统的同步控制提供了新的思路和方法,对提高电力系统的运行效率和稳定性具有重要意义。
2. 电网不平衡的影响电网不平衡是一种常见的电力系统运行状态,它会对电力系统的稳定运行产生不利影响。
电网不平衡主要表现在三相电压或电流的不对称性上,这种不对称性可能由多种因素引起,如单相负载的接入、线路故障、发电机故障等。
(1)影响锁相精度:三相锁相环是依赖于三相电压或电流的对称性进行相位锁定的。
当电网出现不平衡时,三相电压或电流的对称性被破坏,导致锁相环难以准确锁定相位,进而降低系统的控制精度。
(2)增加系统振荡风险:电网不平衡可能导致系统出现负序和零序分量,这些分量会激发系统中的振荡模式,增加系统的不稳定性。

基于dq变换的锁相环设计与仿真何攀;席自强【摘要】针对一般锁相环在电网电压波动时存在锁相误差的问题,提出了一种基于dq变换的锁相环新方案,并对锁相环参数进行了整定.对于电网电压频率变化、相位变化以及谐波注入的影响,利用matlab进行了仿真分析.仿真结果表明,新方案有很好的跟踪效果,跟踪速度快,精度高,能较好实现相位锁定.【期刊名称】《湖北工业大学学报》【年(卷),期】2017(032)005【总页数】3页(P93-95)【关键词】电压波动;dq变换;锁相环【作者】何攀;席自强【作者单位】湖北工业大学太阳能高效利用湖北省协同创新中心,湖北武汉430068;湖北工业大学太阳能高效利用湖北省协同创新中心,湖北武汉 430068【正文语种】中文【中图分类】TM464新能源技术的不断发展,使得越来越多的分布式电源接入电网中,能精确快速锁定电网电压的相位,对于需要并网运行的设备也变得越来越重要。
锁相主要分为硬件锁相和软件锁相两种,由于硬件锁相精确度不高,容易受到干扰,所以现在广泛采用软件锁相技术,数字处理器的大规模发展,也使得软件锁相技术更易于实现[1-4]。
传统的锁相环采用过零锁相的方法,但在电压存在畸变的情况下,锁相效果不太理想;电压不平衡的状态下,可以通过傅里叶变换将基波成分和谐波成分分别提取出来,但必须采集完整的周期数据,不能实时计算[5-7]。
因此,本文根据坐标变换的原理[8],建立了三相电网电压在同步旋转坐标系下的系统模型,详细阐述了锁相环的结构及原理。
并通过仿真验证了锁相环在电压波动时的跟踪效果。
在三相电网电压平衡的情况下,三相电网电压全部为正序分量,其在abc坐标系下的表达式如下:其中,Um为各相电压幅值,ω为电网电压角频率,φ为初始相角。
利用Clark变换,将式(1)中三相电压变换到两相静止αβ坐标系:再利用Park变换,最终转换为dq坐标系下的直流分量Ud、Uq:1.1 同步坐标系锁相环原理根据瞬时无功功率理论,将三相电压合成矢量在同步坐标系下进行分解,图1所示为同步旋转坐标系示意图,图中Us为三相电压合成矢量,与坐标轴的夹角为θ(θ=ωt),θ′为锁相环实际输出电压矢量与坐标轴的夹角,Ud、Uq分别为三相合成矢量在同步旋转坐标系下的d轴和q轴上的直流分量。
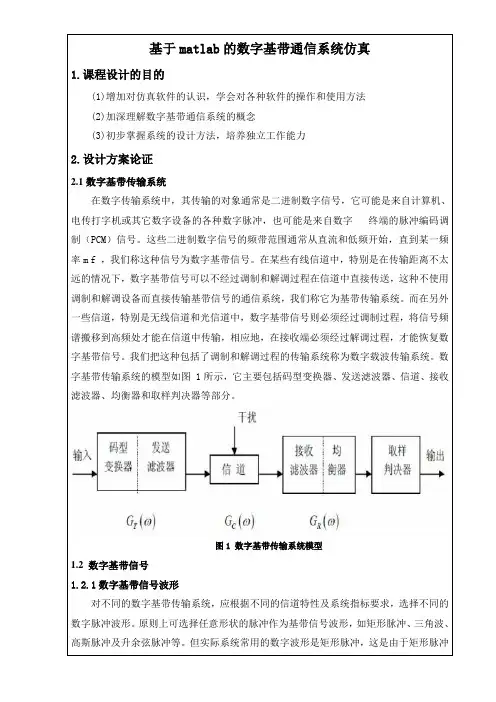
基于matlab的数字基带通信系统仿真1.课程设计的目的(1)增加对仿真软件的认识,学会对各种软件的操作和使用方法(2)加深理解数字基带通信系统的概念(3)初步掌握系统的设计方法,培养独立工作能力2.设计方案论证2.1数字基带传输系统在数字传输系统中,其传输的对象通常是二进制数字信号,它可能是来自计算机、电传打字机或其它数字设备的各种数字脉冲,也可能是来自数字终端的脉冲编码调制(PCM)信号。
这些二进制数字信号的频带范围通常从直流和低频开始,直到某一频率m f ,我们称这种信号为数字基带信号。
在某些有线信道中,特别是在传输距离不太远的情况下,数字基带信号可以不经过调制和解调过程在信道中直接传送,这种不使用调制和解调设备而直接传输基带信号的通信系统,我们称它为基带传输系统。
而在另外一些信道,特别是无线信道和光信道中,数字基带信号则必须经过调制过程,将信号频谱搬移到高频处才能在信道中传输,相应地,在接收端必须经过解调过程,才能恢复数字基带信号。
我们把这种包括了调制和解调过程的传输系统称为数字载波传输系统。
数字基带传输系统的模型如图 1所示,它主要包括码型变换器、发送滤波器、信道、接收滤波器、均衡器和取样判决器等部分。
图1 数字基带传输系统模型1.2 数字基带信号1.2.1数字基带信号波形对不同的数字基带传输系统,应根据不同的信道特性及系统指标要求,选择不同的数字脉冲波形。
原则上可选择任意形状的脉冲作为基带信号波形,如矩形脉冲、三角波、高斯脉冲及升余弦脉冲等。
但实际系统常用的数字波形是矩形脉冲,这是由于矩形脉冲纤数字传输系统中的线路传输码型。
此外,CMI 码和曼彻斯特码一样都是将一位二进制码用一组两位二进制码表示,因此称其为1B2B 码。
(5)4B/3T 码4B/3T 码是1B/1T 码的改进型它把4 个二进制码元变换为3个三进制码元。
显然,在相同信息速率的条件下,4B/3T 码的码元传输速率要比1B/1T 码的低,因而提高了系统的传输效率。

基于SOGI—FLL+NF的复合锁相环三相并网系统中,锁相环能检测出三相电网电压的相位和频率信息,它对整个逆变系统的安全稳定运行有重要作用。
三相电网发生波动时,同步旋转锁相环易受二倍频分量的影响导致锁相不准确。
文章采用SOGI-FLL+NF复合锁相结构,消除三相电网电压波动对锁相效果的影响,通过Matlab/Simulink仿真证明复合结构锁相环的可行性和准确性。
标签:锁相环;二阶广义积分器;陷波器引言對于分布式发电系统而言,为了保证并网逆变器能够向电网输送高质量的电能,这就要求并网电流必须与电压同步。
谐波会使电网电压波动,所以需要锁相环实时准确的获取电网电压的幅值和相位信息,获取信息准确与否直接决定了设备安全稳定运行。
在三相并网逆变器系统中常采用同步旋转坐标系锁相环(SRF-PLL),当三相电压平衡时,有较好的锁相效果,但是当电网电压不平衡时,SRF-PLL容易受二倍频分量影响使精度下降。
二阶广义积分(SOGI)型锁相技术能够抑制谐波分量,但是在精度上有待提高。
陷波器可以看作是一个带宽很小的带阻滤波器,把某一频率的信号滤除。
为了消除谐波对PLL的影响,本文采用SOGI-FLL+NF 复合结构仿真分析锁相效果。
1 三相电网电压不平衡时SRF-PLL性能分析SRF-PLL将输入abc坐标系下的三相电网电压经过Clark和park变换,得到dq系下的电压,调节q轴分量为0,使dq坐标系的旋转角θ与电网电压矢量的相位角相同,来实现锁相[1]。
当电网电压不平衡并采用三相三线的方式接入电网的时候,只考虑正序分量和负序分量。
此时电网电压可以表示为:式中:Vgp、Vgn是电网电压的正序与负序分量的幅值,Φp、Φn正序和负序分量的初始相位,ω代表电网电压角频率。
对式(1)进行Clark变换,再进行Park变换,电网电压矢量在两相旋转坐标系下的表达式为:可以看出,电网电压不平衡时,dq轴下电网电压正序分量变成了直流量,基波负序分量变成了二倍频交流量。

一种实用的5阶电荷泵锁相环性能分析与设计仿真
邓茜;王玫;李加升
【期刊名称】《计算机工程与科学》
【年(卷),期】2009(031)008
【摘要】本文在分析5阶锁相环基本原理和线性化数学模型的基础上,给出了一种实用的4阶环路滤波器的设计方法,用Matlab编程计算锁相环的参数;用ADS工具对系统性能进行仿真,仿真结果与预期结果相吻合;比较了具有相同环路带宽和相位裕度下的高阶锁相环的杂散性能.这对5阶电荷泵锁相环的系统设计和仿真有一定的指导意义.
【总页数】3页(P144-146)
【作者】邓茜;王玫;李加升
【作者单位】桂林电子科技大学信息与通信学院,广西,桂林,541004;桂林电子科技大学信息与通信学院,广西,桂林,541004;桂林电子科技大学信息与通信学院,广西,桂林,541004
【正文语种】中文
【中图分类】TN74
【相关文献】
1.一种高性能4阶电荷泵锁相环的设计 [J], 陈志明;尹勇生;邓红辉;梁上泉
2.基于ADS的三阶电荷泵锁相环的研究及仿真 [J], 赵雪;孙越强;杜起飞
3.一种新型锁相环电荷泵的分析与设计 [J], 谢凤英;孙金中;郭锐
4.基于ADS三阶电荷泵锁相环的分析和仿真 [J], 张明;吴秀龙;张兴建;王诗兵
5.基于ADS三阶电荷泵锁相环的分析和仿真 [J], 张明;吴秀龙;张兴建;王诗兵因版权原因,仅展示原文概要,查看原文内容请购买。


AWGN信道下数字通信系统的蒙特卡洛仿真(基于matlab)数字通信理论课程设计⼀、实验⽬的:1、加深对AWGN 信道下数字通信系统的理解。
2、掌握数字通信系统蒙特卡洛仿真的基本⽅法。
⼆、实验内容:在AWGN 信道下,完成16QAM 系统的误⽐特率性能仿真,绘制系统的BER 曲线,并与理论计算的结果进⾏对⽐。
具体包括如下内容:1、编写程序⽣成随机的⼆元⽐特序列,该序列由{0,1}构成。
2、根据所选择的调制⽅式,将⽐特序列映射为星座图上的点。
3、将所⽣成的信号通过AWGN 信道进⾏传输,编写程序实现随机的加性⾼斯⽩噪声过程,并完成对信号的加噪。
4、实现接收机的解调、检测与判决算法。
要求使⽤相⼲接收机,最⼤似然检测。
5、在不同的⽐特信噪⽐(0/b E N )的条件下统计系统的⽐特错误概率(BER ),画出BER 随0/b E N 变化的曲线。
0/b E N 的变化范围选为0~10dB 。
6、在同⼀幅图中画出理论曲线,并将两者进⾏对⽐。
三、实验要求:1、利⽤计算机仿真完成上述实验。
可以使⽤Matlab 、C 、C++或任何⼀种编程语⾔,但不允许使⽤已有的通信系统仿真模块,例如SIMULINK 中已有的模块。
2、要求画出系统框图,说明仿真流程,给出仿真结果,提供理论的误码率结果及推导过程,进⾏必要的分析和讨论,并在附录中提供程序源代码,列出参考⽂献。
四、实验原理: 1、蒙特卡罗仿真(1)基本概念Monte Carlo 仿真⽅法是通过⼤量的计算机模拟来检验系统的动态特性并归纳出统计结果的⼀种随机分析⽅法,它包括伪随机数的产⽣,Monte Carlo 仿真设计以及结果解释等内容,其作⽤在于⽤数学⽅法模拟真实物理环境,并验证系统的可靠性与可⾏性。
(2)基本⽅法Monte Carlo仿真⽅法⼜称统计实验⽅法,它是⼀种采⽤统计抽样理论近似求解数学、物理及⼯学问题的⽅法。
它解决问题的基本思想是,⾸先建⽴与描述该问题相似的概率模型,然后对模型进⾏随机模拟或统计抽样,在利⽤所得到的结果求出特征的统计估计值作为原问题的近似解,并对解的精度做出某些估计。

台南山学院烟台烟电机与拖动课程设计题目基于Matlab的双闭环三相异步电动机的串级调速仿真姓名:庞超所在学院:计算机与电气自动化学院所学专业:自动化班级:09自动化02班学号: 200902010210指导教师:刘丽丽完成时间: 2012-9-23任务书电机与拖动是自动化专业的一门重要专业基础课。
它主要是研究电机与电力拖动的基本原理,以及它与科学实验、生产实际之间的联系。
通过学习使学生掌握常用交、直流电机、变压器及控制电机的基本结构和工作原理;掌握电力拖动系统的运行性能、分析计算,电动机选择及实验方法等。
电机与拖动课程设计是理论教学之后的一个实践环节,通过完成一定的工程设计任务,学会运用本课程所学的基本理论解决工程技术问题,为学习后续有关课程打好必要的基础。
一、设计课题基于Matlab的异步电动机调压调速系统的仿真二、课程设计的基本要求1.使学生具有自主设计电路原理读图、查阅参考书籍和手册及资料文献的能力。
2.设计、计算、文件选取、画出设计电路图3.撰写严谨的、有理论根据的、实事求是的、文理通顺的字迹端正的电机与拖动课程设计报告。
三、电机与拖动课程设计时间1.设计电路原理读图、查阅参考书籍和手册及资料文献(1.5天)。
2.设计、计算、文件选取、画出设计电路图(1.5天)。
3.验收及校验(0.5天)4.完成课程设计报告(1.5天)四、课程设计报告要求课程设计报告要求字迹工整、文字通顺;其撰写内容包括:1.目录2.课程设计所用的基本知识3.参数计算、电路设计等。
4.总结5.参考文献摘要本文所讨论的是双闭环三相异步电动机的串级调速的基本原理与实现方法。
对于一般交流电动机的调速,我们都是从电动机的定子侧引入控制变量(改变定子供电电压、频率)来实现的,这对于转子处于短路状态的交流鼠笼型转子异步电动机是唯一途径。
但是,对于绕线式异步电动机来说,由于改变其转子绕组控制变量以实现调速,转子侧的控制变量有电流、电动势、电阻等。
simulink锁相环pll用法
Simulink中的锁相环(Phase-Locked Loop,PLL)是一种常用的信号处理器件,用于频率和相位同步。
它可以用于许多应用中,例如通信系统、数据转换、时钟恢复和信号重构等。
在Simulink中使用PLL有几个关键的步骤:
1.模拟输入信号:首先需要生成或获取输入信号,这通常是
一个模拟信号或数字信号。
2.创建PLL模块:打开Simulink环境,创建一个新的模型,
在模型中添加PLL模块。
对于PLL模块的创建,可以在
Simulink库中搜索PLL模块并将其拖放到模型中。
3.设置参数:对于PLL模块,需要设置一些关键参数,例如
参考频率(Reference Frequency)、带宽(Loop Bandwidth)、初始相位(Initial Phase)等。
这些参数决定了PLL的性能
和工作方式。
4.连接信号和参考:将输入信号连接到PLL模块,并指定参
考信号。
参考信号可以是外部提供的,也可以是由PLL根
据输入信号生成的稳定参考。
5.仿真和分析:设置好参数并连接信号后,运行模型进行仿
真。
可以观察输出信号的频率和相位与参考信号的同步情
况,并进行性能分析和优化。
需要注意的是,PLL的具体用法和设置参数会因应用和设计需求而有所差异。
Simulink提供了丰富的库和模块,可以根据具体
应用需求选择和配置适当的PLL模块。
还可以通过自定义模块或编写MATLAB脚本来实现更高级的PLL功能。
MATLAB中环形振荡器仿真振荡器振荡器是将直流电转变为交流电的过程,用来产生一定频率的交流信号,是有源器件,多用于锁相环中。
环形振荡器环形振荡器,是由三个非门或更多奇数个非门输出端和输入端首尾相接,构成环状的机器。
图中所展示的是一种频率可调的环形振荡器,通过增加控制晶体管,控制充放电速度,改变振荡器频率。
HSPICE仿真我首先仿真了三级反相器首尾相接形成的环形振荡器。
振荡周期为200ps。
因为没有增加控制器件,所以充放电波形比较对称。
注意!环振的起振是通过在电源初增加小的扰动即可实现,而不是给某个节点加初始电压,因为环振没有输入输出!(这个问题困扰了我好久接下来,我在第二级反相器上,给nmos串联了4个同样尺寸的nmos,用于调节振荡频率。
开始我只串联了1个nmos,但仿真波形差异不大。
所以多串了几个。
后面思考:应该也可以通过在节点接电容来改变频率。
通过波形可以发现充放电所需时间不同,放电明显比充电时间要长。
这就是因为多串了几个nmos,相当于加长了沟道。
同时,节点的输出幅度不是全摆幅(从0到Vdd)。
周期在260ps左右。
HSPICE代码我使用的是TSMC 0.18um的工艺库,2019版HSPICE。
注意!第一行*标题行一定要加!记得修改库地址哦【三级反相器环振】**buffer.param Supply = 1.8.lib ‘C:\synopsys\Hspice_L-2016.03-2\mm018.L’ TT * Set 0.18um library.opt scale=0.1ump0 out0 in Vdd Vdd pch l=2 w=6 ad=30 pd=6 as=30 ps=6 mn0 out0 in Gnd GND nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mp1 out1 out0 Vdd Vdd pch l=2 w=6 ad=30 pd=6 as=30 ps=6 mn1 out1 out0 Gnd GND nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mp2 in out1 Vdd Vdd pch l=2 w=6 ad=30 pd=6 as=30 ps=6 mn2 in out1 Gnd GND nch l=2 w=3 ad=15 pd=3 as=15 ps=3c in gnd 0.1fvdd vdd gnd pwl(10P 0 100P 1.8).tran 0.01n 5u.op.option captab = 1.OPTION POST=2 TNOM=27 NOMOD LIST METHOD=GEAR.end【频率可调环振】*buffer_2.param Supply = 1.8.lib ‘C:\synopsys\Hspice_L-2016.03-2\mm018.L’ TT * Set 0.18um library.opt scale=0.1ump0 out0 in Vdd Vdd pch l=2 w=6 ad=30 pd=6 as=30 ps=6 mn0 out0 in Gnd GND nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mp1 out1 out0 Vdd Vdd pch l=2 w=6 ad=30 pd=6 as=30 ps=6 mn1 out1 out0 n1 GND nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mn12 n1 vctrl n2 gnd nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mn13 n2 vctrl n3 gnd nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mn14 n3 vctrl n4 gnd nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mn15 n4 vctrl gnd gnd nch l=2 w=3 ad=15 pd=3 as=15 ps=3 mp2 in out1 Vdd Vdd pch l=2 w=6 ad=30 pd=6 as=30 ps=6 mn2 in out1 Gnd GND nch l=2 w=3 ad=15 pd=3 as=15 ps=3c in gnd 0.1fvdd vdd gnd pwl(10P 0 100P 1.8)vctrl vctrl gnd 1.1.tran 0.01n 5u.op.option captab = 1.OPTION POST=2 TNOM=27 NOMOD LIST METHOD=GEAR。
电荷泵锁相环的基础研究随着科技的不断发展,各种电子设备如手机、电视、计算机等已成为人们日常生活和工作中不可或缺的工具。
为了满足人们对电子设备性能和功能不断增长的需求,各种先进的信号处理技术和电路设计方法被引入到这些设备中。
其中,电荷泵锁相环(Charge PumpPhase-Locked Loop,简称CP-PLL)是一种非常重要的技术,它在频率合成、相位跟踪和信号恢复等领域有着广泛的应用。
本文将围绕电荷泵锁相环的基础研究展开讨论。
电荷泵锁相环的研究已经经历了数十年的发展历程。
在国内外相关领域的研究中,理论研究和实验研究都取得了重要的进展。
在理论方面,研究人员对电荷泵锁相环的相位检测、环路控制、输出调节等各个组成部分进行了深入的分析和建模,提出了一系列有效的算法和电路设计。
在实验方面,科研人员通过精心设计的实验方案,验证了电荷泵锁相环在各种不同场景下的性能表现。
电荷泵锁相环是一种基于相位检测和环路控制技术的闭环控制系统。
它通过将输入信号与参考信号进行相位比较,产生一个控制电压,用于调节振荡器的频率和相位,从而使输出信号与参考信号保持同步。
相位检测是电荷泵锁相环的核心组成部分,它通过比较输入信号和反馈信号的相位差,产生一个与相位差成正比的电流或电压。
这个电流或电压作为控制信号输入到环路控制器中,用于调节电荷泵的工作状态。
环路控制器通常由一个运算放大器和一个电荷泵组成。
运算放大器将相位检测器的输出信号进行放大,以产生足够的控制电压。
电荷泵则将控制电压转化为电流,用于调节振荡器的频率和相位。
输出调节部分通常由一个低通滤波器和一个振荡器组成。
低通滤波器用于滤除电荷泵产生的交流分量,只保留直流成分,从而使控制电压能够平滑地调节振荡器的频率和相位。
振荡器则产生最终的输出信号,其频率和相位受控制电压调节。
本文采用文献调研和理论分析相结合的方法,对电荷泵锁相环的相关研究进行了深入的研究。
通过查阅相关文献和专利,了解了电荷泵锁相环的国内外研究现状和发展趋势。
2 o o 6年1 o月 沈阳理工大学学报 第2 5卷第5期TRANSACTIONS OF SHENYANG LIGONG UNIVERSITY Vo1.2 5 No.5
Oct. 2 O O 6
文章编号:1003—1251(2006)05—0051—02
跳频跟踪环在Matlab 6.5上的仿真设计
杨 力 。,滕振宇 ,潘成胜 (1.沈阳理工大学通信与网络工程中心,辽宁沈阳110168;2.南京理工大学) 摘要:介绍了一种跳频跟踪方法延迟锁相环的工作原理,并使用Matlab6.5建立了延 迟锁相环的仿真系统.根据仿真结果对这种跳频跟踪环路跟踪性能进行分析,为跳频系 统的整体仿真实现奠定了一定的基础.
关键词:延迟锁相环;跟踪;计算机仿真 中图分类号:TN914.43 文献标识码:A
跳频同步信息的跟踪可采用自动控制系统常 用的方法,即当跟踪发生偏差时产生误差信号,用 适当的方法检测出误差信号(反映偏差的大小和 方向)作为控制信号,驱动执行部件,使系统回到 正确的平衡状态.一般采用锁相环原理完成同步 信息的跟踪过程.有两种常用的锁相环:.r一抖动锁 相环和延迟锁相环¨ J.这两种锁相环实质上很相 似,都属于”提前一迟后”型锁相环,但产生误差信 号的方法略有不同..r一抖动锁相环采用单个锁相 环检测出误差信号,而延迟锁相环采用两个独立 的相关器检测出误差信号.其中.r一抖动锁相环采 用单个锁相环检测出误差信号,而延迟锁相环采 用两个独立的相关器检测出误差信号.比较两种 锁相环的性能特点,延迟锁相环方法比较适用于 快速跳频系统的同步信息跟踪. 本文针对高跳速的跳频通信系统的同步跟踪 过程进行了理论分析与研究.‘并且利用仿真软件 Matlab6.5¨ 进行仿真. 延迟锁相环工作原理 延迟锁相环用于同步信息跟踪的原理是:环 路中的频率合成器在跳频序列发生器的作用下, 产生两个与接收到的跳频信号的频率超前一段时 收稿日期:2005—11—16 基金项目:国防预研项目重点基金资助. 作者简介:杨力(1982一),女,黑龙江佳木斯人。硕士研究生 间和延迟一段时间的信号,信号频率与接收信号 的频率正好相差一个中频.经带通滤波器和包络 检波器处理后,其输出信号相减,获得超前一段时 间的本振信号同接收信号混频后的中频信号,和 滞后一段时间的本振信号同接收信号混频后的中 频信号相差的电压.这个电压是具有超前迟后鉴 别能力的信号,能实现跳频信号的跟踪.跟踪环路 模型如图1所示.
锁相环的ADS仿真实验报告一.ADF4113芯片介绍1.概述频率合成器中的ADF4113可用于在上变频和下变频上执行本地振荡器,无线接收器和发送器部分。
他们包括一个低噪声数字PFD(相位频率侦测器),一个精密电荷泵,一个可编程参考分频器,可编程A和B计数器和一个双模预置分频器性(P/P+1)。
A(6-bit)和B(13-bit)计数器,会同双模分频器性(P/P+1),实现一个N分频器(N =BP+A)。
此外,14位的参考计数器(R计数器)在PFD 输入时允许投入可选REFIN频率。
如果用合成器被一个外部环路滤波器和电压控制振荡器使用,那么一个完整的PLL(锁相环)就可实现。
该器件工作在2.7 V至5.5 V的电压供应范围内,并且可以不使用时使其开路。
2.电路描述参考输入部分:参考输入级如图24。
SW1和SW2是常闭开关。
SW3是常开。
当电源关闭时,SW3是封闭的和SW1和SW2打开。
这将确保在电源关闭在REFIN引脚上没有加载。
射频输入级:RF输入阶段如图25所示。
其次是一个2级限幅放大器生成一个CML(电流模式逻辑)时钟电平所需的预分频器。
预分频器性(P / P+1)该双模预置分频器性(P / P+1),随着A和B计数器,使大型分频比,N,实现(每组的BP +A)。
该双模预分频器,操作在CML时钟电平,对CMOS A 和B计数器需要设置时钟从射频输入级平台并划分到了可管理的频率。
预分频器是可编程的。
它可以设置软件到达8 / 9,16/17,32/33,或64/65。
它是基于同步4 / 5的核心。
A和B计数器A和B的CMOS计数器连结模数双重预分频器,使其允许在一个广泛的区域的PLL反馈比例不等计数器。
计数器将被指定的工作,当预分频器的输出小于等于200MHz。
因此,随着一个 2.5GHz的RF输入,分频器16/17的频率值是有效的,但对8 / 9值无效。
相位频率侦测器(PFD)和电荷泵在PFD需要从R计数器和N计数器输入(N=BP + A)并且按比例生成的、输出相位和它们之间的频率差。
锁相环仿真 1.锁相环的理论分析 1.1锁相环的基本组成 锁相环路是一种反馈控制电路,简称锁相环(PLL,Phase-Locked Loop)。锁相环的特点是:利用外部输入的参考信号控制环路部振荡信号的频率和相位。因锁相环可以实现输出信号频率对输入信号频率的自动跟踪,所以锁相环通常用于闭环跟踪电路。锁相环在工作的过程中,当输出信号的频率与输入信号的频率相等时,输出电压与输入电压保持固定的相位差值,即输出电压与输入电压的相位被锁住,这就是锁相环名称的由来。锁相环通常由鉴相器(PD,Phase Detector)、环路滤波器(LF,Loop Filter)和压控振荡器(VCO,Voltage Controlled Oscillator)三部分组成,锁相环组成的原理框图如图示:
锁相环中的鉴相器又称为相位比较器,它的作用是检测输入信号和输出信号的相位差,并将检测出的相位差信号转换成uD(t)电压信号输出,该信号经低通滤波器滤波后形成压控振荡器的控制电压uC(t),对振荡器输出信号的频率实施控制。
1.2锁相环的工作原理 1.2.1鉴相器 锁相环中的鉴相器(PD)通常由模拟乘法器组成,利用模拟乘法器组成的鉴相器电路如图示:
鉴相器的工作原理是:设外界输入的信号电压和压控振荡器输出的信号电压分别为:
式中的ω0为压控振荡器在输入控制电压为零或为直流电压时的振荡角频率,称为电路的固有振荡角频率。则模拟乘法器的输出电压uD为:
1.2.2 低通滤波器 低通滤波器(LF)的将上式中的和频分量滤掉,剩下的差频分量作为压控振荡器的输入控制电压uC(t)。即uC(t)为: .. .. . . . .
式中的ωi为输入信号的瞬时振荡角频率,θi(t)和θO(t)分别为输入信号和输出信号的瞬时位相,根据相量的关系可得瞬时频率和瞬时位相的关系为: 即
则,瞬时相位差θd为
对两边求微分,可得频差的关系式为
上式等于零,说明锁相环进入相位锁定的状态,此时输出和输入信号的频率和相位保持恒定不变的状态,uc(t)为恒定值。当上式不等于零时,说明锁相环的相位还未锁定,输入信号和输出信号的频率不等,uc(t)随时间而变。
1.2.3 压控振荡器 压控振荡器(VCO)的压控特性如图示
该特性说明压控振荡器的振荡频率ωu以ω0为中心,随输入信号电压uc(t)线性地变化,变化的关系如下: 上式说明当uc(t)随时间而变时,压控振荡器(VCO)的振荡频率ωu也随时间而变,锁相环进入“频率牵引”,自动跟踪捕捉输入信号的频率,使锁相环进入锁定的状态,并保持ω0=ωi的状态不变。
2.信号流程图 锁相环的原理框图如下:
其工作过程如下: (1)压控振荡器的输出Uo经过采集并分频; (2)输出和基准信号同时输入鉴相器; (3)鉴相器通过比较上述两个信号的频率差,然后输出一个直流脉冲电压Ud; (4)Ud进入到滤波器里面,滤除高频成分后得到信息Ue; (5)Ue进入到压控震荡器VCO里面,控制频率随输入电压线性地变化; (6)这样经过一个很短的时间,VCO的输出就会稳定于某一期望值。 .. .. . . . . 3.二阶环仿真源程序代码及仿真结果 3.1 程序代码: % File: c6_nltvde.m w2b=0; w2c=0; % initialize integrators yd=0; y=0; % initialize differential equation tfinal = 50; % simulation time fs = 100; % sampling frequency delt = 1/fs; % sampling period npts = 1+fs*tfinal; % number of samples simulated ydv = zeros(1,npts); % vector of dy/dt samples yv = zeros(1,npts); % vector of y(t) samples % % beginning of simulation loop for i=1:npts t = (i-1)*delt; % time if t<20 ydd = 4*exp(-t/2)-3*yd*abs(y)-9*y; % de for t<20 else ydd = 4*exp(-t/2)-3*yd-9*y; % de for t>=20 end w1b=ydd+w2b; % first integrator - step 1 w2b=ydd+w1b; % first integrator - step 2 yd=w1b/(2*fs); % first integrator output w1c=yd+w2c; % second integrator - step 1 w2c=yd+w1c; % second integrator - step 2 y=w1c/(2*fs); % second integrator output ydv(1,i) = yd; % build dy/dt vector yv(1,i) = y; % build y(t) vector end % end of simulation loop plot(yv,ydv) % plot phase plane xlabel('y(t)') % label x axis ylabel('dy/dt') % label y zxis % End of script file. % File: pllpost.m % kk = 0; while kk == 0 k = menu('Phase Lock Loop Postprocessor',... 'Input Frequency and VCO Frequency',... 'Input Phase and VCO Phase',... 'Frequency Error','Phase Error','Phase Plane Plot',... 'Phase Plane and Time Domain Plots','Exit Program'); if k == 1 .. .. . . . . plot(t,fin,'k',t,fvco,'k') title('Input Frequency and VCO Freqeuncy') xlabel('Time - Seconds');ylabel('Frequency - Hertz');pause elseif k ==2 pvco=phin-phierror;plot(t,phin,t,pvco) title('Input Phase and VCO Phase') xlabel('Time - Seconds');ylabel('Phase - Radians');pause elseif k == 3 plot(t,freqerror);title('Frequency Error') xlabel('Time - Seconds');ylabel('Frequency Error - Hertz');pause elseif k == 4 plot(t,phierror);title('Phase Error') xlabel('Time - Seconds');ylabel('Phase Error - Radians');pause elseif k == 5 ppplot elseif k == 6 subplot(211);phierrn = phierror/pi; plot(phierrn,freqerror,'k');grid; title('Phase Plane Plot');xlabel('Phase Error /Pi'); ylabel('Frequency Error - Hertz');subplot(212) plot(t,fin,'k',t,fvco,'k');grid title('Input Frequency and VCO Freqeuncy') xlabel('Time - Seconds');ylabel('Frequency - Hertz');subplot(111) elseif k == 7 kk = 1; end end % End of script file. % File: pllpre.m % clear all % be safe disp(' ') % insert blank line fdel = input('Enter the size of the frequency step in Hertz > '); fn = input('Enter the loop natural frequency in Hertz > '); lambda = input('Enter lambda, the relative pole offset > '); disp(' ') disp('Accept default values:') disp(' zeta = 1/sqrt(2) = 0.707,') disp(' fs = 200*fn, and') disp(' tstop = 1') dtype = input('Enter y for yes or n for no > ','s');