《流体力学》(罗惕乾 著)课后习题答案 机械工业出版社
- 格式:pdf
- 大小:572.61 KB
- 文档页数:19

答案 :第一章习题答案选择题(单选题)1.1 按连续介质的概念,流体质点是指:(d)(a )流体的分子;(b)流体内的固体颗粒;(c )几何的点;(d )几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
1.2 作用于流体的质量力包括:(c)(a )压力;(b)摩擦阻力;(c )重力;(d)表面张力。
1.3 单位质量力的国际单位是:(d )(a )N ;(b )Pa ;(c)kg N /;(d )2/s m 。
1.4 与牛顿内摩擦定律直接有关的因素是:(b )(a)剪应力和压强;(b )剪应力和剪应变率;(c)剪应力和剪应变;(d )剪应力和流速。
1.5 水的动力黏度μ随温度的升高:(b )(a )增大;(b )减小;(c )不变;(d )不定。
1.6 流体运动黏度ν的国际单位是:(a )(a )2/s m ;(b )2/m N ;(c )m kg /;(d )2/m s N ⋅。
1.7 无黏性流体的特征是:(c )(a )黏度是常数;(b )不可压缩;(c )无黏性;(d )符合RT p=ρ。
1.8 当水的压强增加1个大气压时,水的密度增大约为:(a )(a )1/20000;(b)1/10000;(c)1/4000;(d)1/2000. 1.9 水的密度为10003kg/m ,2L 水的质量和重量是多少? 解:10000.0022m V ρ==⨯=(kg )29.80719.614G mg ==⨯=(N )答:2L 水的质量是2kg ,重量是19.614N 。
1.10 体积为0.53m 的油料,重量为4410N ,试求该油料的密度是多少? 解:44109.807899.3580.5m G g V V ρ====(kg/m 3) 答:该油料的密度是899.358kg/m 3。
1.11 某液体的动力黏度为0.005Pa s ⋅,其密度为8503/kg m ,试求其运动黏度。
解:60.005 5.88210850μνρ-===⨯(m 2/s )答:其运动黏度为65.88210-⨯m 2/s 。

流体力学答案流体力学课后答案 分析答案 解答BP1.1.1 根据阿佛迦德罗定律,在标准状态下(T = 273°K ,p = 1.013×105 Pa )一摩尔空气(28.96ɡ)含有6.022×10 23个分子。
在地球表面上70 km 高空测量得空气密度为8.75×10 -5㎏/m 3。
试估算此处 10 3μm 3体积的空气中,含多少分子数n (一般认为n <106 时,连续介质假设不再成立)答: n = 1.82×10 3提示:计算每个空气分子的质量和103μm 3体积空气的质量 解: 每个空气分子的质量为 g 1081.410022.6g 96.282323-⨯=⨯=m 设70 km 处103μm 3体积空气的质量为M g 1075.8)m 1010)(kg/m 1075.8(20318335---⨯=⨯⨯=M323201082.1g1081.4g 1075.8⨯=⨯⨯==--m M n 说明在离地面70 km 高空的稀薄大气中连续介质假设不再成立。
BP1.3.1 两无限大平行平板,保持两板的间距δ= 0.2 mm 。
板间充满锭子油,粘度为μ= 0.01Pa ⋅s ,密度为ρ= 800 kg / m 3。
若下板固定,上板以u = 0.5 m / s 的速度滑移,设油内沿板垂直方向y 的速度u (y)为线性分布,试求: (1) 锭子油运动的粘度υ; (2) 上下板的粘性切应力τ1、τ2 。
答: υ= 1.25×10 – 5 m 2/s, τ1=τ2 = 25N/m 2。
提示:用牛顿粘性定侓求解,速度梯度取平均值。
解:(1 ) /s m 1025.1kg/m800/sm kg 0.0125-3⨯===ρμν (2)沿垂直方向(y 轴)速度梯度保持常数,δμμττ/21u dydu==== (0.01Ns /m 2)(0.5m/s)/(0.2×10-3m)=25N/m 2BP1.3.2 20℃的水在两固定的平行平板间作定常层流流动。

删掉的题目:1-14、2-6、2-9、2-11、2-17、3-10、3-19、4-5、4-13《流体力学与流体机械之流体力学》第一章 流体及其物理性质1-8 1.53m 的容器中装满了油。
已知油的重量为12591N 。
求油的重度γ和密度ρ。
解:312591856.5kg/m 9.8 1.5m V ρ===⨯;38394N/m g γρ== 1-11 面积20.5m A =的平板水平放在厚度10mm h =的油膜上。
用 4.8N F =的水平力拉它以0.8m/s U =速度移动(图1-6)。
若油的密度3856kg/m ρ=。
求油的动力粘度和运动粘度。
解:29.6N/m F Aτ==,Uh τμ=,所以,0.12Pa s hUτμ==,42/0.12/856 1.410m /s νμρ-===⨯ 1-12 重量20N G =、面积20.12m A =的平板置于斜面上。
其间充满粘度0.65Pa s μ=的油液(图1-7)。
当油液厚度8mm h =时。
问匀速下滑时平板的速度是多少。
解:sin 20 6.84F G N ==,57Pa s FAτ==, 因为U h τμ=,所以570.0080.7m/s 0.65h U τμ⨯=== 1-13 直径50mm d =的轴颈同心地在50.1mm D =的轴承中转动(图1-8)。
间隙中润滑油的粘度0.45Pa s μ=。
当转速950r/min n =时,求因油膜摩擦而附加的阻力矩M 。
解:将接触面沿圆柱展开,可得接触面的面积为:20.050.10.016m A dL ππ==⨯⨯=接触面上的相对速度为:2 2.49m/s 2260d d nu πω=== 接触面间的距离为:0.05mm 2D dδ-== 接触面之间的作用力:358.44N du F AA dy u δμμ=== 则油膜的附加阻力矩为:8.9N m 2dM F== 1-14 直径为D 的圆盘水平地放在厚度为h 的油膜上。
6-3 圆管流的临界雷诺数(下临界雷诺数):(a )随管径变化; (b )随流体的密度变化; (c )随流体的粘度变化; (d )不随以上各量变化。
6-11 工业管道的沿程摩组系数λ,在紊流过渡区随雷诺数的增加: (a ) 增加 (b ) 减小 (c ) 不变 (d )不定 6_12解:查表得10°时水 /s m 101.312-6⨯=ν230076341031.11.01Re 6>=⨯⨯==-νvd紊流m /s 30.01.023001031.1Re 6=⨯⨯==-d v cc ν 流速为0.30m/s 时流态将发生变化6-13解:查表得20°时空气 /s m 101.57 ,kg/m 20.12-53⨯==νρm /s 144.025.023001057.1Re 5=⨯⨯==d v cc νL/s 07.7/s m 00707.0425.014.3144.04322==⨯⨯==d v Q cc π c mQ Q Q >=⨯==/s m 0462.020.136002003v ρ紊流6-14解:查表得10°时水 /s m 101.312-6⨯=ν cm 61522015202=⨯+⨯=+=h b bh R 57568701031.106.015.0Re 6>=⨯⨯==-νvR 紊流6-15解:m/s 2563.0360015.014.33.164422=⨯⨯⨯==d Q v π 1922102.015.02563.0Re 4=⨯⨯==-νvd0333.0192264Re 64===λ m 744.06.192563.015.010000333.0222=⨯⨯==g v d l h f λ6-16见教材 P 137例6-36-17解:先按层流计算,由泊肃叶公式 408πr μρgJ Q =得 cm 97.0298014.3150035013.08884440=⨯⨯⨯⨯⨯===f gh Ql gJ Q r πνπρμ cm 94.120==r d 检验是不是层流 2300176994.114.3013.03544Re <=⨯⨯⨯===d Q vdνπν是层流,说明计算正确6-18解:皮托管测定的是管轴处的速度m/s 35.202.0)190113600(6.19)1(2=⨯-⨯=-=p p h g u ρρ以管轴处速度为特征流速计算雷诺数 23001958109075.035.2Re 5<=⨯⨯==-νud流动是层流 m/s 175.12==uv L/s 19.5/s m 00519.04075.014.3175.14322==⨯⨯==d v Q π6-19解:铸铁管道,取k s =1.25mm (平均值)3101.430025.1-⨯==d k s m/s 236.03.014.33600/604422=⨯⨯==d Q v π 46104.51031.13.0236.0Re ⨯=⨯⨯==-νvd 查穆迪图得 031.0=λ m 176.06.19236.03.0600031.0222=⨯⨯==g v d l h f λ6-20解:查表,取n =0.135m 075.04==d R 002.05001===l h J f 10.4816/1==R nC 管中流速 m /s 59.0==RJ C v6-21解:m/s 2.166.02.13600/42000=⨯==A Q v m 8.0)6.02.1(26.02.144=+⨯⨯==R d e 得由221v d l p e ρλ=∆ 0145.02.1611.15.06.31128.02122=⨯⨯⨯=∆=v p l d e ρλ 6-22解: πAd A AA d e 2 , 44===圆方 (1)层流 v gd lh f 232ρμ= 785.0422===π圆方方圆e e f f d d h h (2)紊流 g v d l h f 22λ= 886.04===π圆方方圆e e f f d d h h6-23解; m/s 702.105.014.300334.04422=⨯⨯==d Q v π 79.126.1215.0702.16.19222=⨯⨯==j h v g ζ 6-24解:由伯努利方程得 gv g v d l g v l H 222222ζλ++=+d l l H g v λζ+++=1)(2222)1()1(2d )(d dl d Hg l v λζλζ++-+=⇒ 当0d )(d 2<lv 时,管中流速随管长增加而减小,因管直径不变,流量也随管长增加而减小,即 01<-+dHλζ小时流量随管长增加而减λζdH )1(+>⇒6-25解:由伯努利方程得 gv v g v h g v 2)(222212221-++= 由连续性方程得 122212v d d v =)1(])1(1[2222122212122221424121d d d d g v d d d d g v h -=---=⇒ ⇒=0)(d )(d 2d h 由0122221=-d d 122d d = g v h 421m ax =6-26解:由伯努利方程得gv d l g v g v H 222222λζ++=进 m/s 36.6025.0602.05.01136.1912=⨯++⨯=++=dlgH v λζ进流量: L/s 12.3/s m 00312.04025.014.336.64322==⨯⨯==d v Q π 65.16.1936.6025.0102.02122=⨯⨯===g v d l h J fλ 切应力: Pa 1.10165.14025.08.910000=⨯⨯⨯==gRJ ρτ6-27解:m/s 06.305.014.3006.04422=⨯⨯==d Q v π m 15.325.06.12)1(=⨯=-=p f h h 水汞ρρ 022.006.3156.1905.015.3222=⨯⨯⨯==gv d l h f λ 6-28解; m/s 28.81.014.3065.04422=⨯⨯==d Q v π 由伯努利方程得gv d l H 2)3(2λζζζζ++++=出阀弯进6.1928.8)1.020042.0126.08.035.0(2⨯⨯+++⨯+=m 9.43=6-29 如图所示,水池中的水经弯管流入大气中。
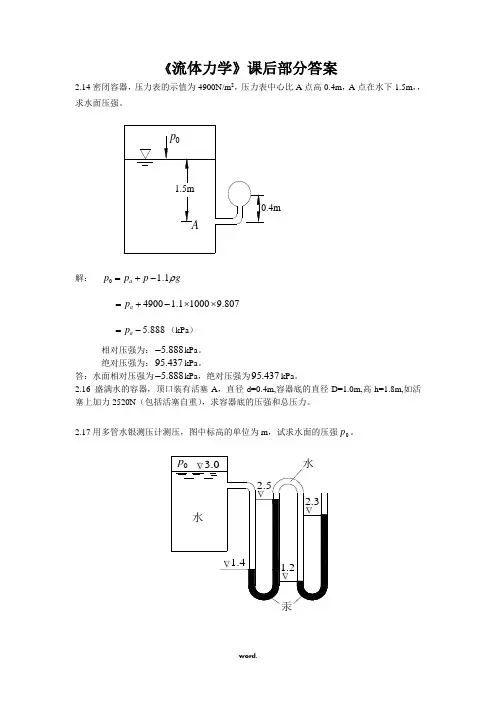
《流体力学》课后部分答案2.14密闭容器,压力表的示值为4900N/m 2,压力表中心比A 点高0.4m ,A 点在水下1.5m ,,求水面压强。
解: 0 1.1a p p p g ρ=+-4900 1.110009.807a p =+-⨯⨯ 5.888a p =-(kPa )相对压强为: 5.888-kPa 。
绝对压强为:95.437kPa 。
答:水面相对压强为 5.888-kPa ,绝对压强为95.437kPa 。
2.16 盛满水的容器,顶口装有活塞A ,直径d=0.4m,容器底的直径D=1.0m,高h=1.8m,如活塞上加力2520N (包括活塞自重),求容器底的压强和总压力。
2.17用多管水银测压计测压,图中标高的单位为m ,试求水面的压强0p 。
解: ()04 3.0 1.4p p g ρ=--()()5 2.5 1.4 3.0 1.4Hg p g g ρρ=+---()()()()2.3 1.2 2.5 1.2 2.5 1.4 3.0 1.4a Hg Hg p g g g g ρρρρ=+---+--- ()()2.3 2.5 1.2 1.4 2.5 3.0 1.2 1.4a Hg p g g ρρ=++---+-- ()()2.3 2.5 1.2 1.413.6 2.5 3.0 1.2 1.4a p g g ρρ=++--⨯-+--⎡⎤⎣⎦265.00a p =+(kPa )答:水面的压强0p 265.00=kPa 。
2.24矩形平板闸门AB ,一侧挡水,已知长l =2m ,宽b =1m ,形心点水深c h =2m ,倾角α=︒45,闸门上缘A 处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力T 。
解:(1)解析法。
10009.80721239.228C C Pp A h g bl ρ=⋅=⋅=⨯⨯⨯⨯=(kN )322212 2.946122sin sin 4512sin 45sin C C D C C C bl I h y y h y A blαα=+=+=+==⨯⋅oo (m ) 对A 点取矩,当开启闸门时,拉力T 满足:()cos 0D A P y y T l θ--⋅=()212sin sin 2sin cos cos C C CD A h h l l P h P y y T l l αααθθ⎡⎤⎛⎫⎢⎥+-- ⎪⎢⎥⋅⎝⎭⋅-⎢⎥⎣⎦==⋅2122sin 3.9228cos C l lP h l αθ⎛⎫ ⎪+ ⎪⋅ ⎪⎝⎭==⋅31.007=(kN )当31.007T ≥kN 时,可以开启闸门。

一元流体动力学基础1.直径为150的给水管道,输水量为h kN /7.980,试求断面平均流速。
解:由流量公式vA Q ρ= 注意:()vA Q s kg h kN ρ=⇒→//A Qv ρ=得:s m v /57.1=2.断面为300×400的矩形风道,风量为2700m 3,求平均流速.如风道出口处断面收缩为150×400,求该断面的平均流速 解:由流量公式vA Q = 得:A Q v =由连续性方程知2211A v A v = 得:s m v /5.122=3.水从水箱流经直径d 1=102=53=2.5的管道流入大气中. 当出口流速10 时,求(1)容积流量与质量流量;(2)1d 与2d 管段的流速解:(1)由s m A v Q /0049.0333== 质量流量s kg Q /9.4=ρ (2)由连续性方程:33223311,A v A v A v A v ==得:s m v s m v /5.2,/625.021==4.设计输水量为h kg /294210的给水管道,流速限制在9.0∽s m /4.1之间。
试确定管道直径,根据所选直径求流速。
直径应是mm 50的倍数。
解:vA Q ρ= 将9.0=v ∽s m /4.1代入得343.0=d ∽m 275.0∵直径是mm 50的倍数,所以取m d 3.0= 代入vA Q ρ= 得m v 18.1=5.圆形风道,流量是10000m 3,,流速不超过20 。
试设计直径,根据所定直径求流速。
直径规定为50 的倍数。
解:vA Q = 将s m v /20≤代入得:mm d 5.420≥ 取mm d 450= 代入vA Q = 得:s m v /5.17=6.在直径为d 圆形风道断面上,用下法选定五个点,以测局部风速。
设想用和管轴同心但不同半径的圆周,将全部断面分为中间是圆,其他是圆环的五个面积相等的部分。
测点即位于等分此部分面积的圆周上,这样测得的流速代表相应断面的平均流速。

一元流体动力学基础1.直径为150mm 的给水管道,输水量为h kN /7.980,试求断面平均流速。
解:由流量公式vA Q ρ= 注意:()vA Q s kg h kN ρ=⇒→//A Qv ρ=得:s m v /57.1=2.断面为300mm ×400mm 的矩形风道,风量为2700m 3/h,求平均流速.如风道出口处断面收缩为150mm ×400mm,求该断面的平均流速 解:由流量公式vA Q = 得:A Q v =由连续性方程知2211A v A v = 得:s m v /5.122=3.水从水箱流经直径d 1=10cm,d 2=5cm,d 3=2.5cm 的管道流入大气中. 当出口流速10m/ 时,求(1)容积流量及质量流量;(2)1d 及2d 管段的流速解:(1)由s m A v Q /0049.0333==质量流量s kg Q /9.4=ρ (2)由连续性方程:33223311,A v A v A v A v ==得:s m v s m v /5.2,/625.021==4.设计输水量为h kg /294210的给水管道,流速限制在9.0∽s m /4.1之间。
试确定管道直径,根据所选直径求流速。
直径应是mm 50的倍数。
解:vA Q ρ= 将9.0=v ∽s m /4.1代入得343.0=d ∽m 275.0 ∵直径是mm 50的倍数,所以取m d 3.0= 代入vA Q ρ= 得m v 18.1=5.圆形风道,流量是10000m 3/h,,流速不超过20 m/s 。
试设计直径,根据所定直径求流速。
直径规定为50 mm 的倍数。
解:vA Q = 将s m v /20≤代入得:mm d 5.420≥ 取mm d 450= 代入vA Q = 得:s m v /5.17=6.在直径为d 圆形风道断面上,用下法选定五个点,以测局部风速。
设想用和管轴同心但不同半径的圆周,将全部断面分为中间是圆,其他是圆环的五个面积相等的部分。

习题【1】1-1 解:已知:120t =℃,1395p kPa '=,250t =℃ 120273293T K =+=,250273323T K =+= 据p RT ρ=,有:11p RT ρ'=,22p RT ρ'= 得:2211p T p T '=',则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解:受到的质量力有两个,一个是重力,一个是惯性力。
重力方向竖直向下,大小为mg ;惯性力方向和重力加速度方向相反为竖直向上,大小为mg ,其合力为0,受到的单位质量力为01-3 解:已知:V=10m 3,50T ∆=℃,0.0005V α=℃-1根据1V V V Tα∆=⋅∆,得:30.000510500.25m V V V T α∆=⋅⋅∆=⨯⨯=1-4 解:已知:419.806710Pa p '=⨯,52 5.884010Pa p '=⨯,150t =℃,278t =℃ 得:1127350273323T t K =+=+=,2227378273351T t K =+=+= 根据mRTp V=,有:111mRT p V '=,222mRT p V '=得:421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯,即210.18V V =体积减小了()10.18100%82%-⨯=G =mg自由落体: 加速度a =g1-5 解:已知:40mm δ=,0.7Pa s μ=⋅,a =60mm ,u =15m/s ,h =10mm根据牛顿内摩擦力定律:u T Ayμ∆=∆ 设平板宽度为b ,则平板面积0.06A a b b =⋅= 上表面单位宽度受到的内摩擦力:1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ,方向水平向左 下表面单位宽度受到的内摩擦力:2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ,方向水平向左 平板单位宽度上受到的阻力:12216384N τττ=+=+=,方向水平向左。

流体力学课后习题答案流体力学是研究流体(液体和气体)在静止和运动状态下的行为及其与固体边界相互作用的科学。
在流体力学的课程中,课后习题是帮助学生巩固理论知识和提高解题能力的重要环节。
以下是一些流体力学课后习题的参考答案:# 习题一:流体静力学问题问题描述:一个长方体水箱,长为L,宽为W,高为H,水箱底部有一个小孔,孔的面积为A。
当水箱装满水后,求水从孔中流出时的流速。
解答:首先,我们应用托里拆利定律,该定律表明流体的静压与流体的深度成正比。
设水的密度为ρ,重力加速度为g,水深为h,孔上表面的压强为P0。
水从孔中流出的流速v可以通过伯努利方程计算:\[ v = \sqrt{\frac{2gh}{1 - \frac{A}{WL}}} \]其中,h是孔到水面的距离,即h = H - x,x是孔到水箱底部的距离。
# 习题二:流体动力学问题问题描述:一个管道的横截面积逐渐增大,管道内流动的流体是不可压缩的。
求管道不同截面处的流速。
解答:根据连续性方程,对于不可压缩流体,流速v与横截面积A之间的关系为:\[ A_1v_1 = A_2v_2 \]其中,A1和v1是管道初始截面的面积和流速,A2和v2是管道末端截面的面积和流速。
# 习题三:边界层问题问题描述:在流体流动过程中,边界层的厚度如何随距离x变化?解答:边界层的厚度δ可以用以下公式近似表示:\[ \delta = \frac{5x}{\sqrt{Rex}} \]其中,Re_x是沿流动方向x处的雷诺数,Rex = ρvx/μ,ρ是流体密度,v是流速,x是距离,μ是流体的动态粘度。
# 结语流体力学的习题答案需要根据具体的题目条件和所用的物理定律来确定。
上述答案仅为示例,实际解题时需要根据题目的具体要求进行详细的计算和分析。
希望这些示例能够帮助你更好地理解和应用流体力学的基本概念。

第四章流体动力学基本定理及其应用4-1欧拉运动微分方程和伯努利方程的前提条件是什么,其中每一项代表什么意义?答:(1)欧拉运动微分方程是牛顿第二定律在理想流体中的具体应用,其矢量表达式为:.:t其物理意义为:从左至右,方程每一项分别表示单位质量理想流体的局部惯性力、迁移惯性力、质量力和压力表面力。
(2)伯努利方程的应用前提条件是:理想流体的定常运动,质量力有势,正压流体,沿流2线积分。
单位质量理想流体的伯努利方程的表达式为:- p g^ C,从左至右方程2 P每项分别表示单位质量理想流体的动能、压力能和位能,方程右端常数称流线常数,因此方程表示沿流线流体质点的机械能守恒。
4-2设进入汽化器的空气体积流量为Q = 0.15m3 / S,进气管最狭窄断面直径D=40mm,喷油嘴直径d=10mm。
试确定汽化器的真空度。
又若喷油嘴内径d=6mm,汽油液面距喷油嘴高度为50cm,试计算喷油量。
汽油的重度=7355N/m3。
答:(1)求A点处空气的速度:设进气管最狭窄处的空气速度为V i,压力为p i,则根据流管的连续方程可以得到:丄二D2_d2V i =Q,44Q因此:v14Q 厂。
江(D2-d2)(2 )求真空度p v选一条流线,流线上一点在无穷远处F,—点为A点;并且:在F点:P F二P o ,V F = 0 ;在A点:P A二P1 二?,V A二W。
将以上述条件代入到伯努利方程中,可以得到:2也.0. v_02g-—;v f , v A = v 2 = ?, z A = h = 50cm = 0.5m ;2在 B 点:P B = p 0, V B = 0,Z B = 0 ; 代入到伯努利方程中,可以得到:Ip 0才v 22rh 』0 0;整理得到:v ;二」V 12 -2gh ;2因此汽油喷出速度为:1V 2 -2gh ;其中空气重度1 = Sg =1.226 9.81 =12N/m 3 ; V 1缪 龙,并注意到喷油嘴的 兀(D -d )直径是6mm ,而不是原来的10mm ,则计算得到:因此汽油流量为:12 _43 3因此真空度为:P v 二 P o - P i4Q冷心2] D2—d 28 322 JI(D 2 —d 2 2若取空气的密度为3::=1.226kg/m ,那么计算得到:8 1.226 0.152pv3.1421 32 =9.95 103Pa 。