门槛回归基本要求

政府科技经费投入、研发规模与高校基础研究科研产出的关系——基于省际面板数据的门槛回归分析张宝生打王天琳打王晓红2(1.哈尔滨师范大学管理学院，黑龙江哈尔滨150025； 2.哈尔滨工业大学管理学院，黑龙江哈尔滨150001)摘要：高等院校是基础研究工作的重要载体，运用Hansen面板门槛模型，以政府科研投入强度和人均政府投入科技经费为门槛变量，基于2010—2017年省际面板数据探讨政府科技经费投入和研发人员规模对高校基础研究科研产出的非线性影响关系。

研究显示，二者对高校基础研究科研产出均存在双重门槛效应；政府投入强度处于中等区间为政府科技经费投入对基础研究产出的最优促进区间；人均科技经费达到一定水平才能充分发挥研发人员规模对基础研究的促进作用；强调资源配置和优化结构比单纯追求投入规模的增加对基础研究活动更有意义。

我国整体上处于政府科研投入强度中等偏高、人均科技经费不足的情况，科研资源配置存在优化空间。

关键词：政府科技经费投入；研发规模；基础研究；科研产出；高等院校中图分类号：F061.2文献标识码：AThe Relationship Between Government Investment in Science and Technology, R&D Personnel Scale and Output of Basic Research in Universities ------Threshold Regression Analysis Based on Provincial Panel DataZhang Baosheng1,Wang Tianlin1,Wang Xiaohong2(1.School of Management,Harbin Normal University,Harbin150025；2. School of Management,Harbin Institute of Technology,Harbin,150001)\i-i r.ici:Colleges and universities are the important carriers of basic research.Based on the Hansen panel threshold model,taking the intensity of government scientific research input and per capita government investment in science and technology as threshold variables, based on2010——2017provincial panel data,it discusses the nonlinear relationship between government science and technology funding and R&D personnel scale on university basic research output.The results are as follows.Both of them have double threshold effect on the output of basic research.The intensity of government input is in the medium range which is the optimal promotion range.Only when the per capita fund reaches a certain level，can the promotion effect of R&D personnel scale on basic research be brought into full基金项目：国家自然科学基金资助项目“网络型知识组织成员错时空的隐性知识合作机制及其实现研究”(71702039),教育部人文社会科学研究一般项目“隐性知识流转网的成员合作机制及网络结构优化研究”(16YJC870019),黑龙江省哲学社会科学研究规划项目“社会变迁视角下大城市生人社会的熟人社区协同共建研究”(16SHD02),黑龙江省哲学社会科学研究规划项目“黑龙江产业集群视角下的企业创新能力与政府补贴关系研究”(2105219031)。

豪斯曼的门槛方法结果解读豪斯曼的门槛方法（Hausman's Threshold Method）是一种用于检测和处理回归模型中的异方差性（heteroscedasticity）的技术。

这种方法由美国经济学家James E. Hausman在1978年提出，旨在解决普通最小二乘法（OLS）在存在异方差性时估计的不准确性。

异方差性指的是在不同的观测值上，误差项的方差不同。

在回归分析中，如果误差项存在异方差性，那么普通最小二乘法的估计结果可能会产生偏误，因为OLS假设误差项具有恒定的方差。

豪斯曼的门槛方法通过引入一个门槛变量来解决这个问题，这个门槛变量通常是解释变量中的一个，用来划分观测值，使得在门槛的两侧，误差项的方差是恒定的。

豪斯曼的门槛方法的结果解读通常包括以下几个方面：1. 门槛效应的存在性：首先，需要判断门槛效应是否存在。

如果存在，这意味着解释变量中的一个或多个对误差项的方差有显著影响。

2. 门槛变量的选择：确定哪个解释变量作为门槛变量。

这通常是通过模型选择过程来确定的，比如使用似然比检验或沃尔德检验来选择最佳门槛变量。

3. 门槛值的确定：确定了门槛变量后，需要确定门槛值。

这通常是通过最大化似然函数或使用交叉验证来确定的最佳门槛值。

4. 回归结果的解读：在确定了门槛值后，需要对回归结果进行解读。

这包括估计系数的符号、大小和统计显著性，以及模型的拟合优度、预测能力等。

5. 异方差性的影响：豪斯曼的门槛方法可以帮助我们了解异方差性对回归估计的影响。

如果门槛方法显著改善了模型的估计，那么可以认为异方差性对原始的OLS估计有显著的影响。

6. 实证经济学的含义：豪斯曼的门槛方法不仅是一个统计技术，它还具有重要的实证经济学含义。

例如，门槛效应可能表明在不同的水平上，经济行为或政策的效果是不同的。

总之，豪斯曼的门槛方法的结果解读需要综合考虑统计显著性、经济意义以及模型的预测能力等多个方面，以得出合理的经济学结论。

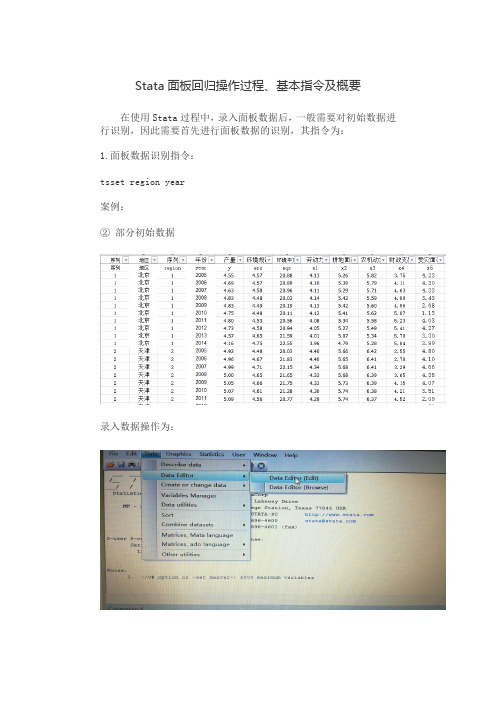
Stata面板回归操作过程、基本指令及概要在使用Stata过程中，录入面板数据后，一般需要对初始数据进行识别，因此需要首先进行面板数据的识别，其指令为：1.面板数据识别指令：tsset region year案例：②部分初始数据录入数据操作为：②将上述初始数据录入stata后（注意：录入数据及首行只能是英文字母或者数字，不能有汉字），显示如下：③输入指令tsset region year，显示如下结果. tsset region yearpanel variable: region (strongly balanced)time variable: year, 2005 to 2014delta: 1 unit2.面板数据固定效应回归指令：xtreg y ers eqs x1 x2 x3 x4 x5,fe案例：录入数据，并进行面板数据识别之后，输入以上指令：xtreg y ers eqs x1 x2 x3 x4 x5,fe其中，xtreg为面板回归指令，y为选取的因变量，ers、eqs、x1、x2、x3、x4、x5为自变量，末尾加fe表示为固定效应，如果末尾加re则是随机效应。

上述回归结果显示如下：3.面板数据随机效应回归指令：xtreg y ers eqs x1 x2 x3 x4 x5,re4.hausman 检验指令：Hausman检验是固定效应或者随机效应回归之后，需要加入的一个检验，具体指令如下：qui xtreg y ers eqs x1 x2 x3 x4 x5,feest store fequi xtreg y ers eqs x1 x2 x3 x4 x5,feest store rehausman fe re5.门限回归指令使用门限（或者门槛）回归模型的，只需要在录入数据后，使用以下指令进行回归即可，xthreg为门限回归指令，y eqs x1 x2 x3 x4 x5分别为自变量和因变量，rx和qx括号中的分别为核心解释变量与门限变量，可以一致也可以不一致。

stata门槛回归指令-回复什么是Stata回归分析？回归分析是一种广泛应用于统计学和经济学领域的数据分析方法。

它用于建立一个或多个自变量与一个因变量之间的关系模型。

Stata是一种常用的统计软件，它提供了强大的回归分析功能。

Stata回归分析可以用于预测、诊断模型、评估因素对因变量的影响等。

Stata中的回归分析命令：Stata提供了丰富的回归分析命令，用于不同类型的回归模型。

其中最常用的回归命令是regress。

下面将逐步介绍如何使用regress命令进行回归分析。

第一步：导入数据在进行回归分析之前，需要首先导入数据。

可以使用import命令将数据从外部文件导入到Stata中。

假设我们有一个名为"data.dta"的Stata数据文件，可以使用以下命令导入数据:use "data.dta", clear第二步：指定回归模型接下来，需要指定回归模型。

在回归模型中，需要指定一个因变量和一个或多个自变量。

以简单线性回归为例，假设我们想要建立一个模型来预测因变量Y与自变量X之间的关系，可以使用以下命令:regress Y X在多重线性回归中，可以使用多个自变量来建立模型。

假设我们有两个自变量X1和X2，可以使用以下命令:regress Y X1 X2可以根据具体的研究问题和数据情况指定不同的回归模型。

第三步：解释回归结果回归分析的一个重要输出是回归系数。

回归系数衡量了自变量对因变量的影响程度。

在Stata中，可以使用regress命令的结果窗口来解释回归系数。

回归系数通常表示为B，然后可以通过解释B的值来说明自变量对因变量的影响。

此外，回归结果还包括一些统计指标，例如R-squared和调整R-squared。

这些指标用于评估回归模型的拟合程度。

R-squared衡量模型解释了因变量变异性的百分比，而调整R-squared还考虑了模型中自由度的数量。

第四步：诊断模型诊断模型是回归分析的重要步骤之一。

面板门槛回归 U型关系1. 引言面板门槛回归是一种经济学中常用的回归方法，用于解决面板数据（Panel Data）中存在的个体效应和时间效应问题。

通过引入个体固定效应变量和时间固定效应变量，可以控制个体和时间的特定影响，从而更准确地估计模型中的参数。

本文将重点探讨面板门槛回归在 U 型关系研究中的应用及其意义。

2. 面板门槛回归的原理面板门槛回归是一种非常灵活的回归方法，可以用于研究个体特征对某一特定变量的影响。

它通过引入一个阈值变量，将样本分为两组，然后在每一组中进行回归分析。

这种方法可以有效地捕捉到个体特征在不同阈值上的不同效应。

面板门槛回归的基本原理可以用以下公式表示：y it=β1D it+β2D it(X it−τ)++αi+δt+εit其中，y it是依变量，D it是阈值变量，X it是解释变量，τ是阈值，αi是个体固定效应，δt是时间固定效应，εit是误差项。

当阈值τ为某一特定值时，模型中的参数β2可以反映出阈值以下和阈值以上两组之间不同变量的效应，从而揭示出 U 型关系。

3. U 型关系的概念及意义U 型关系是指某一变量与另一变量之间存在着一种非线性关系：在变量取值较小或较大时，两者之间关系较弱，而在某一中间区间内，关系较为密切。

U 型关系具有一定的普遍性，可以在不同的领域和问题中观察到。

例如，研究经济增长与环境污染的关系时，经济增长速度在低水平时与环境污染可能呈现 U 型关系。

U 型关系的存在对于政策制定者和经济学家具有一定的意义。

如果能够发现变量之间的 U 型关系，就可以在适当的阈值范围内采取相应的措施，最大程度地实现变量的优化。

而面板门槛回归作为一种探索非线性关系的工具，可以帮助研究者深入理解 U 型关系，并为政策制定提供有针对性的建议。

4. 面板门槛回归在 U 型关系研究中的应用面板门槛回归在 U 型关系研究中具有广泛的应用。

下面将通过一个实例来介绍面板门槛回归在探究投资与经济增长之间关系的应用。

三门槛回归结果解读
一、引言
在众多回归分析方法中，三门槛回归模型作为一种更具解释力的分析手段，被广泛应用于各个领域。

本文将通过对三门槛回归模型的解读，帮助读者更好地理解和运用这一方法。

二、三门槛回归模型概述
三门槛回归模型是在一元线性回归的基础上，引入了三个门槛变量，形成的一种多元回归分析方法。

它能够分析不同门槛变量下，自变量与因变量之间的关系，具有较强的解释能力。

三、门槛回归结果解读
1.门槛值估计
通过最小二乘法估计门槛值，可以得到每个门槛变量对应的最佳阈值。

这些阈值可以帮助我们更好地划分数据样本，分析各组样本之间的差异。

2.门槛效应分析
根据门槛值将数据划分为不同组别，分析自变量在各组别中对因变量的影响。

通过对比各组效应大小，可以揭示自变量与因变量之间的非线性关系。

3.稳健性检验
对门槛回归模型进行稳健性检验，主要包括异方差检验、序列相关检验等。

检验结果表明，模型具有一定的稳健性，分析结果可靠。

四、结果应用与启示
通过对三门槛回归模型的解读，我们可以发现其在实证分析中的广泛应
用。

例如，在经济学、社会学、心理学等领域，可以利用该模型研究不同群体特征下，自变量与因变量之间的关系。

此外，模型结果还可以为我们提供一定的政策建议，如针对不同门槛变量采取差异化政策，以提高政策效果。

五、总结
本文从引言、三门槛回归模型概述、门槛回归结果解读、结果应用与启示等方面，对三门槛回归模型进行了详细解读。

通过本文的阐述，希望读者能够更好地理解与应用这一具有较强解释力的回归分析方法。

stata门槛回归指令Stata门槛回归指令是一种用于分析离散因变量的统计方法。

它通过将连续自变量转化为二值（0或1）变量，以控制门槛值来解决离散因变量的特定问题。

本文将介绍Stata中的门槛回归指令的使用方法，并以一个实例说明其应用。

首先，我们需要安装Stata软件并加载数据集。

假设我们有一个数据集包括因变量“收入”和自变量“教育程度”。

我们想要探索教育程度对收入的影响，并将收入分成两个阶段进行分析：高收入和低收入。

下面的指令将加载数据集并显示前几行数据：```statause "datafile.dta", clearlist in 1/5```接下来，我们需要将收入变量转化为二值变量，并设置一个门槛值来划分高收入和低收入。

假设我们将门槛值设置为5000元，即收入大于等于5000元为高收入，否则为低收入。

下面是实现这一步骤的指令：```statagen high_income = (income >= 5000)```这个指令将创建一个名为“high_income”的二值变量，它的值为1表示高收入，0表示低收入。

现在我们可以使用logit命令来进行门槛回归分析。

Logit模型是一种广义线性模型，适用于解决二值因变量的问题。

下面是一个示例指令：```statalogit high_income education```这个指令将估计一个以“education”为自变量、以“high_income”为因变量的logit模型。

输出结果包括回归系数、标准误、p值等。

另一种常见的门槛回归方法是probit模型，它与logit模型类似，但使用的是累积分布函数。

可以使用probit命令来估计probit模型。

下面是一个示例指令：```stataprobit high_income education```与logit模型类似，这个指令将估计一个以“education”为自变量、以“high_income”为因变量的probit模型，并输出相关统计结果。

门槛回归模型（Threshold Regression Model）是一种特殊的非线性回归模型，主要用于处理因变量与自变量之间存在非线性关系，特别是存在阈值效应的情况。

在这种模型中，自变量的影响随着其跨越某个或多个特定阈值（门槛值）而发生显著变化的现象。

例如，在经济、金融、社会科学等领域，经常出现这样的现象：当某一变量（如GDP、收入、失业率等）低于或高于某个临界值时，其对另一变量（如消费、投资、犯罪率等）的影响会发生改变。

传统的线性回归模型无法捕捉到这种非线性关系和阈值效应。

门槛回归模型的作用主要包括以下几点：
1.揭示变量间的关系结构：通过设定门槛值，可以揭示自变量对因变量影响的
分段性质，描绘出更为复杂的因果关系图景。

2.提升模型拟合效果：在存在阈值效应的数据集中，门槛回归模型往往能够提
供比简单线性回归更好的解释力和预测能力。

3.政策制定依据：在政策分析中，识别出关键的门槛值有助于制定具有针对性
的政策措施，如当经济发展水平达到某个阶段时，可能需要调整相关政策导向。

4.实证研究工具：为实证研究提供了有力工具，帮助研究者深入理解哪些因素
在什么条件下对结果变量产生显著影响。

综上所述，门槛回归模型能够更准确地刻画现实世界中许多变量间的非线性关系，对于理解和预测具有显著转折点或门槛效应的现象非常有用。

三门槛回归结果解读摘要：一、引言- 介绍三门槛回归的基本概念- 阐述三门槛回归在实际问题中的应用及意义二、三门槛回归结果解读1.三门槛回归的基本原理- 门槛变量的定义与作用- 三门槛回归模型的构建2.三门槛回归结果分析- 描述性统计分析- 模型参数估计与解释- 模型显著性检验3.三门槛回归结果的应用- 对现实问题的解释与预测- 与其他回归模型的比较三、结论- 总结三门槛回归的特点与优势- 提出未来研究的方向与建议正文：一、引言三门槛回归是一种在多元线性回归基础上发展起来的回归分析方法，通过引入门槛变量，可以更好地刻画自变量与因变量之间的关系，尤其适用于处理间断性、非线性等问题。

在经济学、社会学、环境科学等领域具有广泛的应用。

本文将对三门槛回归的结果进行解读，以期为实际问题分析提供有益参考。

二、三门槛回归结果解读1.三门槛回归的基本原理三门槛回归是一种非线性回归模型，通过引入门槛变量，可以将原本连续的自变量划分为不同的区间，进而分析不同区间内自变量与因变量之间的关系。

门槛变量可以是一个或多个，根据实际问题需要进行设定。

2.三门槛回归结果分析在三门槛回归分析中，首先进行描述性统计分析，对各变量的分布、关系等进行描述。

然后，构建三门槛回归模型，对模型参数进行估计与解释，分析不同门槛下自变量与因变量之间的关系。

最后，进行模型显著性检验，检验模型是否具有统计学意义。

3.三门槛回归结果的应用根据三门槛回归结果，可以对现实问题进行解释与预测，为政策制定和调整提供依据。

同时，可以与其他回归模型进行比较，评估三门槛回归在特定问题上的适用性。

三、结论三门槛回归作为一种非线性回归方法，在处理间断性、非线性等问题时具有明显优势。

通过对三门槛回归结果的解读，可以为实际问题分析提供有益参考。

门槛回归结果阐述
门槛回归是一种统计方法，用于研究某个自变量对因变量的影响存在阈值和非线性关系的情况。

回归分析通常假设自变量与因变量之间的关系是线性的，但在实际应用中，往往存在非线性的情况。

门槛回归通过引入阈值变量，将样本的数据分为两个或多个子样本，分别进行线性回归分析。

然后，通过比较不同子样本的回归结果，确定自变量与因变量的关系是否存在线性阈值效应。

门槛回归结果的阐述通常包括以下几个方面：
1. 确定阈值：通过统计方法或画图方法，确定自变量和因变量的关系是否存在非线性阈值效应，并确定阈值的位置。

2. 子样本回归结果：一旦确定了阈值，将样本数据分成阈值以下和阈值以上两个或多个子样本，并分别进行线性回归。

分析每个子样本的回归结果。

3. 系数解释：解释不同子样本回归结果中自变量的系数，比较系数的大小和方向，评估阈值以下和阈值以上自变量与因变量之间的关系差异。

4. 模型拟合度：通过评估子样本回归的拟合度指标（如R 方），比较不同子样本的模型拟合度。

评估门槛回归模型的整体拟合度。

5. 假设检验：通过统计检验方法，检验门槛回归模型的显著性和阈值效应的存在性。

综上所述，门槛回归结果的阐述主要是关于阈值的确定、子样本回归结果的比较和解释、模型拟合度的评估以及阈值效应的
显著性检验。

这些阐述可以帮助研究者理解自变量对因变量的影响机制，并对研究结果进行解释和推断。

stata主效应门槛效应-回复Stata主效应与门槛效应是统计学中常见的分析方法，用于研究因变量与自变量之间的关系。

在研究中，主效应指的是自变量对因变量的整体影响，而门槛效应则指的是自变量对因变量的影响在某一特定阈值之后发生显著变化。

本文将针对Stata主效应与门槛效应的分析方法进行详细解释，并通过使用Stata软件来演示具体的步骤和实例。

首先，我们将介绍这两种效应的概念和意义，然后详细解释如何在Stata中进行分析，并给出一个具体的案例来说明。

1. 主效应的概念和意义主效应是指自变量对因变量的整体影响。

在统计学中，我们常常使用线性回归模型来研究自变量与因变量之间的关系。

对于一个简单的线性回归模型：Y = β0 + β1*X + ε，β1就是X（自变量）的主效应，表示X 对Y的整体影响。

主效应的重要性在于它可以帮助我们理解自变量对因变量的作用大小和方向。

例如，如果主效应为正，说明X与Y正相关；如果主效应为负，说明X与Y负相关。

这种主效应的大小和方向信息对于我们做出决策和预测具有重要意义。

2. 门槛效应的概念和意义门槛效应是指自变量对因变量的影响在某一特定阈值之后发生显著变化。

换句话说，当自变量的取值超过或达到某一阈值时，它对因变量的影响发生突变。

门槛效应的研究可以帮助我们找到自变量的最佳切点，从而更好地理解自变量和因变量之间的关系。

3. Stata中的主效应分析在Stata中，我们可以使用reg命令进行主效应的分析。

以下是具体的步骤：步骤1：打开数据文件首先，我们需要在Stata中打开数据文件，使用命令"use 数据文件名"。

确保文件中包含因变量和自变量的数据。

步骤2：运行回归模型接下来，我们可以使用reg命令来对数据进行回归分析。

例如，假设我们的自变量为X，因变量为Y，我们可以使用命令"reg Y X"，即可得到回归结果。

步骤3：解释回归系数回归结果将显示自变量的回归系数。

`thresholdtest` 是Stata 数据分析软件中的一个命令，它用于执行门槛回归（threshold regression）分析。

门槛回归是一种非线性回归技术，它允许研究者考察一个或多个自变量对因变量的影响是否随着某个门槛变量的不同水平而变化。

这种模型特别适用于分析异质性问题，即不同样本点或个体可能受到不同强度的影响。

`thresholdtest` 命令的原理基于以下步骤：1. **模型设定**：门槛回归模型通常设定为线性回归模型的形式，但其中自变量的系数是门槛变量的函数。

门槛变量是一个或多个解释变量，其值将决定模型中其他自变量的系数是否发生变化。

2. **门槛效应的假设**：门槛效应假设存在一个或多个门槛值，当门槛变量的值低于（或高于）这个门槛值时，自变量对因变量的影响会有所不同。

这种影响的变化可能是突然的（即存在跳跃），也可以是连续的（即存在斜率变化）。

3. **估计方法**：`thresholdtest` 使用一种称为“极大似然估计”（Maximum Likelihood Estimation, MLE）的方法来估计模型参数。

MLE 是一种统计方法，它通过寻找能够使似然函数取最大值的参数值来估计模型参数。

4. **似然函数**：似然函数是概率论中的一个概念，它衡量了在给定模型参数的情况下，观察到的数据出现的概率。

在门槛回归中，似然函数是模型参数（包括门槛值和系数）的函数，`thresholdtest` 通过优化似然函数来估计这些参数。

5. **门槛值的确定**：`thresholdtest` 命令可以帮助确定门槛值，这是通过分析似然比检验（Likelihood Ratio Test, LRT）的结果来实现的。

LRT 检验用于比较包含门槛效应的模型与不包含门槛效应的模型（即线性模型）的拟合优度。

如果LRT检验结果表明存在显著的非线性关系，那么可以认为门槛效应是显著的。

6. **结果解读**：`thresholdtest` 命令会输出包括门槛值、系数估计值、标准误、置信区间、P值等在内的结果。

分位数面板门槛回归模型英文回答：Quantile regression is a statistical technique that allows us to estimate the relationship between a set of independent variables and different quantiles of the dependent variable. It is particularly useful when the distribution of the dependent variable is not symmetric and we are interested in understanding how the relationship between the variables changes across different parts of the distribution.Panel data refers to data that is collected over time on multiple individuals or entities. In the context of quantile regression, panel data can be used to estimate the quantile regression coefficients for each individual or entity over time.The threshold regression model, also known as the quantile regression with threshold effects, is an extensionof the quantile regression model that allows for non-linear relationships between the independent variables and the dependent variable. It assumes that the relationship between the variables changes at a certain threshold value. This threshold value can be interpreted as the point at which the relationship between the variables switches from one quantile to another.To estimate the quantile regression coefficients in a panel data setting, we can use a fixed effects or random effects approach. The fixed effects approach controls for individual-specific characteristics that do not vary over time, while the random effects approach allows for individual-specific characteristics that vary over time.For example, let's say we are interested in understanding the relationship between income and education level on different quantiles of happiness. We have panel data on individuals over a period of 10 years. We can estimate the quantile regression coefficients using the fixed effects approach to control for individual-specific characteristics that do not change over time. This wouldallow us to understand how the relationship between income and education level varies across different quantiles of happiness for each individual over time.中文回答：分位数回归是一种统计技术，可以用来估计自变量与因变量不同分位数之间的关系。

单门槛回归结果解读单门槛回归是一种线性回归模型，它假设自变量对因变量的影响存在一个门槛值，当自变量达到该门槛值后，因变量的变化趋势会发生变化。

在单门槛回归中，我们通常会估计两个线性回归模型：一个是低门槛值以下的模型，另一个是高门槛值以上的模型。

以下是单门槛回归结果解读的介绍：1、模型系数在单门槛回归中，每个模型的系数都有特定的含义。

低门槛值以下的模型中，自变量的系数代表在低门槛值以下的自变量对因变量的影响程度；高门槛值以上的模型中，自变量的系数代表在高门槛值以上的自变量对因变量的影响程度。

因此，我们需要分别解读每个模型的系数。

2、门槛值单门槛回归的核心是门槛值，它是自变量对因变量影响发生改变的临界点。

门槛值的估计值通常是通过模型拟合得到的，它代表着自变量对因变量影响发生改变的临界值。

如果自变量达到了这个门槛值，那么因变量的变化趋势就会发生变化。

因此，我们需要关注门槛值的估计值和其显著性。

3、置信区间在单门槛回归中，每个模型的系数都有一个置信区间。

这个置信区间代表着该系数的估计值的不确定性范围。

如果置信区间很窄，那么我们就可以更加确信该系数的估计值是正确的；如果置信区间很宽，那么我们就可以认为该系数的估计值的不确定性很大。

因此，我们需要关注每个系数的置信区间。

4、R方值R方值是衡量模型拟合程度的一个指标，它表示模型能够解释因变量变异的比例。

在单门槛回归中，我们通常会分别计算低门槛值以下和高门槛值以上的R方值。

如果低门槛值以下的R方值很高，那么说明低门槛值以下的模型拟合得很好；如果高门槛值以上的R方值也很高，那么说明高门槛值以上的模型拟合得也很好。

因此，我们需要关注每个模型的R 方值。

5、P值P值是衡量模型系数的显著性的指标。

如果P值小于我们设定的显著性水平（例如0.05），那么我们就可以认为该系数是显著的。

在单门槛回归中，我们需要分别考虑低门槛值以下和高门槛值以上的P值。

如果低门槛值以下的P值很小，那么说明低门槛值以下的模型中自变量的系数是显著的；如果高门槛值以上的P值也很小，那么说明高门槛值以上的模型中自变量的系数也是显著的。

截面门槛回归模型全文共四篇示例，供读者参考第一篇示例：截面门槛回归模型是一种用于建立和分析质变因子的方法，通常应用在金融领域，用于预测和量化不同投资组合的风险收益特征。

在这篇文章中，我们将深入探讨截面门槛回归模型的原理、优势以及应用。

让我们了解一下什么是截面门槛回归模型。

截面门槛回归模型是一种多元回归模型，其中一个或多个解释变量的影响力在达到一定阈值之前是零。

具体来说，当解释变量的值低于门槛值时，其对因变量的影响力忽略不计；而当解释变量的值高于门槛值时，其对因变量的影响力便呈现线性关系。

这种模型有效地捕捉了解释变量在不同阶段对因变量的影响程度，使得模型更加符合实际情况。

截面门槛回归模型的优势在于它能够更准确地描述解释变量与因变量之间的非线性关系。

传统的线性回归模型假设自变量与因变量之间的关系是线性的，而现实情况往往更加复杂。

截面门槛回归模型能够通过设定门槛值，将解释变量的影响力进行分段，更加灵活地适应数据的特征。

这使得模型的预测能力和解释能力都得到了提升，进而增加了模型的准确性和应用价值。

在金融领域，截面门槛回归模型被广泛应用于风险管理和投资组合优化的领域。

通过建立门槛回归模型，投资者可以更好地理解不同因素对资产收益的影响，优化投资组合配置，降低投资风险，提高收益率。

截面门槛回归模型也可以用于量化投资策略的研究，识别并利用影响投资收益的关键因素，制定更加有效的交易策略。

除了金融领域，截面门槛回归模型还可以应用于其他领域，如医学、经济学、社会科学等，帮助研究人员更好地理解数据间的关系，发现隐藏的规律。

通过建立门槛回归模型，研究人员可以更准确地预测和控制各种变量之间的关系，为决策提供有力的支持。

截面门槛回归模型是一种强大的多元回归模型，能够更准确地描述解释变量与因变量之间的复杂关系。

在金融领域，它被广泛应用于风险管理、投资组合优化等领域，在其他领域也有着广泛的应用前景。

通过深入研究截面门槛回归模型的原理和应用，我们可以更好地理解数据的本质，发现数据间隐藏的规律，为决策提供更有力的支持。