全俄物理奥林匹克理论部分竞赛试卷试题包括答案.docx

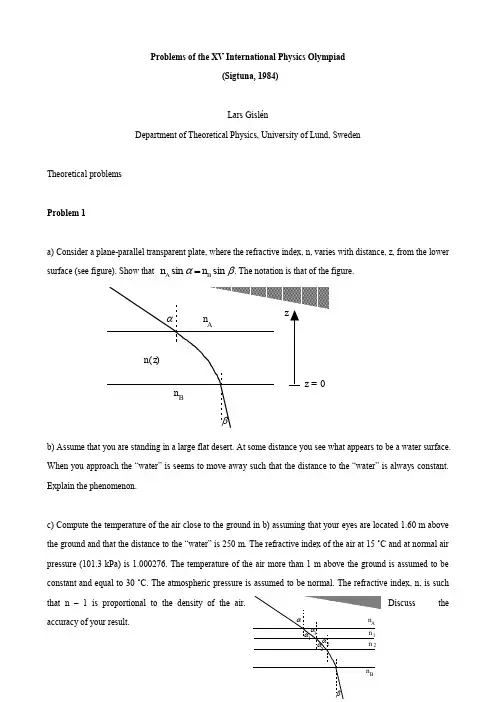
Problems of the XV International Physics Olympiad(Sigtuna, 1984)Lars GislénDepartment of Theoretical Physics, University of Lund, SwedenTheoretical problemsProblem 1a) Consider a plane-parallel transparent plate, where the refractive index, n, varies with distance, z, from the lower surface (see figure). Show that n A sinα=n B sinβ. The notation is that of the figure.b) Assume that you are standing in a large flat desert. At some distance you see what appears to be a water surface. When you approach the “water” is seems to move away such that the distance to the “water” is always constant. Explain the phenomenon.c) Compute the temperature of the air close to the ground in b) assuming that your eyes are located 1.60 m above the ground and that the distance to the “water” is 250 m. The refractive index of the air at 15 ˚C and at normal air pressure (101.3 kPa) is 1.000276. The temperature of the air more than 1 m above the ground is assumed to be constant and equal to 30 ˚C. The atmospheric pressure is assumed to be normal. The refractive index, n, is suchaccuracy of your result.a) From the figure we getn A sin α=n 1sin α1=n 2sin α2=⋯=n B sin βb) The phenomenon is due to total reflexion in a warm layer of air when= 90˚. This givesn A sin α=n Bc) As the density, , of the air is inversely proportional to the absolute temperature, T , for fixed pressure wehaven T ()=1+k ⋅ρ=1+k /TThe value given at 15 ˚C determines the value of k = 0.0795. In order to have total reflexion we have n 30sin α=n T or1+k 303⎛ ⎝ ⎫ ⎭ ⎪ ⋅Lh 2+L 2=1+k T ⎛ ⎝ ⎫ ⎭ ⎪with h = 1.6 m and L = 250 m As h << L we can use a power expansion in h /L :T =303303k +1⎛ ⎝ ⎫ ⎭ ⎪ 11+h 2/L 2-303k ≈3031+303h 22kL 2⎛ ⎝ ⎫ ⎭ ⎪ ⎪ =328K =56ÞCIn certain lakes there is a strange phenomenon called “seiching”phenomenon are normally long compared with the depth and alsonarrow. It is natural to see waves in a lake but not something like theseiching, where the entire water volume oscillates, like the coffee in acup that you carry to a waiting guest.In order to create a model of the seiching we look at water in a rectangular container. The length of the container is L and the depth of the water is h. Assume that the surface of the water to begin with makes a small angle with the horizontal. The seiching will then start, and we assume that the water surface continues to be plane but oscillates around an axis in the horizontal plane and located in the middle of the container.Create a model of the movement of the water and derive a formula for the oscillation period T. The starting conditions are given in figure above. Assume that ξ<<h. The table below shows experimental oscillation periods for different water depths in two containers of different lengths. Check in some reasonable way how well the formula that you have derived agrees with the experimental data. Give your opinion on the quality of your model.Table 1. L = 479 mmh/mm30506988107124142T/s 1.78 1.40 1.18 1.08 1.000.910.82Table 2. L = 143 mmh/mm31385867124T/s0.520.520.430.350.28The graph below shows results from measurements in lake Vättern in Sweden. This lake has a length of 123 kmand a mean depth of 50 m. What is the time scale in the graph?The water surface level in Bastudalen (northern end of lake Vättern) and Jönköping (southern end). Solution:In the coordinate system of the figure, we have for the centre of mass coordinates of the two triangular parts of the waterx 1,y 1()=L /3,h /2+ξ/3()x 2,y 2()=-L /3,h /2-ξ/3().For the entire water mass the centre of mass coordinates will then bex CoM ,y CoM ()=ξL 6h ,ξ26h ⎛ ⎝ ⎫⎭ ⎪ ⎪Due to that the y component is quadratic in will be much much smaller than the x component.The velocities of the water mass arev x ,v y ()=?ξ L 6h ,?ξ ξ3h ⎛ ⎝ ⎫⎭ ⎪ ⎪ ,and again the vertical component is much smaller the the horizontal one.We now in our model neglect the vertical components. The total energy (kinetic + potential) will then beW =W K +W P =12M ?ξ 2L236h 2+Mg ξ26h 2For a harmonic oscillator we haveW =W K +W P =12m ?x 2+12m ω2x 2 Identifying givesω=12ghL orT model =πL 3h . Comparing with the experimental data we findT e xperiment ≈1.1⋅T model, our model gives a slight underestimationof the oscillation period.Applying our corrected model on the Vättern data we have that the oscillation period of the seiching is about 3 hours.Many other models are possible and give equivalent results.Problem 3An electronic frequency filter consists of four components coupled as in the upper figure. The impedance of the source can be neglected and the impedance of the load can be taken as infinite. The filter should be such that the voltage ratio U ou t /U in has a frequency dependence shown in the lower where U in is the input voltage and U out is the output voltage. At frequency f 0 the phase lag between the two voltages is zero.In order to build the filter you can choose from the following components:2 resistors, 10 k Ω 2 capacitors, 10 nF2 solenoids, 160 mH (iron-free and with neglible resistance)Construct, by combining four of these components, a filter that fulfils the stated conditions. Determine the frequency f 0 and the ratio U ou t /U in at this frequency for as many component combinations as possible.Solution:The conditions at very high and very low frequencies can be satisfied with for example the following circuitU U in outCRRCs för afrequencyf 0=12πRCwhen the ratio between the output and input voltages is 2/3. Switching the resistors and the capacitors gives a new circuit with the same frequency f 0. Another two possibilities is to exchange thecapacitors for solenoids where we getf 0=R 2πL. There are further eight solutions with unsymmetric patterns of the electronic components. Experimental problemsProblem 1You have at your disposal the following material:(1) A sine wave voltage generator set to a frequency of 0,Hz. (2) A dual ray oscilloscope. (3) Millimeter graph paper.(4) A diod.(6) An unknown resistor R (red). (7) A coupling plate. (8) Coupling wires.Build the circuit shown in the figure.Connect the terminals A and B to the sine wave generator set to a frequencyof 0.Hz. Determine experimentally the mean power developed in the resistor R when the amplitude of thegenerator voltage is 2.0 V (that is the peak-to-peak voltage is 4.0 V).Solution:The picture to the right shows the oscilloscope voltage over theresistor. The period of the sine wave is 5 ms and this gives therelation 1 horizontal division = 1.5 ms. The actual vertical scalewas 0.85 V / division. The first rising part of the curve is asection of a sine wave, the second falling part is an exponential decay determined by the time constant of the resistor and capacitor. Reading from the display the "half-life" t1/2=RC⋅ln2turns out to be 0.5 ms. This gives R= 7.2 kΩ. The mean power developed in the resistor isP=1TU2t()RT⎰dt. Numerical integration (counting squares) gives U2t()T⎰dt=4,5⋅10-3V2s from whichP≈ 0.1 mW.Problem 2Material:(1) A glow discharge lamp connected to 2, alternating current.(2) A laser producing light of unknown wavelength.(3) A grating.(4) A transparent “micro-ruler”, 1 mm long wi th 100 subdivisions, the ruler is situated exactly in the centre of the circle.(5) A 1 m long ruler(6) Writing material.The spectrum of the glow discharge lamp has a number of spectral lines in the region yellow-orange-red. On of the yellow lines in the short wavelength part of this spectrum is very strong. Determine the wavelength of thisspectral line. Estimate the accuracy of your measurement.Note: If you happen to know the wavelength of the laser light beforehand you are not allowed to use that value in your computation.Warning. Do not look into the laser beam. Do not touch the surface of the grating or the surface of the transparent micro-ruler.Solution:Using the micro-ruler with we can determine the wavelength of the laser light. Knowing this wavelength we can calibrate the grating and then use it to determine the unknown wavelength from the glow discharge lamp. We cannot use the micro-ruler to determine this wavelength because the intensity of the light from the lamp is too weak.。

全国中学生物理竞赛初赛试卷本卷共16题，满分200分，．一、选择题．本题共5小题，每题6分．在每题给出旳4 个项中，有旳小题只有一项符合题意，有旳小题有多项符合题意．把符合题意旳选项前面旳英文字母写在每题背面旳方括号内．所有选对旳得6分，选对但不全旳得3分，有选错或不答旳得0分．1．（6分）一线膨胀系数为α旳正立方体物块，当膨胀量较小时，其体膨胀系数等于A．αB．α1/3C．α3D．3α2．（6分）按如下原理制作一杆可直接测量液体密度旳秤，称为密度秤，其外形和一般旳杆秤差不多，装秤钩旳地方吊着一体积为1 cm3旳较重旳合金块，杆上有表达液体密度数值旳刻度，当秤砣放在Q点处时秤杆正好平衡，如图所示．当合金块完全浸没在待测密度旳液体中时，移动秤砣旳悬挂点，直至秤杆正好重新平衡，便可直接在杆秤上读出液体旳密度，下列说法中错误旳是A．密度秤旳零点刻度在Q点B．秤杆上密度读数较大旳刻度在较小旳刻度旳左边C．密度秤旳刻度都在Q点旳右侧D．密度秤旳刻度都在Q点旳左侧3．（6分）一列简谐横波在均匀旳介质中沿x轴正向传播，两质点P1和p2旳平衡位置在x轴上，它们相距60cm，当P1质点在平衡位置处向上运动时，P2质点处在波谷位置，若波旳传播速度为24m/s，则该波旳频率也许为A．50HzB．60HzC．400HzD.410Hz4．（6分）电磁驱动是与炮弹发射、航空母舰上飞机弹射起飞有关旳一种新型驱动方式．电磁驱动旳原理如图所示，当直流电流忽然加到一固定线圈上，可以将置于线圈上旳环弹射出去．目前同一种固定线圈上，先后置有分别用铜、铝和硅制成旳形状、大小和横截面积均相似旳三种环,当电流忽然接通时，它们所受到旳推力分别为F1、F2和F3。

若环旳重力可忽视，下列说法对旳旳是A. F1> F2> F3B. F2> F3> F1C. F3> F2> F1D. F1 = F2 = F35．（6分）质量为m A旳A球，以某一速度沿光滑水平面向静止旳B球运动，并与B球发生弹性正碰，假设B球旳质量m B可选用为不同旳值，则A．当m B=m A时，碰后B球旳速度最大B．当m B=m A时，碰后B球旳动能最大C．在保持m B>m A旳条件下，m B越小，碰后B球旳速度越大D．在保持m B<m A旳条件下，m B越大，碰后B球旳动量越大二、填空题．把答案填在题中旳横线上．只要给出成果，不需写出求得成果旳过程．6．（10分）用国标一级螺旋测微器（直标度尺最小分度为0. 5mm，丝杆螺距为0.5mm,套管上分为50格刻度）测量小球直径．测微器旳初读数如图(a)历示，其值为______mm，测量时如图(b)所示，其值为_______mm，测得小球直径d=____________________mm.7．（10分）为了缓和都市交通拥堵问题，杭州交通部门在严禁行人步行旳十字路口增设“直行待行区”（行人可从天桥或地下过道过马路），如图所示，当其她车道旳车辆右拐时，直行道上旳车辆可以提迈进入“直行待行区”；当直行绿灯亮起时，可从“直行待行区”直行通过十字路口．假设某十字路口限速50km/h，“直行待行区”旳长度为12m，从提示进入“直行待行区”到直行绿灯亮起旳时间为4s.如果某汽车司机看到上述提示时立即从停车线由静止开始匀加速直线运动，运动到“直行待行区”旳前端虚线处正好直行绿灯亮起，汽车总质量为1. 5t，汽车运动中受到旳阻力恒为车重旳0.1倍，则该汽车旳行驶加速度为________；在这4s内汽车发动机所做旳功为___________。

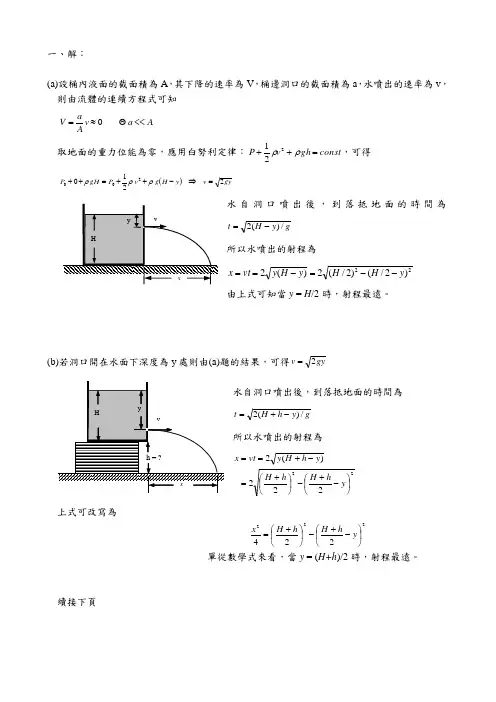
一、解：(a)設桶內液面的截面積為A ，其下降的速率為V ，桶邊洞口的截面積為a ，水噴出的速率為v ，則由流體的連續方程式可知A a v AaV <<≈=取地面的重力位能為零，應用白努利定律：const gh v P =++ρρ221，可得()gy v y H g v P gH P 2210200=⇒-++=++ρρρ 水自洞口噴出後，到落抵地面的時間為g y H t /)(2-=所以水噴出的射程為22)2/()2/(2)(2y H H y H y vt x --=-==由上式可知當y = H /2時，射程最遠。

(b)若洞口開在水面下深度為y 處則由(a)題的結果，可得gy v 2=水自洞口噴出後，到落抵地面的時間為g y h H t /)(2-+=所以水噴出的射程為22222 )(2⎪⎭⎫⎝⎛-+-⎪⎭⎫ ⎝⎛+=-+==y h H h H y h H y vt x 上式可改寫為222224⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛+=y h H h H x 單從數學式來看，當y = (H+h )/2時，射程最遠。

續接下頁上式的函數曲線如下圖：依桶底面離地高度h 的大小可分成三種情況討論：(1)若h < H ，則(H+h )/2 < H ，即能噴水最遠的洞口在桶底面的上方。

在上圖中，y = H 落在y = (H+h )/2的右邊，其對應的水射程不是最遠的。

(2)若h = H ，則(H+h )/2 = H ，即剛好開在桶底面的洞口，可噴水最遠。

在上圖中，y = H 剛好落在y = (H+h )/2的位置，其對應的水射程極大。

(3)若h > H ，則(H+h )/2 > H ，即y = H 落在y = (H+h )/2的左邊，從上圖左半部的單調上升曲線可看出，從桶底面洞口(y = H )所噴出的水，可射得最遠(相較於0<y<H 時的射程)。

結論：需把水桶底面提離地面的高度h ，大於桶內所裝水的深度H ，才可保證愈接近桶底面的洞口所噴出的水，會射得愈遠。

国际物理奥林匹克竞赛试题理论试题题1A 某蹦迪运动员系在一根长弹性绳子的一端，绳的另一端固定在一座高桥上，他自静止高桥向下面的河流下落，末与水面相触，他的质量为m，绳子的自然长度为L，绳子的力常数（使绳子伸长lm所需的力）为k，重力场强度为g。

求出下面各量的表达式。

（a）运动员在第一次达到瞬时静止前所落下的距离y。

（b）他在下落过程中所达到的最大速率v。

（c）他在第一次达到瞬时静止前的下落过程所经历的时间t。

设运动员可以视为系于绳子一端的质点，与m相比绳子的质量可忽略不计，当绳子在伸长时服从胡克定律，在整个下落过程中空气的阻力可忽略不计。

B 一热机工作于两个相同材料的物体之间，两物体的温度分别为T A和T B（T A＞T B），每个物体的质量均为m，比热恒定，均为s。

设两个物体的压强保持不变，且不发生相变。

（a）假定热机能从系统获得理论上允许的最大机械能，求出两物体A和B最终达到的温度T?的表达式，给出解题全部过程。

（b）由此得出允许获得的最大功的表达式。

（c）假定热机工作于两箱水之间，每箱水的体积为2.50m3，一箱水的温度为350K，另一箱水的温度为300K。

计算可获得的最大机械能。

已知水的比热容= 4.19×103kg-1K-1，水的密度=1.00 x 103kgm.-3C 假定地球形成时同位素238U和235U已经存在，但不存在它们的衰变产物。

238U和235U的衰变被用来确定地球的年龄T。

（a）同位素238U以4.50×109年为半衰期衰变，衰变过程中其余放射性衰变产物的半衰期比这都短得多，作为一级近似，可忽略这些衰变产物的存在，衰变过程终止于铅的同位素206Ph。

用238U的半衰期、现在238U的数目238N表示出由放射衰变产生的206Pb原子的数目206n。

（运算中以109年为单位为宜）（b）类似地，235U在通过一系列较短半衰期产物后，以0.710×109年为半衰期衰变，终止于稳定的同位素207Pb。

国际物理奥林匹克竞赛试题一、在双缝干涉实验中，当光屏上某点到双缝的路程差为半个波长时，该点将出现：A. 明条纹B. 暗条纹C. 无法确定明暗D. 既是明条纹又是暗条纹（答案：A）二、一个物体在地球表面附近做匀速圆周运动，其向心加速度与地球同步卫星的向心加速度相比：A. 两者相等B. 物体的大C. 卫星的大D. 无法比较（答案：B）三、关于光的波动性与粒子性，下列说法正确的是：A. 光只具有波动性，不具有粒子性B. 光只具有粒子性，不具有波动性C. 光在某些情况下表现出波动性，在某些情况下表现出粒子性D. 光的波动性与粒子性是相互矛盾的，不能同时存在（答案：C）四、在量子力学中，描述粒子位置不确定度与动量不确定度之间关系的是：A. 牛顿第二定律B. 能量守恒定律C. 海森堡不确定性原理D. 薛定谔方程（答案：C）五、关于电磁感应现象，下列说法错误的是：A. 闭合电路的一部分导体在磁场中做切割磁感线运动时，导体中会产生感应电流B. 感应电流的磁场总是试图阻碍产生它的磁通量的变化C. 感应电动势的大小与线圈匝数成正比D. 在电磁感应现象中，机械能转化为电能（答案：C）六、在相对论中，关于时间膨胀效应，下列说法正确的是：A. 高速运动的物体内部时间流逝速度比静止时快B. 高速运动的物体内部时间流逝速度比静止时慢C. 时间膨胀效应与物体的运动速度无关D. 时间膨胀效应只在接近光速运动时才显著（答案：B）七、关于量子纠缠，下列说法正确的是：A. 量子纠缠是一种超距作用，违反了相对论中的光速限制B. 量子纠缠是量子系统之间的一种特殊关联，不能通过经典通信实现C. 量子纠缠只存在于相同的粒子之间D. 量子纠缠可以被观测而不影响系统的状态（答案：B）八、在杨-米尔斯理论中，描述基本粒子相互作用的是：A. 引力场B. 电磁场C. 规范场D. 标量场（答案：C）。

物理奥赛初赛试题及答案一、选择题（每题5分，共20分）1. 光在真空中的传播速度是：A. 3×10^8 m/sB. 3×10^5 m/sC. 3×10^6 m/sD. 3×10^7 m/s答案：A2. 根据牛顿第二定律，力和加速度的关系是：A. F = maB. F = ma^2C. F = m/aD. F = a/m答案：A3. 以下哪个选项是正确的能量守恒定律表述？A. 能量可以被创造B. 能量可以被消灭C. 能量既不能被创造也不能被消灭D. 能量可以在不同形式之间转换答案：C4. 根据库仑定律，两个点电荷之间的力与它们之间的距离的关系是：A. 与距离成正比B. 与距离成反比C. 与距离的平方成正比D. 与距离的平方成反比答案：D二、填空题（每题5分，共20分）5. 一个物体在水平面上以初速度v0开始滑行，摩擦系数为μ，滑行距离为s，则物体滑行时间t为______。

答案：t = v0 / (μg)6. 一个质量为m的物体从高度h自由落下，忽略空气阻力，其落地时的速度v为______。

答案：v = √(2gh)7. 一个电路中，电阻R、电流I和电压V之间的关系是______。

答案：V = IR8. 根据欧姆定律，电阻R、电流I和电压V之间的关系是______。

答案：I = V / R三、计算题（每题10分，共40分）9. 一辆汽车以恒定加速度a从静止开始加速，经过时间t后，汽车的速度v和位移s分别为多少？答案：v = ats = 1/2 * a * t^210. 一个质量为m的物体从高度h自由落下，求物体落地时的动能。

答案：动能 = 1/2 * m * v^2 = 1/2 * m * (2gh) = mgh11. 一个电阻R与一个电容C串联后接在电压为V的直流电源上，求电路达到稳态时的电流I。

答案：I = V / (R + 1/(C * ω))12. 一个质量为m的物体在弹簧的弹力作用下做简谐振动，弹簧的劲度系数为k，求物体的最大速度。

第五届国际中学生物理奥林匹克竞赛试题(理论部分)(1982年联邦德国基尔)题 1 如图13-1所示，荧光灯接在50Hz的交流电压上；测出的数据如下：总电压(电网电压)U=228.5V，电流强度I=0.6A，荧光灯管两端电压U′=84V，串联镇流器的欧姆电阻R d=26.3Ω。

计算时，可把荧光灯管当作是欧姆电阻器。

试问：(a)串联镇流器的电感量L是多大？(b)电压和电流之间的相移角φ等于多少？(c)这个装置的有功功率P w等于多少？(d)串联镇流器除限流作用外，还有另一个重要功能。

写出这个功能并加以说明。

提示：启动器—S—的触头在接通电源后马上闭合，随即断开，并保持开路状态。

(e)试在定量时间标度图上，画出灯管发出的光通量随时间变化的图像。

(f)虽然所加交变电压每隔一定时间间隔都要通过零值，为什么灯管只需启动一次？(g)根据厂家说明，对这种类型的荧光灯管，可配用电容量为4.7μF的电容器同串联镇流器串联。

这样做对灯管的工作有什么影响，其目的又是什么？(h)试用附带的分光镜对演示用的荧光灯的两半段进行观察。

解释两种光谱之间的差别。

你可以走近荧光灯，并在实验后把分光镜留作纪念。

〔解〕(a)这个装置的总阻抗为Z==380.8(欧姆) 灯管的欧姆阻值是R R==140(欧姆) 因此总欧姆阻值为R=140+26.3=166.3(欧姆) 串联镇流器的感抗为ωL==342.6(欧姆) 从而L==1.09亨利(b)阻抗角可从下式得到：tgφ==2.06 于是φ=64.1° (c)用不同的方法可以求出有功功率1)Pω=UIcosφ=228.5×0.6×cos64.1°=59.88(瓦特) 2)Pω=RI2=166.3×0.62=59.87(瓦特) (d)启动器触头断开时，将使串联镇流器两端产生很高的感应电动势(假定触头不是刚好在电流值为0时断开)。

由此产生的电压足能使灯管启动。

国际物理奥林匹克竞赛试题在紧张的物理奥赛题复习阶段，大家要做好每一次的物理考试复习筹备。

这样才能让大家在即将到来的考试中获得优秀的成绩!下面是本店铺收拾的国际物理奥林匹克竞赛试题，以供大家学习参考。

国际物理奥林匹克竞赛试题物理奥赛题复习资料关于摩擦力的剖析与判断1.摩擦力产生的条件两物体直接接触、相互挤压、接触面粗糙、有相对运动或相对运动的趋势。

这四个条件缺一不可。

两物体间有弹力是这两物体间有摩擦力的必要条件。

2.摩擦力的方向摩擦力方向一直沿着接触面，和物体间相对运动的方向相反。

摩擦力的方向和物体的运动方向可能相同，可能相反，可能垂直，可能成任意角度。

●学习牛顿第肯定律需要要注意的三个问题1.牛顿第肯定律包含了两层含义：①维持匀速直线运动状况或静止状况是物体的固有属性;物体的运动无需力来维持;②要使物体的运动状况改变，需要施加力的用途，力是改变物体运动状况的起因。

2.牛顿第肯定律导出了两个定义：①力的定义。

力是改变物体运动状况的起因。

又依据加速度概念，速度变化就肯定有加速度，所以可以说力是使物体产生加速度的起因。

②惯性的定义。

一切物体都有维持原有运动状况的性质，这就是惯性。

惯性反映了物体运动状况改变的难易程度。

水平是物体惯性大小的量度。

3.牛顿第肯定律描述的是理想状况下物体的运动规律。

它描述了物体在不受任何外力时如何运动。

而不受外力的物体是不存在的。

物体不受外力和物体所受合外力为零是有不同的，所以不可以把牛顿第肯定律当成牛顿第二定律在F=0时的特例，因此不可以说牛顿第肯定律是实验定律。

应用牛顿第二定律的常用办法1.合成法第一确定研究对象，画出受力剖析图，沿着加速度方向将各个力根据力的平行四边形定则在加速度方向上合成，直接求出合力，再依据牛顿第二定律列式求解。

此办法被称为合成法，具有直观方便的特征。

2.分解法确定研究对象，画出受力剖析图，依据力的实质功效成效，将某一个力分解成两个分力，然后依据牛顿第二定律列式求解。