2020届浙江省舟山中学2017级高三3月月考数学试卷无答案
- 格式:pdf
- 大小:373.13 KB
- 文档页数:4


2020届浙江省湖州中学2017级高三下学期一模考试数学试卷★祝考试顺利★(解析版)一、选择题:本大题共10小题,每小题4分,共40分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1. 已知全集U ={1,2,3,4},集合A ={1,2},B ={2,3},则∁U (A ∪B )=( )A. {1,3,4}B. {3,4}C. {3}D. {4}【答案】D【解析】先求得并集,再求补集.【详解】∵A ={1,2},B ={2,3},∴A ∪B ={1,2,3},∴∁U (A ∪B )={4}.故选:D . 2. 已知,R a b ∈则33log log a b >是“1122a b ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭”的( ) A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】由33log log a b >得0a b >>,因为1()2x y = 是减函数,所以1122a b ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭成立,当1122a b ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭时,a b >成立,因为正负不确定,不能推出33log log a b >,故33log log a b >是“1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭”的充分不必要条件,故选A.3. 如果双曲线22221(0,0)x y a b a b -=>>的两条渐近线互相垂直,那么它的离心率是( )C. 2D. 3- 2 - 【答案】A【解析】由渐近线互相垂直判断出渐近线与x 轴夹角为45︒,进而求出a 与b 的关系,再结合222c a b =+即可求出离心率【详解】由题可知,渐近线与x 轴夹角为45︒,故tan 1b k a θ==±=±,得出a b =,再由222c a b =+得出222c a =,即2222c e a ==,2e =故选:A4. 已知5x x ⎛- ⎪⎝⎭的展开式中含32x 的项的系数为30,则a 等于(). A. 3 B. 3- C. 6D. 6- 【答案】D【详解】5215C (1)r r rrr T a x -+=-,令1r =,可得530a -=解得6a =-.故选:D.5. 某几何体的三视图如图所示,则该几何体的体积是( )A. 40B. 48。

2020年高考数学真题试卷(浙江卷)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合P ={x|1<x <4},Q ={x|2<x <3},则P∩Q =( ) A. {x|1<x≤2} B. {x|2<x <3} C. {x|3≤x <4} D. {x|1<x <4}2.已知a ∈R ,若a ﹣1+(a ﹣2)i (i 为虚数单位)是实数,则a =( ) A. 1 B. ﹣1 C. 2 D. ﹣23.若实数x ,y 满足约束条件 {x −3y +1≤0x +y −3≥0 ,则z =x+2y 的取值范围是( )A. (﹣∞,4]B. [4,+∞)C. [5,+∞)D. (﹣∞,+∞) 4.函数y =xcosx+sinx 在区间[﹣π,+π]的图象大致为( )A. B.C. D.5.某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是( )A. 73B. 143 C. 3 D. 66.已知空间中不过同一点的三条直线m ,n ,l ,则“m ,n ,l 在同一平面”是“m ,n ,l 两两相交”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 7.已知等差数列{a n }的前n 项和S n , 公差d≠0, a 1d≤1.记b 1=S 2 , b n+1=S n+2﹣S 2n , n ∈N*,下列等式不可能成立的是( )A. 2a 4=a 2+a 6B. 2b 4=b 2+b 6C. a 42=a 2a 8D. b 42=b 2b 88.已知点O (0,0),A (﹣2,0),B (2,0).设点P 满足|PA|﹣|PB|=2,且P 为函数y =3 √4−x 2 图象上的点,则|OP|=( )A. √222B. 4√105C. √7D. √109.已知a ,b ∈R 且ab≠0,若(x ﹣a )(x ﹣b )(x ﹣2a ﹣b )≥0在x≥0上恒成立,则( ) A. a <0 B. a >0 C. b <0 D. b >0 10.设集合S ,T ,S ⊆N*,T ⊆N*,S ,T 中至少有两个元素,且S ,T 满足:①对于任意x ,y ∈S ,若x≠y ,都有xy ∈T ;②对于任意x ,y ∈T ,若x <y ,则 yx ∈S ;下列命题正确的是( )A. 若S 有4个元素,则S ∪T 有7个元素B. 若S 有4个元素,则S ∪T 有6个元素C. 若S 有3个元素,则S ∪T 有4个元素D. 若S 有3个元素,则S ∪T 有5个元素二、填空题:本大题共7小题,共36分。
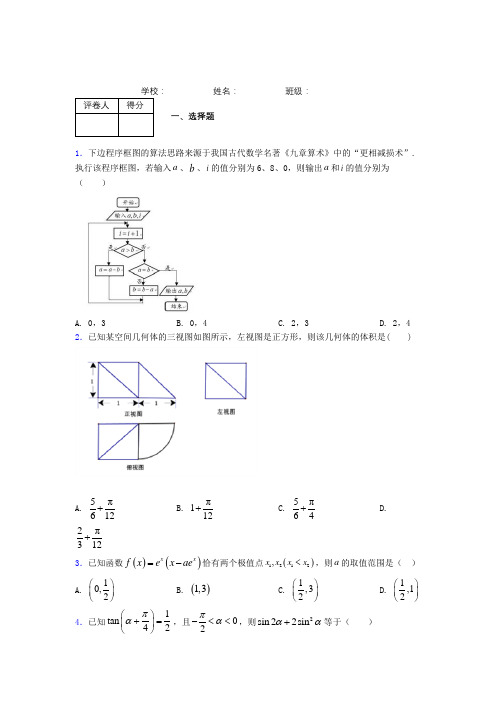
__________ 姓名:__________ 班级:__________评卷人 得分一、选择题1.下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a 、b 、i 的值分别为6、8、0,则输出a 和i 的值分别为( )A. 0,3B. 0,4C. 2,3D. 2,42.已知某空间几何体的三视图如图所示,左视图是正方形,则该几何体的体积是( )A.5π612+ B. π112+C.5π64+ D.2π312+ 3.已知函数()()xxf x ex ae =-恰有两个极值点()1212,x x x x <,则a 的取值范围是( )A. 10,2⎛⎫ ⎪⎝⎭B. ()1,3C. 1,32⎛⎫ ⎪⎝⎭D. 1,12⎛⎫ ⎪⎝⎭4.已知1tan 42πα⎛⎫+= ⎪⎝⎭,且02πα-<<,则2sin 22sin αα+等于( )A. 255-B. 25-C.25D.255评卷人 得分二、填空题5.在平面四边形ABCD 中,75A B C ∠=∠=∠=︒.2BC =,则AB 的取值范围是_____. 【答案】()62,62-+【解析】 【分析】如图所示,延长BA ,CD 交于点E ,在△BCE 与在△BCF 中,分别由正弦定理可求出AB 的取值范围.【详解】如图所示,延长BA ,CD 交于E ,平移AD ,当A 与D 重合与E 点时,AB 最长,在△BCE 中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得sin sin BC BEE C=∠∠,即o o2sin30sin75BE=,解得BE 6+2AD ,当D 与C 重合时,AB 最短,此时与AB交于F ,在△BCF 中,∠B=∠BFC=75°,∠FCB=30°,由正弦定理知,sin sin BF BC FCB BFC =∠∠,即o o2sin30sin75BF =,解得62AB 的取值范围626+2. 故答案为(62,62.【点睛】本题考查求AB 的取值范围,考查三角形中的几何计算及正弦定理的应用,考查学生的计算能力,属于中档题.6.对于三次函数()()220f x ax bx cx d a =+++≠,定义:设()x f ''是函数()y f x =的导数()'y f x =的导数,若方程()''0f x =有实数解0x ,则称点()00()x f x ,为函数()y f x =的“拐点”.任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,函数()3231324f x x x x =-+-,计算1232012...2013201320132013f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=____ 7.设n S 为等差数列{}n a 的前n 项和,若1357910a a a a a ++++=,228236a a -=,则10S 的值为_____.评卷人 得分三、解答题8.为了解某市高三数学复习备考情况,该市教研机构组织了一次检测考试,并随机抽取了部分高三理科学生数学成绩绘制如图所示的频率分布直方图.(1)根据频率分布直方图,估计该市此次检测理科数学的平均成绩0u ;(精确到个位) (2)研究发现,本次检测的理科数学成绩X 近似服从正态分布2(,)N μσ(0u u =,σ约为19.3),按以往的统计数据,理科数学成绩能达到自主招生分数要求的同学约占40%;(i )估计本次检测成绩达到自主招生分数要求的理科数学成绩大约是多少分?(精确到个位)(ii )从该市高三理科学生中随机抽取4人,记理科数学成绩能达到自主招生分数要求的人数为Y ,求Y 的分布列及数学期望()E Y .(说明11()1()x uP X x φσ->=-表示1X x >的概率.参考数据:(0.7257)0.6ϕ=,(0.6554)0.4ϕ=)9.如图,已知椭圆14:221=+y x C 的左、右顶点为1A ,2A ,上、下顶点为1B ,2B ,记四边形1122A B A B 的内切圆为2C . (1)求圆2C 的标准方程;(2)已知圆2C 的一条不与坐标轴平行的切线l 交椭圆1C 于P ,M 两点. (i )求证:OP OM ⊥;(ii )试探究2211OP OM +是否为定值.10.已知圆221:420C x y x y +-+=与圆222:240C x y y +--=.(1)求两圆公共弦所在直线的方程;(2)求过两圆的交点且圆心在直线241x y +=上的圆的方程. 11.(12分)已知函数()xf x xe a =+。
浙江省舟山市高三上学期数学第一次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)设集合,若,则的值是()A . 1B . 2C . 0D .2. (2分)在等比数列{an}中,an>an+1 ,其前n项的积为Tn(n∈NΦ),若T13=4T9 ,则a8•a15=()A . ±2B . ±4C . 2D . 43. (2分)(2020·福州模拟) 已知函数某个周期的图象如图所示,A,B分别是图象的最高点与最低点,C是图象与x轴的交点,则tan∠BAC=()A .B .C .D .4. (2分)如图,当直线l:y=x+t从虚线位置开始,沿图中箭头方向平行匀速移动时,正方形ABCO位于直线l下方(图中阴影部分)的面积记为S,则S与t的函数图象大致是()A .B .C .D .5. (2分) (2020高二下·扶风月考) 给出下列三个类比结论:①(ab)n=anbn与(a+b)n类比,则有(a+b)n=an+bn;②loga(xy)=logax+logay与sin(α+β)类比,则有sin(α+β)=sin αsin β;③(a+b)2=a2+2ab+b2与( + )2类比,则有( + )2= 2+2 · + 2.其中结论正确的个数是().A . 0B . 1C . 2D . 36. (2分) (2016高一上·西湖期中) 已知f(x)为奇函数,且在(0,+∞)上是递增的,若f(﹣3)=0,则xf(x)>0的解集是()A . {x|﹣3<x<0或x>3}B . { x|x<﹣3或0<x<3}C . { x|x<﹣3或x>3}D . { x|﹣3<x<0或0<x<3}7. (2分) (2016高一下·江门期中) 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<)的图象如图所示,则f(0)=()A . 1B .C .D .8. (2分)(2018·德阳模拟) 在中,已知,,点D为BC的三等分点(靠近C),则的取值范围为()A .B .C .D .二、填空题 (共6题;共7分)9. (1分) (2020高二下·绍兴月考) 设,则的值为________.10. (1分) (2020高一下·佛山期中) 在中,,,,则的面积等于________.11. (1分)(2018·重庆模拟) 根据党中央关于“精准”脱贫的要求,我市某农业经济部门决定派出五位相关专家对三个贫困地区进行调研,每个地区至少派遣一位专家,其中甲、乙两位专家需要派遣至同一地区,则不同的派遣方案种数为________(用数字作答).12. (1分)已知点A(﹣1,5)和向量=(2,3),若=3,则点B的坐标为________13. (1分)(2017·上饶模拟) 已知函数f(x)=sin(3x+3φ)﹣2sin(x+φ)cos(2x+2φ),其中|φ|<π,若f(x)在区间上单调递减,则φ的最大值为________.14. (2分) (2019高二下·绍兴期中) 已知函数在上为增函数,则的取值范围为 ________三、解答题 (共6题;共50分)15. (15分) (2018高二上·莆田月考) 在中,角的对边分别为,且.(1)求角的大小;(2)若,求的最大值.16. (5分)(2018·呼和浩特模拟) 为了了解校园噪音情况,学校环保协会对校园噪音值(单位:分贝)进行了天的监测,得到如下统计表:噪音值(单位:分贝)频数(1)根据该统计表,求这天校园噪音值的样本平均数(同一组的数据用该组组间的中点值作代表).(2)根据国家声环境质量标准:“环境噪音值超过分贝,视为重度噪音污染;环境噪音值不超过分贝,视为轻度噪音污染.”如果把由上述统计表算得的频率视作概率,回答下列问题:(i)求周一到周五的五天中恰有两天校园出现重度噪音污染而其余三天都是轻度噪音污染的概率.(ii)学校要举行为期天的“汉字听写大赛”校园选拔赛,把这天校园出现的重度噪音污染天数记为,求的分布列和方差 .17. (10分)(2017·河南模拟) 设函数f(x)=x﹣alnx+ .(Ⅰ)若a>1,求函数f(x)的单调区间;(Ⅱ)若a>3,函数g(x)=a2x2+3,若存在x1 ,x2∈[ ,2],使得|f(x1)﹣g(x2)|<9成立,求a 的取值范围.18. (10分) (2020高一下·吉林期中) 在锐角三角形中,角所对的边分别为,已知.(1)求角C的大小;(2)求的取值范围.19. (5分) (2019高二下·南宁期中) 已知各项均为正数的数列的前n项和为 ,且 .(1)求;(2)设,数列的前n项和,证明 .20. (5分) (2018高三上·邹城期中) 设函数 ( 为常数,是自然对数的底数),若曲线在点处切线的斜率为 .(Ⅰ)求实数的值;(Ⅱ)令,试讨论函数的单调性.参考答案一、单选题 (共8题;共16分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:二、填空题 (共6题;共7分)答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:三、解答题 (共6题;共50分)答案:15-1、答案:15-2、考点:解析:答案:16-1、答案:16-2、考点:解析:答案:17-1、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、考点:解析:。

浙江省舟山中学高三数学文科第四次月考试卷一、选择题:本大题共分10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、定义{}|,A B x x A x B -=∈∉且,若{}1,3,5,7,9A =,{}2,3,5B =,则A B -=A .AB .BC .{}1,2,7,9D .{}1,7,92、若条件2、p :14x +≤,条件q :23x <<,则q ⌝是p ⌝的A .充分不必要条件B .必要不充分条件C .充要条件D .既非充分条件也非必要条件3、已知,x y 满足约束条件50,0,3,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2z x y =+的最小值为A .-3B .3C .-5D . 5 4、若函数()3sin()f x x ωϕ=+对任意实数x 都有()()66f x f x ππ+=-,则()6f π=A .0B .3C .-3D . 3或-3 5、)1()1(5)1(10)1(10)1(5)1(23345-+-+-+-+-+-x x x x x x 等于A .5x B .51x - C .51x + D .5(1)1x --6、设双曲线22169144x y -=的右焦点为2F ,M 是双曲线上任意一点,点A 的坐标为()9,2,则235MA MF +的最小值为 A .9 B .365 C .425 D .5457、已知方程()()22220x mx x nx -+-+=的四个根组成一个首项为12的等比数列,则m n -=A .1B .32C .52D .928、已知棱长为a 的正四面体ABCD 有内切球O ,经过该棱锥A BCD -的中截面为M ,则O 到平面M 的距离为A .4a B .66a C .612a D .28a 9、在OAB ∆中,OA a =,OBb =,OD 是AB 边上的高,若AD AB λ=,则实数λ等于 A .2()a b a a b⋅-- B .2()a a b a b⋅-- C .()a b a a b ⋅-- D .()a ab a b⋅--10、垂直于直线2610x y -+=,且与曲线3231y x x =+-相切的直线方程是 A .320x y ++= B .320x y -+= C .320x y +-= D .320x y --= 二、填空题:本大题共4小题,每小题4分,共16分。
2020年浙江省舟山市市普陀中学高三数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 下列函数中,既是偶函数,又在上单调递增的函数是A. B.C. D.参考答案:C略2. 函数的图象的大致形状是()参考答案:D3. 若函数,当时,,若在区间内恰有一个零点,则实数的取值范围是( )....参考答案:A4. 设函数,则使得成立的取值范围是()A.B.C.D.参考答案:C11.设,则的大小关系为()A.B. C. D.参考答案:A6. 不等式的解集是( )A. B. C. D.参考答案:A略7. i为虚数单位,, 则的共轭复数为 ( )A. 2-iB. 2+iC. -2-iD. -2+i 参考答案:【知识点】复数代数形式的乘除运算;共轭复数.【答案解析】C解析:解:因为,故的共轭复数为,故选C.【思路点拨】先把原式化简,再利用共轭复数的概念即可求得结果.8. 已知i为虚数单位,(1﹣2i)?z=i3.则复数z在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限参考答案:D【考点】复数代数形式的乘除运算;复数的代数表示法及其几何意义.【分析】由(1﹣2i)?z=i3,得,然后利用复数代数形式的乘除运算化简复数z,求出复数z在复平面内对应的点的坐标,则答案可求.【解答】解:由(1﹣2i)?z=i3,得=,则复数z在复平面内对应的点的坐标为:(,),位于第四象限.故选:D.9. 已知函数在点处的切线与的图象有三个公共点,则的取值范围是().A. B.C. D.参考答案:D10. 已知函数,若存在实数满足其中,则的取值范围是()A. B. C. D.参考答案:B试题分析:由题意知,因此,,得,令,得或,由图知,令,得或,,,故答案为B考点:1、函数的图象;2、对数的运算性质二、填空题:本大题共7小题,每小题4分,共28分11. 设,其中实数满足,则的最大值是参考答案: 8 略12. 已知函数的图象为,则下列说法:①图象关于点对称;②图象关于直线对称;③函数在区间内是增函数;④由的图象向左平移个单位长度可以得到图象.其中正确的说法的序号为 .参考答案:②③13. 设函数.若有唯一的零点(),则实数a = .参考答案: 414. 已知函数的值域为,则实数的取值范围是参考答案:[0,1]15. 若变量x,y 满足约束条件则Z=2x-y 的最大值为( )A.2B.5C.1D.4参考答案:B略16. 在二项式的展开式中, 的一次项系数是,则实数的值为 . 参考答案:117. 某项研究表明:在考虑行车安全的情况下,某路段车流量F (单位时间内经过测量点的车辆数,单位:辆/小时)与车流速度v (假设车辆以相同速度v 行驶,单位:米/秒)、平均车长l (单位:米)的值有关,其公式为.(Ⅰ)如果不限定车型,,则最大车流量为 辆/小时;(Ⅱ)如果限定车型,, 则最大车流量比(Ⅰ)中的最大车流量增加 辆/小时.参考答案:(Ⅰ)1900;(Ⅱ)100三、 解答题:本大题共5小题,共72分。
- 1 - 杭州学军2020年4月高三月考 数学试卷 一、选择题 1.已知集合2|230AxRxx,1,0,1,2,3,4B,则( ) A.|13ABxx B.0,1,2AB C.|14ABxx D.1,0,1234AB 【参考答案】B 【试题解析】
先化简集合A,再利用集合的基本运算求解. 因为集合2|230|13AxRxxxRx,1,0,1,2,3,4B, 所以0,1,2AB 故参考答案:B 本题主要考查集合的基本运算,还考查了运算求解的能力,属于基础题. 2.若复数z满足232izi(其中i为虚数单位),则复数z在复平面内对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【参考答案】A 【试题解析】
设zxyi根据复数z满足232izi,得到2232xyyixi,再利用复数相等求解. 设zxyi,,xyR. 因为复数z满足232izi, 所以2232xyyixi, - 2 -
所以2322xyyx, 所以4575xy. 故参考答案:A 本题主要考查复数的运算及几何意义,还考查了运算求解的能力,属于基础题. 3.已知直线1:240laxy,2:(1)20lxay,则“1a”是“12ll”的 A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 【参考答案】C 【试题解析】
先得出两直线平行的充要条件,根据小范围可推导出大范围,可得到答案. 直线1:240laxy,2:120lxay,12ll的充要条件是1221aaaa或,当a=2时,化简后发现两直线是重合的,故舍去,最终a=-1.因
浙江省舟山市定海区中学2020-2021学年高三数学文月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知两个随机变量x,y之间的相关关系如表所示:根据上述数据得到的回归方程为=x+,则大致可以判断()A.>0,>0 B.>0,<0 C.<0,>0 D.<0,<0参考答案:C【考点】BK:线性回归方程.【分析】利用公式求出,,即可得出结论.【解答】解:样本平均数=0.2, =﹣1.7,∴==>0,∴=﹣1.7﹣×0.2<0,故选:C.【点评】本题考查线性回归方程的求法,考查最小二乘法,属于基础题.2. 若集合A={x|0≤x≤2},B={x|x2>1},则A∩B=( )A.{x|x>0或x<﹣1} B.{x|1<x≤2}C.{x|0≤x≤1}D.{x|0≤x≤2}参考答案:B考点:交集及其运算.专题:集合.分析:求解一元二次不等式化简集合B,然后直接利用交集运算求解.解答:解:∵A={x|0≤x≤2},B={x|x2>1}={x|x<﹣1或x>1},∴A∩B={x|1<x≤2}.故选:B.点评:本题考查了交集及其运算,考查了二次不等式的解法,是基础题.3. 正方体ABCD—A1B1C1D1中,E为CC1中点,则异面直线BC1与AE所成角的余弦值为()A. B. C. D .参考答案:答案:A4. 在边长为的正三角形中,设,,若,则的值为()(A )(B )(C )(D)参考答案:D5. (5分)复数等于()A.B.﹣C.i D.﹣i参考答案:D【考点】:复数代数形式的混合运算.【分析】:直接化简分母,然后分子、分母同乘分母的共轭复数并化简.解:=,故选D【点评】:复数代数形式的运算,是基础题目.6. 执行如图所示的程序框图,则输出的结果是A.171B.342C.683D.341参考答案:C根据程序框图可知:;;,. 故选C.7. 某几何体的三视图如图所示,则该几何体中,面积最大的侧面的面积为()A.B.C.D.3参考答案:B【考点】L!:由三视图求面积、体积.【分析】由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A﹣BCDE的高为1,四边形BCDE是边长为1的正方形,分别计算侧面积,即可得出结论.【解答】解:由三视图可知,几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A﹣BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED==,S△ABC=S△ABE==,S△ACD==,故选:B.8. 设是两条不同的直线,是三个不同的平面,则下列为假命题的是.若,则.若.若⊥,⊥,∥,则∥.若参考答案:D9. 在一次贵州省八所中学联合考试后,汇总了3766名理科考生的数学成绩,用表示,我们将不低于120的考分叫“红分”,将这些数据按右图的程序框图进行信息处理,则输出的数据为这3766名考生的.平均分.“红分”人数.“红分”率.“红分”人数与非“红分”人数的比值参考答案:依题意,输出的为红分人数,为红分率.10. 已知定义在R上的函数f(x)满足为偶函数,若f(x)在(03)内单调递减,则下面结论正确的是A. B.C. D.参考答案:A分析】根据以及为偶函数即可得出,并且可得出,根据在内单调递减即可得结果.【详解】,的周期为6,又为偶函数,,,,,又在内单调递减,,,故选A.【点睛】在比较,,,的大小时,首先应该根据函数的奇偶性与周期性将,,,通过等值变形将自变量置于同一个单调区间,然后根据单调性比较大小.二、填空题:本大题共7小题,每小题4分,共28分11. 化简逻辑函数式A+B+BC+AB= .参考答案:A+B【考点】相互独立事件的概率乘法公式.【专题】概率与统计.【分析】相互独立事件同时发生的概率等于两事件发生概率的乘积.【解答】解: =1﹣B , =1﹣C,所以:A+B+BC+AB=A×(1﹣B)+B×(1﹣C)+BC+AB=A+B,故答案为:A+B.【点评】本题考查相互独立事件的概率乘法公式,属于基础题.12. 已知中,过重心的直线交边于点(异于点),交边于点(异于点),设的面积为,面积为,,,则的取值范围为___________.参考答案:略13. 向量a,b,c在正方形网格中的位置如图所示,若,则=.参考答案:14. 如图,正方体的棱线长为,线段上有两个动点,且,则三棱锥的体积为 .参考答案:15. 下列命题:①函数y=sin(2x+)的单调减区间为,k∈Z;②函数y=cos2x﹣sin2x图象的一个对称中心为(,0);③函数y=sin(x﹣)在区间上的值域为;④函数y=cosx的图象可由函数y=sin(x+)的图象向右平移个单位得到;⑤若方程sin(2x+)﹣a=0在区间上有两个不同的实数解x1,x2,则x1+x2=.其中正确命题的序号为.参考答案:①②⑤考点:正弦函数的单调性;正弦函数的对称性;函数y=Asin(ωx+φ)的图象变换.专题:计算题.分析:①令+2kπ可求②利用两角和的余弦公式化简可得y=,令2x+,求出函数的对称中心③由可得,结合正弦函数的图象可求函数的值域④根据函数的图象平移法则:左加右减的平移法则可得⑤根据正弦函数的图象结合函数的对称性可得.解答:解:①令+2kπ,解得+kπ,k∈Z,,故①正确②y=,令2x+,解得x=+kπ,k=0时函数的一个对称中心(,0)②正确③y=,当﹣,结合正弦函数的图象可得﹣≤y≤1,③错误④由函数y=sin(x+)的图象向右平移个单位得到y=sinx的图象,故④错误⑤令y=sin(2x+),当x时,2x+,若使方程有两解,则两解关于x=对称,则x1+x2=,故⑤正确故答案为:①②⑤点评:本题综合考查了三角函数y=Asin(ωx+?)(A>0,ω>0)的性质:函数的单调区间的求解,函数的对称中心的求解,函数在闭区间上的最值的求解及函数图象的平移,还用到了两角和的余弦公式,而解决本题的关键是要熟练掌握并能灵活运用三角函数的图象.16. (本题满分12分)本大题共有2小题,第1小题满分6分,第2小题满分6分.已知函数(,,)的图像与轴的交点为,它在轴右侧的第一个最高点和第一个最低点的坐标分别为和(1)求函数的解析式;(2)若锐角满足,求的值.解:(1)由题意可得……………………………………………………………1分即,……………………………………………… 3分,由且,得………………………………………5分函数…… ………………………………………………6分由于且为锐角,所以…… ………………………………8分 (10)分略17. 已知在等腰梯形中,,,,双曲线以,为焦点,且与线段,(包含端点,)分别有一个交点,则该双曲线的离心率的取值范围是.参考答案:三、解答题:本大题共5小题,共72分。