初中数学统计与概率思维导图精品

初中数学7-9年级教材知识体系梳理思维导图
初中数学（7～9年级）课程标准
一、数与代数
在本学段中，学生将学习实数、整式和分式、方程和方程组、不等式和不等式组、函数等知识，探索数、形及实际问题中蕴涵的关系和规律，初步掌握一些有效地表示、处理和交流数量关系以及变化规律的工具，发展符号感，体会数学与现实生活的紧密联系，增强应用意识，提高运用代数知识与方法解决问题的能力。

在教学中，应注重让学生在实际背景中理解基本的数量关系和变化规律，注重使学生经历从实际问题中建立数学模型、估计、求解、验证解的正确性与合理性的过程，应加强方程、不等式、函数等内容的联系，介绍有关代数内容的几何背景；应避免繁琐的运算。

二、空间与图形
在本学段中，学生将探索基本图形（直线形、圆）的基本性质及其相互关系，进一步丰富对空间图形的认识和感受，学习平移、旋转、对称的基本性质，欣赏并体验变换在现实生活中的广泛应用，学习运用坐标系确定物体位置的方法，发展空间观念。

推理与论证的学习从以下几个方面展开：在探索图形性质、与他人合作交流等活动过程中，发展合情推理，进一步学习有条理地思考与表达；在积累了一定的活动经验与掌握了一定的图形性质的基础上，从几个基本的事实出发，证明一些有关三角形、四边形的基本性质，从而体会证明的必要性，理解证明的基本过程，掌握用综合法证明的格式，初步感受公理化思想。

在教学中，应注重所学内容与现实生活的联系，注重使学生经历观察、操作、推理、想像等探索过程；应注重对证明本身的理解，而不追求证明的数量和技巧。

证明的要求控制在《标准》所规定的范围内。

三、统计与概率
四、综合与实践
思维导图。

初中七年级数学上册思维导图(注：因为字数限制，以下思维导图并非完整版，仅供参考)第一章相识与认识1. 数学的定义1. 数学的由来2. 数学的定义3. 数学与周围世界的关系2. 数学与生活1. 数学在生活中的应用2. 数学的意义和价值3. 数学思维及其特点1. 数学思维的概念2. 数学思维的特点3. 提高数学思维的方法第二章认识数1. 自然数及其运算1. 自然数的概念与基本性质2. 自然数的排序3. 自然数的加减乘除运算2. 整数及其运算1. 整数的概念与性质2. 整数的大小比较3. 整数的加减乘除运算3. 有理数及其运算1. 有理数的概念与性质2. 有理数的大小比较3. 有理数的加减乘除运算4. 实数及其表示1. 实数的概念与性质2. 实数的表示方法第三章代数式与方程1. 代数式及其基本性质1. 代数式的概念与分类2. 代数式的基本性质2. 方程及其解法1. 方程的概念与分类2. 解方程的基本方法3. 解一元一次方程的公式3. 一次方程组及其解法1. 一次方程组的概念与分类2. 解一次方程组的基本方法4. 二元一次方程及其解法1. 二元一次方程的概念与性质2. 用消元法解二元一次方程第四章图形的结构1. 点、线、面的基本概念1. 点的概念及性质2. 线的概念及性质3. 面的概念及性质2. 基本图形及其性质1. 三角形的分类及性质2. 四边形的分类及性质3. 圆的概念及性质3. 同位角和内错角的概念及其性质1. 同位角和内错角的概念2. 相关定理的证明第五章几何运算1. 相似与全等1. 相似的概念与基本性质2. 全等的概念与基本性质3. 合同与全等的区别2. 勾股定理及其应用1. 勾股定理的概念与证明2. 勾股定理的应用3. 三角形的面积及其计算公式1. 三角形的面积的计算公式2. 利用面积公式解决实际问题第六章数据的处理1. 统计量的概念及其计算1. 概率的概念及性质2. 事件的分类及其概率2. 频数分布表及其分析1. 频数分布表的概念2. 分析频数分布表的方法3. 直方图、折线图及其应用1. 直方图、折线图的概念及绘制方法2. 分析直方图、折线图的方法第七章章节综合与实践1. 综合练习及复习2. 数学解决实际问题1. 实际问题解决的方法2. 实际问题的例题分析及解决方法。

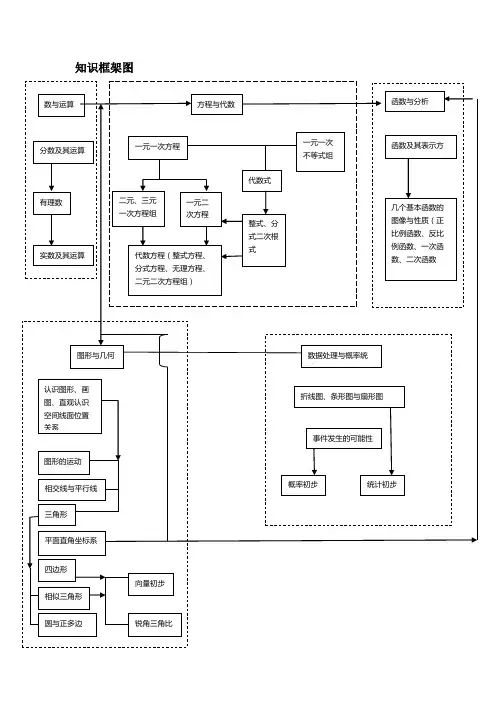
初中数学思维导图导图是一种将信息以图形方式组织和展示的工具。

在学习数学的过程中，使用思维导图可以帮助整理和归纳知识，促进思维的发散和联想。

本文将以初中数学为主题，探讨在学习初中数学过程中如何使用思维导图。

一、数的性质和关系思维导图1. 自然数、整数、有理数和实数的关系和性质- 自然数：介于0和正整数之间的数。

- 整数：正整数、负整数和0的总称。

- 有理数：可以表示为两个整数的比例的数。

- 实数：包括有理数和无理数（无限不循环小数）的总称。

2. 数轴和坐标系- 数轴：以0点为原点，正方向为正数，负方向为负数的直线。

- 坐标系：直角坐标系由x轴和y轴组成，x轴为横轴，y轴为纵轴。

3. 数的比较和大小- 比较运算符：大于（>）、小于（<）、大于等于（≥）、小于等于（≤）。

- 绝对值：数的绝对值是指这个数到0点的距离。

4. 数的逆运算和逆元- 加法逆运算：对于任意实数a，存在一个实数-b，使得a + b = 0。

- 乘法逆运算：对于任意非零实数a，存在一个实数1/a，使得a * (1/a) = 1。

二、代数表达式思维导图1. 代数式和代数方程- 代数式：包含变量、常数和运算符的表达式。

- 代数方程：等号连接的两个代数式。

2. 代数运算- 加法和减法：a + b、a - b。

- 乘法和除法：a * b、a / b。

- 幂运算：a^b。

3. 多项式表达式和因式分解- 多项式表达式：包含不同次数的单项式的代数式。

- 因式分解：将一个多项式或代数方程想成几个因式相乘的形式。

4. 代数式的值- 代入：将某个值代入代数式中计算。

三、几何思维导图1. 图形的分类- 点、线、线段、射线。

- 角的分类：锐角、直角、钝角。

- 三角形的分类：等边三角形、等腰三角形、直角三角形。

2. 图形的性质与关系- 直线：平行线、相交线、垂直线。

- 三角形：内角之和、外角之和。

- 平行四边形：对角线、对边。

3. 三角关系- 正弦定理：a/sinA = b/sinB = c/sinC。

数学八年级思维导图上册数学八年级思维导图上册
一、有理数
1. 有理数的定义
2. 有理数的四则运算
3. 有理数的大小比较
4. 有理数的绝对值
5. 有理数的加减法运算规律
二、代数式与方程式
1. 代数式的概念
2. 代数式的加减乘除
3. 代数式的因式分解
4. 简单一元一次方程式的解法
5. 一元一次方程式的应用
三、平面图形
1. 平面图形的基本概念
2. 三角形的性质及分类
3. 四边形的性质及分类
4. 正多边形的性质及分类
5. 平行线与平面图形的性质
四、函数
1. 函数的定义
2. 常见函数及其图像
3. 函数的性质及变化规律
4. 函数的概念拓展
5. 函数的图像及其在实际问题中的应用
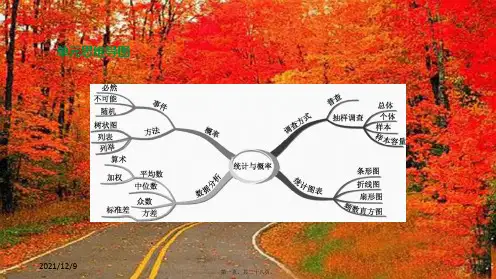
五、统计与概率
1. 统计中的基本概念及统计图
2. 概率的基本概念及概率模型
3. 事件的概念及其运算
4. 概率的应用
5. 统计与概率在实际问题中的应用
六、三角函数
1. 角度制与弧度制
2. 常见三角函数及其性质
3. 三角函数的等式和恒等式
4. 三角函数的运用及其在实际问题中的应用
5. 三角函数的图像和周期性
七、空间图形
1. 空间图形的基本概念及表示方法
2. 立体图形的计算
3. 空间直角坐标系及其应用
4. 空间几何中的关系与定理
5. 空间几何在实际问题中的应用
总结：
数学八年级思维导图上册内容涵盖了初中阶段最重要的数学知识点，包括有理数、代数式与方程式、平面图形、函数、统计与概率、三角函数以及空间图形等方面，是初中数学学习的重要参考资料。

千里之行，始于足下。

...定理、结论图表)-202X年中考数学学问梳理+思维导图202X年中考数学学问梳理+思维导图数学是一门基础学科，涵盖了多个学问领域。

在202X年中考数学考试中，同学需要把握肯定的数学学问，包括一些基本的定理和结论。

本文将对这些学问进行梳理，并结合思维导图进行具体说明。

一、代数学问1. 一次函数的概念及性质：一次函数的表示形式为y=ax+b，其中a、b为常数。

函数图像为一条直线，斜率为a，截距为b。

2. 二次函数的概念及性质：二次函数的表示形式为y=ax^2+bx+c，其中a、b、c为常数，且a不等于0。

函数图像为开口向上或向下的抛物线。

3. 幂函数的概念及性质：幂函数的表示形式为y=ax^k，其中a、k为常数。

幂函数的图像与指数函数的图像相像，但是有些状况下幂函数是奇函数，有些状况下是偶函数。

二、几何学问1. 直角三角形的性质：直角三角形有一个直角和两个锐角，满足勾股定理：c^2=a^2+b^2。

2. 利用勾股定理求解问题：依据已知直角三角形的两个边长，可以通过勾股定理求解第三个边长。

第1页/共3页锲而不舍，金石可镂。

3. 三角形的相像性质：假如两个三角形有相同的夹角，并且对应边的比例相等，则这两个三角形是相像的。

4. 三角形的面积计算公式：通过底边和高的乘积的一半可以计算三角形的面积。

三、概率与统计学问1. 概率的概念：概率是指某个大事在全部可能大事中发生的可能性。

2. 大事的排列组合：排列是指从一组元素中选取部分元素进行排序，组合是指从一组元素中选取部分元素进行组合。

3. 统计的概念：统计是通过对样本进行观看和测量，推断并描述总体的一种方法。

以上只是数学学问中的一小部分，但对于中考来说是比较重要的基础学问。

下面是一个思维导图，用于总结和梳理这些学问点。

[思维导图][图片]通过这个思维导图，我们可以清楚地看到不同学问点之间的关系和联系。

例如，直角三角形和勾股定理是直接相关的；概率和大事的排列组合是亲密相关的。

初中三年数学知识点总结思维导图初中三年的数学学习涵盖了广泛的知识点，从基础的算术运算到复杂的几何图形，再到函数和统计学，这些知识点构成了数学学科的坚实基础。

以下是初中数学知识点的总结思维导图：1. 数与代数- 有理数：包括整数、分数、小数和负数的概念，以及它们的加减乘除运算。

- 无理数：了解无理数的定义，如圆周率π和自然对数的底数e。

- 代数式：学习代数表达式的简化，包括合并同类项和分配律的应用。

- 一元一次方程：解方程的基本步骤，如移项、合并同类项和化简。

- 二元一次方程组：通过代入法或消元法求解方程组。

- 不等式：不等式的基本性质和解法，包括一元一次不等式和不等式组。

- 函数：一次函数、二次函数、反比例函数等的基本性质和图像。

2. 几何- 线段、射线和直线：了解它们的定义和性质。

- 角：锐角、直角、钝角和周角的概念及其度量。

- 三角形：三角形的分类，如等边、等腰、直角三角形，以及三角形的内角和定理。

- 四边形：平行四边形、矩形、菱形、正方形的性质和判定。

- 圆：圆的基本概念，如圆心、半径、直径，以及圆周率π。

- 多边形：正多边形的性质，如正五边形、正六边形等。

- 相似与全等：相似图形和全等图形的判定方法。

- 几何变换：平移、旋转和轴对称等变换的性质和应用。

3. 统计与概率- 数据收集：了解数据的收集方法，如调查、实验等。

- 数据整理：数据的分类、排序和图表表示，如条形图、折线图和饼图。

- 描述统计：平均数、中位数、众数、方差和标准差等统计量的计算。

- 概率：事件的确定性和不确定性，以及概率的计算方法。

- 随机变量：离散型和连续型随机变量的概念及其分布。

通过以上的思维导图，我们可以清晰地看到初中数学的主要知识点，这些知识点不仅为高中数学打下坚实的基础，而且在日常生活中也有着广泛的应用。

掌握这些知识点，对于提高数学素养和解决实际问题都具有重要意义。