连续刚构桥刚度变化对自振频率的影响

钢结构桥梁的自振特性与控制钢结构桥梁是现代交通基础设施中常见的一种桥梁型式，具有承载能力强、稳定性好等特点。

然而，钢结构桥梁的自振特性可能导致其在受到外力激励时发生共振现象，进而引发结构破坏和灾害事故。

为了保证桥梁的安全运行，研究钢结构桥梁的自振特性并采取控制措施变得尤为重要。

一、钢结构桥梁的自振特性钢结构桥梁的自振特性主要受到以下几个因素的影响：1. 材料特性：钢结构桥梁采用的钢材具有一定的弹性模量和密度，这些材料特性会直接影响桥梁的固有频率和自振特性。

2. 结构形式：钢结构桥梁的结构形式多种多样，包括悬索桥、梁桥等。

不同结构形式下的桥梁会有不同的固有频率和自振特性。

3. 外力激励：车辆行驶和风力等外力的作用会引起桥梁的振动。

如果外力的频率接近桥梁的固有频率，就会导致桥梁产生共振现象，从而增加桥梁的振动幅度，甚至引发桥梁的破坏。

二、钢结构桥梁的自振控制技术为了减小钢结构桥梁的自振幅度，提高桥梁的稳定性和安全性，需要采取一系列的自振控制技术。

1. 调整刚度：通过增加或减小构件的刚度，可改变桥梁的固有频率，使其远离外力频率，减小共振风险。

例如，通过加装加劲筋、加固节点等方式，增加整个桥梁的刚度，使其固有频率向低频移动。

2. 吸振器：在桥梁结构中安装吸振器可以吸收并分散桥梁振动的能量，从而减小振幅。

常见的吸振器包括液体阻尼器、摩擦阻尼器等。

3. 主动控制系统：通过在桥梁结构中设置传感器和执行器，实现实时的振动调节和控制。

主动振动控制系统可以根据外界振动信号实时调整构件的刚度和阻尼，从而达到减小自振振幅的目的。

三、案例分析以某钢结构桥梁为例，采用了主动控制技术进行自振控制。

在桥梁结构中安装了传感器，实时监测桥梁的振动状态。

当外界振动频率接近桥梁的固有频率时，控制系统会自动调节构件的刚度和阻尼，抑制共振现象的发生。

通过实验和模拟计算，证明了主动控制技术对钢结构桥梁的自振控制具有良好的效果。

在外界激励下，桥梁振幅显著减小，振动能量得到有效吸收和分散，保证了桥梁的安全运行。

钢结构人行天桥自振频率影响因素研究摘要城市化进程的不断加快对行人出行安全带来新的问题和挑战，城市道路交叉口往往都会修建人行天桥以保障行人的安全通行。

钢结构人行天桥以其自重轻、强度高的特点被广泛采用，根据规范中频率设计法要求，其自振基频不能超过3Hz，这对人行天桥的设计提出了更高的要求。

本文以某一结构人行天桥为例，采用有限元结构分析方法，分别分析主梁参数、约束条件两项变量对人行天桥自振频率的影响，从而改善桥梁结构的合理性，提高结构的安全性和舒适度。

关键词钢结构人行天桥自振频率主梁参数约束条件0 引言钢结构在恒载和活载作用下，变形及内力易满足设计要求，因此在设计时一般重点考虑其动力特性[1-2]。

如何优化钢结构人行天桥的设计，满足频率设计要求，对于保障桥梁结构和行人的安全具有重要的工程意义。

我国CJJ69—95《城市人行天桥与人行地道技术规范》提出的频率设计法规定[3]：人行天桥的竖向自振频率应不小于3Hz，因此文章以频率分析为主线，利用软件仿真分析，选取了梁高、跨径和约束条件几个参数，对钢人行天桥设计合理性展开研究，以期为同类桥梁设计提供借鉴意义。

1 频率设计法人行天桥主要活载为人群荷载，人群荷载一般取5kN/m2，在组合条件，对结构产生的挠度和应力值也远小于允许值，具有较大的安全储备。

根据桥梁的实际使用工况，正常行人的走步频率介于1.6～2.4Hz之间，为避免共振，提高行人的安全感，我国规范要求自振频率应不小于3Hz。

综上，频率设计法是人行天桥的典型计算方法。

对于钢结构人行天桥，在满足应力、挠度限制的基础上，通过调整钢结构梁体参数和边界约束条件，使梁体自振频率满足规范要求。

2 有限元建模以某一字型简支钢箱梁人行天桥为例建模，天桥跨径为23.8m，钢箱梁净宽4.5m，两侧栏杆各0.15m，全宽4.8m。

钢箱梁材料均采用Q355，梁高为100cm。

桥面铺装为40mm厚CF40钢纤维混凝土。

采用Midas Civil 2019有限元分析软件对全桥进行建模分析，定义自重荷载、二期恒载和人群荷载，将荷载转化为质量以便进行自振频率计算分析。

图 ４ 第二 阶振 型 ： 阶纵 向振 动 一
－
厂
Ｏ ５ ０ ０ ●
＃０ ５ ０
．
Ｏ ｏ ０
￡ 恤
Ⅲ ５
ｎ ｎｍ
蝴
，
∞，
－
根据 《 中国地震 动参数 区划 图｝Ｇ １３ ６ ２０ ）桥址区 （Ｂ ８０ — ０ １，
抗 震设 防烈 度属 ６度 区， 设计基本地震加速度值 ａ ０ ５ ， ＝ ． ｇ 设 ０
Ｓ ｉｎ ｅ＆ Ｔｅ ｈ ｏｏ ｙ Ｖｉｏ ｃｅ ｃ ｃ ｎ ｌｇ ｓ ｎ ｉ
公路科技
科 技 视 界
２１ 年 ０ 月第 １期 ０２ ５ ５
典型高墩大跨连续刚构桥抗震性能分析
任 蒙
（ 中交第二公 路 勘察设 计研 究院 有 限公 司 湖北
武汉
４０５ ） ３ ０ ６
ｔ４ 要】 ｇ 对一座典型高墩大跨 连续刚构桥进行 地震 动响应 分析 ， 通过调整连续刚构双肢墩之 间的 系梁连接 ， 究表 明 ， 研 增
图 １ 乌江特 大桥立面图 （ 单位 ： ｍ）
的重要性。高墩大跨预应力混凝土连续 刚构 的抗震性能的进
一
步研究 ， 将有助于防灾减灾 。 高墩大跨连续刚构桥 因其本身 的结构特 点 ， 抗震性 能具
有其特殊性 。本文 以一座典型高墩大跨连续 刚构 桥为背景 ，
研究 了高墩大跨连续 刚构桥 的动力性 能和地震动响应。
阶次
３ ４
周期（） ｓ
３９ ３ ８ ．４１ ３ ２５ ６ ５ ．７ ２ ８
频率（ ） ｈ ｚ
０．５３ ２ ２ ７ ０３ ８ ６ ．８ １
图 ３ 第 一 阶 振 型 ： 阶 横 向振 动 一

立 该 桥 的空 间有 限元 模 型 ， 对 其 自振 特 性 进 行 计 算 分 析 ， 获 得 了该 桥 的 自振 频 率 和振 型 。 关键 词 大 跨 连 续 刚构 桥 有 限 元 自振 特 性
山 区高等 级公 路 连 续 刚构 桥 梁 ， 通 常 以跨越 深谷 沟 壑 ， 受 力合 理 ， 施 工便 利 ， 跨 度 大 为其 特 点 而被 广泛 应用 ｕ ］ 。又 因桥 墩 固结 的特 点 ， 省 去 了 大跨 连续 梁 的支座 ， 同时桥墩 厚度 大大减 小 ， 减 少
邓 果 陈 昊 吴 俊
（ 贵 州 省 交 通 规 划 勘 察 设 计 研 究 院 股 份 有 限公 司 贵 阳 ５ ５ ０ ０ ０ １ ）
摘
要 以 山 区大 跨 连 续 刚 构 桥 —— 鱼 洞 大 桥 为 研 究 对 象 ， 运 用 大 型 通 用 有 限 元 软 件 ＭＩ ＤＡ Ｓ建
阵； 五 ， Ｕ分别 对 应 于系统 加 速度 列 阵 和 位移 列 阵 。 假 定 多 自由度 体 系 的 自 由振 动 是 简 谐 振 动 ， 则 位
移 可 写 成
（ ￡ ） 一 ｓ ｉ ｎ（ ＋ ） （ ２ ）
ｂ ） 第 ２阶 振 型 （ 主梁一阶横弯）
物 线变 化 。主墩 的设 计 形 式 为 双 薄 壁式 实 心 墩 ， 实 心墩横 桥 向 ６ ． ５ ｍ， 顺桥向 ２ ． ２ ｉ ｎ ， 两 片墩 问净
图 ２ 全 桥 有 限元 模 型
收 稿 日期 ： ２ ０ １ ２ － １ ２ ２ ４
２ ０ １ ３年 第 ２ 期
邓
横坡 为单 向 ２ ． ０ （ 左 右 幅相 反 ） 。上 部箱 梁 为 变 截 面单箱 单 室 断 面 ， 箱 顶宽 １ １ ． ２ ５ ｍ， 底宽 ６ ． ５

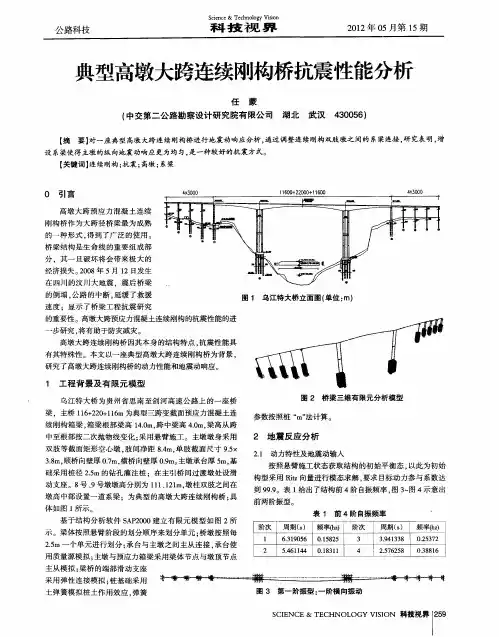
大跨度连续刚构桥抗震性能分析谢群华【摘要】双肢薄壁墩和单柱式墩是连续刚构桥的常用桥墩结构形式,为研究桥墩形式对桥梁的影响,以某连续刚构桥为基础,建立空间有限元模型,对比分析双肢薄壁墩和单柱式墩对连续刚构桥动力特性与地震相应的影响,研究预应力对桥梁地震响应和抗震性能验算的影响.结果表明,相同截面情况下,双肢薄壁墩比单柱式墩受力更为合理,预应力对刚构桥地震响应影响不大,但抗震性能验算时必须考虑预应力作用,且双肢墩的内外两肢受力要协调,避免正常使用状况下内外两肢内力相差过大.【期刊名称】《现代交通技术》【年(卷),期】2016(013)004【总页数】4页(P32-35)【关键词】双肢薄壁墩;单柱式墩;刚构桥;预应力;抗震性能【作者】谢群华【作者单位】东南大学建筑设计研究院有限公司,江苏南京210096【正文语种】中文【中图分类】U442.5+5连续刚构桥具有造型优美、跨越能力强、施工方便、造价低等优点，近年来在我国山高谷深的西南、西北地区大量采用。

2008年在汶川地震中庙子坪大桥是近年国内第一座大跨度连续刚构桥震害实例，主要震害是桥墩开裂和倾斜［1］，并且5号墩水下部分出现横向贯通裂缝，裂缝宽度达0.8 mm。

刚构桥的易损部位位于墩顶和墩底［2-3］，由于刚构桥一般跨越峡谷或河流，震后维修较为不便，因此开展大跨度连续刚构桥的抗震性能评价尤为重要。

汶川地震后国内学者对连续刚构桥进行了较多研究，夏修身、陈兴冲等［4］对铁路刚构桥进行了研究，提出对其进行弹性抗震设计是不经济的，尚维波等［5］对高墩刚构桥体系梁进行了抗震研究，李子春［6］针对不同的桥墩形式对刚构桥的动力特性进行了研究，但是对双肢薄壁刚构桥的协同受力没有研究。

本文针对在公路桥梁上采用双肢薄壁墩或单柱式墩，进行了动力性能比较，并对地震荷载作用下的内力进行了相应对比，分析了预应力钢束对桥墩抗震性能的影响。

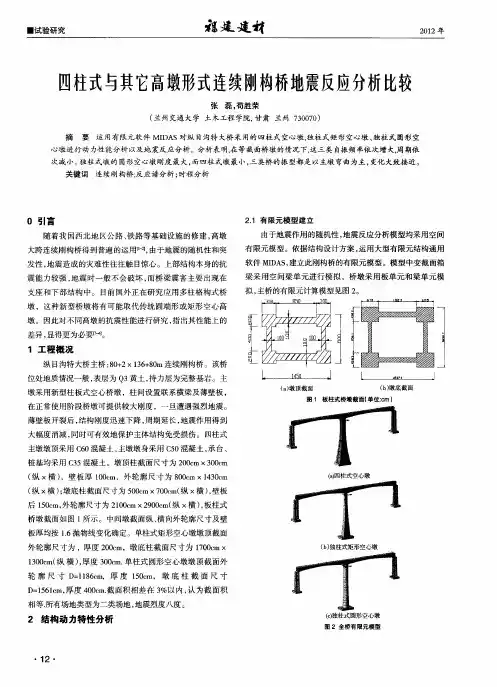
某3跨大跨径连续刚构桥跨径组成为（97+176+ 97）m，全长370 m，桥梁总体布置图见图1。

●验 究 试 研
更 莲 村
２２ ０生 １
四 柱式与其它高墩形式连续冈构桥地震反应分析比 ９ 较
张 磊 ， 胜 荣 苟
（ 兰州交通大学 土木 工程 学院， －兰州 ７ ０７ ） 甘ａ ３０ ０ 摘 要 运用有限元软件 ＭＩ Ａ Ｄ Ｓ对纵 目沟特大桥 采用的四柱式空心墩， 独柱式矩形 空心墩 、 独柱式圆形 空
波作用与结构，直接对结构运动方程进行数值积分而求得结
构地 震反 应的时间历程， 能考虑结构 的弹性和弹塑性状态， 能
反应谱理 论也 称动力法 ， 目前世界各 国应用最 为广 泛 是
的抗震分 析方 法 ， 其优点是考 虑了地震时地面的运动特性 与 结构物 自身的动力特性 ， 只需 要取少数的低阶振型就可 以求 得较 为满意 的结果 ， 且计算 量少 ， 而加 速度反应谱 值是加 速 度反应 的最大值 ， 用它来进行设计 一般 来说是安全的 。该桥 所处场地类型 为 Ⅱ类 ， 反应谱采用 Ⅱ类 场地的标准谱作 为谱
二十阶振型， 振型总参与质量为 ９． ％， ７ ４ 满足规范要求， １ ６ 表 列出 了该桥三种桥墩形式下前 １ ０阶振型的频率周期及振型特征。
表 １ 结构的 自振频率及振型特征
从表 １中三类墩柱 的全桥频率 和周期分 析得出 ： 采用 四
柱式空心桥 墩 、 独柱式矩 形空心 墩 、 独柱式 圆形 空心墩 的 自
墩 ，这种新型桥墩将 有可能取代传统 圆端形或矩形 空心高
墩 。因此 对不 同高墩 的抗震性能进行研究 ， 出其性能上 的 指
差异 ， 显得 更 为 必 要 。
１ 工 程概况
纵 目沟特大桥主桥 ：０ ２×１６ ８ ｍ连续刚构桥 。该桥 ８＋ ３＋０ 位处地质情况一般 ， 表层为 Ｑ 黄土 ， 力层 为完整基岩 。主 ３ 持 墩 采用新 型柱板式空心桥墩 ，柱间设置联系横梁及薄壁板 ， 在正常使用阶段桥墩 可提供较 大刚度 ，一旦遭遇强烈地震。

连续刚构桥健康监测自振频率测试和评估研究
连续刚构桥健康监测自振频率测试和评估研究
在对桥梁进行健康监测时,准确地测量桥梁的自振频率是非常重要的.以某连续刚构桥为例,简要地介绍了加速度传感器在测量桥梁自振频率中的应用,并提出了桥梁自振频率的评估模式,为后期健康监测桥梁结构技术状态的判定提供了依据.
作者：石鹏程陈宇 SHI Peng-cheng CHEN Yu 作者单位：重庆交通大学土木建筑学院刊名：黑龙江交通科技英文刊名：COMMUNICATIONS SCIENCE AND TECHNOLOGY HEILONGJIANG 年，卷(期)：2009 32(2) 分类号：U446.3 关键词：连续刚构桥健康监测自振频率评估。

钢结构自振频率分析与优化设计自振频率是指结构在自身没有外部激励的情况下产生的固有振动频率。

钢结构自振频率的分析与优化设计是工程领域重要的研究课题之一，对于保证结构的安全性和稳定性具有关键作用。

首先，进行钢结构自振频率分析时，需要考虑结构的动力特性、材料特性以及结构的几何形态。

其中，结构的刚度是影响自振频率的重要因素之一。

刚度较大的结构往往具有较高的自振频率，反之亦然。

因此，优化设计时可以通过调整结构的截面尺寸、材料性质以及梁柱等构件的布置方式来改变结构的刚度，从而达到调节自振频率的目的。

在分析钢结构的自振频率时，还需要考虑结构的振型。

振型是指结构在振动时不同部位的位移分布情况。

结构的振型与其自振频率密切相关，不同的频率对应着不同的振型。

例如，自振频率较低的模态往往具有较大的位移响应，而较高的自振频率则对应着较小的位移响应。

因此，通过对结构进行自振频率分析，可以了解到结构的振型特点，从而为结构的设计提供重要的参考依据。

钢结构自振频率分析与优化设计不仅可以用于评估结构的振动性能，还可以用于探测结构的缺陷和隐患。

由于振动会引起结构内部的应力变化和疲劳破坏，因此通过自振频率分析可以对结构的健康状况进行监测。

通过对结构振动响应的采集和分析，可以及时发现结构的变形、裂缝等缺陷，并采取相应的修复和加固措施。

这不仅可以提高结构的使用寿命，还能够保证结构的安全性和可靠性。

然而，钢结构的自振频率分析与优化设计并非一件简单的任务。

首先，钢结构的模型构建需要考虑多个因素，包括结构的材料、几何形态、运载条件等。

其次，自振频率的计算需要进行大量复杂的数值计算和仿真分析，这对计算资源和算法的要求较高。

此外，在操作过程中还需要考虑结构的实际使用条件和约束，使得优化设计结果能够满足实际需求。

最后，钢结构自振频率分析与优化设计是钢结构工程设计中不可或缺的一环。

通过对结构的自振频率进行分析，可以了解结构的动态特性和振动行为，为结构的设计提供依据和指导。

第2P总第262期)2021年2月URBAN ROADS BRIDGES&FLOOD CONTROL桥梁结构D01:10.16799/ki.csdqyfh.2021.02.013钢结构人行桥自振频率影响因素及其分析叶涛!，李亚平"，肖海波1(1.宁波市城建设计研究院有限公司，浙江宁波315012；2•宁波市供排水有限公司工程建设管理分公司，浙江宁波315041)摘要：城市钢结构人行天桥竖向自振频率为设计控制要素之一。

提出了影响桥梁自振频率的因素，并通过有限元分析软件梁单元模型进行分析计算，研究了结构型式、梁高及桥面铺装对桥梁自振频率的影响。

得到的相关结论可对同类工程起到借鉴参考意义。

关键词：钢结构；人行天桥；自振频率中图分类号：U448.11文献标志码：A文章编号：1009-7716(2021)02-0048-030引言城市进程，人行过天桥及公天桥来多。

伴人们日渐提高的审，新的人行天桥相来结构有频率的，行人[常行频，人-桥振，人行桥L 振⑴人行桥对人行桥共振提的设计要有频率响分析城市人行天桥人行(CJJ69—1995)频率£法，要竖向自振频率3Hz。

人行天桥的过振行人来，对结构有一影响有要对人行天桥的竖向振及其影响因素进行深入研究。

1影响桥梁自振频率的因素结构的自振频率公式Y#(%)]2d%!2二一!-------------------------------------------------------------]°&(%)[Y(%)]2d%+"m(Y?(1)(2)式!为圆频率;/为频率；*为模；/为面；$(%)为位移形状函数；Y(为质点&的振幅;&为平均质；I为桥梁跨式(1)、式(2)可知，桥梁的自振频率与以下因素有关：收稿日期：2020-07-17作者简介：叶涛(1989―),男，硕士，工程师，从事桥梁设计工作。

连续刚构桥刚度变化对自振频率的影响摘要：桥梁结构的自振特性对正确进行桥梁的抗震设计、健康检测和维护具有十分重要的意义，因此分析刚构桥各个部位刚度对其自振频率的影响在桥梁设计以及将来桥梁在运营中激振频率对桥体安全性的影响都有很重要的意义。

本文以某连续钢构桥为例建立了有限元计算模型，分别分析了在改变桥梁的梁体、墩和钢筋刚度的情况下，所得出的相应的自振频率的变化，并对计算结果进行了初步分析比较，得出了具有一定指导意义的结论。

关键词：连续刚构桥；有限元；自振频率；ANSYS一、概述刚构桥特别是大跨度连续刚构桥已经在桥梁工程领域得到了广泛的应用，其结构特点主要是：其墩、梁、基础三者固结为一个整体而共同受力；墩身的形式、高度等对桥体结构受力都有影响。

随着刚构桥体系的发展，跨度在不断增大，墩部也在不断加高，因此出现了许多有关此类桥梁结构模态和稳定性等动力特性方面的问题，研究此类桥梁结构的动力特性有着非常重要的意义。

随着振动理论及其相关学科的发展，人们早已改变了仅仅依靠强度理论进行结构设计的观念。

桥梁，特别是大跨度桥梁，必须考虑桥梁上车辆荷载振动的影响，过去和现在都发生过由于共振引起的桥梁毁塌事故。

对桥梁的激振频率应尽量避开其各阶自振频率。

由模态分析的结果，即模态频率等参数，对被测结构进行直接动态性能评估。

对一般结构，要求各阶频率远离激振频率，或激振频率不落在某阶模态的半功率带宽内，已成为工程界的基本方法。

二、算例分析（一）算例介绍该连续钢构桥全长410.65m，最高桥墩56m，主跨为168m。

主跨为预应力混凝土连续刚构桥，主桥按（96＋168＋96）m布置。

梁体为单箱单室变高度变截面箱形梁，支墩处高11.0 m，中跨跨中及边跨梁端处梁高5.5 m，梁体下缘除中中跨跨中部10 m梁段，河边跨部17.8 m梁段为等高直线外，其余按二次抛物线变化。

箱梁顶板宽11.0 m，箱宽7.8 m。

除梁段附近区段外，顶板厚60 cm，底板厚50~110 cm，腹板厚50~100 cm。

结构刚度对桥梁固有频率和模态的影响
傅强;郭正婷
【期刊名称】《山西建筑》
【年(卷),期】2010(036)021
【摘要】基于Euler-Bernoulli梁理论,给出了桥梁在列车移动荷载下的动力学模型,对比分析了考虑刚度效应前后的固有频率和振型模态,结果表明:刚度越大,桥梁固有频率越高,并且固有频率阶数越低,刚度的影响越大,振型模态受刚度的影响不大,主要取决于跨度、边界条件和质量.
【总页数】2页(P305-306)
【作者】傅强;郭正婷
【作者单位】中冶华天工程技术有限公司,安徽,马鞍山,243005;中冶华天工程技术有限公司,安徽,马鞍山,243005
【正文语种】中文
【中图分类】U441
【相关文献】
1.温度对结构模态固有频率的影响研究 [J], 马帅
2.Galerkin模态截断对计算悬臂输液管道固有频率的影响 [J], 齐欢欢;徐鉴
3.矩形薄板通透开裂缝对固有频率和模态的影响分析 [J], 龚健;卢奂采;陈振安;庄一舟;金江明
4.桥梁结构刚度对高速列车—轨道—桥梁耦合系统动力特性的影响 [J], 翟婉明;王少林
5.底架边梁及上弦梁结构刚度对车体结构模态的影响 [J], 孟飞;杨冰;阳光武;肖守讷;朱涛;邓永权
因版权原因，仅展示原文概要，查看原文内容请购买。

影 响 不 大 ， 要取 决 于 跨 度 、 界 条 件 和 质 量 。 主 边
关键词 ： 桥梁 ， 固有频率 ， 态 ， 模 刚度
中 图分 类 号 ： ４ Ｕ４ １ 文献标识 码 ： Ａ
其 中 ， （ 为 彤 状 函数 ， 固有 振 动 的 模 态 。 ） 为
０ 引言
桥梁 在 列 车 荷 载 作 用 下 的 动 力 学 问题 通 常 采 用 移 动 荷 载 下
式 （１ 有 解 的条 件 为 ： １） —ｖ ）㈩ ｔ
Ａ ２＝ Ａ ３＝ Ａ ４＝ ０ ｓｎａ ０ ｉ ｊ
＝
，
（ 优 ＝∑ （ ｖ＋ 一 ） — ｔ Ｌ）
（ ２ ）
Ａ１ 任 意 常数 ， 每 一 阶模 态 有 Ａ１ ｊ 为 对 ＝ｑ。 式 （３为频率方程式 ， 此有 ： １） 冈
郭正婷 （９１ ， ， 授级高级工程师 ， １６ 一）女 教 中冶 华 天 工 程 技 术 有 限 公 司 ， 徽 马 鞍 山 安
Ｅ ＋ｍ ＝０ ㈩
＝ｊｒ （ Ｔｊ＝１ ２ … ， ， ， ”）
将 式（４代人式 （） ： １） ８有
２（） 宇
固有频率为 ：
＝
由于方程 （ ） 自由振动时为谐振 变化 ， 解可假定为 ［ ： １在 其 ］
（， ＝∑ｙ ｘｓ ｏ ） ｊ） ｊ （ ｉｔ ｍ
根据振 型分解的原则 ， 每一阶模 态都需满 足式 （ ） 因此可简 ６，
ｄ ｘ） ｙ（ ｉ
一
四种 ＿ 。描述 连续 弹性 体的梁有 Ｅ ｌ － ｅ ｕ ｉ 和 Ｔ ｍ ｓｅ ｋ １ Ｊ ｕｅ Ｂ ｍｏ ｌ 梁 ｒ ｌ ｉ ｏｈｎ ｏ Ｔｉ ｓｅｋ ｍｏｈｎ ｏ梁模型在其基础上 引入 了剪切应 变和旋转 惯性 ， 使受 力 分 析 更 加 完 整 ＿ 。 但 Ｔｍｏｈｎ ｏ梁 模 型 理 论 分 析 较 为 复 杂 ， ２ Ｊ ｉ ｓｅ ｋ

结构刚度和自振频率结构刚度是指结构体系在外部施加作用力或荷载下，抵抗变形的能力。

在弹性范围内，结构刚度可以通过材料的弹性模量和截面尺寸来确定。

结构刚度越高，结构在受到载荷时，其变形越小。

结构刚度可以通过以下公式来计算：K=F/δ其中，K是结构刚度，F是作用在结构上的力，δ是结构的变形。

结构刚度的大小直接影响着结构的稳定性和延性。

若结构刚度不足，结构在受到外部载荷时容易产生较大的变形，甚至可能导致结构的破坏。

若结构刚度过大，结构受到外部载荷时不能充分吸收载荷能量，容易产生应力集中，从而引发结构破坏。

自振频率是指结构体系在没有外部载荷作用下，自然地以特定的频率来振动。

自振频率可以通过结构的质量和刚度来计算。

结构的自振频率与其固有振动情况密切相关，主要取决于结构的质量和刚度。

对于固定在地基上的结构来说，在自振频率接近结构受到周期性激励的频率时，结构就容易发生共振。

共振会导致结构振动幅值增大，并引起破坏。

因此，设计过程中通常需要考虑结构的自振频率并避免与外部激励频率产生共振。

提高结构刚度可以降低结构的振动频率，而降低结构的刚度则可以增加结构的振动频率。

为了实现理想的结构性能和振动特性，需要在设计过程中进行综合考虑和权衡。

总之，结构刚度和自振频率是结构设计中非常重要的概念。

结构刚度决定了结构对外部载荷的抵抗能力，而自振频率则表示了结构在没有外部载荷作用下自然振动的频率。

在设计过程中，需要合理选择结构刚度和自振频率，以确保结构的稳定性、耐久性和抗震安全性。

刚度布置对连续梁自振特性的影响本文中将建立有限元模型分析典型刚度分配下的连续梁结构的自振特性。

自振特性分析中最重要的问题就是求解出结构的固有频率和固有振型，在本章中将采用ANSYS软件的模态分析部分功能用于求解结构的模态和固有频率, 以此来分析典型刚度分配下连续梁桥的自振特性。

为了方便比较与建模，令模型中跨长度为100m，边中跨比为0.6。

在中跨为100m和边中跨比为0.6保持不变的前提下，改变该模型桥的刚度分配规律，建立有限元模型。

4.1 有限元模型概况有限元模型概况图形式如图3.1和图3.2所示，在此不赘附。

4.2 模态分析及各阶振型边中跨比为0.6时，各阶振型图与图3.3所示形式相似。

如图4.1所示。

（a）第1阶振型（b）第2阶振型（c）第3阶振型（d）第4阶振型（e）第5阶振型（f）第6阶振型（g）第7阶振型（h）第8阶振型（i）第20阶振型图4.1 各阶振型4.3 规律分析为了分析出不同刚度分配规律下其自振特性的变化情况，分别通过改变梁高的变化来改变梁纵向刚度的分配，并以此建立有限元模型，3种刚度分配方案下，1-1、3-3截面梁高不变，2-2截面梁高依次增大，桥的截面形式和其余参数相同。

显然第三种刚度分配情况下桥梁整体的刚度更大。

如图4.2所示。

具体的刚度分配方案为：（a）刚度分配方案1：1-1截面梁高为2m，2-2截面梁高4m，梁高按照二次抛物线变化。

（b）刚度分配方案2：1-1截面梁高为2m，2-2截面梁高6m，梁高按照二次抛物线变化。

（c）刚度分配方案3：1-1截面梁高为2m，2-2截面梁高8m，梁高按照二次抛物线变化。

图4.2 刚度分配示意图经过计算，得出这3种刚度分配方案下的前20阶振型对应的固有频率（TIME/FREQ）并列于表4.1中。

表4.1如下所示。

表4.1 不同刚度分配方案下频率变化表阶数刚度情况刚度分配方案1 刚度分配方案2 刚度分配方案31 0.43256 0.56928 0.697022 0.88186 1.1143 1.32133 1.1219 1.4955 1.81894 1.6552 2.2049 2.70945 2.6807 2.9033 2.96086 3.2773 3.8831 4.70057 3.5278 4.5017 5.42298 3.8577 5.0443 6.17989 5.1853 6.6824 8.017910 6.8995 8.5720 9.710411 7.5948 9.6329 11.34612 8.3960 10.698 12.02513 9.7738 10.869 12.68914 10.844 11.994 13.10115 11.271 13.836 16.05816 12.785 16.011 17.41917 13.344 16.724 19.45618 14.956 17.368 20.44219 16.537 19.073 22.75820 18.270 22.407 23.261图4.2 不同刚度分配方案下频率变化图从表3.2和图4.2中可以发现：随着2-2截面梁高增加，梁桥在不同刚度分配方案下频率随着阶数的变化形式相似；随着梁高增大，梁桥刚度增大，在同一阶振型下，频率随着桥梁刚度增大而增大；采用同一种刚度分配方案时，随着阶数增加，频率增加。

结构刚度和自振频率结构刚度是指物体抵抗变形的能力。

当物体受到外力作用时，其内部会发生一定的形变，这种形变就是结构变形。

而结构刚度就是物体抵抗变形的能力大小。

我们可以想象一下，如果一个物体全然没有刚度，那么它就无法保持其原有形状，而会轻易地变形。

所以，结构刚度是一个物体保持原有形状的重要因素之一。

结构刚度与受力有直接关系。

当一个物体受到定向的力作用时，它会沿着受力方向发生位移，而这种位移就是变形。

结构刚度越大，物体在受力后产生的变形就越小。

如果结构刚度过小，物体就会在承受相同的力时发生较大的位移和变形。

这就会对物体的使用带来一定的损害或者失效。

结构刚度是钢结构、混凝土结构以及木质结构等建筑结构中常用的描述参数。

不同材料的结构刚度不同，一般来说，钢材的刚度最高，混凝土材料次之，木材材料专业度最小。

结构刚度大小因此会影响到建筑物的不同功能，例如，高层建筑中通常采用钢结构来保证其安全和稳定，而木材往往用于制作家具等轻质结构。

自振频率是指物体的固有振动频率，通俗来说，就是一个物体单独存在时自然振荡的频率。

物体固有振动频率是其几何形态、质量以及弹性特性决定的。

物体在固有频率下振动时自发地产生共振，这种共振就是物体自身谐振的状态。

这个状态与可能的外部激励频率相匹配。

自振频率可以作为结构设计和分析中的重要参数来使用。

对于桥梁和建筑等结构，特别是在地震等极端情况下，将结构的自振频率降低至不与激励频率相近，就能避免共振现象的发生产生结构损坏的细节。

由此可见，通过合理的调整自振频率，我们可以提高结构的抵抗能力，从而保证建筑物的安全性和稳定性。

总之，结构刚度和自振频率是建筑结构中非常重要的参数。

结构刚度直接影响建筑物的稳定性和抗力能力，而自振频率则影响结构的共振现象。

了解这两个参数，可以帮助我们更好地理解和设计建筑物。

钢结构的自振与共振分析钢结构是一种重要的结构形式，具有承载能力强、抗震性能好等特点。

然而，在实际运行中，钢结构也会面临自振与共振的问题，可能会引发结构的破坏和安全隐患。

因此，对钢结构的自振与共振进行分析和评估，具有重要的工程意义。

本文将就钢结构的自振与共振问题展开探讨。

1. 振动的基本原理振动是物体在受到外力作用下产生的一种周期性往复运动。

对于钢结构而言，其自振与共振主要由以下因素影响：1.1 结构的固有频率结构的固有频率是指在无外力作用下，结构自身固有振动的频率。

钢结构的固有频率与其几何形状、刚度和质量分布有关，是结构自身的属性。

1.2 外界激励频率外界激励频率是指作用于钢结构的外力或外界环境的振动频率。

外界激励频率可能是恒定的，也可能是变化的，如地震、风力等。

2. 自振与共振的问题2.1 自振当外界激励频率接近或等于结构的固有频率时，钢结构将会发生自振现象。

自振可能引发结构的超载、疲劳和振动破坏等问题。

因此，在钢结构设计和施工过程中，需要合理控制结构的固有频率，以避免自振问题的产生。

2.2 共振当一个物体的振动频率与另一个外部振动源的激励频率相等或接近时，就会发生共振现象。

共振会导致结构受到外力的放大作用，加速结构的疲劳和破坏。

因此，在钢结构的设计和施工中，需要避免共振问题的发生。

3. 自振与共振分析方法为了预测和评估钢结构的自振与共振问题，工程师们通常采用以下方法进行分析：3.1 模态分析模态分析是一种分析结构固有频率和振型的方法。

通过模态分析，可以获得结构的固有频率和相应的振型，从而评估结构的自振问题。

3.2 频率响应分析频率响应分析是一种分析结构对外界激励频率的响应功效的方法。

通过频率响应分析，可以评估结构在不同激励频率下的响应情况，进而判断结构是否存在共振问题。

4. 自振与共振的控制措施为了控制钢结构的自振与共振问题，可以采取以下措施：4.1 结构优化设计在钢结构的设计过程中，可以通过调整结构的几何形状、增加结构的质量或刚度等方式来改变结构的固有频率，以减小自振和共振的风险。

自振频率和刚度的关系哇塞！一听到“自振频率和刚度的关系”这个题目，是不是感觉有点头疼？其实我一开始也这么觉得，但是后来老师一讲，好像也没有那么难理解啦！咱们先来说说啥是自振频率吧。

你可以把它想象成一个东西自己喜欢“抖”的节奏。

比如说，一根琴弦，你轻轻拨动它，它就会按照一个特定的频率抖动起来，这个就是它的自振频率啦。

那刚度又是啥呢？这就好像是一个东西的“脾气”。

刚度大的东西，就像一个脾气很倔的人，很难被改变形状；刚度小的呢，就像个好脾气的人，轻轻一弄就变形啦。

那自振频率和刚度到底有啥关系呢？这就好比跑步的速度和腿的力量！腿的力量越大，也就是刚度越大，那跑起来的节奏，也就是自振频率，不就可能会更快嘛！咱们来假设一下，有两根同样长度的弹簧。

一根弹簧特别硬，很难拉伸或者压缩，这就是刚度大；另一根弹簧很软，轻轻一拉就变长，一压就变短，这就是刚度小。

当我们给它们同样的一个扰动，你说哪个弹簧振动的速度会更快呢？肯定是刚度大的那个呀！因为它更“有力气”，振动起来就更“带劲”，自振频率也就更高啦。

再比如说，一座大桥。

如果这座桥的结构刚度很大，很结实，那它在风吹或者车开过的时候，振动的频率就会比较低，不会轻易地晃来晃去。

可要是这桥的刚度不够，哎呀，稍微有点动静，可能就会晃得厉害，自振频率也就乱七八糟的啦。

你想想看，要是咱们住的房子刚度不够，稍微有点风吹草动就“抖个不停”，那多吓人呀！所以建筑师们在设计房子、桥梁这些东西的时候，就得好好考虑自振频率和刚度的关系，不然出了问题可就糟糕啦！我觉得呀，自振频率和刚度的关系真的太重要啦！咱们生活中的好多东西都得靠它们俩配合好，才能安全又稳定地存在。

要是不搞清楚它们，那可真是会有大麻烦呢！。