2020年辽宁省沈阳市和平区九年级一模试题及答案

2020年辽宁省沈阳市和平区中考语文一模试卷一、积累与运用（15分）1．（2分）下列词语中加点字的字音、字形完全正确的一项是（）A．囫．囵（hú）杜绝．（jué）狩．猎（shòu）自暴．自弃（bào）B．圈订．（dìng）睥．睨（pì）熏陶．（tāo）目眩．神迷（xuàn）C．执着．（zhuó）鹳．鸟（huān）帐蓬．（péng）翻来覆．去（fù）D．修润．（rùn）落弟．（dì）记载．（zài）取义成仁．（rén）2．（2分）依次填入下面句子横线处的词语最恰当的一项是（）“百善孝为先”，________，就是在所有的美德中，“孝”排在第一位。

木兰替父从军，白居易孝亲敬老，郑板桥责行孝道……从这些历史典故中，我们领悟到秉承孝行的可贵和可敬的精神。

________，随着时代的发展，我们的孝行________在不知不觉中________甚至被全然________．一杯茶、一碗饭，点点滴滴见真情；一件衣、一床被，丝丝缕缕连爱心。

孝是稍纵即逝的眷恋，孝是无法重现的幸福。

让我们用行动________孝义，让孝与和谐相伴，让孝与爱心同行。

A．顾名思义虽然也淡化遗忘实现B．望文生义然而却遗忘淡化实现C．顾名思义然而却淡化遗忘践行D．望文生义虽然也遗忘淡化践行3．（3分）下列各项中表述有误的一项是（）网络上，流传着一张钟南山接受新华社记者采访的视频截图．．。

他讲到“相信武汉能够过关，武汉是一座英雄的城市”时，两眼噙泪．．．．，嘴唇紧紧抿成了一道弧线．．。

这张照片把他的刚毅与深情展露无遗。

所谓医者仁心。

医者需要学者严谨坚毅的意志，行医也需要一颗慈爱之心。

钟南山就是二者完美的结合。

智慧与拙朴，硬朗与宽厚，坚毅与脆弱，不屈与妥协，尊严与随和，铁面与柔情……这些性格在．他身上实现了对立统一．．．．：前者更多深藏于．内心，后者却表露在他那张坚毅的脸庞上。

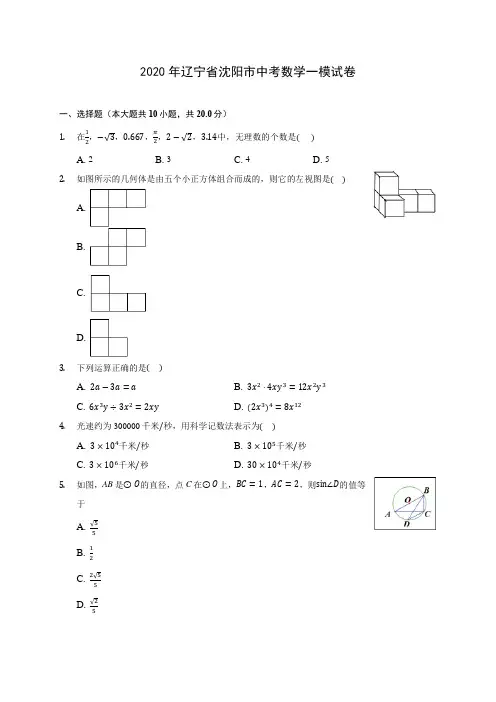
2020年辽宁省沈阳市中考数学一模试卷一、选择题（本大题共10小题，共20.0分）1. 在12，−√3，0.667，π2，2−√2，3.14中，无理数的个数是( ) A. 2 B. 3 C. 4 D. 52. 如图所示的几何体是由五个小正方体组合而成的，则它的左视图是( )A.B.C.D.3. 下列运算正确的是( )A. 2a −3a =aB. 3x 2⋅4xy 3=12x 2y 3C. 6x 3y ÷3x 2=2xyD. (2x 3)4=8x 124. 光速约为300000千米/秒，用科学记数法表示为( )A. 3×104千米/秒B. 3×105千米/秒C. 3×106千米/秒D. 30×104千米/秒5. 如图，AB 是⊙O 的直径，点C 在⊙O 上，BC =1，AC =2，则sin∠D 的值等于A. √55B. 12C. 2√55D. √256.如图，四边形OABC是矩形，四边形ADEF是边长为3的正方形，点A，D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y=kx(x>0)的图象上，且BF=5，则k值为()A. 15B. 714C. 725D. 177.某工厂现在平均每天比原计划多生产25个零件，现在生产600个零件所需时间与原计划生产450个零件所需时间相同，设原计划平均每天生产x个零件，根据题意可列方程为()A. 600x−25=450xB. 600x=450x−25C. 600x+25=450xD. 600x=450x+258.如图，一科珍贵的乌稔树被台风“山竹”吹歪了，处于对它的保护，需要测量它的高度．现采取以下措施：在地面选取一点C，测得∠BCA=45°，AC=20米，∠BAC=60°，则这棵乌稔树的高AB约为()(参考数据：√2≈1.4，√3≈1.7)A. 7米B. 14米C. 20米D. 40米9.一个半径为2cm的圆内接正六边形的面积等于()A. 24cm2B. 6√3cm2C. 12√3cm2D. 8√3cm210.小聪和小慧参加某健身房的半年卡促销活动，若设该半年卡的定价为x元，可列方程：0.8(2x−100)=2×500，则该健身房的促销活动可能是()A. 两人一起办卡每人立减100元，再打八折，优惠后每人只需500元B. 两人一起办卡总价立减100元，再打八折，优惠后每人只需500元C. 两人一起办卡可打八折，折后每人再减100元，优惠后每人只需500元D. 两人一起办卡可打八折，折后总价再减100元，优惠后每人只需500元二、填空题（本大题共6小题，共18.0分）11.当m=__________时，分式的值为0.当x______时，分式xx−3有意义．12.阳阳的身高是1.6m，他在阳光下的影长是1.2m，在同一时刻测得某棵树的影长为3.6m，则这棵树的高度约为______m.13.不等式组{x2≤−1−x+7>4的解集是______．14.在▱ABCD中，∠BAD的平分线AE交BC于点E，BE=3，若▱ABCD的周长是16，则EC=______．15.甲骑自行车从A地出发前往B地，同时乙步行从B地出发前往A地，如图的折线OPQ和线段EF分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(ℎ)之间的函数关系，且OP与EF相交于点M.则经过______小时，甲、乙两人相距3km．16.正方形ABCD中，E为DC边上一点，且DE=1，将AE绕点E顺时针旋转90°得到EF，连接AF，FC，则FC=______．三、计算题（本大题共1小题，共6.0分）17.计算：(−2016)0+(−12)−1+|1−√3|−8sin60°+√27．四、解答题（本大题共8小题，共76.0分）18.2019年3月24日无锡马拉松赛在盛大的樱花雨中鸣枪起跑．无锡马拉松赛的赛事共有三项：A.全程马拉松；B.半程马拉松；C.迷你马拉松．小华、小红和小明参与该项赛事的志愿者服务工作，组委会随机将他们分配到三个项目组．(1)小明被分配到“迷你马拉松”项目组的概率为____________；(2)已知小明被分配到A(全程马拉松)，请利用树状图或列表法求三人被分配到不同项目组的概率．19.如图，把平行四边形纸片ABCD沿BD折叠，点C落在点C′处，BC′与AD相交于点E．(1)连接AC′，则AC′与BD的位置关系是______；(2)EB与ED相等吗？证明你的结论．20.某学校为了解学生课外阅读的情况，对学生“平均每天课外阅读的时间”进行了随机抽样调查，如图是根据调查结果绘制的两幅不完整的统计图．请你根据统计图提供的信息，解答以下问题：(1)平均每天课外阅读的时间为“0.5～1小时”部分的扇形图的圆心角为______度；(2)本次一共调查了______名学生；(3)将条形图补充完整；(4)若该校有1680名学生，请估计该校有多少名学生平均每天课外阅读的时间在0.5小时以下．21.为了迎接“五⋅一”小长假的购物高峰．某服装专卖店老板小王准备购进甲、乙两种夏季服装．其中甲种服装每件的成本价比乙种服装的成本价多20元，甲种服装每件的售价为240元比乙种服装的售价多80元．小王用4000元购进甲种服装的数量与用3200元购进乙种服装的数量相同．(1)甲种服装每件的成本是多少元？(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价−进价)不少于21100元，且不超过21700元，问小王有几种进货方案？22.如图，Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB，连接DO并延长交CB的延长线于点E．(1)判断直线CD与⊙O的位置关系，并说明理由；(2)若BE=4，DE=8，求AC的长．23.如图，已知矩形ABCD中，AB=4，AD=m，动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP，作点D关于直线PC的对称点E，设点P的运动时间为t(s)．(1)若m=6，在点P的运动过程中，① 求当P，E，B三点在同一直线上时对应的t的值．②求当点A与点E距离最近时t的值，并求出该最近距离．(2)已知m满足：在动点P从点D到点A的整个运动过程中，有且只有一个时刻t，使点E到直线BC的距离等于1，求符合条件的m的取值范围．24.在△ABC中，点D、E分别在AB、AC上，BE、CD相交于点O，且∠DCB=∠EBC=1∠A．2(1)如图1，若AB=AC，则BD与CE的数量关系是______；(2)如图2，若AB≠AC，请你补全图2，思考BD与CE是否仍然具有(1)中的数量关系，并说明理由；(3)如图3，∠BDC=105°，BD=3，且BE平分∠ABC，请写出求BE长的思路．(不用写出计算结果)x2+bx+c交25.如图，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，B(3,5)，抛物线y=−12 x轴于点C，D两点，且经过点B．(1)求抛物线的表达式；(2)在抛物线上是否存在点F，使得△ACF的面积等于5，若存在，求出点F的坐标；若不存在，说明理由；(3)点M(4,k)在抛物线上，连接CM，求出在坐标轴的点P，使得△PCM是以∠PCM为顶角以CM为腰的等腰三角形，请直接写出P点的坐标．【答案与解析】1.答案：B解析：本题考查了无理数，无理数是无限不循环小数，注意带根号的数不一定是无理数．根据无理数是无限不循环小数，可得答案．，2−√2是无理数，共有3个．解：−√3，π2故选B．2.答案：D解析：解：此几何体的左视图有两列，左边一列有2个小正方形，右边一列有1个小正方体，故选：D．找出几何体从左边看所得到的图形即可．此题主要考查了简单几何体的三视图，关键是掌握所看的位置．3.答案：C解析：解；A、2a−3a=−a，故此选项错误；B、3x2⋅4xy3=12x3y3，故此选项错误；C、6x3y÷3x2=2xy，故此选项正确；D、(2x3)4=16x12，故此选项错误；故选：C．分别利用合并同类项以及单项式除以单项式和整式的除法运算进而判断得出即可．此题主要考查了合并同类项以及单项式除以单项式和整式的除法运算等知识，熟练应用相关定义是解题关键．4.答案：B解析：解：300000千米/秒，用科学记数法表示为3×105千米/秒，故选：B．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n 为整数，表示时关键要正确确定a的值以及n的值．5.答案：A解析：本题考查了圆周角定理的应用和勾股定理、锐角三角函数的应用，掌握直径所对的圆周角是直角和同弧所对的圆周角相等是解题的关键．根据AB是⊙O的直径，求出∠ACB=90º，根据勾股定理，求出AB的长，再由∠D=∠A，运用锐角三角函数的定义即可求出结论．解：∵AB是⊙O的直径，∴∠ACB=90º，BC=1，AC=2，由勾股定理得：AB=√5，∵∠D=∠A，∴sin∠D=sin∠A=BCAB =√5=√55．故选A．6.答案：C解析：解：设AO=a，∵四边形ADEF是边长为3的正方形，BF=5，∴AB=8，OD=a+3，∴B(a,8)，E(a+3,3)，又∵点B、E在反比例函数y=kx(x>0)的图象上，∴8a=3(a+3)，解得a=95，∴B(95,8)，∴k=95×8=725，故选：C．。

2020年沈阳市和平区中考数学一模试卷一、选择题（本大题共10小题，共20.0分）1.下列四个实数中最小的是()A. √3B. 2C. √2D. 1.42.下列四个选项中，既是轴对称又是中心对称的图形是()A. 矩形B. 等边三角形C. 正五边形D. 正七边形3.一种登革热病毒的直径约为0.00000005m，数据0.00000005m可用科学记数法表示为()A. 5×10−7mB. 5×10−8mC. 0.5×10−7mD. −5×108m4.如图是由若干个正方体组成的几何体的俯视图，数字表示该位置上小正方体的个数，则该几何体左视图可能是()A.B.C.D.5.十二边形的内角和为()A. 180°B. 360°C. 1800°D. 无法计算6.如图，在2×3的方格中，画有格点△ABC，下列选项的方格中所画格点三角形(阴影部分)与△ABC相似的是()A.B.C.D.7.下列说法正确的是()A. 掷一枚质地均匀的骰子，“向上一面的点数是6”是必然事件B. 了解一批电视机的使用寿命，适合用普查的方式C. “明天降雨的概率为1”，表示明天有半天都在降雨2D. 在统计中，样本的方差可以近似地反映总体的波动大小8.一元二次方程x2−2x−3=0的根的情况是()A. 无实根B. 有两相等实根C. 有两不等实根D. 无法判断9.计算(−2a3)2÷a2的结果是()A. −2a3B. −2a4C. 4a3D. 4a410.如图，四边形ABCD是⊙O的内接正方形，点P是CD⏜上不同于点C的任意一点，则∠BPC的大小是()A. 22.5°B. 45°C. 30°D. 50°二、填空题（本大题共6小题，共18.0分）11.一组数据：2，5，3，1，6，则这组数据的中位数是．12.分解因式：4x3−x=______ ．13.如图所示，直线AB//CD，∠A=23°，则∠C=______．14.如图，在平行四边形ABCD中，AB=m，BC=n，AC的垂直平分线交AD于点E，则△CDE的周长是_______．15.一块矩形土地ABCD由篱笆围着，并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计)，当AB=________m时，矩形土地ABCD的面积最大．16.如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是______．三、解答题（本大题共9小题，共82.0分）17.先化简，再求值：⋅−()，其中x=．18.在一个不透明的口袋装有三个完全相同的小球，分别标号为1、2、3.求下列事件的概率：(1)从中任取一球，小球上的数字为偶数；(2)从中任取一球，记下数字作为点A的横坐标x，把小球放回袋中，再从中任取一球记下数字作为点A的纵坐标y，点A(x,y)在函数y=3的图象上．x19.如图，在矩形ABCD中，对角线AC，BD交于点O，过点B作BE//AC，过点C作CE//BD，两直线交于点E．(1)求证：四边形BOCE为菱形．(2)若BE=AB=1，求矩形ABCD的面积．20.某校开展“阳光体育”活动，决定开设乒乓球、篮球、跑步、跳绳这四种运动项目，学生只能选择其中一种，为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成两张不完整的统计图，请你结合图中的信息解答下列问题：(1)样本中喜欢篮球项目的人数百分比是______；其所在扇形统计图中的圆心角的度数是______；(2)把条形统计图补画完整并注明人数；(3)已知该校有1000名学生，根据样本估计全校喜欢乒乓球的人数是多少？21.某商店购进A、B两种商品，购买1个A商品比购买1个B商品多花10元，并且花费300元购买A商品和花费100元购买B商品的数量相等．(1)求购买一个A商品和一个B商品各需要多少元；(2)商店准备购买A、B两种商品共80个，若A商品的数量不少于B商品数量的4倍，并且购买A、B商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？22.如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在AD⏜上.(1)求∠AED的度数：(2)若⊙O的半径为3，则AD⏜的长为多少？x+b 23.如图，矩形OABC的顶点A、C分别在x、y的正半轴上，点B的坐标为(6,8)，一次函数y=−23的图象与边OC、AB分别交于点D、E，并且满足OD=BE.点M是线段DE上的一个动点.(1)求b的值；(2)连接OM，若三角形ODM的面积与四边形OAEM的面积之比为1︰3，求点M的坐标；(3)设点N是x轴上方平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点M的坐标．24.如图，射线AN上有一点B，AB=5，tan∠MAN=4，点C从点A3出发以每秒3个单位长度的速度沿射线AN运动，过点C作CD⊥AN交射线AM于点D，在射线CD上取点F，使得CF=CB，连结AF.设点C的运动时间是t(秒)(t>0)．(1)当点C在点B右侧时，求AD、DF的长．(用含t的代数式表示)(2)连结BD，设△BCD的面积为S平方单位，求S与t之间的函数关系式．(3)当△AFD是轴对称图形时，直接写出t的值．x2+bx+c经过A(3,0)、C(−1,0)两点，与y轴交于B点．25.如图，抛物线y=−43(1)求抛物线的解析式；(2)D为第一象限抛物线上的一点，连接CD交AB于E，当CE=2ED时，求点D的坐标；(3)点P以每秒3个单位长度的速度从点O出发，沿O→B→A匀速运动，同时点Q以每秒1个单位长度的速度从点C出发，沿C→A匀速运动，运动时间为t秒，当一个点到达终点时，另一个点也随之停止运动，是否存在t，使以A、P、Q为顶点的三角形为直角三角形？若存在，直接写出t的值；若不存在，说明理由．【答案与解析】1.答案：D解析：此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数>0>负实数，两个负实数绝对值大的反而小．正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．解：根据实数比较大小的方法，可得1.4<√2<√3<2，∴四个实数中最小的是1.4．故选D．2.答案：A解析：解：A、矩形是轴对称图形，也是中心对称图形，故此选项正确；B、等边三角形是轴对称图形，不是中心对称图形，故此选项错误；C、正五边形是轴对称图形，不是中心对称图形，故此选项错误；D、正七边形是轴对称图形，不是中心对称图形，故此选项错误．故选：A．根据轴对称图形与中心对称图形的概念求解．本题考查的是中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．3.答案：B解析：本题考查用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．解：0.00000005=5×10−8．故选B．4.答案：B解析：由已知条件可知，左视图有2列，每列小正方形数目分别为1，2.据此可画出图形．本题考查几何体的三视图画法．由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视数的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字．左视图的列数与俯视图的行数相同，且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字．解：如图所示：该几何体左视图可能是：．故选B．5.答案：C解析：解：(12−2)⋅180°=1800°．故选C．根据多边形的内角和公式(n−2)⋅180°，列式计算即可得解．本题考查了多边形的内角和定理，熟记多边形内角和公式是解题的关键．6.答案：A解析：利用两组对应边的比相等且夹角对应相等的两个三角形相似对各选项进行判断．本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．解：∠ACB=90°，AC=2，BC=1，AC：BC=2，A选项中，三条线段的长为√2，2√2，√10，因为(√2)2+(2√2)2=(√10)2，此三角形为直角三角形，长直角边与短直角边的比为2，所以A选项的方格中所画格点三角形(阴影部分)与△ABC相似；而B 选项中长直角边与短直角边的比为3，C、D选项中的两直角边的比为1：1．故选A．7.答案：D解析：解：A、掷一枚质地均匀的骰子，“向上一面的点数是6”是随机事件，故此选项错误；B、了解一批电视机的使用寿命，适合用抽样调查的方式，故此选项错误；C、“明天降雨的概率为1”，表示明天50%的可能降雨，故此选项错误；2D、在统计中，样本的方差可以近似地反映总体的波动大小，正确．故选：D．分别利用概率的意义以及抽样调查的意义以及方差的性质和随机事件的定义分别分析得出答案．此题主要考查了概率的意义以及抽样调查的意义以及方差的性质和随机事件的定义，正确把握相关性质是解题关键．8.答案：C解析：此题考查了根的判别式，一元二次方程根的情况与判别式Δ的关系：(1)Δ>0方程有两个不相等的实数根；(2)Δ=0方程有两个相等的实数根；(3)Δ<0方程没有实数根．先求出Δ的值，再判断出其符号即可．解：∵Δ=(−2)2−4×1×(−3)=16>0，∴方程有两个不相等的实数根．故选C．9.答案：D解析：【试题解析】解：原式=4a6÷a2=4a4．故选：D．直接利用积的乘方运算化简，再利用整式的除法运算法则化简即可．此题主要考查了整式的除法运算，正确掌握相关运算法则是解题关键．10.答案：B解析：本题主要考查了正方形的性质和圆周角定理的应用．这里注意：根据90°的圆周角所对的弦是直径，知正方形对角线的交点即为其外接圆的圆心．连接OB、OC，首先根据正方形的性质，得∠BOC=90°，再根据圆周角定理，得∠BPC=45°．解：∵四边形ABCD是⊙O的内接正方形，∴O为正方形ABCD的中心，如图，连接OB、OC，则∠BOC=90°，∠BOC=45°．根据圆周角定理，得：∠BPC=12故选：B．11.答案：3解析：本题考查了中位数的概念：将一组数据按照从小到大(或从大到小)的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．根据中位数的定义求解可得．解：将这5个数据按从小到大的顺序排列为1，2，3，5，6，故这组数据的中位数是3．12.答案：x(2x+1)(2x−1)解析：此题主要考查了提取公因式法、公式法分解因式，正确找出公因式是解题关键．首先直接提取公因式x，进而利用平方差公式分解因式得出答案．解：4x3−x=x(4x2−1)=x(2x+1)(2x−1)．故答案为：x(2x+1)(2x−1)．13.答案：23°解析：本题考查了平行线的性质，熟练运用平行线的性质是本题的关键，属于基础题．由平行线的性质可解．解：∵AB//CD，∴∠C=∠A=23°．故答案为：23°．14.答案：m+n解析：本题考查了平行四边形的性质，线段垂直平分线性质，解此题的关键是求出AD、CD的长和求出△CDE的周长=AD+CD，根据平行四边形的性质求出AD、CD的长，根据线段垂直平分线性质求出AE=CE，求出△CDE的周长=AD+CD，代入求出即可．解：∵四边形ABCD是平行四边形，AB=m，BC=n，∴AD=BC=n，CD=AB=m，∵AC的垂直平分线交AD于点E，∴AE=CE，∴△CDE的周长为DE+CE+DC=DE+AE+CD=AD+CD=m+n．故答案为m+n．15.答案：150解析：本题考查二次函数的应用，根据题意可以用相应的代数式表示出矩形绿地的面积；即可解答本题． 解：设AB =xm ，则BC =12(900−3x)，由题意可得，S =AB ×BC =x ·12(900−3x)=−32(x 2−300x)=−32(x −150)2+33750， ∴当x =150时，S 取得最大值，此时，S =33750，∴AB =150m ，故答案为150． 16.答案：90°解析：解：由ABCD 是正方形，得AD =AB ，∠DAB =∠B =90°．在△ABE 和△DAF 中{AB =AD∠ABE =∠DAF BE =AF，∴△ABE≌△DAF ，∴∠BAE =∠ADF ．∵∠BAE +∠EAD =90°，∴∠OAD +∠ADO =90°，∴∠AOD =90°，故答案为：90°．根据全等三角形的判定与性质，可得∠ODA 与∠BAE 的关系，根据余角的性质，可得∠ODA 与∠OAD 的关系，根据直角三角形的判定，可得答案．本题考查了全等三角形的判定与性质，利用了全等三角形的判定与性质，余角的性质，直角三角形的判定．17.答案：解：原式=x−3(x−1)(x+1)·(x+1)2x−3−x x−1， =x+1x−1−x x−1，=1x−1，当x =√2+1时，原式=√2+1−1=√22．解析：本题主要考查了分式的化简求值，在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．先将原分式进行化简，再代入数值计算即可．18.答案：解：(1)∵在一个不透明的口袋里装有分别标有数字1、2、3三个小球，小球除数字不同外，其它无任何区别，∴从中任取一球，球上的数字为偶数的概率是：13；(2)列表得：则点M坐标的所有可能的结果有九个：(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(3,1)、(3,2)、(3,3)，积为3的有2种，所以点A(x,y)在函数y=3x 的图象上概率为：29．解析：(1)由在一个不透明的口袋里装有分别标有数字1、2、3三个小球，小球除数字不同外，其它无任何区别，直接利用概率公式求解即可求得答案；(2)列表得出所有等可能的情况数，找出点(x,y)落在函数y=3x的图象上的情况数，即可求出所求的概率．考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比．正确的列表或树状图是解答本题的关键，难度不大．19.答案：(1)证明：∵BE//AC，CE//BD，∴四边形BOCE是平行四边形．∵四边形ABCD是矩形，∴OB=OC，∴四边形BOCE是菱形．(2)解：∵四边形BOCE是菱形，∴OC=BE=1．∵四边形ABCD是矩形，∴OA=OC=1，∠ABC=90°．∴AC=1+1=2，∴BC=√AC2−AB2=√3，∴矩形ABCD的面积为√3×1=√3．解析：本题考查矩形的性质、菱形的判定、勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．(1)先根据BE//AC，CE//BD得到四边形BOCE为平行四边形，又因为矩形的对角线相互平分且相等，得到OB=OC，最后根据邻边相等的平行四边形是菱形即可判断；(2)先利用BE=AB=1，可得到AC=2，利用勾股定理求出BC=√3的长即可解决问题．20.答案：(1)20%；72°；(2)调查的总人数是：44÷44%=100(人)，则喜欢篮球的人数是：100×20%=20(人)，；(3)全校喜欢乒乓球的人数是1000×44%=440(人)．答：根据样本估计全校喜欢乒乓球的人数是440人．解析：解：(1)1−44%−8%−28%=20%，所在扇形统计图中的圆心角的度数是：360×20%=72°，故答案为：20%，72°；(2)见答案；(3)见答案．本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．(1)利用1减去其它各组所占的比例即可求得喜欢篮球的人数百分比，利用百分比乘以360度即可求得扇形的圆心角的度数；(2)根据喜欢A乒乓球的有44人，占44%即可求得调查的总人数，乘以对应的百分比即可求得喜欢篮球的人数，补全统计图即可；(3)总人数1000乘以喜欢乒乓球的人数所占的百分比即可求解．21.答案：解：(1)设购买一个B商品需要x元，则购买一个A商品需要(x+10)元，依题意，得：300x+10=100x，解得：x=5，经检验，x=5是原方程的解，且符合题意，∴x+10=15．答：购买一个A商品需要15元，购买一个B商品需要5元．(2)设购买B商品m个，则购买A商品(80−m)个，依题意，得：{80−m≥4m15(80−m)+5m≥1000 15(80−m)+5m≤1050，解得：15≤m≤16．∵m为整数，∴m=15或16．∴商店有2种购买方案，方案①：购进A商品65个、B商品15个；方案②：购进A商品64个、B商品16个．解析：(1)设购买一个B商品需要x元，则购买一个A商品需要(x+10)元，根据数量=总价÷单价结合花费300元购买A商品和花费100元购买B商品的数量相等，即可得出关于x的分式方程，解之经检验后即可得出结论；(2)设购买B商品m个，则购买A商品(80−m)个，根据A商品的数量不少于B商品数量的4倍并且购买A、B商品的总费用不低于1000元且不高于1050元，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为整数即可找出各购买方案．本题考查了分式方程的应用以及一元一次不等式组的应用，解题的关键是：(1)找准等量关系，正确列出分式方程；(2)根据各数量之间的关系，正确列出一元一次不等式组．22.答案：解：(1)连接BD，如图1所示：∵四边形ABCD是⊙O的内接四边形，∴∠BAD+∠C=180°，∵∠C=120°，∴∠BAD=60°，∵AB=AD，∴△ABD是等边三角形，∴∠ABD=60°，∵四边形ABDE是⊙O的内接四边形，∴∠AED+∠ABD=180°，∴∠AED=120°；(2)∵∠AOD=2∠ABD=120°，=2π．∴AD⏜的长为：120×π×3180解析：此题考查了圆的内接四边形的性质、圆周角定理以及等边三角形的判定与性质．注意准确作出辅助线是解此题的关键．(1)连接BD，根据圆的内接四边形的性质得出∠BAD的度数，由AB=AD，可证得△ABD是等边三角形，求得∠ABD=60°，再利用圆的内接四边形的性质，即可求得∠AED的度数；(2)连接OA，由圆周角定理求出∠AOD的度数，由弧长公式即可得出AD⏜的长．23.答案：解：(1)y=−23x+b中，令x=0，解得y=b，则D的坐标是(0,b)，OD=b，∵OD=BE，∴BE=b，则E的坐标是(6,8−b)，把E的坐标代入y=−23x+b得8−b=−23×6+b，解得：b=6，∴y=−23x+6；(2)设M(a,−23a+6)，S△ODM=12×6×a=3a，S四边形AEDO =8×62=24，∵三角形ODM的面积与四边形OAEM的面积之比为1：3，∴3a：24=1:4，∴a=2，则M的坐标是(2,143)；(3)当四边形OMDN是菱形时，如图(1)，M的纵坐标是3，把y=3代入y=−23x+6，得−23x+6=3，解得：x=92，则M的坐标是(92,3)，当四边形OMND是菱形时，如图(2)，OM=OD=6，设M的横坐标是m，则纵坐标是−23m+6，则m2+(−23m+6)2=36，解得：m=7213或0(舍去).则M的坐标是(92,3)或(7213,3013).解析：本题是一次函数与菱形的判定与性质的综合题，主要考查了菱形的判定方法，正确根据菱形的性质求得M的坐标是解决本题的关键．(1)首先在一次函数的解析式中令x=0，即可求得D的坐标，则OD的长度即可求得，OD=b，则E的坐标即可利用b表示出来，然后代入一次函数解析式即可得到关于b的方程，求得b的值；(2)首先设M(a,−23a+6)，根据题意可得S△ODM=3a，S四边形AEDO=24，再根据三角形ODM的面积与四边形OAEM的面积之比为1：3 可得3a：24=1:4，得出a的值，从而求出M的坐标；(3)分成四边形OMDN是菱形和四边形OMND是菱形两种情况进行讨论，四边形OMDN是菱形时，M是OD的中垂线与DE的交点；四边形OMND是菱形时，设出M的坐标，根据OM=OD即可求得M的坐标．24.答案：解：(1)在Rt△ACD中，AC=3t，tan∠MAN=43，∴CD=4t．∴AD=√AC2+CD2=√(3t)2+(4t)2=5t，当点C在点B右侧时，CB=3t−5，∴CF=CB．∴DF=4t−(3t−5)=t+5．(2)当0<t<53时，S=12⋅(5−3t)⋅4t=−6t2+10t．当t>53时，S=12⋅(3t−5)⋅4t=6t2−10t．(3)①如图1中，当DF=AD时，△ADF是轴对称图形．则有5−3t−4t=5t，解得t=512，②如图2中，当AF=DF时，△ADF是轴对称图形．作FH⊥AD．∵FA=DF，∴AH=DH=52t，由cos∠FDH=45，可得52t4t−(5−3t)=45，解得t=4031．③如图3中，当AF=DF时，△ADF是轴对称图形．作FH ⊥AD ．∵FA =DF ，∴AH =DH =52t ，由cos∠FDH =45，可得52t 4t−(3t−5)=45，解得t =4017． 综上所述，满足条件的t 的值为512或4031或4017．解析：(1)解直角三角形求出AD ，DC ，DF 即可．(2)分两种情形：当0<t <53时，当t >53时，分别求解即可解决问题．(3)分三种情形分别画出图形，构建方程即可解决问题．本题属于三角形综合题，考查了解直角三角形，轴对称图形等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型． 25.答案：解：(1)∵抛物线y =−43x 2+bx +c 经过A(3,0)、C(−1,0)两点，{−34×32+3b +c =0−34−b +c =0 解得{b =83c =4 ∴抛物线的解析式是y =−43x 2+83x +4；(2)如图1所示：作DF//AC 交AB 于F ．设直线AB的解析式为y=kx+b，将点A、B的坐标代入得：{b=43k+b=0，解得：k=−43，b=4．∴直线AB的解析式为y=−43x+4．∵FD//AC，∴△ACE∽△FDE，∴FDAC =DECE=DE2DE=12，∵AC=4∴FD=2．设D(a,−43a2+83a+4)，则F(a−2,−43a2+83a+4)，将点F的坐标代入直线AB的解析式得：−43a2+83a+4=−43(a−2)+4，解得a=1或a=2．当a=1时，−43a2+83a+4=163，即点D(1,163).当a=2时，−43a2+83a+4=4，即点D(2,4)．综上所述点D的坐标为(1,163)或(2,4)．(3)存在．如图2所示：当∠APA=90°时．∵∠QPO+∠OPA=90°，∠QPO+∠PQO=90°，∴∠OPA=∠PQO．又∵∠POQ=∠POA=90°，∴△PQO∽△APO．∴POOQ =OAOP，即3t1−2t=33t，解得t=−1+√136或t=−1−√136(舍去)．如图3所示：当点Q与点O重合时，△PQP为直角三角形．∵OC=1，∴t=1．如图4所示：当∠PQA=90°时．由题意可知QA=4−t，AP=9−3t．∵cos∠BAO=OAAB =AQAP=35，∴4−t9−3t =35，解得：t=74．如图5所示：当∠QPA=90°时．由题意可知QA =4−t ，AP =9−3t ．∵cos∠BAO =AP QA =OA AB ═35，∴9−3t 4−t =35，解得：t =114．综上所述，当t 的值为−1+√136或1或74或=114时，△PAQ 为直角三角形．解析：(1)由A 、C 两点的坐标，利用待定系数法可求得抛物线解析式；(2)作DF//AC 交AB 于F ，可证得△ACE∽△FDE ，根据相似三角形的性质可求得FD ，设出设D(a,−43a 2+83a +4)，则F(a −2,−43a 2+83a +4)，然后求得直线AB 的解析式，将点B 的坐标代入直线AB 的解析式可求得a 的值；(3)先依据题意分析可出可能出现的情况，然后画出相应的图形，最后利用相似三角形的性质求解即可．本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、相似三角形的性质和判定，利用相似三角形的性质表示出点F 的坐标是解答问题(2)的关键，根据题意画出符合题意的所有图形是解答问题(3)的关键．。

（B） 2 b （D） 2 b
2a b
（B）
x
y
6， 2
1
（C）
x
y
6， 4
（D）
x y
0， 2
9．如图，菱形 ABCD 的周长为 16，C 120°，E ，F 分别为 AB ， AD 的中点，则 EF 的长为 （A） 2 2
（B） 2 3
（C）4
（D）8
10．若点（
6
，
y1
和平区 2019－2020 学年度第二学期九年级第一次 质量调查数学学科试卷
温馨提示：本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷（非选择题）两部分．第Ⅰ卷为第 1 页至第 3 页，第Ⅱ卷为第 4 页至第 8 页．试卷满分 120 分．考试时间 100 分钟．
祝你考试顺利!
第Ⅰ卷
注意事项： 1．每题选出答案后，用 2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑．如
AC 3 ，求 EA 的长．
D C
A
O
B
C
E
A
O
B
图①
图②
22．（本小题 10 分） 如图，建筑物 BC 上有一宣传牌 AB ，从 D 处测得宣传牌底部 B 的仰角为 35°，前
进 4 m 到达 E 处，从 E 处测得宣传牌顶部 A 的仰角为 45°．已知建筑物 BC 的高是 16 m， 求宣传牌 AB 的高度（结果精确到 0.1 m）．
2
（A） a ＞－2 （C）－2≤ a ＜4
（B） a ＜4 （D）－2＜ a ≤4
第Ⅱ卷
注意事项： 1．用黑色字迹的签字笔将答案写在“答题卡”上(作图可用 2B 铅笔)． 2．本卷共 13 题，共 84 分．
二、填空题（本大题共 6 小题，每小题 3 分，共 18 分）

2020年和平区九年级教学质量监测(一)理化综合试卷(考试时间:150分钟满分:150分)物理部分(满分85分)注意事项1．考生务必将姓名、学校、班级写在答题卡相应位置上。

2．考生应把试题答案答在答题卡上对应题目处，答在试卷上无效装的3．选择题，需用2B铅笔涂黑在题目对应的选项中一、选择题(共21分，其中第1-6小题为单选题，每小题2分。

第7-9小题为多选题，每小题3分，多选、错选不得分，漏选得1分)1．下列估测中，和实际数据最接近的是A．考生步人考场的速度约为4km/hB．一本初中物理教材受到的重力约为30NC．一标准大气压最多能托起760mm高的水柱D．电视机正常工作时的电功率约为8W2．如图所示的光现象中，由于光的直线传播形成的是3．如图，在探究什么因素决定声音的响度时，将正在发声的音叉轻触系在细绳上的乒乓球，这是为了A．使音叉的振动尽快停下来B．将音叉的振动转换为小球的振动C．使音叉振动频率增大D．使声波被多次反射形成回声4．如图，两个完全相同的木块A和B叠放在水平木质桌面上。

在5N的水平拉力F的作用下木块A、B一起向右做匀速直线运动，空气阻力忽略不计，则下列说法正确的是A．A受到的支持力和A对B的压力是一对平衡力B．B受到的重力和桌面对B的支持力是一对平衡力C．桌面对B的摩擦力为5ND．桌面比木块A和B的表面粗糙5．小虎用如图所示装置“探究影响动能大小的因素”，在高度为h的光滑斜槽顶端，将质量不同的钢球由静止释放，观察水平长木板上的木块被撞动的距离，则下列说法正确的是A．质量大的钢球到达水平木板的初速度大B．本实验必须选择光滑的长木板C．本实验可探究木块的动能跟质量大小的关系D．质量大的钢球撞动木块运动的距离远6，防控疫情期间，为了严格控制区分外来车辆出入小区，很多小区装备了门禁系统，内部车辆可以被自动开关识别并启动横杆，外部车辆需要保安闭合手动开关启动横杆。

下列模拟电路中，符合门禁系统要求的是7．小虎分别用密度为ρ甲、ρ乙的两种物质制成形状和体积均相同的甲、乙两个长方体，重力分别为G甲、G甲，将它们置于水平桌面上，此时它们对桌面的压强相等。

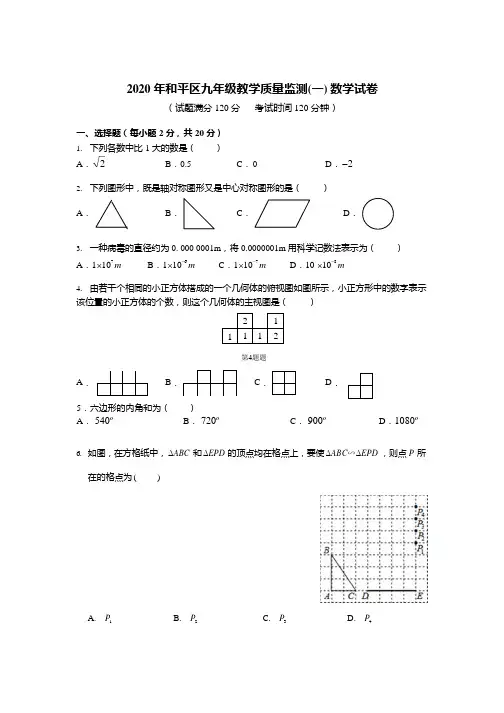
2020 年和平区九年级教学质量监测(一) 数学试卷（试题满分120 分考试时间120 分钟）一、选择题（每小题2 分，共20 分）1.下列各数中比1 大的数是（）A． 2 B．0.5 C．0 D．-22.下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．3.一种病毒的直径约为0. 000 0001m，将0.0000001m 用科学记数法表示为（）A．1⨯107 m B．1⨯10-6 m C．1⨯10-7 m D．10 ⨯10-8 m4.由若干个相同的小正方体搭成的一个几何体的俯视图如图所示，小正方形中的数字表示该位置的小正方体的个数，则这个几何体的主视图是（）211112第4题题A．B．C．D．5．六边形的内角和为（）A．540o B．720o C．900o D．1080o 6.如图，在方格纸中，∆ABC 和∆EPD 的顶点均在格点上，要使∆ABC∽∆EPD ，则点P 所在的格点为( )A.P1B.P2C.P3D.P4FBC7. 下列说法正确的是（ ）A. “三角形任意两边之差小于第三边”是必然事件B. 在连续 5 次的测试中，两名同学的平均分相同，方差较大的同学成绩更稳定C. 某同学连续 10 次抛掷质量均匀的硬币，6 次正面向上，因此正面向上的概率是 60% D ．检测某品牌笔芯的使用寿命，适宜用普查8．方程 x 2 - 2x -1 = 0根 的情况是（ ）A ．有两个相等的实数B ．只有一个实数根C ．没有实数 根D ．有两个不相等的实数 根9．计算： (-x 2 y )2÷ (-2xy ) = （ ）A ． 1xB ． 1x 3 yC ． - 1x 3 yD ． -2x 3 y22 210．在圆内接正方形 ABCD 中，正方形的边长 AB 是 8，则这个正方形的中心角和边心距是 （）A ． 90o ，4B ． 90o ，1C ． 45o ，4D ． 45o ，1二、填空题（每小题 3 分，共 18 分）11.一组数据 15，20，25，30，20，这组数据的中位数为.12.分解因式： 9x - x 3 = .13.如图，直线 a ∥b ，若∠1=139°，则∠2= .DECADabAB第 13 题图第 14 题图第 15 题图14. 如图，在平行四边形 ABCD 中，AB =3cm ，BC =2cm ，连接 BD ，作 BD 的垂直平分线交CD 于点 E ，交 BD 于点 F ，连接 BE ，则△BCE 的周长是cm .15. 如图，假设篱笆（虚线部分）的长度是 8m ，则所围成矩形 ABCD 的最大面积是m .16. 正方形 ABCD ，点 P 为正方形内一点，且满足 PA =3，PB = 2 为 度.，PC =5，则∠APB 的度数三、解答题（第 17 小题 6 分，第 18、19 小题各 8 分，共 22 分）2 c 123O17. 先化简，再求值：()4,2,21222=-=+-⋅⎪⎪⎭⎫ ⎝⎛--y x y y xy x y x x 其中18. 在一个不透明的盒ƒ中放有三张卡片，每张卡片上写有 1 个实数，分别为 1，2，3.（卡片除了实数不同外，其余均相同）（1） 从盒ƒ中随机抽取一张卡片，请直接写出卡片上的实数是 2 的概率；（2） 先从盒ƒ中随机抽取一张卡片，将卡片上的实数作为点 P 的横坐标，卡片不放回，再随机抽取一张卡片，将卡片上的实数作为点 P 的纵坐标，两次抽取的卡片上的实数分别作为点 P 的横纵坐标。

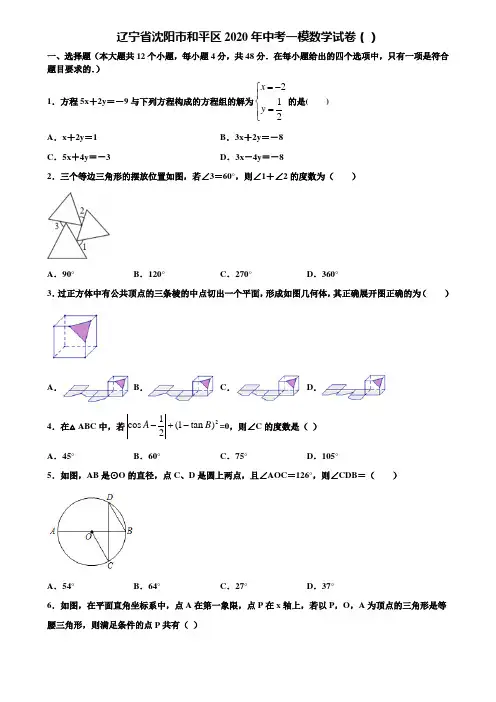
辽宁省沈阳市和平区2020年中考一模数学试卷（）一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．方程5x ＋2y ＝－9与下列方程构成的方程组的解为212xy =-⎧⎪⎨=⎪⎩的是( ) A ．x ＋2y ＝1B ．3x ＋2y ＝－8C ．5x ＋4y ＝－3D ．3x －4y ＝－82．三个等边三角形的摆放位置如图，若∠3＝60°，则∠1＋∠2的度数为（ ）A ．90°B ．120°C ．270°D ．360°3．过正方体中有公共顶点的三条棱的中点切出一个平面，形成如图几何体，其正确展开图正确的为（ ）A ．B ．C ．D ．4．在△ABC 中，若21cos (1tan )2A B -+-=0，则∠C 的度数是（ ） A ．45° B ．60°C ．75°D ．105° 5．如图，AB 是⊙O 的直径，点C 、D 是圆上两点，且∠AOC ＝126°，则∠CDB ＝（ ）A ．54°B ．64°C ．27°D ．37°6．如图，在平面直角坐标系中，点A 在第一象限，点P 在x 轴上，若以P ，O ，A 为顶点的三角形是等腰三角形，则满足条件的点P 共有（ ）A．2个B．3个C．4个D．5个7．如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（）A．1 B．3C．3D．238．如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4：9，则OB′：OB为（）A．2：3 B．3：2 C．4：5 D．4：99．如图，在平行线l1、l2之间放置一块直角三角板，三角板的锐角顶点A，B分别在直线l1、l2上，若∠l=65°，则∠2的度数是（）A．25°B．35°C．45°D．65°10．如图，两个一次函数图象的交点坐标为(2,4)，则关于x，y的方程组111222,y k x by k x b=+⎧⎨=+⎩的解为（）A．2,4xy=⎧⎨=⎩B．4,2xy=⎧⎨=⎩C．4,xy=-⎧⎨=⎩D．3,xy=⎧⎨=⎩11．4的算术平方根为（）A．2±B．2C．2±D．2 12．把多项式x2+ax+b分解因式，得(x+1)(x-3)，则a、b的值分别是（）A．a=2，b=3 B．a=-2，b=-3C．a=-2，b=3 D．a=2，b=-3二、填空题：（本大题共6个小题，每小题4分，共24分．）13．分解因式：3ax2﹣3ay2＝_____．14．请写出一个比2大且比4小的无理数：________.15．不等式组2113242xx x+>-⎧⎨+≥+⎩的整数解是_____．16．一个不透明的袋中共有5个小球，分别为2个红球和3个黄球，它们除颜色外完全相同，随机摸出两个小球，摸出两个颜色相同的小球的概率为____.17．如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S△BDE：S△CDE=1：3，则BE：BC 的值为_________．18．小明把一副含45°，30°的直角三角板如图摆放，其中∠C＝∠F＝90°，∠A＝45°，∠D＝30°，则∠α+∠β等于_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）为有效治理污染，改善生态环境，山西太原成为国内首个实现纯电动出租车的城市，绿色环保的电动出租车受到市民的广泛欢迎，给市民的生活带来了很大的方便，下表是行驶路程在15公里以内时普通燃油出租车和纯电动出租车的运营价格： 车型 起步公里数 起步价格 超出起步公里数后的单价 普通燃油型 3 13元 2.3元/公里纯电动型 3 8元 2元/公里张先生每天从家打出租车去单位上班（路程在15公里以内），结果发现，正常情况下乘坐纯电动出租车比乘坐燃油出租车平均每公里节省0.8元，求张先生家到单位的路程．20．（6分）《孙子算经》是中国传统数学的重要著作之一，其中记载的“荡杯问题”很有趣．《孙子算经》记载“今有妇人河上荡杯．津吏问曰：‘杯何以多？’妇人曰：‘家有客．’津吏曰：‘客几何？’妇人曰：‘二人共饭，三人共羹，四人共肉，凡用杯六十五．’不知客几何？”译文：“2人同吃一碗饭，3人同吃一碗羹，4人同吃一碗肉，共用65个碗，问有多少客人？”21．（6分）计算：()10152cos 4532π-⎛⎫-+︒--+ ⎪⎝⎭． 22．（8分）某超市对今年“元旦”期间销售A 、B 、C 三种品牌的绿色鸡蛋情况进行了统计，并绘制如图所示的扇形统计图和条形统计图．根据图中信息解答下列问题：该超市“元旦”期间共销售 个绿色鸡蛋，A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是 度；补全条形统计图；如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个，请你估计这个分店销售的B 种品牌的绿色鸡蛋的个数？23．（8分）如图，点D 在O e 的直径AB 的延长线上，点C 在O e 上，且AC=CD ，∠ACD=120°.求证：CD 是O e 的切线；若O e 的半径为2，求图中阴影部分的面积. 24．（10分）已知关于x 的方程（a ﹣1）x 2+2x+a ﹣1＝1．若该方程有一根为2，求a 的值及方程的另一根；当a为何值时，方程的根仅有唯一的值？求出此时a的值及方程的根．25．（10分）如图，在△ABC中，BC＝12，tanA＝34，∠B＝30°；求AC和AB的长．26．（12分）某公司为了扩大经营，决定购进6台机器用于生产某活塞．现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示．经过预算，本次购买机器所耗资金不能超过34万元.甲乙价格(万元/台) 7 5每台日产量(个) 100 60(1)按该公司要求可以有几种购买方案？如果该公司购进的6台机器的日生产能力不能低于380个，那么为了节约资金应选择什么样的购买方案？27．（12分）如图，某地方政府决定在相距50km的A、B两站之间的公路旁E点，修建一个土特产加工基地，且使C、D两村到E点的距离相等，已知DA⊥AB于A，CB⊥AB于B，DA=30km，CB=20km，那么基地E应建在离A站多少千米的地方？参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．D【解析】试题分析：将x与y的值代入各项检验即可得到结果．解：方程5x+2y=﹣9与下列方程构成的方程组的解为的是3x﹣4y=﹣1．故选D．点评：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．2．B【解析】【分析】先根据图中是三个等边三角形可知三角形各内角等于60°，用∠1，∠2，∠3表示出△ABC各角的度数，再根据三角形内角和定理即可得出结论．【详解】∵图中是三个等边三角形，∠3=60°，∴∠ABC=180°-60°-60°=60°，∠ACB=180°-60°-∠2=120°-∠2，∠BAC=180°-60°-∠1=120°-∠1，∵∠ABC+∠ACB+∠BAC=180°，∴60°+（120°-∠2）+（120°-∠1）=180°，∴∠1+∠2=120°．故选B.【点睛】考查的是等边三角形的性质，熟知等边三角形各内角均等于60°是解答此题的关键．3．B【解析】试题解析：选项,,A C D折叠后都不符合题意，只有选项B折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点，与正方体三个剪去三角形交于一个顶点符合.故选B.4．C【解析】【分析】根据非负数的性质可得出cosA及tanB的值，继而可得出A和B的度数，根据三角形的内角和定理可得出∠C的度数．【详解】由题意，得 cosA=12，tanB=1，∴∠A=60°，∠B=45°，∴∠C=180°-∠A-∠B=180°-60°-45°=75°．故选C．5．C【解析】【分析】由∠AOC＝126°，可求得∠BOC的度数，然后由圆周角定理，求得∠CDB的度数．【详解】解：∵∠AOC＝126°，∴∠BOC＝180°﹣∠AOC＝54°，∵∠CDB＝12∠BOC＝27°故选：C．【点睛】此题考查了圆周角定理．注意在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．6．C【解析】【分析】分为三种情况：①AP=OP，②AP=OA，③OA=OP，分别画出即可．【详解】如图，分OP=AP（1点），OA=AP（1点），OA=OP（2点）三种情况讨论.∴以P，O，A为顶点的三角形是等腰三角形，则满足条件的点P共有4个.故选C.【点睛】本题考查了等腰三角形的判定和坐标与图形的性质，主要考查学生的动手操作能力和理解能力，注意不要漏解．7．C【解析】连接AE ，OD ，OE ．∵AB 是直径， ∴∠AEB=90°．又∵∠BED=120°，∴∠AED=30°．∴∠AOD=2∠AED=60°．∵OA=OD ．∴△AOD 是等边三角形．∴∠A=60°．又∵点E 为BC 的中点，∠AED=90°，∴AB=AC ．∴△ABC 是等边三角形，∴△EDC 是等边三角形，且边长是△ABC 边长的一半23．∴∠BOE=∠EOD=60°，∴»BE和弦BE 围成的部分的面积=»DE 和弦DE 围成的部分的面积． ∴阴影部分的面积=EDC 1S =23=32∆⋅C ． 8．A【解析】【分析】根据位似的性质得△ABC ∽△A′B′C′，再根据相似三角形的性质进行求解即可得.【详解】由位似变换的性质可知，A′B′∥AB ，A′C′∥AC ，∴△A′B′C′∽△ABC ，∵△A'B'C'与△ABC 的面积的比4：9，∴△A'B'C'与△ABC 的相似比为2：3， ∴23OB OB '= ， 故选A ．【点睛】本题考查了位似变换：如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形，这个点叫做位似中心．9．A【解析】【分析】如图，过点C 作CD ∥a ，再由平行线的性质即可得出结论．【详解】如图，过点C 作CD ∥a ，则∠1=∠ACD ，∵a ∥b ，∴CD ∥b ，∴∠2=∠DCB ，∵∠ACD+∠DCB=90°，∴∠1+∠2=90°，又∵∠1=65°，∴∠2=25°，故选A ．【点睛】本题考查了平行线的性质与判定，根据题意作出辅助线，构造出平行线是解答此题的关键．10．A【解析】【分析】根据任何一个一次函数都可以化为一个二元一次方程，再根据两个函数交点坐标就是二元一次方程组的解可直接得到答案．【详解】解：∵直线y 1=k 1x+b 1与y 2=k 2x+b 2的交点坐标为（2，4），∴二元一次方程组111222,y k x b y k x b =+⎧⎨=+⎩的解为2,4.x y =⎧⎨=⎩ 故选A.【点睛】本题主要考查了函数解析式与图象的关系，满足解析式的点就在函数的图象上，在函数的图象上的点，就一定满足函数解析式．函数图象交点坐标为两函数解析式组成的方程组的解．11．B【解析】 4=2，而2，，故选B．点睛：此题主要考查了算术平方根的定义，解题时应先明确是求哪个数的算术平方根，否则容易出现选A 的错误．12．B【解析】分析：根据整式的乘法，先还原多项式，然后对应求出a、b即可.详解：（x+1）（x-3）=x2-3x+x-3=x2-2x-3所以a=2，b=-3，故选B．点睛：此题主要考查了整式的乘法和因式分解的关系，利用它们之间的互逆运算的关系是解题关键.二、填空题：（本大题共6个小题，每小题4分，共24分．）13．3a（x＋y）（x－y）【解析】【详解】解：3ax2-3ay2=3a（x2-y2）=3a（x+y）（x-y）．【点睛】本题考查提公因式法与公式法的综合运用．14．π【解析】【分析】利用完全平方数和算术平方根对无理数的大小进行估算，然后找出无理数即可【详解】<<x的取值在4~16【点睛】本题考查估算无理数的大小，能够判断出中间数的取值范围是解题关键15．0【解析】【分析】求出不等式组的解集，再找出不等式组的整数解即可． 【详解】2113242x x x +>-⎧⎨+≥+⎩211x +>-,则x>-1 3242x x +≥+,则x 0≤ ∴不等式组的解集为-1<x 0≤. ∴整数解为0. 【点睛】本题考查的是一元一次不等式组的整数解，熟练掌握不等式组是解题的关键. 16．25【解析】 【详解】解：根据题意可得：列表如下共有20种所有等可能的结果，其中两个颜色相同的有8种情况， 故摸出两个颜色相同的小球的概率为82205=． 【点睛】本题考查列表法和树状图法，掌握步骤正确列表是解题关键． 17．1：4 【解析】 【分析】由S △BDE ：S △CDE =1：3，得到 BE 1CE 3=，于是得到 41BE BC =． 【详解】解：:1:3BDE CDE S S V V Q ，= 两个三角形同高，底边之比等于面积比. 13BE CE ∴=， :1:4.BE BC ∴=故答案为1:4. 【点睛】本题考查了三角形的面积，比例的性质等知识，知道等高不同底的三角形的面积的比等于底的比是解题的关键． 18．210° 【解析】 【分析】根据三角形内角和定理得到∠B ＝45°，∠E ＝60°，根据三角形的外角的性质计算即可． 【详解】 解：如图：∵∠C ＝∠F ＝90°，∠A ＝45°，∠D ＝30°， ∴∠B ＝45°，∠E ＝60°， ∴∠2+∠3＝120°，∴∠α+∠β＝∠A+∠1+∠4+∠B ＝∠A+∠B+∠2+∠3＝90°+120°＝210°， 故答案为：210°． 【点睛】本题考查的是三角形的外角的性质、三角形内角和定理，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤． 19．8.2 km 【解析】 【分析】首先设小明家到单位的路程是x 千米，根据题意列出方程进行求解． 【详解】解：设小明家到单位的路程是x 千米．依题意，得13+2.3（x －3）=8+2（x －3）+0.8x ．解得：x=8.2答：小明家到单位的路程是8.2千米． 【点睛】本题考查一元一次方程的应用，找准等量关系是解题关键． 20．x=60 【解析】 【分析】设有x 个客人，根据题意列出方程，解出方程即可得到答案. 【详解】解：设有x 个客人，则65234x x x++= 解得：x=60； ∴有60个客人. 【点睛】本题考查了由实际问题抽象出一元一次方程，找准等量关系，正确列出一元一次方程是解题的关键． 21．1 【解析】 【分析】根据特殊角的三角函数值，零次幂的性质，负整指数幂的性质、绝对值的性质，进行实数的混合运算即可. 【详解】()11532π-⎛⎫-︒--+ ⎪⎝⎭=1+1-3+2 =122．（1）2400，60；（2）见解析；（3）500 【解析】 整体分析：（1）由C 品牌1200个占总数的50%可得鸡蛋的数量，用A 品牌占总数的百分比乘以360°即可；（2）计算出B 品牌的数量；（3）用B 品牌与总数的比乘以1500. 解：（1）共销售绿色鸡蛋：1200÷50%=2400个， A 品牌所占的圆心角：4002400×360°=60°； 故答案为2400，60；（2）B 品牌鸡蛋的数量为：2400﹣400﹣1200=800个，补全统计图如图：（3）分店销售的B种品牌的绿色鸡蛋为：8002400×1500=500个．23．（1）见解析（2）图中阴影部分的面积为2 3π.【解析】【分析】（1）连接OC．只需证明∠OCD＝90°．根据等腰三角形的性质即可证明；（2）先根据直角三角形中30°的锐角所对的直角边是斜边的一半求出OD，然后根据勾股定理求出CD，则阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积．【详解】（1）证明：连接OC．∵AC＝CD，∠ACD＝120°，∴∠A＝∠D＝30°．∵OA＝OC，∴∠2＝∠A＝30°．∴∠OCD＝∠ACD－∠2＝90°，即OC⊥CD，∴CD是⊙O的切线；（2）解：∠1＝∠2＋∠A＝60°．∴S扇形BOC＝2602360π⨯＝23π．在Rt△OCD中，∠D＝30°，∴OD＝2OC＝4，∴CD22OD OC-3∴S Rt △OCD ＝12OC×CD ＝12×2×23＝23． ∴图中阴影部分的面积为：23－23π． 24．（3）a=15，方程的另一根为12；（2）答案见解析. 【解析】 【分析】（3）把x=2代入方程，求出a 的值，再把a 代入原方程，进一步解方程即可；（2）分两种情况探讨：①当a=3时，为一元一次方程；②当a≠3时，利用b 2－4ac ＝3求出a 的值，再代入解方程即可． 【详解】（3）将x ＝2代入方程2(a 1)x 2x a 10-++-=，得4(a 1)4a 10-++-=，解得：a ＝15． 将a ＝15代入原方程得24x 2054x 5-+-=，解得：x 3＝12，x 2＝2．∴a ＝15，方程的另一根为12； （2）①当a ＝3时，方程为2x ＝3，解得：x ＝3.②当a≠3时，由b 2－4ac ＝3得4－4(a －3)2＝3，解得：a ＝2或3． 当a ＝2时， 原方程为：x 2＋2x ＋3＝3，解得：x 3＝x 2＝－3； 当a ＝3时， 原方程为：－x 2＋2x －3＝3，解得：x 3＝x 2＝3． 综上所述，当a ＝3，3，2时，方程仅有一个根，分别为3，3，－3. 考点：3.一元二次方程根的判别式；2.解一元二次方程；3.分类思想的应用. 25．8+63． 【解析】 【分析】如图作CH ⊥AB 于H ．在Rt △BHC 求出CH 、BH ，在Rt △ACH 中求出AH 、AC 即可解决问题； 【详解】解：如图作CH ⊥AB 于H ．在Rt △BCH 中，∵BC ＝12，∠B ＝30°，∴CH ＝12BC ＝6，BH 在Rt △ACH 中，tanA ＝34＝CH AH， ∴AH ＝8，∴AC 10，【点睛】本题考查解直角三角形，锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．26．（1）有3种购买方案①购乙6台，②购甲1台，购乙5台，③购甲2台，购乙4台（2）购买甲种机器1台,购买乙种机器5台, 【解析】 【分析】（1）设购买甲种机器x 台（x≥0），则购买乙种机器（6-x ）台，根据买机器所耗资金不能超过34万元，即购买甲种机器的钱数+购买乙种机器的钱数≤34万元．就可以得到关于x 的不等式，就可以求出x 的范围．（2）该公司购进的6台机器的日生产能力不能低于380个，就是已知不等关系：甲种机器生产的零件数+乙种机器生产的零件数≤380件．根据（1）中的三种方案，可以计算出每种方案的需要资金，从而选择出合适的方案． 【详解】解：(1)设购买甲种机器x 台(x≥0),则购买乙种机器(6-x)台 依题意,得7x+5(6-x)≤34解这个不等式,得x≤2,即x 可取0,1,2三个值. ∴该公司按要求可以有以下三种购买方案: 方案一:不购买甲种机器,购买乙种机器6台. 方案二:购买甲种机器l1台,购买乙种机器5台. 方案三:购买甲种机器2台,购买乙种机器4台 (2)根据题意,100x+60(6-x)≥380 解之得x>12由(1)得x≤2,即12≤x≤2. ∴x 可取1,2俩值. 即有以下两种购买方案：购买甲种机器1台,购买乙种机器5台,所耗资金为1×7+5×5=32万元；购买甲种机器2台,购买乙种机器4台,所耗资金为2×7+4×5=34万元.∴为了节约资金应选择购买甲种机器1台,购买乙种机器5台,.【点睛】解决本题的关键是读懂题意，找到符合题意的不等关系式，正确确定各种情况，确定各种方案．27．20千米【解析】【分析】由勾股定理两直角边的平方和等于斜边的平方即可求，即在直角三角形DAE和直角三角形CBE中利用斜边相等两次利用勾股定理得到AD2+AE2=BE2+BC2，设AE为x，则BE=10﹣x，将DA=8，CB=2代入关系式即可求得．【详解】解：设基地E应建在离A站x千米的地方．则BE=（50﹣x）千米在Rt△ADE中，根据勾股定理得：AD2+AE2=DE2∴302+x2=DE2在Rt△CBE中，根据勾股定理得：CB2+BE2=CE2∴202+（50﹣x）2=CE2又∵C、D两村到E点的距离相等．∴DE=CE∴DE2=CE2∴302+x2=202+（50﹣x）2解得x=20∴基地E应建在离A站20千米的地方．考点：勾股定理的应用．中考模拟数学试卷一．选择题（共10小题，满分30分，每小题3分）1．（3分）下列说法不正确的是（）A．0既不是正数，也不是负数B．绝对值最小的数是0C．绝对值等于自身的数只有0和1D．平方等于自身的数只有0和12．（3分）据悉，超级磁力风力发电机可以大幅度提升风力发电效率，但其造价高昂，每座磁力风力发电机，其建造花费估计要5 300万美元，“5 300万”用科学记数法可表示为（）A．5.3×103B．5.3×104C．5.3×107D．5.3×1083．（3分）下面的计算正确的是（）A．3a﹣2a=1 B．a+2a2=3a3C．﹣（a﹣b）=﹣a+b D．2（a+b）=2a+b4．（3分）如图是用八块完全相同的小正方体搭成的几何体，从左面看几何体得到的图形是（）A．B．C．D．5．（3分）如图，若AB∥CD，则∠α、∠β、∠γ之间关系是（）A．∠α+∠β+∠γ=180° B．∠α+∠β﹣∠γ=360°C．∠α﹣∠β+∠γ=180°D．∠α+∠β﹣∠γ=180°6．（3分）若干名工人某天生产同一种玩具，生产的玩具数整理成条形图（如图所示）．则他们生产的玩具数的平均数、中位数、众数分别为（）A．5，5，4 B．5，5，5 C．5，4，5 D．5，4，47．（3分）如图，在矩形ABCD中，AD=10，AB=14，点E为DC上一个动点，若将△ADE沿AE折叠，当点D的对应点D′落在∠ABC的角平分线上时，则点D′到AB的距离为（）A．6 B．6或8 C．7或8 D．6或78．（3分）已知一元二次方程ax2+bx+c=0（a≠0）中，下列说法：①若a+b+c=0，则b2﹣4ac＞0；②若方程两根为﹣1和2，则2a+c=0；③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；④若b=2a+c，则方程有两个不相等的实根．其中正确的有（）A．①②③B．①②④C．②③④D．①②③④9．（3分）如图，在Rt△ABO中，斜边AB=1，若OC∥BA，∠AOC=36°，则（）A．点B到AO的距离为sin54°B．点A到OC的距离为sin36°sin54°C．点B到AO的距离为tan36°D．点A到OC的距离为cos36°sin54°10．（3分）如图，若a＜0，b＞0，c＜0，则抛物线y=ax2+bx+c的大致图象为（）A．B．C．D．二．填空题（共8小题，满分32分，每小题4分）11．（4分）分解因式（xy﹣1）2﹣（x+y﹣2xy）（2﹣x﹣y）=．12．（4分）已知函数，则x取值范围是．13．（4分）如图，△ABC中，AC=5，BC=12，AB=13，CD是AB边上的中线．则CD=．14．（4分）计算=．15．（4分）若x2+kx+81是完全平方式，则k的值应是．16．（4分）如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转90°得到△OA1B1，若AB=2，则点B走过的路径长为．17．（4分）如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，F是CD 上一点，DF=1，在对角线AC上有一点P，连接PE，PF，则PE+PF的最小值为．18．（4分）在平面直角坐标系中，智多星做走棋的游戏，其走法是：棋子从原点出发，第1步向上走1个单位，第2步向上走2个单位，第3步向右走1个单位，第4步向上走1个单位……依此类推，第n步的走法是：当n被3除，余数为2时，则向上走2个单位；当走完第2018步时，棋子所处位置的坐标是三．解答题（共8小题，满分74分）19．（8分）计算：|﹣|+（π﹣2017）0﹣2sin30°+3﹣1．20．（10分）先化简，再求值：（m+），其中m是方程x2+x﹣3=0的根．21．（10分）已知，如图，点D是△ABC的边AB的中点，四边形BCED是平行四边形，（1）求证：四边形ADCE是平行四边形；（2）当△ABC满足什么条件时，平行四边形ADCE是矩形？22．（10分）如图，一次函数y=k1x+b与反比例函数y=的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC=5．（1）求一次函数与反比例函数的解析式；（2）根据所给条件，请直接写出不等式k1x+b＞的解集；（3）若P（p，y1），Q（﹣2，y2）是函数y=图象上的两点，且y1≥y2，求实数p的取值范围．23．（12分）跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售．若每个甲种零件的进价比每个乙种零件的进价少2元，且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同．（1）求每个甲种零件、每个乙种零件的进价分别为多少元？（2）若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个，购进两种零件的总数量不超过95个，该五金商店每个甲种零件的销售价格为12元，每个乙种零件的销售价格为15元，则将本次购进的甲、乙两种零件全部售出后，可使销售两种零件的总利润（利润=售价﹣进价）超过371元，通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案？请你设计出来．（1）本次抽样调查共抽取了多少名学生？（2）求测试结果为C等级的学生数，并补全条形图；（4）若从体能为A等级的2名男生2名女生中随机的抽取2名学生，做为该校培养运动员的重点对象，请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率．25．（12分）如图，AB是⊙O的直径，⊙O与AC相交于点D，∠BAC=45°，AB=BC．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为2cm，求图中阴影部分的面积．26．如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B 为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P 为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．（1）求经过B、E、C三点的抛物线的解析式；（2）判断△BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；（3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．【解答】解：A、B、D均正确，绝对值等于它自身的数是所有非负数，所以C错误，故选：C．2．【解答】解：5 300万=5 300×103万美元=5.3×107美元．故选C．3．【解答】解：A、3a﹣2a=a，故A错误；B、不是同类项不能合并，故B错误；C、﹣（a﹣b）=﹣a+b，故C正确；D、2（a+b）=2a+2b，故D错误．故选：C．4．【解答】解：从左面看易得上面一层左边有1个正方形，下面一层有2个正方形．故选：A．5．【解答】解：如图，作EF∥AB，∵AB∥CD，∴EF∥CD，∵EF∥AB，∴∠α+∠AEF=180°，∵EF∥CD，∴∠γ=∠DEF，而∠AEF+∠DEF=∠β，∴∠α+∠β=180°+∠γ，即∠α+∠β﹣∠γ=180°．故选：D．6．【解答】解：===5件，中位数为第5、6个数的平均数，为5件，众数为5件．故选：B．7．【解答】解：如图，连接BD′，过D′作MN⊥AB，交AB于点M，CD于点N，作D′P⊥BC交BC于点P∵点D的对应点D′落在∠ABC的角平分线上，∴MD′=PD′，又∵∠D'MB=∠MBP=∠BPD'=90°，∴四边形BPD'M为正方形，设MD′=x，则P D′=BM=x，∴AM=AB﹣BM=14﹣x，又折叠可得AD=AD′=10，∴Rt△AD'M中，x2+（14﹣x）2=102，解得x=6或8，即MD′=6或8，∴点D′到AB的距离为6或8，故选：B．8．【解答】解：①当x=1时，有若a+b+c=0，即方程有实数根了，∴△≥0，故错误；②把x=﹣1代入方程得到：a﹣b+c=0 （1）把x=2代入方程得到：4a+2b+c=0 （2）把（2）式减去（1）式×2得到：6a+3c=0，即：2a+c=0，故正确；③方程ax2+c=0有两个不相等的实数根，则它的△=﹣4ac＞0，∴b2﹣4ac＞0而方程ax2+bx+c=0的△=b2﹣4ac＞0，∴必有两个不相等的实数根．故正确；④若b=2a+c则△=b2﹣4ac=（2a+c）2﹣4ac=4a2+c2，∵a≠0，∴4a2+c2＞0故正确．②③④都正确，故选C．9．【解答】解：B到AO的距离是指BO的长，∵AB∥OC，∴∠BAO=∠AOC=36°，∵在Rt△BOA中，∠BOA=90°，AB=1，∴sin36°=，∴BO=ABsin36°=sin36°，故A、C选项错误；过A作AD⊥OC于D，则AD的长是点A到OC的距离，∵∠BAO=36°，∠AOB=90°，∴∠ABO=54°，∵sin36°=，∴AD=AO•sin36°，∵sin54°=，∴AO=AB•sin54°，∵AB=1，∴AD=AB•sin54°•sin36°=1×sin54°•sin36°=sin54°•sin36°，故B选项正确，D选项错误；故选：B．10．【解答】解：∵a＜0，∴抛物线的开口方向向下，故第三个选项错误；∵c＜0，∴抛物线与y轴的交点为在y轴的负半轴上，故第一个选项错误；∵a＜0、b＞0，对称轴为x=＞0，∴对称轴在y轴右侧，故第四个选项错误．故选：B．二．填空题（共8小题，满分32分，每小题4分）11．【解答】解：令x+y=a，xy=b，则（xy﹣1）2﹣（x+y﹣2xy）（2﹣x﹣y）=（b﹣1）2﹣（a﹣2b）（2﹣a）=b2﹣2b+1+a2﹣2a﹣2ab+4b=（a2﹣2ab+b2）+2b﹣2a+1=（b﹣a）2+2（b﹣a）+1=（b﹣a+1）2；即原式=（xy﹣x﹣y+1）2=[x（y﹣1）﹣（y﹣1）]2=[（y﹣1）（x﹣1）]2=（y﹣1）2（x﹣1）2．故答案为：（y﹣1）2（x﹣1）2．12．【解答】解：由题意得，x﹣2≥0，解得，x≥2，故答案为：x≥2．13．【解答】解：∵在△ABC中，AC=5，BC=12，AB=13，∴AC2+BC2=52+122=132=AB2，∴△ABC为直角三角形，且∠ACB=90°，∵CD是AB边上的中线，∴CD=6.5；故答案为：6.5．14．【解答】解：x4+4=（x2+2）2﹣（2x）2=（x2+2x+2）（x2﹣2x+2）=[（x+1）2+1][（x﹣1）2+1]，∴原式=．故答案为：．15．【解答】解：∵x2+kx+81是完全平方式，∴k=±18．故答案为：±18．16．【解答】解：∵在直角△OAB中，∠AOB=30°，AB=2，∴OB=，∵将△OAB绕点O逆时针旋转90°得到△OA1B1，∴∠BOB1=90°，∴点B走过的路径长为，故答案为π17．【解答】解：如图作EH⊥BC于H．作点F关于AC的对称点F′，连接EF′交AC于P′，此时P′E+P′F 的值最小．∵正方形ABCD的面积为12，∴AB=2，∠ABC=90°，∵△ABE是等边三角形，∴BE=AB=2，∠ABE=60°，∴∠EBH=30°，∴EC=BE=，BH=EH=3，∵BF′=DF=1，∴HF′=2，在Rt△EHF′中，EF′==，∴PE+PF的最小值为，故答案为18．【解答】解：由题意得，每3步为一个循环组依次循环，且一个循环组内向右1个单位，向上3个单位，∵2018÷3=672…2，∴走完第2018步，为第673个循环组的第2步，所处位置的横坐标为672，纵坐标为672×3+3=2019，∴棋子所处位置的坐标是（672，2019）．故答案为：（672，2019）．三．解答题（共8小题，满分74分）19．【解答】解：原式=+1﹣2×+=．20．【解答】解：原式=•=•=m（m+1）=m2+m，∵m是方程x2+x﹣3=0的根，∴m2+m﹣3=0，即m2+m=3，则原式=3．21．【解答】证明：（1）因为四边形BCED是平行四边形，所以BD=CE且BD∥CE，又因为D是△ABC的边AB的中点，所以AD=BD，即DA=CE，又因为CE∥BD，所以四边形ADCE是平行四边形．（2）当△ABC为等腰三角形且AC=BC时，CD是等腰三角形底边AB上的中线，则CD⊥AD，平行四边形ADCE的角∠ADC=90°，因此四边形ADCE是矩形．22．【解答】解：（1）把A（2，m），B（n，﹣2）代入y=得：k2=2m=﹣2n，即m=﹣n，则A（2，﹣n），过A作AE⊥x轴于E，过B作BF⊥y轴于F，延长AE、BF交于D，∵A（2，﹣n），B（n，﹣2），∴BD=2﹣n，AD=﹣n+2，BC=|﹣2|=2，∵S△ABC=•BC•BD∴×2×（2﹣n）=5，解得：n=﹣3，即A（2，3），B（﹣3，﹣2），把A（2，3）代入y=得：k2=6，即反比例函数的解析式是y=；把A（2，3），B（﹣3，﹣2）代入y=k1x+b得：，解得：k1=1，b=1，即一次函数的解析式是y=x+1；（2）∵A（2，3），B（﹣3，﹣2），∴不等式k1x+b＞的解集是﹣3＜x＜0或x＞2；（3）分为两种情况：当点P在第三象限时，要使y1≥y2，实数p的取值范围是P≤﹣2，当点P在第一象限时，要使y1≥y2，实数p的取值范围是P＞0，即P的取值范围是p≤﹣2或p＞0．23．【解答】解：（1）设每个乙种零件进价为x元，则每个甲种零件进价为（x﹣2）元．由题意得：．解得：x=10．检验：当x=10时，x（x﹣2）≠0∴x=10是原分式方程的解．每个甲种零件进价为：x﹣2=10﹣2=8答：每个甲种零件的进价为8元，每个乙种零件的进价为10元．（2）设购进乙种零件y个，则购进甲种零件（3y﹣5）个．由题意得：解得：23＜y≤25∵y为整数∴y=24或25．∴共有2种方案．方案一：购进甲种零件67个，乙种零件24个；方案二：购进甲种零件70个，乙种零件25个．24．【解答】解：（1）10÷20%=50，所以本次抽样调查共抽取了50名学生；（2）测试结果为C等级的学生数为50﹣10﹣20﹣4=16（人）；补全条形图如图所示：（3）700×=56，（4）画树状图为：共有12种等可能的结果数，其中抽取的两人恰好都是男生的结果数为2，所以抽取的两人恰好都是男生的概率==．25．【解答】（1）证明：∵AB=BC，∴∠BAC=∠C=45°，∴∠ABC=180°﹣∠BAC﹣∠C=90°，∴AB⊥BC，∴BC是⊙O的切线；（2）解：连接BD，如图，∵AB是⊙O的直径，∴∠ADB=90°，∴AD=CD=BD，∴=，∴图中阴影部分的面积=S△ABC=××AB×BC=××4×4=4（cm2）．26．【解答】解：（1）B（﹣1，0）E（0，4）C（4，0）设解析式是y=ax2+bx+c，可得，解得，∴y=﹣x2+3x+4；（2）△BDC是直角三角形，∵BD2=BO2+DO2=5，D C2=DO2+CO2=20，BC2=（BO+CO）2=25∴BD2+DC2=BC2，∴△BDC是直角三角形．点A坐标是（﹣2，0），点D坐标是（0，2），设直线AD的解析式是y=kx+b，则，解得：，则直线AD的解析式是y=x+2，设点P坐标是（x，x+2）当OP=OC时x2+（x+2）2=16，解得：x=﹣1±（不符合，舍去）此时点P（﹣1+，1+）当PC=OC时（x+2）2+（4﹣x）2=16，方程无解；当PO=PC时，点P在OC的中垂线上，∴点P横坐标是2，得点P坐标是（2，4）；∴当△POC是等腰三角形时，点P坐标是（﹣1+，1+）或（2，4）；（3）点M坐标是（，点N坐标是（），∴MN=，设点P为（x，x+2），Q（x，﹣x2+3x+4），则PQ=﹣x2+2x+2①若PQNM是菱形，则PQ=MN，可得x1=0.5，x2=1.5当x2=1.5时，点P与点M重合；当x1=0.5时，可求得PM=，所以菱形不存在．②能成为等腰梯形，作QH⊥MN于点H，作PJ⊥MN于点J，则NH=MJ，则﹣（﹣x2+3x+4）=x+2﹣，解得：x=2.5，此时点P的坐标是（2.5，4.5）．。

2020年沈阳市和平区东北育才学校中考数学一模试卷一、选择题（本大题共10小题，共20.0分）1.3的算术平方根是()A. ±3B. √3C. 3D. ±√32.通州区大运河森林公园占地面积10700亩，是北京规模最大的滨河森林公园．将10700用科学记数法表示为A. 10.7×104B. 1.07×105C. 1.7×104D. 1.07×1043.如图所示的是由五个相同的小正方体组成的立体图形，它的左视图是()A.B.C.D.4.下列计算正确的是()A. 3a2⋅4ab=7a3bB. (2ab3)2=4a2b6C. a12÷a6=a2D.4a+4b=8ab5.下列说法正确的是()A. 为了解全省中学生的心理健康状况，宜采用普查方式B. 掷两枚质地均匀的硬币，两枚硬币都是正面朝上这一事件发生的概率为12C. 掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是必然事件D. 甲乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是S甲2=0.4，S乙2=0.6，则甲的射击成绩较稳定6.甲骨文是我国的一种古代文字，是汉字的早期形式．下列甲骨文中，不是轴对称图形的是()A. B. C. D.7.如果不等式组{x<8x>m有解，那么m的取值范围是()A. m>8B. m<8C. m≥8D. m≤88.关于x的方程x2+3x+a=0有一个根为−1，则a的值为()A. 1B. −1C. 2D. −29.如图，△ODC是由△OAB绕点O顺时针旋转30°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠B的度数是()A. 40∘B. 35∘C. 30∘D. 15∘10.抛物线y=ax2+bx+c的顶点为D(−1,2)，与x轴的一个交点A在点(−3,0)和(−2,0)之间，其部分图象如图，则以下结论：①b2−4ac<0；②当x>−1时，y随x增大而减小；③a+b+c<0；④若方程ax2+bx+c−m=0没有实数根，则m>2；⑤3a+c<0.其中正确结论的个数是()A. 2个B. 3个C. 4D. 5个二、填空题（本大题共6小题，共18.0分）11.分解因式：ax2−4ax+4a=______．12.一组数据3，5，7，8，m的平均数为5，则这组数据的中位数是_____．13.如图，在Rt△ABC中，∠C=90∘，∠A=60∘，AC=√3cm，将△ABC绕点B顺时针旋转至△A′BC′的位置，且使点A，B，C′三点在同一直线上，则点A经过的路线长是___________cm．14.如图，直线l为y=√3x，过点A1(1,0)作A1B1⊥x轴，与直线l交于点B1，以原点O为圆心，OB1长为半径画圆弧交x轴于点A2；再作A2B2⊥x轴，交直线l于点B2，以原点O为圆心，OB2长为半⏜ 的长为径画圆弧交x轴于点A3…，按此作法进行下去，则A n B n−1______(用含n，π的式子表示)．15.如图，在平面直角坐标系xOy中，四边形ODEF和四边形ABCD都是正方形，点F在x轴的正半轴上，点C在边DE上，反比例函数y=k(k≠0,x>0)的图象过点B，E.若AB=2，则k的值为________.x16.如图，在等腰直角△ABC中，∠ACB=90°，CO⊥AB于点O，点D、E分别在边AC、BC上，且AD=CE，连结DE交CO于点P，给出以下结论：①△DOE是等腰直角三角形；②∠CDE=∠COE；③若AC=1，则；④AD2+BE2−2OP2=2DP⋅PE，其中四边形CEOD的面积为14所有正确结论的序号是______．三、计算题（本大题共1小题，共6.0分）)−217.计算：2√2sin45°−(−2019)0+|1−√2|+(−12四、解答题（本大题共8小题，共64.0分）18.在直角三角形△ABC中，∠C=90°，点E、F分别在边AB、AC上，将△ABC沿着直线EF折叠，使得A点恰好落在BC边上的D点处，且ED⊥BC．(1)求证四边形AFDE是菱形；(2)若CD=2，AC=6，求线段ED的长度．19.我市某中学为了了解本校学生对电视节目的喜爱情况，随机调查了部分学生最喜爱哪一类节目(被调查的学生只选一类并且没有不选择的)，并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息，完成下列问题：(1)求本次调查的学生人数；(2)请将两个统计图补充完整，并求出新闻节目在扇形统计图中所占圆心角的度数；(3)若该中学有1500名学生，请估计该校喜爱电视剧节目的人数．20.在一个不透明的袋子里装有四只标号分别为1，2，3，4的乒乓球，这些乒乓球除所标数字不同其余均相同．先从袋子里随机摸出一个乒乓球(不放回)，再从袋子里随机摸出一个乒乓球，请用画树状图(或列表)的方法，求两次摸出乒乓球的标号是连续整数的概率．21.甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用l0天．且甲队单独施工15天和乙队单独施工10天的工作量相同．(1)甲、乙两队单独完成此项任务各需多少天？(2)若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队单独继续施工，为了不影响工程进度．甲队的工作效率提高到原来的2倍．要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少单独施工多少天？22.如图，AB为⊙O的直径，C，E为O上的两点，若AC平分∠EAB，CD⊥AE于点D．(1)求证：DC是⊙O切线；(2)若AO=6，DC=3√3，求DE的长；(3)过点C作CF⊥AB于F，如图2，若AD−OA=1.5，AC=3√3，求图中阴影部分面积．23.如图①，在平面直角坐标系中，直线y=34x+32与x轴相交于点A，且经过点B(2,m).已知点C(3,0)．(1)求直线BC的函数表达式；(2)在线段BC上找一点D，使得△ABO与△ABD的面积相等，求出点D的坐标；(3)在y轴上有一动点P，在直线BC上有一动点M，若△APM是以线段AM为斜边的等腰直角三角形，求出点M的坐标；(4)如图②，E为线段AC上一点，连结BE，一动点F从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段EA以每秒√2个单位的速度运动到点A后停止．设点F在整个运动过程中所用时间为t(s)，求t的最小值．24.如图1，在Rt△ABC中，∠A=90°，AB=AC，点D，E分别在边AB，AC上，AD=AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想：图1中，线段PM与PN的数量关系是__，位置关系是__；(2)探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；(3)拓展延伸：把△ADE绕点A在平面内自由旋转，若AD=4，AB=10，请直接写出△PMN面积的最大值．25.如图，抛物线y=ax2+6x+c交x轴于A，B两点，交y轴于点C.直线y=x−5经过点B，C．(1)求抛物线的解析式；(2)过点A的直线交直线BC于点M．①当AM⊥BC时，过抛物线上一动点P(不与点B，C重合)，作直线AM的平行线交直线BC于点Q，若以点A，M，P，Q为顶点的四边形是平行四边形，求点P的横坐标；②连接AC，当直线AM与直线BC的夹角等于∠ACB的2倍时，请直接写出点M的坐标．-------- 答案与解析 --------1.答案：B解析：解：3的算术平方根是√3．故选：B．利用算术平方根的定义求解．本题考查了算术平方根：求一个非负数的算术平方根与求一个数的平方互为逆运算，在求一个非负数的算术平方根时，可以借助乘方运算来寻找．2.答案：D解析：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n 为整数，表示时关键要正确确定a的值以及n的值．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值>1时，n是正数；当原数的绝对值<1时，n是负数．解：将10700用科学记数法表示为1.07×104.故选D.3.答案：B解析：解：从左边看第一层是两个小正方形，第二层左边一个小正方形，故选：B．根据从左边看得到的图形是左视图，可得答案．本题考查了简单组合体的三视图，从左边看得到的图形是左视图．4.答案：B解析：解：∵3a2⋅4ab=12a3b，故选项A错误，∵(2ab3)2=4a2b6，故选项B正确，∵a12÷a6=a6，故选项C错误，∵4a+4b不能合并，故选项D错误，故选：B．根据各个选项中的式子，可以计算出正确的结果，从而可以解答本题．本题考查整式的混合运算，解答本题的关键是明确整式的混合运算的计算方法．5.答案：D解析：解：A、为了解全省中学生的心理健康状况，宜采用抽查方式，故错误；B、掷两枚质地均匀的硬币，两枚硬币都是正面朝上这一事件发生的概率为1；故错误；4C、掷一枚质地均匀的正方体骰子，骰子停止转动后，5点朝上是随机事件；故错误；D、甲乙两人在相同条件下各射击10次，他们成绩的平均数相同，方差分别是S甲2=0.4，S乙2=0.6，则甲的射击成绩较稳定，故正确；故选：D．根据调查与抽样调查、方差的性质以及随机事件与必然事件的定义即可得到结论．本题考查了求概率的方法、全面调查与抽样调查、方差的性质以及随机事件与必然事件；熟记方法和性质是解决问题的关键．6.答案：D解析：本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．根据轴对称图形的概念求解．解：A.是轴对称图形，故本选项错误；B.是轴对称图形，故本选项错误；C.是轴对称图形，故本选项错误；D.不是轴对称图形，故本选项正确．故选D．7.答案：B解析：本题考查了不等式组的解集．先解出不等式组的解集，根据已知解集比较，可求出m 的取值范围即可．解：∵不等式组{x <8x >m有解 ∴m <x <8∴m <8m 的取值范围为m <8．故选B ．8.答案：C解析：本题考查一元二次方程的解的定义，根据方程的解的定义直接把x =−1代入方程x 2+3x +a =0得到关于a 的方程，然后解关于a 的方程即可．解：把x =−1 代入方程得1−3+a =0，解得a =2．故选C ．9.答案：B解析：根据旋转的性质可得∠AOD =∠BOC =30°，AO =DO ，再求出∠BOD ，∠ADO ，然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．本题考查了旋转的性质，等腰三角形的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记各性质并准确识图是解题的关键．解：∵△COD 是△AOB 绕点O 顺时针旋转30°后得到的图形，∴∠AOD =∠BOC =30°，AO =DO ，∵∠AOC =100°，∴∠BOD =100°−30°×2=40°，∠ADO=∠A=12(180°−∠AOD)=12(180°−30°)=75°，由三角形的外角性质得，∠B=∠ADO−∠BOD=75°−40°=35°．故选B．10.答案：C解析：本题考查二次函数图象与系数的关系，根的判别式、抛物线与x轴的交点等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．利用图象信息，以及二次函数的性质即可一一判断．解：∵二次函数与x轴有两个交点，∴b2−4ac>0，故①错误，观察图象可知：当x>−1时，y随x增大而减小，故②正确，∵抛物线与x轴的另一个交点为在(0,0)和(1,0)之间，∴x=1时，y=a+b+c<0，故③正确，∵当m>2时，抛物线与直线y=m没有交点，∴方程ax2+bx+c−m=0没有实数根，故④正确，∵对称轴x=−1=−b2a，∴b=2a，∵a+b+c<0，∴3a+c<0，故⑤正确，故选C．11.答案：a(x−2)2解析：先提取公因式a，再利用完全平方公式进行二次分解．本题考查了提公因式法，公式法分解因式，提取公因式后利用完全平方公式进行二次分解，注意要分解彻底．解：ax2−4ax+4a，=a(x2−4x+4)，=a(x−2)2．12.答案：5解析：本题考查平均数与中位数的意义．平均数是指在一组数据中所有数据之和再除以数据的个数．中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(或最中间两个数的平均数)，叫做这组数据的中位数．先根据平均数的定义求出m的值，然后根据中位数的定义求解即可．【详解】解：由题意可知，(3+5+7+8+m)÷5=5，解得：m=2，这组数据从小到大排列2，3，5，7，8，则中位数是5．故答案为：5．13.答案：5√3π3解析：【试题解析】本题考查旋转的性质以及弧长公式.点A经过的路线即以B为圆心，以AB的长为半径的弧．先根据直角三角形性质求出∠ABC的度数，从而由旋转的性质求得∠ABA′的度数，再根据弧长公式进行计算即可．解：∵∠C=90°，∠A=60°，∴∠ABC=90°−60°=30°，∴∠A′BC′=∠ABC=30°，∴∠ABA′=180°−30°=150°，∵AC=√3cm，∴AB =2AC =2√3cm ，∴点A 经过的路线的长度150×π×2√3180=5√33π(cm )． 故答案为5√33π．14.答案：2n π3解析：解：∵直线l 为y =√3x ，点A 1(1,0)，A 1B 1⊥x 轴，∴当x =1时，y =√3，即B 1(1,√3)，∴tan∠A 1OB 1=√3，∴∠A 1OB 1=60°，∠A 1B 1O =30°，∴OB 1=2OA 1=2，∵以原点O 为圆心，OB 1长为半径画圆弧交x 轴于点A 2，∴A 2(2,0)，同理可得，A 3(4,0)，A 4(8,0)，…，∴点A n 的坐标为(2n−1,0)，∴OA n =2n−1，∴OB n−1=2×2n−1=2n ，∴A n B n−1⏜ =60°×π×2n 180∘=2n π3故答案为2n π3依据直线l 为y =√3x ，点A 1(1,0)，A 1B 1⊥x 轴，可得A 2(2,0)，同理可得，A 3(4,0)，A 4(8,0)，…，依据规律可得点A n 的坐标为(2n−1,0)，可得OB n−1的长，由弧长公式可求解．本题主要考查了一次函数图象上点的坐标特征，找出点A n 坐标规律是本题的关键．15.答案：6+2√5解析：解：设E(x,x)，∴B(2,x +2)，∵反比例函数y =k x (k ≠0,x >0)的图象过点B 、E ．∴x2=2(x+2)，解得x1=1+√5，x2=1−√5(舍去)，∴k=x2=6+2√5，故答案为6+2√5．设E(x,x)，则B(2,x+2)，根据反比例函数系数的几何意义得出x2=2(x+2)，求得E的坐标，从而求得k的值．本题考查了反比例函数图象上点的坐标特征，关键是掌握反比例函数图象上点与反比例函数中系数k的关系．16.答案：①②③④解析：本题考查勾股定理、四点共圆、全等三角形的判定和性质、等腰直角三角形的性质、相似三角形的判定和性质等知识，解题的关键是正确寻找全等三角形，学会利用四点共圆解决问题，题目比较难，用到的知识点比较多．①正确．由ADO≌△CEO，推出DO=OE，∠AOD=∠COE，由此即可判断．②正确．由D、C、E、O四点共圆，即可证明．③正确．由S△ABC=12×1×1=12，S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=12S△ABC即可解决问题．④正确．由D、C、E、O四点共圆，得OP⋅PC=DP⋅PE，所以2OP2+2DP⋅PE=2OP2+2OP⋅PC=2OP(OP+PC)=2OP⋅OC，由△OPE∽△OEC，得到OPOE =OEOC，即可得到2OP2+2DP⋅PE=2OE2=DE2=CD2+CE2，由此即可证明．解：①正确．如图，∵∠ACB=90°，AC=BC，CO⊥AB∴AO=OB=OC，∠A=∠B=∠ACO=∠BCO=45°，在△ADO和△CEO中，{OA=OC∠A=∠ECO AD=CE，∴△ADO≌△CEO，∴DO=OE，∠AOD=∠COE，∴∠AOC=∠DOE=90°，∴△DOE是等腰直角三角形．故①正确．②正确．∵△DOE是等腰直角三角形，∴∠EDO=∠A=45°，∵∠CDE+∠EDO=∠A+∠AOD，∴∠CDE=∠AOD，∵∠AOD=∠COE，∴∠CDE=∠COE，故②正确．③正确．∵AC=BC=1，∴S△ABC=12×1×1=12，S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=12S△ABC=14，故③正确．④正确．∵D、C、E、O四点共圆，∴OP⋅PC=DP⋅PE，∴2OP2+2DP⋅PE=2OP2+2OP⋅PC=2OP(OP+PC)=2OP⋅OC，∵∠OEP=∠DCO=∠OCE=45°，∠POE=∠COE，∴△OPE∽△OEC，∴OPOE =OEOC，∴OP⋅OC=OE2，∴2OP2+2DP⋅PE=2OE2=DE2=CD2+CE2，∵CD=BE，CE=AD，∴AD2+BE2=2OP2+2DP⋅PE，∴AD2+BE2−2OP2=2DP⋅PE．故④正确．17.答案：解：原式=2√2×√22−1+√2−1+4=2−1+√2−1+4=4+√2．解析：原式利用特殊角的三角函数值，零指数幂、负整数指数幂法则，以及绝对值的代数意义计算即可求出值．此题考查了实数的运算，熟练掌握运算法则是解本题的关键．18.答案：解：(1)∵ED⊥BC∴∠EDB=90°，∵∠C=90°，∴∠EDB=∠C，∴AC//ED，∴∠CFD=∠FDE，由翻折可知：∠A=∠FDE，则∠A=∠CFD，∴DF//AE，∴四边形AFDE是平行四边形，由翻折可知：AF=DF，∴平行四边形AFDE是菱形，(2)设CF=x，则由翻折可知：DF=AF=6−x，∴由勾股定理可知：DF2=CF2+CD2，(6−x)2=x2+22，解得：x=83，则DF=6−x=103，∴菱形AFDE中，ED=FD=103．解析：本题考查菱形的综合问题，涉及菱形的性质与判定，勾股定理，解方程，翻折变换等知识，需要学生灵活运用所学知识．(1)易证∠EDB=90°，所以∠EDB=∠C，所以AC//ED，从而可知∠CFD=∠FDE，由翻折可知：∠A=∠FDE，所以∠A=∠CFD，所以DF//AE，所以四边形AFDE是平行四边形，由翻折可知：AF=DF，所以平行四边形AFDE是菱形．(2)设CF=x，则由翻折可知：DF=AF=6−x，根据勾股定理可知(6−x)2=x2+22，解得：x=83，则DF=6−x=103，所以在菱形AFDE中，ED=FD=103．19.答案：解：(1)69÷23%=300(人)∴本次共调查300人；(2)∵喜欢娱乐节目的人数占总人数的20%，∴20%×300=60(人)，补全如图：∵360°×12%=43.2°，∴新闻节目在扇形统计图中所占圆心角的度数为43.2°；(3)1500×23%=345(人)，∴估计该校有345人喜爱电视剧节目．解析：(1)根据电视剧的人数及其百分比可得总人数；(2)总人数乘以B种类的百分比求得其人数，用C种类的人数除以总人数可得其百分比，据此补全图形即可，再用360°乘以D的百分比可得；(3)总人数乘以样本中电视剧的百分比可得答案．本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．20.答案：解：画树状图得：∵共有12种等可能的结果，两次摸出乒乓球的标号是连续整数的有6种情况，∴两次摸出乒乓球的标号是连续整数的概率为：612=12．解析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次摸出乒乓球的标号是连续整数的情况，再利用概率公式即可求得答案．此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．21.答案：解：(1)设乙队单独完成此项任务需要x天，则甲队单独完成此项任务需要(x+10)天，由题意，得15x+10=10x，解得：x=20．经检验，x=20是原方程的解，则x+10=30(天)．答：甲队单独完成此项任务需要30天，乙队单独完成此项任务需要20天；(2)设甲队再单独施工a天，由题意，得3 30+2a30≥2×320，解得：a≥3．答：甲队至少再单独施工3天．解析：(1)设乙队单独完成此项任务需要x天，则甲队单独完成此项任务需要(x+10)天，根据甲队单独施工15天和乙队单独施工10天的工作量相同建立方程求出其解即可；(2)设甲队再单独施工a天，根据甲队总的工作量不少于乙队的工作量的2倍建立不等式求出其解即可．本题是一道工程问题的运用，考查了工作时间×工作效率=工作总量的运用，列分式方程解实际问题的运用，分式方程的解法的运用，一元一次不等式的应用，解答时验根是学生容易忽略的地方．22.答案：(1)证明：连接OC，如图1，∵AC平分∠EAB，∴∠1=∠2，∵OA=OC，∴∠2=∠3，∴∠1=∠3，∴OC//AD，∵AD⊥CD，∴OC⊥CD，C为O上的点，∴DC是⊙O切线；(2)解：连接BE交OC于H，如图1，∵AB为⊙O的直径，∴∠AEB=90°，∵OC//AD，∴∠OHB=90°，∴EH=BH，四边形CDEH为矩形，∴CD=EH=3√3，CH=ED，∴BH=3√3，在Rt△OBH中，OH=√62−(3√3)2=3，∴CH=6−3=3，∴DE=3；(3)解：连接OC，如图2，设⊙O的半径为r，∵AC平分∠BAD，CD⊥AD，CF⊥AB，∴CD=CF，∴AD=AF=AO+OF，∵AD−OA=1.5，∴AO+OF−OA=1.5，即OF=1.5，∵AB为⊙O的直径，∴∠ACB=90°，∵∠CAF=∠BAC，∴△ACF∽△ABC，∴ACAB =AFAC，即3√32r=3√3，解得r=−92(舍去)或r=3，在Rt△OCF中，CO=3=2×1.5=2OF，，∴∠COF=60°，∴CF=√CO2−OF2=3√32，∴图中阴影部分面积=S扇形BOC −S△OCB=60⋅π⋅32360−12×3×3√32=32π−9√34．解析：本题考查了切线的判定与性质：经过半径的外端且垂直于这条半径的直线是圆的切线；圆的切线垂直于经过切点的半径．判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”；有切线时，常常“遇到切点连圆心得半径”.也考查了圆周角定理和垂径定理．(1)连接OC，如图1，先证明∠1=∠3得到OC//AD，再利用平行线的性质得OC⊥CD，然后根据切线的判定定理得到结论；(2)连接BE 交OC 于H ，如图1，利用圆周角定理得∠AEB =90°，易得四边形CDEH 为矩形，则CD =EH =3√3，CH =ED ，利用垂径定理得BH =3√3，然后利用勾股定理计算出OH 后计算出CH ，从而得到DE 的长；(3)连接OC ，如图2，设⊙O 的半径为r ，利用角平分线的性质得CD =CF ，则根据勾股定理得AD =AF ，于是可计算出OF =1.5，再证明△ACF∽△ABC ，利用相似比得到3√32r=3√3，解得r =3，接着在Rt △OCF 中利用含30°角的直角三角形的性质得到∠COF =60°，CF =3√32，然后根据扇形面积公式，利用图中阴影部分面积=S 扇形BOC −S △OCB 进行计算．23.答案：解：(1)将点B(2,m)的坐标代入y =34x +32，得m =3，∴点B(2,3)．设直线BC 的函数表达式为y =kx +b ，把点B(2,3)，C(3,0)的坐标代入， 得{2k +b =3,3k +b =0,∴{k =−3,b =9,∴直线BC 的函数表达式为y =−3x +9． (2)过点O 作OD//AB 交BC 于点D ． 易得S △ABO =S △ABD ，k AB =k OD =34， ∴直线OD 的函数表达式为y = 34x. 联立方程组{y =34x,y =−3x +9,解得{x =125,y =95,∴点D 的坐标为(125,95)．(3)分两种情况讨论：①如解图①，当点P 在y 轴负半轴时，作M 1N ⊥OP 于点N ． ∵直线AB 与x 轴相交于点A ，∴点A 的坐标为(−2,0)． ∵∠APO +∠PAO =90°，∠APO +∠NPM 1=90°，∴∠PAO =∠NPM 1.又∵AP =PM 1，∠POA =∠M 1NP =90°， ∴△AOP≌△PNM 1(AAS)，∴PN =AO =2． 设OP =NM 1=m ，则ON =m −2，∴把点M 1(m,2−m)的坐标代入y =−3x +9，解得m =72， ∴点M 1(72,−32)．②如解图②，当点P在y轴正半轴时，作M2H⊥OP于点H.易证△AOP≌△PHM2．设HM2=n，则OH=n−2，∴点M2(n,n−2).把点M2(n,n−2)的坐标代入y=−3x+9，解得n=114，∴点M2(114,34 )．综上所述，点M的坐标为(72,−32)或(114,34)．(4)如解图③，作射线AQ与x轴正半轴的夹角为45°，过点B作x轴的垂线交射线AQ于点Q，作EK⊥AQ于点K，作BT⊥AQ于点T．∵∠CAQ=45°，BG⊥x轴，点B(2,3)，∴AG=4，∴AQ=4√2，BQ=7，t=BE1√2=BE+EK≥BT．由面积法可得12AQ·BT=12BQ·AG，∴12×4√2BT=12×7×4，∴BT=72√2，故t的最小值为72√2．解析：(1)把B(2,m)代入直线AB解析式可求出m的值，即可得B点坐标，设直线BC的解析式为y=kx+b，把B、C两点坐标代入可求得k、b的值，即可得直线BC的解析式；(2)过点O作OD//AB交BC于点D，可知S△ABC=S△ABD，k AB=k OD=34，联立直线BC与OD的解析式解得交点D的坐标即可；(3)分别讨论P点在y轴的负半轴和正半轴时两种情况；(4)作射线AQ与x轴正半轴的夹角为45°，过点B作x轴的垂线交射线AQ于点Q，作EK⊥AQ于点K，作BT⊥AQ于点T，可求出AG、AQ、BQ的长，根据时间t=BE1+√2=BE+EK≥BT，利用面积法求出BT的值即可．本题考查一次函数的几何应用，待定系数法求一次函数解析式及面积公式的应用，熟练掌握相关知识是解题关键．24.答案：(1)PM=PN；PM⊥PN(2)由旋转知，∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE(SAS)，∴∠ABD=∠ACE，BD=CE，同(1)的方法，利用三角形的中位线得，PN=12BD，PM=12CE，∴PM=PN，∴△PMN是等腰三角形，同(1)的方法得，PM//CE，∴∠DPM=∠DCE，同(1)的方法得，PN//BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形，(3)492．解：如图2，同(2)的方法得，△PMN是等腰直角三角形，∴MN最大时，△PMN的面积最大，∴DE//BC且DE在顶点A上面，∴MN最大=AM+AN，连接AM，AN，在△ADE中，AD=AE=4，∠DAE=90°，∴AM=2√2，在Rt△ABC中，AB=AC=10，AN=5√2，∴MN最大=2√2+5√2=7√2，∴S△PMN最大=12PM2=12×12MN2=14×(7√2)2=492．解析：此题是几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质，是一道中考常考题．解：∵点P，N是BC，CD的中点，∴PN//BD，PN=12BD，∵点P，M是CD，DE的中点，∴PM//CE，PM=12CE，∵AB=AC，AD=AE，∴BD=CE，∴PM=PN，∵PN//BD，∴∠DPN =∠ADC ， ∵PM//CE ， ∴∠DPM =∠DCA ， ∵∠BAC =90°， ∴∠ADC +∠ACD =90°，∴∠MPN =∠DPM +∠DPN =∠DCA +∠ADC =90°， ∴PM ⊥PN ，故答案为PM =PN ，PM ⊥PN ，(2)先判断出△ABD≌△ACE ，得出BD =CE ，同(1)的方法得出PN =12BD ，PM =12CE ，即可得出PM =PN ，同(1)的方法即可得出结论；(3)先判断出MN 最大时，△PMN 的面积最大，进而求出AN ，AM ，即可得出MN 最大=AM +AN ，最后用面积公式即可得出结论．25.答案：解：(1)当x =0时，y =x −5=−5，则C(0,−5)，当y =0时，x −5=0，解得x =5，则B(5,0)，把B(5,0)，C(0,−5)代入y =ax 2+6x +c 得{25a +30+c =0c =−5，解得{a =−1c =−5，∴抛物线解析式为y =−x 2+6x −5；(2)①解方程−x 2+6x −5=0得x 1=1，x 2=5，则A(1,0)， ∵B(5,0)，C(0,−5)， ∴△OCB 为等腰直角三角形， ∴∠OBC =∠OCB =45°， ∵AM ⊥BC ，∴△AMB 为等腰直角三角形， ∴AM =√22AB =√22×4=2√2，∵以点A ，M ，P ，Q 为顶点的四边形是平行四边形，AM//PQ ， ∴PQ =AM =2√2，PQ ⊥BC ，作PD ⊥x 轴交直线BC 于D ，如图1，则∠PDQ =45°， ∴PD =√2PQ =√2×2√2=4，设P(m,−m 2+6m −5)，则D(m,m −5)， 当P 点在直线BC 上方时，PD =−m 2+6m −5−(m −5)=−m 2+5m =4，解得m 1=1，m 2=4， 当P 点在直线BC 下方时，PD =m −5−(−m 2+6m −5)=m 2−5m =4，解得m 1=5+√412，m 2=5−√412，综上所述，P 点的横坐标为4或5+√412或5−√412；②作AN ⊥BC 于N ，NH ⊥x 轴于H ，作AC 的垂直平分线交BC 于M 1，交AC 于E ，如图2， ∵M 1A =M 1C ， ∴∠ACM 1=∠CAM 1， ∴∠AM 1B =2∠ACB ， ∵△ANB 为等腰直角三角形， ∴AH =BH =NH =2， ∴N(3,−2)，易得AC 的解析式为y =5x −5，E 点坐标为(12,−52)， 设直线EM 1的解析式为y =−15x +b ，把E(12,−52)代入得−110+b =−52，解得b =−125， ∴直线EM 1的解析式为y =−15x −125，解方程组{y =x −5y =−15x −125得{x =136y =−176，则M 1(136,−176)； 在直线BC 上作点M 1关于N 点的对称点M 2，如图2，则∠AM 2C =∠AM 1B =2∠ACB ，设M 2(x,x −5)， ∵3=136+x 2，∴x =236，∴M 2(236,−76)，综上所述，点M的坐标为(136,−176)或(236,−76).解析：(1)利用一次函数解析式确定C(0,−5)，B(5,0)，然后利用待定系数法求抛物线解析式；(2)①先解方程−x2+6x−5=0得A(1,0)，再判断△OCB为等腰直角三角形得到∠OBC=∠OCB= 45°，则△AMB为等腰直角三角形，所以AM=2√2，接着根据平行四边形的性质得到PQ=AM=2√2，PQ⊥BC，作PD⊥x轴交直线BC于D，如图1，利用∠PDQ=45°得到PD=√2PQ=4，设P(m,−m2+ 6m−5)，则D(m,m−5)，讨论：当P点在直线BC上方时，PD=−m2+6m−5−(m−5)=4；当P点在直线BC下方时，PD=m−5−(−m2+6m−5)，然后分别解方程即可得到P点的横坐标；②作AN⊥BC于N，NH⊥x轴于H，作AC的垂直平分线交BC于M1，交AC于E，如图2，利用等腰三角形的性质和三角形外角性质得到∠AM1B=2∠ACB，再确定N(3,−2)，AC的解析式为y=5x−5，E点坐标为(12,−52)，利用两直线垂直的问题可设直线EM1的解析式为y=−15x+b，把E(12,−52)代入求出b得到直线EM1的解析式为y=−15x−125，则解方程组{y=x−5y=−15x−125得M1点的坐标；作直线BC上作点M1关于N点的对称点M2，如图2，利用对称性得到∠AM2C=∠AM1B=2∠ACB，设M2(x,x−5)，根据中点坐标公式得到3=136+x2，然后求出x即可得到M2的坐标，从而得到满足条件的点M的坐标．本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角的判定与性质和平行四边形的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；会运用分类讨论的思想解决数学问题．。

2020年和平区一模化学试卷可能用到的相对原子质量：H1C12N14O16Na23Mg24S32Cl35.5K39Ca40Mn55Fe56Cu64Zn65Ag108Ba137一、选择题（本大题共10小题，每小题2分，共20分。

每小题给出的四个选项中，只有一个最符合题意)1.下列实验不涉及化学变化的是A B C D2.人类生存需要清新的空气。

下列一般不会造成空气污染的是A.人工降雨B.燃放烟花C.焚烧垃圾D.汽车尾气3.下列实验操作正确的是A.点燃酒精灯B.稀释浓硫酸C.测溶液的pHD.制取氧气4.认识燃烧原理可以利用和控制燃烧。

下列说法不正确的是A.空气中混有可燃性气体，在有限空间里遇明火可能发生爆炸B.用煤炭烧锅炉时不断鼓入空气，可使煤炭燃烧更剧烈、更充分C.实验桌上少量酒精着火时可用湿布盖灭，是因为降低了酒精的着火点D.森林起火时，可在大火蔓延线路游砍掉一片树木，建立隔离带灭火5.下列说法不正确的是A.细铁丝在氧气中燃烧时，火星四射，生成黑色固体B.红磷在空气中燃烧产生大量的白雾C.硫在氧气中燃烧生成有刺激性气味的气体D.少量氯化铵与少量熟石灰粉未混合、研磨，放出刺激性气味气体6.近期，英国《自然》杂志利发了材料领域的最新研究成果——科学家找到了接近常温的超导材料“超氢化镧”。

下列有关衡的说法错误的是A.镧是金属元素B.元素符号是LaC.中子数是57D.相对原子质量是138.97.如图表示元素的化合价与物质类别关系，若它表示氨元素的部分关系图，则下列说法错误的是A.A点对应的物质类别是单质B.B点表示物质的化学式为NOC.某化合物的化学式为KNO3，它代表的点是FD.写出由D点表示的物质与水发生反应生成的化学方程式：3NO2+H2O=2HNO3+NO8.下列课本实验中，说法正确的是A.测定空气中氧气含量的实验中，可以用硫粉替代红磷B.过滤时，滤纸要紧贴漏斗内壁C.蒸发食盐水时，待蒸发皿内水分蒸干后，才停止加热D.电解水实验中，加入的CuSO4做为催化剂9.下列图像分别对应四个变化过程，不能正确反映对应变化关系的是A B C DA.气体物质的溶解度与温度和压强的关系B.向等质量的氧化锌和氢氧化锌中分别加入相同浓度的稀盐酸至过量C.加热一定质量的氧酸钾和二氧化锰的混合物D.向一定量的盐酸和硫酸钾混合溶液中不断滴加氢氧化钡溶液11.在2A+3B=C+2D反应中，36g A与56g B恰好完全反应生成28g C和一定量的D、若C的相对分子质量为14，则C和D的相对分子质量之比为A.7：1B.7：8C.7：16D.7：32二、选择题（本大题共5小题，每小题2分，共10分。

2020年辽宁省沈阳市和平区中考化学一模试卷一、单选题（本大题共13小题，共39.0分）1.下列变化中，属于化学变化的是()A. 干冰升华B. 钢铁锈蚀C. 汽油挥发D. 电灯发光2.人类的衣、食、住、行都离不开化学，下列化工产品都是重要的材料。

其中属于复合材料的是()A. 钢筋混凝土B. 玻璃C. PE塑料袋D. 铜丝3.下列做法科学的是()A. 用嘴吹灭酒精灯B. 锅内的油着火时，用水浇灭C. 高层建筑内发生火灾时，人们应乘电梯快速下楼D. 逃离浓烟密布的火灾现场时．人应俯身并用湿毛巾掩盖口鼻4.糖醋鱼是百姓喜爱的家常菜。

制作时用到的下列原料，富含蛋白质的是()A. 草鱼B. 白糖C. 淀粉D. 植物油5.下列物质不属于合金的是()A. 青铜B. 硬铝C. 不锈钢D. 氧化铁6.下列实验操作正确的是()A. 铁丝在氧气中燃烧B. 测溶液pHC. 量筒读数D. 称量固体氢氧化钠7.2013年6月5日“世界环境日”的主题是“思前、食后、厉行节约”，低碳环保的意识需深入人心，并付之行动．下列做法不符合低碳环保的理念的是()A. 骑自行车上学B. 尽量少开空调C. 提倡纸张双面使用D. 电器长期处于待机状态8.如图表示的是某化学反应的微观反应过程，其中、表示两种原子，框图ABC为该反应的三个过程，依据该图，下列选项的说法正确的是()A. 该反应属于化合反应B. 该反应中原子的种类不变C. 框图B中的粒子为分子D. 该反应过程中有新的原子生成9.有三个集气瓶中分别装有空气、氧气、二氧化碳三种无色气体，为了把它们一次鉴别开来最好的方法是A. 将带火星的木条放在集气瓶口B. 将燃着的木条伸入集气瓶中C. 分别加入适量的石灰水D. 将带火星的木条放在集气瓶中10.如图所示a、b、c、d四个点，表示可燃物最容易着火的点是()A. a点B. b点C. c点D. d点11.下列四个实验方案的设计中，方案1合理、方案2不合理的是()选项A B C D实验目的除去氢氧化钠中少量的碳酸钠清洗铁制品表面的铁锈鉴别稀盐酸和氯化钠溶液检验一氧化碳中是否混有二氧化碳气体方案1加水溶解加适量稀盐酸加锌粒点燃方案2加稀硫酸用水洗涤加石蕊溶液通入澄清石灰水A. AB. BC. CD. D12.铁画是以低碳钢为主料，经锻打、焊接、酸洗和喷漆等多道工艺制成．下列叙述不正确的是()A. 低碳钢具有延展性B. 给铁画喷漆既美观又防锈蚀C. 制作铁画的多道工艺均属于物理变化D. 制铁画的原料生锈后可用稀盐酸清洗13.某化合物4.6g完全燃烧，生成8.8g二氧化碳和5.4g水，则该化合物的组成中()A. 只含碳、氢元素B. 只含氢、氧元素C. 含有碳、氢元素，可能含氧元素D. 含碳、氢、氧三种元素二、简答题（本大题共3小题，共26.0分）14.结合钠、氯元素在元素周期表中的信息及A、B、C三种粒子的结构示意图，回答下列问题。

辽宁省沈阳市和平区2020年中考物理一模试卷一、单选题1. 下列估测中，和实际数据最接近的是（ ）A . 考生步入考场的速度约为4km/hB . 一本初中物理教材受到的重力约为30NC . 一标准大气压最多能托起 760mm 高的水柱D . 电视机正常工作时的电功率约为8W2. 如图所示的光现象中，由于光的直线传播形成的是（ ）A .水中倒影 B .雨后彩虹 C .海市蜃楼D .金环日食3. 如图，在探究什么因素决定声音的响度时，将正在发声的音叉轻触系在细绳上的乒乓球，这是为了（ ）A . 使音叉的振动尽快停下来B . 将音叉的震动转换为小球的振动C . 使音叉振动频率增大D . 使声波被多次反射形成回声4. 如图，两个完全相同的木块A 和B 叠放在水平木质桌面上。

在5N 的水平拉力F 的作用下，木块A 、B 一起向右做匀速直线运动，空气阻力忽略不计，则下列说法正确的是（ ）A . A 受到的支持力和A 对B 的压力是一对平衡力 B . B 受到的重力和桌面对B 的支持力是一对平衡力C . 桌面对B 的摩擦力为5ND . 桌面比木块A 和B 的表面粗糙5. 小虎用如图所示装置“探究影响动能大小的因素”，在高度为h 的光滑斜槽顶端，将质量不同的钢球由静止释放，观察水平长木板上的木块被撞动的距离，则下列说法正确的是（ ）A . 质量大的钢球达到水平木板的初速度大B . 本实验必须选择光滑的长木板C . 本实验可探究木块的动能跟质量大小的关系D . 质量大的钢球撞动木块运动的距离远6. 防控疫情期间，为了严格控制区分外来车辆出入小区，很多小区装备了门禁系统，内部车辆可以被自动开关识别并启动横杆，外部车辆需要保安闭合手动开关启动横杆，下列模拟电路中符合门禁系统要求的是（ ）A .B .C .D .二、多选题7. 小虎分别用密度为ρ、ρ的两种物质制成形状和体积均相同的甲、乙两个长方体，重力分别为G 、G ，将它们置于水平桌面上，此时它们对桌面的压强相等。

本试卷分为第Ⅰ卷（选择题）、第Ⅱ卷两部分。

第Ⅰ卷为第1页至第4页，第Ⅱ卷为第5页至第8页。

试卷满分120分。

考试时间120分钟。

答卷前，请你务必将自己的姓名、考生号、考点校、考场号、座位号填写在“答题卡”上，并在规定位置粘贴考试用条形码。

答题时，务必将答案涂写在“答题卡”上，答案答在试卷上无效。

考试结束后，将本试卷和“答题卡”一并交回。

祝你考试顺利!第Ⅰ卷注意事项：1．每题选出答案后，用2B铅笔把“答题卡”上对应题目的答案标号的信息点涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号的信息点。

2．本卷共11题，共27分。

一、（本大题共11小题，共27分。

1～4小题，6～7小题，每题2分；5小题，8～11小题，每题3分）1．下面给加点字的注音，完全正确的一项是A．真谛．（dì）哺．育（bǔ）追溯．（shuò）矫．揉造作（jiǎo）B．窈．窕（yǎo）热忱．（chén）恪．守（kè）鲜．为人知（xiǎn）C．拂．晓（fú）绮．丽（qǐ）桑梓．（xīn）梦寐．以求（mèi）D．矜．持（jīn）卓．越（zhuó）惬．意（qiè）开卷．有益（juǎn）2．依次填入下面句中横线处的词语，最恰当的一项是“我们的征途是星辰大海”是纪录片《智慧中国Ⅲ：前沿科学》中的一条弹幕，也是中国科学家心中坚守的。

纪录片带领观众中国科研基地，身临其境感受科技带来的震撼与感动。

主持人与科学家展开深度对话，辅之生动形象的动画剪辑，将科学原理娓娓道来，使纪录片兼具科普性和趣味性。

纪录片不仅中国丰硕的科技成果，同时也致力于传递崇高科学精神。

A．信心探访体现B．信心探求展现C．信念探访展现D．信念探求体现3．下面句子有语病的一项是①作为一档旨在弘扬民族文化的节目《中国地名大会》以地名知识为载体，从地理、历史、语言、文学、民俗等各个角度全方位展现中华大地的万千风貌。

中考数学一模试卷一、选择题（本大题共10小题，共20.0分）1.-的相反数是（）A. 2B. -2C. -D.2.如图是一个正方体纸盒的展开图每个面上都标注了字母或数字，在正方体展开前标注a的面的对面上所标注的数字是（）A. 3B. 4C. 5D. 63.如图，AB∥DF，AC⊥CE于C，BC与DF交于点E，若∠A＝20°，则∠CEF等于（）A. 110°B. 100°C. 80°D. 70°4.在一个暗箱里放有a个除颜色外其它完全相同的球，这a个球中红球只有3个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在25%，那么可以推算出a大约是（）A. 12B. 9C. 4D. 35.把不等式组：的解集表示在数轴上，正确的是（）A. B.C. D.6.下列运算中，正确的是（）A. a4•a2=a8B. a10÷a2=a5C. （-3ab） 2=9a2b2D. （a-b） 2=a2-b27.关于x的一元二次方程x2-2x+1=0的根的情况是（）A. 有两个不相等的实数根B. 有两个相等的实根C. 没有实数根D. 不能确定8.某班体育委员统计了全班45名同学一周的体育锻炼时间（单位：小时），并绘制了如图所示的折线统计图，下列说法中错误的是（）A. 众数是9B. 中位数是9C. 平均数是9D. 锻炼时间不低于9小时的有14人9. 已知三点P 1（x 1，y 1），P 2（x 2，y 2），P 3（1，-2）都在反比例函数的图象上，若x 1＜0，x 2＞0，则下列式子正确的是（ ） A. y 1＜y 2＜0 B. y 1＜0＜y 2 C. y 1＞y 2＞0 D. y 1＞0＞y 2 10. 某市在旧城改造过程中，需要整修一段全长2400m 的道路．为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8小时完成任务．求原计划每小时修路的长度．若设原计划每小时修路xm ，则根据题意可得方程（ ）A.B.C.D.二、填空题（本大题共6小题，共18.0分）11. 分解因式：3a 2-3=______．12. 世界文化遗产长城总长约为6700000m ，将6700000用科学记数法表示应为______． 13. 用同样大小的黑色棋子按图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子______枚．（用含n 的代数式表示）14. 如图，菱形ABCD 中，点E 是对角线AC 上一点，BE 的延长线交边CD 于点F 若∠1+∠2=75°，则∠3的度数为______．15. ⊙O 的半径为1，OP =2，∠MPO =60°，将射线PM 绕点P 旋转α度（0＜α＜180°）得到射线PN ，若直线PN 恰好与⊙O 相切，则α的值为______．16. 如图，矩形ABCD 中，由8个面积均为1的小正方形组成的L 型模板如图放置，则矩形ABCD 的周长为______．三、解答题（本大题共9小题，共82.0分）17.计算：（-2019）0+|-2|-（）-2+3tan30°18.将分别标有数字1，2，3的三张卡片（卡片除所标注数字外其他均相同）洗匀后，背面朝上放在桌面上．（1）随机地抽取一张卡片，直接写出抽到的卡片所标数字是奇数的概率；（2）随机地抽取一张卡片将卡片上标有的数字作为十位上的数字（不放回），再随机地抽取一张卡片，将卡片上标有的数字作为个位上的数字，用列表或树状图的方法求组成的两位数恰好是“32”的概率．19.如图，在平行四边形ABCD中，AE，BF分别平分∠DAB和∠ABC，交边CD于点E，F，线段AE，BF相交于点M．（1）求证：AE⊥BF；（2）若EF＝AD，则BC：AB的值是____．20.为了解某市市民绿色出行”方式的情况某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．根据以上信息，回答下列问题：（1）参与本次问卷调查的市民共有______人，其中选择B类的人数有______人，在扇形统计图中，A类所对应的扇形的圆心角度数是______度；（2）请根据以上信息，直接在答题卡中补全条形统计图；（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为绿色出行”方式，根据抽样调查的结果，请估计该市“绿色出行”方式的人数．21.如图，某中心广场灯柱AB（垂直于地面BC）被钢缆CD定，已知CB=3.6m，且sin∠DCB=．（1）求钢缆CD的长度；（2）若AD=2m，灯的顶端E距离A处1.6m，且∠EAB=120°，求灯的顶端E到地面的距离．22.如图，在R△ABC中，∠ACB=90°，以BC为直径的⊙O交AB于点D，点E是AC的中点，连接DC，DE．（1）求证：DE是⊙O的切线；（2）若AB=2BC=8，求的长．23.国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴20元，种粮大户老王今年种了50亩地，计划明年再多承租50～150亩土地种粮以增加收入，考虑各种因素，预计明年每亩种粮成本y（元）与种粮面积x（亩）之间满足一次函数关系其图象如图所示．（1）今年老王种粮可获得补贴______元；（2）求y与x之间的函数关系式；（3）若老王明年每亩的售粮收入能达到2100元，设老王明年种粮利润为w（元）（种粮利润=售粮收入-种粮成本+种粮补贴）．①求老王明年种粮利润w（元）与种粮面积x（亩）之间的函数关系式；②当种粮面积为多少亩时，老王明年种粮利润最高？24.如图1，在正方形ABCD中，AD=6，点P是对角线BD上任意一点，连接PA，PC，过点P作PE⊥PC交直线AB于点E．（1）求证：PC=PE；（2）延长AP交直线CD于点F．①如图2，若点F是CD的中点，求△APE的面积；②若△APE的面积是，则DF的长为______；（3）如图3，点E在边AB上，连接EC交BD于点M，作点E关于BD的对称点Q，连接PQ，MQ，过点P作PN∥CD交EC于点N连接QN，若PQ=5，MN=，则△MNQ的面积是______．25.如图1，抛物线y=ax2+c与x轴，y轴的正半轴分别交于点B（4，0）和点C（0，4），与x轴负半轴交于点A，动点M从点A出发沿折线AC-B向终点B匀速运动，将线段OM绕点O顺时针旋转60°得到线段ON，连接MN．（1）求抛物线y=ax2+c的函数表达式；（2）如图2，当点N在线段AC上时，求证：AM=CN；（3）当点N在线段BC上时，直接写出此时直线MN与抛物线交点的纵坐标；（4）设BN的长度为n，直接写出在点M移动的过程中，n的取值范围．答案和解析1.【答案】D【解析】解：-的相反数是，故选：D．根据一个数的相反数就是在这个数前面添上“-”号，求解即可．本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．不要把相反数的意义与倒数的意义混淆．2.【答案】A【解析】解：正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，所以在正方体展开前标注a的面的对面上所标注的数字是3．故选：A．由平面图形的折叠及立体图形的表面展开图的特点解题．本题考查了正方体相对两个面上的文字．注意正方体的空间图形，从相对面入手，分析及解答问题．3.【答案】A【解析】解：如图，∵AC⊥BC于C，∴△ABC是直角三角形，∴∠ABC=180°-∠A-∠C=180°-20°-90°=70°，∴∠ABC=∠1=70°，∵AB∥DF，∴∠1+∠CEF=180°，即∠CEF=180°-∠1=180°-70°=110°．故选A．本题比较简单，考查的是平行线的性质及直角三角形的性质．由AC⊥BC于C得到△ABC是直角三角形，然后可以求出∠ABC=180°-∠A-∠C=180°-20°-90°=70°，而∠ABC=∠1=70°，由于AB∥DF可以推出∠1+∠CEF=180°，由此可以求出∠CEF．4.【答案】A【解析】解：∵摸到红球的频率稳定在25%，∴=25%，解得：a=12．故选：A．摸到红球的频率稳定在25%，即=25%，即可即解得a的值．本题考查：频率、频数的关系：频率=．5.【答案】B【解析】解：解不等式①，得x＞-1，解不等式②，得x≤1，所以不等式组的解集是-1＜x≤1．故选：B．分别求出各个不等式的解集，再求出这些解集的公共部分即可．不等式组的解集在数轴上表示的方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画．＜，≤向左画）．在表示解集时“≥”，“≤”要用实心圆点表示．“＜”，“＞”要用空心圆圈表示．6.【答案】C【解析】解：A、a4•a2=a6，故本选项错误；B、a10÷a2=a8，故本选项错误；C、（-3ab） 2=9a2b2，故本选项正确；D、（a-b） 2=a2-2ab+b2，故本选项错误；故选：C．利用同底数幂的乘法法则判断A；利用同底数幂的除法法则判断B；利用积的乘方法则判断C；利用完全平方公式判断D．本题考查了同底数幂的乘法与除法、积的乘方、完全平方公式，熟练掌握运算法则和乘法公式是解题的关键．7.【答案】B【解析】解：∵a=1，b=-2，c=1，∴△=b2-4ac=（-2）2-4×1×1=0，∴方程有两个相等的实数根．故选：B．把a=1，b=-2，c=1代入△=b2-4ac，然后计算△，最后根据计算结果判断方程根的情况．本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．8.【答案】D【解析】解：由图可知，锻炼9小时的有18人，所以9在这组数中出现18次为最多，所以众数是9．把数据从小到大排列，中位数是第23位数，第23位是9，所以中位数是9．平均数是（7×5+8×8+9×18+10×10+11×4）÷45=9，所以平均数是9．锻炼时间不低于9小时的有18+10+4=32，故D错误．故选D．此题根据众数，中位数，平均数的定义解答．此题考查了折线统计图，用到的知识点是平均数、中位数、众数，众数是一组数据中出现次数最多的数，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．平均数是所有数的和除以所有数的个数．9.【答案】D【解析】解：∵点P3（1，-2）都在反比例函数的图象上，∴k=1×（-2）=-2＜0，函数图象在二，四象限，又∵x1＜0，x2＞0，∴P1在第二象限，P2在第四象限，∴y1＞0，y2＜0，∴y1＞0＞y2．故选：D．根据k=xy即横纵坐标相乘得比例系数k，再由反比例函数图象上点的坐标特征即可解答．本题需先求出反比例函数的比例系数．在反比函数中，已知两点的横坐标，比较纵坐标的大小，首先应区分两点是否在同一象限内．10.【答案】A【解析】解：∵原计划用的时间为：，实际用的时间为：，∴可列方程为：，故选：A．关系式为：原计划用的时间-实际用的时间=8，把相关数值代入即可．考查列分式方程；得到关于工作时间的关系式是解决本题的关键．11.【答案】3（a+1）（a-1）【解析】解：3a2-3，=3（a2-1），=3（a+1）（a-1）．故答案为：3（a+1）（a-1）．先提取公因式3，再对余下的多项式利用平方差公式继续分解．本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．12.【答案】6.7×106【解析】解：6 700000=6.7×106，故答案为：6.7×106．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．13.【答案】（3n+1）【解析】【分析】此题考查了平面图形的认识，主要培养学生的观察能力和空间想象能力．解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论．解：第一个图需棋子4；第二个图需棋子4+3=7；第三个图需棋子4+3+3=10；…第n个图需棋子4+3（n-1）=（3n+1）枚．故答案为：（3n+1）．14.【答案】30°【解析】解：∵四边形ABCD为菱形，∴BC=CD，∠BCA=∠DCA，∴△BEC≌△DEC，∴∠EDC=∠1，∵∠1+∠2=75°，∴∠EDC+∠2=75°，∴∠AED=∠EDC+∠2=75°，∴∠BED=2∠AED=150°，∴∠3=30°．故答案为：30°．根据四边形ABCD为菱形得到BC=CD，∠BCA=∠DCA，从而得到△BEC≌△DEC，证得∠EDC=∠1，然后根据∠1+∠2=75°得到∠EDC+∠2=75°，然后利用外角性质得到∠BED=2∠AED=150°，从而求得答案．本题考查了菱形的性质，解题的关键是充分挖掘菱形隐含的条件，难度不大．15.【答案】30°或90°【解析】【分析】当PN与⊙O相切时，可连接圆心与切点，通过构建的直角三角形，求出∠OPN的度数，然后再根据PN的不同位置分类讨论．此题主要考查的是切线的性质，以及解直角三角形的应用；需注意切线的位置有两种情况，不要漏解．【解答】解：如图；①当PN在∠OPM的内部时，设切点为D，连接OD，则∠ODP=90°；Rt△OPD中，OP=2OD，∴∠OPD=30°；∴∠MPN=60°-30°=30°；②当PN在∠OPM的外部时；同①，可求得∠ODP=30°；此时∠MPN=60°+30°=90°；故旋转角α的度数为30°或90°．16.【答案】【解析】解：如图，连接AF，作GH⊥AE于点H，则有AE=EF=HG=4，FG=2，AH=2，∵AG==2，AF==4，∴AF2=AD2+DF2=（AG+GD）2+FD2=AG2+GD2+2AG•GD+FD2，GD2+FD2=FG2∴AF2=AG2+2AG•GD+FG2∴32=20+2×2×GD+4，∴GD=，FD=，∵∠BAE+∠AEB=90°=∠FEC+∠AEB，∴∠BAE=∠FEC，∵∠B=∠C=90°，AE=EF，∴△ABE≌△ECF（AAS），∴AB=CE，CF=BE，∵BC=BE+CE=AD=AG+GD=2+，∴AB+FC=2+，∴矩形ABCD的周长=AB+BC+AD+CD=2BC+AB+CF+DF=2++2++2++=8．故答案为：8．连接AF，作GH⊥AE于点H，则有AE=EF=HG=4，FG=2，AH=2，根据矩形的性质及勾股定理即可求得其周长．本题利用了矩形的性质和勾股定理及全等三角形的性质求解．17.【答案】解：原式=1+2--4+3×=3--4+=-1．【解析】直接利用零指数幂的性质以及绝对值的性质、负指数幂的性质分别化简得出答案．此题主要考查了实数运算，正确化简各数是解题关键．18.【答案】解：（1）抽到的卡片所标数字是奇数的概率=；（2）画树状图为：共有6种等可能的结果数，其中组成的两位数恰好是“32”的结果数为1，所以组成的两位数恰好是“32”的概率=．【解析】（1）直接利用概率公式求解；（2）画树状图展示所有6种等可能的结果数，再找出组成的两位数恰好是“32”的结本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．\ 19.【答案】解：（1）证明：∵在平行四边形ABCD中，AD∥BC，∴∠DAB+∠ABC=180°，∵AE、BF分别平分∠DAB和∠ABC，∴∠DAB=2∠BAE，∠ABC=2∠ABF，∴2∠BAE+2∠ABF=180°，即∠BAE+∠ABF=90°，∴∠AGB=90°，∴AE⊥BF；（2）.【解析】解答：（1）见答案；（2）解：∵在平行四边形ABCD中，CD∥AB，∴∠DEA=∠EAB，又∵AE平分∠DAB，∴∠DAE=∠EAB，∴∠DEA=∠DAE，∴DE=AD，同理可得，CF=BC，又∵在平行四边形ABCD中，AD=BC，∴DE=CF，∴DF=CE，∵EF=AD，∴BC=AD=5EF，∴DE=5EF，∴DF=CE=4EF，∴AB=CD=9EF，∴BC：AB=5：9；故答案为：．【分析】（1）想办法证明∠BAE+∠ABF=90°，即可推出∠AMB=90°即AE⊥BF；（2）想办法证明DE=AD，CF=BC，再利用平行四边形的性质AD=BC，证出DE=CF，得出DF=CE，由已知得出BC=AD=5EF，DE=5EF，求出DF=CE=4EF，得出AB=CD=9EF，即可得出结果．本题考查平行四边形的性质、角平分线的定义，等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．20.【答案】（1）800 240 90（2）条形统计图如图所示．（3）12×80%=9.6（万人），答：估计该市“绿色出行”方式的人数为9.6万人．【解析】解：（1）200÷25%=800（人），800÷30%=240（人），360°×（1-25%-30%-14%-6%）=90°，故答案为：800，240，90．（2）见答案（3）见答案【分析】（1）根据组人数以及百分比求出总人数即可解决问题．（2）求出A组人数画出条形图即可．（3）利用样本估计总体的思想解决问题即可．本题考查条形统计图，扇形统计图，样本估计总体的思想等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．21.【答案】解：（1）∵sin∠DCB=，∴cos∠DCB=，即=，∴CD=6m．（2）∵sin∠DCB=，CD=6m，∴BD=4.8m．过点A作AM∥BC，过点E作EF⊥AM于点F，如图所示．在Rt△AEF中，∠AFE=90°，∠EAF=∠EAB-90°=30°，AE=1.6m，∴EF=AE•sin∠EAF=0.8m，∴灯的顶端E到地面的距离=EF+AD+BD=7.6m．【解析】（1）由sin∠DCB=可得出cos∠DCB=，结合CB的长度即可求出CD的长度；（2）由sin∠DCB=，CD=6m，可得出BD的长度，过点A作AM∥BC，过点E作EF⊥AM于点F，在Rt△AEF中，通过解直角三角形可求出EF的长度，进而可得出灯的顶端E 到地面的距离．本题考查了解直角三角形的应用，解题的关键是：（1）由sin∠DCB=，找出=；（2）通过解直角三角形求出EF的长度．22.【答案】解：（1）连接OD．∵AE=EC，OB=OC，∴OE∥AB，∴OE⊥CD，∵OD=OC，∴∠DOE=∠COE，在△EOD和△EOC中，，∴△EOD≌△EOC（SAS），∴∠EDO=∠ECO=90°，∴OD⊥DE，∴DE是⊙O的切线；（2）∵∠ACB=90°，∵AB=2BC=8，∴∠ABC=60°，∵OC=OB，∴∠DOB=60°，∴的长==π．【解析】（1）欲证明DE是切线，只要证明OD⊥DE即可；（2）连接OD，求出圆心角∠DOB，根据弧长公式，即可解决问题．本题考查了切线的判定和性质，圆周角定理，全等三角形的判定和性质，弧长的计算，熟练掌握切线的判定定理是解题的关键．23.【答案】（1）1000；（2）假设函数解析式为y=kx+b，根据图象可以得出：图象过（205，1000），（275，1280），将两点代入解析式得出：，解得：，则y与x之间的函数关系式为：y=4x+180；（3）根据题意得出：W=（2100-y）x+20x=[2100-（4x+180）]x+20x=-4x2+1940x，则x=-=-=242.5时，∵x≥50+50，x≤50+150，∴100≤x≤200，∴当x=200时，W最大=228000（元）．当种粮面积为200亩时，总收入最高为228000元．【解析】解：（1）∵国家和地方政府为了提高农民种粮的积极性，每亩地每年发放种粮补贴20元，种粮大户老王今年种了50亩地，∴今年老王种粮可获得补贴20×50=1000元；故答案为：1000；（2）见答案；（3）见答案．（1）根据每亩地每年发放种粮补贴20元，种粮大户老王今年种了50亩地，得出老王种粮可获得补贴数目；（2）利用待定系数法求出一次函数解析式即可；（3）根据明年每亩的售粮收入能达到2100元，预计明年每亩种粮成本y（元）与种粮面积x（亩）之间的函数关系为y=4x+180，进而得出W与x的函数关系式，再利用二次函数的最值公式求出即可．此题主要考查了二次函数的应用，一次函数的应用以及待定系数法求一次函数解析式和二次函数的最值问题，根据已知得出W与x的函数关系式是解题关键．24.【答案】（1）证明：如图1，过P作GH⊥AB于G，交CD于H，∵四边形ABCD是正方形，∴AB∥CD，∠BDC=45°，∴GH⊥CD，∴∠EGP=∠PHC=90°，∵PE⊥PC，∴∠EPC=90°，∴∠GEP+∠GPE=∠GPE+∠CPH=90°，∴∠GEP=∠CPH，∵∠BDC=45°，∴△PDH是等腰直角三角形，∴PH=DH=AG，∵AB=CD，∴BG=CH=GP，∴△EGP≌△PHC（AAS），∴PE=PC；（2）解：①过P作GH⊥AB于G，交CD于H，∵F是CD的中点，∴DF=DC=AB，∵DF∥AB，∴△DPF∽△BPA，∴PH=2，PG=4，由（1）知：△EGP≌△PHC，∴EG=PH=DH=AG=2，∴AE=2+2=4，∴S△APE==8；②4 ；（3） .【解析】（1）见答案；（2）解：①见答案；②同理可知：AG=EG=PH=DH，设EG=x，则PG=6-x，S△APE==，x2-6x+=0，（x-3）2=，x1=（舍），x2=，当x=时，PH=，PG=6-=，∵DF∥AB，∴△ABP∽△FDP，∴，∴=，DF=4；故答案为：4；（3）解：如图3，∵点E关于BD的对称点Q，∴PE=PQ=5，BE=BQ，由（1）知：PE=PC，PE⊥PC，∴△PEC是等腰直角三角形，∴CE=5，过Q作QR⊥CE于R，∵∠CRQ=∠CBE=90°，∠RCQ=∠BCE，∴△CQR∽△CEB，∴，∴=，RQ=，∴S△MNQ===，故答案为：．（1）由“AAS”可证△EGP≌△PHC可得结论；（2）①同理作辅助线，证明△DPF∽△BPA，根据相似三角形相似比等于对应高的比得：，计算PH=2，PG=4，从而得AE的长，根据三角形面积公式可得结论；②设EG=x，则PG=6-x，表示三角形APE的面积，得方程：（x-3）2=，解出可得PH的长，证明△ABP∽△FDP，可得DF的长；（3）根据对称的性质得：PE=PQ=5，BE=BQ，由△PEC是等腰直角三角形，得CE=5，计算BE的长，作QR⊥CE于R，证明△CQR∽△CEB，可得RQ的长，由三角形面积公式可得结论．本题是四边形综合题，考查了正方形的性质，全等三角形判定和性质，勾股定理，相似三角形的判定和性质，作辅助线构建△EGP≌△PHC是本题的关键．25.【答案】解：（1）将点B、C代入抛物线，解得c=4，16a+c=0，∴a=-，∴抛物线的解析式为y=-x2+4．（2）令y=0，解得x1=4，x2=-4，∴A（-4，0），∴OA=OC，∠OAC=∠OCA=45°，∵OM=ON，∠MON=60°，∴△OMN为等边三角形，∴∠AMO=∠CNO=120°，∴△AMO≌△CNO（AAS），∴AM=CN．（3）情况一：如图1所示，过点O作OH垂直AC，OQ垂直BC，∴△AOH≌△BOQ（AAS），∴OH=OQ，∵OM=ON，∴△OHM≌△OQN（HL），∴MH=NQ，∴CM=CN，∴△CMO≌△CNO（SAS），∴∠MOC=∠NOC=30°，∴∠MOA=∠NOB=60°，∵∠OMN=∠ONM=60°，∴MN∥x轴，设CE=ME=x，则OE=x，∴x+x=4，∴x=2-2，∴OE=6-2，∴直线MN与抛物线交点的纵坐标为6-2．情况二：当点N再一次落在BC上时，此时M、N都在BC上，则MN与抛物线的交点为点C，∴直线MN与抛物线的交点的纵坐标为4，综上所述：直线MN与抛物线的交点的纵坐标为6-2或4．（4）如图2所示，将△ACB绕点O顺时针旋转60°得到△A′C′B′，∵点M的运动轨迹为AC、BC，当N落A′上时，BN最长，∵A′（-2，2），∴BN最长为4，过点B作B′C′的垂线，此时BN最短，过点E作OB′的垂线，设PE=PB′=y，则OP=y，∴y+y=4，解得y=6-2，∴OE=4-4，BE=8-4，OH=2，∵△OHE∽△BNE，∴，解得BN=-．∴-≤n≤6-2．【解析】（1）代入点B、C的坐标即可解除抛物线的解析式．（2）OM=ON，∠MON=60°，可知△MON为等边三角形，可证明△AMO≌△CNO，则AM=CN．（3）当点N落在线段BC上时，分两种情况讨论，先找到MN，则纵坐标可求．（4）根据点M的运动轨迹，可求出点N的运动轨迹，可以分析出何时BN最长，何时NB最短，则n的范围可知．此题考查了待定系数法求函数解析式及二次函数与几何图形结合的问题，最后一问找到点N的运动轨迹为解题关键．。

2020年和平区九年级教学质量监测（一）物理部分一、选择题（共21分，其中1～6小题为单选题，每小题2分。

7～9小题为多选题，每小题3分，多选、错选不得分，漏选得1分）1、下列估测中，和实际数据最接近的是（）A.考生进入考场的速度约为4Km/hB.一本初中物理教材受到的重力约为30NC.一标准大气压最多托起760mm的水柱D.电视机正常工作时的电功率约为8W2、如图所示的光现象中，由于光的直线传播形成的是（）3、如图，在探究什么因素决定声音的响度时，将正在发生的音叉轻触系在细绳上的乒乓球，这是为了（）A.使音叉的振动尽快停下来B.将音叉的振动转换为小球的振动C.使音叉振动频率增大D.使声波被多次反射形成回声4、如图，两个完全相同的木块A和B叠放在水平木质桌面上。

在5N的水平拉力F的作用下，木块A、B一起向右做匀速直线运动，空气阻力忽略不计，则下列说法正确的是（）A.A受到的支持力和A对B的压力是一对平衡力B.B受到的重力和桌面对B的支持力是一对平衡力C.桌面对B的摩擦力为5ND.桌面比木块A和B的表面粗糙5、小虎用如图所示装置“探究影响动能大小的因素”，在高度为h的光滑斜槽顶端，两质量不同的钢球由静止释放，观察水平长木板上的木块被撞动的距离，则下列说法正确的是（）A.质量大的钢球到达水平木板的初速度大B.本实验必须选择光滑的长木板C.本实验可探究木块的动能跟质量大小的关系D.质量大的钢球撞动木块运动的距离远6、防控疫情期间，为了严格控制区分外来车辆出入小区，很多小区装备了门禁系统，内部车辆可以被自动开关识别并启动横杆，外部车辆需要保安闭合手动开关启动横杆。

下列模拟电路中，符合门禁系统要求的是（）7、小虎分别用密度为ρ甲、ρ乙的两种物质制成形状和体积均相同的甲、乙两个长方体，重力分别为G甲、G乙，将它们置于水平桌面上，此时它们对桌面的压强相等。

接着小虎将两个长方体顺时针旋转90°，如图中虚线所示。