北京将建世界第一大机场9条跑道

76Academic Papers学术交流影响有影响的人北京大兴国际机场对北京市综合交通运输效率的提升作用文／中国人民公安大学 李根摘要：北京市南北交通运输发展不平衡已成为影响综合交通效率的重要因素。

北京大兴国际机场作为国家发展新的动力源、大型综合交通枢纽，可以很大程度上疏解首都国际机场旅客、推动北京市南部经济发展、促进完善北京市南部综合交通基础设施建设，提高综合交通效率，进一步改善市民出行，提升国家形象。

关键字:北京大兴国际机场；北京市；综合交通运输效率北京市是全国政治中心、文化中心、国际交往中心、科技创新中心，也是世界著名古都和现代化国际大都市。

作为国家中心城市、超大城市，交通拥堵等大城市病严重困扰城市发展、市民生活以及国家形象。

业界普遍认为，提升综合交通运输效率，是缓解交通拥堵的有效和必要手段。

多年来，由于北京市南北发展不平衡、南部地区发展不充分，南北综合交通发展也不均衡，导致综合交通效率还有待进一步提高。

而通过建设运营北京大兴国际机场，推动北京市南部经济发展，增加北京市南部对人口的吸引力，促进完善北京市南部综合交通运输设施建设，即可有效提升北京市综合交通运输效率。

1.北京市南北交通运输发展不平衡已成为影响综合交通效率的重要因素党的十九大报告明确指出，中国特色社会主义进入新时代，我国社会主要矛盾已经转化为人民日益增长的美好生活需要与不平衡、不充分的发展之间的矛盾。

这一描述的转变，不但适用于整个中国社会，也同样适用于北京市综合交通运输发展。

北京市综合交通运输，从建国以来的不断建设发展，其主要矛盾已经从供给整体不足转化为整体发展不平衡、局部发展不充分问题，从路不够好、不够用问题转化为综合交图1 2019年8月北京市地铁交通图77TR A M S P O R T C ON S T R UC T I O N & M A N A G E M E N T交通建设与管理 影响有影响的人04. AUGUST . 2019通运输效率不高的问题，其中北京市南北发展不平衡问题已呈现显著特点。

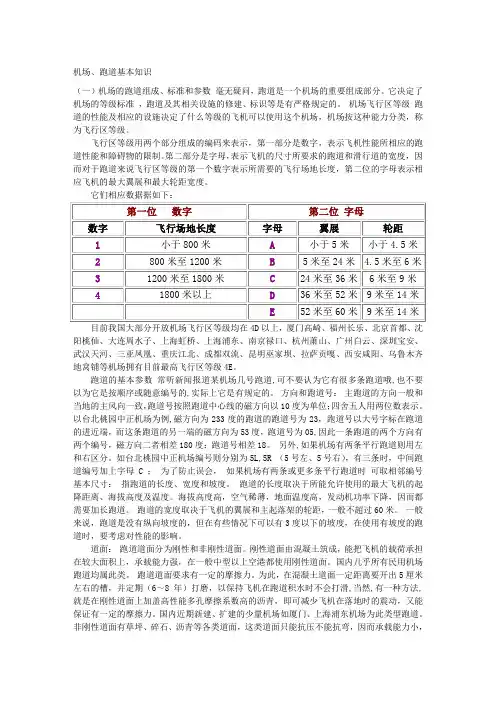
机场、跑道基本知识（一）机场的跑道组成、标准和参数毫无疑问，跑道是一个机场的重要组成部分。

它决定了机场的等级标准，跑道及其相关设施的修建、标识等是有严格规定的。

机场飞行区等级跑道的性能及相应的设施决定了什么等级的飞机可以使用这个机场，机场按这种能力分类，称为飞行区等级。

飞行区等级用两个部分组成的编码来表示，第一部分是数字，表示飞机性能所相应的跑道性能和障碍物的限制。

第二部分是字母，表示飞机的尺寸所要求的跑道和滑行道的宽度，因而对于跑道来说飞行区等级的第一个数字表示所需要的飞行场地长度，第二位的字母表示相应飞机的最大翼展和最大轮距宽度。

它们相应数据据如下：阳桃仙、大连周水子、上海虹桥、上海浦东、南京禄口、杭州萧山、广州白云、深圳宝安、武汉天河、三亚凤凰、重庆江北、成都双流、昆明巫家坝、拉萨贡嘎、西安咸阳、乌鲁木齐地窝铺等机场拥有目前最高飞行区等级4E。

跑道的基本参数常听新闻报道某机场几号跑道,可不要认为它有很多条跑道哦,也不要以为它是按顺序或随意编号的,实际上它是有规定的。

方向和跑道号：主跑道的方向一般和当地的主风向一致，跑道号按照跑道中心线的磁方向以10度为单位；四舍五人用两位数表示。

以台北桃园中正机场为例,磁方向为233度的跑道的跑道号为23，跑道号以大号字标在跑道的进近端，而这条跑道的另一端的磁方向为53度，跑道号为05,因此一条跑道的两个方向有两个编号，磁方向二者相差180度；跑道号相差18。

另外,如果机场有两条平行跑道则用左和右区分。

如台北桃园中正机场编号则分别为5L,5R （5号左、5号右），有三条时，中间跑道编号加上字母 C ；为了防止误会，如果机场有两条或更多条平行跑道时可取相邻编号基本尺寸：指跑道的长度、宽度和坡度。

跑道的长度取决于所能允许使用的最大飞机的起降距离、海拔高度及温度。

海拔高度高，空气稀薄，地面温度高，发动机功率下降，因而都需要加长跑道。

跑道的宽度取决于飞机的翼展和主起落架的轮距，一般不超过60米。

2022-2023学年第二学期初三数学测试题一、选择题（本题共16分，每小题2分）1. 北京大兴国际机场目前是全球建设规模最大的机场，2019年9月25日正式通航，预计到2022年机场旅客吞吐量将达到45000000人次，将45000000用科学记数法表示为（ ）A.64510´ B.74.510´ C.84.510´ D.80.4510´【答案】B 【解析】【分析】根据科学记数法的表示方法，进行表示即可．【详解】将数据45000000用科学记数法可表示为：74.510´．故选B ．【点睛】本题考查科学记数法，熟练掌握科学记数法的表示方法：()11100£´<n a a ，是解题的关键．2. 如图是某个几个几何体的三视图，该几何体是（ ）A. 圆锥B. 圆柱C. 长方体D. 正三棱柱【答案】B 【解析】【分析】由主视图和俯视图确定是柱体，由左视图确定具体形状.【详解】解：从主视图和俯视图可以确定是柱体，然后由左视图可以确定此物体为一个横放着的圆柱.故答案为：B.【点睛】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．3. 正六边形的每个内角度数为（ ）A. 60° B. 120°C. 135°D. 150°【答案】B【解析】【分析】利用多边形的内角和为（n ﹣2）•180°求出正六边形的内角和，再结合其边数即可求解．【详解】解：根据多边形的内角和定理可得：正六边形的每个内角的度数＝（6﹣2）×180°÷6＝120°．故选：B ．【点睛】本题考查了多边形，解决本题的关键是利用多边形的内角和公式即可解决问题．4. 如图，点A 是数轴上一点，点A ，B 表示的数互为相反数，则点B 表示的数可能是（ ）A. 0B. 1C. 1.5D. 2.5【答案】C 【解析】【分析】点A 所表示的数在-2和-1之间，根据相反数的意义，可求出点B 所表示的数在1和2之间，据此即可判断．【详解】解：∵点A 所表示的数在-2和-1之间，∴点B 所表示的数在1和2之间，0、1、1.5、2.5四个数中，只有1.5符合题意，故选：C ．【点睛】本题考查了互为相反数的意义，只有符号不同的两个数互为相反数，在数轴上在原点的两侧，到原点距离相等的两个数互为相反数．5. 如图，直线//AB CD ，AB 平分EAD Ð，1100Ð=°，则2Ð的度数是（ ）A. 60°B.50°C. 40°D. 30°【答案】C 【解析】【分析】根据邻补角求出=80EAD а，由AB 平分EAD Ð可知=40EAB а，根据//AB CD 得到2=40EAB Ð=а．【详解】解：∵1180EAD Ð+Ð=°，1100Ð=°，∴=80EAD а，∵AB 平分EAD Ð，∴1=402EAB EAD ÐÐ=°，∵//AB CD ，∴2=40EAB Ð=а，故选：C ．【点睛】此题考查了邻补角和平行线的性质、角平分线的定义．解题关键是掌握相关定义和性质．6. 如图，将一个正方形纸片沿图中虚线剪开，能拼成下列四个图形，其中是中心对称图形的是（ ）A. B.C. D.【答案】B 【解析】【分析】根据拼成的四个图形是否存在中心对称点，即可判断图形是否为中心对称图形．【详解】解：依照中心对称图形的特征：若图形存在中心对称点，沿中心对称点旋转180°后可与原图形重合．选项A 图形无中心对称点，故不是中心对称图形，不符合题意；选项B 图形有中心对称点，故是中心对称图形，符合题意；选项C 图形无中心对称点，故不是中心对称图形，不符合题意；选项D 图形无中心对称点，故不是中心对称图形，不符合题意；故选：B ．【点睛】本题考查中心对称图形的性质特征，熟练掌握相关知识是解题的关键．7. 某餐厅规定等位时间达到30分钟（包括30分钟）可享受优惠．现统计了某时段顾客的等位时间t （分钟），如图是根据数据绘制的统计图．下列说法正确的是（ ）A. 此时段有1桌顾客等位时间是40分钟B. 此时段平均等位时间小于20分钟C. 此时段等位时间的中位数可能是27D. 此时段有6桌顾客可享受优惠【答案】D 【解析】【分析】根据直方图，逐一进行判断即可．【详解】解：A 、由直方图可知：有1桌顾客等位时间在35至40分钟，不能说是40分钟，选项错误，不符合题意；B 、平均等位时间为：1101515202025253030353540261295124.235222222++++++æö´+´+´+´+´+´»ç÷èø（分钟），大于20分钟，选项错误，不符合题意；C 、因为样本容量是35，中位数落在2025t £<之间，选项错误，不符合题意；D 、30分钟以上的桌数为516+=，选项正确，符合题意．故选：D ．【点睛】本题考查频数分布直方图，求平均数，中位数．解题的关键是从统计图中有效的获取信息．8. 如图，一架梯子AB 靠墙而立，梯子顶端B 到地面的距离BC 为2m ，梯子中点处有一个标记，在梯子顶端B 竖直下滑的过程中，该标记到地面的距离y 与顶端下滑的距离x 满足的函数关系是（ ）A. 正比例函数关系B. 一次函数关系C . 二次函数关系 D. 反比例函数关系【答案】B 【解析】【分析】过梯子中点O 作OD ^地面于点D ．由题意易证A OD A B C ¢¢¢V :V ，即得出A O OD AB BC ¢=¢¢¢．由O 为中点，2B C x ¢-，OD y =，即可推出122y x=-，即112y x =-+．即可选择．【详解】如图，过梯子中点O 作OD ^地面于点D ．∴90ODA B CA ¢¢¢Ð=Ð=°，又∵OA D B A C ¢¢¢Ð=Ð，∴A OD A B C ¢¢¢V :V ，∴A O OD A B B C¢=¢¢¢，根据题意O 为中点，2B C x ¢=-，OD y =．∴122y x =-，整理得：112y x =-+．故y 与x 的函数关系为一次函数关系．故选B ．【点睛】本题考查三角形相似的判定和性质以及一次函数的实际应用．作出辅助线构成相似三角形是解答本题的关键．二、填空题（本题共16分，每小题2分）9.在实数范围内有意义，则x 的取值范围是 _____．【答案】12x ³【解析】【分析】根据二次根式有意义的条件即可求出答案．实数范围内有意义，∴210x -³，解得12x ³，故答案为12x ³．【点睛】本题考查二次根式有意义的条件、解一元一次不等式，解题的关键是熟练运用二次根式有意义的条件．10. 分解因式：2288x x ++=___________．【答案】22()2x +【解析】【分析】直接提取公因式2，再利用完全平方公式分解因式得出答案．【详解】解：2288x x ++=2（x 2+4x+4）=22()2x +．故答案为：22()2x +．【点睛】此题主要考查了提取公因式法以及公式法分解因式，正确应用公式是解题关键．11. 方程1﹣12x +＝0的解为 _____．【答案】=1x -【解析】【分析】先把分式方程化为整检验即可得到答案．【详解】解：1102x -=+去分母得210x +-=，解得=1x -，经检验=1x -是原方程的解，∴原方程的解为=1x -．【点睛】本题主要考查了解分式方程，熟知解分式方程的方法是解题的关键．12. 已知点A (1，2)，B 在反比例函数()0k y x x =>的图象上，若OA=OB ，则点B 的坐标为_________．【答案】（2，1）【解析】【分析】根据点A ，B 关于y =x （y -x =0）的对称，求解即可【详解】解：∵点A (1，2)，B 在反比例函数()0k y x x =>的图象上，OA=OB ，∴点A ，B 关于直线y =x （y -x =0）的对称，设点（1，2）关于直线y =x （y -x =0）的对称点设为（a ，b ）由两点中点在直线y =x 上及过两点的直线垂直直线y =x （斜率之积为-1）可以得到：1222(2)(1)1a bb a ++ì=ïíï--=-î，解得：a =2，b =1，∴点B 的坐标为（2,1）故答案为：（2，1）【点睛】本题考查了反比例函数图象上点的坐标特征，利用已知条件得出：点A ，B 关于直线y =x （y -x =0）的对称是解题的关键．13. 某校学生会在同学中招募志愿者作为校庆活动讲解员，并设置了“即兴演讲”“朗诵短文”“电影片段配音”三个测试项目，报名的同学通过抽签的方式从这三个项目中随机抽取一项进行测试．甲、乙两位同学报名参加测试，恰好都抽到“即兴演讲”项目的概率是______．【答案】19【解析】【分析】列表后，再根据概率公式计算概率即可.【详解】解：列表如下：故P（甲、乙都抽到“即兴演讲”项目）=19，故答案为：19【点睛】此题考查了概率的计算，正确列出表格是解答此题的关键.14. 石拱桥是中国传统桥梁四大基本形式之一，如图，已知一石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，求水面宽AB＝_____m．【答案】8．【解析】【分析】连结OA，先计算OD的长，由勾股定理解得AD的长，再根据垂径定理可得AB=2AD，据此解题．【详解】连结OA，Q 拱桥半径OC 为5cm ，5OA \=cm ，8CD =Q m ，853OD \=-=cm ，224AD OA OD \=-==m2248AB AD \==´=m，故答案为：8．【点睛】本题考查垂径定理及其推论、勾股定理等知识，是重要考点，难度较易，掌握相关知识是解题关键．15. 若关于x的方程22x x m ++=有两个不相等的实数根，则m 的取值范围是_____．【答案】1m <【解析】【分析】利用一元二次方程根的判别式的意义可以得到2240m D =->，然后解关于m的不等式即可．【详解】根据题意得2240m D =->，解得1m <．故答案为1m <．【点睛】本题考查一元二次方程根的判别式.一元二次方程()200ax bx c a ++=¹的根与24b acD =-有如下关系：当0D >时，方程有两个不相等的实数根；当0D =时，方程有两个相等的实数根；当D<0时，方程无实数根．16. 某快递公司的快递件分为甲类件和乙类件，快递员送甲类件每件收入1元，送乙类件每件收入2元．累计工作1小时，只送甲类件，最多可送30件，只送乙类件，最多可送10件；累计工作2小时，只送甲类件，最多可送55件，只送乙类件，最多可送20件；…，理形成统计表如表：经整②180【答案】①. 160.【解析】【分析】（1）根据表格数据得出答案即可；（2）根据x+y＝8，x，y均为正整数，把所有收入可能都计算出，即可得出最大收入．【详解】解：(1)由统计表可知:如该快递员一天工作8小时只送甲类件，则他的收入是1×145=145(元)如果该快递员一天工作8小时只送乙类件，则他的收入是2 × 80= 160 (元)∴他一天的最大收入是160元;(2)依题意可知：x和y均正整数，且x+y= 8①当x=1时，则y=7∴该快递员一天的收入是1 ×30+2×70=30+ 140= 170 (元)；②当x=2时，则y=6∴该快递员-天的收入是1×55+2×60=55+120=175(元)；③当x=3时，则y=5∴该快递员一天的收入是1× 80+2×50= 80+ 100= 180 (元)；④当x=4时，则y=4∴该快递员一天的收入是1×100+2×40= 100+80 = 180 (元)；⑤当x=5时，则y=3∴该快递员一天的收入是1×115+2×30=115十60 = 175 (元)；⑥当x=6时，则y=2∴该快递员一天的收入是1 × 125+ 2× 20= 125+40 = 165 (元)；⑦当x=7时，则y=1∴该快递员一天的收入是1×135+2×10=135+20= 155 (元)综上讨论可知：他一天的最大收入为180元.故填： 160；180.【点睛】本题主要考查二元一次方程的应用，在给定的“x +y ＝8，x ，y 均为正整数”的条件下，分情况讨论出最大收入即可.三、解答题（本题共68分，第17-21题，每小题5分，第22-24题，每小题6分，第25题5分，第26题6分，第27-28题，每小题7分）解答应写出文字说明、演算步骤或证明过程．17. 计算：()113π2cos602-æö---+°+ç÷èø．2+【解析】【分析】直接利用绝对值的性质以及非零数的零次幂、特殊角三角函数值、负整数指数幂的性质分别化简即可得到答案．【详解】解：()113π2cos602-æö--+°+ç÷èø11222-+´+112++2+．【点睛】此题主要考查了实数的运算，正确化简各式是解答此题的关键．18. 解不等式组3(2)22254x x x x -<-ìïí+<ïî．【答案】52＜x ＜4【解析】【分析】先分别求出各不等式的解析，然后各不等式解集的公共部分即为不等式组的解集．【详解】解：3(2)22254x x x x -<-ìïí+<ïî①②由①得x ＜4由②得x ＞52所以不等式组的解集为：52＜x ＜4【点睛】本题考查了解一元一次不等式组，根据不等式的解集确定不等式组的解集是解答本题的关键．19. 已知210x x +-=，求代数式()()212x x x +--的值【答案】9【解析】【分析】根据完全平方公式展开所求代数式，把已知式子代入求解即可；【详解】解：2(31)(2)x x x +--，229612x x x x =++-+，2881x x =++，210x x +-=Q ，21x x \+=，\原式()2818119x x =++=´+=．【点睛】本题主要考查了代数式求值，结合完全平方公式化简是解题的关键．20. 证明下面是三角形中位线定理添加辅助线的方法，请你完成证明．三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．已知：如图，点D 、E 分别是ABC V 的边AB 、AC 的中点．求证：DE BC ∥ 且 12DE BC =．证明：如图，延长DE 到F ，使EF DE =，连接FC 、DC 、AF ．【答案】见解析【解析】【分析】证明AED CEF V V ≌，推出CF AD BD ==，CF AB ∥，得到四边形BDFC 为平行四边形，得到,DF BC DF BC =∥，即可得证．【详解】证明：如图，延长DE 到F ，使EF DE =，连接FC 、DC 、AF ，∵点D 、E 分别是ABC V 的边AB 、AC 的中点，∴,AD BD AE EC ==，又AED CEF Ð=Ð，∴()SAS AEDCEF △≌△，∴,CF AD BD EFC ADE ==Ð=Ð，∴CF AD ∥，∴四边形BDFC 为平行四边形，∴,DF BC DF BC =∥，∵12EF DE DF ==，∴DE BC ∥ 且 12DE BC =．【点睛】本题考查全等三角形的判定和性质，平行四边形的判定和性质．解题的关键是证明四边形BDFC 为平行四边形．21. 如图，在▱ABCD 中，AC ，BD 交于点O ，且AO ＝BO ．（1）求证：四边形ABCD 是矩形；（2）∠ADB 的角平分线DE 交AB 于点E ，当AD ＝3，tan ∠CAB ＝34时，求AE 的长．【答案】（1）见解析；（2）32.【解析】【分析】(1)由平行四边形性质和已知条件得出AC ＝BD ，即可得出结论；(2)过点E 作EG ⊥BD 于点G ，由角平分线的性质得出EG ＝EA ．由三角函数定义得出AB ＝4，sin ∠CAB ＝sin ∠ABD ＝35ADBD=，设AE ＝EG ＝x ，则BE ＝4﹣x ，在Rt △BEG 中，由三角函数定义得出345x x =-，即可得出答案．【详解】(1)证明：∵四边形ABCD 是平行四边形，∴AC ＝2AO ，BD ＝2BO ．∵AO ＝BO ，∴AC ＝BD ．∴平行四边形ABCD 为矩形．(2)过点E 作EG ⊥BD 于点G ，如图所示：∵四边形ABCD 是矩形，∴∠DAB ＝90°，∴EA ⊥AD ，∵DE 为∠ADB 的角平分线，∴EG ＝EA ．∵AO ＝BO ，∴∠CAB ＝∠ABD ．∵AD ＝3，tan ∠CAB ＝34，∴tan ∠CAB ＝tan ∠ABD ＝34＝AD AB．∴AB ＝4．∴BD 5=，sin ∠CAB ＝sin ∠ABD ＝35AD BD =．设AE ＝EG ＝x ，则BE ＝4﹣x ，在△BEG 中，∠BGE ＝90°，∴sin ∠ABD ＝345x x =-．解得：x ＝32，∴AE ＝32．故答案为：32.【点睛】本题考查了矩形的判定与性质、角平分线的性质、勾股定理、三角函数定义等知识；熟练掌握矩形的判定与性质和三角函数定义是解题的关键．22. 平面直角坐标系xOy 中，一次函数1y kx =-的图象经过点(2,3)．（1）求这个一次函数的解析式；（2）当2x <时，对于x 的每一个值，函数y x a =+的值都大于一次函数1y kx =-的值，直接写出a 的取值范围．【答案】（1）21y x =-；（2）1a ³【解析】【分析】（1）直接利用待定系（2）对于21y x =-，当2x =时，求出其y 的值，再由此坐标可求出a 的值．画出函数图象即可求出a 的取值范围．【详解】（1）解：∵一次函数1y kx =-的图象过点(23)，，∴321k =-，解得：2k =．∴这个一次函数的解析式是21y x =-．（2）当2x =时，代入21y x =-，得：3y =，∴当函数y x a =+经过点（2，3）时，1a =．画出两个函数图象如图：由图象可知，当1a ³，在2x <时，函数y x a =+的图象都在一次函数21y x =-的图象上方，即此时y x a =+的值都大于21y x =-的值，故a 的取值范围为1a ³．【点睛】本题考查求一次函数解析式和一次函数与不等式的关系，解题关键是熟练运用待定系数法求解析式，利用数形结合思想确定a 的取值范围．23. 某校在距离冬奥会开幕倒计时300天之际开展了一次冬奥知识答题竞赛，七、八年级各有200名学生参加了本次活动，为了解两个年级的答题情况，从两个年级各随机抽取了20名学生的成绩进行调查分析，过程如下（数据不完整）．收集数据七年级 66 70 71 78 71 78 75 78 58 a 63 90 80 85 80 89 85 86 80 87 八年级 61 65 74 70 71 74 74 76 63 b 91 85 80 84 87 83 82 80 86 c 整理、描述数据格）分析数据两组样本数据的平均数、中位数、众数如下表所示：请根据所给信息，解答下列问题：（1）=a ，m = ，n = ；（2）在此次竞赛中，小冬的成绩在七年级能排在前50%，在八年级只能排在后50%，那么估计小冬的成绩可能是 ；（3）估计七年级和八年级此次测试成绩优秀的总人数为 ．【答案】（1）80，0.45,80 （2）79.5 （3）210【解析】【分析】（1）利用平均数即可求出a ；找出成绩在8089x ££之间的频数即可求出m ，利用中位数即可求出n ；（2）利用中位数的意义列不等式求解即可；（3）求出抽取的20名七年级学生成绩中的优秀率，再乘以200；求出20名八年级学生成绩中的优秀率，再乘以200；最后两者相加即可解答．【小问1详解】解：∵七年级成绩的平均数为6671868087=77.520+++++L ，∴80a =；∵七年级同学成绩在8089x ££之间的频数为9，∴9=0.4520m =；将八年级同学成绩从小到大排序，处在中间的两个数都是80，∴80n =．故答案为：80，0.45,80．【小问2详解】解：∵七年级成绩的中位数是79，八年级成绩的中位数是80，小冬的成绩在七年级能排在前50%，在八年级只能排在后50%，∴小冬成绩在79和80之间∴小冬的成绩可能是79.5．故答案为79.5．【小问3详解】解：∵七年级的成绩为优秀的人数为0.5200=100´人，八年级的成绩为优秀的人数为0.55200=110´人，∴七年级和八年级此次测试成绩优秀的总人数为210人．【点睛】本题主要考查中位数、众数、平均数、频数分布表等知识点，理解中位数、众数、平均数的意义以及频数，频率和总数之间的关系是解题的关键．24. 如图，⊙O是△ABC的外接圆，圆心O在AC上．过点B作直线交AC的延长线于点D，使得∠CBD=∠CAB．过点A作AE⊥BD于点E，交⊙O于点F．（1）求证：BD是⊙O的切线；（2）若AF=4，2sin3D=，求BE的长．【答案】（1）见解析；（2【解析】【分析】（1）要证明BD是⊙O的切线，需要连接OB，通过角的等量代换，求证90CBD OBC°Ð+Ð=，即可．（2）连接CF交OB于点G，由直径所对的角为直角及平行线的判定及性质得出ACF DÐ=Ð，再根据等角的正弦值相等及勾股定理即可求出CF=，易证四边形BEFG是矩形，最后根据矩形的性质即可得出答案．【详解】（1）证明：如图，连接OB，∵AC是直径，∴ABC°90Ð=，90ABO OBC°\Ð+Ð=，Q，OA OB=\Ð=Ð，CAB ABO90CAB OBC°\Ð+Ð=，Q，CBD CABÐ=ÐCBD OBC°90\Ð+Ð=，\^，OB BD∴BD是☉O的切线．（2）解：如图，连接CF交OB于点G，∵AC 是直径，90AFC °\Ð=，AE BD ^Q ，90AED °\Ð=，AFC AED \Ð=Ð．//FC ED \，ACF D \Ð=Ð，2sin 3D Ð=Q ，2in sin 3s ACF D \Ð=Ð=，在Rt ACF D 中，sin AF ACF ACÐ=，23AF AC \=，4AF =Q ，6AC \=．根据勾股定理，得CF =．//,CF BD OB BD ^Q ，OB CF \^，12FG CF \==，90EFG FEB EBG °Ð=Ð=Ð=Q ，∴四边形BEFG 是矩形，∴BE FG ==．【点睛】本题考查圆的切线证明，三角形的勾股定理应用，锐角三角函数的计算以及矩形的性质等相关知识点，能根据题意进行准确的条件分析是解题关键．25. 某公园在垂直于湖面的立柱上安装了一个多孔喷头，从喷头每个孔喷出的水柱形状都相同，可以看作是抛物线的一部分，当喷头向四周同时喷水时，形成一个环状喷泉，安装后，通过测量其中一条水柱，获得如下数据，在距立柱水平距离为d 米的地点，水柱距离湖面的高度为h 米，请解决以下问题：（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；（2）结合表中所给数据或所画图象，直接写出这条水柱最高点距离湖面的高度；（3）求所画图象对应的函数表达式；（4）从安全的角度考虑，需要在这个喷泉外围设立一圈正方形护栏，这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米，请通过计算说明公园至少需要准备多少米的护栏（不考虑接头等其他因素）．【答案】（1）见解析 （2）5（3）()()2135085h d d =--+££ （4）72米【解析】【分析】（1）在表格中建立坐标系，然后描点、连线即可；（2）观察图象即可；（3）由表中点（1.0，4.2），（5.0，4.2），可确定抛物线的对称轴及顶点坐标，则设抛物线解析式为顶点式即可，再找点（1.0，4.2）代入即可求得解析式；（4）在求得的解析式中令h =0，则可求得d 的值，即可确定所需护栏的长度．【小问1详解】坐标系及图象如图所示．【小问2详解】由图象知，水柱最高点距离湖面的高度为5米．【小问3详解】∵抛物线经过点（1.0，4.2），（5.0，4.2），∴抛物线的对称轴为3d =．∴抛物线的顶点坐标为（3.0，5.0）．设抛物线的函数表达式为()235h a d =-+． 把（1.0，4.2）代入，解得15a =-．∴所画图象对应的函数表达式为()()2135085h d d =--+££．【小问4详解】令0h =，解得12d =-（舍），28d =．∴每条水柱在湖面上的落点到立柱的水平距离为8米．∵这个喷泉的任何一条水柱在湖面上的落点到护栏的距离不能小于1米，∴正方形护栏的边长至少为18米．则公园至少需要准备18×4=72（米）的护栏．【点睛】本题是二次函数的实际问题，考查了画二次函数图象，求二次函数解析式，二次函数与一元二次方程的关系等知识，二次函数的相关知识是解题的关键．26. 已知二次函数y ＝ax 2﹣2ax ．（1）二次函数图象的对称轴是直线x ＝ ；（2）当0≤x ≤3时，y 的最大值与最小值的差为4，求该二次函数的表达式；（3）若a ＜0，对于二次函数图象上的两点P （x 1，y 1），Q （x 2，y 2），当t ≤x 1≤t +1，x 2≥3时，均满足y 1≥y 2，请结合函数图象，直接写出t 的取值范围．【答案】（1）1；（2）y ＝x 2﹣2x y ＝﹣x 2+2x ；（3）﹣1≤t ≤2【解析】【分析】（1）由对称轴是直线x ＝2b a-，可求解；（2）分a ＞0或a ＜0两种情况讨论，求出y 的最大值和最小值，即可求解；（3）利用函数图象的性质可求解．【详解】解：（1）由题意可得：对称轴是直线x ＝22a a--＝1，故答案为：1；（2）当a ＞0时，∵对称轴为x ＝1，当x ＝1时，y 有最小值为﹣a ，当x ＝3时，y 有最大值为3a ，∴3a ﹣（﹣a ）＝4．∴a ＝1，∴二次函数的表达式为：y ＝x 2﹣2x ；当a ＜0时，同理可得y 有最大值为﹣a ； y 有最小值为3a ，∴﹣a ﹣3a ＝4，∴a ＝﹣1，∴二次函数的表达式为：y ＝﹣x 2+2x ；综上所述，二次函数的表达式为y ＝x 2﹣2x 或y ＝﹣x 2+2x ；（3）∵a ＜0，对称轴为x ＝1，∴x ≤1时，y 随x 的增大而增大，x ＞1时，y 随x 的增大而减小，x ＝﹣1和x ＝3时的函数值相等，∵t ≤x 1≤t +1，x 2≥3时，均满足y 1≥y 2，∴t ≥﹣1，t +1≤3，∴﹣1≤t ≤2．【点睛】本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识点的综合应用，能利用分类思想解决问题是本题的关键．27. 已知等边ABC V ，D 为边BC 中点，M 为边AC 上一点（不与A ，C 重合），连接DM ．（1）如图1，点E 是边AC 的中点，当M 在线段AE 上（不与A ，E 重合）时，将DM 绕点D 逆时针旋转120°得到线段DF ，连接BF ．①依题意补全图1；②此时EM 与BF 的数量关系为：DBF Ð= °．（2）如图2，若2DM MC =，在边AB 上有一点N ，使得120NDM Ð=°．直接用等式表示线段BN ，ND ，CD 之间的数量关系，并证明．【答案】（1）①见解析；②EM BF =，120；（2）12CD BN ND =+，证明见解析【解析】【分析】（1）①根据提示画出图形即可；②连接DE ，证明△DME ≌△DFB 即可得到结论；（3）取线段AC 中点E ，连接ED ．由三角形中位线定理得12DE BA =，12CE CA =，12BD CD BC ==．根据ABC V 是等边三角形可证明DE BD CD CE ===，60CED EDC B Ð=Ð=Ð=°，再证明EDM BDN @△△得BN EM =，2ND MD MC ==，进一步可得结论．【详解】解：（1）①补全图形如图1．②线段EM 与BF 的数量关系为EM BF =；120DBF Ð=°．连接DE ，∵D 为BC 的中点，E 为AC 的中点，∴DE 为△ABC 的中䏠线，∴DE =12AB ，DE //AB∵ABC V 是等边三角形，∴AB BC AC ==，60Ð=Ð=Ð=°A B C ．∵D 为BC 的中点，∴12BD BC DE ==∵//DE AB∴60CDE ABC Ð=Ð=°，60CED A Ð=Ð=°∴120BDE BDM EDM Ð=°=Ð+Ð∵120BDM BDF Ð+Ð=° ，,DM DF =\ BDF EDM Ð=Ð∴△DME ≌△DFB∴EM BF =；DBF DEM Ð=Ð．∵60CED Ð=°∴120DEM Ð=°∴120DBF Ð=°．故答案为：EM BF =；120DBF Ð=°．（2）证明：取线段AC 中点E ，连接ED ．如图2 ．∵点D 是边BC 的中点，点E 是边AC 的中点，∴12DE BA =，12CE CA =，12BD CD BC ==．∵ABC V 是等边三角形，∴AB BC AC ==，60B C Ð=Ð=°．∴DE BD CD CE ===，60CED EDC B Ð=Ð=Ð=°．∴120Ð=°BDE ，∵120NDM Ð=°，∴EDM BDN Ð=Ð．∴EDM BDN @△△．∴BN EM =，2ND MD MC ==，∵EC EM MC =+，∴12CD BN ND =+．【点睛】此题主要考查了全等三角形的判定与性质，等边三角形的性质以及三角形中位线定理，正确作出辅助线构造全等三角形是解答此题的关键．28. 对于平面直角坐标系xOy 中的图形M ，N ，给出如下定义：P 为图形M 上任意一点，Q 为图形N 上任意一点，如果P ，Q 两点间的距离有最小值，那么称这个最小值为图形M ，N 间的“闭距离”，记作d （M ，N ），特殊地，当图形M 与图形N 有公共点时，规定d （M ，N ）＝0已知点()(2,00)2(30)0()2A B C D m -,，,,,,．（1）①求d （点O ，线段AB ）；②若d （线段CD ，直线AB ）＝1，直接写出m 的值；（2）⊙O 的半径为r ，若d （⊙O ，线段AB ）≤1，直接写出r 的取值范围；（3）若直线y b =+上存在点E ，使d （E ，ABC V ）＝1，直接写出b 的取值范围．【答案】（1）①②2m =-；（2）11r -££；（3）22b --££【解析】【分析】（1）①根据题意作图，由三角形的面积公式及“闭距离”的定义即可求解；②根据题意作图，根据含30°的直角三角形的性质即可求出D 点坐标，故可求解；（2）根据题意作图，由d （⊙O ，线段AB ）≤1，分情况讨论即可求解；（3）根据题意作图，找到d （⊙O ，线段AB ）=1的点，再根据解直角三角形、一次函数的解析式求解方法求出b 的值，故可求解．【详解】（1）①如图，作OH ⊥AB ，∵()020(A B -，,，∴AO =2，BO =，AB 4=根据三角形的面积公式可得1122AO BO AB OH ×=×∴OH=∴d （点O ，线段AB ）②∵AO=2，BO=23，AB4=∴AB=2AO，∴∠ABO=30°如图，作HD⊥AB，∵d（线段CD，直线AB）＝1，∴DH=1∴BD=2HD=2∴DO=BO-BD=-2∴D（-，0）2∴m=-；2（2）如图，OH⊥AB，交⊙O于M点，BI=1当d（⊙O，线段AB）≤1当HM≤1时，由（1）可得OH=3∴r³-当BI≤1时，此时IO=BI+OB=∴1故若d（⊙O，线段AB）≤1时， r的取值范围r11（3）∵ d （E ，ABC V ）＝1，如图，作CM ⊥直线3y x b =+于M 点，此时CM =1设直线y b =+与x 轴交于K 点，则∠CKM =60°∴CK =CM ÷cos60°=3∴K （2+3，0），代入y b =+得20b æ=+ççèø解得b =2-如图，作BG ⊥直线y b =+于G 点，此时BG =1设直线y b =+与y 轴交于N 点，则∠GNB =90°-60°=30°∴BN =2BG =2∴N （0，2+），代入y b =+得20b +=+解得b =2∵存在点E，使d（E，ABCV）＝1，∴b的取值范围是--££+．b2322【点睛】此题主要考查圆与几何综合，解题的关键是根据题意作图，由“闭距离”的定义及解直角三角形、圆的性质特点进行求解．。

北京新机场规划图二期中国未来的航空中心查看全部一主指的是开发区。

两辅为西侧大兴区综合配套服务区和东侧台湖高端总部基地。

《规划》要求构建区域一体化生活圈。

继续发挥开发区的标杆作用，建立多主体供给、多渠道保障、租购并举的住房保障体系。

采育或将成为大兴新机场中央别墅区亦庄新城规划隔空把采育产业园隔空纳入，那么其中必有奥妙，今天南城君来给大家解读解读。

采育拥有3000亩的原始次生森林，广袤丰饶的2万亩葡萄园，富含多种矿物质的地热温泉，以及采育阳光俱乐部高尔夫球场。

目前已知投资110亿美元的迪拜商业项目，以及首都机场集团总部基地、超级万象城等12个大项目相继落户大兴机场临空经济区，这里未来将聚集大量的高端就业人口，同时也就催生了高端住宅需求。

大兴机场临空经济区的航空物流区及自贸区，采育距离大兴机场航空物流区及主要自贸区的距离仅为15公里，通过首都地区环线高速及城际铁路联络线，可以快速直通大兴机场及临空经济区，交通优势明显。

自贸区大兴机场片区将依托大兴机场航空口岸和综合保税区的贸易便利化平台，大力发展航材、进口高端消费品和专业产品的国际贸易业务，推动跨境电商等新型贸易业务的发展。

避开机场噪音，南城低密宜居净土南城君通过研究大大兴机场一体化设计指什么？在2023年的9月也就是北京新机场正是运营前一年的时间点，北京新机场已经被正式命名为北京大兴国际机场。

对于北京新机场的命名，可以说也是情理之中的，但是这种命名还是忽视了京津冀城市群、京津冀一体化这个改变，因此还是留下了一些遗憾的。

打开百度App，看更多图片众所周知，北京新机场与京津冀城市群的发展是密切相关的，而且中国在推进京津冀一体化的大战略的时候，其实已经明了北京新机场就是服务于京津冀地区的。

从这个角度来说，北京新机场命名为北京大兴国际机场，这里面北京本地的改变十足，但是没有突出京津冀城市群的概念壮观的北京新机场从使用的角度，北京新机场也不仅仅是服务于北京的，它位于京津冀城市群的里面，这在北京2035总规中已经得到了明确的说明。

中国民用航空局、国家发展和改革委员会关于推进国际航空枢纽建设的指导意见文章属性•【制定机关】中国民用航空局,国家发展和改革委员会•【公布日期】2024.07.31•【文号】民航发〔2024〕28号•【施行日期】2024.07.31•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】民航正文中国民用航空局国家发展和改革委员会关于推进国际航空枢纽建设的指导意见民航发〔2024〕28号民航各地区管理局、各运输（通用）航空公司、各服务保障公司、各机场公司、民航局属各单位，各省、自治区、直辖市及新疆生产建设兵团发展改革委：国际航空枢纽是航空运输服务体系的核心节点，是现代综合交通运输体系的重要组成，是民航服务国家对外开放和构建新发展格局的重要支撑，对服务国家重大战略实施、服务区域经济社会发展、服务人民群众便捷高效航空出行具有重要作用。

为解决我国国际航空枢纽战略谋划不深、枢纽竞争力不强、协同运行效率不高、国际运输服务能力不足等问题，高水平建设国际航空枢纽，提升民航国际竞争力，更好发挥民航国家重要战略产业作用，提出以下意见。

一、总体要求以习近平新时代中国特色社会主义思想为指导，深入贯彻党的二十大和二十届二中、三中全会精神，完整、准确、全面贯彻新发展理念，着力推动民航高质量发展，服务构建新发展格局。

牢牢把握国家对特定地区的战略定位，落实国家区域重大战略和区域协调发展战略，打造定位清晰、各具特色、竞争力强的航空枢纽功能体系。

以推进一批夯基础、强功能、利长远的重大规划、重点工程、重要政策实施为抓手，以推动国际航空枢纽顶层设计更加完善、规划建设更加优化、运行管理更加协同、运输服务更加高效为重点任务，推动国际航空枢纽资源优化配置，打造2-3家世界级超级航空承运人，强化北京、上海、广州等国际航空枢纽全方位门户复合型功能，打造一批面向特定区域的国际航空枢纽和区域航空枢纽，为更好推动国家重大战略实施，服务高水平对外开放，满足人民美好航空出行需求，加快谱写交通强国建设民航新篇章提供有力支撑。

世界最大的机场排行世界最大的机场是我们几乎每个人都熟悉的概念。

随着航空业的迅猛发展，人们对机场的需求也越来越大。

机场不仅是连接各大城市和国家的重要交通枢纽，还是国际贸易和旅游的重要环节。

在过去的几十年里，世界各地的机场竞相扩建和更新，争夺称为世界最大的机场的荣耀。

本文将为大家介绍一些目前世界上最大的机场，并简要介绍其规模和重要性。

排名第一的世界最大机场是位于中国北京的北京大兴国际机场。

这座机场是为了应对北京和中国日益增长的航空需求而建设的。

它于2019年投入运营，占地面积超过了世界第二大机场迪拜国际机场的两倍以上。

北京大兴国际机场拥有4条跑道，可以同时起降超过200架次的飞机。

机场的设计灵感来自于传统的中国建筑和文化元素，使其成为一个独特的地标。

迪拜国际机场位于阿拉伯联合酋长国迪拜市，是跨大西洋航线和东西方航线的重要枢纽。

它是世界第二大机场，拥有3个航站楼和6条跑道，估计每年处理超过8000万乘客。

这个机场是迪拜经济的关键组成部分，对于吸引游客和促进国际贸易起着重要作用。

排名第三的是美国亚特兰大哈茨菲尔德-杰克逊国际机场。

这个机场是美国国内和国际航班最繁忙的机场之一。

它根据旅客流量被认为是世界第一大机场。

亚特兰大机场拥有充足的停机位和多条跑道，可以同时容纳多达3百万乘客和机组人员。

这个机场是美国南部地区的重要经济引擎，对于贸易和旅游业都起着举足轻重的作用。

除了这些前三大机场外，世界上还有许多其他规模庞大的机场。

例如，伦敦希思罗机场位于英国伦敦，是世界上最繁忙的国际航空枢纽之一。

它拥有两个航站楼和两条跑道，并每年处理数以亿计的旅客。

希思罗机场为英国经济做出了巨大贡献，也是欧洲航空业的重要一环。

另一个世界最大机场的例子是日本东京的成田国际机场。

这个机场是日本最繁忙的国际航空枢纽，也是东京地区的主要机场之一。

成田机场有两个航站楼和三条跑道，每年处理数以千万计的旅客。

机场附近还有许多世界知名的景点，吸引着大量的国际游客。

第1篇一、招标公告根据我国航空运输事业的发展需要，为满足北京大兴国际机场（以下简称“大兴机场”）的建设需求，现面向国内外具有资质的设计单位公开招标大兴机场设计方案。

现将有关事项公告如下：一、项目概况1. 项目名称：北京大兴国际机场设计方案2. 项目地点：北京市大兴区3. 项目规模：4F级国际机场，年旅客吞吐量预计为7200万人次，货运吞吐量预计为130万吨。

4. 项目性质：新建5. 项目总投资：约880亿元人民币二、招标内容1. 设计单位负责大兴机场的整体规划、建筑设计、结构设计、机电设计、景观设计等。

2. 设计单位需充分考虑机场的可持续发展、节能减排、绿色环保等方面。

3. 设计单位需结合机场周边环境，提出合理的交通组织方案。

4. 设计单位需充分考虑机场运营需求，提出高效的运营管理方案。

三、投标人资格要求1. 具有独立法人资格，具备有效的营业执照。

2. 具有国家建设行政主管部门核发的工程设计综合甲级资质。

3. 具有良好的财务状况和信誉，无不良记录。

4. 具有类似大型国际机场设计经验，并在最近三年内承担过至少一个4F级国际机场的设计项目。

5. 设计团队具有丰富经验，具备承担本项目的专业能力。

四、招标文件获取1. 招标文件获取时间：自本公告发布之日起至招标文件发售截止之日止。

2. 招标文件获取方式：有意向的投标人可前往招标代理机构领取招标文件。

3. 招标文件售价：人民币5000元/套。

五、投标文件递交1. 投标文件递交截止时间：详见招标文件。

2. 投标文件递交地点：详见招标文件。

六、开标时间及地点1. 开标时间：详见招标文件。

2. 开标地点：详见招标文件。

七、其他事项1. 本项目采用资格后审方式，招标人将对投标人的资格进行审查。

2. 投标人应严格按照招标文件的要求编制投标文件，投标文件应包含但不限于以下内容：（1）投标函及投标保证金；（2）法定代表人身份证明或授权委托书；（3）企业法人营业执照副本；（4）资质证书副本；（5）类似项目业绩证明；（6）设计团队介绍；（7）投标报价及详细方案；（8）其他相关资料。

第1篇摘要：北京大兴国际机场作为我国乃至世界规模最大的单体机场，其建设过程中涉及到的工程项目管理具有极高的复杂性和重要性。

本文通过对大兴机场工程项目的背景、组织架构、项目管理模式、关键技术及风险控制等方面的分析，旨在为我国大型复杂工程项目管理提供借鉴和启示。

一、引言随着我国经济的快速发展，航空运输业已成为国家战略性新兴产业。

北京大兴国际机场作为我国民航业的重要基础设施，承载着推动京津冀协同发展、服务全国乃至全球旅客的重要使命。

大兴机场工程项目的成功实施，对于提高我国航空运输能力、优化机场布局、促进区域经济发展具有重要意义。

本文将对大兴机场工程项目的管理进行分析，以期对类似大型复杂工程项目提供有益借鉴。

二、大兴机场工程项目背景1. 国家战略需求：为满足国家战略需求，优化京津冀地区航空运输布局，提高我国航空运输能力，国家决定建设北京大兴国际机场。

2. 区域协同发展：大兴机场的建成将促进京津冀地区经济、交通、文化等方面的协同发展，提升区域整体竞争力。

3. 市场需求：随着我国经济持续增长，航空旅客需求不断上升，大兴机场的建成将有效缓解首都国际机场的运输压力，满足市场对航空运输的需求。

三、大兴机场工程项目组织架构1. 项目法人：由北京市政府牵头，联合民航局、国家发改委等部门共同组建项目法人，负责工程项目的总体规划和组织实施。

2. 项目管理机构：设立项目管理机构，负责项目前期、建设、运营等全过程的监督管理。

3. 项目参与单位：包括设计、施工、监理、设备供应商、咨询机构等，共同参与项目的实施。

四、大兴机场工程项目管理模式1. EPC（设计、采购、施工）模式：由一家总承包商负责工程设计、设备采购和施工，提高项目管理效率。

2. 总承包+专业分包模式：将工程划分为若干专业分包，由总承包商负责协调和管理各专业分包，确保工程质量和进度。

3. 信息化管理：采用BIM（建筑信息模型）等先进技术，实现工程项目全生命周期管理。

北京大兴国际机场工程伦理案例分析摘要：北京大兴国际机场是世界首个在建投资的大型枢纽机场，中国政府高度重视新机场的建设。

新机场是高标准高质量推进“一带一路”建设，进一步提升国家形象、增进沿线地区经济发展互信与利益共享所采取的重大举措，也是确保北京这座城市在新时代迈向高质量发展的重要保障。

因此，深入研究北京大兴国际机场工程相关伦理案例是工程伦理研究中重要的内容之一。

关键词：跑道；建设管理；生态环境；伦理治理作者简介：李亚男，北京市建筑科学研究院教授，博士生导师。

本文结合国家政策法规、行业标准、法律规定以及北京大兴国际机场工程建设实践中案例分析报告文本等资料梳理北京大兴国际机场工程伦理案例分析框架和分析方法。

作者从伦理问题产生的背景入手，对相关问题进行论述以及相关的理论阐释。

一、问题概述2016年9月1日，北京大兴国际机场正式投入使用。

在此之前，人们普遍认为该机场应按照“国内首例空管设施机场建设案例”来进行规划设计，也就是将机场打造成“大型空中交通枢纽”。

然而，随着时间的推移及各方面原因的影响，导致规划设计方案在实际运营过程中出现了许多潜在的伦理问题。

随着我国经济社会的不断发展，人们生活水平的不断提高，对生活质量越来越重视，但随之而来的却是对工作效率的不断要求。

为了使工作效率提高，将工作质量与工作效率提高作为发展目标是当今国际通用的一种通行做法。

这也使得人们越来越关注工作中所产生的伦理问题以及它们可能会带来的社会问题。

从工程建设领域来看，工程伦理已成为各国企业和政府在建设项目管理过程中都必须要重视的一个问题。

随着我国社会主义市场经济体制不断完善与发展，建筑市场逐步走向规范化、透明化及制度化，工程伦理也应随着经济社会发展逐步走向规范化、透明化、制度化建设与发展领域。

因此可以将其视为一种建筑市场行为规范来进行研究治理。

二、基本框架分析根据上述文献资料，笔者在总结分析某工程项目在建设管理、发展和传承过程中存在的重大伦理问题基础上，从工程质量、建筑材料和工程管理等三个层面分别对北京大兴国际机场项目各环节中相关伦理问题进行分析并提出相应对策。

中国排名前⼗的机场有哪些 或许有些⼈对那个中国机场⾯积最⼤这个问题有所好奇，以下是由⼩编整理关于中国机场最⼤⾯积排名，希望⼤家喜欢! 中国机场最⼤⾯积排名 1、北京机场 北京⾸都国际机场，简称⾸都机场，为中华⼈民共和国北京市的主要的国际机场，并且是⽬前中国最繁忙的民⽤机场，同时也是中国国际航空公司的基地机场。

2004年，北京⾸都国际机场取代东京国际机场(⽻⽥)成为亚洲飞机起降最为繁忙的机场。

按客运量算，2004年，⾸都机场是亚洲四⼤机场(位列⽻⽥、曼⾕、⾹港之后)之⼀以及全球第⼆⼗⼤机场。

2005年, 北京⾸都国际机场已成为亚洲第⼆⼤机场(仅次于⽻⽥机场)，全球排名第⼗五位。

2、⾹港机场 ⾹港新国际机场作为⾹港唯⼀的机场于1998年7⽉6⽇投⼊营运。

它构成⾹港壮观的门户，巨⼤、轻盈、飘逸的形象令⼈印象深刻，同时它⼜是友好⽽亲切的。

尽管它是世界上最⼤的空港，其尺度并没有给⼈⼀种恐惧或震撼感。

设计赋予了它易于理解、易于接近的特质：庄严⽽⾮势不可挡。

新机场延续发展了福斯特在1991年建成伦敦第三⼤机场――斯坦斯特机场中⾸创的设计理论。

其特征包括：轻型屋⾯、解放设备空间、⼴泛应⽤⾃然光，将环境⽓候控制设备与⾏李处理及运输设施统⼀布置于中央⼤厅之下，使建筑中的流线与运动尽可能⾃由。

新机场周围的⾃然景⾊是壮观的，旅客在空港内任何⼀处均可享受外部宽阔的景⾊，玻璃⾯的最⼩⾼度均⼤于4⽶，并清除视觉范围内各种障碍以减少景观遮挡。

设计强调利⽤周围环境导向远远超过空港建筑本⾝导向：旅客可看到⼤地、海⾯、放眼远处的道路、桥梁和近处的飞机起降。

这种考虑与许多空港采⽤封闭的“盒⼦”或通道的作法⼤相庭径，旅⾏变为⼀种愉悦的过程。

3、上海浦东机场 上海浦东国际机场位于上海浦东长江⼊海⼝南岸的滨海地带，占地40多平⽅公⾥，距上海市中⼼约30公⾥，距虹桥机场约40公⾥。

浦东机场⼀期⼯程1997年10⽉全⾯开⼯，1999年9⽉建成通航。

证券研究报告交运研究前瞻系列大兴机场转场完成，北京航空市场格局展望行业评级交运强于大市（维持）证券分析师张功投资咨询资格编号：S1060521020003邮箱：***********************.CN2021年04月23日严家源投资咨询资格编号：S1060518110001邮箱：************************.CN投资要点⏹大兴机场转场工作提前完成：北京大兴国际机场定位大型国际枢纽，规划年旅客吞吐量超过1亿人次，2021年夏秋航季，在东航集团完成转场工作后，标志着大兴机场转场工作基本完成，与此前的规划方案相比，提前一个航季完成转场工作。

新航季，受国际航线管控影响，机场日均航班900架次不及规划中的1050架次。

⏹主要航空公司网络布局初显：根据民航局最新规划，南航集团、东航集团和国航集团将分别占有机场40%、30%和10%的时刻资源。

新航季，在国际航线管制未放开的情况下，南航集团航班量占比达到47%，东航集团航班量占比37%、国航集团航班量占比12%。

各家公司的航线网络初步搭建完毕，各有特点，其中南航注重精品航线建设，东航注重覆盖范围，国航注重千万级机场通达。

⏹北京航空市场发展推演：在北京市场足够容纳两个大型国际枢纽情况下，我们认为南航在大兴机场重点打造辐射全国联通全球的枢纽网络，并能得到此前在广州很难获取的合作伙伴共建网络优势；东航则能够通过双品牌战略实现高中低端旅客的全覆盖；国航则是巩固首都机场优势同时，涉足大兴机场优质国内航线，分享大兴机场发展成果。

⏹投资建议：大兴机场给南航集团和东航集团带来扩大北京市场影响力的机遇，我们推荐迎来提高国际影响力、提升航线收益品质良机的南方航空以及京沪线优势稳固、双品牌战略扩大北京市场辐射面的东方航空。

⏹风险提示：1、行业政策：政策的调整、变化将直接或间接地影响收入和成本。

2、宏观经济：当宏观经济环境变化将导致市场需求出现变化，影响盈利水平。

起航！北京大兴机场凤凰展翅作者：柯胡端来源：《商业文化》2019年第32期在经历了7次综合模拟演练、3场验证试飞之后，北京大兴国际机场迎来它“凤凰展翅”的高光时刻。

2019年9月25日，北京大兴国际机场投运仪式隆重举行。

北京大兴、河北广阳之间，占地面积140万平方米，相当于63个天安门广场的土地，不到5年时间成为北京的新地标、勾连世界的枢纽。

作为20年内全球范围规划新建设的最大机场之一，北京大兴国际机场“五纵两横”的地面交通网、“四进四出”的空中航班波……这些，必将再次吸引世界目光，注目她的优雅起飞。

【一】大机场大智慧高空俯瞰，北京大兴国际机场苑若展翅的凤凰;走进机场，却是恢弘之下，一个个贴心服务的小细节，一处处让人叹服的大智慧。

值机全程自助无纸化从四层出发层走进这座气势恢宏的单体航站楼，就如同进入了一个白色的梦幻空间。

抬头看，巨大的屋顶线条柔美而又干练;宽阔的空间里，8根C形柱如参天巨树，支撑起整座航站楼的曲面屋檐;阳光从顶端的采光窗倾斜而入，光影交织的美景带给整座机场更多通透感。

航站楼整座屋顶由一个中央天窗、六条条形天窗和八个气泡窗组成，需要用12800块不同形状和材质的玻璃拼接而成，玻璃接缝胶黏长度可以环绕北京四环路一圈。

更不简单的是，看似轻飘飘如云朵一样的屋顶，其实光是网架重量就超过3万吨，相当于大半个鸟巢钢结构的重量。

继续往前走到值机柜台，出发之前的值机手续已经无需人工办理。

在值机环节，大兴机场协同航空公司配备了400余台自助值机和自助托运设备，乘客只需要在电子屏上点击触摸屏，刷身份证，顺利完成打印登机牌、托运行李。

贴上最新投入使用的无线射频的行李条，就可在手机上看到自己的行李到了哪里。

安检通道也引入了人脸识别等智能新技术，旅客从进入航站楼一直到登机口，可以摆脱纸质登机牌，全流程实现自助无纸化。

8分钟到达最远登机口一切办妥后完成安检程序，进入到候机楼内部，面对乘客的将不再是错杂繁复的迷宫，而是站在中央就能一眼望到头的五条指廊。

世界面积最大的机场排行榜1、美国芝加哥奥黑尔国际机场：这是世界上目前最大的飞机场，距离芝加哥市27公里，总共有6个跑道，并且有高速公路穿梭其中，美国所有的航空公司在这都有自己的登机口，在这里，平均不到3分钟就有一班航班起降，这里也是全球第五大航空公司美国联合航空公司的基地之一。

这里每天要起降两千七百次航班，每年大约有七千两百多万名乘客经该机场来往穿梭于世界各地。

奥黑尔国际机场是全美最大两家航空公司的主要中心机场，在这里工作的员工共有五万多人。

这座世界一流的机场位于芝加哥市区外，占地达七千七百英亩，拥有七条跑道和一个庞大的候机楼。

2、美国亚特兰大哈兹菲德国际机场：距离亚特兰大市19公里，这是世界上登机口最多的机场，共有6个航站楼，拥有将近100个近机位，这里是全球飞机数量最多的航空公司美国达美航空公司的总部。

亚特兰大机场建立在亚特兰大市南区与乔治亚大学城相邻的地方。

机场邻近的市镇有福尔顿Fulton、凯尔顿Clayton等，而和亚特兰大是联结的市镇除了大学城，还有东中心East Point、哈皮维利Hapeville等。

哈兹菲尔德-杰克逊机场里主要的航空公司除了达美航空和穿越航空外，还包括有达美连航Delta Connection、大西洋东南航空Atlantic Southeast Airlines等。

3、美国纽约约翰·肯尼迪国际机场：距离纽约市27公里，是世界上最繁忙的机场，她由美国达美航空公司、美国西北航空公司、美国航空公司、美国大陆航空公司、美国环球航空公司五大航空公司、英国航空公司及其他国际航空公司的一共7个候机厅组成。

每个候机厅都比北京首都机场候机厅大，各候机厅之间有公路相连，形成一个长达八公里的环。

他是全球第9大航空公司美国西北航空公司和美国大陆航空公司的总部。

4、英国伦敦希斯罗国际机场：距伦敦市中心20公里，是整个欧洲空中交通的中心，同时他也是世界第一大航空公司英国航空公司的总部，另外，英国米特兰航空公司，英国不列颠航空公司，英国AIR 2000航空公司的总部也在这里。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。