高中物理磁场大题(超全)

专题7 磁场中的三维偏转问题
例题1.（2021·6 浙江·T23）如图甲所示，空间站上某种离子推进器由离子源、间距为d 的中间有小孔的两平行金属板M、N和边长为L的立方体构成，其后端面P为喷口。

以金属板N的中心O为坐标原点，垂直立方体侧面和金属板建立x、y和z坐标轴。

M、N板之间存在场强为E、方向沿z轴正方向的匀强电场；立方体内存在磁场，其磁感应强度沿z方向的分量始
终为零，沿x和y方向的分量B
x 和B
y
随时间周期性变化规律如图乙所示，图中B
可调。

氙离
子（Xe2+）束从离子源小孔S射出，沿z方向匀速运动到M板，经电场加速进入磁场区域，最
后从端面P射出，测得离子经电场加速后在金属板N中心点O处相对推进器的速度为v。

已知单个离子的质量为m、电荷量为2e，忽略离子间的相互作用，且射出的离子总质量远小于推进器的质量。

（1）求离子从小孔S射出时相对推进器的速度大小v；
（2）不考虑在磁场突变时运动的离子，调节B
的值，使得从小孔S射出的离子均能从喷口后
端面P射出，求B
的取范围；
（3）设离子在磁场中的运动时间远小于磁场变化周期T，单位时间从端面P射出的离子数为n，
且B0=√2mv0
5eL 。

求图乙中t
时刻离子束对推进器作用力沿z轴方向的分力。

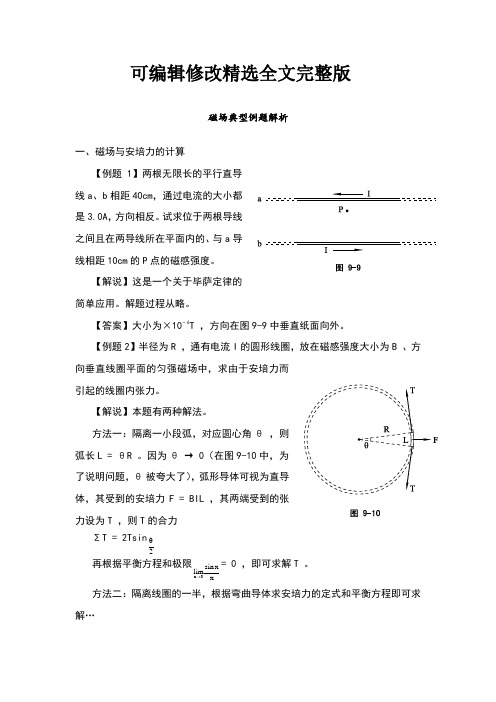
可编辑修改精选全文完整版磁场典型例题解析一、磁场与安培力的计算【例题1】两根无限长的平行直导线a 、b 相距40cm ，通过电流的大小都是3.0A ，方向相反。

试求位于两根导线之间且在两导线所在平面内的、与a 导线相距10cm 的P 点的磁感强度。

【解说】这是一个关于毕萨定律的简单应用。

解题过程从略。

【答案】大小为×10−6T ，方向在图9-9中垂直纸面向外。

【例题2】半径为R ，通有电流I 的圆形线圈，放在磁感强度大小为B 、方向垂直线圈平面的匀强磁场中，求由于安培力而引起的线圈内张力。

【解说】本题有两种解法。

方法一：隔离一小段弧，对应圆心角θ ，则弧长L = θR 。

因为θ → 0（在图9-10中，为了说明问题，θ被夸大了），弧形导体可视为直导体，其受到的安培力F = BIL ，其两端受到的张力设为T ，则T 的合力ΣT = 2Tsin 2θ再根据平衡方程和极限xxsin lim0x →= 0 ，即可求解T 。

方法二：隔离线圈的一半，根据弯曲导体求安培力的定式和平衡方程即可求解…【答案】BIR 。

〖说明〗如果安培力不是背离圆心而是指向圆心，内张力的方向也随之反向，但大小不会变。

〖学员思考〗如果圆环的电流是由于环上的带正电物质顺时针旋转而成（磁场仍然是进去的），且已知单位长度的电量为λ、环的角速度ω、环的总质量为M ，其它条件不变，再求环的内张力。

〖提示〗此时环的张力由两部分引起：①安培力，②离心力。

前者的计算上面已经得出（此处I = ωπλ•π/2R 2 = ωλR ），T 1 = B ωλR 2 ；后者的计算必须．．应用图9-10的思想，只是F 变成了离心力，方程 2T 2 sin 2θ =πθ2M ω2R ，即T 2 =πω2R M 2 。

〖答〗B ωλR 2 + πω2R M 2 。

【例题3】如图9-11所示，半径为R 的圆形线圈共N 匝，处在方向竖直的、磁感强度为B 的匀强磁场中，线圈可绕其水平直径（绝缘）轴OO ′转动。

5年高考1年模拟全国III卷物理试题分项解析专题11 磁场一、全国III卷：（2020年和2021年使用III卷的省份没有发生变化）2020届高考：云南、广西、贵州、四川、西藏2021届高考：云南、贵州、四川、广西、西藏二、2016-2020年全国III卷分布情况概况：考点年份题号题型分数磁场2020 18 选择题6分2019 18 选择题6分2018 24 计算题12分2017 18/24 选择题6分/12分2016 18 选择题6分三、2016-2020年全国III卷试题赏析：1、（2020·全国III卷·T18）真空中有一匀强磁场，磁场边界为两个半径分别为a和3a的同轴圆柱面，磁场的方向与圆柱轴线平行，其横截面如图所示。

一速率为v的电子从圆心沿半径方向进入磁场。

已知电子质量为m，电荷量为e，忽略重力。

为使该电子的运动被限制在图中实线圆围成的区域内，磁场的磁感应强度最小为（）ŒA. 32mvaeB.mvaeC.34mvaeD.35mvae2、（2019·全国III 卷·T18）.如图，在坐标系的第一和第二象限内存在磁感应强度大小分别为12B 和B 、方向均垂直于纸面向外的匀强磁场．一质量为m 、电荷量为q （q >0）的粒子垂直于x 轴射入第二象限，随后垂直于y 轴进入第一象限，最后经过x 轴离开第一象限．粒子在磁场中运动的时间为A. 5π6m qBB. 7π6m qBC. 11π6m qBD.13π6mqB3、（2017·全国III 卷·T18）如图，在磁感应强度大小为B 0的匀强磁场中，两长直导线P 和Q 垂直于纸面固定放置，两者之间的距离为l 。

在两导线中均通有方向垂直于纸面向里的电流I 时，纸面内与两导线距离均为l 的a 点处的磁感应强度为零。

如果让P 中的电流反向、其他条件不变，则a 点处磁感应强度的大小为A ．0B ．033B C ．0233B D ．2B 0 4、（2016·全国III 卷·T18）平面OM 和平面ON 之间的夹角为30°，其横截面（纸面）如图所示，平面OM 上方存在匀强磁场，磁感应强度大小为B 、方向垂直于纸面向外。

高考物理带电粒子在磁场中的运动的技巧及练习题及练习题(含答案)一、带电粒子在磁场中的运动专项训练1．如图所示，一质量为m 、电荷量为+q 的粒子从竖直虚线上的P 点以初速度v 0水平向左射出，在下列不同情形下，粒子经过一段时间后均恰好经过虚线右侧的A 点．巳知P 、A 两点连线长度为l ，连线与虚线的夹角为α=37°，不计粒子的重力，(sin 37°=0.6，cos 37°=0.8).(1)若在虚线左侧存在垂直纸面向外的匀强磁场，求磁感应强度的大小B 1；(2)若在虚线上某点固定一个负点电荷，粒子恰能绕该负点电荷做圆周运动，求该负点电荷的电荷量Q (已知静电力常量为是）；(3)若虚线的左侧空间存在垂直纸面向外的匀强磁场，右侧空间存在竖直向上的匀强电场，粒子从P 点到A 点的过程中在磁场、电场中的运动时间恰好相等，求磁场的磁感应强度的大小B 2和匀强电场的电场强度大小E .【答案】（1）0152mv B ql = （2）2058mv l Q kq = （3）0253mv B ql π= 220(23)9mv E qlππ-=【解析】 【分析】 【详解】（1)粒子从P 到A 的轨迹如图所示：粒子在磁场中做匀速圆周运动，设半径为r 1 由几何关系得112cos 25r l l α== 由洛伦兹力提供向心力可得2011v qv B m r =解得:0 152mv Bql=(2)粒子从P到A的轨迹如图所示：粒子绕负点电荷Q做匀速圆周运动，设半径为r2由几何关系得252cos8lr lα==由库仑力提供向心力得2222vQqk mr r=解得:258mv lQkq=(3)粒子从P到A的轨迹如图所示：粒子在磁场中做匀速圆周运动，在电场中做类平抛运动粒子在电场中的运动时间00sin35l ltv vα==根据题意得，粒子在磁场中运动时间也为t，则2Tt=又22mTqBπ=解得0253mvBqlπ=设粒子在磁场中做圆周运动的半径为r，则0v t rπ=解得:35l r π=粒子在电场中沿虚线方向做匀变速直线运动，21cos 22qE l r t mα-=⋅ 解得:220(23)9mv E qlππ-=2．如图纸面内的矩形 ABCD 区域存在相互垂直的匀强电场和匀强磁场，对边 AB ∥CD 、AD ∥BC ，电场方向平行纸面，磁场方向垂直纸面，磁感应强度大小为 B .一带电粒子从AB 上的 P 点平行于纸面射入该区域，入射方向与 AB 的夹角为 θ（θ<90°），粒子恰好做匀速直线运动并从 CD 射出．若撤去电场，粒子以同样的速度从P 点射入该区域，恰垂直 CD 射出.已知边长 AD=BC=d ，带电粒子的质量为 m ，带电量为 q ，不计粒子的重力.求：(1)带电粒子入射速度的大小；(2)带电粒子在矩形区域内作直线运动的时间； (3)匀强电场的电场强度大小．【答案】（1）cos qBd m θ（2）cos sin m qB θθ （3）2cos qB dm θ【解析】 【分析】画出粒子的轨迹图，由几何关系求解运动的半径，根据牛顿第二定律列方程求解带电粒子入射速度的大小；带电粒子在矩形区域内作直线运动的位移可求解时间；根据电场力与洛伦兹力平衡求解场强. 【详解】（1） 设撤去电场时，粒子在磁场中做匀速圆周运动的半径为R ，画出运动轨迹如图所示，轨迹圆心为O ．由几何关系可知：cos d Rθ=洛伦兹力做向心力：200v qv B m R= 解得0cos qBdv m θ=（2）设带电粒子在矩形区域内作直线运动的位移为x ，有sin d xθ= 粒子作匀速运动：x=v 0t 联立解得cos sin m t qB θθ=（3）带电粒子在矩形区域内作直线运动时，电场力与洛伦兹力平衡：Eq=qv 0B解得2qB dE mcos θ=【点睛】此题关键是能根据粒子的运动情况画出粒子运动的轨迹图，结合几何关系求解半径等物理量；知道粒子作直线运动的条件是洛伦兹力等于电场力.3．如图所示为电子发射器原理图，M 处是电子出射口，它是宽度为d 的狭缝．D 为绝缘外壳，整个装置处于真空中，半径为a 的金属圆柱A 可沿半径向外均匀发射速率为v 的电子；与A 同轴放置的金属网C 的半径为2a.不考虑A 、C 的静电感应电荷对电子的作用和电子之间的相互作用，忽略电子所受重力和相对论效应，已知电子质量为m ，电荷量为e.(1)若A 、C 间加速电压为U ，求电子通过金属网C 发射出来的速度大小v C ；(2)若在A 、C 间不加磁场和电场时，检测到电子从M 射出形成的电流为I ，求圆柱体A 在t 时间内发射电子的数量N.(忽略C 、D 间的距离以及电子碰撞到C 、D 上的反射效应和金属网对电子的吸收)(3)若A 、C 间不加电压，要使由A 发射的电子不从金属网C 射出，可在金属网内环形区域加垂直于圆平面向里的匀强磁场，求所加磁场磁感应强度B 的最小值． 【答案】(1)22e eUv v m=+4alt N ed π=(3) 43mv B ae = 【解析】 【分析】（1）根据动能定理求解求电子通过金属网C 发射出来的速度大小；（2）根据=neI t求解圆柱体A 在时间t 内发射电子的数量N ；（3）使由A 发射的电子不从金属网C 射出，则电子在 CA 间磁场中做圆周运动时，其轨迹圆与金属网相切，由几何关系求解半径，从而求解B. 【详解】（1）对电子经 CA 间的电场加速时，由动能定理得221122e e U mv mv =- 解得：22e eUv v m=+（2）设时间t 从A 中发射的电子数为N ，由M 口射出的电子数为n ， 则 =ne I t224d dNn N a aππ==⨯解得4altN edπ=（3）电子在 CA 间磁场中做圆周运动时，其轨迹圆与金属网相切时，对应的磁感应强度为B ．设此轨迹圆的半径为 r ，则222(2)a r r a -=+2v Bev m r=解得：43mvB ae=4．在如图所示的平面直角坐标系中，存在一个半径R ＝0.2m 的圆形匀强磁场区域，磁感应强度B ＝1.0T ，方向垂直纸面向外，该磁场区域的右边缘与y 坐标轴相切于原点O 点。

高中物理电磁大题和答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN1.（2014年 安徽卷）18．“人造小太阳”托卡马克装置使用强磁场约束高温等离子体，使其中的带电粒子被尽可能限制在装置内部，而不与装置器壁碰撞。

已知等离子体中带电粒子的平均动能与等离子体的温度T 成正比，为约束更高温度的等离子体，则需要更强的磁场，以使带电粒子的运动半径不变。

由此可判断所需的磁感应强度B 正比于A ．TB ．T C．3T D ．2T【答案】A【解析】由于等离子体中带电粒子的平均动能与等离子体的温度T 成正比，即k E T ∝。

带电粒子在磁场中做圆周运动，洛仑磁力提供向心力：2v qvB m R =得mv B qR =。

而212k E mv =故可得：2k mE mvB qR ==又带电粒子的运动半径不变，所以k B E T ∝∝。

A 正确。

2.（2014年 大纲卷）25．(20 分)如图，在第一象限存在匀强磁场，磁感应强度方向垂直于纸面(xy 平面)向外；在第四象限存在匀强电场，方向沿x 轴负向。

在y 轴正半轴上某点以与x 轴正向平行、大小为v 0的速度发射出一带正电荷的粒子，该粒子在(d ，0)点沿垂直于x 轴的方向进人电场。

不计重力。

若该粒子离开电场时速度方向与y 轴负方向的夹角为θ，求： ⑴电场强度大小与磁感应强度大小的比值； ⑵该粒子在电场中运动的时间。

25. 【答案】（１）201tan 2v θ （２）02tan dv θ【考点】带电粒子在电磁场中的运动、牛顿第二定律、【解析】（1）如图粒子进入磁场后做匀速圆周运动，设磁感应强度大小为B ，粒子质量与所带电荷量分别为m 和q ，圆周运动的半径为R 0，由洛伦兹力公式及牛顿第二定律得：2000mv qv B R =由题给条件和几何关系可知：R 0＝d设电场强度大小为E ，粒子进入电场后沿x 轴负方向的加速度大小为a x ，在电场中运动的时间为t ，离开电场时沿x 轴负方向的速度大小为v y 。

高中物理电磁感应练习题及答案一、选择题1、在电磁感应现象中，下列说法正确的是：A.感应电流的磁场总是阻碍原磁通量的变化B.感应电流的磁场方向总是与原磁场的方向相反C.感应电流的磁场方向总是与原磁场的方向相同D.感应电流的磁场方向与原磁场方向无关答案：A.感应电流的磁场总是阻碍原磁通量的变化。

2、一导体在匀强磁场中匀速切割磁感线运动，产生感应电流。

下列哪个选项中的物理量与感应电流大小无关？A.磁感应强度B.导体切割磁感线的速度C.导体切割磁感线的长度D.导体切割磁感线的角度答案：D.导体切割磁感线的角度。

二、填空题3、在电磁感应现象中，当磁通量增大时，感应电流的磁场方向与原磁场方向_ _ _ _ ；当磁通量减小时，感应电流的磁场方向与原磁场方向 _ _ _ _。

答案：相反；相同。

31、一根导体在匀强磁场中以速度v运动，切割磁感线，产生感应电动势。

如果只增大速度v，其他条件不变，则产生的感应电动势将_ _ _ _ ；如果保持速度v不变，只减小磁感应强度B，其他条件不变，则产生的感应电动势将 _ _ _ _。

答案：增大；减小。

三、解答题5、在电磁感应现象中，有一闭合电路，置于匀强磁场中，接上电源后有电流通过，现将回路断开，换用另一电源重新接上，欲使产生的感应电动势增大一倍，应采取的措施是（）A.将回路绕原路转过90°B.使回路长度变为原来的2倍C.使原电源的电动势增大一倍D.使原电源的电动势和回路长度都增大一倍。

答案：A.将回路绕原路转过90°。

法拉第电磁感应定律是电磁学中的重要规律之一，它描述了变化的磁场产生电场，或者变化的电场产生磁场的现象。

这个定律是法拉第在1831年发现的，它为我们打开了一个全新的领域——电磁学，也为我们的科技发展提供了强大的理论支持。

在高中物理中，法拉第电磁感应定律主要通过实验和理论推导来展示，让学生们能够更直观地理解这个重要的规律。

高中的学生们已经对电场和磁场的基本概念有了一定的了解，他们已经掌握了电场线和磁场线的概念，以及安培定则等基本知识。

高中物理必修三磁场磁感线同步练习含答案卷I（选择题）一、选择题（本题共计 10 小题，每题 3 分，共计30分，）1. 科考队进入某一磁矿区域后，发现指南针原来的N极逆时针转过45∘（如图所示的虚线），设该位置地磁场磁感应强度水平分量为B，则磁矿所产生的磁感应强度水平分量的最小值为（）A.BB.2BC.B2D.√2B22. 2002年12月31日上午，举世瞩目的上海磁悬浮列车线首次试运行，它是世界上第一条投入商业运营的磁悬浮列车线．运行全程共30km，最高时速可达552km，单向运行约8min．磁悬浮列车上装有电磁体，铁路底部则安装线圈．通过地面线圈与列车上的电磁体排斥力使列车悬浮起来．地面线圈上的极性与列车上的电磁体下极性总保持（）A.相同 B.相反 C.不能确定 D.以上均不对3. 下列说法中正确的是（）A.磁感线是磁场中客观存在、肉眼看不见的曲线，且总是从磁体的N极指向S极B.两个磁场叠加的区域，磁感线就有可能相交C.穿过线圈的磁通量为零，但该处的磁感应强度不一定为零D.一对通有相同的大小和方向的电流的线圈彼此平行且共轴，当线圈间距调整到适当距离时，两个线圈间可以产生均匀的磁场4. 下列对一些物理现象的描述，错误的是（）A.奥斯特实验说明电流具有磁效应B.磁电式电流表的工作原理是磁场对电流的作用C.安培分子电流假说认为磁体的磁场是由运动电荷产生的D.将一条形磁铁从中间锯断，一块仅为N极，另一块仅为S极5. 下列物品中必须用到磁性材料的是（）A.DVD碟片B.计算机上的磁盘C.电话卡D.喝水用的搪瓷杯子6. 如图所示，a、b、c三根铁棒中有一根没有磁性，则这一根可能是（）A.aB.bC.cD.都有可能7. 若地球磁场是由于地球带电产生的，则地球表面带电情况是（）A.正电B.负电C.不带电D.无法确定8. 下列关于磁场和磁感线的描述正确的是（）A.磁感线从磁体的N极出发，终止于S极，磁场中任意两条磁感线有可能相交B. 磁场的方向就是通电导体在磁场中某点受磁场作用力的方向C. 沿磁感线方向，磁场逐渐减弱D. 在磁场强的地方同一通电导体受的磁场力可能比在磁场弱的地方受的磁场力小9. 以下说法正确的是（）A.第一个提出磁现象的电本质的科学家是奥斯特B.安培通过精密仪器观察到了分子电流从而提出了分子电流假说C.铁钉通常情况不显磁性，是因为它的分子电流的取向杂乱无章D.静止电荷之间的相互作用力是通过磁场而产生的10. 如图所示，电子束沿x轴正方向运动，则电子束产生的磁场在y轴正向A点的方向是（）A.z轴正方向B.z轴负方向C.y轴正方向D.y轴负方向二、多选题（本题共计 5 小题，每题 3 分，共计15分，）11. 下列关于磁场的说法中，正确的是（）A.磁场和电场一样，是客观存在的特殊物质B.磁场是为了解释磁极间相互作用而人为规定的C.磁极与磁极之间，磁极与电流之间的相互作用是通过磁场发生的D.磁场只有在磁极与磁极、磁极与电流发生作用时才产生12. 关于磁场和磁感线，下列叙述正确的是（）A.磁感线可以形象地描述磁场的强弱和方向，其每一点的磁场方向在该处的切线方向上B.磁极间的相互作用是通过磁场产生的C.磁感线总是从磁体的N极指向S极D.磁感线就是磁场中碎铁屑磁化后排列成的曲线13. 如图是几种常见磁场的磁感线分布示意图，下列说法正确的是（）A.图(a)中a端是磁铁的S极，b端是磁铁的N极B.图(a)中a端是磁铁的N极，b端是磁铁的S极C.图(b)是两异名磁极的磁感线分布示意图，c端是N极，d端是S极D.图(b)是两异名磁极的磁感线分布示意图，c端是S极，d端是N极14. 对于右手螺旋定则（安培定则）和左手定则的说法中，正确的是（）A.判断直线电流周围的磁场方向，应用右手螺旋定则，其中大拇指所指的方向与电流方向一致B.判断环形电流中心轴上的磁场方向，应用右手螺旋定则，其中四指和环形电流方向一致C.判断通电螺线管中心轴上的磁场方向，应用左手定则，其中左手弯曲的四指和电流方向一致D.判断磁场方向、电流方向和安培力方向之间的关系，应用安培定则15. 安培分子电流假说可用来解释（）A.运动电荷受磁场力作用的原因B.两通电导体有相互作用的原因C.永久磁铁具有磁性的原因D.软铁棒被磁化的现象卷II（非选择题）三、填空题（本题共计 10 小题，每题 3 分，共计30分，）16. 在光滑水平面上固定一条形磁铁，有一小球以一定的初速度像磁铁方向运动，如果发现小球做减速运动，则小球的材料不可能是________．17. 原先没有磁性的铁，在长期受到磁铁的吸引会产生磁性________．（判断对错）18. 说明下列图中小磁针N极的指向．(a)图中小磁针1北极指向________；小磁针2北极指向________；(b)图中小磁针1北极指向________；小磁针2北极指向________；小磁针3北极指向________；(c)图中小磁针1北极指向________；小磁针2北极指向________．19. 磁铁外部的磁感线是从磁铁的________出来，进入磁铁的________．20. 磁体与________之间、磁体与________之间，以及通电导体与________之间的相互作用，都是通过________来发生的．21. 磁感线：所谓磁感线是在磁场中画出的一些有方向的曲线，在这些曲线上，每一点的磁场方向都在该点的________方向上．磁感线是闭合的曲线，磁铁外部从________极到________极，磁铁内部从________极到________极．22. 直线电流周围的磁场方向可以用安培定则（又称为右手螺旋定则）来判断．这安培定则中用________表示电流方向，用右手自然弯曲的________表示其周围磁感线方向；对于环形电流和通电螺线管，可用安培定则判定，在安培定则中用________表示电流方向，用________表示内部磁感线的方向．23. 如图所示，磁铁的磁极吸引着两根细铁丝，两铁丝下端相斥，这是因为铁丝被________后，远离磁铁磁极的一端极性相________，由于________名磁极相互排斥而远离．24. 磁化了的物体，经过高温或剧烈震动容易________．25. 缝衣针、螺丝刀等钢铁物体，与磁铁接触后就会显示出磁性，这种现象叫做________．原来有磁性的物体，经过高温、剧烈震动或者逐渐减弱的交变磁场的作用，就会失去磁性，这种现象叫做________．四、解答题（本题共计 10 小题，每题 10 分，共计100分，）26. 图(a)是条形磁铁的磁场，请你画出过P点的磁感线；图(b)是一个通电线圈，请你画出过P点的磁感线．27. 你见过只有一个磁极的磁铁吗？能否将一条形磁铁折断得到单个磁极（如图）？为什么？28. 如图所示，有一金属棒ab静止在宽为1m水平光滑轨道上，轨道处在竖直向上B= 0.1T的匀强磁场中，已知电池电动势E=3V，内阻为r=0.2Ω，金属棒接入部分的电阻R=0.4Ω，两轨道的电阻均可忽略不计，开关闭合瞬间，求：（1）通过金属棒ab的电流；（2）金属棒ab所受安培力的大小和方向．29. 长时间放在同一地方的金属物体可能使指南针指针偏转，为什么？30. 如图所示，系在细线下端的回形针受磁铁吸引悬在空中，在回形针的下方用点燃的蜡烛加熬回形针。

高中物理【磁场磁感线】专题练习题[A组基础达标练]1．如图所示，小磁针正上方的直导线与小磁针平行，当导线中有电流时，小磁针会发生偏转。

首先观察到这个实验现象的物理学家和观察到的现象是()A．物理学家伽利略，小磁针的N极转向纸内B．天文学家开普勒，小磁针的S极转向纸内C．物理学家牛顿，小磁针静止不动D．物理学家奥斯特，小磁针的N极转向纸内解析：首先发现电流的磁效应的科学家是奥斯特，根据右手螺旋定则和小磁针N极受力方向为该点磁场方向可知D正确。

答案：D2．指南针是我国古代的四大发明之一。

司南是春秋战国时期发明的一种指南针，如图所示。

它由青铜盘和磁勺组成，磁勺放置在青铜盘的中心，可以自由转动。

由于受地磁场作用，司南的磁勺尾静止时指向南方。

下列说法正确的是()A．磁勺能够指示方向，是利用了地磁场对磁勺的作用B．磁勺的指向不会受到附近磁体的干扰C．磁勺的指向不会受到附近铁块的干扰D．磁勺的N极位于司南的磁勺尾部解析：司南能够指示南北，是由于地球具有磁性，地磁场是南北指向，故A正确；司南的指向会受到附近磁体和铁块的干扰，故B、C错误；由于司南的磁勺尾静止时指向南方，所以磁勺的S极位于司南的磁勺尾部，故D错误。

答案：A3．关于磁场、磁感线和电场线，下列说法正确的是()A．磁感线是闭合曲线，而电场线不是闭合曲线B．磁感线和电场线都是一些相互平行的曲线C．地磁场起始于地球的北极附近，终止于地球的南极附近D．磁感线和电场线都是真实存在的线解析：磁体周围的磁感线从N极出发回到S极，在内部则是从S极回到N极，磁感线是闭合曲线；电场线从正电荷或无限远出发，终止于无限远或负电荷，电场线不是闭合曲线，A正确；磁感线和电场线不一定都是一些互相平行的曲线，B错误；磁体周围的磁感线从N 极出发回到S极，在内部则是从S极回到N极，故在地球外部，地磁场从地球的地理南极附近出来，进入地球的地理北极附近，不是终止，C错误；磁感线和电场线是为了形象描述磁场和电场而引入的假想的线，实际并不存在，D错误。

高中物理带电粒子在磁场中的运动题20套(带答案)含解析一、带电粒子在磁场中的运动专项训练1．如图所示为电子发射器原理图，M 处是电子出射口，它是宽度为d 的狭缝．D 为绝缘外壳，整个装置处于真空中，半径为a 的金属圆柱A 可沿半径向外均匀发射速率为v 的电子；与A 同轴放置的金属网C 的半径为2a.不考虑A 、C 的静电感应电荷对电子的作用和电子之间的相互作用，忽略电子所受重力和相对论效应，已知电子质量为m ，电荷量为e.(1)若A 、C 间加速电压为U ，求电子通过金属网C 发射出来的速度大小v C ；(2)若在A 、C 间不加磁场和电场时，检测到电子从M 射出形成的电流为I ，求圆柱体A 在t 时间内发射电子的数量N.(忽略C 、D 间的距离以及电子碰撞到C 、D 上的反射效应和金属网对电子的吸收)(3)若A 、C 间不加电压，要使由A 发射的电子不从金属网C 射出，可在金属网内环形区域加垂直于圆平面向里的匀强磁场，求所加磁场磁感应强度B 的最小值． 【答案】(1)22e eUv v m=+4alt N ed π=(3) 43mv B ae = 【解析】 【分析】（1）根据动能定理求解求电子通过金属网C 发射出来的速度大小；（2）根据=neI t求解圆柱体A 在时间t 内发射电子的数量N ；（3）使由A 发射的电子不从金属网C 射出，则电子在 CA 间磁场中做圆周运动时，其轨迹圆与金属网相切，由几何关系求解半径，从而求解B. 【详解】（1）对电子经 CA 间的电场加速时，由动能定理得221122e e U mv mv =- 解得：22e eUv v m=+（2）设时间t 从A 中发射的电子数为N ，由M 口射出的电子数为n ， 则 =ne I t224d dNn N a aππ==⨯解得4altN edπ=（3）电子在 CA 间磁场中做圆周运动时，其轨迹圆与金属网相切时，对应的磁感应强度为B ．设此轨迹圆的半径为 r ，则222(2)a r r a -=+2v Bev m r=解得：43mvB ae=2．“太空粒子探测器”是由加速、偏转和收集三部分组成，其原理可简化如下：如图1所示，辐射状的加速电场区域边界为两个同心平行半圆弧面，圆心为O ，外圆弧面AB 的电势为2L()o ϕ>，内圆弧面CD 的电势为φ，足够长的收集板MN 平行边界ACDB ，ACDB 与MN 板的距离为L ．假设太空中漂浮着质量为m ，电量为q 的带正电粒子，它们能均匀地吸附到AB 圆弧面上，并被加速电场从静止开始加速，不计粒子间的相互作用和其它星球对粒子的影响，不考虑过边界ACDB 的粒子再次返回．（1）求粒子到达O 点时速度的大小；（2）如图2所示，在PQ （与ACDB 重合且足够长）和收集板MN 之间区域加一个匀强磁场，方向垂直纸面向内，则发现均匀吸附到AB 圆弧面的粒子经O 点进入磁场后最多有23能打到MN 板上，求所加磁感应强度的大小；（3）如图3所示，在PQ （与ACDB 重合且足够长）和收集板MN 之间区域加一个垂直MN 的匀强电场，电场强度的方向如图所示，大小4E Lφ=，若从AB 圆弧面收集到的某粒子经O 点进入电场后到达收集板MN 离O 点最远，求该粒子到达O 点的速度的方向和它在PQ 与MN 间运动的时间． 【答案】（1）2q v mϕ=；（2）12m B L q ϕ=；（3）060α∴= ；22m L q ϕ【解析】 【分析】 【详解】试题分析：解：（1）带电粒子在电场中加速时，电场力做功，得：2102qU mv =-2U ϕϕϕ=-=2q v mϕ=(2）从AB 圆弧面收集到的粒子有23能打到MN 板上，则上端刚好能打到MN 上的粒子与MN 相切，则入射的方向与OA 之间的夹角是60︒，在磁场中运动的轨迹如图甲，轨迹圆心角060θ=．根据几何关系，粒子圆周运动的半径：2R L =由洛伦兹力提供向心力得：2v qBv m R=联合解得：12m B L qϕ=（3）如图粒子在电场中运动的轨迹与MN 相切时，切点到O 点的距离最远， 这是一个类平抛运动的逆过程． 建立如图坐标.212qE L t m= 222mL mt L qE q ϕ== 22x Eq qEL q v t m m m ϕ===若速度与x 轴方向的夹角为α角 cos x v v α=1cos 2α=060α∴=3．如图甲所示，在直角坐标系中的0≤x≤L 区域内有沿y 轴正方向的匀强电场，右侧有以点（2L ，0）为圆心、半径为L 的圆形区域，与x 轴的交点分别为M 、N ，在xOy 平面内，从电离室产生的质量为m 、带电荷量为e 的电子以几乎为零的初速度从P 点飘入电势差为U 的加速电场中，加速后经过右侧极板上的小孔Q 点沿x 轴正方向进入匀强电场，已知O 、Q 两点之间的距离为2L，飞出电场后从M 点进入圆形区域，不考虑电子所受的重力。

2021年高考物理100考点最新模拟题千题精练（选修3-2）第四部分电磁感应专题4.25 磁场变化产生的感应电动势问题（提高篇）一．选择题1.（2020年3月武汉质检）如图(a)所示，在倾角θ=37°的斜面上放置着一个金属圆环，圆环的上半部分处在垂直斜面向上的匀强磁场（未画出）中，磁感应强度的大小按如图(b)所示的规律变化。

释放圆环后，在t=8t0和t=9t0时刻，圆环均能恰好静止在斜面上。

假设圆环与斜面间的最大静摩擦力等于滑动摩擦力，sin37°=0.6，则圆环和斜面间的动摩擦因数为A ．B ．C ．D ．【参考答案】.D【命题意图】本题以静止在斜面上金属圆环为情景，考查法拉第电磁感应定律、闭合电路欧姆定律、安培力、平衡条件及其相关知识点，考查的核心素养是“运动和力”的观点、场的观点和科学思维能力。

【解题思路】设金属圆环半径为r，则面积为S=πr2，圆环单位长度电阻为R0，则圆环电阻为R=2πr R0，在0~8t0时间内，金属圆环内磁感应强度变化率大小为Bt∆∆=08Bt，根据法拉第电磁感应定律，在金属圆环中产生的感应电动势大小为，E1=0.5SBt∆∆=πr2016Bt，感应电流为I1=E1/R=00032rBR t，在t=8t0时刻，金属圆环所受安培力为F1=B0I1·2r=220016r BR t。

由平衡条件，mgsinθ+F1=μmgcosθ，即0.6mg+220016r BR t=0.8μmg···○1；在9t0~10t0时间内，金属圆环内磁感应强度变化率大小为Bt∆∆=0Bt，根据法拉第电磁感应定律，在金属圆环中产生的感应电动势大小为，E2=0.5SBt∆∆=πr202Bt，感应电流为I2=E2/R=0004rBR t，在t=9t0时刻，金属圆环所受安培力为F 2=B 0I 2·2r=220002r B R t 。