(整理)9广义积分习题课.

第九章 广义积分习题课一、主要内容 1、基本概念无穷限广义积分和无界函数广义积分敛散性的定义、绝对收敛、条件收敛。

2、敛散性判别法Cauchy 收敛准则、比较判别法、Cauchy 判别法、Abel 判别法、Dirichlet 判别法。

3、广义积分的计算4、广义积分与数项级数的关系5、广义积分敛散性的判别原则和程序包括定义在内的广义积分的各种判别法都有特定的作用对象和原则，定义既是定性的――用于判断简单的具体广义积分的敛散性，也是定量的――用于计算广义积分，其它判别法都是定性的，只能用于判断敛散性，Cauchy 判别法可以用于抽象、半抽象及简单的具体广义积分的敛散性，比较判别法和Cauchy 判别法用于不变号函数的具体广义积分和抽象广义积分判别法，Abel 判别法和Dirichlet 判别法处理的广义积分结构更复杂、更一般。

对具体广义积分敛散性判别的程序： 1、比较法。

2、Cauchy 法。

3、Abel 判别法和Dirichlet 判别法。

4、临界情况的定义法。

5、发散性判别的Cauchy 收敛准则。

注、对一个具体的广义积分敛散性的判别，比较法和Cauchy 法所起作用基本相同。

注、在判断广义积分敛散性时要求：1、根据具体题型结构，分析特点，灵活选择方法。

2、处理问题的主要思想：简化矛盾，集中统一，重点处理。

3、重点要掌握的技巧：阶的分析方法。

二、典型例子下述一系列例子，都是要求讨论其敛散性。

注意判别法使用的顺序。

例1 判断广义积分⎰+∞+=0qp x x dxI 的敛散性。

分析 从结构看，主要是分析分母中两个因子的作用。

解、记⎰+=101qp x x dx I ，⎰+∞+=12q p x x dxI对1I ，先讨论简单情形。

q p =时，1<p 时收敛，1≥p 时发散。

q p ≠，不妨设q p <，则⎰-+=11)1(pq p x x dxI ，故，0≤p 时为常义积分，此时收敛。

第五节 广义积分我们前面介绍的定积分有两个最基本的约束条件：积分区间的有限性和被积函数的有界性. 但在某些实际问题中,常常需要突破这些约束条件. 因此在定积分的计算中,我们也要研究无穷区间上的积分和无界函数的积分. 这两类积分通称为广义积分或反常积分,相应地,前面的定积分则称为常义积分或正常积分.分布图示★ 无穷限的广义积分★ 无穷限的广义积分几何解释★ 例1 ★ 例2 ★ 例3 ★ 例4★ 例5 ★ 例6 ★ 无界函数的广义积分★ 例7 ★ 例8 ★ 例9 ★ 例10 ★ 例11 ★ 例12★ 例13 ★ 内容小结 ★ 课堂练习★ 习题5-5 ★ 返回内容要点一、无穷限的广义积分)()(|)()(a F F x F dx x f a a-+∞==∞++∞⎰)()(|)()(-∞-==∞-∞-⎰F b F x F dx x f b b)()(|)()(-∞-+∞==∞+∞-+∞∞-⎰F F x F dx x f二、无界函数的广义积分⎰⎰++→=ba badx x f dx x f εε)(lim )(0.)(lim)(0⎰⎰-+→=εεb aba dx x f dx x f例题选讲无穷限的广义积分例1 (E01) 计算广义积分⎰+∞-0dx e x .解 对任意的,0>b 有⎰-bx dx e 0⎰----=--bbxee 0)1(b e --=1于是⎰-+∞→bx b dx e 0lim)1(lim b b e -+∞→-=01-=1=因此⎰∞+-0dx e x⎰-+∞→=bxb dx e 0lim1=或⎰∞+-0dx e x+∞--=0xe )1(0--=.1=例2 (E02) 判断广义积分⎰+∞sin xdx 的敛散性.解 对任意,0>b⎰bxdx 0sin b xcos -=)0(cos cos +-=b b cos 1-=因为)cos 1(lim b b -+∞→不存在，故由定义知无穷积分⎰+∞sin xdx 发散.例3 (E03) 计算广义积分⎰+∞∞-+21x dx.解 ⎰∞+∞-+21x dx ⎰⎰+∞∞-+++=020211x dx x dx ⎰⎰+++=+∞→-∞→bb a a x dxx dx0221lim 1limb b a a x x 00][arctan lim ][arctan lim +∞→-∞→+=b a b a arctan lim arctan lim +∞→-∞→+=22ππ+⎪⎭⎫ ⎝⎛--=.π=例4 计算广义积分.1sin 1/22⎰∞+πdx x x解 原式⎰∞+⎪⎭⎫⎝⎛-=π211sin x d x ⎰⎪⎭⎫ ⎝⎛-=+∞→bb x d x π211sin limbb x π21cos lim ⎥⎦⎤⎢⎣⎡-=+∞→⎥⎦⎤⎢⎣⎡-=+∞→2cos 1cos lim πb b .1=例5 (E04) 计算广义积分⎰+∞-0dt te pt (p 是常数, 且0>p 时收敛).解⎰∞+-0dt te pt ⎰∞+--=01pttdep⎰∞+-+∞-+-=011dt e pte ppt pt+∞-+∞---=02011pt pte pte p)10(10lim 12--+-=-+∞→p te p pt t .12p= 注: 其中不定式pt t te -+∞→lim ptt e t+∞→=limpt t pe 1lim+∞→=.0=例6 (E05) 讨论广义积分⎰∞+11dx x p的敛散性. 证 )1(,1=p ⎰∞+11dx xp ⎰∞+=11dx x+∞=1ln x ;+∞=)2(,1≠p ⎰∞+11dx x p +∞--=111p x p⎪⎩⎪⎨⎧>-<∞+=1,111,p p p因此，当1>p 时，题设广义积分收敛，其值为;11-p 当1≤p 时，题设广义积分发散.无界函数的广义积分例7 (E06) 计算广义积分).0(022>-⎰a xa dx a解 原式⎰-→-=+εεa x a dx 0220lim εε-→⎥⎦⎤⎢⎣⎡=+a a x 00arcsin lim ⎥⎦⎤⎢⎣⎡--=+→0arcsin lim 0a a εε.2π=例8 (E07) 计算广义积分 ⎰21ln xx dx. 解⎰21ln x x dx⎰+→+=210ln lim εεx x dx⎰+→+=210ln )(ln lim εεxx d 210)][ln(ln lim εε+→+=x ))]1ln(ln()2[ln(ln lim 0εε+-=+→.∞=故题设广义积分发散.例9 (E08) 讨论广义积分⎰11dx x q的敛散性. 证 )1(,1=q ⎰101dx x q⎰=101dx x10ln x =,+∞=)2(,1≠q ⎰101dx x q 1011q x q -=-⎪⎩⎪⎨⎧<->∞+=1,111,q qq 因此，当1<q 时，广义积分收敛，其值为;11q- 当1≥q 时，广义积分发散.例10 计算广义积分⎰=⋅-33/21)1(x x dx瑕点. 解⎰-303/2)1(x dx⎰⎰-+-=313/2103/2)1()1(x dxx dx⎰-103/2)1(x dx 13/1)1(3/211--=x 3=， ⎰-313/2)1(x dx 313/1)1(3/211--=x ,233⋅= ∴⎰-303/2)1(x dx).21(33+=例11 计算广义积分.)1(03⎰∞++x x dx解 此题为混合型广义积分，积分上限为,+∞下限0=x 为被积函数的瑕点. 令,t x =则,2t x =+→0x 时，,0→t +∞→x 时，,+∞→t 于是⎰+∞+03)1(x x dx ⎰∞++=2/32)1(2t t tdt.)1(202/32⎰∞++=t dt再令,tan u t =取,arctan t u =0=t 时,0=u +∞→t 时,2π→u 于是⎰∞++03)1(x x dx ⎰=2032sec sec 2πuudu⎰=20cos 2πudu .2=注: 本题若采用变换t x =+11等，计算会更简单,请读者自行解之.例12 (E09) 计算广义积分⎰-10)1(arcsindx x x x .解 被积函数有两个可疑的瑕点:0=x 和.1=x 因为1)1(arcsin lim 0=-+→x x x x 所以, 1=x 是被积函数的唯一瑕点.从而⎰-1)1(arcsin dx x x x ⎰-=1)1(arcsin dx x x x 102)(arcsin x =.42π=例13 计算.11105⎰∞+++xx x dx解 分母的阶数较高，可利用到代换，令,1tx =则⎰∞+++11051xx x dx ⎰++-=110541dt tt t ⎰++=110541tt dt t再令,5t u =则⎰++110541tt dt t ⎰++=12151u u du ⎰+⎪⎭⎫ ⎝⎛+=12432151u du102121ln 51⎪⎭⎫⎝⎛++++=u u u .321ln 51⎪⎪⎭⎫ ⎝⎛+=课堂练习1. 计算广义积分⎰+∞+122)1(ln dx x xx ;2. 判断广义积分⎰-101ln dx x x的瑕点.。

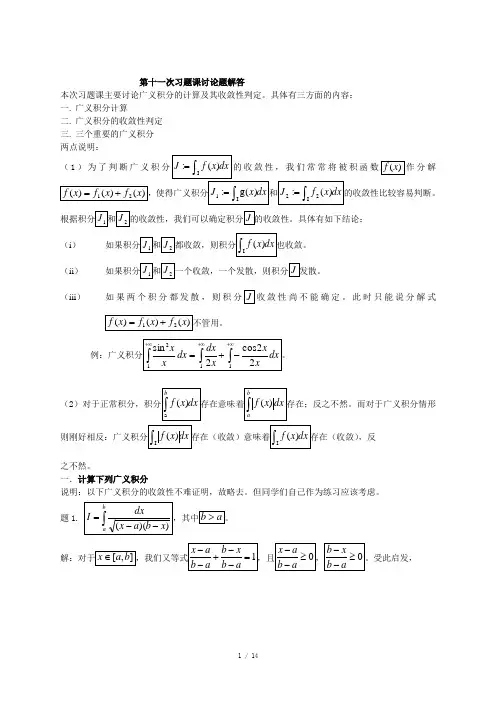
第十一次习题课讨论题解答本次习题课主要讨论广义积分的计算及其收敛性判定。

具体有三方面的内容：一.广义积分计算二.广义积分的收敛性判定三.三个重要的广义积分两点说明：（1）为了判断广义积收敛性，我们常常将被积函分解（i）（ii）（iii）如果两个积分都发散，则积分敛性尚不能确定。

此时只能说分解式（2，反之不然。

一．计算下列广义积分说明：以下广义积分的收敛性不难证明，故略去。

但同学们自己作为练习应该考虑。

题题2．。

另解：原式题3题4二、判断广义积分的收敛性题1题2为考察无穷积分。

题（第六章复习题题2（1），p.206）我们再来考虑积分在无穷远处的收敛性。

我们将被积函数写作题（习题6.2题9（2），p.206）由此可见，积分为条件收敛。

解答完毕。

注：对于无穷区间型的广义积分而言，积分收敛，并不意味着被积函数有界，当然更遑论被 积函数有趋向于零的极限。

题3，p.206）解：注意被积函数没有有限奇点，0。

根据Dirichlet 判别法可知积分收敛。

我们进一步积分的绝对收敛性。

注意从而存使于是题6. 讨论如下广义积分的绝对收敛性和条件收敛性,(i)解：（i ）由于被积函数为非负的，因此它收敛即为绝对收敛。

时， 根据不等式时，根据不等式（ii再根据结论（i）根据不等式（iii三．三个重要的广义积分（1）计算Euler（2）计算Froullani（3）证明概率积分（也称Euler-Poisson（证明有点长，已超出要求，可略去。

但证明不超出我们所学，也不难懂。

）（1）. (课本第六章总复习题9，p.207 ) 计算EulerEuler积分的瑕点。

这里我们略去证明收敛性的证明（不难），只专注我们尝试用配对法来求积分值。

不难证明注：可利用上述Euler积分计算以下积分的值（2）证明Froullani广义积分处理。

因此因此原积分为注1注2：利用上述Froullaniiii（3）证明概率积分（也称Euler-Poisson注1注2：下个学期我们将学习多重积分。

经济数学基础 第6章 定积分第六单元 广义积分一、学习目标通过本节课的学习，了解无穷积分及收敛、发散的概念．二、内容讲解定积分是在有限区间],[b a 上讨论的积分问题，但有的积分问题需要在无穷区间上讨论，这就是广义积分：广义积分（或称无穷积分）⎰⎰∞+∆+∞→=a b a b x x f x x f d )(d )(lim⎰⎰∞-∆-∞→=b b aa xx f x x f d )(d )(lim在上两个定义式中，若左端的极限存在，则称右端的无穷积分收敛；若左端的极限不存在，则称右端的无穷积分发散．三、例题讲解例1计算广义积分⎰∞+12d 1x x ．解：⎰∞+12d 1x x ⎰+∞→=bb x x 12d 1lim bb x 1)1(lim -=+∞→1)11(lim =+-=+∞→b b例2计算广义积分⎰∞+-02d e xx ．解：⎰∞+-02d e x x ⎰-+∞→=b x b x 02d e lim bx b 02e 21lim -+∞→-=21)e 1(21lim 2=-=-+∞→b b 例3计算广义积分⎰∞--0d e 2xx x ．经济数学基础 第6章 定积分解：⎰∞--0d e 2x x x ⎰--∞→=0d e lim 2a x a x x ⎰--=--∞→02)(d e 21lim 2a x a x 02e 21lim a x a --∞→-= 21)e (121lim 2-=--=--∞→a a四、课堂练习计算下列广义积分积分：（1）⎰∞+-022d e3xx x ；（2）⎰∞+132d 1xx．对于无穷积分⎰∞+axx f d )(，先求⎰b axx f d )(，再求⎰+∞→bab xx f d )(lim，若此极限存在，它就是所求的积分值．若此极限不存在，则⎰∞+axx f d )(发散．五、课后作业求下列广义积分：（1）⎰∞+-0d e2xx x；（2）⎰∞+12d ln x x x ；（3）⎰∞+4d 1x x ．。

习题课 广义积分1. 判断dx x x xx ⎰∞+++121arctan 的收敛性.解: 与dx x⎰+∞121比较，由极限比较法，收敛.2. 判断dx x x x ⎰∞++151ln 的收敛性.解: 由0ln lim3=+∞→xx x ，存在0>X ，使得当0>>X x 时，3ln x x <，167,11ln 535>=+<+p x x x x x x ，直接比较法，收敛.3. 判断广义积分dx x⎰πsin 1的收敛性.解: dx x⎰πsin 1dx xdx x⎰⎰+=πππ220sin 1sin 1，第一个积分显然收敛，对第二个积分令dt dx t x ==-,π，dx xdt tdx x⎰⎰⎰=-=2022sin 1sin 1sin 1ππππ，收敛.4. 讨论dx xxp⎰∞+0arctan 的收敛性.解: dx xxp⎰∞+0arctan dx xx p⎰=10arctan dx xx p⎰∞++1arctan对第一个积分，pxx arctan 与11-p x等价（0→x ），2,11<⇒<-p p 收敛.对第二个积分，pxx arctan 与qx1进行比阶，⎪⎩⎪⎨⎧=>=-+∞→qp q p xx qp x 2arctan limπ因此，当1>≥q p 时第二个积分收敛。

综合上述分析，21<<p 时积分收敛。

5. 判断广义积分的收敛性⎰∞+⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+01111ln dx x x解: ⎰∞+⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+01111ln dx x x ⎰⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+=101111ln dx x x ⎰∞+⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++11111ln dx x x,0+→x ⎪⎭⎫ ⎝⎛+x 11ln ∽x ln -，⎰⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛+101111ln dx x x 收敛； ,+∞→x x x +-⎪⎭⎫ ⎝⎛+1111ln ∽221x ，⎰∞+⎥⎦⎤⎢⎣⎡+-⎪⎭⎫ ⎝⎛++11111ln dx x x 收敛。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。