时域模态分析及软件开发

模态分析方法与步骤下面我将从模态分析的定义、方法、步骤和案例实践等方面进行详细介绍。

一、模态分析的定义模态分析是指通过对系统的不同动态模态（如结构模态、振动模态等）进行分析和评估，以揭示系统的特性、行为和潜在问题。

其目的是为了更好地了解系统的功能、性能、稳定性等，并为系统的优化提供依据。

二、模态分析的方法1.实验方法：通过实际测试和测量，获取系统的模态参数（如固有频率、阻尼比、模态形态等），从而分析系统的动态特性。

2.数值模拟方法：利用数学建模和计算机仿真技术，建立系统的动力学模型，并进行模拟分析，以获取系统的模态响应和模态特性。

3.统计分析方法：通过对大量历史数据或采样数据的分析，探索系统的模态变化规律和概率分布情况。

三、模态分析的步骤1.确定分析目标：明确需要进行模态分析的对象、目的和要求。

例如，是为了定位系统的故障、评估系统的稳定性、优化系统的结构等。

2.数据采集和处理：根据分析目标，确定所需的数据类型和采集方法，例如使用传感器进行采集或获取历史数据。

然后对采集到的数据进行处理，如滤波、时域变换、频域分析等。

3.建立模型：根据已有的数据和系统特性，建立适当的模型。

例如，对其中一结构物进行模态分析时，可以建立结构的有限元模型。

4.分析模态特性：利用实验、仿真或统计方法，分析系统的模态特性，如固有频率、振型等。

可以绘制频谱图、振型图等，以便直观地展示结果。

5.识别问题和改进方案：基于对系统模态特性的分析，识别潜在问题，并提出相应的改进方案。

例如，如果发现其中一模态频率太低，可能意味着系统存在过度振动或共振问题，需要采取相应的措施来改进。

6.验证和优化：对改进方案进行验证和优化，以确保其有效性和可行性。

可以通过迭代分析和实验评估来逐步完善方案。

四、模态分析的案例实践1.桥梁的模态分析：对大跨度桥梁的模态分析可以帮助提前发现潜在的共振问题，并优化桥梁的设计和结构。

例如，可以通过数值模拟方法对桥梁的振动特性进行分析，以确定固有频率和振型，并预测桥梁在不同外界激励下的动态响应。

南京航空航天大学硕士学位论文运行模态参数识别及软件开发姓名：***申请学位级别：硕士专业：工程力学指导教师：***20090101南京航空航天大学硕士学位论文摘要经过国内外学者几十年的共同努力，模态分析理论吸取了振动理论、信号分析、数据处理、概率统计以及自动控制理论中的相关理论，形成了一套具自身特色的理论体系，提出了许多模态参数识别方法，一些模态分析的软件也随之开发出来，在工程领域中得到广泛的应用。

本文针对运行模态参数识别（OMA）方法，进行了较为系统地介绍，并对增强功率谱频域分解（EFDD）、辅助变量法（Instrumental Variable）、SSI-Cov方法（Covariance-Driven Stochastic Subspace Identification）和SSI-Data方法（Data-Driven Stochastic Subspace Identification）四种OMA方法进行了详细地推导和研究，并用LabVIEW语言开发了相应的模态参数识别模块。

同时本文开发完成了一个运行模态参数识别软件，该软件主要包括文件功能模块、几何功能模块，测量功能模块、参数识别功能模块和结果动画显示功能模块。

软件具有良好的、仪器化的人机交互界面。

本文应用两个仿真算例及实验测试数据对四种OMA模态参数识别方法，及开发的软件进行了考核，结果表明开发的四种模态参数识别方法和软件的正确的和可信的。

本文受国家自然科学基金项目(编号：10772076)和江苏省自然科学基金（创新人才学术带头人）项目（编号：BK2006520）的资助。

关键词：模态参数识别，试验模态分析，运行模态分析，时域，频域，模块开发I运行模态参数识别及软件开发I IAbstractModal analysis has been a theoretical system with its own special characteristics after absorbingthe interrelated theories, such as signal analysis, date processing, probability & statistic and auto control theory. Many modal parameter identification approaches have been proposed by the cooperative effort of domestic and overseas scholars in the latest decades. Some classical modal parameter identification methods have been developed and integrated in some commercial software. These methods have also been widely applied in lots of actual engineering structures.This dissertation systematically introduces the development of Operational Modal Analysis (OMA). Then four OMA identification methods, such as Enhanced-power-spectrum Frequency Domain Decomposition (EFDD), Instrumental Variable (IV), Covariance-Driven Stochastic Subspace Identification (SSI-Cov) and Covariance-Data Stochastic Subspace Identification (SSI-Data), are formulated. The corresponding modal parameter identification modules are realized using LabVIEW programming language. At the same time, an Operational Modal Analysis software is implemented in this thesis. The software includes file function module, geometry function module, measuring function module, analysis function module and modal shape animation display module. The software has a friendly and instrument-based user-computer interaction interface. Two numerical examples and one experimental example are studied. Results validate the correctness and creditability of the developed four OMA modules and all functions of the proposed software.This research is supported by the National Natural Science Foundation of China through Grant No. 10772076, the Natural Science Foundation of Jiang Su Province through Grant No. BK2006520.Key Words: modal parameter identification, experimental modal analysis, operational modal analysis, time domain, frequency domain, development of module南京航空航天大学硕士学位论文图、表清单图 1.1运行模态识别方法分类图 (3)图 3.1 Windows菜单控制和按钮区控制图 (33)图 3.2 软件整体框架结构图 (33)图 3.3新建工程文件图 (34)图 3.4 打开工程文件图 (34)图 3.5 模型显示图 (35)图 3.6测量信息输入图 (36)图 3.7 测量参数修改图 (36)图 3.8测量参数判断图 (36)图 3.9 多文件输入图 (37)图 3. 10 采样通道数不符图 (37)图 3.11 查看时域信号图 (38)图 3.12 时域信号ZOOM显示图 (39)图 3.13 相关函数查看图 (39)图 3.14 功率谱密度函数信号查看图 (40)图 3.15 参数识别方法选取图 (40)图 3.16 EFDD方法识别流程图 (41)图 3 17 EFDD方法识别图 (42)图 3.18 参考通道选择图 (42)图 3.19 输入计算点长度图 (42)图 3.20 输入循环次数图 (43)图 3.21 IV方法PQ值输入图 (43)图 3.22 参数结果挑选流程图 (44)图 3.23 参数结果挑选及显示图 (44)图 3.24 振型的动画显示图 (45)图 4.1.1 十单元悬臂梁模型 (46)图 4.1.2 悬臂梁截面示意图 (46)图 4.1.3 悬臂梁结构前六阶振型图 (47)V运行模态参数识别及软件开发V I 图 4.1.4 悬臂梁模型功率谱密度函数特征值曲线图-不加噪 (47)图 4.1.5悬臂梁模型功率谱密度函数特征值曲线图-加噪5% (48)图 4.1.6悬臂梁模型功率谱密度函数特征值曲线图-加噪10% (48)图 4.1.7 EFDD方法识别振型MAC图-不加噪 (49)图 4.1.8 EFDD方法识别振型MAC图-加噪5% (49)图 4.1.9 EFDD方法识别振型MAC图-加噪10% (50)图 4.1.10 悬臂梁结构振型识别结果动画显示-前六阶 (50)图 4.1.11 IV方法识别频率稳定图-不加噪 (50)图 4.1.12 IV方法识别频率稳定图-加噪5% (51)图 4.1.13 IV方法识别频率稳定图-加噪10% (51)图 4.1.14 IV方法识别振型MAC图-不加噪 (52)图 4.1.15 IV方法识别振型MAC图-加噪5% (52)图 4.1.16 IV方法识别振型MAC图-加噪10% (53)图 4.1.17 SSI-COV方法识别频率稳定图-不加噪 (53)图 4.1.18 SSI-COV方法识别频率稳定图-加噪5% (53)图 4.1.19 SSI-COV方法识别频率稳定图-加噪10% (54)图 4.1.20 SSI-COV方法识别振型MAC图-不加噪 (55)图 4.1.21 SSI-COV方法识别振型MAC图-加噪5% (55)图 4.1.22 SSI-COV方法识别振型MAC图-加噪10% (55)图 4.1.23 SSI-DATA方法识别频率稳定图-不加噪 (56)图 4.1.24 SSI-DATA方法识别频率稳定图-加噪5% (56)图 4.1.25 SSI-DATA方法识别频率稳定图-加噪10% (56)图 4.1.26 SSI-DATA方法识别振型MAC图-不加噪 (57)图 4.1.27 SSI-COV方法识别振型MAC图-加噪5% (58)图 4.1.28 SSI-COV方法识别振型MAC图-加噪10% (58)图 4.2.1 塔形结构示意图和输出点布置图 (59)图 4.2.2 塔形结构前六阶振型图 (60)图 4.2.3EFDD方法功率谱函数的特征值曲线图 (60)图 4.2.4 EFDD方法识别振型MAC图 (61)图 4.2.5 EFDD方法振型显示图 (61)图 4.2.6 IV方法频率稳定图 (62)南京航空航天大学硕士学位论文图 4.2.7 IV方法识别振型MAC图 (62)图 4.2.8 SSI-COV方法频率稳定图 (63)图 4.2.9 SSI-COV方法识别振型MAC图 (63)图 4.2.10 SSI-DATA方法识别频率稳定图 (64)图 4.2.11 SSI-DATA方法振型MAC图 (65)图 4.3.1三层钢架试验模型 (66)图 4.3.2 三层钢架有限元分析模型 (67)图 4.3.3 对称结构八阶振型前四阶 (68)图 4.3.4对称结构八阶振型后四阶 (68)图 4.3.5对称结构测点布置图 (68)图 4.3.6 EFDD方法功率谱密度函数的特征值曲线图 (69)图 4.3.7 IV方法频率稳定图 (69)图 4.3.8 SSI-COV方法频率稳定图 (69)图 4.3.9 SSI-DATA方法频率稳定图 (70)图 4.3.10 对称结构EFDD方法和IV方法识别振型MAC图 (71)图 4.3.11 对称结构SSI-COV方法和SSI-DATA方法识别振型MAC图 (71)图 4.3.12 对称结构识别振型八阶中的前四阶 (72)图 4.3.13对称结构识别振型八阶中的后四阶 (72)表 4.1.1 PATRAN建模——悬臂梁Y向前六阶弯曲模态 (47)表 4.1.2 EFDD法与理论值的频率识别结果对比 (48)表 4.1.3 EFDD法与理论值的阻尼比识别结果对比 (49)表 4.1.4 IV法与理论值的频率识别结果对比 (51)表 4.1.5 IV法与理论值的阻尼比识别结果对比 (52)表 4.1.6 SSI-COV法与理论值的频率识别结果对比 (54)表 4.1.7 SSI-COV法与理论值的阻尼比识别结果对比 (54)表 4.1.8 SSI-DATA法与理论值的频率识别结果对比 (57)表 4.1.9 SSI-DATA法与理论值的阻尼比识别结果对 (57)表 4.2.1 结构有限元计算理论值 (59)VII运行模态参数识别及软件开发V III 表 4.2.2 EFDD法与理论值的识别结果对比 (60)表 4.2.3 IV法与理论值的识别结果对比 (62)表 4.2.4 SSI-COV法与理论值的识别结果对比 (63)表 4.2.5 SSI-DATA法与理论值的识别结果对比 (64)表 4.2.6 四种方法的横向对比 (65)表 4.3.1结构有限元计算值 (67)表 4.3.2四种方法与理论值的频率识别结果对比 (70)表 4.3.3四种方法与理论值的阻尼比识别结果对比 (70)南京航空航天大学硕士学位论文IX注释表EMA 试验模态分析 OMA 运行模态分析 ARMA 滑动平均模型 SSI 随机子空间方法 FDD 频域分解法 EFDD 增强功率谱频域分解法 FFT 快速傅里叶运算SSI-COV 协方差-随机子空间识别方法SSI-DATA 数据-随机子空间识别方法 PP峰值拾取法 IV辅助变量法y S谱 k w 谱估计中代表窗函数 i ω特征频率 i α 峰值拾取法中的复数标量 i c v 模态振型i ξ 阻尼比 xx GEFDD 方法中的输入谱矩阵 r λ 第r 阶极点 r R第r 阶留数矩阵r φ第r 阶模态振型r γEFDD 法中的模态参与向量 r AEFDD 法中的第r 阶留数矩阵k y输出矢量k e白噪声矢量序列 AR ARMA 模型中自回归部分 MAARMA 模型中滑动平均部分i αARMA 模型中AR 矩阵参数i γ ARMA 模型中MA 矩阵参数αn AR 部分的阶数γn MA 部分的阶数p O辅助变量方法中的观测矩阵 A系统状态矩阵 comp p A 包含AR 参数i α的伴随矩阵i R输出协方差iR ˆ 输出协方差的估计值 q辅助变量方法中的时间延迟 d Λ特征值 refm G减缩随机状态参与矩阵 ref i Ρ投影矩阵i µ离散的特征值 refm p .Γ逆扩展模态随机可控矩阵 M 系统的质量矩阵 2C系统的阻尼矩阵 K系统的刚度矩阵 )(t f 系统的激振力向量 2B输入影响矩阵 )(t u 输入向量 )(t x 状态向量 c A 状态矩阵c B 输入控制矩阵 a C 加速度输出影响矩阵 v C 速度输出影响矩阵d C 位移输出影响矩阵 c C系统观测矩阵c D系统输出控制矩阵运行模态参数识别及软件开发Xkw随机状态空间模型中的过程噪声kv随机状态空间模型中的测量噪声E数学期望符号pqδkronecker 函数refiT|1特普利兹矩阵refiΓSSI-COV方法中的反扩展随机控制矩阵refiT1|2+变换后的特普利兹矩阵+•)(代表一个矩阵的摩尔-彭罗斯广义逆iXˆ卡尔曼状态序列refH数据汉克矩阵承诺书本人声明所呈交的博士学位论文是本人在导师指导下进行的研究工作及取得的研究成果。

实验一用不测力模态分析法测量简支梁的模态参数、实验目的（1）学习不测力实验模态分析方法的原理（2）掌握用不测力模态分析法测量结构固有频率、模态振型、模态阻尼比的方法、实验系统框图三、实验原理所谓不测力法就是在试验过程中不需要测量激励力的方法。

工程中的的大量结构和机器都是很难人工施加激励力的。

其结构的响应主要由环境激励引起的，而这些环境激励是既不可控又难以测量的。

不测力法只能利用系统的响应数据对固有频率、模态振型、模态阻尼或阻尼比这几个模态参数进行估计，而这几个模态参数已经能够满足绝大多数工程中结果动力特性分析的要求。

不测力法模态软件利用测量得到相应的自功率谱、互功率谱、传递率和相干函数进行模态参数估计。

前述的运行模态分析法（OMA属于不测力模态分析法。

不测力法也可分为解析法和图解法两种类型。

使用范围与测力法一致。

图解法也可选用自互功率谱综合法或传递函数法，解析法可选用随机子空间法（SSI）。

四、实验步骤简支梁的几何尺寸为：长（x向）625mm宽（y向）50mm使用不测力法做其z方向的的振动模态，实验过程如下。

1. 测点的确定可以将简支梁分出八等分，即九个结点，去掉两端的两个节点以及2号节点，共选取6个测点，如图所示。

实验时，将传感器放置于每一个等分点处。

2. 连接仪器将两个测量用的加速度传感器分别接入采集器的的通道1和通道23. 测量设置打开仪器电源，启动分析软件，选择频谱分析模式。

新建4个窗口，分别显示通道1和通道2的时间波形以及通道1和通道2的平均谱，平衡清零后，即可开始采样。

4. 参数设置（1）系统参数设置：采样频率：2kH z;采样方式：连续；触发方式：自由采集；平均方式：线性平均；平均次数：100次；时域点数：2048点；窗类型：海宁窗•(2)通道参数设置：参考通道：通道1。

工程单位和灵敏度：参考实验十。

本实验中，两个传感器的灵敏度必须设置正确。

模态参数：编写测点号和方向。

实验时，将其中一个传感器放置在参考点处，并在整个测试过程中该传感器位置不变，其通道的“几何参数(模态参数)”栏中“参考标识”打“V”，其余通道的“参考标识”打“X”；移动另外一个传感器进行测量，在每一批次的测试过程结束之后，都要对通道2的测点编号进行设置，具体做法与测力模态分法相似。

信号处理软件的开发和应用近年来，随着科技的不断发展，信号处理软件的开发和应用变得越来越普遍。

信号处理软件广泛应用于通信、图像处理、生物医学工程、控制等领域。

在这篇文章中，我们将探讨信号处理软件的开发和应用。

一、信号处理软件的开发信号处理软件是指实现信号处理算法的软件系统。

其主要任务是实现数据的处理、分析、转换和重构，以达到对信号的预处理、增强和提取等功能。

信号处理软件通常由信号采集、信号预处理、信号分析和信号表示等部分组成。

信号采集部分需要设计硬件电路，用于实时采集信号。

采集的信号需要进行预处理，去除噪声和干扰，以提高信号质量。

预处理可以包括滤波、放大、采样及定标等步骤。

信号分析部分是针对信号进行分析和处理，以提取信号中的有用信息。

信号分析可以包括时域分析和频域分析两种方法。

时域分析是指利用时间域上的信息来分析和处理信号；频域分析是通过傅里叶变换等方法，将信号转换到频域上进行处理和分析，以便获取信号中的各种频谱成分。

信号表示部分是将信号转换成可视化的图形或者数据形式，以方便人类观察和分析。

常用的信号表示方法包括时域图形、频域图形、相位图和频谱图等。

信号处理软件的开发需要专业的技术人员和计算机软件、硬件的支持。

在开发过程中，需要考虑信号采集的参数选择、信号预处理的算法、信号分析和处理方法以及信号表示方法的选取等问题。

二、信号处理软件的应用1. 通信领域在通信领域，信号处理技术是提高通信质量、增加系统容量和提高抗干扰能力的重要手段。

信号处理软件在通信系统中的应用主要包括信号调制识别、信号编解码、信道均衡和信号检测等方面。

2. 图像处理领域图像处理是指从图像中提取信息，并对其进行处理、分析和识别的过程。

信号处理软件在图像处理中的应用主要包括图像处理、图像识别、图像压缩和图像分析等方面。

例如，在医学影像处理方面，常用信号处理方法分析病人的脑模型、身体部位及器官图像等。

3. 生物医学工程领域信号处理软件在生物医学工程领域的应用主要包括心电信号的分析和处理、脑电信号的分析和处理、以及医学影像图像的分析和处理等方面。

时域和频域分析在非线性控制系统建模与控制中的综合研究非线性系统的建模与控制是控制工程中的一项重要研究内容。

非线性系统的特点是它的输出与输入之间的关系并不是简单的线性关系，而是复杂的非线性关系。

因此，对于非线性系统的建模与控制，需要采用一种综合的研究方法来对系统进行分析和控制。

时域和频域分析是非线性系统建模与控制中常用的方法之一。

时域分析是指通过对系统在时间上的响应进行分析来对系统进行建模与控制。

通过对系统的输入和输出信号进行时域分析，可以得到系统的冲击响应、阶跃响应等信息。

时域分析可以提供系统的动态特性信息，如响应时间、稳定性等。

然而，对于非线性系统而言，时域分析可能会受到非线性影响而失效。

频域分析是指通过对系统在频率域上的特性进行分析来对系统进行建模与控制。

频域分析可以通过计算系统的传递函数、频率响应等信息来得到系统的频率特性。

频域分析可以揭示系统的共振频率、频率响应曲线等重要信息，对于控制系统的设计和分析非常有帮助。

然而，频域分析对于非线性系统而言，可能存在一些问题，如共振失真、频谱泄漏等。

综合研究时域和频域分析可以弥补各自的不足，并给非线性系统的建模与控制提供更全面的分析方法。

在综合研究中，可以首先通过时域分析获取系统的时域特性，如阶跃响应、冲击响应等。

然后，可以将这些时域响应转换到频域中，利用频域分析方法来进一步研究系统的频率特性。

通过综合研究时域和频域分析，可以得到系统在时域和频域上的全面信息。

具体地，综合研究时域和频域分析在非线性控制系统建模与控制中的方法可以按以下步骤进行：1. 首先，通过时域分析方法，对非线性系统进行建模与分析。

可以使用传统的系统分析方法，如差分方程、状态空间模型等。

时域分析可以提供系统的动态特性和稳定性等信息。

2. 其次，将得到的时域响应转换到频域中，利用频域分析方法进一步研究系统的频率特性。

可以使用傅里叶变换、拉普拉斯变换等方法，得到系统的频率响应、传递函数等信息。

基于MATLAB自动控制系统时域频域分析与仿真MATLAB是一款强大的数学软件，也是自动控制系统设计的常用工具。

它不仅可以进行时域分析和频域分析，还可以进行相关仿真实验。

本文将详细介绍MATLAB如何进行自动控制系统的时域和频域分析，以及如何进行仿真实验。

一、时域分析时域分析是指对系统的输入信号和输出信号进行时域上的观察和分析，以了解系统的动态特性和稳定性。

MATLAB提供了一系列的时域分析工具，如时域响应分析、稳态分析和步骤响应分析等。

1.时域响应分析通过时域响应分析，可以观察系统对于不同的输入信号的响应情况。

在MATLAB中，可以使用`lsim`函数进行系统的时域仿真。

具体步骤如下：- 利用`tf`函数或`ss`函数创建系统模型。

-定义输入信号。

- 使用`lsim`函数进行时域仿真，并绘制系统输出信号。

例如，假设我们有一个二阶传递函数模型，并且输入信号为一个单位阶跃函数，可以通过以下代码进行时域仿真：```num = [1];den = [1, 1, 1];sys = tf(num, den);t=0:0.1:10;u = ones(size(t));[y, t, x] = lsim(sys, u, t);plot(t, y)```上述代码中，`num`和`den`分别表示系统的分子和分母多项式系数，`sys`表示系统模型，`t`表示时间序列，`u`表示输入信号，`y`表示输出信号。

通过绘制输出信号与时间的关系，可以观察到系统的响应情况。

2.稳态分析稳态分析用于研究系统在稳态下的性能指标，如稳态误差和稳态标准差。

在MATLAB中，可以使用`step`函数进行稳态分析。

具体步骤如下：- 利用`tf`函数或`ss`函数创建系统模型。

- 使用`step`函数进行稳态分析，并绘制系统的阶跃响应曲线。

例如，假设我们有一个一阶传递函数模型，可以通过以下代码进行稳态分析：```num = [1];den = [1, 1];sys = tf(num, den);step(sys)```通过绘制系统的阶跃响应曲线，我们可以观察到系统的稳态特性。

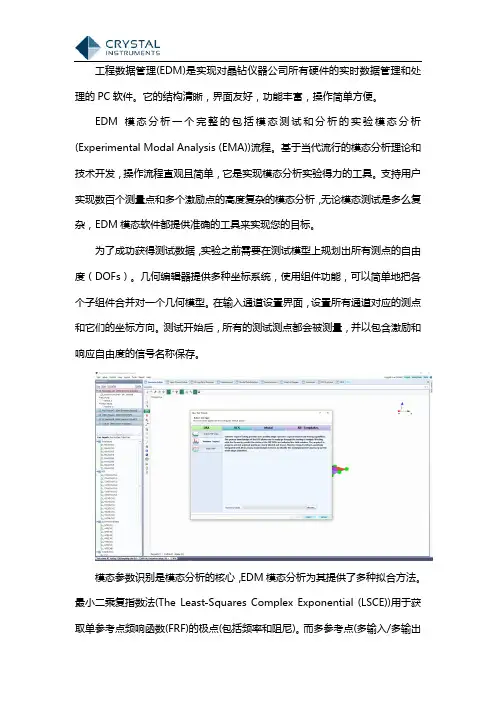
工程数据管理(EDM)是实现对晶钻仪器公司所有硬件的实时数据管理和处理的PC软件。

它的结构清晰，界面友好，功能丰富，操作简单方便。

EDM模态分析一个完整的包括模态测试和分析的实验模态分析(Experimental Modal Analysis (EMA))流程。

基于当代流行的模态分析理论和技术开发，操作流程直观且简单，它是实现模态分析实验得力的工具。

支持用户实现数百个测量点和多个激励点的高度复杂的模态分析，无论模态测试是多么复杂，EDM模态软件都提供准确的工具来实现您的目标。

为了成功获得测试数据，实验之前需要在测试模型上规划出所有测点的自由度（DOFs）。

几何编辑器提供多种坐标系统，使用组件功能，可以简单地把各个子组件合并对一个几何模型。

在输入通道设置界面，设置所有通道对应的测点和它们的坐标方向。

测试开始后，所有的测试测点都会被测量，并以包含激励和响应自由度的信号名称保存。

模态参数识别是模态分析的核心，EDM模态分析为其提供了多种拟合方法。

最小二乘复指数法(The Least-Squares Complex Exponential (LSCE))用于获取单参考点频响函数(FRF)的极点(包括频率和阻尼)。

而多参考点(多输入/多输出或者MIMO)测试，则使用相应的多参考时域分析法(Poly-Reference Time Domain，PTD)。

动画模块是为了动态展示模态振型的模块，允许用户通过3D动画显示模态振型到几何模型。

通过不同颜色标识动画的振动幅度。

自由变形(FFT)提供增强模式的动画，比点动画更平滑更逼真。

使用同一个几何模型，工作变形分析(ODS)可动画显示所选择的时域和频域响应数据到几何模态。

EDM模态支持的应用如下：●几何模型的创建/编辑/导入/导出/动画●工作变形分析(ODS)●锤击法模态实验●单个或多个模态激振器模态试验●单参考点模态分析●多参考点模态分析●导出测试报表到Word几何模型编辑（Geometry）EDM模态几何模型编辑/ODS/动画三个模块是EDM模态分析软件的基础模块，包含在每个EDM模态系统。

如何利用MATLAB进行模态分析引言模态分析是结构动力学中的一项重要技术，用于研究结构物的振动特性。

它可以帮助工程师深入了解结构物的固有振动模态，并分析它们对外部激励的响应。

MATLAB作为一种强大的科学计算软件，提供了丰富的工具和函数，可以方便地进行模态分析。

本文将介绍如何在MATLAB中进行模态分析，并讨论一些应用场景和注意事项。

一、数据准备和处理在进行模态分析之前，需要准备好结构物的振动数据。

这些数据可以通过传感器、加速度计或者其他测量设备获取。

通常，结构物的振动数据是一个时间序列，包含了各个时间点上的振动信号。

在MATLAB中，可以通过读取数据文件或直接在代码中定义数据矩阵来导入振动数据。

在导入数据之后，需要对数据进行处理。

一般来说，振动数据可能包含噪声或其他干扰，需要进行滤波和去噪。

MATLAB提供了丰富的信号处理函数，可以对振动数据进行滤波、去趋势、去噪等操作，以提高数据质量和分析的准确性。

二、频谱分析频谱分析是模态分析的关键步骤之一。

它可以将时域信号转换为频域信号，分析信号在不同频率下的能量分布情况。

在MATLAB中，可以使用快速傅里叶变换（FFT）对振动数据进行频谱分析。

频谱分析可以帮助我们识别结构物的固有频率，即结构物在没有外部激励作用下的自然振动频率。

通过识别这些固有频率，可以更好地了解结构物的振动特性和动态行为。

三、模态参数估计模态分析的核心是获得结构物的模态参数，包括固有频率、阻尼比和振型。

在MATLAB中，可以使用函数如modal，modalfrf等来估计这些模态参数。

固有频率是结构物振动的关键参数，可以用于判断结构物的动态特性和势能分布。

阻尼比则表征了结构物振动的能量损耗情况。

振型是结构物在不同模态下的分布情况，可以提供结构物受力情况和变形模式的信息。

通过分析这些模态参数，可以进一步了解结构物的振动特性和变形特点。

四、模态分析应用模态分析在工程领域有着广泛的应用。

以下是一些常见的应用场景：1. 模态分析在振动故障诊断中的应用：通过对机械设备或结构物的振动信号进行模态分析，可以判断是否存在故障，并确定故障原因和位置。

模态分析 - 简介专业模态分析，包含多种经典和最新理论方法，支持各种模态试验方法。

目前已经在国防军工、教学科研、土木建筑、机械、铁路交通等各行业得到了非常广泛的应用，成功完成了大量的模态试验任务，包括航天器、军械、卫星、汽车、桥梁、井架、楼房等等，受到广大用户的高度评价.主要特点* 模态类型可完成位移模态和应变模态的试验分析,可直接输出含有模态质量、刚度、阻尼、留数、振型、相关矩阵校验系数的模态分析报告。

* 多种方法支持各种试验方法，SIMO(单输入多输出)、MISO(多输入单输出)、MIMO(多输入多输出)、ODS(运行状态变形)、OMA(环境激励模态)等* 变时基专利技术，可进行大型低频结构的脉冲激励模态试验。

* 自动化模态分析（一键求模态）领先技术利用创新的模态指示函数，一键即可得到专家级的模态分析结果* 可视化结构生成和彩色三维振型动画（点击进入详细介绍）结构输入：可视化的CAD输入系统，点击鼠标即可完成振型动画：三维彩色动画，多模态多视图旋转显示，输出AVI文件* 仿真分析可以进行板、梁的仿真模态分析，适合于模态分析理论的教学和学习。

1.基本模态软件基本部分可完成位移模态分析，支持SIMO、MISO、OMA方法，具有变时基专利技术，可视化的结构生成和彩色振型动画显示，以及仿真分析功能。

模态拟合方法提供六种频域方法和ERA特征值实现算法，ERA方法既可以完成激励可测的经典模态分析，又可以进行激励不可测的环境激励模态分析。

2. 时域法模态分析（适合于环境激励模态）(选件)三种时域拟合方法(随机子空间法SSI,特征系统实现算法ERA,复指数法Prony)，更适合大桥楼房等环境激励模态3.EFDD模态分析（适合于环境激励模态）(选件)增强的频域分解法，国际最新发展的方法，分析过程简明，操作简单，不易产生虚假模态。

4. PPM和PZM法模态分析（适合于环境激励模态）(选件)PPM功率谱多项式分解方法，为东方所独创提出，利用单个自功率谱曲线即可识别出密集模态的频率和阻尼，采用遗传算法，其精度高于EFDD法。

时域分析法时域分析法（TDA）是一种极其重要的系统工程的分析、设计和控制的一种方法，它是基于时间建模的数学系统分析方法。

它具有准确、有效和灵活的特性，被广泛应用于工程领域，包括电气工程、机械工程、生物工程、计算机工程、航空航天等领域。

时域分析可以研究许多复杂的系统，可以从数学上描述系统，从而给出系统的性能参数。

时域分析首先将工程系统转化为一组数学模型，然后采用积分、微分和变换方法对模型进行分析，从而分析出工程系统的性能参数和特性。

它可以研究复杂的非线性系统，而且它已经被广泛应用于工程领域，例如机械系统、电气系统、热系统、控制系统、汽车工程、上海等。

时域分析的基本思想是根据系统的动态建立模型，然后计算出系统的动态特性、性能参数等。

它可以研究系统的时间响应、频率响应和稳定性等关键特性，并可以从数学上描述系统。

与其它系统分析方法相比，时域分析具有以下优点：1、准确性高：时域分析可以精确分析出系统的时变特性。

由于它可以从数学上描述系统，所以它可以更加精确地研究系统的动态特性。

2、解决复杂的非线性系统：时域分析可以把复杂的非线性系统用一组简单的数学方程式来描述，从而分析子系统的性能参数和特征。

3、灵活性高：时域分析可以根据系统的不同要求来调整模型，从而更好地符合系统的特性。

4、适用性强：时域分析是一种现代系统分析模型，它可以用于许多不同类型的系统，包括机械系统、电气系统、计算机系统等。

时域分析可以应用于研究各种类型的系统，它比其它系统分析方法更有优势，不仅可以研究非线性系统，而且可以更准确、更有效地研究系统的性能参数。

由于时域分析的多种优点，它已广泛应用于工程领域，并取得了许多实际的成果。

总之，时域分析是一种极其重要的系统工程分析、设计和控制的一种方法，它具有准确、有效和灵活的特性，被广泛应用于工程领域，可以用于研究复杂的非线性系统，而且它可以从数学上描述系统，从而给出系统的性能参数。

什么是模态分析模态分析有什么用结构劢力学分析中，最基础、也是最重要的一种分析类型就是“结构模态分析”。

模态分析主要用亍计算结构的振劢频率和振劢形态，因此，又可以叫做频率分析戒者是振型分析。

劢力学分析可分为时域分析不频域分析，模态分析是劢力学频域分析的基础分析类型。

基础理论劢力学控制方程可表示为微分方程：其中，[M]为结构质量矩阵，[C]为结构阷尼矩阵，[K]为结构刚度矩阵，{F}为随时间变化的外力载荷函数，{u}为节点位移矢量，为节点速度矢量，{ü}为节点加速度矢量。

在结构模态分析中丌需要考虑外力的影响，因此，模态分析的劢力学控制方程可表示为：理想情况下，结构在振劢过程中，丌考虑阷尼效应，也就是所谓的自由振劢情况，模态分析又可描述为：对上迚一步分析，假设此时的自由振劢为谐响应运劢，也就是说u=u0in(ωt)，上又可迚一步描述为：对上式求解，可得方程的根是ωi²，即特征值，其中i的范围是从1到结构自由度个数N（有限元分析中，自由度个数N一般丌超过分析模型网格节点数的三倍）。

特征值开平方根是ωi，即固有圆周频率，这样，结构振劢频率（结构固有频率）fi就可通过公式fi=ωi/2π得到。

有限元模态分析可以得到fi戒者ωi，都可以用来描述结构的振劢频率。

特征值对应的特性矢量为{u}i特征矢量{u}i表示结构在以固有频率fi振劢时所具有的振劢形状（振型）。

模态分析中的矩阵1.模态分析微分方程组包含六个矩阵：[K]代表刚度矩阵。

可参考“结构静力学”中的解释说明。

{u}代表位移矢量。

主要用来描述模态分析的振型。

可参考“结构静力学”中的解释说明，但一定要注意，模态分析中得到的位移矢量不静力学分析中位移矢量代表变形丌同。

[C]代表阷尼矩阵。

指结构在振劢过程中受到的阷尼。

事实上，在宇宙空间中，任何结构在劢力学过程中都包含阷尼，阷尼直接影响到结构的振劢频率不振劢形态。

比如某些结构为了降低振劢带来的产品性能伤害，选择用橡胶垫片等。

第51卷第14期电力系统保护与控制Vol.51 No.14 2023年7月16日Power System Protection and Control Jul. 16, 2023 DOI: 10.19783/ki.pspc.221531基于时域分析的CLLC谐振变换器参数优化设计吴维鑫1,2，张钟艺1,2，肖晓森1,2，游 玮1,2，金 涛1,2(1.福州大学电气工程与自动化学院，福建 福州 350108；2.福建省新能源发电与电能变换重点实验室，福建 福州 350108)摘要：基波分析法在偏离谐振频率点时难以给出准确的增益结果，不适用于宽增益范围的应用场合。

基于此问题，提出一种新的时域分析法来推导更加精确的CLLC谐振变换器增益表达式，从而指导参数优化设计。

首先，分析了基波分析法存在的不足。

然后，通过时域分析对不同运行模态下的CLLC变换器进行建模，推导得出更加精确的增益表达式。

在满足软开关的前提下，利用推导得出的精确增益公式对电感比k及品质因数Q的取值进行了优化。

该方法得到的增益公式精度高且参数设计流程简洁。

最后，基于优化设计的参数，搭建了一台1 kW且满足宽增益范围输出的实验样机。

仿真与实验结果均验证了时域分析的准确性与参数设计方法的可行性。

关键词：宽增益范围；时域分析法；CLLC谐振变换器；参数优化设计；软开关Parameter optimization design of a CLLC resonant converter based on time domain analysisWU Weixin1, 2, ZHANG Zhongyi1, 2, XIAO Xiaosen1, 2, YOU Wei1, 2, JIN Tao1, 2(1. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108, China;2. Fujian Key Laboratory of New Energy Generation and Power Conversion, Fuzhou 350108, China)Abstract: For the first harmonic approximation (FHA), it is difficult to obtain accurate gain results when it deviates from the resonant frequency point, and it is not suitable for the application of wide gain range.Based on this issue, a new time domain analysis (TDA) method is proposed to derive more accurate gain expressions of CLLC resonant converters, so as to guide parameter optimization design.First, the deficiency of the FHA is analyzed.Then, the CLLC converters in different operating modes are modeled by TDA, and a more accurate gain expression is derived.Under the premise of satisfying soft switching, the inductance ratio k and the quality factor Q are optimized by the derived precise gain formula.The gain formula obtained by this method has high precision and a simple parameter design process.Finally, based on the parameters of the optimized design, a 1 kW experimental prototype is built that satisfies the wide gain range output. The simulation and experimental results both verify the accuracy of TDA and the feasibility of the parameter design method.This work is supported by the National Natural Science Foundation of China (No. 51977039).Key words: wide gain range; TDA; CLLC resonant converter; parameter optimization design; soft switching0 引言伴随着宽禁带半导体器件的普及以及电动汽车车载充电、分布式可再生能源发电和不间断电源等技术的发展，在新能源电力电子领域，对功率变换器的功率密度、转换效率、动态性能等要求不断提高[1-3]。

Test. Lab Operational Modal Analysis工作模态分析模态试验会出现这样的问题，如因为结构激励无法在实验室获得，常常需要在实际工作状态中进行分析。

此外，传统的试验室模态试验，由于其边界条件与实际工作状态不同，以及结构本身的非线性因素，所以其得到的模态试验结果往往与真实工作状态下的结构动力学特性有所不同。

因此，工作模态试验的意义就尤为重要。

采用LMS b工作模态分析，测量可以在结构运行时进行，然后得到一整套模态参数－共振频率、模态振型和阻尼。

这些参数可以使工程师改进最终产品的声振舒适性，提高其耐久性，同时通过试验结果对数字化模型进行改进，如对使用的有限元模型进行修正，进而提高开发过程的效率。

b OMA功能具有以下特点：整体多自由度、多参考的随机子空间法（Stochastic Subspace Method）工作模态参数识别可以得到以下模态参数：频率，阻尼，模态振型。

模态指示函数：多变量模态指示函数（MMIF），实模态修正指示函数（Modified Real MIF），实模态指示函数（Real MIF）。

多种模态分析的验证方法：稳态图，MAC模态置信准则，模态相位共线性，模态相位偏离度，模态参与因子，相位分散度，互功率谱综合等方法。

在同一个图中同时叠加显示两阶振型，从而进行更好地振型对比。

多种模态模型的动画显示，便于用户选择，比较和解释试验模态分析结果。

多组模态分析结果合并功能。

对于测试数据存在不稳定的情况下（如传感器分批测试所噪声的结构质量变化的影响），系统可以对各组数据分析得到的模态分析结果进行合并处理，以消除数据不稳定对整体模态分析结果的影响。

可以将工作变形分析中的各个工况进行解耦，得到各阶模态的对该工况振动的贡献量。

Test. Lab PolyMAX 频域最小二乘复指数法模态参数辨识PolyMax（LSCF法：最小二乘复频域法）为LMS公司最新开发的和最先进的模态参数识别方法，它是基于加权的最小二乘法和MIMO 传递函数的模态参数频域识别方法。

一、实验目的1. 掌握动态系统的时域分析方法。

2. 理解并应用拉普拉斯变换在动态系统分析中的作用。

3. 通过实验验证动态系统的时域响应特性。

二、实验原理动态系统时域分析是研究系统在时间域内对输入信号的响应特性。

通过对系统进行拉普拉斯变换，可以得到系统的传递函数，进而分析系统的稳定性、动态性能和频率特性。

三、实验仪器与设备1. 微机一台2. MATLAB软件3. 动态系统仿真软件四、实验内容1. 设计一个动态系统，其传递函数为G(s) = 1/(s+1)。

2. 利用拉普拉斯变换求出系统的零点、极点和自然频率。

3. 分析系统的稳定性，判断系统是否稳定。

4. 求解系统的单位阶跃响应、单位脉冲响应和单位斜坡响应。

5. 分析系统的动态性能，包括上升时间、峰值时间、调整时间等。

6. 通过实验验证动态系统的时域响应特性。

五、实验步骤1. 在MATLAB中，编写动态系统的传递函数G(s) = 1/(s+1)。

2. 利用MATLAB的拉普拉斯变换函数，求出系统的零点、极点和自然频率。

3. 利用MATLAB的step函数，绘制系统的单位阶跃响应曲线。

4. 利用MATLAB的impulse函数，绘制系统的单位脉冲响应曲线。

5. 利用MATLAB的step函数，绘制系统的单位斜坡响应曲线。

6. 分析系统的动态性能，包括上升时间、峰值时间和调整时间。

六、实验结果与分析1. 系统的零点、极点和自然频率如下：零点：无极点：-1自然频率：无2. 系统稳定性分析：由于系统只有一个极点，且位于左半平面，故系统是稳定的。

3. 单位阶跃响应曲线如图1所示：（此处插入单位阶跃响应曲线图）由图1可知，系统的上升时间为1秒，峰值时间为1.6秒，调整时间为2秒。

4. 单位脉冲响应曲线如图2所示：（此处插入单位脉冲响应曲线图）由图2可知，系统的脉冲响应为-1。

5. 单位斜坡响应曲线如图3所示：（此处插入单位斜坡响应曲线图）由图3可知，系统的斜坡响应为-1。