江苏省无锡市2014届高三上学期期末考试数学试题 Word版含答案

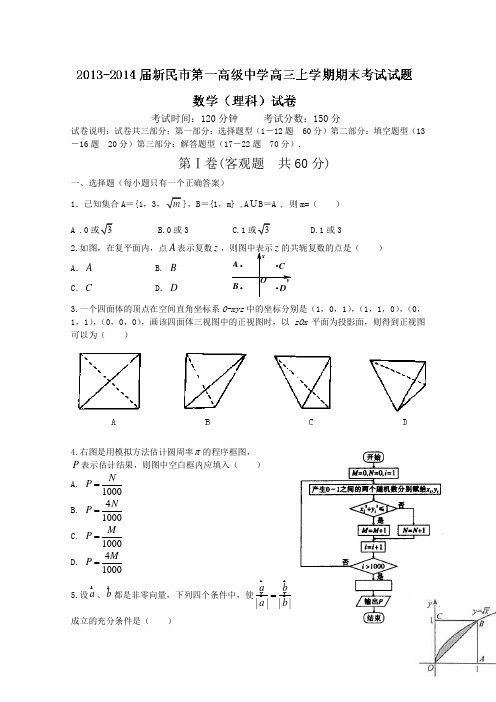
考试时间：120分钟 考试分数：150分试卷说明：试卷共三部分：第一部分：选择题型（1－12题 60分）第二部分：填空题型（13－16题 20分）第三部分：解答题型（17－22题 70分）.第Ⅰ卷(客观题 共60分)一、选择题（每小题只有一个正确答案） 1．已知集合A ＝{1，3}，B ＝{1，m} ,AB ＝A , 则m=（ ）A .0或3 C.1或32.如图，在复平面内，点A 表示复数z ）A ．A B.BC ．CD ．D3.一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为（ ）4.右图是用模拟方法估计圆周率π的程序框图， P 表示估计结果，则图中空白框内应填入（ ）A. 1000NP =B. 41000NP =C. 1000MP =D. 41000MP =5.设a 、b 都是非零向量，下列四个条件中，使||||a ba b =成立的充分条件是（ ）A ．a b =- B.//a b C ．2a b = D ．//a b 且||||a b = 6.如图所示，在边长为1的正方形OABC 中任取一点P ， 则点P 恰好取自阴影部分的概率为（ ） A.14 B. 15 C. 16 D. 177．设等差数列{}n a 的前n 项和为n S ，若0,01615<>S S ，则15152211,,,a S a S a S 中最大的是（ ）A.11a S B. 77a S C. 88a S D. 99a S8.总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字，则选出9.下列说法：①命题“”的否定是“”；②若一个命题的逆命题为真，则它的否命题也一定为真； ③“矩形的两条对角线相等”的逆命题是真命题；④“x ≠3”是|x|≠3成立的充分条件.其中错误的个数是（ ） A ．1 B ．2C ．3D ．410. 设{}n a 是等比数列，11=a ，公比q =n S 为{}n a 的前n 项和，n Q 为数列}{n b 的前n项和，若n n n x b x b x b b x 123121)12(+++++=-+ .记*12,17N n Q S S T n nn n ∈-=+,设0n T 为数列{n T }的最大项，则=0n （ ） A.3B.4C.5D.611．函数()sin()f x A x ωωπ=+（0A >,0>ω）的图像在]43,47[ππ--上单调递增，则ω的最大值是（ ） A ．21 B ． 43C ． 1D ．3212.函数20134321)(2013432x x x x x x f ++-+-+= ，则)(x f 的零点个数是（ ） A.0B.1C.2D.3第Ⅱ卷(主观题 共90分)二、填空题13.设a 为实常数，()y f x =是定义在R 上的奇函数，当0x <时，2()97a f x x x =++，若()1f x a ≥+对一切0x ≥成立，则a 的取值范围为 .14.一个球与正四面体的六条棱都相切，若正四面体的棱长为1，则这个球的体积是 .15.如右图，迎面从左至右悬挂3串气球，分别有两串绑两只，一串绑3只，现在用枪射击气球，假设每枪均能命中一只气球，要求每次射击只能射击每串最下方的气球，则用7枪击爆这7只气球不同的次序有多少种 . 16.][x 表示不超过x 的最大整数，若函数a xx x f -=][)(，当0>x 时，)(x f 有且仅有3个零点，则a 的取值范围为 . 三、解答题17.（本小题满分12分）如图，在△ABC 中，∠ABC ＝90°，AB= 3 ，BC=1，P 为△ABC 内一点，∠BPC ＝90°.（Ⅰ）若PB=12，求PA ；（Ⅱ）若∠APB ＝150°，求tan ∠PBA.18.（本小题满分12分）四棱锥P ABCD -的底面ABCD 是正方形，侧棱PD ⊥底面ABCD ，DC PD =，E 是PC 的中点.（Ⅰ）证明PA //平面BDE ；（Ⅱ）求二面角C DE B --的平面角的余弦值.19.（本小题满分12分）如图，在竖直平面内有一个“游戏滑道”，空白部分表示光滑滑道，黑色正方形表示障碍物，自上而下第一行有1个障碍物，第二行有2个障碍物，……，依次类推．一个半径适当的光滑均匀小球从入口A 投入滑道，小球将自由下落，已知小球每次遇到正方形障碍物上顶点时，向左、右两边下落的概率都是21．记小球遇到第n 行第m 个障碍物（从左至右）上顶点的概率为),(m n P ．（Ⅰ）求)1,4(P ，)2,4(P 的值，并猜想),(m n P 的表达式（不必证明）；（Ⅱ）已知⎩⎨⎧≤<-≤≤-=63,331,4)(x x x x x f ，设小球遇到第6行第m 个障碍物（从左至右）上顶点时，得到的分数为)(m f =ξ，试求ξ的分布列及数学期望．20.（本题满分12分)已知数列}{n a 满足：n n na a a a 2321321=++++ )(*N n ∈. （Ⅰ）求数列}{n a 的通项公式；（Ⅱ）若数列nnn a b 2=)(*N n ∈，试求数列}tan {tan 1+⋅n n b b 的前n 项和n S .21.（本题满分12分) 已知函数).0()1ln(1)(>++=x xx x f（Ⅰ）试判断函数),0()(+∞在x f 上单调性并证明你的结论； （Ⅱ）若1)(+>x kx f 对于(0,)x ∀∈+∞恒成立，求正整数k 的最大值；（Ⅲ）求证：[]2 - 3(112)(123)(134)1(1n n n e +⨯+⨯+⨯⋅⋅⋅++>）．请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分.做答时请写清题号.22.（本题满分10分)选修4－1：几何证明选讲如图，PA 切圆O 于点A ，割线PBC 经过圆心O ，OB=PB=1，OA 绕点O 逆时针旋转60︒到 OD ．（Ⅰ）求线段PD 的长；?若有,指出该线段;若没有,说明理由． 23．（本小题满分10分）选修4—4：坐标系与参数方程已知直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧=+-=ty t x 22221（t 为参数），曲线C 的极坐标方程是2sin 1sin θρθ=-，以极点为原点，极轴为x 轴正方向建立直角坐标系，点(1,0)M -，直线l 与曲线C 交于A 、B 两点．（Ⅰ）写出直线l 的极坐标方程与曲线C 的普通方程；（Ⅱ）线段MA ，MB 长度分别记为||MA ，||MB ，求||||MB MA ⋅的值．24．(本小题满分10分) 选修4-5：不等式选讲 设函数()|1||2|f x x x =-+-（Ⅰ）若m x f ≥)(恒成立，求实数m 的取值范围；（Ⅱ）若不等式||||||||()a b a b a f x +--≤（0a ≠，a R ∈，b R ∈）恒成立，求实数x 的范围．数学(理)试卷答案及评分标准一、本题共12小题，每小题5分，共60分．13．87a ≤-14．π24215．210 16．]54,43( 三．计算题17. （Ⅰ）由已知，∠PBC=60°，所以∠PBA=30°.2011732cos30.424PA =+-=故2PA =（6分） （Ⅱ）设PBA α∠=，由已知得sin PB α=，在∆PBA 中，由正弦定理得00sin sin150sin(30)αα=-4sin αα=，故tan α=.（12分）18. （Ⅰ）以D 为坐标原点，分别以DA 、DC 、DP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系设PD=DC=2，则A （2，0，0），P （0，0，2），E （0，1，1），B （2，2，0）. (2,0,2),(0,1,1),(2,2,0)PA DE DB =-==设 1(,,)n x y z =是平面BDE 的一个法向量，则由111001,(1,1,1).2200n DE y z y n x y n DB ⎧⋅=+=⎧⎪=-=-⎨⎨+=⋅=⎩⎪⎩得取得∵11220,,//.PA n PA n PA BDE PA BDE ⋅=-=∴⊥⊄∴，又平面平面 或使用线面平行定理证明（6分）（II ）由（Ⅰ）知1(1,1,1)n =-是平面BDE 的一个法向量， 又2(2,0,0)n DA ==是平面DEC 的一个法向量. （8分）设二面角B -DE -C 的平面角为θ，由图可知12,n n θ=<>∴121212cos cos ,||||3n n n n n n θ⋅=<>===⋅⨯故二面角B -DE -C 的余弦值为33（12分） 19. （Ⅰ）81)21()1,4(303==C P ，（2分） 83)21()2,4(313==C P ，（4分） 猜想111)21(),(---=n m n C m n P ；（6分） （Ⅱ）=ξ3,2,1161)6,6()1,6()3(=+==P P P ξ， 165)21()5,6()2,6()2(515==+==C P P P ξ，85)4,6()3,6()1(=+==P P P ξ（10分）162385116521613=⨯+⨯+⨯=ξE ．（12分） 20.（Ⅰ）当2≥n ，n a n n 12-=（4分）当1=n ，11=a （5分），故当1≥n ，na n n 12-=（6分）（Ⅱ）n b n 2=（7分），12tan tan tan tan tan 11--=⋅++nn n n b b b b （10分）n n S n --+=2tan 2tan )22tan(（12分）21. （Ⅰ）)]1ln(11[1)]1ln(11[1)(22+++-=+--+='x x x x x x x x f （2分） .0)(,0)1ln(,011,0,02<'∴>+>+>∴>x f x x x x),0()(∞∴在x f 上是减函数.（3分）（Ⅱ）.)]1ln(1)[1()(,1)(恒成立即恒成立k xx x x h x k x f >+++=+>即()h x 的最小值大于k .故正整数k 的最大值是3（7分）（III ）由（Ⅱ）知)0(13)1ln(1>+>++x x x x∴xx x x x 32132113)1ln(->+-=-+>+ （9分） 令*))(1(N n n n x ∈+=，则)1(32)]1(1ln[+->++n n n n （10分）∴[]ln(112)ln(123)ln 1(1)n n +⨯++⨯+⋅⋅⋅+++[]2 - 3(112)(123)(134)1(1n n n e ∴+⨯+⨯+⨯⋅⋅⋅++>）（12分）22．（Ⅰ）∵PA 切圆O 于点A,且B 为PO 中点,∴AB=OB=OA ．∴60,120AOB POD ∠=︒∴∠=︒2222cos 7POD PO DO POD PD ∆=+-⋅∠=∴=在中,PD PO OD （5分）（II ）存在3=PA （10分）23．（Ⅰ）直线l 的极坐标方程1cos sin +=θρθρ，（3分）曲线C 普通方程2x y = （5分）（II）将12x y ⎧=-+⎪⎪⎨⎪=⎪⎩代入2x y =得220t -+=，（8分）2||||||21==⋅t t MB MA （10分）24．（Ⅰ）1≤m （5分） （II ）由a b a b a 2≤--+ ，得)(||2x f a a ≤，由0≠a ，得)(2x f ≤， 解得21≤x 或25≥x （10分）。

江苏省无锡市太湖格致中学2014届九年级英语上学期期中试题第Ⅰ卷（客观题共70分）一、听力测试（本大题共20 分，每小题1分）第一节（共10小题）听下面10段短对话，每段对话后有一个小题，从题中A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话读两遍。

听第1至10段材料，回答第1至10题。

1. Which charity are they talking about?A. B. C.2.What is Susan 's star sign ?A. B. C.3. What does the man like doing better after supper?A. B. C.4. What sport are they doing?A. B. C.5. Who needs to calm down?A. Eve.B. Millie.C. Frank.6. How much does a ticket cost?A. $320.B. $160.C. $230.7. Where is the bank?A. In front of a big market.B. Past a big market.C. Behind the post office.8. What is Tony going to do tonight?A. Work on the Maths problems.B. Enjoy an evening party.C. Visit his grandparents.9. Who was Helen Keller?A. An American writer.B. A blind dancer.C. A famous actress.10. What did Jim do last weekend?A. He flew to another country.B. He had a picnic in the country.C. He had a lot of fun at home.第二节（共10小题）听下面3段长对话和短文，每段对话和短文后有几个小题，从题中A、B、C三个选项中选出最佳选项。

江苏省无锡市硕放中学2014届九年级物理上学期期中试题一、选择题(每小题2分，共24分. 每小题只有一个正确答案，请将正确答案的序号填在下表中)1.如图所示为四种日常生活用具，它们在使用中属于费力杠杆的是( )2.如图所示的四个事例中，用做功方式改变内能的是( )①冬天，搓手会②冬天，嘴对手③炒菜时，铁锅④水蒸气把软木塞冲让手变暖和哈气取暖热得烫手开时，温度会降低A．①②B．②③ C．③④ D．①④3.下列实例中，力对物体没有做功的是（）A.起重机吊起重物B.马拉车，车未动C.跳水运动员从跳台跳下D.举重运动员，将杠铃举起4.一箱汽油用掉一半后，剩下的一半汽油与原来一箱汽油相比较( )A.内能变为原来的一样B.比热容变为原来的一半C.密度变为原来的一半D.热值变为原来的一样5.汽油机是由四个冲程不断循环而工作的，表示内能转化为机械能的冲程是（）6.关于温度、热量、内能，以下说法正确的是（）A.物体的温度越高，所含的热量越多B. 一个物体吸收热量时，温度不一定升高C.0℃的冰没有内能D. 对物体做功，物体的温度一定升高7.在2011年校秋季田径运动会上，九年级男生集体比赛项目为引体向上。

为了粗略估测某位同学引体向上运动的功率时，下列物理量不需要测量的是（）A.学生的质量B.每次身体上升的高度C.做引体向上的时间D.单杠的高度8.关于功率和机械效率，下列说法正确的是（）A．剪子B．起子C．镊子D．钢丝钳A.功率大的机械，机械效率一定高B.做功多的机械，机械效率一定高C.机器的功率越大，做的功就越多D.机器的功率越大，做的功就越快9.如图所示，将同一物体分别沿光滑的斜面AB 、AC 以相同的速度从底部匀速拉到顶点A ，已知AB>AC ，施加的力分别为F 1、F 2，且平行于各自斜面向上，拉力做的功为W 1、W 2，拉力的功率分别为P 1、P 2，则下列判断中正确的是 （ ） A.F 1<F 2 , W 1=W 2 , P 1<P 2B.F 1>F 2 , W 1>W 2 , P 1>P 2C.F 1<F 2 , W 1<W 2 , P 1<P 2D.F 1<F 2 , W 1=W 2 , P 1>P 210．小明用两个相同的滑轮组成不同的滑轮组（如图所示），分别将同一物体匀速提高到相同高度，滑轮组的机械效率分别为η1、η2，下列关系正确的是（忽略绳重及摩擦）（ ） A.F 1 > F 2，η 1 = η2 B.F 1 > F 2，η 1 > η2 C.F 1 < F 2，η 1 = η2 D.F 1 < F 2，η 1 > η211.保密室有两道门，只有当两道门都关上时（关上一道门相当于闭合一个开关），值班室内的指示灯才会发光，表明门都关上了。

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分120分，考试时间100分钟一、单项选择题：本部分包括20题，每题2分，共计40分。

每题只有一个选项最符合题意。

1.下列说法正确的是：（）A．人的各种反射活动都需要多个细胞的参与，不可能由一个细胞独立完成，因此，细胞不可能是生命活动的基本单位B．生命系统的结构层次包括从原子、分子到生物圈的各个层次C．原核生物中既有自养生物，又有异养生物D．SARS、蓝藻和酵母菌都具有细胞质2.如图所示：甲图中①②表示目镜，③④表示物镜，⑤⑥表示物镜与载玻片之间的距离，乙和丙分别表示不同物镜下观察到的图象。

下面描述正确的是（）A．①比②的放大倍数大，③比④放大倍数小B．把视野里的标本从图中的乙转为丙，应选用③，同时提升镜筒C．从图中的乙转为丙，正确调节顺序：转动转换器→调节光圈→移动标本→转动细准焦螺旋D．若使物像放大倍数最大，甲图中的组合一般是②③⑤3. 生物膜将真核细胞分隔成不同的区室，使得细胞内能够同时进行多种化学反应，而不会相互干扰。

下列叙述正确的是（）A.细胞核是mRNA合成的主要场所B.高尔基体是肽链合成和加工的场所C.线粒体将葡萄糖氧化分解成CO2和H2OD.溶酶体合成和分泌多种酸性水解酶4. 下列过程未体现生物膜信息传递功能的是（）A.蔗糖溶液使洋葱表皮细胞发生质壁分离B.抗原刺激引发记忆细胞增殖分化C.胰岛素调节靶细胞对葡萄糖的摄取D.传出神经细胞兴奋引起肌肉收缩5. 下列关于物质跨膜运输的叙述中，错误的是：（）A．海带细胞通过主动运输积累I－等溶质，因而不会在海水中发生质壁分离B．将植物细胞置于蒸馏水中，会因渗透作用吸水而胀破C．人体内红细胞、肾小管上皮细胞吸收葡萄糖的方式都需要载体D．线粒体产生的CO2以自由扩散的方式进入细胞质基质6. 下列有关酶的叙述正确的是：（）A.所有酶用双缩脲试剂进行检验都可以呈现紫色反应B.酶只能在活细胞中起作用C.同一种酶可存在于形态结构不同的活细胞中D.酶分子结构在高温、低温、过酸、过碱条件下均会受到破坏而使酶失去活性7. 下列细胞中，可能已发生癌变的是：（）A．细胞的形态结构发生显著变化的细胞 B．细胞新陈代谢的速率减慢的细胞C ．自由水含量减少的细胞D ．被细菌侵染的细胞8. 下图是探究酵母菌进行呼吸方式类型的装置，下列叙述错误的是：（ ）A ．假设装置一中的液滴左移．装置二中的液滴不动．说明酵母菌只进行有氧呼吸B ．假设装置一中的液滴不移动。

江南中学高三12月月考数学试卷（文科）时量：120分钟 分值：150分一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知i 为虚数单位，复数i i z )1(+=在复平面内对应的点位于（ ） A. 第一象限B. 第二象限C. 第三象限D. 第四象限2．已知命题2:,0p x x ∀∈≥R ；和命题2:,3,q x Q x ∃∈=则下列命题为真的是（ ）A ．p q ∧B ．()p q ⌝∨C ．()p q ∨⌝D ．()()p q ⌝∧⌝3. 在△ABC 中，“B A sin sin >”是“B A >”的( ) A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4． 设0.5323,log 2,cos3a b c π===，则（ ） A ．c b a << B ．a b c << C ．c a b << D ．b c a <<5.已知函数2n y a x =（*0,n a n N ≠∈）的图象在1x =处的切线斜率为121n a -+（*2,n n N ≥∈），且当1n =时，其图象经过()2,8，则7a =（ ）A ．12B ．5C ．6D ．76．函数125)(-+-=x x x f 的零点所在的区间是（ ）A.)1,0(B. )2,1(C. )3,2(D.)4,3(7．已知P 是△ABC 所在平面内一点，PB ＋PC ＋2PA ＝0，现将一粒黄豆随机撒在△ABC 内，则黄豆落在△PBC 内的概率是( )A.14B.13C.23D.12 8.在△ABC 中，BC=1，∠B=3π,△ABC 的面积S =3，则sinC=（ ）A 、1313B 、53 C 、54 D 、13392 9. 已知等差数列{a n }的前n 项和为S n ，若OB →＝a 1O A →＋a 2 014OC →，且A 、B 、C 三点共线(该直线不过点O )，则S 2 014等于 （ ）A ．1 007B ．1 008C ．2 013D ．2 01410.已知函数22,0,()ln(1),0x x x f x x x ⎧-+≤=⎨+>⎩，若|()|1f x ax ≥-恒成立，则a 的取值范围是（A ）[2,0]- （B ）[2,1]- (C) [4,0]- (D) [4,1]-二．填空题：本大题共5小题，每小题5分，共25分，请将答案填在答题卡中对应题号后的横线上。

江苏省苏北四市2020届高三上学期期末考试2020届高三模拟考试试卷数 学 2020.01(满分160分，考试时间120分钟)2020．1 参考公式：1. 样本数据x 1，x 2，…，x n 的方差s 2＝1n ∑n i ＝1(x i －x)2，其中x ＝1n ∑ni ＝1x i； 2. 圆锥的体积V ＝13Sh ，其中S 是圆锥的底面圆面积，h 是圆锥的高．一、 填空题：本大题共14小题，每小题5分，共70分．1. 已知集合A ＝{x|0<x<2}，B ＝{x|－1<x<1)，则A ∪B ＝________． S ←0 I ←1While I ＜6 I ←I ＋1 S ←S ＋I End While Print S(第4题)2. 已知复数z 满足z 2＝－4，且z 的虚部小于0，则z ＝________．3. 若一组数据7，x ，6，8，8的平均数为7，则该组数据的方差是________．4. 执行如图所示的伪代码，则输出的结果为________．5. 函数f(x)＝log 2x －2的定义域为________．6. 某学校高三年级有A ，B 两个自习教室，甲、乙、丙3名学生各自随机选择其中一个教室自习，则甲、乙两人不在同一教室上自习的概率为________．7. 若关于x 的不等式x 2－mx ＋3<0的解集是(1，3)，则实数m 的值为________．8. 在平面直角坐标系xOy 中，双曲线x 23－y 2＝1的右准线与渐近线的交点在抛物线y 2＝2px 上，则实数p 的值为________．9. 已知等差数列{a n }的前n 项和为S n ，a 2＋a 9＝8，S 5＝－5，则S 15的值为________． 10. 已知函数y ＝3sin 2x 的图象与函数y ＝cos 2x 的图象相邻的三个交点分别是A ，B ，C ，则△ABC 的面积为________．11. 在平面直角坐标系xOy 中，已知圆M ：x 2＋y 2－4x －8y ＋12＝0，圆N 与圆M 外切于点(0，m)，且过点(0，－2)，则圆N 的标准方程为______________．12. 已知函数f(x)是定义在R 上的奇函数，其图象关于直线x ＝1对称，当x ∈(0，1]时，f(x)＝－e ax (其中e 是自然对数的底数)．若f(2 020－ln 2)＝8，则实数a 的值为________．(第13题)13. 如图，在△ABC 中，D ，E 是BC 上的两个三等分点，AB →·AD →＝2AC →·AE →，则cos∠ADE 的最小值为________．14. 设函数f(x)＝|x 3－ax －b|，x ∈[－1，1]，其中a ，b ∈R .若f(x)≤M 恒成立，则当M 取得最小值时，a ＋b 的值为________．二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．15. (本小题满分14分)如图，在三棱锥PABC 中，AP ＝AB ，点M ，N 分别为棱PB ，PC 的中点，平面PAB ⊥平面PBC.求证：(1) BC ∥平面AMN ；(2) 平面AMN ⊥平面PBC.16. (本小题满分14分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos A ＝55. (1) 若a ＝5，c ＝25，求b 的值； (2) 若B ＝π4，求tan 2C 的值．17. (本小题满分14分) 如图，在圆锥SO 中，底面半径R 为3，母线长l 为5.用一个平行于底面的平面去截圆锥，截面圆的圆心为O 1，半径为r.现要以截面为底面，圆锥底面圆心O 为顶点挖去一个倒立的小圆锥OO 1，记圆锥OO 1的体积为V.(1) 将V 表示成r 的函数； (2) 求V 的最大值．18. (本小题满分16分)在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a>b>0)的右顶点为A ，过点A 作直线l 与圆O ：x 2＋y 2＝b 2相切，与椭圆C 交于另一点P ，与右准线交于点Q.设直线l 的斜率为k.(1) 用k 表示椭圆C 的离心率；(2) 若OP →·OQ →＝0，求椭圆C 的离心率．19. (本小题满分16分)已知函数f(x)＝(a －12)ln x(a ∈R )．(1) 若曲线y ＝f(x)在点(1，f(1))处的切线方程为x ＋y －1＝0，求a 的值； (2) 若f(x)的导函数f′(x)存在两个不相等的零点，求实数a 的取值范围；(3) 当a ＝2时，是否存在整数λ，使得关于x 的不等式f(x)≥λ恒成立？若存在，求出λ的最大值；若不存在，请说明理由．20. (本小题满分16分)已知数列{a n }的首项a 1＝3，对任意的n ∈N *，都有a n ＋1＝ka n －1(k ≠0)，数列{a n －1}是公比不为1的等比数列．(1) 求实数k 的值；(2) 设b n ＝⎩⎪⎨⎪⎧4－n ，n 为奇数，a n －1，n 为偶数，数列{b n }的前n 项和为S n ，求所有正整数m 的值，使得S 2mS 2m －1恰好为数列{b n }中的项．2020届高三模拟考试试卷(四)数学附加题(满分40分，考试时间30分钟)21. 【选做题】 在A ，B ，C 三小题中只能选做两题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．A. (选修42：矩阵与变换)已知矩阵M ＝⎣⎢⎡⎦⎥⎤23t 1的一个特征值为4，求矩阵M 的逆矩阵M －1.B. (选修44：坐标系与参数方程)在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为ρ(cos θ＋sin θ)＝12，曲线C 的参数方程为⎩⎨⎧x ＝23cos θ，y ＝2sin θ(θ为参数，θ∈R )．在曲线C 上求点M ，使点M 到l 的距离最小，并求出最小值．C. (选修45：不等式选讲)已知正数x ，y ，z 满足x ＋y ＋z ＝1，求1x ＋2y ＋1y ＋2z ＋1z ＋2x的最小值． 【必做题】 第22，23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤．22. 如图，在三棱柱ABCA 1B 1C 1中，侧面AA 1B 1B 为正方形，侧面BB 1C 1C 为菱形，∠BB 1C 1＝60°，平面AA 1B 1B ⊥平面BB 1C 1C.(1) 求直线AC 1与平面AA 1B 1B 所成角的正弦值； (2) 求二面角BAC 1C 的余弦值．23. 已知n 为给定的正整数，设(23＋x)n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，x ∈R .(1) 若n ＝4，求a 0，a 1的值；(2) 若x ＝13，求∑n k ＝0(n －k)a k x k 的值．2020届高三模拟考试试卷(四)(苏北四市)数学参考答案及评分标准1. {x|－1<x<2}2. －2i3. 454. 205. [4，＋∞)6. 127. 48. 149. 135 10.32π 11. (x ＋2)2＋y 2＝8 12. 3 13. 47 14. 3415. 证明：(1) 在△PBC 中，因为点M ，N 分别为棱PB ，PC 的中点，所以MN ∥BC.(3分)又MN ⊂平面AMN ，BC ⊄平面AMN ，所以BC ∥平面AMN.(6分)(2) 在△PAB 中，因为AP ＝AB ，点M 为棱PB 的中点，所以AM ⊥PB.(8分)因为平面PAB ⊥平面PBC ，平面PAB ∩平面PBC ＝PB ，AM ⊂平面PAB ，所以AM ⊥平面PBC.(12分)又AM ⊂平面AMN ，所以平面AMN ⊥平面PBC.(14分)16. 解：(1) 在△ABC 中，由余弦定理b 2＋c 2－2bccos A ＝a 2，得b 2＋20－2×25×55b ＝25，即b 2－4b －5＝0，(4分) 解得b ＝5或b ＝－1(舍)，所以b ＝5.(6分) (2) 由cos A ＝55及0<A<π，得sin A ＝1－cos 2A ＝1－（55）2＝255，(8分) 所以cos C ＝cos [π－(A ＋B)]＝－cos(A ＋π4)＝－22(cos A －sin A)＝1010.因为0<C<π，所以sin C ＝1－cos 2C ＝1－（1010）2＝31010， 从而tan C ＝sin Ccos C ＝310101010＝3，(12分)所以tan 2C ＝2tan C 1－tan 2C ＝2×31－32＝－34.(14分) 17. 解：(1) 在△SAO 中，SO ＝SA 2－AO 2＝52－32＝4.(2分)由△SNO 1∽△SAO 可知SO 1SO ＝r R ，所以SO 1＝43r ，(4分)所以OO 1＝4－43r ，所以V(r)＝13πr 2(4－43r)＝49π(3r 2－r 3)，0<r<3.(7分)(2) 由(1)得V(r)＝49π(3r 2－r 3)，0<r<3，所以V′(r)＝49π(6r －3r 2)，令V′(r)＝0，得r ＝2，(9分)当r ∈(0，2)时，V ′(r)>0，所以V(r)在(0，2)上单调递增； 当r ∈(2，3)时，V ′(r)<0，所以V(r)在(2，3)上单调递减． 所以当r ＝2时，V(r)取得最大值V(2)＝16π9.答：小圆锥的体积V 的最大值为16π9.(14分)18. 解：(1) 直线l 的方程为y ＝k(x －a)，即kx －y －ak ＝0.因为直线l 与圆O ：x 2＋y 2＝b 2相切，所以|－ak|k 2＋1＝b ，故k 2＝b 2a 2－b 2.所以椭圆C 的离心率e ＝1－b 2a 2＝1k 2＋1.(4分) (2) 设椭圆C 的焦距为2c ，则右准线方程为x ＝a 2c.由⎩⎪⎨⎪⎧y ＝k （x －a ），x ＝a 2c 得y ＝k(a 2c －a)＝k a 2－ac c ，所以Q(a 2c ，k （a 2－ac ）c)．(6分)由⎩⎪⎨⎪⎧x 2a 2＋y 2b 2＝1，y ＝k （x －a ）得(b 2＋a 2k 2)x 2－2a 3k 2x ＋a 4k 2－a 2b 2＝0， 解得x P ＝a 3k 2－ab 2b 2＋a 2k 2，则y P ＝k(a 3k 2－ab 2b 2＋a 2k 2－a)＝－2ab 2k b 2＋a 2k 2，所以P(a 3k 2－ab 2b 2＋a 2k 2，－2ab 2kb 2＋a 2k2)．(10分)因为OP →·OQ →＝0，所以a 2c ·a 3k 2－ab 2b 2＋a 2k 2＋k （a 2－ac ）c ·－2ab 2k b 2＋a 2k 2＝0，即a(a 2k 2－b 2)＝2b 2k 2(a －c)．(12分) 由(1)知k 2＝b 2a 2－b 2，所以a(a 2b 2a 2－b 2－b 2)＝2b 4（a －c ）a 2－b 2， 所以a ＝2a －2c ，即a ＝2c ，所以c a ＝12，故椭圆C 的离心率为12.(16分)19. 解：(1) f′(x)＝1x 2ln x ＋(a －1x )1x.因为曲线y ＝f(x)在点(1，f(1))处的切线方程为x ＋y －1＝0，所以f′(1)＝a －1＝－1，解得a ＝0.(2分) (2) 因为f′(x)＝ax －1＋ln xx 2存在两个不相等的零点， 所以g(x)＝ax －1＋ln x 存在两个不相等的零点，则g′(x)＝1x ＋a.①当a ≥0时，g ′(x)>0，所以g(x)单调递增，至多有一个零点．(4分) ②当a<0时，因为当x ∈(0，－1a )时，g ′(x)>0，g(x)单调递增；当x ∈(－1a ，＋∞)时，g ′(x)<0，g(x)单调递减，所以x ＝－1a 时，g(x)max ＝g(－1a )＝ln(－1a)－2.(6分)因为g(x)存在两个零点，所以ln(－1a )－2>0，解得－e －2<a<0.(7分)因为－e －2<a<0，所以－1a>e 2>1.因为g(1)＝a －1<0，所以g(x)在(0，－1a )上存在一个零点．(8分)因为－e －2<a<0，所以(－1a )2>－1a.因为g((－1a )2)＝ln(－1a )2＋1a －1，设t ＝－1a ，则y ＝2ln t －t －1(t>e 2)．因为y′＝2－tt<0，所以y ＝2ln t －t －1(t>e 2)单调递减， 所以y<2ln(e 2)－e 2－1＝3－e 2<0，所以g((－1a )2)＝ln(－1a )2＋1a －1<0，所以g(x)在(－1a，＋∞)上存在一个零点．综上可知，实数a 的取值范围是(－e －2，0)．(10分)(3) 当a ＝2时，f(x)＝(2－1x )ln x ，f ′(x)＝1x 2ln x ＋(2－1x )1x ＝2x －1＋ln xx 2，设g(x)＝2x －1＋ln x ，则g′(x)＝1x ＋2>0，所以g(x)单调递增，且g(12)＝ln 12<0，g(1)＝1>0，所以存在x 0∈(12，1)使得g(x 0)＝0.(12分)因为当x ∈(0，x 0)时，g(x)<0，即f′(x)<0，所以f(x)单调递减； 当x ∈(x 0，＋∞)时，g(x)>0，即f′(x)>0，所以f(x)单调递增， 所以x ＝x 0时，f(x)取得极小值，也是最小值，此时f(x 0)＝(2－1x 0)ln x 0＝(2－1x 0)(1－2x 0)＝－(4x 0＋1x 0)＋4.(14分)因为x 0∈(12，1)，所以f(x 0)∈(－1，0)．因为f(x)≥λ，且λ为整数，所以λ≤－1，即λ的最大值为－1.(16分) 20. 解：(1) 由a n ＋1＝ka n －1，a 1＝3可知，a 2＝3k －1，a 3＝3k 2－k －1. 因为{a n －1}为等比数列，所以(a 2－1)2＝(a 1－1)(a 3－1)，即(3k －2)2＝2×(3k 2－k －2)，即3k 2－10k ＋8＝0，解得k ＝2或k ＝43.(2分)当k ＝43时，a n ＋1－3＝43(a n －3)，所以a n ＝3，则a n －1＝2，所以数列{a n －1}的公比为1，不符合题意；当k ＝2时，a n ＋1－1＝2(a n －1)，所以数列{a n －1}的公比q ＝a n ＋1－1a n －1＝2，所以实数k 的值为2.(4分) (2) 由(1)知a n －1＝2n ，所以b n ＝⎩⎪⎨⎪⎧4－n ， n 为奇数，2n ， n 为偶数，则S 2m ＝(4－1)＋4＋(4－3)＋42＋…＋[4－(2m －1)]＋4m＝(4－1)＋(4－3)＋…＋[4－(2m －1)]＋4＋42＋…＋4m ＝m(4－m)＋4m ＋1－43，(6分)则S 2m －1＝S 2m －b 2m ＝m(4－m)＋4m －43.因为b 2m ＋b 2m ＋1＝3－2m ＋4m ，又(b 2m ＋2＋b 2m ＋3)－(b 2m ＋b 2m ＋1)＝3×4m －2>0， 且b 2＋b 3＝5>0，b 1＝3>0，所以S 2m －1>0，则S 2m >0.设S 2mS 2m －1＝b t >0，t ∈N *，(8分) 则t ＝1，3或t 为偶数，因为b 3＝1不可能，所以t ＝1或t 为偶数．①当S 2mS 2m －1＝b 1时，m （4－m ）＋4m ＋1－43m （4－m ）＋4m －43＝3，化简得6m 2－24m ＋8＝－4m ≤－4， 即m 2－4m ＋2≤0，所以m 可能取值为1，2，3，验证S 2S 1＝73，S 4S 3＝3，S 6S 5＝8723，得当m ＝2时，S 4S 3＝b 1成立．(12分)②当t 为偶数时，S 2m S 2m －1＝m （4－m ）＋4m ＋1－43m （4－m ）＋4m －43＝1＋3－3m 2＋12m －44m ＋1， 设c m ＝－3m 2＋12m －44m ，则c m ＋1－c m ＝9m 2－42m ＋214m ＋1. 由①知m>3，当m ＝4时，c 5－c 4＝－345<0；当m>4时，c m ＋1－c m >0，所以c 4>c 5<c 6<…，所以c m 的最小值为c 5＝－191 024，所以0<S 2m S 2m －1<1＋3－191 024＋1<5.令S 2m S 2m －1＝4＝b 2，则1＋3－3m 2＋12m －44m＋1＝4，即－3m 2＋12m －4＝0，无整数解． 综上，正整数m 的值2.(16分)2020届高三模拟考试试卷(苏北四市) 数学附加题参考答案及评分标准21. A. 解：矩阵M 的特征多项式为f(λ)＝⎪⎪⎪⎪⎪⎪λ－2－3－t λ－1＝(λ－2)(λ－1)－3t.(2分)因为矩阵M 的一个特征值为4，所以f(4)＝6－3t ＝0，所以t ＝2.(5分)所以M ＝⎣⎢⎡⎦⎥⎤2321，所以M －1＝⎣⎢⎢⎡⎦⎥⎥⎤12×1－3×2－32×1－3×2－22×1－3×222×1－3×2＝⎣⎢⎡⎦⎥⎤－14 34 12－12.(10分) B. 解：由l ：ρcos θ＋ρsin φ－12＝0，及x ＝ρcos θ，y ＝ρsin θ， 所以l 的直角坐标方程为x ＋y －12＝0. (2分)在曲线C 上取点M(23cos φ，2sin φ)，则点M 到l 的距离d ＝|23cos φ＋2sin φ－12|2＝⎪⎪⎪⎪4sin （φ＋π3）－122＝12－4sin （φ＋π3）2，(6分)当φ＝π6时，d 取最小值42，(8分)此时点M 的坐标为(3，1)．(10分)C. 解：因为x ，y ，z 都为正数，且x ＋y ＋z ＝1， 所以由柯西不等式，得3(1x ＋2y ＋1y ＋2z ＋1z ＋2x )＝(1x ＋2y ＋1y ＋2z ＋1z ＋2x )·[(x ＋2y)＋(y ＋2z)＋(z ＋2x)](5分) ≥(1x ＋2y·x ＋2y ＋1y ＋2z·y ＋2z ＋1z ＋2x·z ＋2x)2＝9， 当且仅当x ＝y ＝z ＝13时等号成立，所以1x ＋2y ＋1y ＋2z ＋1z ＋2x的最小值为3.(10分)22. 解：(1) 因为四边形AA 1B 1B 为正方形，所以AB ⊥BB 1.因为平面AA 1B 1B ⊥平面BB 1C 1C ，平面AA 1B 1B ∩平面BB 1C 1C ＝BB 1， AB ⊂平面AA 1B 1B ，所以AB ⊥平面BB 1C 1C. (2分)以点B 为坐标原点，分别以BA ，BB 1所在的直线为x ，y 轴，以过点B 且垂直于平面AA 1B 1B 的直线为z 轴，建立如图所示的空间直角坐标系Bxyz.不妨设正方形AA 1B 1B 的边长为2， 则A(2，0 ，0)，B 1(0，2，0)．在菱形BB 1C 1C 中，因为∠BB 1C 1＝60°，所以C 1(0，1，3)，所以AC 1→＝(－2，1，3)． 因为平面AA 1B 1B 的一个法向量为n ＝(0，0，1)， 设直线AC 1与平面AA 1B 1B 所成角为α， 则sin α＝|cos 〈AC 1→，n 〉|＝|3|22×1＝64，即直线AC 1与平面AA 1B 1B 所成角的正弦值为64.(6分) (2) 由(1)可知，C(0，－1，3)，所以CC 1→＝(0，2，0)． 设平面ACC 1的一个法向量为n 1＝(x 1，y 1，z 1)，因为⎩⎪⎨⎪⎧n 1·AC 1→＝0，n 1·CC 1→＝0，即⎩⎨⎧（x 1，y 1，z 1）·（－2，1，3）＝0，（x 1，y 1，z 1）·（0，2，0）＝0，取x 1＝32，y 1＝0，z 1＝1，即n 1＝(32，0，1)． 设平面ABC 1的一个法向量为n 2＝(x 2，y 2，z 2)， 因为BA →＝(2，0，0)，BC 1→＝(0，1, 3)，所以⎩⎨⎧（x 2，y 2，z 2）·（2，0，0）＝0，（x 2，y 2，z 2）·（0，1，3）＝0，取n 2＝(0，3，－1)．(8分)设二面角BAC 1C 的平面角为θ，则cos θ＝－cos 〈n 1，n 2〉＝－n 1·n 2|n 1|·|n 2|＝－－134＋1·3＋1＝77， 所以二面角BAC 1C 的余弦值为77.(10分) 23. 解：(1) 因为n ＝4，所以a 0＝C 04(23)4＝1681，a 1＝C 14(23)3＝3227.(2分) (2) 当x ＝13时，a k x k ＝C k n (23)n －k (13)k ， 因为kC k n ＝k n ！k ！（n －k ）！＝n （n －1）！（k －1）！（n －k ）！＝nC k －1n －1，(4分) ＝n －13n(23＋13)n －1＝23n ，当n ＝1时，也符合． 所以(n －k)a k x k 的值为23n.(10分)。

江苏省无锡市2013-2014学年高一下学期期末考试化学试卷(word版)注意事项及说明：①试卷满分：120分。

考试时间：100分钟②可能用到的相对原子质量：H —1 C —12 N —14 O —16 Na —23第Ⅰ卷 (选择题 共66分)一、选择题(本题包括14个小题，每题3分，共42分。

每题只有1个选项符合题意) 1．2014年“六·五”世界环境日中国主题为“向污染宣战”,旨在体现对治理污染紧迫性和艰巨性的清醒认识，倡导共同行动,努力改善环境,保卫家园。

下列说法正确的是 A ．把硝酸工厂的烟囱建造得更高一些，以减少氮氧化物的排放 B ．推广燃煤发电，停建核电站，以防核泄漏事故发生 C ．将废电池深埋，可以避免其中的重金属污染D ．大量燃烧化石燃料产生的PM2.5是雾霾天气的主要原因之一 2．下列化学用语对应正确的是A ．CH 4分子的比例模型：B ．CCl 4的电子式：C ．H 2O 2的结构式：D ．乙酸的最简式：C 2H 4O 2 3．下列关于有机物存在的叙述，错误的是A ．工业酒精中含有乙醇和甲醇B ．煤中含有苯和甲苯C ．天然油脂中含有高级脂肪酸甘油酯D ．许多水果中含有酯类化合物 4．下列各组物质的晶体中，化学键类型相同、晶体类型也相同的是 A ．SO 2和Si B ．CO 2和H 2O C ．NaCl 和HCl D ．CCl 4和KCl 5．能将化学能转化为热能的是A ．光合作用B ．水力发电C ．燃煤取暖D ．燃料电池 6．下列说法中正确的是A. O 168、O 178、O 188互为同素异形体B. O 2与O 3互为同位素C. CH 3-CH 2-OH 与CH 3-O-CH 3互为同分异构体D.7．下列措施是为了降低化学反应速率的是A ．食品放在冰箱中贮藏B ．双氧水制氧气时加入少量二氧化锰C ．试管中进行镁和水反应时，稍微加热D ．铁粉代替铁钉与稀硫酸反应制取氢气 8．下列叙述错误的是A ．乙烯和苯都能使溴水褪色，褪色的原理相同B ．淀粉、油脂、蛋白质都能水解，但水解产物不同C ．煤油可由石油分馏获得，可用作燃料和保存少量金属钠D ．乙醇、乙酸、乙酸乙酯都能发生取代反应。

江苏省无锡市2017年中考数学试卷（word 精校版）第Ⅰ卷（共30分）一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.5-的倒数是( ) A ．15 B ．5± C ．5 D ．15- 2.函数2x y x=-中自变量x 的取值范围是( )A ．2x ≠B ．2x ≥C ．2x ≤D ．2x > 3.下列运算正确的是( ) A ．()437aa = B ．()22ab ab = C ．824a a a ÷= D ．246a a a ⋅=4.下列图形中，是中心对称图形的是( )A ．B ． C. D ． 5.若2a b -=，3b c -=-，则a c -等于( ) A ．1 B ．1- C.5 D ．5-6.“表1”为初三（1）班全部43名同学某次数学测验成绩的统计结果，则下列说法正确的是 A ．男生的平均成绩大于女生的平均成绩 B ．男生的平均成绩小于女生的平均成绩 C.男生成绩的中位数大于女生成绩的中位数 D ．男生成绩的中位数小于女生成绩的中位数7.某商店今年1月份的销售额是2万元，3月份的销售额是4.5万元，从1月份到3月份，该店销售额平均每月的增长率是( )A ．20%B ．25% C.50% D ．62.5%8.对于命题“若22a b >，则a b >．”下面四组关于a 、b 的值中，能说明这个命题是假命题的是( ) A ．3a =，2b = B ．3a =-，2b = C.3a =，1b =- D ．1a =-，3b = 9.如图，菱形CD AB 的边20AB =，面积为320，D 90∠BA <o，O e 与边AB 、D A 都相切，10AO =，则O e 的半径长等于( )A ．5B ．6 C.25 D ．3210.如图，C ∆AB 中，C 90∠BA =o，3AB =，C 4A =，点D 是C B 的中点，将D ∆AB 沿D A 翻折得到D ∆AE ，连C E ，则线段C E 的长等于( ) A ．2 B ．54 C.53 D ．75第Ⅱ卷（共100分）二、填空题（每题2分，满分16分，将答案填在答题纸上）11.123的值是 ． 12.分解因式：2363a a -+= ．13.贵州F S A T 望远镜是目前世界第一大单口径射电望远镜，反射面总面积约2500002m ，这个数据用科学记数法可表示为 ．14.如图是我市某连续7天的最高气温与最低气温的变化图，根据图中信息可知，这7天中最大的日温差是Co．15.已知反比例函数kyx=的图像经过点()1,2--，则k的值为．16.已知圆锥的底面半径为3cm，母线长为5cm，则它的侧面展开图的面积等于2cm．17.如图，已知矩形CDAB中，3AB=，D2A=，分别以边DA、CB为直径在矩形CDAB的内部作半圆1O和半圆2O，一平行于AB的直线FE与这两个半圆分别交于点E、点F，且F2E=（FE与AB在圆1O和2O的同侧），则由»AE、FE、»F B、AB所围成图形（图中阴影部分）的面积等于．18.在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A、B、C、D都在格点处，AB与CD相交于O，则tan D∠BO的值等于．三、解答题（本大题共10小题，共84分.解答应写出文字说明、证明过程或演算步骤.）19. （本题满分8分）计算：（1）()()03627-+-+；（2）()()()a b a b a a b+---．20. （本题满分8分）（1）解不等式组：()2311222xx x+>⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⎧⎪⎨-≤+⋅⋅⋅⋅⎪⎩①②；（2）解方程：53212x x=-+．21. （本题满分8分）已知，如图，平行四边形CDAB中，E是CB边的中点，连D E并延长交AB的延长线于点F，求证：FAB=B．22. （本题满分8分）甲、乙、丙、丁四人玩扑克牌游戏，他们先取出两张红心和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色的即为游戏搭档．现甲、乙两人各抽取了一张，求两人恰好成为游戏搭档的概率．（请用“画树状图”或“列表”等方法写出分析过程）23. （本题满分8分）某数学学习网站为吸引更多人注册加入，举行了一个为期5天的推广活动．在活动期间，加入该网站的人数变化情况如下表所示：（1）表格中a =，b=；（2）请把下面的条形统计图补充完整；（3）根据以上信息，下列说法正确的是（只要填写正确说法前的序号）．①在活动之前，该网站已有3200人加入；②在活动期间，每天新加入人数逐天递增；③在活动期间，该网站新加入的总人数为2528人．24.（本题满分6分）如图，已知等边C∆AB，请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：（1）作C∆AB的外心O；（2）设D是AB边上一点，在图中作出一个正六边形D FGE HI，使点F，点H分别在边CB和CA 上．25.（本题满分10分）操作：“如图1，P 是平面直角坐标系中一点（x 轴上的点除外），过点P 作C x P ⊥轴于点C ，点C 绕点P 逆时针旋转60o得到点Q ．”我们将此由点P 得到点Q 的操作称为点的T 变换． （1）点(),a b P 经过T 变换后得到的点Q 的坐标为 ；若点M 经过T 变换后得到点()6,3N -，则点M 的坐标为 ．（2）A 是函数3y x =图像上异于原点O 的任意一点，经过T 变换后得到点B ． ①求经过点O 、点B 的直线的函数表达式；②如图2，直线AB 交y 轴于点D ，求∆OAB 的面积与D ∆OA 的面积之比．26.（本题满分10分）某地新建的一个企业，每月将产生1960吨污水．为保护环境，该企业计划购置污水处理器，并在如下两个型号中选择：已知商家售出的2台A 型、3台B 型污水处理器的总价为44万元；售出的1台A 型、4台B 型污水处理器的总价为42万元．（1）求每台A 型、B 型污水处理器的价格；（2）为确保将每月产生的污水全部处理完，该企业决定购买上述的污水处理器，那么他们至少要支付多少钱？27.（本题满分10分）如图，以原点O 为圆心、3为半径的圆与x 轴分别交于A 、B 两点（点B 在点A 的右边），P 是半径OB 上一点，过P 且垂直于AB 的直线与O e 分别交于C 、D 两点（点C 在点D 的上方），直线C A 、D B 交于点E ．若C:C 1:2A E =，（1）求点P 的坐标；（2）求过点A 和点E ，且顶点在直线CD 上的抛物线的函数表达式．28.（本题满分8分）如图，已知矩形CD AB 中，4AB =，D m A =．动点P 从点D 出发，在边D A 上以每秒1个单位的速度向点A 运动，连接C P ，作点D 关于直线C P 的对称点E ．设点P 的运动时间为()s t ． （1）若6m =，求当P 、E 、B 三点在同一直线上时对应的t 的值．（2）已知m 满足：在动点P 从点D 到点A 的整个运动过程中，有且只有一个时刻t ，使点E 到直线C B 的距离等于3，求所有这样的m 的取值范围．（无锡润禾教育提供试卷）润禾教育2016高考成绩榜（部分名单）陈璨 北京大学 王卓颖 中国地质大学 魏逸丹 南京理工大学 钱婧 北京大学 俞濒城 中国地质大学 朱逸凡 南京理工大学 金洋 清华大学 陈昊洋 中国海洋大学 杨曜岭 北京化工大学 王奕韬 清华大学 訾亦轩 中国药科大学 沈菡 东北财经大学 施滢璐 浙江大学 王卓筠 中国政法大学 周舜韬 对外经济贸易大学 陶甄 浙江大学 周文卉 中国政法大学 蔡湲 南京师范大学 关欣欣 复旦大学 邓娴仪 中央财经大学 华宇雯 南京师范大学 吕瑶瑶复旦大学 丁雪卿 中央财经大学 姜炜 南京师范大学 秦晟昊 复旦大学 林欣忆 中央财经大学 吕寅政 南京师范大学 邓智暄 南京大学 蔡尧 北京交通大学 权辰妍 南京师范大学 蒋佳锐 南京大学 杨浩 北京交通大学 尤宗涛 南京师范大学 尤一凡 南京大学 张无极 华东理工大学 周炘 南京师范大学 李雨桐 上海交通大学 华臻浩 华中科技大学 朱韵奇 南京师范大学 刘韵一 上海交通大学 张悦 华中科技大学 惠沁怡 南京中医药大学 邹雨瑶 上海交通大学 沈杰 西安交通大学 张俊怡 南京中医药大学 朱洁仪 上海外国语大学 范一 西南财经大学 方西子 西安电子科技大学 徐笑远 北京外国语大学 邱武强 大连理工大学 王榆杰 西安电子科技大学顾佳晟 北京航空航天大学 尤伟康 大连理工大学 程馨仪 苏州大学 冯嘉颖 北京航空航天大学郑光聪 东北大学 顾珏如 苏州大学 吴梓铃 湖南大学 林家驹 上海海洋大学 顾铭淳 苏州大学 张梦婷 湖南大学 周寅 上海纽约大学 蒋雨菡 苏州大学 林辰 吉林大学 纪宇婕 上海师范大学 李佳航 苏州大学 曹旭璋 厦门大学 王家辉 上海政法大学 刘清源 苏州大学 万昕 山东大学 江柯 哈尔滨工程大学 鲁嘉楠 苏州大学 唐烨四川大学顾茜婷哈尔滨工程大学陆恺苏州大学毛绮妤武汉大学王恒哈尔滨工程大学张铭蕙苏州大学吴瀚文武汉大学袁成哈尔滨工程大学朱梦柯苏州大学周滢武汉大学钱加骏南京航空航天大学顾宇文河海大学杜雅馨东南大学吴泓耘南京航空航天大学顾志远河海大学钱昀东南大学吴嘉昊南京航空航天大学潘佳佳河海大学任彦桥东南大学徐容南京航空航天大学孙梓雯河海大学荣悦东南大学杨正昊南京航空航天大学周辛瑜华中农业大学张权东南大学徐容南京航天航空大学林钰芸江南大学赵威威东南大学郭柯晴西交利物浦钱靖江南大学王维恺中南大学吴知行西交利物浦徐纯熙江南大学范佳怡东华大学周玥西交利物浦盛一珺宁波诺丁汉大学朱奕霖东华大学侯怡琳西交利物浦大学荣尤琦宁波诺丁汉大学周锦宇兰州大学平雪烨西交利物浦大学徐致钦南昌大学马跃成西北工业大学魏逸丹南京理工大学沈雨灏西北大学谭舒菲西北工业大学毛陆霄南京理工大学曹子浩长安大学润禾教育介绍：无锡润禾新课程教育培训中心是一家结合优质教育资源和先进信息技术，专注与研究国家新课程标准、家庭教育及学生课外学习辅导的教育机构，以“倡导优质教育，真诚服务社会”为宗旨，充分发挥教师资源优势，为锡城中小学生提供最优质的课外学习辅导。

江苏省无锡市南菁中学2014届九年级英语上学期第一次阶段性测试试题第一卷（选择题，共70分）一、听力测试（本大题共20分，每小题1分）I．听对话回答问题:本部分共有10道小题，每小题你将听到一段对话，每段对话听两遍。

在听每段对话前，你将有5秒钟的时间阅读题目；听完后，你还有5秒钟的时间选择你认为最合适的备选答案。

1. Which charity are they talking about?A. B. C.2. What is the box like?A. It’s heavy and small.B. It’s small and light.C. It’s big and light.3. Who will repair the bike?A. Li Ping.B. Tom.C. Mary.4. What does the man mean?A. He hasn’t read the story.B. He doesn’t like the story at all.C. He knows something about the story.5. When will the speech be ready?A. On Monday morning.B. On Tuesday afternoon.C. On Tuesday morning.6. Why does the woman walk all the way to the office?A. She takes it as a kind of exercise.B. She wants to save money.C. Her office isn’t very far.7. What’s the woman’s job?A. A waitress.B. A teacher.C. A doctor.8. Who is the woman most probably speaking to?A. A taxi driver.B. A policeman.C. A worker in the post office.9. What can we learn from the conversation?A. The woman won’t go to the movies.B. The woman doesn’t like watching movies.C. The man is too tired to go to the movies.10. How would the woman most probably go to work?A. By bus.B. By bike.C. By train.Ⅱ．听对话和短文回答问题。

江苏省无锡市硕放中学2014届九年级英语上学期期中试题第一卷（客观题共70分）一、听力测试（本大题共20分，每小题1分）I．听对话回答问题:本部分共有10道小题，每小题你将听到一段对话，每段对话听两遍。

在听每段对话前，你将有5秒钟的时间阅读题目；听完后，你还有5秒钟的时间选择你认为最合适的备选答案。

1. Which charity are they talking about?A. B. C.2. What is the box like?A. It’s heavy and small.B. It’s small and light.C.It’s big and light.3. Who will repair the bike?A. Li Ping.B. Tom.C. Mary.4. What does the man mean?A. He ha sn’t read the story.B. He doesn’t like the story at all.C.He knows something about the story.5. When will the speech be ready?A. On Monday morning.B. On Tuesday afternoon.C. On Tuesdaymorning.6. Why does the woman walk all the way to the office?A. She takes it as a kind of exercise.B. She wants to save money.C. Her officeisn’t very far.7. What’s the woman’s job?A. A waitress.B. A teacher.C. A doctor.8. Who is the woman most probably speaking to?A. A taxi driver.B. A policeman.C. A worker inthe post office.9. What can we learn from the conversation?A. The woman won’t go to the movies.B. The woman doesn’t likewatching movies.C. The man is too tired to go to the movies.10. How would the woman most probably go to work?A. By bus.B. By bike.C. By train.Ⅱ．听对话和短文回答问题。