区域综合2附答案

（苏教版•2024秋）小学一年级数学上册第1-4单元期中综合素养提升测评试卷（附答案）时间：90分钟满分：100分注意事项：1．亲爱的同学：答题前填写好自己的学校、班级、姓名等信息。

2．请将答案正确填写在答题区域，注意书写工整，格式正确，卷面整洁。

3．经过两周的认真学习，你一定又掌握了不少新的知识，你作好准备了吗？现在就让我们带着希望、带着微笑来挑战自己吧！相信你会做得很棒！记住：要细心哦！4.转眼学期过半，四年级想举办一场“自然科学技术与历史文化”主题展，丰富学生生活，展示学习成果。

请你帮助同学进行活动策划，布置展厅，加油吧！一、选择题1．“5○5＝0”，在○里应填的运算符号是（）。

A．＋B．－C．×2．被减数是9，减数是5，差是（）。

A．14 B．43．一个数，比6大，比10小，它不可能是（）。

A．7 B．8 C．104．小动物们做同样多的口算题，做对最多的是（）。

A．①B．②C．③5．9再添1是（）。

A．8 B．9 C．106．下面的物体，哪个不是同一类的（）。

A．B．C．7．从第二行移4个到第一行后，第二行比第一行多1个，原来第二行比第一行多（）个。

A．5 B．8 C．98．10个小朋友排成一排，从右边数，明明排第4，从左边数，明明排第几？（）A．5 B．6 C．79．（）是羽毛球。

A．B．C．10．下面三个盒子里原来都有果子，如果往三个盒子里再放入1个、2个、3个果子，这三个盒子的果子数就相等，原来哪个盒子里的果子数最少？（）A．B．C．二、填空题11．括号填上合适的数。

( )＜3 5＞( ) ( )＞8( )＜10 7＝( )12．6后面的第3个数是( )；8前面的第2个数是( )。

13．照样子填一填。

14．画一画，写一写。

15．比7个碗少2个的碗的个数是( )个。

16．在括号里填“＞”“＜”或“＝”。

2＋7( )10 10( )6＋3 10－3( )2＋5 10－1( )7＋3 17．数一数，填一填。

2021-2022学年人教版九年级数学几何部分综合提升训练2（附答案）1．如图，AB为⊙O的直径，弦CD⊥AB于点F，OE⊥AC于点E，若OE＝3，OB＝5，则CD的长度是（）A．9.6B．4C．5D．102．如图，在正方形ABCD中，AB＝6，M是AD边上的一点，AM：MD＝1：2．将△BMA 沿BM对折至△BMN，连接DN，则DN的长是（）A．B．C．3D．3．如图，直线y＝﹣2x+2与坐标轴交于A、B两点，点P是线段AB上的一个动点，过点P 作y轴的平行线交直线y＝﹣x+3于点Q，△OPQ绕点O顺时针旋转45°，边PQ扫过区域（阴影部分）面积的最大值是（）A．πB．πC．πD．π4．将如图所示的长方体牛奶包装盒沿某些棱剪开，且使六个面连在一起，然后铺平，则得到的图形可能是（）A．B．C．D．5．如图，已知点O是△ABC的外心，∠A＝40°，连结BO，CO，则∠BOC的度数是（）A．60°B．70°C．80°D．90°6．如图，已知在△ABC中，∠ABC＜90°，AB≠BC，BE是AC边上的中线．按下列步骤作图：①分别以点B，C为圆心，大于线段BC长度一半的长为半径作弧，相交于点M，N；②过点M，N作直线MN，分别交BC，BE于点D，O；③连接CO，DE．则下列结论错误的是（）A．OB＝OC B．∠BOD＝∠COD C．DE∥AB D．DB＝DE7．如图，已知在矩形ABCD中，AB＝1，BC＝，点P是AD边上的一个动点，连结BP，点C关于直线BP的对称点为C1，当点P运动时，点C1也随之运动．若点P从点A运动到点D，则线段CC1扫过的区域的面积是（）A．πB．π+C．D．2π8．如图，把含30°的直角三角板PMN放置在正方形ABCD中，∠PMN＝30°，直角顶点P在正方形ABCD的对角线BD上，点M，N分别在AB和CD边上，MN与BD交于点O，且点O为MN的中点，则∠AMP的度数为（）A．60°B．65°C．75°D．80°9．下列命题是真命题的是（）A．对角线相等的四边形是平行四边形B．对角线互相平分且相等的四边形是矩C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是正方形10．在锐角△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，有以下结论：＝＝＝2R（其中R为△ABC的外接圆半径）成立．在△ABC中，若∠A＝75°，∠B ＝45°，c＝4，则△ABC的外接圆面积为（）A．B．C．16πD．64π11．如图，⊙O的直径AB＝8，AM，BN是它的两条切线，DE与⊙O相切于点E，并与AM，BN分别相交于D，C两点，BD，OC相交于点F，若CD＝10，则BF的长是（）A．B．C．D．12．由沈康身教授所著，数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事：如图，三姐妹为了平分一块边长为1的祖传正方形地毯，先将地毯分割成七块，再拼成三个小正方形（阴影部分）．则图中AB的长应是．13．如图，三角形纸片ABC中，点D，E，F分别在边AB，AC，BC上，BF＝4，CF＝6，将这张纸片沿直线DE翻折，点A与点F重合．若DE∥BC，AF＝EF，则四边形ADFE 的面积为．14．如图，△ABC中，点D为边BC的中点，连接AD，将△ADC沿直线AD翻折至△ABC 所在平面内，得△ADC′，连接CC′，分别与边AB交于点E，与AD交于点O．若AE ＝BE，BC′＝2，则AD的长为．15．如图，在边长为4的正方形ABCD中，点E是BC的中点，点F在CD上，且CF＝3DF，AE，BF相交于点G，则△AGF的面积是．16．如图，△ABC的顶点均在正方形网格格点上．只用不带刻度的直尺，作出△ABC的角平分线BD（不写作法，保留作图痕迹）．17．如图，在矩形ABCD中，点E、F分别是边AB、CD的中点．求证：DE＝BF．18．如图，在▱ABCD中，AB＞AD．（1）用尺规完成以下基本作图：在AB上截取AE，使AE＝AD；作∠BCD的平分线交AB于点F．（保留作图痕迹，不写作法）（2）在（1）所作的图形中，连接DE交CF于点P，猜想△CDP按角分类的类型，并证明你的结论．19．如图，四边形ABCD为平行四边形，连接AC，且AC＝2AB．请用尺规完成基本作图：作出∠BAC的角平分线与BC交于点E．连接BD交AE于点F，交AC于点O，猜想线段BF和线段DF的数量关系，并证明你的猜想．（尺规作图保留作图痕迹，不写作法）20．在一次数学课外实践活动中，小明所在的学习小组从综合楼顶部B处测得办公楼底部D 处的俯角是53°，从综合楼底部A处测得办公楼顶部C处的仰角恰好是30°，综合楼高24米．请你帮小明求出办公楼的高度．（结果精确到0.1，参考数据tan37°≈0.75，tan53°≈1.33，≈1.73）21．如图，A，B是海面上位于东西方向的两个观测点，有一艘海轮在C点处遇险发出求救信号，此时测得C点位于观测点A的北偏东45°方向上，同时位于观测点B的北偏西60°方向上，且测得C点与观测点A的距离为25海里．（1）求观测点B与C点之间的距离；（2）有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里/小时，求救援船到达C点需要的最少时间．22．如图，点D在以AB为直径的⊙O上，过D作⊙O的切线交AB延长线于点C，AE⊥CD于点E，交⊙O于点F，连接AD，FD．（1）求证：∠DAE＝∠DAC；（2）求证：DF•AC＝AD•DC；（3）若sin∠C＝，AD＝4，求EF的长．23．如图，已知AB是⊙O的直径，∠ACD是所对的圆周角，∠ACD＝30°．（1）求∠DAB的度数；（2）过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．若AB＝4，求DF的长．24．如图，△ABC是⊙O的内接三角形，过点C作⊙O的切线交BA的延长线于点F，AE 是⊙O的直径，连接EC．（1）求证：∠ACF＝∠B；（2）若AB＝BC，AD⊥BC于点D，FC＝4，F A＝2，求AD•AE的值．25．已知在△ACD中，P是CD的中点，B是AD延长线上的一点，连结BC，AP．（1）如图1，若∠ACB＝90°，∠CAD＝60°，BD＝AC，AP＝，求BC的长．（2）过点D作DE∥AC，交AP延长线于点E，如图2所示，若∠CAD＝60°，BD＝AC，求证：BC＝2AP．（3）如图3，若∠CAD＝45°，是否存在实数m，当BD＝mAC时，BC＝2AP？若存在，请直接写出m的值；若不存在，请说明理由．26．在△ABC中，AB＝AC，D是边BC上一动点，连接AD，将AD绕点A逆时针旋转至AE的位置，使得∠DAE+∠BAC＝180°．（1）如图1，当∠BAC＝90°时，连接BE，交AC于点F．若BE平分∠ABC，BD＝2，求AF的长；（2）如图2，连接BE，取BE的中点G，连接AG．猜想AG与CD存在的数量关系，并证明你的猜想；（3）如图3，在（2）的条件下，连接DG，CE．若∠BAC＝120°，当BD＞CD，∠AEC ＝150°时，请直接写出的值．27．在等边△ABC中，AB＝6，BD⊥AC，垂足为D，点E为AB边上一点，点F为直线BD 上一点，连接EF．（1）将线段EF绕点E逆时针旋转60°得到线段EG，连接FG．①如图1，当点E与点B重合，且GF的延长线过点C时，连接DG，求线段DG的长；②如图2，点E不与点A，B重合，GF的延长线交BC边于点H，连接EH，求证：BE+BH＝BF；（2）如图3，当点E为AB中点时，点M为BE中点，点N在边AC上，且DN＝2NC，点F从BD中点Q沿射线QD运动，将线段EF绕点E顺时针旋转60°得到线段EP，连接FP，当NP+MP最小时，直接写出△DPN的面积．参考答案1．解：∵OE⊥AC，∴AE＝EC，∵AB⊥CD，∴∠AFC＝∠AEO＝90°，∵OE＝3，OB＝5，∴AE＝，∴AC＝8，∵∠A＝∠A，∠AEO＝∠AFC，∴△AEO∽△AFC，∴，即：，∴，∵CD⊥AB，∴CD＝2CF＝＝9.6．故选：A．2．解：连接AN交BM于点O，作NH⊥AD于点H．如图：∵AB＝6，AM：MD＝1：2．∴AM＝2，MD＝4．∵四边形ABCD是正方形．∴BM＝．根据折叠性质，AO⊥BM，AO＝ON．AM＝MN＝2．∴．∴＝．∴AN＝．∵NH⊥AD．∴AN2﹣AH2＝MN2﹣MH2．∴．∴．∴．∴．∴DN＝．故选：D．3．解：设P（m，﹣2m+2），则Q（m，﹣m+3）．∴OP2＝m2+（﹣2m+2）2＝5m2﹣8m+4，OQ2＝m2+（﹣m+3）2＝2m2﹣6m+9．∵△OPQ绕点O顺时针旋转45°．∴△OPQ≌△ODC，∠QOC＝∠POD＝45°．∴PQ扫过区域（阴影部分）面积S＝S扇OQC﹣S扇OPD＝＝＝．当m＝时，S的最大值为：．故选：A．4．解：该长方体表面展开图可能是选项A．故选：A．5．解：∵点O为△ABC的外心，∠A＝40°，∴∠A＝∠BOC，∴∠BOC＝2∠A＝80°，故选：C．6．解：由作法得MN垂直平分BC，∴OB＝OC，BD＝CD，OD⊥BC，所以A选项不符合题意；∴OD平分∠BOC，∴∠BOD＝∠COD，所以B选项不符合题意；∵AE＝CE，DB＝DC，∴DE为△ABC的中位线，∴DE∥AB，所以C选项不符合题意；DE＝AB，而BD＝BC，∵AB≠BC，∴BD≠DE，所以D选项符合题意．故选：D．7．解：如图，当P与A重合时，点C关于BP的对称点为C′，当P与D重合时，点C关于BP的对称点为C″，∴点P从点A运动到点D，则线段CC1扫过的区域为：扇形BC'C''和△BCC''，在△BCD中，∵∠BCD＝90°，BC＝，CD＝1，∴tan∠DBC＝，∴∠DBC＝30°，∴∠CBC″＝60°，∵BC＝BC''∴△BCC''为等边三角形，∴S扇形BC′C″＝＝π，作C''F⊥BC于F，∵△BCC''为等边三角形，∴BF＝，∴C''F＝tan60°×＝，∴S△BCC''＝，∴线段CC1扫过的区域的面积为：π+．故选：B．8．解：∵四边形ABCD是正方形，∴∠ABD＝45°，在Rt△PMN中，∠MPN＝90°，∵O为MN的中点，∴OP＝，∵∠PMN＝30°，∴∠MPO＝30°，∴∠AMP＝∠MPO+∠MBP＝30°+45°＝75°，故选：C．9．解：A、对角线互相平分的四边形是平行四边形，对角线相等的四边形也可能是等腰梯形等四边形，故A不符合题意；B、对角线互相平分的四边形是平行四边形，若对角线再相等，则四边形是矩形，故B符合题意；C、对角线互相垂直的四边形不能判定是平行四边形，也就不能判定是菱形，故C不符合题意；D、对角线互相垂直平分的四边形是菱形，不能判断它的内角有直角，故D不符合题意；故选：B．10．解：∵∠A+∠B+∠C＝180°，∴∠C＝180°﹣∠A﹣∠B＝180°﹣75°﹣45°＝60°，∵＝2R，∴2R＝＝＝，∴R＝，∴S＝πR2＝π（）2＝π，故选：A．11．解：如图，构建如图平面直角坐标系，过点D作DH⊥BC于H．∵AB是直径，AB＝8，∴OA＝OB＝4，∵AD，BC，CD是⊙O的切线，∴∠DAB＝∠ABH＝∠DHB＝90°，DA＝DE，CE＝CB，∴四边形ABHD是矩形，∴AD＝BH，AB＝DH＝8，∴CH＝＝＝6，设AD＝DE＝BH＝x，则EC＝CB＝x+6，∴x+x+6＝10，∴x＝2，∴D（2，4），C（8，﹣4），B（0，﹣4），∴直线OC的解析式为y＝﹣x，直线BD的解析式为y＝4x﹣4，由，解得，∴F（，﹣），∴BF＝＝，解法二：设DH交OC于G，利用△OBF∽△GDF求解即可．故选：A．12．解：∵地毯面积被平均分成了3份，∴每一份的边长为＝，∴CD＝3×＝，在Rt△ACD中，根据勾股定理可得AD＝＝，又根据剪裁可知BD＝CK＝1，∴AB＝AD﹣BD＝﹣1．故答案为：﹣1．13．解：∵纸片沿直线DE翻折，点A与点F重合，∴DE垂直平分AF．∴AD＝DF，AE＝EF．∵DE∥BC，∴DE为△ABC的中位线．∴DE＝BC＝（BF+CF）＝×（4+6）＝5．∵AF＝EF，∴△AEF为等边三角形．∴∠F AC＝60°．在Rt△AFC中，∵tan∠F AC＝，∴AF＝＝2．∴四边形ADFE的面积为：DE×AF＝×5×2＝5．故答案为：5．14．解：由题意可得，△DCA≌△DC′A，OC＝OC′，∠COD＝∠C′OD＝90°，∴点O为CC′的中点，∵点D为BC的中点，∴OD是△BCC′的中位线，∴OD＝BC′，OD∥BC′，∴∠COD＝∠EC′B＝90°，∵AE＝BE，BC′＝2，∴OD＝1，在△EC′B和△EOA中，，∴△EC′B≌△EOA（AAS），∴BC′＝AO，∴AO＝2，∴AD＝AO+OD＝2+1＝3，故答案为：3．15．解：作FM⊥AB于点M，作GN⊥AB于点N，如右图所示，∵正方形ABCD的边长为4，点E是BC的中点，点F在CD上，且CF＝3DF，∴BE＝2，MF＝4，BM＝CF＝3，∵GN⊥AB，FM⊥AB，∴GN∥FM，∴△BNG∽△BMF，∴，设BN＝3x，则NG＝4x，AN＝4﹣3x，∵GN⊥AB，EB⊥AB，∴△ANG∽△ABE，∴，即，解得x＝，∴GN＝4x＝，∴△AGF的面积是：＝＝，故答案为：．16．解：如图，线段BD即为所求作．17．证明：∵四边形ABCD是矩形，∴AB∥CD，AB＝CD，又E、F分别是边AB、CD的中点，∴DF＝BE，又AB∥CD，∴四边形DEBF是平行四边形，∴DE＝BF．18．解：（1）如图，AE、CF为所作；（2）△CDP为直角三角形．证明：∵四边形ABCD为平行四边形，∴AB∥CD，AD∥BC，∴∠CDE＝∠AED，∠ADC+∠BCD＝180°，∵AD＝AE，∴∠ADE＝∠AED，∴∠ADE＝∠CDE，∴∠CDE＝∠ADE＝∠ADC，∵CF平分∠BCD，∴∠FCD＝∠BCD，∴∠CDE+∠FCD＝90°，∴∠CPD＝90°，∴△CDP为直角三角形．19．解：如图：猜想：DF＝3BF，证明：∵四边形ABCD为平行四边形，∴OA＝OC，OD＝OB，∵AC＝2AB，∴AO＝AB．∵∠BAC的角平分线与BO交于点F，∴点F是BO的中点，即BF＝FO，∴OB＝OD＝2BF，∴DF＝DO+OF＝3BF，即DF＝3BF．20．解：由题意可知AB＝24米，∠BDA＝53°，∴tan∠BDA＝＝≈1.33，∴AD＝≈18.05（米）．∵tan∠CAD＝tan30°＝＝＝，∴CD＝18.05×≈10.4（米）．故办公楼的高度约为10.4米．21．解：（1）如图，过点C作CE⊥AB于点E，根据题意可知：∠ACE＝∠CAE＝45°，AC＝25海里，∴AE＝CE＝25（海里），∵∠CBE＝30°，∴BE＝25（海里），∴BC＝2CE＝50（海里）．答：观测点B与C点之间的距离为50海里；（2）如图，作CF⊥DB于点F，∵CF⊥DB，FB⊥EB，CE⊥AB，∴四边形CEBF是矩形，∴FB＝CE＝25（海里），CF＝BE＝25（海里），∴DF＝BD+BF＝30+25＝55（海里），在Rt△DCF中，根据勾股定理，得CD＝＝＝70（海里），∴70÷42＝（小时）．答：救援船到达C点需要的最少时间是小时．22．（1）证明：如图，连接OD．∵CD是⊙O的切线，∴OD⊥EC，∵AE⊥CE，∴AE∥OD，∴∠EAD＝∠ADO，∵OA＝OD，∴∠ADO＝∠DAO，∴∠DAE＝∠DAC．（2）证明：如图，连接BF．∵AB是直径，∴∠AFB＝90°，∵AE⊥EC，∴∠AFB＝∠E＝90°，∴BF∥EC，∴∠ABF＝∠C，∵∠ADF＝∠ABF，∴∠ADF＝∠C，∵∠DAF＝∠DAC，∴△DAF∽△CAD，∴＝，∴DF•AC＝AD•DC．（3）解：过点D作DH⊥AC于H．∵CD是⊙O的切线，∴∠ODC＝90°，∵sin∠C＝＝，∴可以假设OD＝k，OC＝4k，则OA＝OD＝k，CD＝k，∵•OD•DC＝•OC•DH，∴DH＝k，∴OH＝＝k，∴AH＝OA+OH＝k，∵AD2＝AH2+DH2，∴（4）2＝（k）2+（k）2∴k＝8或﹣8（舍弃），∴AC＝5k＝40，AB＝2k＝16，∴sin C＝＝＝sin∠ABK＝，∴AE＝10，AF＝4，∴EF＝AE﹣AF＝10﹣4＝6．23．解：（1）如图，连接BD，∵∠ACD＝30°，∴∠B＝∠ACD＝30°，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠DAB＝90°﹣∠B＝60°；（2）∵∠ADB＝90°，∠B＝30°，AB＝4，∴AD＝AB＝2，∵∠DAB＝60°，DE⊥AB，且AB是直径，∴EF＝DE＝AD sin60°＝，∴DF＝2DE＝2．24．（1）证明：如图1，连接OC，∵CF是⊙O的切线，∴∠OCF＝90°，∴∠OCA+∠ACF＝90°，∵OE＝OC，∴∠E＝∠OCE，∵AE是⊙O的直径，∴∠ACE＝90°，∴∠OCA+∠OCE＝90°，∴∠ACF＝∠OCE＝∠E，∵∠B＝∠E，∴∠ACF＝∠B；（2）解：∵∠ACF＝∠B，∠F＝∠F，∴△ACF∽△CBF，∴＝，∵AF＝2，CF＝4，∴，∴BF＝8，∴AB＝BC＝8﹣2＝6，AC＝3，∵AD⊥BC，∴∠ADB＝∠ACE＝90°，∵∠B＝∠E，∴△ABD∽△AEC，∴＝，即AE•AD＝AB×AC＝6×3＝18．25．解：（1）∵∠ACB＝90°，∠CAD＝60°，∴AB＝，∵BD＝AC，∴AD＝AC，∴△ADC是等边三角形，∴∠ACD＝60°，∵P是CD的中点，∴AP⊥CD，在Rt△APC中，AP＝，∴，∴，（2）证明：连接BE，∵DE∥AC，∴∠CAP＝∠DEP，在△CP A和△DPE中，∴△CP A≌△DPE（AAS），∴AP＝EP＝，DE＝AC，∵BD＝AC，∴BD＝DE，又∵DE∥AC，∴∠BDE＝∠CAD＝60°，∴△BDE是等边三角形，∴BD＝BE，∠EBD＝60°，∵BD＝AC，∴AC＝BE，在△CAB和△EBA中，∴△CAB≌△EBA（SAS），∴AE＝BC，∴BC＝2AP，（3）存在这样的m，m＝．理由如下：作DE∥AC交AP延长线于E，连接BE，由（2）同理可得DE＝AC，∠EDB＝∠CAD＝45°，AE＝2AP，当BD＝时，∴BD＝，作BF⊥DE于F，∵∠EDB＝45°，∴BD＝，∴DE＝DF，∴点E，F重合，∴∠BED＝90°，∴∠EBD＝∠EDB＝45°，∴BE＝DE＝AC，同（2）可证：△CAB≌△EBA（SAS），∴BC＝AE＝2AP，∴存在m＝，使得BC＝2AP，26．解：（1）连接CE，过点F作FQ⊥BC于Q，∵BE平分∠ABC，∠BAC＝90°，∴F A＝FQ，∵AB＝AC，∴∠ABC＝∠ACB＝45°，∴FQ＝CF，∵∠BAC+∠DAE＝180°，∴∠DAE＝∠BAC＝90°，∴∠BAD＝∠CAE，由旋转知，AD＝AE，∴△ABD≌△ACE（SAS），∴BD＝CE＝2，∠ABD＝∠ACE＝45°，∴∠BCE＝90°，∴∠CBF+∠BEC＝90°，∵BE平分∠ABC，∴∠ABF＝∠CBF，∴∠ABF+∠BEC＝90°，∵∠BAC＝90°，∴∠ABF+∠AFB＝90°，∴∠AFB＝∠BEC，∵∠AFB＝∠CFE，∴∠BEC＝∠CFE，∴CF＝CE＝2，∴AF＝FQ＝CF＝；（2）AG＝CD，理由：延长BA至点M，使AM＝AB，连接EM，∵G是BE的中点，∴AG＝ME，∵∠BAC+∠DAE＝∠BAC+∠CAM＝180°，∴∠DAE＝∠CAM，∴∠DAC＝∠EAM，∵AB＝AM，AB＝AC，∴AC＝AM，∵AD＝AE，∴△ADC≌△AEM（SAS），∴CD＝EM，∴AG＝CD；（3）如图3，连接DE，AD与BE的交点记作点N，∵∠BAC+∠DAE＝180°，∠BAC＝120°，∴∠DAE＝60°，∵AD＝AE，∴△ADE是等边三角形，∴AE＝DE，∠ADE＝∠AED＝60°，∵∠AEC＝150°，∴∠DEC＝∠AEC﹣∠AED＝90°，在△ABC中，AB＝AC，∠BAC＝120°，∴∠ACB＝∠ABC＝30°，∵∠AEC＝150°，∴∠ABC+∠AEC＝180°，∴点A，B，C，E四点共圆，∴∠BEC＝∠BAC＝120°，∴∠BED＝∠BEC﹣∠DEC＝30°，∴∠DNE＝180°﹣∠BED﹣∠ADE＝90°，∵AE＝DE，∴AN＝DN，∴BE是AD的垂直平分线，∴AG＝DG，BA＝BD＝AC，∴∠ABE＝∠DBE＝∠ABC＝15°，∴∠ACE＝∠ABE＝15°，∴∠DCE＝45°，∵∠DEC＝90°，∴∠EDC＝45°＝∠DCE，∴DE＝CE，∴AD＝DE，设AG＝a，则DG＝a，由（2）知，AG＝CD，∴CD＝2AG＝2a，∴CE＝DE＝CD＝a，∴AD＝a，∴DN＝AD＝a，过点D作DH⊥AC于H，在Rt△AHC中，∠ACB＝30°，CD＝2a，∴DH＝a，根据勾股定理得，CH＝a，在Rt△AHD中，根据勾股定理得，AH＝＝a，∴AC＝AH+CH＝a+a，∴BD＝a+a，∴＝＝．27．解：（1）①过D作DH⊥GC于H，如图：∵线段EF绕点E逆时针旋转60°得到线段EG，点E与点B重合，且GF的延长线过点C，∴BG＝BF，∠FBG＝60°，∴△BGF是等边三角形，∴∠BFG＝∠DFC＝60°，BF＝GF，∵等边△ABC，AB＝6，BD⊥AC，∴∠DCF＝180°﹣∠BDC﹣∠DFC＝30°，∠DBC＝∠ABC＝30°，CD＝AC＝AB ＝3，∴∠BCG＝∠ACB﹣∠DCF＝30°，∴∠BCG＝∠DBC，∴BF＝CF，∴GF＝CF，Rt△FDC中，CF＝＝＝2，∴GF＝2，Rt△CDH中，DH＝CD•sin30°＝，CH＝CD•cos30°＝，∴FH＝CF﹣CH＝，∴GH＝GF+FH＝，Rt△GHD中，DG＝＝；②过E作EP⊥AB交BD于P，过H作MH⊥BC交BD于M，连接PG，作BP中点N，连接EN，如图：∵EF绕点E逆时针旋转60°得到线段EG，∴△EGF是等边三角形，∴∠EFG＝∠EGF＝∠GEF＝60°，∠EFH＝120°，EF＝GF，∵△ABC是等边三角形，∴∠ABC＝60°，∴∠ABC+∠EFH＝180°，∴B、E、F、H共圆，∴∠FBH＝∠FEH，而△ABC是等边三角形，BD⊥AC，∴∠DBC＝∠ABD＝30°，即∠FBH＝30°，∴∠FEH＝30°，∴∠FHE＝180°﹣∠EFH﹣∠FEH＝30°，∴EF＝HF＝GF①，∵EP⊥AB，∠ABD＝30°，∴∠EPB＝60°，∠EPF＝120°，∴∠EPF+∠EGF＝180°，∴E、P、F、G共圆，∴∠GPF＝∠GEF＝60°，∵MH⊥BC，∠DBC＝30°，∴∠BMH＝60°，∴∠BMH＝∠GPF②，而∠GFP＝∠HFM③，由①②③得△GFP≌△HFM（AAS），∴PF＝FM，∵EP⊥AB，BP中点N，∠ABD＝30°，∴EP＝BP＝BN＝NP，∴PF+NP＝FM+BN，∴NF＝BM，Rt△MHB中，MH＝BM，∴NF＝MH，∴NF+BN＝MH+EP，即BF＝MH+EP，Rt△BEP中，EP＝BE•tan30°＝BE，Rt△MHB中，MH＝BH•tan30°＝BH，∴BF＝BE+BH，∴BE+BH＝BF；（2）以M为顶点，MP为一边，作∠PML＝30°，ML交BD于G，过P作PH⊥ML于H，设MP交BD于K，如图：Rt△PMH中，HP＝MP，∴NP+MP最小即是NP+HP最小，此时N、P、H共线，∵将线段EF绕点E顺时针旋转60°得到线段EP，∴F在射线QF上运动，则P在射线MP上运动，根据“瓜豆原理”，F为主动点，P是从动点，E为定点，∠FEP＝60°，则F、P轨迹的夹角∠QKP＝∠FEP＝60°，∴∠BKM＝60°，∵∠ABD＝30°，∴∠BMK＝90°，∵∠PML＝30°，∴∠BML＝60°，∴∠BML＝∠A，∴ML∥AC，∴∠HNA＝180°﹣∠PHM＝90°，而BD⊥AC，∴∠BDC＝∠HNA＝∠PHM＝90°，∴四边形GHND是矩形，∴DN＝GH，∵等边△ABC中，AB＝6，BD⊥AC，∴CD＝3，又DN＝2NC，∴DN＝GH＝2，∵等边△ABC中，AB＝6，点E为AB中点时，点M为BE中点，∴BM＝，BD＝AB•sin A＝6×sin60°＝3，Rt△BGM中，MG＝BM＝，BG＝BM•cos30°＝，∴MH＝MG+GH＝，GD＝BD﹣BG＝，Rt△MHP中，HP＝MH•tan30°＝，∴PN＝HN﹣HP＝GD﹣HP＝，∴S△DPN＝PN•DN＝．。

区域地理综合模拟测试卷一、选择题(本大题共15小题,每小题3分,共45分。

)京津冀都市圈以北京市和天津市为核心,包括河北省石家庄、唐山、张家口等8个地级市。

下表示意2000~2018年京津冀都市圈耕地占区域总面积的比重。

据此完成1~3题。

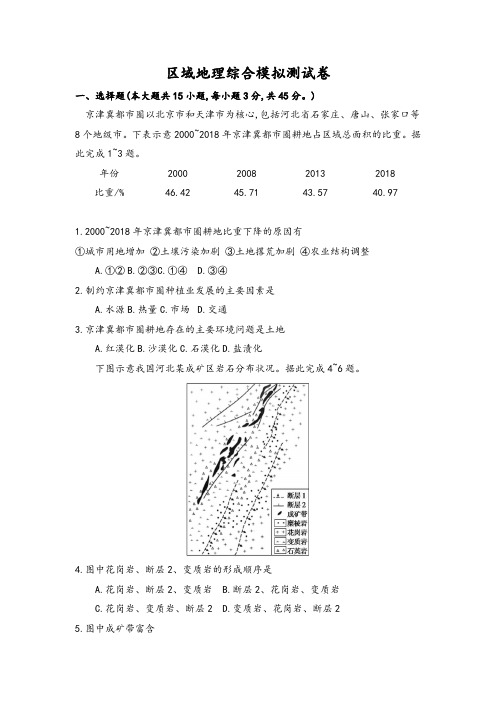
年份2000 2008 2013 2018比重/% 46.42 45.71 43.57 40.971.2000~2018年京津冀都市圈耕地比重下降的原因有①城市用地增加②土壤污染加剧③土地撂荒加剧④农业结构调整A.①②B.②③C.①④D.③④2.制约京津冀都市圈种植业发展的主要因素是A.水源B.热量C.市场D.交通3.京津冀都市圈耕地存在的主要环境问题是土地A.红漠化B.沙漠化C.石漠化D.盐渍化下图示意我国河北某成矿区岩石分布状况。

据此完成4~6题。

4.图中花岗岩、断层2、变质岩的形成顺序是A.花岗岩、断层2、变质岩B.断层2、花岗岩、变质岩C.花岗岩、变质岩、断层2D.变质岩、花岗岩、断层25.图中成矿带富含A.有色金属B.天然气C.石油D.煤炭6.图中糜棱岩属于A.石灰岩B.侵入岩C.喷出岩D.变质岩萨吾尔山坐落在新疆维吾尔自治区阿勒泰地区的西南边缘,最高峰木斯岛山海拔3835米,山顶终年被冰川覆盖。

木斯岛山冰川反照率较大,且时空分布变化大。

近年来,全球气候变暖和频繁的人类活动导致木斯岛山冰川融化加速,有学者建议在冰川下方建一个人工蓄水坝,也叫“冰川修复工程”,以减少冰川消融。

下图示意2018年木斯岛山冰川分布状况。

据此完成7~9题。

7.木斯岛山冰川反照率最低值出现的月份为A.1~2月B.4~5月C.7~8月D.10~11月8.同一时期,图中甲、乙、丙、丁四地中冰川反照率最高的是A.甲B.乙C.丙D.丁9.木斯岛山修建人工蓄水坝可减少冰川消融的原因是A.增加局部降水B.阻挡融水下渗C.降低气温,减少冰川消融量D.夜间气温低,坝内融水结冰我国台湾的甲公司是目前全球最大的半导体和芯片代工制造商,日本的乙公司是甲公司在日本的重要客户。

综合能力测试题(附答案)一、选择题（每题5分，共40分）1. 下列哪个城市被誉为“世界工厂”？A. 北京B. 东莞C. 上海D. 深圳答案：B2. 以下哪个经济体制是社会主义市场经济体制的基础？A. 计划经济B. 混合经济C. 市场经济D. 国有经济答案：C3. 下列哪个科学家提出了相对论？A. 牛顿B. 爱因斯坦C. 陈景润D. 霍金答案：B4. 以下哪个国家是世界上最大的碳排放国？A. 美国B. 中国C. 印度D. 俄罗斯答案：B5. 以下哪个城市是联合国教科文组织评定的“世界设计之都”？A. 北京B. 上海C. 广州D. 深圳答案：D6. 以下哪个古代发明被誉为“四大发明”之一？A. 圆规B. 指南针C. 火药D. 造纸术答案：B7. 下列哪个企业是全球最大的智能手机制造商？A. 苹果B. 三星C. 华为D. 小米答案：B8. 以下哪个地区是我国著名的茶叶产区？A. 福建B. 云南C. 广东D. 浙江答案：B二、填空题（每题5分，共30分）9. 请补全下列句子：我国首颗量子科学实验卫星名为“______”。

答案：墨子号10. 请补全下列句子：2019年，我国国内生产总值达到______万亿元。

答案：99.111. 请补全下列句子：我国著名科学家______被誉为“现代计算机之父”。

答案：冯·诺依曼12. 请补全下列句子：我国著名的“一带一路”倡议于______年提出。

答案：201313. 请补全下列句子：联合国教科文组织将每年的______定为“世界遗产日”。

答案：6月7日14. 请补全下列句子：我国著名的“三山五岳”中的五岳包括：泰山、华山、嵩山、衡山和______。

答案：恒山三、判断题（每题5分，共30分）15. 我国是世界上人口最多的国家。

（）答案：正确16. 量子计算机是一种基于量子力学原理的计算机，具有超强的计算能力。

（）答案：正确17. 马克思主义是我国的指导思想。

（）答案：正确18. 美国是世界上最大的碳排放国。

冀教版六年级数学上册第一、二单元综合素质达标一、填空。

(每空 1 分，共 27 分)1. 圆有( )条半径，半径的长度是它直径的( )，半圆有( )条对称轴。

2. 一张圆形纸片，至少对折( )次可以找到它的圆心；将一张圆形纸片连续对折三次，得到一个扇形，这个扇形的圆心角是( )°。

3. 一个圆的直径是 4.8 cm ，这个圆的半径是( )cm 。

一个圆的半径是 4.8 cm ，这个圆的直径是( )cm 。

4. 如右图，正方形的边长是 36 厘米，圆心角是 180°的扇形所在圆的半径是( )厘米，直径是( )厘米；圆心角是 90°的扇形所在圆的直径是( )厘米。

5. 如图，涂色部分的圆心角是( )°，在同一个圆中，( )决定扇形的大小。

6. 3 ∶ 4＝( )÷( )＝⎝ ⎛⎭⎪⎫＝21 ∶( )＝( )∶ 207. 根据 3×8＝4.8×5 写出两个比例：( )和( )；在一个比例中，两个内项的积是最小的合数，其中一个外项是 0.5，另一个外项是( )。

8. 一块地种了三种蔬菜，黄瓜和豆角种植面积的比是 3 ∶ 5，豆角和西红柿种植面积的比是 4 ∶ 3，黄瓜和西红柿种植面积的比是( )∶( )。

9. 如图，阴影部分的面积是小圆面积的23，是大圆面积的14。

小圆和大圆面积的最简单的整数比是( )。

10. 下面是荣荣今天早上吃的各种食物的质量。

(单位：g)(1)荣荣今天早上吃的蛋糕、牛肉、小米粥的质量比是( )。

(2)荣荣的妈妈按照同样的食物比吃了 810 g 早餐，妈妈吃了蛋糕( )g，牛肉 ( )g，小米粥( )g。

二、选择。

(将正确答案的序号填在括号里)(每题 2 分，共 16 分)1. 井盖平面轮廓采用圆形的一个原因是圆形井盖怎么放都不会掉到井里，并且能恰好盖住井口，这是应用了( )。

A. 圆心确定圆的位置B. 半径决定圆的大小C. 同一圆内所有直径都相等D. 圆是轴对称图形2. 下面图形中阴影部分是扇形的是( )。

北师大版八年级数学下册第二章综合素质评价一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列式子：①3＞0；②4x ＋6＞0；③x ＜2；④x 2＋x ；⑤x ≠－5；⑥x ＋2＞x ＋1，其中不等式有( )A ．3个B ．4个C ．5个D ．6个2．若x ＜y ，且(a －3)x ＞(a －3)y ，则a 的取值范围是( )A ．a ＜3B ．a ＞3C ．a ≥3D ．a ≤33．下列说法中，错误的是( )A ．不等式x ＜2的正整数解只有一个B ．－2是不等式2x －1＜0的一个解C ．不等式－3x ＞9的解集是x ＞－3D ．不等式x ＜10的整数解有无数个4．已知点P (x －2，6－2x )是平面直角坐标系第二象限上一点，则x 的取值范围在数轴上表示正确的是( )5．【2021·娄底】如图，直线y ＝x ＋b 和y ＝kx ＋4与x 轴分别相交于点A (－4，0)，点B (2，0)，则⎩⎨⎧x ＋b ＞0，kx ＋4＞0的解集为( )A ．－4＜x ＜2B ．x ＜－4C ．x ＞2D ．x ＜－4或x ＞2 6．【2022·佛山南海区校级月考】某种商品的进价为400元，出售时标价为500元，由于换季，商店准备打折销售该种商品，但要保证利润率不低于10%，那么至多打( )A ．8折B ．8.5折C ．8.8折D ．9折7．已知不等式组⎩⎨⎧x ＋a >1，2x ＋b <2的解集为－2＜x ＜3，则(a ＋b )2 023的值为( ) A ．1 B ．2 023 C ．－1 D ．－2 0238．现在有住宿生若干名，分住若干间宿舍，若每间住4人，则还有19人无宿舍住；若每间住6人，则有一间宿舍不空也不满，若设宿舍间数为x ，则可以列不等式组为( )A.⎩⎨⎧（4x ＋19）－6（x －1）≥1（4x ＋19）－6（x －1）≤6B.⎩⎨⎧（4x ＋19）－6（x －1）≤1（4x ＋19）－6（x －1）≥6 C.⎩⎨⎧（4x ＋19）－6（x －1）≤1（4x ＋19）－6（x －1）≥5 D.⎩⎨⎧（4x ＋19）－6（x －1）≥1（4x ＋19）－6（x －1）≤59．若关于x ，y 的方程组⎩⎨⎧2x ＋y ＝4，x ＋2y ＝－3m ＋2的解满足x －y ＞－32，则m 的最小整数解为( )A ．－3B ．－2C ．－1D ．010．对于任意实数m 、n ，定义一种新运算：m ※n ＝mn －m －n ＋3，等式的右边是通常的加减和乘法运算，例如：3※5＝3×5－3－5＋3＝10.请根据上述定义解决问题：若a ＜4※x ＜7，且解集中有两个整数解，则a 的取值范围是( )A ．－1＜a ≤4B ．－1≤a ＜2C ．－4≤a ＜－1D ．－4＜a ≤－1二、填空题：本大题共5小题，每小题3分，共15分．11．语句“x 的18与x 的和不超过5”可以表示为____________．12．若不等式(m －3)x |m －2|＋2＞0是关于x 的一元一次不等式，则m 的值为____________．13．不等式组⎩⎨⎧x －2<3a ，－2x >－2a ＋8的解集是x ＜a －4，则a 的取值范围是_____________． 14．对一个实数x ，按如图所示的程序进行操作，规定：程序运行从“输入一个实数x ”到“判断结果是否大于190”为一次操作，如果操作恰好进行两次停止，那么x 的取值范围是____________．15．定义：对于实数a ，b ，符号max{a ，b }表示：当a ≥b 时，max{a ，b }＝a ，当a ＜b 时，max{a ，b }＝b .例如max{－3，5}＝5，max{2，1}＝2.若关于x 的函数y ＝max{x －2，－2x ＋1}，则该函数的最小值为______________．三、解答题(一)：本大题共3小题，每小题8分，共24分．16．【2022·宜昌】解不等式x －13≥x －32＋1，并在如图所示的数轴上表示解集．17．【2022·毕节】解不等式组⎩⎪⎨⎪⎧x －3（x －2）≤8，12x －1<3－32x ，并把解集在数轴上表示出来．18．(1)解不等式5x ＋2≥3(x －1)，并把它的解集在如下数轴上表示出来；(2)写出一个实数k ，使得不等式x ＜k 和(1)中的不等式组成的不等式组恰有3个整数解．四、解答题(二)：本大题共3小题，每小题9分，共27分．19．已知关于x ，y 的方程组⎩⎨⎧2x ＋2y ＝4m ，x －y ＝3m －4，且x ＞0，y ＞0. (1)试用含m 的式子表示方程组的解；(2)求实数m 的取值范围．20．每年11月份脐橙和蜜桔进入销售旺季．某商家购进脐橙和蜜桔共1 000箱．设购进蜜桔x 箱，这两种水果的售价与进价如下表所示：(1)请用含x 的代数式表示该商家售完这1 000箱水果所获得的利润；(2)为了迎接“双11”活动，商家决定进行组合促销活动：两种水果各一箱打包成一组，售价为55元/组，其组数为购进蜜桔箱数的15，未打包的按原价出售．若这两种水果全部卖出，利润不少于6 500元，则该商家至少要购进蜜桔多少箱？21．对x ，y 定义一种新运算T ，规定：T (x ，y )＝(mx ＋ny )(x ＋2y )(其中m ，n 均为非零常数)．例如：T (1，1)＝3m ＋3n .已知T (1，－1)＝0，T (0，2)＝8.(1)求m ，n 的值；(2)若关于p 的不等式组⎩⎨⎧T （2p ，2－p ）>4，T （4p ，3－2p ）≤a恰好有3个整数解，求a 的取值范围．五、解答题(三)：本大题共2小题，每小题12分，共24分．22．某学校需要采购一批演出服装，A ，B 两家制衣公司都愿意成为这批服装的供应商．经了解，两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元．经洽谈协商，A 公司给出的优惠条件是全部服装按单价打七折，但校方需承担2 200元的运费；B 公司给出的优惠条件是男女装均按每套100元打八折，公司承担运费．另外根据大会组委会要求，参加演出的女生人数应比男生人数的2倍少100人，设参加演出的男生有x 人．(1)设学校购买A ，B 两家公司服装所付的总费用分别是y 1元，y 2元，用含x 的代数式分别表示y 1和y 2；(2)该学校购买哪家制衣公司的服装比较合算？23．先阅读下面的例题，再按要求解决问题．例题：解一元二次不等式x 2－9＞0.解：∵x 2－9＝(x ＋3)(x －3)，∴(x ＋3)(x －3)＞0.由有理数的乘法法则“两数相乘，同号得正”，有①⎩⎨⎧x ＋3>0，x －3>0，解不等式组①，得x >3， ②⎩⎨⎧x ＋3<0，x －3<0，解不等式组②，得x ＜－3， 故原不等式的解集为x ＞3或x ＜－3.问题：(1)求关于x 的不等式(x ＋1)(x －2)＞0的解集；(2)求关于x 的两个多项式的商组成的不等式3x －72x －9<0的解集；(3)若a是(2)中不等式的整数解，b＝4，a，b，c为△ABC的三条边长，c是△ABC中的最长的边长(△ABC非等边三角形)．①求c的取值范围；②若c为整数，求这个等腰三角形ABC的周长．答案一、1．C 2．A 3．C 4．C 5．A 6．C 7．C 8．D9．C 提示：⎩⎨⎧2x ＋y ＝4，①x ＋2y ＝－3m ＋2，②①－②得x －y ＝3m ＋2，∵关于x ，y 的方程组⎩⎨⎧2x ＋y ＝4，x ＋2y ＝－3m ＋2的解满足x －y ＞－32，∴3m ＋2＞－32，解得m ＞－76， ∴m 的最小整数解为－1.10．B 提示：根据题意，得4※x ＝4x －4－x ＋3＝3x －1.∴a <3x －1<7，解得a ＋13<x <83.∵解集中有两个整数解，∴0≤a ＋13<1，解得－1≤a <2.二、11．18x ＋x ≤5 12．113．a ≥－3 14．22＜x ≤6415．－1 提示：当x －2≥－2x ＋1时，解得x ≥1，此时y ＝x －2，且y 随x 的增大而增大，∴当x ≥1时，y ≥－1；当x －2<－2x ＋1时，解得x <1，此时y ＝－2x ＋1，且y 随x 的减少而增大，∴x <1时，y >－1.综上可知，函数的最小值为－1.三、16．解：x －13≥x －32＋1，去分母，得2(x －1)≥3(x －3)＋6，去括号，得2x －2≥3x －9＋6，移项，得2x －3x ≥－9＋6＋2，合并同类项，得－x ≥－1，系数化为1，得x ≤1.这个不等式的解集在数轴上表示如下：17．解：⎩⎪⎨⎪⎧x －3（x －2）≤8，①12x －1<3－32x ，② 解不等式①得x ≥－1，解不等式②得x <2，∴原不等式组的解集为－1≤x <2.该不等式组的解集在数轴上表示如下：18．解：(1)5x ＋2≥3(x －1)，去括号，得5x ＋2≥3x －3，移项，得5x －3x ≥－3－2，合并同类项，得2x ≥－5，两边都除以2，得x ≥－2.5，这个不等式的解集在数轴上表示为：(2)∵存在一个实数k ，使得不等式x ＜k 和(1)中的不等式组成的不等式组恰有3个整数解，∴0＜k ≤1，∴k ＝1满足条件(答案不唯一)．四、19．解：(1)方程组整理，得⎩⎨⎧x ＋y ＝2m ， ①x －y ＝3m －4，② ①＋②，得2x ＝5m －4，∴x ＝5m －42，①－②，得2y ＝－m ＋4，∴y ＝－m ＋42，∴原方程组的解为⎩⎪⎨⎪⎧x ＝5m －42，y ＝4－m 2；(2)∵x ＞0，y ＞0，∴⎩⎪⎨⎪⎧5m －42>0，③4－m 2>0，④解不等式③，得m ＞45，解不等式④，得m ＜4，∴不等式组的解集为45＜m ＜4，即实数m 的取值范围为45<m <4.20．解：(1)由题意可得，售完1 000箱水果所获得的利润为(28－20)x ＋(31－25)×(1 000－x )＝2x ＋6 000，即该商家售完这1 000箱水果所获得的利润为(2x ＋6 000)元；(2)由题意可知，购进蜜桔x 箱，则购进脐橙(1 000－x )箱，(28－20)×45x ＋(31－25)×(1 000－x －15x )＋(55－20－25)×15x ≥6 500，解得x ≥41623，∵x 为整数，且为5的倍数，∴该商家至少要购进蜜桔420箱．21．解：(1)由题意，得⎩⎨⎧－（m －n ）＝0，8n ＝8，∴⎩⎨⎧m ＝1，n ＝1； (2)由题意，得⎩⎨⎧（2p ＋2－p ）（2p ＋4－2p ）>4，①（4p ＋3－2p ）（4p ＋6－4p ）≤a ，②解不等式①，得p ＞－1.解不等式②，得p ≤a －1812.∴－1<p ≤a －1812.∵恰好有3个整数解，∴2≤a －1812<3.∴42≤a ＜54.五、22．解：(1)由题意得y 1＝0.7[120x ＋100(2x －100)]＋2 200＝224x －4 800(x ≥50)，即y 1＝224x －4 800(x ≥50)，y 2＝0.8[100(3x －100)]＝240x －8 000(x ≥50)，即y 2＝240x －8 000(x ≥50)；(2)当y 1＞y 2时，即224x －4 800＞240x －8 000，解得x ＜200，由(1)得x ≥50，∴50≤x <200；当y 1＝y 2时，即224x －4 800＝240x －8 000，解得x ＝200；当y 1＜y 2时，即224x －4 800＜240x －8 000，解得x ＞200；综上，当参加演出的男生少于200人且大于等于50人时，购买B 公司的服装比较合算；当参加演出的男生等于200人时，购买两家公司的服装总费用相同，可任选一家公司购买；当参加演出的男生多于200人时，购买A 公司的服装比较合算．23．解：(1)由有理数的乘法法则“两数相乘，同号得正”，有①⎩⎨⎧x ＋1>0，x －2>0，解不等式组①，得x ＞2， ②⎩⎨⎧x ＋1<0，x －2<0，解不等式组②，得x ＜－1， 故原不等式的解集为x ＞2或 x ＜－1；(2)∵3x －72x －9<0， ∴由“两数相除，异号得负”，有①⎩⎨⎧3x －7>0，2x －9<0，解不等式组①，得73<x <92， ②⎩⎨⎧3x －7<0，2x －9>0，解不等式组②，无解， ∴原不等式的解集为73<x <92；(3)①∵a 是(2)中不等式的整数解，∴a ＝3或a ＝4，∵c是△ABC的最大边，且△ABC非等边三角形，∴当a＝3，b＝4时，4≤c＜7；当a＝4，b＝4时，4＜c＜8；②∵△ABC为等腰三角形，c为整数，∴当a＝3，b＝4时，4≤c＜7，∴c＝4，∴C△ABC＝11；∴当a＝4，b＝4时，4＜c＜8，∴c＝5或6或7，∴C△ABC＝13或14或15.综上所述，这个等腰三角形ABC的周长为11或13或14或15.。

吉林省通化市高职单招2021-2022学年综合素质第二次模拟卷(附答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.世界上桥最多的是哪个城市：()A.苏州B.威尼斯C.汉堡2.影响植物萎蔫的主要外因是缺少（）A.光照B.养分C.水分D.乙烯3.生活中有形态各异的建筑结构，下列建筑物主体结构所属类型与另外三项不同的是（）A.B.C.D.4.不属于大气污染物的是()A.二氧化氮B.可吸入颗粒物C.二氧化碳D.二氧化硫5.下列诗文中的“海”不是指代大海的是（）A.曾经沧海难为水，除却巫山不是云B.瀚海阑干百丈冰，愁云惨淡万里凝C.春江潮水连海平，海上明月共潮生D.乘风破浪会有时，直挂云帆济沧海6.世界上有几个联合国城？()A.一个B.两个C.三个D.四个7.孟子强调“亲亲而仁民，仁民而爱物”，反映的是中华传统美德基本精神中的()A.重视整体利益、国家利益和民族利益B.推崇“仁爱”原则，追求人际和谐C.讲求谦敬礼让，强调克骄防矜D.倡导言行一致，强调恪守诚信8.下列历史事件按时间先后排序正确的是（）A.秦始皇统一六国→赤壁之战→陈胜、吴广起义→京杭大运河开通B.贞观之治→王安石变法→蒙古政权建立→郑和下西洋C.戚继光抗倭→林则徐虎门销烟→郑成功收复台湾→邓世昌血战黄海D.红军长征开始→九一八事变→南京国民政府建立→西安事变9.我国第一部关于安全生产的综合性法律是（）A.《中华人民共和国安全生产法》B.《中华人民共和国劳动法》C.《中华人民共和国职业病防治法》10.如果赵和王之间隔一人，以下哪项是不可能的（）A.张排在第一B.李排在第一C.王排在第一D.宋排在第一11.当今世界最大的国际组织是（）A.红十字会B.世界银行C.联合国D.世界贸易组织12.下列土壤中，酸性最强的是()A.pH=10B.pH=7C.pH=4D.pH=1213.儿童学习语言的关键期是()A.0～1岁B.1～3岁C.3～6岁D.5～6岁14.“落霞与孤鹜齐飞，秋水共长天一色”描写的是的()景色。

安徽省淮南市高职单招2022-2023学年综合素质第二次模拟卷(附答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.穿着最普遍、拥有最广泛的消费对象的是()A.日常服B.护士服C.旗袍D.消防服2.国家司法机关在当事人和其他诉讼参与人的参加下，依法查明犯罪事实、惩罚犯罪分子、保障无罪人不受刑事追究的活动，属于（）A.刑事诉讼B.民事诉讼C.行政诉讼D.司法诉讼3.“冬天到了，春天还回远吗？”语出：()A.席勒B.雪莱C.歌德D.舒婷4.关于风力发电，下列说法错误的是（）A.新疆达坂城建有我国规模较大的风能发电基地B.16世纪荷兰已经广泛建立了风力发电系统C.我国已在东南沿海地区建成大型海上风电站D.风力发电利用了电磁感应原理5.汽车：倒车雷达：备用轮胎()A.显示器：打印机：复印机B.手枪：消声器：枪套C.手表：表盘：指针D.手机：电池：耳机6.职业道德是从业人员在职业活动中（）A.必须服从的工作指令B.应该遵循的行为规范C.衡量绩效的根本标准D.自我评价的价值尺度7.关于民族区域自治权的正确表述是（）A.民族区域自治权由民族自治地方的人民政府、法院和检察院行使B.民族区域自治权由民族自治地方的人民代表大会和人民政府行使C.民族区域自治权只有少数民族才能享有D.民族区域自治权的实质是少数民族的自由权8.“女士优先”的含义是男士让女士()A.处处走在前面B.先行进餐C.做简单的工作D.成为受尊重的对象9.()1922年成立于杭州，其成员为应修人、潘谟华、汪静之、冯雪峰四人。

他们出版有四人诗合集《湖畔》。

()A.湖畔诗社B.新月社C.象征诗派D.创造社10.古代“银针验毒”的原理是：4Ag+2H2S+O2═2X+2H2O，X的化学式为（）A.AgSB.Ag2OC.Ag2SD.Ag2O211.下列属于社会实践中最基本的活动是（）A.农民播种小麦B.演员登台表演C.警察侦破案件D.科学家进行实验12.下面不属于河北省的名胜古迹的是()A.避暑山庄B.五台山C.易县的清西陵D.遵化市清东陵13.互联网技术让世界变成了“鸡犬之声相闻”的地球村，相隔万里的人们不再“老死不相往来”。

部编版五年级语文下册第三单元综合素质达标时间：90分钟满分：100分题号一二三四五总分得分一、基础训练营(28分)1. 给下列甲骨文选择相应的现代汉字。

(6分)A. 云B. 牛C. 吴D. 门E. 山F. 来(1) ( ) (2) ( ) (3) ( )(4) ( ) (5) ( ) (6) ( )2. 读谜面，猜字。

(3分)(1)左边是古人，右边是古文，撇去正中间，立即变文人。

( )(2)林字多一半，别当森字猜。

( )(3) 10－8＋1 ( )3. 在横线上填上恰当的同音字。

(3分)实验小学用五个读音相同的字作为校训，激励师生努力创造良好校风：环境整洁突出一个“净”字；秩序安定突出一个“______”字，文明礼貌突出一个“______”字，力争上游突出一个“______”字，强身健体突出一个“劲”字。

4. 请找出下面图片中的错别字，并改正过来。

(2分)______改为______ ______改为______5. 选择题。

(14分)(1)( )和( )都是在象形字的基础上增加声符创造出来的。

A. 蜀B. 凤C. 星D. 祭(2)下面三幅图和字符所表示的字分别是( )A. 北、并、从B. 并、从、北C. 从、并、北D. 从、北、并(3)根据汉字的表意特点，推测“璞”的意思可能是( )A. 美丽的女孩B. 一种职业C. 含玉的石头D. 部落首领(4)下面全是形声字的一组是( )A. 相暮详日B. 站战胆兵C. 峰锋匠雨D. 雾霜江慈(5)下列歇后语的使用有误的一项是( )A. 打扫卫生的同学匆匆将工具“飞回”卫生角，教室和负责区域整洁了，这里的“脏乱差”还是“外甥打灯笼——照旧(舅)”。

B. 一片好心却把事情办糟了，我真是“哑巴吃黄连——有苦说不出”。

C. 李医生的医术可真是“隔着门缝吹喇叭——名(鸣)声在外”啦！连外省的人都来找她治病。

D. 奶奶第一次来我家，做饭的时候找不到盐，我对她说：“这不是‘咸菜烧豆腐——有言(盐)在先’吗？您怎么就看不到呢？”(6)下列关于汉字字体的说法不正确的一项是( )A. 甲骨文是刻在龟甲或兽骨上的文字，主要在商周时期使用。

四川省德阳市高职单招2021-2022学年综合素质第二次模拟卷(附答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.酸雨、温室效应、臭氧空洞是人类面临的三大环境问题，下列说法不准确的是()A.对燃煤预先采取脱硫措施，可以减少酸雨B.逐步使用核能、风能、氢能，可以减少温室效应C.使用无氟冰箱等，可以减少臭氧空洞D.使用液化气代替汽油作汽车燃料，可以减少温室效应2.“音乐之乡”奥地利产生了许多著名音乐家，下列音乐家哪一位不是奥地利人：()A.舒伯特B.莫扎特C.海顿D.斯特劳斯E.肖邦3.下列作品与情节对应不正确的是（）A.《三国演义》——桃园三结义、草船借箭B.《水浒传》——鲁提辖拳打镇关西、林教头风雪山神庙C.《西游记》——大战红孩儿、三打祝家庄D.《红楼梦》——黛玉葬花、葫芦僧判断葫芦案4.人的一生心脏所泵出的血，足够装满大约()个标准游泳池。

()A.50B.70C.90D.1005.“禅让”是我国原始社会推举部落联盟首领的办法。

相传下列首领禅让的顺序是()A.舜→禹→尧B.禹→尧→舜C.尧→禹→舜D.尧→舜→禹6.在商务礼仪中，男士西服如果是两粒扣子，那么扣子的系法应为（）A.两粒都系B.系上面一粒C.系下面一粒D.全部敞开7.世界上最大的区域性贸易集团是()A.欧洲联盟(UN)B.世界贸易组织(WTO)C.石油输出国组织(OPEC)D.东南亚国家联盟(ASEAN)8.酝酿效应是指反复探索一个问题的解决而毫无结果时，把问题暂时搁置几小时、几天或几个星期，由于某种机遇突然使新想法浮现了出来，百思不得其解的问题往往一下子便找到解决办法。

根据上述定义，下列属于酝酿效应的是（）A.小王在上大学期间对某一现象琢磨不透，大量翻阅文献资料，直到研究生期间，通过更多的阅读，终于了解到了该现象产生的根源及实质B.小李为准备一次家庭聚会，将最喜爱的一本书藏好，聚会结束后未能找到这本书。