正方体的展开图word版本

正方体的十一种平面展开图可记忆成下面口诀：一三二，一四一，一在同层可任意，两个三，日状连，三个二，成阶梯，相邻必有日，整体没有田。

相对的两个面之间总隔着一个面正方体：中间四个面，上下各一面（6种摆法-141）中间三个面，一二隔河见（3种摆法-132/231）中间二个面，楼梯天天见（1种摆法-222)中间没有面，三三连一线（1种摆法-33）例1 在图13中（每个小四边形皆为全等的正方形），可以是一个正方体表面展开图的是( ).例2图14是一个正方体包装盒的表面展开图，若在其中的三个正方形A、B、C 内分别填上适当的数,使得这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( ).A.0,-2,1B.0,1,-2C.1,0,-2D.-2,0,1例3图15所示的是一个正方体包装盒的表面展开图，各个面上标注的数字分别为1，2，3，4，5，6。

现将表面展开图复原为正方体包装盒，则标注数字1和3的两个面是互相平行的，请你写出另一组相互平行的面上所对应的数字：_______。

注：例1、例2、例3的答案分别为：C;A;2与5或4与6。

是不是有点多此一举？例4 一个无盖的正方体纸盒，将它展开成平面图形，可能情况总共有（）。

A．12种 B.11种 C.9种 D.8种千万注意，你可不要选B呦！选D才对。

我又在炫耀了，不过你能很快画出这8个平面展开图吗？下面是示意图，黑方块表示展开图，白方块表示空缺。

（一）□■□■■■□■□（二）■■■■■□□□（三）■■■■□■□□（四）■■■■□□■□（五）■■■■□□□■（六）□■□■■■□□■（七）□□■■■■□□■（八）■□□■■■□□■。

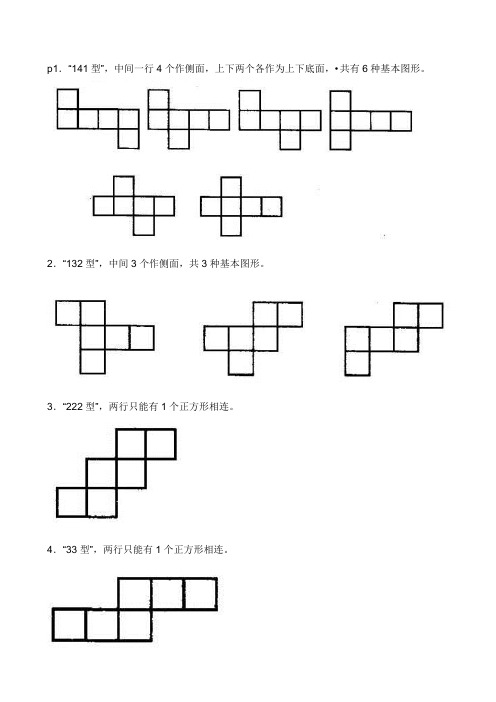
p1．“141型”，中间一行4个作侧面，上下两个各作为上下底面，•共有6种基本图形。

2．“132型”，中间3个作侧面，共3种基本图形。

3．“222型”，两行只能有1个正方形相连。

4．“33型”，两行只能有1个正方形相连。

找“相对面”办法：先找同层隔一面，再找异层隔两面，剩下两面必相对。

（通过正方体展开图找相对面时，首先在同一层四个或三个连续相连的正方形中隔一面寻找，再在异层中隔两面寻找，剩下的两面自然相对。

）1、如图是一个正方体展开图，和“2”对应的面的是分析：同层中有连续四个正方形，优先利用“同层隔一面”寻找相对面，2和5隔一面，所以2和5是对面，4和6隔一面，所以4和6是对面，剩下的1和3是对面。

2、如图是一个正方体展开图，与①对应的面的是分析：含有同层三个连续正方形，优先利用“同层隔一面”寻找，3和5隔一面，所以3和5是对面，再用“异层隔两面”，1和4是对面，剩下2和6是对面。

3、如图是一个的正方体展开图，在正方体中，与2对应的面的是分析：不存在同层三个或四个连续正方形，利用“异层隔两面”的方法找，2和9是对面。

4、一个正方体的每个都有一个汉字，其平面图展开如图所示，那么在该正方体中和“流”字相对应的字是（）分析：含有同层三个连续正方形，利用“同层隔一面”寻找，防与流是对面5、如图一个正方体的六面都标上数字，请问5对面是（）1、如图是一个正方体展开图，和“2”对应的面的是第面2、如图是一个正方体展开图，与①对应的面的是3、如图是一个的正方体展开图，在正方体中，与2对应的面的是4、一个正方体的每个都有一个汉字，其平面图展开如图所示，那么在该正方体中和“流”字相对应的字是（）5、如图一个正方体的六面都标上数字，请问5对面是（）。

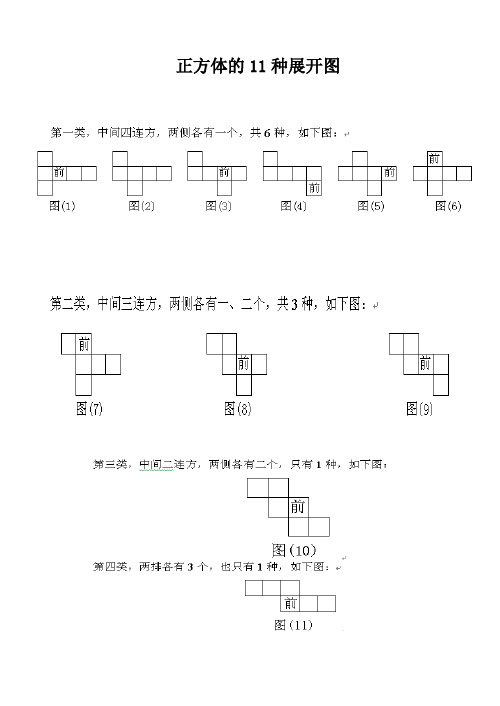
正方体的11种展开图
判断技巧
我们知道，同一个立方体图形，按不同的方式展开得到的平面展开图形一般是不一样的。

常见的正方体平面展开图究竟有几种不同的形状呢？
同学们一定熟悉这样一种操作：把一个正方形纸片平均分成9个小正方形，剪去角上四个小正方形，可以拼成一个无盖的正方体纸盒，其中五个面按习惯不妨记为下、左、右、前、后，如图一。

好啦！现在只要把刚才剪去的一个小正方形作为“上”面，就可拼成一个正方体。

作为正方体平面展开图，这个“上”应该和图1（1）中哪个面拼接在一起呢？观察图1（2），知“上”和前、后、左、右任一个面拼接都行（这四种拼接看作同一种情形），不妨和“后”拼接在一起，如图2。

根据上和下、左和右、前和后相间隔这一规律，现在我们把图2中的“左”或“右”平移，可得图3～图7五种情形。

平移图2中的“前”，可得图8；再平移图8中的“左”，可得图9、图10；把图10中的“上”向左平移，得图11；若移动图8（或图9、图10）中的“左”，又可得图12。

同学们，当你和我一样，把图2～图12这11个图剪下来，动手折一折，得到11个漂亮的小正方体时，你一定为我们的收获感到欢欣鼓舞吧！
对正方体表面展开图的11种情况，为加深记忆，可编成如下口诀：一四一呈6种，一三二有3种，二二二与三三各1种，展开图共有11种。

“动手实践，自主探索和合作交流”是新课程标准倡导学习数学的三种重要方法，而实践活动是培养我们进行主动探索与合作交流的重要途径。

只要通过自己主动观察、实验、猜想、验证等数学活动，就能使我们“建立空间观念，发展几何直觉”，提高思维能力。