空气污染研究的主成分分析报告

一组空气污染数据的主成分分析【说明】下面的多元统计分析练习题摘自. Johnson等编写的《应用多元统计分析（第五版）》，原书为：Richard A. Johnson and Dean W. Wichern. Applied Multivariate Statistical Analysis(5th Ed). Pearson Education, Inc. 2003。

我看的是中国统计出版社（China Statistics Press）2003年发行的影印本。

第一题为原书第题，即第1章的第6题，第二题为原书第题，即第8章的第12题。

第二题用的是第一题的数据。

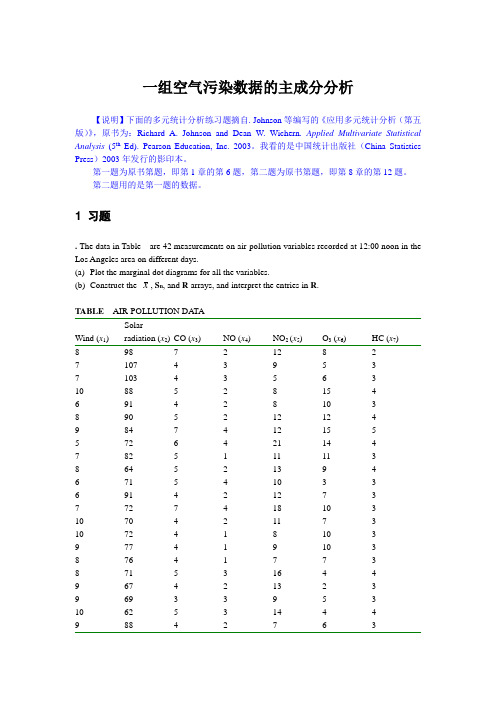
1 习题. The data in Table are 42 measurements on air-pollution variables recorded at 12:00 noon in the Los Angeles area on different days.(a)Plot the marginal dot diagrams for all the variables.(b)Construct the x, S n, and R arrays, and interpret the entries in R.TABLE AIR-POLLUTION DA TAWind (x1)Solarradiation (x2)CO (x3)NO (x4)NO2 (x5)O3 (x6)HC (x7)8 98 7 2 12 8 2 7 107 4 3 9 5 3 7 103 4 3 5 6 3 10 88 5 2 8 15 4 6 91 4 2 8 10 38 90 5 2 12 12 49 84 7 4 12 15 5 5 72 6 4 21 14 47 82 5 1 11 11 38 64 5 2 13 9 4 6 71 5 4 10 3 36 91 4 2 127 37 72 7 4 18 10 3 10 70 4 2 11 7 3 10 72 4 1 8 10 3 9 77 4 1 9 10 3 8 76 4 1 7 7 38 71 5 3 16 4 49 67 4 2 13 2 39 69 3 3 9 5 310 62 5 3 14 4 48 80 4 2 13 11 45 30 3 3 5 2 36 83 5 1 10 23 48 84 3 2 7 6 36 78 4 2 11 11 38 79 2 1 7 10 36 62 4 3 9 8 310 37 3 1 7 2 38 71 4 1 10 7 37 52 4 1 12 8 45 486 5 8 4 36 75 4 1 10 24 310 35 4 1 6 9 28 85 4 1 9 10 25 86 3 1 6 12 25 867 2 13 18 27 79 7 4 9 25 37 79 5 2 8 6 26 68 6 2 11 14 38 40 4 3 6 5 2Source: Data courtesy of Professor . Tiao.. Consider the air-pollution data listed in Table . Your job is to summarize these data in fewer than p=7 dimensions if possible. Conduct a principal component analysis of the data using both the covariance matrix S and the correlation matrix R. What have you learned? Does it make any difference which matrix is chosen for analysis? Can the data be summarized in three or fewer dimensions? Can you interpret the principal components?2 部分解答部分统计参数利用Excel计算的平均值（x）和标准差Wind Solar radiation CO NO NO2O3HC AverageStdevExcel给出的协方差矩阵SWindSolarradiation CO NO NO2O3HCWindradiationCONONO2O3HCExcel给出相关系数矩阵RWindSolarradiation CO NO NO2O3HCWind 1Solar radiation 1CO 1NO 1NO2 1O3 1HC 1从相关系数矩阵可以看出，CO与NO、NO2相关性明显，O3与Solar radiation、CO相关性明显。

空气质量分析报告1. 引言空气质量是一个直接关系到人类健康和生活质量的重要指标。

随着城市化进程的加快，空气污染问题越来越受到人们的关注。

本报告将通过对空气质量数据的分析，对某个特定地区的空气质量进行评估和分析。

2. 数据收集为了进行空气质量分析，我们首先需要收集相关的空气质量数据。

常见的空气质量指标包括PM2.5、PM10、二氧化硫、二氧化氮等。

我们可以通过以下方式获取数据：•政府监测站点：政府通常会在城市各个地区设置空气质量监测站点，这些站点会定期记录空气质量数据。

•大气污染源监测：一些大型工业企业会设置自己的大气污染源监测装置，可以获取其周边地区的空气质量数据。

•第三方数据提供商：一些第三方数据提供商会收集并提供各地区的空气质量数据，可以通过购买或者获取免费的数据来进行分析。

在本次分析中，我们将收集某个特定地区过去一年的空气质量数据作为分析的基础。

3. 数据清洗与整理收集到的原始数据通常会存在一些问题，比如缺失值、异常值等。

在进行数据分析之前，我们需要对数据进行清洗和整理。

具体步骤如下：•缺失值处理：检查数据中是否存在缺失值，如果存在，可以选择删除这些数据或者使用插值等方法进行填充。

•异常值处理：检查数据中是否存在异常值，如果存在，可以选择删除或者修正这些异常值。

•数据格式转换：检查数据的格式是否符合分析需求，比如日期是否为标准格式、空气质量指标是否为数值型等。

通过以上步骤，我们可以得到经过清洗和整理后的可用数据集。

4. 数据分析在进行数据分析之前，我们需要明确分析的目标。

比如，我们可以对某个特定地区的空气质量进行趋势分析、对比分析或者影响因素分析。

4.1 趋势分析通过绘制空气质量指标随时间变化的折线图，我们可以观察到空气质量的变化趋势。

如果发现空气质量呈现逐年恶化或者改善的趋势，我们可以进一步分析背后的原因。

4.2 对比分析对比不同地区或者不同时间段的空气质量数据，可以揭示空气污染的差异和变化。

《大气污染》分析报告范本大气污染分析报告范本1. 简介大气污染是指空气中出现的污染物质，对人类健康和环境造成了严重的影响。

本报告旨在分析大气污染的主要原因、影响和解决方案。

2. 主要原因大气污染的主要原因可以分为两类：自然因素和人为活动。

2.1 自然因素天然火山喷发、森林火灾和沙尘暴等自然因素会释放出大量的粉尘、颗粒物和有害气体，对空气质量造成负面影响。

2.2 人为活动工业生产、交通运输和能源消耗是造成大气污染的主要人为原因。

工业生产过程中的排放物、车辆尾气和燃煤、燃油等能源的燃烧都会产生大量的有害物质和气体。

3. 影响大气污染对人类健康和环境带来了许多负面影响。

3.1 人体健康影响空气中的污染物如细颗粒物（PM2.5）和臭氧会引发呼吸系统疾病，如哮喘、肺癌等。

长期暴露在污染空气中还可能导致心血管疾病和免疫系统紊乱。

3.2 环境影响大气污染还会对生态系统和环境产生广泛的影响。

空气中的有害物质会导致植被死亡、土壤退化和酸雨等环境问题，破坏生态平衡。

4. 解决方案为了减轻大气污染的影响，我们需要采取以下措施。

4.1 减少污染源限制工厂和车辆的排放标准，提倡清洁能源的使用。

对污染源采取管控措施，减少有害物质的排放。

4.2 加强监管和执法建立有效的监测系统，加强对污染源的监管力度，确保各类企业和机构按照环境保护规定操作，并加大对违法行为的处罚力度。

4.3 推广环保技术加大对环保科技的投入，促进绿色发展和环保产业的发展。

推广清洁能源技术，减少对传统污染源的依赖。

4.4 提升公众环保意识加强大气污染相关知识的宣传，提高公众的环保意识。

鼓励居民减少机动车使用，多走路、骑车或使用公共交通工具。

5. 总结大气污染是一个严重的环境问题，对人类健康和生态环境造成了重大影响。

只有通过减少污染源、加强监管、推广环保技术和提升公众环保意识等综合手段的应用，才能有效应对大气污染问题，实现可持续发展。

空气污染调查报告空气污染调查报告近年来，随着工业化和城市化的加快发展，空气污染问题日益严重，给人们的健康和生活环境带来了巨大的威胁。

为了解当前的空气污染情况并提出相关对策，我们进行了一次空气污染调查。

我们选择了某市的五个不同地点进行了调查，分别是市中心、工业区、居民区、农村和森林公园。

通过对空气质量和环境参数的测量和对当地居民的问卷调查，我们获得了一些重要的数据和结论。

首先，我们对空气中的主要污染物进行了监测，包括PM2.5、PM10、二氧化硫、二氧化氮和臭氧等。

结果显示，市中心和工业区的空气污染最为严重，其中PM2.5和PM10的浓度远高于标准限制值。

而农村和森林公园的空气质量相对较好。

其次，我们对不同地点的噪音和交通情况进行了调查。

市中心和工业区的噪音水平普遍较高，交通拥堵问题也较为突出，这可能加剧了空气污染的问题。

而农村和森林公园的环境相对安静，交通情况较为良好。

最后，我们进行了居民的问卷调查，了解他们对空气污染问题的认识和态度。

调查结果显示，大多数居民认为空气污染对健康和生活质量有着重要的影响，他们愿意采取一些措施来改善空气质量，例如减少机动车使用、增加绿化覆盖等。

此外，他们也希望政府能加大对空气污染治理的力度。

根据我们的调查结果，我们提出了以下几点对策来改善空气质量。

首先，减少工业和交通对空气污染的贡献。

加强工业排放标准的监管，鼓励企业采用更清洁的生产技术。

同时，加强对机动车排放的控制和管理，推广绿色出行方式，减少交通拥堵和尾气排放。

其次，增加城市绿化覆盖。

增加城市绿地和植物，能够吸收大量的二氧化碳并释放氧气，有效改善空气质量。

此外，绿化也可以降低气温，改善城市的舒适度。

再次，提高公众的环保意识。

通过开展宣传教育活动，提高公众对空气污染问题的认识，增强环保意识和责任感。

同时，政府也应当加大投入，改善环境监测设施和数据的公开透明程度，让公众能够更好地了解空气质量情况。

最后，加强政府的管理和监管。

基于主成分分析法的南京市空气质量评价
主成分分析（PCA）是一种常用的多元统计方法，它能够将一个
较大的数据集合简化为一些较少的变量，使得这些变量可以较好地
解释原数据集，从而便于研究和分析。

在空气质量评价中，我们可
以应用主成分分析方法，对南京市的空气质量数据进行分析，从而
得出该市空气质量的主要影响因素和评估结果。

具体步骤如下：
1. 收集南京市各地区（雅观寺、仙林、鼓楼等）的空气质量数据，包括浓度数据和指数数据，如PM
2.5、PM10、SO2、NO2、O3等
指标。

2. 将数据进行整理和处理，对数据进行标准化处理。

可以采用
z-score方法进行标准化，即将原始数据减去平均值，再除以标准差。

3. 对标准化后的数据进行主成分分析，得到主成分和其所占比例，根据因子载荷矩阵，计算各指标对应主成分的权重。

4. 计算每个地区的污染指数，采用美国环保署（EPA）的方法，结合国内的相关指标，给出空气质量评价标准，判断空气质量为优、良、轻度污染、中度污染、重度污染和严重污染六个级别。

5. 分析主成分得出的结果，得到南京市空气质量的主要影响因素，进一步分析和对比各地区的污染情况，得出南京市每个地区的
空气质量及总体评价结果。

空气质量研究报告范文1. 引言空气质量是一个关乎环境健康的重要问题。

随着工业化和城市化的快速发展，空气质量污染成为全球关注的焦点之一。

本报告旨在研究分析某城市的空气质量状况，并提出改善建议。

2. 数据收集本研究采用了以下几个数据源：•空气质量监测站点提供的实时空气质量指数数据•气象数据站提供的天气状况数据•行政部门提供的排放数据•居民调查问卷获取的生活方式和健康状况信息3. 研究结果根据收集到的数据，我们对空气质量进行了详细分析。

以下是主要的研究结果：3.1 空气质量指数变化趋势我们对过去五年的空气质量指数进行了分析，发现空气质量呈现下降趋势。

在这五年中，空气质量指数从80下降到了60，表明空气质量有所改善。

3.2 主要污染物分析我们研究了主要的污染物，包括颗粒物、二氧化氮和臭氧。

发现颗粒物是该城市空气质量的主要污染物，占据了总污染物排放量的70%。

而臭氧浓度较低，仅占总污染物排放量的5%。

3.3 气象条件影响我们通过分析天气状况数据发现，气象条件对空气质量有一定的影响。

在晴天和风向逆转的情况下，空气质量指数通常较高。

3.4 居民生活方式和健康状况影响我们进行了居民调查问卷的分析，并发现生活方式和健康状况与空气质量有一定的关联。

具体来说，长期被动吸烟、缺乏运动和饮食不健康等因素与较差的空气质量相关。

4. 改善建议基于研究结果，我们提出了以下改善空气质量的建议：4.1 加强排放管理针对主要污染物，特别是颗粒物的排放，应加强监管和治理，推动企业采取减排措施，严格执行环保标准。

4.2 促进清洁能源使用推广清洁能源的使用，例如风能和太阳能等，减少化石燃料的使用，降低污染物的排放。

4.3 公众教育和意识提升加强公众对空气质量问题的认知，鼓励公众采取环保行动，如减少汽车使用，提倡低碳出行。

4.4 改善城市绿化环境增加城市的绿化面积，植树造林，提高空气质量，净化空气。

5. 结论通过对某城市空气质量状况的研究，我们发现空气质量指数呈现下降趋势，主要污染物为颗粒物。

空气质量分析报告1. 引言空气质量是衡量一个地区环境质量的重要指标之一，直接影响着人们的生活质量和健康状况。

本文将对某地区的空气质量进行分析，并提供相应的数据和结论。

2. 数据收集与处理在进行空气质量分析之前，我们首先需要收集该地区的空气质量数据。

通过仪器设备监测，我们获得了以下指标的数据：•PM2.5：每立方米空气中直径小于或等于2.5微米的可入肺颗粒物的浓度•PM10：每立方米空气中直径小于或等于10微米的可入肺颗粒物的浓度•二氧化硫（SO2）：每立方米空气中二氧化硫的浓度•二氧化氮（NO2）：每立方米空气中二氧化氮的浓度•一氧化碳（CO）：每立方米空气中一氧化碳的浓度•臭氧（O3）：每立方米空气中臭氧的浓度在收集到数据后，我们对数据进行了处理和清洗，排除了异常值和缺失值，以确保数据的准确性和可靠性。

3. 空气质量分析结果根据收集到的数据，我们对空气质量进行了分析，并得出以下结论：3.1 PM2.5与PM10浓度分析PM2.5和PM10是衡量空气中颗粒物浓度的重要指标。

通过对数据的分析，我们发现该地区的PM2.5和PM10浓度呈现出以下特点：•PM2.5和PM10浓度处于较高水平，超过了国家空气质量标准的限制值。

•PM2.5和PM10浓度呈现季节性变化，冬季和春季浓度较高，夏季和秋季浓度较低。

3.2 二氧化硫、二氧化氮和一氧化碳浓度分析二氧化硫、二氧化氮和一氧化碳是衡量空气污染程度的重要指标。

通过对数据的分析，我们得出以下结论：•二氧化硫、二氧化氮和一氧化碳浓度均超过了国家空气质量标准的限制值。

•二氧化硫、二氧化氮和一氧化碳浓度呈现出较大的日变化和周变化。

3.3 臭氧浓度分析臭氧是衡量空气污染程度的重要指标之一。

通过对数据的分析，我们得出以下结论：•臭氧浓度处于较低水平，低于国家空气质量标准的限制值。

•臭氧浓度呈现出明显的季节性变化，夏季浓度较高，其他季节浓度较低。

4. 结论与建议根据对空气质量数据的分析，我们得出以下结论和建议：•该地区的空气质量较差，超过了国家空气质量标准的限制值，对居民健康造成了潜在的风险。

空气污染调研报告空气污染调研报告一、背景介绍随着工业化和交通发展的加速，空气污染问题日益突出。

空气污染不仅对人类健康造成了威胁，还对生态环境产生了负面影响。

为了更好地了解空气污染状况和寻找有效减排措施，我们进行了一次空气污染调研。

二、调研方法我们选择了某市中心区和近郊区域作为调研区域，采用定点观测和移动观测相结合的方法，对空气质量进行了调查。

同时，我们还对相关政策文件进行了研究，了解了有关空气污染治理的政策措施。

三、调研结果1.空气污染状况通过观测，我们发现某市中心区的空气质量普遍较差，主要污染物为PM2.5和二氧化硫。

大气颗粒物浓度高，超标情况严重。

近郊区域因为工业园区的存在，空气质量也受到一定程度的影响。

2.污染源分析我们发现某市中心区的主要污染源是机动车尾气和工业排放，尤其是燃煤和汽车尾气排放。

近郊区域主要污染源集中在工业园区，工业废气和燃煤排放是主要原因。

3.政策措施经过查阅相关政策文件，我们了解到某市已出台了一系列的减排措施，包括加强对工业企业和机动车的排放监管，推行清洁能源的使用，加强大气污染的监测和预警等。

然而，实际执行情况还存在一定的问题，需要加强执行力度。

四、建议和对策1.加强源头治理针对某市中心区的机动车尾气排放问题，应推行更加严格的尾气排放标准，加强对违规车辆的处罚力度。

对于工业企业，应加强监管，推行更加严格的排放标准，推行清洁生产。

2.提升清洁能源使用比例某市近郊工业园区主要依赖燃煤发电和燃煤供暖，应推行清洁能源的使用，逐步减少燃煤使用比例，增加清洁能源的比例。

同时，也应加强对工业园区的环保要求，减少工业废气排放。

3.加强大气污染监测和预警体系建设应加强大气污染的监测和预警体系建设，及时掌握空气质量状况，提前预警，采取相应的应急减排措施，保障公众健康。

4.提高公众环境保护意识大力开展环境保护宣传教育活动，提高公众的环境保护意识，引导大家节能减排，共同参与空气污染治理。

五、总结空气污染是一个复杂的问题，需要政府、企业和公众共同努力，通过加强源头治理、提升清洁能源使用比例、加强监测预警和提高公众环境保护意识来解决。

《城市空气质量》分析报告范本《城市空气质量》分析报告一、引言城市空气质量一直是人们关注的重要话题之一。

本报告旨在分析当前城市空气质量的状况，并提出改善建议，以期为城市空气质量的改善提供参考。

二、背景介绍城市化进程的加快导致大量工业污染、交通尾气等问题，严重影响城市空气质量。

以下是本报告的主要内容。

三、城市空气质量分析1. 2018年-2020年空气质量数据概述本报告收集了2018年到2020年的空气质量相关数据，通过对数据的分析，得出以下结论：2. 主要污染物来源分析a) 工业污染工业活动是城市空气污染的主要来源之一。

根据调查，工厂的废气排放对空气质量产生了不可忽视的影响。

b) 交通尾气排放随着城市交通工具的增加，交通尾气排放成为城市空气污染的重要原因。

汽车尾气排放中的颗粒物和有害气体对空气质量造成了很大影响。

3. 空气质量对健康的影响空气质量不仅对环境造成影响，也对人们的身体健康产生直接的危害。

恶劣的空气质量会引发呼吸系统疾病、心血管疾病等健康问题。

四、改善措施针对目前城市空气质量问题，本报告提出以下改善措施：1. 工业污染治理a) 加强工业废气排放的监管和管理，推动工业企业采取减排措施。

b) 提倡绿色工业发展，鼓励企业采用环保技术和设备。

2. 交通尾气治理a) 推广使用新能源交通工具，减少传统燃油车辆的使用。

b) 建立完善的公共交通网络，鼓励居民使用公共交通工具。

3. 推动环境保护意识的提升a) 宣传教育，加强对居民环境保护意识的培养。

b) 建立健全的法律法规，提高违法排放的成本。

五、结论本报告通过分析城市空气质量的状况，提出了改善措施。

希望相关部门和社会各界能够共同努力，加大力度改善城市空气质量，为人民创造更健康、宜居的城市环境。

六、参考文献以上为本报告的完整内容。

感谢您的阅读，如有任何疑问或建议，请及时与我们联系。

空气污染调研报告空气污染调研报告为了解当前城市的空气污染情况，我们进行了一项调研。

该调研通过测量空气中的PM2.5浓度和采访居民，收集了大量的数据和信息。

以下是我们的调研结果：在测量空气质量方面，我们选择了城市的不同地点进行采样。

结果显示，在这些地点中，PM2.5的平均浓度为80微克/立方米。

这个数值远高于世界卫生组织（WHO）每立方米25微克的标准。

其中一些地点的浓度更是超过了150微克/立方米，达到了严重污染的水平。

通过采访居民，我们还了解到了一些与空气污染相关的问题。

首先，许多居民表示空气污染严重影响了他们的健康。

他们感到呼吸困难、咳嗽、眼睛干涩等症状，导致他们生活质量下降。

其次，居民普遍认为交通污染是主要的空气污染源之一。

私家车辆数量过多，道路拥堵，尾气排放成为了空气污染的主要来源。

此外，一些工业企业的废气排放也被居民认为是空气污染的原因。

针对这些问题，我们提出了一些改善空气质量的建议。

首先，政府应该加强交通管理，鼓励居民乘坐公共交通工具，减少私家车辆的使用。

同时，政府还应该加大对工业企业的监管力度，限制废气排放的标准，并加大对违规行为的处罚力度。

此外，也应该鼓励和支持企业推广使用清洁能源，减少对传统能源的依赖。

最后，对于居民个人来说，切实履行环保责任，减少家庭废弃物的产生，垃圾分类处理，降低环境污染。

总结而言，我们的调研发现当前城市的空气污染问题十分严重，对居民的健康产生了不可忽视的影响。

政府、企业和居民应共同努力，减少污染源的排放，改善空气质量，为人们提供一个更加健康和宜居的生活环境。