ACM经典的题目代码

ACM程序设计东北林业大学陈宇Lg_chenyu@第一讲算法原理和ACM入门(Introduction to ACM)我校的ACM在线评测系统**课件下载地址：*/kj/suanfa01.ppt预期赛事（今后每年）*3~4月，举行校内大赛（暨选拔赛）*4月，ACM全国邀请赛*5月，参加黑龙江省大学生程序设计大赛*6月，参加东北4省大学生程序设计大赛*10~11月，参加ACM/ICPC亚洲区比赛（至少参加4～5个赛区的比赛）*另外，每学期至少有三次月赛以及适当的练习赛第一部分算法概述*算法分析（Algorithm Analysis）：对算法所需要的两种计算机资源——时间和空间进行估算；时间复杂性（Time Complexity）空间复杂性（Space Complexity）算法分析的目的：设计算法——设计出复杂性尽可能低的算法选择算法——在多种算法中选择其中复杂性最低者算法的描述语言：⑴自然语言优点：容易理解缺点：冗长、二义性使用方法：粗线条描述算法思想注意事项：避免写成自然段（2）流程图优点：流程直观缺点：缺少严密性、灵活性使用方法：描述简单算法注意事项：注意抽象层次⑶程序设计语言优点：能由计算机执行缺点：抽象性差，对语言要求高使用方法：算法需要验证注意事项：将算法写成子函数（4）伪代码——算法语言伪代码（Pseudocode）：介于自然语言和程序设计语言之间的方法，它采用某一程序设计语言的基本语法，操作指令可以结合自然语言来设计。

优点：表达能力强，抽象性强，容易理解评价算法*评价算法的三条主要标准是：*(1) 算法实现所耗费的时间；*(2) 算法实现所所耗费的存储空间，其中*主要考虑辅助存储空间；*(3) 算法应易于理解，易于编码，易于调*试等等。

和算法执行时间相关的因素：1）问题中数据存储的数据结构2）算法采用的数学模型3）算法设计的策略4）问题的规模5）实现算法的程序设计语言6）编译算法产生的机器代码的质量7）计算机执行指令的速度算法效率的衡量方法*通常有两种衡量算法效率的方法:*1）事后统计法（有缺点，较少使用）*2）事前分析估算法*算法的时间效率是问题规模的函数。

acm试题及答案2ACM试题及答案21. 问题描述：编写一个程序，计算给定整数序列中的最大子段和。

2. 输入格式：第一行包含一个整数N，表示序列的长度。

第二行包含N个整数，表示序列中的整数。

3. 输出格式：输出一个整数，表示序列中的最大子段和。

4. 样例输入：```51 -2 -34 -1```5. 样例输出：```6```6. 问题分析：该问题可以通过动态规划的方法来解决。

定义一个数组dp，其中dp[i]表示以第i个元素结尾的最大子段和。

状态转移方程为dp[i] = max(dp[i-1] + nums[i], nums[i])。

7. 算法实现：```pythondef maxSubArray(nums):n = len(nums)dp = [0] * ndp[0] = nums[0]max_sum = nums[0]for i in range(1, n):dp[i] = max(dp[i-1] + nums[i], nums[i])max_sum = max(max_sum, dp[i])return max_sum```8. 复杂度分析：时间复杂度为O(n)，其中n为序列的长度。

空间复杂度为O(n)。

9. 测试用例：- 输入：`[3, -2, 4]`输出：`5`- 输入：`[-2, 1, -3, 4, -1, 2, 1, -5, 4]`输出：`6`10. 注意事项：- 确保输入的序列长度N大于等于1。

- 序列中的整数可以是负数或正数。

- 输出结果应该是一个整数。

11. 扩展思考：- 如何优化算法以减少空间复杂度？- 如果序列中的整数是浮点数，算法是否仍然有效？12. 参考答案：- 可以通过只使用一个变量来存储最大子段和，以及一个变量来存储当前子段和，从而将空间复杂度优化到O(1)。

- 如果序列中的整数是浮点数，算法仍然有效，但需要注意浮点数运算的精度问题。

1111111杭电：1000 A + B Problem (4)1001 Sum Problem (5)1002 A + B Problem II (6)1005 Number Sequence (8)1008 Elevator (9)1009 FatMouse' Trade (11)1021 Fibonacci Again (13)1089 A+B for Input-Output Practice (I) (14)1090 A+B for Input-Output Practice (II) (15)1091 A+B for Input-Output Practice (III) (16)1092 A+B for Input-Output Practice (IV) (17)1093 A+B for Input-Output Practice (V) (18)1094 A+B for Input-Output Practice (VI) (20)1095 A+B for Input-Output Practice (VII) (21)1096 A+B for Input-Output Practice (VIII) (22)1176 免费馅饼 (23)1204 糖果大战 (25)1213 How Many Tables (26)2000 ASCII码排序 (32)2001 计算两点间的距离 (34)2002 计算球体积 (35)2003 求绝对值 (36)2004 成绩转换 (37)2005 第几天？ (38)2006 求奇数的乘积 (40)2007 平方和与立方和 (41)2008 数值统计 (42)2009 求数列的和 (43)2010 水仙花数 (44)2011 多项式求和 (46)2012 素数判定 (47)2014 青年歌手大奖赛_评委会打分 (49)2015 偶数求和 (50)2016 数据的交换输出 (52)2017 字符串统计 (54)2019 数列有序! (55)2020 绝对值排序 (56)2021 发工资咯：） (58)2033 人见人爱A+B (59)2037 今年暑假不AC (61)2039 三角形 (63)2040 亲和数 (64)2045 不容易系列之(3)—— LELE的RPG难题 (65)2049 不容易系列之(4)——考新郎 (66)2056 Rectangles (68)2073 无限的路 (69)2084 数塔 (71)2201 熊猫阿波的故事 (72)2212 DFS (73)2304 Electrical Outlets (74)2309 ICPC Score Totalizer Software (75)2317 Nasty Hacks (77)2401 Baskets of Gold Coins (78)2500 做一个正气的杭电人 (79)2501 Tiling_easy version (80)2502 月之数 (81)2503 a/b + c/d (82)2504 又见GCD (83)2519 新生晚会 (84)2520 我是菜鸟，我怕谁 (85)2521 反素数 (86)2522 A simple problem (88)2523 SORT AGAIN (89)2524 矩形A + B (90)2535 Vote (91)2537 8球胜负 (93)2539 点球大战 (95)2547 无剑无我 (98)2548 两军交锋 (99)2549 壮志难酬 (100)2550 百步穿杨 (101)2551 竹青遍野 (103)2552 三足鼎立 (104)2553 N皇后问题 (105)2554 N对数的排列问题 (106)2555 人人都能参加第30届校田径运动会了 (107)2560 Buildings (110)2561 第二小整数 (112)2562 奇偶位互换 (113)2563 统计问题 (114)2564 词组缩写 (115)2565 放大的X (117)2566 统计硬币 (118)2567 寻梦 (119)2568 前进 (121)2569 彼岸 (123)2700 Parity (124)2577 How to Type (126)北京大学：1035 Spell checker (129)1061 青蛙的约会 (133)1142 Smith Numbers (136)1200 Crazy Search (139)1811 Prime Test (141)2262 Goldbach's Conjecture (146)2407 Relatives (150)2447 RSA (152)2503 Babelfish (156)2513 Colored Sticks (159)ACM算法：kurXX最小生成树 (163)Prim (164)堆实现最短路 (166)最短路DIJ普通版 (167)floyd (168)BELL_MAN (168)拓扑排序 (169)DFS强连通分支 (170)最大匹配 (172)还有两个最大匹配模板 (173)最大权匹配,KM算法 (175)两种欧拉路 (177)无向图： (177)有向图： (178)【最大流】Edmonds Karp (178)dinic (179)【最小费用最大流】Edmonds Karp对偶算法 (181)ACM题目：【题目】排球队员站位问题 (182)【题目】把自然数Ｎ分解为若干个自然数之和。

杭电acm练习题100例（删减版）【程序1】题目：有1、2、3、4个数字，能组成多少个互不相同且无重复数字的三位数？都是多少？1.程序分析：可填在百位、十位、个位的数字都是1、2、3、4。

组成所有的排列后再去掉不满足条件的排列。

#include "stdio.h"#include "conio.h"main(){ int i,j,k;printf("\n");for(i=1;i<5;i++) /*以下为三重循环*/for(j=1;j<5;j++)for (k=1;k<5;k++){ if (i!=k&&i!=j&&j!=k) /*确保i、j、k三位互不相同*/printf("%d,%d,%d\n",i,j,k); }getch(); }==============================================================【程序2】题目：企业发放的奖金根据利润提成。

利润(I)低于或等于10万元时，奖金可提10%；利润高于10万元，低于20万元时，低于10万元的部分按10%提成，高于10万元的部分，可可提成7.5%；20万到40万之间时，高于20万元的部分，可提成5%；40万到60万之间时高于40万元的部分，可提成3%；60万到100万之间时，高于60万元的部分，可提成1.5%，高于100万元时，超过100万元的部分按1%提成，从键盘输入当月利润I，求应发放奖金总数？#include "stdio.h" #include "conio.h"main(){ long int i;int bonus1,bonus2,bonus4,bonus6,bonus10,bonus;scanf("%ld",&i);bonus1=100000*0. 1;bonus2=bonus1+100000*0.75;bonus4=bonus2+200000*0.5;bonus6=bonus4+200000*0.3;bonus10=bonus6+400000*0.15;if(i<=100000)bonus=i*0.1;else if(i<=200000)bonus=bonus1+(i-100000)*0.075;else if(i<=400000)bonus=bonus2+(i-200000)*0.05;else if(i<=600000)bonus=bonus4+(i-400000)*0.03;else if(i<=1000000)bonus=bonus6+(i-600000)*0.015;elsebonus=bonus10+(i-1000000)*0.01;printf("bonus=%d",bonus);getch(); }====================================== ========================【程序3】题目：一个整数，它加上100后是一个完全平方数，再加上168又是一个完全平方数，请问该数是多少？#include "math.h"#include "stdio.h"#include "conio.h"main(){ long int i,x,y,z;for (i=1;i<100000;i++){ x=sqrt(i+100); /*x为加上100后开方后的结果*/y=sqrt(i+268); /*y为再加上168后开方后的结果*/if(x*x==i+100&&y*y==i+268)printf("\n%ld\n",i); }getch(); }====================================== ========================【程序4】题目：输入某年某月某日，判断这一天是这一年的第几天？#include "stdio.h" #include "conio.h"main(){ int day,month,year,sum,leap;printf("\nplease input year,month,day\n");scanf("%d,%d,%d",&year,&month,&day);switch(month) /*先计算某月以前月份的总天数*/{ case 1:sum=0;break;case 2:sum=31;break;case 3:sum=59;break;case 4:sum=90;break;case 5:sum=120;break;case 6:sum=151;break;case 7:sum=181;break;case 8:sum=212;break;case 9:sum=243;break;case 10:sum=273;break;case 11:sum=304;break;case 12:sum=334;break;default:printf("data error");break; }sum=sum+day; /*再加上某天的天数*/if(year%400==0||(year%4==0&&year%100!=0)) /*判断是不是闰年*/leap=1;elseleap=0;if(leap==1&&month>2) /*如果是闰年且月份大于2,总天数应该加一天*/sum++;printf("It is the %dth day.",sum);getch(); }====================================== ======================== 【程序5】题目：输入三个整数x,y,z，请把这三个数由小到大输出。

目录一．数论 41.阶乘最后非零位 42. 模线性方程(组) 43. 素数表64. 素数随机判定(miller_rabin) 65. 质因数分解76. 最大公约数欧拉函数8二．图论_匹配91. 二分图最大匹配(hungary邻接表形式) 92. 二分图最大匹配(hungary邻接表形式,邻接阵接口) 103. 二分图最大匹配(hungary邻接阵形式) 104. 二分图最大匹配(hungary正向表形式) 115. 二分图最佳匹配(kuhn_munkras邻接阵形式) 116. 一般图匹配(邻接表形式) 127. 一般图匹配(邻接表形式,邻接阵接口) 138. 一般图匹配(邻接阵形式) 149. 一般图匹配(正向表形式) 15三．图论_生成树161. 最小生成树(kruskal邻接表形式) 162. 最小生成树(kruskal正向表形式) 173. 最小生成树(prim+binary_heap邻接表形式) 194. 最小生成树(prim+binary_heap正向表形式) 205. 最小生成树(prim+mapped_heap邻接表形式) 216. 最小生成树(prim+mapped_heap正向表形式) 227. 最小生成树(prim邻接阵形式) 238. 最小树形图(邻接阵形式) 24四．图论_网络流251. 上下界最大流(邻接表形式) 252. 上下界最大流(邻接阵形式) 263. 上下界最小流(邻接表形式) 274. 上下界最小流(邻接阵形式) 295. 最大流(邻接表形式) 306. 最大流(邻接表形式,邻接阵接口) 317. 最大流(邻接阵形式) 328. 最大流无流量(邻接阵形式) 329. 最小费用最大流(邻接阵形式) 33五. 图论_最短路径341. 最短路径(单源bellman_ford邻接阵形式) 342. 最短路径(单源dijkstra_bfs邻接表形式) 353. 最短路径(单源dijkstra_bfs正向表形式) 354. 最短路径(单源dijkstra+binary_heap邻接表形式) 365. 最短路径(单源dijkstra+binary_heap正向表形式) 376. 最短路径(单源dijkstra+mapped_heap邻接表形式) 387. 最短路径(单源dijkstra+mapped_heap正向表形式) 398. 最短路径(单源dijkstra邻接阵形式) 409. 最短路径(多源floyd_warshall邻接阵形式) 40六. 图论_连通性411. 无向图关键边(dfs邻接阵形式) 412. 无向图关键点(dfs邻接阵形式) 423. 无向图块(bfs邻接阵形式) 434. 无向图连通分支(bfs邻接阵形式) 435. 无向图连通分支(dfs邻接阵形式) 446. 有向图强连通分支(bfs邻接阵形式) 447. 有向图强连通分支(dfs邻接阵形式) 458. 有向图最小点基(邻接阵形式) 46七. 图论_应用461.欧拉回路(邻接阵形式) 462. 前序表转化473. 树的优化算法484. 拓扑排序(邻接阵形式). 495. 最佳边割集506. 最佳顶点割集517. 最小边割集528. 最小顶点割集539. 最小路径覆盖55八. 图论_NP搜索551. 最大团(n小于64)(faster) 552. 最大团58九. 组合591. 排列组合生成592. 生成gray码603. 置换(polya) 614. 字典序全排列615. 字典序组合626. 组合公式62十. 数值计算631. 定积分计算(Romberg) 632. 多项式求根(牛顿法) 643. 周期性方程(追赶法) 66十一. 几何671. 多边形672. 多边形切割703. 浮点函数714. 几何公式765. 面积786. 球面797. 三角形798. 三维几何819. 凸包(graham) 8910. 网格(pick) 9111. 圆9212. 整数函数9413. 注意96十二. 结构971. 并查集972. 并查集扩展(friend_enemy) 983. 堆(binary) 984. 堆(mapped) 995. 矩形切割996. 线段树1007. 线段树扩展1028. 线段树应用1059. 子段和10510. 子阵和105十三. 其他1061. 分数1062. 矩阵1083. 日期1104. 线性方程组(gauss) 1115. 线性相关113十四. 应用1141. joseph 1142. N皇后构造解 1153. 布尔母函数1154. 第k元素1165. 幻方构造1166. 模式匹配(kmp) 1187. 逆序对数1188. 字符串最小表示1199. 最长公共单调子序列11910. 最长子序列12011. 最大子串匹配12112. 最大子段和12213. 最大子阵和123一．数论1.阶乘最后非零位//求阶乘最后非零位,复杂度O(nlogn)//返回该位,n以字符串方式传入#include <string.h>#define MAXN 10000int lastdigit(char* buf){const int mod[20]={1,1,2,6,4,2,2,4,2,8,4,4,8,4,6,8,8,6,8,2};int len=strlen(buf),a[MAXN],i,c,ret=1;if (len==1)return mod[buf[0]-'0'];for (i=0;i<len;i++)a[i]=buf[len-1-i]-'0';for (;len;len-=!a[len-1]){ret=ret*mod[a[1]%2*10+a[0]]%5;for (c=0,i=len-1;i>=0;i--)c=c*10+a[i],a[i]=c/5,c%=5;}return ret+ret%2*5;}2. 模线性方程(组)#ifdef WIN32typedef __int64 i64;#elsetypedef long long i64;#endif//扩展Euclid求解gcd(a,b)=ax+byint ext_gcd(int a,int b,int& x,int& y){int t,ret;if (!b){x=1,y=0;return a;}ret=ext_gcd(b,a%b,x,y);t=x,x=y,y=t-a/b*y;return ret;}//计算m^a, O(loga), 本身没什么用, 注意这个按位处理的方法:-Pint exponent(int m,int a){int ret=1;for (;a;a>>=1,m*=m)if (a&1)ret*=m;return ret;}//计算幂取模a^b mod n, O(logb)int modular_exponent(int a,int b,int n){ //a^b mod nint ret=1;for (;b;b>>=1,a=(int)((i64)a)*a%n)if (b&1)ret=(int)((i64)ret)*a%n;return ret;}//求解模线性方程ax=b (mod n)//返回解的个数,解保存在sol[]中//要求n>0,解的范围0..n-1int modular_linear(int a,int b,int n,int* sol){int d,e,x,y,i;d=ext_gcd(a,n,x,y);if (b%d)return 0;e=(x*(b/d)%n+n)%n;for (i=0;i<d;i++)sol[i]=(e+i*(n/d))%n;return d;}//求解模线性方程组(中国余数定理)// x = b[0] (mod w[0])// x = b[1] (mod w[1])// ...// x = b[k-1] (mod w[k-1])//要求w[i]>0,w[i]与w[j]互质,解的范围1..n,n=w[0]*w[1]*...*w[k-1]int modular_linear_system(int b[],int w[],int k){int d,x,y,a=0,m,n=1,i;for (i=0;i<k;i++)n*=w[i];for (i=0;i<k;i++){m=n/w[i];d=ext_gcd(w[i],m,x,y);a=(a+y*m*b[i])%n;}return (a+n)%n;}3. 素数表//用素数表判定素数,先调用initprimeint plist[10000],pcount=0;int prime(int n){int i;if((n!=2&&!(n%2))||(n!=3&&!(n%3))||(n!=5&&!(n%5))||(n!=7&&! (n%7)))return 0;for (i=0;plist[i]*plist[i]<=n;i++)if (!(n%plist[i]))return 0;return n>1;}void initprime(){int i;for (plist[pcount++]=2,i=3;i<50000;i++)if (prime(i))plist[pcount++]=i;}4. 素数随机判定(miller_rabin)//miller rabin//判断自然数n是否为素数//time越高失败概率越低,一般取10到50#include <stdlib.h>#ifdef WIN32typedef __int64 i64;#elsetypedef long long i64;#endifint modular_exponent(int a,int b,int n){ //a^b mod nint ret;for (;b;b>>=1,a=(int)((i64)a)*a%n)if (b&1)ret=(int)((i64)ret)*a%n;return ret;}// Carmicheal number: 561,41041,,int miller_rabin(int n,int time=10){if(n==1||(n!=2&&!(n%2))||(n!=3&&!(n%3))||(n!=5&&!(n%5))||(n!= 7&&!(n%7)))return 0;while (time--)if(modular_exponent(((rand()&0x7fff<<16)+rand()&0x7fff+rand() &0x7fff)%(n-1)+1,n-1,n)!=1)return 0;return 1;}5. 质因数分解//分解质因数//prime_factor()传入n, 返回不同质因数的个数//f存放质因数，nf存放对应质因数的个数//先调用initprime()，其中第二个initprime()更快#include<iostream>#include<cstdio>#include<cmath>using namespace std;#define MAXN#define PSIZEint plist[PSIZE], pcount=0;int prime(int n){int i;if((n!=2&&!(n%2))||(n!=3&&!(n%3))||(n!=5&&!(n%5))||(n!=7&&! (n%7)))return 0;for (i=0;plist[i]*plist[i]<=n;++i)if (!(n%plist[i]))return 0;return n>1;}void initprime(){int i;for (plist[pcount++]=2,i=3;i<;++i)if (prime(i))plist[pcount++]=i;}int prime_factor(int n, int* f, int *nf) {int cnt = 0;int n2 = sqrt((double)n);for(int i = 0; n > 1 && plist[i] <= n2; ++i)if (n % plist[i] == 0) {for (nf[cnt] = 0; n % plist[i] == 0; ++nf[cnt], n /= plist[i]);f[cnt++] = plist[i];}if (n > 1) nf[cnt] = 1, f[cnt++] = n;return cnt;}/*//产生MAXN以内的所有素数//note:就是//给所有2的倍数赋初值#include <cmath>#include <iostream>using namespace std;#define MAXNunsigned int plist[],pcount;unsigned int isprime[(MAXN>>5)+1];#define setbitzero(a) (isprime[(a)>>5]&=(~(1<<((a)&31))))#define setbitone(a) (isprime[(a)>>5]|=(1<<((a)&31)))#define ISPRIME(a) (isprime[(a)>>5]&(1<<((a)&31)))void initprime(){int i,j,m;int t=(MAXN>>5)+1;for(i=0;i<t;++i)isprime[i]=;plist[0]=2;setbitone(2);setbitzero(1);m=(int)sqrt(MAXN);for(pcount=1,i=3;i<=m;i+=2)if(ISPRIME(i))for(plist[pcount++]=i,j=i<<1;j<=MAXN;j+=i)setbitzero(j);if(!(i&1))++i;for(;i<=MAXN;i+=2)if(ISPRIME(i))plist[pcount++]=i;}6. 最大公约数欧拉函数int gcd(int a,int b){return b?gcd(b,a%b):a;}inline int lcm(int a,int b){return a/gcd(a,b)*b;}//求1..n-1中与n互质的数的个数int eular(int n){int ret=1,i;for (i=2;i*i<=n;i++)if (n%i==0){n/=i,ret*=i-1;while (n%i==0)n/=i,ret*=i;}if (n>1)ret*=n-1;return ret;}二．图论_匹配1. 二分图最大匹配(hungary邻接表形式)//二分图最大匹配,hungary算法,邻接表形式,复杂度O(m*e)//返回最大匹配数,传入二分图大小m,n和邻接表list(只需一边) //match1,match2返回一个最大匹配,未匹配顶点match值为-1 #include <string.h>#define MAXN 310#define _clr(x) memset(x,0xff,sizeof(int)*MAXN)struct edge_t{int from,to;edge_t* next;};int hungary(int m,int n,edge_t* list[],int* match1,int* match2){ int s[MAXN],t[MAXN],p,q,ret=0,i,j,k;edge_t* e;for(_clr(match1),_clr(match2),i=0;i<m;ret+=(match1[i++]>=0))for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for (e=list[k=s[p]];e&&match1[i]<0;e=e->next)if (t[j=e->to]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}return ret; }2. 二分图最大匹配(hungary邻接表形式,邻接阵接口)//二分图最大匹配,hungary算法,邻接表形式,邻接阵接口,复杂度O(m*e)s//返回最大匹配数,传入二分图大小m,n和邻接阵//match1,match2返回一个最大匹配,未匹配顶点match值为-1 #include <string.h>#include <vector>#define MAXN 310#define _clr(x) memset(x,0xff,sizeof(int)*MAXN)int hungary(int m,int n,int mat[][MAXN],int* match1,int*match2){int s[MAXN],t[MAXN],p,q,ret=0,i,j,k,r;vector<int> e[MAXN];//生成邻接表(只需一边)for(i=0;i<m;++i)for(j=0;j<n;++j)if (mat[i][j]) e[i].push_back(j);for(_clr(match1),_clr(match2),i=0;i<m;ret+=(match1[i++]>=0))for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for(r=0,k=s[p];r<e[k].size()&&match1[i]<0;++r)if (t[j=e[k][r]]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}return ret;}3. 二分图最大匹配(hungary邻接阵形式)//二分图最大匹配,hungary算法,邻接阵形式,复杂度O(m*m*n) //返回最大匹配数,传入二分图大小m,n和邻接阵mat,非零元素表示有边//match1,match2返回一个最大匹配,未匹配顶点match值为-1 #include <string.h>#define MAXN 310#define _clr(x) memset(x,0xff,sizeof(int)*MAXN)int hungary(int m,int n,int mat[][MAXN],int* match1,int*match2){int s[MAXN],t[MAXN],p,q,ret=0,i,j,k;for(_clr(match1),_clr(match2),i=0;i<m;ret+=(match1[i++]>=0))for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for (k=s[p],j=0;j<n&&match1[i]<0;j++)if (mat[k][j]&&t[j]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}return ret;}4. 二分图最大匹配(hungary正向表形式)//二分图最大匹配,hungary算法,正向表形式,复杂度O(m*e)//返回最大匹配数,传入二分图大小m,n和正向表list,buf(只需一边)//match1,match2返回一个最大匹配,未匹配顶点match值为-1 #include <string.h>#define MAXN 310#define _clr(x) memset(x,0xff,sizeof(int)*MAXN)int hungary(int m,int n,int* list,int* buf,int* match1,int* match2){ int s[MAXN],t[MAXN],p,q,ret=0,i,j,k,l;for(_clr(match1),_clr(match2),i=0;i<m;ret+=(match1[i++]>=0))for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for(l=list[k=s[p]];l<list[k+1]&&match1[i]<0;l++)if (t[j=buf[l]]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}return ret;}5. 二分图最佳匹配(kuhn_munkras邻接阵形式)//二分图最佳匹配,kuhn munkras算法,邻接阵形式,复杂度O(m*m*n)//返回最佳匹配值,传入二分图大小m,n和邻接阵mat,表示权值//match1,match2返回一个最佳匹配,未匹配顶点match值为-1 //一定注意m<=n,否则循环无法终止//最小权匹配可将权值取相反数#include <string.h>#define MAXN 310#define inf#define _clr(x) memset(x,0xff,sizeof(int)*n)int kuhn_munkras(int m,int n,int mat[][MAXN],int* match1,int* match2){ints[MAXN],t[MAXN],l1[MAXN],l2[MAXN],p,q,ret=0,i,j,k;for (i=0;i<m;i++)for (l1[i]=-inf,j=0;j<n;j++)l1[i]=mat[i][j]>l1[i]?mat[i][j]:l1[i];for (i=0;i<n;l2[i++]=0);for (_clr(match1),_clr(match2),i=0;i<m;i++){for (_clr(t),s[p=q=0]=i;p<=q&&match1[i]<0;p++)for (k=s[p],j=0;j<n&&match1[i]<0;j++)if (l1[k]+l2[j]==mat[k][j]&&t[j]<0){s[++q]=match2[j],t[j]=k;if (s[q]<0)for (p=j;p>=0;j=p)match2[j]=k=t[j],p=match1[k],match1[k]=j;}if (match1[i]<0){for (i--,p=inf,k=0;k<=q;k++)for (j=0;j<n;j++)if(t[j]<0&&l1[s[k]]+l2[j]-mat[s[k]][j]<p)p=l1[s[k]]+l2[j]-mat[s[k]][j];for (j=0;j<n;l2[j]+=t[j]<0?0:p,j++);for (k=0;k<=q;l1[s[k++]]-=p);}}for (i=0;i<m;i++)ret+=mat[i][match1[i]];return ret;}6. 一般图匹配(邻接表形式)//一般图最大匹配,邻接表形式,复杂度O(n*e)//返回匹配顶点对数,match返回匹配,未匹配顶点match值为-1 //传入图的顶点数n和邻接表list#define MAXN 100struct edge_t{int from,to;edge_t* next;};int aug(int n,edge_t* list[],int* match,int* v,int now){int t,ret=0;edge_t* e;v[now]=1;for (e=list[now];e;e=e->next)if (!v[t=e->to]){if (match[t]<0)match[now]=t,match[t]=now,ret=1;else{v[t]=1;if (aug(n,list,match,v,match[t]))match[now]=t,match[t]=now,ret=1;v[t]=0;}if (ret)break;}v[now]=0;return ret;}int graph_match(int n,edge_t* list[],int* match){int v[MAXN],i,j;for (i=0;i<n;i++)v[i]=0,match[i]=-1;for (i=0,j=n;i<n&&j>=2;)if (match[i]<0&&aug(n,list,match,v,i))i=0,j-=2;elsei++;for (i=j=0;i<n;i++)j+=(match[i]>=0);return j/2;}7. 一般图匹配(邻接表形式,邻接阵接口)//一般图最大匹配,邻接表形式,复杂度O(n*e)//返回匹配顶点对数,match返回匹配,未匹配顶点match值为-1 //传入图的顶点数n和邻接表list#include <vector>#define MAXN 100int aug(int n,vector<int> list[],int* match,int* v,int now){ int t,ret=0,r;v[now]=1;// for (e=list[now];e;e=e->next)for (r=0;r<list[now].size();++r)if (!v[t=list[now][r]]){if (match[t]<0)match[now]=t,match[t]=now,ret=1;else{v[t]=1;if (aug(n,list,match,v,match[t]))match[now]=t,match[t]=now,ret=1;v[t]=0;}if (ret)break;}v[now]=0;return ret;}int graph_match(int n,int mat[][MAXN],int* match){int v[MAXN],i,j;vector<int> list[MAXN];for (i=0;i<n;i++)for (j=0;j<n;j++)if (mat[i][j]) list[i].push_back(j);for (i=0;i<n;i++)v[i]=0,match[i]=-1;for (i=0,j=n;i<n&&j>=2;)if (match[i]<0&&aug(n,list,match,v,i))i=0,j-=2;elsei++;for (i=j=0;i<n;i++)j+=(match[i]>=0);return j/2;}8. 一般图匹配(邻接阵形式)//一般图最大匹配,邻接阵形式,复杂度O(n^3)//返回匹配顶点对数,match返回匹配,未匹配顶点match值为-1 //传入图的顶点数n和邻接阵mat#define MAXN 100int aug(int n,int mat[][MAXN],int* match,int* v,int now){ int i,ret=0;v[now]=1;for (i=0;i<n;i++)if (!v[i]&&mat[now][i]){if (match[i]<0)match[now]=i,match[i]=now,ret=1;else{v[i]=1;if (aug(n,mat,match,v,match[i]))match[now]=i,match[i]=now,ret=1;v[i]=0;}if (ret)break;}v[now]=0;return ret;}int graph_match(int n,int mat[][MAXN],int* match){int v[MAXN],i,j;for (i=0;i<n;i++)v[i]=0,match[i]=-1;for (i=0,j=n;i<n&&j>=2;)if (match[i]<0&&aug(n,mat,match,v,i))i=0,j-=2;elsei++;for (i=j=0;i<n;i++)j+=(match[i]>=0);return j/2;}9. 一般图匹配(正向表形式)//一般图最大匹配,正向表形式,复杂度O(n*e)//返回匹配顶点对数,match返回匹配,未匹配顶点match值为-1 //传入图的顶点数n和正向表list,buf#define MAXN 100int aug(int n,int* list,int* buf,int* match,int* v,int now){ int i,t,ret=0;v[now]=1;for (i=list[now];i<list[now+1];i++)if (!v[t=buf[i]]){if (match[t]<0)match[now]=t,match[t]=now,ret=1;else{v[t]=1;if (aug(n,list,buf,match,v,match[t]))match[now]=t,match[t]=now,ret=1;v[t]=0;}if (ret)break;}v[now]=0;return ret;}int graph_match(int n,int* list,int* buf,int* match){int v[MAXN],i,j;for (i=0;i<n;i++)v[i]=0,match[i]=-1;for (i=0,j=n;i<n&&j>=2;)if (match[i]<0&&aug(n,list,buf,match,v,i))i=0,j-=2;elsei++;for (i=j=0;i<n;i++)j+=(match[i]>=0);return j/2;}三．图论_生成树1. 最小生成树(kruskal邻接表形式)//无向图最小生成树,kruskal算法,邻接表形式,复杂度O(mlogm) //返回最小生成树的长度,传入图的大小n和邻接表list//可更改边权的类型,edge[][2]返回树的构造,用边集表示//如果图不连通,则对各连通分支构造最小生成树,返回总长度#include <string.h>#define MAXN 200#define inftypedef double elem_t;struct edge_t{int from,to;elem_t len;edge_t* next;};#define _ufind_run(x) for(;p[t=x];x=p[x],p[t]=(p[x]?p[x]:x))#define _run_both _ufind_run(i);_ufind_run(j)struct ufind{int p[MAXN],t;void init(){memset(p,0,sizeof(p));}void set_friend(int i,int j){_run_both;p[i]=(i==j?0:j);}int is_friend(int i,int j){_run_both;return i==j&&i;}};#define _cp(a,b) ((a).len<(b).len)struct heap_t{int a,b;elem_t len;};struct minheap{heap_t h[MAXN*MAXN];int n,p,c;void init(){n=0;}void ins(heap_t e){for(p=++n;p>1&&_cp(e,h[p>>1]);h[p]=h[p>>1],p>>=1);h[p]=e;}int del(heap_t& e){if (!n) return 0;for(e=h[p=1],c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n ]);h[p]=h[c],p=c,c<<=1);h[p]=h[n--];return 1;}};elem_t kruskal(int n,edge_t* list[],int edge[][2]){ufind u;minheap h;edge_t* t;heap_t e;elem_t ret=0;int i,m=0;u.init(),h.init();for (i=0;i<n;i++)for (t=list[i];t;t=t->next)if (i<t->to)e.a=i,e.b=t->to,e.len=t->len,h.ins(e);while (m<n-1&&h.del(e))if (!u.is_friend(e.a+1,e.b+1))edge[m][0]=e.a,edge[m][1]=e.b,ret+=e.len,u.set_friend(e.a+ 1,e.b+1);return ret;}2. 最小生成树(kruskal正向表形式)//无向图最小生成树,kruskal算法,正向表形式,复杂度O(mlogm) //返回最小生成树的长度,传入图的大小n和正向表list,buf//可更改边权的类型,edge[][2]返回树的构造,用边集表示//如果图不连通,则对各连通分支构造最小生成树,返回总长度#include <string.h>#define MAXN 200#define inftypedef double elem_t;struct edge_t{int to;elem_t len;};#define _ufind_run(x) for(;p[t=x];x=p[x],p[t]=(p[x]?p[x]:x))#define _run_both _ufind_run(i);_ufind_run(j)struct ufind{int p[MAXN],t;void init(){memset(p,0,sizeof(p));}void set_friend(int i,int j){_run_both;p[i]=(i==j?0:j);}int is_friend(int i,int j){_run_both;return i==j&&i;}};#define _cp(a,b) ((a).len<(b).len)struct heap_t{int a,b;elem_t len;};struct minheap{heap_t h[MAXN*MAXN];int n,p,c;void init(){n=0;}void ins(heap_t e){for(p=++n;p>1&&_cp(e,h[p>>1]);h[p]=h[p>>1],p>>=1);h[p]=e;}int del(heap_t& e){if (!n) return 0;for(e=h[p=1],c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n ]);h[p]=h[c],p=c,c<<=1);h[p]=h[n--];return 1;}};elem_t kruskal(int n,int* list,edge_t* buf,int edge[][2]){ ufind u;minheap h;heap_t e;elem_t ret=0;int i,j,m=0;u.init(),h.init();for (i=0;i<n;i++)for (j=list[i];j<list[i+1];j++)if (i<buf[j].to)e.a=i,e.b=buf[j].to,e.len=buf[j].len,h.ins(e);while (m<n-1&&h.del(e))if (!u.is_friend(e.a+1,e.b+1))edge[m][0]=e.a,edge[m][1]=e.b,ret+=e.len,u.set_friend(e.a+ 1,e.b+1);return ret;}3. 最小生成树(prim+binary_heap邻接表形式)//无向图最小生成树,prim算法+二分堆,邻接表形式,复杂度O(mlogm)//返回最小生成树的长度,传入图的大小n和邻接表list//可更改边权的类型,pre[]返回树的构造,用父结点表示,根节点(第一个)pre值为-1//必须保证图的连通的!#define MAXN 200#define inftypedef double elem_t;struct edge_t{int from,to;elem_t len;edge_t* next;};#define _cp(a,b) ((a).d<(b).d)struct heap_t{elem_t d;int v;};struct heap{heap_t h[MAXN*MAXN];int n,p,c;void init(){n=0;}void ins(heap_t e){for(p=++n;p>1&&_cp(e,h[p>>1]);h[p]=h[p>>1],p>>=1);h[p]=e;}int del(heap_t& e){if (!n) return 0;for(e=h[p=1],c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n ]);h[p]=h[c],p=c,c<<=1);h[p]=h[n--];return 1;}};elem_t prim(int n,edge_t* list[],int* pre){heap h;elem_t min[MAXN],ret=0;edge_t* t;heap_t e;int v[MAXN],i;for (i=0;i<n;i++)min[i]=inf,v[i]=0,pre[i]=-1;h.init();e.v=0,e.d=0,h.ins(e);while (h.del(e))if (!v[e.v])for (v[e.v]=1,ret+=e.d,t=list[e.v];t;t=t->next)if (!v[t->to]&&t->len<min[t->to])pre[t->to]=t->from,min[e.v=t->to]=e.d=t->len,h.ins(e);return ret;}4. 最小生成树(prim+binary_heap正向表形式)//无向图最小生成树,prim算法+二分堆,正向表形式,复杂度O(mlogm)//返回最小生成树的长度,传入图的大小n和正向表list,buf//可更改边权的类型,pre[]返回树的构造,用父结点表示,根节点(第一个)pre值为-1//必须保证图的连通的!#define MAXN 200#define inftypedef double elem_t;struct edge_t{int to;elem_t len;};#define _cp(a,b) ((a).d<(b).d)struct heap_t{elem_t d;int v;};struct heap{heap_t h[MAXN*MAXN];int n,p,c;void init(){n=0;}void ins(heap_t e){for(p=++n;p>1&&_cp(e,h[p>>1]);h[p]=h[p>>1],p>>=1);h[p]=e;}int del(heap_t& e){if (!n) return 0;for(e=h[p=1],c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n ]);h[p]=h[c],p=c,c<<=1);h[p]=h[n--];return 1;}};elem_t prim(int n,int* list,edge_t* buf,int* pre){heap h;heap_t e;elem_t min[MAXN],ret=0;int v[MAXN],i,j;for (i=0;i<n;i++)min[i]=inf,v[i]=0,pre[i]=-1;h.init();e.v=0,e.d=0,h.ins(e);while (h.del(e))if (!v[i=e.v])for (v[i]=1,ret+=e.d,j=list[i];j<list[i+1];j++)if(!v[buf[j].to]&&buf[j].len<min[buf[j].to])pre[buf[j].to]=i,min[e.v=buf[j].to]=e.d=buf[j].len,h.ins(e);return ret;}5. 最小生成树(prim+mapped_heap邻接表形式)//无向图最小生成树,prim算法+映射二分堆,邻接表形式,复杂度O(mlogn)//返回最小生成树的长度,传入图的大小n和邻接表list//可更改边权的类型,pre[]返回树的构造,用父结点表示,根节点(第一个)pre值为-1//必须保证图的连通的!#define MAXN 200#define inftypedef double elem_t;struct edge_t{int from,to;elem_t len;edge_t* next;};#define _cp(a,b) ((a)<(b))struct heap{elem_t h[MAXN+1];int ind[MAXN+1],map[MAXN+1],n,p,c;void init(){n=0;}void ins(int i,elem_t e){for(p=++n;p>1&&_cp(e,h[p>>1]);h[map[ind[p]=ind[p>>1]]=p]=h[p >>1],p>>=1);h[map[ind[p]=i]=p]=e;}int del(int i,elem_t& e){i=map[i];if (i<1||i>n) return 0;for(e=h[p=i];p>1;h[map[ind[p]=ind[p>>1]]=p]=h[p>>1],p>>=1);for(c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n]);h[map[i nd[p]=ind[c]]=p]=h[c],p=c,c<<=1);h[map[ind[p]=ind[n]]=p]=h[n];n--;return 1;}int delmin(int& i,elem_t& e){if (n<1) return 0;i=ind[1];for(e=h[p=1],c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n ]);h[map[ind[p]=ind[c]]=p]=h[c],p=c,c<<=1);h[map[ind[p]=ind[n]]=p]=h[n];n--;return 1;}};elem_t prim(int n,edge_t* list[],int* pre){heap h;elem_t min[MAXN],ret=0,e;edge_t* t;int v[MAXN],i;for (h.init(),i=0;i<n;i++)min[i]=(i?inf:0),v[i]=0,pre[i]=-1,h.ins(i,min[i]);while (h.delmin(i,e))for (v[i]=1,ret+=e,t=list[i];t;t=t->next)if (!v[t->to]&&t->len<min[t->to])pre[t->to]=t->from,h.del(t->to,e),h.ins(t->to,min[t->to]=t->l en);return ret; }6. 最小生成树(prim+mapped_heap正向表形式)//无向图最小生成树,prim算法+映射二分堆,正向表形式,复杂度O(mlogn)//返回最小生成树的长度,传入图的大小n和正向表list,buf//可更改边权的类型,pre[]返回树的构造,用父结点表示,根节点(第一个)pre值为-1//必须保证图的连通的!#define MAXN 200#define inftypedef double elem_t;struct edge_t{int to;elem_t len;};#define _cp(a,b) ((a)<(b))struct heap{elem_t h[MAXN+1];int ind[MAXN+1],map[MAXN+1],n,p,c;void init(){n=0;}void ins(int i,elem_t e){for(p=++n;p>1&&_cp(e,h[p>>1]);h[map[ind[p]=ind[p>>1]]=p]=h[p >>1],p>>=1);h[map[ind[p]=i]=p]=e;}int del(int i,elem_t& e){i=map[i];if (i<1||i>n) return 0;for(e=h[p=i];p>1;h[map[ind[p]=ind[p>>1]]=p]=h[p>>1],p>>=1);for(c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n]);h[map[i nd[p]=ind[c]]=p]=h[c],p=c,c<<=1);h[map[ind[p]=ind[n]]=p]=h[n];n--;return 1;}int delmin(int& i,elem_t& e){if (n<1) return 0;i=ind[1];for(e=h[p=1],c=2;c<n&&_cp(h[c+=(c<n-1&&_cp(h[c+1],h[c]))],h[n ]);h[map[ind[p]=ind[c]]=p]=h[c],p=c,c<<=1);h[map[ind[p]=ind[n]]=p]=h[n];n--;return 1;}};elem_t prim(int n,int* list,edge_t* buf,int* pre){heap h;elem_t min[MAXN],ret=0,e;int v[MAXN],i,j;for (h.init(),i=0;i<n;i++)min[i]=(i?inf:0),v[i]=0,pre[i]=-1,h.ins(i,min[i]);while (h.delmin(i,e))for (v[i]=1,ret+=e,j=list[i];j<list[i+1];j++)if (!v[buf[j].to]&&buf[j].len<min[buf[j].to]) pre[buf[j].to]=i,h.del(buf[j].to,e),h.ins(buf[j].to,min[buf[j].to ]=buf[j].len);return ret;}7. 最小生成树(prim邻接阵形式)//无向图最小生成树,prim算法,邻接阵形式,复杂度O(n^2)//返回最小生成树的长度,传入图的大小n和邻接阵mat,不相邻点边权inf//可更改边权的类型,pre[]返回树的构造,用父结点表示,根节点(第一个)pre值为-1//必须保证图的连通的!#define MAXN 200#define inftypedef double elem_t;elem_t prim(int n,elem_t mat[][MAXN],int* pre){elem_t min[MAXN],ret=0;int v[MAXN],i,j,k;for (i=0;i<n;i++)min[i]=inf,v[i]=0,pre[i]=-1;for (min[j=0]=0;j<n;j++){for (k=-1,i=0;i<n;i++)if (!v[i]&&(k==-1||min[i]<min[k]))k=i;for (v[k]=1,ret+=min[k],i=0;i<n;i++)if (!v[i]&&mat[k][i]<min[i])min[i]=mat[pre[i]=k][i];}return ret;}8. 最小树形图(邻接阵形式)//多源最小树形图,edmonds算法,邻接阵形式,复杂度O(n^3)//返回最小生成树的长度,构造失败返回负值//传入图的大小n和邻接阵mat,不相邻点边权inf//可更改边权的类型,pre[]返回树的构造,用父结点表示//传入时pre[]数组清零,用-1标出源点#include <string.h>#define MAXN 120#define inftypedef int elem_t;elem_t edmonds(int n,elem_t mat[][MAXN*2],int* pre){ elem_t ret=0;intc[MAXN*2][MAXN*2],l[MAXN*2],p[MAXN*2],m=n,t,i,j,k;for (i=0;i<n;l[i]=i,i++);do{memset(c,0,sizeof(c)),memset(p,0xff,sizeof(p));for (t=m,i=0;i<m;c[i][i]=1,i++);for (i=0;i<t;i++)if (l[i]==i&&pre[i]!=-1){for (j=0;j<m;j++)if(l[j]==j&&i!=j&&mat[j][i]<inf&&(p[i]==-1||mat[j][i]<mat[p[i]][i ]))p[i]=j;if ((pre[i]=p[i])==-1)return -1;if (c[i][p[i]]){for(j=0;j<=m;mat[j][m]=mat[m][j]=inf,j++);for (k=i;l[k]!=m;l[k]=m,k=p[k])for (j=0;j<m;j++)if (l[j]==j){if(mat[j][k]-mat[p[k]][k]<mat[j][m])mat[j][m]=mat[j][k]-mat[p[k]][k];if(mat[k][j]<mat[m][j])mat[m][j]=mat[k][j];}c[m][m]=1,l[m]=m,m++;}for (j=0;j<m;j++)if (c[i][j])for(k=p[i];k!=-1&&l[k]==k;c[k][j]=1,k=p[k]);}}while (t<m);for (;m-->n;pre[k]=pre[m])for (i=0;i<m;i++)if (l[i]==m){for (j=0;j<m;j++)if(pre[j]==m&&mat[i][j]==mat[m][j])pre[j]=i;if(mat[pre[m]][m]==mat[pre[m]][i]-mat[pre[i]][i])k=i;}for (i=0;i<n;i++)if (pre[i]!=-1)ret+=mat[pre[i]][i];return ret;}四．图论_网络流1. 上下界最大流(邻接表形式)//求上下界网络最大流,邻接表形式//返回最大流量,-1表示无可行流,flow返回每条边的流量//传入网络节点数n,容量mat,流量下界bf,源点source,汇点sink //MAXN应比最大结点数多2,无可行流返回-1时mat未复原! #define MAXN 100#define infint _max_flow(int n,int mat[][MAXN],int source,int sink,intflow[][MAXN]){int pre[MAXN],que[MAXN],d[MAXN],p,q,t,i,j,r;vector<int> e[MAXN];for (i=0;i<n;i++)for (e[i].clear(),j=0;j<n;j++)if (mat[i][j]) e[i].push_back(j),e[j].push_back(i);for (;;){for (i=0;i<n;pre[i++]=0);pre[t=source]=source+1,d[t]=inf;for (p=q=0;p<=q&&!pre[sink];t=que[p++])for (r=0;r<e[t].size();++r){i=e[t][r];if (!pre[i]&&(j=mat[t][i]-flow[t][i])) pre[que[q++]=i]=t+1,d[i]=d[t]<j?d[t]:j;else if (!pre[i]&&(j=flow[i][t]))pre[que[q++]=i]=-t-1,d[i]=d[t]<j?d[t]:j;}if (!pre[sink]) break;for (i=sink;i!=source;)if (pre[i]>0)flow[pre[i]-1][i]+=d[sink],i=pre[i]-1;elseflow[i][-pre[i]-1]-=d[sink],i=-pre[i]-1;}for (j=i=0;i<n;j+=flow[source][i++]);return j;}int limit_max_flow(int n,int mat[][MAXN],int bf[][MAXN],int source,int sink,int flow[][MAXN]){int i,j,sk,ks;if (source==sink) return inf;for(mat[n][n+1]=mat[n+1][n]=mat[n][n]=mat[n+1][n+1]=i=0;i<n;i+ +)for(mat[n][i]=mat[i][n]=mat[n+1][i]=mat[i][n+1]=j=0;j<n;j++) mat[i][j]-=bf[i][j],mat[n][i]+=bf[j][i],mat[i][n+1]+=bf[i][j];sk=mat[source][sink],ks=mat[sink][source],mat[source][sink ]=mat[sink][source]=inf;for (i=0;i<n+2;i++)for (j=0;j<n+2;flow[i][j++]=0);_max_flow(n+2,mat,n,n+1,flow);for (i=0;i<n;i++)if (flow[n][i]<mat[n][i]) return -1;flow[source][sink]=flow[sink][source]=0,mat[source][sink] =sk,mat[sink][source]=ks;_max_flow(n,mat,source,sink,flow);for (i=0;i<n;i++)for (j=0;j<n;j++)mat[i][j]+=bf[i][j],flow[i][j]+=bf[i][j];for (j=i=0;i<n;j+=flow[source][i++]);return j;}2. 上下界最大流(邻接阵形式)//求上下界网络最大流,邻接阵形式//返回最大流量,-1表示无可行流,flow返回每条边的流量//传入网络节点数n,容量mat,流量下界bf,源点source,汇点sink //MAXN应比最大结点数多2,无可行流返回-1时mat未复原! #define MAXN 100#define inf void _max_flow(int n,int mat[][MAXN],int source,int sink,int flow[][MAXN]){int pre[MAXN],que[MAXN],d[MAXN],p,q,t,i,j;for (;;){for (i=0;i<n;pre[i++]=0);pre[t=source]=source+1,d[t]=inf;for (p=q=0;p<=q&&!pre[sink];t=que[p++])for (i=0;i<n;i++)if (!pre[i]&&j=mat[t][i]-flow[t][i]) pre[que[q++]=i]=t+1,d[i]=d[t]<j?d[t]:j;else if (!pre[i]&&j=flow[i][t])pre[que[q++]=i]=-t-1,d[i]=d[t]<j?d[t]:j;if (!pre[sink]) break;for (i=sink;i!=source;)if (pre[i]>0)flow[pre[i]-1][i]+=d[sink],i=pre[i]-1;elseflow[i][-pre[i]-1]-=d[sink],i=-pre[i]-1;}}int limit_max_flow(int n,int mat[][MAXN],int bf[][MAXN],int source,int sink,int flow[][MAXN]){int i,j,sk,ks;if (source==sink) return inf;for(mat[n][n+1]=mat[n+1][n]=mat[n][n]=mat[n+1][n+1]=i=0;i<n;i+ +)for(mat[n][i]=mat[i][n]=mat[n+1][i]=mat[i][n+1]=j=0;j<n;j++) mat[i][j]-=bf[i][j],mat[n][i]+=bf[j][i],mat[i][n+1]+=bf[i][j];sk=mat[source][sink],ks=mat[sink][source],mat[source][sink ]=mat[sink][source]=inf;for (i=0;i<n+2;i++)for (j=0;j<n+2;flow[i][j++]=0);_max_flow(n+2,mat,n,n+1,flow);for (i=0;i<n;i++)if (flow[n][i]<mat[n][i]) return -1;flow[source][sink]=flow[sink][source]=0,mat[source][sink] =sk,mat[sink][source]=ks;_max_flow(n,mat,source,sink,flow);for (i=0;i<n;i++)for (j=0;j<n;j++)mat[i][j]+=bf[i][j],flow[i][j]+=bf[i][j];for (j=i=0;i<n;j+=flow[source][i++]);return j;}3. 上下界最小流(邻接表形式)//求上下界网络最小流,邻接阵形式//返回最大流量,-1表示无可行流,flow返回每条边的流量//传入网络节点数n,容量mat,流量下界bf,源点source,汇点sink //MAXN应比最大结点数多2,无可行流返回-1时mat未复原! #define MAXN 100#define inf。

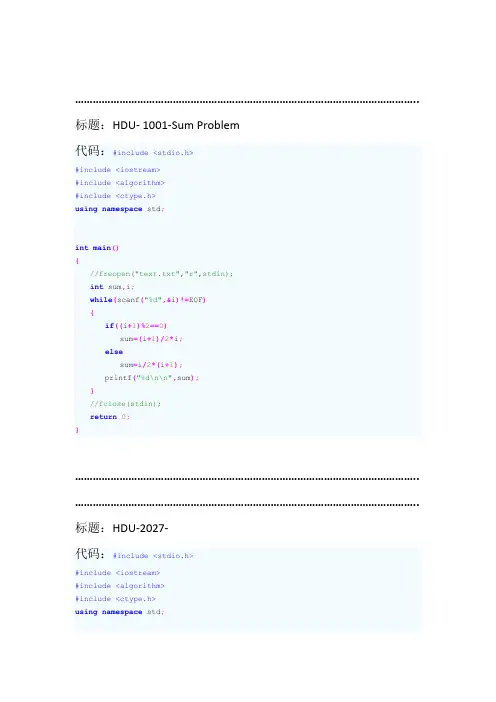
…………………………………………………………………………………………………….. 标题：HDU- 1001-Sum Problem代码：#include <stdio.h>#include <iostream>#include <algorithm>#include <ctype.h>using namespace std;int main(){//freopen("text.txt","r",stdin);int sum,i;while(scanf("%d",&i)!=EOF){if((i+1)%2==0)sum=(i+1)/2*i;elsesum=i/2*(i+1);printf("%d\n\n",sum);}//fclose(stdin);return 0;}…………………………………………………………………………………………………….. …………………………………………………………………………………………………….. 标题：HDU-2027-代码：#include <stdio.h>#include <iostream>#include <algorithm>#include <ctype.h>using namespace std;int main(){//freopen("text.txt","r",stdin);char c[101];int n,j,k,a,e,i,o,u;scanf("%d\n",&n);//注意这里for(j=1;j<=n;j++){a=e=i=o=u=0;gets(c);for(k=0;c[k]!='\0';k++){if(c[k]=='a')a++;if(c[k]=='e')e++;if(c[k]=='i')i++;if(c[k]=='o')o++;if(c[k]=='u')u++;}printf("a:%d\ne:%d\ni:%d\no:%d\nu:%d\n",a,e,i,o,u);if(j<n)printf("\n");}//fclose(stdin);return 0;}…………………………………………………………………………………………………….. …………………………………………………………………………………………………….. 标题：HDU-2025- 查找最大元素代码：#include <stdio.h>#include <iostream>#include <algorithm>#include <ctype.h>using namespace std;int main(){//freopen("text.txt","r",stdin);char a[105],max='A';int i,n;while(scanf("%s",a)!=EOF){n=strlen(a);max='A';for(i=0;i<n;i++){if(a[i]>max) max=a[i];}for(i=0;i<n;i++){printf("%c",a[i]);if(a[i]==max)printf("(max)");}printf("\n");}//fclose(stdin);return 0;}…………………………………………………………………………………………………….. …………………………………………………………………………………………………….. 标题：HDU-1037-Keep on Truckin'代码：#include <stdio.h>#include <iostream>#include <algorithm>#include <ctype.h>using namespace std;int main(){//freopen("text.txt","r",stdin);int a,b,c,min;while(cin >> a >> b >> c){min = a>b?b:a;min = min>c?c:min;if(min<=168)printf("CRASH %d\n",min);elseprintf("NO CRASH\n");}//fclose(stdin);return 0;}…………………………………………………………………………………………………….. …………………………………………………………………………………………………….. 标题：HDU-2052-Picture代码：#include <stdio.h>#include <iostream>#include <algorithm>#include <ctype.h>using namespace std;int main(){//freopen("text.txt","r",stdin);int n,m,i;while(scanf("%d%d",&n,&m)!=EOF){printf("+");for(i=0;i<n;++i){printf("-");}printf("+\n");for(i=0;i<m;++i){printf("|");for(int j=0;j<n;++j){printf(" ");}printf("|\n");}printf("+");for(i=0;i<n;++i){printf("-");}printf("+\n\n");}//fclose(stdin);return 0;}…………………………………………………………………………………………………….. …………………………………………………………………………………………………….. 标题：HDU-1034-Candy Sharing Game代码：#include <stdio.h>#include <iostream>#include <algorithm>#include <ctype.h>using namespace std;const int MAXN=1000;int a[MAXN];int main(){//freopen("text.txt","r",stdin);int n;int i;while(scanf("%d",&n),n){for(i=0;i<n;i++) scanf("%d",&a[i]);int res=0;while(1){for(i=1;i<n;i++)if(a[i-1]!=a[i]) break;if(i>=n) break;res++;int temp=a[n-1]/2;for(i=n-1;i>0;i--){a[i]/=2;a[i]+=a[i-1]/2;}a[0]/=2;a[0]+=temp;for(i=0;i<n;i++)if(a[i]&1) a[i]++;}printf("%d %d\n",res,a[0]);}//fclose(stdin);return 0;}……………………………………………………………………………………………………..。

acm算法经典例题一、数论1: Wolf and Rabbit描述There is a hill with n holes around. The holes are signed from0 to n-1.A rabbit must hide in one of the holes. A wolf searches the rabbit in anticlockwise order. The first hole he get into is the one signed with 0. Then he will get into the hole every m holes. For example, m=2 and n=6, the wolf will get into the holes which are signed 0,2,4,0. If the rabbit hides in the hole which signed 1,3 or 5, she will survive. So we call these holes the safe holes.输入The input starts with a positive integer P which indicates the number of test cases. Then on the following P lines,each line consists 2 positive integer m and n(0<m,n<2147483648).< bdsfid="69" p=""></m,n<2147483648).<>输出For each input m n, if safe holes exist, you should output "YES", else output "NO" in a single line.样例输入21 22 2样例输出NOYES翻译：描述一座山有n个洞，洞被标记为从0到n-1。

hdu 题目分类1001 整数求和 水题1002 C 语言实验题——两个数比较 水题1003 1、2、3、4、5... 简单题1004 渊子赛马 排序+贪心的方法归并1005 Hero In Maze 广度搜索1006 Redraiment 猜想 数论：容斥定理1007 童年生活二三事 递推题 1008 University 简单hash 1009 目标柏林 简单模拟题 1010 Rails 模拟题（堆栈） 1011 Box of Bricks 简单题1012 IMMEDIATE DECODABILITY Huffman 编码1013 STAMPS 搜索or 动态规划 1014 Border 模拟题1015 Simple Arithmetics 高精度计算 1016 Shoot-out 博弈+状态压缩DP 1017 Tour Guide 1018 Card Trick 简单题1019 Necklace Decomposition 贪心1020 Crashing Robots 模拟题1021 Electrical Outlets 简单题 1022 Watchdog 简单题1023 Taxi Cab Scheme 图论：最小路径覆盖--->最大二分匹配1024 Pseudo-random Numbers 数论 1025 Card Game Cheater 简单题 1026 Investment 动态规划 1027 Pipes1028 SETI 数学:高斯消元法1029 Minimax Triangulation 计算几何 1030 Unequalled Consumption 母函数 1031 Declaration of Content 1032 Laserbox 搜索：DFS 1033 Bowlstack 1034 Pesky Heroes1035 Reduced ID Numbers 暴力 1036 Tantrix1037 Guardian of Decency 图论：匈牙利算法求二分图的最大匹配1038 Up the Stairs 简单数学题 1039 Sudoku 搜索：DFS 1040 The SetStack Computer 1041 Pie 二分法1042 Ticket to Ride 动态规划 1043 The Bookcase 动态规划 1044 Printer Queue 模拟题 1045 Prime Path 搜索：BFS1046 Lineland's Airport 1047 Leonardo's Notebook 数学题：群置换 1048 简易版最长序列 简单题 1049 Jesse's problem 搜索：DFS 1050 Error Correction 模拟题 1051 A × B problem 高精度计算 1052 Redraiment 的走法 动态规划 1053 Word Encoding 动态规划 1054 Jesse's Code 组合数学：排列 1055 简单密码破解 水题1056 英文金曲大赛 水题 1057 有假币 水题 1058 寄居蟹与海葵 水题1059 天仙配 水题1060 鹊桥相会 水题 1061 杨辉三角 水题 1062 蟠桃记 水题1063 养兔子 水题 1064 字符统计 水题 1065 完美数 水题 1066 亲和数 水题 1067 成绩评估 水题 1068 找零钱 水题 1069 漂亮菱形 水题 1070 Least Common Multiple 水题 1071 第几天 水题 1072 编辑距离 水题1073 支配值数目 水题 1074 等值数目 水题 1075 两数组最短距离 水题 1076 输入入门(1) 水题 1077 输入入门(2) 水题 1078 输入入门(3) 水题 1079 输出入门 水题1080 Counterfeit Dollar 组合数学 1081 Dividing 动态规划 1082 Sorting It All Out 图论：拓扑排序 1083 False coin 暴力法 1084 File Mapping 1085 Color Me Less 简单题1086 Round and Round We Go 简单题 1087 Microprocessor Simulation 简单题 1088 求奇数的乘积 水题 1089 平方和与立方和 水题1090 绝对值排序 水题 1091 JudgeOnline 水题 1092 More Beautiful 水题 1093 猴子分桃 水题 1094 C 语言实验题——一元二次方程 水题 1095 C 语言实验题——保留字母 水题 1096 C 语言实验题——排列 水题 1097 C 语言实验题——矩阵转置 水题 1098 C 语言实验题——素数 水题1099 Ambiguous permutations 简单题 1100 Home Work 贪心法1101 Redraiment 的遭遇 数学题：找规律 1102 Decorate the wall 搜索or 动态规划 1103 Economic phone calls 动态规划or 贪心 1104 Any fool can do it 记忆化搜索 1105 Wine trading in Gergovia 贪心法 1106 Homogeneous squares 随机算法 1107 Automatic Correction of Misspellings 字符串1108 Black and white painting 简单数学题 1109 Cylinder 计算几何：公式推导 1110 Deli Deli 水题1111 Expressions 数据结构：树的遍历 1112 Flavius Josephus Reloaded 数论：Pollard's R1113 Annoying painting tool 贪心法 1114 Frequent values RMQ 区间最值问题 OR 线段树1115 Anagram Groups 字符串匹配 1116 Let it Bead 组合数学->Polya 定理 1117 Simple Computers 简单题 1118 Mondriaan's Dream 动态规划 1119 Equidistance 计算几何 1120 How many Fibs? 高精度计算 1121 Hike on a Graph 搜索：BFS 1122 ASCII Art 1123 Billing Tables1124 Cellular Automaton 矩阵计算1125 Exchange 1126 Fool's Game 1127 Java vs C++ 字符串处理 1128 Kickdown 字符串处理 1129 Copying Books 贪心+二分法1130 Adding Reversed Numbers 简单题 1131 Glass Beads 字符串的最小表示 1132 The Circumference of the Circle 计算几何题 1133 Knight Moves 搜索：BFS 1134 Eeny Meeny Moo 变形的约瑟夫问题 1135 Lotto 组合数学1136 Humble Numbers 动态规划 1137 Average is not Fast Enough! 简单题 1138 Etaoin Shrdlu 简单题 1139 Hard to Believe, but True! 简单题 1140 Code the Tree 简单题 1141 Fiber Network 图论：全源最短路径，Floyd-Warshall 算法 1142 Global Roaming 3D 几何题 1143 All in All 字符串处理1144 The Sierpinski Fractal 递归 1145 Assistance Required 简单题：预处理 1146 Drink, on Ice 模拟题 1147 All Discs Considered 搜索：BFS 1148 In Danger 模拟题 1149 Run Length Encoding 字符串处理 1150 Bee Maja 模拟题 1151 Friends 表达式求值 1152 John 博弈论 1153 Double Queue 最大堆与最小堆 1154 ‘JBC’1155 Loan Scheduling 贪心+堆 1156 Showstopper 1157 Highway 贪心法 1158 Computers 动态规划 1159 The Stable Marriage Problem 组合数学 1160 Arne Saknussemm 模拟题 1161 Sum Problem 水题 1162 Fire Net 搜索题 1163 统计1到N 之间数字1的个数 推理题 1164 最大公因子 水题1165 C 语言实验题——三个整数 水题 1166 C 语言实验题——大小写转换 水题 1167 C 语言实验题——分数序列 水题 1168 C 语言实验题——最值 水题 1169 C 语言实验题——保留整数 水题 1170 C 语言实验题——矩阵下三角元素之和 水题 1171 C 语言实验题——字符逆序 水题 1172 C 语言实验题——打印菱形 水题 1173 C 语言实验题——分割整数 水题 1174 C 语言实验题——删除指定字符 水题 1175 C 语言实验题——时间间隔 水题 1176 C 语言实验题——数组逆序 水题 1177 C 语言实验题——打印数字图形 水题 1178 C 语言实验题——单词统计 水题 1179 C 语言实验题——最小公倍数和最大公约数 水题 1180 Crashing Balloon 搜索题1181 念数字 模拟题1182 A+B for Input-Output Practice(1) 水题 1183 Anagrams by Stack 搜索：回溯 1184 Elevator 数学：找规律1185 Substrings 字符串处理1186 Calling Extraterrestrial Intelligence Again 搜索：枚举法 1187 Do the Untwist 简单数学题 1188 数字对 水题 1189 A+B for Input-Output Practice (2) 水题 1190 火星A+B 简单题1191 三齿轮问题：三个齿轮啮合 简单数学题 1192 A + B Problem II 高精度计算 1193 The ones to remain 数学题 1194 Chinese Chess 博弈论1195 Page Replacement 数据结构：队列or hash 1196 RSA Signing 数论：Pollard's Rho 算法 1197 Number Guessing 搜索：穷举 1198 求n 的阶乘 高精度计算 1199 Area 计算几何 1200 求两直线的夹角 水题 1201 三角形面积 水题 1202 Max Sum 动态规划 1203 Number Sequence 大数问题1204 u Calculate e 水题 1205 斐波那契数列 高精度计算 1206 Fibonacci Again 大数问题 1207 Let the Balloon Rise 字符串处理 1208 还是A+B 水题1209 A + B 水题1210 The area 简单计算几何1211 Ignatius's puzzle 简单数学问题 1212 Computer Transformation 高精度计算 1213 N! 高精度计算 1217 Text Reverse 水题 1220 填数字游戏 搜索：DFS1221 Tempter of the Bone 搜索：DFS or BFS+剪枝 1226 Last non-zero Digit in N! 数论 1227 三角形 递推求解 1228 回文数猜想 简单题 1229 Factorial 简单题 1230 Specialized Four-Digit Numbers 简单数学题 1231 Lowest Bit 简单题1232 To and Fro 简单题 1233 AC Me 简单题1234 Wolf and Rabbit 数论1235 最大连续子序列 动态规划 1236 开门人和关门人 字符串处理 1237 排名 排序1238 统计难题 字符串处理：字典树1239 Tick and Tick 数学题 1240 Quoit Design 分治法1241 钱币兑换问题 递推求解 1242 求出前m 大的数 简单题 1243 角谷猜想 简单题1244 Reverse Number 简单题1245 寻找素数对 简单题 1246 ZJUTACM 简单题1247 Hat's Fibonacci 高精度计算1248 Encoding 简单题 1249 四数相加 高精度计算 1250 两数相减 高精度计算1251 Square Coins 母函数 1252 Counting Triangles 递推求解 1253 2^x mod n = 1 数论：费尔马小定理 1254 Minimum Inversion Number 简单题 1255 Surround the Trees 计算几何：凸包 1256 Number Steps 简单题 1257 Binary Numbers 简单题 1258 Knight Moves 搜索：BFS 1259 Lotto 组合数学 1260 A Simple Task 简单题 1261 The Drunk Jailer 数论1262 Hanoi Tower Troubles Again! 递推求解 1263 IBM Minus One 水题1264 Definite Values 简单题 1265 Box of Bricks 水题 1266 Perfection 简单题 1267 Reverse Text 水题 1268 Inversion 模拟题1269 Prime Cuts 简单题1270 How Many Fibs? 高精度计算1271 Round and Round We Go 简单题 1272 Red and Black 搜索：DFS 1273 What Day Is It? 简单题1274 String Matching 字符串匹配 1275 A Contesting Decision 简单题 1276 Doubles 简单题 1277 The Snail 简单题1278 Jungle Roads 图论：最小生成树 1279 Prime Ring Problem 搜索：DFS 1280 Big Number 大数问题 1281 Least Common Multiple 简单题 1283 简单排序 水题 1284 Gridland 简单题 1285 An Easy Task 简单题 1286 Calendar Game 模拟题1287 Human Gene Functions 动态规划 1288 计算几何练习题——线段相交 计算几何 1289 计算几何练习题——线段相交II 计算几何 1290 计算几何练习题——直线交点 计算几何 1291 Trees Made to Order 递归求解 1292 排序 简单题 1293 18岁生日 简单题 1294 吃糖果 递推求解 1295 变种汉诺塔 递推求解 1296 洗牌 递推求解 1297 大数求余 数论 1298 圆桌会议 递推求解 1299 畅通工程 并查集 1300 还是畅通工程 最小生成树 1301 统计同成绩学生人数 水题1302 简单计算器 表达式求值：栈的应用 1303 改进版计算器 表达式求值：栈的应用 1304 FatMouse' Trade 贪心法 1305 Digital Roots 大数问题 1306 Uniform Generator 数论 1307 A Mathematical Curiosity 穷举法 1308 Safecracker 穷举法 1309 The 3n + 1 problem 简单题 1310 分享糖果 模拟题 1311 宝物收集 搜索：BFS 1312 Climbing Worm 简单题 1313 搬桌子 贪心法1314 Humble Numbers 动态规划 1315 Dividing 动态规划1316 Rightmost Digit 数学问题 1317 Leftmost Digit 数学问题 1318 Hangover 简单数学问题1319 Exponentiation 高精度计算 1320 I Think I Need a Houseboat 简单题 1321 Girls and Boys DFS+二分图 1322 Monkey and Banana 动态规划 1323 买牛奶 简单题 1324 Matrix Chain Multiplication 数据结构：栈的应用 1325 计算成绩 简单题1326 Holding Bin-Laden Captive! 母函数 1327 You can Solve a Geometry Problem too 计算几何 1328 Super Jumping! Jumping! Jumping! 动态规划 1329 a^b 数论 1330 计算GPA 水题1331 Give me an offer! 动态规划：0-1背包 1332 田忌赛马 贪心法 1333 Asteroids! 搜索：BFS 1334 Oil Deposits 搜索：DFS 1335 营救天使 搜索：BFS 1336 小数化分数 高精度计算 1337 I Hate It 线段树 1338 Strange Billboard 位运算+枚举 1339 Frobenius 递推求解 1340 奇怪的公式 数学题 1341 Fibonacci again and again 博弈论 1342 A New Tetris Game 博弈论 1343 Sum It Up 搜索：DFS 1344 速算24点 搜索 1345 推箱子 搜索：BFS1346 Pushing Boxes 搜索：BFS 1347 The Worm Turns 搜索 1348 Alfredo's Pizza Restaurant 简单题 1349 Broken Keyboard 字符串处理 1350 Convert Kilometers to Miles 简单题 1351 单词数 水题1352 仙人球的残影 简单题 1353 Family planning 简单题1354 Rout 66 简单题 1355 LC-Display 模拟题 1356 A == B ? 高精度计算 1357 不容易系列之一 递推求解 1358 折线分割平面 递推求解1359 find the nth digit 二分查找 1360 奇数阶魔方(II) 简单题 1361 Keep on Truckin' 简单题 1362 Factstone Benchmark 简单题1363 Destroy the Well of Life 模拟题 1365 Brave Game 博弈论 1366 ASCII 码排序 水题 1367 计算两点间的距离 水题1368 计算球体积 水题 1369 求绝对值 水题 1370 数值统计 水题1371 求数列的和 水题1372 水仙花数 水题 1373 多项式求和 水题 1374 素数判定 水题 1375 偶数求和 水题 1376 母牛的故事 水题 1377 数列有序! 水题 1378 发工资咯：） 水题 1379 C 语言合法标识符 水题 1380 海选女主角 水题 1381 查找最大元素 水题 1382 首字母变大写 水题1383 统计元音 水题1384 Palindromes _easy version 水题 1385 汉字统计 水题 1386 进制转换 水题1387 人见人爱A+B 水题 1388 人见人爱A-B 水题 1389 人见人爱A^B 水题 1390 改革春风吹满地 计算几何 1391 今年暑假不AC 动态规划 1392 三角形 水题1393 求平均成绩 水题1394 不容易系列之二 递推求解 1395 密码 水题1396 一只小蜜蜂... 递推求解 1397 不容易系列之(3)—— LELE 的RPG 难题 递推求解1398 骨牌铺方格 递推求解 1399 阿牛的EOF 牛肉串 递推求解 1400 神、上帝以及老天爷 递推求解 1401 不容易系列之(4)——考新郎 递推求解 1402 Bitset 简单题 1403 Picture 简单模拟题1404 Switch Game 找规律1405 An easy problem 简单模拟题 1406 A + B Again 简单题 1407 The sum problem 简单数学题 1408 龟兔赛跑 动态规划 1409 Snooker 简单数学题 1410 Subset sequence 简单题 1411 汉诺塔III 递推求解 1412 "红色病毒"问题 递推求解 1413 小兔的棋盘 递推求解 1414 RPG 的错排 错排+排列组合 1415 无限的路 简单题 1416 夹角有多大 数学题 1417 汉诺塔IV 递推求解 1418 复习时间 简单题 1419 选课时间 暴力求解 1420 手机短号 字符串处理 1421 找单词 母函数1422 简易版之最短距离 数学题 1423 数塔 动态规划 1424 核反应堆 简单题 1425 A1 = ? 公式推导 1426 剪花布条 字符串处理 1427 不要62 数学题 1428 空心三角形 字符串处理 1429 小明A+B 简单题 1430 Sky 数 进制转换 1431 整除的尾数 简单题 1432 分拆素数和 数论 1433 正整数解 数学题 1434 挂盐水 模拟题 1435 {A} + {B} 简单题 1436 小数A+B 高精度计算 1437 Zigzag 简单题 1438 螺旋形 简单题 1439 行李寄存 简单题 1440 判断多边形凹凸 计算几何 1441 The centre of polygon 计算几何 1442 最小正整数 简单题 1443 Elevator Stopping Plan 二分+贪心法 1444 TOYS 计算几何 1445 The Doors 计算几何 1446 Polygon And Segment 计算几何 1447 Fence 计算几何 1448 两圆相交面积 计算几何1449 Area of Circles 计算几何 1450 Pipe 计算几何1451 zero sum 搜索：DFS1452 C 语言实验题——Hello World 水题 1453 C 语言实验题——数日子 水题 1454 C 语言实验题——三个数排序 水题 1455 C 语言实验题——数字串求和 水题 1456 C 语言实验题——拍皮球 水题 1457 C 语言实验题——求一个3*3矩阵对角线元素之和 水题1458 C 语言实验题——数组逆序 水题 1459 C 实验题——求最大值 水题 1460 C 实验题——求绝对值最大值 水题 1461 C 语言实验题——求平均值 水题 1462 C 语言实验题——打印直角三角形 水题 1463 C 语言实验题——相加和最大值 水题 1464 C 语言实验题——简单编码 水题 1465 C 语言实验题——某年某月的天数 水题 1466 C 语言实验题——各位数字之和排序 水题 1467 C 语言实验题——两个数最大 水题 1468 C 语言实验题——求级数值 水题 1469 Pipe II 计算几何 1470 Transmitters 计算几何 1471 Wall 计算几何1472 C 语言实验题——逆置正整数 水题 1473 C 语言实验题——找中间数 水题 1474 C 语言实验题——整数位 水题 1475 C 语言实验题——一元二次方程 II 水题 1476 C 语言实验题——圆周率 水题 1477 C 语言实验题——余弦 水题 1478 C 语言实验题——打印金字塔 水题 1479 C 语言实验题——排序 水题 1480 C 语言实验题——约瑟夫问题 水题 1481 C 语言实验题——鞍点 水题 1482 C 语言实验题——计算表达式 水题 1483 C 语言实验题——汉诺塔 水题 1484 C 语言实验题——字符串排序 水题 1485 C 语言实验题——整除 水题 1486 Solitaire 搜索：（双向）BFS 1487 Abbreviation 水题1488 C 语言实验题——买糖果 水题 1489 C 语言实验题——字符编码 水题 1490 C 语言实验题——合法的C 标识符 水题 1491 C 语言实验题——三角形面积 水题 1492 C 语言实验题——大小写转换 水题 1493 C 语言实验题——圆柱体计算 水题 1494 C 语言实验题——温度转换 水题 1495 C 语言实验题——统计字串 水题1496 C 语言实验题——字符过滤 水题 1497 Coin Change 暴力求解 1498 Beautiful Meadow 搜索题 1499 C 语言实验题——鸡兔同笼 水题 1500 Coins of Luck 数学题：数学期望 1501 Friends 搜索：DFS 1502 Find All M^N Please 数学题 1503 Incredible Cows 搜索：二分+DFS 1504 计算直线的交点数 递推求解 1505 Number Game 动态规划 1506 Sort ZOJ7 字符串处理 1507 Find 7 Faster Than John Von Neumann 高精度计1508 免费馅饼 动态规划 1509 Worm 动态规划1510 Common Subsequence 动态规划 1511 搬寝室 动态规划 1512 Daydream 字符串处理 1513 Ballroom Lights 1514 Drop the Triples 1515 Finding Seats1516 He is offside! 1517 Justice League 1518 星星点点 搜索1519 逆波兰表达式 表达式求解：栈的应用 1520 十六进制 高精度计算 1521 Palindromic sequence 1522 Hotel 模拟题1523 Intersecting Lines 计算几何 1524 Heap Construction 最短路径 1525 Pizza Anyone? 1526 Adam's Genes 1527 Risk1528 Just the Facts 数论 1529 Horse Shoe Scoring 计算几何 1530 哥德巴赫猜想 数论1531 爱的伟大意义 简单题1532 校门外的树 模拟题 1533 最多约数问题 数论 1534 Quicksum 数学题1535 找规律填数字 数学题1536 Accepted Necklace 搜索：DFS1537 除法表达式 数论 1538 A Walk Through the Forest 图论：最短路径 1539 Accurately Say "CocaCola"! 简单题 1540 Build The Electric System 图论：最小生成树 1541 Colorful Rainbows 计算几何 1542 Easy Task 数学题1543 Faster, Higher, Stronger 简单题 1544 Give Me the Number 模拟题 1545 Hurdles of 110m 动态规划 1546 Just Pour the Water 矩阵计算 1547 Kinds of Fuwas 穷举法 1548 复数运算 简单题 1549 元素个数排序 简单题 1550 Fiber Communications 1551 Power Hungry Cows 搜索：BFS 1552 Cow Cycling 动态规划 1553 Rebuilding Roads 树型DP 1554 Triangular Pastures 动态规划 1555 Chores 动态规划 1556 Extra Krunch1557 BUY LOW, BUY LOWER 动态规划 1558 Hypnotic Milk Improvement 1559 Happy Cows1560 Unary Cow Counting 1561 Dairy Route 1562 Calf Numbers 1563 Hide and Seek 1564 Mountain Majesties 1565 Secret Milk Pipes 1566 Circus Tickets 1567 Life Cycle 1568 Wiggle Numbers 1569 Superwords 1570 Cow Brainiacs 1571 Pasture Fences 1572 New Years Party 1573 Strolling Cows 1574 Grazing Sets 1575 Factorial Power 1576 Friday the Thirteenth 1577 Beef McNuggets 1578 Calf Flac 1579 Light Bulbs 1580 Cow Math 图论1581 Cow Imposters 动态规划 1582 Traffic Lights 递推求解 1583 Farm Tour 图论：最短路径 1584 Vertical Histogram 简单题 1585 Cowties 动态规划 1586 Travel Games 搜索：DFS1587 Best Cow Fences 二分法 1588 Cornfields RMQ 问题 1589 Six Degrees of Cowvin Bacon 简单题 1590 Herd Sums 简单题1591 Message Decoding 简单题1592 Mountain Walking 二分+flood fill 1593 Millenium Leapcow 动态规划 1594 Optimal Milking 最大流+二分法1595 Bale Figures 模拟+二分法1596 Jumping Cows 动态规划 1597 Lost Cows SBT 树1598 Bovine Math Geniuses 简单题 1599 Dividing the Path 动态规划 1600 Fence Obstacle Course 动态规划 1601 Cow Ski Area 图论：flood fill 1602 Cleaning Shifts 贪心法 1603 Bad Cowtractors 最大生成树 1604 Tree Cutting 树状动态规划 1605 Navigation Nightmare 并查集 1606 Cow Marathon 树状动态规划 1607 Distance Queries LCA ，tarjan 算法 1608 Distance Statistics 楼天成大牛“男人八题”中的一道 1609 Moo University - Team Tryouts 排序+穷举法 1610 Moo University - Emergency Pizza Order 1611 Moo University - Financial Aid 最大堆、最小堆 1612 Cube Stacking 并查集 1613 The Cow Lineup 穷举法 1614 MooFest 线段树1615 Turning in Homework 动态规划 1616 Alignment of the Planets 1617 Finding Bovine Roots 1618 Cow Bowling1619 Cow Patterns 字符串匹配的扩展 1620 Barn Expansion 二分查找 1621 Layout 差分约束系统 1622 Knights of Ni 搜索：BFS 1623 Cleaning Shifts DP ＋Heap 1624 Scales 搜索+剪枝1625 Secret Milking Machine 二分+网络流 1626 Aggressive cows 二分法1627 Rigging the Bovine Election 穷举法 1628 Feed Accounting 简单模拟题1629 Muddy Fields 穷举法1630 The Wedding Juicer 堆+flood fill 1631 Naptime 动态规划 1632 Sumsets 动态规划1633 Moo Volume 简单题1634 Ombrophobic Bovines Floyd-Warshall 1635 Space Elevator 动态规划1636 Yogurt factory 动态规划 1637 Checking an Alibi 最短路径 1638 Out of Hay 1639 Satellite Photographs 搜索：BFS or DFS 1640 Asteroids 最大网络流 1641 Grazing on the Run 动态规划1642 Walk the Talk 动态规划1643 City Skyline 栈的应用 1644 Cow Acrobats 贪心法1645 Ant Counting 动态规划 1646 Hopscotch 搜索：DFS1647 Securing the Barn 穷举法 1648 Bovine Birthday 递推求解 1649 Max Factor 简单题 1650 Flying Right 1651 Close Encounter 1652 Allowance 1653 Lazy Cows 1654 Expedition 1655 Around the world 1656 Landscaping 1657 Waves1658 Navigating the City1659 Disease Management 1660 Muddy roads 1661 Wormholes 最短路径 1662 The Fewest Coins 动态规划 1663 Milk Patterns 二分法or 后缀树1664 Cow Picnic 搜索：BFS or DFS 1665 Cow Roller Coaster 动态规划 1666 River Hopscotch 二分法+贪心 1667 The Moronic Cowmpouter 进制转换 1668 DNA Assembly 穷举法1669 Cow Phrasebook 二分法 1670 Cellphones 穷举法1671 Steady Cow Assignment 网络流 1672 Treats for the Cows 动态规划 1673 Backward Digit Sums 穷举法 1674 Stump Removal 简单题 1675 Finicky Grazers 动态规划 1676 The Water Bowls 枚举二进制位 1677 Redundant Paths 图论 1678 Roping the Field 动态规划 1679 Corral the Cows 二分法 1680 The Cow Prom 图论 1681 Dollar Dayz 动态规划 1682 The Grove 最短路径 1683 Fence Repair Huffman 编码 1684 Corn Fields 状态压缩DP 1685 Roadblocks 图论：最短路径 1686 Bad Hair Day 搜索 1687 Big Square 穷举法 1688 Round Numbers 枚举二进制位 1689 Building A New Barn 1690 Cow Sorting 置换群 1691 Lilypad Pond 最短路径 1692 The Cow Lexicon 动态规划 1693 Silver Cow Party 最短路径 1694 Problem Solving 动态规划 1695 Cow School1696 Protecting the Flowers 贪心法 1697 Tallest Cow 区间统计 1698 Balanced Lineup RMQ 问题1699 Gold Balanced Lineup RMQ 问题 1700 Ranking the Cows 搜索：DFS 1701 Face The Right Way 穷举法 1702 Cow Traffic 动态规划 1703 Monthly Expense 贪心法 1704 Cheapest Palindrome 动态规划 1705 Dining 贪心+网络流 1706 City Horizon 离散化+ 扫描 1707 Catch That Cow 最短路径 1708 Fliptile 枚举+位压缩 1709 2-Dimensional Rubik's Cube 搜索：BFS 1710 Ball 计算几何1711 3D Camera 三维计算几何 1712 Cipher 模拟题1713 Five in a Row 简单题 1714 Pinhole Imaging 简单计算几何1715 URL 模拟题 1716 Battle of Submarines 集合DP 1717 WOJ 动态规划 1718 钥匙计数之二 递推求解 1719 BrokenLED 模拟题 1722 A+B again and again! 模拟题 1723 Just calculate it! 数论 1724 Guess how much I love you? 简单题 1725 NBA Finals 1726 Find Out an “E” 1727 Judging ACM/ICPC 1728 Cryptography of Alex 1729 Rings of square grid 1730 Fermat's Theorem 1731 Cup 二分法1732 Find the Path DP+二分法1733 Five in a Row, Again 动态规划 1734 Minimum Heap 递推求解1735 Name PK 模拟题 1736 Pendant 动态规划 1737 Radar 计算几何+搜索 1738 Ring 多串模式匹配 1739 Run 计算几何1740 Toxophily 简单题 1741 通讯录编排 简单题 1742 超缘分ACM 队伍 简单题1743 集合运算 简单题 1744 矩阵计算 简单题1745 Arbitrage 动态规划1746 The Tower of Babylon 动态规划 1747 Binomial Showdown 组合数学 1748 Dungeon Master 搜索：BFS1749 Equation Solver 表达式求值应用 1750 Frogger 最短路径 1751 Globetrotter 计算几何1752 Tree Recovery 数据结构：二叉树 1753 Artificial Intelligence? 1754 The Settlers of Catan 搜索 1755 France '98 概率问题1756 Goldbach's Conjecture 数论 1757 Heavy Cargo 最小生成树 1758 Quadtree1759 From Dusk till Dawn or: Vladimir the Vampir1760 Euro Cup 2000 1761 Quadtree II or: Florida Jones strikes back 1762 HTML 简单题1763 Paths on a Grid 组合数学：T 路问题 1764 Balanced Food 动态规划1765 California Jones and the Gate to Freedom 组1766 Diplomatic License 简单计算几何题 1767 Polygon Programming with Ease 数学题 1768 Hall of Fountains 搜索：BFS or DP1769 The Bottom of a Graph 图论：强连通分量 1770 Edge 1771 Fold1772 Largest Rectangle in a Histogram 动态规划 1773 Boolean Logic 1774 Code1775 In Danger 模拟题 1776 Fractran1777 Huffman's Greed 1778 Bullshit Bingo 字符串处理 1779 A Song contest 1780 Message1781 The skatepark's new ramps 1782 Road 1783 Warfare 1784 Blackjack 1785 Robintron1786 Diamond Dealer 计算几何：凸包 1787 Best Compression Ever 1788 Code Theft 1789 Dinner1790 Event Planning 1791 Getting Gold 1792 Introspective Caching1793 Just A Few More Triangles! 1794 Knights of the Round Table 图论：无向图的块1795 The Cow Doctor 穷举法1796 Wild West 线段树1797 Find the Clones 1798 The Warehouse1799 Widget Factory 数论：同余方程组1800 Martian Mining 动态规划 3301 字符串；AC 自动机， 动态规划；状态压缩3302 计算几何 3303 数学；代数运算；高斯消元 3304 图论；强连通分量；2-SAT 3305 动态规划；凸单调性优化 3306 枚举 3307 贪心3308 数学；代数运算 3309 最短路；佛洛伊德 3310 动态规划 3311 贪心3312 计数问题；递推，数状数组，二分查找 3313 数论；欧拉定理，快速幂取模 3314 计数问题，数状数组3315 博弈；Surreal 数；Farey 数列； 3316 计数问题；递推，高精度 3317 计数问题；容斥原理 3318 递推；矩阵乘法 3319 数学；概率 3320 背包 3321 动态规划3322 字符串；AC 自动机 3323 动态规划 3324 博弈 3325 搜索 3326 贪心 3327 最短路3328 数据结构（实现一种数据结构，支持要求的操作），数状数组 3329 图论；二分图最大权匹配 3330 数学；数论 3331 递推；矩阵乘法 3332 数学；数论，二分查找 3333 计算几何 3334 动态规划3335 字符串，后缀数组或拉宾卡普；动态规划 3336 数据结构；并查集 3337 计数问题，递推 3338 二分查找，贪心 3339 数学 3340 计算几何；凸包，图论；佛洛伊德；最小环 3341 动态规划 3342 广搜 3343 动态规划 3344 计算几何 3345 二分图最大匹配3346 树型DP 3347 动态规划 3348 数学；数论；进制 3349 计数问题 3350 贪心3351 数学；数论；进制 3352 动态规划，数论，组合数学 3353 数学；数论 3354 计数；递推 3355 图论；佛洛伊德3356 博弈 3357 动态规划 3358 数据结构；线段树，数状数组3359 计算几何，动态规划 3360 博弈；SG 函数 3361 图论；最近公共祖先 3362 图论；强连通分量；2－SAT 3363 计算几何3364 字符串；AC 自动机，动态规划 3365 搜索，舞蹈链 3366 数学；数论3367 数学；代数运算；高斯消元 3368 动态规划 3369 计数问题；递推 3370 网络流（错题） 3371 树型DP3372 数学；高精度 3373 数学； 3374 RMQ 3376 数学；进制 3377 字符串；后缀数组 3378 动态规划 3379 计算几何 3380 线段树3381 图论；欧拉路 3382 简单题3383 字符串；AC 自动机 3384 广搜 3385 计算几何，矩阵3386 语言处理3387 动态规划；状态压缩 3388 图论；全局最小割 3389 简单题 3390 广搜3391 数学；Pell 方程 3392 背包 3393 计算几何 3394 广搜3395 搜索；迭代加深 3396 数学；计数问题 3397 数学；解方程3398 分析 3399 模拟3400 数学；计数问题，数论。

1089：输入不说明有多少个Input Block,以EOF为结束标志。

#include <stdio.h>int main(){int a,b;while(scanf("%d %d",&a, &b) != EOF)printf("%d\n",a+b);}1090：输入一开始就会说有N个Input Block,下面接着是N个Input Block。

#include <stdio.h>int main(){int n,i,a,b;scanf("%d",&n);for(i=0;i<n;i++){scanf("%d %d",&a, &b);printf("%d\n",a+b);}}1091：输入不说明有多少个Input Block,但以某个特殊输入为结束标志。

#include <stdio.h>int main(){int a,b;while(scanf("%d %d",&a, &b)&&(a!=0 || b!=0))printf("%d\n",a+b);}1096：一个Input Block对应一个Output Block，Output Block之间有空行。

#include <stdio.h>int main(){int icase,n,i,j,a,sum;scanf("%d",&icase);for(i=0;i<icase;i++){sum=0;scanf("%d",&n);for(j=0;j<n;j++){scanf("%d",&a);sum+=a;}if(i<icase-1)printf("%d\n\n",sum);elseprintf("%d\n",sum);}}I.求两个数的最小值：#include "stdafx.h"int main(){ int a, b;scanf("%d%d",&a,&b);if(a>b){printf("%d\n",b);}elseprintf("%d\n",a);}II.输入n个数，找出n个数中的最大值。

acm考试题库及答案1. 题目一：数组的最大子序列和问题描述：给定一个整数数组，请找出该数组中连续子数组的最大和。

答案：可以使用动态规划的方法解决此问题。

首先初始化一个变量`maxSoFar`用来存储遍历过程中的最大和，以及一个变量`maxEndingHere`用来存储以当前元素结尾的最大子数组和。

遍历数组，对于每个元素，更新`maxEndingHere`，如果`maxEndingHere`变为负数，则重置为0。

同时，每次更新`maxSoFar`为`maxSoFar`和`maxEndingHere`中的较大值。

遍历结束后，`maxSoFar`即为所求的最大子序列和。

2. 题目二：无重复字符的最长子串问题描述：给定一个字符串，请找出其中不含有重复字符的最长子串的长度。

答案：可以使用滑动窗口的方法来解决这个问题。

维护一个窗口，记录窗口内字符的出现情况，当遇到重复字符时，移动窗口的左边界，直到窗口内没有重复字符。

同时记录并更新最长子串的长度。

3. 题目三：合并两个有序链表问题描述：给定两个按非递减顺序排列的链表，合并这两个链表并使新链表中的节点仍然是按非递减顺序排列。

答案：可以使用迭代的方法来合并两个链表。

创建一个虚拟头节点`prehead`，然后使用一个指针`prev`指向`prehead`。

遍历两个链表，比较当前节点的值，将较小的节点连接到`prev`后面，并移动`prev`。

最后，将非空链表的剩余部分连接到合并后的链表后面。

4. 题目四：寻找旋转排序数组中的最小值问题描述：假设按照升序排序的数组在某个点上进行了旋转，形成最大值左边的元素都比右边的元素大的数组。

给定这样一个旋转排序数组，找出其中的最小值。

答案：可以使用二分查找的方法来解决这个问题。

首先判断数组是否旋转，然后根据旋转点将数组分为两部分，一部分有序，另一部分无序。

在有序部分使用二分查找，如果中间元素小于其前一个元素，则最小值在中间元素的右边；否则，在左边。