Dynamical localization, measurements and quantum computing

1/4波片quarter-wave plateCG矢量耦合系数Clebsch-Gordan vector coupling coefficient; 简称“CG[矢耦]系数”。

X射线摄谱仪X-ray spectrographX射线衍射X-ray diffractionX射线衍射仪X-ray diffractometer[玻耳兹曼]H定理[Boltzmann] H-theorem[玻耳兹曼]H函数[Boltzmann] H-function[彻]体力body force[冲]击波shock wave[冲]击波前shock front[狄拉克]δ函数[Dirac] δ-function[第二类]拉格朗日方程Lagrange equation[电]极化强度[electric] polarization[反射]镜mirror[光]谱线spectral line[光]谱仪spectrometer[光]照度illuminance[光学]测角计[optical] goniometer[核]同质异能素[nuclear] isomer[化学]平衡常量[chemical] equilibrium constant[基]元电荷elementary charge[激光]散斑speckle[吉布斯]相律[Gibbs] phase rule[可]变形体deformable body[克劳修斯-]克拉珀龙方程[Clausius-] Clapeyron equation[量子]态[quantum] state[麦克斯韦-]玻耳兹曼分布[Maxwell-]Boltzmann distribution[麦克斯韦-]玻耳兹曼统计法[Maxwell-]Boltzmann statistics[普适]气体常量[universal] gas constant[气]泡室bubble chamber[热]对流[heat] convection[热力学]过程[thermodynamic] process[热力学]力[thermodynamic] force[热力学]流[thermodynamic] flux[热力学]循环[thermodynamic] cycle[事件]间隔interval of events[微观粒子]全同性原理identity principle [of microparticles][物]态参量state parameter, state property[相]互作用interaction[相]互作用绘景interaction picture[相]互作用能interaction energy[旋光]糖量计saccharimeter[指]北极north pole, N pole[指]南极south pole, S pole[主]光轴[principal] optical axis[转动]瞬心instantaneous centre [of rotation][转动]瞬轴instantaneous axis [of rotation]t 分布student's t distributiont 检验student's t testＫ俘获K-captureＳ矩阵S-matrixＷＫＢ近似WKB approximationＸ射线X-rayΓ空间Γ-spaceα粒子α-particleα射线α-rayα衰变α-decayβ射线β-rayβ衰变β-decayγ矩阵γ-matrixγ射线γ-rayγ衰变γ-decayλ相变λ-transitionμ空间μ-spaceχ 分布chi square distributionχ 检验chi square test阿贝不变量Abbe invariant阿贝成象原理Abbe principle of image formation阿贝折射计Abbe refractometer阿贝正弦条件Abbe sine condition阿伏伽德罗常量Avogadro constant阿伏伽德罗定律Avogadro law阿基米德原理Archimedes principle阿特伍德机Atwood machine艾里斑Airy disk爱因斯坦-斯莫卢霍夫斯基理论Einstein-Smoluchowski theory 爱因斯坦场方程Einstein field equation爱因斯坦等效原理Einstein equivalence principle爱因斯坦关系Einstein relation爱因斯坦求和约定Einstein summation convention爱因斯坦同步Einstein synchronization爱因斯坦系数Einstein coefficient安[培]匝数ampere-turns安培[分子电流]假说Ampere hypothesis安培定律Ampere law安培环路定理Ampere circuital theorem安培计ammeter安培力Ampere force安培天平Ampere balance昂萨格倒易关系Onsager reciprocal relation凹面光栅concave grating凹面镜concave mirror凹透镜concave lens奥温电桥Owen bridge巴比涅补偿器Babinet compensator巴耳末系Balmer series白光white light摆pendulum板极plate伴线satellite line半波片halfwave plate半波损失half-wave loss半波天线half-wave antenna半导体semiconductor半导体激光器semiconductor laser半衰期half life period半透[明]膜semi-transparent film半影penumbra半周期带half-period zone傍轴近似paraxial approximation傍轴区paraxial region傍轴条件paraxial condition薄膜干涉film interference薄膜光学film optics薄透镜thin lens保守力conservative force保守系conservative system饱和saturation饱和磁化强度saturation magnetization本底background本体瞬心迹polhode本影umbra本征函数eigenfunction本征频率eigenfrequency本征矢[量] eigenvector本征振荡eigen oscillation本征振动eigenvibration本征值eigenvalue本征值方程eigenvalue equation比长仪comparator比荷specific charge; 又称“荷质比(charge-mass ratio)”。

PHYSICAL REVIEW B94,241110(R)(2016)Hubbard band versus oxygen vacancy states in the correlated electron metal SrVO3S.Backes,1T.C.R¨o del,2,3F.Fortuna,2E.Frantzeskakis,2P.Le F`e vre,3F.Bertran,3M.Kobayashi,4R.Yukawa,4 T.Mitsuhashi,4M.Kitamura,4K.Horiba,4H.Kumigashira,4R.Saint-Martin,5A.Fouchet,6B.Berini,6Y.Dumont,6A.J.Kim,1F.Lechermann,7,8H.O.Jeschke,1M.J.Rozenberg,9R.Valent´ı,1,*and A.F.Santander-Syro2,†1Institut f¨u r Theoretische Physik,Goethe-Universit¨a t Frankfurt,Max-von-Laue-Strasse1,60438Frankfurt am Main,Germany 2CSNSM,Univ.Paris-Sud,CNRS/IN2P3,Universit´e Paris-Saclay,91405Orsay Cedex,France3Synchrotron SOLEIL,L’Orme des Merisiers,Saint-Aubin-BP48,91192Gif-sur-Yvette,France 4Photon Factory,Institute of Materials Structure Science,High Energy Accelerator Research Organization(KEK),1-1Oho,Tsukuba305-0801,Japan5SP2M-ICMMO-UMR-CNRS8182Universit´e Paris-Sud,Universit´e Paris-Saclay,91405Orsay Cedex,France 6GEMaC,Universit´e de Versailles St.Quentin en Y.-CNRS,Universit´e Paris-Saclay,Versailles,France7Institut f¨u r Theoretische Physik,Universit¨a t Hamburg,Jungiusstrasse9,20355Hamburg,Germany8Institut f¨u r Keramische Hochleistungswerkstoffe,TU Hamburg-Harburg,D-21073Hamburg,Germany 9Laboratoire de Physique des Solides,CNRS,Univ.Paris-Sud,Universit´e Paris-Saclay,91405Orsay Cedex,France(Received22February2016;published19December2016)We study the effect of oxygen vacancies on the electronic structure of the model strongly correlatedmetal SrVO3.By means of angle-resolved photoemission spectroscopy(ARPES)synchrotron experiments,we investigate the systematic effect of the UV dose on the measured spectra.We observe the onset of a spuriousdose-dependent prominent peak at an energy range where the lower Hubbard band has been previously reportedin this compound,raising questions on its previous interpretation.By a careful analysis of the dose-dependenteffects we succeed in disentangling the contributions coming from the oxygen vacancy states and from the lowerHubbard band.We obtain the ARPES spectrum in the limit of a negligible concentration of vacancies,wherea clear signal of a lower Hubbard band remains.We support our study by means of state-of-the-art ab initiocalculations that include correlation effects and the presence of oxygen vacancies.Our results underscore therelevance of potential spurious states affecting ARPES experiments in correlated metals,which are associatedwith the ubiquitous oxygen vacancies as extensively reported in the context of a two-dimensional electron gas atthe surface of insulating d0transition metal oxides.DOI:10.1103/PhysRevB.94.241110Introduction.A major challenge of modern physics is to understand the fascinating phenomena in strongly correlated transition metal oxides(TMOs),which emerge in the neighbor-hood of the Mott insulator state.Some preeminent examples that have gathered interest for almost30years are high temperature superconductivity,colossal magnetoresistance, heavy fermion physics,and,of course,the Mott metal-insulator transition itself[1].Significant theoretical progress was made with the introduction of dynamical meanfield theory (DMFT)and its combination with ab initio density functional methods[local density approximation(LDA)+DMFT],which allows treatment of the interactions promoting itinerancy and localization of electrons on equal footing[2–4].Among the most emblematic achievements of DMFT is the prediction of a Hubbard satellite,which separates from the conduction band of a metal.This satellite results from the partial localization of conduction electrons due to their mutual Coulomb repulsion. Early DMFT studies also showed that it is the precursor of the localized electronic states of a Mott insulator[5].Since then,these predictions promoted a large number of studies using photoemission spectroscopy,which is a technique to directly probe the presence of Hubbard bands.In this context, the TMO system SrVO3has emerged as the drosophila model system to test the predictions of strongly correlated electron *valenti@itp.uni-frankfurt.de†andres.santander@csnsm.in2p3.fr theories.In fact,SrVO3is arguably the simplest correlated metal.It is a simple cubic perovskite,with nominally one electron per V site,which occupies a threefold degenerate t2g conduction band.While the presence of a satellite in the photoemission spectra of Ni metal was already well known,in the context of correlated TMOs,the Hubbard band was originally reported in a systematic investigation of Ca1−x Sr x VO3[6],which was followed by many subsequent studies,including angle-resolved photoemission spectroscopy (ARPES)[7–9]and comparisons with theoretical predictions (see,for instance,Refs.[10–20],among others).One of the most salient features in SrVO3is the observation of a broad peak at an energy of about−1.5eV in angle integrated photoemission spectra(upper black curve in Fig.1), which is interpreted as a Hubbard satellite linked to the V t2g electrons.This feature is also seen in a large range of 3d1materials[21,22].The ratio of spectral strength between the quasiparticle(QP)state and the incoherent satellite in SrVO3is an important indicator of the magnitude of electron correlations[1,2].However,photoemission experiments using different photon energies or light brilliance have reported very dissimilar values for such a ratio[11],making the quantitative benchmarking of realistic ab initio theories for correlated electron systems difficult[6,11,18,23,24].Moreover,as shown in Fig.1,a broad peak at about the same energy is also observed in several d0TMO cubic perovskites,such as SrTiO3, KTaO3,or anatase TiO2.Nevertheless,in all these cases the feature has been clearly linked to the presence of oxygenS.BACKES et al.PHYSICAL REVIEW B94,241110(R)(2016)FIG.1.Integrated UV photoemission spectra for various per-ovskite oxides,showing a quasiparticle peak at E F and an in-gap state at energies between1and1.5eV.For SrVO3(upper black curve),a correlated-electron metal,the QP peak corresponds to the bulk conduction band,and as will be shown further,the in-gap state is a superposition of the lower Hubbard band and localized electronic states associated with oxygen vacancies.For the other d0 oxides,such as KTaO3(blue curve),anatase TiO2(green curve), or SrTiO3(red curve),the QP peak and in-gap state correspond respectively to a confined quasi-2D electron gas at the sample surface and to localized states,all formed by oxygen vacancies.The crystal orientation(normal to the samples’surface)is indicated in all cases. defects[25–32].Interestingly,recent ab initio calculations show that the spectral weight at−1.3eV in SrTiO3most likely is not of Ti t2g orbital character,but should be understood as an in-gap defect state with Ti e g character[33–36].Thus,we are confronted with the fact that at about1.5eV below the Fermi level(E F),wefind the lower Hubbard bands of d1systems as well as the in-gap states of oxygen-deficient d0systems.In view of these observations one may unavoidably wonder(and worry),despite the great success of DMFT methods,whether the putative Hubbard satellite of SrVO3might also originate from oxygen vacancy states.Moreover,one should also worry about the possibility of these extrinsic states affecting the features of the conduction band dispersion.In the present Rapid Communication we resolve these issues in a thorough manner.We present a systematic photoemission study of SrVO3,to demonstrate dramatic consequences in the spectra due to the creation of oxygen ing ARPES,we directly show that the UV or x-rays used for measurements can produce a large enhancement, of almost an order of magnitude,of the peak at−1.5eV, similar to the effect observed in d0oxide insulators[25–28,37].Despite these significant effects on the energy states around the Mott-Hubbard band,we are able to determine the bulk SrVO3photoemission spectrum in the limit of a negligible concentration of vacancies,where a clear signal of the dispersive correlated Hubbard band remains.We support the interpretation of the experimental data by means of state-of-the-art LDA+DMFT calculations on SrVO3with oxygen vacancies.Consistent with our experimental data,the calculations show that oxygen vacancies produce states(of e g symmetry)at energies near the Hubbard satellite.While our study provides definite evidence of a correlated Hubbard band in SrVO3as predicted by DMFT,it also underlines the significant effects due to oxygen vacancies,which may also affect photoemission data in other TMOs.Methods.The bulk-like relaxed,crystalline(001)oriented SrVO3thinfilms were grown by pulsed laser deposition (PLD)either at the GEMaC laboratory,then measured at the CASSIOPEE beamline of Synchrotron SOLEIL,or in a PLD chamber directly connected to the ARPES setup at beamline2A of KEK-Photon Factory(KEK-PF)[9,38,39]. To clean the surfaces in UHV prior to ARPES experiments at SOLEIL,the SrVO3thinfilms were annealed at550◦C for t=5–20min at pressures lower than2×10−8Torr.At KEK-PF,the PLD growth was performed under a pressure below10−7Torr,to obtain UHV-clean surfaces,using a Sr2V2O7target,which has excess oxygen with respect to SrVO3,thus minimizing the formation of vacancies during the growth.In all cases,the surface quality was confirmed right before ARPES measurements by low-energy electron diffraction(LEED).The thinfilms measured at KEK-PF showed a c(4×4)surface reconstruction,which does not affect the analysis and conclusions of this work.For the ARPES measurements we used linearly polarized photons in the energy range30–110eV and hemispherical electron analyzers with vertical slits at SOLEIL and horizontal slits at KEK-PF.The angular and energy resolutions were0.25◦and 15meV.The mean diameter of the incident photon beam was smaller than100μm.The UV light brilliance,measured using calibrated photodiodes,was≈5×109photons s−1μm−2at SOLEIL,and about100times smaller at KEK-PF.The samples were cooled down to T=20K before measuring.Unless specified otherwise,all data were taken at that temperature. The results were reproduced on more thanfive samples.All through this Rapid Communication,directions and planes are defined in the cubic unit cell of SrVO3.We denote [hkl]the crystallographic directions in real space, hkl the corresponding directions in reciprocal space,and(hkl)the planes orthogonal to those directions.The indices h,k,and l of hkl correspond to the reciprocal lattice vectors of the cubic unit cell of SrVO3.The Supplemental Material[40]presents further details about the sample growth and measurements.Experimental results.Figure2(a)shows the integrated photoemission spectra of SrVO3as a function of the UV dose, measured at CASSIOPEE SOLEIL under the same conditions of light brilliance of any standard ARPES experiment at a third-generation synchrotron.The measurements were done by continuously irradiating the sample with hν=33eV photons while recording the spectra as a function of irradiation time, with an accumulation time of about2min per spectrum.The blue and black curves show spectra for the lowest and highest measured doses,obtained respectively after∼2min and∼2h of irradiation.These data clearly demonstrate that the very UV or x-rays used for photoemission experiments can produce radical changes in the measured spectra of SrVO3.Note in fact that a similar effect has been observed for VO2[41].In particular,from Fig.2(a)we observe that the amplitude ofHUBBARD BAND VERSUS OXYGEN V ACANCY STATES IN THE...PHYSICAL REVIEW B94,241110(R)(2016)FIG.2.(a)Photoemission spectra of SrVO3as a function of UV dose,measured at Synchrotron SOLEIL(hν=33eV).The energy distribution curves(EDCs)were extracted from raw ARPES data around the 002point integrated along the k= 010 direction.(b)Corresponding momentum distribution curves(MDCs)integrated over50meV below E F.Peaks in the MDCs indicate the Fermi momenta.(c),(d)Same as(a),(b)for SrTiO3(hν=47eV).Thefilling of a2DEG upon UV irradiation is evidenced by the formation of QP peaks in the EDCs and MDCs at E F[inset of(c)and(d),respectively].All data were taken at20K.the in-gap state at−1.5eV,and,more significantly,the ratio of in-gap to quasiparticle(QP)amplitudes,strongly increase with increasing UV dose,going from about1:3in a pristine sample to more than2:1in a heavily irradiated sample. Importantly,note that the QP peak position remains basically dose independent,implying that the carriers created by the UV or x irradiation do not significantly dope the conduction band,and form dominantly localized states.This is confirmed in Fig.2(b),which shows that the Fermi momenta of the QP band,given by the peak positions in the momentum distribution curves(MDCs)at E F,are also dose independent. Additional data presented in the Supplemental Material further demonstrate that our measurements yield the expected3D bulk Fermi surface of SrVO3.Thus,the observed increase in intensity of the in-gap state upon UV irradiation cannot be ascribed to a change infilling of the conduction band,which could have affected the electron correlations.Instead,this unambiguously shows the light-assisted formation of localized defect states at essentially the same energy as that of the expected intrinsic lower Hubbard band—which should then resemble the in-gap peak observed at the lowest UV doses.In fact,as mentioned previously,it is well established that strong doses of UV or x-rays create a large concentration of oxygen vacancies in several d0perovskites[25–32,42]. As illustrated in Figs.2(c)and2(d)for the case of SrTiO3, the progressive doping of the surface region with oxygen vacancies,due to synchrotron UV irradiation,has two effects: the formation of a very intense in-gap state at about−1.3eV, and,in contrast to SrVO3,the simultaneous creation of a sharp QP peak at E F corresponding to a confined quasi-2D electron gas(2DEG)at the samples’surface.The effective mass of such2DEG,precisely determined by ARPES,matches the mass expected from density functional theory calcula-tions[25,26,43,44].Thus,as in SrVO3,the increase in intensityof the in-gap state observed in SrTiO3upon UV or x irradiationcannot be due to an onset or increase of electron correlations,and should be ascribed to an extrinsic effect.We therefore conclude that,in SrVO3,exposure to syn-chrotron UV or x-rays creates oxygen vacancies,which are inturn responsible for the extrinsic increase in intensity of thein-gap state evidenced by our measurements.This effect canseriously obscure the determination of the spectral function ofthis model system,thus hampering the advancement of validtheories for correlated electron systems.Thefindings described above imply that the correct ex-perimental determination of the vacancy-free photoemissionspectrum of SrVO3should(i)use samples that from thebeginning have the lowest possible concentration of oxygenvacancies,and(ii)use doses of UV or x-ray light low enoughto avoid light-induced changes in the measured spectra.Tothis end,we measured SrVO3thinfilms grown directly insitu at beamline2A of KEK-PF.As mentioned before,the growth protocol of such thinfilms minimizes the formationof vacancies,while the UV light brilliance at KEK-PF is ∼100times smaller than the one in Figs.2(a)and2(b)from measurements at SOLEIL.We checked(see the SupplementalMaterial)that under these conditions the spectra did notchange with time,even after several hours of measurements.The resulting energy-momentum ARPES map,and its secondderivative,are presented in Figs.3(a)and3(b).One clearlyobserves the dispersing QP band along with an also dispersivein-gap state of weaker intensity,corresponding to the intrinsiclower Hubbard band,as reported in previous works[7].Theintrinsic spectral function of SrVO3will then be given by such aphotoemission spectrum,which approaches the vacancy-freelimit,modulo dipole-transition matrix elements,inherent toS.BACKES et al.PHYSICAL REVIEW B94,241110(R)(2016)FIG.3.(a)Energy-momentum ARPES intensity map measured at KEK-PF with a low UV dose on a SrVO3sample prepared in situ,using a well-established protocol to minimize the formation of oxygen vacancies(see the main text and Supplemental Material).Note that due to the choice of light polarization,the heavy bands along(100)are not observed and only the contribution of the light d xy band is detected.The data were acquired at hν=88eV around ¯103.(b)Second derivative(negative values)of the map in(a).The use of second derivatives allows a better visualization of the dispersion of both the quasiparticle and Mott-Hubbard bands on the same color plot.The dispersionless feature at E F is a spurious effect of such a second derivative on the Fermi-Dirac cutoff.(c),(d)Same as(a),(b)after a strong UV irradiation dose,measured at SOLEIL(hν=33eV),typical of modern third-generation synchrotrons.The measurements were done at hν=33eV close to 002.All data were taken at20K.Note that at constant photon energy,ARPES maps out the electronic structure at a spherical surface of three-dimensional (3D)k space,which can be locally approximated to a plane for all our measurements(details in the Supplemental Material).The different choice of photon energies and k-space positions for measurements at KEK-PF[(a)and(b)]and SOLEIL[(c)and(d)]was dictated by the different geometrical configurations and constraints of the beamlines in both synchrotrons.the photoemission process,which can still modulate the intensity of the QP peak relative to the Hubbard peak.A calculation of such matrix elements requires a full one-step calculation of the photoemission process,which is beyond the scope of this work.By contrast,Figs.3(c)and3(d) show the momentum-resolved electronic structure of a sample, measured at SOLEIL,that was intensively irradiated.There, the peak at−1.5eV becomes broader,more intense,and nondispersive—all characteristic signatures of a high random concentration of oxygen vacancies.Numerical calculations.To rationalize from a microscopic point of view the influence of oxygen vacancies on the electronic structure of SrVO3,we performed charge self-consistent LDA+DMFT calculations for bulk SrVO3and var-ious relaxed oxygen-deficient SrVO3supercells.The latter are computationally demanding calculations.We shall focus here on the case of a2×2×3supercell with two oxygen vacancies located at opposite apical sites of one vanadium atom,as shown in the inset of Fig.4(b).We use such a vacancy arrangement as it is the prototypical one for d0compounds[43].For our LDA+DMFT calculations we chose values of U= 2.5eV and J=0.6eV for vanadium and included the effects of bandwidth renormalization due to dynamically screened Coulomb interactions by following the prescription suggested in Ref.[45](the LDA+DMFT unrenormalized data are shown in the Supplemental Material).In Figs.4(a)and4(c)we show, respectively,the results of the k-integrated and k-resolved spectral functions for bulk SrVO3without oxygen vacancies. Wefind the expected features of a t2g quasiparticle peak at the Fermi level and a lower Hubbard band at negative energies of the same t2g nature,in agreement with the photoemission spectra in Fig.2(a)and Figs.3(a)and3(b).The light band at E F along k 100 [Fig.4(c)]consists of two degenerate bands of d xy and d xz characters,while the heavy band along the same direction has d yz character.While comparing with the measured k-resolved spectral function[Figs.3(a)and3(b)],HUBBARD BAND VERSUS OXYGEN V ACANCY STATES IN THE...PHYSICAL REVIEW B94,241110(R)(2016)FIG.4.LDA+DMFT results for SrVO3including bandwidth renormalization effects[45].(a)k-integrated spectral function for bulk SrVO3.The V t2g orbitals show a quasiparticle peak at E F and a lower Hubbard band at−1.6eV.(b)Spectral function for the2×2×3supercell of SrVO3with two oxygen vacancies.An additional nondispersive V e g vacancy state originating from the V atom neighboring the oxygen vacancies leads to a sharp peak below the Fermi level at∼−1.0eV.The V t2g orbitals show a quasiparticle peak at E F and a lower Hubbard band at−1.8eV.(c)and(d)show the corresponding spectral functions(multiplied by a Fermi-Dirac function at20K)along the X- -X path.one should bear in mind that along -X(or -Y)the heavy d yz(or d xz)bands are silenced by dipole-transition selection rules in the experiment[25].Inclusion of bandwidth renormalization[45]renders the lower Hubbard band at an energy(−1.6eV)in reasonable agreement with experiment (−1.5eV).We adopted typical values for U and J from the literature.We did not attempt to further optimize the values to get a better quantitative agreement with the experimental data, for two reasons:First is the heavy numerical cost,and second, as we show next in the calculations with oxygen vacancies, the adopted values facilitate the distinct visualization of the contributions from the Hubbard and localized states to the incoherent peak at∼−1.5eV.The removal of oxygen atoms in the system leads to the donation of two electrons per oxygen to its surrounding. Already at the level of density functional theory(DFT)in the local density approximation(LDA)(see the Supplemental Material),wefind that most of the charge coming from the additional electrons is transferred to the3d z2orbitals of the neighboring V atom,developing into a sharp peak of e g symmetry located around−1.0eV,i.e.,at an energy close to the position of the experimentally observed oxygen vacancy states.In analogy to the experimental average over many lattice sites,note that averaging among various supercells with differentoxygen vacancy locations and concentrations(which is beyondthe scope of the present work)would result in a wider in-gape g band,as demonstrated for the case of SrTiO3(see Fig.3ofRef.[34])and for some cases in SrVO3(see the SupplementalMaterial,Fig.S7).By including electronic correlations within(bandwidth renormalized)LDA+DMFT we then see that allthe experimental observations qualitatively emerge.In fact,the conducting t2g orbitals develop a lower Hubbard bandpeaked at energies about−1.8eV[Figs.4(b)and4(d)],similarto the bulk case without oxygen vacancies.Most notably,this lower Hubbard satellite does not increase in amplitudewith the introduction of vacancies,but rather broadens.Inaddition,the oxygen vacancy defect states situated at about −1eV remain qualitatively unchanged by the correlation effects,but experience a broadening with respect to the pureLDA case.This is in agreement with the photoemission data,evidencing that the increase in intensity of the in-gap statein the oxygen-deficient SrVO3is not to be attributed to anincrease in population of the lower Hubbard satellite,butinstead to the manifestation of vacancy states of e g character.Conclusions.In summary,we performed a detailed study of the effects of oxygen vacancies in the spectroscopy of the archetypal strongly correlated electron system SrVO3.We found that oxygen vacancy states,which are created by UV or x-ray irradiation,occur at energies close to the Hubbard satellite.This dramatically affects the measured line shape of the Mott-Hubbard band and the ratio of intensities between the quasiparticle and the Mott-Hubbard peaks.By means of a systematic study under a controlled irradiation dose, using samples directly grown in situ,we were able to obtain the photoemission spectrum of the bulk SrVO3system in the limit of a negligible concentration of oxygen vacancies. Our experimental interpretation is supported by LDA+DMFT calculations,which provided further insight into the likely nature of the oxygen vacancy states.Acknowledgments.We thank Silke Biermann,Ralph Claessen,Marc Gabay,and Michael Sing for discussions. This work was supported by public grants from the French National Research Agency(ANR),project LACUNES No. ANR-13-BS04-0006-01,and the“Laboratoire d’Excellence Physique Atomes Lumi`e re Mati`e re”(LabEx PALM project ELECTROX)overseen by the ANR as part of the“Investisse-ments d’Avenir”program(reference:ANR-10-LABX-0039). S.B.,A.J.K.,F.L.,H.O.J.,and R.V.gratefully acknowledge the Deutsche Forschungsgemeinschaft forfinancial support through Grant FOR1346.T.C.R.acknowledges funding from the RTRA–Triangle de la Physique(project PEGASOS).A.F.S.-S.is thankful for support from the Institut Universitairede France.S.B.and T.C.R.contributed equally to this work.[1]M.Imada,A.Fujimori,and Y.Tokura,Metal-insulator transi-tions,Rev.Mod.Phys.70,1039(1998).[2]A.Georges,G.Kotliar,W.Krauth,and M.J.Rozenberg,Dynamical meanfield theory of strongly correlated electronsS.BACKES et al.PHYSICAL REVIEW B94,241110(R)(2016)and the limit of infinite dimensions,Rev.Mod.Phys.68,13 (1996).[3]G.Kotliar and D.V ollhardt,Strongly correlated materials:Insights from dynamical mean-field theory,Phys.Today57(3), 53(2004).[4]G.Kotliar,S.Y.Savrasov,K.Haule,V.S.Oudovenko,O.Parcollet,and C.A.Marianetti,Electronic structure calculations with dynamical mean-field theory,Rev.Mod.Phys.78,865 (2006).[5]X.Y.Zhang,M.J.Rozenberg,and G.Kotliar,Mott Transitionin the d=∞Hubbard Model at Zero Temperature,Phys.Rev.Lett.70,1666(1993).[6]I.H.Inoue,I.Hase,Y.Aiura,A.Fujimori,Y.Haruyama,T.Maruyama,and Y.Nishihara,Systematic Development of the Spectral Function in the3d1Mott-Hubbard System Ca1−x Sr x VO3,Phys.Rev.Lett.74,2539(1995).[7]M.Takizawa,M.Minohara,H.Kumigashira,D.Toyota,M.Oshima,H.Wadati,T.Yoshida,A.Fujimori,M.Lippmaa,M.Kawasaki,H.Koinuma,G.Sordi,and M.Rozenberg,Coherent and incoherent d band dispersions in SrVO3,Phys.Rev.B80, 235104(2009).[8]T.Yoshida,M.Hashimoto,T.Takizawa,A.Fujimori,M.Kubota,K.Ono,and H.Eisaki,Mass renormalization in the bandwidth-controlled Mott-Hubbard systems SrVO3and CaVO3studied by angle-resolved photoemission spectroscopy,Phys.Rev.B 82,085119(2010).[9]S.Aizaki,T.Yoshida,K.Yoshimatsu,M.Takizawa,M.Minohara,S.Ideta,A.Fujimori,K.Gupta,P.Mahadevan,K.Horiba,H.Kumigashira,and M.Oshima,Self-Energy on the Low-to High-Energy Electronic Structure of Correlated Metal SrVO3,Phys.Rev.Lett.109,056401(2012).[10]M.J.Rozenberg,I.Inoue,H.Makino,F.Iga,and Y.Nishihara,Low Frequency Spectroscopy of the Correlated Metallic System Ca1−x Sr x VO3,Phys.Rev.Lett.76,4781(1996).[11]A.Sekiyama,H.Fujiwara,S.Imada,S.Suga,H.Eisaki,S.I.Uchida,K.Takegahara,H.Harima,Y.Saitoh,I. A.Nekrasov,G.Keller,D.E.Kondakov,A.V.Kozhevnikov,Th.Pruschke,K.Held,D.V ollhardt,and V.I.Anisimov,Mutual Experimental and Theoretical Validation of Bulk Photoemis-sion Spectra of Sr1−x Ca x VO3,Phys.Rev.Lett.93,156402 (2004).[12]E.Pavarini,S.Biermann,A.Poteryaev,A.I.Lichtenstein,A.Georges,and O.K.Andersen,Mott Transition and Suppression of Orbital Fluctuations in Orthorhombic3d1Perovskites,Phys.Rev.Lett.92,176403(2004).[13]B.Amadon,F.Lechermann,A.Georges,F.Jollet,T.O.Wehling,and A.I.Lichtenstein,Plane-wave based electronic structure calculations for correlated materials using dynamical mean-field theory and projected local orbitals,Phys.Rev.B77,205112 (2008).[14]M.Aichhorn,L.Pourovskii,V.Vildosola,M.Ferrero,O.Parcollet,T.Miyake,A.Georges,and S.Biermann,Dynamical mean-field theory within an augmented plane-wave framework: Assessing electronic correlations in the iron pnictide LaFeAsO, Phys.Rev.B80,085101(2009).[15]M.Karolak,T.O.Wehling, F.Lechermann,and A.I.Lichtenstein,General DFT++method implemented with pro-jector augmented waves:Electronic structure of SrVO3and the Mott transition in Ca2−x Sr x RuO4,J.Phys.:Condens.Matter23, 085601(2011).[16]H.Lee,K.Foyevtsova,J.Ferber,M.Aichhorn,H.O.Jeschke,and R.Valent´ı,Dynamical cluster approximation within an aug-mented plane wave framework:Spectral properties of SrVO3, Phys.Rev.B85,165103(2012).[17]J.M.Tomczak,M.Casula,T.Miyake, F.Aryasetiawan,and S.Biermann,Combined GW and dynamical mean-field theory:Dynamical screening effects in transition metal oxides, Europhys.Lett.100,67001(2012).[18]C.Taranto,M.Kaltak,N.Parragh,G.Sangiovanni,G.Kresse,A.Toschi,and K.Held,Comparing quasiparticle GW+DMFTand LDA+DMFT for the test bed material SrVO3,Phys.Rev.B 88,165119(2013).[19]J.M.Tomczak,M.Casula,T.Miyake,and S.Biermann,Asymmetry in band widening and quasiparticle lifetimes in SrVO3:Competition between screened exchange and local correlations from combined GW and dynamical mean-field theory GW+DMFT,Phys.Rev.B90,165138(2014).[20]A.van Roekeghem and S.Biermann,Screened exchangedynamical meanfield theory and its relation to density functional theory:SrVO3and SrTiO3,Europhys.Lett.108,57003(2014).[21]A.Fujimori,I.Hase,H.Namatame,Y.Fujishima,Y.Tokura,H.Eisaki,S.Uchida,K.Takegahara,and F.M.F.de Groot,Evolution of the Spectral Function in Mott-Hubbard Systems with d1Configuration,Phys.Rev.Lett.69,1796(1992). [22]K.Morikawa,T.Mizokawa,A.Fujimori,Y.Taguchi,andY.Tokura,Photoemission spectral weight distribution in Y1−x Ca x TiO3,Phys.Rev.B54,8446(1996).[23]I.A.Nekrasov,G.Keller,D.E.Kondakov,A.V.Kozhevnikov,Th.Pruschke,K.Held, D.V ollhardt,and V.I.Anisimov, Comparative study of correlation effects in CaVO3and SrVO3, Phys.Rev.B72,155106(2005).[24]R.Eguchi,T.Kiss,S.Tsuda,T.Shimojima,T.Mizokami,T.Yokoya,A.Chainani,S.Shin,I.H.Inoue,T.Togashi,S.Watanabe,C.Q.Zhang,C.T.Chen,M.Arita,K.Shimada,H.Namatame,and M.Taniguchi,Bulk-and Surface-SensitiveHigh-Resolution Photoemission Study of Two Mott-Hubbard Systems:SrVO3and CaVO3,Phys.Rev.Lett.96,076402 (2006).[25]A.F.Santander-Syro,O.Copie,T.Kondo,F.Fortuna,S.Pailh`e s,R.Weht,X.G.Qiu,F.Bertran,A.Nicolaou,A.Taleb-Ibrahimi, P.Le F`e vre,G.Herranz,M.Bibes,N.Reyren,Y.Apertet,P.Lecoeur,A.Barth´e l´e my,and M.J.Rozenberg,Two-dimensional electron gas with universal subbands at the surface of SrTiO3, Nature(London)469,189(2011).[26]W.Meevasana,P.D.C.King,R.H.He,S.-K.Mo,M.Hashimoto,A.Tamai,P.Songsiriritthigul,F.Baumberger,and Z.-X.Shen,Creation and control of a two-dimensional electron liquid at the bare SrTiO3surface,Nat.Mater.10,114(2011).[27]P.D.C.King,R.H.He,T.Eknapakul,P.Buaphet,S.-K.Mo,Y.Kaneko,S.Harashima,Y.Hikita,M.S.Bahramy,C.Bell,Z.Hussain,Y.Tokura,Z.-X.Shen,H.Y.Hwang,F.Baumberger, and W.Meevasana,Subband Structure of a Two-Dimensional Electron Gas Formed at the Polar Surface of the Strong Spin-Orbit Perovskite KTaO3,Phys.Rev.Lett.108,117602 (2012).[28]T.C.R¨o del,F.Fortuna,F.Bertran,M.Gabay,M.J.Rozenberg,A.F.Santander-Syro,and P.Le F`e vre,Engineering of two-dimensional electron gases at the(001)and(101)surfaces of TiO2anatase using light,Phys.Rev.B92,041106(R) (2015).。

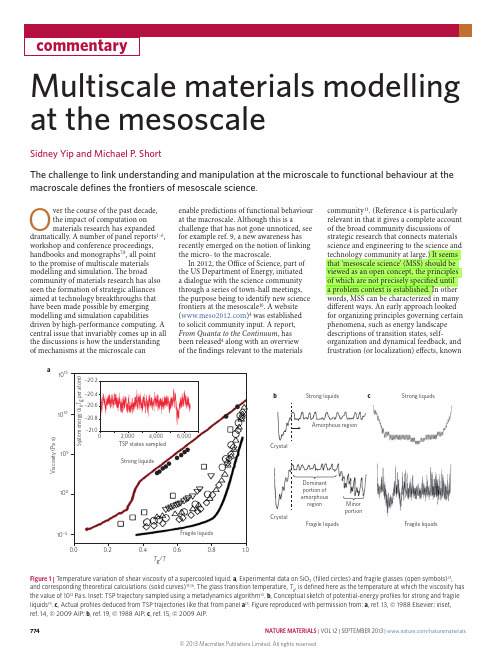
Multiscale materials modelling at the mesoscaleSidney Yip and Michael P. ShortThe challenge to link understanding and manipulation at the microscale to functional behaviour at the macroscale defines the frontiers of mesoscale science.O ver the course of the past decade, the impact of computation onmaterials research has expanded dramatically. A number of panel reports1–6, workshop and conference proceedings, handbooks and monographs7,8, all pointto the promise of multiscale materials modelling and simulation. The broad community of materials research has also seen the formation of strategic alliances aimed at technology breakthroughs that have been made possible by emerging modelling and simulation capabilities driven by high-performance computing. A central issue that invariably comes up in all the discussions is how the understanding of mechanisms at the microscale can enable predictions of functional behaviourat the macroscale. Although this is achallenge that has not gone unnoticed, seefor example ref. 9, a new awareness hasrecently emerged on the notion of linkingthe micro- to the macroscale.In 2012, the Office of Science, part ofthe US Department of Energy, initiateda dialogue with the science communitythrough a series of town-hall meetings,the purpose being to identify new sciencefrontiers at the mesoscale10. A website()4 was establishedto solicit community input. A report,From Quanta to the Continuum, hasbeen released4 along with an overviewof the findings relevant to the materialscommunity11. (Reference 4 is particularlyrelevant in that it gives a complete accountof the broad community discussions ofstrategic research that connects materialsscience and engineering to the science andtechnology community at large.) It seemsthat ‘mesoscale science’ (MSS) should beviewed as an open concept, the principlesof which are not precisely specified untila problem context is established. In otherwords, MSS can be characterized in manydifferent ways. An early approach lookedfor organizing principles governing certainphenomena, such as energy landscapedescriptions of transition states, self-organization and dynamical feedback, andfrustration (or localization) effects, knownFragile liquids Fragile liquidsDominantportion ofamorphousregionStrong liquids Strong liquidsMinorportionCrystalCrystalb cAmorphous region1015Viscosity(Pas)101010510010−50.00.2T g/T0.60.8 1.0Strong liquidsFragile liquidsSystemenergy(kBTgperatom)02,0004,000TSP states sampled6,000–20.8–20.6–20.4–20.2–21.0aFigure 1 | T emperature variation of shear viscosity of a supercooled liquid. a, Experimental data on SiO2 (filled circles) and fragile glasses (open symbols)13, and corresponding theoretical calculations (solid curves)15,16. The glass transition temperature, T g, is defined here as the temperature at which the viscosity has the value of 1012 Pa s.Inset: TSP trajectory sampled using a metadynamics algorithm14. b, Conceptual sketch of potential-energy profiles for strong and fragile liquids19. c, Actual profiles deduced from TSP trajectories like that from panel a15. Figure reproduced with permission from: a, ref. 13, © 1988 Elsevier; inset, ref. 14, © 2009 AIP; b, ref. 19, © 1988 AIP; c, ref. 15, © 2009 AIP.774 NATURE MATERIALS | VOL 12 | SEPTEMBER 2013 | /naturematerialsto be important in the statistical physicsor biophysics domains12. This could be considered a top-down view. A more recent approach, which takes a bottom-up view, focuses on discrete particle systems to identify local spatial and temporal features, such as activated processes, dynamically heterogeneous environments, intermittency and ‘rare’ events11. To promote further discussions, we offer here three materials phenomena as candidates for quantifying MSS in the area of materials ageing and environmental degradation.Materials challenges at the mesoscale The strong variation of the shear viscosity of supercooled liquids with temperature (Fig. 1) is a signature of slow dynamics, a characteristic phenomenon fundamental to our understanding of the glass transition. Two broad classes of behaviour are shown, an Arrhenius variation (filled circles)for an oxide glass such as SiO2, and a distinctly non-Arrhenius variation (open symbols) for several molecular glasses13. The latter, known as ‘fragile’ scaling, is the more intriguing, as it indicates a thermal activation process where the activation barrier is temperature dependent. Howto explain the so-called fragile behaviour using only atomistic concepts has beena topic of enduring interest in the glass science community.Figure 1 also shows that the experimental data can essentially be explained by calculations14–16 (curvesin Fig. 1a). Because these curves can be obtained using information exclusively provided by atomistic simulations, theyprovide a way to understand the nature of fragility in supercooled liquids in terms that are, in effect, quantifiable. According to classical transition-state theory, the shear viscosity of a glassy liquid can be expressed as17η(T) = η0exp[Q(T)/k B T] (1)where η0 is a reference viscosity value generally known or accepted, Q(T)is an effective activation barrier, k B isthe Boltzmann constant and T is the temperature. Within this description, understanding the behaviour of η(T) amounts to an explanation of Q(T). The essential ingredient needed to calculate the curves in Fig. 1a is the trajectory of the transition-state pathway (TSP), which is information obtained by sampling the potential energy landscape14,18. An actual trajectory for a fragile glass model is shown in Fig. 1a. It is an alternating sequence of local energy minima and saddle points (transition states), and associated with each are the known positions of all theparticles in the system. A trajectory thusspecifies the path of the system as itevolves by moving on its potential energylandscape. These physical details are thenprocessed by statistical analysis and coarsegraining to give Q(T) (refs 14,15). TheTSP trajectory can be used to directlycalculate η(T) through linear responsetheory16 without using equation (1). Suchinformation also elucidates our notionof the energy landscape description ofamorphous media. It has been suggested19that the potential-energy surface associatedwith Arrhenius (‘strong’) temperaturedependence should be relatively smooth,whereas the energy surface giving riseto fragile behaviour should be quiterough, as depicted schematically inFig. 1b. Figure 1c displays the actualsurface profiles deduced from the TSPtrajectories15, which provide a quantitativemeasure of the respective landscapetopologies. From the computationalstandpoint it is worth noting that probingglassy dynamics requires simulation atthe mesoscale, because the timescalerelevant to the experimental data lies wellbeyond the capability of conventionalsimulation techniques at the microscale.The thermal activation processes observedin the high-viscosity region in Fig. 1a canbe regarded as rare events in the contextof materials modelling and simulation atthe microscale.The onset of a sharp increase inη(T) over a small temperature range ischaracterized by a crossover (or critical)temperature T x (T c) (ref. 20). What couldbe the change in the atomic configurationsor interatomic interactions underlyingsuch an upturn, or kink behaviour inthe temperature variation? As a resultof the calculations14–16, the increase inthe resistance to viscous flow (curves inFig. 1a) can be interpreted as showingthat the system is becoming intermittentlytrapped in deep energy basins. In theenergy landscape framework the crossoverphenomenon — the transition from gradualto accelerated variations in behaviour —can be expected whenever differentexisting mechanisms compete, and thedominance of one over the other dependson the local environment or driving force.Consider an analogy between viscous flowin glassy fluids and creep deformation inplastic solids. Although glass rheology andcrystal plasticity are seldom regarded asclosely related phenomena, it has recentlybecome appreciated that transition-statetheory, as described by equation (1), isequally suitable in describing stress-drivenresponses where Q(T) is replaced by a stressactivation barrier Q(σ). Such an approachis capable of describing a sudden upturnbehaviour in the variation of yield stresswith strain rate21, which may be comparedto the variation in viscosity with inversetemperature of the fragile liquids shownin Fig. 1. This upturn or kink variation isa characteristic dynamical response seenexperimentally in systems from metals22to colloidal suspensions23. Its widespreadpresence suggests a simple underlyingorigin, basically a localization (orconfinement) process. Thus the crossoverin η(T) would correspond to stresslocalization as the system is trapped in adeep energy basin, whereas the crossoverin the yield stress would correspond tostrain localization when the strain ratereaches a critical value. Whether there is acommon underlying origin in the differentphysical behaviour24 is a question for thedevelopment of MSS.In our second illustration of MSS, wefocus on a specific system, cement. As the 1010105106107108109104101IIIIII102Time (s)Shearelasticmodulus(Pa)103104105SandC3SFigure 2 | Time evolution of complex shearmodulus in a cement paste measured by anultrasonic method. Data from ref. 26. Inset:schematic of cement hydration — dissolutionof clinker C3S grains and precipitation ofC–S–H (black bars)27. Bottom left: magnifiedversion of area encolsed by red box in inset.Bottom right: molecular model of C–S–Hshowing the arrangement of CaO layers, SiO2chains and water molecules31. Blue and whiterepresent oxygen and hydrogen atoms of water,respectively, green and grey denote inter- andintralayer calcium ions, yellow and red representsilicon and oxygen atoms in silica tetrahedra.Figure reproduced with permission from: inset,ref. 27, © 2005 ACS; bottom right, ref. 31,© 2009 NAS.776NATURE MATERIALS | VOL 12 | SEPTEMBER 2013 | /naturematerialsmost widely used structural material on Earth, concrete is irreplaceable in terms of commercial availability and widespread utility. The scientific challenge of concrete lies in understanding the mechanisms of setting (hydration)25, the process by which cement paste, a mixture of cement powder and water, becomes hardened over time. Hardening can be measured directly by an ultrasonic probe that gives the time evolution of the complex shear modulus, as shown in Fig. 2 (ref. 26). The rigidity of the paste rises to a level of ~10 MPa on the order of minutes, stays relatively constant over a few hours, and then rises sharply to several GPa overnight. Unlike theviscosity behaviour shown in Fig. 1 where calculations can be directly compared to experiments, it is not yet feasible to fully analyse the setting curve of cement paste shown in Fig. 2, or its counterpart, the hydration curve 25. There is consensus in the cement and concrete researchcommunity that setting is a key challenge with significant potential for innovation, for example, in the development ofadditives. Our qualitative understanding of cement setting begins with (1) clinker dissolution causing precipitation of the hydration product calcium silicate hydrate (C–S–H, or CaO–SiO 2–H 2O; inset of Fig. 2; ref. 27), (2) growth of the C–S–H phase, and (3) hardening of the evolving paste 28. The latter two stages are especiallylacking in mechanism-based analysis. To address mechanical behaviour from the standpoint of C–S–H growth, one needs to understand how the hydration products affect the packing fraction 29, and the formation and evolution of pores 30, in processes such as the kinetics of dissolution and precipitation (nucleation and growth), the percolation (or jamming) of the emerging network of C–S–H, and the effects of water in the interlayer regions of C–S–H and in the pores. All these can be considered examples of MSS challenges with significant industrial implications 2. At the microscale, a molecular model of C–S–H, which is chemically consistent with neutron scattering measurements (Ca/Si ratio and water density), has been proposed 31 (Fig. 2). It remains an open problem to introduce such atomic-level details in multiscale materials modelling studies to achieve a predictive capability for cement setting 32.Yet another way to identify mesoscale science challenges in the materialsdomain is to consider an interdisciplinary phenomenon. Stress corrosion cracking (SCC), a technologically important process in the area of environmental degradation of materials, is our third illustrative example. The relevant functional behaviour here is the variation of crack velocity with applied stress. Figure 3 shows experimental data on static fatigue, where crack propagation inglass specimens under tensile loading was studied with respect to varying moisture levels in the environment 33. Figure 3 is similar to Fig. 2 in that the interpretations of the macroscale experimental data in terms of underlying mechanisms and processes at the mesoscale are not yet feasible. To facilitate interpretation and guide the eye, lines at six constant moisture levels have been fitted through a large collection of data, only a subset of those at 0.017% and 100% are shown as filled circles. Additionally, the data from a single run at 0.2% are shown as open circles. The variation of crack propagation speed with applied stress v (K ) is seen to follow a three-stage response 34, a schematic of which is shown in Fig. 3b. There is a resemblance to the microstructure evolution in thethree-stage setting of cement paste (Fig. 2). Keeping in mind that both chemistry (corrosion) and mechanics (stress) play a role that is manifest in Fig. 3, we may regard the onset of crack propagation at low stress (stage I) as a threshold effect of corrosion-induced bond breaking. The rapid increase of v (K ) indicates a strong stress-dependence as well as sensitivity to the environment. Stage II in Fig. 3b is characterized by the crack speed becoming stress-independent (compare with stage II in Fig. 2). This may be a consequence of the rate-limiting process of water diffusing to the crack tip, just as the formation of C–S–H in cement limits the rate of cement curing. It would be interesting to probe this region further to clarify the interplay between local reactivity and spatially extended transport. More generally, this coupling is fundamental for identifying the hallmark character of the slow dynamics of SCC. In stage III, the propagation curve reverts back to a second threshold behaviour, now with brittle fracture controlled by the Griffith criterion with corrosion playing at most a minor role. To emphasize the delayed nature of SCC, Fig. 3c explicitly shows the increase in crack length to the critical point of failure on the timescale of observation. Correlating this direct evidence with the ‘mechanism map’ in Fig. 3b will enable one to understand the importance of controlling the growth rate and avoiding the occurrence of a critical crack length 35. Identifying a definitive link between atomistic-level bond breaking or crack formation and a measurable crack speed at the macroscale therefore presents an opportunity for contributions by MSS.Implications for mesoscale scienceCollectively, the macroscale behaviour of glass viscosity, cement setting andL o g v (m s –1)–Time (min)–––aK I (MPa m 1/2)Figure 3 | Data and schematics showing upturn behaviour in fracture toughness curves of glasses exposed to different moisture levels. a , Variation of crack propagation speed in soda-lime silica glass with applied tensile stress K I measured at various moisture levels. b , Schematic showing the behaviour of v (K ) that has three distinct stages of evolution (see main text for explanation)34. c , Time evolution of measured crack length (ΔL ) showing that it corresponds to the expected behaviour of stages II and III (ref. 33). Figure reproduced with permission from: a ,c , ref. 33, © 1967 Wiley.SCC illustrate the capability of MSSto incorporate a range of materials phenomena such as ageing and durability. There are clearly other cases of functional behaviour in need of mesoscale analysis and interpretations. The experience gained in the sampling and analysis of TSP trajectories in understanding viscous flow in glassy states could be useful in other problems. The challenges of quantifyingC–S–H nucleation and growth in cement setting, and the interplay between chemical attack and stress-driven cracking in delayed fracture in glasses all provide opportunities for developing TSP sampling methodsto reach experimental timescales (Fig. 2 and Fig. 3c).The underlying physical phenomenon common to the problems we have highlighted is the evolution kinetics ofthe mesoscale structure. By this we mean the time-dependent relationship between the evolving ‘defect’ configurationsat the mesoscale (for example, glassyconfigurations, granular assembly ofC–S–H and propagating crack tip) and the corresponding functional properties (viscosity, shear modulus and crack speed) at the macroscale. This correlation isan extension of the familiar structure–property correlation, which has beena longstanding paradigm of materials science. The novelty in the present context is dealing with the cross correlations, linking different sets of degrees of freedom associated with different spatial and temporal scales. Although cross correlation has always been part of the spirit of multiscale materials modelling, even in the early days9, quantitatively understanding this correlation in specific problems of broad interest could expand the scope of MSS in new directions.It seems entirely appropriate MSS should play a key role in the quest for coupling scientific advances with technological impact. We also see MSS as the enabling capability essential to strategic alliances, particularly concerning the reliabilityand optimization of materials. In 2010, the US Department of Energy established an Energy Innovation Hub on nuclear modelling and simulation, the Consortium for the Advanced Simulation of Light Water Reactors (CASL)36. Among the ongoing CASL research projects is an effort to better understand and control corrosionin nuclear reactors37. The formation and growth of the corrosion product known as chalk river unidentified deposits (CRUD) on fuel rods, for example, is similar in complexity to the precipitation and growth of C–S–H in the cement setting process. Understanding the properties of CRUD requires treating the phenomena of heattransfer, fluid flow, chemistry, precipitationand dissolution, and the underlyingcorrosion of the fuel cladding in a coupledmanner38, a problem that is much toocomplex for microscale modelling andsimulations alone. Indeed, CRUD ismore challenging than the cases we haveconsidered because, in addition, coupledradiation and neutronic effects are nowinvolved. With CASL being a partnershipof national laboratories, industries anduniversities, solving a problem such asCRUD would demonstrate the importanceof teamwork among the stakeholders, inparticular, partners from industry. Overallthe MSS concept should be applicable toany field where scientific capabilities andtechnology innovations overlap at themesoscale (Fig. 4). The gap between thescience push and technology pull is aninherent part of scientific exploration anddiscovery. How to bridge this gap is worthyof our future efforts. ❐Sidney Yip1,2 and Michael P. Short1 are at1Department of Nuclear Science and Engineering atMassachusetts Institute of Technology, Cambridge,Massachusetts 02139-4307, USA, and 2Departmentof Materials Science and Engineering atMassachusetts Institute of Technology, Cambridge,Massachusetts 02139-4307, USA.e-mail: syip@References1. President’s Information Technology Advisory CommitteeComputational Science: Ensuring America’s Competitiveness(June, 2005); available via /pXa64m2. Report of the National Science Foundation Blue Ribbon Panelon Simulation-based Engineering Science Simulation-BasedFigure 4 | Complexity–capability map showingthe separation between scientific studies atthe microscale and technology innovations atthe macroscale along the capability axis. Theseparation between unit processes associatedwith isolated mechanisms and integratedsystem-level functional behaviour is shown alongthe complexity axis. Bridging the gaps will requirethe development of modelling, simulation andexperimental capabilities in the mesoscale realmto address the relevant functional behaviourextending to the macroscale.UnitSystem-levelEngineering Science: Revolutionizing Engineering Science throughSimulation (February 2006); /pubs/reports/sbes_final_report.pdf3. World Technology Evaluation Center Panel ReportInternational Assessment of Research and Developmentin Simulation-Based Engineering and Science (2009);/sbes4. US Department of Energy Basic Energy Science Report FromQuanta to the Continuum: Opportunities for Mesoscale Science(September, 2012); .5. National Research Council Integrated ComputationalMaterials Engineering: A Transformational Discipline forImproved Competitiveness and National Security (NAS, 2008);/catalog/12199.html6. Materials Genome Initiative for Global Competitiveness(June, 2011); available via /Rkw2mj7. Yip, S. (ed.) Handbook of Materials Modeling (Springer, 2006).8. Konings, R. (ed.) Comprehensive Nuclear Materials(Elsevier, 2012).9. Yip, S. Nature Mater.2, 3–5 (2003).10. Bader, S. APS News21, 8 (2012).11. Crabtree, G. W. & Sarrao, J. L. Mater. Res. Soc. Bull.37, 1079–1088 (2012).12. Laughlin, R. B., Pines, D., Schmalian, J., Stojkovic, B. P. &Wolynes, P. Proc. Natl Acad. Sci. USA97, 32–37 (2000).13. Angell, C. A. J. Phys. Chem. Solids49, 863–871 (1988).14. Kushima, A. et al.J. Chem. Phys.130, 224504 (2009).15. Kushima, A. et al.J. Chem. Phys.131, 164505 (2009).16. Li, J. et al.PLoS ONE6, e17909 (2011).17. Brush, S. G. Chem. Rev.62, 513–548 (1962).18. Liao, A. & Parrinello, M. Proc. Natl Acad. Sci. USA99, 12562–12566 (2002).19. Stillinger, F. H. J. Chem. Phys.88, 7818–7825 (1988).20. Mallamace, F. et al.Proc. Natl Acad. Sci. USA28, 22457–22462 (2010).21. Fan, Y., Osetsky, Y., Yip, S. & Yildiz, B. Phys. Rev. Lett.109, 135503 (2012).22. Armstrong, R. W., Arnold, W. & Zerilli, F. J. Appl. Phys.105, 023511 (2009).23. Chen, L. B., Ackerson, B. J. & Zukoski, C. F. J. Rheology38, 193–216 (1994).24. Kushima, A., Eapen, J., Li, J., Yip, S. & Zhu, T. Eur. Phys. J. B82, 271–293 (2011).25. Gartner, E. M., Y oung, J. F., Dadot, D. A. & Jawed, I. in Structureand Performance of Cements 2nd edn (eds Barnes, P. &Bensted, J.) 57–113 (Spon, 2002).26. Lootens, D., Hebraud, P., Lecolier, E. & Van Damme, H.Oil Gas Sci. Technol.59, 31–40 (2004).27. Jönsson, B., Nonat, A., Labbez, C., Cabane, B. & Wennerström, H.Langmuir21, 9211–9221 (2005).28. Bullard, J. W. et al.Cem. Concr. Res.41, 1208–1223 (2011).29. Masoero, E., Del Gado, E., Pellenq, R. J-M., Ulm, F-J. & Yip, S.Phys. Rev. Lett.109, 155503 (2012).30. Jennings, H. M. Cem. Concr. Res. 37, 275–336 (2007).31. Pellenq, R. J-M. et al.Proc. Natl Acad. Sci. USA106, 16102–16107 (2009).32. Van Vliet, K. et al.Mater. Res. Soc. Bull.37, 395–402 (2012).33. Wiederhorn, S. M. J. Am. Ceram. Soc.50, 407–414 (1967).34. Ciccotti, M. J. Phys. D42, 214006 (2009).35. Proceedings of QMN-4 Fourth Meeting of QuantitativeMicro Nano (QMN) Approach to Predicting Stress CorrosionCracking (Sun Valley, Idaho, June 12–17, 2013); available via/36. 37. Edsinger, K., Stanek, C. R. & Wirth, B. D. JOM63, 49–52 (2011).38. Deshon, J. et al.JOM63, 64–72 (2011).AcknowledgmentsWe thank A.S. Argon, S.-H. Chen, E. Del Gado, Y. Fan,H.M. Jennings, E. Masoero, R.J-M. Pellenq, F.-J. Ulm,K.J. Van Vliet, D. Wolf and B. Yildiz for discussionsof materials behaviour at the mesoscale. M.S. andS.Y. acknowledge support by the Consortium forAdvanced Simulation of Light Water Reactors, anEnergy Innovation Hub for Modeling and Simulationof Nuclear Reactors under US-DOE Contract No.DE-AC05-00OR22725. S.Y. also acknowledges theConcrete Sustainability Hub at MIT sponsored by thePortland Cement Association and the National ReadyMix Concrete Association, and the US-DOE-Basic EnergySciences, Grant No. DE-SC0002633.。

[北京大学《量子信息物理原理》课程讲稿]（I,II）第一章量子测量及相关问题§1.1,量子测量基础1，量子力学的第三公设——测量公设2，测量理论的三个阶段3，塌缩阶段的四个特征4，量子测量分类§1.2, 量子光学一些器件作用分析1，半透片、符合测量、PBS、后选择2，延迟选择、后选择、预选择、杨氏双缝3，斜置偏振片的变换4，斜置半波片的作用5，BBO晶体与参量下转换——极化纠缠光子对产生§1.3,von Neumann正交投影测量模型1, von Neumann正交投影测量模型2,典型例子————Stern-Gerlach装置对电子自旋的测量§1.4, 广义测量与POVM1，广义测量2，局域测量——POVM3，POVM举例4，Neumark定理§1.5, 量子非破坏测量（Quantum nondemolition measurements ——QND）简介1, 标准量子极限（SQL——Standard Quantum Limit）2，量子非破坏测量的定义3，QND所必须满足的充要条件4，QND的局限性§1.6, 量子弱测量1, 量子弱测量含义2, 弱测量初步应用§1.7, 量子测量及相关问题小结1，量子测量中时间塌缩和空间非定域性的问题2，量子测量理论中存在的问题※※※第一章量子测量及相关问题量子测量的物理分析是联系量子理论计算和实验测量的桥樑，是整个量子理论的基础和支柱。

按现在文献情况可以说，不熟习量子测量理论很难理解许多近代重要的实验工作。

更何况，量子测量理论本身就蕴含着量子理论几乎全部的未解决重大基本问题。

这些问题都如此基本，以致于对它们的解答必定会从根本上纠正我们现有的时空观和某些基本概念，导致我们对世界有一个崭新的再认识。

鉴于我国量子力学教材中很少谈及测量问题，而量子信息论必须和经常涉及它，所以课程不得不对量子测量内容作一个简要的介绍。

无人机目标检测量子多模式识别优化算法侯旋1，2，薛飞3，陈涛41.西北政法大学新闻传播学院，西安7101222.空军工程大学航空工程学院，西安7100383.空军研究院航空兵研究所，北京1000764.电子科技大学电子科学技术学院，成都611731摘要：研究了现阶段无人机雷达探测技术的难点与方法，分析了量子多模式识别网络模型与算法，根据Grover 算法优化理论，提出了基于相位旋转的量子多模式识别算法（PRQMPRA ）。

优化算法避免了在带冗余项的量子多模式识别算法（RQMPRA ）中两个相位旋转均为π会导致搜索成功概率降低的缺陷。

利用三种数据集对误差反向传播算法（EBPA ）、基于交叉熵函数的深层自编码器学习算法（CDAA ）以及RQMPRA 与PRQMPRA 进行模式识别能力分析，结果表明在确定限定误差的情况下PRQMPRA 具有更高的识别率与相对较快的运算速度。

提出了一种基于量子多模式识别算法的雷达目标检测方法，通过模式分类的方法研究目标检测问题。

利用上述四种算法进行无人机目标检测实验，研究结果表明PRQMPRA 具有更高的检测精度，在低信噪比的情况下可保持较高的发现概率。

关键词：目标检测；无人机；量子计算；模式识别文献标志码：A中图分类号：TP183doi ：10.3778/j.issn.1002-8331.2001-0143UAV Target Detection on Quantum Multi-pattern Recognition Optimization AlgorithmHOU Xuan 1，2,XUE Fei 3,CHEN Tao 41.School of Journalism and Communication,Northwest University of Politics and Law,Xi ’an 710122,China2.College of Aeronautics Engineering,Air Force Engineering University,Xi ’an 710038,China3.Aviation Institute,Air Force Research Institute,Beijing 100076,China4.College of Electronic Science and Technology,University of Electronic Science and Technology of China,Chengdu 611731,ChinaAbstract ：The difficulties and methods of unmanned aerial vehicle radar detection technology are studied.It analyzes the model and algorithms of Quantum multi-Pattern Recognition Network （QPRN ）.By Grover introducing algorithm optimi-zation theory,Phase Rotation Quantum Multi-Pattern Recognition Algorithm （PRQMPRA ）is proposed.The optimization algorithm avoids the defect that both phase rotations are πin the Redundancy Quantum Multi-Pattern Recognition Algo-rithm （RQMPRA ）,which will lead to a decrease in the probability of successful search.Three types of data sets are used to analyze the pattern recognition ability of Error Back Propagation Algorithm （EBPA ）,Cross-entropy function-Deep Autoencoder learning Algorithm （CDAA ）,RQMPRA and PRQMPRA.In the case of determining the limit error,the results show that PRQMPRA has higher recognition rate and relatively faster operation speed.A multi-pattern recognition algorithm based radar target detection method is proposed to study the target detection problem by pattern ing the above four algorithms for UAV target detection experiments,the results show that PRQMPRA has higher detection accuracy and can maintain a higher discovery probability in the case of low Signal to Noise Ratio （SNR ）.Key words ：target detection;Unmanned Aerial Vehicle （UAV ）;quantum computing;pattern recognition基金项目：国家自然科学基金（51507186）。

量子力学教案主讲周宙安《量子力学》课程主要教材及参考书1、教材：周世勋，《量子力学教程》，高教出版社，19792、主要参考书：[1] 钱伯初，《量子力学》，电子工业出版社，1993[2] 曾谨言，《量子力学》卷I，第三版，科学出版社，2000[3] 曾谨言，《量子力学导论》，科学出版社，2003[4] 钱伯初，《量子力学基本原理及计算方法》，甘肃人民出版社，1984[5] 咯兴林，《高等量子力学》，高教出版社，1999[6] L. I.希夫，《量子力学》，人民教育出版社[7] 钱伯初、曾谨言，《量子力学习题精选与剖析》，上、下册，第二版，科学出版社，1999[8] 曾谨言、钱伯初，《量子力学专题分析（上）》，高教出版社，1990[9] 曾谨言，《量子力学专题分析（下）》，高教出版社，1999[10] P.A.M.Dirac,The Principles of Quantum Mechanics (4th edition), Oxford University Press (Clarendon),Oxford,England,1958；（《量子力学原理》，科学出版社中译本，1979）[11]ndau and E.M.Lifshitz, Quantum Mechanics (Nonrelativistic Theory) (2nd edition),Addison-Wesley,Reading,Mass,1965；（《非相对论量子力学》，人民教育出版社中译本，1980）第一章绪论量子力学的研究对象：量子力学是研究微观粒子运动规律的一种基本理论。

它是上个世纪二十年代在总结大量实验事实和旧量子论的基础上建立起来的。

它不仅在进到物理学中占有及其重要的位置，而且还被广泛地应用到化学、电子学、计算机、天体物理等其他资料。

§1.1经典物理学的困难一、经典物理学是“最终理论”吗？十九世纪末期，物理学理论在当时看来已经发展到相当完善的阶段。