湖北省2018年秋八年级数学上册第十二章检测卷新人教版

第十二章检测卷题号一二三总分得分一、选择题(共10小题，每小题3分，共30分)1．在下列每组图形中，是全等形的是( )2．如图，△AOC≌△BOD，点A与点B是对应点，则下列结论中错误的是( )A．∠A＝∠B B．AO＝BOC．AB＝CD D．AC＝BD第2题图第3题图3．如图，已知AB＝AC，BD＝CD，则可推出( )A．△ABD≌△BCD B．△ABD≌△ACDC．△ACD≌△BCD D．△ACE≌△BDE4．一定能确定△ABC≌△DEF的条件是( )A．∠A＝∠D，AB＝DE，∠B＝∠EB．∠A＝∠E，AB＝EF，∠B＝∠DC．AB＝DE，BC＝EF，∠A＝∠DD．∠A＝∠D，∠B＝∠E，∠C＝∠F5．已知∠AOB的平分线上一点P到OA的距离为5，Q是OB上任意一点，则( ) A．PQ＞5 B．PQ≥5C．PQ＜5 D．PQ≤56．如图，点A、D、C、E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝12，AC＝8，则CD的长为( )A．5.5 B．4 C．4.5 D．3第6题图第7题图第8题图7．如图，MP⊥NP，MQ为∠PMN的平分线，MT＝MP，连接TQ，则下列结论中不正确的是( )A．TQ＝PQ B．∠MQT＝∠MQPC．∠QTN＝90° D．∠NQT＝∠MQT8．如图，BE⊥AC于点D，且AD＝CD，BD＝ED.若∠ABC＝54°，则∠E的度数为( ) A．25° B．27°C．30° D．45°9．如图，已知AD＝BC，AC与BD交于点O，AE⊥BD于点E，CF⊥BD于点F，则图中的全等三角形有( )A．5对B．6对C．7对D．8对第9题图第10题图10．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM＝PN恒成立；②OM＋ON的值不变；③四边形PMON的面积不变；④MN的长不变．其中正确的个数为( )A．4个B．3个C．2个D．1个二、填空题(共6小题，每小题3分，共18分)11．如图，在△ABC与△ADC中，已知AD＝AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，只需再添加的一个条件可以是__________．第11题图第12题图12．如图，要测量池塘的宽度AB，在池塘外选取一点P，连接AP、BP并各自延长，使PC＝PA，PD＝PB，连接CD，测得CD长为25m，则池塘宽AB为________m，依据是________________________．13．如图，AB∥CF，E为AC的中点．若FC＝6cm，DB＝3cm，则AB＝________cm.第13题图第14题图14．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝96cm2，AB＝18cm，BC＝12cm，则DE＝________cm.15．如图，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAC＝80°，则∠CAE的度数是________．第15题图第16题图16．如图，在平面坐标系中，B(3，1)，AB＝OB，∠ABO＝90°，则点A的坐标是____________．三、解答题(共8题，共72分)17．(8分)如图，点C是AE的中点，∠A＝∠ECD，AB＝CD.求证：∠B＝∠D.18．(8分)工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M、N重合，过角尺顶点P的射线OP便是∠AOB的平分线，请说明理由．19.(8分)如图，点D在BC上，∠1＝∠2，AE＝AC，下面有三个条件：①AB＝AD；②BC ＝DE；③∠E＝∠C.请你从所给条件①②③中选一个条件，使△ABC≌△ADE，并证明两三角形全等．20．(8分)如图，在Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一点，E在BC 的延长线上，且AE＝BD，BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系，并证明你的猜想．21．(8分)如图，AD是△ABC的中线，BE⊥AD于点E，CF⊥AD交AD的延长线于点F.求证：AE＋AF＝2AD.22．(10分)如图，在△ABC中，D为BC上一点，E为△ABC外部一点，DE交AC于一点O，AC＝AE，AD＝AB，∠BAC＝∠DAE.(1)求证：△ABC≌△ADE；(2)若∠BAD＝20°，求∠CDE的度数．23．(10分)如图，在△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F.(1)求证：BE＝CF；(2)若AB＝8，AC＝6，求AE，BE的长．24．(12分)在解决线段数量关系的问题时，如果条件中有角平分线，经常采用下面构造全等三角形的解题思路，如：在图①中，若C是∠MON的平分线OP上一点，点A在OM上，此时，在ON上截取OB＝OA，连接BC，根据三角形全等判定(SAS)，容易构造出全等三角形△OBC和△OAC.参考上面的方法，解答下列问题：如图②，在非等边△ABC中，∠B＝60°，AD，CE分别是∠BAC，∠BCA的平分线，且AD，CE交于点F.求证：AC＝AE＋CD.参考答案与解析1．C 2.C 3.B 4.A 5.B 6.B 7.D 8.B 9.C10．B 解析：如图，作PE ⊥OA 于E ，PF ⊥OB 于F ，则∠PEO ＝∠PFO ＝90°，∴∠EPF ＋∠AOB ＝180°.∵∠MPN ＋∠AOB ＝180°，∴∠EPF ＝∠MPN ，∴∠EPM ＝∠FPN .∵OP平分∠AOB ，∴∠POE ＝∠POF .在△POE 和△POF 中， ⎩⎨⎧∠POE ＝∠POF ，∠PEO ＝∠PFO ，PO ＝PO ，∴△POE ≌△POF ，∴PE ＝PF ，OE ＝OF .在△PEM 和△PFN 中， ⎩⎨⎧∠MPE ＝∠NPF ，PE ＝PF ，∠PEM ＝∠PFN ，∴△PEM ≌△PFN ，∴EM ＝NF ，PM ＝PN ，故①正确．∴S △PEM ＝S △PFN ，∴S 四边形PMON＝S 四边形PEOF ＝定值，故③正确．∵OM ＋ON ＝OE ＋ME ＋OF －NF ＝2OE ＝定值，故②正确．MN 的长度是变化的，故④错误．故选B.11．DC ＝BC (或∠DAC ＝∠BAC ) 12．25 全等三角形对应边相等 13．9 14.6.4 15.20°16．(2，4) 解析：如图，过点A 作AC ∥x 轴，过点B 作BD ∥y 轴，两条直线相交于点E ，则CE ＝OD ，DE ＝OC ，∠ODB ＝∠BEA ＝90°.∵B (3，1)，∴OD ＝3，BD ＝1.∵∠DOB ＋∠OBD ＝90°，∠OBD ＋∠ABE ＝90°，∠BAE ＋∠ABE ＝90°，∴∠BOD ＝∠ABE ，∠OBD ＝∠BAE .在△ABE 与△BOD 中，∵⎩⎨⎧∠BOD ＝∠ABE ，AB ＝BO ，∠OBD ＝∠BAE ，∴△ABE ≌△BOD (ASA)，∴AE ＝BD ＝1，BE ＝OD ＝3，∴AC ＝OD －AE ＝3－1＝2，DE ＝BD ＋BE ＝1＋3＝4，∴A (2，4)．17．证明：∵点C 是AE 的中点，∴AC ＝CE .(2分)在△ABC 和△CDE 中，⎩⎨⎧AC ＝CE ，∠A ＝∠ECD ，AB ＝CD ，∴△ABC ≌△CDE (SAS)，(7分)∴∠B ＝∠D .(8分)18．解：在△OMP 和△ONP 中，∵⎩⎨⎧OM ＝ON ，MP ＝NP ，OP ＝OP ，∴△OMP ≌△ONP (SSS)，(6分)∴∠MOP＝∠NOP ，∴OP 平分∠AOB .(8分)19．解：选②BC ＝DE .(1分)证明如下：如图，∵∠1＝∠2，∠3＝∠4，∴∠E ＝∠C .(3分)在△ADE 和△ABC 中，⎩⎨⎧AE ＝AC ，∠E ＝∠C ，DE ＝BC ，∴△ADE ≌△ABC (SAS)．(8分)20．解：猜想BF ⊥AE .(2分)理由如下：∵∠ACB ＝90°，∴∠ACE ＝∠BCD ＝90°.又BC ＝AC ，BD ＝AE ，∴Rt△BDC ≌Rt△AEC (HL)．∴∠CBD ＝∠CAE .(5分)又∵∠CAE ＋∠E ＝90°，∴∠EBF ＋∠E ＝90°.∴∠BFE ＝90°，即BF ⊥AE .(8分)21．证明：∵AD 是△ABC 的中线，∴BD ＝CD .∵BE ⊥AD ，CF ⊥AD ，∴∠BED ＝∠CFD＝90°.(2分)在△BDE 和△CDF 中，⎩⎨⎧∠BED ＝∠CFD ，∠BDE ＝∠CDF ，BD ＝CD ，∴△BDE ≌△CDF (AAS)，∴DE ＝DF .(5分)∵AE ＝AD －DE ，AF ＝AD ＋DF ，∴AE ＋AF ＝AD －DE ＋AD ＋DF ＝2AD .(8分)22．(1)证明：在△ABC 和△ADE 中，⎩⎨⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE (SAS)．(5分)(2)解：由(1)知△ABC ≌△ADE ，∴∠E ＝∠C .∵∠BAC ＝∠DAE ，∠BAC ＝∠BAD ＋∠DAC ，∠DAE ＝∠DAC ＋∠CAE ，∠BAD ＝20°，∴∠CAE ＝∠BAD ＝20°.(7分)∵∠E ＝∠C ，∠AOE ＝∠DOC ，∴∠CAE ＝∠CDE ，∴∠CDE ＝20°.(10分)23．(1)证明：如图，连接DB ，DC .∵DG ⊥BC 且平分BC ，∴∠DGB ＝∠DGC ＝90°，BG ＝CG .又DG ＝DG ，∴△DGB ≌△DGC ，∴DB ＝DC .∵AD 为∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF ，∠DAE ＝∠DAF ，∠BED ＝∠AED ＝∠DFC ＝90°.(3分)在Rt△DBE 和Rt△DCF 中，⎩⎨⎧DB ＝DC ，DE ＝DF ，∴Rt△DBE ≌Rt△DCF (HL)，∴BE ＝CF .(5分)(2)解：在△ADE 和△ADF 中，⎩⎨⎧∠DAE ＝∠DAF ，∠AED ＝∠AFD ，AD ＝AD ，∴△ADE ≌△ADF ，∴AE ＝AF .(7分)∵AC ＋CF ＝AF ，AE ＝AB －BE ，∴AC ＋CF ＝AB －BE ，即6＋BE ＝8－BE ，∴BE ＝1，∴AE ＝8－1＝7.(10分)24．证明：如图，在AC 上截取AG ＝AE ，连接FG .(1分)∵AD 是∠BAC 的平分线，CE是∠BCA 的平分线，∴∠1＝∠2，∠3＝∠4.(2分)在△AEF 和△AGF 中， ⎩⎨⎧AE ＝AG ，∠1＝∠2，AF ＝AF ，∴△AEF ≌△AGF (SAS)，∴∠AFE ＝∠AFG .(6分)∵∠B ＝60°，∴∠BAC ＋∠ACB ＝120°，∴∠2＋∠3＝12(∠BAC ＋∠ACB )＝60°.∵∠AFE ＝∠2＋∠3，∴∠AFE ＝∠CFD ＝∠AFG ＝60°，∴∠CFG ＝180°－∠CFD －∠AFG ＝60°，∴∠CFD ＝∠CFG .(9分)在△CFG 和△CFD 中，⎩⎨⎧ ∠CFG ＝∠CFD ，FC ＝FC ，∠3＝∠4，∴△CFG ≌△CFD (ASA)，∴CG ＝CD .∴AC ＝AG ＋CG ＝AE ＋CD .(12分)。

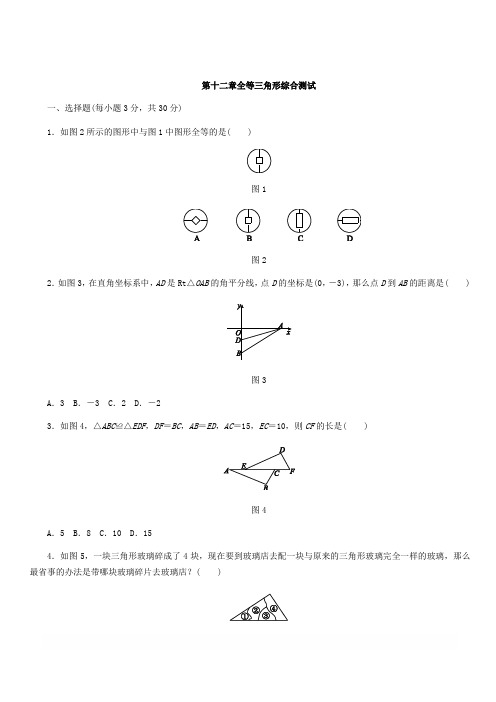
第十二章全等三角形综合测试一、选择题(每小题3分，共30分)1．如图2所示的图形中与图1中图形全等的是( )图1图22．如图3，在直角坐标系中，AD是Rt△OAB的角平分线，点D的坐标是(0，－3)，那么点D到AB的距离是( )图3A．3 B．－3 C．2 D．－23．如图4，△ABC≌△EDF，DF＝BC，AB＝ED，AC＝15，EC＝10，则CF的长是( )图4A．5 B．8 C．10 D．154．如图5，一块三角形玻璃碎成了4块，现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃，那么最省事的办法是带哪块玻璃碎片去玻璃店？( )图5A．① B．② C．③ D．④5．如图6所示，在△ABC和△ABD中，∠C＝∠D＝90°，要利用“HL”判定△ABC≌△ABD成立，还需要添加的条件是( )图6A．∠BAC＝∠BAD B．BC＝BD或AC＝ADC．∠ABC＝∠ABD D．AB为公共边6．已知图7中的两个三角形全等，则∠α的度数为( )图7A．105° B．75°C．60° D．45°7．如图8，点B，E在线段CD上，若∠C＝∠D，则添加下列条件，不一定能使△ABC≌△EFD的是( )图8A．BC＝FD，AC＝ED B．∠A＝∠DEF，AC＝EDC．AC＝ED，AB＝EF D．∠A＝∠DEF，BC＝FD8．如图9，AB⊥BC，BE⊥AC，∠1＝∠2，AD＝AB，则下列结论正确的是( )图9A．∠1＝∠EFD B．BE＝EC C．BF＝CD D．FD∥BC9．现已知线段a，b(a＜b)，∠MON＝90°，求作Rt△ABO，使得∠O＝90°，AB＝b，小惠和小雷的作法分别如下：小惠：①以点O为圆心、线段a的长为半径画弧，交射线ON于点A；②以点A为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．小雷：①以点O为圆心、线段a的长为半径画弧，交射线ON于点A；②以点O为圆心、线段b的长为半径画弧，交射线OM于点B，连接AB，△ABO即为所求．则下列说法中正确的是( )A．小惠的作法正确，小雷的作法错误B．小雷的作法正确，小惠的作法错误C．两人的作法都正确D．两人的作法都错误10．如图10，每个小方格都是边长为1的小正方形，△ABC是格点三角形(即顶点恰好是小正方形的顶点)，在图中与△ABC全等且有一条公共边的所有格点三角形的个数是( )图10A．5 B．4 C．3 D．2请将选择题答案填入下表：第Ⅱ卷 (非选择题 共70分)二、填空题(每小题3分，共18分)11．如图11，△ABC ≌△ADE ，BC 的延长线交DE 于点G.若∠B ＝24°，∠CAB ＝54°，∠DAC ＝16°，则∠DGB ＝________°.图1112．如图12，在Rt △ABC 中，∠C ＝90°，∠B ＝20°，以点A 为圆心，任意长为半径画弧分别交AB ，AC 于点M ，N ，再分别以点M ，N 为圆心，大于12MN 的长为半径画弧，两弧相交于点P ，连接AP 并延长交BC 于点D ，则∠ADB ＝________°.图1213．如图13，D 为Rt △ABC 中斜边BC 上的一点，且BD ＝AB ，过点D 作BC 的垂线，交AC 于点E ，若AE ＝12 cm ，则DE 的长为________cm .1314．如图14，四边形ABCD 的对角线AC ，BD 相交于点O ，△ABO ≌△ADO.有下列结论：①AC ⊥BD ；②CB ＝CD ；③△ABC ≌△ADC ；④DA ＝DC.其中所有正确结论的序号是________．图1415．如图15，△ABC的两条外角平分线BP，CP相交于点P，PE⊥AC交AC的延长线于点E.若△ABC的周长为11，PE＝2，S△BPC＝2，则S△ABC＝________．1516．如图16，在Rt△ABC中，∠C＝90°.E为AB的中点，D为AC上一点，BF∥AC，交DE的延长线于点F，AC ＝6，BC＝5，则四边形FBCD周长的最小值是________．图16三、解答题(共52分)17．(6分)如图17，已知△ABC.求作：直线MN，使MN经过点A，且MN∥BC.(尺规作图，保留作图痕迹，不写作法)图1718.(6分)如图18，△ABC≌△ADE，∠BAD＝40°，∠D＝50°，AD与BC相交于点O.探索线段AD与BC的位置关系，并说明理由．图1819．(6分)如图19，△ACF≌△ADE，AD＝9，AE＝4，求DF的长．图1920．(6分)如图20，C是AB的中点，AD＝CE，CD＝BE.求证：∠A＋∠ECA＝180°.图2021．(6分)如图21所示，海岛上有A，B两个观测点，点B在点A的正东方，海岛C在观测点A的正北方，海岛D在观测点B的正北方，从观测点A看海岛C，D的视角∠CAD与从观测点B看海岛C，D的视角∠CBD相等，那么海岛C，D到观测点A，B所在海岸的距离相等吗？为什么？图2122．(7分)如图22，在∠AOB的两边OA，OB上分别取OM＝ON，OD＝OE，DN和EM相交于点C.求证：点C在∠AOB的平分线上．图2223．(7分)在Rt△ABC中，BC＝AC，∠ACB＝90°，D为射线AB上一点，连接CD，过点C作线段CD的垂线l，在直线l上，分别在点C的两侧截取与线段CD相等的线段CE和CF，连接AE，BF.(1)当点D在线段AB上时(点D不与点A，B重合)，如图23(a)．①请你将图形补充完整；②线段BF，AD所在直线的位置关系为________，线段BF，AD的数量关系为________．(2)当点D在线段AB的延长线上时，如图23(b)．在(1)中②问的结论是否仍然成立？如果成立，请进行证明；如果不成立，请说明理由．图2324．(8分)如图24①，点A，B，C，D在同一直线上，AB＝CD，作EC⊥AD于点C，FB⊥AD于点B，且AE＝DF.(1)求证：EF平分线段BC；(2)若将△BFD沿AD方向平移得到图②时，其他条件不变，(1)中的结论是否仍成立？请说明理由．图24答案1．B2．A3．A4．D5．B6．B7．C8．D9．A10．B11．7012．12513．1214．①②③15．716．1617．解：如图所示，作∠MAB＝∠B，则直线MN即为所求．18．解：AD⊥BC.理由如下：∵△ABC≌△ADE，∠D＝50°，∴∠B＝∠D＝50°.在△AOB中，∠AOB＝180°－∠BAD－∠B＝180°－40°－50°＝90°，∴AD⊥BC.19．解：∵△ACF≌△ADE，∴AF＝AE，∴DF＝AD－AF＝AD－AE＝9－4＝5.20．证明：∵C是AB的中点，∴AC ＝CB.在△ACD 和△CBE 中，AC ＝CB ，AD ＝CE ，CD ＝BE ，∴△ACD ≌△CBE(SSS )，∴∠A ＝∠ECB ，∴AD ∥CE ，∴∠A ＋∠ECA ＝180°.21．解：相等．理由：设AD ，BC 相交于点O.∵∠CAD ＝∠CBD ，∠COA ＝∠DOB ，∴由三角形内角和定理，得∠C ＝∠D.由已知得∠CAB ＝∠DBA ＝90°.在△CAB 和△DBA 中，∠C ＝∠D ，∠CAB ＝∠DBA ，AB ＝BA ，∴△CAB ≌△DBA(AAS )，∴CA ＝DB ，∴海岛C ，D 到观测点A ，B 所在海岸的距离相等．22．证明：过点C 分别作CG ⊥OA 于点G ，CF ⊥OB 于点F ，如图．在△MOE 和△NOD 中，OM ＝ON ，∠MOE ＝∠NOD ，OE ＝OD ，∴△MOE ≌△NOD(SAS )，∴S △MOE ＝S △NOD ，∴S △MOE －S 四边形ODCE ＝S △NOD －S 四边形ODCE ，即S △MDC ＝S △NEC .由三角形面积公式得12DM ·CG ＝12EN ·CF. ∵OM ＝ON ，OD ＝OE ，∴DM＝EN，∴CG＝CF.又∵CG⊥OA，CF⊥OB，∴点C在∠AOB的平分线上．23．解：(1)①如图所示．②∵CD⊥EF，∴∠DCF＝90°.∵∠ACB＝90°，∴∠ACB＝∠DCF，∴∠ACD＝∠BCF.又∵AC＝BC，CD＝CF，∴△ACD≌△BCF，∴AD＝BF，∠BAC＝∠FBC，∴∠ABF＝∠ABC＋∠FBC＝∠ABC＋∠BAC＝90°，即BF⊥AD. 故答案为：垂直，相等．(2)成立．证明：∵CD⊥EF，∴∠DCF＝90°.∵∠ACB＝90°，∴∠DCF＝∠ACB，∴∠DCF＋∠BCD＝∠ACB＋∠BCD，∴∠BCF＝∠ACD.又∵AC＝BC，CD＝CF，∴△ACD≌△BCF，∴AD＝BF，∠BAC＝∠FBC，∴∠ABF＝∠ABC＋∠FBC＝∠ABC＋∠BAC＝90°，即BF⊥AD. 24．解：(1)证明：∵EC⊥AD，FB⊥AD，∴∠ACE＝∠DBF＝90°.∵AB＝CD，∴AB＋BC＝BC＋CD，即AC＝DB.在Rt△ACE和Rt△DBF中，AE＝DF，AC＝DB，∴Rt△ACE≌Rt△DBF(HL)，∴EC＝FB.在△CEG和△BFG中，∠ECG＝∠FBG＝90°，∠EGC＝∠FGB，EC＝FB，∴△CEG≌△BFG(AAS)，∴CG＝BG，即EF平分线段BC.(2)EF平分线段BC仍成立．理由：∵EC⊥AD，FB⊥AD，∴∠ACE＝∠DBF＝90°.∵AB＝CD，∴AB－BC＝CD－BC，即AC＝DB.在Rt△ACE和Rt△DBF中，AE＝DF，AC＝DB，∴Rt△ACE≌Rt△DBF(HL)，∴EC＝FB.在△CEG和△BFG中，∠ECG＝∠FBG＝90°，∠EGC＝∠FGB，EC＝FB，∴△CEG≌△BFG(AAS)，∴CG＝BG，即EF平分线段BC.。

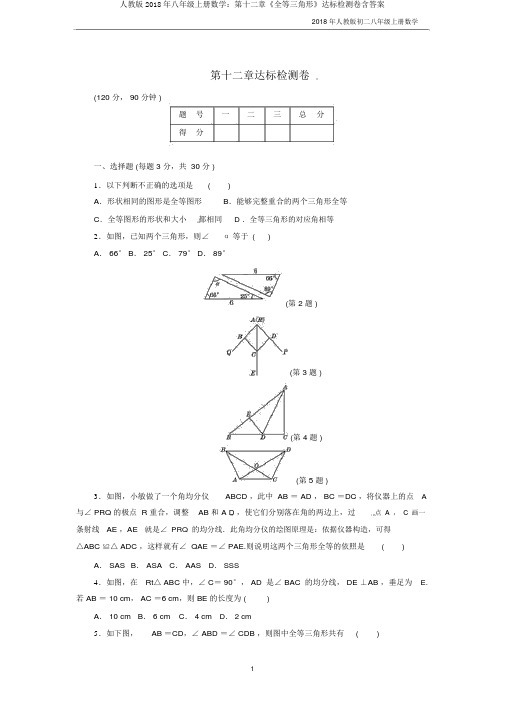
2018 年人教版初二八年级上册数学第十二章达标检测卷(120 分， 90 分钟 )题号一二三总分得分一、选择题 (每题 3 分，共 30 分 )1．以下判断不正确的选项是()A．形状相同的图形是全等图形B．能够完整重合的两个三角形全等C．全等图形的形状和大小都相同 D ．全等三角形的对应角相等2．如图，已知两个三角形，则∠α等于()A． 66° B． 25° C． 79° D． 89°(第 2 题 )(第 3 题 )(第 4 题 )(第 5 题 )3．如图，小敏做了一个角均分仪ABCD ，此中 AB ＝ AD ， BC ＝DC ，将仪器上的点A 与∠ PRQ 的极点 R 重合，调整AB 和 A D ，使它们分别落在角的两边上，过点A，C画一条射线AE ，AE就是∠ PRQ的均分线．此角均分仪的绘图原理是：依据仪器构造，可得△ABC ≌△ ADC ，这样就有∠ QAE ＝∠ PAE.则说明这两个三角形全等的依照是() A． SAS B． ASA C． AAS D． SSS4．如图，在Rt△ ABC 中，∠ C＝ 90°， AD 是∠ BAC 的均分线， DE ⊥AB ，垂足为 E.若 AB ＝ 10 cm， AC ＝6 cm，则 BE 的长度为 ()A． 10 cm B． 6 cm C． 4 cm D． 2 cm5．如下图，AB ＝CD，∠ ABD ＝∠ CDB ，则图中全等三角形共有()A． 5 对B．4 对C． 3 对 D ．2 对6．点P在∠AOB的均分线上，点P 到 OA 边的距离等于5，点 Q 是 OB 边上的随意一点，则以下选项正确的选项是()A．PQ＞5 B．PQ≥5 C． PQ＜ 5D． PQ≤ 57．在△ABC中，∠ B＝∠ C，与△ ABC全等的△ DEF中有一个角是100 °，那么在△ABC 中与这 100°角对应相等的角是()A．∠ A B．∠ B C．∠ C D ．∠ B 或∠ C8．如下图，已知△ABE ≌△ ACD ，∠ 1＝∠ 2，∠ B＝∠ C，则不正确的选项是() A．AB ＝ AC B．∠ BAE ＝∠ CAD C． BE＝ DC D． AD ＝ DE(第 8 题 )(第 9 题 )(第 10 题 )9．如图，直线a， b， c 表示三条公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地点有()A．一处B．两处C．三处D．四周10．已知：如图，在△ABC和△ ADE中，∠ BAC＝∠ DAE＝90°，AB＝AC，AD＝AE ，连结CD ， C， D ， E 三点在同一条直线上，连结BD ， BE.以下四个结论：①BD ＝CE；②∠ ACE ＋∠ DBC ＝ 45°；③ BD⊥ CE ；④∠ BAE ＋∠ DAC ＝ 180 °.此中结论正确的个数是 ()A． 1 B． 2 C．3D． 4二、填空题 (每题 3 分，共 30 分 )11．如图，∠1＝∠2，要使△ABE≌△ACE，还需增添一个条件是：________． (填上你以为适合的一个条件即可)12．如图，点O 在△ ABC内，且到三边的距离相等．若∠ A ＝ 60°，则∠ BOC ＝________ °.13．在△ABC中，AB＝4，AC＝3，AD是△ABC的角均分线，则△ABD 与△ ACD 的面积之比是 ________．[根源学&科&网](第 11 题 )(第 12 题 )(第 15 题 )(第 16 题 )14．已知等腰△ABC 的周长为18 cm， BC＝ 8 cm，若△ ABC ≌△ A′ B′，C则′△ A′ B′ C′的腰长等于 ________．15．如图，BE⊥AC，垂足为 D ，且AD ＝ CD ， BD ＝ ED. 若∠ ABC ＝ 54°，则∠ E＝________ °.16．如图，△ABC≌△DCB，AC与BD订交于点E，若∠ A ＝∠ D ＝ 80°，∠ ABC ＝60°，则∠ BEC 等于 ________．[根源:]17．如图，OP均分∠MON，PE⊥OM于E，PF⊥ ON于F，OA＝OB，则图中共有________对全等三角形．18．如图，已知P(3， 3)，点 B、 A 分别在 x 轴正半轴和y 轴正半轴上，∠APB ＝ 90°，则OA ＋ OB＝________ ．(第 17 题)(第 18 题)(第 19 题 )(第 20 题 )19．如图，AE⊥AB，且AE ＝ AB ， BC ⊥ CD ，且B C ＝ CD ，请依照图中所标明的数据，计算图中实线所围成的图形的面积S 是 ________．20．如图，已知点P 到 BE ， BD ， AC 的距离恰巧相等，则点P 的地点：①在∠DBC 的均分线上；②在∠DAC的均分线上；③在∠ECA 的均分线上；④正是∠DBC ，∠ DAC ，∠ECA 的均分线的交点，上述结论中，正确的有________． (填序号 )三、解答题 (21、 22 题每题 7 分， 23、 24 题每题 8 分， 25～ 27 题每题 10 分，共 60 分)21．如图，按以下要求作图：(1)作出△ ABC 的角均分线CD ；(2)作出△ ABC 的中线 BE；(3)作出△ ABC 的高 AF.(不写作法 )(第 21 题 )[根源:]22．如图，已知△EFG≌△ NMH ，∠ F 与∠ M 是对应角．(1)写出全部相等的线段与相等的角；(2)若 EF＝ 2.1 cm， FH ＝ 1.1 cm， HM ＝ 3.3 cm，求 MN 和 HG 的长度．(第 22 题 )23．如图，AD⊥AE，AB⊥AC，AD＝AE，AB＝AC.求证：△ABD≌△ACE.(第 23 题 )24．如图，AC∥BE，点D在BC上，AB＝DE，∠ABE＝∠CDE.求证： DC ＝ BE－ AC.(第 24 题 )25．如下图，在△ABC 中，∠ C＝ 90°， AD 是∠ BAC 的均分线， DE⊥AB 交 AB 于E， F 在 AC 上， BD ＝DF.求证： (1)CF＝ EB ； (2)AB ＝ AF ＋ 2EB.(第 25 题 )26．如图，A，B两建筑物位于河的两岸，要测得它们之间的距离，能够从 B 点出发在河岸上画一条射线 BF，在 BF 上截取 BC＝ CD，过 D 作 DE ∥ AB ，使 E， C，A 在同向来线上，则 DE 的长就是 A ， B 之间的距离，请你说明道理．(第 26 题 )27．如图(1)，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连结AD，以AD为一边且在 AD 的右边作正方形 ADEF ，连结 CF.(1)假如 AB ＝AC ，∠ BAC ＝ 90°，①当点 D 在线段 BC 上时 (与点 B 不重合 )，如图 (2)，线段 CF， BD 所在直线的地点关系为______，线段 CF，BD 的数目关系为 ________；②当点 D 在线段BC 的延伸线上时，如图(3)，①中的结论能否仍旧建立，并说明理由；(2)假如 AB ≠ AC ，∠ BAC 是锐角，点 D 在线段 BC 上，当∠ ACB 知足什么条件时，CF⊥BC( 点 C、 F 不重合 )，并说明原因．(第 27 题 )答案一、 1.A 2.D 3.D 4.C 5.C 6.B7． A 8.D9． D点拨： 如图，在△ ABC 内部，找一点到三边距离相等，依据到角的两边距离相等的点在角的均分线上，可知，此点在各内角的均分线上，作∠ ABC ，∠ BCA 的角均分线，交于点 O 1，由角均分线的性质可知，O 1 到 AB ， BC ， AC 的距离相等．同理，作∠ACD ，∠ CAE 的角均分线，交于点 O 2，则 O 2 到 AC ， BC ，AB 的距离相等，相同作法得 到点 O 3，O 4.故可供选择的地点有四周．应选D .(第 9 题 )10． D二、 11.∠ B ＝∠ C( 答案不独一 )12． 120 13.4∶ 3 14.8 cm 或 5 cm15． 27 16.100 °17． 3 点拨： △OPE ≌△ OPF ，△ OPA ≌△ OPB ，△ AEP ≌△ BFP ，因此共有 3 对全等三角形．18． 6 点拨： 过点 P 作 PC ⊥ OB 于 C ， PD ⊥ OA 于 D ，则 PD ＝ PC ＝ DO ＝ OC ＝3，可证△ APD ≌△ BPC ，∴ DA ＝ CB ，∴ OA ＋ OB ＝ OA ＋ OC ＋ CB ＝ OA ＋ OC ＋ DA ＝ OC ＋ OD＝ 6.19． 50 点拨： 由题意易知，△ AFE ≌△ BGA ，△ BGC ≌△ CHD. ∴ FA ＝ BG ＝ 3 ， AG1＝EF ＝6， CG ＝ HD ＝ 4， CH ＝ BG ＝ 3.∴ S ＝S 梯形 EFHD －S △ EFA － S △ AGB － S △ BGC － S △CHD ＝ 2(4＋ 6)×(3＋ 6＋ 4＋3) － 1× 3× 6×2－ 1× 3×4× 2＝ 80－ 18－ 12＝50.2 220．①②③④三、 21.解： (1)角均分线 CD 如图①所示．(2) 中线 BE 如图②所示． (3) 高 AF 如图③所示．(第 21 题 )22．解：(1)EF＝MN，EG＝HN，FG＝MH，FH＝GM，∠F＝∠M，∠E＝∠N，∠EGF ＝∠ MHN ，∠ FHN ＝∠ EGM.(2)∵△ EFG≌△ NMH ，∴ MN ＝ EF＝ 2.1 cm， GF＝HM ＝ 3.3 cm，∵FH＝ 1.1 cm，∴ HG＝ GF－ FH ＝ 3.3－ 1.1＝2.2 (cm)．23．证明：∵AD⊥AE，AB⊥AC，∴∠CAB＝∠DAE＝90°.∴∠ CAB ＋∠ CAD ＝∠ DAE ＋∠ CAD ，即∠ BAD ＝∠ CAE.在△ ABD 和△ ACE 中，AB ＝AC ，∠BAD ＝∠ CAE ，[根源学科网]AD ＝AE ，∴△ ABD ≌△ ACE.24．证明：∵AC∥BE，∴∠DBE＝∠C.∵∠CDE＝∠DBE＋∠E，∠ABE＝∠ABC＋∠ C＝∠ DBE ，∠DBE ，∠ABE ＝∠ CDE ，∴∠ E ＝∠ ABC. 在△ ABC与△DEB中，∠ ABC＝∠ E，AB ＝DE，∴△ ABC ≌△ DEB( AAS)．∴ BC＝BE ，AC ＝ BD. ∴ DC＝ BC－ BD ＝ BE－ AC.25．证明：(1)∵AD是∠BAC的均分线，DE⊥AB，DC⊥AC，∴DE＝ DC.又∵ BD＝ DF，∴Rt△ CDF≌ Rt△ EDB( HL )．∴CF＝ EB.(2)由 (1) 可知 DE ＝ DC，又∵ AD ＝ AD ，∴Rt△ ADC ≌ Rt△ADE.∴AC ＝AE.∴AB ＝AE ＋BE ＝ AC ＋ EB＝ AF ＋ CF＋EB ＝AF ＋ 2EB.2018 年人教版初二八年级上册数学点拨： (1)依据角均分线的性质“角均分线上的点到角的两边的距离相等”，可得点D 到AB 的距离＝点 D 到 AC 的距离，即 CD ＝ DE. 再依据 Rt△ CDF≌ Rt△ EDB ，得 CF＝ EB.(2)利用角均分线的性质证明Rt△ADC ≌Rt△ ADE ，∴ AC ＝ AE ，再将线段AB 进行转化．26．解：∵DE∥AB，∴∠A＝∠E.∵ E， C，A 在同向来线上，B， C，D 在同向来线上，∴∠ACB ＝∠ ECD.∠ A ＝∠ E，在△ ABC 与△ EDC 中，∠ ACB＝∠ ECD，BC ＝ CD ，∴△ ABC ≌△ EDC( AAS)．∴ AB ＝DE.27．解：(1)①CF⊥BD；CF＝BD②当点 D 在线段 BC 的延伸线上时，①中的结论仍旧建立．原因：由正方形ADEF 得AD ＝ AF ，∠ DAF ＝ 90°.∵∠ BAC ＝ 90°，∴∠ DAF ＝∠ BAC.∴∠ DAB ＝∠ FAC.又∵ AB ＝ AC ，∴△ DAB ≌△ FAC.∴ CF＝ BD ，∠ ACF ＝∠ ABD.∵∠ BAC ＝ 90°， AB ＝AC ，∴△ ABC 是等腰直角三角形．∴∠ABC ＝∠ ACB ＝45°.∴∠ ACF ＝ 45°.∴∠ BCF ＝∠ ACB ＋∠ ACF ＝ 90°.即 CF⊥BD. 来[源:Z_xx_](第 27 题)(2)当∠ ACB ＝ 45°时， CF⊥ BC( 如图 )．原因：过点 A 作 AG ⊥ AC 交 CB 的延伸线于点G，则∠ GAC ＝90°，∵∠ ACB ＝ 45°，∠AGC ＝ 90°－∠ ACB ，∴∠ AGC ＝ 90°－ 45°＝ 45°，∴∠ ACB ＝∠ AGC ＝ 45°，∴△ AGC 是等腰直角三角形，∴AC ＝ AG. 又∵∠ DAG ＝∠ FAC( 同角的余角相等) ， AD ＝ AF ，∴△ GAD ≌△ CAF ，∴∠ ACF ＝∠ AGC ＝ 45°，∴∠ BCF ＝∠ ACB ＋∠ ACF ＝ 45°＋ 45°＝90°，即 CF⊥ BC.。

一、选择题1．如图，在ABC 中，AB AC =，点D ，E 在BC 上，连接AD ，AE ，若只添加一个条件使DAB EAC ∠=∠，则添加的条件不能为（ ）A ．BD CE =B ．AD AE =C ．BE CD = D ．DA DE = D解析：D【分析】 根据全等三角形的判定与性质，等边对等角的性质对各选项分析判断后利用排除法求解．【详解】解：A 、添加BD ＝CE ，可以利用“边角边”证明△ABD 和△ACE 全等，再根据全等三角形对应角相等得到∠DAB ＝∠EAC ，故本选项不符合题意；B 、添加AD ＝AE ，根据等边对等角可得∠ADE ＝∠AED ，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB ＝∠EAC ，故本选项不符合题意；C 、添加BE ＝CD 可以利用“边角边”证明△ABE 和△ACD 全等，再根据全等三角形对应角相等得到∠BAE=∠CAD ，可得∠DAB ＝∠EAC ，故本选项不符合题意；D 、添加DA ＝DE 无法求出∠DAB ＝∠EAC ，故本选项符合题意．故选：D ．【点睛】本题考查了等腰三角形等边对等角的性质，三角形的一个外角等于与它不相邻的两个内角的和的性质，全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解题的关键．2．如图，已知ABC DCB ∠=∠，添加一个条件使ABC DCB △△≌，下列添加的条件不能使ABC DCB △△≌的是（ ）A ．A D ∠=∠B ．AB DC = C ．AC DB =D ．ACB DBC ∠=∠ C解析：C【分析】 根据全等三角形的判定与性质综合分析即可；【详解】在ABC 和DCB 中，A D ABC DCB BC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩，故ABC DCB △△≌，A 不符合题意；在ABC 和DCB 中，AB DC ABC DCB BC CB =⎧⎪∠=∠⎨⎪=⎩，故ABC DCB △△≌，B 不符合题意；只有AC=BD ，BC=CB ，ABC DCB ∠=∠，不符合全等三角形的判定，故C 符合题意；在ABC 和DCB 中，ACB DBC CB BC ABC DCB ∠=∠⎧⎪=⎨⎪∠=∠⎩，故ABC DCB △△≌，D 不符合题意；故答案选C ．【点睛】本题主要考查了全等三角形的判定与性质，准确分析判断是解题的关键．3．如图，AD 平分BAC ∠交BC 于点D ，DE AB ⊥于点E ，DF AC ⊥于点F ，若ABC S 12=，DF 2=，AC 3=，则AB 的长是 ( )A ．2B ．4C ．7D ．9D解析：D【分析】 求出DE 的值，代入面积公式得出关于AB 的方程，求出即可．【详解】解：∵AD 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，∴DE=DF=2，∵S △ABC =S △ABD +S △ACD ，∴12=12×AB×DE+12×AC×DF ， ∴24=AB×2+3×2，∴AB=9，故选：D ．【点睛】本题考查了角平分线性质，三角形的面积的应用，注意：角平分线上的点到角两边的距离相等．4．如图所示，下面甲、乙、丙三个三角形和ABC 全等的图形是（ ）A ．甲和乙B ．乙和丙C ．只有丙D ．只有乙B解析：B【分析】 甲只有2个已知条件，缺少判定依据；乙可根据SAS 判定与△ABC 全等；丙可根据AAS 判定与△ABC 全等，可得答案．【详解】解：甲三角形只知道两条边长无法判断是否与△ABC 全等；乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC 全等；丙三角形72°内角及所对边与△ABC 对应相等且均有50°内角，可根据AAS 判定乙与△ABC 全等；则与△ABC 全等的有乙和丙，故选：B ．【点睛】本题主要考查全等三角形的判定定理，熟练掌握并充分理解三角形全等的判定定理，注意对应二字的理解很重要．5．如图，123,,l l l 是三条两两相交的公路，现需建一个仓库，要求仓库到三条公路距离相等，则仓库的可能地址有（ ）处．A ．1B ．2C ．3D ．4D解析：D【分析】 到三条相互交叉的公路距离相等的地点应是三条角平分线的交点，把三条公路的中心部位看作三角形，那么这个三角形两个内角平分线的交点以及三个外角两两平分线的交点都满足要求．【详解】（1）三角形两个内角平分线的交点，共一处（2）三个外角两两平分线的交点，共三处，共四处，故选：D．．【点睛】此题考查角平分线的性质：角平分线上的点到角两边的距离相等，熟记性质是正确解题的关键．6．下列说法不正确的是（）A．三边分别相等的两个三角形全等B．有两边及一角对应相等的两个三角形全等C．有两角及一边对应相等的两个三角形全等D．斜边和一条直角边分别相等的两个直角三角形全等B解析：B【分析】直接利用三角形全等的判定条件进行判定，即可求得答案；注意而SSA是不能判定三角形全等的.【详解】解：A，三边分别相等的两个三角形全等，故本选项正确；B，两边和一个角对应相等的两个三角形不一定全等，故本选项错误；C，两个角和一个边对应相等的两个三角形，可利用ASA或AAS判定全等，故本选项正确；D，斜边和一条直角边分别相等的两个直角三角形全等，故本选项正确．故选：B【点睛】此题考查了全等三角形的判定．注意普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等．7．如图，已知AC⊥BC，DE⊥AB，AD平分∠BAC，下面结论错误的是（）A．BD＋ED＝BC B．∠B＝2∠DACC．AD平分∠EDC D．ED＋AC>AD B解析：B【分析】利用角平分线的性质定理判断A；利用直角三角形两锐角互余判断B；证明△AED≌△ACD，由此判断C；利用三角形三边关系得到AC+CD>AD，由此判断D．【详解】∵AC⊥BC，DE⊥AB，AD平分∠BAC，∴DE=DC，∠BAD=∠DAC，∵BD+DC=BC，∴BD+ED=BC，故A正确；∵∠C=90︒，∴∠B+∠BAC=90︒，∴∠B+2∠DAC=90︒，故B错误；∵DE⊥AB，∴∠AED=∠C=90︒,又∵∠BAD=∠DAC，DE=CD，∴△AED≌△ACD，∴∠ADE=∠ADC，∴AD平分∠EDC，故C正确；在△ACD中，AC+CD>AD，∴ED＋AC>AD，故D正确；故选：B．【点睛】此题考查三角形的三边关系，角平分线的性质定理，全等三角形的判定及性质，直角三角形两锐角互余的性质，熟记各知识点并应用解决问题是解题的关键．8．如图，OB平分∠MON，A为OB的中点，AE⊥ON，EA=3，D为OM上的一个动点，C 是DA延长线与BC的交点，BC//OM，则CD的最小值是（）A ．6B ．8C ．10D ．12A解析：A【分析】 根据两条平行线之间的距离可知当CD ⊥OM 时，CD 取最小值，先利用角平分线的性质得出AD =AE =3，利用全等三角形的判定和性质得出AC =AD =AE =3，进而解答即可．【详解】解：由题意得，当CD ⊥OM 时，CD 取最小值，∵OB 平分∠MON ，AE ⊥ON 于点E ，CD ⊥OM ，∴AD =AE =3，∵BC ∥OM ，∴∠DOA =∠B ，∵A 为OB 中点，∴AB =AO ，在△ADO 与△ABC 中B DOA AB AO BAC DAO ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ADO ≌△ABC (SAS ),∴AC =AD =3，∴336CD AC AD =+=+=，故选A ．【点睛】此题考查角平分线的性质、全等三角形的判定和性质、平行线之间的距离，关键是利用全等三角形的判定和性质得出AC =AD =AE =3．9．如图，AD 是ABC 的高，AD BD 8==，E 是AD 上的一点，BE AC 10==，AE 2=，BE 的延长线交AC 于点F ，则EF 的长为（ ）A ．1.2B ．1.5C ．2.5D ．3A 解析：A【分析】先证明Rt ACD ≌()Rt BED HL ，得CD ED AD AE 6==-=，CAD EBD ∠∠=，再证BE AC ⊥，然后由三角形面积关系求出BF 11.2=，则EF BF BE 1.2=-=．【详解】解：AD 是ABC 的高，AD BC ∴⊥，ADC BDE 90∠∠∴==︒，在Rt ACD 和Rt BED 中，AC BE AD BD =⎧⎨=⎩， Rt ACD ∴≌()Rt BED HL ，CD ED AD AE 826∴==-=-=，CAD EBD ∠∠=，C CAD 90∠∠+=︒，C EBD 90∠∠∴+=︒，BFC 90∠∴=︒，BE AC ∴⊥， ABC 的面积ABD =的面积ACD +的面积， 111AC BF AD BD CD AD 222∴⨯=⨯+⨯， AC BF AD BD CD AD ∴⨯=⨯+⨯，即10BF 8886112=⨯+⨯=，BF 11.2∴=，EF BF BE 11.210 1.2∴=-=-=，故选：A ．【点睛】本题考查了全等三角形的判定和性质、直角三角形的性质以及三角形面积等知识；证明三角形全等是解题的关键．10．如图，△ACB ≌△A 'CB '，∠BCB '=25°，则∠ACA '的度数为（ ）A ．35°B ．30°C ．25°D ．20°C解析：C【分析】利用全等三角形的性质可得∠A′CB′=∠ACB ，再利用等式的性质可得答案．【详解】解：∵△ACB ≌△A′CB′，∴∠A′CB′=∠ACB ，∴∠A′CB′-∠A′CB=∠ACB-∠A′CB ，∴∠ACA′=∠BCB′=25°，故选：C ．【点睛】此题主要考查了全等三角形的性质，关键是掌握全等三角形对应角相等．二、填空题11．如图，点C 在AOB ∠的平分线上，CD OA ⊥于点D ，且2CD =，如果E 是射线OB 上一点，那么CE 长度的最小值是___________．2【分析】根据垂线段最短及角平分线的性质定理求解【详解】解：如图由垂线段最短定理可知：当CE ⊥OB 时CE 的长度最小∵点C 在∠AOB 的平分线上CD ⊥OA ∴CE=CD=2故答案为2【点睛】本题是基础题目解析：2【分析】根据垂线段最短及角平分线的性质定理求解 ．【详解】解：如图，由垂线段最短定理可知：当CE⊥OB时，CE 的长度最小，∵点C在∠AOB 的平分线上，CD⊥OA，∴CE=CD=2，故答案为2 ．【点睛】本题是基础题目，熟练掌握垂线段最短及角平分线的性质定理是解题关键．0,3，另12．如图，把等腰直角三角板放平面直角坐标系内，已知直角顶点C的坐标为()8,8，则点A的坐标为____________一个顶点B的坐标为()（5－5）【分析】根据余角的性质可得∠BCP=∠CAQ根据全等三角形的判定与性质可得AQCQ根据线段的和差可得OQ可得答案【详解】解：作BP⊥y轴AQ⊥y轴如图∴∠BPC=∠AQC=90°∵BC=A解析：（5，－5）【分析】根据余角的性质，可得∠BCP=∠CAQ，根据全等三角形的判定与性质，可得AQ，CQ，根据线段的和差，可得OQ，可得答案．【详解】解：作BP⊥y轴，AQ⊥y轴，如图，∴∠BPC=∠AQC=90°∵BC=AC ，∠BCA=90°，∴∠BCP+∠ACQ=90°．又∠CAQ+∠ACQ=90°∴∠BCP=∠CAQ ．在△BPC 和△CQA 中，BPC CQA BCP CAQ BC AC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ Rt △BPC ≌Rt △ACQ （AAS ），AQ=PC=8-3=5；CQ=BP=8．∵QO=QC-CO=8-3=5，∴A （5，-5），故答案为：（5，-5）．【点睛】本题考查了坐标与图形，全等三角形的判定与性质，利用全等三角形的判定与性质得出AQ ，CQ 是解题关键．13．如图，在ABC 中，=6AB ，=4AC ，点D ，E 分别在边AB ，AC 上，2BD AE CE ===，//CE AB 交DE 的延长线于点F ，则CF 的长为_____________．4【分析】根据ASA 证明△ADE ≌△CFE 得CF=AD 再求出AD 的长即可【详解】解：∵AB=6BD=2∴AD=AB-BD=6-2=4∵∴∠BAC=∠FCE 在△ADE 和△CFE 中∴△ADE ≌△CFE ∴解析：4【分析】根据ASA 证明△ADE ≌△CFE 得CF=AD ，再求出AD 的长即可．【详解】解：∵AB=6，BD=2∴AD=AB-BD=6-2=4∵//CE AB∴∠BAC=∠FCE ，在△ADE 和△CFE 中BAC FCE AE CEAED CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△CFE∴CF=AD=4．故答案为：4．【点睛】此题主要考查了全等三角形的判定与性质，证明△ADE≌△CFE是解答此题的关键．14．如图，D，E分别是AB，AC上的点，AD=AE，请添加一个条件，使得ABE≌ACD．这个条件可以为_____（只填一个条件即可）．∠B=∠C（或∠ADC=∠AEB或AB=AC）【分析】根据已知条件知两个三角形已经具有∠A=∠AAD=AE两个条件对应相等故再添加一组对应角相等或是AB=AC即可得到ABE≌ACD【详解】∵∠A=∠解析：∠B=∠C（或∠ADC=∠AEB或AB=AC）【分析】根据已知条件知两个三角形已经具有∠A=∠A，AD=AE两个条件对应相等，故再添加一组对应角相等或是AB=AC即可得到ABE≌ACD．【详解】∵∠A=∠A，AD=AE，∴当∠B=∠C时，可利用AAS证明ABE≌ACD；当∠ADC=∠AEB时，可利用ASA证明ABE≌ACD；当AB=AC时，可利用SAS证明ABE≌ACD；故答案为：∠B=∠C（或∠ADC=∠AEB或AB=AC）．【点睛】此题考查添加一个条件证明三角形全等，熟记三角形全等的判定定理是解题的关键．15．如图，在△ABC中，∠C＝90°，AD是∠BAC的角平分线，若BC＝8cm，BD＝5cm，AB=10cm,则S△ABD=______．15cm2【分析】过点D作DE⊥AB于E根据角平分线的性质可得DE=CD根据三角形的面积公式即可求得△ABD的面积【详解】解：过点D作DE⊥AB于E∵AD是∠BAC的角平分线∠C＝90°DE⊥AB∴解析：15cm2【分析】过点D作DE⊥AB于E，根据角平分线的性质可得DE=CD，根据三角形的面积公式即可求得△ABD的面积．【详解】解：过点D 作DE ⊥AB 于E ，∵AD 是∠BAC 的角平分线，∠C ＝90°，DE ⊥AB∴DE=DC ，∵BC ＝8cm ，BD ＝5cm ，∴DE=DC=3cm ，∴S △ABD =12·AB·DE=12×10×3=15(cm 2)， 故答案为：15cm 2．【点睛】本题考查角平分线的性质、三角形的面积公式，熟练掌握角平分线的性质是解答的关键． 16．如图，点D 在BC 上，DE ⊥AB 于点E ，DF ⊥BC 交AC 于点F ，BD ＝CF ，BE ＝CD ．若∠AFD ＝145°，则∠EDF ＝_____．55°【分析】由∠AFD ＝145°可求得∠CFD=35°证明Rt △BDE ≌△Rt △CFD 根据对应角相等推知∠BDE=∠CFD=35°进而可求出∠EDF 的值【详解】解：∵∠DFC+∠AFD=180°∠解析：55°【分析】由∠AFD ＝145°可求得∠CFD=35°，证明Rt △BDE ≌△Rt △CFD ，根据对应角相等推知∠BDE=∠CFD=35°，进而可求出∠EDF 的值．【详解】解：∵∠DFC+∠AFD=180°，∠AFD=145°，∴∠CFD=35°．又∵DE ⊥AB ，DF ⊥BC ，∴∠BED=∠CDF=90°，在Rt △BDE 与△Rt △CFD 中，BE CD BD CF =⎧⎨=⎩， ∴Rt △BDE ≌△Rt △CFD （HL ），∴∠BDE=∠CFD=35°，∴∠EDF =180°-90°-35°=55°．故答案是：55°．【点睛】本题考查了全等三角形的判定与性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．17．如图，点P 是AOC ∠的角平分线上一点，PD OA ⊥，垂足为点D ，且5PD =，点M 是射线OC 上一动点，则PM 的最小值为__．5【分析】根据角平分线的性质及垂线段最短解答【详解】根据垂线段最短可知：当PM ⊥OC 时PM 最小∵OP 平分PD=5∴PM=PD=5故答案为：5【点睛】此题考查角平分线的性质垂线段最短掌握点到直线的所有 解析：5【分析】根据角平分线的性质及垂线段最短解答.【详解】根据垂线段最短可知：当PM ⊥OC 时，PM 最小，∵OP 平分AOC ∠，PD OA ⊥，PD=5，∴PM=PD=5，故答案为：5.【点睛】此题考查角平分线的性质，垂线段最短，掌握点到直线的所有连线中垂线段最短是解题的关键.18．如图，90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥，垂足分别为,D E ，若9,6AD DE ==，则BE 的长为________________________．3【分析】由AD ⊥CEBE ⊥CE 可以得到∠BEC=∠CDA=90°再根据∠ACB=90°可以得到∠BCE=∠CAD 从而求得△CEB ≌△ADC 然后利用全等三角形的性质可以求得BE 的长【详解】解：∵∠A解析：3【分析】由AD⊥CE，BE⊥CE，可以得到∠BEC=∠CDA=90°，再根据∠ACB=90°，可以得到∠BCE=∠CAD，从而求得△CEB≌△ADC，然后利用全等三角形的性质可以求得BE的长．【详解】解：∵∠ACB=90°，BE⊥CE，AD⊥CE，∴∠BCE+∠DCA=90°，∠BEC=∠CDA=90°，∴∠ACD+∠CAD=90°，∴∠BCE=∠CAD，在△CEB和△ADC中，BCE CADBEC CDA AC BC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CEB≌△ADC（AAS）；∴BE=CD，CE=AD=9．∵DC=CE-DE，DE=6，∴DC=9-6=3，∴BE=3．故答案为：3【点睛】本题考查全等三角形的判定与性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．19．如图，AB＝8cm，AC＝5cm，∠A＝∠B，点P在线段AB上以2cm/s的速度由点A向B 运动，同时，点Q以x cm/s的速度从点B出发在射线BD上运动，则△ACP与△BPQ全等时，x的值为_____________2或【分析】由∠A＝∠B可知△ACP与△BPQ全等时CP和PQ是对应边则分AP＝BQ和AP＝PB两种情况进行讨论即可【详解】设动点的运动时间为t秒则AP＝2tBP＝AB－AP＝8－2tBQ＝xt∵∠解析：2或5 2【分析】由∠A＝∠B，可知△ACP与△BPQ全等时，CP和PQ是对应边，则分AP＝BQ和AP＝PB两种情况进行讨论即可．【详解】设动点的运动时间为t 秒，则AP ＝2t ，BP ＝AB －AP ＝8－2t ，BQ ＝xt ，∵∠A ＝∠B ，∴CP 和PQ 是对应边，当△ACP 与△BPQ 全等时，①AP ＝BQ ，即：2t ＝ xt ，解得：x ＝2，②AP ＝PB ，即：2t ＝8－2t ，解得：t ＝2，此时，BQ ＝AC ，xt ＝5，即：2x ＝5，解得：x ＝52故填：2或52． 【点睛】本题考查全等三角形的性质，“分类讨论”的数学思想是关键．20．如图所示，AB AC =，AD AE =，BAC DAE ∠=∠，点D 在线段BE 上．若125∠=︒，230∠=︒，则3∠=______．55°【分析】先证明△ABD ≌△ACE （SAS ）；再利用全等三角形的性质：对应角相等求得∠2=∠ABE ；最后根据三角形内角与外角的性质即可求出答案【详解】∵∴∠1+∠CAD=∠CAE+∠CAD ∴∠1解析：55°【分析】先证明△ABD ≌△ACE （SAS ）；再利用全等三角形的性质：对应角相等，求得∠2=∠ABE ；最后根据三角形内角与外角的性质即可求出答案．【详解】∵BAC DAE ∠=∠，∴∠1+∠CAD=∠CAE+∠CAD ，∴∠1=∠CAE ；在△ABD 与△ACE 中，1AD AE CAE AB AC =⎧⎪∠=∠⎨⎪=⎩，∴△ABD ≌△ACE （SAS ）；∴∠2=∠ABE ；∵∠3=∠ABE+∠1=∠1+∠2，∠1=25°，∠2=30°，∴∠3=55°．故答案为：55°．【点睛】本题考查了全等三角形的判定及性质，三角形的外角性质；将所求的角与已知角通过全等及内角、外角之间的关系联系起来是解答此题的关键．三、解答题21．（1）如图，∠MAB＝30°，AB＝2cm，点C在射线AM上，画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题，请画出图形，并写出你所选取的BC 的长约为cm（精确到0.lcm）．（2）∠MAB为锐角，AB＝a，点C在射线AM上，点B到射线AM的距离为d，BC＝x，若△ABC的形状、大小是唯一确定的，则x的取值范围是．解析：（1）见解析，1.2；（2）x=d或x≥a【分析】（1）可以取BC＝1.2cm（1cm＜BC＜2cm），画出图形即可；（2）当x＝d或x≥a时，三角形是唯一确定的．【详解】（1）如图，选取的BC的长约为1.2cm，故答案是：1.2；（2）若△ABC的形状、大小是唯一确定的，则x的取值范围是x＝d或x≥a，故答案为：x=d或x≥a．【点睛】本题考查全等三角形的判定，解题的关键是理解题意，掌握“有两边和其中一边的对角分别相等的两个三角形不一定全等”，属于中考常考题型．22．（阅读理解）AB=，课外兴趣小组活动时，老师提出了如下问题：如图1，ABC中，若8AC=，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的6=，请根据小明的方法思考：解决方法：延长AD到点E，使DE AD△的理由是______．（1）由已知和作图能得到ADC≌EDB（2）求得AD的取值范围是______．（感悟）解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．（问题解决）（3）如图2，在ABC 中，点D 是BC 的中点，点M 在AB 边上，点N 在AC 边上，若DM DN ⊥，求证：BM CN MN +>．解析：（1）SAS ；（2）17AD <<；（3）见解析【分析】（1）根据AD=DE ，∠ADC=∠BDE ，BD=DC 推出△ADC 和△EDB 全等即可；（2）根据全等得出BE=AC=6，AE=2AD ，由三角形三边关系定理得出8-6＜2AD ＜8+6，求出即可；（3）延长ND 至点E ，使DE DN =，连接BE 、ME ，证明BED ≌()SAS CND △，得到BE CN =，根据三角形三边关系解答即可．【详解】（1）解：∵在△ADC 和△EDB 中，AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△EDB （SAS ），故答案为：SAS ；（2）解：∵由（1）知：△ADC ≌△EDB ，∴BE=AC=6，AE=2AD ，∵在△ABE 中，AB=8，由三角形三边关系定理得：8-6＜2AD ＜8+6，∴1＜AD ＜7，故答案为：1＜AD ＜7．（3）证明：延长ND 至点E ，使DE DN =，连接BE 、ME ，如图所示：∵点D 是BC 的中点，∴BD CD =．在BED 和CND △中，DE DN BDE CDN BD CD =⎧⎪∠=∠⎨⎪=⎩， ∴BED ≌()SAS CND △，∴BE CN =，∵DM DN ⊥，DE DN =，∴ME MN =，在BEM △中，由三角形的三边关系得：BM BE ME +>，∴BM CN MN +>．【点睛】本题是三角形综合题，主要考查了三角形的中线，三角形的三边关系定理，全等三角形的性质和判定等知识点，主要考查学生运用定理进行推理的能力．23．如图，△ABC 中，AB=AC ，∠BAC=90°，CD 平分∠ACB ，BE ⊥CD ，垂足E 在CD 的延长线上．求证：CD=2BE ．解析：见解析【分析】根据等角的余角相等求出∠ACD=∠ABF ，再利用“角边角”证明△AFB ≌△ADC 可得CD=BF ，利用“角边角”证明△BCE 和△FCE 全等，根据全等三角形对应边相等BE=EF ，整理即可得证．【详解】证明：∵BE ⊥CD ，∠BAC=90°，∴∠ACD+∠F=180°-90°=90°，∠ABF+∠F=180°-90°=90°，∴∠ACD=∠ABF ，在△AFB 和△ADC 中，90ACD ABF AB ACCAD BAF ∠∠⎧⎪⎨⎪∠∠︒⎩＝＝＝＝， ∴△AFB ≌△ADC （ASA ）；∴CD=BF ，∵CD 平分∠ACB ，∴∠BCE=∠FCE ，在△BCE 和△FCE 中，90BCE FCE CE CEBEC FEC ∠∠⎧⎪⎨⎪∠∠︒⎩＝＝＝＝， ∴△BCE ≌△FCE （ASA ），∴BE=EF ，∴BF=2BE∴CD=2BE ．【点睛】本题考查了全等三角形的判定与性质，熟练掌握三角形全等的证明方法并准确识图是解题的关键．24．如图，在ACD △与BCE 中，AC BC =，CD CE =，ECD ACB ∠=∠．（1）求证：AD BE =；（2）若105ACD ∠=︒，32D ∠=︒，求B 的度数．解析：（1）见解析；（2）43°【分析】利用 SAS 证明≌ACD BCE 即可;由全等三角形的性质可知:B A ∠=∠ 再根据三角形内角和为180︒，可求出A ∠的度数，即可求出B ．【详解】（1）证明：∵ECD ACB ∠=∠．∴ECD ACE ACB ACE ∠+∠=∠+∠∴ACD BCE ∠=∠，在ACD △和BCE 中，AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴()ACD BCE SAS ≌∴AD BE =（2）∵105ACD ∠=︒，32D ∠=︒∴1801053243A ∠=︒-︒-︒=︒由（1）得≌ACD BCE∴43B A ∠=∠=︒．【点睛】本题考查了全等三角形的判定和性质，三角形的内角和定理，属于中考常考题型． 25．如图，点B ，F ，C ，E 在一条直线上，FB=CE ，AB ∥ED ，AC ∥FD ． 求证：AB=DE ．解析：见详解【分析】先根据条件求出BC=EF ，根据平行线性质求出∠B=∠E ，∠ACB=∠DFE ，根据ASA 推出△ABC ≌△DEF 即可．【详解】∵FB ＝CE ，∴FB+FC=FC+CE ，即BC=FE ，又∵AB ∥ED ，AC ∥FD ，∴∠B=∠E ，∠ACB=∠DFE ，在△ABC 和△DEF 中，B E BC FEACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△DEF （ASA ）∴AB=DE ．【点睛】本题考查了平行线的性质和全等三角形的性质和判定的应用，主要考查学生的推理论证能力．26．如图，点E ，F 在BC 上，A D ∠=∠，AF DE =，AFC DEB ∠=∠．求证：BE CF =．解析：见详解【分析】先证明∠AFB=∠DEC ，再根据ASA 证明∆AFB ≅∆DEC ，进而即可得到结论．【详解】∵AFC DEB ∠=∠，∴∠AFB=∠DEC ，又∵A D ∠=∠，AF DE =，∴∆AFB ≅∆DEC （ASA ），∴BF=CE ，∴BF-EF= CE-EF ，∴BE CF =．【点睛】本题主要考查三角形全等的判定和性质定理，熟练掌握ASA 证明三角形全等，是解题的关键．27．如图，已知Rt ABC △中，90ACB ︒∠=，CA CB =，D 是AC 上一点，E 在BC 的延长线上，且CE CD =，BD 的延长线与AE 交于点F ．求证：BF AE ⊥．解析：证明见解析【分析】根据题意可以得到△ACE ≌△BCD ，然后根据全等三角形的性质和垂直的定义可以证明结论成立．【详解】证明：∵90ACB ︒∠=∴90ACE BCD ︒∠=∠=在ACE △和BCD △中，CA CB ACE BCD CE CD =⎧⎪∠=∠⎨⎪=⎩∴()ACE BCD SAS =∴CAE CBD ∠=∠∵Rt ACE △中，90CAE E ︒∠+∠=，∴90CBD E ︒∠+∠=，∴90BFE ︒∠=∴BF AE ⊥【点睛】本题考查了全等三角形的判定与性质、垂直的定义，解题的关键是明确题意，利用全等三角形的判定和性质、数形结合的思想作答．28．已知：如图，AB ＝ AD ．请添加一个条件使得△ABC ≌△ADC ，然后再加以证明．解析：BC=CD,证明见解析（答案不唯一）．【分析】已知两组对应边相等，则找另一组边相等或找另一组对应角相等均可证明△ABC ≌△ADC ．【详解】解：若添加条件为：BC=CD,证明如下：在△ABC 和△ADC 中AC AC BC CD AB AD =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC （SSS ）（答案不唯一）．【点睛】本题主要考查了全等三角形的判定，灵活运用全等三角形的判定方法是解答本题的关键．。

第十二章检测卷题号一二三总分得分一、选择题(共10小题，每小题3分，共30分)1．在下列每组图形中，是全等形的是( )2．如图，△AOC≌△BOD，点A与点B是对应点，则下列结论中错误的是( )A．∠A＝∠B B．AO＝BOC．AB＝CD D．AC＝BD第2题图第3题图3．如图，已知AB＝AC，BD＝CD，则可推出( )A．△ABD≌△BCD B．△ABD≌△ACDC．△ACD≌△BCD D．△ACE≌△BDE4．一定能确定△ABC≌△DEF的条件是( )A．∠A＝∠D，AB＝DE，∠B＝∠EB．∠A＝∠E，AB＝EF，∠B＝∠DC．AB＝DE，BC＝EF，∠A＝∠DD．∠A＝∠D，∠B＝∠E，∠C＝∠F5．已知∠AOB的平分线上一点P到OA的距离为5，Q是OB上任意一点，则( ) A．PQ＞5 B．PQ≥5C．PQ＜5 D．PQ≤56．如图，点A、D、C、E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝12，AC ＝8，则CD的长为( )A．5.5 B．4 C．4.5 D．3第6题图第7题图第8题图7．如图，MP⊥NP，MQ为∠PMN的平分线，MT＝MP，连接TQ，则下列结论中不正确的是( )A．TQ＝PQ B．∠MQT＝∠MQPC．∠QTN＝90° D．∠NQT＝∠MQT8．如图，BE⊥AC于点D，且AD＝CD，BD＝ED.若∠ABC＝54°，则∠E的度数为( ) A．25° B．27° C．30° D．45°9．如图，已知AD＝BC，AC与BD交于点O，AE⊥BD于点E，CF⊥BD于点F，则图中的全等三角形有( )A．5对 B．6对 C．7对 D．8对第9题图第10题图10．如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN 在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM＝PN 恒成立；②OM＋ON的值不变；③四边形PMON的面积不变；④MN的长不变．其中正确的个数为( )A．4个 B．3个 C．2个 D．1个二、填空题(共6小题，每小题3分，共18分)11．如图，在△ABC与△ADC中，已知AD＝AB，在不添加任何辅助线的前提下，要使△ABC≌△ADC，只需再添加的一个条件可以是__________．第11题图第12题图12．如图，要测量池塘的宽度AB，在池塘外选取一点P，连接AP、BP并各自延长，使PC＝PA，PD＝PB，连接CD，测得CD长为25m，则池塘宽AB为________m，依据是________________________．13．如图，AB∥CF，E为AC的中点．若FC＝6cm，DB＝3cm，则AB＝________cm.第13题图第14题图14．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝96cm2，AB＝18cm，BC＝12cm，则DE＝________cm.15．如图，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAC＝80°，则∠CAE的度数是________．第15题图第16题图16．如图，在平面坐标系中，B(3，1)，AB＝OB，∠ABO＝90°，则点A的坐标是____________．三、解答题(共8题，共72分)17．(8分)如图，点C是AE的中点，∠A＝∠ECD，AB＝CD.求证：∠B＝∠D.18．(8分)工人师傅常用角尺平分一个任意角，做法如下：如图，∠AOB是一个任意角，在边OA、OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M、N重合，过角尺顶点P的射线OP便是∠AOB的平分线，请说明理由．19.(8分)如图，点D在BC上，∠1＝∠2，AE＝AC，下面有三个条件：①AB＝AD；②BC ＝DE；③∠E＝∠C.请你从所给条件①②③中选一个条件，使△ABC≌△ADE，并证明两三角形全等．20．(8分)如图，在Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一点，E在BC的延长线上，且AE＝BD，BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF 与AE有何特殊的位置关系，并证明你的猜想．21．(8分)如图，AD是△ABC的中线，BE⊥AD于点E，CF⊥AD交AD的延长线于点F.求证：AE＋AF＝2AD.22．(10分)如图，在△ABC中，D为BC上一点，E为△ABC外部一点，DE交AC于一点O，AC＝AE，AD＝AB，∠BAC＝∠DAE.(1)求证：△ABC≌△ADE；(2)若∠BAD＝20°，求∠CDE的度数．23．(10分)如图，在△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC 于F.(1)求证：BE＝CF；(2)若AB＝8，AC＝6，求AE，BE的长．24．(12分)在解决线段数量关系的问题时，如果条件中有角平分线，经常采用下面构造全等三角形的解题思路，如：在图①中，若C是∠MON的平分线OP上一点，点A在OM上，此时，在ON上截取OB＝OA，连接BC，根据三角形全等判定(SAS)，容易构造出全等三角形△OBC和△OAC.参考上面的方法，解答下列问题：如图②，在非等边△ABC中，∠B＝60°，AD，CE分别是∠BAC，∠BCA的平分线，且AD，CE交于点F.求证：AC＝AE＋CD.参考答案与解析1．C 2.C 3.B 4.A 5.B 6.B 7.D 8.B 9.C10．B 解析：如图，作PE ⊥OA 于E ，PF ⊥OB 于F ，则∠PEO ＝∠PFO ＝90°，∴∠EPF ＋∠AOB ＝180°.∵∠MPN ＋∠AOB ＝180°，∴∠EPF ＝∠MPN ，∴∠EPM ＝∠FPN .∵OP 平分∠AOB ，∴∠POE ＝∠POF .在△POE 和△POF 中， ⎩⎪⎨⎪⎧∠POE ＝∠POF ，∠PEO ＝∠PFO ，PO ＝PO ，∴△POE ≌△POF ，∴PE ＝PF ，OE ＝OF .在△PEM 和△PFN 中， ⎩⎪⎨⎪⎧∠MPE ＝∠NPF ，PE ＝PF ，∠PEM ＝∠PFN ，∴△PEM ≌△PFN ，∴EM ＝NF ，PM ＝PN ，故①正确．∴S △PEM ＝S △PFN ，∴S 四边形PMON ＝S 四边形PEOF＝定值，故③正确．∵OM ＋ON ＝OE ＋ME ＋OF －NF ＝2OE ＝定值，故②正确．MN 的长度是变化的，故④错误．故选B.11．DC ＝BC (或∠DAC ＝∠BAC ) 12．25 全等三角形对应边相等 13．9 14.6.4 15.20°16．(2，4) 解析：如图，过点A 作AC ∥x 轴，过点B 作BD ∥y 轴，两条直线相交于点E ，则CE ＝OD ，DE ＝OC ，∠ODB ＝∠BEA ＝90°.∵B (3，1)，∴OD ＝3，BD ＝1.∵∠DOB ＋∠OBD ＝90°，∠OBD ＋∠ABE ＝90°，∠BAE ＋∠ABE ＝90°，∴∠BOD ＝∠ABE ，∠OBD ＝∠BAE .在△ABE 与△BOD 中，∵⎩⎪⎨⎪⎧∠BOD ＝∠ABE ，AB ＝BO ，∠OBD ＝∠BAE ，∴△ABE ≌△BOD (ASA)，∴AE ＝BD ＝1，BE ＝OD ＝3，∴AC ＝OD －AE ＝3－1＝2，DE ＝BD ＋BE ＝1＋3＝4，∴A (2，4)．17．证明：∵点C 是AE 的中点，∴AC ＝CE .(2分)在△ABC 和△CDE 中，⎩⎪⎨⎪⎧AC ＝CE ，∠A ＝∠ECD ，AB ＝CD ，∴△ABC ≌△CDE (SAS)，(7分)∴∠B ＝∠D .(8分)18．解：在△OMP 和△ONP 中，∵⎩⎪⎨⎪⎧OM ＝ON ，MP ＝NP ，OP ＝OP ，∴△OMP ≌△ONP (SSS)，(6分)∴∠MOP ＝∠NOP ，∴OP 平分∠AOB .(8分)19．解：选②BC ＝DE .(1分)证明如下：如图，∵∠1＝∠2，∠3＝∠4，∴∠E ＝∠C .(3分)在△ADE 和△ABC 中，⎩⎪⎨⎪⎧AE ＝AC ，∠E ＝∠C ，DE ＝BC ，∴△ADE ≌△ABC (SAS)．(8分)20．解：猜想BF ⊥AE .(2分)理由如下：∵∠ACB ＝90°，∴∠ACE ＝∠BCD ＝90°.又BC ＝AC ，BD ＝AE ，∴Rt△BDC ≌Rt△AEC (HL)．∴∠CBD ＝∠CAE .(5分)又∵∠CAE ＋∠E ＝90°，∴∠EBF ＋∠E ＝90°.∴∠BFE ＝90°，即BF ⊥AE .(8分)21．证明：∵AD 是△ABC 的中线，∴BD ＝CD .∵BE ⊥AD ，CF ⊥AD ，∴∠BED ＝∠CFD ＝90°.(2分)在△BDE 和△CDF 中，⎩⎪⎨⎪⎧∠BED ＝∠CFD ，∠BDE ＝∠CDF ，BD ＝CD ，∴△BDE ≌△CDF (AAS)，∴DE ＝DF .(5分)∵AE ＝AD －DE ，AF ＝AD ＋DF ，∴AE ＋AF ＝AD －DE ＋AD ＋DF ＝2AD .(8分)22．(1)证明：在△ABC 和△ADE 中，⎩⎪⎨⎪⎧AB ＝AD ，∠BAC ＝∠DAE ，AC ＝AE ，∴△ABC ≌△ADE (SAS)．(5分)(2)解：由(1)知△ABC ≌△ADE ，∴∠E ＝∠C .∵∠BAC ＝∠DAE ，∠BAC ＝∠BAD ＋∠DAC ，∠DAE ＝∠DAC ＋∠CAE ，∠BAD ＝20°，∴∠CAE ＝∠BAD ＝20°.(7分)∵∠E ＝∠C ，∠AOE ＝∠DOC ，∴∠CAE ＝∠CDE ，∴∠CDE ＝20°.(10分)23．(1)证明：如图，连接DB ，DC .∵DG ⊥BC 且平分BC ，∴∠DGB ＝∠DGC ＝90°，BG ＝CG .又DG ＝DG ，∴△DGB ≌△DGC ，∴DB ＝DC .∵AD 为∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF ，∠DAE ＝∠DAF ，∠BED ＝∠AED ＝∠DFC ＝90°.(3分)在Rt△DBE 和Rt△DCF 中，⎩⎪⎨⎪⎧DB ＝DC ，DE ＝DF ，∴Rt△DBE ≌Rt△DCF (HL)，∴BE ＝CF .(5分)(2)解：在△ADE 和△ADF 中，⎩⎪⎨⎪⎧∠DAE ＝∠DAF ，∠AED ＝∠AFD ，AD ＝AD ，∴△ADE ≌△ADF ，∴AE ＝AF .(7分)∵AC＋CF ＝AF ，AE ＝AB －BE ，∴AC ＋CF ＝AB －BE ，即6＋BE ＝8－BE ，∴BE ＝1，∴AE ＝8－1＝7.(10分)24．证明：如图，在AC 上截取AG ＝AE ，连接FG .(1分)∵AD 是∠BAC 的平分线，CE 是∠BCA 的平分线，∴∠1＝∠2，∠3＝∠4.(2分)在△AEF 和△AGF 中， ⎩⎪⎨⎪⎧AE ＝AG ，∠1＝∠2，AF ＝AF ，∴△AEF ≌△AGF (SAS)，∴∠AFE ＝∠AFG .(6分)∵∠B ＝60°，∴∠BAC ＋∠ACB ＝120°，∴∠2＋∠3＝12(∠BAC ＋∠ACB )＝60°.∵∠AFE ＝∠2＋∠3，∴∠AFE ＝∠CFD ＝∠AFG ＝60°，∴∠CFG ＝180°－∠CFD －∠AFG ＝60°，∴∠CFD ＝∠CFG .(9分)在△CFG 和△CFD 中，⎩⎪⎨⎪⎧ ∠CFG ＝∠CFD ，FC ＝FC ，∠3＝∠4，∴△CFG ≌△CFD (ASA)，∴CG ＝CD .∴AC ＝AG ＋CG ＝AE ＋CD .(12分)。