Quantum-Classical Phase Transition of Escape rate in Biaxial Spin Particles
- 格式:pdf
- 大小:148.13 KB
- 文档页数:23

2022年自考专业(英语)英语科技文选考试真题及答案一、阅读理解题Directions: Read through the following passages. Choose the best answer and put the letter in the bracket. (20%)1、 (A) With the recent award of the Nobel Prize in physics, the spectacular work on Bose-Einstein condensation in a dilute gas of atoms has been honored. In such a Bose-Einstein condensate, close to temperatures of absolute zero, the atoms lose their individuality and a wave-like state of matter is created that can be compared in many ways to laser light. Based on such a Bose-Einstein condensate researchers in Munich together with a colleague from the ETH Zurich have now been able to reach a new state of matter in atomic physics. In order to reach this new phase for ultracold atoms, the scientists store a Bose-Einstein condensate in a three-dimensional lattice of microscopic light traps. By increasing the strength of the lattice, the researchers are able to dramatically alter the properties of the gas of atoms and can induce a quantum phase transition from the superfluid phase of a Bose-Einsteincondensate to a Mott insulator phase. In this new state of matter it should now be possible to investigate fundamental problems of solid-state physics, quantum optics and atomic physics. For a weak optical lattice the atoms form a superfluid phase of a Bose-Einstein condensate. In this phase, each atom is spread out over the entire lattice in a wave-like manner as predicted by quantum mechanics. The gas of atoms may then move freely through the lattice. For a strong optical lattice the researchers observe a transition to an insulating phase, with an exact number of atoms at each lattice site. Now the movement of the atoms through the lattice is blocked due to therepulsive interactions between them. Some physicists have been able to show that it is possible to reversibly cross the phase transition between these two states of matter. The transition is called a quantum phase transition because it is driven by quantum fluctuations and can take place even at temperatures of absolute zero. These quantum fluctuations are a direct consequence of Heisenberg’s uncertainty relation. Normally phase transitions are driven by thermal fluctuations, which are absent at zero temperature. With their experiment, the researchers in Munich have been able to enter a new phase in the physics of ultracold atoms. In the Mott insulator state theatoms can no longer be described by the highly successful theories for Bose-Einstein condensates. Now theories are required that take into account the dominating interactions between the atoms and which are far less understood. Here the Mott insulator state may help in solving fundamental questions of strongly correlated systems, which are the basis for our understanding of superconductivity. Furthermore, the Mott insulator state opens many exciting perspectives for precision matter-wave interferometry and quantum computing.What does the passage mainly discuss?A.Bose-Einstein condensation.B.Quantum phase transitions.C.The Mott insulator state.D.Optical lattices.2、What will the scientists possibly do by reaching the new state of matter in atomic physics?A.Store a Bose-Einstein condensate in three-dimensional lattice of microscopic light traps.B.Increase the strength of the lattice.C.Alter the properties of the gas of atoms.D.Examine fundamental problems of atomic physics.3、Which of the following is NOT mentioned in relation to aweak optical lattice?A.The atoms form a superfluid phase of a Bose-Einstein condensate.B.Each atom is spread out over the entire lattice.C.The gas of atoms may move freely through the lattice.D.The superfluid phase changes into an insulating phase.4、What can be said about the quantum phase transition?A.It can take place at temperatures of absolute zero.B.It cannot take place above the temperatures of absolute zero.C.It is driven by thermal fluctuations.D.It is driven by the repulsive interactions between atoms.5、The author implies all the following about the Mott insulator state EXCEPT that______.A.the theory of Bose-Einstein condensation can’t possibly account for the atoms in the Mott insulator stateB.not much is known about the dominating interactions between the atoms in the Mott insulator stateC.it offers new approaches to exact quantum computingD.it forms a superfluid phase of a Bose-Einstein condensate6、 (B) Gene therapy and gene-based drugs are two ways we would benefit from our growing mastery of genetic science. But therewill be others as well. Here is one of the remarkable therapies on the cutting edge of genetic research that could make their way into mainstream medicine in the c oming years. While it’s true that just about every cell in the body has the instructions to make a complete human, most of those instructions are inactivated, and with good reason: the last thing you want for your brain cells is to start churning out stomach acid or your nose to turn into a kidney. The only time cells truly have the potential to turn into any and all body parts is very early in a pregnancy, when so-called stem cells haven’t begun to specialize. Most diseases involve the death of healthy cells—brain cells in Alzheimer’s, cardiac cells in heart disease, pancreatic cells in diabetes, to name a few; if doctors could isolate stem cells, then direct their growth, they might be able to furnish patients with healthy replacement tissue. It was incredibly difficult, but last fall scientists at the University of Wisconsin managed to isolate stem cells and get them to grow into neural, gut, muscle and bone cells. The process still can’t be controlled, and may have unforeseen limitations; but if efforts to understand and master stem-cell development prove successful, doctors will have a therapeutic tool of incredible power. The same applies to cloning, whichis really just the other side of the coin; true cloning, as first shown, with the sheep Dolly two years ago, involves taking a developed cell and reactivating the genome within, resenting its developmental instructions to a pristine state. Once that happens, the rejuvenated cell can develop into a full-fledged animal, genetically identical to its parent. For agriculture, in which purely physical characteristics like milk production in a cow or low fat in a hog have real market value, biological carbon copies could become routine within a few years. This past year scientists have done for mice and cows what Ian Wilmut did for Dolly, and other creatures are bound to join the cloned menagerie in the coming year. Human cloning, on the other hand, may be technically feasible but legally and emotionally more difficult. Still, one day it will happen. The ability to reset body cells to a pristine, undeveloped state could give doctors exactly the same advantages they would get from stem cells: the potential to make healthy body tissues of all sorts. And thus to cure disease.That could prove to be a true “miracle cu re”.What is the passage mainly about?A.Tomorrow’s tissue factory.B.A terrific boon to medicine.C.Human cloning.D.Genetic research.7、 According to the passage, it can be inferred that which of the following reflects the author’s opinion?A.There will inevitably be human cloning in the coming year.B.The potential to make healthy body tissues is undoubtedly a boon to human beings.C.It is illegal to clone any kind of creatures in the world.D.It is legal to clone any kind of creatures in the world except human.8、Which of the following is NOT true according to the passage?A.Nearly every cell in the human brain has the instructions to make a complete human.B.It is impossible for a cell in your nose to turn into a kidney.C.It is possible to turn out healthy replacement tissues with isolated stem cells.D.There will certainly appear some new kind of cloned animal in the near future.9、All of the following are steps involved in true cloning EXCEPT_______.A.selecting a stem cellB.taking a developed cellC.reactivating the genome within the developed cellD.resetting the developmental instructions in the cell to its original state10、The word “rejuvenated” in para. 5 is closest in meaning to_______.A.rescuedB.reactivatedC.recalledD.regulated参考答案:【一、阅读理解题】1~5CDDAD6~10DBBA。



相位跃迁原理及作用Phase transition in quantum mechanics, also known as quantum phase transitions, refers to the abrupt changes in the ground state of a system driven by external parameters such as temperature or magnetic field strength. 相位跃迁是指由外部参数如温度或磁场强度驱动而导致系统基态发生突变的量子力学现象。
This phenomenon is of great interest to researchers as it can lead to the emergence of new phases of matter and exotic quantum states. 这一现象引起研究人员的极大兴趣,因为它可能导致新物质相和异域量子态的出现。
One of the key principles underlying phase transitions is known as the Landau theory, which describes the behavior of order parameters near a critical point in a phase transition. 一个关键原则是朗道理论,它描述了在相位跃迁的临界点附近,有序参数的行为。
The concept of phase transitions has wide-ranging applications in various fields, including condensed matter physics, quantum information theory, and even in understanding the behavior ofcomplex systems in biology and social sciences. 相位跃迁的概念在各个领域有着广泛的应用,包括凝聚态物理学、量子信息理论,甚至在理解生物学和社会科学中复杂系统的行为方面。


凝聚态物理专业导师简介(以姓氏拼音为序)艾保全,男,副教授,硕士生导师。
主研方向是分子马达运动机制、低维材料(纳米)的能量和热的传输、生物非线性噪声效应。
2004年毕业于中山大学,获博士学位。
随后在香港大学及香港浸会大学从事博士后研究工作,2005年9月起华南师范大学教师。
主要从事理论生物物理的研究,包括生物非线性系统中的噪声效应,肌肉运动微观机制,分子马达的运动机制(线性和旋转马达)以及低维材料的热传导等领域的研究。
他以第一作者在Journal of physical chemistry B, Journal of Chemical physics, Physical Review E等 SCI收录国际重要期刊上发表论文32篇。
论文被引用200多次,其中关于肿瘤生长过程中噪声控制的论文被它引50次,关于微管中粒子定向输运的论文被著名综述期刊Reviews Modern of physics引用并介绍我们的相关工作。
主持国家自然科学基金和广东省自然科学基金各一项,并和澳门科技大学,日本产业科技大学以及香港浸会大学等研究组从事合作研究。
主要荣誉:2006年华南师范大学科研优秀工作者.2006年入选广东省“千百十”人才工程培养对象.2005年获得广东省优秀博士学位论文称号.研究兴趣:1.分子马达的研究: 研究分子马达的运动机制,线性分子马达,旋转分子马达,以及分子马达运动方向的控制,效率及其最大值研究,考虑量子效应的分子马达的运动。
2.低维材料(纳米)的能量和热的传输:一维纳米系统中热传导性质的研究及其应用的研究;热二极管,三级管及热(声子)操纵和控制的研究.3.生物非线性系统中的噪声效应: 基因选择过程中的噪声效应; 噪声对肿瘤生长的影响; 细菌生长过程中的噪声效应。
主持科研项目:1.国家自然科学基金2007.1-2009.12,分子马达运动机制的理论研究(旋转).2.广东省自然科学基金2007.1-2008.12,线性分子马达运动机制的基础研究.发表代表性论文(if>2.0)1.Bao-quan Ai and Liang-Gang Liu, Brownian pump in nonlinear diffusive media,The Journal of Physical Chemistry B 112(2008)95402.Bao-quan Ai and Liang-Gang Liu, Phase shift induces currents in a periodictube, Journal of Chemical Physics 126(2007) 2047063.Bao-quan Ai and Liang-Gang Liu, A channel Brownian pump powered by anunbiased external force, Journal of Chemical Physics , 128 (2008)0247064.Bao-quan Ai and Liang-Gang Liu, The tube wall fluctuation can induce a netcurrent in a periodic tube, Chemical Physics, 344 (2008)185-188.5.Bao-quan Ai and Liang-Gang Liu, Thermal noise can facilitate energytransformation in the presence of entropic barriers, Phys. Rev.E 75(2007)061126.6.Bao-quan Ai and Liang-Gang Liu, Reply to comment on correlated noise in alogistic growth model, Phys. Rev. E 77(2008)013902.7.Bao-quan Ai and Liang-Gang Liu, Facilitated movement of inertial Brownianmotors driven by a load under an asymmetric potential, Phys. Rev.E 76(2007)042103.8.Bao-quan Ai and Liang-Gang Liu, Current in a three-dimensional periodictube with unbiased forces, Phys. Rev. E 74(2006) 051114.9.Bao-quan Ai, Liqiu Wang and Liang-Gang Liu, Transport reversal in a thermalratchet, Phys. Rev. E 72, (2005) 031101.10.Bao-quan Ai, Xian-ju Wang, Guo-tao Liu and Liang-Gang Liu, Correlatednoise in a logistic growth model, Phys. Rev. E 67 (2003)022903.11.Bao-quan Ai, Xian-Ju Wang, Guo-Tao Liu, and Liang-Gang Liu, Efficiencyoptimization in a correlation ratchet with asymmetric unbiased fluctuations, Phys.Rev. E 68 (2003)061105.12.Xian-Ju Wang, Bao-quan Ai, Liang-Gang Liu, Modeling translocation ofparticles on one-dimensional polymer lattices,Phys. Rev. E 64, (2001)906-910.13.Bao-quan Ai and Liang-Gang Liu, Stochastic resonance in a stochastic bistablesystem,Journal of Statistical Mechanics: theory and experiment (2007)P02019.14.Bao-quan Ai and Liang-gang Liu,Efficiency in a temporally asymmetricBrownian motor with stochastic potentials, Journal of Statistical Mechanics: Theory and Experiment (2006)P09016.15.Bao-quan Ai, Guo-Tao Liu, Hui-zhang Xie and Liang-Gang Liu, Efficiency andCurrent in a correlated ratchet, Chaos 14(4)(2004)95716.Bao-quan Ai, Liqiu Wang and Liang-Gang Liu, Flashing motor at hightransition rate, Chaos, solitons & fractals 34( 2007 ) 1265-1271.17.Bao-quan Ai, and Liang-gang Liu, Transport driven by a spatially modulatednoise in a periodic tube, Journal of Physics: Condensed Matter 19(2007) 266215.Email:aibq@陈浩,男,教授,硕士生导师。



量子色动力学相变的临界行为量子色动力学(Quantum Chromodynamics,简称QCD)是描述强相互作用的理论,它在粒子物理中起着重要的作用。
在高温和高能量密度条件下,QCD相变会导致强子系统中的自由夸克和胶子相互作用的改变,这种相变被称为量子色动力学相变(Quantum Chromodynamics Phase Transition)。
本文将讨论量子色动力学相变的临界行为。
1. 引言量子色动力学是标准模型的一部分,它描述了夸克和胶子之间的相互作用。
在冷却高温夸克胶子等离子体时,会发生从强子相到夸克-胶子等离子体的相变。
在相变过程中,系统的热力学性质发生了显著变化,这种变化被称为临界现象。
量子色动力学相变的临界行为一直是研究者关注的焦点。
2. 临界行为的表征量子色动力学相变的临界行为可以通过临界指数来表征。
临界指数是指在临界点附近各种物理量的行为方式。
其中,最常用的是比热容、磁化率和相关长度的临界指数。
3. 临界指数(1)比热容的临界指数在量子色动力学相变的临界点附近,比热容的行为可以用下式描述:C_v \sim |T - T_c|^{-\alpha}$$式中,$C_v$为比热容,$T$为温度,$T_c$为临界温度,$\alpha$为比热容的临界指数。
临界指数$\alpha$的数值决定了比热容在临界点附近的行为。
(2)磁化率的临界指数磁化率是描述系统磁现象的物理量,它在临界点附近的行为可以用下式表示:$$\chi \sim |T - T_c|^{-\gamma}$$式中,$\chi$为磁化率,$\gamma$为磁化率的临界指数。
磁化率的临界指数$\gamma$决定了磁化率在临界点附近的变化行为。
(3)相关长度的临界指数临界点附近的相关长度也能够描述临界行为。
相关长度可以用下式表示:$$\xi \sim |T - T_c|^{-\nu}式中,$\xi$为相关长度,$\nu$为相关长度的临界指数。
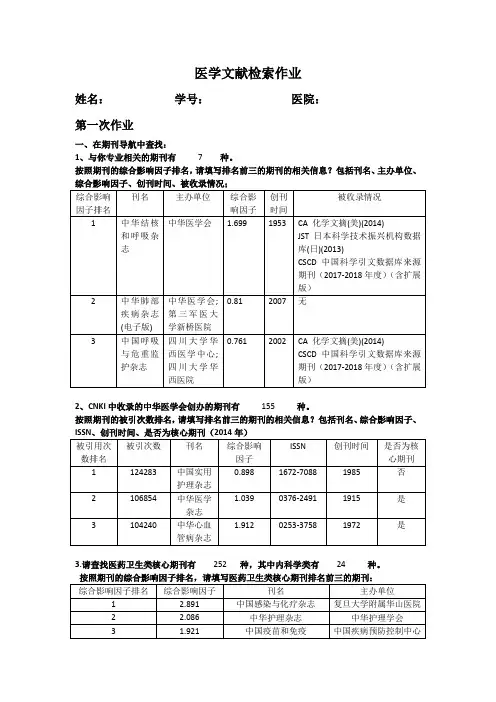
医学文献检索作业姓名:学号:医院:第一次作业一、在期刊导航中查找:1、与你专业相关的期刊有7种。
按照期刊的综合影响因子排名,请填写排名前三的期刊的相关信息?包括刊名、主办单位、2、CNKI中收录的中华医学会创办的期刊有155种。
按照期刊的被引次数排名,请填写排名前三的期刊的相关信息?包括刊名、综合影响因子、3.请查找医药卫生类核心期刊有252种,其中内科学类有24种。
4.自学作业:(提示:在百度上查找)(1)核心期刊的含义以及中国四大核心期刊体系。
核心期:刊是期刊中学术水平较高的刊物,是进行刊物评价而非具体学术评价的工具。
中国四大核心期刊体系:①中国科学技术信息研究所“中国科技论文统计源期刊”(又称“中国科技核心期刊”):②北京大学图书馆“中文核心期刊”;③南京大学“中文社会科学引文索引(CSSCI)来源期刊”;④中国社会科学院文献信息中心“中国人文社会科学核心期刊”。
(2)期刊的影响因子(IF)的定义和计算公式。
①期刊的影响因子(Impact factor,IF),是代表期刊影响大小的一项定量指标。
也就是某刊平均每篇论文的被引用数,它实际上是某刊在某年被全部源刊物引证该刊前两年发表论文的次数,与该刊前两年所发表的全部源论文数之比。
②计算公式:IF(k)= (nk-1+nk-2) / ( Nk-1+Nk-2)说明:k 为某年, Nk-1+Nk-2 为该刊在前一两年发表的论文数量, nk-1 和nk-2 该刊在k 年的被引用数量。
也就是说,某刊在2005年的影响因子是其2004和2003两年刊载的论文在2005年的被引总数除该刊在2004和2003这两年的载文总数(可引论文)。
(3)计算:某期刊2015年影响因子本刊2014年的文章在2015年的被引次数:48 ;本刊2014年的发文量:187本刊2013年的文章在2015年的被引次数:128 ;本刊2013年的发文量:154计算过程及结果:(48+128)/(187+154)=0.5165.(1)以“湖南师范大学医学院”为机构名检索2010~2016发表的论文数量,其中在核心期刊上发表的论文数量,在核心期刊上发文最多的作者;“湖南师范大学医学院”为机构名检索2010~2016发表的论文数量为:797篇;其中在核心期刊上发表的论文数量为:198篇;在核心期刊上发文最多的作者是:曹建国(13篇)。
qstem模拟参数
QSTEM(Quantum-inspired Simulation of Transition Metal Oxide Thin Films)是一种基于密度泛函理论的材料模拟方法,适用于过渡金属氧化物和稀土镁氧化物等薄膜材料的研究。
下面是一些QSTEM模拟的常用参数:
1. 计算精度:QSTEM模拟可以选择不同的计算精度,包括LANL2DZ、PBE0、VWN3DFE等不同的泛函,以及不同的基组和密度泛函紧束缚方法。
2. 计算域:QSTEM模拟的计算域可以根据需要进行调整,通常是一个超胞体(supercell)或者一个周期性边界条件(periodic boundary condition)的结构。
3. 原子类型:QSTEM模拟可以选择不同的原子类型,包括过渡金属、氧、镁等,不同的原子类型会影响材料的结构和性质。
4. 晶格常数:QSTEM模拟可以通过调整晶格常数来模拟不同的晶体结构,例如单斜晶系、正交晶系、菱面晶系等。
5. 界面势:QSTEM模拟可以通过引入界面势来模拟不同的界面结构,
例如氧空位、钙钛矿结构等。
6. 温度:QSTEM模拟可以模拟不同的温度条件,包括室温、高温等,不同的温度条件会影响材料的性质和缺陷结构。
7. 自洽场计算:QSTEM模拟可以通过引入自洽场(HF)计算来提高计算精度,例如引入HSE06计算可以得到更加准确的电子结构和能带结构。
总之,QSTEM模拟是一种非常强大和灵活的材料模拟方法,它可以模拟不同的材料结构和性质,并可以通过调整不同的参数来适应不同的研究需求。
英语科技文选试题课程代码:00836PART A: VOCABULARYI. Directions: Add the affix to each word according to the given Chinese, making changes when necessary. (8%)1. artificial 人工制品 1. __________________2. fiction 虚构的 2. __________________3. coincide 巧合 3. __________________4. organic 无机的 4. __________________5. sphere 半球 5. __________________6. technology 生物技术 6. __________________7. formid 可怕的7. __________________8. harmony 和谐的8. __________________II. Directions: Fill in the blanks, each using one of the given words or phrases below in its proper form.(12%)stand for exposure to at work on the edge of short ofend up focus on a host of give off a sense ofin memory of comply with9. We were on a hill, right _________ the town.10. UNESCO _________ United Nations Educational, Scientific and Cultural Organization.11. I am a bit _________ cash right now, so I can’t lend you anything.12. The milk must be bad, it’s _________ a nasty smell.13. The traveler took the wrong train and _________ at a country village.14. The material will corrode after prolonged _________ acidic gases.15. _________ problems may delay the opening of the conference.16. The congress opened with a minute’s silence _________ those who died in the struggle for the independence of their country.17. Tonight’s TV program _________ homelessness.18. He promised to _________ my request.19. Farmers are _________ in the fields planting.20. She doesn’t sleep enough, so she always has _________ of fatigue.III. Directions: Fill in each blank with a suitable word given below.(10%)birth to unmarried had premature among were between such pastThe more miscarriages or abortions a woman has,the greater are her chances of giving birth to a child that is underweight or premature in the future,the research shows.Low birthweight (under 2500g) and premature birth(less than 37 weeks)are two of the major contributors to deaths 21 newborn babies and infants. Rates of low birthweight and 22 birth were highest among mothers who 23 black, young or old, poorly educated, and 24 . But there was a strong association 25 miscarriage and abortion and an early or underweight 26 , even after adjusting for other influential factors, 27 as smoking, high blood pressure and heavy drinking. Women who had 28 one, two, or three or more miscarriages or abortions in the 29 were almost three, five, and nine times as likely to give birth 30 an underweight child as those without previous miscarriages or abortions.21. _________ 22. _________ 23. _________ 24. _________ 25. _________26. _________ 27. _________ 28. _________ 29. _________ 30. _________PART B: TRANSLATIONIV. Directions: Translate the following sentences into English, each using one of the given words or phrases below.(10%)precede replete with specialize in incompatible with suffice for31.上甜食前,每个用餐者都已吃得很饱了。
f band f 带f center f 心f center laser f 心激光器f center maser f 心微波激射器f layer f 层f value 振子强度f/d ratio f/d 比face centered crystal 面心晶体face centered cubic lattice 面心立方晶格face centered cubic structure 面心立方结构face centered lattice 面心点阵factor 因子factor group 剩余群facula 光斑faddeev equation 法捷耶夫方程faddeev popov ghost 法捷耶夫波波夫鬼态fading 衰退;褪色fahrenheit scale 华氏温标fahrenheit temperature scale 华氏温标fahrenheit thermometer 华氏温度计fall 降低fall of potential 电压降fall time 下降时间falling sphere viscometer 落球粘度计fallout 放射性沉降物false image 鬼象family 族family of asteroids 小行星族family of comets 彗星族fano factor 法诺因子far field pattern 远场图样far infrared 远红外区far infrared laser 远红外激光器far infrared radiation 远红外辐射far infrared rays 远红外线far point 远点far ultraviolet 远紫外区far ultraviolet laser 远紫外激光器far ultraviolet radiation 紫外线辐射far ultraviolet rays 远紫外线farad 法faraday 法拉第faraday cage 法拉第笼faraday cell 法拉第盒faraday constant 法拉第常数faraday cup 法拉第笼faraday dark space 法拉第暗区faraday effect 磁致旋光faraday rotation 磁致旋光faraday tube 法拉第管faraday's law 法拉第定律farvitron 线振质谱仪fast 迅速的fast breeder reactor 快增殖堆fast fission 快中子裂变fast fission effect 快中子裂变效应fast fourier transform 快速傅里叶变换fast neutron 快中子fast neutron reactor 快中子堆fast nova 快新星fast reactor 快中子堆fatigue 疲劳fatigue limit 疲劳极限fatigue strength 疲劳强度fcc structure 面心立方结构feedback 反馈feedback amplifier 反馈放大器feedback circuit 反馈电路feedback control 反馈控制feedback factor 反馈系数feedback ratio 反馈比feeder 馈电线femto 飞femtometer 费密femtosecond 飞秒femtosecond region 飞秒区域fermat's principle 费马原理fermi 费密fermi acceleration 费密加速fermi age 费密年龄fermi dirac statistics 费密统计法fermi distribution 费密分布fermi energy 费密能fermi gas 费密气体fermi glass 费密玻璃fermi hole 费密空穴fermi interaction 费密相互酌fermi level 费密能级fermi liquid 费密液体fermi particle 费密子fermi pasta ulam problem 费密巴斯德乌拉姆问题fermi resonance 费密共振fermi selection rule 费密选择定则fermi statistics 费密统计法fermi surface 费密面fermi temperature 费密温度fermi transition 费密跃迁fermi's golden rule 费密黄金定律fermiology 费密面学fermion 费密子fermionic dark matter 费密子暗物质fermium 镄ferrielectricity 亚电性ferrimagnetic resonance 亚铁磁共振ferrimagnetism 铁氧体磁性ferrite 铁氧体ferrite magnetostrictive vibrator 铁氧体磁致伸缩振子ferro resonance 铁磁共振ferroelastic phase transition 铁弹性相变ferroelasticity 铁弹性ferroelectric 铁电的ferroelectric domain 铁电畴ferroelectric mode 铁电模ferroelectric phase transition 铁电相变ferroelectric semiconductor 铁电半导体ferroelectric substance 铁电性材料ferroelectricity 铁电性ferrofluid 铁磁铃ferromagnet 铁磁体ferromagnetic 铁磁的ferromagnetic dielectrics 铁磁电介质ferromagnetic fluid 铁磁铃ferromagnetic material 铁磁性材料ferromagnetic resonance 铁磁共振ferromagnetic substance 铁磁性材料ferromagnetic superconductor 铁磁超导体ferromagnetic thin film 铁磁薄膜ferromagnetism 铁磁性feynman diagram 费因曼图feynman path integral 费因曼的路径积分feynman spectrum 费因曼谱ffag synchrotron 固定场交变梯度回旋加速器fiber 纤维fiber bundle 纤维丛fiber electrometer 悬丝静电计fiber laser 纤维激光器fiber optics 纤维光学fiber structure 纤维结构fibonacci semiconductor superlattice 菲博纳奇半导体超晶格fibril 小纤维fibril structure 纤维结构fick's law 斐克定律fictitious spin quantum number 假想自旋量子数fictitious year 假年field 场;体field adsorption 场吸附field current 励磁电流field density 场密度field desorption 场致退吸field distortion 场畸变field distribution 场的分布field effect transistor 场效应晶体管field electron emission 场致电子发射field emission 场致发射field emission microscope 场致发射显微镜;自动电子显微镜field emitted electron 场致发射电子field equation 场方程field intensity 场强field ion microscope 场致离子显微镜field lens 场镜field magnet 场磁铁field of forces 力场field of gravity 重力场field of view 视场field of vision 视场field operator 场算符field particle 场粒子field quantum 场量子field stop 场栏field strength 场强field structure 场结构field theory 场论fifth force 第五种力fifth fundamental force 第五种基本力figure 图形figure of merit 优值figure of noise 噪声指数file 文件filled band 满带filled level 满带能级filled shell 满壳层film 软片film badge 胶片剂量计film boiling 膜态沸腾film dosimeter 胶片剂量计film type condensation 膜状凝结filter 滤器滤光器滤波器filtration 过滤final product 最终产物final state interaction 终态相互酌final vacuum 极限真空finder 取景器finding telescope 寻星镜fine particle 微粒子fine structure 精细结构fine structure constant 精细结构常数fine structure splitting 精细结构劈裂finesse 锐度finite difference method 差分法finite element method 有限元法finite group 有限群finite universe 有限宇宙fireball 火球fireball model 火球模型first harmonics 基波first integral 初积分first law of thermodynamics 热力学第一定律first order phase transition 一级相转变first point of aries 春分点first quarter 上弦first resonance 一次共振first sound 第一次声波fish finder 鱼群探测器fissible 可裂变的fissile 可裂变的fissile nucleus 可分裂的核fissility 可分变性fission 分裂fission chain reaction 裂变链式反应fission chamber 裂变室fission counter 裂变计数器fission energy 裂变能量fission event 裂变事件fission fragment 裂变碎片fission neutron 裂变中子fission yield 裂变产额fissionable 可裂变的fissionable nucleus 可裂变核fissioning isomer 裂变同质异能素fit 适合five minute oscillations 五分钟振动fixation 定影fixed capacitor 固定电容器fixed point 定点fixed resistor 固定电阻器fixed star 恒星fixing 定影fixing solution 定影液fizeau fringe 菲佐条纹fizeau interferometer 菲佐干涉仪flame 火焰flame photometer 火焰光度计flame photometry 火焰光度法flame spectrum 火焰光谱flare 太阳耀斑flare star 耀星flash 闪光flash of light 闪光flash photolysis 闪烁光解flash spectrum 闪光光谱flat surface 平面flatness problem 平坦性问题flattening 扁率flavor 味flexibility 挠性flexible polymer 挠性聚合体flexural rigidity 弯曲刚度flexural strength 抗挠强度flexure 挠曲flexure vibration 弯曲振动flicker 闪烁flicker effect 闪烁效应flicker noise 闪变噪声flicker photometer 闪烁光度计flight path 飞越距离flight time 飞越时间flint glass 火石玻璃flip flop 触发器flip flop circuit 双稳态触发电路floating body 浮体floating point representation 浮点表示floating zone melting method 浮区熔炼法flocculation 凝聚flood and ebb 潮汐flooding 溢流floppy disk 软磁盘flow 流flow birefringence 怜双折射flow counter 柳式计数管flow dichroism 怜二色性flow equation 怜方程flow parameter 怜参数flow pattern 镣flow proportional counter 怜正比计数器flow rate 量flow visualization 辽视化flowmeter 量计fluctuating force 涨落力fluctuation 起伏fluctuation dissipation theorem 涨落耗散定理fluctuon 起伏量子fluent 变数fluid 铃fluid dynamics 铃动力学fluid elasticity 水弹性fluid model 铃模型fluidal 铃的fluidic 铃的fluidity 怜性fluorescence 荧光fluorescence center 荧光中心fluorescence dosimeter 荧光剂量计fluorescence spectrophotometer 荧光分光光度计fluorescence spectrum 荧光光谱fluorescence yield 荧光产额fluorescent 萤光的fluorescent indicator tube 荧光指示管fluorescent lamp 荧光灯fluorescent material 萤光材料fluorescent radiation 特狰射fluorescent scattering 荧光散射fluorescent screen 荧光屏fluorescent x rays 荧光 x 射线fluorimeter 荧光计fluorine 氟fluorite structure 萤石型结构fluorography 荧光照相法fluorometer 荧光计fluorometric analysis 荧光分析fluoroscope 荧光镜fluoroscopy 荧光检查法fluorspar structure 萤石型结构flux 通量flux creep 磁通量蠕变flux density 通量密度flux flow 磁通量流flux jump 磁通量跃变flux method 熔剂法flux motion 磁通量运动flux of energy 能通量flux of light 光通量flux of radiation 辐射通量flux pinning 通量锁住flux pump 通量泵flux quantization 磁通量量子化flux quantum 磁通量子fluxmeter 磁通计fluxoid 磁通量子fluxon 磁通量子fly 苍蝇座flying spot electron microscope 扫描电子显微镜fm receiver 档接受器focal distance 焦距focal length 焦距focal line 焦线focal plane 焦面focal point 焦点focal power 光焦度focal surface 焦曲面fock representation 福克表示fock space 福克空间focometer 焦距计focon 聚焦锥focus 焦点focused ion beam 聚焦离子束focusing 倒focusing camera 倒照相机focusing coil 聚焦线圈focusing cone 聚焦锥focusing lens 聚焦透镜focusing quadrupole magnet 聚焦四极磁铁focuson 聚焦子foil 箔fokker planck equation 福克普朗克方程follow up control 随动控制foot pound second system 英尺磅秒单位制forbidden 禁戒的forbidden band 禁带forbidden decay 禁戒衰变forbidden line 禁线forbidden lines in astrophysics 天体物理学中的禁线forbidden reflection 禁戒反射forbidden transition 禁戒跃迁forbiddenness 禁戒force 力force function 力函数force of attraction 引力force of gravity 重力force of inertia 惯性力force of repulsion 斥力force of rolling friction 滚动摩擦力force of sliding friction 滑动摩擦力force polygon 力的多边形force triangle 力的三角形forced circulation 强制循环forced convection 强制对流forced emission 强迫发射forced oscillations 受迫振荡forced vibration 受迫振荡forced vortex 强迫涡流fore vacuum 前级真空forecast 预报forecast of solar activity 太阳活动预告foreign atom 杂质原子forepump 预备真空泵fork mounting 叉式装置form drag 型阻form factor 形状因子formant 共振峰formation of order 秩序形成formula 公式formulation 公式化fornax 天炉座fortran 程序语言forward scattering 前方散射foucault currents 涡电流foucault knife edge test 傅科刀口检验foucault's pendulum 傅科摆fountain effect 喷水效应four current 四维电流four dimensional space 四维空间four dimensional structure of the universe 宇宙四维结构four dimensionality 四维性four factor formula 四因子公式four force 四维力four momentum 四维动量four potential 四维势four terminal network 四端网络four vector 四维矢four velocity 四维速度four wave mixing 四波混合fourier component 谐波分量fourier integral 傅里叶积分fourier number 傅里叶数fourier series 傅里叶级数fourier spectroscopy 傅里叶光谱学fourier transform hologram 傅里叶变换全息图fourier transform spectrometer 傅里叶光谱仪fourier transformation 傅里叶变换fourth sound 第四次声波fractal 分形fractal dimension 分形维数fractional charge 分数电荷fractional crystallization 分级结晶fractional quantum hall effect 分数量子霍尔效应fracton 分形子fracture 破裂fracture mechanics 断裂力学fragility 脆性frame antenna 环形天线frame of reference 参考系francium 钫franck condon principle 富兰克康登原理franck hertz's experiment 富兰克赫兹实验frank read source 弗朗克里德源franklin 富兰克林fraunhofer diffraction 夫琅和费衍射fraunhofer hologram 夫琅和费全息图fraunhofer line 夫琅和费谱线fre 量子free 自由的free charge 自由电荷free convection 自由对流自然对流free electron 自由电子free electron laser 自由电子激光器free energy 自由能free energy of activation 激活的自由能free field 自由场free free transition 自由自由跃迁free group 自由群free gyroscope 自由陀螺仪free motion 自由运动free neutron 自由中子free oscillation 自由振动free path 自由程free pendulum 自由摆free rotation 自由旋转free space 自由空间free state 自由态free surface 自由面free system 自由系free vibration 自由振动free volume 自由体积free volume theory 自由体积理论freedom 自由freezing 凝固freezing mixture 冷冻剂freezing point 凝固点frenkel defect 夫伦克尔缺陷frenkel exciton 夫伦克尔激子frequency 频率frequency analysis 频率分析frequency band 频带frequency characteristic 频率特性frequency converter 变频器frequency converter tube 变频管frequency counter 频率计数器frequency divider 分频器frequency domain 频域frequency factor 频率因子frequency meter 频率计frequency modulation 档frequency multiplier 倍频器频率倍增器frequency range 频率范围frequency response 频率响应frequency response method 频率特性法frequency shift 移频frequency spectrum 频谱frequency stability 频率稳定度frequency stabilized laser 稳频激光器frequency transfer function 频率传递函数fresnel diffraction 菲涅耳衍射fresnel half period zones 菲涅耳半周期带fresnel hologram 菲涅耳全息图fresnel lens 菲涅耳透镜fresnel prism 菲涅耳棱镜fresnel rhomb 菲涅耳斜方系fresnel zone 菲涅耳带fresnel's biprism 菲涅耳双棱镜fresnel's dragging coefficient 菲涅耳曳引系数fresnel's zone plate 菲涅耳波带片friction 摩擦friction coefficient 摩擦系数friction cone 摩擦锥friction layer 摩擦层friction loss 摩擦损失friction of fluid lubrication 液体润滑摩擦frictional drag 摩擦阻力frictional electricity 摩擦电frictional force 摩擦力frictional oscillation 摩擦振动frictional resistance 摩擦阻力friedel sum rule 弗里德尔的求和定则friedmann equation 弗里德曼方程friedmann universe 弗里德曼宇宙frigorimeter 深冷温度计fringes with white light 白光干涉条纹froude number 弗劳德数frozen in magnetic field 冻结磁场frustrated total internal reflection 衰减全内反射frustration 抑止ft value ft 值fuel assembly 燃料组件fuel cell 燃料电池fuel cycle 燃料循环fuel regeneration 燃料再生fuel reprocessing 燃料再生fuel rod 燃料元件棒fugacity 挥发性fulcrum 支点full load 满载full moon 望月full wave rectification 全波整流full width at half maximum 半宽度fullerene 球壳状碳分子function 函数functional 泛函functional analysis 泛函分析functional ceramics 机能陶瓷functional derivative 泛函微分fundamental absorption 基本吸收fundamental catalog 基本星表fundamental constants 基本常数fundamental doublet 基本双重线fundamental frequency 基频率fundamental interaction 基本相互酌fundamental law 基本定律fundamental magnitude 基本量fundamental mode 郑fundamental particle 基础粒子fundamental research 基础研究fundamental series 伯格曼系fundamental star 基本星fundamental theorem 基本定理fundamental tone 基音fundamental unit 基本单位furnace 炉furry's theorem 弗里定理fuse 熔断器保险丝fused quartz 熔融石英fusible alloy 易熔合金fusing point 熔点fusion 熔化fusion fission hybrid reactor 核聚变裂变混合反应堆fusion point 熔点fusion reaction 聚变反应fusion reactor 热核堆fusion temperature 聚变温度。
量子失谐及其应用这篇文章中,简单介绍了一种新的非经典关联形式,量子失谐。
不同于传统的非经典关联,其存在于可分离态中。
对于量子失谐的度量方法,将介绍两种形式,一是采用互信息所定义的度量方式,另一种是经常使用的几何度量。
量子失谐具有某些独特的性质,如在非马尔科夫环境下,衰减的量子失谐可以从环境中恢复。
由于量子失谐优于纠缠的抗环境干扰能力,所以被用来取代纠缠应用于许多方面。
例如,在单量子位确定性计算中具有良好的稳定性;在远程量子态制备中表现出较高的保真度;以及在指示量子相变临界点时,展现出其他物理量所无法企及的准确性。
关键词:量子失谐;非经典关联;马尔科夫环境;非马尔科夫环境;量子信息绪论自20世纪初由爱因斯坦(Einstein)和玻尔(Bohr)等人发展而来的量子力学,以薛定谔(Schrödinger)建立的波动力学和海森堡(Heisenberg)建立的的矩阵力学作为工具,揭示并描述了微观世界物质的运动规律。
量子力学所描述的不同于经典物理的奇特的现象与规律也被一一呈现出来。
与人们从直接的感官所认识到的由波和粒子的运动模式构建的经典的世界不同,物质在微观世界中的运动具有波粒二相性,呈现出了态的叠加,不确定性以及量子相干性等特点。
之后,物理学家提出将这种性质应用于信息领域,从而诞生了量子信息这一新学科。
不同于经典信息,量子信息因其独特的性质天然地具有经典所无法达到的多种性质。
其中一个方面是应用在通信中,因其独特的量子性,使得在量子保密通信的协议中,信息的就收者可以察觉到通信是否被第三人窃听。
另外一个方面是在量子计算中。
传统的经典计算机在模拟量子系统时或者在处理某些算法时会遇到指数墙的问题,即计算量会随对象数量的增加而呈指数增长的现象。
但是利用量子态的叠加的性质,可以得到解决,从而提高计算速度,使得短期无法解决的问题在短时间内得到解决。
对于量子信息的实现方式,一直以来被认为是其核心的量子纠缠(entanglement),但是其在技术实现上存在很多问题,例如在环境噪声的干扰下因退相干而使其量子相干性消失而造成纠缠态的消失。
二维声子晶体中简单旋转操作导致的拓扑相变王健;吴世巧;梅军【期刊名称】《物理学报》【年(卷),期】2017(066)022【摘要】构建了一种简单的二维声子晶体:由两个横截面为三角形的钢柱所组成的复式元胞按三角点阵的形式排列在空气中,等效地形成了一个蜂巢点阵结构.当三角形钢柱的取向与三角点阵的高对称方向一致时,整个体系具有C6v对称性.研究发现:在保持钢柱填充率不变的条件下,只需要将所有三角柱绕着自己的中心旋转180°,就可实现二重简并的p态和d态在布里渊区中心Γ点处的频率反转,且该能带反转过程实质上是一个拓扑相变过程.通过利用Γ点的p态和d态的空间旋转对称性,构造了一个赝时反演对称性,并在声学系统中实现了类似于电子系统中量子自旋霍尔效应的赝自旋态.随后通过k.p微扰法导出了Γ点附近的有效哈密顿量,并分别计算了拓扑平庸和非平庸系统的自旋陈数,揭示了能带反转和拓扑相变的内在联系.最后通过数值模拟演示了受到拓扑不变量保护的声波边界态的单向传输行为和对缺陷的背向散射抑制.文中所研究的声波体系,尽管材料普通常见,但其拓扑带隙的相对宽度超过21%,比己报道的类似体系的带隙都要宽,且工作原理涵盖从次声波到超声波的很大频率范围,从而在实际应用上具有较大的优势和潜力.%We design a two-dimensional acoustic crystal (AC) to obtain topologically protected edge states for sound waves.The AC is composed of a triangular array of a complex unit cell consisting of two identical triangle-shaped steel rods arranged in air.The steel rods are placed on the vertices of the hexagonal unit cell so that the whole lattice possesses the C6v symmetry.We showthat by simply rotating all triangular rods around their respective centers by 180 degrees,a topological phase transition can be achieved,and more importantly,such a transition is accomplished with no need of changing the fill ratios or changing the positions of the rods.Interestingly,the achieved topologically nontrivial band gap has a very large frequency width,which is really beneficial to future applications.The topological properties of the AC are rooted in the spatial symmetries of the eigenstates.It is well known that there are two doubly-degenerate eigenstates at the Γ point for a C6v point group,and they are usually called the p and d states in electronic system.By utilizing the spatial symmetries of the p and d states in the AC,we can construct the pseudo-time reversal symmetry which renders the Kramers doubling in this classical system.We find pseudospin states in the interface between topologically trivial and nontrivial ACs,where anticlockwise (clockwise) rotational behaviors of time-averaged Poynting vectors correspond to the pseudospin-up (pseudospin-down) orientations of the edge states,respectively.These phenomena are very similar to the real spin states of quantum spin Hall effect in electronic systems.We also develop an effective Hamiltonian for the associated bands to characterize the topological properties of the AC around the Brillouin zone center by the k · p perturbation method.We calculate the spin Chern numbers of the ACs,and reveal the inherent link between the band inversion and the topological phase transition.With full-wave simulations,we demonstrate the one-way propagation of sound waves along the interface between topologically distinct ACs,and demonstratethe robustness of the edge states against different types of defects including bends,cavity and disorder.Our design provides a new way to realize acoustic topological effects in a wide frequency range spanning from infrasound to ultrasound.Potential applications and acoustic devices based on our design are expected,so that people can manipulate and transport sound waves in a more efficient.【总页数】8页(P47-54)【作者】王健;吴世巧;梅军【作者单位】华南理工大学物理与光电学院,广州 510641;华南理工大学物理与光电学院,广州 510641;华南理工大学物理与光电学院,广州 510641【正文语种】中文【相关文献】1.一维颗粒声子晶体的拓扑相变及可调界面态 [J], 王青海;李锋;黄学勤;陆久阳;刘正猷2.考虑材料参数的二维固/固声子晶体拓扑优化设计 [J], 许卫锴; 宁金英; 韩世超; 余欣宇; 祁武超3.考虑材料参数的二维固/固声子晶体拓扑优化设计 [J], 许卫锴; 宁金英; 韩世超; 余欣宇; 祁武超4.二维介电光子晶体中的赝自旋态与拓扑相变 [J], 王彦兰; 李妍5.基于结构反转二维光子晶体的拓扑相变及拓扑边界态的构建 [J], 方云团;王张鑫;范尔盼;李小雪;王洪金因版权原因,仅展示原文概要,查看原文内容请购买。
a r X i v :c o n d -m a t /9902066v 1 [c o n d -m a t .s o f t ] 4 F eb 1999Quantum-Classical Phase Transition of Escape Rate in BiaxialSpin ParticlesY.-B.Zhang 1,2∗,J.-Q.Liang 1,2,H.J.W.M¨u ller-Kirsten 2†,S.-P.Kou 1,3,X.-B.Wang 4,F.-C.Pu 3,51.Department of Physics and Institute of Theoretical Physics,Shanxi University,Taiyuan,Shanxi 030006,China 2.Department of Physics,University of Kaiserslautern,D-67653Kaiserslautern,Germany 3.Institute of Physics and Center for Condensed Matter Physics,Chinese Academy of Sciences,Beijing 100080,China 4.Center for Advanced Study and Department of Physics,Tsinghua University,Beijing 100084,China 5.Department of Physics,Guangzhou Normal College,Guangzhou 510400,China Abstract The escape rates of the biaxial single domain spin particles with and without an applied magnetic field are ing the strict potential field de-scription of spin systems developed by Ulyanov and Zaslavskii we obtain new effective Hamiltonians which are considered to be in exact spin-coordinate correspondence unlike the well studied effective Hamiltonians with the ap-proximate correspondence.The sharp first-order transition is found in bothcases.The phase diagram of the transitions depending on the anisotropy con-stant and the external field is also given.PACS numbers:75.45.+j,75.50.TtI.INTRODUCTIONThe decay rate of metastable states or transition rate between degenerate vacua is dom-inated at high temperatures by thermal activation,whereas at temperatures close to zero, quantum tunneling is relevant.At some critical temperature the transition from the clas-sical to the quantum-dominated regime occurs.The transition can befirst-order,with a discontinuousfirst derivative of the escape rate,or smooth with only a jump of the second derivative in which case it is known as of second-order.Based upon the functional-integral approach Affleck[1]and Larkin and Ovchinnikov[2] demonstrated with certain assumptions for the shape of the potential barrier that a second-order phase transition from the thermal to the quantum regime takes place at a critical temperature T0=1/β0,whereβ0is the period of small oscillations near the bottom of the inverted potential well.Chudnovsky,however,showed that the situation is not generic and that the crossover from the thermal to the quantum regime can quite generally be thefirst-order transition[3]that takes place at T c>T0for the case in which the period versus energy curve possesses a minimum.Shortly after the observation of Chudnovsky the sharpfirst-order transitions were found theoretically in spin tunneling for two systems.One of these is a ferromagnetic bistable large-spin particle[4,5]described by the Hamiltonian ˆH=−DˆS2z−B xˆS x which is believed to be a good approximation for the molecular magnet Mn12Ac of spin S=10,and the other is a biaxial anisotropic model,whose effective mass was shown to be position-dependent[6].It was the externalfield B x(infirst model)and the anisotropic constant ratioλ(in second model)that effect the phase transition of the crossover.The same models with the magneticfield applied along alternative axes have also been studied,and the corresponding phase diagrams have been given[7,8].A sufficient criterion for thefirst-order transition in the context of tunneling can be obtained by studying the Euclidean time period in the neighbourhood of the sphaleron configuration at the peak of the potential barrier[9,10].In the present paper we incorporate the two parameters in a single spin tunneling model in order to investigate the dependence of the phase transitionon these.The phenomenon of spin tunneling has attracted considerable attention not only in view of the possible experimental test of the tunneling effect for mesoscopic single domain par-ticles-in which case it is known as macroscopic quantum tunneling-but also because the spin system with an appliedfield provides various potential shapes and therefore serves as a testing ground for theories of instanton induced transitions.The key procedure in deal-ing with spin tunneling is to convert the discrete spin system into a continuous one by a spin-coordinate correspondence.There are various spin variable techniques which result in effective Hamiltonians.It is a long standing question whether the different effective Hamil-tonians for a given quantum spin system lead to the same result[11,12].Following Ulyanov and Zaslavskii we have obtained a new effective Hamiltonian for the spin particle with bi-axial anisotropy in addition to the one of a sine-Gordon potential with position dependent mass already known in the literature[6,7,13,14].The paper is organized as follows.In Sec.II we give a brief review of the general theory of phase transitions of escape ing the effective method of Ref.[11]we then derive in Sec.III an alternative effective Hamiltonian for the ferromagnetic particle with a biaxial anisotropy without an applied magneticfield.It is shown that the sharpfirst-order transition from the classical to the quantum regime indeed exists in agreement with the observation in our previous paper[6].In Sec.IV we then investigate the spin tunneling and phase transition with an externalfield applied along the easy axis which breaks the symmetry and makes one of the degenerate vacua metastable.Our conclusions and discussions are given in Sec.V.II.THE CRITERION FOR THE SHARP FIRST-ORDER PHASE TRANSITIONOF THE ESCAPE RATEAt temperature T the escape rate of a particle through a potential barrier can be obtained by taking the ensemble average of the tunneling probabilityΓt(E),i.e.Γ(T)= Γt(E)e−E2m(φ)[V(φ)−E](3) is evaluated from the periodic pseudoparticle(instanton or bounce)trajectoriesφc between turning pointsφi andφf.The pseudoparticle trajectoryφc minimizes the Euclidean action at the given energy E above the metastable minimum such thatδS(φc)=0with periodic boundary conditionφc(0)=φc(β).The Euclidean action S E and Lagrangian L E areS E= dτL E=W+βE,L E=1,as usual.The prefactor A in Eq.(2)results from aTGaussian functional integration over smallfluctuations around the pseudoparticle trajectory φc.In the semiclassical approximation the escape rate at temperature T is dominated byΓ(T)∼e−S min(T),(5) where S min(T)is the minimum effective Euclidean action which is chosen as the smallest value of S0and S(T)≡S E.Here,S0is the thermodynamic action defined byS0=βE0(6) with E0being the barrier height for the pseudoparticle to tunnel through.Generally speak-ing,at E=0(the bottom of the initial well)the Euler-Lagrange equation leads to the vacuum instanton or bounce solution.When0<E<E0(between the bottom and the top of the barrier)the trajectoryφ(τ)shows periodic motion in the barrier region of thepotential V (φ)which is forbidden for the classical particle.The period of oscillation as a function of energy E is given by the following integralβ(E )= φf (E )φi (E )dφ2)+12)+14V ′′(q s ),g 2(ω)=−2M ′(q s )+V ′′′(q s )M (q s )(10)and M is the position dependent mass.The subscript s stands for the coordinate of the bottom of the well of the inverted potential,i.e.,the coordinate of the sphaleron.This criterion has been applied to various models studied earlier and the results coincide with previous ones.III.EFFECTIVE HAMILTONIAN OF THE FERROMAGNETIC PARTICLEThe model we consider here is that of a nanospin particle which is assumed to have a biaxial anisotropy with XOY easy plane and the easy X-axis in the XY-plane,and is described by the HamiltonianˆH=K1ˆS2z+K2ˆS2y,K1>K2>0(11)which has been extensively studied in the context of tunneling from various aspects such as ground state tunneling[13,15],tunneling atfinite energy,namely,with the periodic instanton [14],and topological quenching of tunneling[16,17].Most recently it was shown that this model possesses afirst-order phase transition from the thermal to the quantum regime[6]. In all these investigations the quantum spin system of Eq.(11)is converted into a potential problem by using the conventional spin coherent state technique with approximate spin-coordinate correspondence(see Appendix).The effective potential is of the sine-Gordon type.In the present investigation we reexamine the quantum spin system in terms of a new method developed by Ulyanov and Zaslavskii[11].The spin operator representation in differential form on the basis of spin coherent states is given by the relationsˆS z =−iddϕ,ˆS y=S sinϕ+cosϕddφ2+K2 S−1dφ+ E−K2S2cos2φ−K2S sin2φ Φ=0where we have shifted the azimuthal angle byπ2.Following Ref.[11],we use the transformationΨ=Φ(φ)(K1−K2sin2φ)−SK1,sinφ=sn x(14) The eigenvalue equation is then transformed to the following effective potential form−K1d2Ψdn2xΨ=EΨ(15) where sn x,cn x and dn x denote Jacobian elliptic functions.The effective Hamiltonian is seen to beˆH=p22K1,U(x)=K2S(S+1)cd2x.(16) with cd x=cn x/dn x.We remark here that this derivation,unlike that in previous inves-tigations,is exact and without a large s limiting procedure.We also emphasize that this Jacobian elliptic potential is of interest on its own and has not been investigated before in the context of instanton considerations.The periodic instanton solution leads to an integral withfinite energy and is obtained asx p=sn−1[k sn(ωτ),˜k](17) The trajectory of one instanton as half of the periodic bounce is shown in Fig.1with added instanton−anti-instanton pair.We choose s=√ω(E)=2K11K2s2−EλK(k)(18)where K(k)is the complete elliptic integral of thefirst kind,andk= n2−λ,n2=K2s21−λλK1 K(k)−(1−λk2)Π(λk2,k) (20)Here we are particularly interested in the phase transition.To this end we show in Fig.2 the shape of the potential for various values ofλ.The peak of the barrier becomesflatter andflatter asλincreases.The curve ofβversus E is given in Fig.3and demonstrates the obviousfirst-order phase transition forλ>1/2.Fig.4shows the action as a function of temperature.Next we apply the criterion for thefirst-order phase transition to the model above.The sphaleron is located at x s=puting the corresponding quantities at the sphaleron position,i.e.V[x s]=K2s2,V′[x s]=0,V′′[x s]=−2K2s2(1−λ),V′′′[x s]=0,V′′′′[x s]=8K2s2(1−λ)(1−2λ)(21)Eq.(8)becomes12at which thefirst-order transition sets in.We see the new effective Hamiltonian with exact spin-coordinate correspondence leads to the same results as those of ref.[6].However,the physical interpretation for the sharpfirst-order phase transition is now different.In the present case the effective mass is constant and the sharp transition from quantum to classical behavior results from aflattening of the peak of the barrier.In Ref.[6]thefirst-order transition resulted from the position dependence of the mass which makes the latter heavier at the top of the barrier.IV.THE PHASE TRANSITION WITH AN APPLIED FIELD ALONG THEEASY AXISThe Hamiltonian with an applied magneticfield h along the easy X-axis is given byˆH=K1ˆS2z+K2ˆS2y−gµB hˆS z,(23)whereµB is the Bohr magneton,and g is the spin g-factor which is taken to be2here.The anisotropy energy associated with this Hamiltonian has two minima:the one on the+X-axis which is a metastable state and the other on the−X-axis.Between these two energy minima there exists an energy barrier,and the spin escapes from the metastable state either by crossing over or by tunneling through the barrier.Following the same procedure as in the previous section,the Hamiltonian of Eq.(23) can be mapped onto a point particle problem with effective HamiltonianˆH=p22K1,V(x)=K2s2(1+α2λ2,˜k)and barrier heightE0=K2s2(1+α2λ44+K2s2α(1+αλ2−1)4(26)Under the barrier a bounce configuration exists as shown in Fig.5.We redraw the period diagram as a function of energy for the same parameter(λ=0.9,α=1)in Fig.6and obtain thefirst-order transition from thermal activation to quantum tunneling as shown in Fig.7.Applying the phase transition criterion to this model,we obtainV′(x s)=0,V′′(x s)=−2K2s2(1−α21−α21−α2λ4−α2λ (λ2−2λ)α4−(7λ2−22λ+7)α2−32λ+16 (27) and the frequencyω20isω20=ω2s=−V′′(x s)8α(1−λ)(1−α24)g2=14)(1−α2λ8+α2(30)The corresponding phase diagram is shown in Fig.8.From the diagram we observe several interesting features.First,the classical-quantum phase transition shows both thefirst-order (region I)and the second-order(region II)transition domains.We see that there is only a second-order transition forλ<0.5.For materials withλlarger than0.5we can see that the order of the phase transition changes fromfirst to second asαincreases and the phase boundary changes withλup to1.An alternative effective Hamiltonian[18,19]with the conventional application of the spin coherent state technique as that for the biaxial anisotropy spin particle without the applied magneticfield[6]has also been investigated.However,the effective Hamiltonian with ap-proximate spin-coordinate correspondence gives rise to a result[19]for the phase transition which differs from that of the Hamiltonian of Eq.(24)with exact spin-coordinate corre-spondence.The center of the position dependent mass in the Hamiltonian with approximate spin-coordinate correspondence in Refs.[18,19]does not coincide with the position of the pseudoparticle,namely,the bounce here.We,therefore,believe that the instanton concept fails in this case.A detailed analysis will be reported elsewhere.V.CONCLUSIONIn summary,we investigated the biaxial spin model with applied magneticfield along the easy X-axis with the effective potential methods developed in Ref.[11].The resultingperiodic instanton solutions with potential in terms of Jacobian elliptic functions and the corresponding phase transitions have been studied for the first time.For the quantum spin particles with anisotropic constant λ>121−(cos θ−α)2,A −=11−(cos θ+α)2−whereα=1/s.Substituting(A4)into Eq.(A3),one has[S x,S y]=s2(−i)sinθA−=i cosθs2α+O(α3)(A5) i.e.[S x,S y]=iS z+O(s−3)(A6)which implies that the usual commutation relation holds only in the large spin limit.Acknowledgment:This work was supported by the National Natural Science Founda-tion of China under Grant Nos.19677101and19775033.J.-Q.L.also acknowledges support by a DAAD-K.C.Wong Fellowship.REFERENCES[1]I.Affleck,Phys.Rev.Lett.46,388(1981).[2]rkin and Yu.N.Ovchinnikov,Sov-Phys.JETP37,382(1983).[3]E.M.Chudnovsky,Phys.Rev.A46,8011(1992).[4]E.M.Chudnovsky and D.A.Garanin,Phys.Rev.Lett.79,4469(1997).[5]D.A.Garanin and E.M.Chudnovsky,Phys.Rev.B56,11102(1997);D.A.Garanin,X.Martines and E.M.Chudnovsky,Phys.Rev.B57,13639(1998).[6]J.Q.Liang,H.J.W.M¨u ller-Kirsten,D.K.Park,and F.Zimmerschiel,Phys.Rev.Lett.81,216(1998).[7]S.-Y.Lee,H.J.W.M¨u ller-Kirsten,D.K.Park,and F.Zimmerschied,Phys.Rev.B58,5554(1998).[8]D.A.Garanin and E.M.Chudnovsky,to appear in Phys.Rev.B,cond-mat/9808037.[9]D.A.Gorokhov and G.Blatter,Phys.Rev.B56,3130(1997).[10]H.J.W.M¨u ller-Kirsten,D.K.Park and J.M.S.Rana,to be published.[11]V.V.Ulyanov and O.B.Zaslavskii,Phys.Rep.216,179(1992).[12]J.L.van Hemmen,A.S¨u t¨o,Europhys.Lett.1,481(1986);Physica B141,37(1986).[13]M.Enz and R.Schilling,J.Phys.C.19,1765(1986);ibid,19,L771(1986).[14]J.-Q.Liang,Y.-B.Zhang,H.J.W.M¨u ller-Kirsten,Jian-Ge Zhou,F.Zimmerschied andF.-C.Pu,Phys.Rev.B57,529(1998).[15]E.M.Chudnovsky and L.Gunther,Phys.Rev.Lett.60,661(1988).[16]D.Loss,D.P.DiVincenzo and G.Grinstein,Phys.Rev.Lett.69,3232(1992).[17]J.Q.Liang,H.J.W.M¨u ller-Kirsten and Jian-Ge Zhou,Z.Phys.B102,525(1997).[18]J.Q.Liang,H.J.W.M¨u ller-Kirsten,Jian-Ge Zhou,F.Zimmerschied and F.-C.Pu,Kaiserslautern Report KL-TH96/13(unpublished)[19]C.S.Park,S.-K.Yoo,D.K.Park and D.-H.Yoon,cond-mat/9807344.Figure Captions:Fig.1:The effective potential and the corresponding periodic instanton configurations. Fig.2:The potentials for different values ofλ.Fig.3:The oscillation period as a function of energy atλ=0.9.Fig.4:The action as a function of temperature indicating thefirst-order transition at λ=0.9.Fig.5:The effective potential in the case with external magneticfield.Fig.6:The oscillation period as a function of energy atλ=0.9andα=1.Fig.7:The action as a function of temperature showing thefirst-order transition in the case with externalfield.Fig.8:The phase diagram for the orders of phase transitions in the(λ,α)plane.Region I: thefirst-order domain,region II:the second-order domain.。