振动特征分析

振动分析原理振动是物体在受到外力作用或者自身受到激励时产生的周期性变化。

振动分析原理是研究物体振动特性的一种方法，通过对振动信号的采集、分析和处理，可以获取物体的振动特征参数，进而对物体的结构和性能进行评估和分析。

振动分析原理在工程领域有着广泛的应用，可以用于机械设备的故障诊断、结构的健康监测、产品的设计优化等方面。

本文将介绍振动分析的基本原理及其在工程实践中的应用。

振动分析的基本原理包括振动信号采集、信号分析和信号处理三个方面。

首先，振动信号的采集是通过传感器将物体振动产生的信号转换成电信号，并进行采样和量化。

常用的传感器包括加速度传感器、速度传感器和位移传感器，它们可以分别测量物体在加速度、速度和位移方面的振动信号。

其次，采集到的振动信号需要进行分析，通过对信号的频域分析、时域分析和轨迹分析，可以获取物体的振动频率、幅值和相位等特征参数。

最后，对振动信号进行处理，可以采用滤波、降噪、特征提取等方法，提高信号的质量和可靠性。

振动分析在工程实践中有着广泛的应用。

首先，它可以用于机械设备的故障诊断。

通过对机械设备振动信号的监测和分析，可以及时发现设备的故障和异常振动，为设备的维护和修理提供依据。

其次，振动分析可以用于结构的健康监测。

对建筑结构、桥梁、飞机等物体进行振动监测，可以了解结构的动态响应和疲劳破坏情况，为结构的安全评估和维护提供支持。

此外，振动分析还可以用于产品的设计优化。

通过对产品振动特性的分析，可以优化产品的结构设计，提高产品的性能和可靠性。

总之，振动分析原理是研究物体振动特性的一种重要方法，它在工程领域有着广泛的应用。

通过对振动信号的采集、分析和处理，可以获取物体的振动特征参数，为设备的故障诊断、结构的健康监测和产品的设计优化提供支持。

振动分析的发展将进一步推动工程技术的进步，为工程实践提供更多的可能性和机遇。

随机振动分析报告1. 引言随机振动是振动工程中的重要研究领域，对于各种结构和系统的设计与分析都具有重要的意义。

本文将介绍随机振动分析的基本概念、方法和步骤，并通过一个示例来说明如何进行随机振动分析。

2. 随机振动的基本概念随机振动是指在一定时间范围内，振动信号的幅值和频率是不确定的、随机变化的。

随机振动的特点是无法通过确定性的数学模型来描述，因此需要采用统计方法进行分析。

3. 随机振动分析的步骤随机振动分析的基本步骤包括：信号采集、数据预处理、频谱分析、统计分析和模型建立等。

3.1 信号采集随机振动信号的采集可以通过传感器等设备进行。

采集到的信号需要进行滤波和采样处理，以便后续分析。

3.2 数据预处理在进行频谱分析和统计分析之前，需要对采集到的数据进行预处理。

常见的预处理方法包括去除噪声、补充缺失数据和归一化处理等。

3.3 频谱分析频谱分析是对随机振动信号进行频域分析的方法。

通过对信号的频谱特性进行分析，可以了解信号的频率分布和主要频率成分。

3.4 统计分析统计分析是对随机振动信号进行统计学特征分析的方法。

常见的统计分析方法包括均值、方差、自相关函数和互相关函数等。

3.5 模型建立通过对随机振动信号的分析，可以建立相应的数学模型，用于预测和仿真。

常见的模型包括自回归模型和自回归移动平均模型等。

4. 示例：汽车发动机的随机振动分析以汽车发动机的随机振动分析为例，介绍随机振动分析的具体步骤。

4.1 信号采集使用加速度传感器对汽车发动机进行振动信号的采集。

将传感器安装在发动机的合适位置，以获取准确的振动信号。

4.2 数据预处理对采集到的振动信号进行滤波和采样处理，去除噪声和不必要的频率成分，并将信号进行归一化处理。

4.3 频谱分析将预处理后的振动信号进行频谱分析，得到信号的频谱特性。

可以使用FFT算法将信号从时域转换为频域，并绘制频谱图。

4.4 统计分析对频谱分析得到的数据进行统计分析，计算信号的均值、方差和自相关函数等统计学特征。

声学振动分析声学振动分析是一项重要的技术，它通过对声音的振动特性进行研究和分析，揭示了许多与声学振动有关的科学原理和应用技术。

本文将探讨声学振动的基本概念、分析方法和应用领域。

一、声学振动的基本概念声学振动是指物体在受到外界力的作用下，产生的机械运动所产生的声音现象。

声音是由空气、液体或固体等介质中的分子振动引起的，它的传播速度和频率与介质的性质有关。

声学振动的基本参数包括频率、振动形态和声压级等。

频率是指声音振动的频率，用赫兹（Hz）表示；振动形态描述了声音的波形特征，可以通过傅里叶变换等方法来分析；声压级是表示声音强度的指标，通常用分贝（dB）来表示。

二、声学振动分析方法声学振动分析主要借助数学模型和计算机模拟来实现。

以下是声学振动分析常用的方法：1. 声学测量方法：通过使用专业的声学测量设备，例如声音分析仪、声级计等，对声音的频率、声压级等进行测量和统计分析。

2. 模态分析方法：模态分析主要用于分析结构体在特定频率下的振动模态和振型。

通过对结构体进行激励，并测量其振动响应，可以得到结构体的固有频率和振型。

3. 有限元分析方法：有限元分析是一种广泛应用于工程领域的数值分析方法，可以用于模拟和分析结构体在声场激励下的振动响应。

该方法基于有限元模型，通过求解结构体的振动方程，得到其频率响应和振型。

4. 声学仿真方法：声学仿真是利用电脑模拟技术，通过建立声学模型和数字计算模型，对声学振动进行数值模拟和分析。

这种方法可以在不同环境和条件下对声学振动进行仿真实验，以便研究其特性和优化设计。

三、声学振动分析的应用领域声学振动分析在许多领域具有重要应用价值，以下列举几个常见的应用领域：1. 声学工程：声学振动分析可以用于声学设计和噪声控制。

通过对声学环境和声音传播特性进行分析，可以优化建筑结构、减少噪声污染，并提高声学性能。

2. 航空航天：声学振动分析在航空航天工程中广泛应用。

它可以用于飞机、火箭、发动机等结构的振动分析和噪声控制，保证飞行器的安全性和舒适性。

两种传递路径不同振动信号的特征分析牛雪梅;李敏;熊晓燕【摘要】In gear fault diagnosis, box vibration acceleration signal pass many transmission link and there is nonlinear cross couple of signals, the torsional vibration signals measured from transmission axle is studied to carry out fault diagnosis. The btspectrum characteristics of vibration signals obtained Through two different kinds of transfer paths are compared. Frequency components of box vibration acceleration signal are complex, while torsional vibration signal transfer links are less, transfer path is direct, thus interference factors are reduced , and frequency components of the signal are simpler. ' Through spectrum analysis, fault feature can be clearly extracted, which is helpful for accurate fault diagnose.%针对齿轮故障诊断中使用的齿轮箱箱体振动加速度信号的传递环节多,信号存在非线性交叉耦合的情况,研究了使用从传动轴端测取的扭转振动信号进行诊断的方法.对比了这两种传递路径不同振动信号的双谱特征,箱体振动加速度信号的传递路径复杂,导致其频率成分复杂；而扭转振动信号的传递环节少,获取信号的路径直接,干扰因素减少,信号频率成分比较单纯,利用通常使用的谱分析,故障特征就可以清晰地提取出来,利于齿轮故障的准确判断.【期刊名称】《中北大学学报（自然科学版）》【年(卷),期】2012(033)003【总页数】4页(P336-339)【关键词】传递路径;振动加速度信号;扭转振动信号;特征分析【作者】牛雪梅;李敏;熊晓燕【作者单位】太原科技大学电子信息工程学院,山西太原030024;太原理工大学机械电子工程研究所,山西太原030024;太原理工大学机械电子工程研究所,山西太原030024【正文语种】中文【中图分类】TP277;TH1650 引言在齿轮故障诊断中,齿轮箱箱体的振动加速度信号是使用最广泛的一种振动信号,已有大量文献研究对其进行各种分析和处理来提取故障特征,在很多情况下也是有效的[1-3].但若齿轮箱内部的传递环节较多时,各种因素会使系统的非线性特征明显,在箱体测得的振动信号是各种信号的交叉耦合,给特征提取带来困难,或者造成故障误判.若从轴端测取扭转振动信号,传递环节少,传递路径简单直接,干扰因素减少,信号比较单纯,经过简单的处理,故障特征就可以清晰地提取出来,利于故障的准确判断.根据实际对象或工业现场的条件,扭振信号的测取可以采取两种方式,一种由高精度编码器信号经变换处理得到[4],另一种使用定子电流信号解调而来.1 扭振信号的获取扭转振动是旋转机械中的一种重要的振动形式,传动轴及与其有关联的部件的损伤或故障的信息都可以反映在扭振信号中,并且由于其未经过复杂的传递路径,因而更容易提取出准确的故障特征.有如下两种方法可以比较有效地获取扭转振动的信号:1)在轴端安装高精度增量型光电编码器.这种编码器可以产生几千甚至几万个脉冲,其角度分辨率很高,可以感测到幅度(角度)较小的扭转振动,再经过频率-电压转换电路,就能获得扭转振动信号;也可以将编码器输出的信号经过希尔伯特变换而获取扭振信号.有些工业现场的旋转机械就安装有测量转速的编码器,经过适当的改造,可在工业现场方便地测得扭振信号.2)使用电流传感器提取电机的电流信号,再经过解调分析来得到轴的扭振信号.2 两种传递路径不同的振动信号的双谱特征齿轮箱在许多机械系统中都是重要的组成部分,其主要作用是传递动力和改变转速.它的结构形式也多种多样.一般来说,齿轮上的振动激励到箱体上安装的振动加速度计的传递路径是:齿轮→轴→轴承→齿轮箱箱体→加速度计.在这个传递过程中,由于结构本身存在的非线性因素(如间隙、磨损及非线性刚度等)以及传递过程中混入的其它噪声,会使测得的信号非线性程度加强,给诊断带来困难.而直接从轴端测得的扭转振动信号,传递路径简单,非线性因素和干扰噪声减少,利于后续的诊断.本文使用高阶谱分析对两种传递路径得到的振动信号进行了研究.这里把传递路径作为系统考虑.对于非线性系统,当谐波信号作用于它时,系统的输出信号既包含输入信号原有的频率成分,又会由于非线性耦合而出现新的频率成分.高阶谱可以识别出非线性相位耦合的情况.这里,高阶谱所检测和描述的信号是指随机激励非线性系统得到的响应信号.设二次非线性系统的输入信号系统的响应信号式中:X为非零常数.信号 z(k)含有余弦项(λ1,h1),(λ2,h2),(2 λ1,2 h1),(2 λ2,2 h2),(λ1- λ2,h1-h2),(λ1+ λ2,h1+h2).响应信号中不但含有激励信号的频率成分,同时也出现了新的频率成分,它等于激励信号某两个频率成分的和(或差),同时其相位也等于两个相位的和(或差),这种现象就称为二次相位耦合.功率谱是不含有相位信息的,故其无法检测二次相位耦合,而双谱(三阶累积量)就能检测及表征二次相位耦合的情况[5-15].齿轮箱-电机实验台如图 1所示,由电机,单级传动齿轮箱,加载装置,振动加速度计和扭转振动测量装置组成.当齿轮箱中的齿轮、轴和轴承均无故障时,对上述两种传递路径不同的振动信号进行双谱分析.由图 2可以看出,在箱体上测得的振动加速度信号已出现了非线性相位耦合现象,若齿轮箱中的零部件再出现故障时,信号的非线性情况会更加严重;若故障很轻微时,故障特征提取就变得较困难,有时也会出现误判的情况.扭振信号没有经过复杂的传递路径,由于传递路径的因素导致的非线性就不严重,当出现轻微故障时,简单的信号处理就能提取出明显的特征.图 3为扭振信号的双谱图,在 6个对称区域的某个区域中,频率成分简单,没有二次相位耦合现象.图1 齿轮箱-电机实验台Fig.1 Test-bed of gearbox-motor图2 箱体振动加速度信号的双谱图Fig.2 Bispectrum of box acceleration sig nal图3 扭振信号的双谱图Fig.3 Bispectrum of to rsional vibration signal3 故障特征提取从上面的分析可以看出,当齿轮传动系统中的零部件有故障或损伤时,箱体振动加速度信号的频率成分就比扭振信号的频率成分复杂的多.当齿轮上存在点蚀、裂纹等故障时,其接触刚度随之发生变化,这会造成扭转刚度的瞬时改变,这种变化会反映在扭振信号中.对于上述齿轮箱-电机实验台,经过理论计算,传动轴的转动频率为 3.4 Hz,齿轮的啮合频率为 100.4 Hz.这个特征也可以从扭振信号的频谱图中非常明显地体现出来,如图 4所示.当发生故障时,齿轮啮合而产生的信号被上述故障信号调制,在频谱图上就表现为在啮合频率及其各次谐频的两侧出现间隔均匀的边频带.图 5为点蚀齿轮扭振信号的频谱图.从图 5中可以明显地得到点蚀齿轮的信号特征:在 3.4 Hz处有一突出谱线,在 100.1 Hz处也有一突出谱线,在其两边,存在以 3.4 Hz为间隔的均匀明显的边频带,这与理论计算是基本吻合的.图4 提取的无损伤齿轮的扭振信号的频谱图Fig.4 Torsional vibration sig nal spectrum of undamag ed gear图5 提取的点蚀齿轮的扭振信号的频谱图Fig.5 Torsional vibration signal spectrum of pitting gear对箱体振动加速度信号施以与扭振信号相同的处理,其故障特征就远没有扭振信号的特征明显,如图 6所示.图6 提取的点蚀齿轮的振动加速度信号的频谱图Fig.6 Vibration acceleration signal spectrum of pitting gear4 结论当齿轮箱中的齿轮、轴和轴承均无故障时,对箱体振动加速度信号和传动轴端测取扭振信号这两种传递路径不同的振动信号进行双谱分析.振动加速度信号频率成分较复杂,出现了非线性相位耦合的现象.若齿轮箱中的零部件在出现故障时,信号的非线性情况会更加严重;若故障很轻微时,故障特征提取就变得较困难,有时也会出现误判的情况.扭振信号没有经过复杂的传递路径,由于传递路径的因素导致的非线性就不严重,双谱图中没有二次相位耦合的现象.当出现轻微故障时,谱分析就能提取出明显的特征.参考文献:[1]EndoH,Randall R B,Gosselin C. Differential diagnosis of spall vs.cracks inthe gear tooth fillet region: experimentalvalidation[J]. Mechanical Systems and Signal Processing,2009,23(3):563.[2]王楠,陈长征 ,孙长城,等.基于应力波与小波分析的低速滚动轴承故障诊断研究 [J].振动工程学报,2007,20(3):280-284.Wang Nan,Chen Changzheng,Sun Changcheng,et al. Studyon fault diagnosis of low-speed rolling bearing using stress waves and wavelet analysis[J].Journal of Vibration Engineering,2007,20(3):280-284.(in Chinese)[3]程发斌,汤宝平,刘文艺.一种抑制维格纳分布交叉项的方法及在故障诊断中应用[J].中国机械工程,2008,19(14):1727-1731.Chen Fabin,Tang Baoping,Liu Wenyi.Method to suppress cross-terms of wigner-ville distribution and its application in fault diagnosis[J].China MechanicalEngineering,2008,19(14):1727-1731.(in Chinese)[4]熊晓燕.高分辨率扭振测量方法及其应用[J].振动、测试与诊断,2003,23(1):41-43.Xiong Xiaoyan.High resolution torsional vibration measurement and its applications[J]. Journal of Vibration Measurement&Diagnosis,2003,23(1):41-43.(in Chinese)[5]张贤达.现代信号处理 [M].北京:北京大学出版社,2002.[6]陈仲生.基于 M ATLAB 7.0的统计信息处理 [M].长沙:湖南科学技术出版社,2005.[7]Proakis J G.统计信号处理算法 [M].汤俊译.北京:清华大学出版社,2006.[8]苏文斌,史维祥,温熙森.故障诊断中非线性耦合特征提取(一)[J].机械研究与应用,1998,11(2):12.Su Wenbin,Shi Weixiang,Wen Xisen.Nonlinear coupling signature extracting in fault diagnosis(one)[J].Mechanical Research& Application,1998,11(2):12.(in Chinese)[9]李学军,蒋玲丽,杨大栋.基于双谱分布区域的齿轮聚类分析与故障诊断 [J].振动工程学报,2011,24(3):304-308.Li Xuejun, Jiang Lingli,Yang Dadong. Cluster analysis and faultdiagnosis forgearbased on bispectrum distribution[J]. Journal of Vibration Engineering,2011,24(3):304-308.(in Chinese)[10]李凌均,韩捷,李朋勇.矢双谱分析及其在机械故障诊断中的应用 [J].机械工程学报,2011,47(17):50-54.Li Lingjun, Han Jie, Li Pengyong. Vectorbispectrum analysis and its application in machinery fault diagnosis [J]. Journal of Mechanical Engineering,2011,47(17):50-54.(in Chinese)[11]苏文斌,史维祥,温熙森.故障诊断中非线性耦合特征综合优化 [J].机械应用与研究,1998,11(3):10-12.Sun Wenbin, Shi Weixiang, Wen prehensive optimization of nonlinearcoupling signature extracting in fault diagnosis [J].Mechanical Research& Application,1998,11(3):10-12.(in Chinese) [12]马瑞,陈予恕.含裂纹故障齿轮的非线性动力学研究[J].机械工程学报,2011,47(21):84-90.Ma Rui,Chen Yushu.Nonlinear dynamic researcher on gear system with cracked failure[J].Journal of Mechanical Engineering,2011,47(21):84-90.(in Chinese)[13]张青峰,唐立伟,郑海起.基于非线性动力学模型的齿根裂纹故障分析 [J].机械传动,2010,34(11):58-65.Zhang Qingfeng, Tang Liwei, Zheng Haiqi.Nonlinear dynamics fault model analysis on gear tooth crack[J].Journal of Mechanical Transmission,2010,34(11):58-65.(in Chinese)[14]李辉,郑海起,唐立伟.基于双谱的齿轮箱升降速过程故障诊断研究 [J].中国机械工程,2006,17(16):1665-1668.Li Hui,Zheng Haiqi,Tang Liwei.Study on order bispectrum to fault diagnosis of gearbox during runup[J].Chinese Mechanical Engineering,2006,17(16):1665-1668.(in Chinese)[15]张园,李力,邹隽.基于双谱的滚动轴承非线性耦合特征提取与故障分类 [J].轴承,2008(7):37-42.Zhang Yuan,Li Li,Zou Jun.Non-linear coupling characteristics extraction and classification for rolling based on bispectrum[J].Bearing,2008(7):37-42.(in Chinese)。

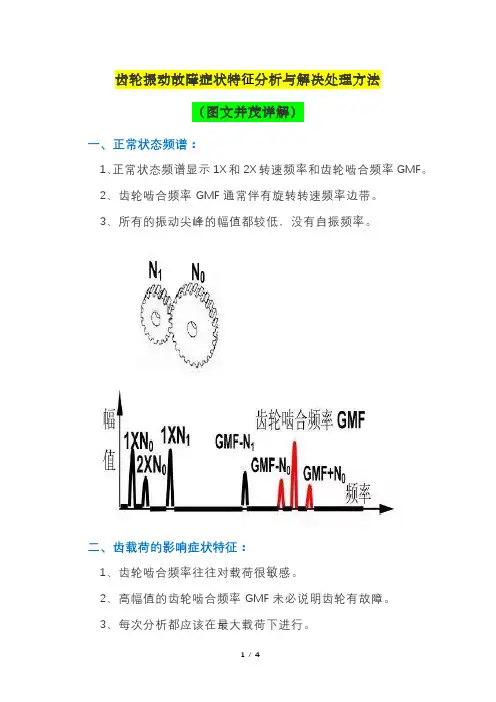
齿轮振动故障症状特征分析与解决处理方法
（图文并茂详解）
一、正常状态频谱：
1、正常状态频谱显示1X和2X转速频率和齿轮啮合频率GMF。

2、齿轮啮合频率GMF通常伴有旋转转速频率边带。

3、所有的振动尖峰的幅值都较低，没有自振频率。

二、齿载荷的影响症状特征：
1、齿轮啮合频率往往对载荷很敏感。

2、高幅值的齿轮啮合频率GMF未必说明齿轮有故障。

3、每次分析都应该在最大载荷下进行。

三、齿磨损症状特征：
1、激起自振频率同时伴有磨损齿轮的1X转速频率的边带说明齿磨损。

2、边带是比齿轮啮合频率GMF更好的磨损指示。

3、当齿轮的齿磨损时齿轮啮合频率的幅值可能不变。

四、齿轮偏心和侧隙游移症状特征：
1、齿轮啮合频率GMF两侧较高幅值的边带说明，齿轮偏心侧隙游移和齿轮轴不平行。

2、有故障的齿轮将调制边带。

3、不正常的侧隙游移通常将激起齿轮自振频率振动。

五、齿轮不对中症状特征：
1、齿轮不对中总是激起二阶或更高阶的齿轮啮合频率的谐波频率，并伴有旋转转速频率边带。

2、齿轮啮合频率基频(1XGMF)的幅值较小，而2X和3X齿轮啮合频率的幅值较高。

3、为了捕捉至少2XGMF频率，设置足够高的最高分析频率很重要。

六、断齿或裂齿症状特征：
1、断齿或裂齿将产生该齿轮的1X转速频率的高幅值的振动。

2、它将激起自振频率振动，并且在其两侧伴有旋转转速基频边带。

3、利用时域波形最佳指示断齿或裂齿故障。

4、两个脉冲之间的时间间隔就是1X转速的倒数。

七、齿磨损症状特征：摆动的齿轮的振动是低频振动，经常忽略它。

振动故障诊断要点振动故障是机械设备常见的故障类型之一，通过振动故障诊断可以帮助工程师找出故障的原因并采取相应的维修措施。

下面是振动故障诊断的要点：1.基本振动概念：了解振动的基本概念和参数，如振动的幅值、频率、相位和加速度等。

这些参数可以帮助工程师判断振动的严重程度和类型。

2.振动特征分析：振动特征分析包括频谱分析、时域分析和轨迹分析等。

频谱分析可以将振动信号转化为频谱图，从而找出频率和幅值异常的情况。

时域分析可以观察振动信号的波形，判断是否存在常见的故障类型。

轨迹分析可以观察旋转机械中旋转部件的运动轨迹，如转子不平衡和轴承故障。

3.振动测量与工具：了解振动测量的原理和方法，掌握常见的振动测量仪器，如加速度计、速度计和位移计等。

这些测量工具可以帮助工程师获取准确的振动数据，并用于故障诊断。

4.振动故障类型：了解振动故障的常见类型，如轴承故障、齿轮故障、不平衡和磨损等。

每种故障类型都有其特定的振动特征，通过分析这些特征可以判断故障的类型和位置。

5.振动诊断方法：根据振动特征和振动测量数据，结合机械设备的工作原理和结构特点，采用不同的振动诊断方法。

常见的方法包括单点测量、多点测量、滤波和波形诊断等。

通过综合应用这些方法，可以准确判断振动故障的原因。

6.振动故障分析：进行振动故障诊断后，需要对振动数据进行进一步的分析。

这包括对振动频谱进行解释和比较，对不同的振动特征进行关联分析，以及对振动故障的可能原因进行推断和验证。

7.故障预防和维护：通过振动故障诊断可以及时找出故障的原因，从而采取相应的维修措施。

然而，更好的方法是在设备正常运行期间进行故障预防和维护工作，包括定期检查和维护设备、定期校准和保养振动测量仪器等。

8.振动故障诊断的案例分析：通过分析实际案例，学习振动故障诊断的方法和技巧。

实际案例可以帮助工程师理解振动故障的原因和机理，并提高振动故障诊断的能力。

振动故障诊断是机械设备维修中重要的一环，能够帮助工程师快速准确地找出故障的原因，避免设备损坏和停机时间的增加。

机械系统振动信号的特征参数提取与分析随着机械工程技术的发展，机械系统振动信号的特征参数提取与分析也日益成为了工程领域的研究热点。

机械系统振动信号的特征参数提取与分析可以帮助工程师诊断和预测机械设备的状态，从而提前进行维护和修复，避免设备故障和生产事故的发生。

一、振动信号特征参数的提取振动信号特征参数的提取是对原始振动信号进行处理和分析，以获得更有价值的信息。

常见的振动信号特征参数有以下几种：1. 频率特征参数：包括振动信号的谱线频率、主频率以及共振频率等。

通过分析频率特征参数，可以确定机械系统的运动状态和周期性变化情况。

2. 振幅特征参数：反映了振动信号的振幅大小和幅值变化的规律。

振幅特征参数的提取可以帮助工程师了解机械系统的振动幅度是否超过了正常范围。

3. 相位特征参数：相位特征参数描述了振动信号中的相对相位差异。

通过分析相位特征参数，可以判断机械系统中是否存在相位不一致或相位错位的情况。

4. 能量特征参数：能量特征参数是振动信号能量与时间的关系。

通过分析能量特征参数，可以评估机械系统的能源消耗情况和能源利用效率。

二、振动信号特征参数的分析振动信号特征参数的分析可以帮助工程师判断机械系统的工作状态和存在的问题，并在必要时采取相应的维修和改进措施。

振动信号特征参数的分析方法多种多样，其中常用的分析方法有以下几种：1. 频谱分析：通过将振动信号从时域转换为频域，得到信号的频率成分和频率分布情况。

常用的频谱分析方法包括傅里叶变换、小波变换和短时傅里叶变换等。

2. 自相关分析：自相关分析可以揭示振动信号中的周期性变化和共振现象。

通过计算振动信号的自相关函数，可以得到信号的周期性特征和自相关时间。

3. 概率分析：概率分析可以用于评估振动信号特征参数的分布情况和变化规律。

常用的概率分析方法包括统计特征、功率谱估计和相关性等。

4. 熵分析：熵分析可以评估振动信号的随机性和复杂性。

通过计算振动信号的熵值，可以得到信号的信息量和不确定性。

振动信号特征提取及识别随着科技的发展和普及，振动信号成为了现代工业中最为常见的一种信号。

振动信号可以反映机械运行状态，是机械故障诊断、监测和预警的重要依据。

为了正确地识别机械故障，需要对振动信号进行特征提取和识别。

本文将介绍振动信号的特征提取和识别方法。

一、振动信号特征提取振动信号是由机械的磨损、摩擦和冲击等产生的，其包含了丰富的信息。

振动信号的特征提取就是从中提取有意义的特征，以便对机械状态进行分析和诊断。

振动信号的特征通常包括时域特征和频域特征。

1.时域特征时域特征指振动信号在时间范围内的性质，常见的包括均值、方差、峰值、脉冲因数、裕度因子等。

这些特征可以很好的反映机械运行状态的变化。

例如，当轴承受损时，峰值会变小，方差会增大。

2.频域特征频域特征包括频谱分析，频带能量分析，小波分析等。

频谱分析通过对振动信号进行傅里叶变换，得到信号的频谱分布，从而得出不同频段内的幅值和峰值。

频带能量分析则是将频谱分为不同的频带，通过测量每个频带内的能量大小，来反映机械运行状态。

小波分析则是将信号在不同尺度下进行分解，可以提取更为细节的信息。

二、振动信号识别振动信号的识别就是将振动信号的特征和已知故障数据库进行对比，从而推断出机械的运行状态。

振动信号的识别需要依靠先进的算法和技术，下面介绍一些常见的振动信号识别方法。

1.神经网络神经网络是一种模拟人类神经系统的计算模型，可以学习和分类振动信号的特征，适用于大规模的数据处理。

通过训练神经网络，可以实现振动信号的分类和故障诊断。

2.支持向量机支持向量机是一种线性分类器，可以通过构造最优分割超平面，将振动信号进行分类。

其优点是对样本数量不敏感，能够处理高维特征数据。

3.小波神经网络小波神经网络将小波分析和神经网络相结合，可以提取更为细节的振动信号特征，并进行更加精准的故障诊断。

4.模糊神经网络模糊神经网络结合了模糊理论和神经网络，可以处理非线性问题。

模糊神经网络适用于复杂的振动信号分类和故障诊断。

振动分析总结报告振动分析总结报告振动分析是一种对物体在振动作用下的响应进行分析和研究的方法。

通过振动分析可以得到物体的振动模态、频率响应以及频率响应函数等重要参数，对物体的设计、制造和运行都具有重要意义。

在振动分析过程中，需要进行实验测量和数值模拟两种方法的结合，以获得准确的结果。

本次振动分析的实验对象是一台电动机，旨在研究其在运行过程中的振动情况，并寻找振动的来源和原因。

实验采用传感器在电动机不同位置处的布置来获取振动信号，再通过信号处理和数据分析得到相应的振动特征参数。

通过实验得到的结果与理论计算和相关指标进行对比和评估，以确定电动机的振动是否正常。

在振动分析的测量过程中，我们发现电动机在运行时产生了较大的振动，振动主要集中在转子轴的两端。

通过分析振动信号的频谱和振动幅值，我们发现电动机存在不平衡的问题。

不平衡可以导致转子轴产生离心力，使其在运动过程中引起振动。

根据实验结果和目标要求，我们对电动机进行了重新调整和平衡处理，从而有效减小了振动的幅值。

然而，实验中我们也遇到了一些挑战。

首先，由于电动机受限于装置结构和使用条件，使用传统的振动传感器进行振动测量并不方便，我们需要寻找到适用的传感器和布置方式。

其次，振动信号的处理和分析也面临一定的困难，我们需要在噪声干扰下提取出有效的振动信号，并进行相应的数据处理以获得准确的振动特征参数。

最后，在振动分析的过程中，我们需要结合相关理论和经验知识，进行数据分析和结果评估，以确保分析结果的可靠性和准确性。

在本次振动分析过程中，我们收集到了丰富的数据和有意义的结果。

通过对电动机的振动特征进行分析，我们确定了振动来源和原因，并针对问题进行了相应的处理和优化。

通过实验和分析，我们得出了以下几点结论和总结：首先，电动机存在不平衡问题，导致了振动的产生。

不平衡可以通过重新调整和平衡来减小振动的幅值。

其次，振动信号的处理和分析是振动分析的关键步骤，需要结合理论和实际经验进行综合分析和评估。

风力发电机组主机架振动分析风力发电机组主机架振动分析风力发电机组主机架振动分析是对风力发电机组运行过程中可能出现的振动问题进行研究和识别的过程。

振动是风力发电机组主机架运行时的常见现象，并且可能会对整个系统的稳定性和性能产生不利影响。

因此，进行振动分析是非常重要的，可以帮助工程师们确定振动的来源，并采取相应的措施来减小振动的影响。

以下是进行风力发电机组主机架振动分析的一些步骤：1. 收集数据：首先，需要收集风力发电机组运行过程中的振动数据。

这些数据可以通过传感器、监测设备或振动测量仪器进行收集。

数据的收集应该涵盖不同工作条件下的振动情况，包括不同风速、不同转速等等。

2. 数据处理：收集到的振动数据需要进行处理，以便更好地理解和分析。

可以使用数据处理软件进行数据的清洗、过滤和调整。

数据处理的目的是消除噪声和杂乱信号，使得振动特征更加清晰和可辨识。

3. 振动特征提取：在数据处理之后，需要提取出振动的特征参数。

这些特征参数可以包括振动的频率、幅值、相位等等。

通过振动特征的分析，可以帮助确定振动的来源和模式，进一步了解主机架的振动机制。

4. 振动源识别：通过振动特征的分析，可以确定振动的源头。

主机架振动的来源可能包括风扇、机械部件、电机等。

通过仔细观察振动特征的变化和振动频率的分析，可以识别出主机架振动的具体来源。

5. 振动控制措施：一旦确定了主机架振动的来源，可以采取相应的振动控制措施。

这些措施可能包括调整机械部件的平衡、加强固定、增加减振装置等。

振动控制的目标是减小振动的幅值和频率，提高系统的稳定性和性能。

6. 振动监测：在采取振动控制措施之后，需要对主机架进行定期的振动监测。

这可以通过在线监测系统或定期的振动测量来实现。

振动监测的目的是确保振动控制的有效性，并及时发现和解决可能的问题。

总之，风力发电机组主机架振动分析是一个复杂而重要的过程。

通过收集、处理和分析振动数据，确定振动的来源，并采取相应的措施来减小振动的影响，可以提高风力发电机组的稳定性和性能。

震动信号的频域分析及特征提取研究近年来，随着现代化工业的发展以及基础设施建设的不断推进，人类的生产和生活与机械设备紧密相连，振动问题逐渐成为工程领域中的重要难题。

震动信号的频域分析及特征提取研究，正是针对这一问题而展开的一种重要研究方向。

一、震动信号的频域分析频域分析，是指将时域信号转换为频域信号，从而更深入地研究信号的特征及物理本质的一种信号分析方法。

在机械振动领域中，采用的最为广泛的分析方法就是频域分析。

首先，震动信号的频域分析需要进行信号采集、滤波和采样三个步骤。

采集信号时，可以将传感器与被测物体进行关联，传感器直接监测被测器件震动的振幅和频率，并输出模拟信号，通过数据采集卡转换为数字信号。

在提取特定频率成分或减少多余噪声时，需要进行数字滤波来优化信号质量。

采样过程中，需要根据所获取的传感器信号，采取适当的时间间隔进行数据采样和储存。

接下来是FFT（快速傅里叶变换）算法的应用。

FFT是一种将时间域信号转换为频域信号的算法，可以在计算机上对信号进行快速的频域变换，分离出原信号中的各个频率分量及其强度，在频谱图上显示出来，从而得出一个完整的频域图像。

如果需要对原始数据进行降噪、滤波或预测，可以通过傅里叶变换、小波变换等算法对其进行进一步的频域分析。

二、震动信号特征提取震动信号特征提取，是指通过算法分析对振动信号中的各种性质进行计算和统计，从而提取出能反映工件运动特性和机械状态的客观指标。

研究特征提取方法，能够有效地评估机械设备的运行状况，提高机械设备的效率，延长机械的使用寿命。

震动信号的特征参数主要包括时间域参数和频域参数两大类。

时间域参数包括波形形态参数和时域统计参数，既可以从整体上反映振动信号的波形水平，也可以从微观特性上揭示振动噪声的随机性和不规则性；频域参数则包括功率谱特征和频域统计特征，对于振动信号的分析具有极其重要的作用。

在实际特征提取过程中，震动信号往往是一个很复杂的非线性系统。

机械振动公式总结机械振动是指物体在受到外力或其他作用下发生的周期性运动。

在研究机械振动时，我们可以利用一些振动公式来描述和分析振动现象。

本文将对机械振动的一些常用公式进行总结和介绍。

1. 振动的基本特征在研究机械振动时，我们常常关注以下几个基本特征：(1) 振动的周期(T)：振动一个完整的往复运动所需要的时间。

(2) 振动的频率(f)：单位时间内振动的次数，即频率的倒数为周期。

(3) 振幅(A)：振动物体从平衡位置最大偏离的距离。

2. 简谐振动公式简谐振动是指振动物体在受到恢复力作用下，其加速度与位移成正比的振动。

简谐振动的公式如下：x(t) = A * sin(ωt + φ)其中，x(t)为时刻t时的位移，A为振幅，ω为角频率，φ为初相位。

3. 简谐振动的频率和周期简谐振动的频率和周期之间存在如下关系：f = 1 / T = ω / 2π其中，f为频率，T为周期，ω为角频率。

4. 简谐振动的角频率与弹性系数和质量的关系对于简谐振动的弹簧振子，角频率与弹性系数k和质量m之间存在如下关系：ω = √(k / m)其中，ω为角频率，k为弹性系数，m为质量。

5. 非简谐振动的公式非简谐振动是指振动物体在受到非线性恢复力作用下的振动。

非简谐振动的公式通常较复杂，常用的一种非简谐振动公式是Duffing 方程：m * x'' + c * x' + k * x + β * x^3 = F0 * cos(ωt)其中，m为质量，x为位移，c为阻尼系数，k为弹性系数，β为非线性系数，F0为驱动力的振幅，ω为驱动力的角频率。

6. 驱动力频率与振动响应在非简谐振动中，驱动力的频率与振动物体的响应存在关系。

当驱动力的频率接近振动系统的固有频率时，振动响应最大。

这个现象称为共振。

共振频率的计算公式如下：ωr = √(k / m)其中，ωr为共振频率，k为弹性系数，m为质量。

7. 多自由度振动的公式多自由度振动是指振动系统中存在多个自由度的振动。

机械振动信号的特征提取与识别一、引言在工业领域中，机械设备的正常运行对于生产效率和安全性至关重要。

机械振动信号是反映机械设备运行状态的重要指标，通过对机械振动信号进行特征提取和识别，可以有效地监测和维护设备状态，提前发现故障，并进行及时维修，从而降低设备故障率和提高生产效率。

本文将介绍机械振动信号的特征提取和识别方法。

二、机械振动信号特征提取机械振动信号的特征提取是将原始信号转化为一组具有代表性的数值指标，以描述信号的特征和状态。

常用的特征提取方法包括时域特征、频域特征和小波分析。

1. 时域特征时域特征是指在时间轴上对振动信号进行采样和统计分析，常用的时域特征包括均值、标准差、峰值、峭度、偏度等。

这些特征能够反映振动信号的整体情况和分布特征，对于正常和异常状态的判断具有一定的能力。

2. 频域特征频域特征是指将时域信号转化为频域信号，通过对频谱进行分析，提取能量、频率等特征。

常用的频域特征包括功率谱密度、频谱熵、主频提取等。

频域特征能够反映信号的频率分布和能量分布，对于频谱分析和频率成分的提取具有重要意义。

3. 小波分析小波分析是一种将信号分解成多个不同频率和幅度的小波基函数，通过对不同尺度和频率上的分析，提取信号的特征。

小波分析具有时频局部化的特点，能够在时域和频域上同时对信号进行分析，提取局部特征。

常用的小波特征包括小波包能量、小波包熵等。

三、机械振动信号的识别方法机械振动信号的识别方法是将特征提取后的信号与已知状态进行比较和判断，从而实现对机械设备运行状态的自动识别。

常用的识别方法包括模式识别、神经网络和支持向量机。

1. 模式识别模式识别是将信号与已有的样本数据进行比对，通过对比样本数据和待识别信号的相似程度，判断待识别信号属于哪一类别。

常用的模式识别方法包括最邻近分类、线性判别分析等。

2. 神经网络神经网络是一种基于生物神经系统的计算模型，它可以通过学习和训练，获得对信号的识别能力。

通过构建适当的神经网络结构和算法，将特征提取后的信号输入神经网络，通过神经网络的学习和模型拟合能力，实现对信号的识别和分类。

复杂边界条件圆柱壳自由振动特性分析1. 引言1.1 背景介绍圆柱壳是一种常见的结构，在工程中具有广泛的应用。

圆柱壳在多种领域中都扮演着重要的角色，比如航空航天领域的发动机壳体、海洋工程领域的钻井平台支柱等。

由于复杂的工作环境和载荷作用，圆柱壳的振动特性对结构的稳定性和安全性有着重要影响。

在实际工程中，圆柱壳往往会受到各种边界条件的限制，如固支、弹簧支座、不同形状的约束等。

这些复杂的边界条件会对圆柱壳的振动特性产生显著影响，因此需要深入研究和分析。

本文旨在通过有限元方法对具有复杂边界条件的圆柱壳进行自由振动特性分析，探讨不同边界条件对圆柱壳振动行为的影响，为工程实践提供理论支持。

通过数值模拟和参数分析，结合实验数据进行模型验证和结果讨论，揭示圆柱壳在不同工况下的振动特性。

通过对圆柱壳振动特性的研究，我们可以进一步了解结构的工作状态和性能，为优化设计和改进提供参考。

1.2 问题提出特别是在一些特殊工况下，比如边界条件不规则或者受到外部扰动等情况下，圆柱壳的振动特性会受到更大的影响，这就需要我们针对不同边界条件下的圆柱壳进行深入研究和分析。

如何解决这一问题成了当前研究的重要课题。

通过对圆柱壳的复杂边界条件进行分析，可以更好地理解结构的振动行为，为工程实践提供重要参考。

本研究旨在通过有限元方法等数值模拟手段，对复杂边界条件下圆柱壳的自由振动特性展开深入研究，为相关工程领域提供理论支持和技术指导。

1.3 研究意义研究圆柱壳的自由振动特性能够为工程设计提供重要参考。

通过深入探究圆柱壳在复杂边界条件下的振动特性，可以为工程师提供更准确的设计参数和指导，从而提高工程结构的性能和安全性。

通过对复杂边界条件下圆柱壳的自由振动特性进行深入分析，可以为工程设计和实际应用提供重要的理论基础和指导，具有重要的研究意义和应用前景。

2. 正文2.1 复杂边界条件对圆柱壳振动影响分析在研究过程中，首先需要建立合适的数学模型来描述圆柱壳的振动行为，并考虑复杂边界条件的影响。

基于声学理论的结构振动特性分析引言：结构振动特性是研究结构动力学的重要内容之一。

在工程实践中，准确分析结构振动特性对于设计和改进结构的性能至关重要。

本文将介绍基于声学理论的结构振动特性分析方法，探讨其在工程实践中的应用。

一、声学理论基础声学理论是研究声波传播的科学，它探讨了声波在介质中的传播规律和与介质相互作用的机制。

在结构振动特性分析中，声学理论提供了一种有效的工具，用于描述结构振动的传播和响应。

二、结构振动的数学模型结构振动可以用数学模型来描述。

常见的数学模型包括弹簧质点模型、连续体模型和有限元模型。

这些模型可以通过声学理论来求解，得到结构的振动频率、振型和振动响应。

三、结构振动的频率分析频率分析是结构振动特性分析的重要内容。

通过声学理论，可以计算出结构的固有频率。

固有频率是结构振动的特征频率，它与结构的几何形状、材料性质和边界条件等因素有关。

通过计算固有频率，可以评估结构的稳定性和动态特性。

四、结构振动的模态分析模态分析是研究结构振动模态的方法。

通过声学理论，可以计算出结构的振型，即结构在不同频率下的振动形态。

振型描述了结构在不同模态下的振动分布情况，它对于结构的设计和优化具有重要意义。

五、结构振动的响应分析响应分析是研究结构在外部激励下的振动响应。

通过声学理论，可以计算出结构在不同激励下的振动响应，包括位移、速度和加速度等。

振动响应分析可以评估结构的动态性能，对于结构的设计和改进具有指导意义。

六、结构振动特性分析的应用基于声学理论的结构振动特性分析在工程实践中有着广泛的应用。

例如，在建筑设计中，可以通过分析结构的振动特性来评估结构的稳定性和舒适性。

在机械设计中，可以通过分析结构的振动特性来评估结构的可靠性和噪声性能。

在桥梁设计中，可以通过分析结构的振动特性来评估结构的抗风性能和耐久性。

结论：基于声学理论的结构振动特性分析方法为工程实践提供了一种有效的工具。

通过分析结构的振动特性，可以评估结构的稳定性、动态性能和舒适性等指标，为结构的设计和改进提供科学依据。

机械振动信号的相关性分析与特征提取机械振动信号是工业生产中常见的一种信号形式，用于监测机械设备的运行状况。

通过对机械振动信号的相关性分析与特征提取，可以有效地判断设备的运行状态和预测故障。

一、相关性分析相关性分析是研究机械振动信号之间关联性的一种方法。

在相关性分析中，通常使用相关系数来衡量信号之间的相关程度。

相关系数的取值范围为-1到1，正值表示正相关，负值表示负相关，而值越接近0表示两个信号之间的相关性越低。

在进行相关性分析时，可以选取不同的频段或时域范围进行计算。

通过观察不同频段或时域范围的相关系数变化情况，可以了解信号在不同频率或时域下的相关性特征。

比如，在高频段中，相关系数较高可能表示设备存在故障，而在低频段中，相关系数较高可能表示设备正常运行。

二、特征提取特征提取是将机械振动信号中的有用信息提取出来，用于判断设备的运行状态。

常用的特征包括时域特征、频域特征和小波特征等。

时域特征是指从时间轴上提取的特征，如峰值、均方根、峭度和偏度等。

这些特征反映了振动信号的幅值、波形和偏度等信息。

通过对时域特征的提取和分析，可以了解设备振动信号的基本特征。

频域特征是指从频谱上提取的特征，如频率峰值、频域能量和频率谱形等。

频域特征可以更加直观地了解信号在不同频率上的能量分布情况。

通过对频域特征的提取和分析，可以判断信号中存在的频率成分，进而判定设备的工作状态。

小波特征是指使用小波分析方法对机械振动信号进行特征提取。

小波分析可以将信号分解为不同频率的成分，通过选择合适的小波基函数，可以提取到信号中的细微变化和瞬态特征。

小波特征的提取可以更准确地刻画机械振动信号的特征。

三、应用案例以工业机械设备故障预测为例，通过对机械振动信号的相关性分析与特征提取，可以提前发现设备可能存在的故障。

首先，对机械振动信号进行相关性分析，计算各信号之间的相关系数。

通过观察相关系数的变化情况，可以找出设备运行状态可能发生变化的频段。

引起发电机组轴承座轴向振动的7种原因及振动特征和案例分析！18-04-0914:01一、轴向振动的机理类似于轴承座的垂赢、水平振动和其他固定结构的振动，引起轴向振动原因通常也是来自轴向激振力过大和轴向动刚度偏弱或轴向共振。

1、转子弯曲当存在永久弯曲或热弯曲的转子旋转时，轴颈中心会产生偏转，这时轴颈在轴瓦内的油膜承力中心将随转速沿轴向发生周期性变化。

由于转子支承系统是由轴承座和基础组成的弹性体，在油膜承力中心周期性变化的作用下，轴承座将沿其某一底边发生周期性的轴向偏转，即造成轴向振动。

特别是当轴承座连接刚度不足时，产生的轴向振动更为明显。

转子弯曲产生的轴向振动值与转子的弯曲度呈正比，当弯曲部位在轴颈附近时，轴承座呈现的轴向振动更大。

当然，通常由转子弯曲产生很大轴向振动的同时，也会伴随转轴振动的增大。

2、轴向电磁力不平衡轴向电磁力不平衡也能引起发电机或励磁机转子轴承座的轴向振动。

当汽轮机驱动发电机转子旋转时，转子旋转磁场切割定子绕组磁力线产生电流，同时定子绕组也产生感应磁场。

正常情况下，发电机转子在定子中沿轴向对称布置，定子绕组感应磁场的磁通量两端基本一致，故电磁力保持平衡。

如果运行中发电机转子与定子沿轴向的对称中心出现偏移，则在定子绕组两端感应磁场的磁通量就不相等，那么两端感应磁场的电磁力也不相等。

使电磁力失去平衡，从而使转子沿轴向产生电磁力不平衡。

一旦出现不平衡电磁力后，转子沿轴向产生位移，不平衡力将力图使转子回到平衡位置，但由于发电机转子两端受联轴器的约束，迫使转子回到先前的偏置位置。

这样，发电机转子就形成沿轴向的振荡，并传递到轴承座形成轴向振动。

同样，当励磁机转子与定子沿轴向出现对称中心线位置偏移时，也会产生不平衡的电磁力，而出现在励磁机转子上的不平衡电磁力使励磁机转子发生轴向串动，并可传递给发电机转子。

发电机转子与定子或励磁机转子与定子沿轴向的对称中心出现偏移时的不平衡电磁力产生100Hz的轴向振动。