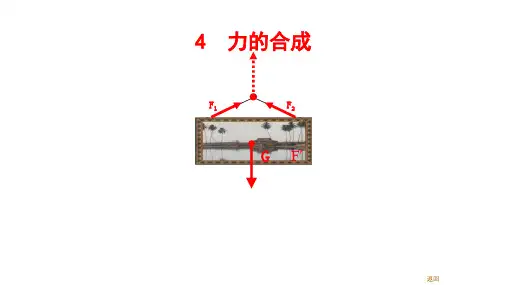
假设斜拉桥中某对钢索与竖直方向的夹角是 30°,每根钢索的拉力都是
3×104 N,那么该对钢索对塔柱形成的合力有多大?方向如何?
解析:把两根钢索的拉力看成沿钢索方向的两个分力,以它们为邻边作出
平行四边形,其对角线就表示它们的合力。由对称性可知,合力方向一定
沿塔柱竖直向下。
法一
作图法(如图甲所示)
自O点引两根有向线段OA和OB,它们跟竖直方向的夹角都为30°。取单位
到一水平向左、大小为10 N的拉力F的作用,则物体所受的合力为(已知物体
与地面间的动摩擦因数为μ=0.5,g取10 m/s2)(
A.0 N
B.20 N,向右
C.20 N,向左
D.10 N,向右
C
)
解析:物体在向右运动,故受到地面的滑动摩擦力,则摩擦力的大小F f =
μmg=10 N;方向与运动方向相反,水平向左;在运动过程中还受到一水平
和,故A、B、C错误;人将弦拉得越紧,则夹角越小,且拉力F1、F2越大,即
箭受到的合力越大,故D正确。
要点二
合力的求解方法
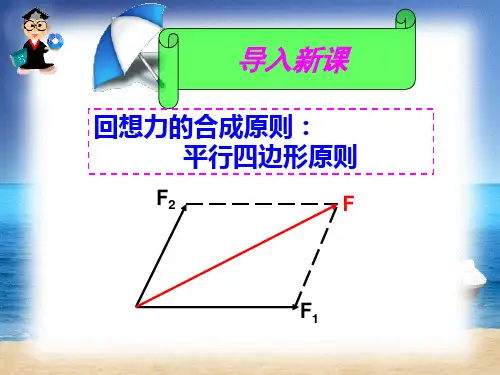
1.作图法(如图所示)
2.计算法
(1)两分力共线时,有两种情况。
①若F1、F2两力同向,则合力F=F1+F2,方向与两力同向。
②若F1、F2两力反向,则合力F=|F1-F2|,方向与两力中较大的同向。
(2)两分力不共线时,根据平行四边形定则作出力的示意图,然后由几何关系
求解对角线所对应的力,即为合力大小。经常遇到以下特殊情况。
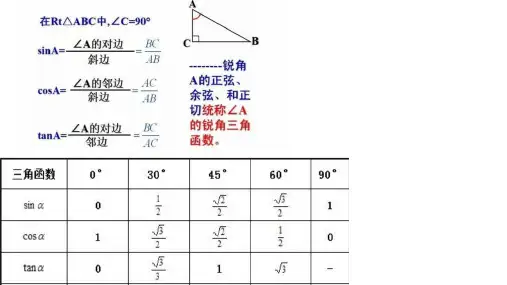
①相互垂直的两个力(即α=90°)的合成,则有 F= + ,F 与 F1 的夹角的正切
值 tan β= ,如图甲所示。
②两个等大的力的合成。两个等大的力的有向线段组成的平行四边形为菱形,其对角