2018年高中数学黄金100题系列第64题空间垂直关系的证明文

【考向解读】1.以选择题、填空题的形式考查，主要利用平面的基本性质及线线、线面和面面的判定与性质定理对命题的真假进行判断，属基础题.2.以解答题的形式考查，主要是对线线、线面与面面平行和垂直关系交汇综合命题，且多以棱柱、棱锥、棱台或其简单组合体为载体进行考查，难度中等.【命题热点突破一】空间线面位置关系的判定(1)根据空间线面平行、垂直关系的判定定理和性质定理逐项判断来解决问题；(2)必要时可以借助空间几何模型，如从长方体、四面体等模型中观察线面位置关系，并结合有关定理来进行判断．例1、(2017·高考全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()C项，作如图③所示的辅助线，则AB∥CD，CD∥MQ，∴AB∥MQ又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ.D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，∴AB∥NQ，又AB⊄平面MNQ，NQ⊂平面MNQ，∴AB∥平面MNQ.故选A.【变式探究】【2016高考江苏卷】(本小题满分14分)如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且，.求证：（1）直线DE∥平面A1C1F；（2）平面B1DE⊥平面A1C1F.【答案】（1）详见解析（2）详见解析所以直线DE//平面（2）在直三棱柱中，因为平面，所以又因为所以平面因为平面，所以又因为所以因为直线，所以【变式探究】(1)若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是( )A．l与l1，l2都不相交B．l与l1，l2都相交C．l至多与l1，l2中的一条相交D．l至少与l1，l2中的一条相交(2)平面α∥平面β的一个充分条件是( )A．存在一条直线a，a∥α，a∥βB．存在一条直线a，a⊂α，a∥βC．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α答案 (1)D (2)D若α∩β＝l，a⊂α，a∥l，b⊂β，b∥l，则a∥β，b∥α，故排除C.故选D.【特别提醒】解决空间点、线、面位置关系的组合判断题，主要是根据平面的基本性质、空间位置关系的各种情况，以及空间线面垂直、平行关系的判定定理和性质定理进行判断，必要时可以利用正方体、长方体、棱锥等几何模型辅助判断，同时要注意平面几何中的结论不能完全引用到立体几何中．【变式探究】已知m，n为两条不同的直线，α，β为两个不重合的平面，给出下列命题：①若m⊥α，n⊥α，则m∥n；②若m⊥α，m⊥n，则n∥α；③若α⊥β，m∥α，则m⊥β；④若m⊥α，m∥β，则α⊥β.A．0 B．1C．2 D．3答案 C【命题热点突破二】空间平行、垂直关系的证明空间平行、垂直关系证明的主要思想是转化，即通过判定、性质定理将线线、线面、面面之间的平行、垂直关系相互转化．例2、(2017·高考全国卷Ⅲ)如图，四面体ABCD中，△ABC是正三角形，AD＝CD.(1)证明：AC⊥BD；(2)已知△ACD是直角三角形，AB＝BD.若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．【变式探究】【2016高考江苏卷】(本小题满分14分)如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且，.求证：（1）直线DE∥平面A1C1F；（2）平面B1DE⊥平面A1C1F.【答案】（1）详见解析（2）详见解析（2）在直三棱柱中，因为平面，所以又因为所以平面因为平面，所以又因为所以因为直线，所以【变式探究】如图，三角形PDC所在的平面与长方形ABCD所在的平面垂直，PD＝PC＝4，AB＝6，BC＝3.(1)证明：BC∥平面PDA；(2)证明： BC⊥PD；(3)求点C到平面PDA的距离．在Rt△PED中，PE＝＝＝.因为平面PDC⊥平面ABCD，平面PDC∩平面ABCD＝CD，PE⊂平面PDC，所以PE⊥平面ABCD，由(2)知：BC⊥平面PDC，由(1)知：BC∥AD，所以AD⊥平面PDC，因为PD⊂平面PDC，所以AD ⊥PD .设点C 到平面PDA 的距离为h ， 因为V 三棱锥CPDA ＝V 三棱锥PACD ， 所以31S △PDA ·h ＝31S △ACD ·PE ， 即h ＝S △PDA S △ACD·PE ＝×3×41＝27， 所以点C 到平面PDA 的距离是27.【特别提醒】 垂直、平行关系的基础是线线垂直和线线平行，常用方法如下：(1)证明线线平行常用的方法：一是利用平行公理，即证两直线同时和第三条直线平行；二是利用平行四边形进行平行转换；三是利用三角形的中位线定理证线线平行；四是利用线面平行、面面平行的性质定理进行平行转换．(2)证明线线垂直常用的方法：①利用等腰三角形底边中线即高线的性质；②勾股定理；③线面垂直的性质：即要证两线垂直，只需证明一线垂直于另一线所在的平面即可，l ⊥α，a ⊂α⇒l ⊥a .【变式探究】如图所示，已知AB ⊥平面ACD ，DE ⊥平面ACD ，△ACD 为等边三角形，AD ＝DE ＝2AB ，F 为CD 的中点．求证：(1)AF ∥平面BCE ； (2)平面BCE ⊥平面CDE .∵DE⊥平面ACD，AF⊂平面ACD，∴DE⊥AF.又CD∩DE＝D，故AF⊥平面CDE.∵BG∥AF，∴BG⊥平面CDE.∵BG⊂平面BCE，∴平面BCE⊥平面CDE.【命题热点突破三】平面图形的折叠问题平面图形经过翻折成为空间图形后，原有的性质有的发生变化、有的没有发生变化，这些发生变化和没有发生变化的性质是解决问题的关键．一般地，在翻折后还在一个平面上的性质不发生变化，不在同一个平面上的性质发生变化，解决这类问题就是要根据这些变与不变，去研究翻折以后的空间图形中的线面关系和各类几何量的度量值，这是化解翻折问题的主要方法．例3、【2016高考新课标2文数】如图，菱形的对角线与交于点，，点分别在上，，交于点．将沿折到位置，．（Ⅰ）证明：平面；（Ⅱ）求二面角的正弦值．【答案】（Ⅰ）详见解析；（Ⅱ）.于是，故.又，而，所以.【变式探究】如图(1)，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图(2)．(1)求证：DE∥平面A1CB；(2)求证：A1F⊥BE；(3)线段A1B上是否存在点Q，使A1C⊥平面DEQ？请说明理由．(3)解线段A1B上存在点Q，使A1C⊥平面DEQ.理由如下：如图，分别取A1C，A1B的中点P，Q，则PQ∥BC.又因为DE∥BC，所以DE∥PQ.所以平面DEQ即为平面DEP.由(2)知，DE⊥平面A1DC，所以DE⊥A1C.又因为P是等腰三角形DA1C底边A1C的中点，所以A1C⊥DP.所以A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.【特别提醒】(1)折叠问题中不变的数量和位置关系是解题的突破口；(2)存在探索性问题可先假设存在，然后在此前提下进行逻辑推理，得出矛盾或肯定结论．【变式探究】如图(1)，四边形ABCD为矩形，PD⊥平面ABCD，AB＝1，BC＝PC＝2，作如图(2)折叠，折痕EF∥DC.其中点E，F分别在线段PD，PC上，沿EF 折叠后点P叠在线段AD上的点记为M，并且MF⊥CF.(1)证明：CF⊥平面MDF；(2)求三棱锥M－CDE的体积．所以MD ＝＝3＝26. S △CDE ＝21DE ·DC ＝21×43×1＝83. 故V M －CDE ＝31MD ·S △CDE ＝31×26×83＝162. 【高考真题解读】1．(2017·高考全国卷Ⅰ)如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是( )∴AB∥平面MNQ.D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，∴AB∥NQ，又AB⊄平面MNQ，NQ⊂平面MNQ，∴AB∥平面MNQ.故选A.2．(2017·全国卷Ⅲ)在正方体ABCDA1B1C1D1中，E为棱CD的中点，则()A．A1E⊥DC1B．A1E⊥BDC．A1E⊥BC1 D．A1E⊥AC答案：C3．(2017·高考全国卷Ⅲ)如图，四面体ABCD中，△ABC是正三角形，AD＝CD.(1)证明：AC⊥BD；(2)已知△ACD是直角三角形，AB＝BD.若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．解：(1)证明：如图，取AC中点O，连OD，OB∵AD＝CD，O为AC中点，∴AC⊥OD，又∵△ABC是等边三角形，∴AC⊥OB，又∵OB∩OD＝O，∴AC⊥平面OBD，BD⊂平面OBD，∴AC⊥BD.(2)设AD＝CD＝2，∴AC＝2，AB＝BC＝2，又∵AB＝BD，∴BD＝2，∴△ABD≌△CBD，∴AE＝EC，又∵AE⊥EC，AC＝2，∴AE＝EC＝2，在△ABD 中，设DE ＝x ，根据余弦定理cos ∠ADB ＝2AD·BD AD2＋BD2－AB2＝2AD·DE AD2＋DE2－AE2＝222＝2×2×x 22＋x2－22.解得x ＝，∴点E 是BD 的中点，则V DACE ＝V EACE ， ∴VBACE VDACE＝1∶1.4.(2017·全国卷Ⅱ)如图，四棱锥P ABCD 中，侧面P AD 为等边三角形且垂直于底面ABCD ，AB ＝BC ＝21AD ，∠BAD ＝∠ABC ＝90°.(1)证明：直线BC ∥平面P AD ；(2)若△PCD 的面积为2，求四棱锥P ABCD 的体积．设BC ＝x ，则CM ＝x ，CD ＝x ，PM ＝x ，PC ＝PD ＝2x ，取CD 的中点N ，连接PN . 则PN ⊥CD ，所以PN ＝214x . 因为△PCD 的面积为2，所以21×x ×214x ＝2，解得x ＝2或x ＝－2(舍去)．(10分)于是AB ＝BC ＝2，AD ＝4，PM ＝2.所以四棱锥P ABCD 的体积V ＝31×22（2＋4）×2＝4.(12分)1.【2016高考新课标2文数】 是两个平面，是两条直线，有下列四个命题：（1）如果，那么.（2）如果，那么. （3）如果，那么.（4）如果，那么与所成的角和与所成的角相等.其中正确的命题有 ． (填写所有正确命题的编号） 【答案】②③④2.【2016高考浙江文数】如图，在△ABC 中，AB =BC =2，∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ，满足PD =DA ，PB =BA ，则四面体PBCD 的体积的最大值是 .【答案】【解析】中，因为，所以.由此可得，将ABD沿BD翻折后可与PBD重合，无论点D在任何位置，只要点D的位置确定，当平面PBD⊥平面BDC时，四面体PBCD的体积最大（欲求最大值可不考虑不垂直的情况）.过作直线的垂线，垂足为.设，则，即，解得.而的面积.当平面PBD⊥平面BDC时：四面体的体积.观察上式，易得，当且仅当，即时取等号，同时我们可以发现当时，取得最小值，故当时，四面体的体积最大，为3.【2016高考新课标1卷】平面过正方体ABCD-A1B1C1D1的顶点A,//平面CB1D1,平面ABCD=m,平面AB B1A1=n,则m、n所成角的正弦值为(A)(B)(C)(D)【答案】A4.【2016高考新课标3文数】在封闭的直三棱柱内有一个体积为的球，若，，，，则的最大值是（）（A）4π（B）（C）6π（D）【答案】B【解析】要使球的体积最大，必须球的半径最大．由题意知球的与直三棱柱的上下底面都相切时，球的半径取得最大值，此时球的体积为，故选B．1．(2015·安徽，5)已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是( )A．若α，β垂直于同一平面，则α与β平行B．若m，n平行于同一平面，则m与n平行C．若α，β不平行，则在α内不存在与β平行的直线D．若m，n不平行，则m与n不可能垂直于同一平面答案 D2．(2015·浙江，8)如图，已知△ABC，D是AB的中点，沿直线CD将△ACD翻折成△A′CD，所成二面角A′－CD－B的平面角为α，则( )A ．∠A ′DB ≤α B ．∠A ′DB ≥αC ．∠A ′CB ≤αD ．∠A ′CB ≥α解析 极限思想：若α＝π，则∠A ′CB ＜π，排除D ；若α＝0，如图，则∠A ′DB ，∠A ′CB 都可以大于0，排除A ，C.故选B.答案 B3．(2015·浙江，13)如图，三棱锥A －BCD 中，AB ＝AC ＝BD ＝CD ＝3，AD ＝BC ＝2，点M ，N 分别是AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是________．解析 连接DN ，作DN 的中点O ，连接MO ，OC .在△AND 中．M 为AD 的中点，则OM 綉21AN .所以异面直线AN ，CM 所成角为∠CMO ，在△ABC 中，AB ＝AC ＝3，BC ＝2，则AN ＝2，∴OM ＝.在△ACD 中，同理可知CM ＝2，在△BCD 中，DN ＝2，在Rt △ONC 中，ON ＝，CN ＝1∴OC ＝.在△CMO 中，由余弦定理cos ∠CMO ＝2|MC|·|MO||MC|2＋|MO|2－|OC|2＝28＋2－3＝87.答案 874．(2015·江苏，16)如图，在直三棱柱ABC －A 1B 1C 1中，已知AC ⊥BC ，BC ＝CC 1.设AB 1的中点为D ，B 1C ∩BC 1＝E .求证：(1)DE∥平面AA1C1C；(2)BC1⊥AB1.所以矩形BCC1B1是正方形，因此BC1⊥B1C.因为AC，B1C⊂平面B1AC，AC∩B1C＝C，所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC，所以BC1⊥AB1.5．(2015·新课标全国Ⅱ，19)如图，长方体ABCD －A 1B 1C 1D 1中，AB ＝16，BC ＝10，AA 1＝8，点E ，F 分别在A 1B 1，D 1C 1上，A 1E ＝D 1F ＝4.过点E ，F 的平面α与此长方体的面相交，交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)；(2)求直线AF 与平面α所成角的正弦值．所以AF 与平面EHGF 所成角的正弦值为155.6．(2015·新课标全国Ⅰ，18)如图，四边形ABCD 为菱形，∠ABC ＝120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE ＝2DF ，AE ⊥EC .(1)证明：平面AEC ⊥平面AFC ， (2)求直线AE 与直线CF 所成角的余弦值．(2)解 如图，以G 为坐标原点，分别以，的方向为x 轴，y 轴正方向，||为单位长，建立空间直角坐标系G －xyz ，由(1)可得A (0，－，0)，E (1，0，)，F 22，C (0，，0)，所以＝(1，，)，＝22.故cos 〈，〉＝＝－33.所以直线AE 与直线CF 所成角的余弦值为33.7．(2014·江苏，16)如图，在三棱锥P －ABC 中，D ，E ，F 分别为棱PC ，AC ，AB 的中点．已知PA ⊥AC ，PA ＝6，BC ＝8，DF ＝5.求证：(1)直线PA∥平面DEF；(2)平面BDE⊥平面ABC.8．(2014·新课标全国Ⅱ，18)如图，四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．(1)证明：PB ∥平面AEC ；(2)设二面角D －AE －C 为60°，AP ＝1，AD ＝，求三棱锥E －ACD 的体积．如图，以A 为坐标原点，的方向为x 轴的正方向，||为单位长，建立空间直角坐标系A －xyz ，则D (0，，0)，E 21，＝21.设B (m ，0，0)(m >0)，则C (m ，，0)，＝(m ，，0)． 设n 1＝(x ，y ，z )为平面ACE 的法向量， 则即z ＝0，1可取n 1＝33.又n 2＝(1，0，0)为平面DAE 的法向量，由题设知|cos 〈n 1，n 2〉|＝21，即3＋4m23＝21，解得m ＝23.因为E 为PD 的中点，所以三棱锥E －ACD 的高为21，三棱锥E －ACD 的体积V ＝31×21××23×21＝83.。

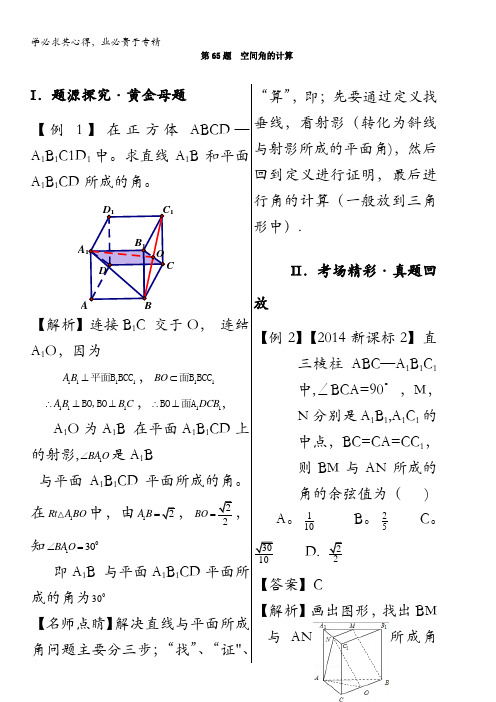
OCC 1D 1D B 1ABA 1第65题 空间角的计算I ．题源探究·黄金母题【例1】在正方体ABCD —A 1B 1C1D 1中。

求直线A 1B 和平面A 1B 1CD 所成的角。

【解析】连接B 1C 交于O ， 连结A 1O ，因为1111A B ⊥平面B BCC ，11BO ⊂面B BCC 111A B B C ∴⊥⊥BO,BO ，11DCB ∴⊥BO 面A ,A 1O 为A 1B 在平面A 1B 1CD 上的射影,1BAO ∠是A 1B与平面A 1B 1CD 平面所成的角。

在1RtA BO 中，由12AB =，22BO =，知0130BAO ∠=即A 1B 与平面A 1B 1CD 平面所成的角为030【名师点睛】解决直线与平面所成角问题主要分三步；“找”、“证"、“算”，即；先要通过定义找垂线，看射影（转化为斜线与射影所成的平面角)，然后回到定义进行证明，最后进行角的计算（一般放到三角形中）.II ．考场精彩·真题回放【例2】【2014新课标2】直三棱柱ABC —A 1B 1C 1中,∠BCA=90°，M ，N 分别是A 1B 1,A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为（ )A 。

110B 。

25C 。

30D.22【答案】C【解析】画出图形，找出BM 与AN所成角的平面角，利用解三角形求出BM 与 AN 所成角的余弦值．解：直三棱柱ABC ﹣A 1B 1C 1中,∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1 的中点，如图：BC 的中点为O,连结ON,1112MN B C OB ==且11MN B C ,则MN0B 是平行四边形,BM 与AN 所成角就是∠ANO ，∵BC=CA=CC 1，设BC=CA=CC 1=2，∴CO=1,AO=，AN=，MB=22211226B M BB +=+=在△ANO 中，由余弦定理可得：cos∠ANO=222630210256AN ON AO AN NO +-==⨯⨯故选:C ．【例3】【2016高考新课标1文数】平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ，11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ，n 所成角的正弦值为( ） （A ）32（B ）22（C ）33（D ）13【答案】A【解析】分析：如图，设平面11CB D 平面ABCD ='m ，平面11CB D 平面11ABB A ='n ，因为//α平面11CB D ,所以//',//'m m n n ，则,m n 所成的角等于','m n 所成的角。

专题限时集训(九) 空间中的平行与垂直关系(对应学生用书第133页)[建议A、B组各用时：45分钟][A组高考达标]一、选择题1．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是( ) A．若l⊥m，m⊂α，则l⊥αB．若l⊥α，l∥m，则m⊥αC．若l∥α，m⊂α，则l∥mD．若l∥α，m∥α，则l∥mB[A中，根据线面垂直的判定定理，只有垂直平面内两条相交直线才行，故A不正确；B中，由线面垂直的性质可知，平行线中的一条垂直于这个平面，则另一条也垂直这个平面，故B正确；C中，l，m可能平行也可能异面，故C不正确；D中，平行于同一平面的两直线可能平行，异面，相交，故D不正确，故选B.]2．设m，n是两条不同的直线，α，β是两个不同的平面，给出下列四个命题：①若m∥n，m⊥β，则n⊥β；②若m∥α，m∥β，则α∥β；③若m∥n，m∥β，则n∥β；④若m⊥α，m⊥β，则α⊥β.其中真命题的个数为( ) 【导学号：68334110】A．1 B．2C．3 D．4A[对于①，由直线与平面垂直的判定定理易知其正确；对于②，平面α与β可能平行或相交，故②错误；对于③，直线n可能平行于平面β，也可能在平面β内，故③错误；对于④，由两平面平行的判定定理易得平面α与β平行，故④错误．综上所述，正确命题的个数为1，故选A.]3．如图9­12所示，直线PA垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长．其中正确的是( )图9­12A．①②B．①②③C．①D．②③B[对于①，∵PA⊥平面ABC，∴PA⊥BC.∵AB为⊙O的直径，∴BC⊥AC.又∵PA∩AC＝A，∴BC⊥平面PAC，又PC⊂平面PAC，∴BC⊥PC.对于②，∵点M为线段PB的中点，∴OM∥PA.∵PA⊂平面PAC，OM⊄平面PAC，∴OM∥平面PAC.对于③，由①知BC⊥平面PAC，∴线段BC的长即是点B到平面PAC的距离，故①②③都正确．]4．已知α，β是两个不同的平面，有下列三个条件：①存在一个平面γ，γ⊥α，γ∥β；②存在一条直线a，a⊂α，a⊥β；③存在两条垂直的直线a，b，a⊥β，b⊥α.其中，所有能成为“α⊥β”的充要条件的序号是( )A．①B．②C．③D．①③D[对于①，存在一个平面γ，γ⊥α，γ∥β，则α⊥β，反之也成立，即“存在一个平面γ，γ⊥α，γ∥β”是“α⊥β”的充要条件，所以①对，可排除B，C.对于③，存在两条垂直的直线a，b，则直线a，b所成的角为90°，因为a⊥β，b⊥α，所以α，β所成的角为90°，即α⊥β，反之也成立，即“存在两条垂直的直线a，b，a⊥β，b⊥α”是“α⊥β”的充要条件，所以③对，可排除A，选D.]5．在三棱锥P­ABC中，已知PA⊥底面ABC，AB⊥BC，E，F分别是线段PB，PC上的动点，则下列说法错误的是( )图9­13A．当AE⊥PB时，△AEF一定为直角三角形B．当AF⊥PC时，△AEF一定为直角三角形C．当EF∥平面ABC时，△AEF一定为直角三角形D．当PC⊥平面AEF时，△AEF一定为直角三角形B[因为AP⊥平面ABC，所以AP⊥BC，又AB⊥BC，且PA和AB是平面PAB上两条相交直线，则BC⊥平面PAB，BC⊥AE.当AE⊥PB时，AE⊥平面PBC，则AE⊥EF，△AEF一定是直角三角形，A正确；当EF∥平面ABC时，EF在平面PBC上，平面PBC与平面ABC相交于BC，则EF∥BC，则EF⊥AE，△AEF一定是直角三角形，C正确；当PC⊥平面AEF时，AE ⊥PC，又AE⊥BC，则AE⊥平面PBC，AE⊥EF，△AEF一定是直角三角形，D正确；B中结论无法证明，故选B.]二、填空题6．已知P为△ABC所在平面外一点，且PA，PB，PC两两垂直，则下列命题：①PA⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.其中正确命题的个数是________. 【导学号：68334111】3[如图所示，∵PA⊥PC，PA⊥PB，PC∩PB＝P，∴PA⊥平面PBC.又∵BC⊂平面PBC，∴PA⊥BC.同理PB⊥AC，PC⊥AB，但AB不一定垂直于BC.]7．在三棱锥C­ABD中(如图9­14)，△ABD与△CBD是全等的等腰直角三角形，O是斜边BD 的中点，AB＝4，二面角A­BD­C的大小为60°，并给出下面结论：①AC⊥BD；②AD⊥CO；③△AOC为正三角形；④cos ∠ADC＝32；⑤四面体ABCD的外接球表面积为32π.其中真命题是________(填序号)．图9­14①③⑤[由题意知BD⊥CO，BD⊥AO，则BD⊥平面AOC，从而BD⊥AC，故①正确；根据二面角A­BD­C的大小为60°，可得∠AOC＝60°，又直线AD在平面AOC的射影为AO，从而AD与CO不垂直，故②错误；根据∠AOC＝60°，AO＝CO可得△AOC为正三角形，故③正确；在△ADC中，AD＝CD＝4，AC＝CO＝22，由余弦定理得cos ∠ADC＝42＋42－222×4×4＝34，故④错误；由题意知，四面体ABCD的外接球的球心为O，半径为22，则外接球的表面积为S＝4π×(22)2＝32π，故⑤正确．]8．正方体ABCD ­A 1B 1C 1D 1中，E 为线段B 1D 1上的一个动点，则下列结论中正确的是________．(填序号) ①AC ⊥BE ； ②B 1E ∥平面ABCD ；③三棱锥E ­ABC 的体积为定值； ④直线B 1E ⊥直线BC 1.①②③ [因为AC ⊥平面BDD 1B 1，故①，②正确；记正方体的体积为V ，则V E ­ABC ＝16V 为定值，故③正确；B 1E 与BC 1不垂直，故④错误．] 三、解答题9．如图9­15，在四棱锥P ­ABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC .图9­15(1)求证：DC ⊥平面PAC . (2)求证：平面PAB ⊥平面PAC .(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得PA ∥平面CEF ？说明理由． [解] (1)证明：因为PC ⊥平面ABCD ，所以PC ⊥DC .2分又因为DC ⊥AC ，且PC ∩AC ＝C ， 所以DC ⊥平面PAC .4分 (2)证明：因为AB ∥DC ，DC ⊥AC ， 所以AB ⊥AC .因为PC ⊥平面ABCD ，所以PC ⊥AB .又因为PC ∩AC ＝C ，所以AB ⊥平面PAC . 8分 又AB ⊂平面PAB ，所以平面PAB ⊥平面PAC . 9分 (3)棱PB 上存在点F ，使得PA ∥平面CEF . 12分理由如下：取PB 的中点F ，连接EF ，CE ，CF . 又因为E 为AB 的中点，所以EF ∥PA . 又因为PA ⊄平面CEF ，且EF ⊂平面CEF ， 所以PA ∥平面CEF .15分 10．(2017·绍兴稽阳联谊学校高三4月联考)如图9­16，四边形ABCD 为梯形，AB ∥CD ，∠C＝60°，点E 在CD 上，AB ＝CE ，BF ＝13BD ＝3，BD ⊥BC .现将△ADE 沿AE 折成如图2△APE位置，使得二面角P ­AE ­C 的大小为π3.图9­16(1)求PB 的长度； (2)求证：PB ⊥平面ABCE ；(3)求直线CE 与平面APE 所成角的正弦值．【导学号：68334112】[解] (1)因为AB 平行且等于EC ，所以四边形ABCE 是平行四边形，所以BC ∥AE ，又因为BD ⊥BC ，所以BD ⊥AE ， 所以AE ⊥FB ，AE ⊥FP ，即∠PFB 为二面角P ­AE ­C 的平面角. 3分又BF ＝3，PF ＝23，由余弦定理得BP 2＝BF 2＋PF 2－2BF ·PF cos ∠BFP ＝9， 所以BP ＝3.5分(2)证明：BF ＝3，PF ＝23，BP ＝3，满足勾股定理， 所以BF ⊥PB .又因为BF ⊥AE ，PF ⊥AE ，BF ∩PF ＝F ， 所以AE ⊥平面PFB ，所以AE ⊥PB . 7分又BF ∩AE ＝F ，则PB ⊥平面ABCE . 9分(3)法一：作BN ⊥PF 于点N ，连接AN ，由(2)可知，AE ⊥平面BFP ，所以平面BFP ⊥平面APE ， 又平面BFP ∩平面APE ＝PF ， 所以BN ⊥平面APE ，12分所以∠BAN 是直线AB 与平面APE 所成的角． 在Rt △FBP 中，BN ＝BF sin π3＝32，sin ∠NAB ＝BN AB ＝322＝34.13分所以直线AB 与平面APE 所成角的正弦值为34，即直线CE 与平面APE 所成角的正弦值为34.15分法二：由于BF ，BP ，BC 两两互相垂直，如图，建立空间直角坐标系，则B (0,0,0)，C (3,0,0)，A (－1，3，0)，E (2，3，0)，P (0,0,3)，则AE →＝(3,0,0)，AP →＝(1，－3，3)，12分设平面APE 的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧n ·AE →＝0，n ·AP →＝0，即⎩⎨⎧3x ＝0，x －3y ＋3z ＝0，取z ＝1，则n ＝(0，3，1)， 13分设直线CE 与平面APE 所成的角为θ，EC →＝(1，－3，0)，则sin θ＝|cos 〈n ，EC →〉|＝|n ·EC →||n ||EC →|＝34，即直线EC 与平面APE 所成角的正弦值为34.15分[B 组 名校冲刺]一、选择题1．已知三棱柱ABC ­A 1B 1C 1的所有棱长相等，若∠AA 1B 1＝∠AA 1C 1＝60°，则异面直线A 1C 与AB 1所成角的余弦值是( ) 【导学号：68334113】图9­17A.36 B.23C.158D.56A [将三棱柱补上一个相同的三棱柱构成一个四棱柱，如图所示，易知图中∠A 1CD 1为所求角．因为三棱柱的所有棱长均相等，不妨设为1，则根据此三棱柱的性质有A 1D 1＝A 1C ＝3，CD 1＝1，则由余弦定理得cos ∠A 1CD 1＝3＋1－323＝36，故选A.]2．如图9­18，四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，将△ADB 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A ­BCD .则在三棱锥A ­BCD 中，下列命题正确的是( )图9­18A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABCD [∵在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，∴BD ⊥CD .又平面ABD ⊥平面BCD ，且平面ABD ∩平面BCD ＝BD ，∴CD ⊥平面ABD ，则CD ⊥AB .又AD ⊥AB ，AD ∩CD ＝D ，∴AB ⊥平面ADC ，又AB ⊂平面ABC ，∴平面ABC ⊥平面ADC ，故选D.]3．如图9­19，在正方形ABCD 中，E ，F 分别是BC ，CD 的中点，沿AE ，AF ，EF 把正方形折成一个四面体，使B ，C ，D 三点重合，重合后的点记为P ，P 点在△AEF 内的射影为O ，则下列说法正确的是( )图9­19A ．O 是△AEF 的垂心B ．O 是△AEF 的内心C ．O 是△AEF 的外心D ．O 是△AEF 的重心A [由题意可知PA ，PE ，PF 两两垂直，∴PA ⊥平面PEF ，从而PA ⊥EF ，而PO ⊥平面AEF ，则PO ⊥EF .∵PO ∩PA ＝P ，∴EF ⊥平面PAO ，∴EF ⊥AO ，同理可知AE ⊥FO ，AF ⊥EO ，∴O 为△AEF 的垂心．故选A.]4．如图9­20，小于90°的二面角α­l ­β中，O ∈l ，A ，B ∈α，且∠AOB 为钝角，∠A ′OB ′是∠AOB 在β内的射影，则下列结论错误的是( )图9­20A ．∠A ′OB ′为钝角 B ．∠A ′OB ′>∠AOBC ．∠AOB ＋∠AOA ′<πD ．∠B ′OB ＋∠AOB ＋∠AOA ′>πD [考虑将图形特殊化，即可将此图形置于正方体中，正方体的一个对角面与底面分别为条件中的平面α，β，如图所示，O 为所在棱的中点，A ，B为所在面对角线上的一个三等分点，A ′，B ′分别为A ，B 在平面β上的射影．设正方体棱长为3，则OA ＝OB ＝172，OA ′＝OB ′＝132，AA ′＝BB ′＝1，则由余弦定理得cos ∠AOB ＝－117，cos ∠A ′OB ′＝－513<－117，所以∠A ′OB ′>∠AOB >π2，所以A ，B 正确；又cos ∠AOA ′＝cos ∠BOB ′＝1317>32，所以∠AOA ′＝∠BOB ′<π6，且由cos ∠AOB ＝－117>－12知∠AOB <2π3，所以∠AOB ＋∠AOA ′<π，∠B ′OB ＋∠AOB ＋∠AOA ′<π，所以C 正确，D 错误，故选D.]二、填空题5．如图9­21，正方形BCDE 的边长为a ，已知AB ＝3BC ，将△ABE 沿边BE 折起，折起后A 点在平面BCDE 上的射影为D 点，关于翻折后的几何体有如下描述：图9­21①AB 与DE 所成角的正切值是2；②AB ∥CE ；③V B ­ACE ＝16a 3；④平面ABC ⊥平面ACD .其中正确的有________．(填序号)①③④ [作出折叠后的几何体直观图如图所示：∵AB ＝3BC ＝3a ，BE ＝a ，∴AE ＝2a .∴AD ＝AE 2－DE 2＝a ，∴AC ＝CD 2＋AD 2＝2a .在△ABC 中，cos ∠ABC ＝AB 2＋BC 2－AC 22AB ×BC＝3a 2＋a 2－2a 223a2＝33. ∴sin ∠ABC ＝1－cos 2∠ABC ＝63. ∴tan ∠ABC ＝sin ∠ABCcos ∠ABC＝ 2.∵BC ∥DE ，∴∠ABC 是异面直线AB ，DE 所成的角，故①正确．连接BD ，CE ，则CE ⊥BD ，又AD ⊥平面BCDE ，CE ⊂平面BCDE ，∴CE ⊥AD .又BD ∩AD ＝D ，BD ⊂平面ABD ，AD ⊂平面ABD ，∴CE ⊥平面ABD .又AB ⊂平面ABD ，∴CE ⊥AB ，故②错误．V B ­ACE ＝V A ­BCE ＝13S △BCE ·AD ＝13×12×a 2×a ＝a 36，故③正确．∵AD ⊥平面BCDE ，BC ⊂平面BCDE ，∴BC ⊥AD .又BC ⊥CD ，CD ∩AD＝D ，CD ，AD ⊂平面ACD ，∴BC ⊥平面ACD .∵BC ⊂平面ABC ，∴平面ABC ⊥平面ACD ，故④正确．故答案为①③④.]6．(2017·金丽衢十二校高三第二次联考)已知△ABC 中，∠C ＝90°，tan A ＝2，M 为AB 的中点．现将△ACM 沿CM 折成三棱锥P ­CBM .当二面角P ­CM ­B 大小为60°时，AB PB＝________.图9­223 [作PE ⊥CM 于点E ，BF ⊥CM 交CM 的延长线于点F ，连接AE ，则AE ⊥CF ，且PE 与BF 所成锐角等于二面角P ­CM ­B 的大小，即为60°.不妨设AC ＝1，则由tan ∠BAC ＝2，∠ACB ＝90°，得BC ＝2，AB ＝3，则由M 是AB 的中点，知MB ＝MC ，则sin ∠BCF ＝sin∠ABC ＝13，∴|PE →|＝|AE →|＝|BF →|＝|BC →|sin ∠BCF ＝23，∴|EF →|＝2|MF →|＝2|BM →|2－|BF →|2＝2⎝ ⎛⎭⎪⎫12|AB →|2－|BF →|2＝13，则由PB →＝PE →＋EF →＋FB →，得|PB →|2＝(PE →＋EF →＋FB →)2＝|PE →|2＋|EF →2|＋|FB →|2－2|PE →||FB →|cos 60°＝23＋13＋23－2×23×23×cos 60°＝1，∴PB ＝1，故AB PB ＝3.]三、解答题7．端午节即将到来，为了做好端午节商场促销活动，某商场打算将进行促销活动的礼品盒重新设计．方案如下：将一块边长为10的正方形纸片ABCD 剪去四个全等的等腰三角形：△SEE ′，△SFF ′，△SGG ′，△SHH ′，再将剩下的阴影部分折成一个四棱锥形状的包装盒S ­EFGH ，其中A ，B ，C ，D 重合于点O ，E 与E ′重合，F 与F ′重合，G 与G ′重合，H 与H ′重合(如图9­23所示)．图9­23(1)求证：平面SEG ⊥平面SFH ；(2)当AE ＝52时，求二面角E ­SH ­F 的余弦值．[解] (1)证明：∵折后A ，B ，C ，D 重合于一点O ，∴拼接成底面EFGH 的四个直角三角形必为全等的等腰直角三角形， ∴底面DFGH 是正方形，EG ⊥FH ，EO ＝OG .2分 连接SO ，由题意知SE ＝SG ，∴EG ⊥SO . 4分 又∵SO ，FH ⊂平面SFH ，SO ∩FH ＝O ， ∴EG ⊥平面SFH .又∵EG ⊂平面SEG ，∴平面SEG ⊥平面SFH .6分(2)过O 作OM ⊥SH 交SH 于M 点，连接EM ，∵EO ⊥平面SFH ，SH ⊂平面SFH ，∴EO ⊥SH ，∴SH ⊥平面EMO ， ∴∠EMO 为二面角E ­SH ­F 的平面角.8分当AE ＝52时，在原平面图形中，可求得SE ＝552.在Rt △SOE 中，可求得SO ＝SE 2－OE 2＝5. 10分Rt △SHO 中，OH ＝52，SO ＝5，SH ＝552，∴OM ＝SO ·OHSH＝5，12分Rt △EMO 中，EM ＝EO 2＋OM 2＝352， cos ∠EMO ＝OM EM ＝5352＝23.14分∴所求二面角的余弦值为23.15分8．(2017·萧山中学高三5月仿真考试)如图9­24，已知矩形ABCD 中，AB ＝4，AD ＝3，现将△DAC 沿着对角线AC 向上翻折到△PAC 位置，此时PA ⊥PB .图9­24(1)求证：平面PAB ⊥平面ABC ；(2)求直线AB 与平面PAC 所成角的正弦值．【导学号：68334114】[解] (1)证明：因为PA ⊥PB ，PA ⊥PC ，PB ∩PC ＝P ， 所以PA ⊥平面PBC ，3分所以PA ⊥BC ，又BC ⊥AB ，AB ∩AP ＝A ， 所以BC ⊥平面PAB ，5分 又BC ⊂平面ABC ，所以平面PAB ⊥平面ABC . 7分(2)法一：如图，作BD ⊥PC 于点D ，连接AD ， 由(1)知PA ⊥平面PBC ，所以PA ⊥BD ， 而BD ⊥PC ，PA ∩PC ＝P ，所以BD ⊥平面PAC ， 所以∠BAD 为直线AB 与平面PAC 所成的角， 10分在Rt △PBC 中，BC ＝3，PC ＝4，PB ＝7，所以BD ＝37413分，又AB ＝4，在Rt △ADB 中，sin ∠BAD ＝BD AB ＝3716，所以直线AB 与平面PAC 所成角的正弦值为3716.15分法二：由(1)知平面PAB ⊥平面ABC ，所以在平面PAB 内，过点P 作PE ⊥AB 于点E ， 则PE ⊥平面ABC ，9分如图，以B 为坐标原点，建立空间直角坐标系(z 轴与直线PE 平行)，在Rt △PBC 中，BC ＝3，PC ＝4，PB ＝7， 在Rt △APB 中，AP ＝3，AB ＝4，PE ＝374，BE ＝74，可知A (0，－4,0)，B (0,0,0)，C (－3,0,0)，P ⎝⎛⎭⎪⎫0，－74，374，12分AC →＝(－3,4,0)，AP →＝⎝⎛⎭⎪⎫0，94，374，则易得平面PAC 的一个法向量为m ＝⎝⎛⎭⎪⎫4，3，－97，AB →＝(0,4,0)，所以cos 〈AB →，m 〉＝AB →·m |AB →||m |＝3716，故直线AB 与平面PAC 所成角的正弦值为3716.15分。

原点，焦点在x 轴上，若曲线C 经过点P (1,3)，则其焦点到准线的距离为________． 2．已知抛物线C ：y 2＝8x 的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点．若FP→＝4FQ →，则QF ＝____________. 3．已知抛物线C ：y 2＝4x ，顶点为O ，动直线l ：y ＝k (x ＋1)与抛物线C 交于A ，B 两点，则OA →·OB→的值为________．4．(2016·长春一模)过抛物线y 2＝2px (p ＞0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A 、B 两点，则AFBF ＝________.5．(2016·无锡模拟)如图，过抛物线y 2＝2px (p ＞0)的焦点F 的直线l 依次交抛物线及其准线于点A ，B ，C ，若BC ＝2BF ，且AF ＝3，则抛物线的方程是______________．6．(2016·黑龙江哈尔滨三中一模)直线l 与抛物线C ：y 2＝2x 交于A ，B 两点，O 为坐标原点．若直线OA ，OB 的斜率k 1，k 2满足k 1k 2＝23，则l 过定点________．7．(2016·常州模拟)如图，抛物线C ：y 2＝2px (p ＞0)的焦点为F ，A 为抛物线C 上的点，以F 为圆心，p2为半径的圆与直线AF 在第一象限的交点为B ，∠AFO ＝120°，A 在y 轴上的投影为N ，则∠ONB ＝________.8．已知抛物线x2＝4y上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为________．9．(2016·福建质检)过抛物线y2＝2px(p＞0)的焦点作倾斜角为30°的直线l与抛物线交于P，Q两点，分别过P，Q两点作PP1，QQ1垂直于抛线物的准线于P1，Q1，若PQ＝2，则四边形PP1Q1Q的面积是________．10．(2016·镇江模拟)已知过拋物线y2＝4x的焦点F的直线交该抛物线于A，B两点，O是坐标原点，AF＝2，则BF＝______，△OAB的面积是________．11．如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米．水位下降1米后，水面宽________米．12．(2016·石家庄质量检测二)设抛物线C：y2＝4x的焦点为F，过F的直线l与抛物线交于A，B两点，M为抛物线C的准线与x轴的交点．若tan∠AMB＝22，则AB＝________.13．过抛物线y2＝4x的焦点F作直线交抛物线于A，B两点，若AB＝8，AF＜BF，则BF＝________.14．(2016·扬州中学月考)已知抛物线的顶点在坐标原点，焦点在x轴上，△ABC的三个顶点都在抛物线上，并且△ABC的重心是抛物线的焦点，BC边所在的直线方程为4x＋y－20＝0，则抛物线的方程为__________．答案精析1.92 2.3 3.5 4.13解析 设抛物线的准线为l ：x ＝－p2，设FB ＝m ，F A ＝n ，过A ，B 两点向准线l 作垂线AC ，BD ，由抛物线定义知AC ＝F A ＝n ，BD ＝FB ＝m ， 过B 作BE ⊥AC ，E 为垂足， AE ＝CE －AC ＝BD －AC ＝m －n ， AB ＝F A ＋FB ＝n ＋m .在Rt △ABE 中，∠BAE ＝60°， cos60°＝AE AB ＝m －n m ＋n ＝12，即m ＝3n . 故AF BF ＝n m ＝m3m ＝13. 5．y 2＝3x解析 分别过点A ，B 作准线的垂线AE ，BD ，分别交准线于点E ，D ，则BF ＝BD ， ∵BC ＝2BF ，∴BC ＝2BD ， ∴∠BCD ＝30°，又AE ＝AF ＝3，∴AC ＝6， 即点F 是AC 的中点， 根据题意得p ＝32， ∴抛物线的方程是y 2＝3x . 6．(－3,0)解析 设直线l 的方程为y ＝kx ＋b ，由⎩⎨⎧y 2＝2x ，y ＝kx ＋b ，得k 2x 2＋(2kb －2)x ＋b 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－2kb －2k 2，x 1x 2＝b 2k 2.由k 1k 2＝y 1y 2x 1x 2＝23，得2x 1x 2－3y 1y 2＝2x 1x 2－3(kx 1＋b )·(kx 2＋b )＝(2－3k 2)x 1x 2－3kb (x 1＋x 2)－3b 2＝0，代入可得b ＝3k ，所以y ＝kx ＋3k ＝k (x ＋3)，所以直线l 一定过点(－3,0)． 7．30°解析 因为点A 到抛物线C 的准线的距离为AN ＋p2，点A 到焦点F 的距离为AB ＋p2，所以AN ＝AB ，因为∠AFO ＝120°，所以∠BAN ＝60°，所以在△ABN 中，∠ANB＝∠ABN ＝60°，则∠ONB ＝30°. 8．2解析 由题意知，抛物线的准线l ：y ＝－1，过点A 作AA 1⊥l 于点A 1，过点B 作BB 1⊥l 于点B 1，设弦AB 的中点为M ，过点M 作MM 1⊥l 于点M 1，则MM 1＝AA 1＋BB 12.因为AB ≤AF ＋BF (F 为抛物线的焦点)，即AF ＋BF ≥6，所以AA 1＋BB 1≥6,2MM 1≥6，MM 1≥3，故点M 到x 轴的距离d ≥2. 9．1解析 由题意得，四边形PP 1Q 1Q 为直角梯形，PP 1＋QQ 1＝PQ ＝2，P 1Q 1＝PQ ·sin30°＝1，∴S ＝PP 1＋QQ 12·P 1Q 1＝1. 10．2 2解析 设A (x 0，y 0)，由抛物线定义知x 0＋1＝2， ∴x 0＝1，则直线AB ⊥x 轴， ∴BF ＝AF ＝2，AB ＝4.故△OAB 的面积S ＝12AB ·OF ＝12×4×1＝2. 11．2 6解析 如图所示，建立平面直角坐标系，设抛物线方程为x 2＝－2py (p ＞0)．由题意将点A (2，－2)代入x 2＝－2py ， 得p ＝1，故x 2＝－2y .设B (x ，－3)，代入x 2＝－2y 中，得x ＝6， 故水面宽为26米．12．8解析 根据对称性，如图所示，不妨设l ：x ＝my ＋1(m ＞0)，A (x 1，y 1)，B (x 2，y 2)．由⎩⎨⎧y 2＝4x ，x ＝my ＋1，得y 2－4my －4＝0，∴y 1＋y 2＝4m ，y 1y 2＝－4，x 1x 2＝y 214·y 224＝1，x 1＋x 2＝m (y 1＋y 2)＋2＝4m 2＋2. ∵tan ∠AMB ＝tan(∠AMF ＋∠BMF )， ∴y 1x 1＋1＋－y 2x 2＋11－y 1x 1＋1·－y 2x 2＋1＝22，即y 1(my 2＋2)－y 2(my 1＋2)(my 1＋2)(my 2＋2)＋y 1y 2＝22，解得y 1－y 2＝42m 2， ∴4m 2＋1＝42m 2， 解得m 2＝1(负值舍去)，∴AB ＝AF ＋BF ＝x 1＋1＋x 2＋1＝4m 2＋4＝8.13．4＋2 2解析 由y 2＝4x ，得焦点F (1,0)．又AB ＝8，故AB 的斜率存在(否则AB ＝4)．设直线AB 的方程为y ＝k (x －1)(k ≠0)，A (x 1，y 1)，B (x 2，y 2)，将y ＝k (x －1)代入y 2＝4x ，得k 2x 2－(2k 2＋4)x ＋k 2＝0，故x 1＋x 2＝2＋4k2，由AB ＝AF ＋BF ＝x 1＋x 2＋2＝8，得x 1＋x 2＝2＋4k 2＝6，即k 2＝1，则x 2－6x ＋1＝0，又AF ＜BF ，所以x 1＝3－22，x 2＝3＋22，故BF ＝x 2＋1＝3＋22＋1＝4＋2 2. 14．y 2＝16x解析 设抛物线的方程为y 2＝2px ， 由⎩⎨⎧4x ＋y －20＝0，y 2＝2px ，可得2y 2＋py －20p ＝0， 由Δ＞0，得p ＞0或p ＜－160， 设B (x 1，y 1)，C (x 2，y 2)， 则y 1＋y 2＝－p2，所以x 1＋x 2＝5－y 14＋5－y 24 ＝10－14(y 1＋y 2)＝10＋p 8，设A (x 3，y 3)，由三角形重心为F (p2，0)，可得x 1＋x 2＋x 33＝p 2，y 1＋y 2＋y 33＝0，所以x 3＝11p 8－10，y 3＝p2， 因为A 在抛物线上， 所以(p 2)2＝2p (118p －10)，从而p ＝8，所以所求抛物线的方程为 y 2＝16x .。

第65题空间角的计算I．题源探究·黄金母题【例1】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.图3.2-7(1)求证:PA//平面EDB;(2)求证:PB⊥平面EFD;(3)求二面角C-PB-D的大小.【答案】（1）见解析（2）见解析（3）600.【解析】如图所示建立空间直角坐标系,点D为坐标原点,设DC=1.（3）解:已知PB⊥EF,由(2)可知PB⊥DF,故∠EFD是二面角C-PB-D的平面角.设点F的坐标为(x,y,z),则)1,,(-=zyx. 因为k=,所以0=⋅,所以(1,1,-1)·(k,k,1-k)=k+k-1+k=3k-1=0,所以31=k，点F的坐标为)32,31,31(。

又点E的坐标为)21,21,0(，所以)61,61,31(--=，因为cosFE FDEFDFEFD⋅∠==，1111121(,,)(,,)16123--⋅---==即∠EFD=600，即二面角C-PB-D的大小为600. 【点睛】直线与平面平行与垂直的证明,二面角大小的求解是高热点中的热点,几乎每年必考,而此例题很好的展现了,用向量方法证明直线与平面平行与垂直,还给出了用向量方法求二面角的大小.II．考场精彩·真题回放【例2】【2017课标II理10】已知直三棱柱111C C AB -A B 中，C 120∠A B=，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为（ ）A．B． C．5D．3【答案】C【解析】分析：如图所示，补成四棱柱1111ABCD A B C D -, 11,BC D BC ∠=则所求角为11BD C D AB ====因此1cos 5BC D ∠== ，故选C 。

【名师点睛】平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面问题化归为共面问题来解决，具体步骤如下：①平移：平移异面直线中的一条或两条，作出异面直线所成的角；②认定：证明作出的角就是所求异面直线所成的角；③计算：求该角的值，常利用解三角形；④取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角。

原点，焦点在x 轴上，若曲线C 经过点P (1,3)，则其焦点到准线的距离为________． 2．已知抛物线C ：y 2＝8x 的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点．若FP→＝4FQ →，则QF ＝____________. 3．已知抛物线C ：y 2＝4x ，顶点为O ，动直线l ：y ＝k (x ＋1)与抛物线C 交于A ，B 两点，则OA →·OB→的值为________．4．(2016·长春一模)过抛物线y 2＝2px (p ＞0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A 、B 两点，则AFBF＝________. 5．(2016·无锡模拟)如图，过抛物线y 2＝2px (p ＞0)的焦点F 的直线l 依次交抛物线及其准线于点A ，B ，C ，若BC ＝2BF ，且AF ＝3，则抛物线的方程是______________．6．(2016·黑龙江哈尔滨三中一模)直线l 与抛物线C ：y 2＝2x 交于A ，B 两点，O 为坐标原点．若直线OA ，OB 的斜率k 1，k 2满足k 1k 2＝23，则l 过定点________． 7．(2016·常州模拟)如图，抛物线C ：y 2＝2px (p ＞0)的焦点为F ，A 为抛物线C 上的点，以F 为圆心，p2为半径的圆与直线AF 在第一象限的交点为B ，∠AFO ＝120°，A 在y 轴上的投影为N ，则∠ONB ＝________.8．已知抛物线x2＝4y上有一条长为6的动弦AB，则AB的中点到x轴的最短距离为________．9．(2016·福建质检)过抛物线y2＝2px(p＞0)的焦点作倾斜角为30°的直线l与抛物线交于P，Q两点，分别过P，Q两点作PP1，QQ1垂直于抛线物的准线于P1，Q1，若PQ＝2，则四边形PP1Q1Q的面积是________．10．(2016·镇江模拟)已知过拋物线y2＝4x的焦点F的直线交该抛物线于A，B两点，O是坐标原点，AF＝2，则BF＝______，△OAB的面积是________．11．如图是抛物线形拱桥，当水面在l时，拱顶离水面2米，水面宽4米．水位下降1米后，水面宽________米．12．(2016·石家庄质量检测二)设抛物线C：y2＝4x的焦点为F，过F的直线l与抛物线交于A，B两点，M为抛物线C的准线与x轴的交点．若tan∠AMB＝22，则AB＝________.13．过抛物线y2＝4x的焦点F作直线交抛物线于A，B两点，若AB＝8，AF＜BF，则BF＝________.14．(2016·扬州中学月考)已知抛物线的顶点在坐标原点，焦点在x轴上，△ABC的三个顶点都在抛物线上，并且△ABC的重心是抛物线的焦点，BC边所在的直线方程为4x＋y－20＝0，则抛物线的方程为__________．答案精析1.92 2.3 3.5 4.13解析 设抛物线的准线为l ：x ＝－p2，设FB ＝m ，F A ＝n ，过A ，B 两点向准线l 作垂线AC ，BD ，由抛物线定义知AC ＝F A ＝n ，BD ＝FB ＝m ， 过B 作BE ⊥AC ，E 为垂足， AE ＝CE －AC ＝BD －AC ＝m －n ， AB ＝F A ＋FB ＝n ＋m . 在Rt △ABE 中，∠BAE ＝60°， cos60°＝AE AB ＝m －n m ＋n ＝12，即m ＝3n . 故AF BF ＝n m ＝m3m ＝13. 5．y 2＝3x解析 分别过点A ，B 作准线的垂线AE ，BD ，分别交准线于点E ，D ，则BF ＝BD ， ∵BC ＝2BF ，∴BC ＝2BD ， ∴∠BCD ＝30°，又AE ＝AF ＝3，∴AC ＝6， 即点F 是AC 的中点， 根据题意得p ＝32， ∴抛物线的方程是y 2＝3x . 6．(－3,0)解析 设直线l 的方程为y ＝kx ＋b ，由⎩⎪⎨⎪⎧y 2＝2x ，y ＝kx ＋b ，得k 2x 2＋(2kb －2)x ＋b 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－2kb －2k 2，x 1x 2＝b 2k 2.由k 1k 2＝y 1y 2x 1x 2＝23，得2x 1x 2－3y 1y 2＝2x 1x 2－3(kx 1＋b )·(kx 2＋b )＝(2－3k 2)x 1x 2－3kb (x 1＋x 2)－3b 2＝0，代入可得b ＝3k ，所以y ＝kx ＋3k ＝k (x ＋3)，所以直线l 一定过点(－3,0)． 7．30°解析 因为点A 到抛物线C 的准线的距离为AN ＋p2，点A 到焦点F 的距离为AB ＋p2，所以AN ＝AB ，因为∠AFO ＝120°，所以∠BAN ＝60°，所以在△ABN 中，∠ANB ＝∠ABN ＝60°，则∠ONB ＝30°. 8．2解析 由题意知，抛物线的准线l ：y ＝－1，过点A 作AA 1⊥l 于点A 1，过点B 作BB 1⊥l 于点B 1，设弦AB 的中点为M ，过点M 作MM 1⊥l 于点M 1，则MM 1＝AA 1＋BB 12.因为AB ≤AF ＋BF (F 为抛物线的焦点)，即AF ＋BF ≥6，所以AA 1＋BB 1≥6,2MM 1≥6，MM 1≥3，故点M 到x 轴的距离d ≥2. 9．1解析 由题意得，四边形PP 1Q 1Q 为直角梯形，PP 1＋QQ 1＝PQ ＝2，P 1Q 1＝PQ ·sin30°＝1，∴S ＝PP 1＋QQ 12·P 1Q 1＝1.10．2 2解析 设A (x 0，y 0)，由抛物线定义知x 0＋1＝2， ∴x 0＝1，则直线AB ⊥x 轴， ∴BF ＝AF ＝2，AB ＝4.故△OAB 的面积S ＝12AB ·OF ＝12×4×1＝2.11．2 6解析 如图所示，建立平面直角坐标系，设抛物线方程为x 2＝－2py (p ＞0)．由题意将点A (2，－2)代入x 2＝－2py ， 得p ＝1，故x 2＝－2y .设B (x ，－3)，代入x 2＝－2y 中，得x ＝6， 故水面宽为26米． 12．8解析 根据对称性，如图所示，不妨设l ：x ＝my ＋1(m ＞0)，A (x 1，y 1)，B (x 2，y 2)．由⎩⎪⎨⎪⎧y 2＝4x ，x ＝my ＋1，得y 2－4my －4＝0，∴y 1＋y 2＝4m ，y 1y 2＝－4，x 1x 2＝y 214·y 224＝1，x 1＋x 2＝m (y 1＋y 2)＋2＝4m 2＋2. ∵tan ∠AMB ＝tan(∠AMF ＋∠BMF )， ∴y 1x 1＋1＋－y 2x 2＋11－y 1x 1＋1·－y 2x 2＋1＝22，即y 1(my 2＋2)－y 2(my 1＋2)(my 1＋2)(my 2＋2)＋y 1y 2＝22，解得y 1－y 2＝42m 2， ∴4m 2＋1＝42m 2，解得m 2＝1(负值舍去)，∴AB ＝AF ＋BF ＝x 1＋1＋x 2＋1＝4m 2＋4＝8.13．4＋2 2解析 由y 2＝4x ，得焦点F (1,0)．又AB ＝8，故AB 的斜率存在(否则AB ＝4)．设直线AB 的方程为y ＝k (x －1)(k ≠0)，A (x 1，y 1)，B (x 2，y 2)，将y ＝k (x －1)代入y 2＝4x ，得k 2x 2－(2k 2＋4)x ＋k 2＝0，故x 1＋x 2＝2＋4k 2，由AB ＝AF ＋BF ＝x 1＋x 2＋2＝8，得x 1＋x 2＝2＋4k 2＝6，即k 2＝1，则x 2－6x ＋1＝0，又AF ＜BF ，所以x 1＝3－22，x 2＝3＋22，故BF ＝x 2＋1＝3＋22＋1＝4＋2 2. 14．y 2＝16x解析 设抛物线的方程为y 2＝2px ， 由⎩⎪⎨⎪⎧4x ＋y －20＝0，y 2＝2px ，可得2y 2＋py －20p ＝0， 由Δ＞0，得p ＞0或p ＜－160， 设B (x 1，y 1)，C (x 2，y 2)， 则y 1＋y 2＝－p 2，所以x 1＋x 2＝5－y 14＋5－y 24 ＝10－14(y 1＋y 2)＝10＋p 8，设A (x 3，y 3)，由三角形重心为F (p2，0)， 可得x 1＋x 2＋x 33＝p 2，y 1＋y 2＋y 33＝0，所以x 3＝11p 8－10，y 3＝p2， 因为A 在抛物线上，所以(p 2)2＝2p (118p －10)，从而p ＝8，所以所求抛物线的方程为 y 2＝16x .。

2018⾼考⽂科数学空间证明专题突破训练（精编有答案）2018年⾼考⽂科数学空间证明冲刺1.如图，直三棱柱111C B A ABC -中，0120=∠ACB 且21===AA BC AC ，E 是棱1CC 中点，F 是AB 的中点.（1）求证：//CF 平⾯1AEB ；（2）求点B 到平⾯1AEB 的距离.2.在如图所⽰的⼏何体中，四边形ABCD 是正⽅形，PA ⊥平⾯ABCD ，EF 分别是线段AD ，PB 的中点，PA=AB=1.()Ⅰ求证： EF ∥平⾯DCP ； ()Ⅱ求F 到平⾯PDC 的距离.3.如图，在四棱锥P ABCD -中，底⾯ABCD 是边长为a 的正⽅形，E F 、分别为PC BD 、的中点，侧⾯PAD ⊥底⾯ABCD ，且2PA PD AD ==．（1）求证：//EF 平⾯PAD ；（2）求三棱锥C PBD -的体积．4.如图，四边形ABCD为正⽅形，PD⊥平⾯ABCD，PD=DC=2，点E，F分别为AD，PC 的中点．（Ⅰ）证明：DF∥平⾯PBE（Ⅱ）求点F到平⾯PBE的距离．5.如图，四棱锥P﹣ABCD中，底⾯ABCD为矩形，PA⊥平⾯ABCD，E为PD的中点．（Ⅰ）证明：PB∥平⾯AEC；（Ⅱ）设AP=1，AD=，三棱锥P﹣ABD的体积V=，求A到平⾯PBC的距离．6.如图，在长⽅体ABCD﹣A1B1C1D1中，AA1=AD=a，AB=2a，E、F分别为C1D1、A1D1的中点．（Ⅰ）求证：DE⊥平⾯BCE；（Ⅱ）求证：AF∥平⾯BDE．7.如图所⽰，在三棱锥P ABC -中，PC ⊥平⾯,3ABC PC =，,D E 分别为线段,AB BC 上的点，且22CD DE CE EB ====.（1）求证：DE ⊥平⾯PCD ；（2）求点B 到平⾯PDE 的距离.8.如图，已知三棱锥A ﹣BPC 中，AP ⊥PC ，AC ⊥BC ，M 为AB 的中点，D 为PB 的中点，且△PMB 为正三⾓形．（I ）求证：BC ⊥平⾯APC ；（Ⅱ）若BC=3，AB=10，求点B 到平⾯DCM 的距离．9.如图所⽰，在四棱锥P﹣ABCD中，底⾯ABCD为平⾏四边形，∠DBA=30°，AB=2BD，PD=AD，PD⊥底⾯ABCD，E为PC上⼀点，且PE=EC．（1）证明：PA⊥BD；（2）若AD=，求三棱锥E﹣CBD的体积．10.如图，在三棱锥VABC中，平⾯VAB⊥平⾯ABC，△VAB为等边三⾓形，AC⊥BC且AC=BC，O，M分别为AB，VA的中点．（1）求证：VB∥平⾯MOC；（2）求证：平⾯MOC⊥平⾯VAB．11.在三棱柱ABC﹣A1B1C1中，侧⾯AA1C1C⊥底⾯ABC，AA1=A1C=AC=AB=BC=2，且点O为AC中点．（Ⅰ）证明：A1O⊥平⾯ABC；（Ⅱ）求三棱锥C1﹣ABC的体积．试卷答案1.（1）取1AB 中点G ，连结FG EG 、，则FG ∥1BB 且121BB FG =. 因为当E 为1CC 中点时，CE ∥1BB 且121BB CE =，所以FG ∥CE 且=FG CE .所以四边形CEGF 为平⾏四边形，CF ∥EG ，⼜因为1AEB CF 平⾯?，1AEB EG 平⾯?，所以//CF 平⾯1AEB ；（2）因为ABC ?中，BC AC =，F 是AB 中点，所以AB CF ⊥. ⼜因为直三棱柱111C B A ABC -中，1BB CF ⊥，B BB AB =1，所以1ABB CF 平⾯⊥，C 到1ABB 平⾯的距离为1=CF .因为//1CC 平⾯1ABB ，所以E 到1ABB 平⾯的距离等于C 到1ABB 平⾯的距离等于1. 设点B 到平⾯1AEB 的距离为d .11ABB E AEB B V V --=，1313111??=??ABB AEB S d S ，易求321=ABB S ，21=AEB S ，解得3=d . 点B 到平⾯1AEB 的距离为3. 2.()Ⅰ⽅法⼀：取PC 中点M ，连接MF DM ,，F M , 分别是PB PC ,中点, CB MF CB MF 21,//=∴，E 为DA 中点，ABCD 为正⽅形，CB DE CB DE 21,//=∴， DE MF DE MF =∴,//,∴四边形DEFM 为平⾏四边形，∴EF DM EF ,//平⾯PDC ，?DM 平⾯PDC ，//EF ∴平⾯PDC .⽅法⼆：取PA 中点N ，连接NE ，NF .E 是AD 中点，N 是PA 中点，//NE DP ∴，⼜F 是PB 中点，N 是PA 中点，//NE AB ∴，//AB CD ，//NF CD ∴，⼜NE NF N = ，NE ?平⾯NEF ，NF ?平⾯NEF ，DP ?平⾯PCD ，CD ?平⾯PCD ，∴平⾯//NEF 平⾯PCD . ⼜EF ? 平⾯NEF ，//EF ∴平⾯PCD .⽅法三：取BC 中点G ，连接EG ，FG ，在正⽅形ABCD 中，E 是AD 中点，G 是BC 中点//GE CD ∴⼜F 是PB 中点，G 是BC 中点，//GF PC ∴，⼜PC CD C = ，,GE GEF GF GEF ??平⾯平⾯， ,PC PCD CD PCD ??平⾯平⾯，∴平⾯GEF //平⾯PCD .EF ? 平⾯GEF//EF ∴平⾯PCD .()Ⅱ⽅法⼀：//EF 平⾯PDC ，F ∴到平⾯PDC 的距离等于E 到平⾯PDC 的距离，⊥PA 平⾯ABCD ，PA DA ⊥∴，1==AD PA ，在PAD Rt ?中2=DP ，⊥PA 平⾯ABCD ，PA CB ⊥∴，⼜⊥CB AB ，A AB PA = ,AB PAB PA PAB ??平⾯，平⾯， CB ⊥∴平⾯PAB ，⼜PB ? 平⾯PAB ，CB PB ⊥∴,故PC .222PD DC PC +=∴，PDC ?∴为直⾓三⾓形， PDE C PDC E V V --=，设E 到平⾯PDC 的距离为h ，则1111111132322h ??，4h =∴F ∴到平⾯PDC 的距离42.⽅法⼆：//EF 平⾯PCD ，∴点F 到平⾯PCD 的距离等于点E 到平⾯PCD 的距离，⼜ AD 平⾯PCD D =,E 是AD 中点，∴点A 到平⾯PCD 的距离等于点E 到平⾯PCD 距离的2倍.取DP 中点H ,连接AH ,由=AD AP 得AH PD ⊥,由AB AP ⊥,AB AD ⊥,AD AP A = , AP ?平⾯PAD ，AD ?平⾯PAD ，AB ⊥∴平⾯PAD ，⼜//AB CD CD ⊥∴平⾯PAD ，∴平⾯PCD ⊥平⾯PAD . ⼜平⾯PCD 平⾯PAD PD =，AH PD ⊥，AH ?平⾯PAD ，AH ⊥∴平⾯PCD ，AH ∴长即为点A 到平⾯PCD 的距离，由1AP AD ==，AP AD ⊥，2AH ∴=.E ∴点到平⾯PCD 的距离为4，即F 点到平⾯PCD .3.（1）连结AC ，则F 是AC 的中点，E 为PC 的中点，故在CPA ?中，//EF PA ，且PA ?平⾯PAD ，EF ?平⾯PAD ，∴//EF 平⾯PAD ；（2）取AD 的中点N ，连结PN ，∵PA PD =，∴PN AD ⊥，⼜平⾯PAD ⊥平⾯ABCD ，平⾯PAD 平⾯ABCD AD =，∴PN ⊥平⾯ABCD ，∴31111332212C PBD P BCD BCD a V V S PN a a a --?==== . 4.【考点】点、线、⾯间的距离计算；直线与平⾯平⾏的判定．【分析】（Ⅰ）取PB 的中点G ，连接EG 、FG ，由已知结合三⾓形中位线定理可得DE ∥FG 且DE=FG ，得四边形DEGF 为平⾏四边形，从⽽可得DF ∥EG ，再由线⾯平⾏的判定可得DF ∥平⾯PBE ；（Ⅱ）利⽤等积法可得：V D﹣PBE=V P﹣BDE，代⼊棱锥体积公式可得点F到平⾯PBE的距离．【解答】（Ⅰ）证明：取PB的中点G，连接EG、FG，则FG∥BC，且FG=．∵DE∥BC且DE=BC，∴DE∥FG且DE=FG，∴四边形DEGF为平⾏四边形，∴DF∥EG，⼜EG?平⾯PBE，DF?平⾯PBE，∴DF∥平⾯PBE；（Ⅱ）解：由（Ⅰ）知，DF∥平⾯PBE，∴点D到平⾯PBE的距离与F到平⾯PBE的距离相等，故转化为求D到平⾯PBE的距离，设为d，利⽤等体积法：V D﹣PBE=V P﹣BDE，即．，∵，，∴．∴d=．5.【考点】点、线、⾯间的距离计算；棱柱、棱锥、棱台的体积；直线与平⾯平⾏的判定．【分析】（Ⅰ）设BD与AC 的交点为O，连结EO，通过直线与平⾯平⾏的判定定理证明PB ∥平⾯AEC；（Ⅱ）通过AP=1，AD=，三棱锥P﹣ABD的体积V=，求出AB，作AH⊥PB⾓PB于H，说明AH就是A到平⾯PBC的距离．通过解三⾓形求解即可．【解答】解：（Ⅰ）证明：设BD与AC 的交点为O，连结EO，∵ABCD是矩形，∴O为BD的中点∵E为PD的中点，∴EO∥PB．EO?平⾯AEC，PB?平⾯AEC∴PB∥平⾯AEC；（Ⅱ）∵AP=1，AD=，三棱锥P﹣ABD的体积V=，∴V==，∴AB=，PB==．作AH⊥PB交PB于H，由题意可知BC⊥平⾯PAB，∴BC⊥AH，故AH⊥平⾯PBC．⼜在三⾓形PAB中，由射影定理可得：A到平⾯PBC的距离．6.【考点】直线与平⾯垂直的判定；直线与平⾯平⾏的判定．【分析】（Ⅰ）证明直线与平⾯垂直，关键要找到两条相交直线与之都垂直：DE⊥BC，DE ⊥EC从⽽得到线⾯垂直．（Ⅱ）要证线⾯平⾏，需要构造线⾯平⾏的判定定理的条件：在平⾯BDE内找⼀条与AF平⾏的直线，通过平⾏关系的相互转化可的线线平⾏继⽽得到线⾯平⾏．【解答】解：（Ⅰ）证明：∵BC⊥侧⾯CDD1C1，DE?侧⾯CDD1C1，∴DE⊥BC，在△CDE中，CD=2a， a，则有CD2=CE2+DE2，∴∠DEC=90°，∴DE ⊥EC ，⼜BC ∩EC=C ∴DE ⊥平⾯BCE ．（Ⅱ）证明：连EF 、A 1C 1，连AC 交BD 于O ，∵EF，AO，∴四边形AOEF 是平⾏四边形，∴AF ∥OE⼜∵OE ?平⾯BDE ，AF ?平⾯BDE ，∴AF ∥平⾯BDE ．7.（1）证明：由PC ⊥平⾯ABC ，DE ?平⾯ABC ，故PC DE ⊥由2CE CD DE ==，CDE ?为等腰直⾓三⾓形，故CD DE ⊥，⼜PC CD C ?=，故DE ⊥平⾯PCD .（2）由（1）知，CDE ?为等腰直⾓三⾓形，4DCE π∠=，过D 作DF 垂直CE 于F ，易知1DF CF EF ===，⼜DE ⊥平⾯PCD ，所以DE PD ⊥，PD = 设点B 到平⾯PDE 的距离为h ，即为三棱锥B PDE -的⾼，由B PDE P BDE V V --=得1133PDE BDE S h S PC =?，113h =??，所以h =，所以B 到平⾯PDE .8.【考点】LW：直线与平⾯垂直的判定；MK：点、线、⾯间的距离计算．【分析】（I）根据正三⾓形三线合⼀，可得MD⊥PB，利⽤三⾓形中位线定理及空间直线夹⾓的定义可得AP⊥PB，由线⾯垂直的判定定理可得AP⊥平⾯PBC，即AP⊥BC，再由AC ⊥BC结合线⾯垂直的判定定理可得BC⊥平⾯APC；（Ⅱ）记点B到平⾯MDC的距离为h，则有V M﹣BCD=V B﹣MDC．分别求出MD长，及△BCD和△MDC ⾯积，利⽤等积法可得答案．【解答】证明：（Ⅰ）如图，∵△PMB为正三⾓形，且D为PB的中点，∴MD⊥PB．⼜∵M为AB的中点，D为PB的中点，∴MD∥AP，∴AP⊥PB．⼜已知AP⊥PC，PB∩PC=P，PB，PC?平⾯PBC∴AP⊥平⾯PBC，∴AP⊥BC，⼜∵AC⊥BC，AC∩AP=A，∴BC⊥平⾯APC，…解：（Ⅱ）记点B到平⾯MDC的距离为h，则有V M﹣BCD=V B﹣MDC．∵AB=10，∴MB=PB=5，⼜BC=3，BC⊥PC，∴PC=4，∴．⼜，∴．在△PBC中，，⼜∵MD⊥DC，∴，∴∴即点B到平⾯DCM的距离为．…9.【考点】棱柱、棱锥、棱台的体积；直线与平⾯垂直的性质．【分析】（1）在△ABD中，不妨设AB=2，BD=，由余弦定理可得AD，则AD2+BD2=BA2，从⽽得到BD⊥AD，结合PD⊥底⾯ABCD，得BD⊥PD，再由线⾯垂直的判定可得BD⊥平⾯PAD，则PA⊥BD；（2）过E作EF⊥CD于F，则三棱锥E﹣CBD的⾼为EF，由已知可得EF．再由（1）知BD，代⼊三棱锥E﹣CBD的体积公式求解．【解答】（1）证明：在△ABD中，由余弦定理可得：AD2=BA2+BD2﹣2BA?BD?cos∠DBA，不妨设AB=2，则由已知AB=2BD，得BD=，∴，则AD2+BD2=BA2，∴∠ADB=90°，即BD⊥AD，⼜PD⊥底⾯ABCD，∴BD⊥PD，⽽AD∩PD=D，∴BD⊥平⾯PAD，则PA⊥BD；（2）解：过E作EF⊥CD于F，则三棱锥E﹣CBD的⾼为EF，由已知可得EF=．由（1）知BD=AD，∴三棱锥E﹣CBD的体积V==．10.【考点】LY：平⾯与平⾯垂直的判定；LS：直线与平⾯平⾏的判定．【分析】（1）由O，M分别为AB，VA的中点，得OM∥VB，即可得VB∥平⾯MOC．（2）由AC=BC，O为AB的中点，得OC⊥AB．⼜平⾯VAB⊥平⾯ABC，得OC⊥平⾯VAB．平⾯MOC⊥平⾯VAB．【解答】解：（1）证明因为O，M分别为AB，VA的中点，所以OM∥VB，⼜因为VB?平⾯MOC，OM?平⾯MOC，所以VB∥平⾯MOC．（2）证明因为AC=BC，O为AB的中点，所以OC⊥AB．⼜因为平⾯VAB⊥平⾯ABC，且OC?平⾯ABC，所以OC⊥平⾯VAB．⼜OC?平⾯MOC，所以平⾯MOC⊥平⾯VAB．【点评】本题考查了空间线⾯平⾏的判定，⾯⾯垂直的判定，属于中档题．11.【考点】LF：棱柱、棱锥、棱台的体积；LW：直线与平⾯垂直的判定．【分析】（Ⅰ）推导出A1O⊥AC，由此能证明A1O⊥平⾯ABC．（Ⅱ）推导出C1到平⾯ABC的距离等于A1到平⾯ABC的距离，从⽽，由此能求出三棱锥C1﹣ABC的体积．【解答】（本⼩题满分12分）证明：（Ⅰ）∵AA1=A1C，且O为AC的中点，∴A1O⊥AC，…⼜∵平⾯AA1C1C⊥平⾯ABC，平⾯AA1C1C∩平⾯ABC=AC…且A1O?平⾯AA1C1C，∴A1O⊥平⾯ABC…解：（Ⅱ）∵A1C1∥AC，A1C1?平⾯ABC，AC?平⾯ABC，∴A1C1∥平⾯ABC，即C1到平⾯ABC的距离等于A1到平⾯ABC的距离…由（Ⅰ）知A1O⊥平⾯ABC且，…∴三棱锥C1﹣ABC的体积：…。

空间中的垂直关系1.(2016·北京)如图，在四棱锥P －ABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC . (1)求证：DC ⊥平面P AC ； (2)求证：平面P AB ⊥平面P AC ；(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得P A ∥平面CEF ？说明理由.2.(2016·江苏)如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且B 1D ⊥A 1F ，A 1C 1⊥A 1B 1. 求证：(1)直线DE ∥平面A 1C 1F ； (2)平面B 1DE ⊥平面A 1C 1F .3.(2016·四川)如图，在四棱锥P －ABCD 中，P A ⊥CD ，AD ∥BC ，∠ADC ＝∠P AB ＝90°，BC ＝CD ＝12AD .(1)在平面P AD 内找一点M ，使得直线CM ∥平面P AB ，并说明理由.(2)证明：平面P AB ⊥平面PBD .1.(2015·湖南)如图，直三棱柱ABC－A1B1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点.(1)证明：平面AEF⊥平面B1BCC1；(2)若直线A1C与平面A1ABB1所成的角为45°，求三棱锥F－AEC的体积.2.(2014·福建)如图所示，三棱锥A－BCD中，AB⊥平面BCD，CD⊥BD.(1)求证：CD⊥平面ABD；(2)若AB＝BD＝CD＝1，M为AD中点，求三棱锥A－MBC的体积.3.(2014·江西)如图所示，三棱柱ABC－A1B1C1中，AA1⊥BC，A1B⊥BB1.(1)求证：A1C⊥CC1；(2)若AB＝2，AC＝3，BC＝7，问AA1为何值时，三棱柱ABC－A1B1C1体积最大，并求此最大值.4.(2014·新课标全国Ⅰ)如图，三棱柱ABC －A 1B 1C 1中，侧面BB 1C 1C 为菱形，B 1C 的中点为O ，且AO ⊥平面BB 1C 1C . (1)证明：B 1C ⊥AB ；(2)若AC ⊥AB 1，∠CBB 1＝60°，BC ＝1，求三棱柱ABC －A 1B 1C 1的高.1.(2015·湖北七市模拟)如图，在△AOB 中，∠AOB ＝π2，∠BAO ＝π6，AB ＝4，D 为线段BA 的中点.△AOC 由△AOB 绕直线AO 旋转而成，记∠BOC ＝θ，θ∈⎝ ⎛⎦⎥⎤0，π2.(1)证明：当θ＝π2时，平面COD ⊥平面AOB ； (2)当三棱锥D －BOC 的体积为1时，求三棱锥A －BOC 的全面积.2.(2016·江西临川模拟)如图，四棱柱ABCD －A 1B 1C 1D 1的底面ABCD 是平行四边形，且AB ＝1，BC ＝2，∠ABC ＝60°，E 为BC 的中点，AA 1⊥平面ABCD . (1)证明：平面A 1AE ⊥平面A 1DE ；(2)若DE ＝A 1E ，试求二面角E －A 1C －D 的余弦值.3.(2015·江西红色六校模拟)如图，已知在四棱锥P －ABCD 中，底面ABCD 是边长为4的正方形，△P AD 是正三角形，平面P AD ⊥平面ABCD ，E ，F ，G 分别是PD ，PC ，BC 的中点.(1)求证：平面EFG ⊥平面P AD ；(2)若M 是线段CD 上一点，求三棱锥M －EFG 的体积.4.(2015·广西江门模拟)如图1，直角梯形ABCD ，∠ADC ＝90°，AB ∥CD ，AD ＝CD ＝12AB ＝2，点E 为AC 的中点，将△ACD 沿AC 折起，使折起后的平面ACD 与平面ABC 垂直(如图2).在图2所示的几何体D －ABC 中：(1)求证：BC ⊥平面ACD ；(2)点F 在棱CD 上，且满足AD ∥平面BEF ，求几何体F －BCE 的体积.空间中的垂直关系【三年高考真题演练】 [2016年高考真题]1.(1)证明 ∵PC ⊥平面ABCD ，DC ⊂平面ABCD ，∴PC ⊥DC .又AC ⊥DC ，PC ∩AC ＝C ，PC ⊂平面P AC ，AC ⊂平面P AC ，∴CD ⊥平面P AC .(2)证明 ∵AB ∥CD ，CD ⊥平面P AC ， ∴AB ⊥平面P AC ，AB ⊂平面P AB ， ∴平面P AB ⊥平面P AC .(3)解 棱PB 上存在点F ，使得P A ∥平面CEF .证明如下：取PB 的中点F ，连接EF ，CE ，CF ，又因为E 为AB 的中点，∴EF 为△P AB 的中位线，∴EF ∥P A .又P A ⊄平面CEF ，EF ⊂平面CEF ，∴P A ∥平面CEF .2.证明 (1)由已知，DE 为△ABC 的中位线， ∴DE ∥AC ，又由三棱柱的性质可得AC ∥A 1C 1， ∴DE ∥A 1C 1，且DE ⊄平面A 1C 1F ，A 1C 1⊂平面A 1C 1F ， ∴DE ∥平面A 1C 1F .(2)在直三棱柱ABC －A 1B 1C 1中，AA 1⊥平面A 1B 1C 1， ∴AA 1⊥A 1C 1，又∵A 1B 1⊥A 1C 1，且A 1B 1∩AA 1＝A ， ∴A 1C 1⊥平面ABB 1A 1，∵B 1D ⊂平面ABB 1A 1， ∴A 1C 1⊥B 1D ，又∵A 1F ⊥B 1D ，且A 1F ∩A 1C 1＝A 1， ∴B 1D ⊥平面A 1C 1F ，又∵B 1D ⊂平面B 1DE ， ∴平面B 1DE ⊥平面A 1C 1F .3.(1)解 取棱AD 的中点M (M ∈平面P AD )，点M 即为所求的一个点，理由如下：因为AD ∥BC ，BC ＝12AD .所以BC ∥AM ，且BC ＝AM . 所以四边形AMCB 是平行四边形，从而CM ∥AB . 又AB ⊂平面P AB .CM ⊄平面P AB .所以CM∥平面P AB.(说明：取棱PD的中点N，则所找的点可以是直线MN上任意一点) (2)证明由已知，P A⊥AB，P A⊥CD.因为AD∥BC，BC＝12AD，所以直线AB与CD相交，所以P A⊥平面ABCD. 从而P A⊥BD.因为AD∥BC，BC＝12AD，所以BC∥MD，且BC＝MD.所以四边形BCDM是平行四边形，所以BM＝CD＝12AD，所以BD⊥AB.又AB∩AP＝A，所以BD⊥平面P AB.又BD⊂平面PBD，所以平面P AB⊥平面PBD.[两年经典高考真题]1.(1)证明∵△ABC为正三角形，E为BC中点，∴AE⊥BC，∴又B1B⊥平面ABC，AE⊂平面ABC，∴B1B⊥AE，∴由B1B∩BC＝B知，AE⊥平面B1BCC1，又由AE⊂平面AEF，∴平面AEF⊥平面B1BCC1.(2)解设AB中点为M，连接CM，则CM⊥AB，由平面A1ABB1⊥平面ABC且平面A1ABB1∩平面ABC＝AB知，CM⊥面A1ABB1，∴∠CA1M即为直线A1C与平面A1ABB1所成的角.∴∠CA1M＝45°，易知CM＝32×2＝3，在等腰Rt△CMA中，AM＝CM＝3，在Rt△A1AM中，A1A＝A1M2－AM2＝ 2.∴FC＝12A1A＝22，又S △AEC ＝12×34×4＝32， ∴V 三棱锥F －AEC ＝13×32×22＝612.2.(1)证明 ∵AB ⊥平面BCD ，CD ⊂平面BCD ，∴AB ⊥CD .又∵CD ⊥BD ，AB ∩BD ＝B ， AB ⊂平面ABD ，BD ⊂平面ABD ， ∴CD ⊥平面ABD .(2)解 由AB ⊥平面BCD ， 得AB ⊥BD .∵AB ＝BD ＝1，∴S △ABD ＝12. ∵M 是AD 的中点， ∴S △ABM ＝12S △ABD ＝14. 由(1)知，CD ⊥平面ABD ，∴三棱锥C －ABM 的高h ＝CD ＝1， 因此三棱锥A －MBC 的体积 V A －MBC ＝V C －ABM ＝13S △ABM ·h ＝112.3.(1)证明 由AA 1⊥BC 知BB 1⊥BC .又BB 1⊥A 1B ，且BC ∩A 1B ＝B ， 故BB 1⊥平面BCA 1， 所以BB 1⊥A 1C .又BB 1∥CC 1，所以A 1C ⊥CC 1. (2)解 设AA 1＝x .在Rt △A 1BB 1中，A 1B ＝A 1B 21－BB 21＝4－x 2. 同理，A 1C ＝A 1C 21－CC 21＝3－x 2.在△A 1BC 中，cos ∠BA 1C ＝A 1B 2＋A 1C 2－BC 22A 1B ·A 1C ＝－x 2（4－x 2）（3－x 2），∴sin ∠BA 1C ＝12－7x 2（4－x 2）（3－x 2），所以S △A 1BC ＝12A 1B ·A 1C ·sin ∠BA 1C ＝12－7x 22.从而三棱柱ABC －A 1B 1C 1的体积V ＝S 直·l ＝S △A 1BC ·AA 1＝x 12－7x 22.因为x 12－7x 2＝12x 2－7x 4＝－7⎝ ⎛⎭⎪⎫x 2－672＋367， 所以当x ＝67＝427，即AA 1＝427时，体积V 取到最大值377.4.(1)证明 连接BC 1，则O 为B 1C 与BC 1的交点. 因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1. 又AO ⊥平面BB 1C 1C ，所以B 1C ⊥AO ， 由于BC 1∩AO ＝O ，故B 1C ⊥平面ABO . 由于AB ⊂平面ABO ，故B 1C ⊥AB .(2)解 作OD ⊥BC ，垂足为D ，连接AD .作OH ⊥AD ，垂足为H . 由于BC ⊥AO ，BC ⊥OD ，且AO ∩OD ＝O ， 故BC ⊥平面AOD ，所以OH ⊥BC . 又OH ⊥AD ，且AD ∩BC ＝D ， 所以OH ⊥平面ABC .因为∠CBB 1＝60°，所以△CBB 1为等边三角形， 又BC ＝1，可得OD ＝34.因为AC ⊥AB 1， 所以OA ＝12B 1C ＝12.由OH ·AD ＝OD ·OA ，且AD ＝OD 2＋OA 2＝74，得OH ＝2114. 又O 为B 1C 的中点，所以点B 1到平面ABC 的距离为217. 故三棱柱ABC －A 1B 1C 1的高为217.【两年模拟试题精练】1. (1)证明当θ＝π2时，∠BOC＝π2，即OC⊥OB，又OC⊥OA，OA∩OB＝O，∴OC⊥平面AOB.∵OC⊂平面COD，∴平面COD⊥平面AOB.(2)解在Rt△AOB中，AB＝4，∠BAO＝π6，∠AOB＝π2，∴OB＝2，OA＝23，取OB的中点E，连接DE，则DE∥AO，∴DE＝ 3.又AO⊥平面BOC，∴DE⊥平面BOC，∴V D－BOC ＝13×S△BOC·DE＝13×12×2×2sin θ×3＝1，∴sin θ＝32，θ＝π3，∴△BOC是等边三角形，∴BC＝2.∴等腰三角形ABC的面积为15，△AOB与△AOC的面积都是23，△BOC的面积为3，∴多面体A－BOC的全面积是53＋15.2.(1)证明依题意BE＝EC＝12BC＝AB＝CD，∠AEB＝60°，∴△ABE是正三角形，∵∠CED＝∠CDE＝12(180°－∠ECD)＝30°，∴∠AED＝180°－∠CED－∠AEB＝90°，∴DE⊥AE.∵AA1⊥平面ABCD，DE⊂平面ABCD，∴DE⊥AA1，∵AA1∩AE＝A，∴DE⊥平面A1AE，∵DE⊂平面A1DE，∴平面A1AE⊥平面A1DE.(2)解连接AC，由题可知AC⊥CD，又DE＝A1E，故AA1＝2，故以C为原点，CD，CA，CC1分别为x，y，z轴建立空间直角坐标系，则C (0，0，0)，D (1，0，0)，E ⎝ ⎛⎭⎪⎫－12，32，0，A 1(0，3，2)，故CE→＝⎝ ⎛⎭⎪⎫－12，32，0，CA 1→＝(0，3，2). 设面EA 1C 的一个法向量n 1＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧n 1·CE →＝0，n 1·CA 1→＝0⇒⎩⎨⎧－12x 1＋32y 1＝0，3y 1＋2z 1＝0令x 1＝3，则y 1＝1，z 1＝－62，∴n 1＝⎝ ⎛⎭⎪⎫3，1，－62.同理可求出面DA 1C 的一个法向量n 2＝(0，－2，3).故cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝555＝5511，而由图可知二面角E －A 1C －D 为钝角，所以二面角E －A 1C －D 的余弦值为－5511.3.(1)证明 ∵平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，CD ⊂平面ABCD ，CD ⊥AD ，∴CD ⊥平面P AD ， 又∵△PCD 中，E 、F 分别是PD 、PC 的中点，∴EF ∥CD ，可得EF ⊥平面P AD ， ∵EF ⊂平面EFG ， ∴平面EFG ⊥平面P AD;(2)解 ∵EF ∥CD ，EF ⊂平面EFG ， CD ⊄平面EFG ， ∴CD ∥平面EFG ，因此CD 上的点M 到平面EFG 的距离等于点D 到平面EFG 的距离，∴V M －EFG ＝V D －EFG ，取AD 的中点H ，连接GH 、EH ，则EF ∥GH ， ∵EF ⊥平面P AD ，EH ⊂平面P AD ，∴EF ⊥EH . 于是S △EFH ＝12EF ×EH ＝2＝S △EFG ，∵平面EFG ⊥平面P AD ，平面EFG ∩平面P AD ＝EH ，△EHD 是正三角形， ∴点D 到平面EFG 的距离等于正△EHD 的高，即为3，因此，三棱锥M －EFG 的体积V M －EFG ＝V D －EFG ＝13×S △EFG ×3＝233. 4.(1)证明 AC ＝AD 2＋CD 2＝22，∠BAC ＝∠ACD ＝45°，AB ＝4，BC 2＝AC 2＋AB 2－2AC ×AB ×cos 45°＝8，∵AB 2＝AC 2＋BC 2＝16，∴∠ACB ＝90°(AC ⊥BC )，∵平面ACD ⊥平面ABC ，平面ACD ∩平面ABC ＝AC ，∴BC ⊥平面ACD .(2)解 ∵AD ∥平面BEF ，AD ⊂平面ACD ，平面ACD ∩平面BEF ＝EF ，∴ AD ∥EF .∵点E 为AC 的中点，∴EF 为△ACD 的中位线，由(1)知，几何体F －BCE 的体积V F －BCE ＝V B －CEF ＝13×S △CEF ×BC S △CEF ＝14S △ACD ＝12，V F －BCE ＝13×12×22＝23.。

专题限时集训(九)空间中的平行与垂直关系(对应学生用书第133页)[建议A、B组各用时：45分钟][A组高考达标]一、选择题1．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是( ) A．若l⊥m，m⊂α，则l⊥αB．若l⊥α，l∥m，则m⊥αC．若l∥α，m⊂α，则l∥mD．若l∥α，m∥α，则l∥mB[A中，根据线面垂直的判定定理，只有垂直平面内两条相交直线才行，故A不正确；B中，由线面垂直的性质可知，平行线中的一条垂直于这个平面，则另一条也垂直这个平面，故B 正确；C中，l，m可能平行也可能异面，故C不正确；D中，平行于同一平面的两直线可能平行，异面，相交，故D不正确，故选B.]2．设m，n是两条不同的直线，α，β是两个不同的平面，给出下列四个命题：①若m∥n，m⊥β，则n⊥β；②若m∥α，m∥β，则α∥β；③若m∥n，m∥β，则n∥β；④若m⊥α，m⊥β，则α⊥β.其中真命题的个数为( ) 【导学号：68334110】A．1 B．2C．3 D．4A[对于①，由直线与平面垂直的判定定理易知其正确；对于②，平面α与β可能平行或相交，故②错误；对于③，直线n可能平行于平面β，也可能在平面β内，故③错误；对于④，由两平面平行的判定定理易得平面α与β平行，故④错误．综上所述，正确命题的个数为1，故选A.]3．如图9­12所示，直线PA垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长．其中正确的是( )图9­12A．①②B．①②③C．①D．②③B[对于①，∵PA⊥平面ABC，∴PA⊥BC.∵AB为⊙O的直径，∴BC⊥AC.又∵PA∩AC＝A，∴BC⊥平面PAC，又PC⊂平面PAC，∴BC⊥PC.对于②，∵点M为线段PB的中点，∴OM∥PA.∵PA⊂平面PAC，OM⊄平面PAC，∴OM∥平面PAC.对于③，由①知BC⊥平面PAC，∴线段BC的长即是点B到平面PAC的距离，故①②③都正确．]4．已知α，β是两个不同的平面，有下列三个条件：①存在一个平面γ，γ⊥α，γ∥β；②存在一条直线a，a⊂α，a⊥β；③存在两条垂直的直线a，b，a⊥β，b⊥α.其中，所有能成为“α⊥β”的充要条件的序号是( )A．①B．②C．③D．①③D[对于①，存在一个平面γ，γ⊥α，γ∥β，则α⊥β，反之也成立，即“存在一个平面γ，γ⊥α，γ∥β”是“α⊥β”的充要条件，所以①对，可排除B，C.对于③，存在两条垂直的直线a，b，则直线a，b所成的角为90°，因为a⊥β，b⊥α，所以α，β所成的角为90°，即α⊥β，反之也成立，即“存在两条垂直的直线a，b，a⊥β，b⊥α”是“α⊥β”的充要条件，所以③对，可排除A，选D.]5．在三棱锥P­ABC中，已知PA⊥底面ABC，AB⊥BC，E，F分别是线段PB，PC上的动点，则下列说法错误的是( )图9­13A．当AE⊥PB时，△AEF一定为直角三角形B．当AF⊥PC时，△AEF一定为直角三角形C．当EF∥平面ABC时，△AEF一定为直角三角形D．当PC⊥平面AEF时，△AEF一定为直角三角形B[因为AP⊥平面ABC，所以AP⊥BC，又AB⊥BC，且PA和AB是平面PAB上两条相交直线，则BC⊥平面PAB，BC⊥AE.当AE⊥PB时，AE⊥平面PBC，则AE⊥EF，△AEF一定是直角三角形，A正确；当EF∥平面ABC时，EF在平面PBC上，平面PBC与平面ABC相交于BC，则EF∥BC，则EF⊥AE，△AEF一定是直角三角形，C正确；当PC⊥平面AEF时，AE⊥PC，又AE⊥BC，则AE⊥平面PBC，AE⊥EF，△AEF一定是直角三角形，D正确；B中结论无法证明，故选B.] 二、填空题6．已知P为△ABC所在平面外一点，且PA，PB，PC两两垂直，则下列命题：①PA⊥BC；②PB⊥AC；③PC⊥AB；④AB⊥BC.其中正确命题的个数是________. 【导学号：68334111】3[如图所示，∵PA⊥PC，PA⊥PB，PC∩PB＝P，∴PA⊥平面PBC.又∵BC⊂平面PBC，∴PA⊥BC.同理PB⊥AC，PC⊥AB，但AB不一定垂直于BC.]7．在三棱锥C­ABD中(如图9­14)，△ABD与△CBD是全等的等腰直角三角形，O是斜边BD的中点，AB＝4，二面角A­BD­C的大小为60°，并给出下面结论：①AC⊥BD；②AD⊥CO；③△AOC为正三角形；④cos ∠ADC＝32；⑤四面体ABCD的外接球表面积为32π.其中真命题是________(填序号)．图9­14①③⑤[由题意知BD⊥CO，BD⊥AO，则BD⊥平面AOC，从而BD⊥AC，故①正确；根据二面角A­BD­C的大小为60°，可得∠AOC＝60°，又直线AD在平面AOC的射影为AO，从而AD与CO 不垂直，故②错误；根据∠AOC ＝60°，AO ＝CO 可得△AOC 为正三角形，故③正确；在△ADC中 ，AD ＝CD ＝4，AC ＝CO ＝22，由余弦定理得cos ∠ADC ＝42＋42－222×4×4＝34，故④错误；由题意知，四面体ABCD 的外接球的球心为O ，半径为22，则外接球的表面积为S ＝4π×(22)2＝32π，故⑤正确．]8．正方体ABCD ­A 1B 1C 1D 1中，E 为线段B 1D 1上的一个动点，则下列结论中正确的是________．(填序号) ①AC ⊥BE ； ②B 1E ∥平面ABCD ；③三棱锥E ­ABC 的体积为定值； ④直线B 1E ⊥直线BC 1.①②③ [因为AC ⊥平面BDD 1B 1，故①，②正确；记正方体的体积为V ，则V E ­ABC ＝16V 为定值，故③正确；B 1E 与BC 1不垂直，故④错误．] 三、解答题9．如图9­15，在四棱锥P ­ABCD 中，PC ⊥平面ABCD ，AB ∥DC ，DC ⊥AC .图9­15(1)求证：DC ⊥平面PAC . (2)求证：平面PAB ⊥平面PAC .(3)设点E 为AB 的中点，在棱PB 上是否存在点F ，使得PA ∥平面CEF ？说明理由． [解] (1)证明：因为PC ⊥平面ABCD ，所以PC ⊥DC .2分又因为DC ⊥AC ，且PC ∩AC ＝C ， 所以DC ⊥平面PAC .4分 (2)证明：因为AB ∥DC ，DC ⊥AC ， 所以AB ⊥AC .因为PC ⊥平面ABCD ，所以PC ⊥AB .又因为PC ∩AC ＝C ，所以AB ⊥平面PAC . 8分 又AB ⊂平面PAB ，所以平面PAB ⊥平面PAC . 9分 (3)棱PB 上存在点F ，使得PA ∥平面CEF .12分理由如下：取PB 的中点F ，连接EF ，CE ，CF . 又因为E 为AB 的中点，所以EF ∥PA . 又因为PA ⊄平面CEF ，且EF ⊂平面CEF ， 所以PA ∥平面CEF .15分10．(2017·绍兴稽阳联谊学校高三4月联考)如图9­16，四边形ABCD 为梯形，AB ∥CD ，∠C ＝60°，点E 在CD 上，AB ＝CE ，BF ＝13BD ＝3，BD ⊥BC .现将△ADE 沿AE 折成如图2△APE 位置，使得二面角P ­AE ­C 的大小为π3.图9­16(1)求PB 的长度； (2)求证：PB ⊥平面ABCE ；(3)求直线CE 与平面APE 所成角的正弦值．【导学号：68334112】[解] (1)因为AB 平行且等于EC ，所以四边形ABCE 是平行四边形，所以BC ∥AE ，又因为BD ⊥BC ，所以BD ⊥AE ， 所以AE ⊥FB ，AE ⊥FP ，即∠PFB 为二面角P ­AE ­C 的平面角. 3分又BF ＝3，PF ＝23，由余弦定理得BP 2＝BF 2＋PF 2－2BF ·PF cos ∠BFP ＝9， 所以BP ＝3.5分(2)证明：BF ＝3，PF ＝23，BP ＝3，满足勾股定理， 所以BF ⊥PB .又因为BF ⊥AE ，PF ⊥AE ，BF ∩PF ＝F ， 所以AE ⊥平面PFB ，所以AE ⊥PB . 7分又BF ∩AE ＝F ，则PB ⊥平面ABCE . 9分(3)法一：作BN ⊥PF 于点N ，连接AN ，由(2)可知，AE ⊥平面BFP ，所以平面BFP ⊥平面APE ，又平面BFP ∩平面APE ＝PF ， 所以BN ⊥平面APE ，12分所以∠BAN 是直线AB 与平面APE 所成的角． 在Rt △FBP 中，BN ＝BF sin π3＝32，sin ∠NAB ＝BN AB ＝322＝34.13分所以直线AB 与平面APE 所成角的正弦值为34，即直线CE 与平面APE 所成角的正弦值为34.15分法二：由于BF ，BP ，BC 两两互相垂直，如图，建立空间直角坐标系，则B (0,0,0)，C (3,0,0)，A (－1，3，0)，E (2，3，0)，P (0,0,3)，则AE →＝(3,0,0)，AP →＝(1，－3，3)，12分设平面APE 的法向量为n ＝(x ，y ，z )， 则⎩⎪⎨⎪⎧n ·AE →＝0，n ·AP →＝0，即⎩⎨⎧3x ＝0，x －3y ＋3z ＝0，取z ＝1，则n ＝(0，3，1)， 13分设直线CE 与平面APE 所成的角为θ，EC →＝(1，－3，0)，则sin θ＝|cos 〈n ，EC →〉|＝|n ·EC →||n ||EC →|＝34，即直线EC 与平面APE 所成角的正弦值为34.15分[B 组 名校冲刺]一、选择题1．已知三棱柱ABC ­A 1B 1C 1的所有棱长相等，若∠AA 1B 1＝∠AA 1C 1＝60°，则异面直线A 1C 与AB 1所成角的余弦值是( ) 【导学号：68334113】图9­17A.36 B.23C.158D.56A [将三棱柱补上一个相同的三棱柱构成一个四棱柱，如图所示，易知图中∠A 1CD 1为所求角．因为三棱柱的所有棱长均相等，不妨设为1，则根据此三棱柱的性质有A 1D 1＝A 1C ＝3，CD 1＝1，则由余弦定理得cos ∠A 1CD 1＝3＋1－323＝36，故选A.]2．如图9­18，四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，将△ADB 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A ­BCD .则在三棱锥A ­BCD 中，下列命题正确的是( )图9­18A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDC C ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABCD [∵在四边形ABCD 中，AD ∥BC ，AD ＝AB ，∠BCD ＝45°，∠BAD ＝90°，∴BD ⊥CD .又平面ABD ⊥平面BCD ，且平面ABD ∩平面BCD ＝BD ，∴CD ⊥平面ABD ，则CD ⊥AB .又AD ⊥AB ，AD ∩CD＝D ，∴AB ⊥平面ADC ，又AB ⊂平面ABC ，∴平面ABC ⊥平面ADC ，故选D.]3．如图9­19，在正方形ABCD 中，E ，F 分别是BC ，CD 的中点，沿AE ，AF ，EF 把正方形折成一个四面体，使B ，C ，D 三点重合，重合后的点记为P ，P 点在△AEF 内的射影为O ，则下列说法正确的是( )图9­19A ．O 是△AEF 的垂心B ．O 是△AEF 的内心C ．O 是△AEF 的外心D ．O 是△AEF 的重心A [由题意可知PA ，PE ，PF 两两垂直，∴PA ⊥平面PEF ，从而PA ⊥EF ，而PO ⊥平面AEF ，则PO ⊥EF .∵PO ∩PA ＝P ，∴EF ⊥平面PAO ，∴EF ⊥AO ，同理可知AE ⊥FO ，AF ⊥EO ，∴O 为△AEF 的垂心．故选A.]4．如图9­20，小于90°的二面角α­l ­β中，O ∈l ，A ，B ∈α，且∠AOB 为钝角，∠A ′OB ′是∠AOB 在β内的射影，则下列结论错误的是( )图9­20A ．∠A ′OB ′为钝角 B ．∠A ′OB ′>∠AOBC ．∠AOB ＋∠AOA ′<πD ．∠B ′OB ＋∠AOB ＋∠AOA ′>πD [考虑将图形特殊化，即可将此图形置于正方体中，正方体的一个对角面与底面分别为条件中的平面α，β，如图所示，O 为所在棱的中点，A ，B 为所在面对角线上的一个三等分点，A ′，B ′分别为A ，B 在平面β上的射影．设正方体棱长为3，则OA ＝OB ＝172，OA ′＝OB ′＝132，AA ′＝BB ′＝1，则由余弦定理得cos ∠AOB ＝－117，cos ∠A ′OB ′＝－513<－117，所以∠A ′OB ′>∠AOB >π2，所以A ，B 正确；又cos ∠AOA ′＝cos ∠BOB ′＝1317>32，所以∠AOA ′＝∠BOB ′<π6，且由cos ∠AOB ＝－117>－12知∠AOB <2π3，所以∠AOB ＋∠AOA ′<π，∠B ′OB ＋∠AOB ＋∠AOA ′<π，所以C 正确，D 错误，故选D.]二、填空题5．如图9­21，正方形BCDE 的边长为a ，已知AB ＝3BC ，将△ABE 沿边BE 折起，折起后A 点在平面BCDE 上的射影为D 点，关于翻折后的几何体有如下描述：图9­21①AB 与DE 所成角的正切值是2；②AB ∥CE ；③V B ­ACE ＝16a 3；④平面ABC ⊥平面ACD .其中正确的有________．(填序号)①③④ [作出折叠后的几何体直观图如图所示：∵AB ＝3BC ＝3a ，BE ＝a ，∴AE ＝2a .∴AD ＝AE 2－DE 2＝a ，∴AC ＝CD 2＋AD 2＝2a .在△ABC 中，cos ∠ABC ＝AB 2＋BC 2－AC 22AB ×BC＝3a 2＋a 2－2a 223a2＝33. ∴sin ∠ABC ＝1－cos 2∠ABC ＝63. ∴tan ∠ABC ＝sin ∠ABCcos ∠ABC＝ 2.∵BC ∥DE ，∴∠ABC 是异面直线AB ，DE 所成的角，故①正确．连接BD ，CE ，则CE ⊥BD ，又AD ⊥平面BCDE ，CE ⊂平面BCDE ，∴CE ⊥AD .又BD ∩AD ＝D ，BD ⊂平面ABD ，AD ⊂平面ABD ，∴CE ⊥平面ABD .又AB ⊂平面ABD ，∴CE ⊥AB ，故②错误．V B ­ACE ＝V A ­BCE ＝13S △BCE ·AD ＝13×12×a 2×a＝a 36，故③正确．∵AD ⊥平面BCDE ，BC ⊂平面BCDE ，∴BC ⊥AD .又BC ⊥CD ，CD ∩AD ＝D ，CD ，AD ⊂平面ACD ，∴BC ⊥平面ACD .∵BC ⊂平面ABC ，∴平面ABC ⊥平面ACD ，故④正确．故答案为①③④.]6．(2017·金丽衢十二校高三第二次联考)已知△ABC 中，∠C ＝90°，tan A ＝2，M 为AB 的中点．现将△ACM 沿CM 折成三棱锥P ­CBM .当二面角P ­CM ­B 大小为60°时，AB PB＝________.图9­223 [作PE ⊥CM 于点E ，BF ⊥CM 交CM 的延长线于点F ，连接AE ，则AE ⊥CF ，且PE 与BF 所成锐角等于二面角P ­CM ­B 的大小，即为60°.不妨设AC ＝1，则由tan ∠BAC ＝2，∠ACB ＝90°，得BC ＝2，AB ＝3，则由M 是AB 的中点，知MB ＝MC ，则sin ∠BCF ＝sin ∠ABC ＝13，∴|PE →|＝|AE →|＝|BF →|＝|BC →|sin ∠BCF ＝23，∴|EF →|＝2|MF →|＝2|BM →|2－|BF →|2＝2⎝ ⎛⎭⎪⎫12|AB→|2－|BF →|2＝13，则由PB →＝PE →＋EF →＋FB →，得|PB →|2＝(PE →＋EF →＋FB →)2＝|PE →|2＋|EF →2|＋|FB →|2－2|PE →||FB →|cos 60°＝23＋13＋23－2×23×23×cos 60°＝1，∴PB ＝1，故ABPB ＝ 3.]三、解答题7．端午节即将到来，为了做好端午节商场促销活动，某商场打算将进行促销活动的礼品盒重新设计．方案如下：将一块边长为10的正方形纸片ABCD 剪去四个全等的等腰三角形：△SEE ′，△SFF ′，△SGG ′，△SHH ′，再将剩下的阴影部分折成一个四棱锥形状的包装盒S ­EFGH ，其中A ，B ，C ，D 重合于点O ，E 与E ′重合，F 与F ′重合，G 与G ′重合，H 与H ′重合(如图9­23所示)．图9­23(1)求证：平面SEG ⊥平面SFH ；(2)当AE ＝52时，求二面角E ­SH ­F 的余弦值．[解] (1)证明：∵折后A ，B ，C ，D 重合于一点O ，∴拼接成底面EFGH 的四个直角三角形必为全等的等腰直角三角形， ∴底面DFGH 是正方形，EG ⊥FH ，EO ＝OG .2分 连接SO ，由题意知SE ＝SG ，∴EG ⊥SO . 4分 又∵SO ，FH ⊂平面SFH ，SO ∩FH ＝O ， ∴EG ⊥平面SFH .又∵EG ⊂平面SEG ，∴平面SEG ⊥平面SFH .6分(2)过O 作OM ⊥SH 交SH 于M 点，连接EM ，∵EO ⊥平面SFH ，SH ⊂平面SFH ，∴EO ⊥SH ，∴SH ⊥平面EMO ， ∴∠EMO 为二面角E ­SH ­F 的平面角.8分当AE ＝52时，在原平面图形中，可求得SE ＝552.在Rt △SOE 中，可求得SO ＝SE 2－OE 2＝5. 10分Rt △SHO 中，OH ＝52，SO ＝5，SH ＝552，∴OM ＝SO ·OHSH＝5，12分Rt △EMO 中，EM ＝EO 2＋OM 2＝352， cos ∠EMO ＝OM EM ＝5352＝23.14分∴所求二面角的余弦值为23.15分8．(2017·萧山中学高三5月仿真考试)如图9­24，已知矩形ABCD 中，AB ＝4，AD ＝3，现将△DAC 沿着对角线AC 向上翻折到△PAC 位置，此时PA ⊥PB .图9­24(1)求证：平面PAB ⊥平面ABC ；(2)求直线AB 与平面PAC 所成角的正弦值．【导学号：68334114】[解] (1)证明：因为PA ⊥PB ，PA ⊥PC ，PB ∩PC ＝P ， 所以PA ⊥平面PBC ，3分所以PA ⊥BC ，又BC ⊥AB ，AB ∩AP ＝A ， 所以BC ⊥平面PAB ，5分 又BC ⊂平面ABC ，所以平面PAB ⊥平面ABC . 7分(2)法一：如图，作BD ⊥PC 于点D ，连接AD ， 由(1)知PA ⊥平面PBC ，所以PA ⊥BD ， 而BD ⊥PC ，PA ∩PC ＝P ，所以BD ⊥平面PAC ， 所以∠BAD 为直线AB 与平面PAC 所成的角， 10分在Rt △PBC 中，BC ＝3，PC ＝4，PB ＝7，所以BD ＝37413分，又AB ＝4，在Rt △ADB 中，sin ∠BAD ＝BD AB ＝3716，所以直线AB 与平面PAC 所成角的正弦值为3716.15分法二：由(1)知平面PAB ⊥平面ABC ，所以在平面PAB 内，过点P 作PE ⊥AB 于点E ， 则PE ⊥平面ABC ，9分如图，以B 为坐标原点，建立空间直角坐标系(z 轴与直线PE 平行)，在Rt △PBC 中，BC ＝3，PC ＝4，PB ＝7， 在Rt △APB 中，AP ＝3，AB ＝4，PE ＝374，BE ＝74，可知A (0，－4,0)，B (0,0,0)，C (－3,0,0)，P ⎝⎛⎭⎪⎫0，－74，374，12分AC →＝(－3,4,0)，AP →＝⎝⎛⎭⎪⎫0，94，374，则易得平面PAC 的一个法向量为m ＝⎝⎛⎭⎪⎫4，3，－97，AB →＝(0,4,0)，所以cos 〈AB →，m 〉＝AB →·m |AB →||m |＝3716，故直线AB 与平面PAC 所成角的正弦值为3716.15分。

一．学习目标及知识点方法规律总结（一）.【学习目标】（1）．熟练掌握线面平行、面面平行的判定定理和性质，会把空间问题转化为平面问题．（2）．学会应用“化归思想”进行“线线问题、线面问题、面面问题”的互相转化．（3）．能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题．（4）．熟练掌握空间中线面垂直的有关性质与判定定理；运用公理、定理证明或判定空间图形的垂直关系的简单命题．不论何种“垂直”都能化归到“线线垂直”(二).知识点及方法归纳1．直线与平面平行的判定(1)判定定理：如果平面外一条直线和这个平面内的一条直线，那么这条直线和这个平面平行，即a∥b，a ⊄α，b⊂α⇒a∥α.(2)如果两个平面平行，那么一个平面内的直线与另一个平面平行，则a∥β.2．直线与平面平行的性质如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交；那么这条直线就和平面平行，即a∥α，a⊂β，α∩β＝b，．3．直线与平面垂直的判定(1)(定义)如果一条直线和平面内任意一条直线都垂直，那么这条直线和这个平面垂直．(2)(判定定理1)如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面．用符号语言表示为：若m⊂α，n⊂α，m∩n＝B，l⊥m，l⊥n，则l⊥α.(3)如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面．用符号语言表示为：若a∥b，a⊥α，则b⊥α.(4)(面面垂直的性质定理)如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．(5)(两平面平行的性质定理)如果两个平面平行，那么与其中一个平面垂直的直线也与另一个平面垂直．(6)如果两个相交平面都垂直于第三个平面，那么它们的交线也垂直于第三个平面．4..两平面平行的判断方法(1)依定义采用反证法.(2)依判定定理通过说明一平面内有两相交直线与另一平面平行来判断两平面平行.(3)依据垂直于同一直线的两平面平行来判定.(4)依据平行于同一平面的两平面平行来判定.5.平行关系的转化程序 线线平行线面平行面面平行从上易知三者之间可以进行任意转化，因此要判定某一平行的过程就是从一平行出发不断转化的过程.在解题时要把握这一点，灵活确定转化思路和方向.1．证明直线与平面平行和直线与平面垂直常运用判定定理，即转化为线线的平行与垂直关系来证明．2．直线与平面平行的判定方法：(1)a ∩α＝∅⇒a ∥α(定义法)，(2) ⎭⎪⎬⎪⎫a ∥b a ⊄αb ⊂α⇒a ∥α，这里α表示平面，a ，b 表示直线．3．证明线面垂直的方法主要有：(以下A 为点，m ，n ，l ，a ，b 表示直线，α，β表示平面)(1)利用线面垂直的定义：a 与α内任何直线垂直⇒a ⊥α；(2)利用判定定理：⎭⎪⎬⎪⎫m ，n ⊂α，m ∩n ＝A l ⊥m ，l ⊥n ⇒l ⊥α； (3)利用第二判定定理：a ∥b ，a ⊥α，则b ⊥α；(4)利用面面平行的性质定理：α∥β，a ⊥α，则a ⊥β.(5)利用面面垂直的性质定理：α⊥β，α∩β＝l ，a ⊂α，a ⊥l ，则a ⊥β.4.面面垂直的证明方法：(1)利用定义：α和β所成的二面角为直二面角⇒α⊥β；(2)利用判定定理：若a⊥β，a ⊂α，则α⊥β.5.性质定理的恰当应用：(1)若α⊥β，α∩β＝l ，a ⊂α，a ⊥l ，则a⊥β，用来证明线面垂直，也用来确定点到平面的垂线段.(2)若α⊥β，点P∈α，P ∈a ，a ⊥β，则a ⊂α.5.垂直关系的转化程序 线线垂直线面垂直面面垂直.二．命题陷阱类型1.平行垂直判断2.平行垂直证明3.翻折中的平行垂直4.平行垂直中的探索性问题三．题型1.平行垂直判断例1．已知,αβ是相异两平面， ,m n 是相异两直线，则下列命题中错误．．的是（ ） A. 若//,m n m α⊥，则n α⊥ B. 若,m m αβ⊥⊥，则//αβC. 若,//m m αβ⊥，则αβ⊥D. 若//,m n ααβ⋂=，则//m n【答案】D【解析】由线面垂直的性质可知选项A ,B ,C 正确，如图所示，对于选项D ，在正方体1111ABCD A BC D -中，取直线m 为AD ，平面α为上顶面1111A B C D ，平面β为平面11CDD C ，则直线n 为11C D ，此时有//,m n ααβ⋂=，直线m 与n 为异面直线，即选项D 的说法是错误的；本题选择D 选项.1．设,,l m n 表示不同的直线， α表示平面，已知m l ，下列结论错误的是（ ）A. 若m n ，则l nB. 若m n ⊥，则l n ⊥C. 若m α，则l αD. 若m α⊥，则l α⊥【答案】C【解析】由于l 可能含于α，故C 选项错误.2．已知α、β是两个不同的平面,m 、n 是两条不同的直线,下列命题中错误的是A. 若m ⊥α、m ∥n ，n β⊂，则α⊥βB. 若α∥β，m ⊥α，n ⊥β，则m ∥nC. 若α∥β， m α⊂， n β⊂，则m ∥nD. 若α⊥β，m α⊂， α n β⋂=，,m ⊥n ，则m ⊥β【答案】B【点睛】本题主要考查空间直线和平面之间的位置关系的判断，要求熟练掌握平行和垂直的判定定理和性质定理．3．已知,αβ是两个平面， ,m n 是两条直线，则下列命题是真命题的是（ ）A. 若//,//,//m n m m αβ，则//αβB. 若,//,//m n m n αβ⊥，则αβ⊥C. 若,,//m n m n αβ⊥⊥，则//αβD. 若//,,m n m n αβ⊂⊥，则αβ⊥【答案】D【解析】若//,//,//m n m m αβ， αβ与可能相交，A 错；若,//,//m n m n αβ⊥，则αβ与不一定垂直，甚至可能重合，B 错；若,,//m n m n αβ⊥⊥，则αβ与可能相交，C 错；若//,,m n m n αβ⊂⊥，则m β⊥，所以αβ⊥，D 正确，故选D.【方法总结】：空间线面间的位置关系判断，实际上可以借助于特殊的几何体来说明，如正方体，这样容易想象，直观性强，便于判断，本题中，如在正方体1111ABCD A BC D -，m AB =， 11n A B =， α是平面11CDD C ， β是平面ABCD ，这说明A 错误．同样可说明B 、C 错误．4．下图是一几何体的平面展开图，其中四边形ABCD 为正方形， PDC ∆， PBC ∆， PAB ∆， PDA ∆为全等的等边三角形， E F 、分别为PA PD 、的中点.在此几何体中，下列结论中错误的为（ ）A. 直线BE 与直线CF 共面B. 直线BE 与直线AF 是异面直线C. 平面BCE ⊥平面PADD. 面PAD 与面PBC 的交线与BC 平行【答案】C 【解析】画出几何体的图形，如图，故答案选C ．5．已知,m n 是两条直线， ,αβ是两个平面，则下列命题中正确的是（ ）A. ,,////m m n n ααββ⊥⊥⇒B. //,//m n n m ααβ⋂=⇒C. //,//,m m n n αβαβ⊥⇒⊥D. ,,////m n m n αβαβ⊥⊥⇒【答案】D【解析】A 不正确，因为n 可能在平面β内；B 两条直线可以不平行；C 当m 在平面β内时，n 此时也可以在平面β内。