深圳市必修第二册第五单元《概率》测试卷(包含答案解析)

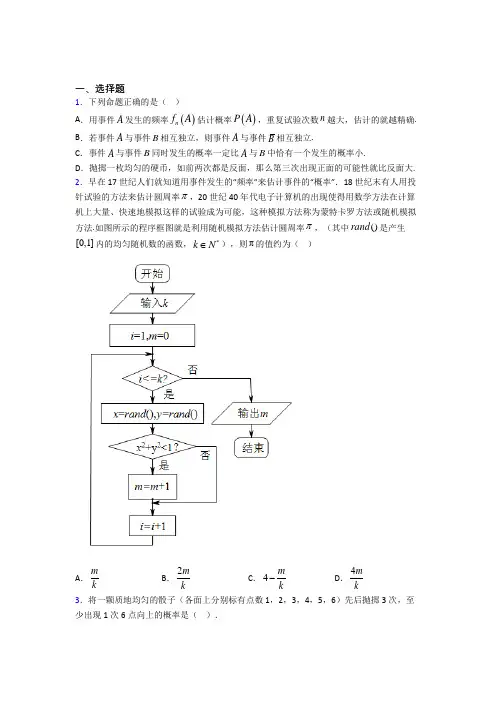
一、选择题1．下列命题正确的是（ ）A ．用事件A 发生的频率()n f A 估计概率()P A ，重复试验次数n 越大，估计的就越精确.B ．若事件A 与事件B 相互独立，则事件A 与事件B 相互独立.C ．事件A 与事件B 同时发生的概率一定比A 与B 中恰有一个发生的概率小.D ．抛掷一枚均匀的硬币，如前两次都是反面，那么第三次出现正面的可能性就比反面大. 2．早在17世纪人们就知道用事件发生的“频率”来估计事件的“概率”．18世纪末有人用投针试验的方法来估计圆周率π，20世纪40年代电子计算机的出现使得用数学方法在计算机上大量、快速地模拟这样的试验成为可能，这种模拟方法称为蒙特卡罗方法或随机模拟方法.如图所示的程序框图就是利用随机模拟方法估计圆周率π，（其中()rand 是产生[0,1]内的均匀随机数的函数，*k N ∈），则π的值约为（ ）A ．m kB ．2m kC ．4m k-D ．4m k3．将一颗质地均匀的骰子（各面上分别标有点数1，2，3，4，5，6）先后抛掷3次，至少出现1次6点向上的概率是（ ）．A ．5216B ．25216C ．31216D ．912164．一袋中有红、黄、蓝三种颜色的小球各一个，每次从中取出一个，记下颜色后放回，当三种颜色的球全部取出时停止取球，则恰好取5次球时停止取球的概率为（ ） A ．581B ．1481C ．2281D ．25815．随机抛掷一枚质地均匀的骰子，记正面向上的点数为a ，则函数()224f x x ax =++至多有一个零点的概率为（ ） A ．13B ．12C ．23D ．566．从1,2,3,4这四个数字中依次取（不放回）两个数字,a b ，使得()()lg 3lg 4a b ≥成立的概率是（ ） A ．13B ．512C ．12D ．7127．近年来，某市为促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000t 生活垃圾．经分拣以后数据统计如下表（单位：t ）：根据样本估计本市生活垃圾投放情况，下列说法错误的是（ ）A ．厨余垃圾投放正确的概率为23B ．居民生活垃圾投放错误的概率为310C ．该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱D ．厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000 8．袋中装有白球3个，黑球4个，从中任取3个，下列各对事件中互为对立事件的是（ ）A ．恰有1个白球和全是白球B ．至少有1个白球和全是黑球C ．至少有1个白球和至少有2个白球D ．至少有1个白球和至少有1个黑球9．甲、乙二人进行围棋比赛，采取“三局两胜制”，已知甲每局取胜的概率为23，则甲获胜的概率为 ( )．A．22213221333C⎛⎫⎛⎫⎛⎫+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B．22232233C⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭C．22112221333C⎛⎫⎛⎫⎛⎫+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D．21112221333C⎛⎫⎛⎫⎛⎫+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭10．齐王有上等、中等、下等马各一匹，田忌也有上等、中等、下等马各一匹．田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马．现在从双方的马匹中随机各选一匹进行一场比赛，若有优势的马一定获胜，则齐王的马获胜得概率为（）A．49B．59C．23D．7911．有3位男生和2位女生在周日去参加社区志愿活动，从该5位同学中任取3人，至少有1名女生的概率为（）A．110B．25C．35D．91012．在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率为710的事件是（）A．至多有一张移动卡B．恰有一张移动卡C．都不是移动卡D．至少有一张移动卡13．甲、乙两人独立地对同一目标各射击一次，其命中率分别为0.6,0.5，现已知目标被击中，则它是被甲击中的概率是()A．0.45 B．0.6 C．0.65 D．0.75二、解答题14．有四个编有1､2､3､4的四个不同的盒子，有编有1､2､3､4的四个不同的小球，现把四个小球逐个随机放入四个盒子里.（1）小球全部放入盒子中有多少种不同的放法？（2）在（1）的条件下求恰有一个盒子没放球的概率？（3）若没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？15．高考改革后，学生除了语数外三门必选外，可在A类科目：物理、化学、生物和B类科目：政治、地理、历史共6个科目中任选3门．（1）求小明同学选A类科目数X的分布列．（2）求小明同学从A类和B类科目中均至少选择1门科目的概率．16．甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题，按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成，2道题不能完成；应聘者乙每题正确完成的概率都是23，且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列，并计算其数学期望;(2)请分析比较甲、乙两人谁的面试通过的可能性较大?17．已知某校甲、乙、丙三个兴趣小组的学生人数分别为36，24，12.现采用分层抽样的方法从中抽取6人，进行睡眠质量的调查.（Ⅰ）应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人？（Ⅱ）现从6人中随机抽取2人做进一步的身体检查，求抽取的2人来自同一兴趣小组的概率.18．“每天锻炼一小时，健康工作五十年，幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关，从单位随机抽取30名员工进行了同卷调查，得到了如下列联表：（1）请将上面的列联表补充完整（在答题卡上直接填写结果，不需要写求解过程）；（2）能否有95%的把握认为爱好运动与性别有关？（3）若在接受调查的所有男生中按照“爱好与不爱好运动”进行分层抽样，现随机抽取8人，再从8人中抽取3人，求至少有2人“爱好运动”的概率.附：()()()()()22n ad bcKa b c d a c b d-=++++19．某学校需要从甲、乙两名学生中选一人参加数学竞赛，抽取了近期两人5次数学考试的成绩，统计结果如下表：（Ⅰ）已知甲、乙两名学生这5次数学考试成绩的平均分都为83分，若从甲、乙两名学生中选一人参加数学竞赛，请从统计学的角度考虑，你认为选谁参加数学竞赛较合适？并说明理由；（Ⅱ）若数学竞赛分初赛和复赛，在初赛中有两种答题方案：方案一：每人从5道备选题中任意抽出1道，若答对，则可参加复赛，否则被淘汰.方案二：每人从5道备选题中任意抽出3道，若至少答对其中2道，则可参加复赛，否则被淘汰.已知学生甲、乙都只会5道备选题中的3道，那么你推荐的选手选择哪种答题方案进入复赛的可能性更大？并说明理由.20．在全面抗击新冠肺炎疫情这一特殊时期，某大型企业组织员工进行爱心捐款活动．原则上以自愿为基础，每人捐款不超过300元，捐款活动负责人统计全体员工数据后，随机抽取的10名员工的捐款数额如下表：员工编号12345678910捐款数额120802155013019530090200225（1）若从这10名员工中随机选取2人，则选取的人中捐款恰有一人高于200元，一人低于200元的概率；（2）若从这10名员工中任意选取4人，记选到的4人中捐款数额大于200元的人数为X，求X的分布列和数学期望．21．为了保证食品安全，保障公众身体健康和生命安全，2018年国家对《食品安全法》进行了修正.2020，年春节前夕，某市质检部门随机抽取了20包某种品牌的速冻水饺，对某项质量指标进行检测.经统计，质量指标均在区间[0，50]内，将其按[0，10)､[10，20)､[20，30)､[30，40)､[40，50]分成5组，制成如图所示的频率分布直方图.（1）求该频率分布直方图中x的值；（2）若同组中的每个数据用该组区间中点值代替，估计该品牌速冻水饺的该项质量指标的平均值：（3）从质量指标大于等于30的速冻水饺中任选2包，进行深度检测，求这2包处于不同区间的概率.22．某组织在某市征集志愿者参加志愿活动，现随机抽出60名男生和40名女生共100人进行调查，统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况，具体数据如图所示.(1)完成下列22⨯列联表，并判断是否有99%的把握认为愿意参与志愿活动与性别有关？愿意 不愿意 总计男生 女生 总计(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者，再从中抽取2人作为队长，求抽取的2人至少有一名女生的概率. 参考数据及公式：()20P K k ≥ 0.1 0.05 0.025 0.010k2.7063.8415.0246.635()()()()()()22n ad bc K n a b c d a b c d a c b d -==+++++++.23．一款小游戏的规则如下：每轮游戏要进行三次，每次游戏都需要从装有大小相同的2个红球，3个白球的袋中随机摸出2个球，一轮游戏中，若“摸出的两个都是红球”出现3次获得200积分，若“摸出的两个都是红球”出现1次或2次获得20积分，若“摸出的两个都是红球”出现0次则扣除10积分（即获得-10积分）. （1）求每次游戏中，“摸出的两个都是红球”的概率p ； （2）设每轮游戏获得的积分为X ，求X 的分布列与数学期望；（3）玩过这款游戏的许多人发现，若干轮游戏后，与最初的积分0相比，积分没有增加反而减少了，请运用概率统计的相关知识分析解释上述现象.24．2020年5月28日，十三届全国人大三次会议表决通过了《中华人民共和国民法典》，此法典被称为“社会生活的百科全书”，是新中国第一部以法典命名的法律，在法律体系中居于基础性地位，也是市场经济的基本法.民法典与百姓生活密切相关，某大学为了解学生对民法典的认识程度，选取了120人进行测试，测试得分情况如图所示.（1）试求出图中实数a 的值，并求出成绩落在[]90,100的人数；（2）如果抽查的测试平均分超过75分，就表示该学校通过测试.试判断该校能否通过测试；（3）如果在[)80,90中抽取3人，在[]90,100中抽取2人，再从抽取的5人中选取2人进行民法典的宣传，那么选取的2人中恰好1人成绩落在[]90,100的概率是多少？ 25．某厂接受了一项加工业务，加工出来的产品(单位：件)按标准分为A ，B ，C ，D 四个等级.加工业务约定：对于A 级品、B 级品、C 级品，厂家每件分别收取加工费90元，50元，20元；对于D 级品，厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如下：甲分厂产品等级的频数分布表 等级 A B C D 频数40202020等级 A B C D 频数28173421（2）分别求甲、乙两分厂加工出来的100件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务?26．某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[)25,30，第2组[)30,35，第3组[)35,40，第4组[)40,45，第5组[]45,50，得到的频率分布直方图如图所示. 区间 [)25,30 [)30,35 [)35,40 [)40,45 []45,50人5050a150b数（1）上表是年龄的频数分布表，求正整数,a b的值；（2）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第1，2，3组的人数分别是多少？（3）在（2）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率.参考答案【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】根据概率的定义，事件的独立性概念判断各选项．【详解】在相同的条件下做大量重复试验,一个事件A出现的次数和总的试验次数n之比,称为事件A在这n次试验中出现的频率.当试验次数n很大时,频率将稳定在一个常数附近. n越大,频率偏离这个常数较大的可能性越小.这个常数称为这个事件的概率，并不是说n越大，估计的精度越精确，A错；事件A与事件B相互独立，即A是否发生与B是否发生无关，∴事件A是否发生与事件B是否发生也无关，它们相互独立，B正确；抛一枚骰子，出现的点数不大于5记为事件A，出现的点为不小于2记为事件B，则事件A与事件B同时发生是指点数为2，3，4，5，概率为4263=，而事件A与B中恰有一个发生是指点为1或6，概率为212633=<．C错；抛掷一枚均匀的硬币，如前两次都是反面，那么第三次出现正面的可能性与出现反面的可能性还是一样．D错．故选：B．【点睛】本题考查概率的定义，考查事件的独立性．掌握概念的定义是解题关键．2．D解析：D 【分析】根据[0,1]x ∈，[0,1]y ∈，而221x y +<表示14个圆，则4m k π=，故4mkπ=. 【详解】根据程序框图，知[0,1]x ∈，[0,1]y ∈，而221x y +<表示14个圆，如图所示：则落在阴影部分的面积与正方形面积比为4m k π=，得4mkπ=. 故选：D. 【点睛】本题考查了程序框图，几何概型，频率的理解与应用，属于中档题.3．D解析：D 【分析】根据正难则反原则，先求出“抛掷3次都没有出现6点向上”事件的概率，由对立事件的概率性质，计算可得答案. 【详解】解：将一颗质地均匀的骰子先后掷3次，这3次之间是相互独立， 记事件A 为“抛掷3次，至少出现一次6点向上”， 则A 为“抛掷3次都没有出现6点向上”，记事件i B 为“第i 次中，没有出现6点向上”，1,2,3i =，则123A B B B =，又()56i P B =，所以()351256216P A ⎛⎫== ⎪⎝⎭，所以()()1259111216216P A P A =-=-=. 故选：D. 【点睛】本题考查对立事件的性质和概率计算，利用了正难则反的原则，属于基础题.4．B解析：B 【分析】恰好取5次球时停止取球，分两种情况3，1，1及2，2，1，这两种情况是互斥的，利用等可能事件的概率计算每一种情况的概率，再根据互斥事件的概率得到结果． 【详解】分两种情况3，1，1及2，2，1这两种情况是互斥的，下面计算每一种情况的概率， 当取球的个数是3，1，1时，试验发生包含的基本事件总数事件是53， 满足条件的事件数是131342C C C∴这种结果发生的概率是13134258381C C C = 同理求得第二种结果的概率是12234256381C C C =根据互斥事件的概率公式得到8614818181P =+=. 故选：B ． 【点睛】此题考查根据古典概型求解概率，关键在于准确分类，求出基本事件总数和某一事件包含的基本事件个数.5．A解析：A 【分析】由函数()f x 至多有一个零点，求得22a -≤≤，得到a 的取值有1，2，共2个可能结果，结合古典概型及概率的计算公式，即可求解. 【详解】由题意，抛掷一枚质地的均匀的骰子，正面向上的点数包含6个可能结果，又由函数()224f x x ax =++至多有一个零点，则24160a ∆=-≤，解得22a -≤≤，又因为a 为正整数，故a 的取值有1，2，共2个可能结果， 所以函数()224f x x ax =++至多有一个零点的概率为13. 故选：A .本题主要考查的是古典概型及其概率计算公式，解题时准确找出试验包含的基本事件的个数，求得函数至多一个零点所包含的的个数，利用古典概型及其概率的计算公式求解是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.6．C解析：C 【分析】列出样本空间Ω,以及事件A =“()()lg 3lg 4a b ≥”包含的基本事件，计算概率. 【详解】因为()()lg 3lg 4a b ≥，所以34a b ≥.从1,2,3,4这四个数字中依次取两个数字的样本空间()()()()()()()()()()()(){}1,2,2,1,1,3,3,1 ,1,4,4,1,2,3,3,2,2,4,4,2,3,4,4,3Ω=，共12个样本点，符合条件34a b ≥的样本点有()()()()()()2,1,3,1,4,1,3,2,4,2,4,3，共6个，所以所求概率为12，故选C . 【点睛】本题考查了古典概型，考查了学生实际应用以及数学运算的能力，属于基础题.7．D解析：D 【分析】由表格可求得：厨余垃圾投放正确的概率，可回收物投放正确的概率，其他垃圾投放正确的概率，再结合选项进行分析即可. 【详解】由表格可得：厨余垃圾投放正确的概率40024001001003==++；可回收物投放正确的概率240424030305==++；其他垃圾投放正确的概率6032020605==++．对A ，厨余垃圾投放正确的概率为23，故A 正确； 对B ，生活垃圾投放错误有200602020300+++=，故生活垃圾投放错误的概率为3003100010=，故B 正确； 对C ，该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱，故C 正确． 对D ，厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的的投放量的平均数600300100100033x ++==，可得方差22221100010001000[(600)(300)(100)]3333s =⨯-+-+-=380000200009≠，故D 错误；【点睛】本题考查概率与统计的计算，考查推理能力与数据处理能力，属于中档题．8．B解析：B【分析】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，进而可分析四个事件的关系；【详解】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，故①恰有1个白球和全是白球，是互斥事件，但不是对立事件，②至少有1个白球和全是黑球是对立事件；③至少有1个白球和至少有2个白球不是互斥事件，④至少有1个白球和至少有1个黑球不是互斥事件，故选B．【点睛】本题考查互斥事件和对立事件的关系，对于题目中出现的两个事件，观察两个事件之间的关系，这是解决概率问题一定要分析的问题，本题是一个基础题．9．C解析：C【分析】先确定事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，再利用独立重复试验的概率公式和概率加法公式可求出所求事件的概率．【详解】事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，若甲三局赢两局，则第三局必须是甲赢，前面两局甲赢一局，所求概率为2121233C⎛⎫⋅⋅ ⎪⎝⎭，若前两局都是甲赢，所求概率为223⎛⎫⎪⎝⎭，因此，甲获胜的概率为22112221333C⎛⎫⎛⎫⎛⎫+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选C．【点睛】本题考查独立重复事件的概率，考查概率的加法公式，解题时要弄清楚事件所包含的基本情况，考查分类讨论思想，考查计算能力，属于中等题．10．C解析：C【分析】现从双方的马匹中随机各选一匹进行一场比赛 ,利用列举法求出基本事件有9种，齐王的马获胜包含的基本事件有6种，利用古典概型概率公式可求出齐王的马获胜的概率. 【详解】设齐王上等、中等、下等马分別为,,A B C ，田忌上等、中等、下等马分别为,,a b c ， 现从双方的马匹中随机各选一匹进行一场比赛,基本事件有：()()()()()()()()(),,,,,,,,,,,,,,,,,A a A b A c B a B b B c C a C b C c ，共9种，有优势的马一定获胜，齐王的马获胜包含的基本事件有：()()()()()(),,,,,,,,,,,A a A b A c B b B c C c ，共 6种,∴齐王的马获胜的概率为6293P ==，故选C. 【点睛】本题主要考查古典概型概率公式的应用，属于中档题，利用古典概型概率公式求概率时，找准基本事件个数是解题的关键，基本亊件的探求方法有 (1)枚举法：适合给定的基本事件个数较少且易一一列举出的；(2)树状图法：适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时，一定要按顺序逐个写出：先11(,)A B ，12(,)A B …. 1(,)n A B ，再21(,)A B ，22(,)A B …..2(,)n A B 依次31(,)A B 32(,)A B ….3(,)n A B … 这样才能避免多写、漏写现象的发生.11．D解析：D 【分析】将3位男生分别记为A 、B 、C ，2位女生分别记为a 、b ，列举出所有的基本事件，并确定事件“从这5位同学中任取3人，至少有1名女生”所包含的基本事件数，利用古典概型的概率公式可求得所求事件的概率. 【详解】将3位男生分别记为A 、B 、C ，2位女生分别记为a 、b ，从这5位同学中任取3人，所有的基本事件有：ABC 、ABa 、ABb 、ACa 、ACb 、Aab 、BCa 、BCb 、Bab 、Cab ，共10种，其中，事件“从这5位同学中任取3人，至少有1名女生”包含的基本事件有：ABa 、ABb 、ACa 、ACb 、Aab 、BCa 、BCb 、Bab 、Cab ，共9种，因此，所求概率为910P =. 故选：D. 【点睛】方法点睛：求解古典概型概率的方法如下： （1）列举法； （2）列表法； （3）树状图法； （4）排列、组合数的应用.12．A 解析：A 【分析】概率710的事件可以认为是概率为310的对立事件．【详解】事件“2张全是移动卡”的概率是310，由对立事件的概率和为1，可知它的对立事件的概率是710，事件为“2张不全是移动卡”，也即为“2张至多有一张是移动卡”．故选：A．【点睛】关键点点睛：本题考查对立事件，解题关键是掌握对立事件的概率性质：即对立事件的概率和为1，考查学生的逻辑推理能力，属于基础题.13．D解析：D【解析】根据题意，记甲击中目标为事件A，乙击中目标为事件B，目标被击中为事件C，则()1()()1(10.6)(10.5)0.8P C P A P B=-=---=.∴目标是被甲击中的概率是0.60.750.8P==故选D.二、解答题14．（1）256种；（2）916；（3）23种.【分析】（1）用分步乘法计数原理计算，考虑每个球的放法可得；（2）选取2球放在一起作为一个球，共3个球放到3个盒子中，用排列求得放法后由古典概型概率公式可计算出概率；（3）4个球的全排列数减去编号全相同的排法1即可得．【详解】（1）每个球都有4种方法，故有4444256⨯⨯⨯=种（2）从4个小球中选两个作为一个元素，同另外两个元素在三个位置全排列，故共有23 44144C A=种不同的放法.概率为：144925616=（3）每个盒子不空，共有4424A=，24123-=种．【点睛】关键点点睛：本题考查计数原理，古典概型，排列的应用．难点是事件“4个盒子中恰有一个盒子没放球”，解题关键是确定完成这件事的方法，4个球放到3个盒子中，其中有一个盒子中必有2个球，由此可选取2个球放在一起作为一个球，4个球看作3个球放入4个盒子中的3个中，用排列知识可求解． 15．（1）分布列见解析；（2）910. 【分析】（1）确定X 的所有取值为0，1，2，3，X 服从超几何分布，代入超几何分布的概率公式，计算每个X 的取值对应的概率，列出X 的分布列即可；（2）即两门A 类科目一门B 类科目或者一门A 类科目两门B 类科目的概率，则概率()()12P P X P X ==+=，从而计算可得；【详解】解：（1）小明同学选A 类科目数X 可能的取值为0，1，2，3，则X 服从超几何分布，()0333361020C C P X C ===， ()1233369120C C P X C ===，()2133369220C C P X C ===，()3033361320C C P X C ===． X 的分布列为：()()()99912202010P C P X P X ==+==+= 【点睛】本题考查了离散型随机变量的概率分布列，考查了超几何分布，古典概型的概率计算，计数原理．属于中档题．16．(1) 甲、乙的分布列见解析；甲的数学期望2、乙的数学期望2； (2)甲通过面试的概率较大． 【分析】（1）设出甲、乙正确完成面试题的数量分别为X ，Y ，由于~(6,3,4)X H ，2~3,3Y B ⎛⎫⎪⎝⎭，分别写出分布列，再求期望值均为2；（2）由于均值相等，可通过比较各自的方差. 【详解】（1）设X 为甲正确完成面试题的数量，Y 为乙正确完成面试题的数量， 依题意可得：~(6,3,4)X H ，∴1223461(1)5C C P X C ⋅===，4212363(2)5C C P X C ⋅===，3042361(3)5C C P X C ⋅===， ∴X 的分布列为：∴1232555EX =⨯+⨯+⨯=． 2~3,3Y B ⎛⎫ ⎪⎝⎭，∴0303211(0)3327P Y C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，12132162(1)C 33279P Y ⎛⎫⎛⎫==== ⎪⎪⎝⎭⎝⎭， 212321124(2)C 33279P Y ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭，333218(3)3327P Y C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， ∴Y 的分布列为：∴01232279927EY =⨯+⨯+⨯+⨯=． （2）2221312(12)(22)(32)5555DX =⨯-+-⨯+-⨯=，2121333(3)DY np p =-=⨯⨯=，∵DX DY <，∴甲发挥的稳定性更强，则甲通过面试的概率较大． 【点睛】本题考查超几何分布和二项分布的应用、期望和方差的计算，考查数据处理能力，求解时注意概率计算的准确性.17．（1）甲、乙、丙分别抽取3人、2人、1人；（2）415【分析】（1）根据分层抽样的比例原则，由36:24:123:2:1=即可求抽取6人从甲、乙、丙三个兴趣小组的学生中各抽取的人数；（2）从6人中随机抽取2人且来自同一兴趣小组的事件{来自甲小组，来自乙小组}，根据无放回试验的概率，分别求出2人来自甲小组、来自乙小组的概率，它们的和即为所求【详解】（1）由甲、乙、丙三个兴趣小组的学生人数分别为36，24，12，根据分层抽样原则 甲、乙、丙分别占总学生人数的比为12、13、16∴采用分层抽样的方法从中抽取6人中：甲中抽取1632⨯=人，乙中抽取1623⨯=人，丙中抽取1616⨯=人 （2）由（1）知：抽取的2人来自同一兴趣小组：{来自甲小组，来自乙小组} ∴2人为甲小组的概率：1121255P =⨯=；2人为乙小组的概率：21113515P =⨯= 故抽取的2人来自同一兴趣小组的概率：1211451515P P P =+=+= 【点睛】本题考查了概率，根据分层抽样的原则，按不同层次总体数量比例抽取固定数量个体，求各层次个体抽取的数量，利用无放回试验，结合概率加法公式求概率 18．（1）填表见解析；（2）没有；（3）57. 【分析】（1）根据题目所给的数据填写22⨯列联表即可；（2）利用公式计算K 的观测值2K ，对照题目表格中的数据，得出统计结论． （3）利用分层抽样可得抽取的8人中有5人爱好运动，3人不爱好运动，结合组合的应用，由古典概型概率公式计算概率即可； 【详解】 （1）列联表：由列联表的数据得k 的观测值（2）()()()()()()2223010866 1.158 3.84116141416n ad bc K a b a c a c b d -⨯⨯-⨯==≈<++++⨯⨯⨯∴没有95%的把握认为爱好运动与性别有关. （3）抽取的8人中有5人爱好运动，3人不爱好运动 设“从8人中抽取3人，至少有2人爱好运动”为事件A ，则()2135353857C C C P A C +==. 【点睛】本题主要考查列联表、古典概型概率公式以及独立性检验，属于中档题.独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.19．（Ⅰ）乙参加，理由见解析；（Ⅱ）方案二，理由见解析. 【分析】（Ⅰ）求出83x x ==甲乙，甲成绩的方差250.8S =甲，乙成绩的方差248.8S =乙，从而选派乙参加数学竞赛较合适．（Ⅱ）5道备选题中学生会的3道分别记为a ，b ，c ，不会的2道分别记为E ，F ，列举法求出方案一学生可参加复赛的概率135P =．方案二学生可参加复赛的概率2710P =．从而推荐的选手选择方案二答题方案进入复赛的可能性更大． 【详解】（Ⅰ）选派乙参加数学竞赛较合适． 理由如下： 由题知1=80+85+71+92+87835x =甲（），10+76+75+92+82835x ==乙（9），∴甲成绩的方差52211()50.85i i Sx x ==-=∑甲甲， 乙成绩的方差()5221148.85i i S x x ==-=∑乙乙，由x x =甲乙，22S S >乙甲，可知甲乙平均分相同，但乙的成绩比甲稳定，故选派乙参加数学竞赛较合适．（Ⅱ）5道备选题中学生会的3道分别记为a ，b ，c ，不会的2道分别记为E ，F ， 方案一：学生从5道备选题中任意抽出1道的结果有：a ，b ，c ，E ，F ，共5 种， 抽中会的备选题的结果有a ，b ，c ，共3种，∴此方案学生可参加复赛的概率135P =． 方案二：学生从5道备选题中任意抽出3道的结果有：(a ，b ，)c ，(a ，b ，)E ，(a ，b ，)F ，(a ，c ，)E ，(a ，c ，)F ，(a ，E ，。

高一数学必修第二册全册复习测试题卷（共22题）一、选择题（共10题）1. 向量 a ⃗=(1,2)，b ⃗⃗=(2,λ)，且 a ⃗⊥b ⃗⃗，则实数 λ= ( ) A ． 3 B ． −3 C ． 7 D ． −12. 袋中共有完全相同的 4 只小球，编号为 1，2，3，4，现从中任取 2 只小球，则取出的 2 只球编号之和是偶数的概率为 ( ) A ． 25B ． 35C ． 13D ． 233. 下列命题正确的是 ( ) A ．三点确定一个平面B ．一条直线和一个点确定一个平面C ．圆心和圆上两点可确定一个平面D ．梯形可确定一个平面4. 复数 1+i 2= ( ) A ． 0B ． 2C ． 2iD ． 1−i5. 已知 ∣a ⃗∣=1，∣b ⃗⃗∣=2，a ⃗ 与 b ⃗⃗ 的夹角为 π3，则 a ⃗⋅b ⃗⃗ 等于 ( ) A ． 1B ． 2C ． 3D ． 46. 已知平面向量 a ⃗=(1,x )，b ⃗⃗=(y,1)，若 a ⃗∥b ⃗⃗，则实数 x ，y 一定满足 ( ) A ．xy −1=0B ．xy +1=0C ．x −y =0D ．x +y =07. 在平行四边形 ABCD 中，A (1,2)，B (3,5)，AD ⃗⃗⃗⃗⃗⃗=(−1,2)，则 AC ⃗⃗⃗⃗⃗⃗+BD ⃗⃗⃗⃗⃗⃗⃗= ( ) A ． (−2,4)B ． (4,6)C ． (−6,−2)D ． (−1,9)8. 若 AB ⃗⃗⃗⃗⃗⃗=(1,1)，AD ⃗⃗⃗⃗⃗⃗=(0,1)，BC ⃗⃗⃗⃗⃗⃗+CD ⃗⃗⃗⃗⃗⃗=(a,b )，则 a +b = ( ) A ． −1B ． 0C ． 1D ． 29. 已知直线 a 在平面 γ 外，则 ( ) A ． a ∥γ B ． a 与 γ 至少有一个公共点 C ． a ∩γ=AD ． a 与 γ 至多有一个公共点10. 下列四个长方体中，由图中的纸板折成的是 ( )A．B．C．D．二、填空题（共6题）11.思考辨析判断正误当向量的始点在坐标原点时，向量的坐标就是向量终点的坐标．( )12.复数加法与减法的运算法则设z1=a+bi，z2=c+di(a,b,c,d∈R)是任意两个复数，则（1）z1+z2=；（2）z1−z2=．13.利用“斜二测”法作多面体直观图时，需考虑个方向上的尺度．14.若向量a⃗与b⃗⃗的夹角为120∘，且∣a⃗∣=1，∣∣b⃗⃗∣∣=1，则∣∣a⃗−b⃗⃗∣∣=．15.当时，λa⃗=0⃗⃗．16.“直线a经过平面α外一点P”用集合符号表示为．三、解答题（共6题）=bsinA．17.△ABC的内角A，B，C的对边分别为a，b，c，已知asin A+C2(1) 求B；(2) 若△ABC为锐角三角形，且a=2，求△ABC面积的取值范围．18.画出如图水平放置的直角梯形的直观图．19.按图示的建系方法，画出水平放置的正五边形ABCDE的直观图．20. 根据图形用符号表示下列点、直线、平面之间的位置关系．(1) 点 P 与直线 AB ； (2) 点 C 与直线 AB ； (3) 点 M 与平面 AC ； (4) 点 A 1 与平面 AC ； (5) 直线 AB 与直线 BC ； (6) 直线 AB 与平面 AC ； (7) 平面 A 1B 与平面 AC ．21. 有 4 条长为 2 的线段和 2 条长为 a 的线段，用这 6 条线段作为棱，构成一个三棱锥．问 a为何值时，可构成一个最大体积的三棱锥，最大值为多少？22. 类似于平面直角坐标系，我们可以定义平面斜坐标系：设数轴 x ，y 的交点为 O ，与 x ，y 轴正方向同向的单位向量分别是 i ⃗，j ⃗，且 i ⃗ 与 j ⃗ 的夹角为 θ，其中 θ∈(0,π2)∪(π2,π)．由平面向量基本定理，对于平面内的向量 OP ⃗⃗⃗⃗⃗⃗，存在唯一有序实数对 (x,y )，使得 OP ⃗⃗⃗⃗⃗⃗=xi ⃗+yj ⃗，把 (x,y ) 叫做点 P 在斜坐标系 xOy 中的坐标，也叫做向量 OP⃗⃗⃗⃗⃗⃗ 在斜坐标系 xOy 中的坐标．在平面斜坐标系内，直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义，如 θ=45∘ 时，方程x−24=y−1−5表示斜坐标系内一条过点 (2,1)，且方向向量为(4,−5)的直线．)，a⃗=(2,1)，b⃗⃗=(m,6)，且a⃗与b⃗⃗的夹角为锐角，求实数m的取值(1) 若θ=arccos(−13范围；(2) 若θ=60∘，已知点A(2,1)和直线l:3x−y+2=0．①求l一个法向量；②求点A到直线l的距离．答案一、选择题（共10题）1. 【答案】D【解析】由a⃗⊥b⃗⃗，所以有a⃗⋅b⃗⃗=1×2+2×λ=0⇒λ=−1．【知识点】平面向量数量积的坐标运算2. 【答案】C【解析】在编号为1，2，3，4的小球中任取2只小球，则有{1,2}，{1,3}，{1,4}，{2,3}，{2,4}，{3,4}，共6种取法，则取出的2只球编号之和是偶数的有{1,3}，{2,4}，共2种取法，即取出的2只球编号之和是偶数的概率为26=13，故选：C．【知识点】古典概型3. 【答案】D【解析】由不共线的三点确定一个平面，故A错误；由一条直线和该直线外一点确定一个平面，故B错误；当圆心和圆上两点在圆的直径上，不能说明该三点确定一个平面，故C错误；由于梯形是有一组对边平行的四边形，可得梯形确定一个平面，故D正确．故选：D．【知识点】平面向量的概念与表示4. 【答案】A【解析】因为i2=−1，所以1+i2=0．故选：A．【知识点】复数的乘除运算5. 【答案】A【解析】a⃗⋅b⃗⃗=∣a⃗∣∣b⃗⃗∣cosπ3=1×2×cosπ3=1．【知识点】平面向量的数量积与垂直6. 【答案】A【解析】因为a⃗∥b⃗⃗，所以1×1−xy=0，即xy−1=0．【知识点】平面向量数乘的坐标运算7. 【答案】A【解析】在平行四边形ABCD中，因为 A (1,2)，B (3,5)，所以 AB⃗⃗⃗⃗⃗⃗=(2,3)， 又 AD ⃗⃗⃗⃗⃗⃗=(−1,2)， 所以 AC ⃗⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗⃗+AD ⃗⃗⃗⃗⃗⃗=(1,5)，BD ⃗⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗−AB ⃗⃗⃗⃗⃗⃗=(−3,−1)， 所以 AC ⃗⃗⃗⃗⃗⃗+BD ⃗⃗⃗⃗⃗⃗⃗=(−2,4)， 故选A ．【知识点】平面向量和与差的坐标运算8. 【答案】A【解析】 BC ⃗⃗⃗⃗⃗⃗+CD ⃗⃗⃗⃗⃗⃗=BD ⃗⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗−AB⃗⃗⃗⃗⃗⃗=(0,1)−(1,1)=(−1,0)， 故 a =−1，b =0， 所以 a +b =−1．【知识点】平面向量和与差的坐标运算9. 【答案】D【解析】直线在平面外，故直线与平面相交或直线与平面平行，直线 a 与平面 γ 平行时没有公共点，直线 a 与平面 γ 相交时有一个公共点，故选D ． 【知识点】直线与平面的位置关系10. 【答案】A【解析】根据题图中纸板的形状及特殊面的阴影部分可以判断B ，C ，D 不正确，故选A ． 【知识点】棱柱的结构特征二、填空题（共6题） 11. 【答案】 √【知识点】平面向量和与差的坐标运算12. 【答案】 (a +c)+(b +d)i ； (a −c)+(b −d)i【知识点】复数的加减运算13. 【答案】三【知识点】直观图14. 【答案】 √3【解析】因为向量 a ⃗ 与 b ⃗⃗ 的夹角为 120∘，∣a ⃗∣=1，∣∣b ⃗⃗∣∣=1，所以 a ⃗⋅b ⃗⃗=∣a ⃗∣∣∣b ⃗⃗∣∣cos120∘=−12，因此 ∣∣a ⃗−b ⃗⃗∣∣=√(a ⃗−b ⃗⃗)2=√∣a ⃗∣2+∣∣b ⃗⃗∣∣2−2a⃗⋅b ⃗⃗=√1+1+1=√3． 【知识点】平面向量的数量积与垂直15. 【答案】 λ=0 或 a ⃗=0⃗⃗【解析】若 λa ⃗=0⃗⃗，则 λ=0 或 a ⃗=0⃗⃗．【知识点】平面向量的数乘及其几何意义16. 【答案】 P ∈a ，P ∉α【知识点】平面的概念与基本性质三、解答题（共6题） 17. 【答案】(1) asinA+C 2=bsinA ，由正弦定理 sinAsinA+C 2=sinBsinA ．因为 A ，B ，C 是 △ABC 的内角，sinA ≠0， 所以 sin A+C 2=sinB =sin (π−B )=sin (A +C )， 所以 sinA+C 2=2sinA+C 2cosA+C 2，因为 0<A +C <π， 所以 0<A+C 2<π2．所以 sinA+C 2≠0，cosA+C 2=12，A+C 2=π3，所以 A +C =2π3，B =π−(A +C )=π−2π3=π3(2) 由正弦定理得 asinA =bsinB =csinC =2sinA ， 所以 c =2sinC sinA，由三角形内角和知 A +C =120∘， 所以 C =120∘−A ， 所以 c =2sin (120∘−A )sinA=√3tanA+1，又 △ABC 为锐角三角形， 所以 120∘−A <90∘ 且 A <90∘， 即 30∘<A <90∘， 又 S △ABC =12acsinB =12ac ×√32=√32c =√32×(√3tanA +1)，30∘<A <90∘，因为30∘<A<90∘，所以tanA>√33，得√3tanA <3，即1<√3tanA+1<4，所以S△ABC=√32×(√3tanA+1)∈(√32,2√3)．【知识点】正弦定理18. 【答案】（1）在已知的直角梯形OBCD中，以OB所在直线为x轴，垂直于OB的腰OD所在直线为y轴建立平面直角坐标系．画出相应的xʹ轴和yʹ轴，使∠xʹOʹyʹ=45∘，如图①②所示．（2）在xʹ轴上截取OʹBʹ=OB，在yʹ轴上截取OʹDʹ=12OD，过点Dʹ作xʹ轴的平行线l，在l上沿xʹ轴正方向取点Cʹ，使得DʹCʹ=DC．连接BʹCʹ，如图②所示．（3）所得四边形OʹBʹCʹDʹ就是直角梯形OBCD的直观图，如图③所示．【知识点】直观图19. 【答案】画法：（1）在图①中作AG⊥x轴于G，作DH⊥x轴于H．（2）在图②中画相应的xʹ轴与yʹ轴，两轴相交于点Oʹ，使∠xʹOʹyʹ=45∘．（3）在图②中的xʹ轴上取OʹBʹ=OB，OʹGʹ=OG，OʹCʹ=OC，OʹHʹ=OH，yʹ轴上取OʹEʹ=1 2OE，分别过Gʹ和Hʹ作yʹ轴的平行线，并在相应的平行线上取GʹAʹ=12GA，HʹDʹ=12HD．（4）连接AʹBʹ，AʹEʹ，EʹDʹ，DʹCʹ，并擦去辅助线GʹAʹ，HʹDʹ，xʹ轴与yʹ轴，便得到水平放置的正五边形ABCDE的直观图五边形AʹBʹCʹDʹEʹ（如图③）．【知识点】直观图20. 【答案】(1) 点P∈直线AB．(2) 点C∉直线AB．(3) 点M∈平面AC．(4) 点A1∉平面AC．(5) 直线AB∩直线BC=点B．(6) 直线AB⊂平面AC．(7) 平面A1B∩平面AC=直线AB．【知识点】点、线、面的位置关系、直线与平面的位置关系、平面与平面的位置关系、直线与直线的位置关系21. 【答案】构成三棱锥，这6条线段作为棱有两种摆放方式．（1）2条长为a的线段放在同一个三角形中．如图所示，不妨设底面 BCD 是一个边长为 2 的正三角形．欲使体积达到最大，必有 BA ⊥底面BCD ，且 BA =2，AC =AD =a =2√2， 此时 V =13×√34×22×2=23√3．（2）2 条长为 a 的线段不在同一个三角形中，此时长为 a 的两条线段必处在三棱锥的对棱，不妨设 AD =BC =a ，BD =CD =AB =AC =2． 取 BC 中点 E ，连接 AE ，DE （见下图）．则 AE ⊥BC,DE ⊥BC ⇒BC ⊥平面AED ，V =13S △AED ⋅BC ， 在 △AED 中，AE =DE =√4−a 24，AD =a ，S △AED =12a √4−a 24−a 24=12a √4−a 22，所以 V =16a 2√4−a 22=16√a 2a 2(16−2a 2)⋅14，由均值不等式 a 2a 2(16−2a 2)≤(163)3，等号当且仅当 a 2=163时成立，即 a =43√3， 所以此时 V max =16√(163)3⋅14=1627√3．【知识点】棱锥的表面积与体积22. 【答案】(1) 由已知 a ⃗=2i ⃗+j ⃗，b ⃗⃗=mi ⃗+6j ⃗，且 a ⃗⋅b ⃗⃗=2m +6+(12+m )(i ⃗⋅j ⃗)=53m +2>0，得 m >−65；若 a ⃗ 和 b ⃗⃗ 同向，则存在正数 t ，使得 t (2i ⃗+j ⃗)=mi ⃗+6j ⃗， 由 i ⃗ 和 j ⃗ 不平行得，{2t =m t =6 得 m =12．故所求为 m >−65，m ≠12．(2) ①方程可变形为x−01=y−23，方向向量为 d⃗=(1,3)， 设法向量为 n ⃗⃗=(a,b )，由 n ⃗⃗⋅d ⃗=0 得 a +3b +12(3a +b )=52a +72b =0， 令 a =−7，b =−5，n ⃗⃗=(−7,5)；②取直线 l 上一点 B (0,2)，则 BA⃗⃗⃗⃗⃗⃗=(2,−1)，所求为 ∣∣BA ⃗⃗⃗⃗⃗⃗⋅n ⃗⃗∣∣∣n⃗⃗∣=∣√(⃗+5j ⃗)2=7√3926．【知识点】直线的点法向式方程（沪教版）、平面向量数量积的坐标运算。

高一数学必修第二册第十章《概率》单元练习题卷11（共22题）一、选择题（共10题）1.甲、乙、丙、丁4个人进行网球比赛，首先甲、乙一组，丙、丁一组进行比赛，两组的胜者进入决赛，决赛的胜者为冠军、败者为亚军，4个人相互比赛的胜率如表所示，表中的数字表示所在行选手击败其所在列选手的概率．甲乙丙丁甲:0.30.30.8乙0.7:0.60.4丙0.70.4:0.5丁0.20.60.5:那么甲得冠军且丙得亚军的概率是( )A．0.21B．0.15C．0.105D．0.0452.设A，B是两个概率大于0的随机事件，则下列论述正确的是( )A．事件A⊆B，则P(A)<P(B)B．若A和B互斥，则A和B一定相互独立C．若A和B相互独立，则A和B一定不互斥D．P(A)+P(B)≤13.一个口袋中装有大小、形状完全相同的白球4个、黑球5个，从中随机摸出1个球，则摸出白球的概率为( )A．14B．45C．59D．494.某中学的学生积极参加体育锻炼，其中有96%的学生喜欢足球或游泳，60%的学生喜欢足球，82%的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( ) A．62%B．56%C．46%D．42%5.“某彩票的中奖概率为11000”意味着( )A．买1000张彩票就一定能中奖B．买1000张彩票中一次奖C．买1000张彩票一次奖也不中D．购买彩票中奖的可能性是110006.袋中有2个白球，2个黑球，从中任意摸出2个，则至少摸出1个黑球的概率是( )A．34B．56C．16D．137.在集合A={2,3}中随机取一个元素m，在集合B={1,2,3}中随机取一个元素n，得到点P(m,n)，则点P在圆x2+y2=9内部的概率为( )A．12B．13C．34D．258.在此次抗击新冠肺炎疫情过程中，中医治疗起到了重要作用．中医理论讲究食物相生相克，合理搭配饮食可以增强体质，提高免疫力，但不恰当的搭配也可能引起身体的不适．食物相克是指事物之间存在着相互拮抗、制约的关系，若搭配不当，会引起中毒反应．已知猪肉与菊花，猪肉与百合，螃蟹与茄子相克．现从猪肉、螃蟹、茄子、菊花、百合这五种食物中任意选取两种，则它们相克的概率为( )A．13B．23C．310D．7109.从一副不含大、小王的52张扑克牌中任意抽出5张，则至少有3张A的概率为( )A．C43C482C525B．C483C42C525C．1−C481C44C525D．C43C482+C44C481C52510.设O为正方形ABCD的中心，在O，A，B，C，D中任取3点，则取到的3点共线的概率为( )A．15B．25C．12D．45二、填空题（共6题）11.已知Y=3+2X，若P(Y>7)=0.3，则P(X≤2)=．12.在100张奖券中，有4张中奖，从中任取两张，则两张都中奖的概率是．13.判断下列结论是否正确．（请在括号中打“√”或“×”）（1）事件发生的频率与概率是相同的．( )（2）在大量重复试验中，概率是频率的稳定值．( )（3）两个事件的和事件是指两个事件都得发生．( )（4）掷一枚硬币两次，出现“两个正面”“一正一反”“两个反面”，这三个结果是等可能的．( )14.加工某一零件需经过三道工序，设第一、二、三道工序的次品率分别为170、169、168，且各道工序互不影响，则加工出来的零件的次品率为．15.判断正误．用古典概型的概率公式可求“在线段[0,5]上任取一点，此点小于2”的概率．16.判断正误．从甲地到乙地共n条线路，且这n条线路长短各不相同，求某人任选一条路线正好选中最短路线的概率是古典概型问题．三、解答题（共6题）17.某条公共汽车线路沿线共有11个车站（包括起点站和终点站），在起点站开出的—辆公共汽车上有6位乘客，假设每位乘客在起点站之外的各个车站下车是等可能的，求：(1) 这6位乘客在其不相同的车站下车的概率；(2) 这6位乘客中恰有3人在终点站下车的概率；18.一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆） 轿车A轿车B轿车C舒适型100150z标准型300450600现按分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类10辆．(1) 求z的值．(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本，将该样本视为一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；(3) 用简单随机抽样的方法从B类舒适型轿车中抽取8辆，经检测，它们的得分如下（单位：分）：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2．从这8个数任取一个数，求该数与样本平均数之差的绝对值不超过0.5的概率．19.某医院治疗一种疾病的治愈率为10%，那么，前9个患者都没有治愈，第10个患者就一定能治愈吗？20.袋中有红、黄、白3种颜色的球各1个，从中每次任取1个，有放回地抽取3次，求(1) “3个球颜色全相同”的概率；(2) “3个球颜色不全相同”的概率．21.运动会前夕，某省派两名女乒乓球运动员参加单打比赛，她们获得冠军的概率分别为37和16，所以她们的粉丝认为该省获得乒乓球女子单打冠军的概率是 16+37．该种想法正确吗？为什么？22. 甲、乙两位同学参加某高校的入学面试．入学面试中有 3 道难度相当的题目，已知甲答对每道题目的概率都是 35，乙答对每道题目的概率都是 12．若每位面试者共有三次机会，一旦某次答对抽到的题目，则面试通过，否则就一直抽题到第 3 次为止．假设对抽到的不同题目能否答对是独立的，且甲、乙两人互不影响．(1) 求甲第二次答题通过面试的概率； (2) 求乙最终通过面试的概率；(3) 求甲、乙两人至少有一人通过面试的概率．答案一、选择题（共10题）1. 【答案】D【解析】甲，乙比赛甲获胜的概率是0.3，丙，丁比赛丙获胜的概率是0.5，甲，丙比赛甲获胜的概率是0.3，根据相互独立事件的概率乘法公式，所以甲得冠军丙得亚军的概率为0.3×0.5×0.3=0.045．【知识点】事件的关系与运算2. 【答案】C【解析】若事件B包含事件A，则P(A)≤P(B)，故A错误；若事件A，B互斥，则P(AB)=0，若事件A，B相互独立，则P(AB)=P(A)P(B)>0，故B错误，C正确；若事件A，B相互独立，且P(A)>12，P(B)>12，则P(A)+P(B)>1，故D错误．【知识点】事件的关系与运算3. 【答案】D【知识点】古典概型4. 【答案】C【解析】记“该中学学生喜欢足球”为事件A，“该中学学生喜欢游泳”为事件B，则“该中学学生喜欢足球或游泳”为事件A+B，“该中学学生既喜欢足球又喜欢游泳”为事件A⋅B，则P(A)=0.6，P(B)=0.82，P(A+B)=0.96，所以P(AB)=P(A)+P(B)−P(A+B)=0.6+0.82−0.96=0.46．所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为46%．【知识点】事件的关系与运算5. 【答案】D【知识点】频率与概率6. 【答案】B【解析】试验中会出现（白1，白2），（白1，黑1），（白1，黑2），（白2，黑1），（白2，黑2）和（黑1，黑2）共6种等可能的结果，事件“至少摸出1个黑球”所含有的基本事件为（白1，黑1），（白1，黑2），（白2，黑1），（白2，黑2）和（黑1，黑2）共5种，据古典概型概率公式，得事件“至少摸出1个黑球”的概率是56．【知识点】古典概型7. 【答案】B【解析】点P(m,n)共有(2,1)，(2,2)，(2,3)，(3,1)，(3,2)，(3,3)，6种情况，只有(2,1)，(2,2)这2个点在圆x2+y2=9的内部，所求概率为26=13．【知识点】古典概型8. 【答案】C【解析】因为从猪肉、螃蟹、茄子、菊花、百合这五种食物中任意选取两种有C52=10种，相克的有3种，则相克的概率为P=310．【知识点】古典概型9. 【答案】D【解析】设X为抽出的5张扑克牌中含A的张数，则P(X≥3)=P(X=3)+P(X=4)= C43C482+C44C481C525．【知识点】古典概型10. 【答案】A【解析】如图，从O，A，B，C，D5个点中任取3个有{O,A,B}，{O,A,C}，{O,A,D}，{O,B,C}，{O,B,D}，{O,C,D}，{A,B,C}，{A,B,D}，{A,C,D}，{B,C,D}共10种不同取法，3点共线只有{A,O,C}与{B,O,D}共2种情况，由古典概型的概率计算公式知，取到3点共线的概率为210=15．【知识点】古典概型二、填空题（共6题）11. 【答案】0.7【解析】因为P(Y>7)=P(3+2X>7)=P(X>2)=0.3，所以P(X≤2)=1−0.3=0.7．【知识点】事件的关系与运算12. 【答案】1825【知识点】古典概型13. 【答案】 × ； √ ； × ； ×【知识点】频率与概率14. 【答案】370【解析】正品率为 P =(1−170)×(1−169)×(1−168)=6770，所以次品率为 Pʹ=1−6770=370． 【知识点】事件的关系与运算、事件的独立性与条件概率15. 【答案】 ×【知识点】古典概型16. 【答案】 √【知识点】古典概型三、解答题（共6题） 17. 【答案】(1) P =P 106106=151200106=0.1512 (2) P =P 63×93106=1458106=0.001458【知识点】古典概型18. 【答案】(1) 依题意知，从每层抽取的比例为 140，从而轿车的总数为 50×40=2000（辆）， 所以 z =2000−100−150−300−450−600=400． (2) 由（1）知 C 类轿车共 1000 辆，又样本容量为 5， 故抽取的比例为1200，即抽取的 5 辆轿车中有 2 辆舒适型、 3 辆标准型，从中任取 2 辆，一共有 10 种等可能的不同取法，记事件 A 为“至少有 1 辆舒适型轿车”，则事件 A 表示抽取到 2 辆标准型轿车，共有 3 种不同取法，从而事件 A 包含的基本事件数为 7， 所以 P (A )=710．(3) 样本平均数 x =18×(9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2)=9.0，记事件 D 为“从这8 个数中任取一个数，该数与样本平均数之差的绝对值不超过 0.5”，则事件 D 包含的基本事件有 6 个，所以 P (D )=68=34．【知识点】古典概型、分层抽样19. 【答案】如果把治疗一个患者作为一次试验，治愈率是 10% 指随着试验次数的增加，有 10%的患者能够治愈，对于一次试验来说，其结果是随机的，但治愈的可能性是 10%，前 9 个患者是这样，第 10 个患者仍是这样，可能治愈，也可能不能治愈，被治愈的可能性仍是 10%．【知识点】频率与概率20. 【答案】(1) “3 个球颜色全相同”包括“3 个全是红球”（事件 A ），“3 个全是黄球”（事件 B ），“3 个全是白球”（事件 C ），且它们彼此互斥，故“3 个球颜色全相同”这个事件可记为 A +B +C ，又 P (A )=P (B )=P (C )=127．故 P (A +B +C )=P (A )+P (B )+P (C )=19．(2) 记“3 个球颜色不全相同”为事件 D ，则事件 D 为“3 个球颜色全相同”，又 P(D)=P (A +B +C )=19．所以 P (D )=1−P(D)=1−19=89，故“3 个球颜色不全相同”的概率为 89． 【知识点】事件的关系与运算21. 【答案】正确．因为两个人分别获得冠军是互斥事件，所以两个人只要有一人获得冠军，则该省就获得冠军，故该省获得冠军的概率为 16+37=2542．【知识点】事件的关系与运算22. 【答案】(1) 设甲第二次答题通过面试为事件 A ， 则 P (A )=(1−35)×35=625．(2) 设乙最终通过面试为事件 B ，对立事件为乙最终没通过面试， ∵P(B)=(1−12)(1−12)(1−12)=18，∴P (B )=1−18=78．(3) 设甲、乙两人至少有一人通过面试为事件 C ，对立事件为甲、乙两人都没有通过面试， ∵P(C)=(1−35)(1−35)(1−35)×18=1125，∴P(C)=1−1125=124125．【知识点】事件的相互独立性。

一、选择题1．某地有A ，B ，C ，D 四人先后感染了传染性肺炎，其中只有A 到过疫区，B 确定是受A 感染的.对于C 因为难以判定是受A 还是受B 感染的，于是假定他受A 和B 感染的概率都是12.同样也假定D 受A ，B 和C 感染的概率都是13.在这种假定下，B ，C ，D 中恰有两人直接受A 感染的概率是（ ） A ．16B ．13C ．12D ．232．从1,2,3,4这四个数字中依次取（不放回）两个数字,a b ，使得()()lg 3lg 4a b ≥成立的概率是（ ） A ．13B ．512C ．12D ．7123．甲、乙两人对同一个靶各射击一次，设事件A =“甲击中靶”，事件B =“乙击中靶”，事件E =“靶未被击中”，事件F=“靶被击中”，事件G =“恰一人击中靶”，对下列关系式（A 表示A 的对立事件，B 表示B 的对立事件）：①E AB =，②F AB =，③F A B =+，④G A B =+，⑤G AB AB =+，⑥()()1P F P E =-，⑦()()()P F P A P B =+．其中正确的关系式的个数是（ ） A ．3B ．4C ．5D ．64．将－颗骰子先后投掷两次分别得到点数,a b ，则关于,x y 方程组228040ax by x y +-=⎧⎨+-=⎩，有实数解的概率为（ ） A ．29B ．79C ．736D ．9365．袋中装有白球3个，黑球4个，从中任取3个，下列各对事件中互为对立事件的是（ ）A ．恰有1个白球和全是白球B ．至少有1个白球和全是黑球C ．至少有1个白球和至少有2个白球D ．至少有1个白球和至少有1个黑球6．学校将5个不同颜色的奖牌分给5个班，每班分得1个，则事件“1班分得黄色的奖牌”与“2班分得黄色的奖牌”是( ) A ．对立事件B ．不可能事件C ．互斥但不对立事件D ．不是互斥事件7．某商场进行购物摸奖活动，规则是：在一个封闭的纸箱中装有标号分别为1，2，3，4，5，6的六个小球，每次摸奖需要同时取出两个球，每位顾客最多有两次摸奖机会，并规定：若第一次取出的两球号码连号，则中奖，摸奖结束；若第一次未中奖，则将这两个小球放回后进行第二次摸球，若与第一次取出的两个小球号码相同，则为中奖，按照这样的规则摸奖，中奖的概率为（ ）A ．13B ．1745C ．245D ．171008．甲、乙二人进行围棋比赛，采取“三局两胜制”，已知甲每局取胜的概率为23，则甲获胜的概率为 ( )．A ．22213221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B ．22232233C ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭C ．22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D ．21112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭9．若从集合{}2,1,2A =-中随机取一个数a ，从集合{}1,1,3B =-中随机取一个数b ，则直线0ax y b -+=一定．．经过第四象限的概率为( ) A ．29B ．13C ．49D ．5910．在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率为710的事件是（ ） A ．至多有一张移动卡 B ．恰有一张移动卡 C ．都不是移动卡D ．至少有一张移动卡11．某校3名教师和5名学生共8人去北京参加学习方法研讨会，需乘坐两辆车，每车坐4人，则恰有两名教师在同一车上的概率（ ） A ．78B ．67C ．37D ．1312．数学与文学有许多奇妙的联系，如诗中有回文诗：“垂帘画阁画帘垂，谁系怀思怀系谁？”既可以顺读也可以逆读，数学中有回文数，如343、12521等，两位数的回文数有11、22、33、…、99共9个，则三位数的回文数中为偶数的概率是（ ） A ．19B ．29C ．39D ．4913．高三年级7位体育老师的身高(单位：cm )数据如茎叶图所示，其中一位老师的身高记录看不清了，但他们的平均身高为177cm ，若从中任选2位老师参加年级的教职工篮球赛，则身高均高于177cm 的概率为（ ）A ．27B ．37C ．1021D ．1121二、解答题14．某班倡议假期每位学生每天至少锻炼一小时.为了解学生的锻炼情况，对该班全部34名学生在某周的锻炼时间进行了调查，调查结果如下表:（Ⅱ）若从锻炼8小时的学生中任选2人参加一项活动，求选到男生和女生各1人的概率；（Ⅲ）试判断该班男生锻炼时长的方差21s 与女生锻炼时长的方差22s 的大小.（直接写出结果）15．空气质量指数是定量描述空气质量状况的指数，空气质量指数的值越高，就代表空气污染越严重，其分级如下表：现分别从甲、乙两个城市12月份监测的空气质量指数的数据中随机抽取6天的数据，记录如下：（2）分别从甲、乙两个城市的统计数据中任取一个，求这两个数据对应的空气质量类别都为轻度污染的概率；（3）记甲城市这6天空气质量指数的方差为20S ．从甲城市12月份空气质量指数的数据中再随机抽取一个记为a ，若99a =，与原有的6天的数据构成新样本的方差记为21S ；若169a =，与原有的6天的数据构成新样本的方差记为22S ，试比较20S 、21S 、22S 的大小．（结论不要求证明）16．国际电子竞技和围棋比赛通常采用双败淘汰制.双败淘汰制即一支队伍失败两场被淘汰出局，直到最后剩下一支队伍夺得冠军(决赛只赛一场).以八支战队的比赛为例(如图所示)，第一轮比赛，由8支战队抽签后交战，获胜战队继续留在获胜组，失败战队则掉人失败组，进人下一轮比赛.失败战队在失败组一旦再失败即被淘汰，最后由胜者组和败者组的冠军决出总冠军.某项国际电子竞技比赛有甲等8名选手参加，比赛采用了双败淘汰制，若这8名选手相互之间每场比赛获胜的概率均为0.5. 双败流程示意图（以八支战队为例）（1）求甲获得冠军的概率；（2）记甲在这次比赛中参加比赛的场次为X，求随机变量X的分布列和期望.17．某校高二期中考试后，教务处计划对全年级数学成绩进行统计分析，从男、女生中各随机抽取100名学生，分别制成了男生和女生数学成绩的频率分布直方图，如图所示.（1）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？（2）在（1）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意任取2人，求至少有1名男生的概率．18．随着科学技术的飞速发展，手机的功能逐渐强大，很大程度上代替了电脑电视.为了了解某高校学生平均每天使用手机的时间与性别是否有关，某调查小组随机抽取了30名男生，20名女生进行为期一周的跟踪调查，调查结果如表所示：平均每天使用手机超过3小时平均每天使用手机不超过3小时合计男生25530（1）能否在犯错误的概率不超过0.01的前提下认为学生使用手机的时间长短与性别有关？（2）在这20名女生中，调查小组发现共有15人使用国产手机，在未使用国产手机的人中，平均每天使用手机不超过3小时的共有2人.从未使用国产手机的人中任意选取3人，求至多有一人使用手机不超过3小时的概率.参考公式：()()()()()22n ad bcKa cb d a bc d-=++++（n a b c d=+++）.19．5月4日，修水第二届“放肆青春放肆跑”全民健身彩跑活动在信华城举行，全程约5.4km，共有2500余名参与者.某单位为了解员工参加彩跑活动是否与性别有关，从单位随机抽取30名员工进行问卷调查，得到了如下22⨯列联表：已知在这30人中随机抽取1人抽到参加彩跑活动的员工的概率是8 15.（1）完成答题卡上的22⨯列联表，并判断能否有90%的把握认为参加彩跑活动与性别有关？（2）已知参加彩跑的女性中共有4人跑完了全程，若从参加彩跑的6名女性中任选两人，求选出的两人均跑完了全程的概率.附：()()()()()22n ad bcKa b c d a c b d-=++++，其中n a b c d=+++.k 2.072 2.706 3.841 5.024 6.6357.87910.82820．为普及抗疫知识、弘扬抗疫精神，某学校组织防疫知识竞赛.比赛共分为两轮，每位参赛选手均须参加两轮比赛，若其在两轮比赛中均胜出，则视为赢得比赛.已知在第一轮比赛中，选手甲、乙胜出的概率分别为35，34；在第二轮比赛中，甲、乙胜出的概率分别为2 3，25.甲、乙两人在每轮比赛中是否胜出互不影响.（1）从甲、乙两人中选取1人参加比赛，派谁参赛赢得比赛的概率更大？（2）若甲、乙两人均参加比赛，求两人中至少有一人赢得比赛的概率.21．在某城市气象部门的数据库中，随机抽取30天的空气质量指数的监测数据，整理得如下表格：空气质量指数优良好轻度污染中度污染重度污染天数5a84b空气质量指数为优或良好，规定为Ⅰ级，轻度或中度污染，规定为Ⅱ级，重度污染规定为Ⅲ级.若按等级用分层抽样的方法从中抽取10天的数据，则空气质量为Ⅰ级的恰好有5天.（1）求a，b的值；（2）若以这30天的空气质量指数来估计一年的空气质量情况，试问一年（按366天计算）中大约有多少天的空气质量指数为优？（3）若从抽取的10天的数据中再随机抽取4天的数据进行深入研究，记其中空气质量为Ⅰ级的天数为X，求X的分布列及数学期望.22．某企业为了解该企业工人组装某产品所用时间，对每个工人组装一个该产品的用时作了记录，得到大量统计数据．从这些统计数据中随机抽取了9个数据作为样本，得到如图所示的茎叶图（单位：分钟）．若用时不超过40（分钟），则称这个工人为优秀员工．（1）求这个样本数据的中位数和众数；（2）从样本数据用时不超过50分钟的工人中随机抽取2个，求至少有一个工人是优秀员工的概率．23．某种产品的广告费支出x 与销售额y （单位：万元）之间有如下对应数据：（1）若广告费与销售额具有相关关系，求回归直线方程；（2）在已有的五组数据中任意抽取两组，求两组数据其预测值与实际值之差的绝对值都不超过5的概率.参考公式：1221ni ii nii x y nx yb xnx==-⋅=-∑∑，a y bx =-.24．2019年《少年的你》自上映以来引发了社会的广泛关注，特别引起了在校学生情感共鸣，现假如男生认为《少年的你》值得看的概率为45，女生认为《少年的你》值得看的概率为34，某机构就《少年的你》是否值得看的问题随机采访了4名学生（其中2男2女） （1）求这4名学生中女生认为值得看的人数比男生认为值得看的人数多的概率；（2）设ζ表示这4名学生中认为《少年的你》值得看的人数，求ζ的分布列与数学期望.25．2020年是全面建成小康社会目标实现之年，也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户，结合当地实际情况采取多项精准扶贫措施，每年新脱贫户数如下表（1）根据2015-2019年的数据，求出y 关于x 的线性回归方程y bx a =+，并预测到2020年底该乡镇500户贫困户是否能全部脱贫；（2）2019年的新脱贫户中有20户五保户，20户低保户，60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访，了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫，随机抽取这5户中的2户进行每月跟踪帮扶，求抽取的2户中至少有1户是扶贫户的概率. 参考数据：5115526838049251001299i ii x y==⨯+⨯+⨯+⨯+⨯=∑参考公式：()()()1122211nni iiii i nniii i x ynx y xxy y b xnxxx====---==--∑∑∑∑，a y bx =-26．某厂接受了一项加工业务，加工出来的产品(单位：件)按标准分为A ，B ，C ，D 四个等级.加工业务约定：对于A 级品、B 级品、C 级品，厂家每件分别收取加工费90元，50元，20元；对于D 级品，厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务，在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如下：甲分厂产品等级的频数分布表（2）分别求甲、乙两分厂加工出来的100件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务?【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】设,,B C D 直接受A 感染为事件B 、C 、D ，分析题意得出()1P B =，1()2P C =，1()3P D =，B ，C ，D 中恰有两人直接受A 感染为事件CD CD +，利用公式求得结果. 【详解】根据题意得出：因为直接受A 感染的人至少是B ， 而C 、D 二人也有可能是由A 感染的， 设,,B C D 直接受A 感染为事件B 、C 、D ， 则事件B 、C 、D 是相互独立的，()1P B =，1()2P C =，1()3P D =， 表明除了B 外，,C D 二人中恰有一人是由A 感染的， 所以12111()()()23232P CD CD P CD P CD +=+=⨯+⨯=， 所以B 、C 、D 中直接受A 传染的人数为2的概率为12， 故选：C. 【点睛】该题考查的是有关概率的问题，涉及到的知识点有随机事件发生的概率，相互独立事件同时发生的概率公式和互斥事件有一个发生的概率公式，属于简单题目.2．C解析：C 【分析】列出样本空间Ω,以及事件A =“()()lg 3lg 4a b ≥”包含的基本事件，计算概率. 【详解】因为()()lg 3lg 4a b ≥，所以34a b ≥.从1,2,3,4这四个数字中依次取两个数字的样本空间()()()()()()()()()()()(){}1,2,2,1,1,3,3,1 ,1,4,4,1,2,3,3,2,2,4,4,2,3,4,4,3Ω=，共12个样本点，符合条件34a b ≥的样本点有()()()()()()2,1,3,1,4,1,3,2,4,2,4,3，共6个，所以所求概率为12，故选C . 【点睛】本题考查了古典概型，考查了学生实际应用以及数学运算的能力，属于基础题.3．B解析：B 【分析】根据事件关系，靶为被击中即甲乙均未击中；靶被击中即至少一人击中，分为恰有一人击中或两人都击中，依次判定即可. 【详解】由题可得：①E AB =，正确；②事件F=“靶被击中”，AB 表示甲乙同时击中，F AB AB AB =++，所以②错误；③F A B =+，正确，④A B +表示靶被击中，所以④错误；⑤G AB AB =+，正确；⑥,E F 互为对立事件，()()1P F P E =-，正确；⑦()()()()P F P A P B P AB =+-，所以⑦不正确． 正确的是①③⑤⑥． 故选：B【点睛】此题考查事件关系和概率关系的辨析，需要熟练掌握事件的关系及其运算，弄清事件特征及其概率特征准确辨析.4．B解析：B 【分析】利用圆心到直线的距离不大于半径可得,a b 的不等式关系，从而得到方程组有解的(),a b 个数，利用古典概型的概率公式可求概率. 【详解】因为方程组228040ax by x y +-=⎧⎨+-=⎩有解，故直线80ax by +-=与圆224x y +=有公共点，2≤即2216a b +≥，当1a =时，4,5,6b =，有3种情形；当2a =时，4,5,6b =，有3种情形； 当3a =时，3,4,5,6b =，有4种情形； 当4,5,6a =时，1,2,3,4,5,6b =，有18种情形；故方程有解有28种情形，而(),a b 共有36种不同的情形，故所求的概率为287369=. 故选：B. 【点睛】古典概型的概率的计算，关键是基本事件的总数和随机事件中基本事件的个数的计算，计算时可采用枚举法、树形图等帮助计数（个数较少时），也可以利用排列组合的方法来计数（个数较大时）.5．B解析：B 【分析】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，进而可分析四个事件的关系； 【详解】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，故①恰有1个白球和全是白球，是互斥事件，但不是对立事件， ②至少有1个白球和全是黑球是对立事件； ③至少有1个白球和至少有2个白球不是互斥事件， ④至少有1个白球和至少有1个黑球不是互斥事件， 故选B ． 【点睛】本题考查互斥事件和对立事件的关系，对于题目中出现的两个事件，观察两个事件之间的关系，这是解决概率问题一定要分析的问题，本题是一个基础题．6．C解析：C 【分析】对与黄色奖牌而言，可能是1班分得，可能是2班分得，也可能1班与2班均没有分得，然后根据对立事件和互斥事件的概念进行判断． 【详解】由题意，1班和2班不可能同时分得黄色的奖牌，因而这两个事件是互斥事件；又1班和2班可能都得不到黄色的奖牌，故这两个事件不是对立事件，所以事件“1班分得黄色的奖牌”与“2班分得黄色的奖牌”是互斥但不对立事件.故选C 【点睛】本题考查了互斥事件和对立事件，关键是对概念的理解，属于基础题．7．B解析：B 【分析】可将中奖的情况分成第一次两球连号和第二次取出的小球与第一次取出的号码相同两种情况，分别计算两种情况的概率，根据和事件概率公式可求得结果. 【详解】中奖的情况分为：第一次取出两球号码连号和第二次取出两个小球与第一次取出的号码相同两种情况第一次取出两球连号的概率为：26513C =第二次取出两个小球与第一次取出号码相同的概率为：261121345C ⎛⎫-⨯= ⎪⎝⎭∴中奖的概率为：121734545+=本题正确选项：B 【点睛】本题考查和事件概率问题的求解，关键是能够根据题意将所求情况进行分类，进而通过古典概型和积事件概率求解方法求出每种情况对应的概率.8．C解析：C 【分析】先确定事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，再利用独立重复试验的概率公式和概率加法公式可求出所求事件的概率． 【详解】事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，若甲三局赢两局，则第三局必须是甲赢，前面两局甲赢一局，所求概率为2121233C ⎛⎫⋅⋅ ⎪⎝⎭，若前两局都是甲赢，所求概率为223⎛⎫ ⎪⎝⎭，因此，甲获胜的概率为22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选C ． 【点睛】本题考查独立重复事件的概率，考查概率的加法公式，解题时要弄清楚事件所包含的基本情况，考查分类讨论思想，考查计算能力，属于中等题．9．D解析：D 【分析】由题意，利用列举法求得基本事件(),a b 的总数，再列举出所求事件所包含的基本事件的个数，利用古典概型及其概率的计算公式，即可求解. 【详解】由题意，从集合{}2,1,2A =-中随机取一个数a ，从集合{}1,1,3B =-中随机取一个数b ，得到(),a b 的取值的所有可能了结果共有：()()()()()()()()()2,1,2,1,2,3,1,1,1,1,1,3,2,1,2,1,2,3------，共计9种结果，由直线0ax y b -+=，即y ax b =+，其中当0a b ≥⎧⎨≥⎩时，直线不过第四象限， 共有()()()()1,1,1,3,2,1,2,3，共计4种，所以当直线0ax y b -+=一定．．经过第四象限时，共有5中情况， 所以概率为59P =，故选D. 【点睛】本题主要考查了古典概型及其概率的计算，以及直线方程的应用，其中解答中根据题意列举出基本事件的总数，进而利用古典概型及其概率的计算公式求解是解答的关键，着重考查了推理与计算能力，属于基础题.10．A解析：A 【分析】概率710的事件可以认为是概率为310的对立事件． 【详解】事件“2张全是移动卡”的概率是310，由对立事件的概率和为1，可知它的对立事件的概率是710，事件为“2张不全是移动卡”，也即为“2张至多有一张是移动卡”． 故选：A ． 【点睛】关键点点睛：本题考查对立事件，解题关键是掌握对立事件的概率性质：即对立事件的概率和为1，考查学生的逻辑推理能力，属于基础题.11．B解析：B 【分析】易得出8人乘车，每车4人的乘车方法是48C ，然后考虑从3名教师中选2人，从5名学生中选2人乘同一辆车，注意有两辆车，求出方法后可得概率． 【详解】8人乘车，每车4人的乘车方法是4870C =，从3名教师中选2人，从5名学生中选2人乘同一辆车的方法娄得2235260C C ⨯=，∴所求概率为606707P ==． 故选：B ． 【点睛】本题考查古典概型，解题关键是求出事件“恰有两名教师在同一车上”的方法数，易错点是不考虑两辆车．12．D解析：D 【分析】利用列举法列举出所有的三位回文数的个数，再列举出其中所有的偶数的个数，由此能求出结果 【详解】解：三位数的回文数为ABA ，A 共有1到9共9种可能，即11B 、22B 、33B ⋯B 共有0到9共10种可能，即0A A 、1A A 、2A A 、3A A 、⋯ 共有91090⨯=个，其中偶数为A 是偶数，共4种可能，即22B ，44B ，66B ，88B ， B 共有0到9共10种可能，即0A A 、1A A 、2A A 、3A A 、⋯ 其有41040⨯=个，∴三位数的回文数中，偶数的概率404909P ==； 故选：D ． 【点睛】本题考查概率的求法，注意列举法在使用时一定做到不重不漏，属于中档题．13．C解析：C 【分析】由平均数求出8x =，进而可得7人中身高高于177cm 的有5人，用古典概型求出概率即可. 【详解】 根据题意，得1801811701731701781791777x +++++++=，解得8x =，这7人中取2人的情况共2721C =种，身高高于177cm 的5人中取2人的情况共2510C =种，所以身高的高于177cm 的概率为1021故选：C. 【点睛】本题考查了茎叶图和古典概型问题，考查了计算能力和逻辑推理能力，属于基础题目.二、解答题14．（Ⅰ）6.5小时（Ⅱ）35（Ⅲ）2212s s > 【分析】（Ⅰ）由表中数据计算平均数即可；（Ⅱ）列举出任选2人的所有情况，再由古典概型的概率公式计算即可； （Ⅲ）根据数据的离散程度结合方差的性质得出2212s s > 【详解】（Ⅰ）这个班级女生在该周的平均锻炼时长为53687682911306.53862120⨯+⨯+⨯+⨯+⨯==++++小时（Ⅱ）由表中数据可知，锻炼8小时的学生中男生有3人，记为,,a b c ，女生有2人，记为,A B从中任选2人的所有情况为{,},{,},{,},{,}a b a c a A a B ，{,},{,},{,}b c b A b B ，{,},{,},{,}c A c B A B ，共10种，其中选到男生和女生各1人的共有6种 故选到男生和女生各1人的概率63105P == （Ⅲ）2212s s > 【点睛】关键点睛：在第二问中，关键是利用列举法得出所有的情况，再结合古典概型的概率公式进行求解. 15．（1）13；（2）19；（3）222102S S S <<．【分析】（1）甲城市这6天内空气质量类别为良的有2天，利用频率估计概率的思想可求得结果； （2）列举出所有的基本事件，并利用古典概型的概率公式可求得结果； （3）根据题意可得出20S 、21S 、22S 的大小关系. 【详解】（1）甲城市这6天内空气质量类别为良的有2天，则估计甲城市12月份某一天空气质量类别为良的概率为13； （2）由题意，分别从甲、乙两个城市的统计数据中任取一个，所有的基本事件有：()48,80、()48,67、()48,108、()48,150、()48,205、()48,62、()65,80、()65,67、()65,108、()65,150、()65,205、()65,62、()104,80、()104,67、()104,108、()104,150、()104,205、()104,62、()132,80、()132,67、()132,108、()132,150、()132,205、()132,62、()166,80、()166,67、()166,108、()166,150、()166,205、()166,62、()79,80、()79,67、()79,108、()79,150、()79,205、()79,62，共36个，用A 表示“这两个数据对应的空气质量类别都为轻度污染”，则事件A 包含的基本事件有：()104,108、()104,150、()132,108、()132,150，共4个基本事件， 所以，()41369P A ==； （3）222102S S S <<． 【点睛】方法点睛：求解古典概型概率的问题有如下方法： （1）列举法； （2）列表法； （3）树状图法； （4）排列组合数的应用. 16．（1）18；（2）分布列答案见解析，数学期望为3.5. 【分析】（1）由“双败淘汰制”可知，甲获得冠军可能是由获胜者组进入决赛并最终夺冠，也可能由失败者组进入决赛最终夺冠，根据相互独立事件的概率公式，即可求出甲获得冠军的概率．（2）X 的可能取值为2，3，4，5，6，分别求出相应的概率，由此能求出X 的分布列和数学期望． 【详解】（1）由“双败淘汰制”可知，甲获得冠军可能是由获胜者进入决赛并最终夺冠，也可能是由失败者组进入决赛最终夺冠的，所以4322451111111812222222648P ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+++⨯+⨯== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭（2）依题意，X 的可能取值为2，3，4，5，6. ()211224P X ⎛⎫=== ⎪⎝⎭，()2121113224P X C ⎛⎫==⨯⨯= ⎪⎝⎭， ()33131115422216P X C ⎛⎫⎛⎫==+⨯⨯= ⎪ ⎪⎝⎭⎝⎭， 当5X =时，有如下情况：①前两场胜利，第三场失败；②第一场失败或第二场失败，则第5场必失败.()4511152228P X ⎛⎫⎛⎫==+⨯= ⎪ ⎪⎝⎭⎝⎭，当6X =时，前5场只可能失败一次，且只可能是在第一场失败或第二场失败，()51162216P X ⎛⎫==⨯= ⎪⎝⎭，所以X 的分布列为所以X 的数学期望为()23456 3.54416816E X =⨯+⨯+⨯+⨯+⨯=. 【点睛】本题主要考查了相互独立事件概率乘法公式、离散型随机变量的分布列、数学期望的求法等基础知识，考查分析能力和计算能力，属于中档题． 17．（1）男30人，女45人（2）710【分析】（1）根据频率分布直方图求出男、女生优秀人数即可；（2）求出样本中的男生和女生的人数，写出所有的基本事件以及满足条件的基本事件的个数，从而求出满足条件的概率即可． 【详解】（1）由题可得，男生优秀人数为()1000.010.021030⨯+⨯=人， 女生优秀人数为()1000.0150.031045⨯+⨯=人； （2）因为样本容量与总体中的个体数的比是51304515=+，所以样本中包含男生人数为130215⨯=人，女生人数为145315⨯=人． 设两名男生为1A ，2A ，三名女生为1B ，2B 3B ． 则从5人中任意选取2人构成的所有基本事件为：{}12,A A ，{}11,A B ，{}12,A B ，{}13,A B ，{}21,A B ，{}22,A B ，{}23,A B ，{}12,B B ，{}13,B B ，{}23,B B 共10个，记事件C ：“选取的2人中至少有一名男生”， 则事件C 包含的基本事件有：{}12,A A ，{}11,A B ，{}12,A B ，{}13,A B ，{}21,A B ，{}22,A B ，{}23,A B 共7个．所以()710P C =． 【点睛】本题考查了频率分布问题，考查了古典概型概率问题，是一道中档题． 18．（1）不能；（2）910. 【分析】（1）根据已知条件计算出2K 的值，然后与6.635比较即可得出结论； （2）根据组合知识和古典概率公式可求得答案. 【详解】（1）()22502510105 6.349 6.63535153020K ⨯⨯-⨯=≈<⨯⨯⨯ . 所以不能在犯错误的概率不超过0.01的前提下认为学生使用手机的时间长短与性别有关． （2）因为在未使用国产手机的5人中，平均每天使用手机不超过3小时的共有2人， 所以从未使用国产手机的人中任意选取3人，至多有一人使用手机不超过3小时的概率为32133235+910C C C P C ==. 【点睛】本题考查计算2K ，进行独立性检验，古典概率公式，属于中档题.19．（1）表格见解析，没有90%的把握认为参加彩跑活动与性别有关；（2）25.【分析】（1）由条件可知参加彩跑的有8301615⨯=人，结合条件补全22⨯列联表，并计算2K ，再和临界值表的数值比较；（2）首先为参加彩跑的6名女性编号，再通过列举的方法，计算概率. 【详解】解：（1）参加彩跑的有8301615⨯=人，由已知数据可求得：230(10866) 1.158 2.70616141416χ⨯-⨯=≈<⨯⨯⨯.所以没有90%的把握认为参加彩跑活动与性别有关.（2）将跑完全程的4人记为A ，B ，C ，D ；没跑完全程的2人记为x ，y . 从这6人中随机选取2人所有可能的情况为AB ，AC ，AD ，BC ，BD ，CD ，Ax ，Ay ，Bx ，By ，Cx ，Cy ，Dx ，Dy ，xy ，共15种.设“选出的两人均跑完了全程”为事件A ， 选出的两人均跑完了全程的情况有6种， 所以所求概率为()62155P A ==. 【点睛】本题考查独立性检验，古典概型，重点考查数据分析，计算能力，属于基础题型. 20．（1）派甲参赛获胜的概率更大；（2）2950. 【分析】（1）利用相互独立事件概率乘法公式分别求出甲赢得比赛的概率和乙赢得比赛的概率，由此得解．（2）设C 表示“甲赢得比赛”， D 表示“乙赢得比赛”， C D 表示“两人中至少有一个赢得比赛”， ()1()1()()P C D P CD P C P D =-=-，由此能求出两人中至少有一人赢得比赛的概率． 【详解】解：（1）设1A =“甲在第一轮比赛中胜出”，2A =“甲在第二轮比赛中胜出”，1B =“乙在第一轮比赛中胜出”，2B =“乙在第二轮比赛中胜出”，则。

一、选择题1．某次战役中，狙击手A 受命射击敌机，若要击落敌机，需命中机首2次或命中机中3次或命中机尾1次，已知A 每次射击，命中机首、机中、机尾的概率分别为0.2、0.4、0.1，未命中敌机的概率为0.3，且各次射击相互独立．若A 至多射击两次，则他能击落敌机的概率为（ ） A ．0.23B ．0.2C ．0.16D ．0.12．法国的数学家费马（PierredeFermat ）曾在一本数学书的空白处写下一个看起来很简单的猜想：当整数2n >时，找不到满足n n n x y z +=的正整数解．该定理史称费马最后定理，也被称为费马大定理．现任取{},,,1,2,3,4,5x y z n ∈，则等式n n n x y z +=成立的概率为（ ） A ．112B ．12625C ．14625D ．76253．甲､乙､丙､丁四位同学站成一排照相,则甲.乙两人中至少有一人站在两端的概率为（ ） A ．56B ．12C ．13 D ．234．教室有4扇编号分别为a b c d ,,,的窗户和2扇编号分别为,x y 的门，窗户d 敞开，其余窗户和门均被关闭.为保持教室空气流通，班长在这些关闭的门和窗户中随机地敞开2扇，则至少有1扇门被敞开的概率为（ ）A ．23 B ．49C ．710D ．7125．设A ，B ，C 是三个事件，给出下列四个事件： （Ⅰ）A ，B ，C 中至少有一个发生； （Ⅱ）A ，B ，C 中最多有一个发生； （Ⅲ）A ，B ，C 中至少有两个发生； （Ⅳ）A ，B ，C 最多有两个发生； 其中相互为对立事件的是（ ）A ．Ⅰ和ⅡB ．Ⅱ和ⅢC ．Ⅲ和ⅣD ．Ⅳ和Ⅰ6．袋中装有白球3个，黑球4个，从中任取3个，下列各对事件中互为对立事件的是（ ）A ．恰有1个白球和全是白球B ．至少有1个白球和全是黑球C ．至少有1个白球和至少有2个白球D ．至少有1个白球和至少有1个黑球7．将一颗质地均匀的骰子先后抛掷3次，至少出现一次6点向上的概率是（ ） A ．91216B ．31216C ．25216D ．52168．古代“五行”学说认为：“物质分金、木、水、火、土五种属性，金克木，木克土，土克水，水克火，火克金”，从五种不同属性的物质中随机抽取两种，则抽取的两种物质不相克的概率为 A ．310B ．25C ．12D ．359．投掷一枚均匀硬币和一枚均匀骰子各一次，记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A ，B 中至少有一件发生的概率是( )A ．512B ．12C ．712D ．3410．下列说法正确的是（ ）A ．天气预报说明天下雨的概率为0900，则明天一定会下雨B ．不可能事件不是确定事件C ．统计中用相关系数r 来衡量两个变量的线性关系的强弱，若[]0.75,1,r ∈则两个变量正相关很强D ．某种彩票的中奖率是11000，则买1000张这种彩票一定能中奖 11．齐王有上等、中等、下等马各一匹，田忌也有上等、中等、下等马各一匹．田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马．现在从双方的马匹中随机各选一匹进行一场比赛，若有优势的马一定获胜，则齐王的马获胜得概率为（ ） A ．49B ．59C ．23D ．7912．一个三位数的百位，十位，个位上的数字依次是,,a b c ，当且仅当a b c b >>且时称为“凹数”，若{},,1234a b c ∈，，，，从这些三位数中任取一个，则它为“凹数”的概率是 A ．13B ．532C ．732D ．71213．在3张卡片上分别写上3位同学的学号后，再把卡片随机分给这3位同学，每人1张，则恰有1位学生分到写有自己学号卡片的概率为（ ） A ．16B ．13C ．12D ．23二、解答题14．进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会､经济､生态等多方面的效益，是关乎生态文明建设全局的大事.为了普及垃圾分类知识，某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为p ，乙同学答对每题的概率都为()q p q >，且在考试中每人各题答题结果互不影响.已知每题甲，乙同时答对的概率为12，恰有一人答对的概率为512. （1）求p 和q 的值；（2）试求两人共答对3道题的概率.15．随着我国中医学的发展，药用昆虫的使用越来越多，每年春暖以后至寒冬前，昆虫大量活动与繁殖，易于采集各种药用昆虫，已知某种药用昆虫的产卵数y （单位：个）与一定范围内的温度x （单位：°C ）有关，于是科研人员在3月份的31天中随机挑选了5天进行研究，收集了该种药用昆虫的5组观测数据如下表： 日期 2日 7日 15日 22日 30日 温度x 10 11 13 12 8 产卵数y2325302616m ，n ，求事件“m ，n 均不小于26”的概率；（2）科研人员确定的研究方案是：先从这5组数据中任选2组，用剩下的3组数据建立y 关于x 的线性回归方程，再对被选取的2组数据进行检验；①若选取的是3月2日和30日这两组数据，请根据7日、15日、22日这3组数据求出y 关于x 的线性回归方程；②若由线性回归方程得到的估计产卵数与所选出的检验数据的误差不超过2个，则认为得到的线性回归方程是可靠的．按照此标准①中得到的线性回归方程是否可靠？说明理由．参考公式：最小二乘法求线性回归方程系数公式：()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-． 16．某校从高一年级的一次月考成绩中随机抽取了50名学生的成绩，这50名学生的成绩都在[50，100]内，按成绩分为[50，60)，[60，70)，[70，80)，[80，90)，[90，100]五组，得到如图所示的频率分布直方图.（1）求图中的a 值；（2）根据频率分布直方图估计该校高一年级本次考试成绩的中位数；（3）用分层抽样的方法从成绩在[80，100]内的学生中抽取6人，再从这6人中随机抽取2名学生进行调查，求月考成绩在[90，100]内至少有1名学生被抽到的概率.17．“每天锻炼一小时，健康工作五十年，幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关，从单位随机抽取30名员工进行了同卷调查，得到了如下列联表：（1）请将上面的列联表补充完整（在答题卡上直接填写结果，不需要写求解过程）； （2）能否有95%的把握认为爱好运动与性别有关？（3）若在接受调查的所有男生中按照“爱好与不爱好运动”进行分层抽样，现随机抽取8人，再从8人中抽取3人，求至少有2人“爱好运动”的概率.附：()()()()()22n ad bc K a b c d a c b d -=++++18．某县为了帮助农户脱贫致富，鼓励农户利用荒地山坡种植果树，某农户考察了三种不同的果树苗A 、B 、C ．经过引种实验发现，引种树苗A 的自然成活率为0.7，引种树苗B 、C 的自然成活率均为()0.60.8p p ≤≤．（1）任取树苗A 、B 、C 各一棵，估计自然成活的棵数为X ，求X 的分布列及其数学期望；（2）将（1）中的数学期望取得最大值时p 的值作为B 种树苗自然成活的概率．该农户决定引种n 棵B 种树苗，引种后没有自然成活的树苗有75%的树苗可经过人工栽培技术处理，处理后成活的概率为0.8，其余的树苗不能成活． ①求一棵B 种树苗最终成活的概率；②若每棵树苗引种最终成活可获利400元，不成活的每棵亏损80元，该农户为了获利期望不低于10万元，问至少要引种B 种树苗多少棵？19．某中学高一年级举行了一次数学竞赛，从中随机抽取了一批学生的成绩，经统计，这批学生的成绩全部介于50至100之间，将数据按照[)50,60，[)60,70，[)70,80，[)80,90，[]90,100的分组作出频率分布直方图如图所示.（1）求频率分布直方图中a 的值，并估计本次竞赛成绩的第80百分位数；（2）若按照分层随机抽样从成绩在[)80,90，(]90,100的两组中抽取6人，再从这6人中随机抽取2人，求至少有1人的成绩在[]90,100内的概率.20．某组织在某市征集志愿者参加志愿活动，现随机抽出60名男生和40名女生共100人进行调查，统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况，具体数据如图所示.(1)完成下列22⨯列联表，并判断是否有99%的把握认为愿意参与志愿活动与性别有关？愿意 不愿意 总计男生 女生 总计(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者，再从中抽取2人作为队长，求抽取的2人至少有一名女生的概率. 参考数据及公式：()20P K k ≥ 0.1 0.05 0.025 0.010k2.7063.8415.0246.635()()()()()()22n ad bc K n a b c d a b c d a c b d -==+++++++.21．有n 名学生，在一次数学测试后，老师将他们的分数（得分取正整数，满分为100分），按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图（如图1），并作出样本分数的茎叶图（如图2）（图中仅列出了得分在[60，70），[90，100]的数据）．（1）求样本容量n 和频率分布直方图中x 、y 的值；（2）从成绩在80分以上（含80分）的学生中随机抽取2名学生参加校数学竞赛，求所抽取的2名学生中至少有一人得分在[90，100]内的概率；（3）分数在[80，100]的学生中，男生有2人，现从该组抽取三人“座谈”，求至少有两名女生的概率．22．北京市政府为做好APEC 会议接待服务工作，对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测，只有两轮都合格才能进行销售，否则不能销售.已知该海产品第一轮检测不合格的概率为16，第二轮检测不合格的概率为110，两轮检测是否合格相互没有影响.（1）求该海产品不能销售的概率.（2）如果该海产品可以销售，则每件产品可获利40元；如果该海产品不能销售，则每件产品亏损80元（即获利-80元）.已知一箱中有该海产品4件，记一箱该海产品获利X 元，求X 的分布列，并求出数学期望()E X .23．从4名男生和2名女生中任选2人参加抗疫志愿服务活动.（1）设X 表示所选2人中男生的人数，求X 的分布列和数学期望E （X ）；（2）已知选出了A ，B 这两人参加此次服务活动，A 的服务满意率为0.87，B 的服务满意率为0.91，用“Y A ＝1，Y B ＝1，”分别表示对A ，B 的服务满意，“Y A ＝0，Y B ＝0，”分别表示对A ，B 的服务不满意，写出方差D （Y A ），D （Y B ）的大小关系.（只需写出结论） 24．某种产品的广告费支出x 与销售额y （单位：万元）之间有如下对应数据：x2 4 5 6 8（1）若广告费与销售额具有相关关系，求回归直线方程；（2）在已有的五组数据中任意抽取两组，求两组数据其预测值与实际值之差的绝对值都不超过5的概率.参考公式：1221ni ii nii x y nx yb xnx ==-⋅=-∑∑，a y bx =-.25．2020年是全面建成小康社会目标实现之年，也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户，结合当地实际情况采取多项精准扶贫措施，每年新脱贫户数如下表（1）根据2015-2019年的数据，求出y 关于x 的线性回归方程y bx a =+，并预测到2020年底该乡镇500户贫困户是否能全部脱贫；（2）2019年的新脱贫户中有20户五保户，20户低保户，60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访，了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫，随机抽取这5户中的2户进行每月跟踪帮扶，求抽取的2户中至少有1户是扶贫户的概率. 参考数据：5115526838049251001299i ii x y==⨯+⨯+⨯+⨯+⨯=∑参考公式：()()()1122211nni iiii i nniii i x ynx y xxy y b xnxxx====---==--∑∑∑∑，a y bx =-26．某中学高二年级从甲、乙两个班中各选出7名学生参加数学竞赛，他们取得成绩的茎叶图如下，其中甲班学生的平均分是85分，乙班学生成绩的中位数是83.（1）求,x y 的值；（2）在成绩高于90分的学生中任选两人，求这两人来自不同班级的概率.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】A 每次射击，命中机首、机中、机尾的概率分别为0.20.40.1、、,未命中敌机的概率为0.3,且各次射击相互独立，若A 射击一次就击落敌机，则他击中利敌机的机尾，故概率为0.1；若A 射击2次就击落敌机，则他2次都击中利敌机的机首，概率为0.20.20.04⨯=；或者A 第一次没有击中机尾、且第二次击中了机尾，概率为 0.90.1? 0.09⨯=,若A 至多射击两次，则他能击落敌机的概率为0.1? 0.04? 0.09? 0.23++= ,故选A . 2．B解析：B 【分析】根据分步计数原理，得到基本事件总数，再利用列举法，求得所求事件所包含的基本事件的个数，利用古典概型的概率计算公式，即可求解. 【详解】由任取{},,,1,2,3,4,5x y z n ∈，使得n n n x y z +=，共有5555625⨯⨯⨯=种不同的情形，当1n =时，可得x y z +=， 可得112,123,134,145,213,224,235,314,325,415+=+=+=+=+=+=+=+=+=+=，共有10种情况，满足题意；当2n =时，可得222x y z +=，可得222222345,435+=+=，共有2种情况，满足题意； 当3,4,5n =时，没有满足n n n x y z +=成立的情况，所以等式n n n x y z +=成立的概率为12625P =. 故选：B. 【点睛】本题主要考查了古典概型的概率的计算，其中解答中求得基本事件的总数，利用列举法求得所求事件所包含的基本事件的个数是解答的关键，着重考查推理与运算能力.3．A解析：A 【分析】本题先求基本事件总数，再求要求事件是基本事件个数，最后根据古典概型解题即可. 【详解】∵甲､乙､丙､丁四位同学站成一排照相，基本事件总数4424n A ==，甲､乙两人中至少有一人站在两端包含的基本事件个数42242220m A A A =-= ∴甲,乙两人中至少有一人站在两端的概率为：205246m P n ===.. 故选：A. 【点睛】本题考查古典概型，是简单题.4．C解析：C 【解析】 【分析】列出样本空间Ω,以及事件A =“至少有1扇门被敞开”包含的基本事件，计算概率. 【详解】 样本空间()()()()()()()()()(){},,,,,,,,,,,,,,,,,,,a b a c a x a y b c b x b y c x c y x y Ω=.记事件A =“至少有1扇门被敞开”，则()()()()()()(){},,,,,,,,,,,,,A a x a y b x b y c x c y x y =，所以()710P A =，故选C . 【点睛】本题考查了古典概型，考查了学生实际应用以及数学运算的能力，属于基础题.5．B解析：B 【分析】利用互斥事件、对立事件的定义直接求解． 【详解】解：A ，B ，C 是三个事件，给出下列四个事件： （Ⅰ）A ，B ，C 中至少有一个发生；（Ⅱ）A，B，C中最多有一个发生；（Ⅲ）A，B，C中至少有两个发生（Ⅳ）A，B，C最多有两个发生；在A中，Ⅰ和Ⅱ能同时发生，不是互斥事件，故A中的两个事件不能相互为对立事件；在B中，Ⅱ和Ⅲ既不能同时发生，也不能同时不发生，故B中的两个事件相互为对立事件；在C中，Ⅲ和Ⅳ能同时发生，不是互斥事件，故C中的两个事件不能相互为对立事件；在D中，Ⅳ和Ⅰ能同时发生，不是互斥事件，故D中的两个事件不能相互为对立事件．故选：B．【点睛】本题考查相互为对立事件的判断，考查互斥事件、对立事件的定义等基础知识，考查运算求解能力，属于基础题．6．B解析：B【分析】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，进而可分析四个事件的关系；【详解】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，故①恰有1个白球和全是白球，是互斥事件，但不是对立事件，②至少有1个白球和全是黑球是对立事件；③至少有1个白球和至少有2个白球不是互斥事件，④至少有1个白球和至少有1个黑球不是互斥事件，故选B．【点睛】本题考查互斥事件和对立事件的关系，对于题目中出现的两个事件，观察两个事件之间的关系，这是解决概率问题一定要分析的问题，本题是一个基础题．7．A解析：A【解析】【分析】事件“至少出现一次6点向上”的对立事件是“出现零次6点向上”，由此借助对立事件的概率进行求解．【详解】由题事件“至少出现一次6点向上”的对立事件是“出现零次6点向上”所以至少出现一次6点向上的概率0331112591 11166216216 p C⎛⎫⎛⎫=--=-=⎪ ⎪⎝⎭⎝⎭故选A. 【点睛】本题考查应用对立事件求概率，属于一般题．8．C解析：C 【解析】 【分析】从五种物质中随机抽取两种，所有抽法共有10种，而相克的有5种情况，得到抽取的两种物质相克的概率是12，进而得到抽取两种物质不相克的概率，即可得到答案. 【详解】从五种物质中随机抽取两种，所有抽法共有2510C =种，而相克的有5种情况，则抽取的两种物质相克的概率是51102=，故抽取两种物质不相克的概率是11122-=， 故选C. 【点睛】本题主要考查了古典概型及其概率的计算公式的应用，以及相互对立事件的应用，其中解答正确理解题意，合理利用对立事件的概率求解是解答的关键，着重考查了运算与求解能力，属于基础题.9．C解析：C 【解析】试题分析：由题意可知，事件A 与事件B 是相互独立的，而事件A 、B 中至少有一件发生的事件包含AB 、AB 、AB ，又()12P A =，()16P B =，所以所事件的概率为()()()()11711112612P P AB P AB P AB P AB ⎛⎫⎛⎫=++=-=--⨯-= ⎪ ⎪⎝⎭⎝⎭，故选C ．考点：相互独立事件概率的计算．10．C解析：C 【分析】运用概率的相关知识对四个选项逐一进行分析即可 【详解】对于A ，天气预报说明天下雨的概率为90%，表示下雨的可能性比较大，是不确定事件，在一定条件下可能下雨，也可能不下雨，但明天一定会下雨是不正确的，故错误； 对于B ，根据定义可知不可能事件是确定事件，故错误；对于C ，统计中用相关系数r 来衡量两个变量的线性关系的强弱，若[]0.75,1,r ∈则两个变量正相关很强，故正确；对于D ，某种彩票的中奖率是11000，每一次买彩票的中奖是独立的，并不是买1000张这种彩票一定能中奖，故错误 故选C 【点睛】本题主要考查了辨别生活中的概率，理解并运用概率知识即可判断，较为基础．11．C解析：C 【分析】现从双方的马匹中随机各选一匹进行一场比赛 ,利用列举法求出基本事件有9种，齐王的马获胜包含的基本事件有6种，利用古典概型概率公式可求出齐王的马获胜的概率. 【详解】设齐王上等、中等、下等马分別为,,A B C ，田忌上等、中等、下等马分别为,,a b c ， 现从双方的马匹中随机各选一匹进行一场比赛,基本事件有：()()()()()()()()(),,,,,,,,,,,,,,,,,A a A b A c B a B b B c C a C b C c ，共9种，有优势的马一定获胜，齐王的马获胜包含的基本事件有：()()()()()(),,,,,,,,,,,A a A b A c B b B c C c ，共 6种,∴齐王的马获胜的概率为6293P ==，故选C. 【点睛】本题主要考查古典概型概率公式的应用，属于中档题，利用古典概型概率公式求概率时，找准基本事件个数是解题的关键，基本亊件的探求方法有 (1)枚举法：适合给定的基本事件个数较少且易一一列举出的；(2)树状图法：适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时，一定要按顺序逐个写出：先11(,)A B ，12(,)A B …. 1(,)n A B ，再21(,)A B ，22(,)A B …..2(,)n A B 依次31(,)A B 32(,)A B ….3(,)n A B … 这样才能避免多写、漏写现象的发生.12．C解析：C 【解析】 【分析】先分类讨论求出所有的三位数，再求其中的凹数的个数，最后利用古典概型的概率公式求解. 【详解】先求所有的三位数，个位有4种排法，十位有4种排法，百位有4种排法，所以共有44464⨯⨯=个三位数.再求其中的凹数，第一类：凹数中有三个不同的数，把最小的放在中间，共有3428C ⨯=种，第二类，凹数中有两个不同的数，将小的放在中间即可，共有2416C ⨯=种方法，所以共有凹数8+6=14个， 由古典概型的概率公式得P=1476432=. 故答案为：C 【点睛】本题主要考查排列组合的运用，考查古典概型的概率，意在考查学生对这些知识的掌握水平和分析推理能力.13．C解析：C 【分析】由题意列出所有可能的结果，然后利用古典概型计算公式即可求得满足题意的概率值. 【详解】设三位同学分别为,,A B C ，他们的学号分别为1,2,3，用有序实数列表示三人拿到的卡片种类，如()1,3,2表示A 同学拿到1号，B 同学拿到3号，C 同学拿到2号.三人可能拿到的卡片结果为：()()()()()()1,2,3,1,3,2,2,1,3,2,3,1,3,1,2,3,2,1，共6种，其中满足题意的结果有()()()1,3,2,2,1,3,3,2,1，共3种， 结合古典概型计算公式可得满足题意的概率值为：3162p ==. 故选：C. 【点睛】 方法点睛：有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数． (1)基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏． (2)注意区分排列与组合，以及计数原理的正确使用.二、解答题14．（1）34p =，23q =；（2）512.【分析】（1）由互斥事件和对立事件的概率公式列方程组可解得,p q ；（2）分别求出两人答对1道的概率，答对两道题的概率，两人共答对3道题，则是一人答对2道题另一人答对1道题，由互斥事件和独立事件概率公式可得结论． 【详解】解：（1）设A ={甲同学答对第一题}，B ={乙同学答对第一题}，则()P A p =，()P B q =.设C ={甲、乙二人均答对第一题}，D {甲、乙二人中恰有一人答对第一题}，则C AB =，D AB AB =+.由于二人答题互不影响，且每人各题答题结果互不影响，所以A 与B 相互独立，AB 与AB 相互互斥，所以()()()()P C P AB P A P B ==，()()P D P AB AB =+()()()()()()()()()()()()11P AB P AB P A P B P A P B P A P B P A P B =+=+=-+-.由题意可得()()1,2511,12pq p q q p ⎧=⎪⎪⎨⎪-+-=⎪⎩即1,217.12pq p q ⎧=⎪⎪⎨⎪+=⎪⎩解得3,42,3p q ⎧=⎪⎪⎨⎪=⎪⎩或2,33.4p q ⎧=⎪⎪⎨⎪=⎪⎩由于p q >，所以34p =，23q =.（2）设=i A {甲同学答对了i 道题}，i B ={乙同学答对了i 道题}，0i =，1，2. 由题意得，()11331344448P A =⨯+⨯=，()23394416P A =⨯=， ()12112433339P B =⨯+⨯=，()2224339P B =⨯=.设E ={甲乙二人共答对3道题}，则1221E A B A B =+. 由于i A 和i B 相互独立，12A B 与21A B 相互互斥，所以()()()()()()()12211221349458916912P E P A B P A B P A P B P A P B =+=+=⨯+⨯=. 所以，甲乙二人共答对3道题的概率为512. 【点睛】关键点点睛：本题考查互斥事件与独立事件的概率公式，解题关键是把所求概率事件用互斥事件表示，然后求概率，如设A ={甲同学答对第一题}，B ={乙同学答对第一题}，设C ={甲、乙二人均答对第一题}，D {甲、乙二人中恰有一人答对第一题}，则C AB =，D AB AB =+．同样两人共答对3题分拆成甲答对2题乙答对1题与甲答对1题乙答对2题两个互斥事件．15．（1）110；（2）①532y x ∧=-；②可靠，理由见解析.【分析】（1）根据题意写出所有的基本事件，即可求解：“不小于26”的概率； （2）①由题意求出x ，y ，代入公式求值，从而得到回归直线方程；②分别将x 的值代入，检验数据的误差均是否不超过2个，即可判断． 【详解】（1）依题意得，m 、n 的所有情况有：{}23,25、{}23,30、{}23,26、{}23,16、{}25,30、{}25,26、{}25,16、{}30,26、{}30,16、{}26,16共有10个；则“m 、n 均不小于26”的事件只有{}30,26，所以110P =，即事件“m 、n 均不小于26”的概率为110； （2）①由数据得111312123x ++==，253026273y ++==， ()322221(1112)(1312)(1212)2i i x x =-=-+-+-=∑，()()31(1112)(2527)(1312)(3027)05iii x x y y =--=--+--+=∑，()()()31321522iii ii x x y y b x x ∧==--==-=∑∑，552712322a y x ∧=-=-⨯=-.所以y 关于x 的线性回归方程为532y x ∧=-.②可靠；由①知，y 关于x 的线性回归方程为532y x ∧=-.对于2日数据，将10x =代入线性回归方程得5103222y ∧=⨯-=，其误差为|2223|12-=<，对于30日数据，将8x =代入线性回归方程得583172y ∧=⨯-=，其误差为|1716|12-=<，所以，所得到的线性回归方程是可靠的. 【点睛】方法点睛：本题考查了线性回归方程的求法及应用，求线性回归方程的步骤： （1）首先求出x 的平均数x 和y 的平均数y（2）代入公式求回归方程的斜率()()()121ˆniii nii x x y y bx x ==--=-∑∑（3）代入公式求出回归方程的截距ˆˆay bx =-，考查学生的计算能力，属于基础题.16．（1）0.016；（2）约为74.1；（3）35． 【分析】（1）由频率分布直方图中所有频率和为1可求得a ；（2）频率分布直方图中将所有小矩形面积二等分的点对应的值为中位数；（3）根据频率分布直方图求出成绩在[80,90)和[90,100]上的人数，然后利用对立事件的概率公式计算． 【详解】（1）由题意(0.0080.0240.0440.008)101a ++++⨯=，解得0.016a =； （2）在频率分布直方图中前两组频率和为(0.0080.024)100.32+⨯=， 第三组频率为0.044100.44⨯=，中位数在第三组，设中位数为x ，则70100.50.320.44x -=-，解得74.1x ≈；（3）由频率分布直方图成绩在[80,90)和[90,100]和频率分别是0.16和0.08，共抽取6人，∴成绩在[80,90)上的有4人，成绩在[90,100]上的有2人，从6人中任意抽取2人共有2615C =种方法，2人成绩都在[80,90)上的方法有246C =种，∴月考成绩在[90，100]内至少有1名学生被抽到的概率为631155P =-=． 【点睛】本题考查频率分布直方图，考查由频率分布直方图计算中位数，考查分层抽样与古典概型，，考查了学生的数据处理能力与运算求解能力，属于中档题． 17．（1）填表见解析；（2）没有；（3）57. 【分析】（1）根据题目所给的数据填写22⨯列联表即可；（2）利用公式计算K 的观测值2K ，对照题目表格中的数据，得出统计结论． （3）利用分层抽样可得抽取的8人中有5人爱好运动，3人不爱好运动，结合组合的应用，由古典概型概率公式计算概率即可； 【详解】 （1）列联表：由列联表的数据得k 的观测值（2）()()()()()()2223010866 1.158 3.84116141416n ad bc K a b a c a c b d -⨯⨯-⨯==≈<++++⨯⨯⨯∴没有95%的把握认为爱好运动与性别有关. （3）抽取的8人中有5人爱好运动，3人不爱好运动 设“从8人中抽取3人，至少有2人爱好运动”为事件A ，则()2135353857C C C P A C +==. 【点睛】本题主要考查列联表、古典概型概率公式以及独立性检验，属于中档题.独立性检验的一般步骤：（1）根据样本数据制成22⨯列联表；（2）根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值；(3) 查表比较2K 与临界值的大小关系，作统计判断.18．（1）分布列见解析，()20.7E X p =+；（2）①0.92；②277棵. 【分析】（1）根据题意得出随机变量X 的可能取值有0、1、2、3，计算出随机变量X 在不同取值下的概率，可得出随机变量X 的分布列，进而可求得随机变量X 的数学期望； （2）①由（1）知当0.8p =时，()E X 最大，然后分一棵B 种树苗自然成活和非自然成活两种情况，可求得所求事件的概率；②记Y 为n 棵树苗的成活棵数，由题意可知(),0.92Y B n ~，利用二项分布的期望公式得出()0.92E Y n =，根据题意得出关于n 的不等式，解出n 的取值范围即可得解. 【详解】（1）依题意，X 的所有可能值为0、1、2、3， 则()()2200.310.30.60.3P X p p p ==-=-+，()()()2210.710.3210.10.80.7P X p p p p p ==-+⨯-=-+，()()22220.710.3 1.1 1.4P X p p p p p ==⨯-+=-+， ()230.7P X p ==.所以，随机变量X 的分布列为：22210.10.80.72 1.1 1.430.720.7E X p p p p p p ∴=⨯-++⨯-++⨯=+；（2）由（1）知当0.8p =时，()E X 取得最大值．①一棵B 种树苗最终成活的概率为：()0.810.80.750.80.92+-⨯⨯=， ②记Y 为n 棵树苗的成活棵数，则(),0.92Y B n ~，()0.92E Y n =，()0.924000.0880100000n ∴⨯-⨯≥，100000276.55361.6n ≈≥． 所以该农户至少要种植277棵树苗，才可获利不低于10万元．【点睛】本题通过“果树种植”的例子，第（1）问考查了随机变量及其分布列，数学期望等基础知识点，第（2）问考查了考生数学建模的能力，即把实际问题转化为数学问题，再运算求解的能力，对于考生的综合分析能力提出较高要求，属中等题． 19．（1）0.020a =；85；（2）35. 【分析】（1）根据小矩形的面积代表概率，所以所有小矩形面积之和等于1 ，即可得a 的值， 成绩在以下的频率为0.7，成绩在90分以下的频率为0.9，第80百分位数()80,90p ∈，0.80.78010850.2p -=+⨯=. （2）先利用频率之比求出[)80,90，(]90,100的两组中应抽的人数，然后列出从这6人中随机抽取2人包括的基本事件，至少有1人的成绩在[]90,100内包括的基本事件，利用概率公式即可求概率. 【详解】（1）由题意可知，()100.0050.0300.0350.0101a ++++= 解得0.020a =.∵100.0050.05⨯=，100.0300.3⨯=，100.0350.35⨯=，100.020.2⨯=，100.010.1⨯=∴成绩在80分以下的频率为0.050.30.350.70.8++=<， 成绩在90分以下的频率为0.050.30.350.20.90.8+++=>， ∴第80百分位数()80,90p ∈，.0.80.78010850.2p -=+⨯=. （2）∵[)80,90，[]90,100的频率之比为0.2:0.12:1= ∴从[)80,90中随机抽取2643⨯=人.从[]90,100中随机抽取1623⨯=人. 从[)80,90中随机抽取的4人记为1，2，3，4，从[]90,100中随凯抽取的2人记为a ，b ，。

《第3章概率》试卷(答案在后面)一、单选题（本大题有8小题，每小题5分，共40分）1、（从以下选项中选择一个正确的答案）袋中有红球若干个，白球6个，现从袋中任意取出2个球，取出的两球颜色相同的概率是：A. 1/7B. 2/7C. 3/7D. 4/72、若袋中有5个红球和7个蓝球，从中随机取出一个球，则取出红球的概率是：A. 5/12B. 7/12C. 12/22D. 22/123、某袋子里有5个红球和3个蓝球，随机从中摸出2个球，其中一个是红色球的概率是（）A. 1/2B. 3/5C. 1/3D. 2/54、袋子里装有5个红球和3个蓝球，每次随机从袋子里抽取一个球，然后放回。

求连续抽两次都抽取到红球的概率。

A.58B.2564C.1532D.5165、某班有40名学生，其中男生25名，女生15名。

现从中随机抽取3名学生，则抽取的3名学生都是女生的概率是（ ）A. 1/56B. 1/24C. 1/120D. 1/406、将三颗骰子各抛掷一次，记事件A 为“三个骰子中至少有一个骰子的点数为6”，则事件A 的概率为（ ）。

A.(563)B.(1−563)C.(163)D.(1−163)7、若一个袋子里有3个红球、2个蓝球和1个白球，从中随机抽取一个球，则抽取到白球的概率是（ ）。

A.16B.14C.12D.258、一个袋子里装有5个红球、3个蓝球和2个白球，从中随机取出一个球，取出红球的概率是多少？A. 1/2B. 2/3C. 1/4D. 3/10二、多选题（本大题有3小题，每小题6分，共18分）1、某班级有男生15人，女生10人，现随机选一名学生，则选中女生的概率是（）。

A. 1/3B. 2/5C. 1/2D. 3/52、在一个装有5个红球、4个蓝球和3个绿球的袋子里，随机取出3个球。

以下说法中正确的是（）。

A. 取出的3个球都是红色的概率是1/90B. 取出的3个球颜色不全相同的概率是3/10C. 取出的3个球中至少有2个球是绿色的概率是1/15D. 取出的3个球相邻且颜色各不相同的概率是3/143、设随机变量X的概率分布如下表所示，则下列选项正确的是：X123P0.20.50.3A.(E(X)=2.2)B.(D(X)=0.76)C.(P(X≤2)=0.7)D.(P(X>2)=0.3)三、填空题（本大题有3小题，每小题5分，共15分）1、若袋中有5个红球和3个蓝球，每次从袋中随机取出一个球，连续取两次，则取出两个红球的概率是_______ 。

高一数学必修第二册第十章《概率》单元练习题卷2（共22题）一、选择题（共10题）1.某校为了增强学生的记忆力和辨识力，组织了一场类似《最强大脑》的PK赛，A，B两队各由4名选手组成，每局两队各派一名选手PK，比赛四局．除第三局胜者得2分外，其余各局胜者均得1分，每局的负者得0分．假设每局比赛A队选手获胜的概率均为23，且各局比赛结果相互独立，比赛结束时A队的得分高于B队的得分的概率为( )A．1627B．5281C．2027D．792.从4名男生2名女生中任选3人参加演讲比赛，则所选3人中恰有1名女生的概率为( )A．15B．12C．35D．453.正方体ABCD−A1B1C1D1中，直线AD与平面A1BC1所成角的正弦值为( )A．12B．√32C．√33D．√634.甲、乙两名同学参加一项射击游戏，游戏规定每击中一次目标得2分，未击中目标得0分．若甲、乙两人射击的命中率分别为35和p，且甲、乙两人各射击一次得分之和为2的概率为920．假设甲、乙两人射击互不影响，则p的值为( )A．35B．45C．34D．145.已知集合A={x∣ x2−2x−3≥0}，B={x∣ −2≤x<2}，则A∩B=( )A．[−2,−1]B．[−1,1]C．[−1,2)D．[1,2)6.从2名男同学和3名女同学中任选2人参加社区服务，则选中的2人都是女同学的概率为( )A．0.6B．0.5C．0.4D．0.3董仲舒扩充为“仁、义、礼、智、信”．若将“仁、义、礼、智、信”排成一排，则“仁”排在第一位，且“智、信”相邻的概率为( )A．110B．15C．310D．258.从分别写有1，2，3，4，5的5张卡片中随机抽取1张，放回后再随机抽取1张，观察抽得的2张数字，设抽得的第1张卡片上的数大于第2张卡片上的数为事件Q，则事件Q含有的样本点个数为( )A．8B．10C．11D．159.从一堆产品（其中正品与次品都多于2件）中任取2件，下列事件是互斥事件但不是对立事件的是( )A．恰好有1件次品和恰好有2件次品B．至少有1件次品和全是次品C．至少有1件正品和至少有1件次品D．至少有1件次品和全是正品10.某公交线路某区间内共设四个站点（如图），分别记为A0，A1，A2，A3，现有甲、乙两人同时从A0站点上车，且他们中的每个人在站点A i(i=1,2,3)下车是等可能的，则甲、乙两人不在同一站点下车的概率为( )A．23B．34C．35D．12二、填空题（共6题）11.甲、乙、丙三人独立解答一道数学竞赛试题，甲解出它的概率为0.9，乙解出它的概率为0.8，丙解出它的概率为0.85．只有甲解出的概率为．12.若一个布袋中有大小、质地相同的三个黑球和两个白球，从中任取两个球，则取出的两球中恰是一个白球和一个黑球的概率是．13.甲、乙两人进行投篮比赛，设两人每次投篮是否命中相互之间不受影响，己知甲、乙两人每次投篮命中的概率分别是0.7，0.6．若甲、乙各投篮一次，则甲命中且乙未命中的概率为；若甲、乙各投篮两次，则甲比乙多命中一次的概率是．14.有一批书共100本，其中文科书40本，理科书60本，按装潢可分精装、平装两种，精装书70本，某人从这100本书中任取一书，恰是文科书，放回后再任取1本，恰是精装书，这一事件的概率是 ．15. 如图，三行三列的方阵有 9 个数 a ij (i =1,2,3;j =1,2,3)，从中任取三个数，则至少有两个数位于同行或同列的概率是 ． (a 11a 12a 13a 21a 22a 23a 31a 32a 33)16. 在三角形的每条边上各取三个分点（如图），以这 9 个分点为顶点可画出若干个三角形，若从中任意抽取一个三角形，则其三个顶点分别落在原三角形的三条不同边上的概率为 ．（用数字作答）三、解答题（共6题）17. 青岛二中有羽毛球社、乒乓球社和篮球社，三个社团的人数分别为 27，9，18，现采用分层抽样的方法从这三个社团中抽取 6 人参加活动． (1) 求应从这三个社团中分别抽取的学生人数．(2) 将抽取的 6 名学生进行编号，编号分别为 A 1，A 2，A 3，A 4，A 5，A 6，从这 6 名学生中随机抽出 2 名参加体育测试．①用所给的编号列出所有可能的结果．②设事件 A 是“编号为 A 1，A 2 的两名学生至少有一人被抽到”，求事件 A 发生的概率．18. 近年来，郑州经济快速发展，跻身新一线城市行列，备受全国瞩目．无论是市内的井字形快速交通网，还是辐射全国的米字形高速铁路网，郑州的交通优势在同级别的城市内无出其右．为了调查郑州市民对出行的满意程度，研究人员随机抽取了 1000 名市民进行调查，并将其满意程度（单位：分）统计成如图所示的频率分布直方图，其中 a =4b ．(1) 求a，b的值；(2) 求被调查的市民的满意程度的平均数、众数、中位数（同一组中的数据用该组区间的中点值作代表）；(3) 若按照分层随机抽样的方式从满意程度在[50,60)，[60,70)的市民中随机抽取8人，再从这8人中随机抽取2人，求至少有1人的满意程度在[50,60)的概率．19.某大学就业部从该大学2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查，其中有一项是他们的月薪情况，经调查统计发现，他们的月薪分布在3000元到10000元之间，根据统计数据得到如图所示的频率分布直方图：若月薪落在区间(x−2s,x+2s)的左侧，则认为该学生属于“就业不理想”的学生，学校将联系本人，咨询其月薪过低的原因，从而为本科毕业生就业提供更好的指导意见，其中x，s分别为样本平均数和样本标准差，计算可得s≈1500元（同一组中的数据用该组区间的中点值代表）．(1) 现该校：2018年大学本科毕业生张茗的月薪为3600元，试判断张茗是不是“就业不理想”的学生；(2) 为感谢同学们对这项调查工作的支持，该校利用分层随机抽样的方法从样本的前3组中抽出6人，各赠送一份礼品，并从这6人中再抽取2人，各赠送某款智能手机1部，求获赠智能手机的2人中恰有1人月薪不超过5000元的概率；(3) 位于某省的一高校2018年某专业的本科毕业生共200人，现他们决定于2021年元旦期间举办一次同学联谊会，并收取一定的活动费用．假定这200人与所抽取的样本的月薪分布情况相同，并用样本频率估计总体频率，现有两种收费方案：方案一：按每人一个月薪水的10%收取；方案二：月薪高于样本平均数的每人收取800元，月薪不低于4000元但低于样本平均数的每人收取400元，月薪低于4000元的不收取任何费用．问：哪一种收费方案最终收取的活动总费用较少？20.从含有两件正品a1，a2和一件次品b1的3件产品中每次任取1件，连续取两次．(1) 若每次取出后不放回，连续取两次，求取出的产品中恰有一件是次品的概率；(2) 若每次取出后又放回，求取出的两件产品中恰有一件是次品的概率．21.现有8名马拉松比赛志愿者（他们都只通晓一门外语），其中志愿者A1，A2，A3通晓日语，B1，B2，B3通晓俄语，C1，C2通晓英语，从中选出通晓日语、俄语和英语的志愿者各1名，组成一个小组．(1) 列出该试验包含的所有样本点．(2) 求A1被选中的概率．(3) 求B1和C1不全被选中的概率．22.现有8名奥运会志愿者，其中志愿者A1，A2，A3通晓日语，B1，B2，B3通晓俄语，C1，C2通晓韩语，从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组．(1) 求A1被选中的概率；(2) 求B1和C1不全被选中的概率．答案一、选择题（共10题） 1. 【答案】C【解析】比赛结束时 A 队的得分高于 B 队的得分的情况有 3 种；A 全胜，A 三胜一负，A 第三局胜，另外三局两胜一负，所以比赛结束时 A 队的得分高于 B 队的得分的概率为：P =(23)4+C 43(23)3(13)+23C 31(23)(13)2=2027．【知识点】事件的相互独立性2. 【答案】C【解析】列举出所有结果易得 P =35． 【知识点】古典概型3. 【答案】C【解析】如图所示，正方体 ABCD −A 1B 1C 1D 1 中，直线 AD 与 B 1C 1 平行，则直线 AD 与平面 A 1BC 1 所成角的正弦值即为 B 1C 1 与平面 A 1BC 1 所成角的正弦值， 因为 △A 1BC 1 为等边三角形，则 B 1 在平面 A 1BC 1 上的投影即为 △A 1BC 1 的中心 O ， 则 ∠B 1C 1O 为 B 1C 1 与平面 A 1BC 1 所成角， 可设正方体边长为 1，显然 BO =√33×√2=√63， 因此 B 1O =√1−(√63)2=√33， 则 sin∠B 1C 1O =B 1OB 1C 1=√33．【知识点】线面角4. 【答案】C【解析】设“甲射击一次，击中目标”为事件 A ，“乙射击一次，击中目标”为事件 B ，则“甲射击一次，未击中目标”为事件 A ，“乙射击一次，未击中目标”为事件 B ，则 P (A )=35，P(A)=1−35=25，P (B )=p ，P(B)=1−p ，依题意得 35×(1−p )+25×p =920，解得 p =34，故选C ．【知识点】事件的相互独立性5. 【答案】A【解析】 A ={x∣ x 2−2x −3≥0}={x ∣∣ x ≥3 或 x ≤−1}，B ={x∣ −2≤x <2}， 则 A ∩B ={x∣ −2≤x ≤−1}． 【知识点】事件的关系与运算6. 【答案】D【解析】设 2 名男同学分别为 A 1，A 2，3 名女同学分别为 B 1，B 2，B 3，从以上 5 名同学中任选 2 人有 A 1A 2，A 1B 1，A 1B 2，A 1B 3，A 2B 1，A 2B 2，A 2B 3，B 1B 2，B 1B 3，B 2B 3，共 10 种可能，其中选中的 2 人都是女同学的情况有 B 1B 2，B 1B 3，B 2B 3，共 3 种可能，则选中的 2 人都是女同学的概率为 310=0.3． 【知识点】古典概型7. 【答案】A【解析】将“仁、义、礼、智、信”排成一排，无限制条件时有 A 55 种排法，其中“仁”排在第一位，且“智、信”相邻的排法有 A 22A 33种，故所求概率为A 22A 33A 55=110，故选A ．【知识点】古典概型8. 【答案】B【解析】如表所示，表中点的横坐标表示第一次取到的数，纵坐标表示第二次取到的数．123451(1,1)(1,2)(1,3)(1,4)(1,5)2(2,1)(2,2)(2,3)(2,4)(2,5)3(3,1)(3,2)(3,3)(3,4)(3,5)4(4,1)(4,2)(4,3)(4,4)(4,5)5(5,1)(5,2)(5,3)(5,4)(5,5)则 Q ={(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4)}． 所以 Q 中含有 10 个样本点． 【知识点】事件与基本事件空间9. 【答案】A【解析】依据互斥和对立事件的定义知，B ，C 都不是互斥事件；D 不但是互斥事件而且是对立事件；只有A 是互斥事件但不是对立事件． 【知识点】事件的关系与运算10. 【答案】A【解析】设事件A为“甲、乙两人不在同一站点下车”，由题意知甲、乙两人同在A1站点下车的概率为13×13=19；甲、乙两人同在A2站点下车的概率为13×13=19；甲、乙两人同在A3站点下车的概率为13×13=19；所以甲、乙两人在同一站点下车的概率P(A)=3×19=13，则P(A)=1−13=23．【知识点】事件的关系与运算二、填空题（共6题）11. 【答案】0.027【知识点】事件的相互独立性12. 【答案】0.6【知识点】古典概型13. 【答案】0.28；0.3024【知识点】事件的相互独立性14. 【答案】725【解析】设“任取一书是文科书”的事件为A，“任取一书是精装书”的事件为B，则A，B是相互独立的事件，所求概率为P(AB)．据题意可知P(A)=40100=25，P(B)=70100=710，故P(AB)=P(A)⋅P(B)=25×710=725．【知识点】事件的相互独立性15. 【答案】1314【知识点】事件的关系与运算、古典概型16. 【答案】13【知识点】频率与概率三、解答题（共6题）17. 【答案】(1) 羽球出国人数：6×2727+9+18=3；兵乓球社人数：6×927+9+18=1；篮球社人数：6×1827+9+18=2．(2) ① {A1,A2}，{A1,A3}，{A1,A4}，{A1,A5}，{A1,A6}，{A1,A6}，{A2,A3}，{A2,A4}，{A2,A5}，{A2,A6}，{A3,A4}，{A3,A5}，{A3,A6}，{A4,A5}，{A4,A6}，{A5,A6}．②两名学生至少有一人被抽到包括一人抽到一人没抽到和两人都抽到两种情况，设P1为事件“一人抽到一人没抽到”，则P1=2×415=815，设P2为事件“两人都抽到”，则P2=115，则事件A发生的概率P A=P1+P2=815+115=35．【知识点】分层抽样、古典概型18. 【答案】(1) 依题意得(a+b+0.008+0.027+0.035)×10=1，所以a+b=0.03，又a=4b，所以a=0.024，b=0.006．(2) 平均数为55×0.08+65×0.24+75×0.35+85×0.27+95×0.06=74.9（分）；众数为70+802=75（分）；中位数为70+0.5−0.08−0.240.035≈75.14（分）．(3) 依题意知，从满意程度在[50,60)的市民中抽取了2人，分别记为a，b，满意程度在[60,70)的市民中抽取了6人，分别记为1，2，3，4，5，6，所以从这8人中随机抽取2人的所有可能情况为(a,b)，(a,1)，(a,2)，(a,3)，(a,4)，(a,5)，(a,6)，(b,1)，(b,2)，(b,3)，(b,4)，(b,5)，(b,6)，(1,2)，(1,3)，(1,4)，(1,5)，(1,6)，(2,3)，(2,4)，(2,5)，(2,6)，(3,4)，(3,5)，(3,6)，(4,5)，(4,6)，(5,6)，共28种，其中满足条件的为(a,b)，(a,1)，(a,2)，(a,3)，(a,4)，(a,5)，(a,6)，(b,1)，(b,2)，(b,3)，(b,4)，(b,5)，(b,6)，共13种．则至少有1人的满意程度在[50,60)的概率为1328．【知识点】样本数据的数字特征、频率分布直方图、古典概型19. 【答案】(1) x=3500×1000×0.00005+4500×1000×0.00010+5500×1000×0.00015 +6500×1000×0.00030+7500×1000×0.00020+8500×1000×0.00015 +9500×1000×0.00005=6650,x−2s=6650−3000=3650>3600，所以张茗是“就为不理想”的学生．(2) 第一组有1000×0.00005×100=5（人），第二组有1000×0.00010×100=10（人），第三组有1000×0.00015×100=15（人），按照分层随机抽样从中抽6人时，第一组抽1人，记为A；第二组抽2人，分别记为B，C；第三组抽了3人，分别记为D，E，F．从这6人中抽2人共有15种情况：(A,B)，(A,C)，(A,D)，(A,E)，(A,F)，(B,C)，(B,D)，(B,E)，(B,F)，(C,D)，(C,E)，(C,F)，(D,E)，(D,F)，(E,F)．其中恰有1人月薪不超过5000元的有9种情况：(A,D)，(A,E)，(A,F)，(B,D)，(B,E)，(B,F)，(C,D)，(C,E)，(C,F)．由古典概型的概率公式可得所求概率P=915=35．(3) 方案一：月薪在3000∼4000元之间的共收取1000×0.00005×200×3500×0.1=3500（元）；月薪在4000∼5000元之间的共收取1000×0.00010×200×4500×0.1=9000（元）；月薪在5000∼6000元之间的共收取1000×0.00015×200×5500×0.1=16500（元）；月薪在6000∼7000元之间的共收取1000×0.00030×200×6500×0.1=39000（元）；月薪在7000∼8000元之间的共收取1000×0.00020×200×7500×0.1=30000（元）；月薪在8000∼9000元之间的共收取1000×0.00015×200×8500×0.1=25500（元）；月薪在9000∼10000元之间的共收取1000×0.00005×200×9500×0.1=9500（元）．故按方案一收取的最终活动总费用为133000元．方案二：月薪高于6650元的共收取800×200×[(7000−6650)×0.00030+1000×(0.00020+0.00015+0.00005)]=80800（元）；月薪不低于4000元但低于6650元的共收取400×200×[(6650−6000)×0.00030+ 1000×(0.00010+0.00015)]=35600（元）．故按方案二收取的最终活动总费用为116400元．因为116400<133000，所以方案二最终收取的活动总费用较少．【知识点】样本数据的数字特征、古典概型、频率分布直方图20. 【答案】(1) 每次取一件，取后不放回地连续取两次，样本空问Ω={(a1,a2),(a1,b1),(a2,a1),(a2,b1),(b1,a1),(b1,a2)}，其中小括号内左边的字母表示第1次取出的产品，右边的字母表示第2次取出的产品，由6个样本点组成，而且这些样本点的出现是等可能的．用A表示“取出的两件中恰好有一件次品”这一事件，则A={(a1,b1),(a2,b1),(b1,a1),(b1,a2)}．事件A由4个样本点组成，所以P(A)=46=23．(2) 有放回地连续取出两次，样本空间Ω={(a1,a1),(a1,a2),(a1,b1),(a2,a1),(a2,a2),(a2,b1),(b1,a1),(b1,a2),(b1,b1)}，共9个样本点，由于每一件产品被取到的机会均等，因此这些样本点的出现是等可能的．用B表示“恰有一件次品”这事件，则B={(a1,b1),(a2,b1),(b1,a1),(b1,a2)}．事件B由4个样本点组成，因而P(B)=49．【知识点】古典概型21. 【答案】(1) 该试验的样本空间Ω={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),(A1,B3,C1),(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3,B2,C1),(A3,B2,C2),(A3,B3,C1),(A3,B3,C2)},共18个样本点．(2) 因为每个样本点出现的机会相等，所以这些样本点是等可能发生的，用M表示事件“A1被选中”，则M={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),(A1,B3,C1),(A1,B3,C2)}，含有6个样本点，所以A1被选中的概率P(M)=618=13．(3) 用N表示事件“B1和C1不全被选中”，则N表示事件“B1和C1全被选中”，因为N={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}，含有3个样本点，所以B1和C1不全被选中的概率P(N)=1−318=56．【知识点】事件的关系与运算、古典概型22. 【答案】(1) 从8人中选出日语、俄语和韩语志愿者各1名，其一切可能的结果组成的基本事件为(A1,B1,C1)，(A1,B1,C2)，(A1,B2,C1)，(A1,B2,C2)，(A1,B3,C1)，(A1,B3,C2)，(A2,B1,C1)，(A2,B1,C2)，(A2,B2,C1)，(A2,B2,C2)，(A2,B3,C1)，(A2,B3,C2)，(A3,B1,C1)，(A3,B1,C2)，(A3,B2,C1)，(A3,B2,C2)，(A3,B3,C1)，(A3,B3,C2)，共18个基本事件，由于每一个基本事件被抽取的机会均等，因此这些基本事件的发生是等可能的，用M表示“A1恰被选中”这一事件，则M= {(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2,C2),(A1,B3,C1),(A1,B3,C2)}，事件M由6个基本事件组成，因此P(M)=618=13．(2) 用N表示“B1，C1不全被选中”这一事件，则其对立事件N表示“B1，C1全被选中”这一事件，由于N={(A1,B1,C1),(A2,B1,C1),(A3,B1,C1)}，事件N由3个基本事件组成，所以P(N)=318=16，由对立事件的概率公式得P(N)=1−P(N)=1−16=56．【知识点】古典概型。

一、选择题1．抛掷一个质地均匀的骰子的试验，事件A表示“小于5的偶数点出现”，事件B表示“不小于5的点数出现”，则一次试验中，事件A或事件B至少有一个发生的概率为（）A．23B．13C．12D．562．传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数，如图所示的图形表示的数就是他们研究过的三角形数．现从1到50这50个整数中，随机抽取3个整数，则这3个数恰好都是三角形数的概率为（）A．3700B．1350C．4455D．39103．下列命题：①对立事件一定是互斥事件；②若A，B为两个随机事件，则P(A∪B)＝P(A)＋P(B)；③若事件A，B，C彼此互斥，则P(A)＋P(B)＋P(C)＝1；④若事件A，B满足P(A)＋P(B)＝1，则A与B是对立事件．其中正确命题的个数是()A．1 B．2 C．3 D．44．在如图所示的电路中，5个格子表示保险匣，格子中所示数据表示通电时保险丝被熔断的概率，则当开关合上时，电路畅通的概率是（）A．2936B．551720C．2972D．291445．党的十八提出：倡导“富强、民主、文明、和谐、自由、平等、公正、法治、爱国、敬业、诚信、友善”社会主义核心价值观.现将这十二个词依次．．写在六张规格相同的卡片的正反面（无区分），（如“富强、民主”写在同一张卡片的两面），从中任意抽取1张卡片，则写有“爱国”“诚信”两词中的一个的概率是（）A ．13B ．16C ．56D ．236．某学校组织高一和高二两个年级的同学，开展“学雷锋敬老爱老”志愿服务活动，利用暑期到敬老院进行打扫卫生、表演文艺节目、倾听老人的嘱咐和教诲等一系列活动.现有来自高一年级的4名同学，其中男生2名、女生2名；高二年级的5名同学，其中男生3名、女生2名.现从这9名同学中随机选择4名打扫卫生，则选出的4名同学中恰有2名男生，且这2名男生来自同一个年级的概率是（ ）A ．1126B ．521C ．635D ．4217．下列说法正确的是（ ）A ．天气预报说明天下雨的概率为0900，则明天一定会下雨B ．不可能事件不是确定事件C ．统计中用相关系数r 来衡量两个变量的线性关系的强弱，若[]0.75,1,r ∈则两个变量正相关很强D ．某种彩票的中奖率是11000，则买1000张这种彩票一定能中奖 8．齐王有上等、中等、下等马各一匹，田忌也有上等、中等、下等马各一匹．田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马．现在从双方的马匹中随机各选一匹进行一场比赛，若有优势的马一定获胜，则齐王的马获胜得概率为（ ） A ．49B ．59C ．23D ．799．“微信抢红包”自2015年以来异常火爆，在某个微信群某次进行的抢红包活动中，若所发红包的总金额为8元，被随机分配为1.72元，1.83元，2.28元，1.55元，0.62元， 5份供甲、乙等5人抢，每人只能抢一次，则甲、乙二人抢到的金额之和不低于3元的概率是 （ ） A ．310B ．25C ．12D ．35第II 卷（非选择题）请点击修改第II 卷的文字说明参考答案10．今年“五一”小长假期间，某博物馆准备举办－次主题展览，为了引导游客有序参观，该博物馆每天分别在10时，13时，16时公布实时观展的人数．下表记录了5月1日至5日的实时观展人数：通常用实时观展的人数与博物馆的最大承载量（同一时段观展人数的饱和量）之比来表示观展的舒适度，50%以下称为“舒适”，已知该博物馆的最大承载量是1万人．若从5月1日至5日中任选2天，则这2天中，恰有1天这3个时刻的观展舒适度都是“舒适”的概率为（）A．12B．25C．35D．3411．我省明年高考将实行312++模式，即语文数学英语必修，物理、历史二选一，化学、生物、政治、地理四选二，今年高一的小明与小芳进行选科，假若他们对六科没有偏好，则他们选课没有相同科目的概率为（）A．16B．112C．56D．111212．从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是()A．110B．310C．35D．91013．中国古典乐器一般按“八音”分类．这是我国最早按乐器的制造材料来对乐器进行分类的方法，最先见于《周礼•春官•大师》，分为“金、石、土、革、丝、木、匏（páo）、竹”八音．其中“金、石、木、革”为打击乐器，“土、匏、竹”为吹奏乐器，“丝”为弹拨乐器，现从“金、石、土、革、丝、木”任取“两音”，则“两音”同为打击乐器的概率为（）A．15B．25C．35D．27二、解答题14．“工资条里显红利，个税新政人民心”，随着2021年新年钟声的敲响，我国自1980年以来，力度最大的一次个人所得税（简称个税）改革至2019年实施以来发挥巨大作用.个税新政主要内容包括：（1）个税起征点为5000元；（2）每月应纳税所得额（含税）=收入-个税起征点-专项附加扣除；（3）专项附加扣除包括住房､子女教育和赡养老人等.新旧个税政策下每月应纳税所得额（含税）计算方法及其对应的税率表如表：年的人均月收入24000元.统计资料还表明，他们均符合住房专项扣除；同时，他们每人至多只有一个符合子女教育扣除的孩子，并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1；此外，他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为：住房1000元/月，子女教育每孩1000元/月，赡养老人2000元/月等.假设该市该收入层级的IT从业者都独自享受专项附加扣除，将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入.根据样本估计总体的思想，解决如下问题：（1）求该市该收入层级的IT从业者2021年月缴个税的所有可能及其概率.（2）根据新旧个税方案，估计从2021年1月开始，经过多少个月，该市该收入层级的IT 从业者各月少缴交的个税之和就超过2019年的月收入？15．日前，《北京传媒蓝皮书：北京新闻出版广电发展报告（2016~2017）》公布，其中提到，2015年9月至2016年9月，北京市年度综合阅读率较上年增长1%，且数字媒体阅读率首次超过了纸质图书阅读率.为了调查某校450名高一学生（其中女生210名）对这两种阅读方式的时间分配情况，该校阅读研究小组通过按性别分层抽样的方式随机抽取了15名学生进行调查，得到这15名学生分别采用这两种阅读方式的平均每周阅读时间，数据如下（单位：小时）：学生编号123456789101112131415数字阅读时间235830604151645355675125334547纸质阅读时间28663653456248474252521304242（2）请用茎叶图表示上面的数据，并通过观察茎叶图，对这两种阅读方式进行比较，写出两个统计结论；（3）平均每周纸质阅读时长超过数字阅读时长的学生中，随机抽取两名学生，求这两名学生中至少有一名学生数字阅读时间不超过40小时的概率.16．某部门为了对该城市共享单车加强监管，随机选取了100人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照[)90,100分成5组，制成如图所示频率分布直方图.50,60，[)60,70，…[]（1）求图中x的值；（2）求这组数据的平均数；50,60内的男生数与女生数的比为3：2，若在满意度评分值（3）已知满意度评分值在[)50,60的人中随机抽取2人进行座谈，求恰有1名女生的概率.为[)17．某医院首批援鄂人员中有2名医生，3名护士和1名管理人员.采用抽签的方式，从这六名援鄂人员中随机选取两人在总结表彰大会上发言.（Ⅰ）写出发言人员所有可能的结果构成的样本空间；（Ⅱ）求选中1名医生和1名护士发言的概率；（Ⅲ）求至少选中1名护士发言的概率.18．某校高二期中考试后，教务处计划对全年级数学成绩进行统计分析，从男、女生中各随机抽取100名学生，分别制成了男生和女生数学成绩的频率分布直方图，如图所示.（1）若所得分数大于等于80分认定为优秀，求男、女生优秀人数各有多少人？（2）在（1）中的优秀学生中用分层抽样的方法抽取5人，从这5人中任意任取2人，求至少有1名男生的概率．19．11分制乒乓球比赛，每赢一球得1分，当某局打成10:10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束.甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立.在某局双方10:10平后，甲先发球，两人又打了X个球该局比赛结束.（1）求P（X=2）；（2）求事件“X=4且甲获胜”的概率.20．“每天锻炼一小时，健康工作五十年，幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关，从单位随机抽取30名员工进行了同卷调查，得到了如下列联表：（1）请将上面的列联表补充完整（在答题卡上直接填写结果，不需要写求解过程）；（2）能否有95%的把握认为爱好运动与性别有关？（3）若在接受调查的所有男生中按照“爱好与不爱好运动”进行分层抽样，现随机抽取8人，再从8人中抽取3人，求至少有2人“爱好运动”的概率.附：()()()()()22n ad bcKa b c d a c b d-=++++21．某校学生社团组织活动丰富，学生会为了解同学对社团活动的满意程度，随机选取了100位同学进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照(40,50)，[50,60)，[60,70)，…，[]90,100分成6组，制成如图所示频率分布直方图.（1）求图中x 的值.（2）现从被调查的问卷满意度评分值在[)60,80的学生中按分层抽样的方法抽取5人进行座谈了解，再从这5人中随机抽取2人作主题发言，求抽取的2人恰在同一组的概率. 22．某中学高一年级由1000名学生, 他们选着选考科目的情况如下表所示： 科目 人数物理 化学 生物 政治 历史 地理300 √ √ √200√ √√100 √√√200√ √ √100√√√100√√√从这1000名学生中随机抽取1人，分别设：A =“该生选了物理”；B =“该生选了化学”；G =“该生选了生物”； D =“该生选了政治”；E =“该生选了历史”；F =“该生选了地理”. （1）求(),()P B P DEF . （2）求(),()PC E P B F ⋃⋃.（3）事件A 与D 是否相互独立？请说明理由.23．某组织在某市征集志愿者参加志愿活动，现随机抽出60名男生和40名女生共100人进行调查，统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况，具体数据如图所示.(1)完成下列22⨯列联表，并判断是否有99%的把握认为愿意参与志愿活动与性别有关？愿意 不愿意 总计男生 女生 总计(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者，再从中抽取2人作为队长，求抽取的2人至少有一名女生的概率. 参考数据及公式：()20P K k ≥ 0.1 0.05 0.025 0.010k2.7063.8415.0246.635()()()()()()22n ad bc K n a b c d a b c d a c b d -==+++++++.24．一款小游戏的规则如下：每轮游戏要进行三次，每次游戏都需要从装有大小相同的2个红球，3个白球的袋中随机摸出2个球，一轮游戏中，若“摸出的两个都是红球”出现3次获得200积分，若“摸出的两个都是红球”出现1次或2次获得20积分，若“摸出的两个都是红球”出现0次则扣除10积分（即获得-10积分）. （1）求每次游戏中，“摸出的两个都是红球”的概率p ； （2）设每轮游戏获得的积分为X ，求X 的分布列与数学期望；（3）玩过这款游戏的许多人发现，若干轮游戏后，与最初的积分0相比，积分没有增加反而减少了，请运用概率统计的相关知识分析解释上述现象.25．2019年《少年的你》自上映以来引发了社会的广泛关注，特别引起了在校学生情感共鸣，现假如男生认为《少年的你》值得看的概率为45，女生认为《少年的你》值得看的概率为34，某机构就《少年的你》是否值得看的问题随机采访了4名学生（其中2男2女） （1）求这4名学生中女生认为值得看的人数比男生认为值得看的人数多的概率；（2）设ζ表示这4名学生中认为《少年的你》值得看的人数，求ζ的分布列与数学期望.26．盒子里放有外形相同且编号为1，2，3，4，5的五个小球，其中1号与2号是黑球，3号、4号与5号是红球，从中有放回地每次取出1个球，共取两次. （1）求取到的2个球中恰好有1个是黑球的概率； （2）求取到的2个球中至少有1个是红球的概率.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】由古典概型概率公式分别计算出事件A 和事件B 发生的概率，又通过列举可得事件A 和事件B 为互斥事件，进而得出事件A 或事件B 至少有一个发生的概率即为事件A 和事件B 的概率之和． 【详解】事件A 表示“小于5的偶数点出现”，事件B 表示“不小于5的点数出现”， ∴P (A )2163==，P (B )2163==， 又小于5的偶数点有2和4，不小于5的点数有5和6， 所以事件A 和事件B 为互斥事件，则一次试验中，事件A 或事件B 至少有一个发生的概率为 P （A ∪B ）＝P (A )+P (B )112333=+=， 故选：A ． 【点睛】本题主要考查古典概型计算公式，以及互斥事件概率加法公式的应用，属于中档题．2．A解析：A 【分析】根据图形，归纳出三角形数从小到大可构成数列{}n a ，且()12n n n a +=，n *∈N ，然后利用组合知识以及古典概型概率公式求解即可. 【详解】由题意可得，三角形数从小到大可构成数列{}n a，且()12nn na+=，n*∈N．从1到50这50个整数中，所有的三角形数依次为1,3，6，10，15，21，28，36，45，共9个图形．因此从1到50这50个整数中，随机抽取3个整数的所有方法种数为35019600C=，其中这3个数恰好都是三角形数的取法种数为3984C=．由古典概型的概率公式，可得概率393503700CPC==．【点睛】本题主要考查归纳推理的应用，考查了古典概型概率公式，同时考查了数形结合思想以及特殊与一般思想的应用，属于中档题.3．A解析：A【分析】根据互斥之间和对立事件的概念，及互斥事件和对立事件的关系和概率的计算，即可作出判断，得到答案．【详解】由题意①中，根据对立事件与互斥事件的关系，可得是正确；②中，当A与B是互斥事件时，才有P(A∪B)＝P(A)＋P(B)，对于任意两个事件A，B满足P(A∪B)＝P(A)＋P(B)－P(AB)，所以是不正确的；③也不正确．P(A)＋P(B)＋P(C)不一定等于1，还可能小于1；④也不正确．例如：袋中有大小相同的红、黄、黑、绿4个球，从袋中任摸一个球，设事件A＝{摸到红球或黄球}，事件B＝{摸到黄球或黑球}，显然事件A与B不互斥，但P(A)＋P(B)＝＋＝1.【点睛】本题主要考查了互斥事件和对立事件的基本概念、互斥事件与对立时间的关系及其应用，其中熟记互斥事件和对立事件的概念和关系是解答的关键，着重考查了推理与论证能力，属于基础题．4．A解析：A【分析】先求出A至B畅通的概率,再求出B至C畅通的概率,再利用独立事件的概率求法求出电路通畅的概率.【详解】当开关合上时,电路畅通即表示A至B畅通且B至C畅通,A至B畅通的概率11115 11114236P⎡⎤⎛⎫⎛⎫=-⨯--⨯-=⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,B 至C 畅通的概率2112915630P =-⨯=, 所以电路畅通的概率125292963036P PP =⨯==, 故选:A. 【点睛】本题考查求独立事件的概率,需要学生有一定的计算分析能力,属于中档题.5．A解析：A 【分析】由题意知，基本事件有6个，其中抽取到含有“爱国”“诚信”两词中的一个的事件有2个基本事件，根据古典概型概率公式计算即可. 【详解】由题意，基本事件为抽到写有富强、民主；文明、和谐；自由、平等；公正、法治；爱国、敬业；诚信、友善的卡片，共有6个，其中抽到写有“爱国”“诚信”两词中的一个的事件为：抽到写有爱国、敬业的卡片，抽到写有诚信、友善的卡片，共有2个， 所以由古典概型概率公式知：2163P ==， 故选：A 【点睛】本题主要考查了古典概型概率的求法，属于中档题.6．D解析：D 【分析】对这两名男生来自高一或高二两种情况讨论，当男生来自高一时，同时任选2名女生，有2224C C 种方法，当男生来自高二时，有2234C C 种方法，并求概率.【详解】当两名男生来自高一年级，2224149121C C P C ==，当两名男生来自高二，223424917C C P C == 1211421721P P P =+=+=, 故选D. 【点睛】本题考查了古典概型的概率，难度不大，关键是能正确分类.7．C解析：C 【分析】运用概率的相关知识对四个选项逐一进行分析即可 【详解】对于A ，天气预报说明天下雨的概率为90%，表示下雨的可能性比较大，是不确定事件，在一定条件下可能下雨，也可能不下雨，但明天一定会下雨是不正确的，故错误； 对于B ，根据定义可知不可能事件是确定事件，故错误；对于C ，统计中用相关系数r 来衡量两个变量的线性关系的强弱，若[]0.75,1,r ∈则两个变量正相关很强，故正确； 对于D ，某种彩票的中奖率是11000，每一次买彩票的中奖是独立的，并不是买1000张这种彩票一定能中奖，故错误 故选C 【点睛】本题主要考查了辨别生活中的概率，理解并运用概率知识即可判断，较为基础．8．C解析：C 【分析】现从双方的马匹中随机各选一匹进行一场比赛 ,利用列举法求出基本事件有9种，齐王的马获胜包含的基本事件有6种，利用古典概型概率公式可求出齐王的马获胜的概率. 【详解】设齐王上等、中等、下等马分別为,,A B C ，田忌上等、中等、下等马分别为,,a b c ， 现从双方的马匹中随机各选一匹进行一场比赛,基本事件有：()()()()()()()()(),,,,,,,,,,,,,,,,,A a A b A c B a B b B c C a C b C c ，共9种，有优势的马一定获胜，齐王的马获胜包含的基本事件有：()()()()()(),,,,,,,,,,,A a A b A c B b B c C c ，共 6种,∴齐王的马获胜的概率为6293P ==，故选C. 【点睛】本题主要考查古典概型概率公式的应用，属于中档题，利用古典概型概率公式求概率时，找准基本事件个数是解题的关键，基本亊件的探求方法有 (1)枚举法：适合给定的基本事件个数较少且易一一列举出的；(2)树状图法：适合于较为复杂的问题中的基本亊件的探求.在找基本事件个数时，一定要按顺序逐个写出：先11(,)A B ，12(,)A B …. 1(,)n A B ，再21(,)A B ，22(,)A B …..2(,)n A B 依次31(,)A B 32(,)A B ….3(,)n A B … 这样才能避免多写、漏写现象的发生.9．D解析：D 【解析】 【分析】甲、乙二人抢到的金额之和包含的基本事件的总数2510n C==，甲、乙二人抢到的金额之和不低于3元包含基本事件有6个，由此能求出甲、乙二人抢到的金额之和不低于3元的概率.【详解】由题意，所发红包的总金额为8元，被随机分配为1.72元、1.83元、2.28元、1.55元、0.62元、5分，供甲、乙等5人抢，每人只能抢一次，甲乙二人抢到的金额之和包含的基本事件的总数为2510n C==，甲乙二人抢到的金额之和不低于3元包含的基本事件有6个，分别为(1.72,1.83),(1.72,2.28),(1.72,1.55),(1.83,2.28),(1.83,1.55),(2.28,1.55)所以甲乙二人抢到的金额之和不低于3元的概率为63105p==，故选D.【点睛】本题主要考查了古典概型及其概率的计算问题，其中解答中正确理解题意，找出基本事件的总数和不低于3元的事件中所包含的基本事件的个数是解答的关键,着重考查了分析问题和解答问题的能力，属于基础题.10．C解析：C【分析】5月1日至5日中，该博物馆每天在10时，13时，16时这3个时刻的观展舒适度都是“舒适”的有2天，从5月1日至5日中任选2天，基本事件总数2510n C==，这2天中，恰有1天这3个时刻的观展舒适度都是"舒适"包含的基本事件个数11236m C C==，由此能求出这2天中，恰有1天这3个时刻的观展舒适度都是“舒适”的概率.【详解】5月1日至5日中，该博物馆每天在10时，13时，16时这3个时刻的观展舒适度都是“舒适”的有2天，分别为5月4日和5月5日，从5月1日至5日中任选2天，基本事件总数2510n C==，这2天中，恰有1天这3个时刻的观展舒适度都是“舒适”包含的基本事件个数11 236m C C==，所以这2天中，恰有1天这3个时刻的观展舒适度都是“舒适”的概率63105mPn===.故选：C【点睛】本题主要考查了概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，属于基础题.11．B解析：B【分析】基本事件总数22221144144n C C C C ==，他们选课他们选课没有相同科目的基本事件个数122412m C C ==，由此能求出他们选课没有相同科目的概率．【详解】解：由题意知，基本事件总数22221144144n C C C C ==，他们选课没有相同科目包含的基本事件个数122412m C C ==∴他们选课没有相同科目的概率为：12114412m P n ===． 故选:B. 【点睛】本题考查了古典概型概率求解，考查了组合的思想，考查了分类的思想.本题的关键是结合组合的思想计算事件数量，属于中档题.12．D解析：D 【解析】试题分析：从装有3个红球，2个白球的袋中任取3个球，共有基本事件3510C =种，则全取红球的基本事件只有一种，所以所取3个球中至少有1个白球的概率为1911010-=，故选D.考点：古典概型及其概率的计算.13．B解析：B 【分析】由条件列举从“金、石、土、革、丝、木”中任取“两音”的所有基本事件的个数，再计算“两音”同为打击乐器所包含的所有基本事件个数，最后求其概率. 【详解】从“金、石、土、革、丝、木”中任取“两音”，组成的基本事件包含：{金、石}，{金、土}，{金、革}，{金、丝}，{金、木}，{石、土}，{石、革}，{石、丝}，{石、木}，{土、革}，{土、丝}，{土、木}，{革、丝}，{革、木}，{丝、木}，共15种情况，其中“两音”同为打击乐器的有{金、石}，{金、革}，{金、木}，{石、革}，{石、木}，{革、木}，共包含6种情况，则“两音”同为打击乐器的概率62155P ==. 故选：B 【点睛】本题考查数学文化与古典概型相结合的考查，重点考查读懂题意，属于基础题型.二、解答题14．（1）答案见解析；（2）经过12个月. 【分析】（1）计算出题中四类人群每月应纳税所得额，结合题意求出每类人群的月缴个税及其概率；（2）计算出在旧政策下，该收入阶层的IT 从业者每月应纳税所得额，可求得新政策下，每月少缴个税额，设经过x 个月该市该收入阶层的IT 从业者各月少缴交的个税之和就超过2019年的月收入，根据已知条件可得出关于x 的不等式，结合x ∈N 可求得结果. 【详解】（1）由题意，既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1.①既不符合子女教育扣除又不符合赡养老人扣除的人群每月应纳税所得额为240005000100018000--=元，月缴个税为30000.0390000.160000.22190⨯+⨯+⨯=元，其概率为25； ②只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为2400050001000100017000---=元，月缴个税为30000.0390000.150000.21990⨯+⨯+⨯=元，其概率为15； ③只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为2400050001000200016000---=元，月缴个税为30000.0390000.140000.21790⨯+⨯+⨯=元，其概率为15； ④既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为24000500010001000200015000----=元，月缴个税为30000.0390000.130000.21590⨯+⨯+⨯=元，其概率为15； （2）在旧政策下，该收入阶层的IT 从业者每月应纳税所得额为24000350020500-=元，故月缴个税为15000.0330000.145000.2115000.254120⨯+⨯+⨯+⨯=元， 在新政策下，该收入阶层的IT 从业者每月应纳税所得额为()212190199017901590195055⨯+++⨯=元，每月少缴个税412019502170-=元，设经过x 个月该市该收入阶层的IT 从业者各月少缴交的个税之和就超过2019年的月收入，则217024000x ≥，又x ∈N ，解得()12x x N ≥∈，所以经过12个月，该市该收入阶层的IT 从业者各月少缴交的个税之和就超过2019年的月收入.【点睛】关键点点睛：解决本题第一问的关键在于理解题中个税新旧政策中的扣税方案，并依据题意计算出各类人群所扣的税额；解决本题第二问的关键在于求出新旧政策下所扣的税额，并结合题意列不等式求解.15．（1）8；（2）答案见解析；（3）7 10.【分析】（1）根据分层抽样的原理计算可得答案；（2）由已知数据得出被调查的15名学生分别采用两种阅读方式的平均每周阅读时间茎叶图，由表中的数据可得统计结论；（3）由表中数据可知平均每周纸质阅读时间超过数字阅读时间的学生的编号分别是1，2，3，5，6，其中数字阅读时间不超过40小时的学生的编号是1，3.运用列举法所有的基本事件，再由古典概率公式可得答案．【详解】（1）450210158450-⨯=（名）.所以被调查的15名学生中共有8名男生.（2）被调查的15名学生分别采用两种阅读方式的平均每周阅读时间茎叶图如下：通过观察比较分析可知，平均每周的数字阅读时间比纸质阅读时间长，纸质阅读时间数据更集中；（3）由表中数据可知平均每周纸质阅读时间超过数字阅读时间的学生的编号分别是1，2，3，5，6，其中数字阅读时间不超过40小时的学生的编号是1，3.从这5名学生中，随机抽取两名学生，所有可能的抽取结果为(1,2)，(1,3)，(1,5)，(1,6)，(2,3)，(2,5)，(2,6)，(3,5)，(3,6)，(5,6)，共10个基本事件，设“从这5名学生中随机抽取两名学生，这两名学生中至少有一名学生数字阅读时间不超过40小时”为事件A，共有7个基本事件，分别为(1,2)，(1,3)，(1,5)，(1,6)，(2,3)，(3,5)，(3,6)，则7 ()10 P A=.【点睛】方法点睛：在解决概率统计的应用问题时，注意理解问题的情景，将生活中的数据转化成数学统计中的数据，再运用相应的统计知识解决．。

一、选择题1．传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数，如图所示的图形表示的数就是他们研究过的三角形数．现从1到50这50个整数中，随机抽取3个整数，则这3个数恰好都是三角形数的概率为（ ）A ．3700B ．1350C ．4455D ．39102．两个实习生每人加工一个零件．加工为一等品的概率分别为23和34，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为A ．12B ．512C ．14D ．163．袋中装有标号为1，2，3，4，5，6且大小相同的6个小球，从袋子中一次性摸出两个球，记下号码并放回，如果两个号码的和是3的倍数，则获奖，若有5人参与摸球，则恰好2人获奖的概率是（ ） A ．40243B ．70243C ．80243D ．382434．甲、乙两人对同一个靶各射击一次，设事件A =“甲击中靶”，事件B =“乙击中靶”，事件E =“靶未被击中”，事件F=“靶被击中”，事件G =“恰一人击中靶”，对下列关系式（A 表示A 的对立事件，B 表示B 的对立事件）：①E AB =，②F AB =，③F A B =+，④G A B =+，⑤G AB AB =+，⑥()()1P F P E =-，⑦()()()P F P A P B =+．其中正确的关系式的个数是（ ） A ．3B ．4C ．5D ．65．已知{0,1,2}a ∈,{1,1,35}b ∈-，,则函数2()2f x ax bx =-在区间(1,)+∞上为增函数的概率是（ ） A ．512B ．13C ．14D ．166．甲、乙二人进行围棋比赛，采取“三局两胜制”，已知甲每局取胜的概率为23，则甲获胜的概率为 ( )．A ．22213221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B ．22232233C ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭C ．22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D ．21112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭7．口袋内有一些大小相同的红球、黄球和白球，从中任意摸出一球，摸出的球是红球或黄球的概率为0.4，摸出的球是红球或白球的概率为0.9，那么摸出的球是黄球或白球的概率为（ ） A ．0.7B ．0.5C ．0.3D ．0.68．有3位男生和2位女生在周日去参加社区志愿活动，从该5位同学中任取3人，至少有1名女生的概率为（ ）A ．110B ．25C ．35D ．9109．甲、乙两名同学相约学习某种技能，该技能需要通过两项考核才能拿到证书，每项考核结果互不影响.已知甲同学通过第一项考核的概率是45，通过第二项考核的概率是12；乙同学拿到该技能证书的概率是13， 那么甲、乙两人至少有一人拿到该技能证书的概率是（ ） A ．1315B ．1115C ．23D ．3510．素数分布是数论研究的核心领域之一，含有众多著名的猜想.19世纪中叶，法国数学家波利尼亚克提出了“广义孪生素数猜想”：对所有自然数k ，存在无穷多个素数对(2)p p k +，.其中当1k =时，称(2)p p +，为“孪生素数”，2k =时，称(4)p p +，为“表兄弟素数”.在不超过30的素数中，任选两个不同的素数p ､q (p q <)，令事件(){A p q =，为孪生素数}，(){B p q =，为表兄弟素数}，{()|4}C p q q p =-≤，，记事件A ､B ､C 发生的概率分别为()P A ､()P B ､(C)P ，则下列关系式成立的是（ ） A ．()()()P A P B P C = B ．()()()P A P B P C += C ．()()()P A P B P C +> D ．()()()P A P B P C +<11．某普通高校招生体育专业测试合格分数线确定为60分，甲、乙、丙三名考生独立参加测试，他们能达到合格的概率分别是0.9，0.8，0.75，则三人中至少有一人达标的概率为（ ） A ．0.015B ．0.005C ．0.985D ．0.99512．我省明年高考将实行312++模式，即语文数学英语必修，物理、历史二选一，化学、生物、政治、地理四选二，今年高一的小明与小芳进行选科，假若他们对六科没有偏好，则他们选课没有相同科目的概率为（ ） A ．16B ．112C ．56D ．111213．数学与文学有许多奇妙的联系，如诗中有回文诗：“垂帘画阁画帘垂，谁系怀思怀系谁？”既可以顺读也可以逆读，数学中有回文数，如343、12521等，两位数的回文数有11、22、33、…、99共9个，则三位数的回文数中为偶数的概率是（ ） A ．19B ．29C ．39D ．49二、解答题14．2020年国庆节期间，甲、乙等5名游客准备从庐山、三清山、婺源、井冈山4个景点中选取一个景点游览，设每人只选择一个景点，且选择任一个景点是等可能的． （1）分别求“恰有2人选择井冈山”和“甲选择井冈山且乙不选择庐山”的概率； （2）记X 表示5人中选择景点的个数，求X 的分布列与数学期望．15．进行垃圾分类收集可以减少垃圾处理量和处理设备，降低处理成本，减少土地资源的消耗，具有社会､经济､生态等多方面的效益，是关乎生态文明建设全局的大事.为了普及垃圾分类知识，某学校举行了垃圾分类知识考试，试卷中只有两道题目，已知甲同学答对每题的概率都为p ，乙同学答对每题的概率都为()q p q >，且在考试中每人各题答题结果互不影响.已知每题甲，乙同时答对的概率为12，恰有一人答对的概率为512. （1）求p 和q 的值；（2）试求两人共答对3道题的概率.16．有四个编有1､2､3､4的四个不同的盒子，有编有1､2､3､4的四个不同的小球，现把四个小球逐个随机放入四个盒子里.（1）小球全部放入盒子中有多少种不同的放法？ （2）在（1）的条件下求恰有一个盒子没放球的概率？（3）若没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？ 17．2020年9月份，南京出台了<南京市生活垃圾管理条例>，提出2020年11月1日起，实现单位生活垃圾强制分类全覆盖，居民区普遍推行生活垃圾分类制度.为加强社区居民的垃圾分类意识，推动社区垃圾分类正确投放，某社区在健身广场举办了“垃圾分类，从我做起”生活垃圾分类大型宣传活动，号召社区居民用实际行动为建设绿色家园贡献一份力量，为此需征集一部分垃圾分类志愿者.已知某垃圾站的日垃圾分拣量y (千克)与垃圾分类志愿者人数x (人)满足线性回归直线方程ˆybx a =+，数据统计如下：（1）已知511405i i y y ===∑，120ii x==∑，1885i i i x y ==∑，根据所给数据求t 和线性回归直线方程ˆybx a =+. （2）用（1）中所求的线性回归方程得到与i x 对应的口垃圾分拣量的估计值ˆi y.当分拣数据i y 与估计值ˆi y满足ˆi i y y -≤2时，则将分拣数据(i x ，i y )称为一个“正常数据”.现从题中5个分拣数据中任取2个，求2个都是“正常数据”的概率.参考公式：()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-. 18．随着我国中医学的发展，药用昆虫的使用越来越多，每年春暖以后至寒冬前，昆虫大量活动与繁殖，易于采集各种药用昆虫，已知某种药用昆虫的产卵数y （单位：个）与一定范围内的温度x （单位：°C ）有关，于是科研人员在3月份的31天中随机挑选了5天进行研究，收集了该种药用昆虫的5组观测数据如下表：m ，n ，求事件“m ，n 均不小于26”的概率；（2）科研人员确定的研究方案是：先从这5组数据中任选2组，用剩下的3组数据建立y 关于x 的线性回归方程，再对被选取的2组数据进行检验；①若选取的是3月2日和30日这两组数据，请根据7日、15日、22日这3组数据求出y 关于x 的线性回归方程；②若由线性回归方程得到的估计产卵数与所选出的检验数据的误差不超过2个，则认为得到的线性回归方程是可靠的．按照此标准①中得到的线性回归方程是否可靠？说明理由．参考公式：最小二乘法求线性回归方程系数公式：()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-． 19．海关对同时从,,A B C 三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如下表所示，工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测． （2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．20．在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱.（1）摸出的3个球为白球的概率是多少？（2）摸出的3个球为2个黄球1个白球的概率是多少？（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？21．某校从高一年级的一次月考成绩中随机抽取了50名学生的成绩，这50名学生的成绩都在[50，100]内，按成绩分为[50，60)，[60，70)，[70，80)，[80，90)，[90，100]五组，得到如图所示的频率分布直方图.（1）求图中的a 值；（2）根据频率分布直方图估计该校高一年级本次考试成绩的中位数；（3）用分层抽样的方法从成绩在[80，100]内的学生中抽取6人，再从这6人中随机抽取2名学生进行调查，求月考成绩在[90，100]内至少有1名学生被抽到的概率.22．为了检测某种零件的一条生产线的生产过程，从生产线上随机抽取一批零件，根据其尺寸的数据得到如图所示的频率分布直方图.若尺寸落在区间（2x s -，2x s +）之外，则认为该零件属“不合格”的零件，其中x ，s ，分别为样本平均数和样本标准差，计算可得：15s ≈（同一组中的数据用该组区间的中点值作代表）.（1）若一个零件的尺寸是97cm ，试判断该零件是否属于“不合格”的零件；（2）工厂利用分层抽样的方法从样本的前3组中抽出6个零件，标上记号，并从这6个零件中再抽取2个，求再次抽取的2个零件中恰有1个尺寸不超过50cm 的概率. 23．北京市政府为做好APEC 会议接待服务工作，对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测，只有两轮都合格才能进行销售，否则不能销售.已知该海产品第一轮检测不合格的概率为16，第二轮检测不合格的概率为110，两轮检测是否合格相互没有影响.（1）求该海产品不能销售的概率.（2）如果该海产品可以销售，则每件产品可获利40元；如果该海产品不能销售，则每件产品亏损80元（即获利-80元）.已知一箱中有该海产品4件，记一箱该海产品获利X 元，求X 的分布列，并求出数学期望()E X .24．盒子里放有外形相同且编号为1，2，3，4，5的五个小球，其中1号与2号是黑球，3号、4号与5号是红球，从中有放回地每次取出1个球，共取两次. （1）求取到的2个球中恰好有1个是黑球的概率； （2）求取到的2个球中至少有1个是红球的概率.25．2020年是全面建成小康社会目标实现之年，也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户，结合当地实际情况采取多项精准扶贫措施，每年新脱贫户数如下表（1）根据2015-2019年的数据，求出y 关于x 的线性回归方程y bx a =+，并预测到2020年底该乡镇500户贫困户是否能全部脱贫；（2）2019年的新脱贫户中有20户五保户，20户低保户，60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访，了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫，随机抽取这5户中的2户进行每月跟踪帮扶，求抽取的2户中至少有1户是扶贫户的概率. 参考数据：5115526838049251001299i ii x y==⨯+⨯+⨯+⨯+⨯=∑参考公式：()()()1122211nni iiii i nniii i x ynx y xxy y b xnxxx====---==--∑∑∑∑，a y bx =-26．某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[)25,30，第2组[)30,35，第3组[)35,40，第4组[)40,45，第5组[]45,50，得到的频率分布直方图如图所示.（1）上表是年龄的频数分布表，求正整数,a b的值；（2）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第1，2，3组的人数分别是多少？（3）在（2）的前提下，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率.参考答案【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】根据图形，归纳出三角形数从小到大可构成数列{}n a，且()12nn na+=，n*∈N，然后利用组合知识以及古典概型概率公式求解即可.【详解】由题意可得，三角形数从小到大可构成数列{}n a，且()12nn na+=，n*∈N．从1到50这50个整数中，所有的三角形数依次为1,3，6，10，15，21，28，36，45，共9个图形．因此从1到50这50个整数中，随机抽取3个整数的所有方法种数为35019600C=，其中这3个数恰好都是三角形数的取法种数为3984C=．由古典概型的概率公式，可得概率393503700CPC==．【点睛】本题主要考查归纳推理的应用，考查了古典概型概率公式，同时考查了数形结合思想以及特殊与一般思想的应用，属于中档题.2．B解析：B 【解析】记两个零件中恰好有一个一等品的事件为A ，即仅第一个实习生加工一等品(A 1)与仅第二个实习生加工一等品(A 2)两种情况， 则P (A )=P (A 1)+P (A 2)=2 3×14+13×34=512故选B.3．C解析：C 【分析】先确定摸一次中奖的概率，5个人摸奖，相当于发生5次试验，根据每一次发生的概率，利用独立重复试验的公式得到结果． 【详解】从6个球中摸出2个，共有2615C =种结果，两个球的号码之和是3的倍数，共有(1,2),(1,5),(2,4),(3,6),(4,5)∴摸一次中奖的概率是51153=， 5个人摸奖，相当于发生5次试验，且每一次发生的概率是13， ∴有5人参与摸奖，恰好有2人获奖的概率是35222180()()33243C ⋅⋅=， 故选：C ． 【点睛】本题主要考查了n 次独立重复试验中恰好发生k 次的概率，考查独立重复试验的概率，解题时主要是看清摸奖5次，相当于做了5次独立重复试验，利用公式做出结果，属于中档题．4．B解析：B 【分析】根据事件关系，靶为被击中即甲乙均未击中；靶被击中即至少一人击中，分为恰有一人击中或两人都击中，依次判定即可. 【详解】由题可得：①E AB =，正确；②事件F=“靶被击中”，AB 表示甲乙同时击中，F AB AB AB =++，所以②错误；③F A B =+，正确，④A B +表示靶被击中，所以④错误；⑤G AB AB =+，正确；⑥,E F 互为对立事件，()()1P F P E =-，正确；⑦()()()()P F P A P B P AB =+-，所以⑦不正确．正确的是①③⑤⑥． 故选：B 【点睛】此题考查事件关系和概率关系的辨析，需要熟练掌握事件的关系及其运算，弄清事件特征及其概率特征准确辨析.5．A解析：A 【分析】利用枚举法分情况将所有满足条件的情况举出,再利用古典概型求概率的方法求解即可. 【详解】{0,1,2}a ∈,{1,1,3,5}b ∈-,∴基本事件总数3412n =⨯=.用(,)a b 表示,a b 的取值.若函数2()2f x ax bx =-在区间(1,)+∞上为增函数,则①当0a =时,()2f x bx =-,符合条件的只有(0,1)-,即0a =,1b =-; ②当0a ≠时,则由题意0a >，只需满足1ba,符合条件的有(1,1)-,(1,1),(2,1)-,(2,1),共4种.∴函数2()2f x ax bx =-在区间(1,)+∞上为增函数的概率512P =. 故选：A 【点睛】本题主要考查了分类讨论的思想以及古典概型求概率的方法,属于中等题型.6．C解析：C 【分析】先确定事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，再利用独立重复试验的概率公式和概率加法公式可求出所求事件的概率． 【详解】事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，若甲三局赢两局，则第三局必须是甲赢，前面两局甲赢一局，所求概率为2121233C ⎛⎫⋅⋅ ⎪⎝⎭， 若前两局都是甲赢，所求概率为223⎛⎫ ⎪⎝⎭，因此，甲获胜的概率为22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选C ． 【点睛】本题考查独立重复事件的概率，考查概率的加法公式，解题时要弄清楚事件所包含的基本情况，考查分类讨论思想，考查计算能力，属于中等题．7．A解析：A【分析】设摸出红球的概率为()P A ，摸出黄球的概率是()P B ，摸出白球的概率为(C)P ，求出()P B 、(C)P 的值，相加即可求解．【详解】设摸出红球的概率为()P A ，摸出黄球的概率是()P B ，摸出白球的概率为(C)P ， 所以()()0.4,()()0.9P A P B P A P C +=+=，且()()()1P A P B P C ++=， 所以()1()()0.6P C P A P B =--=，()1()()0.1P B P A P C =--=， 所以()()0.7P B P C += 【点睛】本题主要考查了互斥事件的概率加法公式的应用，其中解答中熟记互斥事件的概率加法公式，准确计算是解答的关键，着重考查了推理与运算能力，属于基础题．8．D解析：D 【分析】将3位男生分别记为A 、B 、C ，2位女生分别记为a 、b ，列举出所有的基本事件，并确定事件“从这5位同学中任取3人，至少有1名女生”所包含的基本事件数，利用古典概型的概率公式可求得所求事件的概率. 【详解】将3位男生分别记为A 、B 、C ，2位女生分别记为a 、b ，从这5位同学中任取3人，所有的基本事件有：ABC 、ABa 、ABb 、ACa 、ACb 、Aab 、BCa 、BCb 、Bab 、Cab ，共10种，其中，事件“从这5位同学中任取3人，至少有1名女生”包含的基本事件有：ABa 、ABb 、ACa 、ACb 、Aab 、BCa 、BCb 、Bab 、Cab ，共9种，因此，所求概率为910P =. 故选：D. 【点睛】方法点睛：求解古典概型概率的方法如下： （1）列举法； （2）列表法； （3）树状图法； （4）排列、组合数的应用.9．D解析：D 【分析】由已知先求得甲取得证书的概率，再求得甲，乙两人都取不到证书的概率，由对立事件的概率公式可得选项. 【详解】由已知得甲拿到该技能证书的概率为412525⨯=，则甲，乙两人都没有拿到证书的概率为：21211535⎛⎫⎛⎫-⨯-= ⎪ ⎪⎝⎭⎝⎭， 所以甲、乙两人至少有一人拿到该技能证书的概率是23155-=， 故选：D. 【点睛】方法点睛：在解决含有“至少”，“至多”等一类问题的概率问题时，正面求解时情况较复杂，可以求其对立事件的概率，再用1减去所求的对立事件的概率，就是所求的概率.10．D解析：D 【分析】根据素数的定义，一一列举出不超过30的所有素数，共10个，根据组合运算，得出随机选取两个不同的素数p 、q (p q <)，有21045C =(种)选法，从而可列举出事件A 、B 、C的所有基本事件，最后根据古典概率分别求出(),()P A P B 和(C)P ，从而可得出结果. 【详解】解：不超过30的素数有2、3、5、7、11、13、17、19、23、29，共10个，随机选取两个不同的素数p 、q (p q <)，有21045C =(种)选法，事件A 发生的样本点为(3)5，、(57)，、(1113)，、(1719)，共4个， 事件B 发生的样本点为(37)，、(711)，、(1317)，、(1923)，共4个， 事件C 发生的样本点为(2)3，、(25)，、(3)5，、(37)，、(57)，、 (711)，、(1113)，、(1317)，、(1719)，、(1923)，，共10个，∴4()()45P A P B ==，102()459P C ==， 故()()()P A P B P C +<.故选：D. 【点睛】关键点点睛：本题考查与素数相关的新定义，考查古典概型的实际应用和利用列举法求古典概型，考查组合数的计算，解题的关键在于理解素数的定义，以及对题目新定义的理解，考查知识运用能力.11．D解析：D 【分析】设出每一个每一个考生达标的事件，并求其对立事件的概率，根据相互独立事件的概率的和事件求解出答案. 【详解】设 “甲考生达标” 为事件A ， “乙考生达标” 为事件B ， “丙考生达标” 为事件C ，则()0.9P A =，()0.8P B =，()0.75P C =，()10.90.1P A =-=，()10.80.2P B =-=，()10.750.25P C =-=，设 “三人中至少有一人达标” 为事件D ，则()()110.10.20.2510.0050.995P D P ABC =-=-⨯⨯=-=， 故选：D. 【点睛】本题以实际问题为背景考查相互独立事件的概念及其发生的概率的计算，考查分析问题和解决问题的能力，属于中档题.12．B解析：B 【分析】基本事件总数22221144144n C C C C ==，他们选课他们选课没有相同科目的基本事件个数122412m C C ==，由此能求出他们选课没有相同科目的概率．【详解】解：由题意知，基本事件总数22221144144n C C C C ==，他们选课没有相同科目包含的基本事件个数122412m C C ==∴他们选课没有相同科目的概率为：12114412m P n ===． 故选:B. 【点睛】本题考查了古典概型概率求解，考查了组合的思想，考查了分类的思想.本题的关键是结合组合的思想计算事件数量，属于中档题.13．D解析：D 【分析】利用列举法列举出所有的三位回文数的个数，再列举出其中所有的偶数的个数，由此能求出结果 【详解】解：三位数的回文数为ABA ，A 共有1到9共9种可能，即11B 、22B 、33B ⋯B 共有0到9共10种可能，即0A A 、1A A 、2A A 、3A A 、⋯ 共有91090⨯=个，其中偶数为A 是偶数，共4种可能，即22B ，44B ，66B ，88B ， B 共有0到9共10种可能，即0A A 、1A A 、2A A 、3A A 、⋯ 其有41040⨯=个，∴三位数的回文数中，偶数的概率404909P ==； 故选：D ． 【点睛】本题考查概率的求法，注意列举法在使用时一定做到不重不漏，属于中档题．二、解答题14．（1）316；（2）分布列见解析，781256. 【分析】（1）利用排列组合计算方法种数，利用古典概型求概率；（2）先分析X 的所有可能取值，计算概率，写出分布列，套公式计算数学期望即可. 【详解】（1）所有可能的选择方式有54种，“恰有2人选择井冈山”的方式有235C 3⋅种，从而“恰有2人选择井冈山”的概率为2355C 31354512⋅=． “甲选择井冈山且乙不选择庐山”的方式有334⋅种，从而“甲选择井冈山且乙不选择庐山”的概率为35343416⋅=．（2）X 的所有可能值为1，2，3，4．又145C 1(1)4256P X ===， ()2324245252545(2)4256C C A C A P X +===， 2233335343535C C C A C ?A 2!150(3)4256P X ⎛⎫+ ⎪⎝⎭===， 24545C ?A 60(4)4256P X ===． 故X 的分布列为X ∴的数学期望()1234256256256256256E X =⨯+⨯+⨯+⨯=． 【点睛】求离散型随机变量的分布列，应按以下三个步骤进行：（1）明确离散型随机变量的所有可能取值以及取每个值所表示的意义；（2）利用概率的有关知识求出随机变量每个取值的概率； （3）按规范形式写出分布列并用分布列的性质进行检验. 15．（1）34p =，23q =；（2）512.【分析】（1）由互斥事件和对立事件的概率公式列方程组可解得,p q ；（2）分别求出两人答对1道的概率，答对两道题的概率，两人共答对3道题，则是一人答对2道题另一人答对1道题，由互斥事件和独立事件概率公式可得结论． 【详解】解：（1）设A ={甲同学答对第一题}，B ={乙同学答对第一题}，则()P A p =，()P B q =.设C ={甲、乙二人均答对第一题}，D {甲、乙二人中恰有一人答对第一题}，则C AB =，D AB AB =+.由于二人答题互不影响，且每人各题答题结果互不影响，所以A 与B 相互独立，AB 与AB 相互互斥，所以()()()()P C P AB P A P B ==，()()P D P AB AB =+()()()()()()()()()()()()11P AB P AB P A P B P A P B P A P B P A P B =+=+=-+-.由题意可得()()1,2511,12pq p q q p ⎧=⎪⎪⎨⎪-+-=⎪⎩即1,217.12pq p q ⎧=⎪⎪⎨⎪+=⎪⎩解得3,42,3p q ⎧=⎪⎪⎨⎪=⎪⎩或2,33.4p q ⎧=⎪⎪⎨⎪=⎪⎩由于p q >，所以34p =，23q =.（2）设=i A {甲同学答对了i 道题}，i B ={乙同学答对了i 道题}，0i =，1，2. 由题意得，()11331344448P A =⨯+⨯=，()23394416P A =⨯=， ()12112433339P B =⨯+⨯=，()2224339P B =⨯=.设E ={甲乙二人共答对3道题}，则1221E A B A B =+. 由于i A 和i B 相互独立，12A B 与21A B 相互互斥，所以()()()()()()()12211221349458916912P E P A B P A B P A P B P A P B =+=+=⨯+⨯=.所以，甲乙二人共答对3道题的概率为512. 【点睛】关键点点睛：本题考查互斥事件与独立事件的概率公式，解题关键是把所求概率事件用互斥事件表示，然后求概率，如设A ={甲同学答对第一题}，B ={乙同学答对第一题}，设C ={甲、乙二人均答对第一题}，D {甲、乙二人中恰有一人答对第一题}，则C AB =，D AB AB =+．同样两人共答对3题分拆成甲答对2题乙答对1题与甲答对1题乙答对2题两个互斥事件．16．（1）256种；（2）916；（3）23种.【分析】（1）用分步乘法计数原理计算，考虑每个球的放法可得；（2）选取2球放在一起作为一个球，共3个球放到3个盒子中，用排列求得放法后由古典概型概率公式可计算出概率；（3）4个球的全排列数减去编号全相同的排法1即可得． 【详解】（1）每个球都有4种方法，故有4444256⨯⨯⨯=种（2）从4个小球中选两个作为一个元素，同另外两个元素在三个位置全排列，故共有2344144C A =种不同的放法.概率为：144925616= （3）每个盒子不空，共有4424A =，24123-=种．【点睛】关键点点睛：本题考查计数原理，古典概型，排列的应用．难点是事件“4个盒子中恰有一个盒子没放球”，解题关键是确定完成这件事的方法，4个球放到3个盒子中，其中有一个盒子中必有2个球，由此可选取2个球放在一起作为一个球，4个球看作3个球放入4个盒子中的3个中，用排列知识可求解．17．（1）60t =，ˆ8.56yx =+；（2）310P = 【分析】（1）根据40y =，求t ，再根据参考公式求ˆˆ,ba ，求回归直线方程；（2）首先计算“正常数据”的个数，再求两个都是“正常数据”的概率. 【详解】 （1）由条件可知25304045405t++++=，解得：60t =，2045x ==， ()()()()()()()()51242540343040 (646040i)ii x x y y =--=--+--++--∑85=()()()()()()52222221243444546410i i x x =-=-+-+-+-+-=∑，()()()12185ˆ8.510niii ni i x x y y bx x==--∴===-∑∑，ˆˆ408.546a y bx=-=-⨯=， 所以回归直线方程是ˆ8.56yx =+； （2）12x =时，1ˆ23y=，232522-=≤，是正常数据，23x =时，2ˆ31.5y =，31.530 1.52-=≤是正常数据，34x =时，3ˆ40y=，404002-=≤，是正常数据， 45x =时，4ˆ48.5y= 48.545 3.52-=>，不是正常数据，56x =时，5ˆ57y =，576032-=>，不是在正常数据，则5个数据中正常数据是3个，不正常数据是2个， 现从题中5个分拣数据中任取2个，求2个都是“正常数据”的概率2325310C P C ==. 【点睛】关键点点睛：本题的关键是正确理解题意，并能根据参考公式计算求值.18．（1）110；（2）①532y x ∧=-；②可靠，理由见解析.【分析】（1）根据题意写出所有的基本事件，即可求解：“不小于26”的概率； （2）①由题意求出x ，y ，代入公式求值，从而得到回归直线方程； ②分别将x 的值代入，检验数据的误差均是否不超过2个，即可判断． 【详解】（1）依题意得，m 、n 的所有情况有：{}23,25、{}23,30、{}23,26、{}23,16、{}25,30、{}25,26、{}25,16、{}30,26、{}30,16、{}26,16共有10个；则“m 、n 均不小于26”的事件只有{}30,26，所以110P =，即事件“m 、n 均不小于26”的概率为110； （2）①由数据得111312123x ++==，253026273y ++==， ()322221(1112)(1312)(1212)2i i x x =-=-+-+-=∑，()()31(1112)(2527)(1312)(3027)05iii x x y y =--=--+--+=∑，()()()31321522iii ii x x y y b x x ∧==--==-=∑∑，552712322a y x ∧=-=-⨯=-. 所以y 关于x 的线性回归方程为532y x ∧=-. ②可靠；由①知，y 关于x 的线性回归方程为532y x ∧=-.对于2日数据，将10x =代入线性回归方程得5103222y ∧=⨯-=，其误差为|2223|12-=<，对于30日数据，将8x =代入线性回归方程得583172y ∧=⨯-=，其误差为|1716|12-=<，所以，所得到的线性回归方程是可靠的. 【点睛】方法点睛：本题考查了线性回归方程的求法及应用，求线性回归方程的步骤： （1）首先求出x 的平均数x 和y 的平均数y（2）代入公式求回归方程的斜率()()()121ˆniii nii x x y y bx x ==--=-∑∑（3）代入公式求出回归方程的截距ˆˆay bx =-，考查学生的计算能力，属于基础题. 19．（1）1，3，2；（2）415. 【分析】（1）由分层抽样的性质运算即可得解；（2）利用列举法，结合古典概型概率的计算公式，即可得解. 【详解】（1）由题意，样品中来自A 地区商品的数量为650150150100⨯=++，来自B 地区商品的数量为6150350150100⨯=++，来自C 地区商品的数量为6100250150100⨯=++；（2）设来自A 地区的样品编号为a ，来自B 地区的样品编号为1b ,2b ,3b ， 来自C 地区的样品编号为1c ,2c ，则从6件样品中抽取2件产品的所有基本事件为:()1,a b ,()2,a b ,()3,a b ,()1,a c ,()2,a c ,()12,b b ,()13,b b ,()11,b c ,()12,b c ,()23,b b ,()21,b c ,()22,b c ,()31,b c ,()32,b c ,()12,c c ,共15个；抽取的这2件产品来自相同地区的基本事件有:()12,b b ,()13,b b ,()23,b b ,()12,c c ,共4个；故所求概率415P =. 【点睛】本题考查了分层抽样的应用及古典概型概率的求解，考查了运算求解能力，属于中档题. 20．（1）0．05；（2）0．45；（3）1200. 【分析】（1）先列举出所有的事件共有20种结果，摸出的3个球为白球只有一种结果，根据概率公式得到要求的概率，本题应用列举来解，是一个好方法；（2）先列举出所有的事件共有20种结果，摸出的3个球为1个黄球2个白球从前面可以看出共有9种结果种结果，根据概率公式得到要求的概率；（3）先列举出所有的事件共有20种结果，根据摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱，算一下摸出的球是同一色球的概率，估计出结果. 【详解】把3只黄色乒乓球标记为A 、B 、C ，3只白色的乒乓球标记为1、2、3．从6个球中随机摸出3个的基本事件为：ABC 、AB1、AB2、AB3、AC1、AC2、AC3、A12、A13、A23、BC1、BC2、BC3、B12、B13、B23、C12、C13、C23、123，共20个. (1)事件E={摸出的3个球为白球}，事件E 包含的基本事件有1个，即摸出123号3个球，P （E ）=120=0．05. (2)事件F={摸出的3个球为2个黄球1个白球}，事件F 包含的基本事件有9个，P （F ）=920=0．45. （3）事件G={摸出的3个球为同一颜色}={摸出的3个球为白球或摸出的3个球为黄球}，P （G ）=220=0．1，假定一天中有100人次摸奖， 由摸出的3个球为同一颜色的概率可估计事件G 发生有10次，不发生90次． 则一天可赚，每月可赚1200元．考点：1．互斥事件的概率加法公式；2．概率的意义 21．（1）0.016；（2）约为74.1；（3）35． 【分析】（1）由频率分布直方图中所有频率和为1可求得a ；（2）频率分布直方图中将所有小矩形面积二等分的点对应的值为中位数；（3）根据频率分布直方图求出成绩在[80,90)和[90,100]上的人数，然后利用对立事件的。

《第8章概率》试卷(答案在后面)一、单选题（本大题有8小题，每小题5分，共40分）1、下列事件中，不可能事件是（）。

A、抛一枚硬币，正面朝上B、明天会下雨C、地球围绕太阳转D、掷一枚骰子，得点数为72、从一个装有3个红球和2个白球的袋中随机取出两个球，则取出的两球颜色相同的概率是多少？A. 1/10B. 3/10C. 2/5D. 1/23、袋中有5个红球和3个蓝球，现在从袋中随机抽取一个球，抽出红球的概率是（）A、4/8B、5/8C、3/8D、1/24、从装有2个红球和2个白球的袋子中随机取出2个球，取出的两个球颜色相同的情况有（）种。

A. 1B. 2C. 3D. 45、someone is rolling two fair six-sided dice. What is the probability that the sum of the two dice is 7 given that the two dice show the same number？A. 1/6B. 1/9C. 1/16D. 1/126、某班级有40名学生，其中有20名喜欢篮球，15名喜欢足球，10名既喜欢篮球又喜欢足球。

以下关于这个班级学生喜好篮球或足球的描述正确的是（）A、喜欢篮球或足球的学生有35名B、喜欢篮球或足球的学生有25名C、既不喜欢篮球也不喜欢足球的学生有5名D、喜欢篮球的学生中至少有5人同时喜欢足球7、已知一袋中有4个红球和6个白球，从中任取2个球，则取出的2个球都是红球的概率是（）。

A、1/15B、2/15C、1/38、一个袋子里装有5个红球和6个蓝球，从中连续摸出两个球，不放回。

若第一次摸出的是红球，则第二次摸出蓝球的概率是多少？A.511B.16C.611D.3091二、多选题（本大题有3小题，每小题6分，共18分）1、设随机变量(X)的概率分布列为：[X012 P0.20.50.3]则下列哪些选项正确？A.(E(X)=1.1)B.(D(X)=0.69)C.(P(0<X<2)=0.5)D.(P(X≥1)=0.8)2、某学校有男生和女生共500人，为了研究学生在某些方面的共同点，学校决定采用分层抽样进行调查。

人教版（2019）高中英语选择性必修第二册Unit 5单元综合能力测试卷时间：100分钟满分：120分选择题部分第二部分阅读理解(共两节，满分40分)第一节(共15小题；每小题2分，满分30分)阅读下列短文，从每题所给的A、B、C和D四个选项中，选出最佳选项。

ADo you know a child who has used first aid to save a life or help an injured person?St.John Ambulance is seeking young people who have acted quickly，calmly and effectively at a real emergency for its annual Young First Aider of the Year awards.The awards are open to all those under 18，and the closing date for nomination (提名) is April 30，2017.The winners will be invited to attend a special ceremony in June，2020.“St.John Ambulance believes it is essential for young people to learn first aid so that they can help anyone who is injured，” said Sandra Stocker，director of St.John Ambulance Awards Committee.“The Young Fir st Aider of the Year is a wonderful way to celebrate their bravery and quick­thinking.”Nomination for the Young First Aider of the Year is now open.Please complete and return the nomination forms as soon as possible and certainly no later than April 30，2020.The committee will decide which of the nominees will receive the Young First Aider of the Year awards by considering the actions of the nominees along with their ages and other factors.You should send any evidence you have with the nomination form，showing the nominees' actions.Examples of evidence could include：◆ Newspaper clippings (剪报) of the incident.◆ Police incident record numbers.Once a nomination form is received，the nominee or nominator may be approached for further details of the incident.For further information please get in touch with Sandra Stocker by e-mail or on 020－73244082 or 020－73244083.Find out who our winners will be for 2020.1．What does the passage intend to tell the readers?A．Young people should learn first aid to help the injured.B．Learning first aid can help young people win an award.C．The injured are encouraged to act quickly and calmly.D．St.John Ambulance makes profit by training first aiders.2．If you suggest someone for the awards，you should ．A．attend the awards ceremonyB．make a speech introducing yourselfC．provide the details of the incidentD．have a good knowledge about first aid3．Which of the following is the best title for the passage?A．Demand for First AidersB．Importance of First AidC．St.John Ambulance AwardsD．Young First Aider of the YearBIn summer the extreme heat often makes people sweaty and restless.While people are annoyed by it，experts suggest summer is the best season to discharge (排放) your body's toxins (毒素) and recover your energy.One popular option is hot-stone massage (按摩)．Therapists use smooth and heated stones，usually river rocks，to massage certain parts of the body，or place them on key points of the body.The warmth of the hot stones will improve blood circulation and also help relax muscles，while sweating is also believed to be good for discharging the body's toxins.Another popular option is hot-stone baths.The hot-stone bath will help the body discharge toxins and humidity that accumulated during the last winter.Summer is the best season to build a good body.Rather than use water or steam to heat and wash the body，people simply wear a coat or something comfortable，and then lie on heated stone tablets made of hot stones，which are warmed to around 45℃.The body will gradually warm up and blood circulation will also be improved.More sweat will come out quickly.The sweat is smooth and fresh，not smelly like that released after sportsactivities.Such baths bring a number of health benefits，such as anti-aging，improved blood circulation and stress relief.The slimming effect of dieting can even be promoted.Using hot stones for healing dates back to ancient times，but the modern renewal of hot-stone massage is generally credited to Mary Nelson，a native of Tucson，Arizona，America，whose trademark is “LaStone Therapy”．The therapy is gaining wide popularity with many people，especially those who have jobs in cool air-conditioned rooms.The hot-stone therapy can help cure many diseases，including back pain.4．Which of the following could be the best title for the text?A．The origin and development of the hot-stone therapyB．The amazing functions of the hot-stone therapyC．A healthy and comfortable lifestyleD．How to live comfortably in summer5．What do people use to release toxins in our body according to the text?A．Washing the body with cold water.B．Discharging lots of sweat.C．Relaxing muscles.D．Lying on the warm beds.6．What can we know from the text?A．Sports have greater effects on the health than hot-stone massage.B．There are no toxins and humidity in the body in summer.C．Using water of about 45℃ to wash the body is good for the health.D．People should take advantage of summer to improve their health.7．What can be learned about the hot-stone therapy?A．It was invented by Mary Nelson，an American.B．It successfully cured many people of cancer.C．It is popular with people with its excellent effects.D．It can help people avoid sweating too much in hot summer.CSunstroke (中暑) is a condition that can quickly go from dangerous to deadly，especially if proper care isn't given immediately.Sunstroke，sometimes called heatstroke，is a result of the body temperature rising above the safe limit.This causes the body's necessary functions to stop working.It's usually pretty easy to avoid sunstroke，as long as proper action is taken.In that case，you need to act as quickly as possible to return that person's body to a safe temperature.Here are a few tips to help treat sunstroke.Call for helpCall to get an ambulance as quickly as possible.This should be the first thing you do，especially if the sunstroke person has fainted (昏倒)．Also，call for help from anyone nearby if you're in a public place.If there's no one around，call someone nearby if they can get there sooner than an ambulance.Ask everyone to bring you as much water as possible，if there isn't much nearby.Get the person to a cooler areaIf there's a building nearby，aim for that.Anywhere with plenty of air conditioners and water is perfect.If a building isn't available，bring the person to a well-shaded area.Get the water flowingIf the person is still conscious，get him or her to drink water.If there's a bathtub available，fill it with cool water and put the person in it.If your water supply is limited，you have to save it.Dampen a towel or shirt and put it on the person's body.Focus on the face，neck，and chest.Fan the personGetting moving air over the person cools him or her e anything，a towel or sheet，a shirt，your hands，or a piece of board.This is where having many people around really helps，as they can combine to fan the entire body.8．Which of the following is NOT mentioned in the text?A．Call for assistance from others.B．Leave the sunstroke person in the shade.C．Put a wet towel on the person's face.D．Help the person take some medicine.9．What is mainly discussed in the passage?A．The first aid for sunstroke.B．The causes of sunstroke.C．The chief symptoms of sunstroke.D．The essential prevention of sunstroke.10．The text probably comes from a(n) ．A．guidebook B．book reviewC．medical magazine D．official document11．When does a person get sunstroke?A．When the body doesn't function.B．When proper care is given immediately.C．When someone is exposed to the sun too long.D．When the body temperature goes up beyond what one can bear.DWhen your pet has an emergency，first aid is not a substitute for veterinary(兽医的) treatment.However，before you are able to get your pet to a veterinarian，knowing some basic first aid can help.Bite WoundsApproach the pet carefully to avoid getting bitten.Wear a mask for the animal and then check the wound.Clean the wound with large amounts of saline(盐水)．If these are not available，then regular water may be used.Wrap large open wounds to keep them clean.BleedingApply firm，direct pressure over the bleeding area until the bleeding stops.Hold the pressure for at least 10 minutes.Avoid bandages that cut off circulation.Breathing StopsCheck to see if the animal is choking(窒息) on a foreign object.If an animal is not breathing，place it on a firm surface with its left side up.Check for a heartbeat.If you hear a heartbeat but not breathing，close the animal's mouth and breathe directly into its nose—not the mouth—until the chest expands.Repeat 12 to 15 times per minute.BurnsWash the burn immediately with large amounts of cool，running water.Apply an ice pack for 15－20 minutes.Do not place an ice pack directly on the skin.Wrap the pack in a light towel or other cover.If the animal has large quantities of dry chemicals on its skin，brush them off.Water may activate some dry chemicals.Fractures(骨折)Symptoms include pain，inability to use a limb(腿)．Wear a mask for the pet and look for bleeding.If you can control bleeding without causing more injury，then do so.Watch for signs of shock.Don't try to set the fractures by pulling the limb.Transport the pet to the veterinarian immediately，supporting the injured part as best as you can.12．If your pet is burned by chemicals，you should ．A．wash away the chemicals with salineB．put an ice pack directly on the skinC．bind up the cut with a bandageD．get rid of them before washing13．The passage is mainly about ．A．doing pet first aidB．treating sick petsC．dealing with an emergencyD．working as a veterinarian14．The underlined word “substitute” in the first paragraph means something ．A．that is necessaryB．that can replace other thingsC．that is familiar with usD．that can calm people第二节(共5小题；每小题2分，满分10分)根据短文内容，从短文后的选项中选出能填入空白处的最佳选项。

第十章测评(时间:120分钟满分:150分)一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.一部三册的小说,任意排放在书架的同一层上,观察其排放次序,这一试验的样本空间包含的样本点个数n等于( ) A.3 B.4C.6D.121,2,3分别表示这三册小说,排序有(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1)共6种,故样本空间包含6个样本点.2.奥林匹克运动会会旗,由5个尺寸相同、互相套连的圆环组成,环的颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这样的5个环分发给甲、乙、丙、丁、戊五名同学制作,每人分得1个,则事件“甲分得红色”与“乙分得红色”是( )A.对立事件B.不可能事件C.互斥但不对立事件D.既不互斥也不对立事件A=“甲分得红色”,B=“乙分得红色”,则A∩B=⌀,A∪B≠Ω,故事件A与B互斥,但不对立.3.有分别写着数字1到120的120张卡片,从中任意取出1张,取出的卡片上的数字是2的倍数或3的倍数的概率是( )A.12B.34C.47D.23120,其中是2的倍数的数有60个,是3的倍数的数有40个,是6的倍数的数有20个,故所求概率P=60120+40 120−20120=23.4.甲在聊天群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完.若三人均领到整数元,且每人至少领到1元,则乙获得“手气最佳”(即乙领取的钱数不少于其他任何人)的概率是( )A.34B.13C.310D.25丙、丁分别领到x元、y元、z元,用数组(x,y,z)表示该试验的一个样本点,则样本空间Ω={(1,1,4),(1,4,1),(4,1,1),(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3, 1,2),(3,2,1),(2,2,2)},共10个样本点.记事件A=“乙获得‘手气最佳’”,则= A={(4,1,1),(3,1,2),(3,2,1),(2,2,2)},共有4个样本点,故P(A)=4102.55.某校在秋季运动会中,安排了篮球投篮比赛,现有20名同学参加篮球投篮比赛,已知每名同学投进的概率均为0.4,每名同学有2次投篮机会,且各同学投篮之间没有影响.现规定:投进两个得4分,投进一个得2分,一个未进得0分,则其中一名同学得2分的概率为( )A.0.5B.0.48C.0.4D.0.32A,“第二次投进球”为事件B,则得2分的概率为P=P(A B)+P(A B)=0.4×0.6+0.6×0.4=0.48.6.某班有男生30人、女生20人,按性别进行分层,用比例分配的分层随机抽样的方法从该班中选出5人负责校园开放日的接待工作,现从这5人中随机选取2人,至少有1名男生的概率是( )A.110B.310C.710D.910,男生应抽取3030+20×5=3(人),分别记为A,B,C;女生应抽取2人,分别记为甲、乙.从这5人中随机选取2人,试验的样本空间Ω={(A,B),(A,C),(A,甲),(A,乙),(B,C),(B,甲),(B,乙),(C,甲),(C,乙),(甲,乙)},共有10个样本点. 其中1名男生也没有的事件包含的样本点为(甲,乙),只有1个,所以至少有1名男生的概率为P=1-110=910.7.设每个工作日甲、乙、丙3人需使用某种设备的概率分别为0.2,0.5,0.6,若各人是否需使用该设备相互独立,则同一工作日中至少有1人需使用该设备的概率为( )A.0.84B.0.16C.0.94D.0.34,设A=“同一工作日中至少有1人需使用该设备”,则A的对立事件A=“同一工作日中三人都不需要使用该设备”,所以P(A)=1-P(A)=1-(1-0.2)×(1-0.5)×(1-0.6)=0.84.8.若一个三位数的各位数字互不相同,且各数字之和等于10,则称此三位数为“十全十美三位数”(如235),任取一个“十全十美三位数”,该数为奇数的概率为( )A.1320B.720C.12D.512Ω={109,190,901,910,127,172,217,271,712,721,136,163,316,361,613 ,631,145,154,415,451,514,541,208,280,802,820,235,253,325,352,52 3,532,307,370,703,730,406,460,604,640},共有40个样本点,其中该数为奇数包含的样本点有20个,所以任取一个“十全十美三位数”,该数为奇数的概率为2040=12.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知A={-1,0,1},点P的坐标为(x,y),其中x∈A,y∈A,任取一点P,观察点P的坐标,则下列点的坐标是试验的样本点的有( )A.(0,0)B.(-1,1)C.(1,1)D.(1,2)x ∈A,y ∈A,所以A,B,C 都满足条件;D 中,2∉A,所以(1,2)不是试验的样本点,故选ABC.10.甲、乙、丙三名学生用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲及格的概率为45,乙及格的概率为35,丙及格的概率为710,三人各答一次.则( ) A.三人中恰有1人及格的概率为47250 B.三人中恰有2人及格的概率为113250C.三人中至少有1人及格的概率为80125D.三人都不及格的概率为3125中,三人中恰有1人及格的概率P 1=45×(1-35)×(1-710)+(1-45)×35×(1-710)+(1-45)×(1-35)×710=47250,故A 正确;B 中,三人中恰有2人及格的概率P 2=45×35×(1-710)+45×(1-35)×710+(1-45)×35×710=113250, 故B 正确;D 中,三人都不及格的概率P 3=(1-45)×(1-35)×(1-710)=3125,故D 正确.C中,“三人中至少有1人及格”的对立事件为“三人都不及格”,所以三人中至少有1人及格的概率P4=1-3125=122125,故C不正确.11.国庆假期期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中抽取了40名驾驶员进行询问调查,将他们在某段高速公路的车速(单位:km/h)分成六组:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90],得到的频率分布直方图如图所示.下列结论正确的是( )A.这40辆小型汽车车速的众数的估计值为77.5B.在该服务区任意抽取一辆小型汽车,车速超过80 km/h的概率约为0.35C.若从车速在区间[60,70)内的小型汽车中任意抽取2辆,则至少有一辆小型汽车的车速在区间[65,70)内的概率为1415D.若从车速在区间[60,70)内的小型汽车中任意抽取2辆,则车速都在区间[60,65)内的概率为13A中,由题图可知,众数的估计值为最高小矩形底边中点的横坐标75+802=77.5,故A正确;选项B中,车速超过80km/h的频率为0.05×5+0.02×5=0.35,用频率估计概率,知B正确;选项C,D中,由题图知,在40辆被抽查的小型汽车中,车速在区间[60,65)内的车辆数为0.01×5×40=2,记为a,b;车速在区间[65,70)内的车辆数为0.02×5×40=4,记为1,2,3,4,则任意抽取2辆对应的样本空间Ω={(a,b),(a,1),(a,2),(a,3),(a,4),(b,1),(b,2),(b,3),(b,4),(1,2) ,(1,3),(1,4),(2,3),(2,4),(3,4)},共有15个样本点.记事件A=“2辆车速都在区间[60,65)内”,则A={(a,b)},共有1个样本点,故P(A)=115;记事件B=“至少有1辆的车速在区间[65,70)内”,则A与B互为对立事件,即P(B)=1-P(A)=1415.故C正确,D错误.三、填空题:本题共3小题,每小题5分,共15分.12.从集合{1,2,3,4,5,6,7,8,9}中任取一个数记为x,则log2x为整数的概率为.21=0,log22=1,log24=2,log28=3,则log2x为整数的概率为49.13.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:则该营业窗口上午9点钟时,至少有2人排队的概率是.14.袋里装有5个球,每个球都记有1~5中的一个号码,设号码为x的球质量为(x2-5x+30)克,这些球以同等的机会(不受质量的影响)从袋里取出.若同时从袋内任意取出2个球,则它们质量相等的概率是.2个球的号码分别是m,n,其中m≠n,则有m2-5m+30=n2-5n+30,所以m+n=5.5个球中任意取2个球的样本空间Ω={(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5) },共10个样本点.满足m+n=5的样本点有(1,4)和(2,3).所以P=210=15.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)对某班一次测验成绩进行统计,统计结果如下表所示.若从该班学生中,随机抽取一名,求:(1)他的这次测验成绩在区间[80,100]上的概率;(2)他的这次测验成绩在区间[60,100]上的概率.[60,70),[70,80),[80,90),[90,100]内依次为事件A,B,C,D,由题意知事件A,B,C,D两两互斥.(1)他的这次测验成绩在区间[80,100]上的概率是P(C∪D)=P(C)+P(D)=0.25+0.15=0.4.(2)他的这次测验成绩在区间[60,100]上的概率是P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D)=0.17+0.36+0.25+0.15=0.93.16.(15分)假设甲、乙两种品牌的同类产品在某地区市场上销售量相等,为了解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进行测试,统计结果如图所示.甲品牌乙品牌(1)估计甲品牌产品使用寿命小于200 h的概率;(2)这两种品牌产品中,某个产品已使用了200 h,试估计该产品是甲品牌的概率.甲品牌产品使用寿命小于200h的频率为5+20100=14,用频率估计概率,所以估计甲品牌产品使用寿命小于200h的概率为14.(2)根据频数分布图可得使用寿命不低于200h的两种品牌产品共有75+70=145(个),其中甲品牌产品有75个,所以在样本中,使用寿命不低于200h的产品是甲品牌的频率是75145=1529,据此估计已使用了200h的该产品是甲品牌的概率为1529.17.(15分)某同学参加科普知识竞赛,需回答三个问题,竞赛规则规定:答对第一、二、三个问题分别得100分、100分、200分,答错得零分.假设这名同学答对第一、二、三个问题的概率分别为0.8,0.7,0.6,且各题答对与否相互之间没有影响.(1)求这名同学得300分的概率;(2)求这名同学至少得300分的概率.A i(i=1,2,3)=“这名同学答对第i个问题”,则P(A1)=0.8,P(A2)=0.7,P(A3)=0.6,且A1,A2,A3相互独立.(1)这名同学得300分的概率P1=P(A1A2A3)+P(A1A2A3)=P(A1)P(A2)P(A3)+P(A1)P(A2)P(A3)=0.8×0.3×0.6+0.2×0.7×0.6=0.228.(2)这名同学至少得300分的概率P2=P1+P(A1A2A3)=0.228+P(A1)P(A2)P(A3)=0.228+0.8×0.7×0.6=0.564.18.(17分)某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中随机抽取10件作为样本,其质量指标列表如下:(1)利用上表提供的样本数据估计该批产品的一等品率.(2)在该样本的一等品中,随机抽取2件产品,①用产品编号写出试验的样本空间;②设事件B=“在取出的2件产品中,每件产品的综合指标S都等于4”,求P(B).计算10件产品的综合指标S,如下表:其中S≤4的有A 1,A 2,A 4,A 5,A 7,A 9,共6件,故该样本的一等品率为610=0.6,从而可估计该批产品的一等品率为0.6.(2)①在该样本的一等品中,随机抽取2件产品对应的样本空间Ω={(A 1,A 2),(A 1,A 4),(A 1,A 5),(A 1,A 7),(A 1,A 9),(A 2,A 4),(A 2,A 5),(A 2,A 7),(A 2,A 9),(A 4,A 5),(A 4,A 7),(A 4,A 9),(A 5,A 7),(A 5,A 9),(A 7,A 9)},共有15个样本点. ②在该样本的一等品中,综合指标S 等于4的产品编号分别为A 1,A 2,A 5,A 7,则事件B={(A 1,A 2),(A 1,A 5),(A 1,A 7),(A 2,A 5),(A 2,A 7),(A 5,A 7)},共有6个样本点.所以P(B)=615=25.19.(17分)在奥运知识有奖问答竞赛中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲答对这道题的概率是34,甲、乙两人都回答错误的概率是112,乙、丙两人都回答正确的概率是14.设每人回答问题正确与否是相互独立的.(1)求乙答对这道题的概率;(2)求甲、乙、丙三人中,至少有一人答对这道题的概率.记事件A=“甲答对这道题”,B=“乙答对这道题”,C=“丙答对这道题”,设P(B)=x,由于每人回答问题正确与否是相互独立的,故A,B,C 是相互独立事件.由题意得,P(AB )=P(A )P(B )=(1-34)×(1-x)=112,解得x=23,所以乙答对这道题的概率为23.(2)设丙答对这道题的概率P(C)=y,由(1)得,P(BC)=P(B)P(C)=23×y=14,解得y=38.记事件M=“甲、乙、丙三人中,至少有一人答对这道题”,则事件M 的对立事件M =“甲、乙、丙三人都回答错误”,因为P(M )=P(ABC )=P(A )P(B )P(C )=(1-34)×(1-23)×(1-38)=596.所以所求概率P(M)=1-P(M )=1-596=9196.。

一、选择题1．我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”.下图是在“赵爽弦图”的基础上创作出的一个“数学风车”，其中正方形ABCD 内部为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的.我们将图中阴影所在的四个三角形称为同一片“风叶”的概率为（ ）A ．37B ．47C ．314D ．11142．甲、乙两人独立地对同一目标各射击一次，命中率分别为0.6和0.8，在目标被击中的条件下，甲、乙同时击中目标的概率为（ ） A ．2144B ．1223C ．1225D ．21113．斐波那契数列（Fibonacci sequence ）又称黄金分割数列，因数学家列昂纳多·斐波那契（Leonardoda Fibonacci ）以兔子繁殖为例子而引入，故又称为“兔子数列”．在数学上，斐波纳契数列被以下递推的方法定义：数列{}n a 满足：121a a ==，21++=+n n n a a a ，现从数列的前2019项中随机抽取1项，能被3整除的概率是（ ） A ．14B ．2522019C ．5042019D ．50520194．两个实习生每人加工一个零件．加工为一等品的概率分别为23和34，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为A ．12B ．512C ．14D ．165．甲乙两运动员进行乒乓球比赛，采用7局4胜制.在一局比赛中，先得11分的运动员为胜方，但打到10平以后，先多得2分者为胜方.在10平后，双方实行轮换发球法，每人每次只发1个球.若在某局比赛中，甲发球时甲得分的概率为23，乙发球时甲得分的概率为12，各球的结果相互独立，在某局双方10:10平后，甲先发球，则甲以13:11赢下此局的概率为（ ） A ．29B ．19C ．16D ．1186．一个不透明的袋子中装有4个完全相同的小球，球上分别标有数字为0，1，2，3.现甲从中摸出1个球后放回，乙再从中摸出1个球，谁摸出的球上的数字大谁获胜，则甲、乙各摸一次球后，甲获胜且乙摸出的球上数字为偶数的概率为（ ） A ．14B ．13C ．49D ．3167．袋中装有白球3个，黑球4个，从中任取3个，下列各对事件中互为对立事件的是（ ）A ．恰有1个白球和全是白球B ．至少有1个白球和全是黑球C ．至少有1个白球和至少有2个白球D ．至少有1个白球和至少有1个黑球8．“三个臭皮匠，赛过诸葛亮”，这是我们常说的口头禅，主要是说集体智慧的强大. 假设李某智商较高，他独自一人解决项目M 的概率为10.3P =；同时，有n 个水平相同的人也在研究项目M ，他们各自独立地解决项目M 的概率都是0.1.现在李某单独研究项目M ，且这n 个人组成的团队也同时研究项目M ，设这个n 人团队解决项目M 的概率为2P ，若21P P ≥，则n 的最小值是( ) A ．3B ．4C ．5D ．69．将一颗质地均匀的骰子先后抛掷3次，至少出现一次6点向上的概率是（ ） A ．91216B ．31216C ．25216D ．521610．若从集合{}2,1,2A =-中随机取一个数a ，从集合{}1,1,3B =-中随机取一个数b ，则直线0ax y b -+=一定．．经过第四象限的概率为( ) A ．29B ．13C ．49D ．5911．素数分布是数论研究的核心领域之一，含有众多著名的猜想.19世纪中叶，法国数学家波利尼亚克提出了“广义孪生素数猜想”：对所有自然数k ，存在无穷多个素数对(2)p p k +，.其中当1k =时，称(2)p p +，为“孪生素数”，2k =时，称(4)p p +，为“表兄弟素数”.在不超过30的素数中，任选两个不同的素数p ､q (p q <)，令事件(){A p q =，为孪生素数}，(){B p q =，为表兄弟素数}，{()|4}C p q q p =-≤，，记事件A ､B ､C 发生的概率分别为()P A ､()P B ､(C)P ，则下列关系式成立的是（ ） A ．()()()P A P B P C =B ．()()()P A P B PC += C ．()()()P A P B P C +>D ．()()()P A P B P C +<12．某普通高校招生体育专业测试合格分数线确定为60分，甲、乙、丙三名考生独立参加测试，他们能达到合格的概率分别是0.9，0.8，0.75，则三人中至少有一人达标的概率为（ ） A ．0.015B ．0.005C ．0.985D ．0.99513．甲、乙两人独立地对同一目标各射击一次，其命中率分别为0.6,0.5，现已知目标被击中，则它是被甲击中的概率是( ) A ．0.45B ．0.6C ．0.65D ．0.75二、解答题14．某校为了了解高三学生某次月考数学成绩的情况，抽取这次月考100名学生的数学成绩(分数都在[]50,150内)，按数学成绩分成[)50,70、[)70,90、[)90,110、[)110,130、[]130,150这5组，得到频率分布直方图如图所示.（1）估计这次月考该校高三学生数学成绩的中位数（结果保留一位小数）；（2）若从数学成绩在[]110,150内的学生中采用分层抽样的方法随机抽取5人，再从这5人中随机抽取2人，求至少有1人的数学成绩在[]130,150内的概率.15．在新冠肺炎疫情期间，为了认真贯彻落实北京市教委关于做好中小学生延期开学期间“停课不停学”工作要求，各校以教师线上指导帮助和学生居家自主学习相结合的教学模式积极开展工作.为了解学生居家自主学习的情况，从某校高二年级随机抽取了100名学生，获得了他们一天中用于居家自主学习的时间分别在[)[)[)0,1,1,2,2,3，[)[)[)3,4,4,5,5,6，[)[]677,8,,（单位：小时）的数据，整理得到的数据绘制成频率分布直方图（如图）.（1）由图中数据，求a 的值，并估计从该校高二年级中随机抽取一名学生，这名学生该天居家自主学习的时间在[)3,4的概率；（2）现从抽取的100名学生该天居家自主学习的时间在[)0,1和[)1,2的人中任选2人，进一步了解学生的具体情况，求其中学习时间在[)0,1中至少有1人的概率；（3）假设同一时间段中的每个数据可用该时间段的中点值代替，试估计样本中的100名学生该天居家自主学习时间的平均数.16．袋中装有6个形状、大小完全相同的球，其中黑球2个、白球2个、红球2个，规定取出一个黑球记0分，取出一个白球记1分，取出一个红球记2分，抽取这些球的时候，谁也无法看到球的颜色，首先由甲取出3个球，并不再将它们放回原袋中，然后由乙取出剩余的3个球，规定取出球的总积分多者获胜. （1）求甲、乙成平局的概率；（2）从概率的角度分析先后取球的顺序是否影响比赛的公平性.17．甲､乙两队举行围棋擂台赛，规则如下：两队各出3人，排定1，2，3号.第一局，双方1号队员出场比赛，负的一方淘汰，该队下一号队员上场比赛.当某队3名队员都被淘汰完，比赛结束，未淘汰完的一方获胜.如图表格中，第m 行､第n 列的数据是甲队第m 号队员能战胜乙队第n 号队员的概率. 0.5 0.3 0.2 0.6 0.5 0.3 0.8 0.7 0.63名队员都淘汰的概率；（2）比较第三局比赛，甲队队员和乙队队员哪个获胜的概率更大一些？18．某医院首批援鄂人员中有2名医生，3名护士和1名管理人员.采用抽签的方式，从这六名援鄂人员中随机选取两人在总结表彰大会上发言.（Ⅰ）写出发言人员所有可能的结果构成的样本空间；（Ⅱ）求选中1名医生和1名护士发言的概率；（Ⅲ）求至少选中1名护士发言的概率.19．“每天锻炼一小时，健康工作五十年，幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关，从单位随机抽取30名员工进行了同卷调查，得到了如下列联表：（1）请将上面的列联表补充完整（在答题卡上直接填写结果，不需要写求解过程）；（2）能否有95%的把握认为爱好运动与性别有关？（3）若在接受调查的所有男生中按照“爱好与不爱好运动”进行分层抽样，现随机抽取8人，再从8人中抽取3人，求至少有2人“爱好运动”的概率.附：()()()()()22n ad bcKa b c d a c b d-=++++20．随着科学技术的飞速发展，手机的功能逐渐强大，很大程度上代替了电脑电视.为了了解某高校学生平均每天使用手机的时间与性别是否有关，某调查小组随机抽取了30名男生，20名女生进行为期一周的跟踪调查，调查结果如表所示：（1）能否在犯错误的概率不超过0.01的前提下认为学生使用手机的时间长短与性别有关？（2）在这20名女生中，调查小组发现共有15人使用国产手机，在未使用国产手机的人中，平均每天使用手机不超过3小时的共有2人.从未使用国产手机的人中任意选取3人，求至多有一人使用手机不超过3小时的概率.()20P K k ≥ 0.500 0.400 0.250 0.150 0.100 0.050 0.025 0.010 0k0.4550.7081.3232.0722.7063.8415.0246.635参考公式：()()()()()22n ad bc K a c b d a b c d -=++++（n a b c d =+++）.21．为普及抗疫知识、弘扬抗疫精神，某学校组织防疫知识竞赛.比赛共分为两轮，每位参赛选手均须参加两轮比赛，若其在两轮比赛中均胜出，则视为赢得比赛.已知在第一轮比赛中，选手甲、乙胜出的概率分别为35，34；在第二轮比赛中，甲、乙胜出的概率分别为23，25.甲、乙两人在每轮比赛中是否胜出互不影响. （1）从甲、乙两人中选取1人参加比赛，派谁参赛赢得比赛的概率更大？ （2）若甲、乙两人均参加比赛，求两人中至少有一人赢得比赛的概率.22．为了保证食品安全，保障公众身体健康和生命安全，2018年国家对《食品安全法》进行了修正.2020，年春节前夕，某市质检部门随机抽取了20包某种品牌的速冻水饺，对某项质量指标进行检测.经统计，质量指标均在区间[0，50]内，将其按[0，10)､[10，20)､[20，30)､[30，40)､[40，50]分成5组，制成如图所示的频率分布直方图.（1）求该频率分布直方图中x 的值；（2）若同组中的每个数据用该组区间中点值代替，估计该品牌速冻水饺的该项质量指标的平均值：（3）从质量指标大于等于30的速冻水饺中任选2包，进行深度检测，求这2包处于不同区间的概率.23．有n名学生，在一次数学测试后，老师将他们的分数（得分取正整数，满分为100分），按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图（如图1），并作出样本分数的茎叶图（如图2）（图中仅列出了得分在[60，70），[90，100]的数据）．（1）求样本容量n和频率分布直方图中x、y的值；（2）从成绩在80分以上（含80分）的学生中随机抽取2名学生参加校数学竞赛，求所抽取的2名学生中至少有一人得分在[90，100]内的概率；（3）分数在[80，100]的学生中，男生有2人，现从该组抽取三人“座谈”，求至少有两名女生的概率．24．2020年是全面建成小康社会目标实现之年，也是全面打赢脱贫攻坚战收官之年.某乡镇在2014年通过精准识别确定建档立卡的贫困户共有500户，结合当地实际情况采取多项精准扶贫措施，每年新脱贫户数如下表年份2015201620172018209年份代码x12345脱贫户数y55688092100=+，并预测到2020（1）根据2015-2019年的数据，求出y关于x的线性回归方程y bx a年底该乡镇500户贫困户是否能全部脱贫；（2）2019年的新脱贫户中有20户五保户，20户低保户，60户扶贫户.该乡镇某干部打算按照分层抽样的方法对2019年新脱贫户中的5户进行回访，了解生产生活、帮扶工作开展情况.为防止这些脱贫户再度返贫，随机抽取这5户中的2户进行每月跟踪帮扶，求抽取的2户中至少有1户是扶贫户的概率.参考数据：5115526838049251001299 i iix y==⨯+⨯+⨯+⨯+⨯=∑参考公式：()() ()1122211n ni i i ii in ni ii ix y nx y x x y ybx nx x x====---==--∑∑∑∑，a y bx=-25．某重点中学为了了解学生在期末市统考中的数学考试情况，抽取了100名学生的数学成绩．以[)80,90，[)90,100，[)100,110，[)110,120，[)120130,，[)130140,，[]140,150分组的频率分布直方图如下图所示：（1）求直方图中x的值；（2）求数学成绩的中位数；（3）在数学成绩为[)120130,，[)130140,，[]140,150的三组学生中，用分层抽样的方法抽取6名学生，在这6名学生中选出2名学生参加数学竞赛，求至少有一名学生在[)130140,分组的概率．26．2020年开始，山东推行全新的高考制度，新高考不再分文理科，采用“3+3”模式，其中语文、数学、外语三科为必考科目，满分各150分，另外考生还需要依据想考取的高校及专业要求，结合自己的兴趣爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科满分100分，2020年初受疫情影响，全国各地推迟开学，开展线上教学．为了了解高一学生的选科意向，某学校对学生所选科目进行线上检测，下面是100名学生的物理、化学、生物三科总分成绩，以组距20分成7组：[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300]，画出频率分布直方图如图所示．（1）求频率分布直方图中a 的值； （2）由频率分布直方图；（i ）求物理、化学、生物三科总分成绩的中位数；（ii ）估计这100名学生的物理、化学、生物三科总分成绩的平均数（同一组中的数据用该组区间的中点值作代表）；（3）为了进一步了解选科情况，由频率分布直方图，在物理、化学、生物三科总分成绩在[220，240）和[260，280）的两组中，用分层随机抽样的方法抽取7名学生，再从这7名学生中随机抽取2名学生进行问卷调查，求抽取的这2名学生来自不同组的概率．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】由从“数学风车”的八个顶点中任取两个顶点，得到基本事件的个数为28C 种，这两个顶点取自同一片“风叶”的基本事件有234C 种，结合古典概型的概率计算公式，即可求解. 【详解】由题意，从“数学风车”的八个顶点中任取两个顶点的基本事件有2828C =种，其中这两个顶点取自同一片“风叶”的基本事件有234C 12=， 根据古典概型的概率计算公式，可得所求概率123287P ==. 故选：A.【点睛】本题主要考查了古典概型的概率计算，以及组合的概念及组合数的计算，其中解答中正确理解题意，根据组合数的计算公式求得基本事件的总数及所求事件所含有的基本事件的个数是解答的关键，着重考查分析问题和解答问题的能力.2．B解析：B 【分析】根据题意,记甲击中目标为事件A ,乙击中目标为事件B ,目标被击中为事件C ,由相互独立事件的概率公式,计算可得目标被击中的概率,进而计算在目标被击中的情况下,甲、乙同时击中目标的概率,可得答案. 【详解】根据题意,记甲击中目标为事件A ,乙击中目标为事件B ,目标被击中为事件C , 则()()()()()1110.610.80.92P C P A P B =-=--⨯-=； 则在目标被击中的情况下,甲、乙同时击中目标的概率为0.60.80.921223P ⨯==. 故选：B. 【点睛】本题考查条件概率的计算,是基础题,注意认清事件之间的关系,结合条件概率的计算公式正确计算即可.属于基础题.3．C解析：C 【分析】依次写出数列各项除以3所得余数，寻找后可得结论． 【详解】根据斐波纳契数列的定义，数列各项除以3所得余数依次为：1,1,2,0,2,2,1,0,1,1,2,，余数数列是周期数列，周期为8，201925283=⨯+，所以数列的前2019项中能被3整除的项有2522504⨯=，所求概率为5042019P =． 故选：C ． 【点睛】本题考查古典概型，考查斐波纳契数列，考查数列的周期性．解题关键是依次写出波纳契数列各项除以3所得余数形成的新数列．4．B解析：B 【解析】记两个零件中恰好有一个一等品的事件为A ，即仅第一个实习生加工一等品(A 1)与仅第二个实习生加工一等品(A 2)两种情况，则P (A )=P (A 1)+P (A 2)=2 3×14+13×34=512故选B.5．C解析：C 【分析】本题先判断所求事件的两种情况，根据事件的独立性，直接求解即可. 【详解】在比分为10:10后甲先发球的情况下，甲以13:11赢下此局分两种情况： ①后四球胜方依次为甲乙甲甲，概率为12121132329P =⋅⋅⋅=； ②后四球胜方依次为乙甲甲甲，概率为211211323218P =⋅⋅⋅=， 所以，所求事件概率为：121119186P P +=+=， 故选：C. 【点睛】本题考查事件的独立性，分类讨论思想，是中档题.6．A解析：A 【分析】先求得甲、乙各摸一次球所包含的基本事件，在列举出甲、乙各摸一次球后，甲获胜且乙摸出的球上数字为偶数所包含的基本事件的个数，结合古典概型的概率计算公式，即可求解. 【详解】由题意，甲、乙各摸一次球，所有可能的结果有4416⨯=（种），甲摸的数字在前，乙摸的数字在后，则甲获胜的情况有()1,0，()2,0，()2,1，()3,0，()3,1，()3,2，共6种，其中甲、乙各摸一次球后，甲获胜且乙摸出的球上数字为偶数有()1,0，()2,0，()3,0，()3,2，共有4种，所求概率为41164P ==. 故选：A. 【点睛】本题主要考查的是古典概型及其概率计算公式，属于基础题，解题时要准确理解题意，正确求得试验中包含的基本事件的总数数和所求事件所包含的基本事件的个数，利用古典概型及其概率的计算公式求解是解答的关键，着重考查了分析问题和解答问题的能力.7．B解析：B 【分析】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，进而可分析四个事件的关系； 【详解】从白球3个，黑球4个中任取3个，共有四种可能，全是白球，两白一黑，一白两黑和全是黑球，故①恰有1个白球和全是白球，是互斥事件，但不是对立事件， ②至少有1个白球和全是黑球是对立事件； ③至少有1个白球和至少有2个白球不是互斥事件， ④至少有1个白球和至少有1个黑球不是互斥事件， 故选B ． 【点睛】本题考查互斥事件和对立事件的关系，对于题目中出现的两个事件，观察两个事件之间的关系，这是解决概率问题一定要分析的问题，本题是一个基础题．8．B解析：B 【解析】 【分析】设这个n 人团队解决项目M 的概率为2P ，则021(0.9)n n P C =-，由21P P ，得10.90.3n -， 由此能求出n 的最小值． 【详解】李某智商较高，他独自一人解决项目M 的概率为10.3P =，有n 个水平相同的人也在研究项目M ，他们各自独立地解决项目M 的概率都是0.1， 现在李某单独研究项目M ，且这n 个人组成的团队也同时研究M ， 设这个n 人团队解决项目M 的概率为2P ，则021(0.9)n nP C =-， 21P P ，10.90.3n∴-， 解得4n ≥．n ∴的最小值是4．故选B ． 【点睛】本题考查实数的最小值的求法，考查n 次独立重复试验中事件A 恰好发生k 次的概率的计算公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．9．A解析：A【解析】 【分析】事件“至少出现一次6点向上”的对立事件是“出现零次6点向上”，由此借助对立事件的概率进行求解． 【详解】由题事件“至少出现一次6点向上”的对立事件是“出现零次6点向上”所以至少出现一次6点向上的概率0303111259111166216216p C ⎛⎫⎛⎫=--=-= ⎪ ⎪⎝⎭⎝⎭故选A. 【点睛】本题考查应用对立事件求概率，属于一般题．10．D解析：D 【分析】由题意，利用列举法求得基本事件(),a b 的总数，再列举出所求事件所包含的基本事件的个数，利用古典概型及其概率的计算公式，即可求解. 【详解】由题意，从集合{}2,1,2A =-中随机取一个数a ，从集合{}1,1,3B =-中随机取一个数b ，得到(),a b 的取值的所有可能了结果共有：()()()()()()()()()2,1,2,1,2,3,1,1,1,1,1,3,2,1,2,1,2,3------，共计9种结果，由直线0ax y b -+=，即y ax b =+，其中当0a b ≥⎧⎨≥⎩时，直线不过第四象限， 共有()()()()1,1,1,3,2,1,2,3，共计4种，所以当直线0ax y b -+=一定．．经过第四象限时，共有5中情况， 所以概率为59P =，故选D. 【点睛】本题主要考查了古典概型及其概率的计算，以及直线方程的应用，其中解答中根据题意列举出基本事件的总数，进而利用古典概型及其概率的计算公式求解是解答的关键，着重考查了推理与计算能力，属于基础题.11．D解析：D 【分析】根据素数的定义，一一列举出不超过30的所有素数，共10个，根据组合运算，得出随机选取两个不同的素数p 、q (p q <)，有21045C =(种)选法，从而可列举出事件A 、B 、C的所有基本事件，最后根据古典概率分别求出(),()P A P B 和(C)P ，从而可得出结果. 【详解】解：不超过30的素数有2、3、5、7、11、13、17、19、23、29，共10个，随机选取两个不同的素数p 、q (p q <)，有21045C =(种)选法，事件A 发生的样本点为(3)5，、(57)，、(1113)，、(1719)，共4个， 事件B 发生的样本点为(37)，、(711)，、(1317)，、(1923)，共4个， 事件C 发生的样本点为(2)3，、(25)，、(3)5，、(37)，、(57)，、 (711)，、(1113)，、(1317)，、(1719)，、(1923)，，共10个，∴4()()45P A P B ==，102()459P C ==， 故()()()P A P B P C +<.故选：D. 【点睛】关键点点睛：本题考查与素数相关的新定义，考查古典概型的实际应用和利用列举法求古典概型，考查组合数的计算，解题的关键在于理解素数的定义，以及对题目新定义的理解，考查知识运用能力.12．D解析：D 【分析】设出每一个每一个考生达标的事件，并求其对立事件的概率，根据相互独立事件的概率的和事件求解出答案. 【详解】设 “甲考生达标” 为事件A ， “乙考生达标” 为事件B ， “丙考生达标” 为事件C ，则()0.9P A =，()0.8P B =，()0.75P C =，()10.90.1P A =-=，()10.80.2P B =-=，()10.750.25P C =-=，设 “三人中至少有一人达标” 为事件D ，则()()110.10.20.2510.0050.995P D P ABC =-=-⨯⨯=-=， 故选：D. 【点睛】本题以实际问题为背景考查相互独立事件的概念及其发生的概率的计算，考查分析问题和解决问题的能力，属于中档题.13．D解析：D 【解析】根据题意，记甲击中目标为事件A ，乙击中目标为事件B ，目标被击中为事件C ，则()1()()1(10.6)(10.5)0.8P C P A P B =-=---=.∴目标是被甲击中的概率是0.60.750.8P == 故选D.二、解答题14．（1）中位数为100.5分；（2）710. 【分析】（1）设中位数为m ，利用中位数左边的矩形面积之和为0.5列等式可求得m 的值； （2）计算出所抽取的5人中数学成绩在[)110,130的学生有3人，记为a 、b 、c ，数学成绩在[]130,150的学生有2人，记为D 、E ，列举出所有的基本事件，并确定事件“抽取的2人中至少有1人的数学成绩在[]130,150内”所包含的基本事件数，利用古典概型的概率公式可求得所求事件的概率. 【详解】（1）因为()0.0040.010200.280.5+⨯=<，()0.0040.0100.021200.70.5++⨯=>，所以中位数在[)90,110内.设中位数为m ，则()0.28900.0210.5x +-⨯=，解得100.5m ≈， 即这次月考该校高三学生数学成绩的中位数约为100.5分；（2）由题意可得这次月考数学成绩在[)110,130的人数为1000.0092018⨯⨯=， 这次月考数学成绩在[]130,150的人数为1000.0062012⨯⨯=，则采用分层抽样的方法随机抽取的5人中，数学成绩在[)110,130的学生有3人，记为a 、b 、c ，数学成绩在[]130,150的学生有2人，记为D 、E .从这人中随机抽取2人的情况有ab 、ac 、aD 、aE 、bc 、bD 、bE 、cD 、cE 、DE ，共10种，其中符合条件的情况有aD 、aE 、bD 、bE 、cD 、cE 、DE ，共7种， 故所求概率710P =. 【点睛】方法点睛：求解古典概型概率的方法如下： （1）列举法； （2）列表法； （3）树状图法； （4）排列组合数的应用.15．（1）0.1a =；0.1；（2）710；（3）5.38小时. 【分析】（1）由频率之和等于1求出a 的值，这名学生该天居家自主学习的时间在[)3,4的概率； （2）由频率分布直方图可知自主学习时间在[)0,1和[)1,2的人分别有2人和3人，设在[)0,1的2人分别为,a b ，在[)1,2的3人分别,,A B C ，利用列举法结合古典概型的概率公式得出概率；（3）由频率分布直方图中的数据，求解平均数即可. 【详解】解：（1）因为(0.02+0.03+0.05+0.1520.20.3)11a +⨯++⨯=，所以0.1a =. 由图可得：随机抽取的100名学生中居家自主学习时间该天在[)3,4的频率为0.110.1⨯= 所以从该校高二年级中随机抽取一名学生，这名学生该天居家自主学习时间在[)3,4的概率为0.1.（2）设“抽取的2人其中学习时间在[)0,1中至少有1人”为事件A由图中数据可知：该天居家自主学习时间在[)0,1和[)1,2的人分别有2人和3人. 设在[)0,1的2人分别为,a b ，在[)1,2的3人分别,,A B C则从这5人中任选2人的样本空间{}ab,aA,aB,aC,bA,bB,bC,AB,AC,BC =， 共有10个，样本点事件A {}ab,aA,aB,aC,bA,bB,bC =， 共有7个样本点()710P A =所以学习时间在[)0,1中至少有1人的概率为710（3）样本平均数：()0.50.02 1.50.03 2.50.05 3.50.1 4.57.50.15 5.50.2 6.50.3x =⨯+⨯+⨯+⨯++⨯+⨯+⨯5.38=.样本中的100名学生该天居家自主学习时间的平均数为5.38小时. 【点睛】关键点睛：在第一问中，关键是利用频率之和等于1求出a 的值，在第二问中主要是利用列举法求解概率.16．（1）25；（2）不影响比赛的公平性..【分析】（1）将甲的可能取球基本事件一一列举出来，甲乙平局时的基本事件列举出来，根据古典概型概率公式计算即可；（2）结合（1）计算先取者（甲）获胜的概率，后取者（乙）获胜的概率，比较即可得出结论. 【详解】解：（1）记黑球为1，2号，白球为3，4号，红球为5，6号，则甲的可能取球共有以下20种情况：123，124，125，126，134，135，136，145，146，156，234，235，236，245，246，256，345，346，356，456，甲乙平局时都得3分，所以甲取出的三个小球是一黑一白一红，共8种情况， 故平局的概率182205P ==. （2）甲获胜时，得分只能是4分或5分，即取出的是2红1白，1红2白，2红1黑共6种情况，故先取者（甲）获胜的概率2632010P ==， 后取者（乙）获胜的概率3233151010P =--=， 所以23P P =，故先取后取获胜的概率一样. 【点睛】求古典概型概率的步骤：（1）判断本试验的结果是否为等可能事件，设出所求事件A ；（2）分别求出基本事件的总数n 与所求事件A 中所包含的基本事件个数m ； （3）利用公式()mP A n=，求出事件A 的概率． 17．（1）0.045；（2）甲队队员获胜的概率更大一些. 【分析】（1）甲队2号队员把乙队3名队员都淘汰这个事件的发生应是甲队1号输给乙队1号，然后甲队2号上场，三场全胜，由独立事件概率公式计算可得；（2）第三局比赛甲胜可分为3个互斥事件：甲队1号胜乙队3号，甲队2号胜乙队2号，甲队3号胜乙队1号，分别计算概率后相加可得．然后由对立事件概率得出乙队胜的概率，比较后要得结论． 【详解】解：（1）甲队2号队员把乙队3名队员都淘汰的概率为0.50.60.50.30.045⨯⨯⨯= （2）第3局比赛甲队队员获胜可分为3个互斥事件 （i ）甲队1号胜乙队3号，概率为0.50.30.20.03⨯⨯=；（ii ）甲队2号胜乙队2号，概率为0.50.70.50.50.60.50.325⨯⨯+⨯⨯=； (iii )甲队3号胜乙队1号，概率为0.50.40.80.16⨯⨯= 故第3局甲队队员胜的概率为0.030.3250.160.515++=. 则第3局乙队队员胜的概率为10.5150.485-= 因为0.5150.485>，故甲队队员获胜的概率更大一些． 【点睛】。

2021年人教A 版（2019）必修第二册数学第十章 概率单元测试卷（1）一、选择题1. 下列事件中，随机事件的个数为( )①在学校运动会上，学生张涛获得100m 短跑冠军；②在体育课上，体育老师随机抽取一名学生去拿体育器材，抽到李凯；③从标有1，2，3，4的4张号签中任取一张，恰为1号签；④在标准大气压下，水在 4∘C 时结冰.A.1B.2C.3D.42. 下列事件：①连续两次抛掷同一个骰子，两次都出现2点；②明天下雨；③某人买彩票中奖；④从集合{1, 2, 3}中任取两个元素，它们的和大于2；⑤在标准大气压下，水加热到90∘C 时会沸腾，其中是随机事件的个数有( )A.1B.2C.3D.43. 从0，1，2，3这四个数字中任取三个不同的数字，则所抽取的三个数字之和能被6整除的概率为( )A.12B.15C.14D.254. 甲，乙两人参加一次考试，他们合格的概率分别为13，14，那么两人中恰有1人合格的概率是( )A.712B.512C.12D.1125. 甲、乙两人玩猜数字游戏，先由甲心中想一个数字，记为a ，再由乙猜甲刚才所想的数字，把乙猜的数字记为b ，其中a ，b ∈{1, 2, 3, 4, 5, 6}，若|a −b|≤1，就称甲乙“心有灵犀”．现任意找两人玩这个游戏，则他们“心有灵犀”的概率为( )A.19B.29C.718D.496. 甲、乙两人下棋，两人下成和棋的概率是12，甲获胜的概率是13，则甲不输的概率为( )A.56B.25C.16D.137. 将一枚硬币连续抛掷n 次，若使得至少有一次正面向上的概率不小于1516，则n 的最小值为( )A.4B.5C.6D.78.袋子中有大小、形状完全相同的四个小球,分别写有“和”、“谐”、“校”、“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率.利用电脑随机产生1到4之间取整数值的随机数分别用1,2,3,4代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下18组随机数:343 432 341 342 234 142 243 331 112342 241 244 431 233 214 344 142 134由此可以估计,恰好第三次就停止摸球的概率为( )A.19B.16C.29D.5189. 某重点中学为了解本校高二年级的900名学生利用假期时间参加社会实践的情况，从年级学生中随机的抽取了50名学生进行调查，统计所收集的数据，得到下面的频率分布表：估计该校高二学生参加社会实践情况正确的是( )A.参加活动次数是3次的学生的频率约为20%B.参加活动次数是2次或4次的学生的频率约为44%C.参加活动次数不高于2次的学生约为342人D.参加活动次数不低于4次的学生约为162人10. 已知甲射击命中目标的概率为12，乙射击命中目标的概率为13，甲，乙是否命中目标相互之间无影响.现在甲，乙两人同时射击目标一次，则目标被击中的概率是( )A.16B.13C.23D.5611. 在掷一个骰子的试验中，事件A 表示“出现小于5的偶数点数”，事件B 表示“出现小于5的点数”，则一次试验中，事件A ∪B ¯发生的概率为( )A.13B.12C.23D.5612. 某电视台的夏日水上闯关节目中的前四关的过关率分别为56，45，35，12，只有通过前一关才能进入下一关，其中，第三关有两次闯关机会,且通过每关相互独立. 一选手参加该节目,则该选手能进入第四关的概率为( )A.725B.25C.1225D.1425 二、填空题13. 在试验中，若事件A 发生的概率为0.3，则事件A 对立事件发生的概率为________.14. 某中学有学生3600名，从中随机抽取300名调查他们的居住地与学校之间的距离，其中不超过1公里的学生共有15人，不超过2公里的学生共有45人，由此估计该学校所有学生中居住地到学校的距离在(1,2]公里的学生有________人．15. 已知甲、乙、丙3名运动员击中目标的概率分布为12，23，23，若他们3人分别向目标各发1枪，则三枪中至少命中2次的概率为________.16. 甲、乙两队进行篮球决赛，采取七场四胜制（当一队赢得四场胜利时，该队获胜，决赛结束）．根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”．设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4:1获胜的概率是________．三、解答题17. 一个袋中装有6个大小形状完全相同的小球，其中红球2个，白球4个．现从袋中有放回地取球，每次随机取1个球．(1)求连续两次取出的球都是白球的概率；(2)若取到红球一次得3分，取到白球一次得2分，求连续两次取球后的得分不等于5的概率．18. 由经验得知，在某商场付款处排队等候付款的人数及概率如表：(1)至多有2人排队的概率是多少？(2)至少有2人排队的概率是多少．19. 2020年春季，受疫情的影响，学校推迟了开学时间．上级部门倡导“停课不停学”，鼓励学生在家学习，复课后，某校为了解学生在家学习的周均时长（单位：小时），随机调查了部分学生，根据他们学习的周均时长，得到如图所示的频率分布直方图．(1)求该校学生学习的周均时长的众数的估计值；(2)估计该校学生学习的周均时长不少于30小时的概率．20. 学校达标运动会后，为了解学生的体质状况，从中抽取了部分学生的成绩，得到一个容量为n的样本，按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出了下面的频率分布直方图，已知[50,60)与[90,100]两组的频数分别为24与6.(1)求n及频率分布直方图中的x，y的值；(2)估计本次达标运动会中，学生成绩的中位数和平均数；(3)已知[90,100]组中有2名男生，4名女生，为掌握性别与学生体质的关系，从本组选2名学生作进一步调查，求2名学生中至少有1名男生的概率.21. 盒子里有6个红球，4个白球，现从中任取3个球，设事件A={3个球中有1个红球、2个白球}，事件B={3个球中有2个红球、1个白球}，事件C={3个球中至少有1个红球}，事件D={3个球中既有红球又有白球}．(1)事件D与A，B是什么运算关系？(2)事件C与A的交事件是什么事件？22. 先后2次抛掷一枚骰子，将得到的点数分别记为a，b．(1)求直线ax+by+5=0与圆x2+y2=1相切的概率；(2)将a，b，5的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．参考答案与试题解析2021年人教A版（2019）必修第二册数学第十章概率单元测试卷（1）一、选择题1.【答案】C【考点】随机事件【解析】利用随机事件的概念直接判断．【解答】解：在①中，在学校运动会上，学生张涛获得100m短跑冠军，是随机事件；在②中，在体育课上，体育老师随机抽取一名学生去拿体育器材，抽到李凯，是随机事件；在③中，从标有1，2，3，4的4张号签中任取一张，恰为1号签，是随机事件；在④中，在标准大气压下，水在4∘C时结冰是不可能事件.综上，随机事件的个数为3.故选C.2.【答案】C【考点】随机事件【解析】因为随机事件指的是在一定条件下，可能发生，也可能不发生的事件，只需逐一判断5个事件哪一个符合这种情况即可．【解答】解：连续两次抛掷同一个骰子，两次都出现2点这一事件可能发生也可能不发生，∴①是随机事件.明天下雨这一事件可能发生也可能不发生，∴ ②是随机事件.某人买彩票中奖这一事件可能发生也可能不发生，∴ ③是随机事件.从集合{1, 2, 3}中任取两个元素，它们的和必大于2，∴ ④是必然事件.在标准大气压下，水加热到100∘C时才会沸腾，∴ ⑤是不可能事件.综上，随机事件的个数有3个.故选C.3.【答案】C【考点】古典概型及其概率计算公式【解析】此题暂无解析【解答】解：从0，1，2，3这四个数字中任取三个不同的数字，共有(0,1,2),(0,1,3),(0,2,3),(1,2,3)这四种情况，其中三个数字之和能被6整除的情况为(1,2,3)，故所求概率为14.故选C .4.【答案】B【考点】相互独立事件的概率乘法公式【解析】【解答】解：甲，乙两人参加一次考试，他们合格的概率分别为13，14，那么两人中恰有1人合格的概率是 13×34+14×23=512.故选B .5.【答案】D【考点】古典概型及其概率计算公式【解析】本题是一个古典概型，试验包含的所有事件是任意找两人玩这个游戏，其中满足条件的满足|a −b|≤1的情形包括6种，列举出所有结果，根据计数原理得到共有的事件数，根据古典概型概率公式得到结果．【解答】解：由题意知本题是一个古典概型，∵ 试验包含的所有事件共有6×6＝36种猜字结果，其中满足|a −b|≤1的有如下情形：①若a =1，则b =1，2；②若a =2，则b =1，2，3；③若a =3，则b =2，3，4；④若a =4，则b =3，4，5；⑤若a =5，则b =4，5，6；⑥若a =6，则b =5，6，总共16种，∴ “心有灵犀”的概率为P =1636=49.故选D .6.【答案】A【考点】互斥事件的概率加法公式【解析】此题暂无解析【解答】解：甲不输包括两人下成和棋和甲获胜两种情况，由已知条件及互斥事件的概率公式可得，甲不输的概率为P =12+13=56．故选A ．7.【答案】A【考点】对立事件的概率公式及运用n 次独立重复试验【解析】由题意，1−(12)n ≥1516，即可求出n 的最小值．【解答】由题意，1−(12)n ≥1516，∴ n ≥4，∴ n 的最小值为4，故选A.8.【答案】C【考点】模拟方法估计概率【解析】此题暂无解析【解答】解：由题意可知，符合题意的随机数有：142 112 241 142，共4组，所以恰好第三次就停止摸球的概率为：P =418=29.故选C .9.【答案】C【考点】用频率估计概率【解析】利用题设给出的频率，逐项分析得解.【解答】解：A ,参加活动次数是3次的学生的频率约为26%，故错误.B ,参加活动次数是2次或4次的学生的频率约为20%+18%=38%，故错误.C ,参加活动次数不高于2次的学生约为900×(8%+10%+20%)=342，故正确.D ,参加活动次数不低于4次的学生约为900×(18%+12%+5%+1%)=324，故错误. 故选C .10.【答案】C【考点】相互独立事件的概率乘法公式相互独立事件【解析】目标被击中的对立事件是甲、乙同时没有击中目标，由此能求出目标被击中的概率．【解答】解：甲射击命中目标的概率为12，乙射击命中目标的概率为13，甲，乙是否命中目标相互之间无影响．现在甲，乙两人同时射击目标一次，目标被击中的对立事件是甲，乙同时没有击中目标，则目标被击中的概率是：P =1−(1−12)(1−13)=23.故选C .11.【答案】C【考点】事件的运算（并和关系、交积运算）互斥事件的概率加法公式【解析】由已知得P(A)=13，P(B ¯)=13，由此能求出一次试验中，事件A ∪B ¯发生的概率．【解答】解：∵ 在掷一个骰子的试验中，事件A 表示“出现小于5的偶数点数”，事件B 表示“出现小于5的点数”，∴ P(A)=26=13，P(B ¯)=26=13， ∴ 一次试验中，事件A ∪B ¯发生的概率为：P(A ∪B ¯)=P(A)+P(B ¯)=13+13=23．故选C ．12.【答案】D【考点】相互独立事件的概率乘法公式【解析】此题暂无解析【解答】解：该选手能进入第四关的概率为：5 6×45×35+56×45×(1−35)×35=1425.故选D.二、填空题13.【答案】0.7【考点】对立事件的概率公式及运用【解析】此题暂无解析【解答】解：事件A对立事件发生的概率为1−0.3=0.7.故答案为：0.7.14.【答案】360【考点】用频率估计概率【解析】根据题目条件可以求得样本中满足题目条件的学生占110，此时我们就可以利用样本的频率来估计总体的概率，从而求得满足题目条件的学生人数。

一、选择题1．斐波那契数列（Fibonacci sequence ）又称黄金分割数列，因为数学家昂纳多斐波那契以兔子繁殖为例子引入，故又称为“兔子数列”，在数学上斐波那契数列被以下递推方法定义：数列{}n a 满足：121a a ==，()*21N n n n a a a n ++=+∈，现从该数列的前10项中随机的抽取一项，则该数除以3余数为1的概率为（ ） A ．18B ．14C ．38D ．122．下列命题：①对立事件一定是互斥事件；②若A ，B 为两个随机事件，则P(A ∪B)＝P(A)＋P(B)；③若事件A ，B ，C 彼此互斥，则P(A)＋P(B)＋P(C)＝1；④若事件A ，B 满足P(A)＋P(B)＝1，则A 与B 是对立事件． 其中正确命题的个数是( ) A ．1B ．2C ．3D ．43．将一颗质地均匀的骰子（各面上分别标有点数1，2，3，4，5，6）先后抛掷3次，至少出现1次6点向上的概率是（ ）． A ．5216B ．25216C ．31216D ．912164．袋中装有标号为1，2，3，4，5，6且大小相同的6个小球，从袋子中一次性摸出两个球，记下号码并放回，如果两个号码的和是3的倍数，则获奖，若有5人参与摸球，则恰好2人获奖的概率是（ ）A ．40243B ．70243 C ．80243 D ．382435．教室有4扇编号分别为a b c d ,,,的窗户和2扇编号分别为,x y 的门，窗户d 敞开，其余窗户和门均被关闭.为保持教室空气流通，班长在这些关闭的门和窗户中随机地敞开2扇，则至少有1扇门被敞开的概率为（ ） A ．23B ．49C ．710D ．7126．党的十八提出：倡导“富强、民主、文明、和谐、自由、平等、公正、法治、爱国、敬业、诚信、友善”社会主义核心价值观.现将这十二个词依次．．写在六张规格相同的卡片的正反面（无区分），（如“富强、民主”写在同一张卡片的两面），从中任意抽取1张卡片，则写有“爱国”“诚信”两词中的一个的概率是（ ） A ．13B ．16C ．56D ．237．近年来，某市为促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000t 生活垃圾．经分拣以后数据统计如下表（单位：t ）：根据样本估计本市生活垃圾投放情况，下列说法错误的是（ ）A．厨余垃圾投放正确的概率为2 3B．居民生活垃圾投放错误的概率为3 10C．该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱D．厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000 8．从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是（）A．“至少有1个白球”和“都是红球”B．“至少有2个白球”和“至多有1个红球”C．“恰有1个白球” 和“恰有2个白球”D．“至多有1个白球”和“都是红球”9．古代“五行”学说认为：“物质分金、木、水、火、土五种属性，金克木，木克土，土克水，水克火，火克金”，从五种不同属性的物质中随机抽取两种，则抽取的两种物质不相克的概率为A．310B．25C．12D．3510．甲、乙两名同学相约学习某种技能，该技能需要通过两项考核才能拿到证书，每项考核结果互不影响.已知甲同学通过第一项考核的概率是45，通过第二项考核的概率是12；乙同学拿到该技能证书的概率是13，那么甲、乙两人至少有一人拿到该技能证书的概率是（）A．1315B．1115C．23D．3511．在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是310，那么概率为710的事件是（）A．至多有一张移动卡B．恰有一张移动卡C．都不是移动卡D．至少有一张移动卡12．某校3名教师和5名学生共8人去北京参加学习方法研讨会，需乘坐两辆车，每车坐4人，则恰有两名教师在同一车上的概率（）A ．78B ．67C ．37D ．1313．中国古典乐器一般按“八音”分类．这是我国最早按乐器的制造材料来对乐器进行分类的方法，最先见于《周礼•春官•大师》，分为“金、石、土、革、丝、木、匏（páo ）、竹”八音．其中“金、石、木、革”为打击乐器，“土、匏、竹”为吹奏乐器，“丝”为弹拨乐器，现从“金、石、土、革、丝、木”任取“两音”，则“两音”同为打击乐器的概率为（ ） A ．15B ．25C ．35D ．27二、解答题14．2020年是全面建成小康社会目标实现之年，是全面打赢脱贫攻坚战收官之年.为帮助某村巩固扶贫成果，该村的结对帮扶共建企业在该村建立了一座精米加工厂，并对粮食原料进行深加工，研发出一种新产品，已知该产品的质量以某项指标值()60100k k ≤<为衡量标准，质量指标的等级划分如表： 质量指标值k 90100k ≤< 8090k ≤<7080k ≤<6070k ≤<产品等级ABCD件产品的指标值，得到如下的产品质量指标值的频率分布直方图；设M =频率组距，当[)()10,101068,k n n n n N ∈+≤≤∈时，满足52200n M -=.（1）试估计样本质量指标值k 的中位数m ；（2）从样本质量指标值不小于80的产品中采用分层抽样的方法抽取7件产品，然后从这7件产品中任取2件产品，求至少有1件A 级品的概率.15．2020年9月份，南京出台了<南京市生活垃圾管理条例>，提出2020年11月1日起，实现单位生活垃圾强制分类全覆盖，居民区普遍推行生活垃圾分类制度.为加强社区居民的垃圾分类意识，推动社区垃圾分类正确投放，某社区在健身广场举办了“垃圾分类，从我做起”生活垃圾分类大型宣传活动，号召社区居民用实际行动为建设绿色家园贡献一份力量，为此需征集一部分垃圾分类志愿者.已知某垃圾站的日垃圾分拣量y (千克)与垃圾分类志愿者人数x (人)满足线性回归直线方程ˆybx a =+，数据统计如下： 志愿者人数x (人) 2 34 5 6 日垃圾分拣量y (千克)25304045t（1）已知511405i i y y ===∑，120ii x==∑，1885i i i x y ==∑，根据所给数据求t 和线性回归直线方程ˆybx a =+. （2）用（1）中所求的线性回归方程得到与i x 对应的口垃圾分拣量的估计值ˆi y.当分拣数据i y 与估计值ˆi y满足ˆi i y y -≤2时，则将分拣数据(i x ，i y )称为一个“正常数据”.现从题中5个分拣数据中任取2个，求2个都是“正常数据”的概率.参考公式：()()()121ˆniii nii x x y y bx x ==--=-∑∑，ˆˆay bx =-. 16．2020年初，一场突如其来的疫情打乱了人们的生活节奏，也改变了很多人的消费方式，某集团在各地区共有20家商品销售门店，为应对疫情，确保公司商品销售营业额，集团决定在所有门店重点推行线上销售模式，经过半年的努力，公司统计了所有门店在1月~6月的商品销售营业额，发现营业额均分布在600万元~1100万元之间，其频率分布直方图如图.（Ⅰ）估计集团20家门店在上半年的平均营业额（同一组中的数据用该组区间的中点值作代表）；（Ⅱ）为帮助营业额落后的门店，集团决定在营业额超过900万元的门店中抽取若干家对销售额不超过700万元的门店实施一对一帮扶，规定销售额超过1000万元的门店必须参与，若甲门店上半年的销售额为950万元，求甲门店被选中的概率.17．2018年，在《我是演说家》第四季这档节目中，英国华威大学留学生游斯彬的“数学之美”的演讲视频在微信朋友圈不断被转发，他的视角独特，语言幽默，给观众留下了深刻的印象．某机构为了了解观众对该演讲的喜爱程度，随机调查了观看了该演讲的140名观众，得到如下的列联表：（单位：名）（1）根据以上列联表，问能否在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关．（精确到0．001）（2）从这60名男观众中按对该演讲是否喜爱采取分层抽样，抽取一个容量为6的样本，然后随机选取两名作跟踪调查，求选到的两名观众都喜爱该演讲的概率．附：临界值表参考公式：22()=)()()()n ad bcKa b c d a c b d（-++++，+n a b c d=++．18．2018年2月9~25日，第23届冬奥会在韩国平昌举行，4年后，第24届冬奥会将在中国北京和张家口举行，为了宣传冬奥会，某大学在平昌冬奥会开幕后的第二天，从全校学生中随机抽取了120名学生，对是否收看奥运会开幕式进行了问卷调查，统计数据如下：（1）根据上表说明，能否有99%的把握认为，收看开幕式与性别有关？（2）现从参与收看了开幕式的学生中，采用分层抽样的方法选取8人，参加2022年北京冬奥会志愿者宣传活动.①问男、女学生各选取多少人？②若从这8人中随机选取2人到校广播站宣传冬奥会，求恰好选到一名男生为主播一名女生为副播的概率P.附：22()()()()()n ad bcka b c d a c b d-=++++，其中n a b c d=+++.20()P K k ≥ 0.1000.050 0.025 0.010 0.005 0k2.7063.8415.0246.6357.87919．在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱. （1）摸出的3个球为白球的概率是多少？（2）摸出的3个球为2个黄球1个白球的概率是多少？（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？20．某综艺节目邀请嘉宾进行答题闯关挑战，每位嘉宾挑战时，节目组用电脑出题的方式，从题库中随机出4道题，编号为1A ，2A ，3A ，4A ，电脑依次出题，嘉宾按规则作答，挑战规则如下：①嘉宾每答对一道题目得5分，每答错一道题目扣3分；②嘉宾若答对第i A 题，则继续作答第1i A +题；嘉宾若答错第i A 题，则失去第1i A +题的答题机会，从第2i A +题开始继续答题；直到4道题目出完，挑战结束；③每位嘉宾初始分为0分，若挑战结束后，累计得分不低于7分，则嘉宾闯关成功，否则闯关失败．嘉宾小源即将参与挑战，已知小源答对题库中每道题的概率均为23，各次作答结果相互独立，且他不会主动放弃任何一次作答机会，求： （Ⅰ）挑战结束时，小源共答对3道题的概率1P ； （Ⅱ）挑战结束时，小源恰好作答了3道题的概率2P ； （Ⅲ）小源闯关成功的概率3P ．21．某校学生社团组织活动丰富，学生会为了解同学对社团活动的满意程度，随机选取了100位同学进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照(40,50)，[50,60)，[60,70)，…，[]90,100分成6组，制成如图所示频率分布直方图.（1）求图中x的值.60,80的学生中按分层抽样的方法抽取5人进行（2）现从被调查的问卷满意度评分值在[)座谈了解，再从这5人中随机抽取2人作主题发言，求抽取的2人恰在同一组的概率. 22．甲､乙､丙三名射箭选手每次射箭命中各环的概率分布如下面三个表格所示.甲选手乙选手丙选手（1）若甲､乙､丙各射箭一次，假设三位选手射箭所得环数相互独立，求这三位选手射箭所得总环数为28的概率；（2）经过三个月的集训后，甲选手每次射箭命中各环的概率分布如下表所示：若在集训后甲连续射箭两次，假设每次射箭所得环数相互独立，记这两次命中总环数为X，求X的分布列及数学期望.23．为了保证食品安全，保障公众身体健康和生命安全，2018年国家对《食品安全法》进行了修正.2020，年春节前夕，某市质检部门随机抽取了20包某种品牌的速冻水饺，对某项质量指标进行检测.经统计，质量指标均在区间[0，50]内，将其按[0，10)､[10，20)､[20，30)､[30，40)､[40，50]分成5组，制成如图所示的频率分布直方图.（1）求该频率分布直方图中x的值；（2）若同组中的每个数据用该组区间中点值代替，估计该品牌速冻水饺的该项质量指标的平均值：（3）从质量指标大于等于30的速冻水饺中任选2包，进行深度检测，求这2包处于不同区间的概率.24．北京市政府为做好APEC会议接待服务工作，对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测，只有两轮都合格才能进行销售，否则不能销售.已知该海产品第一轮检测不合格的概率为16，第二轮检测不合格的概率为110，两轮检测是否合格相互没有影响.（1）求该海产品不能销售的概率.（2）如果该海产品可以销售，则每件产品可获利40元；如果该海产品不能销售，则每件产品亏损80元（即获利-80元）.已知一箱中有该海产品4件，记一箱该海产品获利X 元，求X的分布列，并求出数学期望()E X.25．从4名男生和2名女生中任选2人参加抗疫志愿服务活动.（1）设X表示所选2人中男生的人数，求X的分布列和数学期望E（X）；（2）已知选出了A，B这两人参加此次服务活动，A的服务满意率为0.87，B的服务满意率为0.91，用“Y A＝1，Y B＝1，”分别表示对A，B的服务满意，“Y A＝0，Y B＝0，”分别表示对A，B的服务不满意，写出方差D（Y A），D（Y B）的大小关系.（只需写出结论）26．盒子里放有外形相同且编号为1，2，3，4，5的五个小球，其中1号与2号是黑球，3号、4号与5号是红球，从中有放回地每次取出1个球，共取两次.（1）求取到的2个球中恰好有1个是黑球的概率；（2）求取到的2个球中至少有1个是红球的概率.【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D 【分析】写出斐波那契数列的前10项，列举出被3除所得的余数，由概率公式可得答案. 【详解】数列{}n a 满足：121a a ==，()*21Nn n n a a a n ++=+∈，数列的前10项为：1，1，2，3，5，8，13，21，34，55 该数列被3除所得的余数为1，1，2，0，2，2，1，0，1，1 所以10项中共有5项满足除以3余数为1， 故概率为51102P . 故选：D 【点睛】本题考查概率的求法，考查列举法的应用，属于基础题.2．A解析：A 【分析】根据互斥之间和对立事件的概念，及互斥事件和对立事件的关系和概率的计算，即可作出判断，得到答案． 【详解】由题意①中，根据对立事件与互斥事件的关系，可得是正确；②中，当A 与B 是互斥事件时，才有P(A ∪B)＝P(A)＋P(B)，对于任意两个事件A ，B 满足P(A ∪B)＝P(A)＋P(B)－P(AB)，所以是不正确的；③也不正确．P(A)＋P(B)＋P(C)不一定等于1，还可能小于1；④也不正确．例如：袋中有大小相同的红、黄、黑、绿4个球，从袋中任摸一个球，设事件A ＝{摸到红球或黄球}，事件B ＝{摸到黄球或黑球}，显然事件A 与B 不互斥，但P(A)＋P(B)＝＋＝1. 【点睛】本题主要考查了互斥事件和对立事件的基本概念、互斥事件与对立时间的关系及其应用，其中熟记互斥事件和对立事件的概念和关系是解答的关键，着重考查了推理与论证能力，属于基础题．3．D解析：D 【分析】根据正难则反原则，先求出“抛掷3次都没有出现6点向上”事件的概率，由对立事件的概率性质，计算可得答案. 【详解】解：将一颗质地均匀的骰子先后掷3次，这3次之间是相互独立， 记事件A 为“抛掷3次，至少出现一次6点向上”， 则A 为“抛掷3次都没有出现6点向上”，记事件i B 为“第i 次中，没有出现6点向上”，1,2,3i =，则123A B B B =，又()56i P B =，所以()351256216P A ⎛⎫== ⎪⎝⎭，所以()()1259111216216P A P A =-=-=. 故选：D. 【点睛】本题考查对立事件的性质和概率计算，利用了正难则反的原则，属于基础题.4．C解析：C 【分析】先确定摸一次中奖的概率，5个人摸奖，相当于发生5次试验，根据每一次发生的概率，利用独立重复试验的公式得到结果． 【详解】从6个球中摸出2个，共有2615C =种结果，两个球的号码之和是3的倍数，共有(1,2),(1,5),(2,4),(3,6),(4,5)∴摸一次中奖的概率是51153=， 5个人摸奖，相当于发生5次试验，且每一次发生的概率是13， ∴有5人参与摸奖，恰好有2人获奖的概率是35222180()()33243C ⋅⋅=， 故选：C ． 【点睛】本题主要考查了n 次独立重复试验中恰好发生k 次的概率，考查独立重复试验的概率，解题时主要是看清摸奖5次，相当于做了5次独立重复试验，利用公式做出结果，属于中档题．5．C解析：C 【解析】 【分析】列出样本空间Ω,以及事件A =“至少有1扇门被敞开”包含的基本事件，计算概率. 【详解】 样本空间()()()()()()()()()(){},,,,,,,,,,,,,,,,,,,a b a c a x a y b c b x b y c x c y x y Ω=.记事件A =“至少有1扇门被敞开”，则()()()()()()(){},,,,,,,,,,,,,A a x a y b x b y c x c y x y =，所以()710P A =，故选C . 【点睛】本题考查了古典概型，考查了学生实际应用以及数学运算的能力，属于基础题.6．A解析：A 【分析】由题意知，基本事件有6个，其中抽取到含有“爱国”“诚信”两词中的一个的事件有2个基本事件，根据古典概型概率公式计算即可. 【详解】由题意，基本事件为抽到写有富强、民主；文明、和谐；自由、平等；公正、法治；爱国、敬业；诚信、友善的卡片，共有6个，其中抽到写有“爱国”“诚信”两词中的一个的事件为：抽到写有爱国、敬业的卡片，抽到写有诚信、友善的卡片，共有2个， 所以由古典概型概率公式知：2163P ==， 故选：A 【点睛】本题主要考查了古典概型概率的求法，属于中档题.7．D解析：D 【分析】由表格可求得：厨余垃圾投放正确的概率，可回收物投放正确的概率，其他垃圾投放正确的概率，再结合选项进行分析即可. 【详解】由表格可得：厨余垃圾投放正确的概率40024001001003==++；可回收物投放正确的概率240424030305==++；其他垃圾投放正确的概率6032020605==++．对A ，厨余垃圾投放正确的概率为23，故A 正确； 对B ，生活垃圾投放错误有200602020300+++=，故生活垃圾投放错误的概率为3003100010=，故B 正确； 对C ，该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱，故C 正确． 对D ，厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的的投放量的平均数600300100100033x ++==，可得方差22221100010001000[(600)(300)(100)]3333s =⨯-+-+-=380000200009≠，故D 错误；故选：D ．本题考查概率与统计的计算，考查推理能力与数据处理能力，属于中档题．8．C解析：C【分析】结合互斥事件与对立事件的概念,对选项逐个分析可选出答案.【详解】对于选项A, “至少有1个白球”和“都是红球”是对立事件,不符合题意;对于选项B, “至少有2个白球”表示取出2个球都是白色的,而“至多有1个红球”表示取出的球1个红球1个白球,或者2个都是白球,二者不是互斥事件,不符合题意;对于选项C, “恰有1个白球”表示取出2个球1个红球1个白球, 与“恰有2个白球”是互斥而不对立的两个事件,符合题意;对于选项D, “至多有1个白球”表示取出的2个球1个红球1个白球,或者2个都是红球,与“都是红球”不是互斥事件,不符合题意.故选C.【点睛】本题考查了互斥事件和对立事件的定义的运用,考查了学生对知识的理解和掌握,属于基础题. 9．C解析：C【解析】【分析】从五种物质中随机抽取两种，所有抽法共有10种，而相克的有5种情况，得到抽取的两种物质相克的概率是12，进而得到抽取两种物质不相克的概率，即可得到答案.【详解】从五种物质中随机抽取两种，所有抽法共有2510C=种，而相克的有5种情况，则抽取的两种物质相克的概率是51102=，故抽取两种物质不相克的概率是11122-=，故选C.【点睛】本题主要考查了古典概型及其概率的计算公式的应用，以及相互对立事件的应用，其中解答正确理解题意，合理利用对立事件的概率求解是解答的关键，着重考查了运算与求解能力，属于基础题.10．D解析：D【分析】由已知先求得甲取得证书的概率，再求得甲，乙两人都取不到证书的概率，由对立事件的概率公式可得选项.由已知得甲拿到该技能证书的概率为412525⨯=，则甲，乙两人都没有拿到证书的概率为：21211535⎛⎫⎛⎫-⨯-= ⎪ ⎪⎝⎭⎝⎭， 所以甲、乙两人至少有一人拿到该技能证书的概率是23155-=， 故选：D. 【点睛】方法点睛：在解决含有“至少”，“至多”等一类问题的概率问题时，正面求解时情况较复杂，可以求其对立事件的概率，再用1减去所求的对立事件的概率，就是所求的概率.11．A解析：A 【分析】概率710的事件可以认为是概率为310的对立事件． 【详解】事件“2张全是移动卡”的概率是310，由对立事件的概率和为1，可知它的对立事件的概率是710，事件为“2张不全是移动卡”，也即为“2张至多有一张是移动卡”． 故选：A ． 【点睛】关键点点睛：本题考查对立事件，解题关键是掌握对立事件的概率性质：即对立事件的概率和为1，考查学生的逻辑推理能力，属于基础题.12．B解析：B 【分析】易得出8人乘车，每车4人的乘车方法是48C ，然后考虑从3名教师中选2人，从5名学生中选2人乘同一辆车，注意有两辆车，求出方法后可得概率． 【详解】8人乘车，每车4人的乘车方法是4870C =，从3名教师中选2人，从5名学生中选2人乘同一辆车的方法娄得2235260C C ⨯=，∴所求概率为606707P ==． 故选：B ． 【点睛】本题考查古典概型，解题关键是求出事件“恰有两名教师在同一车上”的方法数，易错点是不考虑两辆车．13．B解析：B 【分析】由条件列举从“金、石、土、革、丝、木”中任取“两音”的所有基本事件的个数，再计算“两音”同为打击乐器所包含的所有基本事件个数，最后求其概率. 【详解】从“金、石、土、革、丝、木”中任取“两音”，组成的基本事件包含：{金、石}，{金、土}，{金、革}，{金、丝}，{金、木}，{石、土}，{石、革}，{石、丝}，{石、木}，{土、革}，{土、丝}，{土、木}，{革、丝}，{革、木}，{丝、木}，共15种情况，其中“两音”同为打击乐器的有{金、石}，{金、革}，{金、木}，{石、革}，{石、木}，{革、木}，共包含6种情况，则“两音”同为打击乐器的概率62155P ==. 故选：B 【点睛】本题考查数学文化与古典概型相结合的考查，重点考查读懂题意，属于基础题型.二、解答题14．（1）85m =；（2）57. 【分析】（1）计算出各产品等级的频率，利用中位数左边的矩形面积之和为0.5可求得m 的值； （2）计算得出7件产品中A 级品共3件，分别记为1A 、2A 、3A ，B 级品共4件，分别记为1B 、2B 、3B 、4B ，列举出所有的基本事件，并确定事件“所抽的2件产品中至少有1件A 级品”所包含的基本事件数，利用古典概型的概率公式可求得所求事件的概率. 【详解】（1）当6n =时，[)60,70k ∈，1100M =，频率为11100.1100p =⨯=； 当7n =时，[)70,80k ∈，150M =，频率为21100.250p =⨯=； 当8n =时，[)80,90k ∈，125M =，频率为31100.425p =⨯=. 各产品等级的频率如下表所示：0.10.20.50.10.20.4+<<++，80,90m ∴∈，所以，800.10.20.40.510m -++⨯=，解得85m =； （2）所抽取的7件产品中，A 级品的数量为0.3730.30.4⨯=+，分别记为1A 、2A 、3A ，B 级品的数量为4，分别记为1B 、2B 、3B 、4B ，从这7件产品中任取2件产品，所有的基本事件有：12A A 、13A A 、11A B 、12A B 、13A B 、14A B 、23A A 、21A B 、22A B 、23A B 、24A B 、31A B 、32A B 、33A B 、34A B 、12B B 、13B B 、14B B 、23B B 、24B B 、34B B ，共21个基本事件，其中，事件“所抽的2件产品中至少有1件A 级品”包含15个基本事件， 因此，所求事件的概率为155217P ==. 【点睛】方法点睛：求解古典概型概率的方法如下： （1）列举法； （2）列表法； （3）数状图法； （4）排列组合数的应用.15．（1）60t =，ˆ8.56yx =+；（2）310P = 【分析】（1）根据40y =，求t ，再根据参考公式求ˆˆ,ba ，求回归直线方程；（2）首先计算“正常数据”的个数，再求两个都是“正常数据”的概率. 【详解】 （1）由条件可知25304045405t++++=，解得：60t =，2045x ==， ()()()()()()()()51242540343040 (646040i)ii x x y y =--=--+--++--∑85=()()()()()()52222221243444546410i i x x =-=-+-+-+-+-=∑，()()()12185ˆ8.510niii nii x x y y bx x ==--∴===-∑∑，ˆˆ408.546a y bx=-=-⨯=， 所以回归直线方程是ˆ8.56yx =+； （2）12x =时，1ˆ23y=，232522-=≤，是正常数据，23x =时，2ˆ31.5y =，31.530 1.52-=≤是正常数据，34x =时，3ˆ40y=，404002-=≤，是正常数据， 45x =时，4ˆ48.5y= 48.545 3.52-=>，不是正常数据，56x =时，5ˆ57y =，576032-=>，不是在正常数据，则5个数据中正常数据是3个，不正常数据是2个， 现从题中5个分拣数据中任取2个，求2个都是“正常数据”的概率2325310C P C ==. 【点睛】关键点点睛：本题的关键是正确理解题意，并能根据参考公式计算求值. 16．（Ⅰ）835万元；（Ⅱ）25. 【分析】（Ⅰ）根据每组数据的区间中点值，直接代入平均数公式，即可得解；（Ⅱ）计算可得营业额不超过700万元的门店有3家，营业额超过900~1000万元的门店有5家， 由题意知需要在营业额在900~1000万元的5家门店中再抽取两家，求出所有可能以及甲门店被选中的可能，代入古典概型公式，即可得解. 【详解】（Ⅰ）根据频率分布直方图，设该集团20家门店上半年的平均营业额为x ， 则6500.157500.28500.359500.2510500.05835x =⨯+⨯+⨯+⨯+⨯=（万元）， （Ⅱ）可计算得营业额不超过700万元的门店有3家，营业额在900~1000万元的门店有5家，1000万元以上的有1家，由题意知需要在营业额在900~1000万元的5家门店中再抽取两家. 设“甲门店被选中”为事件A ，用a ，b ，c ，d 表示5家门店中的另4家，则组合方式列举如下：甲a ，甲b ，甲c ，甲d ，ab ，ac ，ad ，bc ，bd ，cd ，共10种情形，其中表示甲门店被选中的有4种情形， 故()42105P A ==， ∴甲门店被选中的概率为25. 【点睛】本题考查了求平均数和古典概型问题，考查了频率分布直方图，同时考查了分类讨论思想和计算能力，属于中档题.17．（1）见解析；（2）0.4 【分析】(1)根据独立性检验求出()221406020402071.167 3.8418060100406K ⨯⨯-⨯==≈<⨯⨯⨯，即得不能在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关．（2）利用古典概型求选到的两名观众都喜爱该演讲的概率． 【详解】（1）假设：观众性别与喜爱该演讲无关，由已知数据可求得，()221406020402071.167 3.8418060100406K ⨯⨯-⨯==≈<⨯⨯⨯ ∴ 不能在犯错误的概率不超过0.05的前提下认为观众性别与喜爱该演讲有关．（2）抽样比为616010=，样本中喜爱的观众有40×110=4名， 不喜爱的观众有6﹣4=2名．记喜爱该演讲的4名男性观众为a ，b ，c ，d ，不喜爱该演讲的2名男性观众为1，2，则 基本事件分别为：（a ，b ），（a ，c ），（a ，d ），（a ，1），（a ，2），（b ，c ），（b ，d ），（b ，1），（b ，2），（c ，d ），（c ，1），（c ，2），（d ，1），（d ，2），（1，2）．其中选到的两名观众都喜爱该演讲的事件有6个， 故其概率为P （A ）=60.415= 【点睛】本题主要考查独立性检验和古典概型，意在考查学生对这些知识的理解能力，掌握水平和应用能力.18．（1）有99%的把握；（2）①男生6人，女生2人；②37. 【分析】（1）列出22⨯列联表，求出2k 的值，根据附表可得答案；（2）①根据分层抽样的方法可得，男、女学生各选取的人数；②从这8人中随机选取2人，共有28C 种不同的选法，其中恰好选到一名男生为主播一名女生为副播共有1162C C 种不同的选法，根据古典概型的概率计算公式可得概率. 【详解】（1）22⨯列联表：。

一、选择题1．我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”.下图是在“赵爽弦图”的基础上创作出的一个“数学风车”，其中正方形ABCD 内部为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的.我们将图中阴影所在的四个三角形称为同一片“风叶”的概率为（ ）A ．37B ．47C ．314D ．11142．斐波那契数列（Fibonacci sequence ）又称黄金分割数列，因数学家列昂纳多·斐波那契（Leonardoda Fibonacci ）以兔子繁殖为例子而引入，故又称为“兔子数列”．在数学上，斐波纳契数列被以下递推的方法定义：数列{}n a 满足：121a a ==，21++=+n n n a a a ，现从数列的前2019项中随机抽取1项，能被3整除的概率是（ ）A ．14B ．2522019C ．5042019D ．50520193．下列命题正确的是（ ）A ．用事件A 发生的频率()n f A 估计概率()P A ，重复试验次数n 越大，估计的就越精确.B ．若事件A 与事件B 相互独立，则事件A 与事件B 相互独立.C ．事件A 与事件B 同时发生的概率一定比A 与B 中恰有一个发生的概率小.D ．抛掷一枚均匀的硬币，如前两次都是反面，那么第三次出现正面的可能性就比反面大. 4．从分别写有a ，b ，c ，d ，e 的5个乒乓球中，任取2个，这2个乒乓球上的字母恰好是按字母顺序相邻排列的概率为（ ）. A ．25B ．15C ．35D ．3105．从装有若干个大小相同的红球、白球和黄球的袋中随机摸出1个球，摸到红球、白球和黄球的概率分别为111,,236，从袋中随机摸出一个球，记下颜色后放回，连续摸3次，则记下的颜色中有红有白，但没有黄的概率为（ ）A ．536B ．56C ．512D ．126．设两个独立事件A 和B 同时不发生的概率是p ,A 发生B 不发生与A 不发生B 发生的概率相同,则事件A 发生的概率为( ) A ．2pB ．2p C ．1p - D ．12p -7．某商场进行购物摸奖活动，规则是：在一个封闭的纸箱中装有标号分别为1，2，3，4，5，6的六个小球，每次摸奖需要同时取出两个球，每位顾客最多有两次摸奖机会，并规定：若第一次取出的两球号码连号，则中奖，摸奖结束；若第一次未中奖，则将这两个小球放回后进行第二次摸球，若与第一次取出的两个小球号码相同，则为中奖，按照这样的规则摸奖，中奖的概率为（ ） A ．13B ．1745C ．245D ．171008．甲、乙二人进行围棋比赛，采取“三局两胜制”，已知甲每局取胜的概率为23，则甲获胜的概率为 ( )．A ．22213221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B ．22232233C ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭C ．22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D ．21112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭9．“三个臭皮匠，赛过诸葛亮”，这是我们常说的口头禅，主要是说集体智慧的强大. 假设李某智商较高，他独自一人解决项目M 的概率为10.3P =；同时，有n 个水平相同的人也在研究项目M ，他们各自独立地解决项目M 的概率都是0.1.现在李某单独研究项目M ，且这n 个人组成的团队也同时研究项目M ，设这个n 人团队解决项目M 的概率为2P ，若21P P ≥，则n 的最小值是( ) A ．3B ．4C ．5D ．610．《易经》是中国传统文化中的精髓，如图是易经八卦图(含乾､坤､巽､震､坎､离､艮､兑八卦)，每一卦由三根线组成(表示一根阳线，表示一根阴线)，现有3人各自随机的从八卦中任取两卦，恰有2人两卦的六根线中有四根阳线和两根阴线的概率为（ ）A．2972744B．992744C．67521952D．2252195211．已知在10件产品中可能存在次品，从中抽取2件检查，记次品数为X，已知16(1)45P X==，且该产品的次品率不超过40%，则这10件产品的次品数为（）A．2件B．4件C．6件D．8件12．如果从1，2，3，4，5中任取2个不同的数，则这2个数的和能被3整除的概率为（）A．25B．310C．15D．1213．某校3名教师和5名学生共8人去北京参加学习方法研讨会，需乘坐两辆车，每车坐4人，则恰有两名教师在同一车上的概率（）A．78B．67C．37D．13二、解答题14．某校的课外兴趣小组的同学们进行了一次关于全市“双创双修”知识答题的问卷调查活动，收集到的200张问卷统计得分汇总制成了一张频率直方图.（1）求问卷得分的中位数和平均数；（2）若得分不低于80则为优秀，按分层抽样再次回访8名参加过问卷调查并得分优秀的人，在这8人中还需随机挑选2人做深入访谈，求这两名访谈对象中至少有一人问卷得分超过90的概率.15．“工资条里显红利，个税新政人民心”，随着2021年新年钟声的敲响，我国自1980年以来，力度最大的一次个人所得税（简称个税）改革至2019年实施以来发挥巨大作用.个税新政主要内容包括：（1）个税起征点为5000元；（2）每月应纳税所得额（含税）=收入-个税起征点-专项附加扣除；（3）专项附加扣除包括住房､子女教育和赡养老人等.新旧个税政策下每月应纳税所得额（含税）计算方法及其对应的税率表如表：年的人均月收入24000元.统计资料还表明，他们均符合住房专项扣除；同时，他们每人至多只有一个符合子女教育扣除的孩子，并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1；此外，他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为：住房1000元/月，子女教育每孩1000元/月，赡养老人2000元/月等.假设该市该收入层级的IT从业者都独自享受专项附加扣除，将预估的该市该收入层级的IT从业者的人均月收入视为其个人月收入.根据样本估计总体的思想，解决如下问题：（1）求该市该收入层级的IT 从业者2021年月缴个税的所有可能及其概率.（2）根据新旧个税方案，估计从2021年1月开始，经过多少个月，该市该收入层级的IT 从业者各月少缴交的个税之和就超过2019年的月收入？16．在新冠肺炎疫情期间，为了认真贯彻落实北京市教委关于做好中小学生延期开学期间“停课不停学”工作要求，各校以教师线上指导帮助和学生居家自主学习相结合的教学模式积极开展工作.为了解学生居家自主学习的情况，从某校高二年级随机抽取了100名学生，获得了他们一天中用于居家自主学习的时间分别在[)[)[)0,1,1,2,2,3，[)[)[)3,4,4,5,5,6，[)[]677,8,,（单位：小时）的数据，整理得到的数据绘制成频率分布直方图（如图）.（1）由图中数据，求a 的值，并估计从该校高二年级中随机抽取一名学生，这名学生该天居家自主学习的时间在[)3,4的概率；（2）现从抽取的100名学生该天居家自主学习的时间在[)0,1和[)1,2的人中任选2人，进一步了解学生的具体情况，求其中学习时间在[)0,1中至少有1人的概率；（3）假设同一时间段中的每个数据可用该时间段的中点值代替，试估计样本中的100名学生该天居家自主学习时间的平均数.17．新冠肺炎疫情期间，为确保“停课不停学”，各校精心组织了线上教学活动.开学后，某校采用分层抽样的方法从高中三个年级的学生中抽取一个容量为150的样本进行关于线上教学实施情况的问卷调查. 已知该校高一年级共有学生660人，高三年级共有540人，抽取的样本中高二年级有50人. 下表是根据抽样调查情况得到的高二学生日睡眠时间(单位：h )的频率分布表.分组频数频率[6,6.5)50.10[6,5.7)x y[7,7.5)70.14[7.5,8)120.24[8,8.5)z0.20[8.5,9]80.16合计501x y z的值（2）求频率分布表中实数,,（3）已知日睡眠时间在区间[6,6.5)内的5名高二学生中，有2名女生，3名男生，若从中任选3人进行面谈，求选中的3人恰好为两男一女的概率.18．某部门为了对该城市共享单车加强监管，随机选取了100人就该城市共享单车的推行情况进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照[)90,100分成5组，制成如图所示频率分布直方图.50,60，[)60,70，…[]（1）求图中x的值；（2）求这组数据的平均数；（3）已知满意度评分值在[)50,60内的男生数与女生数的比为3：2，若在满意度评分值为[)50,60的人中随机抽取2人进行座谈，求恰有1名女生的概率.19．甲、乙两名运动员各投篮一次，甲投中的概率为0.8，乙投中的概率为0.9，求下列事件的概率： （Ⅰ）两人都投中； （Ⅱ）恰好有一人投中； （Ⅲ）至少有一人投中.20．在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱. （1）摸出的3个球为白球的概率是多少？（2）摸出的3个球为2个黄球1个白球的概率是多少？（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？21．甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题，按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成，2道题不能完成；应聘者乙每题正确完成的概率都是23，且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列，并计算其数学期望; (2)请分析比较甲、乙两人谁的面试通过的可能性较大?22．为了解一大片经济林的生长情况，随机抽样测量其中20株树木的底部周长（单位cm ），得到如下频数分布表和频率分布直方图： 分组 [)85,95[)95,105[)105,115[)115,125[]125,135频数27ab2（1）请求出频数分布表中a ，b 的值；（2）估计这片经济林树木底部周长的平均值（同一组中的数据用该组区间的中点值作代表）；（3）从样本中底部周长在115cm 以上的树木中任选2株进行嫁接试验，求至少有一株树木的底部周长在125cm 以上的概率.23．随着科学技术的飞速发展，手机的功能逐渐强大，很大程度上代替了电脑电视.为了了解某高校学生平均每天使用手机的时间与性别是否有关，某调查小组随机抽取了30名男生，20名女生进行为期一周的跟踪调查，调查结果如表所示：平均每天使用手机超过3小时 平均每天使用手机不超过3小时 合计 男生 25 5 30 女生 10 10 20 合计351550（1）能否在犯错误的概率不超过0.01的前提下认为学生使用手机的时间长短与性别有关？（2）在这20名女生中，调查小组发现共有15人使用国产手机，在未使用国产手机的人中，平均每天使用手机不超过3小时的共有2人.从未使用国产手机的人中任意选取3人，求至多有一人使用手机不超过3小时的概率.()20P K k ≥ 0.500 0.400 0.250 0.150 0.100 0.050 0.025 0.010 0k0.4550.7081.3232.0722.7063.8415.0246.635参考公式：()()()()()22n ad bc K a c b d a b c d -=++++（n a b c d =+++）.24．某校学生社团组织活动丰富，学生会为了解同学对社团活动的满意程度，随机选取了100位同学进行问卷调查，并将问卷中的这100人根据其满意度评分值（百分制）按照(40,50)，[50,60)，[60,70)，…，[]90,100分成6组，制成如图所示频率分布直方图.（1）求图中x 的值.（2）现从被调查的问卷满意度评分值在[)60,80的学生中按分层抽样的方法抽取5人进行座谈了解，再从这5人中随机抽取2人作主题发言，求抽取的2人恰在同一组的概率. 25．某组织在某市征集志愿者参加志愿活动，现随机抽出60名男生和40名女生共100人进行调查，统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况，具体数据如图所示.(1)完成下列22⨯列联表，并判断是否有99%的把握认为愿意参与志愿活动与性别有关？愿意 不愿意 总计男生 女生 总计(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者，再从中抽取2人作为队长，求抽取的2人至少有一名女生的概率. 参考数据及公式：()20P K k ≥ 0.1 0.05 0.025 0.010k2.7063.8415.0246.635()()()()()()22n ad bc K n a b c d a b c d a c b d -==+++++++.26．2020年5月28日，十三届全国人大三次会议表决通过了《中华人民共和国民法典》，此法典被称为“社会生活的百科全书”，是新中国第一部以法典命名的法律，在法律体系中居于基础性地位，也是市场经济的基本法.民法典与百姓生活密切相关，某大学为了解学生对民法典的认识程度，选取了120人进行测试，测试得分情况如图所示.（1）试求出图中实数a 的值，并求出成绩落在[]90,100的人数；（2）如果抽查的测试平均分超过75分，就表示该学校通过测试.试判断该校能否通过测试；（3）如果在[)80,90中抽取3人，在[]90,100中抽取2人，再从抽取的5人中选取2人进行民法典的宣传，那么选取的2人中恰好1人成绩落在[]90,100的概率是多少？【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】由从“数学风车”的八个顶点中任取两个顶点，得到基本事件的个数为28C 种，这两个顶点取自同一片“风叶”的基本事件有234C 种，结合古典概型的概率计算公式，即可求解. 【详解】由题意，从“数学风车”的八个顶点中任取两个顶点的基本事件有2828C =种，其中这两个顶点取自同一片“风叶”的基本事件有234C 12=， 根据古典概型的概率计算公式，可得所求概率123287P ==. 故选：A. 【点睛】本题主要考查了古典概型的概率计算，以及组合的概念及组合数的计算，其中解答中正确理解题意，根据组合数的计算公式求得基本事件的总数及所求事件所含有的基本事件的个数是解答的关键，着重考查分析问题和解答问题的能力.2．C解析：C 【分析】依次写出数列各项除以3所得余数，寻找后可得结论． 【详解】根据斐波纳契数列的定义，数列各项除以3所得余数依次为：1,1,2,0,2,2,1,0,1,1,2,，余数数列是周期数列，周期为8，201925283=⨯+，所以数列的前2019项中能被3整除的项有2522504⨯=，所求概率为5042019P =． 故选：C ． 【点睛】本题考查古典概型，考查斐波纳契数列，考查数列的周期性．解题关键是依次写出波纳契数列各项除以3所得余数形成的新数列．3．B解析：B【分析】根据概率的定义，事件的独立性概念判断各选项．【详解】在相同的条件下做大量重复试验,一个事件A出现的次数和总的试验次数n之比,称为事件A在这n次试验中出现的频率.当试验次数n很大时,频率将稳定在一个常数附近. n越大,频率偏离这个常数较大的可能性越小.这个常数称为这个事件的概率，并不是说n越大，估计的精度越精确，A错；事件A与事件B相互独立，即A是否发生与B是否发生无关，∴事件A是否发生与事件B是否发生也无关，它们相互独立，B正确；抛一枚骰子，出现的点数不大于5记为事件A，出现的点为不小于2记为事件B，则事件A与事件B同时发生是指点数为2，3，4，5，概率为4263=，而事件A与B中恰有一个发生是指点为1或6，概率为212633=<．C错；抛掷一枚均匀的硬币，如前两次都是反面，那么第三次出现正面的可能性与出现反面的可能性还是一样．D错．故选：B．【点睛】本题考查概率的定义，考查事件的独立性．掌握概念的定义是解题关键．4．A解析：A【分析】基本事件总数2510n C==，利用列举法求出这2个乒乓球上的字母恰好是按字母顺序相邻排列包含的基本事件有4个，由此能求出这2个乒乓球上的字母恰好是按字母顺序相邻排列的概率．【详解】解：从分别写有a，b，c，d，e的5个乒乓球中，任取2个，基本事件总数2510n C==，这2个乒乓球上的字母恰好是按字母顺序相邻排列包含的基本事件有：ab，bc，cd，de，共4个，∴这2个乒乓球上的字母恰好是按字母顺序相邻排列的概率为42105p==．故选：A．【点睛】本题考概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题．5．C解析：C 【分析】概率等于没有黄球的概率减去只有白球或只有红球的概率，计算到答案. 【详解】根据题意：概率等于没有黄球的概率减去只有白球或只有红球的概率.即3331115162312p ⎛⎫⎛⎫⎛⎫=---=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选：C . 【点睛】本题考查了概率的计算，意在考查学生的计算能力和应用能力.6．C解析：C 【分析】利用A 发生B 不发生与A 不发生B 发生的概率相同，事件A 和B 同时不发生的概率是p ，建立方程，即可求得事件A 发生的概率． 【详解】根据题意设事件A 发生的概率为a ，事件B 发生的概率为b ， 则有(1)(1)(1)(1)a b p a b a b --=⎧⎨-=-⎩①②由②知a b =，代入①得1a =故选：C . 【点睛】本题主要考查相互独立事件的概率的计算，解题的关键是正确理解题意，列出方程，属于中档题.7．B解析：B 【分析】可将中奖的情况分成第一次两球连号和第二次取出的小球与第一次取出的号码相同两种情况，分别计算两种情况的概率，根据和事件概率公式可求得结果. 【详解】中奖的情况分为：第一次取出两球号码连号和第二次取出两个小球与第一次取出的号码相同两种情况第一次取出两球连号的概率为：26513C =第二次取出两个小球与第一次取出号码相同的概率为：261121345C ⎛⎫-⨯= ⎪⎝⎭ ∴中奖的概率为：121734545+= 本题正确选项：B 【点睛】本题考查和事件概率问题的求解，关键是能够根据题意将所求情况进行分类，进而通过古典概型和积事件概率求解方法求出每种情况对应的概率.8．C解析：C 【分析】先确定事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，再利用独立重复试验的概率公式和概率加法公式可求出所求事件的概率． 【详解】事件“甲获胜”包含“甲三局赢两局”和“前两局甲赢”，若甲三局赢两局，则第三局必须是甲赢，前面两局甲赢一局，所求概率为2121233C ⎛⎫⋅⋅ ⎪⎝⎭， 若前两局都是甲赢，所求概率为223⎛⎫ ⎪⎝⎭，因此，甲获胜的概率为22112221333C ⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选C ． 【点睛】本题考查独立重复事件的概率，考查概率的加法公式，解题时要弄清楚事件所包含的基本情况，考查分类讨论思想，考查计算能力，属于中等题．9．B解析：B 【解析】 【分析】设这个n 人团队解决项目M 的概率为2P ，则021(0.9)n n P C =-，由21P P ，得10.90.3n -， 由此能求出n 的最小值． 【详解】李某智商较高，他独自一人解决项目M 的概率为10.3P =，有n 个水平相同的人也在研究项目M ，他们各自独立地解决项目M 的概率都是0.1， 现在李某单独研究项目M ，且这n 个人组成的团队也同时研究M ， 设这个n 人团队解决项目M 的概率为2P ，则021(0.9)n nP C =-， 21P P ，10.90.3n∴-， 解得4n ≥．n ∴的最小值是4．故选B ． 【点睛】本题考查实数的最小值的求法，考查n 次独立重复试验中事件A 恰好发生k 次的概率的计算公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．10．A解析：A 【分析】求出3人每个人任取2卦的方法总数，确定3人中哪一个人的两卦中六根线不是4阳2阴，并求出方法数，另外2人分别取两卦且满足题意的方法，相乘可得基本事件的个数，从而可得概率． 【详解】8卦可分为四类：1阳3阴共3个，3阳1阴共3个，3阳共1个，3阴共1个，3人各取2卦的法为222388828C C C =，2卦的六根线中有四根阳线和两根阴线的方法数为21336C C +=，因此3人中恰有2人两卦的六根线中有四根阳线和两根阴线方法为123338(6)662311C C ⨯-⨯⨯=⨯⨯，∴所求概率为3332311297282744P ⨯⨯==． 故选：A ． 【点睛】方法点睛：本题考查古典概型，解题关键是求茁基本事件的个数．解题步骤：第一步分清8卦中阳线和阴线的条件，同类（相同阴线和阳线）的个数，第二步求出任取两卦时，两卦的六根线中有四根阳线和两根阴线方法，第三步用分步乘法原理求出3人中恰有2人两卦的六根线中有四根阳线和两根阴线方法数．这样条理清晰，不易出错．11．A解析：A 【分析】设10件产品中存在n 件次品，根据题意列出方程求出n 的值． 【详解】设10件产品中存在n 件次品，从中抽取2件，其次品数为X ，由16(1)45P X ==得，11102101645n n C C C -=， 化简得210160n n -+=， 解得2n =或8n =；又该产品的次品率不超过40%，4n ∴；应取2n =， 故选：A 【点睛】本题考查了古典概型的概率计算问题，也考查了离散型随机变量的分布列问题，是基础题．12．A解析：A 【分析】从5个数中任取两个不同数，取法为2510C =，列举和能被3整除的情况有4种，利用古典概型得解 【详解】从1,2,3,4,5中任取两个数，取法总数为2510C =这2个数的和能被3整除的情况有：()()()()1,21,52,44,5,，， ∴这2个数的和能被3整除的概率为：42105= 故选：A 【点睛】本题考查古典概型求概率，属于基础题.13．B解析：B 【分析】易得出8人乘车，每车4人的乘车方法是48C ，然后考虑从3名教师中选2人，从5名学生中选2人乘同一辆车，注意有两辆车，求出方法后可得概率． 【详解】8人乘车，每车4人的乘车方法是4870C =，从3名教师中选2人，从5名学生中选2人乘同一辆车的方法娄得2235260C C ⨯=，∴所求概率为606707P ==． 故选：B ． 【点睛】本题考查古典概型，解题关键是求出事件“恰有两名教师在同一车上”的方法数，易错点是不考虑两辆车．二、解答题14．（1）中位数是72.5，平均值为72；（2）1328． 【分析】（1）求出频率0.5对应的数值即为中位数，取各组数据中间值乘以频率相加即得平均值； （2）按分层抽样求出[80,90),[90,100]两组为抽取的人数，然后求挑选2的方法数和至少有一人问卷得分超过90的方法数后可计算出概率． 【详解】（1）由题意分数在[50,70)间的频率为(0.0150.025)100.4+⨯=， 因此中位数在[70,80]间，设中位数为x ，则700.50.4100.4x --=，解得72.5x =． 平均值为：(550.015650.025750.04850.015950.005)10⨯+⨯+⨯+⨯+⨯⨯=72；（2）由频率分布直方图知[80,90),[90,100]两组人数比为0.1530.051=，因此8人中[80,90)这组有6人，[90,100]这组有2人，∴所求概率为112622281328C C C P C +==． 【点睛】关键点点睛：本题考查频率分布直方图，由频率分布直方图求中位数，均值等，考查古典概型．解题关键是正确认识频率分布直方图，由频率分布直方图确定所有数据．然后根据各个数据特征进行计算．15．（1）答案见解析；（2）经过12个月. 【分析】（1）计算出题中四类人群每月应纳税所得额，结合题意求出每类人群的月缴个税及其概率；（2）计算出在旧政策下，该收入阶层的IT 从业者每月应纳税所得额，可求得新政策下，每月少缴个税额，设经过x 个月该市该收入阶层的IT 从业者各月少缴交的个税之和就超过2019年的月收入，根据已知条件可得出关于x 的不等式，结合x ∈N 可求得结果. 【详解】（1）由题意，既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1.①既不符合子女教育扣除又不符合赡养老人扣除的人群每月应纳税所得额为240005000100018000--=元，月缴个税为30000.0390000.160000.22190⨯+⨯+⨯=元，其概率为25； ②只符合子女教育扣除但不符合赡养老人扣除的人群每月应纳税所得额为2400050001000100017000---=元，月缴个税为30000.0390000.150000.21990⨯+⨯+⨯=元，其概率为15； ③只符合赡养老人扣除但不符合子女教育扣除的人群每月应纳税所得额为2400050001000200016000---=元，月缴个税为30000.0390000.140000.21790⨯+⨯+⨯=元，其概率为15； ④既符合子女教育扣除又符合赡养老人扣除的人群每月应纳税所得额为24000500010001000200015000----=元，月缴个税为30000.0390000.130000.21590⨯+⨯+⨯=元，其概率为15； （2）在旧政策下，该收入阶层的IT 从业者每月应纳税所得额为24000350020500-=元，故月缴个税为15000.0330000.145000.2115000.254120⨯+⨯+⨯+⨯=元， 在新政策下，该收入阶层的IT 从业者每月应纳税所得额为()212190199017901590195055⨯+++⨯=元，每月少缴个税412019502170-=元，设经过x 个月该市该收入阶层的IT 从业者各月少缴交的个税之和就超过2019年的月收入，则217024000x ≥，又x ∈N ，解得()12x x N ≥∈，所以经过12个月，该市该收入阶层的IT 从业者各月少缴交的个税之和就超过2019年的月收入. 【点睛】关键点点睛：解决本题第一问的关键在于理解题中个税新旧政策中的扣税方案，并依据题意计算出各类人群所扣的税额；解决本题第二问的关键在于求出新旧政策下所扣的税额，并结合题意列不等式求解. 16．（1）0.1a =；0.1；（2）710；（3）5.38小时. 【分析】（1）由频率之和等于1求出a 的值，这名学生该天居家自主学习的时间在[)3,4的概率； （2）由频率分布直方图可知自主学习时间在[)0,1和[)1,2的人分别有2人和3人，设在[)0,1的2人分别为,a b ，在[)1,2的3人分别,,A B C ，利用列举法结合古典概型的概率公式得出概率；（3）由频率分布直方图中的数据，求解平均数即可. 【详解】解：（1）因为(0.02+0.03+0.05+0.1520.20.3)11a +⨯++⨯=，所以0.1a =. 由图可得：随机抽取的100名学生中居家自主学习时间该天在[)3,4的频率为0.110.1⨯=。