2011年丰台二模试题及解析(理科)

丰台区2011年高三年级第二学期统一练习（二）理科综合 (物理)13. 下列理论的提出标志着量子理论诞生的是A．爱因斯坦提出光量子理论B．玻尔提出原子结构理论C．普朗克提出能量子理论D．爱因斯坦提出相对论14. 能说明光是一种横波的光学现象是A．光的偏振现象 B．光的干涉现象C．光的衍射现象 D．光的色散现象15. 电子是组成原子的基本粒子之一。

下列对电子的说法中正确的是A．密立根发现电子，汤姆生最早测量出电子电荷量为1.6×10-19CB．氢原子的电子由激发态向基态跃迁时，向外辐射光子，原子能量增加C．金属中的电子吸收光子逸出成为光电子，光电子最大初动能等于入射光电能量D．天然放射现象中的β射线实际是高速电子流，穿透能力比α射线强16. “神舟七号”宇宙飞船绕地球做匀速圆周运动，它比地球同步卫星轨道低很多，则“神舟七号”宇宙飞船与同步卫星相比A．线速度小一些 B．周期小一些C．向心加速度小一些 D．角速度小一些17. 图甲为一列简谐横波在t=0.10s时刻的波形图，P是平衡位置为x=1 m处的质点，Q是平衡位置为x=4 m处的质点，图乙为质点Q的振动图象，则A．t=0.10s时，质点Q的速度方向向上B．该波沿x轴正方向的传播C．该波的传播速度为40m/sD．从t=0.10s到t=0.25s，质点P通过的路程为30 cm18. 如图甲所示为一台小型发电机构造的示意图，线圈逆时针转动，产生的电动势随时间变化的正弦规律图象如图乙所示。

发电机线圈内电阻为1.0Ω，外接灯泡的电阻为9.0Ω。

则图甲－－－A ．在t =0.01s 的时刻，穿过线圈磁通量为零B ．瞬时电动势的表达式为t e π50sin 26=(V)C ．电压表的示数为6VD ．通过灯泡的电流为0.6A19. 如图所示，水平向左的匀强电场场强大小为E ，一根不可伸长的绝缘细线长度为L ，细线一端拴一个质量为m 、电荷量为q 的带负电小球，另一端固定在O 点。

海淀区高三年级第二学期期末练习数 学 （理科） 2011.5一、选择题：1. 复数11i+在复平面上对应的点的坐标是A ．(1,1) B. (1,1)- C. (1,1)-- D. (1,1)- 2. 已知全集R,U = 集合{}1,2,3,4,5A =,{|2}B x x =∈≥R ，下图中阴影部分所表示的集合为A {1} B. {0,1} C. {1,2} D. {0,1,2}3．函数21()log f x x x=-的零点所在区间A ．1(0,)2 B. 1(,1)2C. (1,2)D. (2,3)4.若直线l 的参数方程为13()24x tt y t =+⎧⎨=-⎩为参数，则直线l 倾斜角的余弦值为A ．45-B ． 35-C ． 35D ． 455. 某赛季甲、乙两名篮球运动员各13场比赛得分情况用茎叶图表示如下：甲 乙 9 8 8 1 7 7 9 9 6 1 0 2 2 5 6 7 9 9 5 3 2 0 3 0 2 3 7 1 0 4 根据上图，对这两名运动员的成绩进行比较，下列四个结论中，不正确．．．的是 A ．甲运动员得分的极差大于乙运动员得分的极差B ．甲运动员得分的的中位数大于乙运动员得分的的中位数C ．甲运动员的得分平均值大于乙运动员的得分平均值D ．甲运动员的成绩比乙运动员的成绩稳定．可能是．．．该锥体的俯视图的是C主视图左视图1C ：1212212=+b y a x （011>>b a ）和椭圆2C ：1222222=+b y a x （022>>b a ）的焦点相同且12a a >.给出如下四个结论：① 椭圆1C 和椭圆2C 一定没有公共点； ②1122a b a b >； ③ 22212221b b a a -=-； ④1212a a b b -<-.其中，所有正确结论的序号是A ．②③④B ①③④C ．①②④ D. ①②③在一个正方体1111ABCD A BC D -中，P 为正方形1111A B C D 四边上的动点，O 为底面正方形ABCD 的中心，,M N 分别为,AB BC 中点，点Q 为平面ABCD 内一点，线段1D Q 与OP 互相平分，则满足MQ MN λ=的实数λ的值有A. 0个B. 1个 C 2个 D. 3个非选择题（共110分）二、填空题:本大题共6小题,每小题5分,共30分.9．点(,)P x y 在不等式组2,,2y x y x x ≤⎧⎪≥-⎨⎪≤⎩表示的平面区域内，则z x y =+的最大值为_______.10．运行如图所示的程序框图，若输入4n =，则输出S 的值为 . 11．若4234512345(1)x mx a x a x a x a x a x -=++++， 其中26a =-，则实数m 的值为 ；12345a a a a a ++++的值为 .12．如图，已知O 的弦AB 交半径OC 于点D ，若3AD =，2BD =，且D 为OC 的中点，则CD 的长为 .{}n a 满足1,a t =，120n n a a +-+= (,)t n ∈∈**N N ，记数列{}n a 的前n 项和的最大值为()f t ，则()f t = .A1D 1A 1C 1B DC BOPNM Q已知函数sin ()xf x x=（1）判断下列三个命题的真假：①()f x 是偶函数；②()1f x < ；③当32x π=时，()f x 取得极小值. 其中真命题有____________________；（写出所有真命题的序号） （2）满足()()666n n f f πππ<+的正整数n 的最小值为___________. 三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15. （本小题共13分）已知函数2()cos cos f x x x x ωωω= (0)ω>的最小正周期为π.（Ⅰ）求2()3f π的值；（Ⅱ）求函数()f x 的单调区间及其图象的对称轴方程. 16.（本小题共13分）某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客，假设每位乘客在2、3、4层下电梯是等可能的.(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率；(Ⅱ) 用X 表示4名乘客在第4层下电梯的人数，求X 的分布列和数学期望.17.(本小题共14分)如图，四棱锥P ABCD -的底面是直角梯形，//AB CD ，AB AD ⊥，PAB ∆和PAD ∆是两个边长为2的正三角形，4DC =，O 为BD 的中点，E 为PA 的中点．(Ⅰ)求证：PO ⊥平面ABCD ；(Ⅱ)求证：//OE 平面PDC ；(Ⅲ)求直线CB 与平面PDC 所成角的正弦值．18. (本小题共14分）已知函数221()()ln 2f x ax x x ax x =--+.()a ∈R . （I ）当0a =时，求曲线()y f x =在(e,(e))f 处的切线方程（e 2.718...=）； （II ）求函数()f x 的单调区间. 19．(本小题共13分）在平面直角坐标系xOy 中，设点(,),(,4)P x y M x -，以线段PM 为直径的圆经过ADOCPBE原点O .（Ⅰ）求动点P 的轨迹W 的方程；（Ⅱ）过点(0,4)E -的直线l 与轨迹W 交于两点,A B ，点A 关于y 轴的对称点为'A ，试判断直线'A B 是否恒过一定点，并证明你的结论.20. (本小题共13分）对于数列12n A a a a ：，，，，若满足{}0,1(1,2,3,,)i a i n ∈=⋅⋅⋅，则称数列A 为“0-1数列”.定义变换T ，T 将“0-1数列”A 中原有的每个1都变成0，1，原有的每个0都变成1，0. 例如A :1,0,1，则():0,1,1,0,0,1.T A 设0A 是“0-1数列”，令1(),k k A T A -=12k = ，，3,.(Ⅰ) 若数列2A ：1,0,0,1,0,1,1,0,1,0,0,1. 求数列10,A A ；(Ⅱ) 若数列0A 共有10项，则数列2A 中连续两项相等的数对至少有多少对？请说明理由； (Ⅲ)若0A 为0，1，记数列k A 中连续两项都是0的数对个数为k l ，1,2,3,k =⋅⋅⋅.求k l 关于k 的表达式.海淀区高三年级第二学期期末练习数 学（理）答案及评分参考 2011．5选择题 （共40分）一、选择题（本大题共8小题,每小题5分,共40分）非选择题 （共110分）二、填空题（本大题共6小题,每小题5分. 共30分.有两空的题目，第一空3分，第二空2分）9. 6 10. 11 11.32， 11613. 222, (4(1), (4t tt t t ⎧+⎪⎪⎨+⎪⎪⎩为偶数)为奇数) 14. ①② , 9 三、解答题(本大题共6小题,共80分) 15. （共13分） 解：（Ⅰ）1()(1cos 2)22f x x x =+ωω………………………2分1sin(2)26x =++πω, …………………………3分 因为()f x 最小正周期为π,所以22ππω=，解得1ω=, …………………………4分所以1()sin(2)62πf x x =++, ………………………… 5分 所以21()32πf =-. …………………………6分 （Ⅱ）分别由222,()262k x k k Z πππππ-≤+≤+∈，3222,()262k x k k Z πππππ+≤+≤+∈可得,()36k x k k Z ππππ-≤≤+∈，2,().63k x k k Z ππππ+≤≤+∈………………8分所以,函数()f x 的单调增区间为[,],()36k k k Z ππππ-+∈； ()f x 的单调减区间为2[,],().63k k k Z ππππ++∈………………………10分 由2,(62ππx k πk Z +=+∈）得,()26k πx πk Z =+∈. 所以，()f x 图象的对称轴方程为()26k πx πk Z =+∈. …………………………13分16.（共13分）解：(Ⅰ) 设4位乘客中至少有一名乘客在第2层下电梯的事件为A , …………………………1分由题意可得每位乘客在第2层下电梯的概率都是13， ……………………………3分 则4265()1()1381P A P A ⎛⎫=-=-=⎪⎝⎭ .……………………………6分(Ⅱ) X 的可能取值为0,1,2,3,4, …………………………7分 由题意可得每个人在第4层下电梯的概率均为13，且每个人下电梯互不影响， 所以，1(4,3X B . …………………………………11分14()433E X =⨯=. ………………………………13分17.(共14分)（Ⅰ）证明：设F 为DC 的中点，连接BF ，则DF AB = ∵AB AD ⊥，AB AD =，//AB DC ， ∴四边形ABFD 为正方形， ∵O 为BD 的中点， ∴O 为,AF BD 的交点，∵2PD PB ==，∴PO BD ⊥， ………………………………..2分∵BD ==∴PO=12AO BD == 在三角形PAO 中，2224PO AO PA +==，∴PO AO ⊥，……………………………4分 ∵AO BD O = ，∴PO ⊥平面ABCD ； ……………………………5分 (Ⅱ)方法1：连接PF ，∵O 为AF 的中点，E 为PA 中点， ∴//OE PF ，∵OE ⊄平面PDC ，PF ⊂平面PDC ，∴//OE 平面PDC . ……………………………9分方法2：由(Ⅰ)知PO ⊥平面ABCD ，又AB AD ⊥，所以过O 分别做,AD AB 的平行线，以它们做,x y 轴，以OP 为z 轴建立如图所示的空间直角坐标系， 由已知得：(1,1,0)A --，(1,1,0)B -，(1,1,0)D -(1,1,0)F ，(1,3,0)C，P ，11(,22E --，则11(,22OE =--，(1,1,PF =，(1,1,PD =-，(1,3,PC = .A DO CPB EF∴12OE PF =-∴//OE PF∵OE ⊄平面PDC ，PF ⊂平面PDC ，∴//OE 平面PDC ； …………………………………9分(Ⅲ) 设平面PDC 的法向量为111(,,)n x y z =，直线CB 与平面PDC 所成角θ，则00n PC n PD ⎧⋅=⎪⎨⋅=⎪⎩，即111111300x y x y ⎧+-=⎪⎨-=⎪⎩，解得1110y x =⎧⎪⎨=⎪⎩，令11z =，则平面PDC的一个法向量为)n = ，又(2,2,0)CB =--则sin cos ,θn CB =<>==， ∴直线CB 与平面PDC所成角的正弦值为3. ………………………………………14分18. (共14分）解：（I ）当0a =时，()ln f x x x x =-，'()ln f x x =-， ………………………2分 所以()0f e =，'()1f e =-， ………………………4分 所以曲线()y f x =在(e,(e))f 处的切线方程为y x e =-+.………………………5分 （II ）函数()f x 的定义域为(0,)+∞21'()()(21)ln 1(21)ln f x ax x ax x ax ax x x=-+--+=-，…………………………6分①当0a ≤时，210ax -<，在(0,1)上'()0f x >，在(1,)+∞上'()0f x <所以()f x 在(0,1)上单调递增，在(1,)+∞上递减； ……………………………………………8分②当102a <<时，在(0,1)和1(,)2a +∞上'()0f x >，在1(1,)2a上'()0f x < 所以()f x 在(0,1)和1(,)2a +∞上单调递增，在1(1,)2a上递减；………………………10分③当12a =时，在(0,)+∞上'()0f x ≥且仅有'(1)0f =，所以()f x 在(0,)+∞上单调递增； ……………………………………………12分④当12a >时，在1(0,)2a 和(1,)+∞上'()0f x >，在1(,1)2a上'()0f x < 所以()f x 在1(0,)2a 和(1,)+∞上单调递增，在1(,1)2a上递减……………………………14分19．(共13分） 解：（I ）由题意可得OP OM ⊥， ……………………………2分所以O POM⋅= ，即(,xy x -= ………………………………4分即240x y -=，即动点P 的轨迹W 的方程为24x y = ……………5分 （II ）设直线l 的方程为4y kx =-,1122(,),(,)A x y B x y ，则11'(,)A x y -. 由244y kx x y=-⎧⎨=⎩消y整理得24160x kx -+=， ………………………………6分则216640k ∆=->，即|k >. ………………………………7分12124,16x x k x x +==. …………………………………9分直线212221':()y y A B y y x x x x --=-+212221222212212222121222112()1()4()41444 y 44y y y x x y x x x x y x x x x x x x x x x y x x x x x x x -∴=-++-∴=-++--∴=-+-∴=+……………………………………12分即2144x x y x -=+ 所以，直线'A B恒过定点(0,4). ……………………………………13分20. (共13分）解：(Ⅰ)由变换T 的定义可得1:0,1,1,0,0,1A …………………………………2分0:1,0,1A (4)分(Ⅱ) 数列0A 中连续两项相等的数对至少有10对 …………………………………5分证明：对于任意一个“0-1数列”0A ，0A 中每一个1在2A 中对应连续四项1,0,0,1，在0A 中每一个0在2A 中对应的连续四项为0,1,1,0，因此，共有10项的“0-1数列”0A 中的每一个项在2A 中都会对应一个连续相等的数对， 所以2A 中至少有10对连续相等的数对. …………………………………………………………8分 (Ⅲ) 设k A 中有k b 个01数对，1k A +中的00数对只能由k A 中的01数对得到，所以1k k l b +=，1k A +中的01数对有两个产生途径：①由k A 中的1得到； ②由k A 中00得到，由变换T 的定义及0:0,1A 可得k A 中0和1的个数总相等，且共有12k +个，所以12k k k b l +=+， 所以22k k k l l +=+，由0:0,1A 可得1:1,0,0,1A ，2:0,1,1,0,1,0,0,1A 所以121,1l l ==， 当3k ≥时，若k 为偶数，222k k k l l --=+4242k k k l l ---=+ 2422l l =+上述各式相加可得122421(14)11222(21)143k k kk l ---=++++==-- ，经检验，2k =时，也满足1(21)3k k l =-若k 为奇数，222k k k l l --=+ 4242k k k l l ---=+ 312l l =+上述各式相加可得12322(14)112221(21)143k k kk l ---=++++=+=+- ，经检验，1k =时，也满足1(21)3k k l =+所以1(21),31(21),3kk k k l k ⎧+⎪⎪=⎨⎪-⎪⎩为奇数为偶数…………………………………………………………………………………..13分说明：其它正确解法按相应步骤给分.北京市西城区2011年高三二模试卷数学（理科） 2011.5第Ⅰ卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题列出的四个选项中，选出符合题目要求的一项.1.已知集合{0,1}A =，{1,0,3}B a =-+，且A B ⊆，则a 等于 （A ）1（B ）0（C ）2- （D ）3-2.已知i 是虚数单位，则复数23z i+2i 3i =+所对应的点落在 （A ）第一象限 （B ）第二象限 （C ）第三象限（D ）第四象限3.在ABC ∆中，“0AB BC ⋅>”是“ABC ∆为钝角三角形”的（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件（D ）既不充分又不必要条件4.已知六棱锥P ABCDEF -的底面是正六边形，PA ⊥平面ABC .则下列结论不正确．．．的是 （A ）//CD 平面PAF （B ）DF ⊥平面PAF （C ）//CF 平面PAB （D ）CF ⊥平面PAD5.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切，则双曲线离心率为（A（B（C ）2（D ）36.函数sin()(0)y x ϕϕ=π+>的部分图象如右图所示，设P 是图象的最高点，,A B 是图象与x 轴的交点，则tan APB ∠=（A ）10 （B ）8 （C ）87（D ）77．已知数列{}n a 的通项公式为13n a n =-，那么满足119102k k k a a a +++++= 的整数k （A ）有3个 （B ）有2个 （C ）有1个（D ）不存在8．设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +（A ）最小值为15 （B）最小值为5 （C ）最大值为15（D）最大值为5第Ⅱ卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9．在ABC ∆中，若2B A =，:a b =A =_____. 10.在521()x x+的展开式中，2x 的系数是_____. 11．如图，AB 是圆O 的直径，P 在AB 的延长线上，PD切圆O 于点C .已知圆O2OP =，则PC =______；ACD ∠的大小为______.12.在极坐标系中，点(2,)2A π关于直线:cos 1l ρθ=的对称点的一个极坐标为_____.13．定义某种运算⊗，a b ⊗的运算原理如右图所示.设()(0)(2)f x x x x =⊗-⊗. 则(2)f =______；()f x 在区间[2,2]-上的最小值为______.14.数列{}n a 满足11a =，11n n n a a n λ+-=+，其中λ∈R ， 12n = ，，．①当0λ=时，20a =_____；②若存在正整数m ，当n m >时总有0n a <，则λ的取值范围是_____.三、解答题：本大题共6小题，共80分. 解答应写出必要的文字说明、证明过程或演算步骤.15.（本小题满分13分）已知函数cos 2()sin()4x f x x π=+.（Ⅰ）求函数()f x 的定义域； （Ⅱ）若4()3f x =，求s i n 2x 的值.16.（本小题满分13分）如图，已知菱形ABCD 的边长为6，60BAD ∠=,AC BD O = .将菱形ABCD 沿对角线AC折起，使BD =B ACD -.（Ⅰ）若点M 是棱BC 的中点，求证://OM 平面ABD ； （Ⅱ）求二面角A B D O --的余弦值；（Ⅲ）设点N 是线段BD 上一个动点，试确定N点的位置，使得CN =你的结论.17.（本小题满分13分）甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.（Ⅰ）求选出的4名选手均为男选手的概率.（Ⅱ）记X 为选出的4名选手中女选手的人数，求X 的分布列和期望.18.（本小题满分14分）已知函数()(1)e (0)xa f x x x=->，其中e 为自然对数的底数.（Ⅰ）当2a =时，求曲线()y f x =在(1,(1))f 处的切线与坐标轴围成的面积； （Ⅱ）若函数()f x 存在一个极大值点和一个极小值点，且极大值与极小值的积为5e ，求a 的值.19.（本小题满分14分）已知椭圆2222:1x y M a b +=(0)a b >>，且椭圆上一点与椭圆的两个焦点构成的三角形周长为246+．M（Ⅰ）求椭圆M 的方程；（Ⅱ）设直线l 与椭圆M 交于,A B 两点，且以AB 为直径的圆过椭圆的右顶点C ， 求ABC ∆面积的最大值．20.（本小题满分13分）若m A A A ,,,21 为集合2}(,,2,1{≥=n n A 且)n ∈*N 的子集，且满足两个条件： ①12m A A A A = ；②对任意的A y x ⊆},{，至少存在一个},,3,2,1{m i ∈，使}{},{x y x A i = 或}{y . 则称集合组m A A A ,,,21 具有性质P .如图，作n 行m 列数表，定义数表中的第k 行第l 列的数为⎩⎨⎧∉∈=)(0)(1l l kl A k A k a .（Ⅰ）当4n =时，判断下列两个集合组是否具有性质P ，如果是请画出所对应的表格，如果不是请说明理由；集合组1：123{1,3},{2,3},{4}A A A ===； 集合组2：123{2,3,4},{2,3},{1,4}A A A ===. （Ⅱ）当7n =时，若集合组123,,A A A 具有性质P ，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合123,,A A A ；（Ⅲ）当100n =时，集合组12,,,t A A A 是具有性质P 且所含集合个数最小的集合组，求t 的值及12||||||t A A A ++ 的最小值.（其中||i A 表示集合i A 所含元素的个数）北京市西城区2011年高三二模试卷参考答案及评分标准数学（理科） 2011.5一、选择题：本大题共8小题，每小题5分，共40分.题号1 2 3 4 5 6 7 8 答案C C AD C B B A二、填空题：本大题共6小题，每小题5分，共30分.9. 30 10. 5 11.1；7512.)4π（或其它等价写法） 13.2-；6- 14.120；(21,2),k k k -∈*N . 注：11、13、14题第一问2分，第二问3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分.15.（本小题满分13分） 解：（Ⅰ）由题意，sin()04x π+≠， ………………2分 所以()4x k k π+≠π∈Z ， ………………3分 所以()4x k k π≠π-∈Z ， ………………4分函数()f x 的定义域为{x x ≠,4k k ππ-∈Z }. ………………5分（Ⅱ）c o s 2c o s 2()sin()sin cos cos sin444x x f x x x x ==πππ++ ………………7分2sin cos xx x=+ ………………8分22sin )sin )sin cos x x x x x x-==-+. ………………10分因为4()3f x =，所以cos sin 3x x -=. ………………11分 所以，2sin 21(cos sin )x x x =-- ………………12分81199=-= . ………………13分16.（本小题满分13分）（Ⅰ）证明：因为点O 是菱形ABCD 的对角线的交点，所以O 是AC 的中点.又点M 是棱BC 的中点，所以OM 是ABC ∆的中位线，//OM AB . ………………1分因为OM ⊄平面ABD ,AB ⊂平面ABD ,所以//OM 平面ABD . ………………3分 （Ⅱ）解：由题意，3OB OD ==，因为BD =所以90BOD ∠=，OB OD ⊥. ………………4分 又因为菱形ABCD ，所以OB AC ⊥，OD AC ⊥. 建立空间直角坐标系O xyz -，如图所示.(0,3,0),A D (0,0,3)B .所以((AB AD =-=-………………6分设平面ABD 的法向量为n =(,,)x y z ，则有0,0AB AD ⎧⋅=⎪⎨⋅=⎪⎩n n即：30,30z y ⎧-+=⎪⎨-+=⎪⎩令1x =，则y z ==n=(1. ………………7分 因为,AC OB AC OD ⊥⊥,所以AC ⊥平面BOD . 平面BOD 的法向量与AC 平行，所以平面BOD 的法向量为0(1,0,0)=n . ………………8分000cos ,⋅〈〉===n n n n n n 因为二面角A B D O --是锐角，所以二面角A B D O --的余弦值为. ……………9分 （Ⅲ）解：因为N 是线段BD 上一个动点，设111(,,)N x y z ，BN BD λ=，则111(,,3)(0,3,3)x y z λ-=-，所以1110,3,33x y z λλ===-， ……………10分则(0,3,33)N λλ-，,33)CN λλ=-，由CN ==，即29920λλ-+=，…………11分解得13λ=或3λ=， ……………12分 所以N 点的坐标为(0,2,1)或(0,1,2). ……………13分（也可以答是线段BD 的三等分点，2BN ND = 或2BN ND =）17.（本小题满分13分）解：（Ⅰ）事件A 表示“选出的4名选手均为男选手”.由题意知232254()C P A C C = ………………3分11110220=⨯=. ………………5分 （Ⅱ）X 的可能取值为0,1,2,3. ………………6分23225431(0)10620C P X C C ====⨯， ………………7分11212333225423337(1)10620C C C C P X C C +⨯⨯+====⨯， ………………9分 21332254333(3)10620C C P X C C ⨯====⨯， ………………10分 (2)1(0)(1)(3)P X P X P X P X ==-=-=-=920=. ………………11分 X 的分布列：X0 1 2 3 P120 720 920320………………12分179317()01232020202010E X =⨯+⨯+⨯+⨯=. ………………13分18、（本小题满分14分）解：（Ⅰ）22()e xx ax a f x x -+'=， ………………3分 当2a =时，2222()e xx x f x x -+'=， 12122(1)e e 1f -+'=⨯=，(1)e f =-， 所以曲线()y f x =在(1,(1))f 处的切线方程为e 2e y x =-， ………………5分 切线与x 轴、y 轴的交点坐标分别为(2,0)，(0,2e)-， ………………6分 所以，所求面积为122e 2e 2⨯⨯-=. ………………7分 （Ⅱ）因为函数()f x 存在一个极大值点和一个极小值点，所以，方程20x ax a -+=在(0,)+∞内存在两个不等实根， ………………8分则240,0.a a a ⎧∆=->⎨>⎩ ………………9分 所以4a >. ………………10分 设12,x x 为函数()f x 的极大值点和极小值点，则12x x a +=，12x x a =， ………………11分 因为，512()()e f x f x =， 所以，1251212e e e x x x a x a x x --⨯=， ………………12分 即1225121212()e e x x x x a x x a x x +-++=，225e e a a a a a -+=，5e e a =， 解得，5a =，此时()f x 有两个极值点，所以5a =. ………………14分19.（本小题满分14分）解：（Ⅰ）因为椭圆M 上一点和它的两个焦点构成的三角形周长为246+，所以24622+=+c a ， ……………1分又椭圆的离心率为3，即3c a =，所以3c a =， ………………2分所以3a =，c =………………4分所以1b =，椭圆M 的方程为1922=+y x . ………………5分 （Ⅱ）方法一：不妨设BC 的方程(3),(0)y n x n =->，则AC 的方程为)3(1--=x ny . 由22(3),19y n x x y =-⎧⎪⎨+=⎪⎩得0196)91(2222=-+-+n x n x n ， ………………6分 设),(11y x A ，),(22y x B ，因为222819391n x n -=+，所以19327222+-=n n x ， ………………7分同理可得2219327nn x +-=， ………………8分所以1961||22++=n n BC ，222961||nn n n AC ++=， ………………10分 964)1()1(2||||212+++==∆n n n n AC BC S ABC ， ………………12分 设21≥+=n n t ，则22236464899t S t t t ==≤++， ………………13分当且仅当38=t 时取等号，所以ABC ∆面积的最大值为83. ………………14分方法二：不妨设直线AB 的方程x ky m =+.由22,1,9x ky m x y =+⎧⎪⎨+=⎪⎩ 消去x 得222(9)290k y kmy m +++-=， ………………6分 设),(11y x A ，),(22y x B ，则有12229km y y k +=-+，212299m y y k -=+. ① ………………7分因为以AB 为直径的圆过点C ，所以 0CA CB ⋅=.由 1122(3,),(3,)CA x y CB x y =-=-，得 1212(3)(3)0x x y y --+=. ………………8分 将1122,x ky m x ky m =+=+代入上式，得 221212(1)(3)()(3)0k y y k m y y m ++-++-=.将 ① 代入上式，解得 125m =或3m =（舍）. ………………10分 所以125m =（此时直线AB 经过定点12(,0)5D ，与椭圆有两个交点），所以121||||2ABC S DC y y ∆=-12==……………12分设211,099t t k =<≤+，则ABC S ∆=所以当251(0,]2889t =∈时，ABC S ∆取得最大值83. ……………14分20.（本小题满分13分）（Ⅰ）解：集合组1具有性质P . ………………1分所对应的数表为： (3)分集合组2不具有性质P . ………………4分 因为存在{{2,3}1,2,3,4}⊆，有123{2,3}{2,3},{2,3}{2,3},{2,3}A A A ===∅ ， 与对任意的A y x ⊆},{，都至少存在一个{1,2,3}i ∈，有}{},{x y x A i = 或}{y 矛盾，所以集合组123{2,3,4},{2,3},{1,4}A A A ===不具有性质P . ………………5分（Ⅱ）……………7分123{3,4,5,7},{2,4,6,7},{1,5,6,7}A A A ===. ………………8分 （注：表格中的7行可以交换得到不同的表格，它们所对应的集合组也不同） （Ⅲ）设12,,,t A A A 所对应的数表为数表M ，因为集合组12,,,t A A A 为具有性质P 的集合组， 所以集合组12,,,t A A A 满足条件①和②， 由条件①：12t A A A A = ，可得对任意x A ∈，都存在{1,2,3,,}i t ∈ 有i A x ∈， 所以1=xi a ，即第x 行不全为0，所以由条件①可知数表M 中任意一行不全为0. ………………9分1 1 1 1 1 1 1 1 1 11 1 0 0 0 00 0 0 0 0 01 1 0 0 00 1 1 0 0 1由条件②知，对任意的A y x ⊆},{，都至少存在一个{1,2,3,,}i t ∈ ，使}{},{x y x A i = 或}{y ，所以yi xi a a ,一定是一个1一个0，即第x 行与第y 行的第i 列的两个数一定不同.所以由条件②可得数表M 中任意两行不完全相同. ………………10分 因为由0,1所构成的t 元有序数组共有2t个，去掉全是0的t 元有序数组，共有21t-个，又因数表M 中任意两行都不完全相同，所以10021t≤-，所以7t ≥.又7t =时，由0,1所构成的7元有序数组共有128个，去掉全是0的数组，共127个，选择其中的100个数组构造100行7列数表，则数表对应的集合组满足条件①②，即具有性质P .所以7t =. ………………12分 因为12||||||t A A A +++ 等于表格中数字1的个数，所以，要使12||||||t A A A +++ 取得最小值，只需使表中1的个数尽可能少， 而7t =时，在数表M 中，1的个数为1的行最多7行；1的个数为2的行最多2721C =行； 1的个数为3的行最多3735C =行； 1的个数为4的行最多4735C =行；因为上述共有98行，所以还有2行各有5个1，所以此时表格中最少有722133543552304+⨯+⨯+⨯+⨯=个1.所以12||||||t A A A +++ 的最小值为304. ………………14分北京市东城区2010-2011学年第二学期高三综合练习数学 （理科）学校_____________班级_______________姓名______________考号___________ 本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

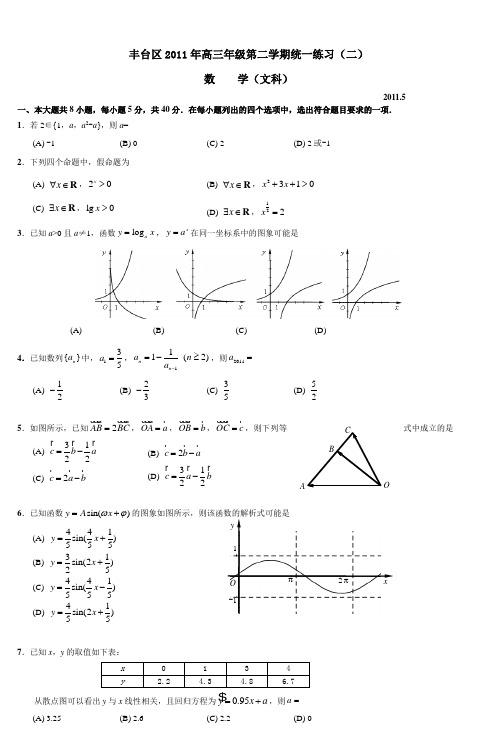
xyO π2π1-1丰台区2011年高三年级第二学期统一练习（二）数 学（文科）2011.5一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．若2∈{1，a ，a 2-a }，则a =(A) -1(B) 0(C) 2(D) 2或-12．下列四个命题中，假命题为(A) x ∀∈R ，20x>(B) x ∀∈R ，2310x x ++>(C) x ∃∈R ，lg 0x >(D) x ∃∈R ，122x =3．已知a >0且a ≠1，函数log a y x =，x y a =在同一坐标系中的图象可能是(A)(B)(C)(D)4．已知数列{}n a 中，135a =，111(2)n n a n a -=-≥，则2011a = (A) 12- (B) 23-(C)35(D)525．如图所示，已知2AB BC = ，OA a = ，OB b = ，OC c =，则下列等式中成立的是(A) 3122c b a =-(B) 2c b a =-(C) 2c a b =-(D) 3122c a b =-6．已知函数sin()y A x ωϕ=+的图象如图所示，则该函数的解析式可能是(A) 441sin()555y x =+ (B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+7．已知x ，y 的取值如下表：从散点图可以看出y 与x 线性相关，且回归方程为 0.95y x a =+，则a = (A) 3.25 (B) 2.6(C) 2.2(D) 0O8．用max{}a b ，表示a ，b 两个数中的最大数，设22()max{84,log }f x x x x =-+-，若函数()()g x f x kx =-有2个零点，则k 的取值范围是 (A) (0,3)(B) (0,3](C) (0,4)(D) [0,4]二、填空题：本大题共6小题，每小题5分，共30分． 9．在复平面内，复数121iz i-=+对应的点位于第 象限． 10．圆C ：222220x y x y ++--=的圆心到直线3x +4y +14=0的距离是 ． 11．若[0,2]x ∈π，则函数sin cos y x x x =-的单调递增区间是 ．12．已知签字笔2元一只，练习本1元一本．某学生欲购买的签字笔不少于3只，练习本不少于5本，但买签字笔和练习本的总数量不超过10，则支出的钱数最多是___元．13．一个几何体的三视图如图所示，则该几何体的体积是 ．14．如图所示，已知正方形ABCD 的边长为1，以A 为圆心，AD 长为半径画弧，交BA 的延长线于P 1，然后以B 为圆心，BP 1长为半径画弧，交CB 的延长线于P 2，再以C 为圆心，CP 2长为半径画弧，交DC 的延长线于P 3，再以D 为圆心，DP 3长为半径画弧，交AD 的延长线于P 4，再以A 为圆心，AP 4长为半径画弧，…，如此继续下去，画出的第8道弧的半径是___，画出第n 道弧时，这n 道弧的弧长之和为___．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数21()sin cos 2f x x x x =+-． （Ⅰ）求()12f π-的值； （Ⅱ）若[0,]2x π∈，求函数()y f x =的最小值及取得最小值时的x 值．16.（本小题共13分）已知梯形ABCD 中，//BC AD ，112BC AD ==，CD G ，E ，F 分别是AD ，BC ，CD的中点，且CG =CG 将△CDG 翻折到△CD G '． （Ⅰ）求证：EF //平面AD B '；（Ⅱ）求证：平面CD G '⊥平面AD G '．17.（本小题共13分）AB C A D P 1 P 2P 3P 4P 5正视图侧视图俯视图FGE ABCD 'AB C EDFG某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩（均为整数）分成六段：[)50,40，[)60,50，…，[]100,90后得到如下频率分布直方图．（Ⅰ）求分数在[)70,80内的频率；（Ⅱ）根据频率分布直方图，估计该校高一年级学生期中 考试数学成绩的平均分；（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率． 18.（本小题共14分）已知函数21(),(0)2af x x a x=+≠． （Ⅰ）当1x =时函数()y f x =取得极小值，求a 的值； （Ⅱ）求函数()y f x =的单调区间． 19.（本小题共14分）已知椭圆C 的长轴长为(1,0)．（Ⅰ）求椭圆C 的标准方程； （Ⅱ）设直线l ：y =kx 与椭圆C 交于A ，B 两点，点P 为椭圆的右顶点．（ⅰ）若直线l 斜率k =1，求△ABP 的面积；（ⅱ）若直线AP ，BP 的斜率分别为1k ，2k ，求证：12k k ⋅为定值． 20.（本小题共13分）已知数列{}n a 的前n 项和为n S ，且2n S n =．数列{}n b 为等比数列，且11b =，48b =． （Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ）若数列{}n c 满足n n b c a =，求数列{}n c 的前n 项和n T ；（Ⅲ）在（Ⅱ）的条件下，数列{}n c 中是否存在三项，使得这三项成等差数列？若存在，求出此三项；若不存在，说明理由．丰台区2011年高三年级第二学期统一练习（二）数 学（文科）参考答案2011.5二、填空题：本大题共6小题，每小题5分，共30分．9．Ⅲ 10．3 11．(0,)π写成闭区间也给满分 12．15 13．12 14． 8，(1)4n n +π注：两个空的填空题第一个空填对得2分，第二个空填对得3分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数21()sin cos 2f x x x x =+-． （Ⅰ）求()12f π-的值；（Ⅱ）求函数(),[0,]2y f x x π=∈的最小值，及取得最小值时的x 的值．解：（Ⅰ）∵21()sin cos 2f x x x x =+-1sin 2cos 222x x =- sin(2)6x π=-， ………………5分∴()sin(2)sin()1212632f ππππ-=-⨯-=-=-． ………………7分 （Ⅱ）∵02x π≤≤∴02x π≤≤．∴52666x πππ-≤-≤． ………………9分∴1sin(2)126x π-≤-≤， 即1()12f x -≤≤． ………………11分∴min 1()2f x =- 此时266x ππ-=- ∴0x =． ………………12分∴当0x =时，min 1()2f x =-． ………………13分16.（本小题共13分）已知梯形ABCD 中，//BC AD ，112BC AD ==，CD =G ，E ，F 分别是AD ，BC ，CD 的中点，且CG =CG 将△CDG 翻折成△CD G '． （Ⅰ）求证：EF //平面AD B '；（Ⅱ）求证：平面CD G '⊥平面AD G '．证明：（Ⅰ）∵E ，F 分别是BC ，CD 的中点，即E ，F 分别是BC ，C D '的中点， ∴EF 为△D BC '的中位线．∴EF //D B '． ………………2分又∵EF ⊄平面AD B '，D B '⊂平面AD B '， ………………4分 ∴EF // 平面AD B '． ………………6分 （Ⅱ）∵G 是AD 的中点，112BC AD ==，即2AD =， ∴1DG =．又∵CD =CG =∴在DGC ∆中，222DG GC DC += ∴DG GC ⊥． ………………9分 ∴GC D G '⊥，GC AG ⊥． ∵AG ∩D G '=G ，∴GC ⊥平面AD G '． ………………12分 又∵GC ⊂平面CD G '，∴平面CD G '⊥平面AD G '． ………………13分17.（本小题共13分）某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩（均为整数）分成六段[)50,40，[)60,50，…，[]100,90后得到如下频率分布直方图．（Ⅰ）求分数在[)70,80内的频率；（Ⅱ）根据频率分布直方图，估计该校高一年级学生期中考试数学成绩的平均分；（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率． 解：（Ⅰ）分数在[)70,80内的频率为：1(0.0100.0150.0150.0250.005)10-++++⨯10.70.3=-=． ………………3分（Ⅱ）平均分为：450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=． ………………6分 （Ⅲ）由题意，[)80,90分数段的人数为：0.256015⨯=人； ………………7分[]90,100分数段的人数为：0.05603⨯=人； ………………8分∵用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本， ∴[)80,90分数段抽取5人，分别记为A ，B ，C ，D ，E ；[]90,100分数段抽取1人，记为M ． ………………9分因为从样本中任取2人，其中恰有1人的分数不低于90分，FGEABCD 'ABC EDFG则另一人的分数一定是在[)80,90分数段，所以只需在分数段[)80,90抽取的5人中确定1人． 设“从样本中任取2人，其中恰有1人的分数不低于90分为”事件A ， ………………10分 则基本事件空间包含的基本事件有：(A ，B )，(A ，C)，(A ，D)，(A ，E )，(B ，C )，(B ，D )， (B ，E )，(C ，D )，(C ，E )，(D ，E)，(A ，M )，(B ，M )，(C ，M )，(D ，M )，(E ，M )共15种． 事件A 包含的基本事件有(A ，M )，(B ，M )，(C ，M )，(D ，M )，(E ，M )5种．………………12分 ∴恰有1人的分数不低于90分的概率为51()153P A ==． ………………13分18.（本小题共14分）已知函数21(),(0)2af x x a x=+≠． （Ⅰ）当1x =时函数()y f x =取得极小值，求a 的值； （Ⅱ）求函数()y f x =的单调区间．解：（Ⅰ）函数()f x 的定义域为(,0)-∞∪(0,)+∞， ………………1分2()af x x x '=-． ………………3分 ∵1x =时函数()y f x =取得极小值，∴(1)0f '=． ………………4分 ∴1a =． ………………5分 当1a =时，在(0,1)内()0f x '<，在(1,)+∞内()0f x '>， ………………6分 ∴1x =是函数()y f x =的极小值点．∴1a =有意义． ………………7分 （Ⅱ）()f x 的定义域为(,0)-∞∪(0,)+∞，322()a x af x x x x -'=-=．令()0f x '=，得x = ………………9分0a <………………11分综上所述： ………………13分当0a <时，函数()y f x =的单调递减区间为(-∞，单调递增区间为，(0,)+∞；当0a >时，函数()y f x =的单调递减区间为(,0)-∞，，单调递增区间为)+∞．………………14分19.（本小题共14分）已知椭圆C的长轴长为(1,0)．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设直线l ：y =kx 与椭圆C 交于A ，B 两点，点P 为椭圆的右顶点．（ⅰ）若直线l 斜率k =1，求△ABP 的面积；（ⅱ）若直线AP ，BP 的斜率分别为1k ，2k ，求证：12k k ⋅为定值．（实际上，P 是不同于A ，B 的任一点，结论都成立．）解：（Ⅰ）依题意椭圆的焦点在x 轴上，且1c =，2a =， ………………1分∴a =2221b a c =-=． ………………2分∴椭圆C 的标准方程为2212x y +=． ………………4分 （Ⅱ）（ⅰ） 2222x y y x⎧+=⎨=⎩ ………………5分∴x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧=⎪⎪⎨⎪=⎪⎩………………7分即A，(B ，P ．所以12ABP S ∆==． ………………9分 （ⅱ）证明：设11(,)A x y ，22(,)B x y ．椭圆的右顶点为P2222x y y kx⎧+=⎨=⎩ ， 消y 整理得 22(21)2k x +=， 不妨设x 1>0>x 2， ∴1x =2x =1y =2y =-．……………12分AP BP k k ⋅==………………13分 2222212221k k k -+=-+22212422k k -==--++ ∴ AP BP k k ⋅为定值12-． ………………14分20.（本小题共13分）已知数列{}n a 的前n 项和为n S ，且2n S n =．数列{}n b 为等比数列，且首项11b =，48b =． （Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ）若数列{}n c 满足n n b c a =，求数列{}n c 的前n 项和为n T ；（Ⅲ）在（Ⅱ）的条件下，问数列{}n c 中是否存在三项，使得这三项成等差数列．若存在，求出此三项，若不存在，说明理由．解：（Ⅰ）∵ 数列{}n a 的前n 项和为n S ，且2n S n =，∴ 当2n ≥时，221(1)21n n n a S S n n n -=-=--=-．当1n =时，111a S ==亦满足上式，故21n a n =-，(*)n ∈N ． ………………3分又 数列{}n b 为等比数列，设公比为q ，∵ 11b =，3418b b q ==， ∴2q =．∴ 12n n b -= (*)n ∈N ． ………………6分 （Ⅱ）2121n n n b n c a b ==-=-．123n n T c c c c =+++ 12(21)(21)(21)n =-+-++- 12(222)n n =++-2(12)12n n -=--．所以 122n n T n +=--． ………………9分 （Ⅲ）假设数列{}n c 中存在三项,,m k l c c c 成等差数列，不妨设(,,*)m k l m k l <<∈N因为 21n n c =-，所以 m k l c c c <<，且三者成等差数列．所以 2k l m c c c =+，即2(21)(21)(21)k m l -=-+-，2222k m l ⋅=+， 即222m k l k --=+．（方法一）因为 (,,*)m k l m k l <<∈N ， 所以1l k -≥，0m k -<． 所以 22l k-≥，20m k ->，所以 222m kl k --+> 与222m k l k --=+矛盾． 所以数列{}n c 中不存在成等差数列的三项． ………………13分（方法二）2222k m l ⋅=+2(12)m l m-=+所以 12122k l mm +-=+， 即1212k m l m +--=+． 所以 1221k ml m +---=．因为(,,*)m k l m k l <<∈N ， 所以 12k m+-，2l m-均为偶数，而1为奇数，所以等式不成立．所以数列{}n c 中不存在三项，使得这三项成等差数列． ………………13分。

北京市丰台区2010—2011学年第二学期高三综合练习（二）（二模）（理科综合）本试卷分为选择题和非选择题两部分。

满分300分。

考试时间150分钟。

注意事项：1．答题前，考生务必先将机读卡和答题卡上的学校、班级、姓名、准考证号用黑色字迹签字笔填写清楚。

2．本次考试选择题在机读卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项。

非选择题在答题卡上作答。

非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3．请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试题、草稿纸上答题无效。

可能用到的相对原子质量为：H l C 12 N 14 O 16 Fe 56 Al 27选择题共120分选择题（在每小题给出的四个选项中只有一项是符合题目要求的）。

1．细菌和病毒所共有的特征是（）A．有核糖体B．进行有丝分裂C．属于异养生物D．以核酸为遗传物质2．下列生物学研究所选择的技术（方法）恰当的是（）A．用标志重捕法调查鼠的种群密度B．用纸层析法提取叶绿体中的色素C．用显微镜观察染色体确认基因突变D．用18O标记H2O和CO2证明CO2是光合作用的原料3．下列说法正确的是（）A．酶、激素和抗体发挥作用后，立即被灭活B．伴性遗传无稳定的性状分离比，故不遵循孟德尔定律C．发育中的蝌蚪尾部的消失属于细胞凋亡，是由基因决定的D．醋酸菌和蓝藻均没有线粒体，所以不能进行有氧呼吸4．下列有关微生物培养的叙述，不正确．．．的是（）A．测定土壤样品中的细菌数目，常用稀释涂布平板法进行菌落计数B．在对微生物进行培养前，需要对微生物和培养基进行灭菌C．酵母菌发酵过程产生的酒精，对其他微生物生长有一定的抑制作用D．分离能分解尿素的细菌，要以尿素作为培养基中唯一的氮源5．图示为患甲病（A对a为显性）和乙病（B对b为显性）两种遗传病的家系图，其中有一种遗传病的致病基因位于X染色体上，若Ⅱ-7不携带致病基因，下列分析不正确的是（）A．甲病是伴X显性遗传病，乙病是常染色体隐性遗传病B．I一2可产生4种类型卵细胞，Ⅲ一9可产生4种类型精子C．如果Ⅲ一8是一个女孩，则她不可能患甲病D．Ⅱ—6不携带甲、乙致病基因的概率是1／36．下列说法不正确．．．的是（）A．凡是吸热反应都不能自发进行B．硅胶常用作袋装食品和瓶装药品的干燥剂C．油脂在碱性溶液中可发生水解，工业上利用该反应制造肥皂D．长期大量使用阿司匹林会导致水杨酸中毒，应立即停药，并静脉滴注：NaHCO3溶液7．下列说法不正确．．．的是（）A．与铜质水龙头连接处的钢制水管易发生腐蚀B．把被保护的钢铁设备作为阴极，外加直流电源可进行保护C．原电池产生电流时，阳离子移向正极，阴离子移向负极D．铅蓄电池是最常见的二次电池，正极板上覆盖有Pb8．下列实验过程中，始终无明显现象的是（）A．SO2通入溴水中B．NH3通入AlCl3溶液中C．CO2通人Ba（NO3）2溶液中D．向白色AgCl悬浊液中加入KI溶液9．下列说法中正确的是（）A．含有碳碳双键的有机物均有顺反异构B．乙烯和聚乙烯均能使酸性KMnO4溶液褪色C．利用电石与水反应制取C2H2时，可采用CuSO4溶液除去杂质气体D．苯酚与甲醛在酸性条件下生成酚醛树脂的结构简式为10．有X、Y、Z三种短周期主族元素，它们在周期表中的位置关系如图，下列有关说法中一定正确的是（）A．原子半径大小为：Y>Z>XB．Y与Z形成化合物是离子化合物C．若Y为金属元素，则X为金属元素D．若Z的最高价氧化物对应水化物是强酸，则Y元素的最高价氧化物具有两性11．一定条件下，在体积为2L的密闭容器中，3molX和3mol Y发生反应：3X（g）+Y（g）2Z （g），经60s达到平衡，生成0．4mol Z。

丰台区2011年高三年级第二学期统一练习（二）理科综合 (物理) 2011.513. 下列理论的提出标志着量子理论诞生的是A ．爱因斯坦提出光量子理论B ．玻尔提出原子结构理论C ．普朗克提出能量子理论D ．爱因斯坦提出相对论14. 能说明光是一种横波的光学现象是A ．光的偏振现象B ．光的干涉现象C ．光的衍射现象D ．光的色散现象 15. 电子是组成原子的基本粒子之一。

下列对电子的说法中正确的是A ．密立根发现电子，汤姆生最早测量出电子电荷量为1.6×10-19CB ．氢原子的电子由激发态向基态跃迁时，向外辐射光子，原子能量增加C ．金属中的电子吸收光子逸出成为光电子，光电子最大初动能等于入射光电能量D ．天然放射现象中的β射线实际是高速电子流，穿透能力比α射线强16. “神舟七号”宇宙飞船绕地球做匀速圆周运动，它比地球同步卫星轨道低很多，则“神舟七号”宇宙飞船与同步卫星相比A ．线速度小一些B ．周期小一些C ．向心加速度小一些D ．角速度小一些 17. 图甲为一列简谐横波在t =0.10s 时刻的波形图，P 是平衡位置为x =1 m 处的质点，Q 是平衡位置为x =4 m 处的质点，图乙为质点Q 的振动图象，则A ．t=0.10s 时，质点Q 的速度方向向上B ．该波沿x 轴正方向的传播C ．该波的传播速度为40m/sD ．从 t =0.10s 到 t =0.25s ，质点P 通过的路程为30 cm18. 如图甲所示为一台小型发电机构造的示意图，线圈逆时针转动，产生的电动势随时间变化的正弦规律图象如图乙所示。

发电机线圈内电阻为1.0Ω，外接灯泡的电阻为9.0Ω。

则A ．在t =0.01s 的时刻，穿过线圈磁通量为零图甲－－－B ．瞬时电动势的表达式为t e π50sin 26=(V)C ．电压表的示数为6VD ．通过灯泡的电流为0.6A19. 如图所示，水平向左的匀强电场场强大小为E ，一根不可伸长的绝缘细线长度为L ，细线一端拴一个质量为m 、电荷量为q 的带负电小球，另一端固定在O 点。

丰台区2011年初三统一练习（二）
数 学 试 卷 2011.6.
学校 姓名 考号
一、选择题 （本题共32分, 每小题4分）
下列各题均有四个选项，其中只有一个．．是符合题意的 1．5-的相反数是
A ．5
B ．5-
C ．1
5
-
D ．
15
2. 根据北京缓解拥堵网站公布的数据，截止2011年4月9日零时，北京小客车指标个人申请累计约为492000个，用科学记数法表示492000是
A. 449.210⨯
B. 349210⨯
C.54.9210
⨯ D.6
0.49210⨯
3. 若一个正多边形的每个内角都为120°，则这个正多边形的边数是 A ．9 Ｂ．8 Ｃ．7 Ｄ．6
4. 一个扇形的圆心角为90°，半径为2，则这个扇形的面积是
A.6π
B. 4π
C. 2π
D.π
5．在五张质地大小完全相同的卡片上分别印有直角三角形、平行四边形、菱形、正方形、等腰梯形的图案，现将印有图案的一面朝下，混合后从中随机抽取一张，则抽到的卡片上的图案既是轴对称图形又是中心对称图形的概率是
A ．15 B. 25 C. 35 D. 45
6．如图，BD 是⊙O 的直径，⊙CBD =30，则⊙A 的度数是
A ．30
B ．45
C ．60
D ．75
7. 某居民小区开展节约用电活动，有关部门对该小区100户家庭的节电量情况进行了统计, 4月份与3月份相比，节电量情况如下表：
则A. 35、30 B. 30、20 C. 30、35 D. 30、30
8．如图所示的正方体的展开图是（ ）。

OA BCD2011年丰台区中考二模数学试卷一、选择题 （本题共32分， 每小题4分）下列各题均有四个选项，其中只有一个．．是符合题意的 1．5-的相反数是（ ）．A ．5B ．5-C ．15-D ．152．根据北京缓解拥堵网站公布的数据，截止2011年4月9日零时，北京小客车指标个人申请累计约为492000个，用科学记数法表示492000是（ ）． A ．449.210⨯ B ．349210⨯ C ．54.9210⨯ D ．60.49210⨯3．若一个正多边形的每个内角都为120︒，则这个正多边形的边数是（ ）． A ．9 B ．8 C ．7 D ．64．一个扇形的圆心角为90︒，半径为2，则这个扇形的面积是（ ）．A ．6πB ．4πC ．2πD ．π5．在五张质地大小完全相同的卡片上分别印有直角三角形、平行四边形、菱形、正方形、等腰梯形的图案，现将印有图案的一面朝下，混合后从中随机抽取一张，则抽到的卡片上的图案既是轴对称图形又是中心对称图形的概率是（ ）．A ．15B ．25C ．35D ．456．如图，BD 是⊙O 的直径，30CBD ∠=︒，则A ∠的度数是（ ）．A ．30︒B ．45︒C ．60︒D ．75︒7．某居民小区开展节约用电活动，有关部门对该小区100户家庭的节电量情况进行了统计，4月份与3月份相比，节电量情况如下表：节电量（千瓦时）20 30 40 50 户 数10403020则4月份这100户家庭节电量的中位数、众数分别是（ ）．A ．35、30B ．30、20C ．30、35D ．30、308．如图所示的正方体的展开图是（）．A ．B ．C ．D ．D 4D 1D 2D 3ABCE 3E 2E 1A BCD E二、填空题 （本题共16分，每小题4分）9．分解因式：228a -= ．10．如图，在ABC △中，点D 、E 分别是AB 、AC 边的中点．若2DE =， 则BC = ．11．若分式34x x -+的值为0，则x 的值是 ．12．已知：如图，在Rt ABC △中，点1D 是斜边AB 的中点，过点1D 作11D E AC ⊥于点1E ，连结1BE 交1CD 于点2D ；过点2D 作22D E AC ⊥于点2E ，连结2BE 交1CD 于点3D ；过点3D 作33D E AC ⊥于点3E ，如此继续，可以依次得到点4D 、5D 、…、n D ，分别记11BD E △、22BD E △、33BD E △…、n n BD E △的面积为1S 、2S 、3S 、…n S ．设ABC △的面积是1， 1S ，n S = （用含n 的代数式表示）．三、解答题（本题共30分，每小题5分） 13．计算：()011()33π2cos454------+︒．14．解方程：211+1x x x x++=．AB CD E F 15．已知：如图，点B 、、E 、C 在同一条直线上，且DF BE ⊥于点F ，AC BE ⊥于点C ，BF CE =，DF AC =．求证：AB DE =．16．已知2315x x +=，求代数式22(1)(21)x x x --++的值．17．列方程或方程组解应用题：某市为更有效地利用水资源，制定了居民用水收费标准：如果一户每月用水量不超过15立方米，每立方米按1.8元收费；如果超过15立方米，超过部分按每立方米2.3元收费，其余仍按每立方米1.8元计算．另外，每立方米加收．．污水处理费1元．若某户一月份共支付水费58.5元，求该户一月份用水量．O D C B A E OABCD18．如图，反比例函数(0)ky x x=>的图象过点A ．（1）求反比例函数的解析式；（2）若点B 在(0)ky x x=>的图象上，求直线AB 的解析式；（3）当一次函数的值大于反比例函数的值时，根据图象写出x 的取值范围．四、解答题（本题共20分，每小题5分）19．已知：如图，在梯形ABCD 中，AD BC ∥，BD CD =，BD CD ⊥，2AD =，6BC =．求si n ABC ∠的值．20．已知：如图，在Rt ABC △中，90C ∠=︒，点E 在斜边AB 上，以AE 为直径的⊙O 与BC 边相切于点D ，连结AD ．（1）求证：AD 是BAC ∠的平分线；（2）若3AC =，3tan 4B ∠=，求⊙O 的半径．xy A B O 1616图⑤图④图③GF FC'G D'F AB CDEA BC DE A B C DE 21．某校数学兴趣小组成员小华对本班上学期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数分布表和频数分布直方图．请你根据图表提供的信息，解答下列问题：（1）频数分布表中a = ，b = ；（2）补全频数分布直方图； （3）数学老师准备从不低于90分的学生中选1人介绍学习经验，那么取得了93分的小华被选上的概率是多少？ 频数分布表22．猜想、探究题： （1）观察与发现小明将三角形纸片()ABC AB AC >沿过点A 的直线折叠，使得AC 落在AB 边上，折痕为，展开纸片（如图①）；再次折叠该三角形纸片，使点A 和点D 重合，折痕为EF ，展平纸片后得到AEF △（如图②）．你认为AEF △是什么形状的三角形？（2）实践与运用将矩形纸片()ABCD AB CD <沿过点B 的直线折叠，使点A 落在BC 边上的点F 处，折痕为BE （如图③）；再沿过点E 的直线折叠，使点D 落在BE 上的点'D 处，折痕为EG （如图④）；再展平纸片（如图⑤）．猜想EBG △的形状，证明你的猜想，并求图⑤中FEG ∠的大小．分组（分） 频数 频率 50~60 20．04 60~70 a0．16 70~80 20 0．40 80~90 16 0．32 90~1004 b合计 501A CD B 图① ACDB 图②FEx y MNOCBA五、解答题（本题共22分，第23题7分，第24题8分，第25题7分） 23．已知：关于x 的方程2(23)30kx k x k +-+-=． （1）求证：方程总有实数根；（2）当k 取哪些整数时，关于x 的方程2(23)30kx k x k +-+-=的两个实数根均为负整数？24．已知：矩形OABC 的顶点O 在平面直角坐标系的原点，边OA 、OC 分别在x 、y 轴的正半轴上，且3cm OA =，=4cm OC ，点M 从点A 出发沿AB 向终点B 运动，点N 从点C 出发沿CA 向终点A 运动，点M 、N 同时出发，且运动的速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t 秒．（1）当点N 运动1秒时，求点N 的坐标；（2）试求出多边形OAMN 的面积S 与t 的函数关系式；（3）t 为何值时，以OAN △的一边所在直线为对称轴翻折OAN △，翻折前后的两个三角形所组成的四边形为菱形．25．已知：如图，二次函数图象的顶点坐标为(1,2)C -，直线y kx m =+的图象与该二次函数的图象交于A 、B 两点，其中A 点坐标为(3,0)，B 点在y 轴上．点P 为线段AB 上的一个动点（点P 与点A 、B 不重合），过点P 且垂直于x 轴的直线与这个二次函数的图象交于点E ． （1）求这个二次函数的解析式；（2）设点P 的横坐标为x ，求线段PE 的长(用含x 的代数式表示)；（3）点D 为直线与这个二次函数图象对称轴的交点，若以点P 、E 、D 为顶点的三角形与AOB △相似，请求出P 点的坐标．xyOABC DEP2011年丰台区中考二模数学试卷答案一、选择题（本题共32分， 每小题4分）题号1 2 3 4 5 6 7 8 答案ACDDBCAC二、填空题（本题共16分，每小题4分）9．2(+2)(2)a a - 10．4 11．3 12．14；21(1)n +三、解答题（本题共30分，每小题5分）13．解：原式=4312---+ =82-+．14．解：2(1)(21)(1)x x x x x ++=++解这个整式方程得：12x =-，经检验：12x =-是原方程的解．∴原方程的解为12x =-．15．证明：∵DF BE ⊥，AC BE ⊥， ∴90ACB DFE ∠=∠=︒， ∵BF CE =∴BF EF CE EF +=+ ∴BC EF =， 在ACB △和DFE △中 AC DF ACB DFE BC EF =⎧⎪∠=∠⎨⎪=⎩∴ACB DFE ≅△△， ∴AB DE =．16．解：原式22(22)(441)x x x x =--+++ 2222441x x x x =-++++ 2=261x x ++当2315x x +=时，原式2=2(3)1215131x x ++=⨯+=．231DCBAOE 17解：∵若某户每月用水量为15立方米，则需支付水费15(1.8142⨯+=）元， 而4258.5<，∴该户一月份用水量超过15立方米．设该户一月份用水量为x 立方米，根据题意，得 42(2.31)(15)58.5x ++-=（或15 1.8 2.3(15)58.5)x x ⨯+-+= 解得20x =．答：该户一月份用水量为20立方米．18．解：（1）∵反比例函数(0)ky x x=>的图象过点A ，∴6k =．∴反比例函数的解析式为6y x=． （2）∵点B 在6y x=的图象上，且其横坐标为6， ∴点B 的坐标为(6,1)．设直线AB 的解析式为(0)y kx b k =+≠， 把点A 和点B 的坐标分别代入(0)y kx b k =+≠， 616k bk b =+⎧⎨=+⎩解得 17k b =-⎧⎨=⎩∴直线AB 的解析式为7y x =-+．（3）16x <<．19．解：如图，分别过点A 、D 作AE BC ⊥于点E ，DF BC ⊥于点F ． ∵AE DF ∥． 又AD BC ∥，∴四边形AEFD 是矩形．∴2EF AD ==．∵BD DC ⊥，BD DC =，6BC =， ∴是等腰直角三角形，∴132DF BF AE BC ====．∴3DF BF ==，1BE BF EF =-=．在Rt ABE △中，90ABE ∠=︒，∴2210AB AE BE =+=， ∴3310sin 1010AE ABC =AB ∠==． ．5分20．（1）证明：连结OD ，xy AB O1616F EODCBA∴OD OA =， ∴12∠=∠，∵BC 为⊙O 的切线， ∴90ODB ∠=︒， ∵90C ∠=︒， ∴ODB C ∠=∠， ∴OD AC ∥， ∴32∠=∠， ∴13∠=∠，AD 是BAC ∠的平分线．（2）解：在Rt ABC △中，90C ∠=︒，3tan 4B ∠=，3AC =， ∴4BC =，5AB =，在Rt ODB △中，3tan 4OD B BD ∠==， 设一份为x ，则3OD OA x ==，则4BD x =，5OB x =， ∴8AB x =，∴85x =，解得58x =，∴半径158OA =．21．解：（1）8a =，0.08b = （2）500.168a =⨯=，40.0850b ==（3）90分以上的有4人，故小华被选上的概率是14．22．解：（1）AEF △的形状是等腰三角形； （2）猜想：EBG △的形状是等腰三角形；由折叠知，四边形ABFE 是正方形，45AEB ∠=︒，∴135BED ∠=︒．又由折叠知，67.5BEG DEG ∠=∠=︒， 又∵AD BC ∥， ∴BGE DEG ∠=∠， ∴BG BE =，即AEF △为等腰三角形． 又∵45BEF ∠=︒，x y FEABC ONMy A'BC NM∴67.54522.5FEG ∠=︒-︒=︒．23．解：（1）分类讨论：若0k =，则此方程为一元一次方程，即330x --=，∴1x =-有根， 若0k ≠，则此方程为一元二次方程， ∴()()2=234390k k k ∆---=>， ∴方程有两个不相等的实数根， 综上所述，方程总有实数根． （2）∵方程有两个实数根 ∴方程为一元二次方程． ∵利用求根公式()2392k x k--±=，得162312k x k k-==-；21x =-， ∵方程有两个负整数根∴31k-是负整数，即k 是3的约数． ∴1k =±，3± 但1k =、3时根不是负整数， ∴1k =-、3-．24．解：（1）∵1t = ∴1CN =，1AM =过N 作NE y ⊥轴，作NF x ⊥轴 ∴CEN COA ∽△△，∴CN EN CA OA =，即153EN= ∴35EN =．由勾股定理得：45CE =，416455EO =-=，∴316,55N ⎛⎫ ⎪⎝⎭．（2）由（1）得CN EN CECA OA CO==， ∴35EN t =，45CE t =∴N 点坐标为34(,4)55t t -．∵多边形OAMN 由ONA △和AMN △组成xyOABC DEP xy G N'NA B COMy HO'A B CON M ∴1344225ONA S OA NF t ⎛⎫=⋅=- ⎪⎝⎭△665t =-1t 33225AMN S AM AF t ⎛⎫=⋅=- ⎪⎝⎭△233210t t =- ∴多边形OAMN 的面积233+61010S t t =-+．(04)t ≤≤ （3）①直线ON 为对称轴时，翻折OAN △得到'OA N △， 此时组成的四边形为'OANA ，当''AN A N A O OA ===，四边形'OANA 是菱形． 即AN OA =，∴53t -= ∴2t =．②直线OA 为对称轴时，翻折OAN △得到'OAN △，此时组成的四边形为'ONAN ，连结'NN ，交OA 于点G ． 当'NN 与OA 互相垂直平分时，四边形'ONAN 是菱形．即'OA NN ⊥，1322OG AG AO ===， ∴NG CO ∥，∴点N 是AC 的中点， ∴52CN =，∴52t = ③直线AN 为对称轴时，翻折OAN △得到'O AN △， 此时组成的四边形为'ONO A ，连结'OO ，交AN 于点H ． 当'OO 与AN 互相垂直平分时，四边形'ONO A 是菱形． 即OH AC ⊥，1522t AH NH AN -===， 由面积法可求得125OH =， 在Rt OAH △中，由勾股定理得，95AH =．∴5925t -=， 75t =． 综上所述，t 的值为2，52或75．25．解：（1）设二次函数的解析式为2(1)2y a x =-- ∵(3,0)A 在抛物线上， ∴20(31)2a =-- ∴12a =∴21(1)22y x =--（2）抛物线与y 轴交点B 的坐标为3(0,)2-设直线AB 的解析式为y kx m =+，3032k m m +=⎧⎪⎨=-⎪⎩ 解得1232k m ⎧=⎪⎪⎨⎪=-⎪⎩ ∴直线AB 的解析式是1322y x =-． ∵P 为线段AB 上的一个动点， ∴P 点坐标为13(,)22x x -．(03)x <<由题意可知PE y ∥轴， ∴E 点坐标为213(,)22x x x --∵03x <<∴22131313()()222222PE x x x x x =----=-+．（3）由题意可知D 点横坐标为1x =，又D 点在直线AB 上， ∴D 点坐标(1,1)-．①当90EDP ∠=︒时，AOB EDP ∽△△，∴AB PEOB DP=． 过点D 作DQ PE ⊥于Q ， ∴Q P x x x ==，1Q y =- ∴DQP AOB EDP ∽∽△△△ ∴DP ABDQ OA=， 又3OA =，32OB =，352AB =又1DQ x =- ∴5(1)2DP x =-∴2351322235(1)22x x x -+=-，解得16x =-±（负舍）． ∴64(61,)2P --（如图中的1P 点）． ②当90DEP ∠=︒时，AOB DEP ∽△△， ∴OA DEOB PE=． 由（2）21322PE x x =-+，1DE x =-∴231322231x xx -+=-，解得12x =±（负舍）． ∴2(12,1)2P +-（如图中的2P 点）． 综上所述，P 点坐标为2(12,1)2+-或64(61,)2--．2011年丰台区中考二模数学试卷答案部分解析一、选择题1. 【答案】A【解析】5-的相反数是5，故选A ．2. 【答案】C【解析】492000用科学记数法表示为54.9210⨯，选C ．3. 【答案】D【解析】正多边形的每个内角都为120︒，每个外角为60︒，外角和始终是360︒，360660n ︒==︒，故选D ．4. 【答案】D【解析】扇形的圆心角为90︒，半径为2，扇形的面积22π90π2π360360n r S ︒⨯===︒︒，故选D ．5. 【答案】B【解析】既是轴对称图形又是中心对称图形是菱形、正方形，所以抽到的卡片上的图案既是轴对称图形又是中心对称图形的概率是25，故选B ．6. 【答案】C【解析】BD 是⊙O 的直径，90BCD ∠=︒，90D CBD ∠+∠=︒，30CBD ∠=︒，60A D ∠=∠=︒，故选C ．7. 【答案】A【解析】这组数据中中位数是按大小排列第50和51个数的中位数40+30=352，众数是30，故选A ．8. 【答案】C【解析】正方体的展开图，仔细观察图可知答案是C ．故选C二、填空题9. 【答案】2(+2)(2)a a -【解析】分解因式：22282(4)2(2)(2)a a a a -=-=+- ． 故答案为：2(+2)(2)a a -．10. 【答案】4【解析】由中点中点中位线可知，12DE BC =，2DE =，4BC =． 故答案为：4．11. 【答案】3【解析】分式34x x -+的值为0，分子为0，分母不为0，即30x -=，3x =． 故答案为：3．12. 【答案】 14；21(1)n +【解析】11AD BD =，11D E BC ∥，1112D E BC =，1111111=44BD E CD E ACB S S S S ===△△△；112233n n CD E CD E CD E CD E ∽∽△△△△111221=2D E D D BC CD =，2123CD CD =，2222112221==()39BD E CD E CD E S S S S ==△△△，22112=3D E D E ，2322313D D D E BC CD ==，3234CD CD =，3333222331==()416BD E CD E CD E S S S S ==△△△， 33223=4D E D E ，3334414D E D D BC CD ==，4345CD CD =，4444332441==()=525BD E CD E CD E S S S S =△△△， 11221=n n n n D E n D E n -----，1111n n n n n D E D D BC CD n ---==，11n n CD nCD n -=+，11221==()1(1)n n n n n n n BD E CD E CD E n S S S S n n --==++△△△． 故答案为：14；21(1)n +．。

十二、圆锥曲线1、（2011朝阳二模理6）点P 是抛物线x y 42=上一动点，则点P 到点(0,1)A -的距离与到直线1-=x 的距离和的最小值是 ( D ) （A（B（C ）2 （D ）22、（2011东城二模理6）已知双曲线22221(0,0)x y a b a b-=>>，过其右焦点且垂直于实轴的直线与双曲线交于,M N 两点，O 为坐标原点.若OM ON ⊥，则双曲线的离心率为（D ） （A）12-+ （B）12+ （C）12-+ （D）123、（2011海淀二模理7）若椭圆1C ：1212212=+b y a x （011>>b a ）和椭圆2C ：1222222=+b y a x （022>>b a ）的焦点相同且12a a >.给出如下四个结论：① 椭圆1C 和椭圆2C 一定没有公共点； ②1122a b a b >； ③ 22212221b b a a -=-； ④1212a a b b -<-.其中，所有正确结论的序号是（B ）A ．②③④ B. ①③④ C ．①②④ D. ①②③4、（2011顺义二模理5）.设抛物线x y 82-=的焦点为F,准线为l ，P 为抛物线上一点，l PA ⊥，A 为垂足，如果直线AF 的斜率为3，那么=PF （C ）A 34B 38C 8D 165、（2011西城二模理5）.双曲线22221x y a b-=的渐近线与圆22(2)1x y +-=相切，则双曲线离心率为（C ）（A（BC ）2（D ）36、（2011东城二模文6）已知点(1,2)A 是抛物线C ：22y px =与直线l ：(1)y k x =+的一个交点，则抛物线C 的焦点到直线l 的距离是(B) （A ）22 （B ）2 （C ）223（D ）227、（2011朝阳二模文4）双曲线221169x y -=的焦点到渐近线的距离为(B) （A ）2 （B ）3 （C ）4 （D ）5 8、（2011海淀二模文8）若椭圆1C ：1212212=+b y a x （011>>b a ）和椭圆2C ：1222222=+b y a x （022>>b a ）的焦点相同且12a a >.给出如下四个结论：② 椭圆1C 和椭圆2C 一定没有公共点 ② 22212221b b a a -=-③1122a b a b > ④1212a a b b -<- 其中，所有正确结论的序号是(C)A ．②③④ B. ①③④ C ．①②④ D. ①②③9、（2011顺义二模文5）设抛物线px y =2的焦点与椭圆12622=+y x 的右焦点重合，则p 的值为( D )，A -4B 4C - 8D 810、（2011西城二模文8）已知点(1,0),(1,0)A B -及抛物线22y x =，若抛物线上点P 满足PA m PB =，则m 的最大值为(C)（A ）3（B ）2（C（D1、（2011昌平二模文13） 已知抛物线的方程是x y 82=，双曲线的右焦点是抛物线的焦点，离心率为2，则双曲线的标准方程是 _1322=-y x _，其渐近线方程是____x y 3±=_______2、（2011丰台二模文10）圆C ：222220x y x y ++--=的圆心到直线3x +4y +14=0的距离是 3 ．3、（2011海淀二模文9）双曲线C ：22122x y -=的渐近线方程为 y x =±；若双曲线C 的右焦点和抛物线22y px =的焦点相同，则抛物线的准线方程为 2x =-解答1、(2011朝阳二模理19)（本小题满分14分）已知椭圆2222:1(0)x y C a b a b+=>>经过点(2, 1)A，离心率为2．过点(3, 0)B 的直线l 与椭圆C 交于不同的两点,M N ． （Ⅰ）求椭圆C 的方程； （Ⅱ）求BM BN ⋅的取值范围；（Ⅲ）设直线AM 和直线AN 的斜率分别为AM k 和AN k ，求证:AM AN k k +为定值．解：（Ⅰ）由题意得22222411,,a b a b c c a⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩解得a =b =故椭圆C 的方程为22163x y +=． ……………………………………4分 （Ⅱ）由题意显然直线l 的斜率存在，设直线l 方程为(3)y k x =-，由22(3),1,63y k x x y =-⎧⎪⎨+=⎪⎩得2222(12)121860k x k x k +-+-=. …………………5分因为直线l 与椭圆C 交于不同的两点M ，N ，所以42221444(12)(186)24(1)0k k k k ∆=-+-=->，解得11k -<<. ……6分 设M ，N 的坐标分别为11(,)x y ，22(,)x y ，则21221212k x x k +=+，212218612k x x k-=+，11(3)y k x =-，22(3)y k x =-．… 7分 所以1212(3)(3)BM BN x x y y ⋅=--+ ……………………………………8分21212(1)[3()9]k x x x x =+-++223312k k +=+23322(12)k =++． ……………………………………9分 因为11k -<<，所以2332322(12)k <++≤． 故BM BN ⋅的取值范围为(2, 3]． ……………………………………10分 （Ⅲ）由（Ⅱ）得AM AN k k +12121122y y x x --=+-- ……………………………………11分 122112(31)(2)(31)(2)(2)(2)kx k x kx k x x x ---+---=--121212122(51)()1242()4kx x k x x k x x x x -++++=-++2222222(186)(51)12(124)(12)186244(12)k k k k k k k k k --+⋅+++=--++2244222k k -+==--． 所以AM AN k k +为定值2-． 2、（2011昌平二模理18）. (本小题满分14分)已知椭圆C ：)0(12222>>=+b a by a x ，左焦点)0,3(-F ，且离心率23=e(Ⅰ）求椭圆C 的方程；(Ⅱ)若直线)0(:≠+=k m kx y l 与椭圆C 交于不同的两点N M ,（N M ,不是左、右顶点），且以MN 为直径的圆经过椭圆C 的右顶点A. 求证：直线l 过定点,并求出定点的坐标.解：（Ⅰ）由题意可知：⎪⎪⎩⎪⎪⎨⎧+====222233c b a a c e c ……1分解得 1,2==b a ………2分所以椭圆的方程为：1422=+y x ……3分 （II ）证明：由方程组⎪⎩⎪⎨⎧+==+m kx y y x 14220448)k 41222=-+++m k m x x 得（….4分 0)44)(41(4)8(222>-+-=∆m k km整理得01422>+-m k ………..5分 设),(),,(2221y x N x x M则22212214144,418k m x x k km x x +-=+-=+ …….6分由已知，AN AM ⊥且椭圆的右顶点为)0,2(A ………7分0)2)(2(2121=+--∴y y x x ……… 8分 2212122121)())((m x x km x x k m kx m kx y y +++=++=即04))(2()1(221212=+++-++m x x km x x k也即04418)2(4144))1(22222=+++-∙-++-∙+m kkm km k m k …… 10分 整理得：01216522=++k mk m ……11分 解得562k m k m -=-=或均满足01422>+-m k ……12分 当k m 2-=时，直线的l 方程为k kx y 2-=，过定点（2，0）与题意矛盾舍去……13分当56k m -=时，直线的l 方程为)56(-=x k y ,过定点)0,56( 故直线l 过定点，且定点的坐标为)0,56(3、（2011东城二模理19）（本小题共13分）在平面直角坐标系xOy 中，动点P 到定点1(0,)4F 的距离比点P 到x 轴的距离大14，设动点P 的轨迹为曲线C ，直线:1l y kx =+交曲线C 于,A B 两点，M 是线段AB 的中点，过点M 作x 轴的垂线交曲线C 于点N ． （Ⅰ）求曲线C 的方程；（Ⅱ）证明：曲线C 在点N 处的切线与AB 平行；（Ⅲ）若曲线C 上存在关于直线l 对称的两点，求k 的取值范围．（Ⅰ）解：由已知，动点P 到定点1(0,)4F 的距离与动点P 到直线14y =-的距离相等． 由抛物线定义可知，动点P 的轨迹为以1(0,)4为焦点，直线14y =-为准线的抛物线．所以曲线C 的方程为2y x =． ………………3分（Ⅱ）证明：设11(,)A x y ，22(,)B x y ．由2,1,y x y kx ⎧=⎨=+⎩得210x kx --=． 所以12x x k +=，121x x =-． 设00(,)M x y ，则02k x =． 因为MN x ⊥轴， 所以N 点的横坐标为2k ． 由2y x =，可得'2y x = 所以当2kx =时，'y k =． 所以曲线C 在点N 处的切线斜率为k ，与直线AB 平行．………………8分（Ⅲ）解：由已知，0k ≠．设直线l 的垂线为'l ：1y x b k=-+． 代入2y x =，可得210x x b k+-= （*） 若存在两点3344(,),(,)D x y E x y 关于直线l 对称，则34122x x k +=-，342122y y b k+=+又3434(,)22x x y y ++在l 上， 所以211()122b k k k +=-+， 21122b k =-． 由方程（*）有两个不等实根 所以21()40b k∆=+>，即221220k k +->所以212k <，解得k <或2k >． …4、（2011丰台二模理19）.（本小题共14分）已知抛物线P ：x 2=2py (p >0)． （Ⅰ）若抛物线上点(,2)M m 到焦点F 的距离为3．（ⅰ）求抛物线P 的方程；（ⅱ）设抛物线P 的准线与y 轴的交点为E ，过E 作抛物线P 的切线，求此切线方程； （Ⅱ）设过焦点F 的动直线l 交抛物线于A ，B 两点，连接AO ，BO 并延长分别交抛物线的准线于C ，D 两点，求证：以CD 为直径的圆过焦点F ．解：（Ⅰ）（ⅰ）由抛物线定义可知，抛物线上点(,2)M m 到焦点F 的距离与到准线距离相等， 即(,2)M m 到2py =-的距离为3； ∴ 232p-+=，解得2p =． ∴抛物线P的方程为24x y =． ………………4分（ⅱ）抛物线焦点(0,1)F ，抛物线准线与y 轴交点为(0,1)E -，显然过点E 的抛物线的切线斜率存在，设为k ，切线方程为1y kx =-．由241x y y kx ⎧=⎨=-⎩， 消y 得2440x kx -+=， ………………6分216160k ∆=-=，解得1k =±． ………………7分∴切线方程为1y x =±-． ………………8分（Ⅱ）直线l 的斜率显然存在，设l ：2p y kx =+， 设11(,)A x y ，22(,)B x y ，由222x py py kx ⎧=⎪⎨=+⎪⎩ 消y 得 2220x pkx p --=． 且0∆>． ∴ 122x x pk +=，212x x p ⋅=-；∵ 11(,)A x y ， ∴ 直线OA ：11y y x x =， 与2p y =-联立可得11(,)22px pC y --， 同理得22(,)22px pD y --． ………………10分 ∵ 焦点(0,)2pF ， ∴11(,)2px FC p y =--，22(,)2px FD p y =--， ………………12分 ∴ 1212(,)(,)22px px FC FD p p y y ⋅=--⋅--22212121212224px px p x x p p y y y y =+=+ 2442221222212120422p x x p p p p p x x x x p p p=+=+=+=- ∴ 以CD 为直径的圆过焦点F ． 5、（2011海淀二模理19）(本小题共13分）在平面直角坐标系xOy 中，设点(,),(,4)P x y M x -，以线段PM 为直径的圆经过原点O .（Ⅰ）求动点P 的轨迹W 的方程；（Ⅱ）过点(0,4)E -的直线l 与轨迹W 交于两点,A B ，点A 关于y 轴的对称点为'A ，试判断直线'A B 是否恒过一定点，并证明你的结论. 解：（I ）由题意可得OP OM ⊥， ……………………………2分所以0OP OM ⋅=，即(,)(,4)0x y x -= ………………………………4分即240x y -=，即动点P 的轨迹W 的方程为24x y = ……………5分 （II ）设直线l 的方程为4y kx =-,1122(,),(,)A x y B x y ，则11'(,)A x y -.由244y kx x y=-⎧⎨=⎩消y 整理得24160x kx -+=， ………………………………6分则216640k ∆=->，即||2k >. ………………………………7分12124,16x x k x x +==. …………………………………9分直线212221':()y y A B y y x x x x --=-+212221222212212222121222112()1()4()41444 y 44y y y x x y x x x x y x x x x x x x x x x y x x x x x x x -∴=-++-∴=-++--∴=-+-∴=+ (12)分即2144x x y x -=+ 所以，直线'A B 恒过定点(0,4). 6、（2011顺义二模理19）. （本小题满分14分） 已知椭圆C 的左，右焦点坐标分别为()()0,3,0,321F F -,离心率是23。

xyO π2π1-1丰台区2011年高三年级第二学期统一练习（二）数 学（理科）2011.5一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．在复平面内，复数121iz i-=+对应的点位于 (A) 第一象限 (B) 第二象限 (C) 第三象限(D) 第四象限2．下列四个命题中，假命题为(A) x ∀∈R ，20x>(B) x ∀∈R ，2310x x ++>(C) x ∃∈R ，lg 0x >(D) x ∃∈R ，122x =3．已知a >0且a ≠1，函数log a y x =，x y a =，y x a =+在同一坐标系中的图象可能是(A)(B) (C) (D)4．参数方程2cos (3sin x y θθθ=⎧⎨=⎩，，为参数)和极坐标方程4sin ρθ=所表示的图形分别是(A) 圆和直线 (B) 直线和直线 (C) 椭圆和直线 (D) 椭圆和圆 5．由1,2,3,4,5组成没有重复数字且2与5不相邻的四位数的个数是(A) 120 (B) 84 (C) 60 (D) 486．已知函数sin()y A x ωϕ=+的图象如图所示，则该函数的解析式可能是(A) 441sin()555y x =+(B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+7．已知直线l ：0Ax By C ++=(A ，B 不全为0)，两点111(,)P x y ，222(,)P x y ，若1122()()0Ax By C Ax By C ++++>，且1122Ax By C Ax By C ++>++，则(A) 直线l 与直线P 1P 2不相交(B) 直线l 与线段P 2 P 1的延长线相交 (C) 直线l 与线段P 1 P 2的延长线相交(D) 直线l 与线段P 1P 2相交OO O O x xxxyyyy1 11 1111 18．已知函数2()2f x x x =-，()2g x ax =+(a >0)，若1[1,2]x ∀∈-，2[1,2]x ∃∈-，使得f (x 1)= g (x 2)，则实数a 的取值范围是 (A) 1(0,]2(B) 1[,3]2(C) (0,3] (D) [3,)+∞二、填空题：本大题共6小题，每小题5分，共30分．9．圆C ：222220x y x y ++--=的圆心到直线3x +4y +14=0的距离是 ． 10．如图所示，DB ，DC 是⊙O 的两条切线，A 是圆上一点，已知 ∠D =46°，则∠A = ．11．函数23sin cos sin y x x x =-的最小正周期为 ，最大值 为 ．12．一个几何体的三视图如图所示，则该几何体的体积是 ．13．如果执行右面的程序框图，那么输出的a =___．14．如图所示，∠AOB =1rad ，点A l ，A 2，…在OA 上，点B 1，B 2，…在OB 上，其中的每一个实线段和虚线段的长均为1个长度单位，一个动点M 从O 点出发，沿着实线段和以O 为圆心的圆弧匀速运动，速度为l 长度单位／秒，则质点M 到达A 3点处所需要的时间为__秒，质点M 到达A n 点处所需要的时间为__秒．O A 1 A 2 A 3 A 4B 1 B 2 B 3 B 4 AB1 1正视图侧视图20.62.4 俯视图0.6ABC DO开始35a =，1n =结束11a a=-1n n =+2011n ≤输出a 是否三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知等差数列{}n a 的前n 项和为n S ，a 2=4， S 5=35． （Ⅰ）求数列{}n a 的前n 项和n S ；（Ⅱ）若数列{}n b 满足n an b e =，求数列{}n b 的前n 项和n T ．16.（本小题共14分）张先生家住H 小区，他在C 科技园区工作，从家开车到公司上班有L 1，L 2两条路线（如图），L 1路线上有A 1，A 2，A 3三个路口，各路口遇到红灯的概率均为12；L 2路线上有B 1，B 2两个路口，各路口遇到红灯的概率依次为34，35．（Ⅰ）若走L 1路线，求最多．．遇到1次红灯的概率； （Ⅱ）若走L 2路线，求遇到红灯次数X 的数学期望；（Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．17.（本小题共13分）已知平行四边形ABCD 中，AB =6，AD =10，BD =8，E 是线段AD 的中点．沿BD 将△BCD 翻折到△BC D '，使得平面BC D '⊥平面ABD ． （Ⅰ）求证：C D '⊥平面ABD ； （Ⅱ）求直线BD 与平面BEC '所成角的正弦值； （Ⅲ）求二面角D BE C '--的余弦值．HCA 1 A 2B 1B 2L 1 L 2A 3A B D E C ' C18.（本小题共13分）已知函数2()ln (2)f x x ax a x =-+-． （Ⅰ）若()f x 在1x =处取得极值，求a 的值； （Ⅱ）求函数()y f x =在2[,]a a 上的最大值．19.（本小题共14分）已知抛物线P ：x 2=2py (p >0)．（Ⅰ）若抛物线上点(,2)M m 到焦点F 的距离为3．（ⅰ）求抛物线P 的方程；（ⅱ）设抛物线P 的准线与y 轴的交点为E ，过E 作抛物线P 的切线，求此切线方程；（Ⅱ）设过焦点F 的动直线l 交抛物线于A ，B 两点，连接AO ，BO 并延长分别交抛物线的准线于C ，D 两点，求证：以CD 为直径的圆过焦点F ．20.（本小题共13分）用[]a 表示不大于a 的最大整数．令集合{1,2,3,4,5}P =，对任意k P ∈和N*m ∈，定义511(,)[]1i k f m k mi =+=+∑，集合{1|N*,}A m k m k P =+∈∈，并将集合A 中的元素按照从小到大的顺序排列，记为数列{}n a ． （Ⅰ）求(1,2)f 的值； （Ⅱ）求9a 的值；（Ⅲ）求证：在数列{}n a 中，不大于001m k +的项共有00(,)f m k 项．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011年高三年级第二学期数学统一练习（二）数 学（理科）参考答案2011.5一、选择题：本大题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案CBCDBACD二、填空题：本大题共6小题，每小题5分，共30分． 9．3 10．67° 11．π，1212．12 13．23- 14．6，(1),2(3),2n n n n a n n n +⎧⎪⎪=⎨+⎪⎪⎩为奇数，为偶数.注：两个空的填空题第一个空填对得2分，第二个空填对得3分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知等差数列{}n a 的前n 项和为n S ，a 2=4， S 5=35． （Ⅰ）求数列{}n a 的前n 项和n S ；（Ⅱ）若数列{}n b 满足n an b e =，求数列{}n b 的前n 项的和n T ．解：（Ⅰ）设数列{}n a 的首项为a 1，公差为d ．则1145(51)5352a d a d +=⎧⎪⎨-+=⎪⎩ ∴113a d =⎧⎨=⎩， ∴ 32n a n =-． ∴ 前n 项和(132)(31)22n n n n n S +--==． ………………7分（Ⅱ）∵32n a n =-， ∴ 32n n b e -=，且b 1=e ．当n ≥2时，3233(1)21n n n n b e e b e----==为定值，∴ 数列{}n b 构成首项为e ，公比为e 3的等比数列．∴数列{}n b 的前n 项的和33133(1)11n n n e e e e T e e +--==--． 即3131n n e eT e +-=-． ………………13分16.（本小题共14分）张先生家住H 小区，他工作在C 科技园区，从家开车到公司上班路上有L 1，L 2两条路线（如图），L 1路线上有A 1，A 2，A 3三个路口，各路口遇到红灯的概率均为12；L 2路线上有B 1，B 2两个路口，各路口遇到红灯的概率依次为34，35． （Ⅰ）若走L 1路线，求最多．．遇到1次红灯的概率； （Ⅱ）若走L 2路线，求遇到红灯次数X 的数学期望；（Ⅲ）按照“平均遇到红灯次数最少”的要求，请你帮助张先生从上述两条路线中选择一条最好的上班路线，并说明理由．解：（Ⅰ）设“走L 1路线最多遇到1次红灯”为A 事件，则0312331111()=()()2222P A C C ⨯+⨯⨯=． 所以走L 1路线，最多遇到1次红灯的概率为12． ………………4分 （Ⅱ）依题意，X 的可能取值为0，1，2．331(=0)=(1)(1)4510P X -⨯-=， 33339(=1)=(1)(1)454520P X ⨯-+-⨯=，339(=2)=4520P X ⨯=．随机变量X 的分布列为：X0 1 2 P110 920 9201992701210202020EX =⨯+⨯+⨯=． ………………10分（Ⅲ）设选择L 1路线遇到红灯次数为Y ，随机变量Y 服从二项分布，1(3,)2Y B ，所以13322EY =⨯=． ………………12分因为EX EY <，所以选择L 2路线上班最好． ………………14分17.（本小题共13分）已知平行四边形ABCD 中，AB =6，AD =10，BD =8，E 是线段AD 的中点．沿直线BD 将△BCD 翻折成△BC D '，使得平面BC D '⊥平面ABD ．（Ⅰ）求证：C D '⊥平面ABD ；（Ⅱ）求直线BD 与平面BEC '所成角的正弦值； （Ⅲ）求二面角D BE C '--的余弦值．证明：（Ⅰ）平行四边形ABCD 中，AB =6，AD =10，BD =8， 沿直线BD 将△BCD 翻折成△BC D ' 可知CD =6，BC ’=BC =10，BD =8，即222''BC C D BD =+， 故'C D BD ⊥． ∵平面BC D '⊥平面ABD ，平面BC D ' 平面ABD =BD ，C D '⊂平面BC D '，∴C D '⊥平面ABD ． ………………5分 （Ⅱ）由（Ⅰ）知C D '⊥平面ABD ，且CD BD ⊥，如图，以D 为原点，建立空间直角坐标系D xyz -．HCA 1A 2B 1B 2L 1 L 2A 3AB DEC ' C则(0,0,0)D ，(8,6,0)A ，(8,0,0)B ，'(0,0,6)C ．∵E 是线段AD 的中点， ∴(4,3,0)E ，(8,0,0)BD =-． 在平面BEC '中，(4,3,0)BE =- ，'(8,0,6)BC =-，设平面BEC '法向量为(,,)n x y z =，∴ 0'0BE n BC n ⎧⋅=⎪⎨⋅=⎪⎩，即430860x y y z -+=⎧⎨-+=⎩， 令3x =，得4,4y z ==，故(3,4,4)n =． 设直线BD 与平面BEC '所成角为θ，则||341sin |cos ,|41||||n BD n BD n BD θ⋅=<>==⋅． ∴ 直线BD 与平面BEC '所成角的正弦值为34141． ………………10分 （Ⅲ）由（Ⅱ）知平面BEC '的法向量为(3,4,4)n = ， 而平面DBE 的法向量为(0,0,6)DC '=，∴ 441cos ,41||||n C D n C D n C D '⋅'<>=='⋅，因为二面角D BE C '--为锐角，所以二面角D BE C '--的余弦值为44141． ………………13分18.（本小题共13分）已知函数2()ln (2)f x x ax a x =-+-． （Ⅰ）若()f x 在1x =处取得极值，求a 的值； （Ⅱ）求函数()y f x =在2[,]a a 上的最大值．解：（Ⅰ）∵2()ln (2)f x x ax a x =-+-， ∴函数的定义域为(0,)+∞．∴2112(2)(21)(1)()2(2)ax a x x ax f x ax a x x x-+---+'=-+-==．∵()f x 在1x =处取得极值， 即(1)(21)(1)0f a '=--+=， ∴1a =-． 当1a =-时，在1(,1)2内()0f x '<，在(1,)+∞内()0f x '>，∴1x =是函数()y f x =的极小值点． ∴1a =-． ………………6分ABDEC 'Cxyz（Ⅱ）∵2a a <，∴01a <<．2112(2)(21)(1)()2(2)ax a x x ax f x ax a x x x-+--+'=-+-==-∵ x ∈(0,)+∞， ∴10ax +>， ∴()f x 在1(0,)2上单调递增；在1(,)2+∞上单调递减， ①当102a <≤时， ()f x 在2[,]a a 单调递增， ∴32max ()()ln 2f x f a a a a a ==-+-；②当21212a a ⎧>⎪⎪⎨⎪<⎪⎩，即1222a <<时，()f x 在21(,)2a 单调递增，在1(,)2a 单调递减，∴max 12()()ln 21ln 22424a a a f x f -==--+=--； ③当212a ≤，即212a ≤<时，()f x 在2[,]a a 单调递减， ∴2532max ()()2ln 2f x f a a a a a ==-+-． ………………12分 综上所述，当102a <≤时，函数()y f x =在2[,]a a 上的最大值是32ln 2a a a a -+-； 当1222a <<时，函数()y f x =在2[,]a a 上的最大值是1ln 24a --； 当22a ≥时，函数()y f x =在2[,]a a 上的最大值是5322ln 2a a a a -+-．…………13分19.（本小题共14分）已知抛物线P ：x 2=2py (p >0)．（Ⅰ）若抛物线上点(,2)M m 到焦点F 的距离为3．（ⅰ）求抛物线P 的方程；（ⅱ）设抛物线P 的准线与y 轴的交点为E ，过E 作抛物线P 的切线，求此切线方程；（Ⅱ）设过焦点F 的动直线l 交抛物线于A ，B 两点，连接AO ，BO 并延长分别交抛物线的准线于C ，D 两点，求证：以CD 为直径的圆过焦点F ． 解：（Ⅰ）（ⅰ）由抛物线定义可知，抛物线上点(,2)M m 到焦点F 的距离与到准线距离相等， ∴ 232p-+=，解得2p =． ∴ 抛物线P 的方程为24x y =． ………………4分（ⅱ）抛物线焦点(0,1)F ，抛物线准线与y 轴交点为(0,1)E -，显然过点E 的抛物线的切线斜率存在，设为k ，切线方程为1y kx =-．由241x y y kx ⎧=⎨=-⎩， 消y 得2440x kx -+=， 216160k ∆=-=，解得1k =±． ∴切线方程为1y x =±-． ………………8分（Ⅱ）直线l 的斜率显然存在，设l ：2py kx =+， 设11(,)A x y ，22(,)B x y ， 由222x py p y kx ⎧=⎪⎨=+⎪⎩ 消y 得 2220x pkx p --=． 且0∆>． ∴ 122x x pk +=，212x x p ⋅=-； ∵ 11(,)A x y ， ∴ 直线OA ：11y y x x =， 与2p y =-联立可得11(,)22px pC y --， 同理得22(,)22px pD y --． ∵ 焦点(0,)2p F ， ∴ 11(,)2px FC p y =-- ，22(,)2pxFD p y =-- ，∴ 1212(,)(,)22px px FC FD p p y y ⋅=--⋅-- 22212121212224px px p x x p p y y y y =+=+2442221222212120422p x x p p p p p x x x x p p p=+=+=+=- ∴ 以CD 为直径的圆过焦点F ． ………………14分20.（本小题共13分）用[]a 表示不大于a 的最大整数．令集合{1,2,3,4,5}P =，对任意k P ∈和N*m ∈，定义511(,)[]1i k f m k mi =+=+∑，集合{1|N*,}A m k m k P =+∈∈，并将集合A 中的元素按照从小到大的顺序排列，记为数列{}n a ．（Ⅰ）求(1,2)f 的值； （Ⅱ）求9a 的值；（Ⅲ）求证：在数列{}n a 中，不大于001m k +的项共有00(,)f m k 项．解：（Ⅰ）由已知知33333(1,2)[][][][][]23456f =++++110002=++++=． 所以(1,2)2f =． ………………4分 （Ⅱ）因为数列{}n a 是将集合{1|N*,}A m k m k P =+∈∈中的元素按从小到大的顺序排成而成，所以我们可设计如下表格12345 ‥‥ 0m1 2 22 32 42‥‥ ‥‥ 2 3 23 33 43‥‥ 3 42434‥‥ ‥‥ 4 5 25 35 ‥‥ ‥‥ 562636‥‥‥‥从上表可知，每一行从左到右数字逐渐增大，每一列从上到下数字逐渐增大． 且2<3<4<5<6<22<23<24<32<25<‥‥所以 932a =． ………………8分（Ⅲ）任取12,*m m ∈N ，12,k k P ∈，若112211m k m k +=+，则必有1212,m m k k ==． 即在（Ⅱ）表格中不会有两项的值相等．对于001m k +而言，若在（Ⅱ）表格中的第一行共有1m 的数不大于001m k +， 则1m 2001m k ≤+，即1m 0012m k +≤，所以1m 001[]2m k +=，同理，第二行共有2m 的数不大于001m k +，有2m 001[]3m k +=，第i 行共有i m 的数不大于001m k +，有i m 001[]1m k i +=+．所以，在数列{}n a 中，不大于001m k +的项共有50011[]1i k m i =++∑项，即00(,)f m k 项．……13分 （若用其他方法解题，请酌情给分）k m。

xyO π2π1-1丰台区2011年高三年级第二学期统一练习（二）数 学（文科）2011.5一、本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．若2∈{1，a ，a 2-a }，则a =(A) -1(B) 0(C) 2(D) 2或-12．下列四个命题中，假命题为(A) x ∀∈R ，20x>(B) x ∀∈R ，2310x x ++>(C) x ∃∈R ，lg 0x >(D) x ∃∈R ，122x =3．已知a >0且a ≠1，函数log a y x =，x y a =在同一坐标系中的图象可能是(A)(B)(C)(D)4．已知数列{}n a 中，135a =，111(2)n n a n a -=-≥，则2011a = (A) 12- (B) 23-(C)35(D)525．如图所示，已知2AB BC = ，OA a = ，OB b = ，OC c =，则下列等式中成立的是(A) 3122c b a =-(B) 2c b a =-(C) 2c a b =-(D) 3122c a b =-6．已知函数sin()y A x ωϕ=+的图象如图所示，则该函数的解析式可能是(A) 441sin()555y x =+(B) 31sin(2)25y x =+(C) 441sin()555y x =-(D) 41sin(2)55y x =+7．已知x ，y 的取值如下表：从散点图可以看出y 与x 线性相关，且回归方程为 0.95y x a =+，则a = (A) 3.25(B) 2.6(C) 2.2(D) 0O8．用m a x {}a b ，表示a ，b 两个数中的最大数，设22()max{84,log }f x x x x =-+-，若函数()()g x f x kx =-有2个零点，则k 的取值范围是 (A) (0,3)(B) (0,3](C) (0,4)(D) [0,4]二、填空题：本大题共6小题，每小题5分，共30分． 9．在复平面内，复数121iz i-=+对应的点位于第 象限． 10．圆C ：222220x y x y ++--=的圆心到直线3x +4y +14=0的距离是 ． 11．若[0,2]x ∈π，则函数sin cos y x x x =-的单调递增区间是 ．12．已知签字笔2元一只，练习本1元一本．某学生欲购买的签字笔不少于3只，练习本不少于5本，但买签字笔和练习本的总数量不超过10，则支出的钱数最多是___元．13．一个几何体的三视图如图所示，则该几何体的体积是 ．14．如图所示，已知正方形ABCD 的边长为1，以A 为圆心，AD 长为半径画弧，交BA 的延长线于P 1，然后以B 为圆心，BP 1长为半径画弧，交CB 的延长线于P 2，再以C 为圆心，CP 2长为半径画弧，交DC 的延长线于P 3，再以D 为圆心，DP 3长为半径画弧，交AD 的延长线于P 4，再以A 为圆心，AP 4长为半径画弧，…，如此继续下去，画出的第8道弧的半径是___，画出第n 道弧时，这n 道弧的弧长之和为___．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数21()sin cos 2f x x x x =+-． （Ⅰ）求()12f π-的值； （Ⅱ）若[0,]2x π∈，求函数()y f x =的最小值及取得最小值时的x 值．16.（本小题共13分）已知梯形ABCD 中，//BC AD ，112BC AD ==，CD =G ，E ，F 分别是AD ，BC ，CD的中点，且CG CG 将△CDG 翻折到△CD G '． （Ⅰ）求证：EF //平面AD B '；（Ⅱ）求证：平面CD G '⊥平面AD G '．AB C A DP 1 P 2P 3P 4P 5正视图侧视图俯视图FGE ABCD 'AB C EDFG17.（本小题共13分）某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩（均为整数）分成六段：[)50,40，[)60,50，…，[]100,90后得到如下频率分布直方图．（Ⅰ）求分数在[)70,80内的频率；（Ⅱ）根据频率分布直方图，估计该校高一年级学生期中考试数学成绩的平均分；（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率． 18.（本小题共14分）已知函数21(),(0)2af x x a x=+≠． （Ⅰ）当1x =时函数()y f x =取得极小值，求a 的值； （Ⅱ）求函数()y f x =的单调区间． 19.（本小题共14分）已知椭圆C 的长轴长为(1,0)．（Ⅰ）求椭圆C 的标准方程； （Ⅱ）设直线l ：y =kx 与椭圆C 交于A ，B 两点，点P 为椭圆的右顶点．（ⅰ）若直线l 斜率k =1，求△ABP 的面积；（ⅱ）若直线AP ，BP 的斜率分别为1k ，2k ，求证：12k k ⋅为定值． 20.（本小题共13分）已知数列{}n a 的前n 项和为n S ，且2n S n =．数列{}n b 为等比数列，且11b =，48b =． （Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ）若数列{}n c 满足n n b c a =，求数列{}n c 的前n 项和n T ；（Ⅲ）在（Ⅱ）的条件下，数列{}n c 中是否存在三项，使得这三项成等差数列？若存在，求出此三项；若不存在，说明理由．丰台区2011年高三年级第二学期统一练习（二）数 学（文科）参考答案2011.5一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9．Ⅲ 10．3 11．(0,)π写成闭区间也给满分 12．15 13．12 14． 8，(1)4n n +π注：两个空的填空题第一个空填对得2分，第二个空填对得3分．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数21()sin cos 2f x x x x =+-． （Ⅰ）求()12f π-的值；（Ⅱ）求函数(),[0,]2y f x x π=∈的最小值，及取得最小值时的x 的值．解：（Ⅰ）∵21()sin cos 2f x x x x =+-12cos 22x x =- sin(2)6x π=-， ………………5分∴()sin(2)sin()121263f ππππ-=-⨯-=-= ． ………………7分 （Ⅱ）∵02x π≤≤∴02x π≤≤．∴52666x πππ-≤-≤． ………………9分∴1sin(2)126x π-≤-≤， 即1()12f x -≤≤． ………………11分∴min 1()2f x =- 此时266x ππ-=- ∴0x =． ………………12分∴当0x =时，min 1()2f x =-． ………………13分16.（本小题共13分）已知梯形ABCD 中，//BC AD ，112BC AD ==，CD =G ，E ，F 分别是AD ，BC ，CD 的中点，且CG 直线CG 将△CDG 翻折成△CD G '． （Ⅰ）求证：EF //平面AD B '；（Ⅱ）求证：平面CD G '⊥平面AD G '．证明：（Ⅰ）∵E ，F 分别是BC ，CD 的中点，即E ，F 分别是BC ，C D '的中点， ∴EF 为△D BC '的中位线．∴EF //D B '． ………………2分又∵EF ⊄平面AD B '，D B '⊂平面AD B '， ………………4分 ∴EF // 平面AD B '． ………………6分 （Ⅱ）∵G 是AD 的中点，112BC AD ==，即2AD =， ∴1DG =．又∵CD =CG =∴在DGC ∆中，222DG GC DC += ∴DG GC ⊥． ………………9分 ∴GC D G '⊥，GC AG ⊥． ∵AG ∩D G '=G ，∴GC ⊥平面AD G '． ………………12分 又∵GC ⊂平面CD G '，∴平面CD G '⊥平面AD G '． ………………13分17.（本小题共13分）某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩（均为整数）分成六段[)50,40，[)60,50，…，[]100,90后得到如下频率分布直方图．（Ⅰ）求分数在[)70,80内的频率；（Ⅱ）根据频率分布直方图，估计该校高一年级学生期中考试数学成绩的平均分；（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率． 解：（Ⅰ）分数在[)70,80内的频率为：1(0.0100.0150.0150.0250.005)10-++++⨯10.70.3=-=． ………………3分（Ⅱ）平均分为：450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=． ………………6分 （Ⅲ）由题意，[)80,90分数段的人数为：0.256015⨯=人； ………………7分[]90,100分数段的人数为：0.05603⨯=人； ………………8分∵用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本， ∴[)80,90分数段抽取5人，分别记为A ，B ，C ，D ，E ；[]90,100分数段抽取1人，记为M ． ………………9分因为从样本中任取2人，其中恰有1人的分数不低于90分，FGEABCD 'ABCEDFG则另一人的分数一定是在[)80,90分数段，所以只需在分数段[)80,90抽取的5人中确定1人． 设“从样本中任取2人，其中恰有1人的分数不低于90分为”事件A ， ………………10分 则基本事件空间包含的基本事件有：(A ，B )，(A ，C)，(A ，D)，(A ，E )，(B ，C )，(B ，D )， (B ，E )，(C ，D )，(C ，E )，(D ，E)，(A ，M )，(B ，M )，(C ，M )，(D ，M )，(E ，M )共15种． 事件A 包含的基本事件有(A ，M )，(B ，M )，(C ，M )，(D ，M )，(E ，M )5种．………………12分 ∴恰有1人的分数不低于90分的概率为51()153P A ==． ………………13分18.（本小题共14分）已知函数21(),(0)2af x x a x=+≠． （Ⅰ）当1x =时函数()y f x =取得极小值，求a 的值； （Ⅱ）求函数()y f x =的单调区间．解：（Ⅰ）函数()f x 的定义域为(,0)-∞∪(0,)+∞， ………………1分2()af x x x '=-． ………………3分 ∵1x =时函数()y f x =取得极小值，∴(1)0f '=． ………………4分 ∴1a =． ………………5分 当1a =时，在(0,1)内()0f x '<，在(1,)+∞内()0f x '>， ………………6分 ∴1x =是函数()y f x =的极小值点．∴1a =有意义． ………………7分 （Ⅱ）()f x 的定义域为(,0)-∞∪(0,)+∞，322()a x af x x x x-'=-=．令()0f x '=，得x = ………………9分………………11分0a >………………13分当0a <时，函数()y f x =的单调递减区间为(-∞，单调递增区间为，(0,)+∞；当0a >时，函数()y f x =的单调递减区间为(,0)-∞，，单调递增区间为)+∞．………………14分19.（本小题共14分）已知椭圆C的长轴长为(1,0)．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）设直线l ：y =kx 与椭圆C 交于A ，B 两点，点P 为椭圆的右顶点．（ⅰ）若直线l 斜率k =1，求△ABP 的面积；（ⅱ）若直线AP ，BP 的斜率分别为1k ，2k ，求证：12k k ⋅为定值．（实际上，P 是不同于A ，B 的任一点，结论都成立．）解：（Ⅰ）依题意椭圆的焦点在x 轴上，且1c =，2a =， ………………1分∴a =2221b a c =-=． ………………2分∴椭圆C 的标准方程为2212x y +=． ………………4分 （Ⅱ）（ⅰ） 2222x y y x⎧+=⎨=⎩ ………………5分∴3x y ⎧=⎪⎪⎨⎪=⎪⎩或3x y ⎧=⎪⎪⎨⎪=-⎪⎩， ………………7分即(33A，(33B --，P ．所以12ABP S ∆==． ………………9分 （ⅱ）证明：设11(,)A x y ，22(,)B x y ．椭圆的右顶点为P2222x y y kx⎧+=⎨=⎩ ， 消y 整理得 22(21)2k x +=， 不妨设x 1>0>x 2， ∴1x =2x =1y =2y =-12分AP BP k k ⋅== ………………13分2222212221k k k -+=-+22212422k k -==--++ ∴ AP BP k k ⋅为定值12-． ………………14分20.（本小题共13分）已知数列{}n a 的前n 项和为n S ，且2n S n =．数列{}n b 为等比数列，且首项11b =，48b =． （Ⅰ）求数列{}n a ，{}n b 的通项公式；（Ⅱ）若数列{}n c 满足n n b c a =，求数列{}n c 的前n 项和为n T ；（Ⅲ）在（Ⅱ）的条件下，问数列{}n c 中是否存在三项，使得这三项成等差数列．若存在，求出此三项，若不存在，说明理由．解：（Ⅰ）∵ 数列{}n a 的前n 项和为n S ，且2n S n =，∴ 当2n ≥时，221(1)21n n n a S S n n n -=-=--=-．当1n =时，111a S ==亦满足上式，故21n a n =-，(*)n ∈N ． ………………3分又 数列{}n b 为等比数列，设公比为q ，∵ 11b =，3418b b q ==， ∴2q =．∴ 12n n b -= (*)n ∈N ． ………………6分 （Ⅱ）2121n n n b n c a b ==-=-．123n n T c c c c =+++ 12(21)(21)(21)n =-+-++- 12(222)n n =++-2(12)12n n -=--．所以 122n n T n +=--． ………………9分 （Ⅲ）假设数列{}n c 中存在三项,,m k l c c c 成等差数列，不妨设(,,*)m k l m k l <<∈N因为 21n n c =-，所以 m k l c c c <<，且三者成等差数列．所以 2k l m c c c =+，即2(21)(21)(21)k m l -=-+-，2222k m l ⋅=+， 即222m k l k --=+．（方法一）因为 (,,*)m k l m k l <<∈N ， 所以1l k -≥，0m k -<． 所以 22l k-≥，20m k ->，所以 222m kl k --+> 与222m k l k --=+矛盾． 所以数列{}n c 中不存在成等差数列的三项． ………………13分（方法二）2222k m l ⋅=+2(12)m l m-=+所以 12122k l mm +-=+， 即1212k m l m +--=+． 所以 1221k ml m +---=．因为(,,*)m k l m k l <<∈N ， 所以 12k m+-，2l m-均为偶数，而1为奇数，所以等式不成立．所以数列{}n c 中不存在三项，使得这三项成等差数列． ………………13分。