下载文档原格式
南开大学22春“信息安全”《密码学》期末考试高频考点版（带答案）一.综合考核(共50题)1.高级数字加密标准算法AES的明文分组位数是?()A.64B.56C.7D.128参考答案：D2.流密码可以分为同步流密码和异步流密码，其中密钥流的产生并不是独立于明文流和密文流的流密码称为同步流密码。
()T.对F.错参考答案：F3.为了保证安全性，密码算法应该进行保密。
()A.正确B.错误参考答案：B4.在RSA公钥密码算法中，设p=11，q=23，n=pq=253，则有RSA密码体制RSA-253，选取加密密钥e=11，设明文为m=55，则密文c为()A.11B.23C.220D.231参考答案：D暴力破解与字典攻击属于同类网络攻击方式，其中暴力破解中所采用的字典要比字典攻击中使用的字典范围要大。
()A.正确B.错误参考答案：A6.下列哪些密码属于序列密码()A.一次一密密码B.RC4密码C.A5密码D.单表代换密码参考答案：ABC7.下列哪些算法属于公钥密码算法()A.RSA算法B.ElGamal算法C.AES算法D.椭圆曲线密码算法ECC参考答案：ABD8.网站信息管理员需要把提供给用户下载的文件生成一个特殊字符串，用户通过它可以检查该文件是否被非法篡改。
则管理员可以使用()算法来实现这个安全服务。
A.VPNB.SHAC.RC4D.DES参考答案：B9.在混合加密方式下，真正用来加解密通信过程中所传输数据明文的密钥是()。
C.非对称算法的私钥D.CA中心的公钥参考答案：B10.数字证书不包含()A.颁发机构的名称B.证书的有效期C.证书持有者的私有密钥信息D.签发证书时所使用的签名算法参考答案：C11.“一次一密”密码属于序列密码中的一种。
()A.正确B.错误参考答案：A12.在RSA密码算法中，选p=11，q=23，则模n的欧拉函数φ(n)的值为()A.253B.220C.139D.5参考答案：C13.在数据加密标准DES中，其加密的核心部件为S-盒运算，则每一个S-盒的输入是()比特位。
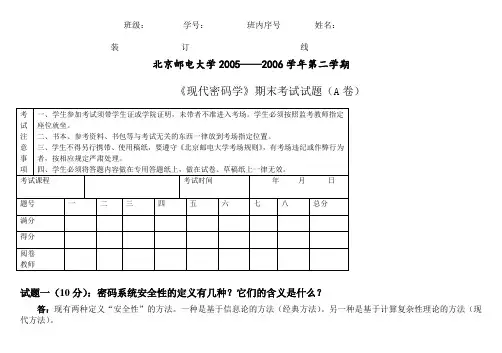
班级：________学号：_______ 班内序号_____ 姓名：_________--------------------------------装----------------------订---------------------------------------线-------------------------------------------------北京邮电大学2005——2006学年第二学期《现代密码学》期末考试试题（A卷）试题一（10分）：密码系统安全性的定义有几种？它们的含义是什么？答：现有两种定义“安全性”的方法。
一种是基于信息论的方法（经典方法）。
另一种是基于计算复杂性理论的方法（现代方法）。
基于信息论的定义是用密文中是否蕴含明文的信息作为标准。
不严格地说，若密文中不含明文的任何信息，则认为该密码体制是安全的，否则就认为是不安全的。
基于计算复杂性理论的安全性定义则不考虑密文中是否蕴含明文的信息，而是考虑这些信息是否能有效地被提取出来。
换句话说，把搭线者提取明文信息的可能性改为搭线者提取明文信息的可行性，这种安全性称为有条件安全性，即搭线者在一定的计算资源条件下，他不能从密文恢复出明文。
试题二(10分)： 假设Hill 密码加密使用密钥⎪⎪⎭⎫⎝⎛=73811K ，试对明文abcd 加密。
答：（a,b ）=(0,1)加密后变为（0,1）⨯⎪⎪⎭⎫ ⎝⎛73811=(3,7)=(d,h)； 同理（c,d ）=(2,3) 加密后变为（2,3）⨯⎪⎪⎭⎫⎝⎛73811=(31,37)=(5,11)=(F,L)。
所以，明文(abcd)经过Hill 密码加密后，变为密文（DHFL ）。
试题三（10分）：设有这样一个密码系统，它的明文空间{}y x P ,=的概率分布为4/3)(,4/1)(==y p x p P P ；它的密钥空间{}c b a K ,,=的概率分布为4/1)()(,2/1)(===c p b p a p K K K ；它的密文空间{}4,3,2,1=C ，假定该密码系统的加密函数为：4)(,3)(;3)(,2)(;2)(,1)(======y e x e y e x e y e x e c c b b a a 。
密码题及答案密码题在生活中往往起着非常重要的作用，可以保证个人信息的安全性。
然而，达到这个目的的密码不能是太简单，还得是足够强的，传统的四位数字密码早已经不能满足需求。
那么，什么才是一个强密码呢？如何才能制定出足够安全且好记的密码呢？本文将探讨密码学的基础知识，并给出几个实用的密码策略。
一. 密码学的基础知识1. 密码强度密码强度可以通过其长度和复杂度来度量。
长度是指密码字符数，复杂度通常表示密码中所包含的字符种类。
仅包含小写字母的六位密码有26^6种组合方式，但增加数字和大写字母后，它就变成了62^6，组合数量大大增加。
通常认为，一个密码字符数越多，密码位数越长，判断密码的强度就会越高。
而每多一种字符，组合数量都会指数级增加，这也解释了为什么提高密码复杂度可以增加安全性的原因。
2. 加盐在实际应用中为了让密码更加安全可靠，常常采用加盐技术。
所谓加盐，就是在密码前或后加入一段随机字符串的做法，以此增加密码的破解难度。
加盐的主要思想是让每个用户都拥有自己的加密密钥。
即使每个用户都使用同样的密码，由于盐值不同，生成的缺省铭文也都不同，直接保证了用户的密码安全。
二. 密码策略1. 长度至少12位现在密码位数越来越长了，因为手机和电脑都支持存储和记住很长很长的密码了。
而通常12位长度以上的密码显得更加严谨和安全，至少需要大写字母，小写字母，数字和符号这四类内容，建议使用符号&、#、$等等，但另外不要使用常见的密码如123456等等。
2. 使用密码管理工具密码管理工具是一种安全的电子记录和存储密码的方式，这种方式可让用户快速、轻松地在多个应用程序中使用更强的密码。
大多数密码管理工具都支持多平台同步。
3. 改变密码每几个月就改变一次密码，这是一个良好的密码协议。
即使你有一个安全密码，保持密码安全仍然是许多人解决密码问题的最佳方法。
不要重复使用同一密码。
4. 支持双因素身份验证双因素身份验证是保护在线账户免受未经授权的访问的强大工具。
信息安全理论与技术期末考试试题答案第一题1.1 常见的计算机安全威胁包括哪些？常见的计算机安全威胁包括：恶意软件、网络攻击、数据泄露、社会工程学攻击等。
1.2 什么是恶意软件？列举几种常见的恶意软件类型。
恶意软件，指的是具有恶意目的的计算机程序。
常见的恶意软件类型包括：病毒、蠕虫、木马、间谍软件和广告软件等。
第二题2.1 什么是加密算法？列举几种常见的加密算法类型。
加密算法是一种将明文转换为密文的数学计算方法。
常见的加密算法类型包括对称加密算法（如DES、AES）、非对称加密算法（如RSA、DSA）和哈希算法（如MD5、SHA）等。
2.2 对称加密算法和非对称加密算法有什么区别？对称加密算法使用相同的密钥进行加密和解密，加密速度快，但密钥管理困难。
非对称加密算法使用一对密钥，公钥用于加密，私钥用于解密，安全性更高但加密速度较慢。
第三题3.1 什么是防火墙？它的作用是什么？防火墙是一种网络安全设备，用于监控并控制网络流量，保护内部网络免受未经授权的访问和攻击。
防火墙的作用包括：过滤网络流量、进行访问控制、检测和阻止恶意流量、保护网络免受攻击等。
3.2 防火墙有哪几种常见的部署方式？常见的防火墙部署方式包括：网络层防火墙、主机层防火墙和虚拟专用网络（VPN）。
第四题4.1 什么是网络钓鱼？列举几种常见的网络钓鱼手法。
网络钓鱼是一种通过虚假身份和欺骗手法诱使用户透露敏感信息的网络攻击手段。
常见的网络钓鱼手法包括：伪造网站、钓鱼邮件、钓鱼短信、伪装社交媒体账号等。
4.2 如何防范网络钓鱼攻击？防范网络钓鱼攻击的方法包括：不点击可疑链接、不登录可疑网站、保持警惕、使用多因素认证、定期更新密码、学习如何识别钓鱼攻击等。
第五题5.1 什么是数据备份？为什么数据备份重要？数据备份是将数据从一个位置复制到另一个位置的过程，以防止数据丢失。
数据备份重要的原因包括：防止误删除或硬件故障导致的数据丢失，保护数据免受恶意软件和攻击事件的影响，恢复数据至先前可用状态等。
1、字母频率分析法对（单表代换密码）算法最有效。
2、（希尔密码）算法抵抗频率分析攻击能力最强，而对已知明文攻击最弱。
3、重合指数法对（多表代换密码）算法的破解最有效。
4、维吉利亚密码是古典密码体制比较有代表性的一种密码，其密码体制采用的是（多表代换密码）。
期中考试1. 公钥密码体制与对称密码体制相比有什么有点和不足？优点：密钥的分发相对容易；密钥管理简单；可以有效地实现数字签名。
缺点：与对称密码体制相比，费对称密码体制加解密速度比较慢；同等安全强度下，费对称密码体制要求的密钥位数要多一些；密文的长度往往大于明文长度。
2. 简述单表代换和多表代换密码的基本思想及其优缺点。
答：单表代换密码是指明文消息中相同的字母，在加密时都使用同意固定的字母来代换。
单表代替的优缺点优点：明文字符的形态一般将面目全非缺点：（A）明文的位置不变；（B）明文字符相同，则密文字符也相同；从而导致在密文字符的统计规律之中.形态变但位置不变单表代换即使有大量的密钥，也不能提供足够的安全性，因为密文中残留了大量的明文结构。
多表代换密码是以一系列代换表依次对明文消息的字母序列代换的加密方法即明文消息中岀现的同一个字母，在加密时不是完全被同一固定的字母代换，而是根据其岀现的位置次序用不同的字母代换。
优缺点：优点：同一字母在明文序列的位置不同就具有不同的密文，从而可以更好地抵抗统计密码分析；缺点：周期性的多表代换密码降低了安全性.3..简述DES与AES的异同：相似之处：二者的轮函数都是由3层构成，非线性层，线性混合层，子密钥异或，只是顺序不同；AES的子密钥异或对应于DES中S盒之前的子密钥异或；AES的列混合运算的目的是让不同的字节相互影响，而DES中的F函数的输岀与左边的一半数据相加也有类似的效果；AES的非线性运算是字节代换，对应于DES中唯一的非线性运算S盒：行移位运算保证了每一行的字节不仅仅影响其他行对应的字节，而且影响其他行所有的字节，这与DES中置换P相似。
2012级本科新大学计算机基础期末考试试题试卷满分：70分考试时间：2012年12月29日9：00—10：30一、选择题（共45分，每小题1.5分）1、网络的主要功能是_________。
A．数据通信和资源共享B．生产过程、实时控制C．并行处理、分布计算D．联网游戏、聊天考试2、衡量计算机运算速度性能指标的是_________。
A.字长B.主频C.存储容量D.软件3、杀毒软件的病毒库应及时更新，才能更有效地起到杀毒与防毒作用，这主要是为了保证信息的_________。
A.共享性B.载体依附性C.时效性D.传递性4、小黄有一个旧的笔记本电脑想卖掉，可又不知道谁想要，现在很流行的网上购物交易，请问他最好到以下_________网站出售。
A.搜狐B.网易C.百度D.淘宝5、人们通常所说的计算机系统包括_________。
A.主机及外部设备B.主机,键盘,显示器和打印机C.系统软件和应用软件D.硬件系统和软件系统6、汉字系统中汉字字库里存放的是汉字的_________。
A.机内码B.输入码C.字形码D.国标码7、与十六进制数(BC)等值的二进制数是_________。
A.10111011B.10111100C.11001100D.110010118、非对称数字用户线路的英文缩写是_________。
A.ADSLB.DSLC.RDSLD.SDSL9、Word2003中，有三种方法为表格添加边框线，________不能为表格添加边框。
A.表格和边框工具栏B.绘图工具栏C.边框和底绞D.表格属性10、小林在Word2003中输入英文“taecher”后，发现该单词变为“teacher”，这是因为Word字处理软件具有_________。
A.批注功能B.自动更正功能C.修订功能D.复制功能11、可以保存正在编辑的文档的按钮是_________。
A. B. C. D.12、当在Excel2003中进行操作时，若某单元格中出现“#####”的信息时，其含义是________。
密码学期末试题本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March密码学期末试题一．选择题1、关于密码学的讨论中，下列（ D ）观点是不正确的。
A 、密码学是研究与信息安全相关的方面如机密性、完整性、实体鉴别、抗否认等的综 合技术B 、密码学的两大分支是密码编码学和密码分析学C 、密码并不是提供安全的单一的手段，而是一组技术D 、密码学中存在一次一密的密码体制，它是绝对安全的2、在以下古典密码体制中，属于置换密码的是（B ）。
A 、移位密码B 、倒序密码C 、仿射密码D 、PlayFair 密码 3、一个完整的密码体制，不包括以下（ C）要素。
A 、明文空间 B 、密文空间 C 、数字签名 D 、密钥空间4、关于 DES 算法，除了（C ）以外，下列描述 DES 算法子密钥产生过程是正确的。
A 、首先将 DES 算法所接受的输入密钥 K （64 位），去除奇偶校验位，得到 56 位密钥（即经过 PC-1 置换， 得到 56 位密钥）B 、在计算第 i 轮迭代所需的子密钥时，首先进行循环左移，循环左移的位数取决于 i 的值，这些经过循环 移位的值作为下一次循环左移的输入C 、在计算第 i 轮迭代所需的子密钥时，首先进行循环左移，每轮循环左移的位数都相同，这些经过循环移 位的值作为下一次循环左移的输入D 、然后将每轮循环移位后的值经 PC-2 置换，所得到的置换结果即为第 i 轮所需的子密钥 Ki5、2000 年 10 月 2 日，NIST 正式宣布将（ B ）候选算法作为高级数据加密标准，该算法是由两位比利时密 码学者提出的。
A 、MARSB 、RijndaelC 、TwofishD 、Bluefish*6、根据所依据的数学难题，除了（ A ）以外，公钥密码体制可以分为以下几类。
A 、模幂运算问题C 、离散对数问题 B 、大整数因子分解问题D 、椭圆曲线离散对数问题7、密码学中的杂凑函数（Hash 函数）按照是否使用密钥分为两大类：带密钥的杂凑函数和不带密钥的杂凑函数，下面（ C ）是带密钥的杂凑函数。
CS255:Cryptography and Computer Security Winter2012Final ExamInstructions:−Answer allfive questions.−The exam is open book and open notes.Wireless devices are not allowed.−Students are bound by the Stanford honor code.−You have two hours and thirty minutes.Problem1.Questions from all over.a.Suppose G:{0,1}s→{0,1}n is a secure PRG.Is G (x)=G(x⊕1s)a secure PRG?If so,explain why.If not,describe an attack.b.Suppose F:K×{0,1}n→{0,1}n is a secure PRF.Is F (k,x)=F(k,x)⊕F(k,x⊕1n)a secure PRF?If so,explain why.If not,describe an attack.c.Let(S,V)be a secure MAC with message space{0,1}n for some large n.Define the MAC(S ,V )asS (k,m)=S(k,m),S(k,0n)andVk,m,(t1,t2)=1if V(k,m,t1)=V(k,0n,t2)=10otherwiseIs this(S ,V )a secure MAC?If so,explain why.If not,describe an attack.d.Suppose an attacker intercepts a ciphertext c which is the encryption of a messages m∈{0,1}n under nonce-based counter mode.Can the attacker create the encryption of m⊕1n just given c?If so,explain how.If not,explain why not.e.Same question as part(d)except that now m is encrypted using Galois Counter Mode(GCM).Can the attacker create the encryption of m⊕1n just given c?If so,explain how.If not,explain why not.f.Let G be a group in which the Computational Diffie-Hellman problem(CDH)is easy.Thatis,there is an efficient algorithm A that for all x,y∈Z,given(g,g x,g y)∈G3outputsg xy.Can this algorithm be used to break the ElGamal encryption system in G?If so,explain how.If not,explain why not.1Problem2.Luby-RackoffRecall that the Luby-Rackofftheorem states that using a secure PRF in a three round Feistel network results in a secure block cipher.Let’s see what goes wrong if we only use a two round Feistel.Let F:K×{0,1}32→{0,1}32by a secure PRF.Recall that a2-round Feistel defines the following block cipher F2:K2×{0,1}64→{0,1}64:Here R is the right32bits of the64-bit string and L is the left32bits.a.Draw the circuit for F−1(k,·).2b.Show that F2can be distinguished from a truly random one-to-one function with advantageclose to1.Hint:Think about querying the PRF challenger at two points and xoring the results.Then see if you canfind a relation among the returned values that will let you distinguishthe PRF from random.Problem3.Recall that Lamport signatures are one-time signatures built from a one-way func-tion f.Key generation outputs a public key containing O(n)points in the image of f.A signature on an n-bit message is a set of O(n)pre-images of certain points in the public key.Show that the length of Lamport signatures can be reduced by a factor of t at the cost of expanding the public and secret keys by a factor of at most2t.Make sure to describe your key generation,signing,and verification algorithms.Hint:Think of signing t bits of the message at a time as opposed to just one bit at a time.(in fact,one can shrink the size of Lamport signatures by a factor of t without expanding the public key.This is a little harder and not discussed here.)2Problem4.Private equality test.Suppose Alice has a secret number a∈Z q and Bob has a secret number b∈Z q,for some prime q.They wish to design a private equality protocol,namely a protocol such that at the end,if a=b Alice learns that fact,but if a=b then Alice learns nothing else about b.Either way Bob learn nothing about a.Think of a and b as hashes of afile.The two want to test if they have the samefile without leaking any other information about the contents of theirfiles.Let E be a public key encryption system with message space Z q.E satisfies the following property:given pk and c1=E(pk,x)and c2=E(pk,y)for x,y in Z q it is possible to createa new ciphertext c that is a fresh random encryption of x+y,namely c=E(pk,x+y)and cis independent of c1and c2.An encryption scheme with this property is said to be additively homomorphic.Now,Alice proposes the following protocol:–Alice generates a pk/sk pair for E and sends pk and c1:=E(pk,a)to Bob.–Bob chooses random s R←Z q∗and computes the encryption of E(pk,s(a−b)).Call the resulting ciphertext c2.Bob sends c2back to Alice.a.Explain how Bob computes c2given pk,c1and s.Hint:you will need to use a variant of the repeated squaring algorithm.b.Explain how Alice uses c2and her secret key to test if a=b.If a=b,explain why Alicelearns nothing about b other than the fact that a=b.c.Let G be a group of order q where the Decision Diffie Hellman problem is hard.Let g bea generator of G and let E be the following variant of ElGamal encryption:the publickey is pk=(g,h=g d)and the secret key is d.The“encryption”of a message a∈Z q isdefined as:E(pk,a)=(g r,h r+a)where r R←Z qShow that given E(pk,a)Alice can use her secret key d to compute h a.Note that thissystem is not really an encryption system since Alice cannot fully recover the plaintext afrom a given ciphertext.d.Explain how to instantiate the protocol above using the system from part(c).Describeexactly what message Alice would send to Bob,how Bob would respond,and how Alicewould learn the comparison result.3Problem5.Challenge response from weak PRFs.Let F:K×X→{0,1}n be a PRF where the input space X is large(so that1/|X|is negligible).We say that F is weakly secure if the adversary cannot distinguish F from a truly random function f:X→{0,1}n when the adversary only sees the evaluation of F(k,·)at random points.That is,the adversary is given pairs(x i,f(x i))for i=1,...,q where all x i are chosen at random in X,and is supposed to distinguish the case where f is a truly random function from the case where f is a random instance of the PRF.a.Write the precise security game defining a weakly secure PRF and define the advantagefunction for this game.Say that F is weakly secure if no efficient adversary can win thegame with non-negligible advantage.b.Let F:K×X→{0,1}n be a secure PRF(in the standard sense)and defineF (k,x)=k if x=0 F(k,x)otherwiseb.1.Is F a secure PRF in the standard sense?If so explain why,if not give an attack.b.2.Is F a weakly secure PRF?If so explain why,if not give an attack.c.Suppose we use a weakly secure PRF in the standard MAC-based challenge-response pro-tocol.That is,we directly use the weakly secure PRF as the MAC in this protocol.Is the resulting authentication protocol secure against active attacks?Hint:Give an example weakly secure PRF for which there is an active attack on the resulting challenge-response protocol.Note:it is possible to design an authentication protocol secure against active attacks from a weakly secure PRF,but we will leave that as a puzzle for another time.4。
密码学作业作业要求1按下面各题要求回答问题；2上机进行实验3索引二篇公开发表有关计算机密码学的文章。
时间发表在2009年以后4考试当日，答题前交到监考老师处（二篇文章，本作业）二.密码体制分类密码体制从原理上可分为两大类，即单钥体制和双钥体制。
单钥体制的加密密钥和解密密钥相同。
采用单钥体制的系统的保密性主要取决于密钥的保密性，与算法的保密性无关，即由密文和加解密算法不可能得到明文。
换句话说，算法无需保密，需保密的仅是密钥。
换句话说，算法无需保密，需保密的仅是密钥。
根据单钥密码体制的这种特性，单钥加解密算法可通过低费用的芯片来实现。
密钥可由发送方产生然后再经一个安全可靠的途径（如信使递送）送至接收方，或由第三方产生后安全可靠地分配给通信双方。
如何产生满足保密要求的密钥以及如何将密钥安全可靠地分配给通信双方是这类体制设计和实现的主要课题。
密钥产生、分配、存储、销毁等问题，统称为密钥管理。
这是影响系统安全的关键因素，即使密码算法再好，若密钥管理问题处理不好，就很难保证系统的安全保密。
单钥体制对明文消息的加密有两种方式：一是明文消息按字符（如二元数字）逐位地加密，称之为流密码；另一种是将明文消息分组（含有多个字符），逐组地进行加密，称之为分组密码。
单钥体制不仅可用于数据加密，也可用于消息的认证。
双钥体制是由Diffie和Hellman于1976年首先引入的。
采用双钥体制的每个用户都有一对选定的密钥：一个是可以公开的，可以像电话号码一样进行注册公布；另一个则是秘密的。
因此双钥体制又称为公钥体制。
双钥密码体制的主要特点是将加密和解密能力分开，因而可以实现多个用户加密的消息只能由一个用户解读，或由一个用户加密的消息而使多个用户可以解读。
前者可用于公共网络中实现保密通信，而后者可用于实现对用户的认证。
三.扩散和混淆扩散和混淆是由Shannon提出的设计密码系统的两个基本方法，目的是抗击敌手对密码系统的统计分析。
所谓扩散，就是将明文的统计特性散布到密文中去，实现方式是使得明文的每一位影响密文中多位的值，等价于说密文中每一位均受明文中多位影响。
混淆是使密文和密钥之间的统计关系变得尽可能复杂，以使敌手无法得到密钥。
因此即使敌手能得到密文的一些统计关系，由于密钥和密文之间的统计关系复杂化，敌手也无法得到密钥。
七.什么是零知识证明?下图表示一个简单的迷宫，C与D之间有一道门，需要知道秘密口令才能将其打开。
P向V证明自己能打开这道门，但又不愿向V泄露秘密口令。
可采用什么协议?零知识证明起源于最小泄露证明。
在交互证明系统中，设P知道某一秘密，并向V证明自己掌握这一秘密，但又不向V泄露这一秘密，这就是最小泄露证明。
进一步，如果V除了知道P能证明某一事实外，不能得到其他任何信息，则称P实现了零知识证明，相应的协议称为零知识证明协议。
① V在协议开始时停留在位置A。
② P一直走到迷宫深处，随机选择位置C或位置D。
③ P消失后，V走到位置B，然后命令P从某个出口返回位置B。
④ P服从V的命令，必要时利用秘密口令打开C与D之间的门。
⑤ P和V重复以上过程n次。
协议中，如果P不知道秘密口令，就只能从来路返回B，而不能走另外一条路。
此外，P每次猜对V要求走哪一条路的概率是1/2，因此每一轮中P能够欺骗V的概率是1/2。
假定n取16，则执行16轮后，P成功欺骗V的概率是1/216=1/65536。
于是，如果P16次都能按V的要求返回，V即能证明P确实知道秘密口令。
还可以看出，V无法从上述证明过程中获取丝毫关于P的秘密口令的信息，所以这是一个零知识证明协议。
四.什么是密码分组链接（CBC）模式,请画出加密\解密示意图它一次对一个明文分组加密，每次加密使用同一密钥,加密算法的输入是当前明文分组和前一次密文分组的异或，因此加密算法的输入不会显示出与这次的明文分组之间的固定关系，所以重复的明文分组不会在密文中暴露出这种重复关系。
一根据下面图解释名词,明文,密文,加密,解密,加密算法,解密算法, 加密密钥和解密密钥通信双方采用保密通信系统可以隐蔽和保护需要发送的消息，使未授权者不能提取信息。
发送方将要发送的消息称为明文，明文被变换成看似无意义的随机消息，称为密文，这种变换过程称为加密；其逆过程，即由密文恢复出原明文的过程称为解密。
对明文进行加密操作的人员称为加密员或密码员。
密码员对明文进行加密时所采用的一组规则称为加密算法。
传送消息的预定对象称为接收者，接收者对密文进行解密时所采用的一组规则称为解密算法。
加密和解密算法的操作通常都是在一组密钥控制下进行的，分别称为加密密钥和解密密钥。
五.杂凑(Hash)函数应满足的条件杂凑函数应满足以下条件：①函数的输入可以是任意长。
②函数的输出是固定长。
③已知x，求H(x)较为容易，可用硬件或软件实现。
④已知h，求使得H(x)=h的x在计算上是不可行的，这一性质称为函数的单向性，称H(x)为单向杂凑函数。
⑤已知x，找出y(y≠x)使得H(y)=H(x)在计算上是不可行的。
如果单向杂凑函数满足这一性质，则称其为弱单向杂凑函数。
⑥找出任意两个不同的输入x、y，使得H(y)=H(x)在计算上是不可行的。
如果单向杂凑函数满足这一性质，则称其为强单向杂凑函数。
第⑤和第⑥个条件给出了杂凑函数无碰撞性的概念，如果杂凑函数对不同的输入可产生相同的输出，则称该函数具有碰撞性。
六.迭代型杂凑函数的一般结构其中函数的输入M被分为L个分组Y0,Y1,…,YL-1，每一个分组的长度为b比特，最后一个分组的长度不够的话，需对其做填充。
算法中重复使用函数ff 的输入有两项，一项是上一轮（第i-1轮）输出的n比特值CVi-1，称为链接变量，另一项是算法在本轮（第i轮）的b比特输入分组Yi。
f 的输出为n比特值CVi，CVi又作为下一轮的输入。
算法开始时还需对链接变量指定一个初值IV，最后一轮输出的链接变量CVL 即为最终产生的杂凑值。
通常有b>n，因此称函数f为压缩函数。
算法可表达如下：CV0=IV=n比特长的初值；CVi=f(CVi-1,Yi-1)；1≤i≤L；H(M)=CVL算法的核心技术是设计无碰撞的压缩函数f，而敌手对算法的攻击重点是f 的内部结构，由于f 和分组密码一样是由若干轮处理过程组成，所以对f 的攻击需通过对各轮之间的位模式的分析来进行，分析过程常常需要先找出f 的碰撞。
由于f 是压缩函数，其碰撞是不可避免的，因此在设计f 时就应保证找出其碰撞在计算上是不可行的。
八.AES高级加密标准的轮函数由4个不同的计算部件组成，分别是：字节代换（ByteSub）、行移位（ShiftRow）、列混合（MixColumn）、密钥加（AddRoundKey）。
根据下图写出字节代换（ByteSub）、行移位（ShiftRow）、(1) 字节代换（ByteSub）字节代换是非线形变换，独立地对状态的每个字节进行。
代换表（即S-盒）是可逆的，由以下两个变换的合成得到：①首先，将字节看作GF(28)上的元素，映射到自己的乘法逆元，‘00’映射到自己。
②其次，对字节做如下的（GF(2)上的，可逆的）仿射变换：(2) 行移位（ShiftRow）行移位是将状态阵列的各行进行循环移位，不同状态行的位移量不同。
第0行不移动，第1行循环左移C1个字节，第2行循环左移C2个字节，第3行循环左移C3个字节。
位移量C1、C2、C3的取值与Nb有关，由表3.10给出。
（见66页表3.10）按指定的位移量对状态的行进行的行移位运算记为ShiftRow (State)图3.20是行移位示意图。
十二、在RSA算法中,设公钥KU={7,187},私钥KR={23,187},设明文M=88, 求密文C（16分）答：88^7mod187=[(88^4mod187)( 88^2mod187)( 88^1mod187)] mod18788^1mod187=8888^2mod187=7744mod187=7788^4mod187=59969536 mod187=13288^7mod187=(88*77*132) mod187=894432mod187=11所以 M=88 在公钥KU={7,187}的计算下得到的密问C=11,解密时，我们计算M=11^23 mod18711^23 mod187=[(11^1 mod187)( 11^2 mod187)( 11^4 mod187(11^8 mod187)( 11^8mod187)) mod18711^1 mod187=1111^2 mod187=12111^4 mod187=14641 mod187=5511^8 mod187=214365881 mod187=3311^23 mod187=(11*121*55*33*33) mod187=79720245 mod187=88用私钥KR={23,187}计算出明文M=88,十三、根据下图S-DES收、发双方共享的10位密钥，计算出两个8位子密钥分别用在加密、解密的不同阶段。
图中的P10、P8如下表，初始10位密钥为（1010000010）求图中的K1、K2P10 3 5 2 7 4 10 1 9 8 6P8 6 3 7 4 8 5 10 9LS-1 循环左移一位LS-2 循环左移二位初始10位密钥为（1010000010）P10=1000001100LS1左=00001LS1右=11000K1= P8=10010010LS2左=00100LS2右=00011K2= P8=00001001十四、根据下图S-DES加密算法计算出当明文M=11110011，求密文？算法中的变换如表解答如下：（S0）1=00（S1）1=10（S0）2=10（S1）2=00明文C=10010110十五、通信双方使用RSA加密体制，接收放的公开密钥是（e,n）=（5，119）接收到的密文是C=66，求明文m=? p(96例4.8)解：求n=119=p×q，选p=7，q=17。
φ(n)=(p-1)(q-1)=96。
取e=5，满足1<e<φ(n)，且gcd(φ(n),e)=1。
确定满足d·e=1 mod 96且小于96的d，因为77×5=385=4×96+1，所以d为77，因此公开钥为{5，119}，秘密钥为{77，119}。
设明文m=19，则由加密过程得密文为c≡195 mod 119≡2476099 mod 119≡66解密为6677mod 119≡19练习题用RSA算法对下列数据实现加密和解密1）p=3;q=11;e=7;m=52) p=5;q=11;e=3m=93) p=7;q=11;e=1;m=84）p=11;q=13;e=11;m=75）p=17;q=31;e=7;m=2十六、是密钥分配的一个实例。
