(完整版)立体几何动态问题(二轮)含答案.,推荐文档

高考数学二轮复习立体几何多选题练习题及解析一、立体几何多选题1．如图①，矩形ABCD 的边2BC =，设AB x =，0x >，三角形BCM 为等边三角形，沿BC 将三角形BCM 折起，构成四棱锥M ABCD -如图②，则下列说法正确的有（ ）A ．若T 为BC 中点，则在线段MC 上存在点P ，使得//PD 平面MATB ．当)3,2x ∈时，则在翻折过程中，不存在某个位置满足平面MAD ⊥平面ABCDC ．若使点M 在平面ABCD 内的射影落在线段AD 上，则此时该四棱锥的体积最大值为1 D ．若1x =，且当点M 在平面ABCD 内的射影点H 落在线段AD 上时，三棱锥M HAB -6322++【答案】BCD 【分析】对于A ，延长AT 与DC 的延长线交于点N ，此时，DP 与MN 必有交点； 对于B ，取AD 的中点H ，表示出2223MH MT HT x --，验证当)3,2x ∈时，无解即可； 对于C ，利用体积公式21233V x x =⨯⨯-，借助基本不等式求最值即可； 对于D ，要求外接球半径与内切球半径，找外接圆的圆心，又内接圆半径为2323r =++【详解】对于A ，如图，延长AT 与DC 的延长线交于点N ，则面ATM ⋂面()MDC N MN =．此时，DP 与MN 必有交点，则DP 与面ATM 相交，故A 错误； 对于B ，取AD 的中点H ，连接MH ，则MH AD ⊥．若面MAD ⊥面ABCD ，则有2223MH MT HT x =-=- 当)3,2x ∈时，无解，所以在翻折过程中，不存在某个位置满足平面MAD ⊥平面ABCD故B 正确；对于C ，由题可知，此时面MAD ⊥面ABCD ，由B 可知，(3x ∈，所以()22222221223232331333232x x V x x x x ⎛⎫+-⎛⎫=⨯⨯-=-≤== ⎪ ⎪⎝⎭⎝⎭当且仅当223x x =-，即6x =时等号成立．故C 正确； 对于D ，由题可知，此时面MAD ⊥面ABCD ，且2MH =因为AHB ，MHB 都是直角三角形，所以M ABH -底面外接圆的圆心是中点，所以1R =，由等体积法，可求得内接圆半径为2323r =++，故61322R r +=，故D 正确．故选：BCD ． 【点睛】本题从多个角度深度考查了立体几何的相关内容，注意辅助线的作法，以及求内接圆半径的公式、基本不等式、构造函数等核心思想．2．已知三棱锥A BCD -的三条侧棱AB ，AC ，AD 两两垂直，其长度分别为a ，b ，c ．点A 在底面BCD 内的射影为O ，点A ，B ，C ，D 所对面的面积分别为A S ，B S ，C S ，D S ．在下列所给的命题中，正确的有（ ） A ．2A BCO D S SS ⋅=； B ．3333A B C D S S S S <++；C ．若三条侧棱与底面所成的角分别为1α，1β，1γ，则222111sin sin sin 1αβγ++=；D ．若点M 是面BCD 内一个动点，且AM 与三条侧棱所成的角分别为2α，2β，2γ，则22cos α+2222cos cos 1βγ+=．【答案】ACD 【分析】由Rt O OA '与Rt O AD '相似，得边长关系，进而判断A 正确；当M 与O 重合时，注意线面角与线线角的关系，即可得C 正确；构造长方体，建立直角坐标系，代入夹角公式计算可得D 正确；代入特殊值，可得B 错误. 【详解】由三棱锥A BCD -的三条侧棱AB ，AC ，AD 两两垂直，则将三棱锥A BCD -补成长方体ABFC DGHE -，连接DO 并延长交BC 于O '， 则AO BC ⊥．对A ：由Rt O OA '与Rt O AD '相似，则2O A O O O D '''=⨯ 又12A S BC O D '=⋅，12BCOS BC O O '=⋅， 22221124D S BC O A BC O A ⎛⎫''=⋅=⋅ ⎪⎝⎭所以2A BCOD S SS ⋅=，故A 正确．对B ：当1a b c ===时，33318B C D S S S ===，则33338B C D S S S ++=，而332333322288A S ⎛⎫=⨯⨯=> ⎪ ⎪⎝⎭，此时3333A B C D S S S S >++，故B 不正确． 对D ：分别以AB ，AC ，AD 为x ，y ，z 轴，建立空间直角坐标系． 设(),,M x y z ，则(),,AM x y z =，222AM x y z =++，(),0,0AB a =，()0,,0AC b =，()0,0,AD c =所以222222222cos cos cos AM AB AM AC AM AD AM ABAM ACAM ADαβγ⎛⎫⎛⎫⎛⎫⋅⋅⋅++=++ ⎪ ⎪ ⎪ ⎪⎪⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭2222221x y z AMAMAM=++=，所以D 正确．对C ：当M 与O 重合时，AO ⊥面BCD ，由D 有222222cos cos cos 1αβγ++=，由各侧棱与底面所成角与侧棱与所AO 成角互为余角，可得C 正确． 故选：ACD.【点睛】关键点睛：本题考查空间线面角、线线角、面积关系的问题，计算角的问题关键是建立空间直角坐标系，写出点的坐标，利用数量积的公式代入计算，解决这道题目还要结合线面角与线线角的关系判断.3．已知四面体ABCD 的所有棱长均为2，则下列结论正确的是（ ） A ．异面直线AC 与BD 所成角为60︒B ．点A 到平面BCD 的距离为3C ．四面体ABCDD ．动点P 在平面BCD 上，且AP 与AC 所成角为60︒，则点P 的轨迹是椭圆 【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ，通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误；在四面体ABCD 中，过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心，因为所有棱长均为2,AF ==即点A 到平面BCD 的距离为3,故B 正确；设O 为正四面体的中心则OF 为内切球的半径，OA 我外接球的半径， 因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△，所以4AF OF =，即2=6OF AO =,所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确；建系如图：,A C ⎛⎛⎫⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ，则,,0,,333AP x y AC →→⎛⎛=-=- ⎝⎭⎝⎭，因为cos 60AP AC AP AC →→→→⋅=，所以241392y +=，83y +，平方化简可得：22400399y x y ----，可知点P 的轨迹为双曲线,故D 错误. 故选：BC ．【点睛】方法点睛：立体几何中动点轨迹的求解问题，解决此类问题可采用空间向量法，利用空间向量法表示出已知的角度或距离的等量关系，从而得到轨迹方程.4．如图所示，在长方体1111ABCD A B C D -中，11,2,AB BC AA P ===是1A B 上的一动点，则下列选项正确的是( )A ．DP 35B ．DP 5C ．1AP PC +6D ．1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值，即求1DA B △底边1A B 上的高即可；旋转11A BC 所在平面到平面11ABB A ，1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值，即求1DA B △底边1A B 上的高，易知115,2A B A D BD ===，所以1A B 边上的高为355h =111,AC BC ，得11A BC ，以1A B 所在直线为轴，将11A BC 所在平面旋转到平面11ABB A ，设点1C 的新位置为C '，连接AC '，则AC '即为所求的最小值，易知11122,2,cos AA AC AAC ''==∠=-， 所以217042222()105AC '=+-⨯⨯⨯-=. 故选：AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否， (1)点的变化，点与点的重合及点的位置变化；(2)线的变化，翻折、旋转前后应注意其位置关系的变化；(3)长度、角度等几何度量的变化．5．M ，N 分别为菱形ABCD 的边BC ，CD 的中点，将菱形沿对角线AC 折起，使点D 不在平面ABC 内，则在翻折过程中，下列结论正确的有（ ）A ．MN ∥平面ABDB ．异面直线AC 与MN 所成的角为定值C ．在二面角D AC B --逐渐变小的过程中，三棱锥D ABC -外接球的半径先变小后变大D ．若存在某个位置，使得直线AD 与直线BC 垂直，则ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭【答案】ABD 【分析】利用线面平行的判定即可判断选项A ；利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ；借助极限状态，当平面DAC 与平面ABC 重合时，三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心，外接圆的半径为球的半径，当二面角D AC B --逐渐变大时，利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D. 【详解】对于选项A:因为M ，N 分别为菱形ABCD 的边BC ，CD 的中点，所以MN 为BCD ∆的中位线，所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ，所以MN ∥平面ABD ,故选项A 正确；对于选项B ：取AC 的中点O ，连接,DO BO ,作图如下：则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知，AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90，故选项B 正确；对于选项C:借助极限状态，当平面DAC 与平面ABC 重合时，三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心，外接圆的半径为球的半径，当二面角D AC B --逐渐变大时，球心离开平面ABC ，但是球心在底面的投影仍然是ABC ∆外接圆圆心，故二面角D AC B --逐渐变小的过程中，三棱锥D ABC -外接球的半径不可能先变小后变大， 故选项C 错误；对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角，H 在线段BC 上；若ABC ∠为直角，H 与B 重合；若ABC ∠为钝角，H 在线段BC 的延长线上；若存在某个位置，使得直线AD 与直线BC 垂直，因为AH BC ⊥，所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角，H 与B 重合，所以CB BD ⊥,在CBD ∆中，因为CB CD =, 所以CB BD ⊥不可能成立，即ABC ∠为直角不可能成立；若ABC ∠为钝角，H 在线段BC 的延长线上，则在原平面图菱形ABCD 中，DCB ∠为锐角，由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小，，所以DCB ∠为锐角，CB HD ⊥，故点H 在线段BC 与H 在线段BC 的延长线上矛盾，因此ABC ∠不可能为钝角；综上可知，ABC ∠的取值范围是0,2π⎛⎫⎪⎝⎭.故选项D 正确;故选：ABD 【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题；考查空间想象能力和逻辑推理能力；借助极限状态和反证法思想的运用是求解本题的关键；属于综合型强、难度大型试题.6．在正方体1111ABCD A B C D -中，如图，,M N 分别是正方形ABCD ，11BCC B 的中心.则下列结论正确的是（ ）A ．平面1D MN 与11BC 的交点是11B C 的中点 B ．平面1D MN 与BC 的交点是BC 的三点分点 C ．平面1D MN 与AD 的交点是AD 的三等分点 D ．平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ，延长DE ，1D N ，并交于点F ，连FM 并延长分别交,BC AD 于,P Q ，连1,D Q PN 并延长交11B C 与H ，平面四边形1D HPQ 为所求的截面，进而求出,,P Q H 在各边的位置，利用割补法求出多面体11QPHD C CD 的体积，即可求出结论.【详解】如图，取BC 的中点E ，延长DE ，1D N ，并交于点F ， 连接FM 并延长，设FM BC P ⋂=，FM AD Q ⋂=， 连接PN 并延长交11B C 于点H .连接1D Q ，1D H ，则平面四边形1D HPQ 就是平面1D MN 与正方体的截面，如图所示.111111////,22NE CC DD NE CC DD ==，NE ∴为1DD F ∆的中位线，E ∴为DF 中点，连BF ， ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒， ,,A B F ∴三点共线，取AB 中点S ，连MS ，则12//,,23BP FB MS BP MS BC MS FS =∴==， 22111,33236BP MS BC BC PE BC ∴==⨯=∴=，E 为DF 中点，11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心，11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点， 点Q 是线段AD 靠近点D 的三等分点， 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P '， 做出线段11A D 靠近1D 的三等分点G ，连接QP '，HP '，QG ，GH ，1H QPP Q GHD V V '--=， 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积，确定出平面与正方体的交线是解题的关键，考查直观想象、逻辑推理能力，属于较难题.7．如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点P 在线段B 1C 上运动，则（ ）A ．直线BD 1⊥平面A 1C 1DB ．三棱锥P ﹣A 1C 1D 的体积为定值C ．异面直线AP 与A 1D 所成角的取值范用是[45°，90°]D ．直线C 1P 与平面A 1C 1D所成角的正弦值的最大值为3【答案】ABD【分析】 在A 中，推导出A 1C 1⊥BD 1，DC 1⊥BD 1，从而直线BD 1⊥平面A 1C 1D ；在B 中，由B 1C ∥平面 A 1C 1D ，得到P 到平面A 1C 1D 的距离为定值，再由△A 1C 1D 的面积是定值，从而三棱锥P ﹣A 1C 1D 的体积为定值；在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，利用向量法能求出直线C 1P 与平面A 1C 1D． 【详解】解：在A 中，∵A 1C 1⊥B 1D 1，A 1C 1⊥BB 1，B 1D 1∩BB 1＝B 1，∴A 1C 1⊥平面BB 1D 1，∴A 1C 1⊥BD 1，同理，DC 1⊥BD 1，∵A 1C 1∩DC 1＝C 1，∴直线BD 1⊥平面A 1C 1D ，故A 正确；在B 中，∵A 1D ∥B 1C ，A 1D ⊂平面A 1C 1D ，B 1C ⊄平面A 1C 1D ，∴B 1C ∥平面 A 1C 1D ，∵点P 在线段B 1C 上运动，∴P 到平面A 1C 1D 的距离为定值，又△A 1C 1D 的面积是定值，∴三棱锥P ﹣A 1C 1D 的体积为定值，故B 正确；在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]，故C 错误；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1，P （a ，1，a ），则D （0，0，0），A 1（1，0，1），C 1（0，1，1），1DA ＝（1，0，1），1DC ＝（0，1，1），1C P ＝（a ，0，a ﹣1），设平面A 1C 1D 的法向量(),,n x y z =， 则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x ＝1，得1,1,1n ，∴直线C 1P 与平面A 1C 1D 所成角的正弦值为： 11||||||C P n C Pn ⋅⋅＝∴当a ＝12时，直线C 1P 与平面A 1C 1D ，故D 正确． 故选：ABD ．【点睛】求直线与平面所成的角的一般步骤：（1）、①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解；（2）、用空间向量坐标公式求解.8．如图所示，在棱长为1的正方体1111ABCD A B C D 中，过对角线1BD 的一个平面交棱1AA 于点E ，交棱1CC 于点F ，得四边形1BFD E ，在以下结论中，正确的是（ ）A ．四边形1BFD E 有可能是梯形B ．四边形1BFD E 在底面ABCD 内的投影一定是正方形C ．四边形1BFDE 有可能垂直于平面11BB D DD ．四边形1BFDE 面积的最小值为62 【答案】BCD【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形；1BFD E 在底面ABCD 内的投影是四边形ABCD ；当与两条棱上的交点是中点时，四边形1BFD E 垂直于面11BB D D ；当E ，F 分别是两条棱的中点时，四边形1BFD E 6【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E ，如图所示，因为平面11//ABB A 平面11DCC D ，且平面1BFD E平面11ABB A BE =. 平面1BFD E 平面1111,//DCC D D F BE D F =，因此，同理1//D E BF ，故四边形1BFD E 为平行四边形，因此A 错误；对于选项B ，四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ，因此B 正确； 对于选项C ，当点E F 、分别为11,AA CC 的中点时，EF ⊥平面11BB D D ，又EF ⊂平面1BFD E ，则平面1BFD E ⊥平面11BB D D ，因此C 正确；对于选项D ，当F 点到线段1BD 的距离最小时，此时平行四边形1BFD E 的面积最小，此时点E F 、分别为11,AA CC 的中点，此时最小值为162322⨯⨯=，因此D 正确. 故选：BCD【点睛】关键点睛：解题的关键是理解想象出要画的平面是怎么样的平面，有哪些特殊的性质，考虑全面即可正确解题.。

立体几何1．一个物体的三视图的排列规则是俯视图放在正(主)视图下面，长度与正(主)视图一样，侧(左)视图放在正(主)视图右面，高度与正(主)视图一样，宽度与俯视图一样，即“长对正，高平齐，宽相等”．在画一个物体的三视图时，一定注意实线与虚线要分明．[问题1] 如图，若一个几何体的正(主)视图、侧(左)视图、俯视图均为面积等于2的等腰直角三角形，则该几何体的体积为________． 答案 432．在斜二测画法中，要确定关键点及关键线段．“平行于x 轴的线段平行性不变，长度不变；平行于y 轴的线段平行性不变，长度减半．”[问题2] 如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图，则这个平面图形的面积是________． 答案 2 23．简单几何体的表面积和体积(1)S 直棱柱侧＝c ·h (c 为底面的周长，h 为高)． (2)S 正棱锥侧＝12ch ′(c 为底面周长，h ′为斜高)．(3)S 正棱台侧＝12(c ′＋c )h ′(c 与c ′分别为上、下底面周长，h ′为斜高)．(4)圆柱、圆锥、圆台的侧面积公式 S 圆柱侧＝2πrl (r 为底面半径，l 为母线)， S 圆锥侧＝πrl (同上)，S 圆台侧＝π(r ′＋r )l (r ′、r 分别为上、下底的半径，l 为母线)． (5)体积公式V 柱＝S ·h (S 为底面面积，h 为高)， V 锥＝13S ·h (S 为底面面积，h 为高)，V 台＝13(S ＋SS ′＋S ′)h (S 、S ′为上、下底面面积，h 为高)．(6)球的表面积和体积 S 球＝4πR 2，V 球＝43πR 3.[问题3] 如图所示，一个空间几何体的正(主)视图和俯视图都是边长为1的正方形，侧(左)视图是一个直径为1的圆，那么这个几何体的表面积为( ) A ．4π B ．3π C ．2π D.32π 答案 D4．空间直线的位置关系：①相交直线——有且只有一个公共点．②平行直线——在同一平面内，没有公共点．③异面直线——不在同一平面内，也没有公共点．[问题4] 在空间四边形ABCD 中，E 、F 、G 、H 分别是四边上的中点，则直线EG 和FH 的位置关系是________． 答案 相交5．空间直线与平面、平面与平面的位置关系 (1)直线与平面①位置关系：平行、直线在平面内、直线与平面相交． ②直线与平面平行的判定定理和性质定理：判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行．性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行．③直线与平面垂直的判定定理和性质定理：判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直． 性质定理：垂直于同一个平面的两条直线平行． (2)平面与平面①位置关系：平行、相交(垂直是相交的一种特殊情况)． ②平面与平面平行的判定定理和性质定理：判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行． 性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行． ③平面与平面垂直的判定定理和性质定理：判定定理：一个平面过另一个平面的垂线，则这两个平面垂直．性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．[问题5] 已知b ，c 是平面α内的两条直线，则“直线a ⊥α”是“直线a ⊥b ，直线a ⊥c ”的________条件． 答案 充分不必要 6．空间向量(1)用空间向量求角的方法步骤①异面直线所成的角若异面直线l 1和l 2的方向向量分别为v 1和v 2，它们所成的角为θ，则cos θ＝|cos 〈v 1，v 2〉|. ②直线和平面所成的角利用空间向量求直线与平面所成的角，可以有两种方法：方法一 分别求出斜线和它在平面内的射影直线的方向向量，转化为求两条直线的方向向量的夹角(或其补角)．方法二 通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角． ③利用空间向量求二面角也有两种方法：方法一 分别在二面角的两个面内找到一个与棱垂直且从垂足出发的两个向量，则这两个向量的夹角的大小就是二面角的平面角的大小．方法二 通过平面的法向量来求，设二面角的两个面的法向量分别为n 1和n 2，则二面角的大小等于〈n 1，n 2〉(或π－〈n 1，n 2〉)．易错警示：①求线面角时，得到的是直线方向向量和平面法向量的夹角的余弦，容易误以为是线面角的余弦．②求二面角时，两法向量的夹角有可能是二面角的补角，要注意从图中分析． (2)用空间向量求A 到平面α的距离： 可表示为d ＝|n ·AB →||n |.[问题6] (1)已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则AB 1与侧面ACC 1A 1所成角的正弦值等于________．(2)正方体ABCD －A 1B 1C 1D 1的棱长为1，O 是底面A 1B 1C 1D 1的中心，则点O 到平面ABC 1D 1的距离为________． 答案 (1)64 (2)24解析 (1)方法一 取A 1C 1的中点E ，连接AE ，B 1E ，如图． 由题意知B 1E ⊥平面ACC 1A 1，则∠B 1AE 为AB 1与侧面ACC 1A 1所成的角． 设正三棱柱侧棱长与底面边长为1， 则sin ∠B 1AE ＝B 1E AB 1＝322＝64.方法二 如图，以A 1C 1中点E 为原点建立空间直角坐标系E －xyz ，设棱长为1，则A ⎝⎛⎭⎫12，0，1，B 1⎝⎛⎭⎫0，32，0， 设AB 1与平面ACC 1A 1所成的角为θ，EB 1→为平面ACC 1A 1的法向量． 则sin θ＝|cos 〈AB 1→，EB 1→〉|＝⎪⎪⎪⎪⎪⎪⎝⎛⎭⎫－12，32，－1·⎝⎛⎭⎫0，32，02×32＝64. (2)建立如图所示的空间直角坐标系，则A (1,0,0)，B (1,1,0)，D 1(0,0,1)，C 1(0,1,1)，O ⎝⎛⎭⎫12，12，1. 设平面ABC 1D 1的法向量为n ＝(x ，y ，z )，则 ⎩⎪⎨⎪⎧n ·AB →＝0，n ·AD 1→＝0，∴⎩⎪⎨⎪⎧y ＝0，－x ＋z ＝0.令z ＝1，得⎩⎪⎨⎪⎧x ＝1，y ＝0，∴n ＝(1,0,1)，又OD 1→＝⎝⎛⎭⎫－12，－12，0， ∴O 到平面ABC 1D 1的距离d ＝|n ·OD 1→||n|＝122＝24.易错点1 三视图认识不清致误例1 一个空间几何体的三视图如图所示，则该几何体的表面积为( )A ．48B ．32＋817C ．48＋817D ．80错解 由三视图知，该几何体的直观图如图所示，该几何体的下底面是边长为4的正方形；上底面是长为4，宽为2的矩形；两个梯形侧面垂直于底面，上底长为2，下底长为4，高为4；另两个侧面是正方形，边长为4. 所以表面积S ＝42×3＋2×4＋2×12(2＋4)×4＝48＋8＋24＝80.找准失分点 不能准确把握三视图和几何体之间的数量关系，根据正视图可知，侧视图中等腰梯形的高为4，而错认为等腰梯形的腰为4.正解 由三视图知该几何体的直观图如图所示，该几何体的下底面是边长为4的正方形；上底面是长为4、宽为2的矩形；两个梯形侧面垂直于底面，上底长为2，下底长为4，高为4；另两个侧面是矩形，宽为4，长为42＋12 ＝17.所以S 表＝42＋2×4＋12×(2＋4)×4×2＋4×17×2＝48＋817.答案 C易错点2 对几何概念理解不透致误例2 给出下列四个命题：①有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱； ②若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱； ③底面是平行四边形的四棱柱是平行六面体； ④底面是矩形的平行六面体是长方体．其中正确的命题是__________(写出所有正确命题的序号)． 错解1 ①②③ 错解2 ②③④找准失分点 ①是错误的，因为棱柱的侧棱要都平行且相等；④是错误的，因为长方体的侧棱必须与底面垂直． 正解 ②③易错点3 对线面关系定理条件把握不准致误例3 已知m 、n 是不同的直线，α、β、γ是不同的平面．给出下列命题： ①若α⊥β，α∩β＝m ，n ⊥m ，则n ⊥α，或n ⊥β； ②若α∥β，α∩γ＝m ，β∩γ＝n ，则m ∥n ；③若m 不垂直于α，则m 不可能垂直于α内的无数条直线； ④若α∩β＝m ，n ∥m ，且n ⊄α，n ⊄β，则n ∥α，且n ∥β； ⑤若m 、n 为异面直线，则存在平面α过m 且使n ⊥α. 其中正确的命题序号是________． 错解 ②③④⑤找准失分点③是错误的；⑤是错误的．正解①是错误的．如正方体中面ABB′A′⊥面ADD′A′，交线为AA′.直线AC⊥AA′，但AC不垂直面ABB′A′，同时AC也不垂直面ADD′A′.②正确．实质上是两平面平行的性质定理．③是错误的．在上面的正方体中，A′C不垂直于平面A′B′C′D′，但与B′D′垂直．这样A′C就垂直于平面A′B′C′D′内与直线B′D′平行的无数条直线．④正确．利用线面平行的判定定理即可．⑤错误．从结论考虑，若n⊥α且m⊂α，则必有m⊥n，事实上，条件并不能保证m⊥n.故错误．答案②④1．已知三条不同直线m，n，l与三个不同平面α，β，γ，有下列命题：①若m∥α，n∥α，则m∥n；②若α∥β，l⊂α，则l∥β；③α⊥γ，β⊥γ，则α∥β；④若m，n为异面直线，m⊂α，n⊂β，m∥β，n∥α，则α∥β.其中正确命题的个数是()A．0 B．1 C．2 D．3答案 C解析因为平行于同一平面的两条直线除了平行，还可能相交或成异面直线，所以命题①错误；由直线与平面平行的定义知命题②正确；由于垂直于同一个平面的两个平面可能平行还可能相交，因此命题③错误；过两条异面直线分别作平面互相平行，这两个平面是唯一存在的，因此命题④正确．故选C.2．设m，n是空间两条直线，α，β是空间两个平面，则下列选项中不正确的是()A．当m⊂α时，“n∥α”是“m∥n”的必要不充分条件B．当m⊂α时，“m⊥β”是“α⊥β”的充分不必要条件C．当n⊥α时，“n⊥β”是“α∥β”成立的充要条件D．当m⊂α时，“n⊥α”是“m⊥n”的充分不必要条件答案 A解析当m⊂α时，若n∥α可得m∥n或m，n异面；若m∥n可得n∥α或n⊂α，所以“n∥α”是“m∥n”的既不充分也不必要条件，答案选A.3．一个几何体的三视图如图所示，则该几何体的体积是()A ．64B ．72C ．80D ．112答案 B解析 根据三视图，该几何体为下面是一个立方体、上面两个三棱锥，所以V ＝4×4×4＋2×13×(12·4·2)×3＝72，故选B.4．如图所示，在正方体ABCD －A 1B 1C 1D 1中，M ，N ，P ，Q 分别是AA 1，A 1D 1，CC 1，BC 的中点，给出以下四个结论：①A 1C ⊥MN ；②A 1C ∥平面MNPQ ；③A 1C 与PM 相交；④NC 与PM 异面．其中不正确的结论是( ) A ．① B ．② C ．③ D ．④ 答案 C解析 作出过M ，N ，P ，Q 四点的截面交C 1D 1于点S ，交AB 于点R ，如图所示中的六边形MNSPQR ，显然点A 1，C 分别位于这个平面的两侧，故A 1C 与平面MNPQ 一定相交，不可能平行，故结论②不正确．5．一个几何体的三视图如图所示，则该几何体的表面积为( )A ．2＋ 2B ．3＋ 2C ．1＋2 2D ．5答案 A解析 由三视图可知，该几何体是一个四棱锥，如图所示． 该几何体的底面是边长为1的正方形，故S 1＝12＝1. 侧棱P A ⊥面ABCD ，且P A ＝1， 故S △P AB ＝S △P AD ＝12×1×1＝12，而PD ⊥DC ，CB ⊥PB ，且PB ＝PD ＝2， 所以S △PBC ＝S △PDC ＝12×2×1＝22.所以该几何体的表面积为S ＝1＋2×12＋2×22＝2＋ 2.故选A.6．如图，已知六棱锥P —ABCDEF 的底面是正六边形，P A ⊥平面ABC ，P A ＝2AB ，则下列结论正确的是( ) A ．PB ⊥ADB ．平面P AB ⊥平面PBC C ．直线BC ∥平面P AED ．直线PD 与平面ABC 所成的角为45° 答案 D解析 若PB ⊥AD ，则AD ⊥AB ，但AD 与AB 成60°角，A 错误；平面P AB 与平面ABD 垂直，所以平面P AB 一定不与平面PBC 垂直，B 错误；BC 与AE 是相交直线，所以BC 一定不与平面P AE 平行，C 错误；直线PD 与平面ABC 所成角为∠PDA ，在Rt △P AD 中，AD ＝P A ， ∴∠PDA ＝45°，D 正确．7．对于四面体ABCD ，给出下列四个命题： ①若AB ＝AC ，BD ＝CD ，则BC ⊥AD ； ②若AB ＝CD ，AC ＝BD ，则BC ⊥AD ； ③若AB ⊥AC ，BD ⊥CD ，则BC ⊥AD ； ④若AB ⊥CD ，AC ⊥BD ，则BC ⊥AD .其中正确的是________．(填序号) 答案 ①④解析 取线段BC 的中点E ，连接AE ，DE ， ∵AB ＝AC ，BD ＝CD ， ∴BC ⊥AE ，BC ⊥DE ， ∴BC ⊥平面ADE ， ∵AD ⊂平面ADE ， ∴BC ⊥AD ，故①正确．设点O 为点A 在平面BCD 上的射影， 连接OB ，OC ，OD ， ∵AB ⊥CD ，AC ⊥BD ， ∴OB ⊥CD ，OC ⊥BD ， ∴点O 为△BCD 的垂心， ∴OD ⊥BC ，∴BC ⊥AD ，故④正确，易知②③不正确，填①④.8.如图，四面体ABCD 中，AB ＝1，AD ＝23，BC ＝3，CD ＝2，∠ABC ＝∠DCB ＝π2，则二面角A －BC －D 的大小为________．答案 π3解析 由∠ABC ＝∠DCB ＝π2知，BA →与CD →的夹角θ就是二面角A －BC －D 的平面角． 又AD →＝AB →＋BC →＋CD →，∴AD →2＝(AB →＋BC →＋CD →)2 ＝AB →2＋BC 2→＋CD →2＋2AB →·CD →.因此2AB →·CD →＝(23)2－12－32－22＝－2， ∴cos(π－θ)＝－12，且0<π－θ<π，则π－θ＝23π，故θ＝π3.9．已知直线l ，m ，平面α，β，且l ⊥α，m ⊂β，给出四个命题：①若α∥β，则l ⊥m ；②若l ⊥m ，则α∥β；③若α⊥β，则l ∥m ；④若l ∥m ，则α⊥β. 其中为真命题的是________．(填序号) 答案 ①④解析 对命题①，则l ⊥α，α∥β得，l ⊥β，m ⊂β，∴l⊥m，故①正确．对命题②，l⊥mD⇒/l⊥β，则l⊥mD⇒/α∥β，故②错误．对命题③，当α⊥β时，l与m也可能相交或异面或平行，故③错误．对命题④，由l⊥α，l∥m得m⊥α，又m⊂β，∴α⊥β，故④正确．10．三棱锥D－ABC及其三视图中的正(主)视图和侧(左)视图如图所示，则棱BD的长为________．答案4 2解析由正(主)视图知CD⊥平面ABC，设AC中点为E，则BE⊥AC，且AE＝CE＝2；由侧(左)视图知CD＝4，BE＝23，在Rt△BCE中，BC＝BE2＋EC2＝(23)2＋22＝4，在Rt△BCD中，BD＝BC2＋CD2＝42＋42＝4 2.故答案为4 2.。

第1页共5页2024年高考数学总复习：立体几何中的动态问题[解题策略]立体几何中的“动态”问题就变化起因而言大致可分为两类：一是平移；二是旋转．就所求变量而言可分为三类：一是相关线、面、体的测度；二是角度；三是距离．立体几何动态问题的解决需要较高的空间想象能力与化归处理能力，在各省市的高考选择题与填空题中也时有出现．在解“动态”立体几何题时，如果我们能努力探寻运动过程中“静”的一面，动中求静，往往能以静制动、克难致胜．1．去掉枝蔓见本质——大道至简在解决立体几何中的“动态”问题时，需从复杂的图形中分化出最简单的具有实质性意义的点、线、面，让几何图形的实质“形销骨立”，即从混沌中找出秩序，是解决“动态”问题的关键．例1如图1，直线l ⊥平面α，垂足为O .正方体ABCD －A 1B 1C 1D 1的棱长为2.点A 是直线l 上的动点，点B 1在平面α内，则点O 到线段CD 1中点P 的距离的最大值为________．图1答案2＋2解析从图形分化出4个点O ，A ，B 1，P ，其中△AOB 1为直角三角形，固定AOB 1，点P 的轨迹是在与AB 1垂直的平面上且以AB 1的中点Q 为圆心的圆，从而OP ≤OQ ＋QP ＝12AB 1＋2＝2＋2，当且仅当OQ ⊥AB 1，且点O ，Q ，P 共线时取到等号，此时直线AB 1与平面α成45°角．2．极端位置巧分析——穷妙极巧在解决立体几何中的“动态”问题时，对于移动问题，由图形变化的连续性，穷尽极端特殊之要害，往往能直取答案．例2在正四面体A －BCD 中，E 为棱BC 的中点，F 为直线BD 上的动点，则平面AEF 与平面ACD 所成二面角的正弦值的取值范围是________．答案1解析本例可用极端位置法来加以分析．。

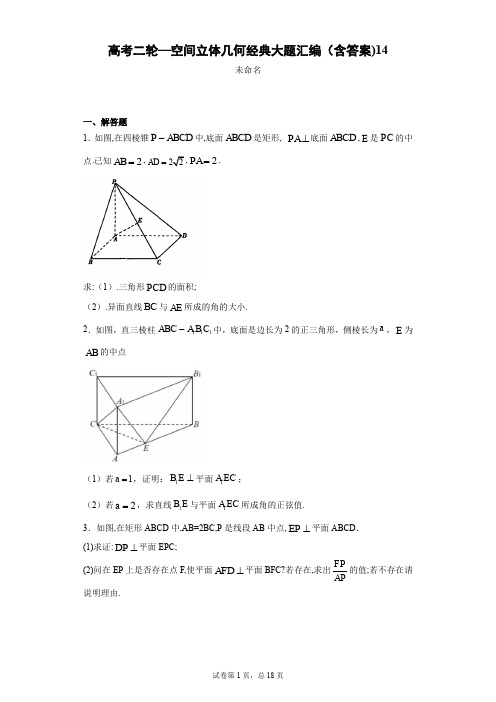
高考二轮—空间立体几何经典大题汇编（含答案)14未命名一、解答题1．如图,在四棱锥P ABCD -中,底面ABCD 是矩形, PA ⊥底面ABCD ,E 是PC 的中点.已知2AB =,AD =2PA =.求:（1）.三角形PCD 的面积;（2）.异面直线BC 与AE 所成的角的大小.2．如图，直三棱柱111ABC A B C -中，底面是边长为2的正三角形，侧棱长为a ，E 为AB 的中点（1）若1a =，证明：1B E ⊥平面1A EC ；（2）若2a =，求直线1B E 与平面1A EC 所成角的正弦值.3．如图,在矩形ABCD 中,AB=2BC,P 是线段AB 中点,EP ⊥平面ABCD ．(1)求证:DP ⊥平面EPC;(2)问在EP 上是否存在点F,使平面AFD ⊥平面BFC?若存在,求出FP AP的值;若不存在请说明理由.4．如图，AB是圆O的直径，C是圆O上不同于A，B的一点，PA⊥平面ABC，E是PC的中点，AB=PA=AC=1．（1）求证：AE⊥PB;（2）求三棱锥C-ABE的体积.（3）求二面角A-PB-C的正弦值．5．如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E、F分别是PC、AD中点，(1)求证：DE//平面PFB；(2)求PB与面PCD所成角的正切值。

-中，底面ABCD是边长为2的正方形，其它四个侧面都6．如图，四棱锥V ABCDE为AB的中点.（1）在侧棱VC 上找一点F ，使BF ∥平面VDE ，并证明你的结论；（2）在（1）的条件下求三棱锥E BDF -的体积．7．如图，在三棱柱111ABC A B C -中，1AA ⊥底面ABC ，90BAC ∠=，2AB AC ==，1AA ,M N 分别为1,BC CC 的中点，P 为侧棱1BB 上的动点（Ⅰ）求证：平面APM ⊥平面11BB C C ；（Ⅱ）若P 为线段1BB 的中点，求证：1//A N 平面APM ；（Ⅲ）试判断直线1BC 与平面APM 是否能够垂直。

立体几何的动态问题立体几何的动态问题，主要有五种：动点问题、翻折问题、旋转问题、投影与截面问题以及轨 迹问题。

基本类型：点动问题；线动问题；面动问题；体动问题；多动问题等。

解题时一般可以通过改变视角、平面化或者寻找变化过程中的不变因素而把问题回归到最本质的定义、定理或现有的结论中，若能再配以沉着冷静的心态去计算，那么相信绝大多数问题可以迎刃而解。

动点轨迹问题空间中动点轨迹问题变化并不多，一般此类问题可以从三个角度进行分析处理，一是从曲线定义或函数关系出发给出合理解释；二是平面与平面交线得直线或线段；三是平面和曲面（圆锥，圆柱侧面，球面）交线得圆，圆锥曲线。

很少有题目会脱离这三个方向。

（注意：阿波罗尼斯圆，圆锥曲线第二定义）1．（2015·浙江卷8）如图，斜线段AB 与平面α所成的角为60°，B 为斜足，平面α上的动点P 满足∠P AB ＝30°，则点P 的轨迹是( C )A ．直线B ．抛物线C ．椭圆D ．双曲线的一支式题 如图，平面α的斜线AB 交α于B 点，且与α所成的角为θ，平面α内有一动点C 满足∠BAC ＝π6，若动点C的轨迹为椭圆，则θ的取值范围为 ．(π6,π2)3．（2015春•龙泉驿区校级期中）在棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中，M 是A 1D 1的中点，点P 在侧面BCC 1B 1上运动．现有下列命题：①若点P 总保持P A ⊥BD 1，则动点P 的轨迹所在的曲线是直线； ②若点P 到点A 的距离为，则动点P 的轨迹所在的曲线是圆；③若P 满足∠MAP ＝∠MAC 1，则动点P 的轨迹所在的曲线是椭圆；④若P 到直线BC 与直线C 1D 1的距离比为2：1，则动点P 的轨迹所在的曲线是双曲线； ⑤若P 到直线AD 与直线CC 1的距离相等，则动点P 的轨迹所在的曲线是抛物线． 其中真命题的个数为（ C ）A ．4B ．3C ．2D ．14．（2018•温州模拟）已知线段AB垂直于定圆所在的平面，B，C是圆上的两点，H是点B在AC上的射影，当C 运动，点H运动的轨迹（A）A．是圆B．是椭圆C．是抛物线D．不是平面图形5．（2013•铁岭模拟）如图所示，△P AB所在的平面α和四边形ABCD所在的平面β互相垂直，且AD⊥α，BC⊥α，AD＝4，BC＝8，AB＝6．若tan∠ADP﹣2tan∠BCP＝1，则动点P在平面α内的轨迹是（D）A．椭圆的一部分B．线段C．双曲线的一部分D．以上都不是6．（2013•嘉兴二模）设m是平面α内的一条定直线，P是平面α外的一个定点，动直线n经过点P且与m成30°角，则直线n与平面α的交点Q的轨迹是（C）A．圆B．椭圆C．双曲线D．抛物线7．（2008•浙江）如图，AB是平面a的斜线段，A为斜足，若点P在平面a内运动，使得△ABP的面积为定值，则动点P的轨迹是（B）A．圆B．椭圆C．一条直线D．两条平行直线8．（2015春•台州校级月考）AB是平面α的斜线段，长度为2，点A是斜足，若点P在平面α内运动，当△ABP的面积等于3 时，点P的轨迹是（B）A．圆B．椭圆C．双曲线D．抛物线9．（2016•浙江二模）在正三棱柱（底面是正三角形的直棱柱）ABC﹣A1B1C1中，AB＝AA1＝2．若点M在△ABC所在平面上运动，且使得△AC1M的面积为1，则动点M的轨迹为（B）A．圆B．椭圆C．双曲线D．抛物线10．（2016•武汉校级模拟）如图，AB是平面α外的固定斜线段，B为斜足，若点C在平面α内运动，且∠CAB等于直线AB与平面α所成的角，则动点C的轨迹为（B）A．圆B．椭圆C．双曲线D．抛物线11．（2008年浙江·理10）如图，AB是平面a的斜线段，A为斜足，若点P在平面a内运动使得△ABP的面积为定值，则动点P的轨迹是（B ）（A）圆（B）椭圆（C）一条直线（D）两条平行直线12.（2014年金华高二十校联考·文10）圆柱的轴截面ABCD是边长为2的正方形，M为正方形ABCD对角线的交点，动点P在圆柱下底面内（包括圆周），若直线BM与直线MP所成角为45°，则点P形成的轨迹为( B) A．椭圆的一部分B．抛物线的一部分C．双曲线的一部分D.圆的一部分13．（2014•杭州二模）在等腰梯形ABCD中，E，F分别是底边AB，BC的中点，把四边形AEFD沿直线EF折起后所在的平面记为α，p∈α，设PB，PC与α所成的角分别为θ1，θ2（θ1，θ2均不为零）．若θ1＝θ2，则满足条件的P所形成的轨迹是圆．BACDMPABP14．（2018秋•诸暨市校级期中）如图，在底面为平行四边形的四棱锥P﹣ABCD中，E，F分别是棱AD，BP上的动点，且满足AE＝2BF，则线段EF中点的轨迹是（A）A．一条线段B．一段圆弧C．抛物线的一部分D．一个平行四边形15．（2015秋•太原期末）如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，P为棱A1B1的中点，点Q在侧面DCC1D1内运动，给出下列结论：①若BQ⊥A1C，则动点Q的轨迹是线段；②若|BQ|＝，则动点Q的轨迹是圆的一部分；③若∠QBD1＝∠PBD1，则动点Q的轨迹是椭圆的一部分；④若点Q到AB与DD1的距离相等，则动点Q的轨迹是抛物线的一部分．其中结论正确的是①③（写出所有正确结论的序号）．16．如图，长方体ABCD﹣A′B′C′D′中，AB＝BC＝，AA，上底面A′B′C′D′的中心为O′，当点E在线段CC′上从C移动到C′时，点O′在平面BDE上的射影G的轨迹长度为（B）A．B．C．D．17．（2016秋•温州期末）点P为棱长是2的正方体ABCD﹣A1B1C1D1的内切球O球面上的动点，点M为B1C1的中点，若满足DP⊥BM，则动点P的轨迹的长度为（C）A．B．C．D．18．（2018•宁波二模）已知棱长为1的正方体ABCD ﹣A 1B 1C 1D 1中，E 为侧面BB 1C 1C 中心，F 在棱AD 上运动，正方体表面上有一点P 满足＝x（x ≥0，y ≥0），则所有满足条件的P点构成图形的面积为．11819．（2017•定海区校级模拟）已知异面直线a ，b 所成角为60°，直线AB 与a ，b 均垂直，且垂足分别是点A ，B 若动点P ∈a ，Q ∈b ，|P A |+|QB |＝m ，则线段PQ 中点M 的轨迹围成的区域的面积是 ．√34m 220．（2017秋•赣州期末）如图，在等腰梯形ABCD 中，CD ＝2AB ＝2EF ＝2a ，E ，F 分别是底边AB ，CD 的中点，把四边形BEFC 沿直线EF 折起，使得平面BEFC ⊥平面ADFE ．若动点P ∈平面ADFE ，设PB ，PC 与平面ADFE 所成的角分别为θ1，θ2（θ1，θ2均不为0）．若θ1＝θ2，则动点P 的轨迹围成的图形的面积为（ D ）A ．B ．C ．D ．翻折问题面（动问题）翻折问题的一线五结论.DF AE ⊥一线：垂直于折痕的线即五结论：1）折线同侧的几何量和位置关系保持不变；折线两侧的几何量和位置关系发生改变； 2--D HF D H F ''∠）是二面角的平面角；3D DF '）在底面上的投影一定射线上；4) ''D H D H 点的轨迹是以为圆心，为半径的圆；5AD'E AE .）面绕翻折形成两个同底的圆锥1、（2016年联考试题）平面四边形ABCD 中，AD=AB=2，CD=CB= 5,且AD AB ⊥，现将△ABD 沿对角线BD 翻折成'A BD ∆，则在'A BD ∆折起至转到平面BCD 的过程中，直线'A C 与平面BCD 所成最大角的正切值为_______ .解：由题意知点A 运动的轨迹是以E 为圆心,EA 为半径的圆，当点A 运动到与圆相切的时候所称的角最大， 所以3tan '3A CB ∠=。

题型专项训练7 立体几何(解答题专项) 1.(2017浙江湖州高三期末)在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心. (1)求证:AA1⊥BC; (2)求直线A1B与平面BCC1B1所成角的大小.

2.如图,在四棱锥P-ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点. (1)求证:PD∥平面OCM; (2)若AP与平面PBD所成的角为60°,求线段PB的长.

3.在三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC. (1)求证:AE⊥BD; (2)若DB=2DC=AB=2,且二面角A-BD-C为60°,求AD与平面BCD所成角的正弦值.

4.如图,在三棱锥P-ABC中,△ABC是等边三角形,D是AC的中点,PA=PC,二面角P-AC-B的大小为60°. (1)求证:平面PBD⊥平面PAC; (2)求AB与平面PAC所成角的正弦值. 5.如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点. (1)求证:EF⊥BD; (2)若异面直线EF,BC1所成的角为30°,求二面角C1-AB-D的平面角的正切值.

6.(2017浙江台州实验中学模拟)如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. (1)求证:AD⊥BM; (2)点E是线段DB上的一动点,当二面角E-AM-D大小为时,试确定点E的位置.

参考答案 题型专项训练7 立体几何(解答题专项) 1.(1)证明 如图,设O为底面三角形的中心, ∵A1O⊥底面ABC,∴A1O⊥BC,

∵△ABC为正三角形,

连接AO交BC于点D,则AD⊥BC, 又AD∩A1O=O,∴BC⊥平面A1AD, 则AA1⊥BC. (2)解 取B1C1的中点D1,连接A1D1,DD1, 由(1)知,BC⊥平面ADD1A1, ∴平面ADD1A1⊥平面BB1C1C,且平面ADD1A1∩平面BB1C1C=DD1,

专题13 立体几何中的计算问题【自主热身，归纳总结】1、若正三棱锥的底面边长为2，侧棱长为1，则此三棱锥的体积为 ． 【答案】：61【解析】：设此正三棱锥的高为h ，则，所以312=h ，33=h ，故此三棱锥的体积．2、 如图，在长方体ABCDA 1B 1C 1D 1中，AB ＝AD ＝3 cm ，AA 1＝2 cm ，则三棱锥AB 1D 1D 的体积为________cm 3.【答案】 3【解析】VAB 1D 1D ＝VB 1AD 1D ＝13S △ADD 1×A 1B 1＝13×12×AD ×D 1D ×A 1B 1＝13×12×3×2×3＝3.3、将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27π cm 3，则该圆柱的侧面积为________cm 2. 【答案】：18π【解析】：设正方形的边长为x cm ，则圆柱的体积为πx 2·x ＝27π，解得x ＝3，所以该圆柱的侧面积为2π×3×3＝18π(cm 2)．4、如图，正四棱锥PABCD 的底面一边AB 的长为2 3 cm ，侧面积为8 3 cm 2，则它的体积为________cm 3.【答案】 4【解析】：如图，过点P 作PO 垂直于底面ABCD ，且垂足为O ，在平面ABCD 中，过点O 作直线AB 的垂线，垂足为E ，连结PE.由正四棱锥的性质知，PE ⊥AB ，所以S 侧＝(12×23×PE )×4＝83，解得PE＝2，在Rt △POE 中，PO ＝PE 2－EO2＝22－3＝1，所以正四棱锥的体积为13×(23)2×1＝4.5、已知正四棱柱的底面边长为3 cm ，侧面的对角线长是35cm ，则这个正四棱柱的体积是________cm 3. 【答案】54【解析】：设该正四棱柱的侧棱长为h cm ，则(35)2＝32＋h 2，解得h ＝6(负值舍去)，从而这个正四棱柱的体积是V ＝32×6＝54(cm 3)．6、若圆锥的侧面展开图是面积为3π且圆心角为2π3的扇形，则此圆锥的体积为________．【答案】 223π7、现有一正四棱柱形铁块，底面边长为高的8倍，将其熔化锻造成一个底面积不变的正四棱锥形铁件（不计材料损耗）．设正四棱柱与正四棱锥的侧面积分别为1S ,2S ,则12S S 的值为 ． 【答案】25【解析】设正四棱柱得高为a ，所以底面边长为8a ，根据体积相等，且高相等，所以正四棱锥的高为3a ，则正棱锥侧面的高为,所以.8、以一个圆柱的下底面为底面，并以圆柱的上底面圆心为顶点作圆锥，若所得的圆锥底面半径等于圆锥的高，则圆锥的侧面积与圆柱的侧面积之比为________． 【答案】22【解析】：如图，由题意可得圆柱的侧面积为S 1＝2πrh ＝2πr 2.圆锥的母线l ＝h 2＋r 2＝2r ，故圆锥的侧面积为S 2＝12×2πr ×l ＝2πr 2，所以S 2∶S 1＝2∶2.9、如图，正三棱柱ABCA 1B 1C 1中，AB ＝4，AA 1＝6.若E ，F 分别是棱BB 1，CC 1上的点，则三棱锥AA 1EF 的体积是________．【答案】：23【解法1】过B 点作BE AC ⊥，垂足为E ，平面ABC ⊥平面11ACC A ，且平面ABC ⋂平面11ACC A =AC ,所以BE ⊥平面11ACC A ，又因为梯形1ACC D 的面积为=6，所以.【解法2】,而=1323⨯⨯,所以四棱锥1B ACC D -的体积为23.【关联1】、如图，铜质六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知正六棱柱的底面边长、高都为4 cm ，圆柱的底面积为9 3 cm 2.若将该螺帽熔化后铸成一个高为6 cm 的正三棱柱零件，则该正三棱柱的底面边长为________cm (不计损耗)．【答案】. 210 由题意知，熔化前后的体积相等，熔化前的体积为6×34×42×4－93×4＝603，设所求正三棱柱的底面边长为x cm ，则有34x 2·6＝603，解得x ＝210，所以所求边长为210cm .【关联2】、在棱长为2的正四面体P ABC -中，M ，N 分别为PA ，BC 的中点，点D 是线段PN 上一点，且2PD DN =，则三棱锥D MBC -的体积为 ．【答案】：2思路分析：解决空间几何体的体积计算问题常常有两个途径：一是直接利用体积公式求解，另一种是利用等体积转化的思想进行计算.解题过程：连结MB ，MC ，MN ，过点D 作MN DH ⊥于H ，因为BP BA =，M 为PA 的中点，所以BM PA ⊥，同理CM PA ⊥，又因为，所以，又因为，所以MN PA ⊥，又因为MN DH ⊥，所以PA DH //，从而，故DH 为点D 到平面MBC 的高.在MBC ∆中，MC MB =，N 为BC 的中点，则，MBC ∆的面积，在NPM ∆中，因为PM DH //，2PD DN =，所以，从而三棱锥D MBC -的体积．【关联3】、如图，在正三棱柱中，已知，点P 在棱1CC 上，则三棱锥1P ABA -的体积为 ．【答案】．439 【解析】： 因为正三棱柱中，11//CC AA ，因为，，所以，因为点P 在棱1CC 上，所以点C 到平面B B AA 11的距离就是点P 到平面B B AA 11的距离．作AB CD ⊥，垂直为点D ，因为正三棱柱中，⊥1AA 面ABC ，⊂CD 面ABC ，所以1AA CD ⊥，而，，，所以．因为正三棱柱中，，所以233=CD ，1ABA ∆的面积，所以三棱锥1ABA P -的体积．例2、已知矩形ABCD 的边AB ＝4，BC ＝3，若沿对角线AC 折叠，使平面DAC ⊥平面BAC ，则三棱锥DABC 的体积为________． 【答案】. 245【解析】：在平面DAC 内作DO ⊥AC ，垂足为点O ，因为平面DAC ⊥平面BAC ，且平面DAC ∩平面BAC ＝AC ，所以DO ⊥平面BAC ，因为AB ＝4，BC ＝3，所以DO ＝125，S △ABC ＝12×3×4＝6，所以三棱锥DABC 的体积为V ＝13×6×125＝245. 【变式1】、．已知一个空间几何体的所有棱长均为1 cm ，其表面展开图如图所示，则该空 间几何体的体积V= cm 3．【答案】216+【解析】空间几何体为一正方体和一正四棱锥的组合体，显然，正方体的体 积为1，正四棱锥的底面边长为1，侧棱长为1，所以，棱锥的高为22，所以，正四棱锥的体积为26，即组合体的体积为216+【变式2】、已知△ABC 为等腰直角三角形，斜边BC 上的中线AD = 2，将△ABC 沿AD 折成60°的二面角，连结BC ，则三棱锥C ABD 的体积为 ． 【答案】：23易错警示 由于二面角平面角的概念在必做部分考查较少形成了复习中的知识盲点在边长为4的正方形ABCD 内剪去四个全等的等腰三角形(如图1中阴影部分)，【关联1】、折叠成底面边长为2的正四棱锥SEFGH(如图2)，则正四棱锥SEFGH 的体积为________．（图1）（图2）【答案】：. 43【解析】：连结EG ，HF ，交点为O ，正方形EFGH 的对角线EG ＝2，EO ＝1，则点E 到线段AB 的距离为1，EB ＝12＋22＝ 5.SO ＝SE 2－OE 2＝5－1＝2，故正四棱锥SEFGH 的体积为13×(2)2×2＝43.【关联2】、已知圆锥的底面半径和高相等，侧面积为42π，过圆锥的两条母线作截面，截面为等边三角形，则圆锥底面中心到截面的距离为 【答案】233【解析】设底面半径为r ，由题意可得：母线长为2r .又侧面展开图面积为，所以2r =.又截面三角形ABD 为等边三角形，故，又，故BOD V 为等角直角三角形.设圆锥底面中心到截面的距离为d ，又，所以.又,2OBD S =V ,2AO r ==，故.【关联3】、 如图，在圆锥VO 中，O 为底面圆心，半径OA ⊥OB ，且OA ＝VO ＝1，则O 到平面VAB 的距离为________．【答案】：33思路分析 在立体几何求点到平面的距离问题中，往往有两种途径：(1) 利用等体积法，这种方法一般不需要作出高线；(2) 利用面面垂直的性质作出高线，再进行计算．解法1 因为VO ⊥平面AOB ，OA ⊂平面AOB ，所以VO ⊥OA ，同理VO ⊥OB ，又因为OA ⊥OB ，OA ＝VO ＝OB ＝1，所以VA ＝VB ＝AB ＝2，所以S △VAB ＝12VA ×AB sin60°＝32.设O 到平面VAB 的距离为h ，由V VAOB ＝V OVAB ，得13S △AOB ×VO＝13S △VAB ×h ，得12OA ×OB ×VO ＝32h ，解得h ＝33. 解法2 取AB 中点M ，连结VM ，过点O 作OH ⊥VM 于H .因为OA ＝OB ，M 是AB 中点，所以OM ⊥AB ，因为VO ⊥平面AOB ，AB ⊂平面AOB ，所以VO ⊥AB ，又因为OM ⊥AB ，VO ∩OM ＝O ，所以AB ⊥平面VOM ，又因为AB ⊂平面VAB ，所以面VAB ⊥平面VOM ，又因为OH ⊥VM ，OH ⊂平面VOM ，平面VAB ∩平面VOM ＝VH ，所以OH ⊥平面VAB ，所以OH 为点O 到平面VAB 的距离，且OH ＝VO ×OM VM ＝33.例3、如图，在直三棱柱A 1B 1C 1ABC 中，AB ⊥BC ，E ，F 分别是A 1B ，AC 1的中点． (1) 求证：EF ∥平面ABC ； (2) 求证：平面AEF ⊥平面AA 1B 1B ；(3) 若A 1A ＝2AB ＝2BC ＝2a ，求三棱锥FABC 的体积．)【解析】 (1) 连结A 1C .因为直三棱柱A 1B 1C 1ABC 中，四边形AA 1C 1C 是矩形，所以点F 在A 1C 上，且为A 1C 的中点．在△A 1BC 中，因为E ，F 分别是A 1B ，A 1C 的中点，所以EF ∥BC .(2分) 又因为BC ⊂平面ABC ，EF ⊄平面ABC ，所以EF ∥平面ABC .(4分) (2) 因为在直三棱柱A 1B 1C 1ABC 中，B 1B ⊥平面ABC ，所以B 1B ⊥BC . 因为EF ∥BC ，AB ⊥BC ，所以AB ⊥EF ，B 1B ⊥EF .(6分) 因为B 1B ∩AB ＝B ，所以EF ⊥平面ABB 1A 1.(8分)因为EF ⊂平面AEF ，所以平面AEF ⊥平面ABB 1A 1.(10分) (3) V FABC ＝12VA 1ABC ＝12×13×S △ABC ×AA 1(12分)＝12×13×12a 2×2a ＝a36.(14分)【变式1】、如图，在五面体ABCDEF 中，已知DE ⊥平面ABCD ，//AD BC ，o 60BAD ∠=，2AB =，1DE EF ==．（1）求证：//BC EF ； （2）求三棱锥B DEF -的体积．【解析】（1）因为//AD BC ，AD ⊂平面ADEF ，BC ⊄平面ADEF ， 所以//BC 平面ADEF ， （3分） 又BC ⊂平面BCEF ，平面BCEF I 平面ADEF EF =， 所以//BC EF ． （6分） （2）如图，在平面ABCD 内过点B 作BH AD ⊥于点H ．因为DE ⊥平面ABCD ，BH ⊂平面ABCD ，所以DE BH ⊥．又AD ，DE ⊂平面ADEF ，，所以BH ⊥平面ADEF ，所以BH 是三棱锥B DEF -的高． （9分） 在直角三角形ABH 中，o 60BAD ∠=，2AB =，所以3BH =． 因为DE ⊥平面ABCD ，AD ⊂平面ABCD ，所以DE AD ⊥．又由（1）知，//BC EF ，且//AD BC ，所以//AD EF ，所以DE EF ⊥， （12分）所以三棱锥B DEF -的体积． （14分）易错警示 在证明线线、线面、面面的位置关系时，一定要注意条件的完备性，不能少写条件．另外，在求几何体的体积时， 一定要证明某条线为高的原因，即证明它与某个平面垂直，否则将导致丢分． 【变式2】、如图，在矩形ABCD 中，AD ＝2，AB ＝4，E ，F 分别为边AB ，AD 的中点．现将△ADE 沿DE 折起，得四棱锥ABCDE. （1）求证：EF ∥平面ABC ；（2）若平面ADE ⊥平面BCDE ，求四面体FDCE 的体积．【解析】 (1) 证法1 如图1，取线段AC 的中点M ，连结MF ，MB. 因为F ，M 为AD ，AC 的中点， 所以MF ∥CD ，且MF ＝12CD.图1在折叠前，四边形ABCD 为矩形，E 为AB 的中点，所以BE ∥CD ，且BE ＝12CD.所以MF ∥BE ，且MF ＝BE.所以四边形BEFM 为平行四边形，故EF ∥BM. 又EF ⊄平面ABC ，BM ⊂平面ABC ， 所以EF ∥平面ABC.证法2 如图2，延长DE 交CB 的延长线于点N ，连结AN.在折叠前，四边形ABCD 为矩形，E 为AB 的中点，所以BE ∥CD ，且BE ＝12CD.图2所以∠NBE ＝∠NCD ，∠NEB ＝∠NDC. 所以△NEB ∽△NDC.所以NE ND ＝BE CD ＝12，即E 为DN 的中点．又F 为AD 的中点，所以EF ∥NA. 又EF ⊄平面ABC ，NA ⊂平面ABC ， 所以EF ∥平面ABC.证法3 如图3，取CD 的中点O ，连结OE ，OF.图3(2) 解法1 在折叠前，四边形ABCD 为矩形，AD ＝2，AB ＝4，E 为AB 的中点，所以△A DE ，△CBE 都是等腰直角三角形，且AD ＝AE ＝EB ＝BC ＝2.所以∠DEA ＝∠CEB ＝45°，且DE ＝EC ＝2 2.又∠DEA ＋∠DEC ＋∠CEB ＝180°，所以∠DEC ＝90°，即DE ⊥CE.又平面ADE ⊥平面BCDE ，平面ADE∩平面BCDE ＝DE ，CE ⊂平面BCDE ，所以CE ⊥平面ADE ，即CE 为三棱锥CEFD 的高．因为F 为AD 的中点，所以S △EFD ＝12×12×AD×AE＝14×2×2＝1. 所以四面体FDCE 的体积V ＝13×S △EFD ×CE＝13×1×22＝223. 解法2 如图4，过F 作FH ⊥DE ，H 为垂足．图4因为平面ADE ⊥平面BCDE ，平面ADE∩平面BCDE ＝DE ，FH ⊂平面ADE ，所以FH ⊥平面BCDE ，即FH 为三棱锥FECD 的高．在折叠前，四边形ABCD 为矩形，且AD ＝2，AB ＝4，E 为AB 的中点，所以△ADE 是等腰直角三角形． 又F 为AD 的中点，所以DF ＝1.所以FH ＝DF·sin45°＝22. 又S △EDC ＝12×CD×BC＝12×4×2＝4， 所以四面体FDCE 的体积V ＝13×S △EDC ×FH＝13×4×22＝223. 解法3 如图5，过A 作AG ⊥DE ，G 为垂足．图5因为平面ADE ⊥平面BCDE ，平面ADE∩平面BCDE ＝DE ，AG ⊂平面ADE ，所以AG ⊥平面BCDE ，即AG 为三棱锥AECD 的高．在折叠前，四边形ABCD 为矩形，且AD ＝2，AB ＝4，E 为AB 的中点，所以△ADE 是等腰直角三角形．所以AG ＝AD·sin45°＝ 2.又S △EDC ＝12×DC×BC＝12×4×2＝4， 所以三棱锥AECD 的体积V AECD ＝13×S △EDC ×AG＝13×4×2＝423. 因为F 为AD 的中点，所以S △EFD ＝12S △EAD . 所以V CEFD ＝12V CEAD ＝12V AECD ＝223. 即四面体FDCE 的体积为223. 【关联】、如图，直四棱柱ABCD-A 1B 1C 1D 1的底面ABCD 是菱形，∠ADC ＝120°，AA 1＝AB ＝1，点O 1，O 分别是上、下底面菱形的对角线的交点．（1）求证：A 1O ∥平面CB 1D 1；（2）求点O 到平面CB 1D 1的距离．【解析】 (1) 因为AA 1∥C C 1且AA 1＝C C 1，所以四边形A 1ACC 1是 平行四边形，所以AC ∥A 1C 1且AC ＝A 1C 1.因为O 1，O 分别是A 1C 1，AC 的中点，故O C ∥A 1O 1且O C ＝A 1O 1. 所以四边形A 1O 1C O 为平行四边形，所以A 1O ∥O 1C.又A 1O ⊄平面CB 1D 1，O 1C ⊂平面CB 1D 1，所以A 1O ∥平面CB 1D 1.（2）解法1 等体积法．设点O 到平面CB 1D 1的距离为h.因为D 1D ⊥平面ABCD ，所以D 1D ⊥C O.因为AC ，BD 为菱形ABCD 的对角线，所以C O ⊥BD.因为D 1D∩BD＝D ，所以C O ⊥平面BB 1D 1D.在菱形ABC D 中，BC ＝1，∠BCD ＝60°，C O ＝32. 解法2 作垂线．因为AA 1⊥平面A 1B 1C 1D 1，所以AA 1⊥B 1D 1.因为A 1C 1，B 1D 1为菱形A 1B 1C 1D 1的对角线，所以B 1D 1⊥A 1C 1. 因为AA 1∩A 1C 1＝A 1，所以B 1D 1⊥平面AA 1C 1C.因为B 1D 1⊂平面CB 1D 1，所以平面CB 1D 1⊥平面AA 1C 1C.在平面AA 1C 1C 内，作OH ⊥C O 1，H 为垂足，而平面CB 1D 1∩平面AA 1C 1C ＝CO 1， 所以OH ⊥平面CB 1D 1，即线段OH 的长为点O 到平面CB 1D 1的距离．在矩形AA 1C 1C 中，∠O CH ＝∠C O 1C 1，sin ∠CO 1C 1＝C C 1C O 1＝172＝27， sin ∠OCH ＝OH O C ＝OH 32＝2OH 3，所以27＝2OH 3，故OH ＝217. 因此，点O 到平面CB 1D 1的距离为217.。

立体几何动态问题在立体几何中，判定和证明空间的线线、线面以及面面之间的位置关系(主要是平行与垂直的位置关系)，计算空间图形中的几何量(主要是角与距离)是两类基本问题．正确揭示空间图形与平面图形的联系，并有效地实施空间图形与平面图形的转换是分析和解决这两类问题的关键．立体几何压轴题多以选择题、填空题形式出现，往往与不等式、导数、三角函数等相结合，具有一定的综合性.类型一 翻折、折叠问题【例1】【2020云南玉溪一中月考】如图，矩形ABCD 中，4,2AB BC ==，E 为边AB 的中点，沿DE 将ADE ∆折起，点A 折至1A 处（1A ∉平面ABCD ），若M 为线段1A C 的中点，则在ADE ∆折起过程中，下列说法错误的是（ ）A ．始终有MB //平面1A DE B ．不存在某个位置，使得1AC ⊥平面1A DE C ．三棱锥1A ADE -体积的最大值是223D ．一定存在某个位置，使得异面直线BM 与1AE 所成角为30【解析】连结AC 交DE 于N ，取CD 的中点O ，连结OM ，OB ，1A N ，对A ，易证，平面//OMB 平面1A DE ，BM ⊂平面OMB ，所以始终有//MB /平面1A DE ，故A 正确；对B ，因为4,2AB BC ==，假设1A C ⊥平面1A DE ，则1A C ⊥1A D ，11A C A E ⊥，则222211CD A D CE A E CD CE -=-⇒=，因为4,2CD CE ==CD DE =不成立，所以假设错误，故不存在某个位置，使得1A C ⊥平面1A DE ，故B 正确； 对C ，当平面1A DE ⊥平面ABCD 时，三棱锥1A ADE -的体积最大，11122(22)2332ADE V S h ∆=⋅⋅=⋅⋅⋅=，故C 正确，故选D【举一反三】1.【2020·吉林吉林一中期中】等腰直角三角形BCD 与等边三角形ABD 中，90C ∠=︒，6BD =，现将ABD △沿BD 折起，则当直线AD 与平面BCD 所成角为45︒时，直线AC 与平面ABD 所成角的正弦值为（ ）A 3B ．22C 3D 23【解析】设E 为BD 中点，连接AE 、CE ，由题可知AE BD ⊥，CE BD ⊥，所以BD ⊥平面AEC ，过A 作AO CE ⊥于点O ，连接DO ，则AO ⊥平面BDC ，所以ADO ∠即为直线AD 与平面BCD 所成角的平面角，所以2sin 2AOADO AD∠==，可得32AO =AOE △中可得3OE =，又132OC BD ==，即点O 与点C 重合，此时有AC ⊥平面BCD ，过C 作CF AE ⊥与点F ，又BD AEC ⊥平面，所以BD CF ⊥，所以CF ⊥平面ABD ，从而角CAE ∠即为直线AC 与平面ABD 所成角，3sin 33CE CAE AE ∠===，故选A.2.【2020·四川双流中学月考】在边长为2的菱形ABCD 中，23BD =ABCD 沿对角线AC 对折，使二面角B AC D --的余弦值为13，则所得三棱锥A BCD -的外接球的表面积为（ ） A ．23π B ．2πC ．4πD ．6π【解析】如图，由题意易知ABC 与ADC 均为正三角形，取AC 中点N ，连接BN ，DN ，则BN AC ⊥，DN AC ⊥，∴BND ∠即为二面角B AC D --的平面角，过点B 作BO DN ⊥于O ，则BO ⊥平面ACD ，由3BN ND ==1cos 3BND ∠=可得3cos ON BN BND =⋅∠=，23OD =，2326333OB ⎛⎫=-= ⎪ ⎪⎝⎭，∴13ON ND =即点O 为ADC 的中心，∴三棱锥A BCD -的外接球球心在直线BO 上，设球心为1O ，半径为r ，∴11BO DO r ==，126OO r =-, ∴2222623r r ⎛⎫⎛⎫-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭解得6r =，∴三棱锥A BCD -的外接球的表面积为234462S r πππ==⨯=，故选D.类型二 截面问题【例3】 【2020山西运城一中月考】如图，在棱长为1的正方体1111ABCD A B C D -中，,,M P Q 分别是棱11A D ，,AB BC 的中点若经过点,,M P Q 的平面与平面11CDD C 的交线为l ，则l 与直线1QB 所成角的余弦值为（ ）A ．33B ．105C 5D ．32【解析】由线面平行的性质及面面平行的性质定理，可得经过点,,M P Q 2的正六边形MGPQFE ,连接1MB ,MQ ,如图所示，则易知若经过点,,M P Q 的平面与平面11CDD C 的交线为EF ,即为直线l ，又EF MQ ,所以1MQB ∠即为l 与直线1QB 所成角，在1MQB ∆中，可得1152QB MB ==，2MQ =,由余弦定理可得：22211115521044cos 25222QB MQ MB MQB QB MQ +-+-∠===⨯⨯⨯⨯,故选 B.【指点迷津】(1)要善于将空间问题转化为平面问题：这一步要求我们具备较强的空间想象能力，对几何体的结构特征要牢牢抓住，如求解与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径等.通过作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．这样才能进一步将空间问题转化为平面内的问题；(2)转化后如何算？因为已经是平面内的问题，那么方法就比较多了，如三角函数法、均值不等式、坐标法，甚至导数都是可以考虑使用的工具． 【举一反三】1.【2018年理新课标I 卷】已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为（ ） A.B.C.D.【解析】根据相互平行的直线与平面所成的角是相等的，所以在正方体中，平面与线所成的角是相等的，所以平面与正方体的每条棱所在的直线所成角都是相等的，同理平面也满足与正方体的每条棱所在的直线所成角都是相等，要求截面面积最大，则截面的位置为夹在两个面与中间的，且过棱的中点的正六边形，且边长为，所以其面积为，2.【2020·湖北随州一中期末】已知三棱锥S ABC -的所有顶点在球O 的球面上，SA ⊥平面ABC ，ABC 是等腰直角三角形，2SA AB AC ===，D 是BC 的中点，过点D 作球O 的截面，则截面面积的最小值是( ) A ．πB ．2πC ．3πD ．4π【解析】点D 是Rt ABC 的外心，过点D 作DO ⊥平面ABC 使112DOSA ==，O 是外接球球心，半径设为R ，则OA OS R ==，在直角梯形SADO 中，2SA =，1OD =，2AD =，得3R =，过点D 作球O 的截面，当OD ⊥截面时，截面面积最小，此时截面圆的半径为222R OD -=，∴截面面积的最小值是2π，故选B .类型三 角的计算问题【例4】【2020江西省临川一中月考】在长方体1111ABCD A B C D -中，二面角1D AB D --的大小为60︒，1DC 与平面ABCD 所成角的大小为30，那么异面直线1AD 与1DC 所成角的余弦值是（ ）A 2B 3C 2D 3 【解析】连接1AB ，由11//AB DC 可得11B AD ∠为异面直线1AD 与1DC 所成角，如图，由二面角1D AB D --的大小为60，可知1160,3D AD AD AA ∠=∴=，又1DC 与平面ABCD 所成角的大小为30，1111122,33DC CC AA DC CC AA ∴===，连接111,AB B D ，设133AD AA ==，则3AB a =，11112323,2,AD a AB a B D ∴==11AB D ∆中，由余弦定理可得，22211444333cos 2322a a a B AD a a+-∠==⨯⨯∴异面直线1AD 与1DC 3 B.【举一反三】1.【2017全国高考卷1】平面过正方体ABCD—A1B1C1D1的顶点A，，，则m，n所成角的正切值为（）A．B．C．D．【解析】如图，由正方体的性质可知为等边三角形，，，，由面面平行的性质，可得，，m，n所成角与相等，即m，n所成角为，则m，n所成角的正切值为.三．强化训练1.【2020黑龙江哈尔滨六中月考】如图，将两个全等等腰直角三角形拼成一个平行四边形ABCD，将平行四边形ABCD沿对角线BD折起，使平面ABD 平面BCD，则直线AC与BD所成角余弦值为（）A 22B6C3D．13【解析】由平面ABD ⊥平面BCD ，AB BD ⊥，平面ABD ⋂平面BCD BD =，AB平面ABD ，所以AB ⊥平面BCD ，又DC ⊂平面BCD ，所以AB DC ⊥，又DB DC ⊥，所以作z 轴//AB ,建立空间直角坐标系B xyz -，如图设1AB =，所以1,1,2BD DC BC ===()()()()0,1,1,0,1,0,1,0,0,0,0,0A B C D ，所以()()1,1,1,0,1,0AC BD =---，所以3cos ,3AC BD AC BD AC BD⋅===，故选C 2.【2020·广东深圳外国语月考】点D 是直角ABC ∆斜边AB 上一动点，3,4AC BC ==，将直角ABC ∆沿着CD 翻折，使'B DC ∆与ADC ∆构成直二面角，则翻折后'AB 的最小值是（ ） A 21 B 13C ．22D 7【答案】B【解析】过点B ′作B E CD '⊥于点E ，连接,BE AE ，如下图所示，设BCD B CD α∠=∠'=，则有4sin 4cos 2B E CE ACE πααα'==∠=-，，，在AEC ∆中，由余弦定理得，2222cos 2AE AC CE AC CE πα⎛⎫=+-⋅⋅- ⎪⎝⎭2916cos 24cos sin ααα=+-，在Rt AEB ∆'中，由勾股定理得，22222916cos 24cos sin 16sin AB AE B E αααα'+'+-+==2512sin 2α=-，∴当4πα=时，AB '13B ．3.【2020广西南宁三中月考】如图，在边长为1的正方体1111ABCD A B C D -中，,,E F H 分别是11,,AB BC C D 的中点．（1）作出过点,,E F H 与正方体1111ABCD A B C D -的截面；（不必说明画法和理由） （2）求点1C 到平面EFH 的距离． 【解析】（1）截面如图所示．（2）∵1//BC EH ，EH ⊂平面EFH ，∴1//BC 平面EFH ， 则点1C 到平面EFH 的距离等于点B 到平面EFH 的距离．在EFH △中，262,22EF HE HF ===， 所以222EF HF HE +=，所以EF HF ⊥，∴12632EFHS==． ∵B EFH H EBF V V --=，∴11133EFHEBFS h S CC =⋅，∴3148h ⋅=， ∴36h =1C 到平面EFH 3。