理论力学习题解答第八章

论力学课后习题答案-第8章--动量定理及其应用第8章 动量定理及其应用8－1 计算下列图示情况下系统的动量。

(1) 已知OA ＝AB ＝l ，θ＝45°，ω为常量，均质连杆AB 的质量为m ，而曲柄OA 和滑块B 的质量不计（图a ）。

(2) 质量均为m 的均质细杆AB 、BC 和均质圆盘CD 用铰链联结在一起并支承如图。

已知AB = BC = CD = 2R ，图示瞬时A 、B 、C 处于同一水平直线位置，而CD 铅直，AB 杆以角速度ω转动（图b ）。

(3) 图示小球M 质量为m 1，固结在长为l 、质量为m 2的均质细杆OM 上，杆的一端O 铰接在不计质量且以速度v 运动的小车上，杆OM 以角速度ω绕O 轴转动（图c ）。

解：（1）p = mv C =ωm l 25，方向同Cv （解图（a ））；（2）p = mv C 1 + mv C 2 = mv B = 2Rm ω，方向同Bv ，垂直AC （解图（b ））； （3）j i p )60sin 260sin ()]60cos 2()60cos ([2121︒+︒+︒-+︒-=ωωωωlm l m l v m l v m j i 423]42)[(212121m m l l m m v m m +++-+=ωω（解图（c ））。

习题8-1图ABOθω ABCDωOMvω 60˚(a)(b)(c)8－2 图示机构中，已知均质杆AB 质量为m ，长为l ；均质杆BC 质量为4m ，长为2l 。

图示瞬时AB 杆的角速度为ω，求此时系统的动量。

解：杆BC 瞬时平移，其速度为v Bωωωm l m l l m p p p BCAB 2942=+=+= 方向同v B 。

8－3 两均质杆AC 和BC 的质量分别为m 1和m 2，在C 点用铰链连接，两杆立于铅垂平面内，如图所示。

设地面光滑，两杆在图示位置无初速倒向地面。

问：当m 1= m 2和m 1= 2m 2时，点C 的运动轨迹是否相同。

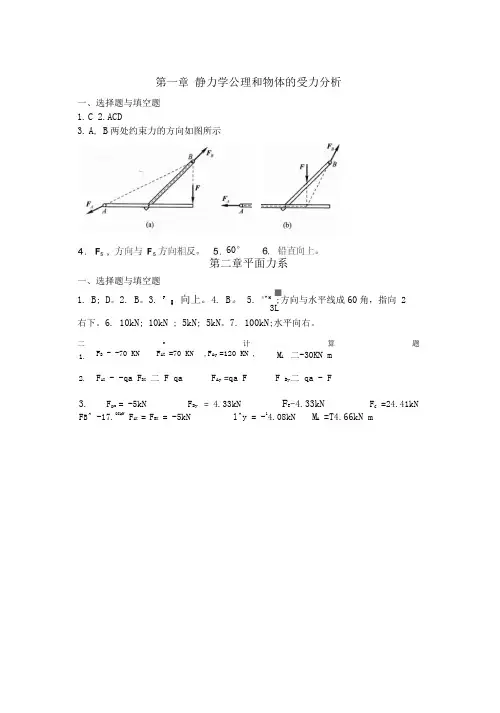
第一章静力学公理和物体的受力分析一、选择题与填空题1.C2.ACD3.A, B两处约束力的方向如图所示60°第二章平面力系一、选择题与填空题■1. B; D。

2. B。

3. F；向上。

4. B。

5. 4^M;方向与水平线成60角，指向 23L右下。

6. 10kN; 10kN ; 5kN; 5kN。

7. 100kN;水平向右。

二•计算题1. F B - -70 KN F AX =70 KN ,F Ay =120 KN , M A二-30KN m2. F AX - -qa F BX二 F qa F Ay =qa F F By 二 qa - F3. F= -5kN F Dy = 4.33kN F E-4.33kN F C =24.41kND xF B^ -17.08kN F AX=F BX = -5kN l^y = -14.08kN M A=T4.66kN mF AX =10N FAy =20N M A =15N mF CD =14.1N6F Ax=2.5kN F Ay=—2.16kN M A=」kN ，m F c =20.33kN7 F B=40kNF AX = —10kNFA ^-20kN M -50kN m F cx = 40kNF ey = 0F HX =300N F Hy =100N第三章空间力系少2(-8. F A ^ = -100N F Ay 二-300N F Ex 二-300N F Ey =100N F °y 二 200N整=一一A > X Y m 一：J E £c X一、选择题与填空题f—- - Fa 6 Fa 1.B。

2.B。

3. M x(F)=O ; M y(F) —H2 44.F x=-40.2N; F y=30-2N; M z=240.2 N m。

5.F z= F sin :；F y= F cos ：cos :;M x(F)二 F(ccos'cos ： bsin )。

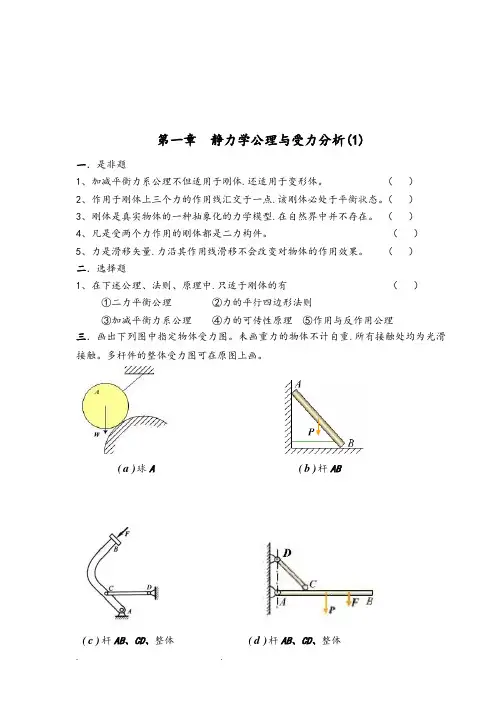
第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体.还适用于变形体。

（）2、作用于刚体上三个力的作用线汇交于一点.该刚体必处于平衡状态。

（）3、刚体是真实物体的一种抽象化的力学模型.在自然界中并不存在。

（）4、凡是受两个力作用的刚体都是二力构件。

（）5、力是滑移矢量.力沿其作用线滑移不会改变对物体的作用效果。

（）二．选择题1、在下述公理、法则、原理中.只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。

未画重力的物体不计自重.所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

b(杆ABa(球A ))d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受力图。

未画重力的物体不计自重.所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析（2）一．画出下列图中指定物体受力图。

未画重力的物体不计自重.所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F= - F’.所以力偶的合力等于零。

（）2、用解析法求平面汇交力系的合力时.若选用不同的直角坐标系.则所求得的合力不同。

（）3、力偶矩就是力偶。

（）二．电动机重P=500N.放在水平梁AC的中央.如图所示。

8-1 8-2 8-7 8-6、8、98-15、16、17、208-1 图示四杆机构1OABO 中，ABB O OA211==；曲柄OA 的角速度srad /3=ω。

求当090=ϕ而曲柄B O 1重合于1OO 的延长线上时，杆AB和曲柄B O 1的角速度。

)/1(2.5),/1(31s s B O AB ==ωω参考答案：OA 杆和O1B 杆为定轴转动，AB 杆为平面运动(瞬心在O 点)。

OA OA v A 3=⋅=ω； 由瞬心法知：s rad OAv A AB 3===ωω（逆时针）根据速度投影定理： 60cos 30cos ⋅=⋅B A v v 故：OA v v A B 333=⋅=；s rad s rad BO OA BO v B BO 196.53333111====ω（逆时针）8-2 四连杆机构中，连杆AB 上固联一块三角板 ABD 。

机构由曲柄A O 1带动。

已知：曲柄的角速度s rad A O /21=ω；曲柄cm A O 101=，水平距离cm O O 521=；AD=5cm ,当A O 1铅垂时，AB平行于21O O ，且AD 与1AO 在同一直线上；角030=ϕ。

求三角板ABD 的角速度和D 点的速度。

s cm v s D ABD /35.25),/1(07.1==ω参考答案：O1A 杆和O2B 杆为定轴转动，ABD 三角板为平面运动(瞬心在C 点)。

由O1A 杆作定轴转动：s cm A O v A O A /2011=⋅=ω，方向水平向左，如图。

由O2B 杆作定轴转动，B v 方向如图。

故三角板ABD 的速度瞬心在图示C 点。

则：s rad CO A O v ACv AA ABD /0718.135102011=+=+==ωs rad CD CD v ABD ABD D /359.25=⋅=⋅=ωω（方向水平向左，如图）8-7 如图所示，在振动机构中，筛子的摆动由曲柄连杆机构所带动。

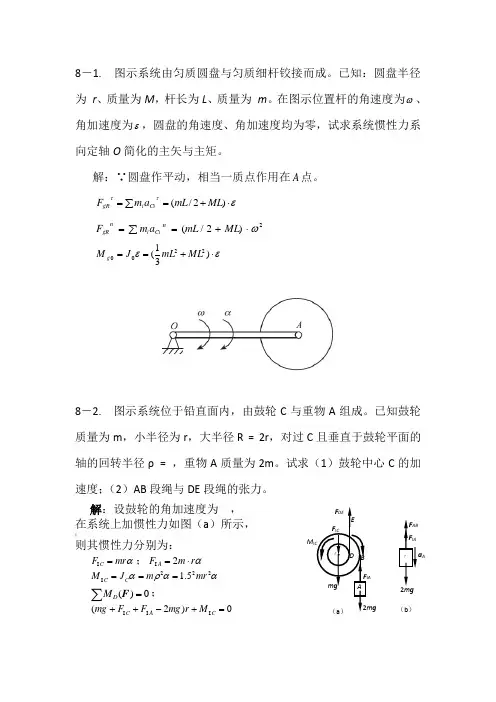
8－1. 图示系统由匀质圆盘与匀质细杆铰接而成。

已知：圆盘半径为 r 、质量为M ，杆长为L 、质量为 m 。

在图示位置杆的角速度为ω、角加速度为ε，圆盘的角速度、角加速度均为零，试求系统惯性力系向定轴O 简化的主矢与主矩。

解：∵圆盘作平动，相当一质点作用在A 点。

εττ⋅+==∑)2/(ML mL a m F Ci i gR 2)2/(ω⋅+==∑ML mL a m F n Ci i ngR εε⋅+==)31(2200ML mL J M g8－2. 图示系统位于铅直面内，由鼓轮C 与重物A 组成。

已知鼓轮质量为m ，小半径为r ，大半径R = 2r ，对过C 且垂直于鼓轮平面的轴的回转半径ρ = ，重物A 质量为2m 。

试求（1）鼓轮中心C 的加速度；（2）AB 段绳与DE 段绳的张力。

解：设鼓轮的角加速度为， 在系统上加惯性力如图（a ）所示， |则其惯性力分别为：αmr F C =I ；αr m F A ⋅=2I ααρα222I 5.1mr m J M C C === ∑=0)(F D M ；0)2(I I I =+-++C A C M r mg F F mg？AM I CF I Cm g F DE （a ）A B 《D E2gF A F I A F AB （b ）g g r a C 2145.132=+==α ∑=0y F ；02I I =--+-mg mg F F F A C DE ；mg mr mg F DE 21593=-=α 取重物A 为研究对象，受力如图（b ）所示，∑=0y F ；02I =-+mg F F A AB ；mg mg mr mg F AB 2134)2141(222=-=-=α：8－3. 11－15重力的大小为100N 的平板置于水平面上，其间的摩擦因数f = ，板上有一重力的大小为300N ，半径为20cm 的均质圆柱。

圆柱与板之间无相对滑动，滚动摩阻可略去不计。

第八章习题解答8-1匀质杆AB 长l ，重G ，沿光滑的圆弧轨道运动如图示。

设当OA 在水平位置时，3arcisn =θ，125gl v A =，求此时轨道对于杆AB 的约束力。

题8－1图解：以杆AB 为研究对象，受力分析A F N 、B F N、G 如图示，杆AB 作定轴转动。

∵53arcsin =θ 53sin =∴θ 54cos =θ 25242sin =θ 2572cos =θ ∵ l R 85=、125gl v A = l g R v A 1516==∴ω l OC 83=AB 杆的质心加速度为OC a ⋅=21ω，OC a ⋅=α2 惯性力主矢*F和主矩*M 方向如图所示，大小为mg l l g m a m F 528315161*1=⋅⋅=⋅=l m a m F 832*2⋅⋅=⋅=ααα222*19243])83(121[ml l m ml M =+=题8－1答案图列平衡方程式∑=0)(F m zO 01924353832=−⋅⋅αml l mg l g 215216=α 0=∑ixF 0sin cos 2cos N *1*2N =−++⋅A B F F F F θθθ 0=∑iyF0cos sin 2sin *1*2N =−−+⋅mg F F F B θθθ mg l g ml F 2158121521683*2=⋅=代入上式得：mg F B4349N =，mg F A 4337N =8-2 匀质杆AB 长l ，重G ，用两根软绳悬挂如图示。

求当其中一根软绳切断，杆AB 开始运动时，另一根软绳中的拉力。

题8－2图解：建立参考基e C−，连体基1e O −和2e B −设当AO 被切断时，BO 的角加速度为1α，AB 杆的角加速度为2α题8－2答案图以杆AB 为研究对象，受力分析如图示重力G ，绳中张力T F 。

杆AB 作平面运动，惯性力主矢*F 和主矩*M 方向如图所示，大小为：C ma F =*，2*αC J M =e C e C e tC C a a a a αω222 ++= ， 02=eC a ω e B e B e tC a a a αω112 +=, 01=e B a ω , B e B a a=α1 e C e B C a a a αα21 +=, eC e B C a m a m a m αα21 += 11*122ααl m ma F e B ==∴ 22*22ααl m ma F e C == 22*121αml M =0)(=∑F m Dz0121442222=+⋅−⋅ααml lmg l ml lg 562=α0)(=∑F m Cz012122222T =−⋅⋅αml l Fmg F 52T =8-3 匀质杆AB 长2l ，重G ，一端A 用长l 的软绳OA 拉住，一端B 放在光滑地面上如图示。

第8章 刚体平面运动概述和运动分解三、选择题1．( D )2． ( B )。

3． ( B )4． ( D )5．( C )6． ( C )7．( C )。

8． ( B )。

四、计算题8-1 如图8.30所示的两齿条以1v 和2v 同方向运动。

在两齿条间夹一齿轮，其半径为r ，求齿轮的角速度及其中心O 的速度。

解：齿轮作平面运动，以B 为基点，分析A 点的速度。

由AB B A v v v +=作A 点的速度合成图如图所示。

由图可知21v v v v v B A AB -=-= 齿轮的角速度为rv v ABv AB O 221-==ω再以B 为基点，分析O 点的速度。

由OB B O v v v +=作O 点的速度合成图如图所示。

由图可知齿轮中心O 的速度2212v v r v v v v O OB B O +=+=+=ω8-2 曲柄OA = 17cm ，绕定轴O 转动的角速度1rads O A /ω=，已知AB = 12cm ，BD = 44cm ，BC = 15cm ，滑块C 、D 分别沿着铅垂与水平滑道运动，如图8.31所示瞬时OA 铅垂，求滑块C 与D 的速度。

图8.30 图8.31解：由A v 和D v 的速度方向，可知杆BD 作瞬时平动。

从而可知B v 方向水平向左。

C 点的速度方向垂直向下。

BD 作瞬时平动，可知滑块D 的速度为 )/(17171s cm OA v v OA A D =⨯=⋅==ω 杆BC 作平面运动，上速度投影定理，有)90cos(cos o ϕϕ-=C B v v根据图示的结构，经过数学计算，可知6778.040157cos ==ϕ，7352.0sin =ϕ，代入上式，可得)/(6.15sin cos sin cos s cm v v v A B C ===ϕϕϕϕ8-3 曲柄OA 绕定轴O 转动的角速度25rad s O A ./ω=，OA = 28cm ，AB = 75cm ，BC = 15cm ，r = 10cm ，轮子沿水平面滚动而不滑动。

理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

如曲柄OA 以匀角加速度a 绕O 轴转动，且当运动开始时，角速度00=w ，转角0=j 。

求动齿轮以中心Ａ为基点的平面运动方程。

解：图示，A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2，故有 ∠CAC 2=r R /j ，所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ，N 用铰C 连结，作平面平行运动。

已知AC=BC=600mm ，在题附图所示位置s mm v s mm v B A /100,/200==，方向如图所示。

试求C 点的速度。

解：由速度投影定理得()()0==BC C BC B v v 。

则v C 必垂直于BC 连线，v C 与AC 连线的夹角为30°。

由()()AC A AC C v v = 即得：s mm v v A C /200== ，方向如题4-6附图示。

解毕。

8-9 图所示为一曲柄机构，曲柄OA 可绕O 轴转动，带动杆AC 在套管B 内滑动，套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。

已知：OA ＝BD ＝300mm ，OB ＝400mm ，当OA 转至铅直位置时，其角速度ωo ＝2rad/s ，试求D 点的速度。

C 12Aj C解 (1)平面运动方法： 由题可知：BD AC w w =确定AC 杆平面运动的速度瞬心。

套筒中AC 杆上一点速度沿套筒(为什么？)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析？关键求AC 杆角加速度(=BD 杆角速度) 基点法，分析AC 杆上在套筒内的点(B’)：(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小：× ∠ ∠ × 方位：× ∠ ∠ ∠ 再利用合成运动方法：动点：套筒内AC 杆上的点B’，动系：套筒。

【关键字】活动、情况、方法、条件、动力、空间、质量、地方、问题、系统、密切、主动、整体、平衡、保持、提升、合力、规律、位置、支撑、作用、结构、水平、速度、关系、分析、简化、倾斜、满足、带动、支持、方向、推动、推进、中心第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体，还适用于变形体。

（）2、作用于刚体上三个力的作用线汇交于一点，该刚体必处于平衡状态。

（）3、刚体是真实物体的一种抽象化的力学模型，在自然界中并不存在。

（）4、凡是受两个力作用的刚体都是二力构件。

（）5、力是滑移矢量，力沿其作用线滑移不会改变对物体的作用效果。

（）二．选择题1、在下述公理、法则、原理中，只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

a(球A )b(杆AB)d(杆AB、CD、整体)c(杆AB、CD、整体)f(杆AC、CD、整体)e(杆AC、CB、整体)四．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

a(球A、球B、整体)b(杆BC、杆AC、整体)第一章 静力学公理与受力分析（2）一．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体 )c (杆AB 、CD 、整体)d (杆BC 带铰、杆AC 、整体 )e (杆CE 、AH 、整体)f (杆AD 、杆DB 、整体 )g (杆AB 带轮及较A 、整体)h (杆AB 、AC 、AD 、整体 第二章 平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F = - F ’，所以力偶的合力等于零。

（ ）2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。

理论力学第8章习题解答第八章质点系动力学：矢量方法习题解答8-1 一个质量为5 kg 弹头M 以水平速度v = 60 m/s 飞行，在D 处爆炸成位于同一水平面内如图示速度方向的两块碎片A 和B 。

已知碎片A 的速度大小v A = 90 m/s 。

试求：(1) 碎片A 的质量m A ；(2) 碎片B 的速度大小v B 。

解：取弹头M 为研究对象，弹头爆炸前后动量守恒 () 30cos B A v m M Mv -= () 30sin 0B A A A v m M v m --=解得M v vm A A 33=，AA B v v vv v 32--=，代入数据得：kg 92.1=A m ，m/s 64.112=B v .8-2 一个质量为m 1的人手里拿着质量为m 2的物体，以仰角θ，速度v 0向前跳起。

当他到达最高点时将物体以相对速度u 水平地向后抛出。

如果不计空气阻力，问由于物体的抛出，跳远距离增加了多少？解：取m 1和m 2物体系统为研究对象，人跳至最高点时只有水平速度 ?c o s 01v v =，所费时间 gv t ?sin 0=。

抛物前后系统水平动量守恒，即 ()()u v m v m v m m -+=+1211021c o s ?，式中1v 为抛物后人的速度。

解得21201c o s m m um v v ++=?，可见，人的速度增量为2121Δm m um v +=，从而跳远距离增加()gm m uv m v t s 21021sin ΔΔ+==?.8-3质量为m 1的平台AB 放在水平面上，平台与水平面间的滑动摩擦因数为f 。

质量为m 2的小车D 由绞车拖动，相对平台的运动规律为221bt s =，其中b 为已知常数。

不计绞车质量，求平台的加速度。

解：1）设平台与水平面间的滑动摩擦因数比较小，当小车D 相对平台运动时，平台AB 的有速度1v （向左），小车D 的相对速度bt sv == r ，（向右），小车D 的绝对速度bt v v v v +-=+-=1r e a ，（向右），滑动摩擦力为 N fF F = 题8-3图题8-3受力图题8-1图由动量定理，()[]F v bt m v m t=-+-1211d d()021=++-N F g m m解得()212121m m g m m f b m a ++-=， ()g m m bm f 212+≤.当()gm m bm f 212+>时，01=a .8-4 质量为m 1的矩形板可在如图所示的光滑水平面上运动。