1.1.1正弦定理2解的个数

第一章 1.1.1正弦定理（2）学习目标：加深对正弦定理的理解，熟练掌握正弦定理的应用。

1．正弦定理有哪几种变形？问题探究：探究问题（一）画图判断三角形的解的个数 （1）已知 △ABC 中，A= 30°，a=1，b=2，则 （ ） A 、有一解 B 、有两解 C 、无解 D 、不能确定 （2）已知△ABC 中,A=30°, a= 2，b=2，则 （ ）A 、有一解B 、有两解C 、无解D 、不能确定（3）已知 △ABC 中,A=30°, a= 21，b=2，则 （ ）A 、有一解B 、有两解C 、无解D 、不能确定总结：已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?探究问题（一）已知a, b 和A, 用正弦定理求B 时的各种情况: （1）若A 为锐角时:⎪⎪⎩⎪⎪⎨⎧≥<<=<)( b a ) ,(b a bsinA )( bsinAasin 锐角一解一钝一锐二解直角一解无解A b a已知边a,b 和∠A有两个解仅有一个解无解CH=bsinA<a<b a=CH=bsinA a<CH=bsinA（2）若A 为直角或钝角时:⎩⎨⎧>≤)( b a 锐角一解无解b a说明：已知两边及其中一边的对角判断三角形解的个数的方法：①应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数；②在△ABC 中，已知a ，b 和A ，以点C 为圆心，以边长a 为半径画弧，此弧与除去顶点A 的射线AB 的公共点的个数即为三角形的个数。

练习.画图判断满足下列条件的三角形的个数:(1)b=11, a=20, B=30o (2)c=54, b=39, C=120o (3)b=26, c=15, C=30o (4)a=2,b=6,A=30o探究问题（二） 利用正弦定理证明两个结论： 1、三角形内角平分线定理的证明：已知：如图，在ΔABC 中，∠A 的平分线AD 与边BC 相交于点D ，求证：BD ABDC AC=证明：如图在ΔABD 和ΔCAD 中，由正弦定理，得sin sin BD AB βα=，0sin sin(180)sin DC AC ACβαα==-，两式相除得BD ABDC AC = 三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比。

1.1.1 正弦定理(二)【学习目标】1．能应用正弦定理解三角形；2．掌握三角形面积公式；3．能利用条件判断三角形解的个数【重点难点】正弦定理及其应用；解三角形中知两边一对角型中解的判断.【知识梳理】1．正弦定理：a sin A ＝b sin B ＝c sin C＝2R 的常见变形： (1)sin A ∶sin B ∶sin C ＝a ∶b ∶c ；(2)a sin A ＝b sin B ＝c sin C ＝a ＋b ＋c sin A ＋sin B ＋sin C＝2R ； (3)a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ；(4)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R. 2．正弦定理的应用 从理论上正弦定理可解决两类问题：（1）两角和任意一边，求其它两边和一角；（2）两边和其中一边对角，求另一边的对角，进而可求其它的边和角 3．三角形面积公式：S ＝12ab sin C ＝12bc sin A ＝12acsin B . 4．ABC ∆中，已知,a b 及锐角A ，则a 、b 、sin A 满足什么关系时，三角形无解，有一解，有两解？⑴若A 为锐角时:⎪⎪⎩⎪⎪⎨⎧≥<<=<)( b a ),( b a bsinA )( bsinA a sin 锐角一解一钝一锐二解直角一解无解A b a ⑵若A 为直角或钝角时:⎩⎨⎧>≤)( b a 锐角一解无解b a【课内练习】1、已知△ABC 的面积为23，且3,2==c b ，则∠A 等于 （ ） A ．30° B ．30°或150° C ．60°D ．60°或120° 2．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知A ＝60°，a ＝3， b ＝1，则c ＝________.3．（1）在C A a c B b ABC ,,1,60,30和求中，===∆；（2）在C B b a A c ABC ,,2,45,60和求中，===∆.4．在△ABC 中，a ，b ，c 分别是三个内角A ，B ，C 的对边，若a ＝2，C ＝π4， cos B 2＝255，求△ABC 的面积S .【课外练习】1．△ABC 中,∠A、∠B 的对边分别为a ,b ，且∠A=60°,4,6==b a ,那么满足条件的△ABC（ ）A ．有一个解B ．有两个解C ．无解D ．不能确定2．已知三角形面积为14，外接圆面积为π，则这个三角形的三边之积为( ) A ．1 B ．2C. 12D ．4 3．在△ABC 中，已知a ＝32，cos C ＝13，S △ABC ＝43，则b ＝________. 4．（1）在ABC △中，3,6,30a c A ===o ，求ABC △的面积S .（2）在ABC △中，4,30,45a B C ===o o，求ABC △的外接圆半径R 和面积S .。

1.1.1正弦定理(二)学习目标 1.熟记并能应用正弦定理的有关变形公式解决三角形中的问题(重点)；2.能根据条件，判断三角形解的个数(难点)；3.能利用正弦定理、三角恒等变换解决较为复杂的三角形问题(难点).知识点1对三角形解的个数的判断已知三角形的两角和任意一边，求另两边和另一角，此时有唯一解，三角形被唯一确定.已知两边和其中一边的对角，求其他的边和角，此时可能出现一解、两解或无解的情况，三角形不能被唯一确定，现以已知a，b和A解三角形为例，从两个角度予以说明：(1)代数角度由正弦定理得sin B ＝b sin A a，①若b sin Aa＞1，则满足条件的三角形个数为0，即无解.②若b sin Aa＝1，则满足条件的三角形个数为1，即一解.③若b sin Aa＜1，则满足条件的三角形个数为1或2.(2)几何角度图形关系式解的个数A为锐角①a＝b sin A；②a≥b一解b sin A＜a＜b 两解a＜b sin A 无解A 为 钝角 或直 角a ＞b 一解a ≤b 无解【预习评价】1.已知三角形的两边及其中一边的对角往往得出不同情形的解，有时需舍去一解，有时又不能舍.那么我们怎么把握舍不舍的问题？提示 例如在△ABC 中，已知a ，b 及A 的值.由正弦定理a sin A ＝bsin B ，可求得sin B ＝b sin Aa .在由sin B 求B 时，如果a ＞b ，则有A ＞B ，所以B 为锐角，此时B的值唯一；如果a ＜b ，则有A ＜B ，所以B 为锐角或钝角，此时B 的值有两个. 2.已知三角形的两边及其夹角，为什么不必考虑解的个数？提示 如果两个三角形有两边及其夹角分别相等，则这两个三角形全等.即三角形的两边及其夹角确定时，三角形的六个元素即可完全确定，故不必考虑解的个数的问题.知识点2 三角形面积公式 任意三角形的面积公式为：(1)S △ABC ＝12bc sin__A ＝12ac sin__B ＝12ab sin__C ，即任意三角形的面积等于任意两边与它们夹角的正弦的乘积的一半.(2)S △ABC ＝12ah ，其中a 为△ABC 的一边长，而h 为该边上的高的长.(3)S △ABC ＝12r (a ＋b ＋c )＝12rl ，其中r ，l 分别为△ABC 的内切圆半径及△ABC 的周长.(4)S △ABC ＝p （p －a ）（p －b ）（p －c ）⎝ ⎛⎭⎪⎫其中p ＝a ＋b ＋c 2. 【预习评价】1.在△ABC 中，若B ＝30°，a ＝2，c ＝4，则△ABC 的面积为________.2.在△ABC 中，若B ＝30°，AB ＝23，AC ＝2，则△ABC 的面积是________.题型一 三角形解的个数的判断【例1】 已知下列各三角形中的两边及其一边的对角，判断三角形是否有解，有解的作出解答.(1)a ＝10，b ＝20，A ＝80°； (2)a ＝23，b ＝6，A ＝30°.规律方法 判断三角形解的情况：先判断角，若有一个为钝角，则有一解或无解；若无钝角，则有一解、两解或无解，然后再由大边对大角来具体判断解的情况.【训练1】 根据下列条件，判断三角形是否有解，若有解，有几个解： (1)a ＝3，b ＝2，A ＝120°； (2)a ＝60，b ＝48，B ＝60°； (3)a ＝7，b ＝5，A ＝80°； (4)a ＝14，b ＝16，A ＝45°.题型二 判断三角形形状问题【例2】 在△ABC 中，若sin A ＝2sin B cos C ，且sin 2A ＝sin 2B ＋sin 2C ，试判断△ABC 的形状.规律方法 判断三角形形状的常用方法有：(1)化边为角.将题目中的条件，利用正弦定理化边为角⎝ ⎛⎭⎪⎫若sin 2A ＝sin 2B ，则A ＝B 或A ＋B ＝π2，再根据三角函数的有关知识得到三个内角的关系，进而确定三角形的形状；(2)化角为边.将题目中的所有条件，利用正弦定理化角为边，再根据代数恒等变换得到边的关系(如a ＝b ，a 2＋b 2＝c 2)，进而确定三角形的形状.【训练2】在△ABC中，已知3b＝23a sin B，且cos B＝cos C，角A是锐角，则△ABC的形状是()A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形方向1 三角函数式的化简、证明及求值【例3－1】如图所示，D是Rt△ABC的斜边BC上一点，AB＝AD，记∠CAD＝α，∠ABC ＝β.(1)求证：sin α＋cos 2β＝0；(2)若AC＝3DC，求β的值.规律方法在三角形中，进行三角函数式的化简、证明或求值时，一要注意边角互化，二要注意三角函数公式的灵活应用，特别是三角恒等式变形的技巧.方向2 与三角形面积有关的问题【例3－2】在△ABC中，∠A＝60°，c＝3 7a.(1)求sin C的值；(2)若a＝7，求△ABC的面积．方向3 求范围或最值【例3－3】在锐角△ABC中，角A，B，C分别对应边a，b，c，且a＝2b sin A，求cos A＋sin C的取值范围.规律方法 三角函数、三角恒等变换与解三角形的综合问题是近几年高考的热点，在高考试题中频繁出现.解决此类问题，要根据已知条件，灵活运用正弦定理，能够对边角关系进行互相转化.课堂达标1.△ABC 满足下列条件：①b ＝3，c ＝4，B ＝30°；②a ＝5，b ＝8，A ＝30°；③c ＝6，b ＝33，B ＝60°；④c ＝9，b ＝12，C ＝60°.其中有两个解的是( ) A.①② B.①④ C.①②③ D.③④2.在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若a ＝1，b ＝3，B ＝60°，则△ABC 的面积为( ) A.12 B.32 C.1 D. 33．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .若△ABC 为锐角三角形，且满足sin B (1＋2cos C )＝2sin A cos C ＋cos A sin C ，则下列等式成立的是( ) A ．a ＝2b B ．b ＝2a C ．A ＝2BD ．B ＝2A4.在△ABC 中，lg(sin A ＋sin C )＝2lg sin B －lg(sin C －sin A )，则此三角形的形状是________.5.在△ABC 中，求证：a －c cos B b －c cos A ＝sin Bsin A.课堂小结1.已知两边和其中一边的对角，求第三边和其他两个角，这时三角形解的情况：可能无解，也可能一解或两解.首先求出另一边的对角的正弦值，当正弦值大于1或小于0时，这时三角形解的情况为无解；当正弦值大于0小于1时，再根据已知的两边的大小情况来确定该角有一个值或者两个值.2.判断三角形的形状，最终目的是判断三角形是不是特殊三角形，当所给条件含有边和角时，应利用正弦定理将条件统一为“边”之间的关系式或“角”之间的关系式.3.结合正弦定理，同时注意三角形内角和定理及三角形面积公式、三角恒等变换等知识进行综合应用.基础过关1.在锐角△ABC 中，角A ，B 所对的边长分别为a ，b .若2a sin B ＝3b ，则角A 等于( ) A.π12 B.π6 C.π4 D.π32.在△ABC 中，A ＝60°，a ＝6，b ＝4，则满足条件的△ABC ( ) A.有一个解 B.有两个解 C.无解 D.不能确定3.在△ABC 中，a cos B ＝bcos A，则△ABC 一定是( ) A.等腰三角形 B.直角三角形 C.等腰直角三角形D.等腰三角形或直角三角形4.已知c＝50，b＝72，C＝135°，则三角形解的个数为________.5.在△ABC中，角A，B，C所对的边分别为a，b，c.若a cos A＝b sin B，则sin A cos A＋cos2B＝________.6.在△ABC中，a，b，c分别是角A，B，C的对边，若tan A＝3，cos C＝5 5，(1)求角B的大小；(2)若c＝4，求△ABC的面积.7.在△ABC中，求证：a2－b2c2＝sin（A－B）sin C.能力提升8.已知方程x2－(b cos A)x＋a cos B＝0的两根之积等于两根之和，且A，B为△ABC 的两内角，a，b为角A，B的对边，则此三角形为()A.等腰直角三角形B.等边三角形C.等腰三角形D.直角三角形9.在△ABC中，∠BAC＝120°，AD为角A的平分线，AC＝3，AB＝6，则AD等于()A.2B.2或4C.1或2D.510.在△ABC中，A＝π3，BC＝3，则△ABC的周长为________(用B表示).11.在△ABC中，C＝90°，M是BC的中点，若sin∠BAM＝13，则sin∠BAC＝________.12.在△ABC中，已知c＝10，cos Acos B＝ba＝43，求a、b及△ABC的内切圆半径.创新突破13.在△ABC中，角A，B，C所对的边分别为a，b，c，已知m＝(2b－3c，cosC)，n＝(3a，cos A)，且m∥n.(1)求角A的大小；(2)求2cos2B＋sin(A－2B)的最小值.。

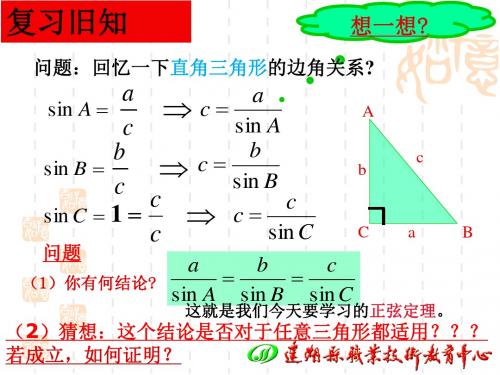
第一章 解三角形1.1 正弦定理和余弦定理1.1.1 正弦定理1．正弦定理在ABC △中，若角A ，B ，C 对应的三边分别是a ，b ，c ，则各边和它所对角的正弦的比相等，即____________．正弦定理对任意三角形都成立．2．解三角形一般地，把三角形的三个角A ，B ，C 和它们的对边a ，b ，c 叫做三角形的____________．已知三角形的几个元素求其他元素的过程叫做____________．K 知识参考答案：1．sin sin sin a b c ==A B C2．元素 解三角形K —重点 正弦定理的变形和推广、正弦定理在解三角形中的应用 K —难点 三角形解的个数的探究、三角形形状的判断K —易错 解三角形时要明确角的取值范围，同时注意对角的讨论正弦定理的常见变形及推广（1）sin sin sin ,,,sin sin ,sin sin ,sin sin sin sin sin A a C c B ba Bb A a Cc A b C c B B b A a C c ======． （2）sin sin sin sin sin sin sin sin sin sin sin sin a b c a b a c b c a b cA B C A B A C B C A B C+++++======+++++． （3）::sin :sin :sin a b c A B C =． （4）正弦定理的推广：2sin sin sin a b cR A B C===，其中R 为ABC △外接圆的半径． （1）已知△ABC 中，sin :sin :sin =1:2:3A B C ，则a:b:c =_____________；（2）已知△ABC 中，∠A =60︒，3a ，则++sin +sin +sin a b cA B C=_____________．【答案】（1）1:2:3；（2）2．【解析】（1）根据正弦定理的变形，可得=sin :sin :sin =1:2:3a:b:c A B C ． （2）方法1：设=sin sin a b A B ==(>0)sin ck k C，则有sin sin sin a k Ab k Bc k C ===，，， 从而sin sin sin sin sin sin sin sin sin a b c k A k B k C k A B C A B C ++++++++==，又32sin sin60a k A ===︒，所以sin sin sin a b c A B C ++++=2． 方法2：根据正弦定理的变形，可得2sin sin sin sin a b c aA B C A++++==．【名师点睛】熟记正弦定理的变形，可使解题过程更加简捷，从而达到事半功倍的效果．在ABC △中，求证：22sin 2sin 22sin a B b A ab C +=．【答案】证明见解析．【解析】设ABC △外接圆的半径为R ，则2sin ,2sin ,a R A b R B == 于是222222sin 2sin 2(2sin )sin 2(2sin )sin 28sin sin (sin cos cos sin )8sin sin sin 22sin 2sin sin 2sin ,a Bb A R A B R B A R A B A B A B R A B CR A R B C ab C +=+=+==⋅⋅⋅=所以22sin 2sin 22sin a B b A ab C +=． 【解题技巧】===2sin sin sin a b c R A B C的两种变形的应用： （1）（边化角）2sin ,2sin ,2sin a R A b R B c R C ===； （2）（角化边）sin ,sin ,sin 222a b cA B C R R R===． 正弦定理在解三角形中的应用、三角形解的个数的探究1．正弦定理可以用来解决下列两类解三角形的问题：（1）已知两角和任意一边，求其他的边和角； （2）已知两边和其中一边的对角，求其他的边和角． 2．三角形解的个数的探究（以已知a b ，和A 解三角形为例） （1）从代数角度来看①若sin sin 1b AB=a >，则满足条件的三角形的个数为0，即无解； ②若sin sin 1b AB=a=，则满足条件的三角形的个数为1；③若sin sin 1b AB=a<，则满足条件的三角形的个数为1或2． 注：对于（3），由sin 0sin 1b AB=a<<可知B 可能为锐角，也可能为钝角，此时应由“大边对大角”、“三角形内角和等于180°”等进行讨论． （2）从几何角度来看①当A 为锐角时：一解一解 两解 无解②当A 为钝角或直角时：一解 一解 无解 无解（1）已知在ABC △中，10,45,30c A C ==︒=︒，则a =_______，b =_______，B =_______；（2）已知在ABC △中，3,60,1b B c ==︒=，则a =_______，A =_______，C =_______； （3）已知在ABC △中，6,45,2c A a ==︒=，求b 和,B C ．【答案】（1）102，5652+，105︒；（2）2，90︒，30︒；（3）见解析． 【解析】（1）10,45,30180()105c A C B A C ==︒=︒∴=︒-+=︒，，由sin sin a c A C =，得sin 10sin 45102sin sin 30c A a C ⨯︒===︒， 由sin sin b c B C =，得sin 10sin10562205652sin sin 304c B b C ⨯︒+===⨯=+︒．（2）∵sin 1sin 601,sin sin sin 23b c c B C B C b ⨯︒=∴===， ,60,b c B C B >=︒∴<，C 为锐角，30,90C A ∴=︒=︒，∴222=+=c b a ．（3）sin 6sin 453,sin sin sin 22a c c A C A C a ⨯︒=∴===， sin ,60c A a c C <<∴=︒或120︒，∴当60C =︒时，sin 6sin 7575,31sin sin 60c B B b C︒=︒===+︒，当120C =︒时，sin 6sin1515,31sin sin 60c B B b C ︒=︒===-︒． 31,75,60b B C ∴=+=︒=︒或31,15,120b B C =-=︒=︒．【解题技巧】（1）已知三角形的两角与一边解三角形时，由三角形内角和定理可以计算出三角形的另一角，由正弦定理可计算出三角形的另两边．（2）已知两边和其中一边的对角解三角形时，先用正弦定理求出另一边所对的角的正弦值，若这个角不是直角，则利用三角形中“大边对大角”看能否判断所求这个角是锐角，①当已知的角为大边所对的角时，则能判断另一边所对的角为锐角；②当已知的角为小边所对的角时，则不能判断，此时就有两解，再分别求解即可；③然后由三角形内角和定理求出第三个角；④最后根据正弦定理求出第三条边．三角形形状的判断判断三角形形状的常用方法——边化角，已知条件中同时包含边角关系，判断三角形形状时，将边化为角，从三角变换的角度来研究角的关系和特征，进而判断三角形的形状．一般来说，这种方法能够判断的三角形都是特殊的三角形，如直角三角形、等腰三角形、等边三角形、等腰直角三角形．在ABC △中，已知sin sin sin a b Ba B A+=-，且cos()cos 1cos 2A B C C -+=-，则ABC △是 A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形【答案】B【解析】设ABC △的外接圆半径为R ，由正弦定理的推广，得sin 2a A R =，sin 2bB R=，代入sin sin sin a b B a B A +=-，可得a b ba b a+=-，即22b a ab -=． 因为cos()cos 1cos 2A B C C -+=-，所以2cos()cos()2sin A B A B C -++=， 即2sin sin sin A B C =． 由正弦定理的推广可得2()222a b cR R R⋅=，所以2ab c =， 由22b a ab -=及2ab c =可得222b a c =+，所以ABC △是直角三角形． 故选B ．【名师点睛】注意到a ，b ，c 在条件式中是齐次线性关系，因此可以考虑利用正弦定理将边化为角．通过角的特征或者关系来判断三角形的形状．忽略角的取值范围而出错在ABC △中，若3C B =，求cb的取值范围． 【错解】由正弦定理，可得22sin sin 3sin 2cos cos 2sin =2cos cos 24cos 1sin sin sin c C B B B B B B B B b B B B +===+=-， 220cos 1,14cos 13B B ≤<∴-≤-<，由0,0b c >>，可得03cb<<． 故cb的取值范围为(0,3)． 【错因分析】错解中没有考虑角B 的取值范围，误认为角B 的取值范围为(0,180)︒︒． 【正解】由正弦定理可得22sin sin 3sin 2cos cos 2sin =2cos cos 24cos 1sin sin sin c C B B B B B B B B b B B B +===+=-， 2180,3,045,cos 12A B C C B B B ++=︒=∴︒<<︒<<， 214cos 13B ∴≤-<，即13cb<<， 故cb的取值范围为(1,3)． 【名师点睛】解三角形时要注意三角形的内角为正角且必须满足三角形内角和定理，这是解题中的隐含条件，应特别注意．忽略对角的讨论而出错已知在ABC △中，4,22,30,a b B ===︒ 求角,A C 和边c ．【错解】由正弦定理sin sin a b A B =可得422sin sin 30A =︒， 2sin ,452A A ∴==︒，1803045105C ∴=︒-︒-︒=︒，62,sin105sin sin 4c b C B +=︒=，sin 232sin b C c B ∴==+． 【错因分析】错解中由正弦定理求出角A 的正弦值后误认为角A 是锐角，从而导致错误． 【正解】由正弦定理,sin sin a b A B =得422sin sin 30A =︒， 2sin ,2A ∴=,45a b A >∴=︒或135︒．当45A =︒时，1803045105C =︒-︒-︒=︒，62sin ,sin105,232sin sin 4sin c b b Cc C B B+=︒=∴==+；当135A =︒时，1803013515C =︒-︒-︒=︒，62sin ,sin15,232sin sin 4sin c b b Cc C B B-=︒=∴==-． 综上，45,105,232A C c =︒=︒=+或135,15,232A C c =︒=︒=-．【名师点睛】在ABC △中，已知两边和其中一边的对角解三角形时，可先用正弦定理求出另一边的对角，此时解的个数可能不确定，应注意讨论，避免漏解导致错误．1．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，83,6,60a b A ===︒，则sin B = A ．2B 6C 2D 32．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若a =45B =︒，2b =，则A =A ．30︒或150︒B ．30︒C ．150︒D ．45︒3．在ABC △中，若∠A ＝60°，∠B ＝45°，BC ＝AC ＝A ．B ．CD 4．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，已知A :B :C ＝1:2:3，则a :b :c ＝A ．1:2:3B ．C ．D ．5．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，b =，4B π∠=，tan A =，则a =A ．210B ．C ．10D ．26．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos sin b C c B a A +=，则ABC △的形状为A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定7．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，15,18,30a b A ===︒，则此三角形解的个数为 A ．0 B ．1 C ．2D ．不能确定8．已知ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，且cos A :cos B ＝b :a ，则ABC △是 A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形9．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若8a =，60B =︒，75C =︒，则b =______________．10．在ABC △中，角A ，C 的对边分别为a ，c ，其中1=a ，33=c 3A π=，则角=C ______________．11．在ABC △中，若B ＝30°，AB ＝23，AC ＝2，则ABC △的周长为______________． 12．ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，己知A −C =90°，a +c =2b ，求C ．13．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若a ＝52b ，A ＝2B ，则cos B = A 5 B 5C 5 D 5 14．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，已知π,3,23A a b ===，则B = A ．π6 B ．π4 C ．π3D ．π215．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，已知π3,6,3a b A ===，则角B 等于 A ．π4B ．3π4C ．π4或3π4D ．以上都不正确16．在ABC △中，角A ，B ，C 的对边为a ，b ，c ，若cos (2)cos c a B a b A -=-，则ABC △是A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形17．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若cos cos cos A B Ca b c==，则ABC △是 A ．有一内角是30°的三角形 B ．等边三角形C ．等腰直角三角形D ．有一内角是30°的等腰三角形18．在ABC △中，已知31,6,15b c B =-==︒，则边长a =A ．31+或2B ．31+C ．2D ．2319．在ABC △中，已知2AB AC =，30B =︒，则A =______________．20．如图所示，在一个坡度一定的山坡AC 的顶上有一高度为25m 的建筑物CD ．为了测量该山坡相对于水平地面的坡角θ，在山坡的A 处测得15DAC ∠=︒，沿山坡前进50m 到达B 处，又测得45DBC ∠=︒．根据以上数据计算可得cos θ=______________．21．如图，在ABC △中，点D 在BC 边上，π72cos 42CAD AC ADB ∠==∠=，，． （1）求sin C 的值；（2）若5BD =，求AD 的长．22．（2017山东理）在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ．若ABC △为锐角三角形，且满足sin (12cos )2sin cos cos sin B C A C A C +=+，则下列等式成立的是 A ．2a b = B ．2b a = C ．2A B =D ．2B A =23．（2017新课标全国Ⅰ文）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ．已知sin sin (sin cos )0B A C C +-=，a =2，c 2，则C =A ．π12 B ．π6 C ．π4D ．π324．（2017新课标全国Ⅱ文）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，若2cos cos cos b B a C c A =+，则B =______________．25．（2017新课标全国Ⅲ文）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ．已知C =60°，b ，c =3，则A =______________．26．（2018北京理）在△ABC 中，7a =，8b =，1cos 7B =-． （1）求A ∠；（2）求AC 边上的高．1．【答案】D【解析】∵83,6,60a b A ===，由sin sin a b A B =得sin 3sin .8b A B a ==故选D ． 2．【答案】B【解析】在ABC △中，由sin sin a b A B =得21sin sin sin 4522a A Bb ===︒，由于a b <，所以A B <，所以30A =︒，故选B ． 3．【答案】B【解析】由正弦定理得23sin 60sin 45AC =︒︒，所以AC ＝23sin 452 2.sin 60︒=︒故选B ．4．【答案】C【解析】因为在ABC △中，A ＋B ＋C ＝π，且A :B :C ＝1:2:3，所以A ＝6π，B =3π，C =2π，由正弦定理的变形，得a :b :c ＝sin A :sin B :sin C 13=1=22：：1:3:2．故选C ．6．【答案】B【解析】由已知可得2sin cos cos sin sin B C B C A +=，∴2sin()sin B C A +=，∴sin 1A =，∴π2A =，三角形为直角三角形．故选B ． 7．【答案】C【解析】由正弦定理可得sin 18sin 303sin 155b A B a ︒===，因为b a >，所以30B A >=︒，所以角B 可能是锐角，也可能是钝角，所以此三角形有两解，故选C ．8．【答案】D【解析】由正弦定理可得cos sin cos sin A b BB a A==，即sin A cos A ＝sin B cos B ，所以sin2A ＝sin2B ，即2A ＝2B 或2A ＋2B ＝π，即A ＝B 或A ＋B ＝2π，故ABC △是等腰或直角三角形．故选D ．9．【答案】46【解析】∵60B =︒，75C =︒，∴45A =︒，∵sin sin a bA B=，∴82322b=，∴46b =． 10．【答案】π6【解析】由正弦定理可得313πsin sin 3C =，即212333sin =⨯=C ，所以π6C =或5π6，又a c <，所以π6C =．12．【答案】o =15C ．【解析】由正弦定理可得sin sin 2A C B +=，又由于o o90=180()A C B A C -=-+，，故cos sin 2)C C A C +=+o 22)22C C =+=，即22sin cos 2,22C C C +=o cos(45)cos 2C C -=． 因为o o 090C <<，所以o 2=45C C -，即o =15C ． 13．【答案】B【解析】由正弦定理，得sin sin a A b B =，所以a ＝52b 可化为sin sin A B ＝52．又A ＝2B ，所以sin 2sin B B ＝52，所以cos B ＝54．故选B ． 14．【答案】D【解析】在ABC △中，由正弦定理可得2πsin sin sin 133b B A a ==⨯=，又0πB <<，所以B =π2，故选D ． 15．【答案】 A【解析】在ABC △中，∵π3,6,3a b A ===，∴36πsin sin sin sin 3a b A B B =⇒=2sin 2B ⇒=，又63b a =<=，∴π03B A <<=，∴π4B =，故选A ．16．【答案】D【解析】由正弦定理和已知条件可得sin sin cos 2sin cos sin cos C A B A A B A -=-， 所以sin()sin cos 2sin cos sin cos ,A B A B A A B A +-=- 即cos (sin sin )0A B A -=，所以cos 0A =或sin sin 0B A -=，即90A =︒或=A B ．故ABC △是等腰三角形或直角三角形． 故选D ．18．【答案】A【解析】由正弦定理可得，sin 63sin 231c B C b ===-， 在ABC △中，c b >，60C ∴=或120．当60C =时，105A =︒，sin 6sin10531sin c A a C ︒∴===； 当120C =时，45A =︒，此时sin 6sin 452sin c A a C ︒∴===． 综上，可得31a =或2．故选A ．19．【答案】105︒或15︒【解析】由正弦定理得sin sin AB AC C B =，得sin 2sin 2sin 302AB B C AC ==︒=， 由AB AC >，得C B >，所以45C =︒或135︒，从而105A =︒或15︒．21．【答案】（1）45；（2）22． 【解析】（1）因为2cos ADB ∠=72sin ADB ∠= 又π4CAD ∠=，所以π4C ADB =∠-， 所以πππ722224sin sin()sin coscos sin 4445C ADB ADB ADB =∠-=∠⋅-∠⋅==． （2）在ACD △中，由sin sin AD ACC ADC =∠，可得sin 22sin AC C AD ADC⋅==∠． 22．【答案】A【解析】由题意知sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+， 所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=，故选A ． 23．【答案】B【解析】由sin()sin (sin cos )0A C A C C ++-=可得sin cos cos sin sin sin A C A C A C ++-sin cos 0A C =，即πsin (sin cos )2sin()04C A A C A +=+=，所以3π4A =．由正弦定理sin sin a c A C =可得223πsin sin 4C =，即1sin 2C =，因为c a <，所以C A <，所以π6C =，故选B ． 24．【答案】π3【解析】由正弦定理可得12sin cos sin cos sin cos sin()sin cos 2B B A C C A A C B B =+=+=⇒=π3B ⇒=． 25．【答案】75︒【解析】由正弦定理sin sin b c B C=，可得36sin 22sin 32b C Bc ⨯===，结合b c <可得45B =︒，则18075A B C =︒--=︒. 26．【答案】（1）π3A ∠=；（2）AC 边上的高为332． 【解析】（1）在△ABC 中，因为1cos 7B =-，所以π(,)2B ∈π，所以243sin 1cos 7B B =-=． 由正弦定理7sin sin sin a b A B A =⇒=8437，所以3sin 2A =． 因为π(,)2B ∈π，所以π(0,)2A ∈，所以π3A ∠=（2）在△ABC 中，3114333sin sin()sin cos sin cos ()272714C A B A B B A =+=+=⨯-+⨯=． 如图所示，在△ABC 中，sin h C BC =，所以3333sin 7142h BC C =⋅=⨯=， 所以AC 边上的高为332．。