东华小学小升初数学考试题知识讲解

2023年广东省东莞市东华初级中学小升初数学试卷一.选择题（每题3分，5小题共15分）1．（3分）如图，大正方形由9个相同的小正方形拼成。

图中已有3个小正方形床上了颜色。

如果在图中再涂上1个小正方形，使涂色部分成为一个轴对称图形，一共有（ ）种不同的涂法。

A．2B．3C．4D．52．（3分）如图中，甲的面积与乙的面积相比较，（ ）A．甲的面积大B．乙的面积大C．甲、乙面积相等D．无法比较3．（3分）一杯牛奶，喝去，加满水摇匀，再喝去，再加满水，这时杯中牛奶的水与牛奶之比是（ ）A．3：7B．2：3C．2：5D．1：14．（3分）已知M＝4322×1233，N＝4321×1234，下面结论正确的是（ ）A．M＞N B．M＝N C．M＜N D．无法判断5．（3分）古希腊毕达哥拉斯学派把1，3，6，10，…这样的数称为“三角形数”，而把1，4，9，16，…这样的数称为“正方形数”。

从图中可以发现，任何一个大于1的“正方形数”都可以看成两个相邻“三角形数”之和。

下面的等式中，符合这一规律的是（ ）A．13＝3+10B．25＝19+6C．36＝15+21D．49＝18+31二.填空题（每题3分，5小题共15分）6．（3分）某市出租车夜间收费（单位：元）与行驶路程（单位：千米）之间的关系如图所示，如果勇勇乘出租车最远能到8公里，那么他恰有 元。

7．（3分）一座大楼上的彩灯按红、黄、蓝、绿、紫的顺序依次排列组装，一共有37个灯泡。

最后一只灯泡的颜色是 。

8．（3分）3米长的木材，锯成每段一样长的小段，共锯了7次，每段长 米。

9．（3分）如图是一个正方形，甲和乙分别是等腰三角形的两种不同的内接正方形，则图中甲与乙的面积比是 ．10．（3分）7只鸽子飞进了3个鸽笼，总有一个鸽笼至少飞进了 只鸽子．三.判断题（每题2分，5小题共10分）11．（2分）任意翻阅2014年的台历，翻到星期一的可能性比翻到1号的可能性大． 12．（2分）图上距离总是比实际距离小． 13．（2分）如果两个圆柱的侧面积相等，那么它们的表面积也相等． ．14．（2分）任意两个素数的和都是偶数． 15．（2分）一次抽奖活动的中奖率是1%，抽100次一定会中奖． ．四、计算题（每题6分，2小题共12分）16．（6分）列式计算。

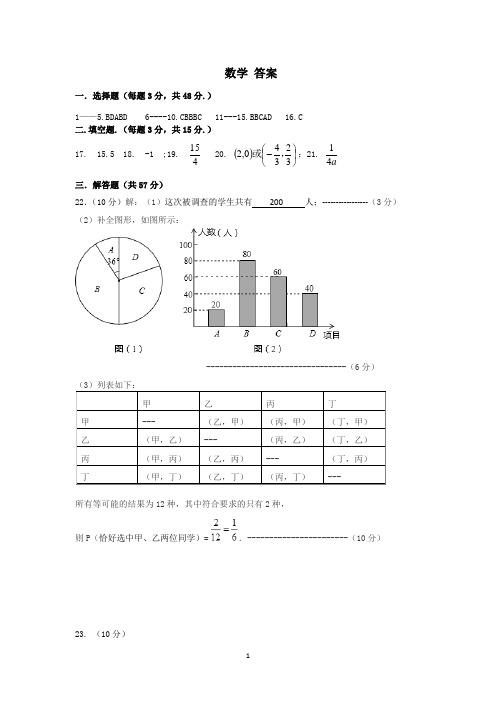
数学 答案一．选择题（每题3分，共48分.）1——5.BDABD 6----10.CBBBC 11---15.BBCAD 16.C 二.填空题.（每题3分，共15分.） 17. 15.5 18. -1 ;19. 415 20. ()⎪⎭⎫⎝⎛-32340,2，或；21. a 41三．解答题（共57分）22．（10分）解：（1）这次被调查的学生共有 200 人；-----------------（3分） （2）补全图形，如图所示：--------------------------------（6分） （3）列表如下： 甲 乙 丙 丁 甲 --- （乙，甲） （丙，甲） （丁，甲） 乙 （甲，乙） --- （丙，乙） （丁，乙） 丙 （甲，丙） （乙，丙） --- （丁，丙） 丁（甲，丁）（乙，丁）（丙，丁）---所有等可能的结果为12种，其中符合要求的只有2种，则P （恰好选中甲、乙两位同学）=．-----------------------（10分）23. （10分）--------------------------------（5分）--------------------------------（10分）24. （10分）解：（1）设直线DE 的解析式为:y=kx+b ∵点D ,E 的坐标为（0,3）、（6,0）, ∴ b= 3 6k+b=0 6k+3=0 6k=-3 k=-0.5得 k=-0.5 b=3∴y =-0.5x+3 --------------------------------（2分） ∵ 点M 在AB 边上,B （4,2）,而四边形OABC 是矩形, ∴ 点M 的纵坐标为2．又 ∵ 点M 在直线y=-0.5x+b 上, ∴-0.5x+b =2 ∵ b=3 ∴ x = 2． ∴ M （2,2）． --------------------------------（4分） （2）∵y=xm（x ＞0）经过点M （2,2）,∴ m=4 ∴.y=x4--------------------------------（6分） 又 ∵ 点N 在BC 边上,B （4,2）, ∴点N 的横坐标为4．∵ 点N 在直线y=-0.5x+b 上, ∴ y=1∴ N （4,1）．∵ 当x=4时,y = 1,∴点N 在函数 的图象上． --------------------------------（8分） （3）4≤ m ≤8 --------------------------------（10分）25. （10分） 解：（1）∵bx ax y +=2的顶点为（-），抛物线的顶点在直线y=kx 上，k=1，抛物线水线最大高度达3m ，∴，，解得，.2,31=-=b a即k=1，且喷出的抛物线水线最大高度达3m ，此时a 、b 的值分别是.2,31=-=b a ；（3分）（2）∵k=1，喷出的水恰好达到岸边，出水口离岸边18m ，抛物线的顶点在直线y=kx 上， ∴此时抛物线的对称轴为x=9，y=x=9，即此时喷出的抛物线水线最大高度是9米；------------------------------（6分）（3）∵bx ax y +=2的顶点为（-）在直线y=3x 上，72-=a ， ∴，解得，b=6，∴抛物线x x y 6722+-=， 当y=0时，x x 67202+-=， 解得，;0,2121==x x ∵21＞18， ∴若72,3-==a k ，则喷出的抛物线水线能达到岸边。

wo最新文件---------------- 仅供参考--------------------已改成-----------word文本--------------------- 方便更改rd2015年小升初东华第一批面试数学题1、如图，已知直角等腰三角形的面积是12平方厘米，求两个小半圆面积．2、一个长方形的长是15cm，宽是6cm，把它切割之后拼成一个长10cm，宽7cm的长方形，你将怎么切割和拼？3、同学折千纸鹤，平均每人折76只。

已知每人至少折70只，其中一位折了88只，如果不算这个同学，那么平均每个人折74只，折得最快的同学最多折多少只？解析：如果把折88个的人算进去，每人折了76个，他一共给其他人给了88-76=12个，如果不算，每人就损失了76-74=2个，所以一共有88-74=142＝7人。

解答：88-74=14，142=7人，74*6=444，5*70=350，444-350=94个。

答：折得最快的同学折了94只.4、（盈亏问题）幼儿园老师给小朋友分梨子，每人分4个，则多9个，如果每人分5个，则少6个。

问有多少个小朋友？多少个梨子？解析：运用（盈亏差）／（方案差）=人数注：盈亏差等于盈＋亏解答：（9＋6）／（5-4）＝15（人）15*4+9=69（个）答：有15个小朋友，69个梨子。

5、（逻辑问题）有三个嫌疑犯来到了法院。

法官审问谁是罪犯。

甲说：“我是罪犯。

”乙说：“我不是罪犯。

”丙说：“甲不是罪犯。

”他们三人中有一人说的是真话，二个人说的是假话。

问：你知道谁是罪犯吗？解析：一三和二对立，如果一说真话，那二就说他是罪犯，如果二说真话，那三就说一是罪犯，故只有三说真话，如果三说真话，那一就不是罪犯，二就是罪犯，三也于一意见符合，故二是罪犯答：三说了真话，二是罪犯6、商店同时卖出两台洗衣机，每台2400元，其中一台比进价高20%，另一台比进价低20%，总的来看商店卖出这两台洗衣机是赚钱还是赔钱？你是怎样想的？解析：根据关系式卖价／卖价的分率＝进价解答2400/（1＋20%）＝2000元2400/（1-20%）＝3000元2400-2000<3000-2400答：总的来看商店卖出这两台洗衣机是赔钱。

2020年广东省东莞市东华初级中学小升初分班数学试卷一．填空题（共10小题，满分40分，每小题4分）1．一列火车装运一批货物，原计划每节车皮装46吨，结果有100吨没装上去，后来每节多装4吨，不但货物全部装完，而且剩两节车皮，则这批货物有 吨．2．一根长1米的圆柱形木棒，锯成3段后，表面积增加了64平方分米，这根木棒的体积是 ．3．甲杯中有水25克，乙杯中有水30克，甲杯中放入10克糖，乙杯中放入 克糖，那么两杯水一样甜．4．6时整，时针和分针又形成 角，2时30分，时针和分针成 角．5．今年“十一黄金周”期间，某景点的门票从平时的150元降到120元，票价降低了 %，“十一黄金周”期间的票价是平时的 %．6．小李、小王同时从甲地出发前往乙地，7小时后小王到达乙地，小李还需要行驶2小时才能到达乙地，此时小李和小王一共行驶了144千米．甲、乙两地相距 千米． 7．□÷35＝28…□中，余数最大是 ，被除数最大是 ． 8．找规律，在横线里填适当的数． （1）34，89，1316， ，2336；（2）12，16，112， ，130．9．有甲、乙两个工地，要完成一个相同的任务．上午工作4小时，派到甲工地的人数是乙工地的3倍．到了中午，老板发现这些人没有办法完成这个任务，又派了一批人去工地．下午新派去甲工地的人数占新派总人数的712，剩下的人都去了乙工地．下午两批人一起工作了4小时，最后甲工地完工，乙工地还需要4名工人再做8小时．如果所有工人每小时的工作效率相同，那么这一天老板一共派出 位工人．10．男女混合接力赛，每组有3名男生和2名女生，要求男女间隔排列，一共有 种排法．二．计算题（共1小题，满分24分，每小题24分） 11．（24分）计算题（1）114−920+1130−1342+1556−1772+1990（2）1−58÷2528−310（3）（415+125）×15×25（4）17.5+17.5×145÷（310−0.06）（5）4x ﹣3（20﹣x ）＝3 （6）x−13−x+26=1−2x−12三．解答题（共5小题，满分36分）12．（7分）用拖拉机耕地，甲拖拉机7小时耕地6公顷，乙拖拉机每小时耕地56公顷．甲拖拉机比乙拖拉机平均每小时多耕地多少公顷？13．（7分）甲、乙、丙三个工程队完成某项工程的天数和日工资如下表：工程队 单独完成工程所用天数每日总工资（万元）甲 10 18 乙 15 12 丙208请你选择两个工程队合做这项工程，如果工期很紧，想尽快完工，应选择哪两个队合做？几天可以完工？完工后两队各得多少工资？14．（7分）已知AB ＝4cm ，AD ＝7cm ，三角形ABE 和三角形ADF 的面积各占长方形ABCD 的13，求三角形AEF 的面积．15．（7分）科技书有75本，故事书有多少本？16．（8分）连日来哈市降雪不断，在清雪工作中，某驻哈武警部队出动兵力600人参加三条街道的清雪劳动．其中A街道清雪人数占此次出动兵力总人数的40%，余下的人参加B街道和C街道的清雪劳动．（1）求参加A街道清雪劳动的共有多少人？（2）若参加B街道清雪人数与参加C街道清雪人数的比是2：3，求参加B街道和C街道清雪劳动的各有多少人？（3）在（2）的条件下，因其它工作需要，调走了在A街道清雪的一部分兵力，又从C 街道处调来一部分兵力参加A街道的劳动，且从C街道处调来的人数占C街道处原来人数的百分比是从A街道调走人数占原来A街道人数百分比的2倍，此时在A街道清雪的人数比在C街道清雪人数的2倍少60人，求此时在A街道清冰雪的有多少人？2020年广东省东莞市东华初级中学小升初分班数学试卷参考答案与试题解析一．填空题（共10小题，满分40分，每小题4分）1．一列火车装运一批货物，原计划每节车皮装46吨，结果有100吨没装上去，后来每节多装4吨，不但货物全部装完，而且剩两节车皮，则这批货物有2400吨．解：车皮节数：[100+（46+4）×2]÷4，＝[100+50×2]÷4，＝200÷4，＝50（节）；这批货物共有：46×50+100，＝2300+100，＝2400（吨）；答：这批货物有2400吨．故答案为：2400．2．一根长1米的圆柱形木棒，锯成3段后，表面积增加了64平方分米，这根木棒的体积是160立方分米．解：1米＝10分米64÷4×10＝16×10＝160（立方分米）答：这根木棒的体积是160立方分米．故答案为：160立方分米．3．甲杯中有水25克，乙杯中有水30克，甲杯中放入10克糖，乙杯中放入12克糖，那么两杯水一样甜．解：30×（10÷25）＝30×2 5＝12（克）答：乙杯中放入12克糖，那么两杯水一样甜．故答案为：12．4．6时整，时针和分针又形成平角，2时30分，时针和分针成105角．解：当钟面上6时整，时针与分针之间有6个大格，30×6＝180（度）180°是平角当钟面上2时30分时，时针与分针之间有3.5个大格，30×3.5＝105（度）答：6时整，时针和分针又形成平角，2时30分，时针和分针成105角．故答案为：平；105．5．今年“十一黄金周”期间，某景点的门票从平时的150元降到120元，票价降低了20%，“十一黄金周”期间的票价是平时的80%．解：（150﹣120）÷150＝30÷150＝20%；1﹣20%＝80%答：票价降低了20%，“十一黄金周”期间的票价是平时的80%．故答案为：20，80．6．小李、小王同时从甲地出发前往乙地，7小时后小王到达乙地，小李还需要行驶2小时才能到达乙地，此时小李和小王一共行驶了144千米．甲、乙两地相距81千米．解：设甲、乙两地相距x千米．7+2＝9（小时）（144﹣x）÷7×（7+2）＝x（144﹣x）÷7×9＝x（144﹣x）×9＝7x144×9﹣9x＝7x16x＝144×9x＝81答：甲、乙两地相距81千米．故答案为：81．7．□÷35＝28…□中，余数最大是 34 ，被除数最大是 1014 ． 解：余数最大为：35﹣1＝34， 28×35+34， ＝980+34， ＝1014；故答案为：34，1014．8．找规律，在横线里填适当的数． （1）34，89，1316，1825，2336；（2）12，16，112，120，130．解：（1）要求的数分子是：13+5＝18 要求的数分母是：52＝5×5＝25 这个分数就是1825；这个数列就是：34，89，1316，1825，2336；（2）要求数的分子是1， 分母是：4×5＝20 这个分数就是120；这个数列就是：12，16，112，120，130．故答案为：1825，120．9．有甲、乙两个工地，要完成一个相同的任务．上午工作4小时，派到甲工地的人数是乙工地的3倍．到了中午，老板发现这些人没有办法完成这个任务，又派了一批人去工地．下午新派去甲工地的人数占新派总人数的712，剩下的人都去了乙工地．下午两批人一起工作了4小时，最后甲工地完工，乙工地还需要4名工人再做8小时．如果所有工人每小时的工作效率相同，那么这一天老板一共派出 28 位工人． 解：设上午派出4x 人，其中甲工地3x 人，乙工地x 人， 下午又派出12y 人其中甲工地7y 人，乙工地5y 人， 并设每人每小时工作效率为1 则甲工地的工程量为：（4+4）×3x+4×7y＝24x+28y乙工地的工程量为（4+4）x+4×5y+4×8＝8x+20y+32由于两个工地的工程量相等所以，24x+28y＝8x+20y+32即：2x+y＝4正整数解只有：x＝1，y＝2所以，共派去：4×1+12×2＝28（人）答：这一天老板共派去28人．10．男女混合接力赛，每组有3名男生和2名女生，要求男女间隔排列，一共有12种排法．解：（3×2×1）×（2×1）＝6×2＝12（种）答：要求男女间隔排列，一共有12种排法．故答案为：12．二．计算题（共1小题，满分24分，每小题24分）11．（24分）计算题（1）114−920+1130−1342+15 56−1772+1990（2）1−58÷2528−310（3）（415+125）×15×25（4）17.5+17.5×14 5÷（310−0.06）（5）4x﹣3（20﹣x）＝3（6）x−13−x+26=1−2x−12解：（1）114−920+1130−1342+1556−1772+1990=54−4+54×5+5+65×6−6+76×7+7+87×8−8+98×9+9+109×10=54−14−15+15+16−16−17+17+18−18−19+19+110＝1+1 10=1110（2）1−58÷2528−310＝1−58×2825−310＝1−710−310＝1﹣（710+3 10）＝1﹣1＝0（3）(415+125)×15×25=415×15×25+125×15×25＝100+15＝115（4）17.5+17.5×145÷(310−0.06)＝17.5+17.5×1.8÷0.24＝17.5×（1+7.5）＝17.5×8.5＝148.75（5）4x﹣3（20﹣x）＝34x+3x﹣60＝37x﹣60+60＝3+607x＝63x＝63÷7x＝9（6）x−13−x+26=1−2x−122x ﹣2﹣x ﹣2＝6﹣6x +3 7x ＝13 x =137 三．解答题（共5小题，满分36分）12．（7分）用拖拉机耕地，甲拖拉机7小时耕地6公顷，乙拖拉机每小时耕地56公顷．甲拖拉机比乙拖拉机平均每小时多耕地多少公顷？ 解：6÷7−56 =67−56 =142（公顷）答：甲拖拉机比乙拖拉机平均每小时多耕地142公顷．13．（7分）甲、乙、丙三个工程队完成某项工程的天数和日工资如下表：工程队 单独完成工程所用天数每日总工资（万元）甲 10 18 乙 15 12 丙208请你选择两个工程队合做这项工程，如果工期很紧，想尽快完工，应选择哪两个队合做？几天可以完工？完工后两队各得多少工资？ 解：因为110＞115＞120，所以选甲乙两队合做．1÷（110+115），＝1÷16， ＝6（天）；18×6＝108（万元）， 12×6＝72（万元）；答：应选甲乙两队合做，6天可以完工，完工后甲队可得工资108万元，乙队可得工资72万元．14．（7分）已知AB ＝4cm ，AD ＝7cm ，三角形ABE 和三角形ADF 的面积各占长方形ABCD的13，求三角形AEF 的面积．解：4×7×13=283（平方厘米）DF =283×2÷7=83（厘米）CF ＝4−83=43（厘米）BE =283×2÷4=143（厘米）EC ＝7−143=73（厘米）S △CEF =43×73÷2=149（平方厘米）S △AEF =283−149=709（平方厘米）答：三角形AEF 的面积是709平方厘米．15．（7分）科技书有75本，故事书有多少本？解：16．（8分）连日来哈市降雪不断，在清雪工作中，某驻哈武警部队出动兵力600人参加三条街道的清雪劳动．其中A街道清雪人数占此次出动兵力总人数的40%，余下的人参加B街道和C街道的清雪劳动．（1）求参加A街道清雪劳动的共有多少人？（2）若参加B街道清雪人数与参加C街道清雪人数的比是2：3，求参加B街道和C街道清雪劳动的各有多少人？（3）在（2）的条件下，因其它工作需要，调走了在A街道清雪的一部分兵力，又从C 街道处调来一部分兵力参加A街道的劳动，且从C街道处调来的人数占C街道处原来人数的百分比是从A街道调走人数占原来A街道人数百分比的2倍，此时在A街道清雪的人数比在C街道清雪人数的2倍少60人，求此时在A街道清冰雪的有多少人？解：（1）600×40%＝240（人）答：参加A街道清雪劳动的共有240人．（2）（600﹣240）÷（2+3）＝360÷5＝72（人）72×2＝144（人）72×3＝216（人）答：参加B街道清雪劳动的有144人，参加C街道清雪劳动的有216人．（3）设从A街道调走人数占原来A街道人数百分比是x，则：240﹣240x+216×2x＝（216﹣216×2x）×2﹣60240+192x＝（216﹣432x）×2﹣60240+192x＝432﹣864x﹣601056x+240＝3721056x＝132x＝12.5% 240﹣240×12.5%+216×（12.5×2）＝240﹣30+54＝210+54＝264（人）答：此时在A街道清冰雪的有264人．。

东华小升初数学真题试卷及答案东华小升初数学真题试卷一、填空每个括号0.5分，共18分。

1、40%=8( )=10:( )=( )(小数：)2.、1千米20米=( )米4.3吨=( )吨( )千克3时15分=( )时2.07立方米=( )立方分米3、四百二十万六千五百写作( )，四舍五入到万位约是( )万。

4、把单位1平均分成7份，表示其中的5份的数是( )，这个数的分数单位是( )。

5、4、8、12的最大公约数是( );最小公倍数是( )，把它分解质因数是( )。

6、0.25：的比值是( )，化成最简单整数比是( )。

7、在1 、1.83和1.83%中，最大的数是( )，最小的数是( )。

8、在1、2、310十个数中，所有的质数比所有的合数少( )%。

9、晚上8时24时记时法就是( )时，从上午7时30分到下午4时30分经过了( )小时。

10、常用的统计图有( )统计图，( )统计图和扇形统计图。

11、能被2、3、5整除的最小两位数是( )最大三位数是( )。

12、六(1)班期中考试及格的有48人及格，2人不及格，及格率是( )，优秀率(80分及以上)达到60%,优秀人数有( )人。

14、一个正方体棱长总和是24厘米，这个正方体的一个面的面积是( )平方厘米，体积是( )立方厘米。

15、一个圆柱体底面直径是4厘米，高3厘米，底面积是( )平方厘米，体积是( )立方厘米，与它等底等高的圆锥体体积是( )立方厘米。

16.20xx年是( )(填平年或闰年)，全年共有( )天。

二.火眼金睛辩正误(对的打，错的打X，共10分)17.圆的周长和直径成正比例。

( )18.兴趣小组做发芽实验，浸泡了20粒种子，结果16课发芽了，发芽率是16%。

( )19.不相交的两条直线是平行线。

( )20.联合国在调查200个国家中，发现缺水的国家有100个，严重缺水的国家有40个，严重缺水的国家占调查国家的40%。

( )21.一个半圆的半径是r，它的周长是(+2)r。

东华小升初试题一、数学1. 小明有5个苹果，小红给了他3个苹果，然后小明又吃掉了2个苹果，最后还剩下多少个苹果？解析：苹果的数量：5个 + 3个 - 2个 = 6个答案：最后剩下6个苹果。

2. 甲、乙、丙三个人在一起比赛，甲赢了乙，乙赢了丙，丙输给了甲。

他们都进行了几次比赛？解析：甲乙之间进行了一次比赛；乙丙之间进行了一次比赛；丙甲之间进行了一次比赛。

答案：他们总共进行了3次比赛。

3. 从1到100，共有几个数字是偶数？解析：偶数是能被2整除的数。

从1到100，每两个数就有一个偶数。

所以，偶数的个数为100 / 2 = 50个。

答案：共有50个数字是偶数。

二、语文1. 下面的词语中，哪个是形容词？A. 高高的B. 跑步C. 漂亮D. 吃饭解析：形容词是用来描述事物的特征或性质的词语。

在选项中，只有A. 高高的是形容词。

答案：A. 高高的2. 下面的诗句中，哪句有错别字？A. 春天来了，万物开始发芽。

B. 梅花的香气，飘荡在清风中。

C. 昨夜的星光，点缀了夜空。

D. 阳光从天空倾泻下来。

解析：仔细阅读每一句诗句，发现没有错别字。

答案：没有错别字。

3. 下面的短文中，哪个词语可以填入横线处？横线处：______ 树叶已经变黄了。

短文：秋天到了，天气渐渐凉爽起来，______ 树叶已经变黄了。

松鼠拿着栗子，在______ 树上跳来跳去。

解析：根据短文的意思，描写的是秋天的景象。

所以，可以填入形容秋天的词语。

答案：金黄色的三、英语1. 用英语写出下面的数字：10解析： 10的英文为：ten答案：ten2. 下列单词中，属于动物的是：A. appleB. catC. bookD. flower解析：动物是指一类有机体，具有感觉和自主运动能力的生物。

只有B. cat （猫）是动物。

答案：B. cat3. 把下列两句话合并成一句：She is reading a book. Her brother is drawing.解析：合并两句话时，可以使用连词来连接。

2021年东莞市东华小学小升初数学试卷一．填空题（共12小题，满分24分）1．（2分）地球是一个美丽的蓝色星球，它距离太阳约149597870千米，画“横线”的数读作，这个数四舍五入到万位约是万。

2．（2分）在如图中标出1.5，0.9和1.1的位置，比较它们的大小。

＜＜。

3．（2分）7÷=()8=25%＝4：＝（填小数）4．（2分）一本书有a页，张华每天看5页，看了b天。

5b表示，a﹣5b表示。

5．（2分）一个等腰三角形的一个底角是30°，它的顶角是°，如果按角来分它是一个三角形．6．（2分）一个长方体，如果高增加2厘米，就变成一个棱长是5厘米的正方体。

原来这个长方体的体积是立方厘米。

7．（2分）一根铁丝围成了一个边长7.85厘米的正方形，如果把这根铁丝围成一个圆，那么圆的周长是厘米．如果用圆规画出这个圆，圆规两脚间的距离是厘米．8．（2分）已知圆锥和圆柱的底面积相等，且圆锥和圆柱的体积比是1：6，圆锥高4.8cm，圆柱高。

9．（2分）下面哪组中的两个比可以组成比例？把能组成比例的在横线里打“√”，不能的打“×”。

（1）2：6和3：1．（2）1：2和0.5：1．（3）0.8：0.2和16：4．（4）7：3和3：7．10．（2分）机械厂第一车间有工人100人，其中女工人有35人，女工人占全车间人数的%，男工人占全车间人数的%。

11．（2分）速度一定，路程和时间成比例；圆的周长和直径成比例．12．（2分）如图，按照前面四幅图的规律，写出第五幅图中的正方形里共有个圆．二．判断题（共5小题，满分5分，每小题1分）13．（1分）9、15、21都是奇数，也都是合数．（判断对错）14．（1分）自然数（0除外）的倒数都是真分数．（判断对错）15．（1分）淘气家10月份各项支出占总支出的百分比，适合用扇形统计图。

（判断对错）16．（1分）如图温度计上的温度可以读作9℃。

（判断对错）17．（1分）小芳家在学校北偏东40°方向，也可以表示为小芳家在学校东偏北50°方向。

东华小升初数学试题大综合_(卢老师)东华小升初数学试题大综合_(卢老师)-东莞最专业的课外辅导决战小升初名校之试题分类精练每个课时的内容课时第1课时第2课时第3课时第4课时第5课时第6课时第7课时第8课时第9课时第10课时第11课时第12课时第13课时第14课时第15课时第16课时第17课时第18课时第19课时第20课时第21课时第22课时第23课时第24课时课题大数的读与写、单位换算、分数、比、百分率、除法、小数的转化比、比例尺、比例（填空、判断、选择）比、比例尺、比例（应用题）比大小质数、合数、偶数、用字母表示数、近似数统计图、三角形的度数、余数、数的整除、年月日、轴对称图形、可能性间隔问题、近似数、循环小数、平均数问题、可能性、抽屉原理、年龄问题、鸡兔同笼与假设法、平均速度找规律、最大公因数、最小公倍数长方形的周长、面积、正方体的表面积、圆的周长、面积、多边形的面积多边形、圆的周长及面积的综合图形计算圆柱、圆锥分数的意义、分数除法、百分率（填空、判断、选择）分数的意义、分数除法、百分率（应用题1）分数的意义、分数除法、百分率（应用题2）分数的意义、分数除法、百分率（应用题3）工程问题行程问题计算（解方程、解比例）计算（递等式计算、简便计算）计算（口算、列式计算、只列式不计算）归总及归一问题、方案设计型、实践与操作第1页共64页1东莞最专业的课外辅导决战小升初名校之试题分类精练会议1（一）大数的读与写（2022东华）9。

写出12.09080亿，省略10亿后的尾数。

（2022东华）11.66亿17381写作（），四舍五入到1亿是（）亿。

（2022东华）2。

数千万的数字是1，10万的数字是7，千的数字是5，其他的数字是0。

这个数字写为（），四舍五入为10000。

(2021东华)1.一个数千万位上是5，十万位是4，千位上是8，其余各位都是0，这个数读作()，省略万位后面的尾数约是()。

（2022东华）1。

东莞市东华小升初面试50道经典奥数思维题(含答案)东华小升初面试50道经典奥数思维题1、已知一张桌子的价钱是一把椅子的10倍，又知一张桌子比一把椅子多288元，一张桌子和一把椅子各多少元?2、3箱苹果重45千克。

一箱梨比一箱苹果多5千克，3箱梨重多少千克?3、甲乙二人从两地同时相对而行，经过4小时，在距离中点4千米处相遇。

甲比乙速度快，甲每小时比乙快多少千米?4、李军和张强付同样多的钱买了同一种铅笔，李军要了13支，张强要了7支，李军又给张强0.6元钱。

每支铅笔多少钱?5、甲乙两辆客车上午8时同时从两个车站出发，相向而行，经过一段时间，两车同时到达一条河的两岸。

由于河上的桥正在维修，车辆禁止通行，两车需交换乘客，然后按原路返回各自出发的车站，到站时已是下午2点。

甲车每小时行40千米，乙车每小时行 45千米，两地相距多少千米?(交换乘客的时间略去不计)6、学校组织两个课外兴趣小组去郊外活动。

第一小组每小时走4.5千米，第二小组每小时行3.5千米。

两组同时出发1小时后，第一小组停下来参观一个果园，用了1小时，再去追第二小组。

多长时间能追上第二小组?7、有甲乙两个仓库，每个仓库平均储存粮食32.5吨。

甲仓的存粮吨数比乙仓的4倍少5吨，甲、乙两仓各储存粮食多少吨?8、甲、乙两队共同修一条长400米的公路，甲队从东往西修4天，乙队从西往东修5天，正好修完，甲队比乙队每天多修10米。

甲、乙两队每天共修多少米?9、学校买来6张桌子和5把椅子共付455元，已知每张桌子比每把椅子贵30元，桌子和椅子的单价各是多少元?10、一列火车和一列慢车，同时分别从甲乙两地相对开出。

快车每小时行75千米，慢车每小时行65千米，相遇时快车比慢车多行了40千米，甲乙两地相距多少千米?11、某玻璃厂托运玻璃250箱，合同规定每箱运费20元，如果损坏一箱，不但不付运费还要赔偿100元。

运后结算时，共付运费4400元。

托运中损坏了多少箱玻璃?12、五年级一中队和二中队要到距学校20千米的地方去春游。

2021年广东东莞东华中学小升初数学真题及答案解析一、细心审题，准确填写．〔每空1分，共23分〕2．〔4分〕_____3____ ÷8== ______ %==6：__16_______ ．考点：比与分数、除法的关系；小数、分数和百分数之间的关系及其转化解析：的分子3做被除数，分母8做除数可转化成除法算式为3÷8；用分子除以分母得小数商为0.375，0.375的小数点向右移动两位，同时添上百分号可化成37.5%；的分子和分母同乘3可化成；的分子3做比的前项，分母8做比的后项也可转化成比为3：8，3：8的前项和后项同乘2可化成6：16；3．〔4分〕4.3M= ___43______ 分M 3600克= ______ 千克75分= ________ 小时 0.2公顷= ___2000______ 平方M．考点：长度的单位换算；时、分、秒单位换算；质量的单位换算；面积单位换算．解析：把4.3M换算成分M数，用4.3乘进率10；把3600克换算成千克数，用3600除以进率1000；把75分换算成小时数，用75除以进率60；把 0.2公顷换算成数，用 0.2乘进率10000．4．〔1分〕甲数是a，乙数比甲数的2倍少b，乙数是__2a﹣b_______ ．考点：用字母表示数解析：根据“乙数比甲数的2倍少b，〞知道乙数=甲数的2倍少b，把甲数a代入关系式，5．〔4分〕一个三角形三个角度数的比是1：1：4，这个三角形的三个角的度数分别是______30___ 度、_____30____ 度和____120____ 度．这个三角形有__1_______ 条对称轴．考点：三角形的内角和；按比例分配应用题；确定轴对称图形的对称轴条数及位置．解析：1+1+4=6，180×=30〔度〕，180×=30〔度〕，180×=120〔度〕，这是一个钝角三角形，也是等腰三角形，有一条对称轴；6．〔1分〕在比例尺1：50000的地图上，量的A、B两地的距离为4厘M，A、B两地的实际距离是_2000________ M．考点：图上距离与实际距离的换算解析：依据“实际距离=图上距离÷比例尺〞即实际距离=4÷=200000〔厘M〕=2000〔M〕；7．〔1分〕梁老师在给班上同学们分组，假设想要一定有两个同学的生日在同一个月份，那么这组至少有______13___ 名同学．考点：抽屉原理．解析：建立抽屉：一年有12个月分别看做12个抽屉，把学生看做元素，考虑最差情况：每个抽屉都有1个元素，即一共有12名同学，此时再多一个同学无论放到哪个抽屉都会出现一个抽屉有2个元素，12+1=13〔名〕8．〔1分〕甲车间女职工人数比男职工人数多，男职工与全车间人数的比是_3：7________ 考点：比的意义；分数的意义解析：把男职工人数看作单位“1〞，那么女生人数是男生人数的〔1+〕，全车间人数是男职工人数的〔1++1〕所以男职工与全车间人数的比=1：〔1++1〕，=1：，=3：7；9．〔2分〕把8M绳子平均剪成5段，2段占全长的______，每段长________ M．考点：分数的意义；分数除法．解析：〔1〕把8M绳子平均剪成5段，就是把8M绳子看作单位“1〞平均分为5份，求2段占全长的几分之几，用2÷5=；〔2〕求每段长多少M，用绳子的总M数除以段数5即用．8÷5=〔M〕10．〔1分〕小明在2021年3月1日把3000元压岁钱存入银行，定期2年，年利率为2.5%，到期时，他可以从银行取出本金和利息共__3150_______ 元．〔已取消利息税〕考点：存款利息与纳税相关问题．解析：本息=本金+本金×时间×利率3000+3000×2×2.5%，=3000+150，=315011．〔1分〕10以内〔包含10〕所有合数的和与所有质数的和相差__20_______ ．考点：合数与质数．解析：10以内的质数有：2，3，5，7，2+3+5+7=17，10以内的合数有：4，6，8，9，10，4+6+8+9+10=37，37﹣17=20；12．〔1分〕全班52人外出春游，共租了11条船．每条大船乘6人，小船乘4人．现在每条船都坐满．大船租了____4_____ 条．考点：列方程解含有两个未知数的应用题解析：解：设大船租了x条，那么小船租了〔11﹣x〕条，得6x+〔11﹣x〕×4=52，解得：x=413．〔1分〕一种商品按定价的8折出售，仍可获利20%，假设按定价出售可获利_50__%．考点：百分数的实际应用．解析：打八折是指现价是原价的80%．设该商品的进价看做单位“1〞，出售获利20%，它的出售价为：1+20%=1.2，因为定价的八折为出售价，所以，定价为：〔1+20%〕÷÷﹣1〕÷1==50%；14．〔1分〕胜利工厂第一车间有40人，由于工作需要，调出10%的人到第二车间．这时第一车间的人数比第二车间的80%少4人．第二车间现在有___50______ 人．考点：百分数的实际应用．解析：第一车间：40×〔1﹣10%〕=40×90%=36〔人〕第一车间：〔36+4〕÷80%=40÷80%=50〔人〕二、灵活处理，细心计算．〔共34分〕15．〔10分〕10×12=120，1﹣0.04=，2+5.8=，÷0.45=10，×4÷4=，+=，﹣=，÷=，+÷+=1，0÷〔﹣〕=0．考点：整数的乘法及应用；分数的四那么混合运算；小数的加法和减法、乘法、除法．解析：运用整数、分数、小数的运算法那么计算。