2016北京市中考数学专题突破六：圆的有关计算(含答案)

专题15圆的有关计算与证明问题（北京真题10道+模拟30道）【方法归纳】题型概述，方法小结，有的放矢考点考查年份考查频率圆的有关计算与证明问题（大题） 2013.2014.2015.2016.2017十年10考2018.2019.2020.2021.2022圆的证明与计算是中考取的一类重要的问题，在北京市的2013-2022年10年中考中出现了10次，常见的圆的基础知识和解题技巧如下：1、圆中的重要定理:(1)圆的定义: 主要用来证明四点共圆和点到或直线圆的最值距离问题.(2)垂径定理: 主要用来证明——弧相等、线段相等、垂直关系等等.(3)三者之间的关系定理: 主要用来证明——弧相等、线段相等、圆心角相等.(4)圆周角性质定理及其推论 : 主要用来证明——直角、角相等、弧相等.(5)切线的性质定理: 主要用来证明垂直关系 .(6)切线的判断定理: 主要用来证明直线是圆的切线 .(7)切线长定理:线段相等、垂直关系、角相等 .2.圆中几个要点元素之间的相互转变 : 弧、弦、圆心角、圆周角等都能够经过相等来相互转变 . 这在圆中的证明和计算中常常用到 .3.判断切线的方法：（ 1）若切点明确，则“连半径，证垂直”。

常有手法有：全等转变；平行转变；直径转变；中线转变等；有时可经过计算联合相像、勾股定理证垂直；（ 2）若切点不明确，则“作垂直，证半径”。

常有手法：角均分线定理；等腰三角形三线合一，隐蔽角均分线；4、考题形式剖析：主要以解答题的形式出现, 第 1 问主要判断切线、证明角或线段相等；第2 问主要与圆有关的计算：①求线段长（或面积）；②求线段比；③求角度的三角函数值（本质仍是求线段比）【典例剖析】典例精讲，方法提炼，精准提分【例1】（2021·北京·中考真题）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E．（1）求证：∠BAD=∠CAD；（2）连接BO并延长，交AC于点F，交⊙O于点G，连接GC．若⊙O的半径为5，OE=3，求GC和OF的长．【答案】（1）见详解；（2）GC=6，OF=2511【解析】【分析】（1）由题意易得BD⌢=CD⌢，然后问题可求证；（2）由题意可先作图，由（1）可得点E为BC的中点，则有OE=12CG,OE//CG，进而可得△AOF∽△CGF，然后根据相似三角形的性质可进行求解．【详解】（1）证明：∵AD是⊙O的直径，AD⊥BC，∵BD⌢=CD⌢，∵∠BAD=∠CAD；（2）解：由题意可得如图所示：由（1）可得点E为BC的中点，∵点O是BG的中点，∵OE=12CG,OE//CG，∵△AOF∽△CGF，∵OA CG =OFGF，∵OE=3，∵CG=6，∵⊙O的半径为5，∵OA=OG=5，∵5 6=OFGF，∵OF=511OG=2511．【点睛】本题主要考查垂径定理、三角形中位线及相似三角形的性质与判定，熟练掌握垂径定理、三角形中位线及相似三角形的性质与判定是解题的关键．【例2】（2022·北京·中考真题）如图，AB是⊙O的直径，CD是⊙O的一条弦，AB⊥CD,连接AC,OD.(1)求证：∠BOD=2∠A;(2)连接DB,过点C作CE⊥DB,交DB的延长线于点E，延长DO,交AC于点F，若F为AC的中点，求证：直线CE为⊙O的切线．【答案】(1)答案见解析(2)答案见解析【解析】【分析】（1）设AB交CD于点H，连接OC，证明RtΔCOH≅RtΔDOH，故可得∠COH=∠DOH，于是BC⌢=BD⌢，即可得到∠BOD=2∠A；（2）连接，解出∠COB=60°，根据AB为直径得到∠ADB=90°，进而得到∠ABD=60°，即可证明OC//DB，故可证明直线CE为⊙O的切线．(1)证明：设AB交CD于点H，连接OC，由题可知，∴OC=OD，∠OHC=∠OHD=90°，∵OH=OH，∴RtΔCOH≅RtΔDOH(HL)，∴∠COH=∠DOH，∴BC⌢=BD⌢，∴∠COB=∠BOD，∵∠COB=2∠A，∴∠BOD=2∠A；(2)证明：连接AD，∵OA=OD，∴∠OAD=∠ODA，同理可得：∠OAC=∠OCA,∠OCD=∠ODC，∵点H是CD的中点，点F是AC的中点，∴∠OAD=∠ODA=∠OAC=∠OCA=∠OCD=∠ODC，∵∠OAD+∠ODA+∠OAC+∠OCA+∠OCD+∠ODC=180°，∴∠OAD=∠ODA=∠OAC=∠OCA=∠OCD=∠ODC=30°，∴∠COB=2∠CAO=2×30°=60°，∵AB为⊙O的直径，∴∠ADB=90°，∴∠ABD=90−∠DAO=90°−30°=60°，∴∠ABD=∠COB=60°，∴OC//DE，∵CE⊥BE，∴CE⊥OC，∴直线CE为⊙O的切线．【点睛】本题主要考查三角形全等的判定与性质，同弧所对的圆周角相等，圆周角定理，直线平行的判定与性质，三角形的内角和公式，证明三角形全等以及证明平行线是解题的关键．【真题再现】必刷真题，关注素养，把握核心1．（2013·北京·中考真题）如图，AB是∵O的直径，PA，PC分别与∵O 相切于点A，C，PC交AB的延长线于点D，DE∵PO交PO的延长线于点E．（1）求证：∵EPD=∵EDO（2）若PC=6，tan∵PDA=，求OE的长．【答案】（1）见解析（2）√5【解析】【详解】试题分析：（1）根据切线长定理和切线的性质即可证明：∵EPD=∵EDO；（2）连接OC，利用tan∵PDA=34，可求出CD=4，再证明∵OED∵∵DEP，根据相似三角形的性质和勾股定理即可求出OE的长．试题解析：（1）证明：PA，PC与∵O分别相切于点A，C，∵∵APO=∵EPD且PA∵AO，∵∵PAO=90°，∵∵AOP=∵EOD，∵PAO=∵E=90°，∵∵APO=∵EDO，∵∵EPD=∵EDO；（2）解：连接OC，∵PA=PC=6，∵tan∵PDA=34，∵在Rt∵PAD中，AD=8，PD=10，∵CD=4，∵tan∵PDA=34，∵在Rt∵OCD中，OC=OA=3，OD=5，∵∵EPD=∵ODE，∵∵OED∵∵DEP，∵PD DO =PEDE=EDOE=2，∵DE=2OE在Rt∵OED中，OE2+DE2=OD2，即5OE2=52，∵OE=√5．考点：1．切线的性质；2．相似三角形的判定与性质．⌢的中点，⊙O的切线BD交AC的延长线于点D，E是2．（2014·北京·中考真题）如图，AB是⊙O的直径，C是ABOB的中点，CE的延长线交切线BD于点F，AF交⊙O于点H，连接BH.（1）求证：AC=CD；（2）若OB=2，求BH的长.【答案】(1)证明见解析(2)BH=4√55【解析】【分析】⌢的中点，可知OC∵AB，又BD是切(1)连接OC，若要证明C为AD的中点，只需证OC//BD，已知C是AB线，可知BD∵AB，问题得证(2)由（1）及E为OB中点可知∵COE∵∵FBE，从而可知BF=CO=BO=2，由勾股定理可得AF的长，由面积法即可求出BH的长【详解】（1）连接OC⌢的中点，AB是∵O的直径∵C是AB∵OC∵AB∵BD是∵O的切线∵BD∵AB∵OC//BD∵AO=BO∵AC=CD（2）∵E是OB的中点∵OE=BE在∵COE和∵FBE中{∠CEO=∠FEB OE=BE ∠COE=∠FBE∵∵COE∵∵FBE（ASA)∵BF=CO∵OB=2∵BF=2∵AF=√AB2+BF2=2√5∵AB是直径∵BH∵AFBH=AB⋅BFAF=2√5=4√55考点：1、平行线分线段成比例定理；2、切线的性质；3勾股定理；4、全等三角形3．（2015·北京·中考真题）如图，AB是∵O的直径，过点B作∵O的切线BM，弦CD//BM，交AB于点F，且DA⌢=DC⌢，连接AC，AD，延长AD交BM于点E．（l）求证：∵ACD是等边三角形；（2）连接OE，若DE＝2，求OE的长．【答案】（1）见解析；（2）2√7【解析】【分析】（1）根据切线的定义可知AB∵BM，又∵BM//CD，∵AB∵CD，根据圆的对称性可得AD=AC，再根据等弧对等弦得DA=DC，即DA=DC=AC，所以可得∵ACD是等边三角形；（2）∵ACD为等边三角形，AB∵CD，由三线合一可得∵DAB=30°，连接BD，根据直径所对的角是直角和三角形的内角和可得∵∵EBD＝∵DAB＝30°，因为DE＝2，求出BE＝4，根据勾股定理得BD=2√3，直角三角形中30°角所对的直角边等于斜边的一半得，AB=4√3，OB=2√3，在Rt∵OBE中，根据勾股定理即可得出OE的长．【详解】解：（1）∵BM是∵O切线，AB为∵O直径，∵AB∵BM，∵BM//CD，∵AB∵CD，∵AD＝AC，∵AD＝AC，∵DA＝DC，∵DC＝AD，∵AD＝CD＝AC，∵∵ACD为等边三角形.（2）∵ACD为等边三角形，AB∵CD，∵∵DAB＝30°，连结BD，∵BD∵AD.∵EBD＝∵DAB＝30°，∵DE＝2，∵BE＝4，BD=2√3，AB=4√3，OB=2√3，在Rt∵OBE中，OE=√OB2+BE2=√12+16=2√7．【点睛】本题考查圆的有关性质，直角三角形的性质；勾股定理．4．（2016·北京·中考真题）如图，AB为∵O的直径，F为弦AC的中点，连接OF并延长交AC⌢于点D，过点D作∵O的切线，交BA的延长线于点E．（1）求证：AC∵DE；（2）连接CD，若OA=AE=a，写出求四边形ACDE面积的思路．【答案】（1）证明见解析；（2）32a2.【解析】【详解】试题分析：（1）欲证明AC∵DE，只要证明AC∵OD，ED∵OD即可．（2）作DM∵OA于M，连接CD，CO，AD，首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE=AE•DM，只要求出DM即可．试题解析：（1）∵ED与∵O相切于D，∵OD∵DE，∵F为弦AC中点，∵OD∵AC，∵AC∵DE．（2）作DM∵OA于M，连接CD，CO，AD．首先证明四边形ACDE是平行四边形，根据S平行四边形ACDE=AE•DM，只要求出DM即可．∵AC∵DE，AE=AO，∵OF=DF，∵AF∵DO，∵AD=AO，∵AD=AO=OD，∵∵ADO是等边三角形，同理∵CDO 也是等边三角形，∵∵CDO=∵DOA=60°，AE=CD=AD=AO=DD=a，∵AO∵CD，又AE=CD，∵四边形ACDE是平行四边形，易知DM=√32a，∵平行四边形ACDE面积=√32a2．考点：切线的性质．5．（2017·北京·中考真题）如图，AB是∵O的一条弦，E是AB的中点，过点E作EC∵OA于点C，过点B 作∵O的切线交CE的延长线于点D．（1）求证：DB=DE;（2）若AB=12，BD=5，求∵O的半径.【答案】（1）证明见解析；（2）152【解析】【详解】试题分析:(1)由切线性质及等量代换推出∵4=∵5，再利用等角对等边可得出结论；（2）由已知条件得出sin∵DEF和sin∵AOE的值，利用对应角的三角函数值相等推出结论.试题解析：（1）∵DC∵OA，∵∵1+∵3=90°，∵BD为切线，∵OB∵BD，∵∵2+∵5=90°，∵OA=OB，∵∵1=∵2，∵∵3=∵4，∵∵4=∵5，在∵DEB中，∵4=∵5，∵DE=DB.(2)作DF∵AB于F，连接OE，∵DB=DE，∵EF=12BE=3，在RT∵DEF中，EF=3，DE=BD=5，EF=3 ，∵DF=√52−32=4∵sin∵DEF=DFDE = 45，∵∵AOE=∵DEF，∵在RT∵AOE中，sin∵AOE=AEAO =45，∵AE=6，∵AO=152.【点睛】本题考查了圆的性质，切线定理，三角形相似，三角函数等知识，结合图形正确地选择相应的知识点与方法进行解题是关键.6．（2018·北京·中考真题）如图，AB是⊙O的直径，过⊙O外一点P作⊙O的两条切线PC，PD，切点分别为C，D，连接OP，CD．（1）求证：OP⊥CD；（2）连接AD，BC，若∠DAB=50°，∠CBA=70°，OA=2，求OP的长．【答案】（1）证明见解析；（2）4√33.【解析】【分析】（1）根据切线的性质定理得到PC=PD，OP平分∠CPD．根据等腰三角形的性质即可得到PQ⊥CD于Q，即OP⊥CD．（2）连接OC、OD．根据等腰三角形的性质和平角的性质得到∠COD=180°−∠AOD−∠BOC=60°．进而得到∠DOQ=12∠COD=30°．在Rt△ODP中，解直角三角形即可.【详解】（1）证明：∵PC、PD与⊙O相切于C、D．∵PC=PD，OP平分∠CPD．在等腰△PCD中，PC=PD，PQ平分∠CPD．∵PQ⊥CD于Q，即OP⊥CD．（2）解：连接OC、OD．∵OA=OD∵∠OAD=∠ODA=50°∵∠AOD=180°−∠OAD−∠ODA=80°同理：∠BOC=40°∵∠COD=180°−∠AOD−∠BOC=60°．在等腰△COD中，OC=OD．OQ⊥CD∵∠DOQ=12∠COD=30°．∵PD与⊙O相切于D．∵OD⊥DP．∵∠ODP=90°．在Rt△ODP中，∠ODP=90°，∠POD=30°∵OP=ODcos∠POD=OAcos30°=√32=43√3．【点睛】本题考查了切线的性质和判定，圆周角定理，解直角三角形等，题目比较典型，综合性比较强，难度适中．7．（2019·北京·中考真题）在平面内，给定不在同一直线上的点A，B，C，如图所示．点O到点A，B，C 的距离均等于a（a为常数），到点O的距离等于a的所有点组成图形G，∠ABC的平分线交图形G于点D，连接AD，CD．（1）求证：AD=CD；（2）过点D作DE⊥BA，垂足为E，作DF⊥BC，垂足为F，延长DF交图形G于点M，连接CM．若AD=CM，求直线DE与图形G的公共点个数．【答案】依题意画出图形G为∵O，如图所示,见解析；（1）证明见解析；（2）直线DE与图形G的公共点个数为1个.【解析】【分析】（1）根据线段垂直平分线的性质得出图形G为∵O，再根据在同圆或等圆中相等的圆周角所对的弧相等得⌢=CD⌢；从而得出弦相等即可．出AD（2）先根据HL得出△CDF∵∵CMF，得出DF=MF，从而得出BC为弦DM的垂直平分线，根据圆心角和圆周角之间的关系定理得出∵ABC=∵COD，再证得DE为∵O的切线即可【详解】如图所示，依题意画出图形G为∵O，如图所示（1）证明：∵BD平分∵ABC，∵∵ABD=∵CBD，⌢=CD⌢，∵AD=CD∵AD（2）解：∵AD=CD，AD=CM，∵CD=CM.∵DF∵BC，∵∵DFC=∵CFM=90°在Rt△CDF和Rt△CMF中{CD=CMCF=CF，∵Rt△CDF∵Rt△CMF（HL），∵DF=MF，∵BC为弦DM的垂直平分线∵BC为∵O的直径，连接OD∵∵COD=2∵CBD，∵ABC=2∵CBD，∵∵ABC=∵COD，∵OD∵BE.又∵DE∵BA，∵∵DEB=90°，∵∵ODE=90°，即OD∵DE，∵DE为∵O的切线.∵直线DE与图形G的公共点个数为1个.【点睛】本题考查了垂直平分线的性质，圆心角和圆周角之间的关系定理，切线的判定，熟练掌握相关的知识是解题的关键．8．（2020·北京·中考真题）如图，AB为∵O的直径，C为BA延长线上一点，CD是∵O的切线，D为切点，OF∵AD于点E，交CD于点F．（1）求证：∵ADC=∵AOF；（2）若sinC=13，BD=8，求EF的长．【答案】（1）见解析；（2）2．【解析】【分析】（1）连接OD，根据CD是∵O的切线，可推出∵ADC+∵ODA=90°，根据OF∵AD，∵AOF+∵DAO=90°，根据OD=OA，可得∵ODA=∵DAO，即可证明；（2）设半径为r，根据在Rt∵OCD中，sinC=13，可得OD=r，OC=3r，AC=2r，由AB为∵O的直径，得出∵ADB=90°，再根据推出OF∵AD，OF∵BD，然后由平行线分线段成比例定理可得OEBD =OAAB=12，求出OE，OFBD =OCBC=34，求出OF，即可求出EF．【详解】（1）证明：连接OD，∵CD是∵O的切线，∵OD∵CD，∵∵ADC+∵ODA=90°，∵OF∵AD，∵∵AOF+∵DAO=90°，∵OD=OA，∵∵ODA=∵DAO，∵∵ADC=∵AOF；（2）设半径为r，在Rt∵OCD中，sinC=13，∵OD OC =13，∵OD=r，OC=3r，∵OA=r，∵AC=OC-OA=2r，∵AB为∵O的直径，∵∵ADB=90°，又∵OF∵AD，∵OF∵BD，∵OE BD =OAAB=12，∵OE=4，∵OF BD =OCBC=34，∵OF=6，∵EF=OF−OE=2．【点睛】本题考查了平行线分线段成比例定理，锐角三角函数，切线的性质，直径所对的圆周角是90°，灵活运用知识点是解题关键．【模拟精练】押题必刷，巅峰冲刺，提分培优一、解答题1．（2022·北京市广渠门中学模拟预测）如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，E为BC⌢上一点，过点E作⊙O的切线，分别交DC,AB的延长线于点F，G连接AE，交CD于点P．(1)求证：EF=FP；(2)连接AD，若AD∥FG,CD=8,cosF=45，求⊙O半径．【答案】(1)见解析(2)256【解析】【分析】（1）连接OE，要使EF=FP，需要∵FEP=∵FPE，通过切线和垂直的已知条件，利用等角的余角相等可得∵FEP=∵FPE，结论可得．（2）设圆的半径为r，在Rt∵ODH中，利用勾股定理可以求得半径r．(1)证明：连接OE，∵EF是圆的切线，∵OE∵EF．∵∵OEF=90°．∵∵OEA+∵AEF=90°．∵CD∵AB，∵∵AHC=90°．∵∵OAE+∵APH=90°．∵OA=OE，∵∵OAE=∵OEA．∵∵AEF=∵APH．∵∵APH=∵EPF，∵∵EPF=∵AEF．∵EF=PF．(2)连接OD，设圆的半径为r，∵直径AB∵CD于H，CD=8，∵CH=DH=4．∵AD∵FG，∵∵ADH=∵F．∵cos∵ADH=cos F=45∴AD=CHcos∠ADH=5∴AH=√AD2−DH2=3∵OH=OA-AH=r-3．在Rt∵ODH中，∵OH2+DH2=OD2,∵（r-3）2+42=r2．∴OE=r=25 6【点睛】本题主要考查了圆的切线的性质，勾股定理，垂径定理，圆周角定理和解直角三角形的知识．使用添加圆中常添加的辅助线是解题的关键．2．（2022·北京房山·二模）如图，已知AB是半⊙O的直径，点H在⊙O上，E是HB⌢的中点，连接AE，过点E作EC⊥AH交AH的延长线于点C．过点E作EF⊥AB于点F．(1)求证：CE是⊙O的切线；(2)若FB=2,EFAF =√22，求OF的长．【答案】(1)见解析(2)OF=1【解析】【分析】（1）连接OE，由于E为HB⌢的中点，根据圆周角定理可知∵1=∵2，而AO=EO，则∵3=∵2，于是∵1=∵3，根据平行线的判定知OE∥AC，而AC∵CE，根据平行线的性质知∵OEC=90°，即OE∵CE，根据切线的判定可知CE是∵O的切线；（2）由于AB是直径，故∵AED=90°，而EF∵AB，易知∵2=∵4=∵1，那么tan∵1=tan∵2=tan∵4=EFAF =√22，在Rt∵EFB中，利用正切可求出EF，同理在Rt∵AEF中，可求出AF，得半径OB=3，进而可求出OF．(1)证明：连结OE，∵点E为HB⌢的中点，∵ ∵1=∵2，∵OE=OA，∵∵3=∵2，∵∵3=∵1，∵OE∵AC，∵AC∵CE，∵OE∵CE，∵点E在∵O上，∵CE是∵O的切线．(2)连结EB，∵AB是∵O的直径，∵∵AEB=90°，∵EF∵AB于点F，∵∵AFE=∵EFB=90°，∵∵2+∵AEF=∵4+∵AEF=90°，∵∵2=∵4=∵1，∵EF AF =√22，∵tan∠1=√22，∵tan∵4 =√22，在Rt∵EFB中，∵EFB=90°，FB=2，tan∵4 =√22，∵EF=2√2，设OE=x，则OB= x．∵FB=2，∵OF=x-2，∵在Rt∵OEF中，∵EFO=90°，∵x2=(x-2)2+(2√2)2，∵x=3，∵OF=1．【点睛】本题主要考查了切线的判定，圆周角定理，平行线的性质，等腰三角形的性质，勾股定理，三角函数的定义，作出辅助线，熟练掌握圆的切线判定方法，是解题的关键．3．（2022·北京朝阳·二模）如图，AB为∵O的直径，C为∵O上的一点，OD⊥AB交AC于点E，DE=DC．(1)求证：DC是∵O的切线；(2)若OA=4，OE=2，求cos D．【答案】(1)见解析(2)35【解析】【分析】（1）连接OC．证∵OCD=90°，即可得出结论；（2）先求出OC=4．再同由勾股定理求出DC=3，OD=5，最后由余弦定义cosD=DC求解．OD(1)证明：如图，连接OC．∵OD⊥AB交AC于点E，∵∠AOD=90∘,∵∠A+∠AEO=90∘．∵∠AEO=∠DEC，∵∠A+∠DEC=90∘．∵DE=DC，∵∠DEC=∠DCE,∵OA=OC，∵∠A=∠ACO，∵∵OCD=∠ACO+∠DCE=90∘，∵DC⊥OC，∵DC是∵O的切线，(2)解：∵∠OCD=90∘，∵DC2+OC2=OD2，∵OA=4，∵OC=4．设DC=x，∵OE=2，∵x2+42=(x+2)2．解得x=3，∵DC=3，OD=5．∵在Rt∵OCD中，cosD=DCOD =35．【点睛】本师考查切线的判定，解直角三角形，掌握切线的判定定理是解题的关键．4．（2022·北京东城·二模）如图，在△ABC中，AB>AC，∠BAC=90°，在CB上截取CD=CA，过点D作DE⊥AB 于点E，连接AD，以点A为圆心、AE的长为半径作⊙A．(1)求证：BC是∵A的切线；(2)若AC=5，BD=3，求DE的长．【答案】(1)见解析(2)158【解析】【分析】（1）过点A作AF⊥BC于F，根据同旁内角互补证得DE//AC，可证得∠DAC=∠ADE，利用AAS可证得△ADE≅△ADF，则可证得AF=AE，根据切线的判定即可求证结论．（2）根据角相等即可得△BDE∼△BCA，利用相似三角形的性质即可求解．(1)过点A作AF⊥BC于F，如图所示，∵DE⊥AB，∴∠AED=90°，∵∠BAC=90°，∴∠AED+∠BAC=180°，∴DE//AC，∴∠DAC=∠ADE，∵CD=AC，∴∠DAC=∠ADC，∴∠ADE=∠ADC，在△ADE和△ADF中，{∠AED=∠AFD ∠ADE=∠ADFAD=AD，∴△ADE≅△ADF(AAS)，∴AF=AE，且AE为⊙A的半径，∴AF是⊙A的半径，∴BC是⊙A的切线．(2)∵AC=5，∴CD=AC=5，∴BC=BD+CD=3+5=8，∵∠DEB=∠BAC=90°，∠B=∠B，∴△BDE∼△BCA，∴DEAC =BDBC，∴DE5=38，解得DE=158，∴DE的长为158．【点睛】本题考查了切线判定、三角形全等的判定及性质、相似三角形的判定及性质，熟练掌握全等三角形的判定及性质，切线的判定及相似三角形判定及性质是解题的关键．5．（2022·北京平谷·二模）如图，AB是∵O的直径，过B作∵O的切线，与弦AD的延长线交于点C，AD=DC，E是直径AB上一点，连接DE并延长与直线BC交于点F，连接AF．(1)求证：AD⌢=BD⌢；(2)若tan∠BAF=14，∵O的半径长为6，求EF的长．【答案】(1)证明见解析(2)√13【解析】【分析】（1）连接BD，根据圆周角定理、切线性质以及题中AD=DC可得∠BAD=∠ABD=∠CBD=∠C=45°，从而得出结论；（2）连接OD，由（1）知DO⊥AB，得出ΔDOE∼ΔFBE，得出DOBF =OEBE，在RtΔABF中，tan∠BAF=14，∵O的半径长为6，解得BF=3，从而63=OEBE，设BE=x,OE=2x，则BE+OE=OB=6，解得x=2，即BE=2，在RtΔEBF中，利用勾股定理得结论．(1)证明：连接BD，如图所示：∵AB是∵O的直径，∴∠ABD=90°，即BD⊥AC，∵过B作∵O的切线，∴AB⊥BC，∵AD=DC，∴∠BAD=∠ABD=∠CBD=∠C=45°，∴BD=AD，∴AD⌢=BD⌢；(2)解：连接OD，如图所示：在等腰RtΔABD中，∠ADB=90°，∴DO⊥AB，∵∠DEO=∠BEF,∠DOE=∠FBE=90°，∴ΔDOE∼ΔFBE，∴DOBF =OEBE，在RtΔABF中，tan∠BAF=14，∵O的半径长为6，则tan∠BAF=14=BFAB=BF12，解得BF=3，∴63=OEBE，设BE=x,OE=2x，则BE+OE=x+2x=OB=6，解得x=2，在RtΔEBF中，∠EBF=90°，BE=2,BF=3，则利用勾股定理得EF=√BE2+BF2=√22+32=√13．【点睛】本题考查圆综合，涉及到圆周角定理、直角三角形的性质、切线的性质、相似三角形的判定与性质、正切函数求线段长、勾股定理等知识点，根据题意准确作出辅助线是解决问题的关键．6．（2022·北京北京·二模）如图，AB为⊙O的直径，BD⌢=CD⌢，过点A作⊙O的切线，交DO的延长线于点E．(1)求证：AC∥DE；(2)若AC=2，t an E=1，求OE的长．2【答案】(1)见解析(2)5【解析】【分析】（1）根据同圆中，等弧相等性质可得∠BAD=∠CAD，再利用等边对等角及等量代换即可证得∠CAD=∠D从而证得结论．（2）连接BC，利用直径所对的圆周角是直角结合（1）中平行线的性质可求得∠B=∠E，从而得到tanB=tanE，根据直角三角形的锐角三角函数的值结合勾股定理即可求得答案．(1)⌢=CD⌢，证明：∵BD∵∠BAD=∠CAD，∵OA=OD，∵∠D=∠BAD，∵∠CAD=∠D，∵AC∥DE．(2)如图，连接BC，∵AB为⊙O的直径，∵∠C=90°，∵AC∥DE，∵∠BAC=∠AOE，∵AE是⊙O的切线，∵OA⊥AE，∵∠C=∠OAE=90°，∵∠B=∠E，∵tanB=tanE=12，在Rt△OAE中，tanB=12，AC=2，∵tanB=ACBC =2BC=12，解得BC=4，∴AB=√AC2+BC2=√22+C2=2√5，∵OA=√5，∵在Rt△OAE中，tanE=12，∵tanE=AOAE =√5AE=12，解得AE=2√5，∵OE=√OA2+AE2=√(√5)2+(2√5)2=5．【点睛】本题考查了平行线的判定及性质、切线的性质、圆周角定理、锐角三角函数值及勾股定理解直角三角形的应用，熟练掌握圆周角定理及平行线的判定及锐角三角函数值及勾股定理解直角三角形的应用是解题的关键．7．（2022·北京丰台·二模）如图，AB是∵O的直径，C为BA延长线上一点，过点C作∵O的切线，切点为D，过点B作BE∵CD于点E，连接AD，BD．(1)求证：∠ABD=∠DBE；(2)如果CA＝AB，BD＝4，求BE的长．【答案】(1)证明见解析；(2)43√6．【解析】【分析】（1）如图1，连接OD，由CD切∵O于点A得OD⊥CD，从而得OD∥BE，进而得∠ODB=∠DBE，另外由∠ODB=∠ABD即可得出结论；（2）解：设OA=x，则CA=AB=2x，CO=CA+OA=3x，先证明△COD∽△CBE，得ODBE =COCB=3x4x从而有x=34BE，另外由△ABD∽△DBE得ABBD =DBBE，即可求得BE=43√6．(1)证明：如图，连接OD，∵CD切∵O于点A，∴OD⊥CD，∵BE∵CD，∴OD∥BE，∴∠ODB=∠DBE，∵OD=OB，∴∠ODB=∠ABD，∴∠ABD=∠DBE；(2)解：如图，设OA=x，则CA=AB=2x，CO=CA+OA=3x，∵OD∥BE，∴∠CDO=∠E,∠COD=∠CBE，∴△COD∽△CBE，∴ODBE =COCB=3x4x即xBE=34，∴x=34BE，∵AB是∵O的直径，∴∠ADB=90°，∵BE∵CD，∴∠E=∠ADB=90°，∵∠ABD=∠DBE，∴△ABD∽△DBE，∴ABBD =DBBE，∵BD＝4，∴2×34BE4=4BE，解得BE=43√6．【点睛】本题主要考查了圆的切线、勾股定理、相似三角形的判定及性质以及平行线的判定及性质，熟练掌握相似三角形的判定及性质是解题的关键．8．（2022·北京密云·二模）如图，在△ABC中，AB=BC，以BC为直径的∵O与AC交于点D，DE是∵O的切线．(1)计算∠AED的度数；(2)若tanA=12，BC=2√5，求线段DE的长．【答案】(1)90°(2)4√55【解析】【分析】（1）连接OD，BD，由直径所对圆周角等于90度得∵BDO+∵ODC=∵BDC=90°，再由切线的性质得∵BDE+∵BDO=∵ODE=90°，所以∵BDE=∵ODC，∵ADE=∵BDO，然后由OB-OC，则∵C=∵ODC，BA=BC，则∵C=∵A，所以∵A+∵ADE=90°，最后由三角形内角和定理即可求解；（2）由（1）知：∵AED=∵ADB=90°，则tan∵A=DEAE =BDAD=12，所以AD=2BD，AE=2DE，又因为AB=BC=2√5，在Rt△ADB中，由勾股定理，可求出BD=2，AD=4，再在Rt△ADE中，由勾股定理可求出DE长．(1)解：如图，连接OD，BD，∵BC是∵O的直径，∵∵BDO+∵ODC=∵BDC=90°，∵∵BDE+∵ADE=∵BDA=90°，∵DE是∵O的切线，∵∵BDE+∵BDO=∵ODE=90°，∵∵BDE=∵ODC，∵ADE=∵BDO，∵OD=OC，∵∵C=∵ODC，∵∵C+∵ADE=∵C+∵BDO=90°，∵BA=BC，∵∵C=∵A，∵∵A+∵ADE=90°，∵∵AED=180°-（∵A+∵ADE）=90°；(2)解：由（1）知：∵AED=∵ADB=90°，∵tan∵A=DEAE =BDAD=12，∵AD=2BD，AE=2DE，∵AB=BC=2√5，∵在Rt△ADB中，由勾股定理，得AD2+BD2=AB2，∵（2BD）2+BD2=（2√5）2，∵BD=2，∵AD=4，在Rt△ADE中，由勾股定理，得AE2+DE2=AD2，（2DE）2+DE2=42，∵DE=4√5．5【点睛】本题考查切线的性质，圆周角定理的推论，勾股定理，正切的定义，熟练掌握切线的性质、圆周角定理的推论、正切的定义是解题的关键．9．（2022·北京大兴·二模）如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA 为半径的⊙O经过点D．(1)求证：BC是⊙O切线；(2)若BD=5,DC=3，求AC的长．【答案】(1)见解析(2)6【解析】【分析】（1）要证BC是∵O的切线，只要连接OD，再证OD∵BC即可．（2）过点D作DE∵AB，根据角平分线的性质可知CD=DE=3，由勾股定理得到BE的长，再通过证明△BDE∵∵BAC，根据相似三角形的性质得出AC的长．(1)连接OD；∵AD是∵BAC的平分线，∵∵1=∵3．∵OA=OD，∵∵1=∵2．∵∵2=∵3．∵OD∵AC．∵∵ODB=∵ACB=90°．∵OD∵BC．∵OD是∵O的半径，∵BC是∵O切线．(2)过点D作DE∵AB，∵AD是∵BAC的平分线，∵CD=DE=3．在Rt△BDE中，∵BED=90°，由勾股定理得：BE=√BD2−DE2=√52−32=4,∵∵BED=∵ACB=90°，∵B=∵B，∵∵BDE∵∵BAC．∵BE BC =DEAC．∵4 8=3AC．∵AC=6．【点睛】^$本题综合性较强，既考查了切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．同时考查了角平分线的性质，勾股定理得到BE的长，及相似三角形的性质．10．（2022·北京西城·二模）如图，AB是⊙O的直径，CB，CD分别与⊙O相切于点B，D，连接OC，点E 在AB的延长线上，延长AD，EC交于点F．(1)求证：FA∥CO；(2)若FA=FE，CD=4，BE=2，求F A的长．【答案】(1)见解析(2)3√5【解析】【分析】（1）连接OD，证明△CDO∵△CBO（SSS），得∵COD=∵COB，即∵BOD=2∵COB，又因为OD=OA，得∵OAD=∵ODA，所以∵BOD=∵OAD+∵ODA=2∵OAD，即可证得∵COB=∵OAD，即可由平行线的判定定理，得出结论；（2）由F A=FE，得∵F AE=∵FEA，又由（1）知：∵COB=∵OAD，所以∵COE=∵CEO，则CO=CE，又由切线的性质得OB∵CB，根据等腰三角形“三线合一”性质得OB=BE=2，从而求出AE=6，OE=4，再由切线性质得CB=CD=4，然后在Rt△CBE中，由勾股定理，得CF=√CB2+BE2=√42+22=2√5，最后证△EOC∵△EAF，得OEAE =CEFE，即46=2√5FE，可求得FE=3√5，即可由F A=FE得出答案．(1)证明：如图，连接OD，∵CB，CD分别与⊙O相切于点B，D，∵CD=CB，∵OD=OB，OC=OC，∵∵CDO∵△CBO（SSS），∵∵COD=∵COB，即∵BOD=2∵COB，∵OD=OA，∵∵OAD=∵ODA，∵∵BOD=∵OAD+∵ODA=2∵OAD，∵2∵COB=2∵OAD，即∵COB=∵OAD，∵F A∥OC；(2)解：∵F A=FE，∵∵F AE=∵FEA，由（1）知：∵COB=∵OAD，∵∵COE=∵CEO，∵CO=CE，∵CB是∵O的切线，∵OB∵CB，∵OB=BE=2，∵OA=OB=2，∵AE=6，OE=4，∵CB、CD是∵O的切线，∵CB=CD=4，在Rt△CBE中，由勾股定理，得CE=√CB2+BE2=√42+22=2√5，∵F A∥OC，∵∵EOC∵∵EAF，∵OE AE =CEFE，即46=2√5FE，∵FE=3√5，∵F A=FE=3√5．【点睛】本题考查切线的性质，全等三角形的判定与性质，相似三角形的判定与性质，等腰三角形的判定与性质，熟练掌握相关性质与判定是解题的关键．11．（2022·北京顺义·二模）如图，△ABC内接于⊙O，AB是⊙O的直径，点D在AB的延长线上，且∠BCD=∠A，点E为AC的中点，连接OE并延长与DC的延长线交于点F．(1)求证：CD是⊙O的切线；(2)若CD=4，tanA=12，求CF的长．【答案】(1)见解析(2)6【解析】【分析】（1）根据AB是⊙O的直径，可得∠ACB=90°，由OA=OC得∠A=∠ACO，结合已知条件，根据可得∠BCD+∠OCB=90°，即可得证；（2）证明△DCB∽△DAC，得出CDAD =DBDC=CBAC，根据tanA=12，可得CBAC=12，从而求得DB的长，进而求得OD的长，由点E为AC的中点，根据垂径定理以及∠ACB=90°，证明OF∥BC，根据平行线分线段成比例即可求解．(1)证明：如图，连接OC，∵OA=OC，∴∠A=∠ACO，∵∠BCD=∠A，∴∠BCD=∠ACO∵AB是⊙O的直径，∴∠ACB=90°,∴∠ACO+∠OCB=90°，∴∠BCD+∠OCB=90°，即∠OCD=90°，∵OC是半径，∴CD是⊙O的切线；(2)∵∠BCD=∠A，∠D=∠D，∴△DCB∽△DAC，∴CDAD =DBDC=CBAC，∵tanA=12，可得CBAC=12，∴4AD =DB4=12，∴AD=8,DB=2，∴OB=12AB=12(AD−BD)=3，∵点E为AC的中点，∴OF⊥AC，又∵∠ACB=90°，∴OF∥BC，∴DCCF =BDOB，即4CF=23，∴CF=6．【点睛】本题考查了切线的判定，直径所对的圆周角是直角，垂径定理的推论，相似三角形的性质与判定，正切，平行线分线段成比例，掌握以上知识是解题的关键．12．（2022·北京房山·二模）如图，在△ABC中，∠C=90°,∠ABC的平分线BE交AC于点E，过点E作直线BE 的垂线于交AB于点F，⊙O是△BEF的外接圆．(1)求证：AC是⊙O的切线；(2)过点E作EH⊥AB于点H，若CD=2，求HF的长度．【答案】(1)见详解(2)2【解析】【分析】（1）连接OE，先证明BF是圆的直径，OE是圆的半径，再证明OE∥BC在，则有∵OEA=∵C=90°，结论得证；（2）连接ED，根据角平分线的性质证明EH=EC，再证∵EHF∵∵ECD，则HF可求．(1)连接OE，如图，∵EF∵BE，∵∵BEF=90°，∵∵O是∵BEF的外接圆，∵BF是∵O的直径，OE是∵O的半径，∵∵OEB=∵OBE，∵BE是∵ABC的角平分线，∵∵OBE=∵CBE，∵∵OEB=∵CBE，∵OE∥BC，∵∵OEA=∵C=90°，即OE∵AC，∵OE是半径，∵AC是∵O的切线；(2)连接ED，如图，∵BE平分∵ABC，且EH∵BA，EC∵BC，∵EH=EC，∵四边形BDEF是∵O的内接四边形，∵∵EFH=∵EDC，∵∵EHF=∵C=90°，∵∵EHF∵∵ECD，∵HF=CD=2，即HF的值为2．【点睛】此题考查了圆的切线的判定、圆周角定理、平行线的判定与性质、全等三角形的判定与性质等知识，解题的关键是正确的作出所需辅助线．13．（2022·北京昌平·二模）如图，在△ABC中，∠C=90°，BC，AC与⊙O交于点F，D，BE为⊙O直径，点E在AB上，连接BD，DE，∠ADE=∠DBE．(1)求证：AC是⊙O的切线；(2)若sinA=35，⊙O的半径为3，求BC的长．【答案】(1)过程见详解(2)245【解析】【分析】（1）连接OD，OD=OB=OE，即有∵OBD=∵ODB，∵ODE=∵OED，再根据BE是直径，得到∵BDE=90°=∵DBE+∵DEB=∵ODB+∵ODE，即有∵DBE+∵ODE=90°，再根据∵ADE=∵DBE，有∵ADE+∵ODE=90°，即有OD∵AC，则结论得证；（2）先证OD∥BC，则有BCOD =ABOA，利用sinA=ODOA=35可求出OA，即可求出BC的值．(1)连接OD，如图，∵OD=OB=OE，∵∵OBD=∵ODB，∵ODE=∵OED，∵BE是直径，∵∵BDE=90°=∵DBE+∵DEB=∵ODB+∵ODE，∵∵DBE+∵ODE=90°，∵∵ADE=∵DBE，∵∵ADE+∵ODE=90°，∵OD∵AC，∵OD为半径，∵AC是∵O的切线；(2)根据（1）的结论，有OD∵AC，∵∵C=90°，∵BC∵AC，∵OD∥BC，∵BC OD =ABOA，∵在Rt△ADO中，sinA=ODOA =35，又∵OD=OB=3，∵OA=5，∵AB=OA+OB=8，∵BC OD =ABOA，∵BC=ABOA ×OD=85×3=245．即BC为245．【点睛】本题考查了切线的判定与性质、直径作对圆周角为90°、平行的性质、勾股定理、三角函数等知识，证明切线是解答本题的关键．14．（2022·北京海淀·二模）如图，AB为∵O的直径，CD为弦，CD∵AB于点E，连接DO并延长交∵O于点F，连接AF交CD于点G，CG =AG，连接AC．(1)求证：AC∵DF；(2)若AB = 12，求AC和GD的长．【答案】(1)见解析(2)AC =6，DG=4√3【解析】【分析】（1）根据圆周角定理得到∵C=∵F，由GA=GC推出∵CAF=∵C，得到∵CAF=∵F，即可得到结论AC∵DF．∠2，进而证得△AOD是等边三角形，（2）连接AD，利用AC∵DF推出∵C=∵1，根据圆周角定理得到∠C=12AB=6．利用垂径定理求出AC=AD=6，利用三角函数求出AG．得到AD=AO=12(1)证明：∵ C，F都在∵O上，∵ ∵C=∵F．∵ GA=GC，∵ ∵CAF=∵C．∵ ∵CAF=∵F．∵ AC∵DF．(2)解：连接AD．∵ AC∵DF，∵ ∵C=∵1，⌢=AD⌢，∵AD∠2．∵∠C=12∠2．∵∵∠1=12∵ AB∵CD于E，∵ ∵BED=90°．∵∠1+∠2=90°．∵∵由∵，∵得∵1=30°，∵2=60°．∵ OA=OD，∵ ∵AOD是等边三角形．AB=6．∵AD=AO=12∵直径AB∵CD于E，∵AC⌢=AD⌢．∵ AC=AD=6．∵ ∵AOD是等边三角形，∵ ∵ADO=60°，∵1=30°．∵ ∵3=∵AOD-∵1=30°∵ DF是∵O的直径，∵ ∵F AD=90°．=4√3．∵ 在Rt∵GAD中，DG=ADcos∠3【点睛】此题考查了圆周角定理，垂径定理，等边三角形的判定及性质，锐角三角函数，平行线的判定定理，熟记圆周角定理及垂径定理是解题的关键．15．（2022·北京市十一学校模拟预测）如图，AB 是⊙O 的弦，C 为⊙O 上一点，过点C 作AB 的垂线与AB 的延长线交于点D ，连接BO 并延长，与⊙O 交于点E ，连接EC ，CD 是⊙O 的切线．(1)求证：∠ABE =2∠E ；(2)若tanE =13，AB =8，求BD 的长．【答案】(1)证明见解析(2)1【解析】【分析】（1）连接OC ，根据切线的性质易得AD ∥CO ，由平行线的性质得到∠ABE =∠BOC ，再结合等腰三角形的性质得到∠OCE =∠OEC ，由三角形外角性质易得∠BOC =∠OCE +∠OEC =2∠BCE 即可求解；（2）连接BC 和AC ，CO ，根据BE 是⊙O 的直径和切线的性质易得∠BCD =∠E ，由圆周角定理得到∠A =∠E ，结合tanE =13得到BD CD =DC AD =13，进而可得CD =3BD ，将AB =8，AD =AB +BD =8+BD 代入即可求解．（1）证明：连接OC ，如下图．∵CD 是⊙O 的切线，过点C 作AB 的垂线与AB 的延长线交于点D ，∵∠CDA =∠DCO =90°，∵AD ∥CO ，∵∠ABE =∠BOC ．∵OC =OE ，∵∠OCE =∠OEC ，∵∠BOC =∠OCE +∠OEC =2∠BCE，∵∠ABE=2∠E；（2）解：连接BC和AC，CO，如下图．∵BE是⊙O的直径，∵∠BCE=90°，∵∠OCE+∠OCB=90°．∵CD是⊙O的切线，∵∠OCB+∠BCD=90°，∵∠BCD=∠OCE，∵∠BCD=∠E，∵∠A=∠E，tanE=13，∵BDCD=DC AD =13，∵CD=3BD．∵AB=8，AD=AB+BD=8+BD，∵3BD8+BD=13，∵BD=1．【点睛】本题主要考查了圆周角定理、切线的性质，平行线的性质，等腰三角形的性质，三角形外角性质，锐角三角函数值的求法，作出辅助线是解答关键．16．（2022·北京东城·一模）如图，在△ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交AC于点E，过点B作⊙O的切线交OD的延长线于点F．(1)求证：∠A=∠BOF；(2)若AB=4，DF=1，求AE的长．【答案】(1)见解析(2)AE=83【解析】【分析】(1)首先根据等边对等角可证得∠C=∠ODB，再根据平行线的判定与性质，即可证得结论；(2)首先根据圆周角定理及切线的性质，可证得∠AEB=∠OBF，即可证得△ABE∽△OFB，再根据相似三角形的性质即可求得．(1)证明：∵AB=AC∴∠C=∠ABC∵OB=OD∴∠ODB=∠OBD∴∠C=∠ODB∴AC∥OD∴∠A=∠BOF(2)解：如图：连接BE∵AB是⊙O的直径，AB=4AB=2∴∠AEB=90°，OB=OD=12∵BF是⊙O的切线∴∠OBF=90°。

2016年全国中考数学真题分类与圆有关的位置关系一、选择题10．（2016安徽，10，4分）如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC 内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）A．B．2 C．D．【考点】点与圆的位置关系；圆周角定理．【分析】首先证明点P在以AB为直径的⊙O上，连接OC与⊙O交于点P，此时PC最小，利用勾股定理求出OC即可解决问题．【解答】解：∵∠ABC=90°，∴∠ABP+∠PBC=90°，∵∠PAB=∠PBC，∴∠BAP+∠ABP=90°，∴∠APB=90°，∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，在RT△BCO中，∵∠OBC=90°，BC=4，OB=3，∴OC==5，∴PC=OC=OP=5﹣3=2．∴PC最小值为2．故选B．18．（2016湖南湘西，18，4分）在RT△ABC中，∠C=90°，BC=3cm，AC=4cm，以点C为圆心，以2.5cm为半径画圆，则⊙C与直线AB的位置关系是（）A．相交 B．相切 C．相离 D．不能确定【考点】直线与圆的位置关系．【分析】过C作CD⊥AB于D，根据勾股定理求出AB，根据三角形的面积公式求出CD，得出d＜r，根据直线和圆的位置关系即可得出结论．【解答】解：过C作CD⊥AB于D，如图所示：∵在Rt△ABC中，∠C=90，AC=4，BC=3，∴AB==5，∵△ABC的面积=AC×BC=AB×CD，∴3×4=5CD，∴CD=2.4＜2.5，即d＜r，∴以2.5为半径的⊙C与直线AB的关系是相交；故选A．【点评】本题考查了直线和圆的位置关系，用到的知识点是勾股定理，三角形的面积公式；解此题的关键是能正确作出辅助线，并进一步求出CD的长，注意：直线和圆的位置关系有：相离，相切，相交．11．（2016•四川凉山州，11，4分）已知，一元二次方程x2﹣8x+15=0的两根分别是⊙O1和⊙O2的半径，当⊙O1和⊙O2相切时，O1O2的长度是（）A．2 B．8 C．2或8 D．2＜O2O2＜8【分析】先解方程求出⊙O1、⊙O2的半径，再分两圆外切和两圆内切两种情况讨论求解．【解答】解：∵⊙O1、⊙O2的半径分别是方程x2﹣8x+15=0的两根，解得⊙O1、⊙O2的半径分别是3和5．∴①当两圆外切时，圆心距O1O2=3+5=8；②当两圆内切时，圆心距O1O2=5﹣2=2．故选C．【点评】考查解一元二次方程﹣因式分解法和圆与圆的位置关系，同时考查综合应用能力及推理能力．注意：两圆相切，应考虑内切或外切两种情况是解本题的难点．6．(2016上海，6，4分)如图1，在Rt△ABC中，∠C＝90°，AC＝4，BC＝7，点D在边沉BC上，CD＝3，⊙A的半径长为3，⊙D与⊙A相交，且点B在⊙D 外，那么⊙D的半径长r的取值范围是( )A．1＜r＜4 B．2＜r＜4 C．1＜r＜8 D．2＜r＜8【答案】B．二、填空题16. (2016四川泸州，16，3分）如图，在平面直角坐标系中，已知点A （1，0），B （1a -，0），C （1a +，0）（0a >），点P 在以D （4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a 的最大值是 .【答案】6（2016湖南永州，20，4分）如图，给定一个半径长为2的圆，圆心O 到水平直线l 的距离为d ，即OM=d ．我们把圆上到直线l 的距离等于1的点的个数记为m ．如d=0时，l 为经过圆心O 的一条直线，此时圆上有四个到直线l 的距离等于1的点，即m=4，由此可知：（1）当d=3时，m= 1 ；（2）当m=2时，d 的取值范围是 0＜d ＜3 ．【考点】直线与圆的位置关系．y xP A O D B C【分析】根据直线与圆的位置关系和直线与圆的交点个数以及命题中的数据分析即可得到答案．【解答】解：（1）当d=3时，∵3＞2，即d＞r，∴直线与圆相离，则m=1，故答案为：1；（2）当m=2时，则圆上到直线l的距离等于1的点的个数记为2，∴直线与圆相交或相切或相离，∴0＜d＜3，∴d的取值范围是0＜d＜3，故答案为：0＜d＜3．三、解答题24．（2016湖北省十堰市，24，10分）如图1，AB为半圆O的直径，D为BA 的延长线上一点，DC为半圆O的切线，切点为C．（1）求证：∠ACD=∠B；（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；①求tan∠CFE的值；②若AC=3，BC=4，求CE的长．【考点】切线的性质．【分析】（1）利用等角的余角相等即可证明．（2）①只要证明∠CEF=∠CFE即可．②由△DCA∽△DBC，得===，设DC=3k，DB=4k，由CD2=DA•DB，得9k2=（4k﹣5）•4k，由此求出DC，DB，再由△DCE∽△DBF，得=，设EC=CF=x，列出方程即可解决问题．【解答】（1）证明：如图1中，连接OC．∵OA=OC，∴∠1=∠2，∵CD是⊙O切线，∴OC⊥CD，∴∠DCO=90°，∴∠3+∠2=90°，∵AB是直径，∴∠1+∠B=90°，∴∠3=∠B．（2）解：①∵∠CEF=∠ECD+∠CDE，∠CFE=∠B+∠FDB，∵∠CDE=∠FDB，∠ECD=∠B，∴∠CEF=∠CFE，∵∠ECF=90°，∴∠CEF=∠CFE=45°，∴tan∠CFE=tan45°=1．②在RT△ABC中，∵AC=3，BC=4，∴AB==5，∵∠CDA=∠BDC，∠DCA=∠B，∴△DCA∽△DBC，∴===，设DC=3k，DB=4k，∵CD2=DA•DB，∴9k2=（4k﹣5）•4k，∴k=，∴CD=，DB=，∵∠CDE=∠BDF，∠DCE=∠B，∴△DCE∽△DBF，∴=，设EC=CF=x，∴=，∴x=．∴CE=．（2016广东梅州，20，9分）如图，点D在⊙O的直径AB的延长线上，点C 在⊙O上，AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．（1）证明：连接O C．………………………1分∵AC =CD ，∠ACD =120°，∴∠CAD =∠D =30°． ………………………2分 ∵OA =OC ，∴∠2=∠CAD =30°．（或 ∠ACO =∠CAD =30° ） ……………3分 ∴∠OCD =∠ACD —∠ACO =90°，即OC ⊥CD ．∴CD 是⊙O 的切线． ………………………4分（2）解：由（1）知∠2=∠CAD =30°．（或 ∠ACO =∠CAD =30° ）， ∴∠1=60°．（或∠COD =60°） …………………5分∴323602602ππ=⨯=BOC S 扇形． ………………………6分 在R t △OCD 中，∵OCCD =︒60tan ，2=OC ∴32=CD ． (7)分∴323222121=⨯⨯=⨯=∆CD OC S OCD Rt，…………………8分 ∴图中阴影部分的面积为3232π-=阴影S ． …………………9分 20．（2016四川资阳，20，8分）如图，在⊙O 中，点C 是直径AB 延长线上一点，过点C 作⊙O 的切线，切点为D ，连结BD ．（1）求证：∠A=∠BDC ；（2）若CM 平分∠ACD ，且分别交AD 、BD 于点M 、N ，当DM=1时，求MN 的长．【分析】（1）由圆周角推论可得∠A+∠ABD=90°，由切线性质可得∠CDB+∠ODB=90°，而∠ABD=∠ODB ，可得答案；（2）由角平分线及三角形外角性质可得∠A+∠ACM=∠BDC+∠DC M ，即∠DMN=∠DNM ，根据勾股定理可求得MN 的长．【解答】解：（1）如图，连接OD ，∵AB 为⊙O 的直径，∴∠ADB=90°，即∠A+∠ABD=90°，又∵CD 与⊙O 相切于点D ，∴∠CDB+∠ODB=90°， ∵OD=OB ，∴∠ABD=∠ODB ，∴∠A=∠BDC ；（2）∵CM 平分∠ACD ，∴∠DCM=∠ACM ，又∵∠A=∠BDC ，∴∠A+∠ACM=∠BDC+∠DCM ，即∠DMN=∠DNM ，∵∠ADB=90°，DM=1，∴DN=DM=1，∴MN==．（2016青海西宁，26，10分）如图11，D 为⊙O 上一点，点C 在直径BA 的延长线上，且CBD CDA ∠=∠．（1）求证：CD 是⊙O 的切线；（2）过点B 作⊙O 的切线交CD 的延长线于点E ，6=BC ，32=BD AD ．求BE 的长．（1）证明：连结OD∵OD OB =∴BDO OBD ∠=∠∵CBD CDA ∠=∠∴ODB CDA ∠=∠又∵AB 是O ⊙的直径∴90ADB ∠=︒（直径所对的圆周角是直角）∴︒=∠+∠90ODB ADO∴︒=∠+∠90CDA ADO 即︒=∠90CDO ∴CD OD ⊥ ∵OD 是O ⊙半径∴CD 是O ⊙的切线（经过半径外端并且垂直于这条半径的直线是圆的切线）（2）解：∵C C ∠=∠，CBD CDA ∠=∠∴CDA ∆∽CBD ∆∴BD AD BC CD = ∵32=BD AD 6=BC ∴4=CD ∵CE ，BE 是O ⊙的切线∴DE BE = ， BC BE ⊥∴222EC BC BE =+ 即()22264BE BE +=+ 解得25=BE EO D A23．（2016四川宜宾，23，10分）如图1，在△APE中，∠PAE=90°，PO是△APE的角平分线，以O为圆心，OA为半径作圆交AE于点G．（1）求证：直线PE是⊙O的切线；（2）在图2中，设PE与⊙O相切于点H，连结AH，点D是⊙O的劣弧上一点，过点D作⊙O的切线，交PA于点B，交PE于点C，已知△PBC的周长为4，tan∠EAH=，求EH的长．【考点】切线的判定与性质．【分析】（1）作OH⊥PE，由PO是∠APE的角平分线，得到∠APO=∠EPO，判断出△PAO≌△PHO，得到OH=OA，用“圆心到直线的距离等于半径”来得出直线PE是⊙O的切线；（2）先利用切线的性质和△PBC的周长为4求出PA=2，再用三角函数求出OA，AG，然后用三角形相似，得到EH=2EG，AE=2EH，用勾股定理求出EG，最后用切割线定理即可．【解答】证明：（1）如图1，作OH⊥PE，∴∠OHP=90°，∵∠PAE=90，∴∠OHP=∠OAP，∵PO是∠APE的角平分线，∴∠APO=∠EPO，在△PAO和△PHO中，∴△PAO≌△PHO，∴OH=OA，∵OA是⊙O的半径，∴OH是⊙O的半径，∵OH⊥PE，∴直线PE是⊙O的切线．（2）如图2，连接GH，∵BC，PA，PB是⊙O的切线，∴DB=DA，DC=CH，∵△PBC的周长为4，∴PB+PC+BC=4，∴PB+PC+DB+DC=4，∴PB+AB+PC+CH=4，∴PA+PH=4，∵PA，PH是⊙O的切线，∴PA=PH，∴PA=2，由（1）得，△PAO≌△PHO，∴∠OFA=90°，∴∠EAH+∠AOP=90°，∵∠OAP=90°，∴∠AOP+∠APO=90°，∴∠APO=∠EAH，∵tan∠EAH=，∴tan∠APO==，∴OA=PA=1，∴AG=2，∵∠AHG=90°，∵tan∠EAH==，∵△EGH∽△EHA，∴===，∴EH=2EG，AE=2EH，∴AE=4EG，∵AE=EG+AG，∴EG+AG=4EG，∴EG=AG=，∵EH是⊙O的切线，EGA是⊙O的割线，∴EH2=EG×EA=EG×（EG+AG）=×（+2）=，∴EH=．（2016湖南娄底，25，10分）如图所示，在Rt△ABC与Rt△OCD中，∠ACB=∠DCO=90°，O为AB的中点．（1）求证：∠B=∠ACD．（2）已知点E在AB上，且BC2=AB•BE．（i）若tan∠ACD=，BC=10，求CE的长；（ii）试判定CD与以A为圆心、AE为半径的⊙A的位置关系，并请说明理由．【分析】（1）因为∠ACB=∠DCO=90°，所以∠ACD=∠OCB，又因为点O是Rt△ACB中斜边AB的中点，所以OC=OB，所以∠OCB=∠B，利用等量代换可知∠ACD=∠B；（2）（i）因为BC2=AB•BE，所以△ABC∽△CBE，所以∠ACB=∠CEB=90°，因为tan∠ACD=tan∠B，利用勾股定理即可求出CE的值；（ii）过点A作AF⊥CD于点F，易证∠DCA=∠ACE，所以CA是∠DCE 的平分线，所以AF=AE，所以直线CD与⊙A相切．【解答】解：（1）∵∠ACB=∠DCO=90°，∴∠ACB﹣∠ACO=∠DCO﹣∠ACO，即∠ACD=∠OCB，又∵点O是AB的中点，∴OC=OB，∴∠OCB=∠B，∴∠ACD=∠B，（2）（i）∵BC2=AB•BE，∴=，∵∠B=∠B，∴△ABC∽△CBE，∴∠ACB=∠CEB=90°，∵∠ACD=∠B，∴tan∠ACD=tan∠B=，设BE=4x，CE=3x，由勾股定理可知：BE2+CE2=BC2，∴（4x）2+（3x）2=100，∴解得x=2，∴CE=6；（ii）过点A作AF⊥CD于点F，∵∠CEB=90°，∴∠B+∠ECB=90°，∵∠ACE+∠ECB=90°，∴∠B=∠ACE，∵∠ACD=∠B，∴∠ACD=∠ACE，∴CA平分∠DCE，∵AF⊥CE，AE⊥CE，∴AF=AE，∴直线CD与⊙A相切．（2016新疆内高班，22，11分）如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．（1）求证：直线BF是⊙O的切线；（2）若AB=5，sin∠CBF=，求BC和BF的长．【分析】（1）连接AE，利用直径所对的圆周角是直角，从而判定直角三角形，利用直角三角形两锐角相等得到直角，从而证明∠ABF=90°．（2）利用已知条件证得△AGC∽△ABF，利用比例式求得线段的长即可．【解答】（1）证明：连接AE，∵AB是⊙O的直径，∴∠AEB=90°，∴∠1+∠2=90°．∵AB=AC，∴∠1=∠CAB．∵∠CBF=∠CAB，∴∠1=∠CBF∴∠CBF+∠2=90°即∠ABF=90°∵AB是⊙O的直径，∴直线BF是⊙O的切线．（2）解：过点C作CG⊥AB于G．∵sin∠CBF=，∠1=∠CBF，∴sin∠1=，∵在Rt△AEB中，∠AEB=90°，AB=5，∴BE=AB•sin∠1=，∵AB=AC，∠AEB=90°，∴BC=2BE=2，在Rt△ABE中，由勾股定理得AE==2，∴sin∠2===，cos∠2===，在Rt△CBG中，可求得GC=4，GB=2，∴AG=3，∵GC∥BF，∴△AGC∽△ABF，∴∴BF==（2016湖南永州，25，10分）如图，△ABC是⊙O的内接三角形，AB 为直径，过点B的切线与AC的延长线交于点D，E是BD中点，连接CE．（1）求证：CE是⊙O的切线；（2）若AC=4，BC=2，求BD和CE的长．【分析】（1）连接OC，由弦切角定理和切线的性质得出∠CBE=∠A，∠ABD=90°，由圆周角定理得出∠ACB=90°，得出∠ACO+∠BCO=90°，∠BCD=90°，由直角三角形斜边上的中线性质得出CE=BD=BE，得出∠BCE=∠CBE=∠A，证出∠ACO=∠BCE，得出∠BCE+∠BCO=90°，得出CE⊥OC，即可得出结论；（2）由勾股定理求出AB，再由三角函数得出tanA===，求出BD=AB=，即可得出CE的长．【解答】（1）证明：连接OC，如图所示：∵BD是⊙O的切线，∴∠CBE=∠A，∠ABD=90°，∵AB是⊙O的直径，∴∠ACB=90°，∴∠ACO+∠BCO=90°，∠BCD=90°，∵E是BD中点，∴CE=BD=BE，∴∠BCE=∠CBE=∠A，∵OA=OC，∴∠ACO=∠A，∴∠ACO=∠BCE，∴∠BCE+∠BCO=90°，即∠OCE=90°，CE⊥OC，∴CE是⊙O的切线；（2）解：∵∠ACB=90°，∴AB===2，∵tanA====，∴BD=AB=，∴CE=BD=．（2016江苏苏州，27，10分）如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N 落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3m/s，以O为圆心，0.8cm为半径作⊙O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜）．（1）如图1，连接DQ平分∠BDC时，t的值为；（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；（3）请你继续进行探究，并解答下列问题：①证明：在运动过程中，点O始终在QM所在直线的左侧；②如图3，在运动过程中，当QM与⊙O相切时，求t的值；并判断此时PM与⊙O是否也相切？说明理由．【分析】（1）先利用△PBQ∽△CBD求出PQ、BQ，再根据角平分线性质，列出方程解决问题．（2）由△QTM∽△BCD，得=列出方程即可解决．（3）①如图2中，由此QM交CD于E，求出DE、DO利用差值比较即可解决问题．②如图3中，由①可知⊙O只有在左侧与直线QM相切于点H，QM与CD交于点E．由△OHE∽△BCD，得=，列出方程即可解决问题．利用反证法证明直线PM不可能由⊙O相切．【解答】（1）解：如图1中，∵四边形ABCD是矩形，∴∠A=∠C=∠ADC=∠ABC=90°，AB=CD=6．AD=BC=8，∴BD===10，∵PQ⊥BD，∴∠BPQ=90°=∠C，∵∠PBQ=∠DBC，∴△PBQ∽△CBD，∴==，∴==，∴PQ=3t，BQ=5t，∵DQ平分∠BDC，QP⊥DB，QC⊥DC，∴QP=QC，∴3t=6﹣5t，∴t=，故答案为．（2）解：如图2中，作MT⊥BC于T．∵MC=MQ，MT⊥CQ，∴TC=TQ，由（1）可知TQ=（8﹣5t），QM=3t，∵MQ∥BD，∴∠MQT=∠DBC，∵∠MTQ=∠BCD=90°，∴△QTM∽△BCD，∴=，∴=，∴t=（s），∴t=s时，△CMQ是以CQ为底的等腰三角形．（3）①证明：如图2中，由此QM交CD于E，∵EQ∥BD，∴=，∴EC=（8﹣5t），ED=DC﹣EC=6﹣（8﹣5t）=t，∵DO=3t，∴DE﹣DO=t﹣3t=t＞0，∴点O在直线QM左侧．②解：如图3中，由①可知⊙O只有在左侧与直线QM相切于点H，QM 与CD交于点E．∵EC=（8﹣5t），DO=3t，∴OE=6﹣3t﹣（8﹣5t）=t，∵OH⊥MQ，∴∠OHE=90°，∵∠HEO=∠CEQ，∴∠HOE=∠CQE=∠CBD，∵∠OHE=∠C=90°，∴△OHE∽△BCD，∴=，∴=，∴t=．∴t=s时，⊙O与直线QM相切．连接PM，假设PM与⊙O相切，则∠OMH=PMQ=22.5°，在MH上取一点F，使得MF=FO，则∠FMO=∠FOM=22.5°，∴∠OFH=∠FOH=45°，∴OH=FH=0.8，FO=FM=0.8，∴MH=0.8（+1），由=得到HE=，由=得到EQ=，∴MH=MQ﹣HE﹣EQ=4﹣﹣=，∴0.8（+1）≠，矛盾，∴假设不成立．∴直线MQ与⊙O不相切．25.（2016北京，25，5分） 如图，AB 为于点D ，过点D作的切线，交BA 的延长线于点E.(1) 求证：AC ∥DE:(2) 连接CD ，若OA ＝AE ＝a ，写出求四边形ACDE 面积的思路。

中考数学专题训练：与圆有关的计算（附参考答案）1．如图，一条公路的转弯处是一段圆弧(AC⏜)，点O是这段弧所在圆的圆心，B 为AC⏜上一点，OB⊥AC于D.若AC＝300√3 m，BD＝150 m，则AC⏜的长为( )A．300π m B．200π mC．150π m D．100√3π m2．将一半径为6的圆形纸片，沿着两条半径剪开形成两个扇形．若其中一个扇形的弧长为5π，则另一个扇形的圆心角度数是( )A．30°B．60°C．105°D．210°3．如图，公园内有一个半径为18米的圆形草坪，从A地走到B地有观赏路(劣弧AB)和便民路(线段AB)．已知A，B是圆上的两点，O为圆心，∠AOB＝120°，小强从点A走到点B，走便民路比走观赏路少走( )A．(6π－6√3)米B．(6π－9√3)米C．(12π－9√3)米D．(12π－18√3)米4．如图，在Rt△ABC中，∠ACB＝90°，AB＝√5，BC＝2，以点A为圆心，AC的长为半径画弧，交AB于点D，以点B为圆心，AC的长为半径画弧，交AB于点E，交BC于点F，则图中阴影部分的面积为( )A．8－πB．4－πC．2－π4D．1－π45．如图，两个半径长均为√2的直角扇形的圆心分别在对方的圆弧上，扇形FCD的圆心C 是AB⏜的中点，且扇形FCD 绕着点C 旋转，半径AE ，CF 交于点G ，半径BE ，CD 交于点H ，则图中阴影部分的面积等于( )A ．π2－1 B ．π2－2 C ．π－1D ．π－26．如图，正六边形ABCDEF 内接于⊙O ，点M 在AB⏜上，则∠CME 的度数为( )A ．30°B ．36°C ．45°D ．60°7．如图，在以AB 为直径的⊙O 中，C 为圆上的一点，BC⏜＝3AC ⏜，弦CD ⊥AB 于点E ，弦AF 交CE 于点H ，交BC 于点G .若H 是AG 的中点，则∠CBF 的度数为( )A ．18°B ．21°C ．22.5°D ．30°8．设圆锥的底面圆半径为r ，圆锥的母线长为l ，满足2r ＋l ＝6，这样的圆锥的侧面积( ) A ．有最大值94π B ．有最小值94π C ．有最大值92πD ．有最小值92π9．如图，从一块直径是2的圆形铁片上剪出一个圆心角为90°的扇形，将剪下来的扇形围成一个圆锥，这个圆锥的底面圆的半径是( )A ．π4 B ．√24 C ．12D ．110．圆心角为90°，半径为3的扇形弧长为( ) A ．2π B ．3π C ．32πD ．12π11．如图，⊙O 是△ABC 的外接圆，半径为4，连接OB ，OC ，OA .若∠CAO ＝40°，∠ACB ＝70°，则阴影部分的面积是( )A ．43π B ．83π C ．163πD ．323π12．如图，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为3∶1，则圆的面积约为正方形面积的( )A ．27倍B ．14倍C ．9倍D ．3倍13．如图所示，点A ，B ，C 对应的刻度分别为1，3，5，将线段CA 绕点C 按顺时针方向旋转，当点A 首次落在矩形BCDE 的边BE 上时，记为点A ′，则此时线段CA 扫过的图形的面积为( )A ．4√3B ．6C ．43πD ．83π14．如图，要用一张扇形纸片围成一个无底的圆锥(接缝处忽略不计)．若该圆锥的底面圆周长为20π cm ，侧面积为240π cm 2，则这个扇形的圆心角的度数是_______度．15．如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝2√3，半径为1的⊙O 在Rt △ABC 内平移(⊙O 可以与该三角形的边相切)，则点A 到⊙O 上的点的距离的最大值为__________．16．如图，在矩形ABCD 中，AB ＝2，BC ＝4，E 为BC 的中点，连接AE ，DE ，以E 为圆心，EB 长为半径画弧，分别与AE ，DE 交于点M ，N ，则图中阴影部分的面积为________．(结果保留π)17．已知AB 为⊙O 的直径，AB ＝6，C 为⊙O 上一点，连接CA ，CB .(1)如图1，若C 为AB⏜的中点，求∠CAB 的大小和AC 的长； (2)如图2，若AC ＝2，OD 为⊙O 的半径，且OD ⊥CB ，垂足为点E ，过点D 作⊙O 的切线，与AC 的延长线相交于点F ，求FD 的长．18．如图，⊙O是正方形ABCD的内切圆，切点分别为E，F，G，H，ED与⊙O相交于点M，则sin ∠MFG的值为______．19．一块圆形玻璃镜面碎成了几块，其中一块如图所示，测得弦AB长20厘米，弓形高CD为2厘米，则镜面半径为______厘米．20．如图，AB，CD为⊙O的直径，C为⊙O上一点，过点C的切线与AB的延长线⏜的中点，弦CE，BD相交于点F.交于点P，∠ABC＝2∠BCP，E是BD(1)求∠OCB的度数；(2)若EF＝3，求⊙O的直径长．21．如图，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD，垂足为点H，过点C作直线分别与AB，AD的延长线交于点E，F，且∠ECD＝2∠BAD.(1)求证：CF是⊙O的切线．(2)如果AB＝10，CD＝6.①求AE的长；②求△AEF的面积．参考答案1．B 2．D 3．D 4．D 5．D6．D 7．C8．C 9．B10．C 11．C 12．B 13．D14．150 15．2√7＋1 16．4－π17．(1)∠CAB＝45°AC＝3√2(2)FD＝2√2 18．√5519.2620．(1)∠OCB＝60°(2)⊙O的直径长为6√321．(1)证明略(2)①AE＝454②△AEF的面积为2258。

2006-2011年北京中考试卷中圆的题目汇总（06年大纲卷）1． 如图，AB 是O e 的直径，点C 在AB 的延长线上，CD 与O e 相切，切点为D ．如果35A ∠=o ，那么C ∠等于（ ）Ａ．20oＢ．30oＣ．35oＤ．55o2．如果圆锥的底面半径为2cm ，母线长为4cm ，那么它的侧面积等于2cm ．3．已知：AB 是半圆O 的直径，点C 在BA 的延长线上运动（点C 与点A 不重合），以OC为直径的半圆M 与半圆O 交于点D ，DCB ∠的平分线与半圆M 交于点E ． （1）求证：CD 是半圆O 的切线（图1）；（2）作EF AB ⊥于点F （图2），猜想EF 与已有的哪条线段的一半相等，并加以证明；（3）在上述条件下，过点E 作CB 的平行线交CD 于点N ，当NA 与半圆O 相切时（图3），求EOC ∠的正切值． （06年课标卷）4．已知：如图，ABC ∆内接于O ⊙，点D 在OC 的延长线上，1sin 302B CAD =∠=︒，．（1）求证：AD 是O ⊙的切线；（2）若OD AB ⊥，5BC =，求AD 的长．OEDCBA（07年课标卷）5. 已知：如图，A 是O ⊙上一点，半径OC 的延长线与过点A的直线交于B 点，OC BC =，12AC OB =．（1）求证：AB 是O ⊙的切线；（2）若452ACD OC ∠=︒=，，求弦CD 的长． （08年课标卷）6．若两圆的半径分别是1cm 和5cm ，圆心距为6cm ，则这两圆的位置关系是（ ）A ．内切B ．相交C ．外切D ．外离7．已知：如图，在Rt ABC △中，90C ∠=o ，点O 在AB 上，以O 为圆心，OA 长为半径的圆与AC AB ，分别交于点D E ，，且CBD A ∠=∠．（1）判断直线BD 与O e 的位置关系，并证明你的结论； （2）若:8:5AD AO =，2BC =，求BD 的长． （09年课标卷）8．如图，C 为O ⊙直径AB 上一动点，过点C 的直线交O ⊙于D 、E 两点，且45ACD ∠=︒，DF AB ⊥于点F ，EG AB ⊥于点G ．当点C 在AB 上运动时，设AF x =，DE y =，下列图象中，能表示y 与x 的函数关系的图象大致是9．如图，AB 为O ⊙的直径，弦CD AB ⊥，E 为»BC上一点，若28CEA ∠=︒，则ABD ∠=______︒．10．已知：如图，在ABC ∆中，AB AC =，AE 是角平分线，BM 平分ABC ∠交AE 于点M ，经过B ，M 两点的O⊙交BC于点G，交AB于点F，FB恰为O⊙的直径．⑴求证：AE与O⊙相切；⑵当4BC=，1cos3C=时，求O⊙的半径．(2010年北京中考)11. 如图，AB为圆O的直径，弦CD AB，垂足为点E OC，若OC=5，CD=8，则AE=_______________.12. 已知：如图，在△ABC中，D是AB边上一点，圆O过D、B、C三点，DOC=2ACD=90.(1) 求证：直线AC是圆O的切线；(2) 如果ACB=75，圆O的半径为2，求BD的长.(2011年北京中考)13如图，在△ABC，AB＝AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF＝ 12∠CAB．(1)求证：直线BF是⊙O的切线；(2)若AB＝5，sin∠CBF＝55，求BC和BF的长．2006-2011年北京中考试卷中圆的题目答案（06年大纲卷）1. A2. 8π3. 解：（1）证明：如图1，连结OD，则OD为半圆O的半径．OCQ为半圆M的直径，CD∴是半圆O的OB CDEAB CDODEO BAMC图1切线． （2）猜想：12EF =OA ． 证法一：如图2-1，连结OD OE ，，延长OE 交CD 于点K ，作EG CD ⊥于点G ，则EG OD ∥．CE Q 平分DCB ∠， OC Q 是半圆M 的直径，E为半圆M 上的一点，CE Q 为公共边，证法二：如图2-2，以OC 为直径作M e ，延长EF 交M e 于点P ，连结OD ．12EF PF EP ∴==，»»EOPO =． CE Q 平分DCB ∠， 证法三：如图2-3，连结OD ME OD ME ，，，相交于点H ．CE Q 平分DCB ∠，（3）解：如图3，延长OE 交CD 于点K ． 设OF x EF y ==，，则2OA y =．NE CB Q ∥，EF CB ⊥，NA 切C图2-2OBA MC图2-3F BOA MC图2-1F半圆O 于点A ，∴四边形AFEN 是矩形． 同（2）证法一，得E 是OK的中点．N ∴是CK 的中点． 2(43)y x y x ∴=-．解得3y x =或1yx=． 当3y x =时，tan 3EF yEOC OF x ∠===．当1yx=时，点C 与点A 重合，不符合题意，故舍去．（06年课标卷）4. （07年课标卷）5. 解：（1）证明： 如图，连结OA ∴ ACO ∆是等边三角形 故 60O ∠=o又可得 30B ∠=o ∴ 90OAB ∠=o ∴ AB 是O e 的切线. （2）解：作AE CD ⊥于E 点.又 45ACD ∠=o ，2AC OC ==，∴在Rt ACE ∆中，2CE AE == 在Rt ACE ∆中，∵ 30D ∠=o ，∴ 22AD = 由勾股定理，可求得 6DE = （08年课标卷） 6. C7. 解：（1）直线BD 与O e 相切．D K OBA MC图3 E F N证明：如图1，连结OD ．90C ∠=o Q ， 90CBD CDB ∴∠+∠=o ．又CBD A ∠=∠Q ，∴直线BD 与O e 相切．（2）解法一：如图1，连结DE ．AE Q 是O e 的直径， 90ADE ∴∠=o ．解法二：如图2，过点O 作OH AD ⊥于点H ． 12AH DH AD ∴==．:8:5AD AO =Q ，（09年课标卷） 8. A 9. 2810．⑴证明：连结OM ，则OM OB =． ∵BM 平分ABC ∠，在ABC ∆中，AB AC =，AE 是角平分线，∴AE 与O e 相切．⑵解：在ABC ∆中，AB AC =，AE 是角平分线， 在ABE ∆中，90AEB ∠=︒，设O e 的半径为r ，则6AO r =-． ∴626r r -=． 解得32r =．∴O e 的半径为32． 11. 212. (1) 证明：∵OD=OC ，DOC=90，∴ODC=OCD=45， ∵DOC=2ACD=90，∴ACD=45，∴ACD OCD=OCA=90，∵点C 在圆O 上，∴直线AC 是圆O 的切线。

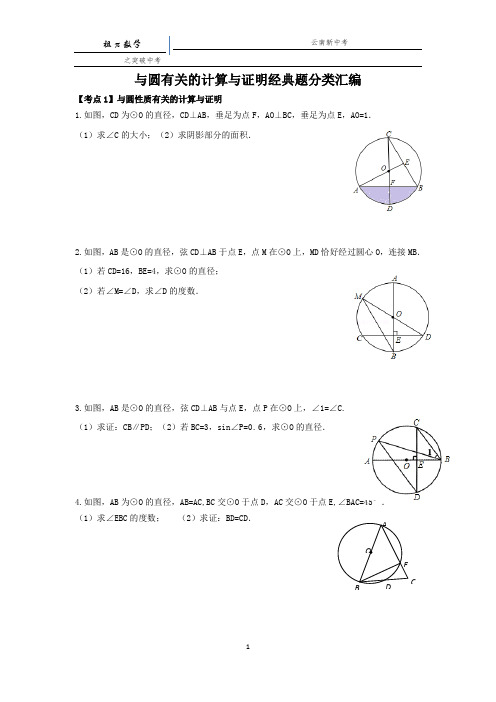
与圆有关的计算与证明经典题分类汇编【考点1】与圆性质有关的计算与证明1.如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．（1）求∠C的大小；（2）求阴影部分的面积．2.如图，AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，MD恰好经过圆心O，连接MB．（1）若CD=16，BE=4，求⊙O的直径；（2）若∠M=∠D，求∠D的度数．3.如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C.（1）求证：CB∥PD；（2）若BC=3，sin∠P=0.6，求⊙O的直径．4.如图，AB为⊙O的直径，AB=AC,BC交⊙O于点D，AC交⊙O于点E,∠BAC=45°．（1）求∠EBC的度数；（2）求证：BD=CD．AOECDB【考点2】与切线性质有关的证明与计算1.如图，PA、PB、EF分别与⊙O相切于点A、B、C，若△PEF的周长为18cm，且∠APB=60°,求⊙O的半径.2.如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB=18cm，BC=28cm，CA=26cm，求AF，BD，CE的长.3.如图，BE是O的直径，点A和点D是⊙O上的两点，过点A作⊙O的切线交BE延长线于点．（1）若∠ADE=25°，求∠C的度数；（2）若AB=AC，CE=2，求⊙O半径的长．4.如图，AB是⊙O的切线，B为切点，圆心在AC上，∠A=30°，D为弧BC的中点．（1）求证：AB=BC；（2）求证：四边形BOCD是菱形．5.如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF=∠ABC．（1）求证：AB=AC；（2）若AD=4，cos∠ABF=45，求DE的长．6.直线PD垂直平分⊙O的半径OA，交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．（1）若⊙O的半径为8，求CD的长；（2）证明：PE=PF；（3）若PF=13，sin A=513，求EF的长．【考点3】与切线的判定有关的证明与计算1.如图，已知⊙O的半径为1，DE是⊙O的直径，过点D作⊙O的切线AD，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．（1）求AD的长；（2）证明BC是⊙O的切线．2.如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．（1）求证：AC是⊙O的切线；（2）若BF=8，DF=40，求⊙O的半径r．3.如图，AB是⊙O的直径，点C在⊙O上，若∠BAC=∠CAM，过点C作直线L垂直于射线AM，垂足为点D．（1）试判断CD与⊙O的位置关系，并说明理由；（2）若直线L与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°，求CE的长．4.如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC 的延长线于点E，与⊙O相交于G、F两点．（1）求证：AB与⊙O相切；（2）若等边三角形ABC的边长是4，求线段BF的长.【考点4】与阴影面积有关的计算与证明1.如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．（1）求证：EF是⊙O的切线；（2）求证：AC2=AD•AB；（3）若⊙O的半径为2，∠ACD=30°，求图中阴影部分的面积．2.如图，在△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O 经过点E，交BC于点F.(1)求证：AC是⊙O的切线；(2)已知cos A＝32，⊙O的半径为3，求图中阴影部分的面积．3.如图，在△ABC中，∠ACB=90°，E为BC上一点，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=2．（1）求证：∠A=2∠DCB；（2）求图中阴影部分的面积．4.如图，BE是⊙O的直径，点A和点D是⊙O上的两点，连接AE，AD，DE，过点A作射线交BE的延长线于点C，使∠EAC＝∠EDA.(1)求证：AC是⊙O的切线；(2)若CE＝AE＝23，求阴影部分的面积．5.如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC与⊙O的交点，连接AF.(1)求证：CB是⊙O的切线；(2)若∠ECB＝60°，AB＝6，求图中阴影部分的面积．6.如图，AB 是⊙O 的直径，∠BAC=90°，四边形EBOC 是平行四边形，EB 交⊙O 于点D ，连接CD 并延长交AB 的延长线于点F ． （1）求证：CF 是⊙O 的切线；（2）若∠F=30°，EB=4，求图中阴影部分的面积.【考点5】与圆有关的计算与证明综合1.如图，AE 为⊙O 的直径，D 是弧BC 的中点BC 与AD ，OD 分别交于点E ，F. （1）求证：OD ∥AC ；（2）求证：DE.DA=DC 2；（3）若tan ∠CAD=21,求tan ∠CDA 的值.2.如图，⊙O 与直线MN 相切于点A ，点B 是⊙O 上异于点A 的一点，∠BAN 的平分线与⊙O 交于点C ．(1)求证：△ABC 是等腰三角形；(2)①若∠CAN ＝15°，⊙O 的半径为23，则AB ＝ ；②当∠CAN ＝ 时，四边形OACB 为菱形．FEDOAC3.如图，PA为⊙O的切线，A为切点，直线PO交⊙O与点E，F过点A作PO的垂线AB垂足为D，交⊙O与点B，延长BO与⊙O交与点C，连接AC，BF．（1）求证：PB与⊙O相切；（2）试探究线段EF，OD，OP之间的数量关系，并加以证明；（3）若AC=12，tan∠F=12，求cos∠ACB的值．4.如图，△ABC 内接于⊙O ，AB 为直径，∠CBA 的平分线交AC 于点F ，交⊙O 于点D, DE ⊥AB 于点E ，且交AC 于点P ，连接AD.(1)求证：∠DAC ＝∠DBA ；(2)求证：P 是线段AF 的中点； (3)若⊙O 的半径为5, AD ＝6，求ADDB的值．5.如图1，⊙O 是△ABC 的外接圆，AB ＝AC ，BC ＝2，cos ∠ABC ＝1010.点D 为AC ︵上的动点，连接AD 并延长，交BC 的延长线于点E. (1)试求AB 的长；(2)试判断AD ·AE 的值是否为定值？若为定值；请求出这个定值；若不为定值，请说明理由； (3)如图2，连接BD ，过点A 作AH ⊥BD 于点H ，连接CD ，求证：BH ＝CD ＋DH.图1图2。

2016年各区二模《圆》汇总1.（西城）如图，四边形ABCD 内接于⊙O ，点E 在CB 的延长线上，连接AC ，AE ，∠ACB =∠BAE =45°． （1）求证：AE 是⊙O 的切线；（2）若AB =AD ，AC =22，tan ∠ADC =3，求CD 的长．（1）证明：连接OA ，OB ，如图1．∵∠ACB =45°，∴∠AOB=2∠ACB = 90°． ……………1分 ∵OA =OB ，∴∠OAB =∠OBA=45°． ∵∠BAE=45°，∴∠OAE =∠OAB+∠BAE =90°． ∴OA ⊥AE ．∵点A 在⊙O 上，∴AE 是⊙O 的切线． ………………………………………………………2分 （2）解：过点A 作AF ⊥CD 于点F ，如图2．∵AB =AD ，∴ = ．∴∠ACB =∠ACD =45°．…………………3分 ∵AF ⊥CD 于点F ， ∴∠AFC =∠AFD =90°． ∵AC =22，∴在Rt △AFC 中，AF =CF =AC ·sin ∠ACF =2． ……………………………4分 ∵在Rt △AFD 中，tan 3AFD DF∠==， ∴DF =23． ∴CD = CF +DF =83． …………………………………………………………5分2.（通州）如图：ΔABC 是⊙O 的内接三角形，∠ACB =45°，∠AOC =150°，过点C 作⊙O 的切线交AB 的延长线于点D . （1）求证：CD=CB ； （2）如果⊙O 的半径为2，求AC 的长.（1）证明：连结OB .∵»»AB AB =，∠ACB ＝45°，∴290AOB ACB ∠=∠=︒， ………………… 1分；AB CD 图2∵OA=OB ，∴45OAB OBA ∠=∠=︒ ∵∠AOC =150°，∴60COB ∠=︒ ∵OC=OB ，∴△OCB 是等边三角形， ………………… 2分； ∴60OCB OBC ∠=∠=︒， ∴75CBD ∠=︒， ∵CD 是⊙O 的切线，∴90OCD OCB BCD ∠=∠+∠=︒， ∴30BCD ∠=︒， ∴75D CBD ∠=∠=︒，∴CD =CB . ………………… 3分；（2）解：过点B 作BE ⊥AC 于点E ，∵△OCB 是等边三角形， ∴2BC OC ==，∵∠ACB ＝45°，∴1CE BE ==， ………………… 4分；∵»»BC BC =，∠BOC ＝60°，∴1302EAB BOC ∠=∠=︒， ∴tan BEEAB AE∠=，∴313AE=， ∴3AE =，∴31AC AE CE =+=+， ………………… 5分；3. （昌平）如图，以△ABC 的边AB 为直径作⊙O ，与BC 交于点D ，点E 是弧BD 的中点，连接AE 交BC 于点F ，2ACB BAE ∠=∠. （1）求证：AC 是⊙O 的切线； （2）若2sin 3B =，BD=5，求BF 的长. 连接AD .∵ E 是弧BD 的中点，∴弧BE = 弧ED ，O E DFCBAEDCBOA∴∠1=∠2.∴∠BAD= 2∠1.∵∠ACB= 2∠1,∴∠C=∠BAD. ……………………………………………………………1分∵AB为⊙O直径,∴∠ADB=∠ADC=90°.∴∠DAC+∠C =90°.∵∠C=∠BAD，∴∠DAC+∠BAD =90°.∴∠BAC =90°.即AB⊥AC.又∵AC过半径外端，∴AC是⊙O的切线. ……………………………………2分（2）解：过点F作FG⊥AB于点G.在Rt△ABD中，∠ADB=90°，2 sin3ADBAB==，设AD=2m，则AB=3m，利用勾股定理求得BD=5m .∵BD=5，∴m=5.∴AD=25, AB=35. ………………………3分∵∠1=∠2,∠ADB=90°，∴FG=FD. …………………………………4分设BF =x,则FG = FD =5- x.在Rt△BGF中，∠BGF=90°，2 sin3B=，∴523xx-=.解得，x=3.∴BF=3.……………………………………………5分4. （丰台）如图，AB 是⊙O 的直径，BD 交⊙O 于点C ，E 为 BC ⌒的中点，连接AE 交BD 于点F ，作AB FG ⊥，垂足为G ，连接AD ，且BAE D ∠2=∠． （1）求证：AD 为⊙O 的切线；（2）若cosD =53，AD = 6，求FG 的长．证明：连接AC .∵AB 是O 的直径∴90ACB ∠=.∴90CAB B ∠+∠=︒. ∵E 为BC 的中点, ∴CAE EAB ∠=∠.∴2CAB EAB ∠=∠. ∵BAE D ∠2=∠,∴CAB D ∠=∠. ------- 1分 ∴90B D ∠+∠=︒.∴90DAB ∠=︒.即AB AD ⊥.又∵AB 是直径,∴AD 是O 的切线. ------- 2分 （2）∵在Rt △ACD 中,3cos 5DC D AD ==，6AD =, 18.5DC ∴=------- 3分 ∵在Rt △ABD 中,3cos 5AD D BD ==，6AD =, ∴10BD =.∵CAF EAB ∠=∠,90ACB ∠=,AB FG ⊥， ∴CF FG =. ------- 4分 设CF FG x ==. ∵AB FG ⊥， ∴GFB D ∠=∠. ∴3cos 5FG GFB FB ∠==. ∴53FB x =. ∵10DC CF FB ++=.G O F DC B A E G O FDC B A E∴1851053x x ++=. 解得125x =.∴125FG =. ------- 5分5. （海淀）如图，在△ABC 中，∠C =90°，点E 在AB 上，以AE为直径的⊙O 切BC 于点D ，连接AD ． （1）求证：AD 平分∠BAC ；（2）若⊙O 的半径为5，sin ∠DAC =55，求BD 的长.（1）证明：连接OD ．………………………1分∵⊙O 切BC 于点D ， 90C ∠=︒， ∴90ODB C ∠=∠=︒． ∴OD ∥AC ． ∴DAC ODA ∠=∠． ∵OD OA =， ∴OAD ODA ∠=∠． ∴DAC OAD ∠=∠．∴AD 平分BAC ∠．………………………2分（2）解：连接DE ． ∵AE 为直径， ∴︒=∠90ADE ．∵OAD DAC ∠=∠，sin 55DAC ∠=， ∴sin 55OAD ∠=． ∵5OA =， ∴10AE =．∴45AD =．………………………3分 ∴4CD =，8AC =． ∵OD ∥AC ，E ODBACEOD BACE ACOBD∴BOD BAC △∽△．………………………4分∴OD BDAC BC =． 即584BD BD =+． ∴203BD =．………………………5分6. （石景山）如图，在Rt △ACB 中，∠C =90°，D 是AB 上一点，以BD 为直径的⊙O 切AC 于点E ，交BC 于点F ，连接DF ． （1）求证：DF=2CE ；（2）若BC =3，sin B =54，求线段BF 的长．（1）证明：连接OE 交DF 于G ，∵AC 切⊙O 于E ，∴∠CEO =90°．又∵BD 为⊙O 的直径，∴∠DFC =∠DFB =90°． ∵∠C =90°，∴四边形CEGF 为矩形．∴CE =GF ，∠EGF =90°…………………1分 ∴DF =2CE ．………………………………2分（2）解：在Rt △ABC 中，∠C =90°，∵BC =3，4sin 5B =，∴AB =5．…………………………………3分 设OE =x ，∵OE //BC ，∴△AOE ∽△ABC ．∴OE AO BC AB =，∴535x x -=，∴158x =．………………………4分 ∴BD =154．在Rt △BDF 中，∠DFB =90°，∴BF =94…………………………5分7. （怀柔） 如图，在Rt △ABC 中，∠ACB=90°，BD 是∠ABC 的平分线，点O 在AB 上，⊙O 经过B ，D 两点，交BC 于点E ． (1)求证：AC 是⊙O 的切线； (2)若3BC=6,tan A=4∠,求CD 的长． (1)证明：如图，连接OD ，∵⊙O 经过B ，D 两点， FO ED C BA∴OB=OD.∴∠OBD=∠ODB. ……………………………………………………………………………1分 又∵BD 是∠ABC 的平分线, ∴∠OBD=∠CBD.∴∠ODB=∠CBD.∴OD ∥BC ， ∵∠ACB=90°，即BC ⊥AC ，∴OD ⊥AC.又OD 是⊙O 的半径，∴AC 是⊙O 的切线. ……………………………………………………………………………2分 (2) 解：在Rt △ABC 中，∠ACB=90°， ∵BC=6,tan ∠BAC=43AC BC =,， ∴AC=8. …………………………………………………………………………………………3分∵OD ∥BC ，∴△AOD ∽△ABC. ∴ABOABC OD =，即10R 106R -=. 解得：415R =. …………………………………………………………………………………4分 ∴415OD =. 在Rt △ABC 中，OD ⊥AC ， ∴tan ∠A=43AD OD =. ∴AD=5.∴CD=3. ……………………………………………………………………………………5分8. （东城）如图，在△ABC 中，BA =BC ，以AB 为直径的⊙O 分别交AC ，BC 于点D ，E ，BC 的延长线与⊙O 的切线AF 交于点F ． （1）求证：∠ABC =2∠CAF ； （2）若AC =210，10sin 10CAF ∠=，求BE 的长． （1）证明：连结BD .∵AB 是O 的直径， ∴90ADB ∠=︒.∴90DAB DBA ∠+∠=︒. ∵AB AC =，E A CO BD∴2ABD ABC ∠=∠，12AD AC =. ∵AF 为⊙O 的切线， ∴∠F AB =90°.∴90FAC CAB ∠+∠=︒. ∴FAC ABD ∠=∠.∴2.ABC CAF ∠=∠ …………2分⑵ 解：连接AE.∴∠AEB =∠AEC =90°.∵10sin 10CAF ABD CAF CBD CAE ∠=∠=∠=∠=∠，，∴10sin sin 10ABD CAF ∠=∠=．∵90210ABD AC ∠=︒=，，∴10AD =，10sin ADAB ABD==∠=BC .∵90210AEC AC ∠=︒=，， ∴sin 2CE AC CAE =⋅∠=.∴1028BE BC CE =-=-=. …………5分9. （顺义）已知：如图，在ABC ∆中，以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，且A D D C =. （1）求证：AB BC =；（2）过点B 作⊙O 的切线，交AC 的延长线于点F ，且CF DC =，求sin CAE ∠的值.（1）证明：∵AB 为⊙O 的直径， ∴90ADB ∠=︒.………………………………………………………………………..……1分又∵AD DC =，∴AB BC =.…………………………………………………………………………………2分 （2）解：∵BF 切⊙O 于点B ，∴90ABF ∠=︒.…………………………………………………………………………………………………..…………3分 ∴90BAF F ∠+∠=︒.又∵90BAF ABD ∠+∠=︒， OFEDCBA∴ABD F ∠=∠， ∴△ABD ∽△BFD ， ∴AD BDBD DF=， ∴2BD AD DF =⋅. 又∵CF DC =， ∴CF DC AD ==，设=CF DC AD k ==，则2222BD AD DF k k k =⋅=⋅=， ∴=2BD k .在RT △BCD 中，=3BC k ，3sin 33k CBD k∠==, 又∵CBD CAE ∠=∠，……………………..………………………………………………………………….……4分 ∴3sin 3CAE ∠=.…………………………………………………………..…………5分10.（房山）如图，△ABC 中，AB =AC ，以AB 为直径的⊙O 与BC 相交于点D ，与CA 的延长线相交于点E ，DF 过点D 作⊙O 的切线交AC 于点F ．（1）求证：DF ⊥AC ；（2）如果33sin =C ，AE 的长为2.求⊙O 的半径． （1）证明：连接OD ．∵DF 是⊙O 的切线，∴ OD ⊥DF ．------------1分 ∵ OB =OD ，∴ ∠B =∠ODB ． ∵AB =AC ．∴ ∠B =∠C ． ∴ ∠ODB =∠C∴ OD ∥AC ． --------------------------2分FDECBOAFDECBO A∴DF ⊥AC ， --------------------------3分 （2）解：连结BE ，AD ．∵ AB 是直径， ∴ ∠ADB =∠AEB =90° ∵ AB =AC ，∴BD =CD ． ∵ DF ⊥AC ∴FD ∥BE ∴可得点F 是CE 的中点.∴sin ∠ABD= sin ∠ACB= sin ∠ADF=33 设⊙O 的半径为r,则AB=2r,AC=2r∴AD =r 332,AF =r-1 ∵sin ∠ADF==AD AF33=r r 3321-----------------------------------------4分∴r=3 --------------------------------5分∴⊙O 的半径为3. 11. （朝阳） 如图，O 是∠MAN 的边AN 上一点，以OA 为半径作⊙O ，交∠MAN 的平分线于点D ，DE ⊥AM 于E ．（1）求证：DE 是⊙O 的切线；（2）连接OE ，若∠EDA =30º，AE =1，求OE 的长． （1）证明：连接OD ．∵AD 平分MAN ∠， ∴EAD OAD ∠=∠． ∵OA OD =， ∴ODA OAD ∠=∠．∴EAD ODA ∠=∠．……………………………1分 ∵DE AM ⊥于E ， ∴90AED ∠=︒．FDECBOAO H F E D C BA O H G F EDC B A ∴90EAD EDA ∠+∠=︒，∴90ODA EDA ∠+∠=︒．∴OD ED ⊥．∴DE 是⊙O 的切线． ………………2分（2）解：∵30EDA ∠=︒，∴60ODA ∠=︒．∵OA OD =，∴△ADO 为等边三角形．…………………………………………………3分在Rt △AED 中，1AE =，可得2AD =，3ED =．………………4分 ∴2OD AD ==．在Rt △ODE 中，由勾股定理可得7OE =． ………………………5分12. （平谷）如图，△ABC 中，AB=AC ,以边BC 为直径的⊙O 与边AB ，AC 分别交于D ，F 两点，过点D 作⊙O 的切线DE ，使DE ⊥AC 于E ．（1）求证：△ABC 是等边三角形；（2）过点E 作EH ⊥BC ，垂足为点H ，连接FH ，若BC =4，求FH 的长．（1）证明：连接OD ， ∵ DE 是⊙O 的切线，∴ OD ⊥DE . (1)∵ DE ⊥AC ，∴ OD ∥AC .∴∠A =∠ODB .∵ OB =OD ，∴∠OBD =∠ODB .∴ ∠A =∠OBD .∴ AC =BC .∵ AB =AC ，∴ AB =AC =BC .∴ △ABC 是等边三角形. ……………2 （2）解：连接BF ，作FG ⊥BC 于点G . ∵ BC 是⊙O 的直径,∴ ∠BFC =90°.∵ △ABC 为等边三角形，∴ CF =12AC =12BC =2. ……………3 ∠C=60°.∵ FG ⊥BC ，∴FG=3，CG=1.在Rt△EHC中，可求CE=3，CH=3/2.∴HG=12 (4)在Rt△FGH中，由勾股定理可得FH=132 (5)初中数学试卷鼎尚图文**整理制作。

圆中有关计算圆的中档解答题分值为5分，难度中等偏上，是每一位考生力争满分的题型之一，所考查知识点相对稳定，主要考查学生对圆、相似、解直角三角形等内容的综合应用能力和计算能力．从题目本身来看，一般都采取标准的两问式子.2015年随着考试改革，本题的位置调整为23题，难度等同于去年．1．[2015·北京] 如图Z6－1，AB 是⊙O 的直径，过点B 作⊙O 的切线BM ，弦CD ∥BM ，交AB 于点F ，且DA ︵＝DC ︵，连接AC ，AD ，延长AD 交BM 于点E .(1)求证：△ACD 是等边三角形； (2)连接OE ，若DE ＝2，求OE 的长．图Z6－12．[2014·北京] 如图Z6－2，AB 是⊙O 的直径，C 是AB ︵的中点，⊙O 的切线BD 交AC 的延长线于点D ，E 是OB 的中点，CE 的延长线交切线BD 于点F ，AF 交⊙O 于点H ，连接BH . (1)求证：AC ＝CD ；(2)若OB ＝2，求BH 的长．图Z6－23．[2013·北京] 如图Z6－3，AB 是⊙O 的直径，PA ，PC 分别与⊙O 相切于点A ，C ，PC 交AB 的延长线于点D ，DE ⊥PO 交PO 的延长线于点E . (1)求证：∠EPD ＝∠EDO ；(2)若PC ＝6，tan ∠PDA ＝34，求OE 的长．图Z6－34．[2012·北京] 如图Z6－4，已知AB 是⊙O 的直径，C 是⊙O 上的一点，OD ⊥BC 于点D ，过点C 作⊙O 的切线，交OD 的延长线于点E ，连接BE . (1)求证：BE 与⊙O 相切；(2)连接AD 并延长交BE 于点F ，若OB ＝9，sin ∠ABC ＝23，求BF 的长．图Z6－45．[2011·北京] 如图Z6－5，在△ABC 中，AB ＝AC ，以AB 为直径的⊙O 分别交AC ，BC 于点D ，E ，点F 在AC 的延长线上，且∠CBF ＝12∠CA B.(1)求证：直线BF 是⊙O 的切线； (2)若AB ＝5，sin ∠CBF ＝55，求BC 和BF 的长．图Z6－51．[2014·东城一模] 如图Z6－6，AB 是⊙O 的直径，点E 是BD ︵上的一点，∠DAC ＝∠AE D. (1)求证：AC 是⊙O 的切线；(2)若点E 是BD ︵的中点，连接AE 交BD 于点F ，当BD ＝5，CD ＝4时，求DF 的值．图Z6－62．[2014·海淀一模] 如图Z6－7，在△ABC 中，AB ＝AC ，以AB 为直径的⊙O 与边BC ，AC 分别交于D ，E 两点，DF ⊥AC 于点F . (1)求证：DF 为⊙O 的切线； (2)若cos C ＝35，CF ＝9，求AE 的长．图Z6－73．[2014·西城一摸] 如图Z6－8，在△ABC 中，AB ＝AC ，以AB 为直径作⊙O ，交BC 于点D ，连接OD ，过点D 作⊙O 的切线，交AB 的延长线于点E ，交AC 于点F . (1)求证：OD ∥AC ； (2)当AB ＝10，cos ∠ABC ＝55时，求AF 及BE 的长．图Z6－84．[2015·东城一模] 如图Z6－9，在⊙O 中，AB 为直径，OC ⊥AB ，弦CD 与OB 交于点F ，过点D ，A 分别作⊙O 的切线交于点G ，且GD 与AB 的延长线交于点E . (1)求证：∠1＝∠2；(2)已知OF ∶OB ＝1∶3，⊙O 的半径为3，求AG 的长．图Z6－95．[2015·海淀二模] 如图Z6－10，AB 为⊙O 的直径，C ，D 为⊙O 上不同于A ，B 的两点，∠ABD ＝2∠BAC ，连接C D.过点C 作CE ⊥DB ，垂足为E ，直线AB 与CE 相交于点F . (1)求证：CF 为⊙O 的切线；(2)当BF ＝5，sin F ＝35时，求BD 的长．图Z6－106．[2015·青山区一模] 如图Z6－11，AB 是⊙O 的直径，BC 交⊙O 于点D ，E 是BD ︵的中点，连接AE 交BC 于点F ，∠ACB ＝2∠EA B. (1)求证：AC 是⊙O 的切线； (2)若cos C ＝23，AC ＝6，求BF 的长．图Z6－117．[2015·朝阳一模] 如图Z6－12，△ABC 内接于⊙O ，AB 为直径，点D 在⊙O 上，过点D 作⊙O 的切线与AC 的延长线交于点E ，ED ∥BC ，连接AD 交BC 于点F . (1)求证：∠BAD ＝∠DAE ；(2)若AB ＝6，AD ＝5，求DF 的长．图Z6－128．[2015·丰台一模] 如图Z6－13，⊙O 的直径AB 垂直于弦CD ，垂足为E ，过点C 作⊙O 的切线，交AB 的延长线于点P ，连接P D.(1)判断直线PD 与⊙O 的位置关系，并加以证明；(2)连接CO 并延长交⊙O 于点F ，连接FP 交CD 于点G .如果CF ＝10，cos ∠APC ＝45，求EG的长．图Z6－139．[2015·海淀一模] 如图Z6－14，在△ABC 中，AB ＝AC ，AD ⊥BC 于点D ，过点C 作⊙O 与边AB 相切于点E ，交BC 于点F ，CE 为⊙O 的直径．(1)求证：OD⊥CE；(2)若DF＝1，DC＝3，求AE的长．图Z6－1410．[2015·西城一模] 如图Z6－15，AB为⊙O的直径，M为⊙O外一点，连接MA与⊙O交于点C，连接MB并延长交⊙O于点D，经过点M的直线l与MA所在直线关于直线MD对称．作BE⊥l于点E，连接AD，DE.(1)依题意补全图形；(2)在不添加新的线段的条件下，写出图中与∠BED相等的角，并加以证明．图Z6－15参考答案1.解：(1)∴AB ⊥BM .∵BM ∥CD ，∴AB ⊥CD ， ∴AD ︵＝AC ︵，∴AD ＝AC. ∵DA ︵＝DC ︵，∴DC ＝AD ，∴AD ＝CD ＝AC ，∴△ACD 为等边三角形．(2)∵△ACD 为等边三角形，AB ⊥CD ， ∴∠DAB ＝30°. 连接BD.∵AB 为⊙O 的直径，∴BD ⊥AD ，∠EBD ＝∠DAB ＝30°. ∵DE ＝2，∴BE ＝4，BD ＝2 3，AB ＝4 3，OB ＝2 3. 在Rt △OBE 中，OE ＝OB 2＋BE 2＝12＋16＝2 7. 2.解：(1)证明：如图，连接OC.∵C 是AB ︵的中点，AB 是⊙O 的直径， ∴OC ⊥A B.∵BD 是⊙O 的切线，∴BD ⊥AB ， ∴OC ∥BD .∵AO ＝BO ，∴AC ＝CD. (2)∵E 是OB 的中点， ∴OE ＝BE .在△COE 与△FBE 中，∠CEO ＝∠FEB ，OE ＝BE ，∠COE ＝∠FBE ， ∴△COE ≌△FBE (ASA )， ∴CO ＝BF .∵OB ＝2，∴BF ＝OC ＝2，∴AF ＝42＋22＝2 5.∵AB 是⊙O 的直径，∴BH ⊥AF ，∴△ABF ∽△BHF ，∴AB ·BF ＝AF ·BH ， ∴BH ＝AB·BF AF ＝4×22 5＝4 55.3．解：(1)证明：∵PA ，PC 与⊙O 分别相切于点A ，C ， ∴∠APO ＝∠EPD ，PA ⊥AO ，即∠PAO ＝90°. ∵∠AOP ＝∠EOD ，∠PAO ＝∠E ＝90°， ∴∠APO ＝∠EDO ， ∴∠EPD ＝∠EDO . (2)连接OC .∵PA ＝PC ＝6，tan ∠PDA ＝34，∴在Rt △PAD 中，AD ＝8，PD ＝10， ∴CD ＝4. ∵tan ∠PDA ＝34，∴在Rt △OCD 中，OC ＝3，OD ＝5. ∵∠EPD ＝∠EDO ，∴△OED ∽△DEP ， ∴PD OD ＝DE OE ＝105＝21，∴DE ＝2OE .在Rt △OED 中，OE 2＋DE 2＝52，∴OE ＝ 5.4．解：(1)证明：连接OC. ∵EC 与⊙O 相切，C 为切点， ∴∠ECO ＝90°.∵OB ＝OC ，∴∠OCB ＝∠OBC. ∵OD ⊥BC ，∴DB ＝DC ，∴直线OE 是线段BC 的垂直平分线， ∴EB ＝EC ，∴∠ECB ＝∠EBC ， ∴∠ECO ＝∠EBO ，即∠EBO ＝90°. ∵AB 是⊙O 的直径， ∴BE 与⊙O 相切．(2)过点D 作DM ⊥AB 于点M ，则DM ∥FB. 在Rt △ODB 中，∵∠ODB ＝90°，OB ＝9，sin ∠ABC ＝23，∴OD ＝OB ·sin ∠ABC ＝6.由勾股定理，得BD ＝OB 2－OD 2＝3 5. 在Rt △DMB 中，同理得DM ＝BD ·sin ∠ABC ＝2 5， BM ＝BD 2－DM 2＝5.∵O 是AB 的中点，∴AB ＝18， ∴AM ＝AB －BM ＝13.∵DM ∥FB ，∴△AMD ∽△ABF ， ∴MD BF ＝AM AB， ∴BF ＝MD ·AB AM ＝36 513.5．解：(1)证明：如图，连接AE . ∵AB 是⊙O 的直径，∴∠AEB ＝90°，∴∠1＋∠2＝90°. ∵AB ＝AC ，∴∠1＝12∠CAB .∵∠CBF ＝12∠CAB ，∴∠1＝∠CBF ，∴∠CBF ＋∠2＝90°， 即∠ABF ＝90°. ∵AB 是⊙O 的直径，∴直线BF 是⊙O 的切线．(2)如图，过点C 作CG ⊥AB 于点G .∵sin ∠CBF ＝55，∠1＝∠CBF ，∴sin ∠1＝55. ∵∠AEB ＝90°，AB ＝5，∴BE ＝AB ·sin ∠1＝ 5.∵AB ＝AC ，∠AEB ＝90°，∴BC ＝2BE ＝2 5. 在Rt △ABE 中，由勾股定理，得AE ＝2 5， ∴sin ∠2＝2 55，cos ∠2＝55.在Rt △CBG 中，可求得GC ＝4，GB ＝2，∴AG ＝3. ∵GC ∥BF ，∴△AGC ∽△ABF ，∴GC BF ＝AG AB， ∴BF ＝GC ·AB AG ＝203.1.解：(1)∴∠ADB ＝∠ADC ＝90°.∵∠B ＝∠AED ＝∠CAD ，∠C ＝∠C ， ∴∠C ＋∠CAD ＝∠C ＋∠B ＝90°， ∴∠BAC ＝∠ADC ＝90°. 又∵AB 是⊙O 的直径， ∴AC 是⊙O 的切线． (2)可证△ADC ∽△BAC ， ∴AC BC ＝CD AC，即AC 2＝BC ·CD ＝36. 解得AC ＝6. ∵E 是BD ︵的中点，∴∠DAE ＝∠BAE .∵∠CAF ＝∠CAD ＋∠DAE ＝∠ABF ＋∠BAE ＝∠AFD ，∴CA ＝CF ＝6， ∴DF ＝CF －CD ＝2.2．解：(1)证明：如图，连接OD ，AD . ∵AB 是⊙O 的直径， ∴∠ADB ＝90°. 又∵AB ＝AC ，∴D 为BC 的中点． 又∵O 为AB 的中点， ∴OD ∥A C. ∵DF ⊥AC ， ∴DF ⊥OD.又∵OD 为⊙O 的半径， ∴DF 为⊙O 的切线．(2)如图，连接BE .∵DF ⊥AC ，CF ＝9， ∴cos C ＝CF CD， ∴CD ＝CFcos C ＝9÷35＝15. ∵∠ADB ＝90°， ∴∠ADC ＝90°， ∴cos C ＝CD AC， ∴AC ＝CDcos C ＝15÷35＝25. ∵AB 是⊙O 的直径， ∴∠AEB ＝90°. 又∵DF ⊥AC ， ∴DF ∥BE ， ∴CF EF ＝CD BD＝1，∴EF ＝CF ＝9，∴AE ＝AC －EF －CF ＝25－9－9＝7. 3．解：(1)证明：如图，连接AD. ∵AB 是⊙O 的直径， ∴∠ADB ＝90°， ∴AD ⊥BC . ∵AB ＝AC ，∴∠1＝∠2.又∵OA ＝OD ，∴∠1＝∠ODA ，∴∠2＝∠ODA ，∴OD ∥A C.(2)∵EF 是⊙O 的切线，∴∠ODE ＝90°.由(1)知OD ∥AC ，∠1＝∠2，∠ADB ＝90°，∴∠AFE ＝∠ODE ＝90°，∠ADF ＝∠ABC.在Rt △ADB 中，AB ＝10，cos ∠ABC ＝55， ∴AD ＝4 5，BD ＝2 5，OD ＝5.在Rt △AFD 中，cos ∠ADF ＝cos ∠ABC ＝55， ∴DF ＝4，∴AF ＝8.∵OD ∥AC ，∴OD AF ＝OE AE， 即58＝BE ＋5BE ＋10， ∴BE ＝103. 4．解：(1)证明：如图，连接OD .∵DE 为⊙O 的切线，OD 为⊙O 的半径，∴OD ⊥DE ，∴∠ODE ＝90°，即∠2＋∠ODC ＝90°.∵OC ＝OD ，∴∠C ＝∠ODC ，∴∠2＋∠C ＝90°.而OC ⊥OB ，∴∠3＋∠C ＝90°，∴∠2＝∠3.∵∠1＝∠3，∴∠1＝∠2.(2)∵OF ∶OB ＝1∶3，⊙O 的半径为3，∴OF ＝1.∵∠1＝∠2，∴EF ＝ED.在Rt △ODE 中，OD ＝3，设DE ＝x ，则EF ＝x ，OE ＝1＋x .∵OD 2＋DE 2＝OE 2，∴32＋x 2＝()x ＋12，解得x ＝4， ∴DE ＝4，OE ＝5.∵AG 为⊙O 的切线，OA 为⊙O 的半径，GD 为⊙O 的切线， ∴AG ⊥AE ，GA ＝GD ，∴∠GAE ＝90°.在Rt △AGE 中，设DG ＝AG ＝t ，则GE ＝t ＋4.∵AG 2＋AE 2＝GE 2，∴t 2＋82＝()t ＋42，解得t ＝6， ∴AG ＝6. 5.解：(1)证明：如图，连接OC .∵OA ＝OC ，∴∠1＝∠2.又∵∠3＝∠1＋∠2，∴∠3＝2∠1.又∵∠4＝2∠1，∴∠4＝∠3，∴OC ∥DB .∵CE ⊥DB ，∴OC ⊥CF .又∵OC 为⊙O 的半径，∴CF 为⊙O 的切线．(2)如图，连接AD .在Rt △BEF 中，∠BEF ＝90°，BF ＝5，sin F ＝35， ∴BE ＝3.∵OC ∥BE ，∴△FBE ∽△FOC ，∴FB FO ＝BE OC.设⊙O 的半径为r ，∴55＋r ＝3r ， 解得r ＝152. ∵AB 为⊙O 的直径，∴AB ＝15，∠ADB ＝90°.∵∠4＝∠EBF ，∴∠F ＝∠BAD ，∴sin ∠BAD ＝BD AB ＝sin F ＝35， ∴BD 15＝35， ∴BD ＝9.6．解：(1)证明：如图，连接AD.∵E 是BD ︵的中点，∴DE ︵＝BE ︵，∴∠EAB ＝∠EAD.∵∠ACB ＝2∠EAB ，∴∠ACB ＝∠DAB .∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠DAC ＋∠ACB ＝90°，∴∠DAC ＋∠DAB ＝90°，即∠BAC ＝90°，∴AC ⊥A B.又∵AB 是⊙O 的直径，∴AC 是⊙O 的切线．(2)如图，过点F 作FH ⊥AB 于点H .在Rt △ACD 中，∵cos C ＝CD AC ＝23，AC ＝6， ∴CD ＝23×6＝4. 在Rt △ACB 中，∵cos C ＝AC BC ＝23， ∴BC ＝32×6＝9， ∴BD ＝BC －CD ＝9－4＝5.∵∠EAB ＝∠EAD ，即AF 平分∠BAD ，而FD ⊥AD ，FH ⊥AB ，∴FD ＝FH .设BF ＝x ，则DF ＝FH ＝5－x .∵FH ∥AC ，∴∠HFB ＝∠C.在Rt △BFH 中，∵cos ∠BFH ＝cos C ＝23＝FH BF， ∴5－x x ＝23，解得x ＝3，即BF 的长为3.7．解：(1)如图，连接OD.∵ED 为⊙O 的切线，∴OD ⊥ED.∵AB 为⊙O 的直径，∴∠ACB ＝90°.∵BC ∥ED ，∴∠ACB ＝∠E ＝∠EDO ＝90°，∴AE ∥OD ，∴∠DAE ＝∠ADO .∵OA ＝OD ，∴∠BAD ＝∠ADO ，∴∠BAD ＝∠DAE .(2)如图，连接BD.∵AB 是⊙O 的直径，∴∠ADB ＝90°.∵AB ＝6，AD ＝5，∴BD ＝AB 2－AD 2＝11.∵∠BAD ＝∠DAE ＝∠CBD ，∴tan ∠CBD ＝tan ∠BAD ＝115. 在Rt △BDF 中，∴DF ＝BD ·tan ∠CBD ＝115. 8．解：(1)PD 与⊙O 相切．证明：如图，连接OD.∵在⊙O 中，OD ＝OC ，AB ⊥CD 于点E ，∴∠1＝∠2.又∵OP ＝OP ，∴△OCP ≌△ODP ，∴∠OCP ＝∠ODP .又∵PC 切⊙O 于点C ，OC 为⊙O 的半径，∴OC ⊥PC ，∴∠OCP ＝90°，∴∠ODP ＝90°，∴OD ⊥PD.又∵点D 在⊙O 上，∴PD 与⊙O 相切于点D.(2)如图，过点F 作FM ⊥AB 于点M .∵∠OCP ＝90°，CE ⊥OP 于点E ，∴∠3＋∠4＝90°，∠APC ＋∠4＝90°，∴∠3＝∠AP C.∵cos ∠APC ＝45，∴Rt △OCE 中，cos ∠3＝CE OC ＝45. ∵CF ＝10，∴OF ＝OC ＝12CF ＝5， ∴CE ＝4，OE ＝3.又∵FM ⊥AB ，AB ⊥CD ，∴∠FMO ＝∠CEO ＝90°.∵∠5＝∠1，OF ＝OC ，∴△OFM ≌△OCE ，∴FM ＝CE ＝4，OM ＝OE ＝3.∵在Rt △OCP 中，cos ∠APC ＝PC OP ＝45， 设PC ＝4k ，OP ＝5k ，∴OC ＝3k .∴3k ＝5，解得k ＝53.∴OP ＝253. ∴PE ＝OP －OE ＝163，PM ＝OP ＋OM ＝343. 又∵∠FMO ＝∠GEP ＝90°，∴FM ∥GE ，∴△PGE ∽△PFM ，∴GE FM ＝PE PM ，即GE 4＝163343， ∴GE ＝3217. 9．解：(1)证明：∵⊙O 与边AB 相切于点E ，且CE 为⊙O 的直径， ∴CE ⊥AB.∵AB ＝AC ，AD ⊥BC ，∴BD ＝DC .又∵OE ＝OC ，∴OD ∥EB ，∴OD ⊥CE .(2)如图，连接EF .∵CE 为⊙O 的直径，且点F 在⊙O 上，∴∠EFC ＝90°.∵CE ⊥AB ，∴∠BEC ＝90°，∴∠BEF ＋∠FEC ＝∠FEC ＋∠ECF ＝90°，∴∠BEF ＝∠ECF ，∴tan ∠BEF ＝tan ∠ECF ，∴BF EF ＝EF FC.又∵DF ＝1，BD ＝DC ＝3，∴BF ＝2，FC ＝4，∴EF ＝2 2.∵∠EFC ＝90°，∴∠BFE ＝90°.由勾股定理，得BE ＝BF 2＋EF 2＝2 3. ∵EF ∥AD ， ∴BE EA ＝BF FD ＝21， ∴AE ＝ 3.10．解：(1)依题意，补全图形如图．(2)图中与∠BED 相等的角为∠BAD . 证明：如图，连接BC ，CD .∵直线l 与直线MA 关于直线MD 对称， ∴∠1＝∠2.∵AB 为⊙O 的直径，∴∠ACB ＝90°，即BC ⊥MA.又∵BE ⊥l ，∴易证△MBC ≌△MBE ， ∴MC ＝ME .又∵C ，E 两点分别在直线MA 与直线l 上， ∴C ，E 两点关于直线MD 对称． ∴∠3＝∠BED.又∵∠3＝∠BAD ，∴∠BAD ＝∠BE D.。

中考专题复习圆形(含答案)本文档为中考数学专题复，主要涵盖了圆形的相关知识点及答案。

以下是题目及对应的答案：1. 求圆的面积题目：已知圆的半径为4cm，求圆的面积。

答案：圆的面积公式为$S = \pi \cdot r^2$，代入半径$r = 4$，得到$S = \pi \cdot 4^2 = 16\pi cm^2$。

2. 求圆的周长题目：已知圆的直径为6cm，求圆的周长。

答案：圆的周长公式为$C = \pi \cdot d$，代入直径$d = 6$，得到$C = \pi \cdot 6 = 6\pi cm$。

3. 求圆的直径题目：已知圆的周长为10π cm，求圆的直径。

答案：圆的周长公式为$C = \pi \cdot d$，代入周长$C = 10\pi$，解方程得到$d = \frac{C}{\pi} = \frac{10\pi}{\pi} = 10 cm$。

4. 求圆柱体的体积题目：已知圆柱体的底面积为9π $cm^2$，高度为5cm，求圆柱体的体积。

答案：圆柱体的体积公式为$V = \pi \cdot r^2 \cdot h$，代入底面积$S = 9\pi$，高度$h = 5$，得到$V = \pi \cdot 3^2 \cdot 5 = 45\pi cm^3$。

5. 求扇形的面积题目：已知扇形的半径为8cm，弧长为12cm，求扇形的面积。

答案：扇形的面积公式为$S = \frac{1}{2} \cdot r \cdot l$，代入半径$r = 8$，弧长$l = 12$，得到$S = \frac{1}{2} \cdot 8 \cdot 12 =48 cm^2$。

6. 求圆锥的体积题目：已知圆锥的底面积为16π $cm^2$，高度为6cm，求圆锥的体积。

答案：圆锥的体积公式为$V = \frac{1}{3} \cdot \pi \cdot r^2\cdot h$，代入底面积$S = 16\pi$，高度$h = 6$，得到$V =\frac{1}{3} \cdot \pi \cdot 4^2 \cdot 6 = 32\pi cm^3$。

2016年北京模拟专题---圆朝阳24．（本小题5分）如图，以△ABC 的一边BC 为直径的⊙O ，交AB 于点D ，连接CD ，OD ， 已知∠A+12∠1=90°． （1）求证：AC是⊙O 的切线；（2）若∠B=30°，AD=2，求⊙O 的半径．朝阳24.（1）证明：依题意，得 ∠B=12∠1． …………………………………1分 ∵∠A+12∠1=90°，∴∠A+∠B=90°.∴∠ACB=90°.∴AC ⊥BC. ∵BC 是⊙O 的直径，∴AC 是⊙O 的切线． …… …………………………………2分（2） 解：∵BC 是⊙O 的直径，∴∠CDB=∠ADC=90°． ……………………………………3分∵∠B=30°，∴∠A=60°，∠ACD=30°．∴AC=2AD=4． ………………………………4分∴43tan ACBC B==∠． ∴⊙O 的半径为23． …………………5分东城25. 如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，与BA 的延长线交于点D ，DE ⊥PO 交PO 延长线于点E ，连接PB ，∠EDB=∠EPB ．（1）求证：PB 是⊙O 的切线．（2）若PB=3，DB=4，求DE 的长．东城25. 解：（1）证明：∵ ∠EDB=∠EPB ，∠DOE=∠POB ，∴ ∠E=∠PBO=90゜，∴ PB 是⊙O 的切线．…………2分 （2）∵ PB=3，DB=4，∴ PD=5. 设⊙O 的半径的半径是r ，连接OC. ∵ PD 切⊙O 于点C ，∴ OC ⊥PD.∴ .222OD OC CD=+∴ .)4(2222r r -=+∴.23=r 可求出352PO =.易证△DEP ∽△OBP.∴ DE DP OB OP=.解得 5DE =. ……5分1ODBCA房山24．如图，AB 为⊙O 的直径，点C 在⊙O 上，且∠CAB =30°，点D 为弧AB 的中点，AC =43.求CD 的长.房山24．解法1：连结BC∵AB 为⊙O 的直径，点C 在⊙O 上，∴∠ACB =90°. -------------1分 ∵∠CAB =30°，∴∠D =60°. ---------------2分∵点D 为弧AB 的中点，∴∠ACD =45°.过点A 作AE ⊥CD ，∵AC=43，∴AE=CE =26. ------------3分∴DE =22. -------------4分 ∴CD =2622+. --------5分 解法2：∵AB 为⊙O 的直径，点D 为弧AB 的中点，∴∠DAB =∠ACD =45°. ------1分 ∵∠CAB =30°，∴弧BC=60°，弧AC =120°.∴∠ADC =60°. --------2分 过点A 作AE ⊥CD ， ∵AC=43，∴AE=CE =26. ------3分 ∴DE =22. -----------4分 ∴CD =2622+.--------5分海淀24．如图，AB ，AD 是⊙O 的弦，AO 平分.过点B 作⊙O 的切线交AO 的延长线于点C ，连接CD ，BO .延长BO 交⊙O 于点E ，交AD 于点F ，连接AE ，DE .（1）求证：是⊙O 的切线；（2）若，求的长.海淀24. (1) 证明：如图，连接． ………………………1分 ∵为⊙的切线，∴． ∵平分BAD ∠，∴．∵OA OB OD ==，∴1=4=2=5∠∠∠∠． ∴．∴△△．∴90CBO CDO ∠=∠=︒． ∴为⊙的切线． ……………2分 (2) ∵,∴AE DE =.∴. ………………………3分∵124∠=∠=∠，∴.∵为⊙的直径,∴.∴.………………………4分∴ ．在Rt △AFE 中，∵，︒=∠303，∴. ………………………5分BAD ∠CD 3AE DE ==AF CBAO E CB AO ECBAO怀柔24.如图，在⊙O 中，AB 为直径，OC AB ⊥，弦CF 与OB 交于点E ，过点F ，A 分别作⊙O 的切线交于点H ，且HF 与AB 的延长线交于点D ．（1）求证：DF=DE;（2）若tan ∠OCE＝12，⊙O 的半径为4，求A H 的长．怀柔24. (1)证明：连结OF ，如图.∴OF⊥DH.∵DH 为⊙O 的切线，OF 为半径，∴∠OFD=90°。