2021年高考永州市第一次模拟考试分析数据(全)

湖南省永州市2021届新高考物理模拟试题（1）一、单项选择题：本题共6小题，每小题5分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的1．双星系统由两颗相距较近的恒星组成，每颗恒星的半径都远小于两颗星球之间的距离，而且双星系统一般远离其他天体。

如图所示，相距为L 的M 、N 两恒星绕共同的圆心O 做圆周运动，M 、N 的质量分别为m 1、m 2，周期均为T 。

若另有间距也为L 的双星P 、Q ，P 、Q 的质量分别为2m 1、2m 2，则( )A ．P 、Q 运动的轨道半径之比为m 1∶m 2B ．P 、Q 运动的角速度之比为m 2∶m 1C ．P 、Q 运动的周期均为22T D ．P 与M 的运动速率相等【答案】C【解析】【详解】双星系统的两颗恒星运动的角速度相等，由万有引力提供向心力，对M 、N 有 G 122m m L＝m 1·r 122π()T G122m m L ＝m 2·r 222π()T 对P 、Q 有 G 12222m m L ⋅＝2m 1·r′122π()TG12222m m L ⋅＝2m 2·r′222π()T 其中r 1＋r 2＝L ，r′1＋r′2＝L联立解得T′＝22T 由2m1r′1＝2m2r′2可知r′1∶r′2＝m2∶m1则可知r1＝r′1结合v＝2rT可知P与M的运动速率不相等，故ABD错误，C正确。

故选C。

2．如图所示为两辆汽车同时同地沿同一平直的公路同向行驶时，通过DIS系统在计算机中描绘出的速度时间图像。

则下列说法正确的是（）A．汽车A的运动轨迹为直线，汽车B的运动轨迹为曲线B．t1时刻两辆汽车相遇C．t1时刻汽车A的加速度大于汽车B的加速度D．在0~t1时间内，两辆汽车之间的距离增大后减小【答案】C【解析】【分析】【详解】A．由图像可知：汽车A做匀加速直线运动，汽车B做加速度逐渐减小的加速直线运动，A错误；B．A、B两v-t图像的交点表示此时两辆汽车共速，B错误；C．v-t图像的斜率表示加速度，由于t1时刻图线A的斜率较大，因此t1时刻汽车A的加速度大于汽车B 的加速度，C正确；D．在0~t1时间内，由于汽车B的速度一直大于汽车A的速度，因此两辆汽车之间的距离一直增大，D错误。

永州市2021年高考第一次模拟考试试卷数 学注意事项：1．全部答案在答题卡上完成，答在本试题卷上无效． 2．考试结束后，只交答题卡．一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知全集U R =，集合{}{}21,3xM x N x x =≥=≤，则MN =A ．](-3∞，B ．[]0,1C ．[]0,3D ．[]13，2．若复数11i z i-=+，则=zA ．1B ．2 CD ．23．已知向量a ，b 满足()1,a m =，()2,1b =-，且(2)a b b +，则m =A ．-2B ．-12C ．12D ．24．已知双曲线2222:1x y C a b-=的渐近线方程为y x =±，则该双曲线的离心率为AB C ． 2 D ． 35．某县政府为了加大对一贫困村的扶贫力度，研究决定将6名优秀干部安排到该村进行督导巡视，周一至周四这四天各安排1名，周五安排2名，则不同的安排方法共有 A ．320种B ．360种C ．370种D ．390种6．苏格兰数学家科林麦克劳林(Colin Maclaurin)研究出了著名的Maclaurin 级数展开式，受到了世界上顶尖数学家的广泛认可，下面是麦克劳林建立的其中一个公式：()()2341ln 1+1234nn x x x xx x n-=-+-+-+...+...，试根据此公式估计下面代数式()141...(5)3n n -+-+≥+...+的近似值为（可能用到数值ln2.4140.881,ln3.414 1.23==）A ．2.788B ．2.881C ．2.886D ．2.9027．在四面体S ABC -中，SA ABC ⊥平面，901ABC SA AC AB ︒∠===，，，则该四面体的外接球的表面积为A ．3π2 B ．43π C ．4π D ．5π 8．已知()f x 为定义在R 上的奇函数，当0x ≥时，22()log (1)f x x x =++，则不等式(1)2f x +>-的解集为 A ．(,1)-∞- B ．(,2)-∞-C ．(1,)-+∞D ．(2,)-+∞二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分，有选错的得0分.部分选对的得3分.9．2020年新型冠状病毒肺炎疫情对消费饮食行业造成了很大影响，为了解A ，B 两家大型餐饮店受影响的程度，现统计了2020年2月到7月A ，B 两店每月营业额，得到如图所示的折线图，根据营业额折线图可知，下列说法正确的是 A ．A 店营业额的平均值超过B 店营业额的平均值 B ．A 店营业额在6月份达到最大值C ．A 店营业额的极差比B 店营业额的极差小D ．A 店5月份的营业额比B 店5月份的营业额小 10．已知0a >，0b >，则下列关系中正确的是 A ．2lg lg a b≥B ．若2a b +=，则2a b +≤C ．若1a b k >>>，则b b a k >D ．若1ab =，则112a b+≥ 11．若函数()cos()f x x ωϕ=-（0ω>，||2πϕ<）的两相邻对称轴之间的距离为2π，且6x π=-时()f x 有最大值，则下列结论成立的是A ．()012f π=B ．函数()f x 的一个单调递减区间为[42,]ππC ．函数()f x 的图象关于点(,0)3π对称D ．函数()f x 的图象关于直线23x π=-对称12．已知O 为坐标原点，椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12F F 、，长轴长为22，焦距为2c ，点P 在椭圆C 上且满足12OP OF OF c ===，直线2PF 与椭圆C交于另一个点Q ，若124cos 5FQF ∠=，点M 在圆228:9G x y +=上，则下列说法正确的是A ．椭圆C 的焦距为2B ．三角形12MF F 面积的最大值为22C ．圆G 在椭圆C 的内部D ．过点2F 的圆G 的切线斜率为2±三、填空题：本题共4小题，每小题5分,共20分.13．在等比数列{}n a 中，若510a =，则19lg lg a a +＝ .（第9题图）14．若tan 1α=，则cos()sin(3)3παπα+-的值为________.15．甲、乙两人参加“社会主义价值观”知识竞赛，两人获一等奖的概率分别为13和12，若两人是否获得一等奖相互独立，则这两人中恰有一人获得一等奖的概率为_____.16．已知四棱锥S ABCD -的底面是边长为4的正方形，SD ABCD ⊥面,点M 、N 分别是AD CD 、的中点,P 为SD 上一点，且33SD PD ==，H 为正方形ABCD 内一点, 若SHPMN 面，则SH 的最小值为 .四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．（本题满分10分）请从①6,sin()2b B π=-=；②42a c b +=+=，sin sin c bA C-=+ 18．（本题满分12分）设数列{}n a 的前n 项和为n S ，已知11a =，*11()n n a S n N +=+∈. （1）求数列{}n a 的通项公式；（2）若n a ，1b ，2b ，…n b ，1n a +组成一个2n +项的等差数列，记其公差为n d ，求数列1n d ⎧⎫⎨⎬⎩⎭的前n 项和n T . 19．（本题满分12分）某市为了在全市营造“浪费可耻、节约为荣”的氛围,制定施行“光盘行动”有关政策，为进一步了解此项政策对市民的影响程度，市政府在全市随机抽取了100名市民进行调查，其中男士与女士的人数之比为3:2，男士中有10人表示政策无效，女士中有25人表示政策有效.（1）根据下列22⨯列联表写出a 和b 的值，并判断能否有99%的把握认为“政策是否1010抽取4名，对政策的有效性进行调研分析，设随机变量X 表示抽取到的4名市民中女士的人数，求X 的分布列及数学期望．参考公式：22()()()()()()n ad bc K n a b c d a b c d a c b d -==+++++++．2()P K k > 0.15 0.10 0.05 0.025 0.010 0.005 0.001k 2.072 2.706 3.842 5.024 6.635 7.879 10.82820．（本题满分12分）已知在直三棱柱111ABC A B C -中，AC BC ⊥,2,AC BC ==13AA =，点O 、E 分别为11AB A C 、中点.三棱柱外一点D 满足DO ⊥平面ABC ,2DO =. （1）求证：//DE 平面11BB C C ； （2）求二面角E BC D --的余弦值．21．（本题满分12分）已知抛物线2:2(0)C x py p =>的焦点为F ，过点F 且斜率为12的直线与抛物线C 交于A ，B 两点，||5AB =. （1）求抛物线C 的标准方程；（2）过点F 的直线l 交抛物线C 于D ,E 两点．过D ,E 分别作抛物线C 的切线，两切线交于点M ，若直线l 与抛物线C 的准线交于第四象限的点N ，且MN DE =，求直线l 的方程.22．（本题满分12分）已知函数()ln x f x ae a =+，()()ln 11g x x =++（其中a 为常数，e 是自然对数的底数）.若函数()ln y f x a =-在点()0,A a 处的切线为1l ，函数 (1)1y g x =--在点(),0B a 处的切线为2l ．（1）若12l l ，求1l 和2l 的方程；（2）若()()f x g x >恒成立，求a 的取值范围.（第20题图）永州市2021年高考第一次模拟考试试卷数学参考答案一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中， 只有一项是符合题目要求的．二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题三、填空题：本大题共4小题，每小题5分，共20分. 把答案填在答题卡中对应题号后的横线上.13．2 14．1 15．1216．四、解答题：本大题共70分，解答应写出文字说明、证明过程或演算步骤. 17．（本小题满分10分）解：选择条件①：（1） sin sin sin c a c bB AC --=+， ∴由正弦定理可得：c a c bb a c--=+，整理可得：222b c a bc +-=， ················2分 根据余弦定理可知22201cos ,60b c a A A +==∴=-··································3分综上所述：()93743,2ABC a S ∆+==·········································10分选择条件②：（1）sin sin sin c a c bB AC --=+， ∴由正弦定理可得：c a c bb a c--=+，整理可得：222b c a bc +-=， ················2分 又2b =，423a c +=+；()()2244232423a a a ∴+---=+-；化简整理可得：()()2436423443,23,4a a c +=+--∴== ·················6分 （2）由（1）知222a b c +=，故三角形为直角三角形，1223232ABC S ∆∴=⨯⨯=综上所述：23,23ABC a S ∆==···························································10分18．（本小题满分12分）解：因为*11()n n a S n N +=+∈ 所以，当2n ≥时，-11n n a S =+，两式相减得，1n n n a a a +-=，即，当2n ≥时12n naa +=， ·······························3分又当1n =时，211a a =+，而11a =，则212a a =，·····································4分 所以数列{}n a 是首项为1，公比为2的等比数列，所以12n n a -= . ··················································································6分 （2）依题意可知，1(1)n n n a n d a +++=，由（1）得，12(1)2n n n n d -++=，即1112n n n d -+=，·······································8分 则012123412222n n n T -+=++++， 123112*********n n n n n T -+=+++++， 两式相减得12311111112222222n n nn T -+=+++++-， ·································10分 即11113213122212n n n n n n T -++=+-=--， 所以，1362n n n T -+=- ··········································································12分19．（本小题满分12分）解：（1）由题意知，男士人数为3100605⨯=，女士人数为2100405⨯=，············································································································1分由此填写22⨯列联表如下：可知50a = ，15b = ·································3分 由表中数据，计算22100(50152510) 5.556 6.63560407525K ⨯⨯-⨯==<⨯⨯⨯ ·····················5分 所以没有99%的把握认为对“政策是否有效与性别有关”； ························6分（2）从被调查的该餐饮机构的市民中，利用分层抽样抽取10名市民，男士抽取60106100⨯=人，女士抽取4人， ············································7分 随机变量X 的可能取值为0，1，2，3，4，464101(0)14C P X C ===，13464108(1)21C C P X C ===，22464103(2)7C C P X C ===31464104(3)35C C P X C ===，444101(4)210C P X C ===········································10分所以X 的分布列为数学期望为：1()01234142183521057E X =⨯+⨯+⨯+⨯+⨯=． ·····················12分 20．（本小题满分12分）解：（1）（坐标法略）几何法：取11A B 的中点为Q ，连接,OQ 易知,,.D O Q 三点共线,Q E 分别为1111,A B A C 的中点11QE C B ∴ ·············································1分又DQ ⊥平面ABC ,1BB ⊥平面ABC ,1BB DQ ∴ ····································4分QEDQ Q =，QE DQE ⊂平面，DQ DQE ⊂平面 11DQEBB CC ∴面面，又DE DQE ⊂平面 11DEBB CC ∴平面 ················································5分（2）（几何法略）坐标法：取BC ，AC 的中点分别为F ，H ，,,OH BC OF AC 由题意知ABC 又三角形为等腰直角三角形，AB BC =，°=90ACB 所以∠，°=90.FOH ∠所以OD OH OF ,,两两垂直，以O 为坐标原点， OD OH OF ,,所在直线分别为z y x ,,轴建立空间直角坐标系， ·······································6分 则(1,1,0)B -， 2)D ，(0,1,3)E ，(1,1,0)C ， 从而(0,2,0)BC =，(2)BD =-，(1,2,3)BE =-. 设平面BDC 的法向量为),,(z y x =，则00BC m BD m ⋅=⋅=⎧⎪⎨⎪⎩，即2020y x y z =-++=⎧⎨⎩，得y=0,取2=x ，则1=z ， 因而)1,0,2(=m . ··········································································8分设平面EBC 的法向量为),,(c b a =，则⎪⎩⎪⎨⎧=⋅=⋅00n BE n BC ，即⎩⎨⎧=-+-=03202c b a b ， 得b =0,取3=a ，则1-=c ，因而)1,0,3(-=n ， ································10分从而63232316||||,cos -=⨯-=⋅>=<n m n m n m .······························11分易知二面角D BC E --为钝二面角，因而二面角D BC E --的余弦值为6233-.······································································································12分21．（本小题满分12分）解：（1）由抛物线的方程可得焦点(0,)2p F ，由题意可得直线AB 的方程为：122py x =+，即2x y p =-，设11)(,A x y ，22)(,B x y ， 联立直线AB 与抛物线的方程：222x p y px y ⎩=⎧⎨=-，整理可得22460y py p -+= ··························································2分 1232y y p +=，2124y p y =································································3分 由抛物线的性质可得123||52pAB y y p p =++=+=，解得2p =，所以抛物线的方程为：24x y =························································4分 （2）易知直线l 的斜率存在且不为零，又由（1）知(0,1)F故可设直线l 的方程为(1)x m y =-，代入抛物线的方程24x y =得，22222(2)0m y m y m -++=设33)(,D x y ，44)(,E x y ，则34242y y m +=+，341y y =，344x x m +=，344x x =- 3424||||||4DE DF EF y y p m∴=+=++=+， ··································6分由抛物线24x y =得214y x =，则12y x '=，所以抛物线在33)(,D x y ，44)(,E x y 两点处的切线的斜率分别为312x ，412x ，故两切线的方程分别为333()2x y y x x -=-，444()2xy y x x -=-，即332()y y x x =+，442()y y x x =+， ················································8分 解得两切线的交点为3434(,)24x x x x M +，即2(,1)M m-， 又准线的方程为1-=x ，由(1)1x m y y ⎩=-=⎧⎨-，得(2,1)N m --···················9分 则1||2||MN m m=+， 由||||MN DE =，得2112||41m m m ⎛⎫+=+ ⎪⎝⎭，得2m =±， ·····················10分 因为直线l 与准线交于第四象限的点N ，故有2m =-，从而直线l 的方程为.2(1)x y =--，即220x y +-=. ························12分22．（本小题满分12分）解：（1）根据题意可知：函数()ln x y f x a ae =-=在点()0,A a 处的切线为1l ， 函数(1)1ln y g x x =--=在点(),0B a 处的切线为2l ，而1'x y ae =，21'y x=， ································································1分 12//l l ，根据导函数在该点的函数值相等可得1a a=， ························2分 又0a >，1a ∴=． ∴切线1l 过点(0,1)，斜率为011k e ==； 切线2l 过点(1,0)，斜率为2k =1，1:10l x y -+=，2:10l x y --=，综上所述，所求的直线方程为：1:10l x y -+=，2:10l x y --=， ··········4分 （2）方法一：()ln x f x ae a =+，()()ln 11g x x =++故不等式()()f x g x >恒成立可等价转化为：ln(1)ln 10x ae x a -++->在(1,)-+∞上恒成立，记()ln(1)ln 1xh x ae x a =-++-，(1,)x ∈-+∞，当01a <≤ 时，(0)ln 10h a a =+-≤，不合题意；···························5分 当1a >时，1(1)1()11x xa x e h x ae x x +-'=-=++， 记()(1)1xx a x e ϕ=+-，[1,)x ∈-+∞， 则()(2)0xx a x e ϕ'=+>，所以()x ϕ在[1,)-+∞是增函数，又(1)1ϕ-=-，(0)10a ϕ=->所以0(1,0)x ∃∈-使得0()0x ϕ=，即00(1)10xa x e +-=①， ···············6分 则当0(1,)x x ∈-时，()0x ϕ<，即()0h x '<， 当0(,)x x ∈+∞时，()0x ϕ>，即()0h x '<，故()h x 在0(1,)x -上单调递减，在0(,)x +∞上单调递增，所以0min 00()()ln(1)ln 1xh x h x ae x a ==-++-②， ··························8分 由①式可得0011x ae x =+，00ln ln(1)a x x =-+-代入②式得min 0001()-(1)-2ln(1)1h x x x x =+++， ··························10分 因为0(1,0)x ∈-，即01(0,1)x +∈， 故001(1)01x x -+>+，02ln(1)0x +<，即min ()0h x >， 所以1a >时()0h x >恒成立，故a 的取值范围为(1,)+∞ . ··················12分 方法二：根据已知条件可得：()ln x f x ae a =+，()()ln 11g x x =++ .且()()f x g x >恒成立；故可等价转化为：)1()1ln()ln(+++>+x x ae ae x x 恒成立 ·················7分 设t t t h ln )(+=，则011)(>+='tt h ，)(t h 单调递增， 因而1+>x ae x 恒成立，即x ex a 1+>恒成立. ····································9分 令x e x x s 1)(+=，则x e x x s -=')(， 当)0,1(-∈x 时，0)(>'x s ，)(x s 单调递增， 当),0(+∞∈x 时，0)(<'x s ，)(x s 单调递减，所以1)0()(=≤s x s ，从而1>a 即为所求。

永州市2021年高考第一次模拟考试试卷地理注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共15小题，每小题3分，共45分。

每小题只有一个选项符合题目要求。

2000多年前，埃及著名的地理学家埃拉托色尼发现在阿斯旺附近，有一口深井，夏至这一天中午，阳光会直射井底。

同一天在阿斯旺近乎正北方的亚历山大城，埃拉托色尼在一个方尖碑下，通过测量方尖碑中午时影子的长度，获得了直立方尖碑与太阳光线之间的夹角。

他又委托商队测量了两城之间的距离，由此计算出了地球周长39690千米。

后人把埃拉托色尼称为“地理学之父”。

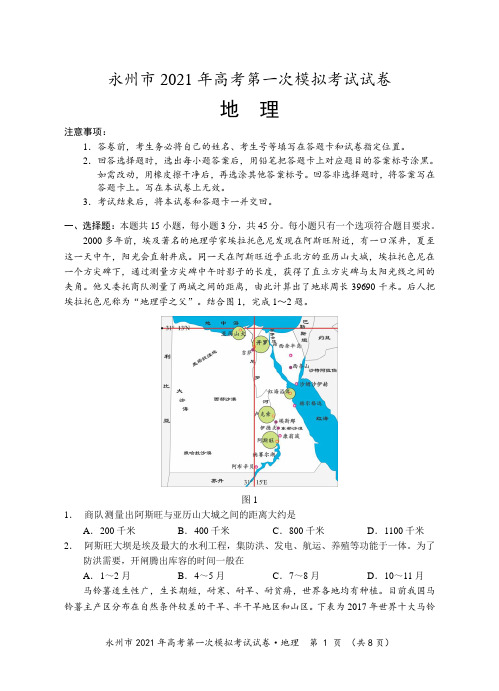
结合图1，完成1～2题。

图11．商队测量出阿斯旺与亚历山大城之间的距离大约是A．200千米B．400千米C．800千米D．1100千米2．阿斯旺大坝是埃及最大的水利工程，集防洪、发电、航运、养殖等功能于一体。

为了防洪需要，开闸腾出库容的时间一般在A．1～2月B．4～5月C．7～8月D．10～11月马铃薯适生性广，生长期短，耐寒、耐旱、耐贫瘠，世界各地均有种植。

目前我国马铃薯主产区分布在自然条件较差的干旱、半干旱地区和山区。

下表为2017年世界十大马铃薯生产国的产量统计表，据此完成3～4题。

国家中国印度俄罗斯乌克兰美国德国孟加拉国波兰荷兰法国其他国家产量（万吨）9921 4861 2959 2221 2002 1172 1022 917 739 734 12271 占比25.6% 12.5% 7.6% 5.7% 5.2% 3% 2.6% 2.4% 1.9% 1.9% 31.6% 3．欧洲六国的马铃薯产量较高的主要原因有①气候比较冷湿②土壤比较贫瘠③地形比较平坦④传统饮食习惯A．①②③B．①②④C．①③④D．②③④4．重视马铃薯的种植，事关我国的粮食安全。

湖南省永州市2021届新高考物理一月模拟试卷一、单项选择题：本题共6小题，每小题5分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的1．如图所示，MON 是竖直平面内的光滑直角支架，小球p 和q 通过一根轻绳连接且它们都套在支架上。

对p 球施加一个沿ON 杆水平向右的拉力F ，使q 球缓慢上升，则此过程中（ ）A ．力F 增大B ．力F 减小C ．p 球受到的支持力增大D ．p 球受到的支持力减小【答案】A 【解析】 【详解】CD ．p 和q 整体分析，p 球受到的支持力等于整体重力，故p 球受到的支持力不变；故CD 错误； AB ．p 和q 整体分析，拉力F 等于OM 杆对q 球的弹力N F ；对q 球分析，设轻绳与OM 杆的夹角为θ，则tan N q F G θ=q 球上升过程中，θ角变大、N F 变大，故F 变大，A 正确，B 错误。

故选A 。

2．半径相同的两个金属小球A 、B 带有等量的电荷，相隔较远的距离，两球之间的吸引力大小为F ，今用第三个半径相同的不带电的金属小球先后与A 、B 两球接触后移开，这时A 、B 两球之间作用力的大小是（ ） A ．4F B ．34F C ．8F D ．38F 【答案】C 【解析】 【分析】 【详解】两球之间是吸引力，故假设A 的带电量为Q ，B 的带电量为-Q ，两球之间的相互吸引力的大小是：22kQ F r=，第三个不带电的金属小球C 与A 接触后，A 和C 的电量都为2Q，C 与B 接触时先中和再平分，则C 、B分开后电量均为4Q-，这时，A、B两球之间的相互作用力的大小：22212488Q Qk kQF Fr r'⋅⋅===故C正确ABD错误。

故选C。

3．某同学按如图1所示连接电路，利用电压传感器研究电容器的放电过程。

先使开关S接1，电容器充电完毕后将开关掷向2，可视为理想电压表的电压传感器将电压信息传入计算机，屏幕上显示出电压随时间变化的U-t曲线，如图2所示。

永州市2021年高考第一次模拟考试试卷地理注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共15小题，每小题3分，共45分。

每小题只有一个选项符合题目要求。

2000多年前，埃及著名的地理学家埃拉托色尼发现在阿斯旺附近，有一口深井，夏至这一天中午，阳光会直射井底。

同一天在阿斯旺近乎正北方的亚历山大城，埃拉托色尼在一个方尖碑下，通过测量方尖碑中午时影子的长度，获得了直立方尖碑与太阳光线之间的夹角。

他又委托商队测量了两城之间的距离，由此计算出了地球周长39690千米。

后人把埃拉托色尼称为“地理学之父”。

结合图1，完成1～2题。

图11．商队测量出阿斯旺与亚历山大城之间的距离大约是A．200千米B．400千米C．800千米D．1100千米2．阿斯旺大坝是埃及最大的水利工程，集防洪、发电、航运、养殖等功能于一体。

为了防洪需要，开闸腾出库容的时间一般在A．1～2月B．4～5月C．7～8月D．10～11月马铃薯适生性广，生长期短，耐寒、耐旱、耐贫瘠，世界各地均有种植。

目前我国马铃薯主产区分布在自然条件较差的干旱、半干旱地区和山区。

下表为2017年世界十大马铃薯生产国的产量统计表，据此完成3～4题。

国家中国印度俄罗斯乌克兰美国德国孟加拉国波兰荷兰法国其他国家产量（万吨）9921 4861 2959 2221 2002 1172 1022 917 739 734 12271 占比25.6% 12.5% 7.6% 5.7% 5.2% 3% 2.6% 2.4% 1.9% 1.9% 31.6% 3．欧洲六国的马铃薯产量较高的主要原因有①气候比较冷湿②土壤比较贫瘠③地形比较平坦④传统饮食习惯A．①②③B．①②④C．①③④D．②③④4．重视马铃薯的种植，事关我国的粮食安全。

湖南省永州市2021届新高考数学一月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．将函数()sin 2f x x =的图象向左平移02πϕϕ⎛⎫≤≤ ⎪⎝⎭个单位长度，得到的函数为偶函数，则ϕ的值为（ ） A ．12π B ．6π C ．3π D ．4π 【答案】D 【解析】 【分析】利用三角函数的图象变换求得函数的解析式，再根据三角函数的性质，即可求解，得到答案． 【详解】将将函数()sin 2f x x =的图象向左平移ϕ个单位长度， 可得函数()sin[2()]sin(22)g x x x ϕϕ=+=+ 又由函数()g x 为偶函数，所以2,2k k Z πϕπ=+∈，解得,42k k Z ππϕ=+∈， 因为02πϕ≤≤，当0k =时，4πϕ=，故选D ．【点睛】本题主要考查了三角函数的图象变换，以及三角函数的性质的应用，其中解答中熟记三角函数的图象变换，合理应用三角函数的图象与性质是解答的关键，着重考查了推理与运算能力，属于基础题． 2．已知i 是虚数单位，若1zi i=-，则||z =（ ）A B ．2C D ．3【答案】A 【解析】 【分析】 直接将1zi i=-两边同时乘以1i -求出复数z ，再求其模即可. 【详解】 解：将1zi i=-两边同时乘以1i -，得 ()11z i i i =-=+考查复数的运算及其模的求法，是基础题.3．已知函数21()log 1||f x x ⎛⎫=+⎪⎝⎭(lg )3f x >的解集为（ ）A ．1,1010⎛⎫⎪⎝⎭B ．1,(10,)10⎛⎫-∞⋃+∞ ⎪⎝⎭C ．(1,10)D ．1,1(1,10)10⎛⎫⋃⎪⎝⎭【答案】D 【解析】 【分析】先判断函数的奇偶性和单调性，得到1lg 1x -<<，且lg 0x ≠，解不等式得解. 【详解】由题得函数的定义域为(,0)(0,)-∞+∞U . 因为()()f x f x -=，所以()f x 为(,0)(0,)-∞+∞U 上的偶函数，因为函数11||y y x =+=，都是在(0,)+∞上单调递减. 所以函数()f x 在(0,)+∞上单调递减. 因为(1)3,(lg )3(1)f f x f =>=， 所以1lg 1x -<<，且lg 0x ≠，解得1,1(1,10)10x ⎛⎫∈⋃ ⎪⎝⎭.故选：D 【点睛】本题主要考查函数的奇偶性和单调性的判断，考查函数的奇偶性和单调性的应用，意在考查学生对这些知识的理解掌握水平.4．已知函数()ln f x x =，()()23g x m x n =++，若对任意的()0,x ∈+∞总有()()f x g x ≤恒成立，记()23m n +的最小值为(),f m n ，则(),f m n 最大值为（ ）A ．1B ．1eC ．21eD对任意的()0,x ∈+∞总有()()f x g x ≤恒成立，因为ln (23)x m x n ≤++，对()0,x ∈+∞恒成立，可得230m +>，令ln (23)y x m x n =-+-，可得1(23)y m x'=-+，结合已知，即可求得答案. 【详解】Q 对任意的()0,x ∈+∞总有()()f x g x ≤恒成立∴ln (23)x m x n ≤++，对()0,x ∈+∞恒成立， ∴230m +>令ln (23)y x m x n =-+-，可得1(23)y m x'=-+ 令0y '=，得123x m =+ 当123x m >+，0y '<当1023x m <<+0y '> ∴123x m =+，max 1ln1023y n m =--≤+，123n m e --+≥ 故1(23)(,)n nm n f m n e ++≥=Q 11(,)n nf m n e+-'=令110n ne+-=，得 1n = ∴当1n >时，(,)0f m n '<当1n <，(,)0f m n '>∴当1n =时，max 21(,)f m n e =故选：C. 【点睛】本题主要考查了根据不等式恒成立求最值问题，解题关键是掌握不等式恒成立的解法和导数求函数单调性的解法，考查了分析能力和计算能力,属于难题. 5．已知复数z ，满足(34)5z i i -=，则z =（ ）A ．1B ．CD ．5首先根据复数代数形式的除法运算求出z ，求出z 的模即可． 【详解】 解：55(34)4334255i i i iz i +-+===-，1z ∴==，故选：A 【点睛】本题考查了复数求模问题，考查复数的除法运算，属于基础题．6．已知函数()2sin()(0,0)3f x x A ωωπ=->>，将函数()f x 的图象向左平移3π个单位长度，得到函数()g x 的图象，若函数()g x 的图象的一条对称轴是6x π=，则ω的最小值为A ．16B ．23C ．53D ．56【答案】C 【解析】 【分析】 【详解】将函数()f x 的图象向左平移3π个单位长度，得到函数()2sin()33g x x ωωππ=+-的图象，因为函数()g x 的图象的一条对称轴是6x π=，所以sin()1633ωωπππ+-=±，即,6332k k ωωππππ+-=+π∈Z ，所以52,3k k ω=+∈Z ，又0>ω，所以ω的最小值为53．故选C ． 7．已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右两个焦点分别为1F ，2F ，若存在点P 满足1212::4:6:5PF PF F F =，则该双曲线的离心率为（ ）A ．2B ．52C ．53D ．5【答案】B 【解析】 【分析】利用双曲线的定义和条件中的比例关系可求.122155642F F e PF PF ===--.选B. 【点睛】本题主要考查双曲线的定义及离心率，离心率求解时，一般是把已知条件，转化为a,b,c 的关系式.8．在复平面内，复数z a bi =+（a ，b R ∈）对应向量OZ uuu r（O 为坐标原点），设OZ r =u u u r ，以射线Ox为始边，OZ 为终边旋转的角为θ，则()cos sin z r i θθ=+，法国数学家棣莫弗发现了棣莫弗定理：()1111cos sin z r i θθ=+，()2222cos sin z r i θθ=+，则()()12121212cos sin z z rr i θθθθ=+++⎡⎤⎣⎦，由棣莫弗定理可以导出复数乘方公式：()()cos sin cos sin nnr i rn i n θθθθ+=+⎡⎤⎣⎦，已知)4z i =，则z =（ ）A．B ．4C．D ．16【答案】D 【解析】 【分析】根据复数乘方公式：()()cos sin cos sin nn r i r n i n θθθθ+=+⎡⎤⎣⎦，直接求解即可. 【详解】)4441216cos sin 266z ii i ππ⎡⎤⎫⎛⎫==+=+⎢⎥⎪ ⎪⎪⎝⎭⎢⎥⎝⎭⎣⎦16cos 4sin 4866i ππ⎡⎤⎛⎫⎛⎫=⨯+⨯=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，16z ==.故选：D 【点睛】本题考查了复数的新定义题目、同时考查了复数模的求法，解题的关键是理解棣莫弗定理，将复数化为棣莫弗定理形式，属于基础题.9．已知函数()()f x x R ∈满足(1)1f =，且()1f x '<，则不等式()22lg lg f x x <的解集为（ ）A ．10,10⎛⎫ ⎪⎝⎭B ．()10,10,10骣琪??琪桫C ．1,1010⎛⎫⎪⎝⎭D ．()10,+∞ 【答案】B构造函数()()g x f x x =-,利用导数研究函数的单调性，即可得到结论. 【详解】设()()g x f x x =-,则函数的导数()()1g x f x ''=-,()1f x Q '<，()0g x '∴<，即函数()g x 为减函数,(1)1f =Q ,(1)(1)1110g f ∴=-=-=，则不等式()0<g x 等价为()(1)g x g <，则不等式的解集为1x >,即()f x x <的解为1x >，22(1)1f g x g x Q <，由211g x >得11gx >或11gx <-，解得10x >或1010x <<, 故不等式的解集为10,(10,)10⎛⎫⋃+∞ ⎪⎝⎭.故选:B . 【点睛】本题主要考查利用导数研究函数单调性，根据函数的单调性解不等式，考查学生分析问题解决问题的能力,是难题.10．已知奇函数()f x 是R 上的减函数，若,m n 满足不等式组()(2)0(1)0()0f m f n f m n f m +-≥⎧⎪--≥⎨⎪≤⎩，则2m n -的最小值为（ ） A ．-4 B ．-2C ．0D ．4【答案】B 【解析】 【分析】根据函数的奇偶性和单调性得到可行域，画出可行域和目标函数，根据目标函数的几何意义平移得到答案. 【详解】奇函数()f x 是R 上的减函数，则()00f =，且2100m nm n m ≤-⎧⎪--≤⎨⎪≥⎩，画出可行域和目标函数，2z m n =-，即2n m z =-，z 表示直线与y 轴截距的相反数，根据平移得到：当直线过点()0,2，即0.2m n ==时，2z m n =-有最小值为2-. 故选：B .【点睛】本题考查了函数的单调性和奇偶性，线性规划问题，意在考查学生的综合应用能力，画出图像是解题的关键.11．某网店2019年全年的月收支数据如图所示，则针对2019年这一年的收支情况，下列说法中错误的是（）A．月收入的极差为60 B．7月份的利润最大C．这12个月利润的中位数与众数均为30 D．这一年的总利润超过400万元【答案】D【解析】【分析】直接根据折线图依次判断每个选项得到答案.【详解】-=，故选项A正确；由图可知月收入的极差为9030601至12月份的利润分别为20，30，20，10，30，30，60，40，30，30，50，30，7月份的利润最高，故选项B正确；易求得总利润为380万元，众数为30，中位数为30，故选项C正确，选项D错误.故选：D.12．已知函22()(sin cos )2cos f x x x x =++，,44x ππ⎡⎤∈-⎢⎥⎣⎦，则()f x 的最小值为（ ） A．2-B ．1C ．0D．【答案】B 【解析】 【分析】())2,4f x x π=++,44x ππ⎡⎤∈-⎢⎥⎣⎦，32444x πππ-≤+≤利用整体换元法求最小值.【详解】由已知，2()12sin cos 2cos sin 2cos22f x x x x x x =++=++)2,4x π=++又44x ππ-≤≤，32444x πππ∴-≤+≤，故当244x ππ+=-，即4πx =-时，min ()1f x =.故选：B. 【点睛】本题考查整体换元法求正弦型函数的最值，涉及到二倍角公式的应用，是一道中档题. 二、填空题：本题共4小题，每小题5分，共20分。

湖南省永州市2021 2021学年高考第一次模拟考试物理试题 Word 版含答案----5681de59-6eb7-11ec-8277-7cb59b590d7d湖南省永州市2021-2021学年高考第一次模拟考试物理试题word版含答案永州市2022-2022学年第一份高考模拟试卷物理第一卷（选择题，共48分）一、选择题（本题共12小题，每小题4分，共48分。

第1~8小题给出的四个选项中，只有如果一个选项是正确的，并且问题9~12中给出的四个选项中有一个以上是正确的，如果所有选项都正确，则得4分；如果正确但不完整，则得2分；如果错误，则得0分。

）1．如图所示，小明在水平桌面上将三个形状不规则的石块成功叠放在一起，下列说法正确的是a、石头a只能承受两种力b．石块b对a的支持力与a受到的重力是一对相互作用力c．石块c受到水平桌面向左的摩擦力d、地面对石头C的支撑力等于三块石头的重力之和2．假设摩托艇受到的阻力的大小与它的速率平方成正比，如果摩托艇的最大速率变为原来的2倍，则摩托艇发动机的输出功率变为原来的a、 4次B.6次c.8次d.9次3．一名跳伞运动员从悬停在高空的直升机中跳下，研究人员利用运动员随身携带的仪器记录下了他的运动情况，通过分析数据，定性画出了运动员从跳离飞机到落地的过程中在空中沿竖直方向运动的v－t图像如图所示，规定向下的方向为正方向，下列说法正确的是a、加速度在0~10s内逐渐减小，在10s~15s内逐渐增大。

B.0~10s内自由下落运动，10s~15s内匀速减速直线运动，C.0~10s内加速度方向垂直向上，10s~15s内加速度方向垂直向下abcd、电阻在0~10s内逐渐增大，在10s~15s内逐渐减小4．水平线上的o点放置一点电荷，图中画出了电荷周围对称分布的几条电场线，如图所示，以水平线上的某点o′为圆心画一个圆，与电场线分别相交于a、b、c、d、e。

下列说法正确的是a、 C和D的电场强度相同b．b、c两点间电势差等于e、d两点间电势差c、 a点的电势高于D点的电势d．电子在c点的电势能大于在b点的电势能5.如图所示，在台秤上放置一块上表面光滑的平板，左侧固定一块挡板，挡板与一块条形磁铁连接一个轻弹簧。

永州市2021年高考第一次模拟考试语文参考答案及评分标准1．A（选项把材料一第一段“节约粮食是中华民族的美德，是尊重劳动的体现，也是勤俭持家的好习惯，更是维护国家安全的具体行动”中的“节约粮食”换成了“勤俭节约”。

）2．C（对材料二中“特别是群众反映强烈的公款餐饮浪费行为得到有效遏制”一句理解错误，原句并没有说公款餐饮浪费是节约粮食行动的最大障碍。

）3．B（有剩菜剩饭是典型的浪费，与节约理念相违背。

）4．①每个人从自身做起，在家吃饭要合理定量，做到坚持“光盘”。

②在外吃饭不讲排场，合理点菜，不贪丰求盛，同时要养成剩菜打包的习惯，不让盛宴变“剩”宴，造成舌尖上的浪费。

③本着节约精神，厉行节约，反对铺张浪费，养成生活中珍惜粮食、厉行节约、反对浪费的习惯。

（答出①②即可得4分，如果答出①③或②③只能得3分）5．①加强宣传教育，切实培养节约习惯，在全社会营造浪费可耻、节约光荣的氛围，让每个人都成为节约粮食的坚定践行者。

②既要节流，也要开源，以科技提升耕地亩产量，扩大粮食耕种面积，让大国粮仓的根基更加牢固。

③保证粮食生产，确保粮食安全，藏粮于技、藏粮于地，加强粮食储备。

（每点2分）6．C（根据原文，“在嘉峪关生活得安心踏实”是因为作者熟悉了这座城市的风景面貌与世俗人情。

）7．D（“这是从正面赞美嘉峪关的味道”分析有误，这里运用了侧面描写的手法。

）8．（4分）①文中写长城兜风、戈壁撒欢、书店、服装城等往事，不仅体现了嘉峪关味道的多样性，而且还丰富了文章的内容；②作者借助这些往事，表达了自己对嘉峪关这座城市的喜爱之情，已经把这座城市当成自己的家乡。

③作者写这些往事与文章开头部分形成鲜明对比，既突出了嘉峪关这座城市的巨大变化，也强调了作者心理变化的起因和过程。

（答出一点得2分，答出两点得3分，全部答出得4分）9．（6分）①椿树代表的是现今嘉峪关的美好生活环境，（1分）表达了作者对嘉峪关这座城市的赞美和热爱。

（1分）②小树苗是韧劲、沧桑与执着的象征，（1分）更是作者初到嘉峪关时的精神力量。

2021届湖南省永州市特优生高考物理模拟试卷(一)一、单选题（本大题共5小题，共20.0分）1.如图所示，在光滑的水平面上，A、B两物体的质量m A=2m B，A物体与轻质弹簧相连，弹簧的另一端固定在竖直墙上，开始时，弹簧处于自由状态，当物体B沿水平向左运动，使弹簧压缩到最短时，A、B两物体间作用力为F，则弹簧给A物体的作用力的大小为()A. FB. 2FC. 3FD. 4F2.如图所示，物体M放在粗糙水平面上受到两个水平力的作用，F1=4N，F2=8N，物体处于静止状态，如果将水平力F1大小增加5N，方向保持不变，则()A. 物体M受到合力向右，开始向右运动B. 物体M仍处于静止C. 物体M受到的合力向左，开始向左运动D. 物体M受到的摩擦力大小增加5N3.如图所示，两个靠摩擦传动(不打滑)的轮P和Q水平放置，A、B二个物块如图放置，已知两轮半径R p：R Q=2：1，A、B物块距转轴距离r A：r B=1：1.且m A：m B=1：2.当主动轮P匀速转动时，两物块与圆盘均保持相对静止，则()A. A、B二个物块的角速度之比为1：1B. A、B二个物块的线速度之比为1：1C. A、B二个物块的加速度之比为1：4D. A、B二个物块所受的静摩擦力之比为1：44.从空中以40m/s的初速度平抛一重为10N的物体，物体在空中运动3s落地，不计空气阻力，取g=10m/s2，则物体落地前瞬间，重力的瞬时功率及落地过程中重力势能的变化量分别为()A. 300W−450JB. 400W50JC. 500W300JD.700W05.空间中存在竖直向上的匀强电场和垂直纸面的磁场(图中未画出)，一带电小球在竖直平面内沿逆针方向做匀速圆周运动，最高点为a，最低点为b，不计空气阻力，则下列说法不正确的是()A. 小球带正电B. 磁场方向垂直纸面向外C. 小球在从a点运动到b点的过程中，电势能增加D. 运动过程突然将磁场反向，小球仍能做匀速圆周运动二、多选题（本大题共6小题，共29.0分）6.用如图甲所示的装置研究光电效应现象。