数学符号英文表示

数学符号读法大全大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德耳塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζit a 西塔Ηηiota iota 约塔Κθkappa kappa 卡帕∧ιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξμxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon 衣普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作e xa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同a^xlog b a 以b为底a的对数；b log b a = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos x符号含义cot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yζ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

、希腊字母：α——阿尔法β——贝塔γ——伽马Δ——德尔塔ξ——可sei ψ——可赛ω——奥秘噶μ——米哟λ——南木打σ——西格玛τ——套φ——fai2、数学运算符：∑—连加号∏—连乘号∪—并∩—补∈—属于∵—因为∴—所以√—根号‖—平行⊥—垂直∠—角⌒—弧⊙—圆∝—正比于∞—无穷∫—积分≈—约等≡—恒等3、三角函数：sin—赛因cos—考赛因tan—叹近体cot—考叹近体sec—赛看近体csc —考赛看近体序号大写小写英文注音国际音标注音中文注音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Ε ε epsilon ep`silon 伊普西龙6 Ζ ζ zeta zat 截塔7 Η η eta eit 艾塔8 Θ θ thet θit 西塔9 Ι ι iot aiot 约塔10 Κ κ k appa kap 卡帕11 Λ λ lambda lambd 兰布达12 Μ μ mu mju 缪13 Ν ν nu nju 纽14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 Π π pi pai 派17 Ρ ρ rho rou 肉18 Σ σ sigma `sigma 西格马19 Τ τ tau tau 套20 Υ υ upsilon jup`silon 宇普西龙21 Φ φ phi fai 佛爱22 Χ χ c hi phai 西23 Ψ ψ psi psai 普西24 Ω ω omega o`miga 欧米伽希腊字母的正确读法是什么？1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Δ δ delta delt 德尔塔5 Ε ε epsilon ep`silon 伊普西龙6 Ζ ζ zeta zat 截塔7 Η η eta eit 艾塔8 Θ θ thet θit 西塔9 Ι ι iot aiot 约塔10 Κ κ kappa kap 卡帕11 ∧λ lambda lambd 兰布达12 Μ μ mu mju 缪13 Ν ν nu nju 纽磁阻系数14 Ξ ξ xi ksi 克西15 Ο ο omicron omik`ron 奥密克戎16 ∏ π pi pai 派17 Ρ ρ rho rou 肉18 ∑ σ sigma `sigma 西格马19 Τ τ tau tau 套20 Υ υ upsilon jup`silon 宇普西龙21 Φ φ phi f ai 佛爱22 Χ χ chi phai 西23 Ψ ψ psi psai 普西角速；24 Ω ω omega o`miga 欧米伽希腊字母读法Αα：阿尔法AlphaΒβ：贝塔BetaΓγ：伽玛GammaΔδ：德尔塔DelteΕε：艾普西龙Epsilonζ ：捷塔ZetaΖη：依塔EtaΘθ：西塔ThetaΙι：艾欧塔IotaΚκ：喀帕Kappa∧λ：拉姆达LambdaΜμ：缪MuΝν：拗NuΞξ：克西XiΟο：欧麦克轮Omicron∏π：派PiΡρ：柔Rho∑σ：西格玛SigmaΤτ：套TauΥυ：宇普西龙UpsilonΦφ：fai PhiΧχ：器ChiΨψ：普赛PsiΩω：欧米伽Omega数学符号大全2008年01月29日星期二 15:25因为自然科学的讨论经常要用到数学，但用文本方式只能表达L!t d5w x r ^ |$s Y 左右结构的数学公式，上下结构、根式、指数等都很难表达。

数学运算符号的英文表达小数、分数、百分数和运算符号1. 小数表示法(1) 小数的读法小数点左边的数通常按基数词读，若为三位以上的数，也可按编码式读法读出，即将数字单个读出；小数点右边的数通常按编码式读法单个读出。

如：6.86 six point eight six14.15 fourteen point one five345.456 three four five point four five six或three hundred and forty－five point four five six(2) 小数中“0”的读法“0”在小数中通常读作nought（英）或zero（美），也可读作字母o。

如：0.08 （nought）point nought eight 或（zero）point zero eight9.07 nine point o seven2. 百分数表示法百分数中的百分号％读作percent。

如：6% 读作 six percent0.6% 读作（nought） point six percent500% 读作five hundred percent3. 倍数表示法倍数表示方法很多，如：This room is four times as big as mine. 这个房间是我房间的四倍。

This room is three times larger than that one. 这个房间比那个房间大两倍。

The output of coal has doubled. 煤的产量增加了一倍。

My aunt is as old again as I am. 我姑姑年龄比我大一倍。

Productivity is increased three fold. 生产效率提高了两倍。

The volume of the Sun is about 1,300,000 times that of the Earth.太阳的体积约为地球的1300000倍。

+plus加号；正号-minus减号；负号±plus or minus正负号×is multiplied by乘号÷is divided by除号＝is equal to等于号≠is not equal to不等于号≡is equivalent to全等于号≌is equal to or approximately equal to等于或约等于号≈is approximately equal to约等于号＜is less than小于号＞is greater than大于号≮is not less than不小于号≯is not more than不大于号≤is less than or equal to小于或等于号≥is more than or equal to大于或等于号%per cent百分之…‰per mill千分之…∞infinity无限大号∝varies as与…成比例√(square) root平方根∵since; because因为∴hence所以∷equals, as (proportion)等于，成比例∠angle角≲semicircle半圆≰circle圆○circumference圆周πpi 圆周率△triangle三角形≱perpendicular to垂直于∪union of并，合集∩intersection of 交，通集∫the integral of …的积分∑(sigma) summation of总和°degree度′minute分″second秒℃Celsius system摄氏度{open brace, open curly左花括号}close brace, close curly右花括号(open parenthesis, open paren左圆括号)close parenthesis, close paren右圆括号() brakets/ parentheses括号[open bracket 左方括号]close bracket 右方括号[] square brackets方括号.period, dot句号，点|vertical bar, vertical virgule竖线&ampersand, and, reference, ref和，引用*asterisk, multiply, star, pointer星号，乘号，星，指针/slash, divide, oblique 斜线，斜杠，除号//slash-slash, comment 双斜线，注释符#pound井号\backslash, sometimes escape反斜线转义符，有时表示转义符或续行符~tilde波浪符.full stop句号,comma逗号:colon冒号;semicolon分号?question mark问号!exclamation mark (英式英语) exclamation point (美式英语)'apostrophe撇号-hyphen连字号-- dash 破折号...dots/ ellipsis省略号"single quotation marks 单引号""double quotation marks 双引号‖parallel 双线号&ampersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号。

数学欧米伽符号
数学欧米伽符号，又称omega符号或横杆符，是数学符号Ω 的英文表达。

它是一个希腊字母符号，代表无穷大，表示相反的概念“无穷小”的欧拉符号是字母μ（μ），及其英文名称micro。

欧米伽符号Ω主要用于数学表达式中，它表达的是某种语义或意思，在一定的情况下可以说，它有时优先考虑的是某种特定的抽象概念，而不是三维空间维度上的确定性。

在欧拉计算机科学中，ω欧米伽符号表示计算机程序在某个操作执行完毕后所需要的时间，通常是指无穷大量程序完成计算任务的时间。

例如某算法的执行时间为Ω（log（n）），表示在最坏情况下，需要按照log（n）的次数完成计算任务。

在概率论中欧米伽符号ω，也用于表示一种概率分布的聚集性指标，即一定的概率分布的每一个样本值的总和（或平均值）在归结到真实取值范围时具有无穷大的能力，均值可以符号表达为均值≤ ∫∞ 0f (x) dx。

从上述的解释中可以看出，数学欧米伽符号在数学和计算机中都有它独特的功能，深刻体现了无限大、无限小、无穷计算以及概率聚集性等概念。

常用数学符号读法大全数学中有很多运算用希腊字母来表示，这些字母通用性很强，往往用来表示分类标示、数学运算符，物理或化学中也经常应用。

但有些比较复杂，好多同学不会读，下面就是小编给大家带来的数学符号读法，希望能帮助到大家！下面就将常用列表如下：大写小写英文注音国际音标注音中文注音Αα alpha alfa 阿耳法Ββ beta beta 贝塔Γγ gamma gamma 伽马Δδ deta delta 德耳塔Εε epsilon epsilon 艾普西隆Ζζ zeta zeta 截塔Ηη eta eta 艾塔Θθ theta θita西塔Ιι iota iota 约塔Κκ kappa kappa 卡帕∧λ lambda lambda 兰姆达Μμ mu miu 缪Νν nu niu 纽Ξξ xi ksi 可塞Οο omicron omikron 奥密可戎∏π pi pai 派Ρρ rho rou 柔∑σ sigma sigma 西格马Ττ tau tau 套Υυ upsilon jupsilon 衣普西隆Φφ phi fai 斐Χχ chi khai 喜Ψψ psi psai 普西Ωω omega omiga 欧米伽· 数学符号：(1)数量符号：如：i，2+i，a，x，自然对数底e，圆周率π。

(2)运算符号：如加号(+)，减号(-)，乘号(×或·)，除号(÷或/)，两个集合的并集(∪)，交集(∩)，根号(√)，对数(log，lg，ln)，比(：)，微分(dx)，积分(∫)等。

(3)关系符号：如“=”是等号，“≈”是近似符号，“≠”是不等号，“>”是大于符号，“<”是小于符号，“→ ”表示变量变化的趋势，“∽”是相似符号，“≌”是全等号，“∥”是平行符号，“⊥”是垂直符号，“∝”是反比例符号，“∈”是属于符号，“C”或“C 下面加一横”是“包含”符号等。

1、希腊字母：α——阿尔法β——贝塔γ——伽马Γ——德尔塔μ——可sei ψ——可赛ω——奥秘噶κ——米哟ι——南木打ζ——西格玛η——套θ——fai2、数学运算符：ⅲ—连加号ⅱ—连乘号ⅻ—并ⅺ—补ⅰ—属于ⅿ—因为ⅾ—所以ⅳ—根号‖—平行↌—垂直ⅶ—角↍—弧↋—圆ⅴ—正比于ⅵ—无穷ⅼ—积分Ↄ—约等ↆ—恒等3、三角函数：sin—赛因cos—考赛因tan—叹近体cot—考叹近体sec—赛看近体csc —考赛看近体序号大写小写英文注音国际音标注音中文注音1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Θ θ kappa kap 卡帕11 Ι ι lambda lambd 兰布达12 Κ κ mu mju 缪13 Λ λ nu n ju 纽14 Μ μ xi ksi 克西15 Ν ν omicron omik`ron 奥密克戎16 Ξ π pi pai 派17 Ο ξ rho rou 肉18 Π ζ sigma `sigma 西格马19 Ρ η tau tau 套20 ΢ υ upsilon jup`silon 宇普西龙21 Φ θ phi fai 佛爱22 Σ χ chi phai 西23 Τ ψ psi psai 普西24 Υ ω omega o`miga 欧米伽希腊字母的正确读法是什么？1 Α α alpha a:lf 阿尔法2 Β β beta bet 贝塔3 Γ γ gamma ga:m 伽马4 Γ δ delta delt 德尔塔5 Δ ε epsilon ep`silon 伊普西龙6 Ε δ zeta zat 截塔7 Ζ ε eta eit 艾塔8 Θ ζ thet ζit 西塔9 Η η iot aiot 约塔10 Κ θ kappa kap 卡帕11 ⅸι lambda lambd 兰布达12 Μ κ mu mju 缪13 Ν λ nu nju 纽磁阻系数14 Ξ μ xi ksi 克西15 Ο ν omicron omik`ron 奥密克戎16 ∏ π pi pai 派17 Ρ ξ rho rou 肉18 ∑ ζ sigma `sigma 西格马19 Σ η tau tau 套20 Τ υ upsilon jup`silon 宇普西龙21 Φ θ phi fai 佛爱22 Υ χ chi phai 西23 Φ ψ psi psai 普西角速；24 Χ ω omega o`miga 欧米伽希腊字母读法Αα：阿尔法AlphaΒβ：贝塔BetaΓγ：伽玛GammaΓδ：德尔塔DelteΔε：艾普西龙Epsilonδ ：捷塔ZetaΕε：依塔EtaΘζ：西塔ThetaΗη：艾欧塔IotaΚθ：喀帕Kappaⅸι：拉姆达LambdaΜκ：缪MuΝλ：拗NuΞμ：克西XiΟν：欧麦克轮Omicron∏π：派PiΡξ：柔Rho∑ζ：西格玛SigmaΣη：套TauΤυ：宇普西龙UpsilonΦθ：fai PhiΥχ：器ChiΦψ：普赛PsiΧω：欧米伽Omega数学符号大全各种符号的英文读法'exclam'＝'!''at'＝'@''numbersign'＝'#''dollar'＝'$''percent'＝'%''caret'＝'^''ampersand'＝'&''asterisk'＝'*''parenleft'＝'(''parenright'＝')''minus'＝'-''underscore'＝'_''equal'＝'=''plus'＝'+''bracketleft'＝'''braceright'＝'}''semicolon'＝';''colon'＝':''quote'＝''''doublequote'＝'"''backquote'＝''''tilde'＝'~''backslash'＝'\''bar'＝'|''comma'＝',''less'＝'<''period'＝'.''greater'＝'>''slash'＝'/''question'＝'?''space'＝' '~~~~~~~~~~~~~~~~~~~~~~｡ hyphen 连字符' apostrophe 省略号；所有格符号— dash 破折号‘ ’single quotation marks 单引号“ ”double quotation m arks 双引号( ) parentheses 圆括号square brackets 方括号Angle bracket{} Brace《》French quotes 法文引号；书名号... ellipsis 省略号¨ tandem colon 双点号" ditto 同上‖ parallel 双线号／ virgule 斜线号＆ ampersand = and～ swung dash 代字号§ section; division 分节号Ⅾ arrow 箭号；参见号＋ plus 加号；正号－ minus 减号；负号ª plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号＝ is equal to 等于号ↅ is not equal to 不等于号ↆ is equivalent to 全等于号ↄ is equal to or approximately equal to 等于或约等于号Ↄ is approximately equal to 约等于号＜ is less than 小于号＞ is more than 大于号↉ is not less than 不小于号↊ is not more than 不大于号ↇ is less than or equal to 小于或等于号ↈ is more than or equal to 大于或等于号％ per cent 百分之…‟ per mill 千分之…ⅵ infinity 无限大号ⅴ varies as 与…成比例ⅳ (square) root 平方根ⅿ since; b ecause 因为ⅾ hence 所以ↁ equals, as (proportion) 等于，成比例ⅶ angle 角↍ semicircle 半圆↋ circle 圆◈ circumference 圆周π pi 圆周率△ triangle 三角形↌ perpendicular to 垂直于ⅻ union of 并，合集ⅺ intersection of 交，通集ⅼ the integral of …的积分ⅲ (sigma) summation of 总和© degree 度† minute 分‡ second 秒＃number …号‣ Celsius system 摄氏度＠ at 单价x'是x prime(比如转置矩阵)x"是x double-prime数学符号大全1 几何符号↌ⅷⅶ↍↋ↆↄ△‖2 代数符号ⅴⅸⅹ～ⅼↅↇↈↃⅵↀ3运算符号×÷ⅳª4集合符号ⅻⅺⅰⅰↇↈ⊆⊂5特殊符号ⅲπ（圆周率）6推理符号|a| ↌ↂ△ⅶⅺⅻↅↆªↈↇⅰⅬⅭⅮⅯ↖↗↘↙ⅷⅸⅹ&; §↎↏←↑→↓↔↕↖↗ΓΓΘΛΞΟΠ΢ΦΥΦΧαβγδεδεζηθικλμνπξζηυθχψωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ﹪﹫﹬﹭﹮﹯ﹰﹱﹲﹳⅰⅱⅲ↚ⅳⅴⅵ↛ⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↀↁↂↃↄ↝ↅↆↇↈ↞↟↉↊？↋↌↠↍‣上述符号所表示的意义和读法（中英文参照）＋plus 加号；正号－minus 减号；负号±plus or minus 正负号×is multiplied by 乘号÷is divided by 除号＝is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号ↄis approximately equal to 约等于≈ is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号≤ is less than or equal to 小于或等于≥ is more than or equal to 大于或等于％per cent 百分之…∞ infinity 无限大号√ (square) root 平方根X squared X的平方X cubed X的立方ⅿsince; because 因为ⅾhence 所以ⅶangle 角↍semicircle 半圆↋circle 圆○ circumference 圆周△triangle 三角形↌perpendicular to 垂直于ⅻintersection of 并，合集∩ union of 交，通集∫ the integral of …的积分∑ (sigma) summation of 总和°degree 度′ minute 分〃second 秒＃number …号＠at 单价符号意义ⅵ无穷大PI 圆周率|x| 函数的绝对值ⅻ集合并ⅺ集合交ↈ大于等于ↇ小于等于ↆ恒等于或同余ln(x) 自然对数lg(x) 以2为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分 x - floor(x)ⅼf(x)δx 不定积分ⅼ[a:b]f(x)δx a到b的定积分[P] P为真等于1否则等于0ⅲ[1ↇkↇn]f(k) 对n进行求和,可以拓广至很多情况如：ⅲ[n is prime][n < 10]f(n)ⅲⅲ[1ↇiↇjↇn]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm↌n m与n互质a ⅰ A a属于集合A#A 集合A中的元素个数ⅰⅱⅲⅳⅵⅶ↜ⅷⅸⅹⅺⅻⅼⅽⅾⅿↂↃↄↅↆↇↈ↞↟？↋↌ &#8226;数学符号大全收藏运算符： ± × ÷ ↀ∫ ⅽↆↄ≈ ↂⅴ↝≠ ↆ≤ ≥ ↞↟↉↊／√ ‰ ∑ ∏ ＆关系运算符：ⅸⅹ集合符号：ⅻⅺⅰ↜⊆序号：↎↏←↑→↓↔↕↖↗ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ﹪﹫﹬﹭﹮﹯ﹰﹱﹲﹳ≈㈠㈡㈢㈣㈤㈥㈦㈧㈨㈩其它：～ ± × ÷ ∑ⅻⅺⅰ√ⅷⅶ↋ↆↄ≈ↂ≠↉↊≤≥∞ⅿⅾ☈☇‣｟‰☆★○●◉◇◆□■△▲ⅮⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ＊ΟαβγδεζηθικλμνξποστυφχψωΑ Β Γ Δ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ ΢ Σ Τ Υ Φ Ωα β γ δ ε ζ η θ ι κ λ μ μ ν ξ π ο σ τ υ φ χψ ωⅬⅭⅮⅯ↖↗↘↙∞ ⅾⅿↀↁ° ′ ″ ‣▝↠△↋ⅶ↍↌ⅷ〓〔〈〉《》「」『』〕〖【】（）［］｛｝ﹶ§ № •＃＆＠☆★○● ◉△▲◇◆□ ■〒▙▛▚▘☇☈ⅬⅭⅮⅯ↖↗↘↙ⅰ∏∑↌↠∕√ⅴ∞↛ⅶ↜ⅷⅸⅹⅺⅻ∫ⅽⅾⅿↀↁↂ≈ↄ↝≠ↆ≤≥↞↟↉↊﹞﹟﹠﹡﹢﹣﹤﹥﹦﹧﹨﹩！﹖﹗＂＃＄％＆＇＊＼＾＿｀｜～｟｠ﹴ｡﹵｢▝↋↍▔▕■□▲△▖▗◆◇◈◉●▘▙▚▛★☆▜☇☈、。

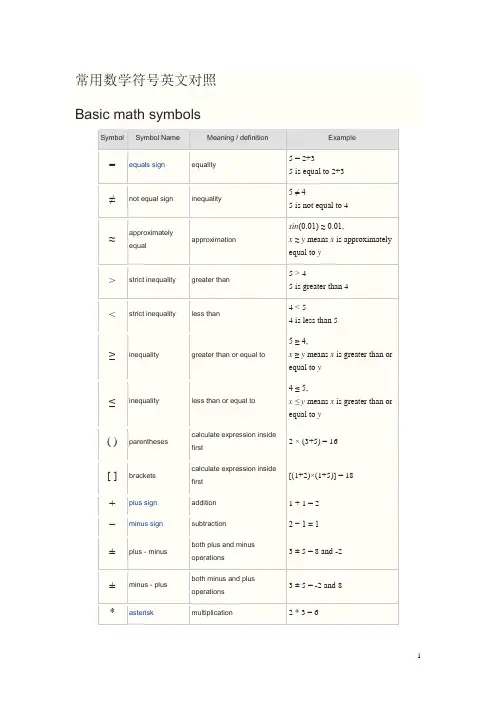
常用数学符号英文对照Basic math symbolsSymbol Symbol Name Meaning / definition Example= equals sign equality 5 = 2+35 is equal to 2+3≠not equal sign inequality 5 ≠ 45 is not equal to 4≈approximatelyequal approximationsin(0.01) ≈ 0.01,x≈y means x is approximatelyequal to y> strict inequality greater than 5 > 45 is greater than 4< strict inequality less than 4 < 54 is less than 5≥inequality greater than or equal to 5 ≥ 4,x≥y means x is greater than or equal to y≤inequality less than or equal to 4 ≤ 5,x ≤ y means x is greater than or equal to y( ) parentheses calculate expression insidefirst2 × (3+5) = 16[ ] brackets calculate expression insidefirst[(1+2)×(1+5)] = 18 + plus sign addition 1 + 1 = 2−minus sign subtraction 2 − 1 = 1±plus - minus both plus and minusoperations3 ± 5 = 8 and -2±minus - plus both minus and plusoperations3 ± 5 = -2 and 8 * asterisk multiplication 2 * 3 = 6×times sign multiplication 2 × 3 = 6 ·multiplication dot multiplication 2 · 3 = 6÷division sign /division 6 ÷ 2 = 3obelus/ division slash division 6 / 2 = 3–horizontal line division / fractionmod modulo remainder calculation 7 mod 2 = 1. period decimal point, decimal2.56 = 2+56/100separatora b power exponent 23= 8a^b caret exponent 2 ^ 3= 8√a square root √a ·√a = a√9 = ±33√a cube root 3√a ·3√a ·3√a = a3√8 = 24√a fourth root 4√a ·4√a ·4√a ·4√a = a4√16 = ±2n√a n-th root (radical) for n=3, n√8 = 2% percent1% = 1/100 10% × 30 = 3‰per-mille1‰ = 1/1000 = 0.1%10‰ × 30 = 0.3ppm per-million1ppm = 1/1000000 10ppm × 30 = 0.0003ppb per-billion 1ppb = 1/1000000000 10ppb × 30 = 3×10-7ppt per-trillion 1ppt = 10-1210ppt × 30 = 3×10-10ABC = 30°AOB = 30°°degree 1 turn = 360°α = 60°deg degree 1 turn = 360deg α = 60deg′prime arcminute, 1° = 60′α = 60°59′″double prime arcsecond, 1′ = 60″α = 60°59′59″line infinite lineAB line segment line from point A to point Bray line that start from point Aarc arc from point A to point B= 60°⊥perpendicular perpendicular lines (90° angle) AC ⊥ BC| | parallel parallel lines AB | | CD≅congruent to equivalence of geometric shapes and size ∆ABC≅∆XYZ ~ similarity same shapes, not same size ∆ABC~ ∆XYZ Δtriangle triangle shape ΔABC≅ΔBCD |x-y| distance distance between points x and y | x-y | = 5πpi constant π = 3.141592654...is the ratio between the circumference and diameter of acirclec = π·d = 2·π·rrad radians radians angle unit 360° = 2π rad c radians radians angle unit 360° = 2πcgrad gradians / gons grads angle unit 360° = 400 gradg gradians / gons grads angle unit 360° = 400 gx x variableto findwhen 2x = 4, then x = 2≡equivalence identical to≜equal by definition equal bydefinition:= equal by definition equal bydefinition~ approximately equal weakapproximation11 ~ 10≈approximately equal approximation sin(0.01) ≈ 0.01∝proportional to proportional to y∝x when y = kx, k constant ∞lemniscate infinity symbol≪much less than much less than 1 ≪1000000≫much greater than much greaterthan1000000 ≫1( ) parentheses calculateexpressioninside first2 * (3+5) = 16[ ] brackets calculateexpressioninside first[(1+2)*(1+5)] = 18{ } braces set⌊x⌋floor brackets rounds numberto lower integer⌊4.3⌋ = 4⌈x⌉ceiling brackets rounds numberto upper integer⌈4.3⌉ = 5x! exclamation mark factorial4! = 1*2*3*4 = 24 | x | single vertical bar absolute value | -5 | = 5f (x) function of x maps values ofx to f(x)f (x) = 3x+5(f∘g) function composition (f∘g) (x)= f (g(x))f (x)=3x,g(x)=x-1 ⇒(f∘g)(x)=3(x-1)(a,b) open interval (a,b) = x∈(2,6)[a ,b ] closed interval[a ,b ] = {x | a ≤ x ≤ b }x ∈ [2,6]∆ delta change / difference∆t = t 1 - t 0∆ discriminantΔ = b 2 - 4ac∑sigmasummation -sum of all values in range of series ∑ x i = x 1+x 2+...+x n∑∑sigmadouble summation∏capital piproduct -product of all values in range of series∏ x i =x 1∙x 2∙...∙x ne e constant / Euler's numbere =2.718281828... e = lim (1+1/x )x , x →∞γ Euler-Mascheroni constant γ =0.527721566...φgolden ratio golden ratio constantπpi constant π =3.141592654...is the ratiobetween the circumference and diameter of a circlec = π·d = 2·π·rA ⊗Btensor product tensor product of A and BA ⊗ Binner product[ ] brackets matrix of numbers ( ) parentheses matrix of numbers| A | determinant determinant of matrix A det(A ) determinant determinant of matrix A|| x || double vertical bars normA T transpose matrix transpose(A T )ij = (A )ji A † Hermitian matrix matrix conjugate transpose (A †)ij = (A )ji A * Hermitian matrix matrix conjugate transpose(A *)ij = (A )jiA -1inverse matrixA A -1 = Irank(A ) matrix rank rank of matrix A rank(A ) = 3 dim(U )dimensiondimension of matrix Arank(U ) = 3Probability and statistics symbolsSymbolSymbol Name Meaning / definitionExampleP (A )probability function probability of event A P (A ) = 0.5P (A ∩ B ) probability ofeventsintersection probability that of events A and BP (A ∩B ) = 0.5P (A ∪B ) probability ofevents unionprobability that of events A or B P (A ∪B ) = 0.5P (A | B )conditionalprobability function probability of event A given event B occuredP (A | B ) = 0.3f (x ) probabilitydensity function (pdf) P (a ≤ x ≤ b ) = ∫ f (x ) dxF (x )cumulativeF (x ) = P (X ≤ x )distribution function (cdf)μ population mean mean of population valuesμ = 10E (X )expectation valueexpected value of random variable X E (X ) = 10E (X | Y )conditional expectationexpected value of random variable X given YE (X | Y=2) = 5var (X ) variance variance of random variable X var (X ) = 4σ2variancevariance of population values σ2 = 4std (X ) standard deviationstandard deviation of random variable X std (X ) = 2σXstandard deviationstandard deviation value of random variable X σX = 2medianmiddle value of random variable xcov (X ,Y )covariance covariance ofrandom variables X and Y cov (X,Y ) = 4corr (X ,Y ) correlationcorrelation ofrandom variables X and Y corr (X,Y ) = 0.6ρX ,Ycorrelation correlation ofrandom variables X and YρX ,Y = 0.6∑summation summation - sum ofall values in range of series∑∑double summationdouble summationMo mode value that occurs most frequently in populationMR mid-range MR = (x max+x min)/2 Md sample median half the population isbelow this valueQ1lower / firstquartile 25% of population are below this valueQ2median /second quartile 50% of population are below this value = median of samplesQ3upper / thirdquartile 75% of population are below this valuex sample mean average / arithmeticmeanx = (2+5+9) / 3 = 5.333s2samplevariance population samples variance estimators2 = 4s samplestandarddeviationpopulation samplesstandard deviationestimators = 2z x standard score z x = (x-x) / s xX ~ distribution of X distribution ofrandom variable XX ~ N(0,3)N(μ,σ2) normaldistributiongaussian distribution X ~ N(0,3)U(a,b) uniformdistributionequal probability inrange a,bX ~ U(0,3)exp(λ)exponentialdistributionf (x) = λe-λx , x≥0gamma(c, λ)gammadistributionf (x) = λ c x c-1e-λx /Γ(c), x≥0χ 2(k) chi-squaredistributionf (x) = x k/2-1e-x/2 /( 2k/2 Γ(k/2) )F (k1, k2) F distributionBin (n ,p )binomial distribution f (k ) = n C k p k (1-p )n-kPoisson (λ)Poisson distribution f (k ) = λk e -λ / k !Geom (p )geometric distribution f (k ) = p (1-p ) kHG (N ,K ,n ) hyper-geometric distributionBern (p ) Bernoulli distributionsubset the set {9,14,28} A ⊄ B not subset left set not a subset of right set{9,66} ⊄{9,14,28} A ⊇B supersetset A has more elements or equalto the set B{9,14,28} ⊇{9,14,28} A ⊃Bproper superset / strictsupersetset A has more elements than setB{9,14,28} ⊃{9,14}A ⊅B not superset set A is not a superset of set B{9,14,28} ⊅{9,66} 2A power set all subsets of Apower set all subsets of AA =B equalityboth sets have the samemembersA={3,9,14},B={3,9,14},A=BA c complementall the objects that do not belongto set AA \B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A - B relative complementobjects that belong to A and notto BA = {3,9,14},B = {1,2,3},A-B = {9,14} A ∆ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ∆B ={1,2,9,14} A ⊖ B symmetric differenceobjects that belong to A or B butnot to their intersectionA = {3,9,14},B = {1,2,3},A ⊖B ={1,2,9,14}a∈A element of set membership A={3,9,14}, 3 ∈Ax∉A not element of no set membership A={3,9,14}, 1 ∉A(a ,b ) ordered pair collection of 2 elementsA×B cartesian product set of all ordered pairs from Aand B|A| cardinality the number of elements of set AA={3,9,14}, |A|=3 #A cardinality the number of elements of set AA={3,9,14}, #A=3aleph-nullinfinite cardinality of naturalnumbers setaleph-one cardinality of countable ordinalnumbers setØ empty set Ø = { }C = {Ø}universal set set of all possible valuesnatural numbers / whole numbers set (with zero) 0 = {0,1,2,3,4,...}0 ∈ 01natural numbers / wholenumbers set (withoutzero)1 = {1,2,3,4,5,...}6 ∈ 1integer numbers set= {...-3,-2,-1,0,1,2,3,...} -6 ∈rational numbers set= {x | x =a /b , a ,b ∈}2/6 ∈real numbers set= {x | -∞ < x <∞} 6.343434∈complex numbers set= {z | z=a +bi ,-∞<a <∞, -∞<b <∞}6+2i ∈∨reversed caret or x∨y | vertical line or x | y x' single quote not - negation x'x bar not - negation x¬not not - negation ¬x ! exclamation mark not - negation ! x ⊕circled plus / oplus exclusive or - xor x⊕y ~ tilde negation ~ x ⇒implies⇔equivalent if and only if (iff)↔equivalent if and only if (iff)∀for all∃there exists∄there does not exists∴therefore∵because / sincee e constant / Euler'snumber e = 2.718281828...e = lim(1+1/x)x ,x→∞y ' derivative derivative - Lagrange's notation (3x3)' = 9x2y '' second derivative derivative of derivative (3x3)'' = 18xy(n)nth derivative n times derivation (3x3)(3) = 18derivative derivative - Leibniz's notation d(3x3)/dx = 9x2second derivative derivative of derivative d2(3x3)/dx2 = 18xnth derivative n times derivationtime derivative derivative by time - Newton's notationtime secondderivativederivative of derivativeD x y derivative derivative - Euler's notationD x2y second derivative derivative of derivativepartial derivative ∂(x2+y2)/∂x = 2x ∫integral opposite to derivation ∫f(x)dx∫∫double integral integration of function of 2variables∫∫f(x,y)dxdy∫∫∫triple integral integration of function of 3variables∫∫∫f(x,y,z)dxdydz∮closed contour / lineintegral∯closed surfaceintegral∰closed volumeintegral[a,b] closed interval [a,b] = {x | a ≤ x ≤ b}(a,b) open interval (a,b) = {x | a < x < b}i imaginary unit i≡ √-1 z = 3 + 2i z* complex conjugate z = a+bi→z*=a-bi z* = 3 - 2i z complex conjugate z = a+bi→z = a-bi z = 3 - 2i ∇nabla / del gradient / divergence operator ∇f (x,y,z)vectorunit vectorx * y convolution y(t) = x(t) * h(t)Laplace transform F(s) = {f (t)}Fourier transform X(ω) = {f (t)}δdelta function∞lemniscate infinity symbol。

section; division
分节号
→
arrow
箭号；参见号
＋
plus
加号；正号
－
minus
减号；负号
±
plus or minus
正负号
×
is multiplied by
乘号
÷
is divided by
除号
＝
is equal to
等于号
≠
is not equal to
不等于号
≡
is equivalent to
Ν
（纽）
Ξ
（可系）
Ο
（奥密克戎）
Π
（派）
Ρ
（若）
Σ
（西格马）
Τ
（套）
Υ
（英文或拉丁字母）
Φ
（斐）
Χ
（喜）
Ψ
（普西）
Ω
（欧米伽）
Mu
Ν ν： 拗
Nu
Ξ ξ： 克西
KeXi
Ο ο： 欧麦克轮 Omicron
∏ π： 派
Pi
Ρ ρ： 柔
Rho
∑ σ： 西格玛
Sigma
Τ τ： 套
Tau
Υ υ： 宇普西龙 Upsilon
Φ φ： fai
Phi
Χ χ： 器
Chi
Ψ ψ： 普赛
Psi
Ω ω： 欧米伽
Omega
希腊字母怎么打:打开 Office 文档之后，在你需要输入希腊字母的时候，先将输入法切换为
ω（欧米伽）。
更全面：
1 Α α alpha a:lf
阿尔法 角度系数
2 Β β beta bet
贝塔 磁通系数 角度系数

各种数学符号和表达式的英文读法.txt52每个人都一条抛物线，天赋决定其开口，而最高点则需后天的努力。

没有秋日落叶的飘零，何来新春绿芽的饿明丽？只有懂得失去，才会重新拥有。

各种数学符号和表达式的英文读法一、一般符号对应的英文单词．period 句号，comma 逗号：colon 冒号；semicolon 分号！exclamation 惊叹号？question mark 问号￣hyphen 连字符'apostrophe 省略号；所有格符号—dash 破折号‘ ’single quotat ion marks 单引号“ ”double quotation marks 双引号( )parentheses 圆括号[ ]square brackets 方括号《》French quotes 法文引号；书名号...ellipsis 省略号¨tandem colon 双点号"ditto 同上‖parallel 平行／virgule 斜线号＆ampersand = and～swung dash 代字号§section; division 分节号→arrow 箭号；参见号＋plus 加号；正号－minus 减号；负号ªplus or minus 正负号×is multiplied by or cross 叉乘÷is divided by 除号＝is equal to 等于号≠is not equal to 不等于号≡is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于号≈is approximately equal to 约等于号＜is less than 小于号＞is more than （is greater than在数学中更常用）大于号≤is not less than 不小于号≥is not more than 不大于号≢is less than or equal to 小于或等于号≣is more than or equal to 大于或等于号％per cent 百分之…‟per mill 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于，成比例∟angle 角≨semicircle 半圆≦circle 圆○circumference 圆周πpi 圆周率△triangle 三角形≧perpendicular to 垂直于；另外normal to，right to也都有垂直的意思。

university
university
∫ the integral of [ˈ ɪntɪgrəl] n.整体; 积分; …的积分 ∑(sigma) the summation of …的和 ∏(pi) the product of …的积 lim x→ 0 + the limit as x approaches zero from above lim x→ 0 − the limit as x approaches zero from below dy the derivative of y [dɪˈr ɪvətɪv] n.导数，微商 f'( x ) f prime x / f dash x / the (first) derivative of f with respect to x f''( x ) f doublend derivative of f with respect to x f'''( x ) f triple-prime x / f triple-dash x / the third derivative of f with respect to x
Mean Valve Theorem
Theorem: If f’(x) = 0 on [a,b] The f’(x) constant on [a,b]. i.e. f(x) = f(a) for all x belong to (a,b] Proof: Assume there is a special x-value and f(x)≠f(a) Then (f(x)-f(a)) / (x-a) = m ave ≠0 There is a point C in (a,x) with f’(c) = m ave ≠0 Then this contradicts the given fact that f’(x) =0 for all x belong to (a,b) So the assumption f(x) ≠f(a) must be fake and instead, f(x)=f(a) for all x belong to (a,b]. Theorem : [ˈθ ɪərəm] n.定理 i.e. : [ˈa ɪ ˈi:]abbr.(=that is) 即，换言之

数学符号英语表达
数学符号是用来表示数学概念和运算的特殊符号。

在数学中，不同的符号有不同的含义和用法。

下面是一些常见的数学符号及其英语表达：
+ 加 (plus)
- 减 (minus)
×乘 (times)
÷除 (divided by)
= 等于 (equals)
≠不等于 (not equal to)
< 小于 (less than)
> 大于 (greater than)
≤小于等于 (less than or equal to)
≥大于等于 (greater than or equal to)
√开方 (square root)
^ 幂 (exponent)
% 百分号 (percent)
π圆周率 (pi)
e 自然对数的底数 (Euler's number)
除了这些常见的数学符号外，还有很多其他符号，如集合符号、积分符号、极限符号等等。

掌握这些符号的英语表达，可以帮助我们更好地理解和应用数学知识。

数学字母符号数学领域有许多非常重要的符号，这些符号在数学研究中起着至关重要的作用。

下面，我将简单地介绍一些常见的数学字母符号。

一、希腊字母符号：1. α (alpha)：希腊字母中的第一个字母，往往用于表示角度、系数等。

2. β (beta)：希腊字母中的第二个字母，往往用于表示系数、角度等。

3. γ (gamma)：希腊字母中的第三个字母，往往用于表示角度、系数等。

4. δ (delta)：希腊字母中的第四个字母，往往用于表示差异、微小变化等。

5. ε (epsilon)：希腊字母中的第五个字母，往往用于表示误差、极小量等。

6. ζ (zeta)：希腊字母中的第六个字母，往往用于表示函数中的变量。

7. η (eta)：希腊字母中的第七个字母，往往用于表示数据中的变量。

8. θ (theta)：希腊字母中的第八个字母，往往用于表示角度、温度等。

9. ι (iota)：希腊字母中的第九个字母，往往用于表示一个很小的数字。

10. κ (kappa)：希腊字母中的第十个字母，往往用于表示系数、角度等。

11. λ (lambda)：希腊字母中的第十一个字母，往往用于表示常数、波长等。

12. μ (mu)：希腊字母中的第十二个字母，往往用于表示平均数、质量等。

13. ν (nu)：希腊字母中的第十三个字母，往往用于表示频率、速度等。

14. ξ (xi)：希腊字母中的第十四个字母，往往用于表示未知数、角度等。

15. π (pi)：希腊字母中的第十五个字母，往往用于表示圆的周长与直径之比。

16. ρ (rho)：希腊字母中的第十六个字母，往往用于表示电阻、电导率等。

17. σ (sigma)：希腊字母中的第十七个字母，往往用于表示标准差、总体方差等。

18. τ (tau)：希腊字母中的第十八个字母，往往用于表示时间常数、力矩等。

19. υ (upsilon)：希腊字母中的第十九个字母，往往用于表示平均速度、位移等。

数学运算符号的英文表达数学运算符号的英文表达小数、分数、百分数和运算符号小数、分数、百分数和运算符号1. 小数表示法小数表示法(1) 小数的读法小数的读法小数点左边的数通常按基数词读，小数点左边的数通常按基数词读，若为三位以上的数，若为三位以上的数，也可按编码式读法读出，即将数字单个读出；小数点右边的数通常按编码式读法单个读出。

如：个读出；小数点右边的数通常按编码式读法单个读出。

如：6.86 six point eight six 14.15 fourteen point one five 345.456 three four five point four five six 或three hundred and forty －five point four five six (2) 小数中“0”的读法的读法“0”在小数中通常读作nought （英）或zero （美），也可读作字母o 。

如：。

如：0.08 （nought ）point nought eight 或 （zero ）point zero eight 9.07 nine point o seven 2. 百分数表示法百分数表示法百分数中的百分号％读作percent 。

如：。

如：6% 读作读作 six percent 0.6% 读作读作 （nought ） point six percent 500% 读作读作 five hundred percent 3. 倍数表示法倍数表示法倍数表示方法很多，如：倍数表示方法很多，如：This room is four mes as big as mine. 这个房间是我房间的四倍。

这个房间是我房间的四倍。

This room is three mes larger than that one. 这个房间比那个房间大两倍。

这个房间比那个房间大两倍。

The output of coal has doubled. 煤的产量增加了一倍。

数学运算符号的英文表达小数、分数、百分数和运算符号1. 小数表示法(1) 小数的读法小数点左边的数通常按基数词读，若为三位以上的数，也可按编码式读法读出，即将数字单个读出；小数点右边的数通常按编码式读法单个读出。

如：6.86 six point eight six14.15 fourteen point one five345.456 three four five point four five six或three hundred and forty－five point four five six(2) 小数中“0”的读法“0”在小数中通常读作nought（英）或zero（美），也可读作字母o。

如：0.08 （nought）point nought eight 或（zero）point zero eight9.07 nine point o seven2. 百分数表示法百分数中的百分号％读作percent。

如：6% 读作 six percent0.6% 读作（nought） point six percent500% 读作five hundred percent3. 倍数表示法倍数表示方法很多，如：This room is four times as big as mine. 这个房间是我房间的四倍。

This room is three times larger than that one. 这个房间比那个房间大两倍。

The output of coal has doubled. 煤的产量增加了一倍。

My aunt is as old again as I am. 我姑姑年龄比我大一倍。

Productivity is increased three fold. 生产效率提高了两倍。

The volume of the Sun is about 1,300,000 times that of the Earth.太阳的体积约为地球的1300000倍。

表⽰各种数学符号的英⽂单词 由于有各种各样的数学符号，那么数学符号的英⽂单词也是有很多的。

以下是百分⽹店铺为⼤家整理了关于表⽰⼀些数学符号的部分英⽂单词，⼀起来看看吧! 表⽰减号的英⽂单词：minus 1. 它应该拥有的加号数⽬⼤于减号数⽬，⽽且它应该有你的直觉的赞同。

It should have more plus signs than negative signs, and it should have your intuition's approval. 2. 如果你这样下去，那么它会成为⼀个减号。

If you let that go, then it`ll become a minus. 3. 如果你在你的物理⽅程式的中间插⼊⼀个减号，那将会发⽣? What would happen if you inserted a minus sign in the middle of your physics equation? 4. 如果没有物减号就⼀个引的打吧 If there is no minus sign on a matter of playing it cited other 5. 这个⽅法⽤减号说明了他是⼀个实例⽅法。

The declaration is preceded by a minus sign, which indicates that this is an instance method. 6. TVS_HASBUTTONS=紧接于⽗选项显⽰加号和减号按钮。

TVS_HASBUTTONS == Displays plus and minus buttons next to parent items. 7. 若要执⾏此，拖动标题的减号⼤纲符号或加号⼤纲符号 To promote to higher level heading, drag plus outline symbol to left. 8. 间张，以及好的牌型⽽增值的牌。

数学符号英文说法和发音大全！！各路出国党不妨看过来！Symbols+ plus /'pl?s/- minus /'ma?n?s/±plus or minus /'pl?s ?: 'ma?n?s/x multiplied by /'m?lt?pla?d ba?// over; divided by /'??v?/ /d?'va?d?d/÷divided /d?'va?d?d/= equals /'?:kw?lz/≈approximately, similar /?'pr?ks?m?tl?/ /'s?m?l? t?/≡equivalent to; identical /?k'w?v?l?nt t?/ /a?'dent?kl t?/≠　not equal to /'n?t 'i?kw?l t?/> greater than /'gre?t? e?n/< less than /'les e?n/≥　greater than or equal to /'gre?t? e?n ?r 'i?kw?l t?/≤　less than or equal to /'les e?n ?r' i?kw?l t?/?not greater than /'n?t 'gre?t? e?n/?not less than /'n?t 'les e?n/?much greater than /'m?? 'gre?t? e?n/?much less than /'m?? 'les e?n/⊥perpendicular to /p??p?n'd?kj?l? t?/∣∣parallel to /'p?r?lel t?/?not equivalent to, not identical to /'n?t ?k'w?v?l?nt t?/ /'n?t a?'dent?kl t? ??not similar to /'n?t 's?m?l? t?/2squared /'skwe?d/3cubed /'kju:bd/4 to the fourth; to the power four /t? e? 'f??θ/ /te e? 'pɑ?? f??/n to the n; to the nth; to the power n /t? e? en; t? d?enθ; t? e? pɑ??r en/√root; square root /ru:t/ /skwe? ru:t/?cube root /kju:b ru:t/?fourth root /f??θ ru?t/! factorial /f?k't??r??l/% percent /p?'sent/∞infinity /?n'f?n?t?/∝varies as; proportional to /'v??r?z/ /pr?'p????n?l/˙dot /d?t/¨double dot /d?bl d?t/: is to, ratio of /re?????/f(x) fx f; function /ef/ /'f??k??n/f'(x) f dash; derivative /d??/ /d?'r?v?t?v/f''x f double-dash; second derivative /'d?bl d??/ /'sek?nd d?'r?v?t?v/f'''(x) f triple-dash; f treble-dash; third derivative /'tr?pl d??/ / trebl d??/ /θ？:d d?'r?v?t?v'r?v?t?v/f(4) f four; fourth derivative /f??θ d??partial derivative, delta /pa???l d?'r?v?t?v/ /delt?/∫integral /'?nt?gr?l/∑sum /s?m/w.r.t. with respect to /w?e 'r?spekt/log log /l?g/log?x log to the base 2 of x /l?g t? e? be?s tu: ?v eks/∴therefore /'e??f??/∵because /b?'k?z/→gives, leads to, approaches /g?vz/ /li:dz t?/ /?pr????z// per /p?:/∈belongs to; a member of; an element of /b?'l??z/ /'memb?/ /'el?m?nt/?does not belong to; is not a member of; is not an element of /n?t b?'l??/ /n?t ? 'memb?/ /n?t ?n 'e ?contained in; a proper subset of /k?n'te?nd ?n/ /'pr?p? 's?bset/?contained in; subset /'s?bset/?intersection /'?nt?sek??n/?union /'ju?n??n/?for all /f? r?:l/cos x cos x; cosine x /k?z/sin x sine x /sa?n/tan x tangent x /tan/cosec x cosec x /'k??sek/sinh x shine x /'?a?n/cosh x cosh x /'k??/tanh x than x /θ?n/|x| mod x; modulus x /m?d/ /'m?dj?l?s/℃degrees Centigrade /d?'gri:z 'sent?gre?d/℉degrees Fahrenheit /d?'gri:z 'f?r?nha?t/°K degrees Kelvin /d?'gri:z 'kelv?n/C absolute zero /abs?lu:t zi:r??/0°K, –273.15 °mm millimetre /'m?l?mi?t?/cm centimetre /'sent?mi?t?/cc, cm3cubic centimetre, centimetre cubed /'kju?b?k 'sent?mi?t?/ /'sent?mi?t? 'kju: m metre /'mi?t?/km kilometre /k?'l?m?t?/mg milligram /'m?l?gr?m/g gram /gr?m/kg kilogram /'k?l?gr?m/AC A.C. /e? si:/DC D.C. /di: si:/Examplesx + 1 x plus onex -1 x minus onex ± 1 x plus or minus onexy x y; x times y; x multiplied by y(x — y)(x + y) x minus y, x plus yx/y x over y; x divided by y;x ÷ y x divided by yx = 5 x equals 5; x is equal to 5x ≈ y x is approximately equal to yx ≡ y x is equivalent to y; x is identical with yx ≠ y x is not equal to yx > y x is greater than yx < y x is less than yx ≥ y x is greater than or equal to yx ≤ y x is less than or equal to y0 < x < 1 zero is less than x is less than 1; x is greater than zero and less than 10 ≤ x ≤ 1zero is less than or equal to x is less than or equal to 1; x is greater than or equal to zero and less than or equal to 1x2x squaredx3x cubedx4 x to the fourth; x to the power fourxn x to the n; x to the nth; x to the power nx-n x to the minus n; x to the power of minus n√root x; square root x; the square root of x?the cube root of x?the fourth root of xthe nth root of x(x + y)2x plus y all squared(x/y)2x over y all squaredn! n factorial; factorial nx% x percent∞infinityx ∝y x varies as y; x is (directly) proportional to yx ∝1/y x varies as one over y; x is indirectly proportional to y?x dot?x double dotf(x) fx f of x; the function of xf'(x) f dash x; the (first) derivative of with respect to xf''x f double-dash x; the second derivative of f with respect to xf'''(x) f triple-dash x; f treble-dash x; the third derivative of f with respect to xf(4) f four x; the fourth derivative of f with respect to x?v the partial derivative of v?v?θdelta v by delta theta, the partial derivative of v with respect to θ?2v?θ２delta two v by delta theta squared; the second partial derivative of v with respect to dv the derivative of vdvdθ d v by d theta, the derivative of v with respect to thetad2vdθ２ d 2 v by d theta squared, the second derivative of v with respect to theta,∫integralintegral from zero to infinity∑sumthe sum from i equals 1 to nw.r.t. with respect tologey log to the base e of y; log y to the base e; natural log (of) y∴therefore∵because→gives, approachesΔx → 0delta x approaches zerolimΔx→０the limit as delta x approaches zero, the limit as delta x tends to zeroLtΔx→０the limit as delta x approaches zero, the limit as delta x tends to zerom/sec metres per secondx ∈ A x belongs to A; x is a member of A; x is an element of Ax? A x does not belong to A; x is not a member of A; x is not an element of AA? B A is contained in B; A is a proper subset of BA ?B A is contained in B; A is a subset of BA ?B A intersection BA ?B A union Bcos x cos x; cosine xsin x sine xtan x tangent x, tan xcosec x cosec xsinh x shine xcosh x cosh xtanh x than x|x| mod x; modulus x18 ℃eighteen degrees Centigrade70 ℉seventy degrees FahrenheitGreek alphabetΑαalpha /'?lf?/Ββbeta /'bi:t?/Γγgamma /'g?m?/Δδdelta /'delt?/Εεepsilon /'epsil?n/Ζζzeta /'zi?t?/Ηηeta /'i?t?//Θθtheta /'θi?t?Ιιiota /a?'??t?/Κκkappa /'k?p?/Λλlamda /'l?md?/Μμmu /'mju?/Ννnu /'nju?/Ξξxi /'ksa?/Οοomicron /'??m?kr?n/ Ππpi /'pa?/Ρρ？rho /'r??/Σσsigma /'s?gm?/Ττtau /'tɑ?/Υυupsilon /'j?ps?l?n/ Φφphi /'fa?/Χχchi /'ka?/Ψψ psi /'psa?/Ωω omega /'??m?g?/ ^Roman alphabetA a /'e?/B b /'bi?/C c /'si?/D d /'di?/E e /'i?/F f /'ef/G g /'?i?/H h /'e??/I i /'a?/J j /'?e?/K k /'ke?/L l /'el/M m /'em/N n /'en/O o /'??/P p /'pi?/Q q /'kju?/R r /'ɑ?/S s /'es/T t /'ti:/U u /'ju:/V v /'vi:/W w /'d?blju?/X x /'eks/Y y /'wa?/Z z /'zed/^Fractions? a half /? 'hɑ:f/? a quarter /? 'kw??t?/z/? three quarters /θri? 'kw??t?:d/? a third /?'θ？:dz/? two thirds /tu: 'θ？?a fifth /? 'f?fθ／?t wo fifths /tu: 'f?fθs/?t hree fifths /θri? 'f?fθs/?f our fifths /f?? 'f?fθs/?a sixth /? 's?ksθ／?f ive sixths /fa?v 's?ksθs/? an eighth /?n 'e?tθ／? three eighths /θri? 'e?tθs/? five eighths /fa?v 'e?tθs/? seven eighths /sev?n 'e?tθs/^Decimal Fractions0.1 nought point one /n?:t p??nt w?n/0.01 nought point oh one /n?:t p??nt ?? w?n/0.0001 nought point oh oh oh one /ten p??nt ?????? w?n/1.1 one point one /w?n p??nt w?n/1.2 one point two /w?n p??nt tu:/1.23 one point two three /w?n p??nt tu: θri:/1.0123 one point oh one two three /w?n p??nt ?? w?n tu: θri:/10.01 ten point oh one /ten p??nt ?? w?n/21.57 twenty-one point five seven /'twent? w?n p??nt fa?v 'sev?n/2.6666666666.... two point six recurring /tu: p??nt s?ks r?'k?:r??/'k?:r??/ 2.612361236123... two point six one two three recurring /tu: p??nt s?ks w?n tu: θri: r? 2.5 million two point five million /tu: p??nt fa?v 'm?lj?n/^SI Units: Prefixes10-24 yocto y /'j?kt??/10-21 zepto z /'zept??/10-18 atto a /'at??/10-15 femto f /'femt??/10-12 pico p /'pi:k??/10-9 nano n /'nan??/10-6 micro μ/'ma?kr??/10-3 milli m /'m?l?/10-2 centi c /'sent?/10-1 deci d /'des?/103 kilo k /'k?l??/106 mega M /'meg?/109 giga G /'g?g?/1012 tera T /'ter?/1015 peta P /'pet?/1018 exa E /'eks?/1021 zetta Z /'zet?/1024 yotta Y /'j?t?/1027 xona X /'z??n?/1030 weka W /'wek?/1033 vunda V /'v?nd?/^Cardinal Numbers1 one /w?n/2 two /tu:/3 three /θri:/4 four /f??/5 five /fa?v/6 six /s?ks/7 seven /'sev?n/8 eight /e?t/9 nine /na?n/10 ten /ten/11 eleven /?'lev?n/12 twelve /twelv/:'ti:n/13 thirteen /θ？14 fourteen /f??'ti:n/15 fifteen /f?f'ti:n/16 sixteen /s?kst'i:n/17 seventeen /seven'ti:n/18 eighteen /e?'ti:n/19 nineteen /na?n'ti:n/20 twenty /'twent?/21 twenty-one /twent?'w?n/22 twenty-two /twent?'tu:/23 twenty-three /twent?'θri:/24 twenty-four /twent?'f??/25 twenty-five /twent?'fa?v/26 twenty-six /twent?'s?ks/27 twenty-seven /twent?'sev?n/28 twenty-eight /twent?'e?t/29 twenty-nine /twent?'na?n/:t?/30 thirty /'θ？40 forty /'f??t?/50 fifty /'f?ft?/60 sixty /'s?kst?/70 seventy /'sev?nt?/80 eighty /'e?t?/90 ninety /'na?nt?/100 a hundred; one hundred /? 'h?ndr?d/ /w 101 a hundred and one /? 'h?ndr?d ?n 102 a hundred and two /? 'h?ndr?d ?n 110 a hundred and ten /? 'h?ndr?d ?n 120 a hundred and twenty /? 'h?ndr?d ?n 200 two hundred /tu: 'h?ndr?d/ 300 three hundred /θri: 'h?ndr?d 400 four hundred /f?? 'h?ndr?d/ 500 five hundred /fa?v 'h?ndr?d/ 600 six hundred /s?ks 'h?ndr?d/ 700 seven hundred /'sev?n 'h?ndr? 800 eight hundred /e?t 'h?ndr?d/ 900 nine hundred /na?n 'h?ndr?d/ 1 000 a thousand, one thousand /?θ'ɑ?z?nd 1 001 a thousand and one /?'θɑ?z?nd 1 010 a thousand and ten /?'θɑ?z?nd 1 020 a thousand and twenty /?'θɑ?z?nd 1 100 one thousand, one hunded /w?n 'θɑ?z 1 101 one thousand, one hundred and one /w?n 'θɑ?z 1 110 one thousand, one hundred and ten /w?n 'θɑ?z9 999 nine thousand, nine hundred and ninety-nine /na?n 'θɑ?10 000 ten thousand /ten 'θɑ?15 356 fifteen thousand, three hundred and fifty six /'f?fti:n 'θ100 000 a hundred thousand /? 'h?ndr?d 'θ1 000 000 a million /? 'm?lj?n/100 000 000 a hundred million /? 'h?ndr?d 'm?1 000 000 000 a billion /? 'b?lj?n/100 000 000 000 a hundred billion /? 'h?ndr?d 'b?l 1 000 000 000 000 a trillion /? 'tr?lj?n/1 000 000 000 000 000 a quadrillion /? kw?dr?lj?n/ 1 000 000 000 000 000 000 a quintillian /? kw?n't?lj?n/ 1 000 000 000 000 000 000 000 a sextillion /? seks't?lj?n/1 000 000 000 000 000 000 000 000 a septillion /? sep't?lj?n/1 000 000 000 000 000 000 000 000 000 an ocillion /?n ?kt't?lj?n/1 000 000 000 000 000 000 000 000 000 000 a nonillion /? n?n'?lj?n/1 000 000 000 000 000 000 000 000 000 000 000 a decillion /? de's?lj?n/^Ordinal Numbers1st first /f?:st/2nd second /'sek?nd/:d/3rd third /θ？4th fourth /f?:θ／5th fifth /f?fθ／6th sixth /s?ksθ／7th seventh /'sev?nθ／8th eighth /e?tθ／9th ninth /na?nθ／10th tenth /tenθ／11th eleventh /?'lev?nθ／12th twelfth /'twelfθ／:'ti:nθ／13th thirteenth /θ？14th fourtheenth /f??'ti:nθ／15th fidteenth /f?f'ti:nθ/16th sixteenth /s?ks'ti:nθ／17th seventeenth /seven'ti:nθ／18th eighteenth /e?'ti:nθ／19th nineteenth /na?n'ti:nθ／20th twentieth /'twent??θ／21st twenty-first /twent?'f?:st/22nd twenty-second /twent?'sek?nd/:d/23rd twenty-third /twent?'θ？24th twenty-fourth /twent?'f?:θ／25th twenty-fifth /twent?'f?fθ／26th twenty-sixth /twent?'s?ksθ／27th twenty-seventh /twent?'sev?nθ／28th twenty-eighth /twent?'e?tθ／29th twenty-ninth /twent?'na?nθ／30th thirtieth /'θ??t??θ／'f?:st/31st thirty-first /θ??t?40th fortieth /'f?:t??θ／50th fiftieth /'f?ft??θ／100th hundredth /'h?ndr?dθ／1 000th thousandth /'θɑ?z?ndθ／1 000 000th millionth /'m?lj?nθ／。