第五讲试题

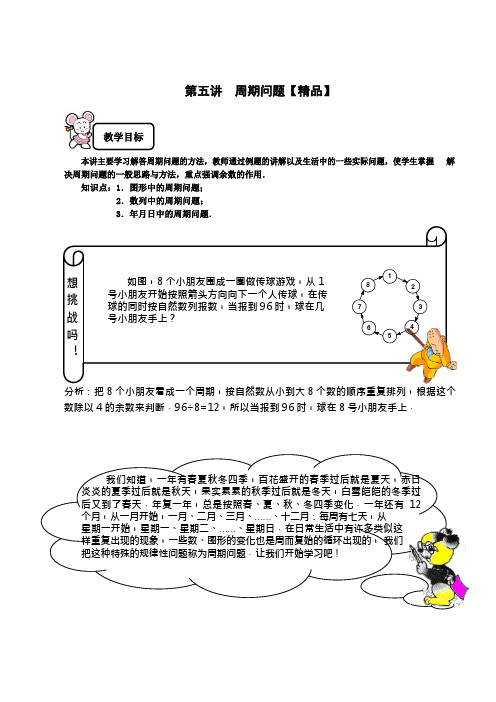
如图，8 个小朋友围成一圈做传球游戏，从 1 号小朋友开始按照箭头方向向下一个人传球，在传球的同时按自然数列报数，当报到 96 时，球在几 号小朋友手上？18 2 7 364 5第五讲 周期问题【精品】本讲主要学习解答周期问题的方法，教师通过例题的讲解以及生活中的一些实际问题，使学生掌握 解决周期问题的一般思路与方法，重点强调余数的作用．知识点：1．图形中的周期问题；2．数列中的周期问题； 3．年月日中的周期问题．分析：把 8 个小朋友看成一个周期，按自然数从小到大 8 个数的顺序重复排列，根据这个 数除以 4 的余数来判断．96÷8=12，所以当报到 96 时，球在 8 号小朋友手上．教学目标想 挑 战 吗 ？我们知道，一年有春夏秋冬四季，百花盛开的春季过后就是夏天，赤日炎炎的夏季过后就是秋天，果实累累的秋季过后就是冬天，白雪皑皑的冬季过后又到了春天．年复一年，总是按照春、夏、秋、冬四季变化．一年还有 12 个月，从一月开始，一月、二月、三月、……、十二月；每周有七天，从 星期一开始，星期一、星期二、……、星期日．在日常生活中有许多类似这样重复出现的现象，一些数、图形的变化也是周而复始的循环出现的， 我们把这种特殊的规律性问题称为周期问题．让我们开始学习吧！黑珠、白珠共 102 个，排列成○●○○○●○○○●○○○……，这串珠子中， 最后一个珠子应是什么颜色，这种颜色在这串珠子中共有多少个？分析：观察可以发现，这串珠子是按“一白、一黑、二白”4 个珠子组成一组，并且不断重复出现的．我们先算出 102 个珠子可以这样排列成多少组，还余多少．我们可以根据排列周期判断出最后一个珠子的颜色，还可以求出有多少个这样的珠子．因为 102÷4=25…2，所以最后一个珠子是第 26 个周期中的第二个，即为黑色． 在每一个周期中只有 1 个黑珠子，所以黑色珠子在这串珠子中共有 25＋1=26（个）[巩固]按下面的摆法，摆一百个三角形，请问第 100 个三角形是什么颜色的？在这 100 个三角形中有多少个白色的三角形？△△△▲▲▲△△△▲▲▲△△△▲▲▲……从图中可以看出，按照 6 个为一个周期，因为 100÷6=16……4，所以第 100 个三角形应该是这一个周期 当中的第四个，应该是黑色的．每个周期里有 3 个白色的，一共有 16 个周期就有 48 个白色三角形，余下的 4 个三角形中还有 3 个白色的，所以一共有 16×3＋3=51 个．流水线上给小木球涂色的次序是：先 5 个红、再 4 个黄、再 3 个绿、在 2 个黑、再 1 个白，然后又依次是 5 红、4 黄、3 绿、2 黑、1 白……如此继续涂下去，到第 2003 个小球该涂什么颜色？分析：小木球的涂色顺序是：“5 红、4 黄、 3 绿、2 黑、1 白”，也就是每涂过“5 红、4 黄、3 绿、2 黑、1 白”循环一次，给小木球涂色的一个周期是 5＋4＋3＋2＋1=15，因此只要用 2003 除以 15，根据余数是 8 就可以判断：第 2003 个小木球出现在上面所列一个周期中第 8 个，所以第 2003 个小球是涂黄色2003÷15=133 (8)专题精讲解答周期问题的关键是找规律，找出周期．确定周期后，用总量除以周期，如果正好有整数个周期，结果就为周期里的最后一个；例如：1，2，1，2，1，2，…那么第 18 个数是多少？这个数列的周期是 2，18÷2=9，所以第 18 个数是2． 如果比整数个周期多 n 个，那么为下个周期里的第 n 个；例如：1，2，3，1，2，3，1，2，3，…那么第 16 个数是多少？这个数列的周期是 3，16÷3=5…1，所以第 16 个数是 1．如果不是从第一个开始循环，可以从总量里减掉不是循环的个数后，再继续算． 例如：1，2，3，2，3，2，3，…那么第 16 个数是多少？ 这个数列从第二个数开始循环，周期是 2，（16-1）÷3=5，所以第 16 个数是 3．例1 例2作弊沙僧参加数学考试，监考老师盯着他脖子上的珠子看了半天，冷笑道：“嘿嘿，把算盘伪装成这样了！休想作弊，快摘下来！”节日的校园内挂起了一盏盏小电灯，小明看出每两个白灯之间有红、黄、绿各一盏彩灯．也就是说，从第一盏白灯起，每一盏白灯后面都紧接着有 3 盏彩灯．那么第 73 盏灯是什么颜色的灯？分析： 从第一盏白灯开始，每隔三盏彩灯就又出现一盏白灯，不难看出白灯的编号依次是： 1，5，9，13，……，这些编号被 4 除所得的余数都是 1．73=4×18＋1，即 73 被 4 除的余数是 1，因此第 73 盏灯是白灯．小莉把平时积存下来的 200 枚硬币按 3 个 1 分，2 个 2 分，1 个 5 分的顺序排列起来．（1） 最后 1 枚是几分硬币（2） 这 200 枚硬币一共价值多少钱？分析：（1）每个周期有 3＋2＋1=6 枚硬币，要求最后一枚，用这个数除以 6，根据余数来判断 200÷6=33……2，所以最后一枚是 1 分硬币（2）每个周期中 6 枚硬币共价值 1×3＋2×2＋1×5=12（分），用这个数乘以周期次数再加上余下的， 就可以得到一共价值多少了 12×33＋2=398（分）所以，这 200 枚硬币一共价值 398 分．有 249 朵花，按 5 朵红花，9 朵黄花，13 朵绿花的顺序轮流排列，最后一朵是什么颜色的花？这249 朵花中，什么花最多，什么花最少？最少的花比最多的花少几朵？分析：这些花按 5 红、9 黄、13 绿的顺序轮流排列，它的一个周期内有 5＋9＋13=27（朵）花．因为 249÷27=9……6，所以，这 249 朵花中含有 9 个周期还余下 6 朵花．按花的排列规律，这 6 朵花中前 5 朵应是红花，最后一朵应是黄花．在这一个周期里，绿花最多，红花最少，所以在 249 朵花中，自然也是绿花最多，红花最少．少几朵呢？有两种解法：（方法 1）249÷（5＋9＋13）=9 (6)红花有：5×9＋5=50（朵） 绿花有：13×9=117（朵）红花比绿花少：117－50=67（朵） （方法 2）249÷（5＋9＋13）=9 (6)一个周期少的：13－5=8（朵）9×8=72（朵） 余下的 6 朵中还有 5 朵红花，所以 72－5=67（朵）例 3 例 4 例5在图所示的表中，将每列上、下两个字组成一组，例如 第一组为（新奥），第二组为（北林），那么第 50 组是什么？新北京新奥运新北京新奥运新北京新奥运…… 奥林匹克运动会奥林匹克运动会奥林匹克运动会……分析：要知道第 50 组是哪两个数，我们首先要弄清楚第一行和第二行的第 50 个字分别应该是什么． 第一行“新北京新奥运”是 6 个字一个周期，50÷6=8……2，第 50 个字就是北．再看第二行“奥林匹 克运动会”是 7 个字一个周期，50÷7=7……1，第 50 个字就是奥．把第一行和第二行合在一起，第 50 组就是“北奥”．[前铺]“北京欢迎你北京欢迎你北京欢迎你……”依次排列，第 28 个字是什么字？分析：这道题是按“北京欢迎你”的规律重复排列，即 5 个字为一个周期．因为 28÷5=5…3，所以 28 个字里含有 5 个周期还多 3 个字，即第 28 个字就是所列一个周期中的第 3 个字，所以第 28 个字是“欢”字．如图所示，每列上、下两个字（字母）组成一组，例如，第一组是“我，A”， 第二组是“们，B”……我 们 爱 科 学 我 们 爱 科 学 我 …… ABCDEFGABCD……（1） 写出第 62 组是什么？（2） 如果“爱、C”代表 1991 年，那么“科、D”代表 1992 年……问 2008 年对应怎样的组？分析：（1）要求第 62 组是什么数，我们要分别求出上、下两行是什么字（字母），上面一行是以“我们爱科学”五个字为一个周期，下面一行则是以“ABCDEFG”七个字母为一个周期 62÷5=12......2 62÷7=8 (6)所以第 62 组是“们，F”（2）2008 是 1991 之后的第 17 组，现在上面一行按“科学我们爱”五个字为一个周期，下面一行则按 “DEFGABC” 七个字母为一个周期2008－1991=17（组） 17÷5=3......2 17÷7=2 (3)所以 2008 年对应的组为“学、F”2002 年的 6 月 1 日是星期六，问这一年的 10 月 1 日是星期几？分析：我们只要算出 6 月 1 日到 10 月 1 日要经过多少天，然后按照 7 天为一个周期， 运用周期变化规律解答．例6 例7 例86 月 1 日到 10 月 1 日要经过的天数：30＋31＋31＋30＋1=123（天） 123÷7=17……4 这个周期从周六开始，那么第 4 天正好是星期二．[拓展]2008 年 3 月 3 号是星期一，算一算 2008 年 8 月 8 号奥运会开幕是星期几？首先我们应该算出 2008 年 3 月 3 号到 8 月 8 号一共有多少天，（31－2）＋30＋31＋30＋31＋8=15（9 天）．按 照 7 天为一个周期，159÷7=22……5，这个周期的第一天是星期一，那么第五天就应该是星期五，所以 2008 年 8 月 8 号奥运会开幕是星期五．今天是星期三，那么从明天起第 365 天是星期几？分析：题中所说的第 365 天，不包括今天在内，是说“从今天之后的第 365 天”． 365÷7=52（星期）……1（天）所以，从明天起，到第 365 天是星期三．[前铺]今天是星期三，从今天算起，到第 50 天是星期几？分析：题中所说的第 50 天，包括今天在内，所以“从今天算起，到第 50 天”只是相当于“从今天之后 第 49 天”．49 天正好是 7 个星期，所以还是星期三． 50－1=49（天）49÷7=7（星期）所以，从今天算起，到第 50 天是星期三阳历 1978 年 1 月 1 日是星期日，阳历 2000 年 1 月 1 日是星期几？分析：每四年有一个闰年，闰年的年份倍 4 整除，所以从 1978 年至 1999 年共有 17 个平年，5 个闰年， 由此可以算出总天数，用总天数除以 7，余 1 是星期一，余 2 是星期二，依次类推365×17＋366×5=8035（天）8035÷7=1147（星期）……6（天）所以，阳历 2000 年 1 月 1 日是星期六．[前铺]6 月 1 日是星期六，问 6 月 27 日是星期几？分析：从日历上可以看到，每个星期有 7 天，就是以 7 天为一个周期不断地重复．6 月 1 日是星期六， 那么再过 7 天，即 6 月 8 日，还是星期六；如果再过 14 天，即 6 月 15 日，还是星期六，……所以要知 道 6 月 27 日是星期几，首先要求出 6 月 27 日是 6 月 1 日后的第几天，27－1=26（天）；因为每个星期 都是 7 天，也就是周期为 7，所以 26÷7=3（星期）……5（天）．这样，从 6 月 1 日开 始经过 3 个星期，最后一天是星期六，从这最后一天再过 5 天就是星期四27－1=26（天）一三五七八十腊，三十一天永不差， 四六九冬是小月，每月天数整三十， 平年二月二十八，闰年二月二十九．（腊是 12 月，冬是 11 月）例10 例926÷7=3（星期）……5（天）所以，6 月 27 日是星期四．周期问题很神奇，由简到繁细分析，列表计算找周期，整除周期末一个，余几周期里第几．专题展望在我们的生活当中经常会遇到类似周期问题的实际问题，希望同学们在学习完本讲后，可以应用到自己的生活中．以后我们还会学习到更为复杂的周期问题，敬请期待吧！练习五1. ★○○○★★○○○★★○○○……这样的一排图形中第 87 个是什么图形，在 87 个图形中一共有多少个五角星？分析：87÷（2＋3）= 17……2．第87 个图形是圆形．17×2＋1=35（个）2. 有一列数：7，0，2，5，3，7，0，2，5，3…（1）第81 个数是多少？（2）这81 个数相加的和是多少？分析：（1）从排列上可以看出这组数按7，0，2，5，3依次重复排列，那么每个周期就有5个数．81个数则是 16 个周期还多 1 个，第 1 个数是 7，所以第 81 个数是 781÷5=16 (1)（2）每个周期各个数之和是：7＋0＋2＋5＋3=17．再用每个周期各数之和乘以周期次数再加上余下的各数，即可得到答案．17×16＋7=279所以，这 81 个数相加的和是 279．3.同学们在科技馆参加活动，谁最先参加游戏呢？同学们想了个好办法，大家排成一排 1—2 报数，报 2 的同学再 1—2 报数，这样依次进行下去，最后报 2 的这名同学先玩，如果这列一共有 12 人，最先玩的同学是这一列中的第几个？分析：第一次 1—2 报数，报 2 的是第 2，4，6，8，10，12 这几个同学，这些同学再 1—2 报数，报 2的是第 4，，8，12 这三名同学，最后这三名同学再 1—2 报数，就只剩下第 8 个同学是报 2，所以最先玩的这个同学是这列中的第 8 个．4.甲、乙、丙三名学生，每天早晨轮流为李奶奶取牛奶．甲第一次取奶是星期一，那么，他第 100 次取奶是星期几？分析：2l 天内，每人取奶 7 次，甲第 8 次取奶又是星期一，即每取 7 次奶为一个周期．100÷7=14…2，所以甲第 100 次取奶是星期二．5.今天是星期五，从今天算起，到第 200 天是星期几？分析：200－1=199（天）199÷7=28（星期）……3（天），所以从今天算起，到第 200 天是星期日．推理小故事巧断小偷美哼百货大厦新进了一批金表，囚提前作了促销宣传，所以当新表上市的时候，到柜台卖金表的人络绎不绝，都想一睹为快，许多人都向前挤．营业员一看不好，急忙说：“大家不要向前挤，注意安全．”但已经挤起来的人群，怎么还能听进去?人群在挤呀挤．“啪”地一声，柜台被挤晃动了．一些不安分的人动手了．“谁偷了金表?”营业员喊．大厅的保卫人员听到喊声，马上过来维持秩序，并抓了四名嫌疑犯．因金表被盗，所以大家就打电话让大侦探欧门前来协助审案．营业员提供的线索是：“金表丢失了一块；所以这四个人中有一人是小偷．”下面是四名嫌疑人提供的证词：为了记录上的方便，他们的名字就用甲、乙、丙、丁来表示．甲说：“我看见手表是乙偷的．”乙说：“不是我!手表是丙偷的．”丙说：“乙在撒谎，他是要陷害我．”丁说：“手表是谁偷的我不知道，反正我没有偷．”大侦探欧门对案情进行了深入地调查研究，经过分析与推理，终于从这四个嫌疑人的谈话中找到了线索，使案情真相大白．原来，小偷确实在他们四人之中，并且只有一个人说的是真话，其余三人的供词都是假话．亲爱的同学们，你能根据上面的线索，分析出谁是真正的小偷吗?答案见第六讲．第四讲“真假辨别”答案：原来，数学上有一条规律:9 乘以任何整数，其积无论是几位数，各位数字相加的和总是 9 的倍数．审判员正是以此作为前提进行推理的．王某诈骗的钱，是 9 位顾客相等的数额(即是 9 的倍数);而把王某交待的金额每位数字相加:1+9+8+4=22，这不是9 的倍数．所以，可以断定王某交代的金额是假的．接着，审判员又进一步推论:22+5 才能构成 9 的倍数，可见王某交代的数额差 5．如果把 5 加到个位，这不大可能，因为大的数字都交代了，隐瞒5 块钱，没有什么价值．如果把5 加到十位数或百位数上，更不可能，因为十位数已经是8，百位数已经是9．只有加到千位数才合乎情理．所以，断定王某故意隐瞒的 5，是一个千位数，即把 6984 元说成 1984 元，以此避重就轻，既可取得坦白从宽的“优待”又可以隐瞒诈骗的大量金额，一举两得．谁知具有逻辑知识的审判员通过严密的逻辑思维，终于机智地揭穿了王某欺骗手段．同学们，你答对了吗？。

P DCBA 第五讲 直线型几何综合题一、学习指引 1.知识要点：三角形及四边形的根本性质，特殊三角形、特殊四边形、全等三角形的断定和性质，轴对称、平移、旋转、相似等变换的性质，一次函数图象和性质。

2.方法指导：〔1〕解决动态几何型问题的策略：化“动〞为“静〞——利用运动中特殊点的位置将图形分类；“静〞中求“动〞——针对各类图形，分别解决动态问题。

〔2〕解决图形分割问题的思维方式是：从详细问题出发→观察猜测→实验操作→形成方案→严密计算与论证；图形分割问题的解题策略：比拟原图形与分割后图形在边、角、面积等方面的变化是解决图形分割问题的着手点；〔3〕新概念性几何题解题策略：正确理解问题中的“新概念〞，然后抓住 “新概念〞的特征，结合相关的数学知识综合解决问题。

二、 典型例题例1．如图，在矩形ABCD 中，AB=2，BC=1，动点P 从点B 出发，沿道路B→C→D 作匀速运动，那么△ABP 的面积S 与点P 运动的路程x 之间的函数图象大致是〔 〕例2．如图，在矩形ABCD中，BC =20cm ，P，Q ，M ，N分别从A ，B ，C ，D 出发沿AD ，BC ，CB ，DA 方向在矩形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停顿．在一样时间是内，假设BQ =x cm(0x )，那么AP =2x cm ，CM =3x cm ，DN =x 2cm ．〔1〕当x 为何值时，以PQ ，MN 为两边,以矩形的边〔AD 或者BC 〕的一局部为第三边构成一个三角形；〔2〕当x 为何值时，以P ，Q ，M ，N 为顶点的四边形是平行四边形；〔3〕以P ，Q ，M ，N 为顶点的四边形能否为等腰梯形?假如能，求x 的值；假如不能，请说明理由．例3．三张形状、大小完全一样的平行四边形透明纸片，分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合〔如图1、图2、图3〕．分别在图1、图2、图3中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两局部，并把这两局部重新拼成符合以下要求的几何图形．要求如下：〔1〕在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形；〔2〕裁成的两局部在拼成几何图形时要互不重叠且不留空隙； 〔3〕所画出的几何图形的各顶点必须与小正方形的顶点重合．ABDCPQ MN例4．如图，两个边长分别为4和3的正方形，请用线段将它们进展适当分割，剪拼成一个大正方形，请在以下图中分别画出两种不同的拼法，并将剪拼前、后的一样区域用一样数字序号标出．例5．如图，在梯形OABC 中，O 为直角坐标系的原点，A 、B 、C 的坐标分别为(14，0)，(14，3)，(4，3)．点P 、Q 同时从原点出发，分别做匀速运动，其中点P 沿OA 向终点A 运动，速度为每秒1个单位，点Q 沿OC 、CB 向终点B 运动．当这两点中有一点到达自己的终点时，另一点也停顿运动．图1矩形〔非正方形〕图2正方形图3有一个角是135°的三角形〔例3图〕拼法二备用图二备用图一拼法一〔1〕设从出发起运动了x秒，假如点Q的速度为每秒2个单位，试分别写出这时点Q在OC 上或者CB上时的坐标(用含x的代数式表示，不要求写出x的取值范围)；〔2〕设从出发起运动了x秒，假如点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半．①试用含x的代数式表示这时点Q所经过的路程和它的速度；②试问：这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两局部？假如有可能，求出相应的x的值和P、Q的坐标，如不可能，请说明理由．例6．如图，在等腰梯形ABCD中，AB∥DC，∠A=45°，AB=10cm，CD=4cm，等腰直角三角形PMN的斜边MN=10cm，A点与N点重合，MN和AB在一条直线上，设等腰梯形ABCD不动，等腰直角三角形PMN沿AB所在直线以1cm/s的速度向右挪动，直到点N与点B重合为止。

第五讲 基本盈亏问题1.1.老师拿来10个苹果，平均分给5个同学，每个人分几个呢？如果再来两个同学，还是每人分那么多，还差几个苹果呢？2. 2. 羊村村长给小羊们发青草丸子，每只羊分到的一样多，还剩下20个青草丸子。

后来又来了一只小羊，分给它同样多的丸子后，只剩下10个青草丸子了，请问每只小羊分到几个青草丸子？3．老师拿来一些苹果，分给5个同学，每个人分到的一样多，还剩下1个，如果又来1个同学，分给他同样多的苹果后，还差1个，那么每个同学分几个苹果呢？老师原来有几个苹果？ 4．老师拿来一些苹果，分给3个同学，每个人一样多，还剩下10个，又来了两个同学，分给他们同样多的苹果后，还剩下2个，每个同学分几个苹果呢？老师原来有几个苹果？例1老师拿来很多剪纸，分给5个同学，每人分到的一样多，还剩下22张，又来了两个同学，分给他们一样多的剪纸后，就只剩下6张了。

请问每个同学分几张剪纸？老师一共拿来了多少张剪纸？【练习】1.羊村村长给小羊们发青草丸子，每只羊分到的一样多，还剩下20个青草丸子。

后来又来了两只小羊，分给它同样多的丸子后，只剩下10个青草丸子了，请问每只小羊分到几个青草丸子？2.乐乐准备了一些棒棒糖发给班里的同学，开始发给7个同学，还剩下14根。

后来又来了3名同学，发给他们同样多的棒棒糖后，就只剩下5根了。

请问每个同学发几根棒棒糖？乐乐开始一共准备了多少根棒棒糖？3.老师给同学们发作业本，每个人发同样多的作业本后，还剩下20本。

后来给新来的2个同学也发了同样多的作业本，就只剩下12本，请问每个同学发几本？剩下的作业本还能发给几个同学？例2裁缝要往一些西服上缝扣子，如果每件西服缝3个扣子的，还会剩下26个扣子；如果每件缝5个，就只剩下4个扣子了。

请问：裁缝一共有多少个扣子？几件西服？【练习】1.把一些桃子分给猴子们，如果每只猴子分5个，那么还剩下12个桃子；如果每只猴子分8个，就只剩下3个桃子了，问有多少只猴子？有多少个桃子？2.某车队买回来一些新轮胎，要是把每辆车的2个前胎全部换掉，还能剩下20个轮胎；要是把每辆车的4个轮胎全部换掉，就只剩下6个轮胎了。

整式方程（组）1．一个等腰三角形的底边长是5，腰长是一元二次方程x2﹣6x+8＝0的一个根，则此三角形的周长是（）A．12B．13C．14D．12或142．若一个直角三角形的两条直角边长之和为14，面积为24，则其斜边的长是（）A．2B．4C．8D．103．已知菱形的两条对角线长是一元二次方程x2﹣3x+2＝0的根，则此菱形的边长是（）A．B．C．D．4．已知关于x的一元二次方程mx2﹣nx＝p（m≠0）的两个根为x1＝3，x2＝5，则方程m（2x+5）2﹣n（2x+5）﹣p＝0的根为（）A．x1＝3，x2＝5B．x1＝﹣1，x2＝0C．x1＝﹣2，x2＝0D．x1＝11，x2＝155．若x2﹣2px+3q＝0的两根分别是﹣3与5，则多项式2x2﹣4px+6q可以分解为（）A．（x+3）（x﹣5）B．（x﹣3）（x+5）C．2（x+3）（x﹣5）D．2（x﹣3）（x+5）6．实数x，y满足（x2+y2）（x2+y2+1）＝2，则x2+y2的值为（）A．1B．2C．﹣2或1D．2或﹣17．已知当x＞0时，反比例函数y＝的函数值随自变量的增大而减小，此时关于x的方程x2﹣2（k+1）x+k2﹣1＝0的根的情况为（）A．有两个相等的实数根B．没有实数根C．有两个不相等的实数根D．无法确定8．如果的解都是正数，那么a的取值范围是（）A．a＜2B．a＞﹣C．﹣2＜a＜D．a＜﹣9．关于x的方程m2x2﹣8mx+12＝0至少有一个正整数解，且m是整数，则满足条件的m 的值的个数是（）A．5个B．4个C．3个D．2个10．阅读：关于x方程ax＝b在不同的条件下解的情况如下：（1）当a≠0时，有唯一解x＝；（2）当a＝0，b＝0时有无数解；（3）当a＝0，b≠0时无解．请你根据以上知识作答：已知关于x的方程•a＝﹣（x﹣6）无解，则a的值是（）A．1B．﹣1C．±1D．a≠111．关于x的一元二次方程kx2﹣4x+3＝0有实数根，则k应满足的条件是．12．已知关于x，y的二元一次方程（2m﹣1）x+（m+1）y﹣m+2＝0，无论实数m取何值，此二元一次方程都有一个相同的解，则这个相同的解是．13．关于x、y的方程2x+ay＝7仅有一组正整数解，则满足条件的正整数a的值为．14．如图，两个正方形的边长分别为4，3，两阴影部分的面积分别为a，b（a＞b），则a﹣b等于．15．如图，用如图①中的a张长方形和b张正方形纸板作侧面和底面，做成如图②的竖式和横式两种无盖纸盒，若295＜a+b＜305，用完这些纸板做竖式纸盒比横式纸盒多30个，则a＝，b＝．16．已知方程组的解x、y满足x+y＜1，且m为正数，求m的取值范围．17．如图，在Rt△ABC中，∠B＝90°，AB＝5cm，BC＝7cm．点P从点A开始沿AB边向终点B以1cm/s的速度移动，点Q从点B开始沿BC边向终点C以2cm/s的速度移动，当其中一点到达终点时，另一点随之停止．点P，Q分别从点A，B同时出发．（1）求出发多少秒时PQ的长度等于5cm；（2）出发秒时，△BPQ中有一个角与∠A相等．整式方程（组）参考答案与试题解析1.【解答】解：解方程x2﹣6x+8＝0得：x＝4或2，当三角形的三边为5，2，2时，2+2+＜5，不符合三角形三边关系定理，此时不能组成三角形；当三角形的三边为5，4，4时，符合三角形三边关系定理，此时三角形的周长为5+4+4＝13，故选：B．\2．【解答】解：设其中一条直角边的长为x，则另一条直角边为（14﹣x），根据题意得：x （14﹣x）＝24，整理得：x2﹣14x+48＝0．解得x1＝6，x2＝8，所以斜边长为：＝10．故选：D．3．【解答】解：方程x2﹣3x+2＝0，分解得：（x﹣1）（x﹣2）＝0，解得：x＝1或x＝2，∵菱形的对角线互相垂直∴根据勾股定理得：＝，故选：C．4【解答】解：∵关于x的一元二次方程mx2﹣nx＝p（m≠0）的两个根为x1＝3，x2＝5，∴方程m（2x+5）2﹣n（2x+5）﹣p＝0中2x+5＝3或2x+5＝5，解得：x＝﹣1或x＝0，即x1＝﹣1，x2＝0，故选：B．5【解答】解：∵x2﹣2px+3q＝0的两根分别是﹣3与5，∴2x2﹣4px+6q＝2（x2﹣2px+3p）＝2（x+3）（x﹣5），故选：C．6．【解答】解：（x2+y2）（x2+y2+1）＝2，设x2+y2＝a，则原方程化为：a（a+1）＝2，即a2+a﹣2＝0，解得：a＝﹣2或1，∵不论xy为何值，x2+y2不能为负数，所以x2+y2只能等于1，故选：A．7．【解答】解：∵当x＞0时，反比例函数y＝的函数值随自变量的增大而减小，∴k＞0，∵x2﹣2（k+1）x+k2﹣1＝0，∴△＝[﹣2（k+1）]2﹣4×1×（k2﹣1）＝8k+8＞0，∴关于x的方程x2﹣2（k+1）x+k2﹣1＝0有两个不相等的实数根，故选：C．8．【解答】解：，①×2+②得：5x＝2a+4，解得：x＝，①×3﹣②得：﹣5y＝3a﹣4，解得：y＝，即方程组的解是，∵方程组的解都是正数，∴＞0，＞0，解得：﹣2＜a＜，故选：C．9．【解答】解：m2x2﹣8mx+12＝0，解法一：△＝（﹣8m）2﹣4m2×12＝16m2，∴x＝＝，∴x1＝，x2＝，解法二：（mx﹣2）（mx﹣6）＝0，∴x1＝，x2＝，∵关于x的方程m2x2﹣8mx+12＝0至少有一个正整数解，且m是整数，∴＞0，＞0，∴m＝1或2或3或6，则满足条件的m的值的个数是4个，故选：B．10．【解答】解：去分母得：2ax＝3x﹣（x﹣6），去括号得：2ax＝2x+6移项，合并得，x＝，因为无解；所以a﹣1＝0，即a＝1．故选：A．11．【解答】解：∵关于x的一元二次方程kx2﹣4x+3＝0有实数根∴k≠0且△＝（﹣4）2﹣4•k•3＝16﹣12k≥0，解得：k≤且k≠0，故答案为：k≤且k≠0．12【解答】解：将方程（2m﹣1）x+（m+1）y﹣m+2＝0整理得：（2x+y﹣1）m﹣x+y+2＝0∵无论实数m取何值，此二元一次方程都有一个相同的解∴解得：故答案为：．13．【解答】解：2x+ay＝7，ay＝7﹣2x，①当x＝1时，7﹣2x＝5，∴ay＝5，∴a＝1，y＝5（舍）或a＝5，y＝1，②当x＝2时，7﹣2x＝3，∴ay＝3，∴a＝1，y＝3（舍）或a＝3，y＝1，③当x＝3时，7﹣2x＝1，∴ay＝1，∴a＝1，y＝1（舍），综上，满足条件的正整数a的值为5或3，故答案为：5或3．14．【解答】解：设空白出图形的面积为x，根据题意得：a+x＝16，b+x＝9，则a﹣b＝7．故答案为：7．15．【解答】解：设横式纸盒x个，则竖式纸盒为（x+30）个，a＝4（x+30）+3x，b＝（x+30）+2x，∵295＜a+b＜305，∴295＜4（x+30）+3x+（x+30）+2x＜305，解得：14.5≤x≤15.5，∵x为整数，∴x＝15当x＝15时，a＝225，b＝75，故答案为：225，75．16．【解答】解：①×2﹣②，得3x＝1+7mx＝，把x＝代入①得+y＝1+3m，y＝，∵x+y＜1，m．∵m＞0，∴0．17．【解答】解：（1）设出发t秒时PQ的长度等于5cm，PQ＝5，则PQ2＝25＝BP2+BQ2，即25＝（5﹣t）2+（2t）2，解得：t＝0（舍）或2．故2秒后，PQ的长度为5cm．（2）设出发x秒时，△BPQ中有一个角与∠A相等．∵AB＝5cm，BC＝7cm∴PB＝（5﹣x）cm，BQ＝2xcm当∠BPQ＝∠A时，又∵∠B＝∠B∴△ABC∽△PBQ∴＝∴＝解得：x＝；当∠BQP＝∠A时，又∵∠B＝∠B∴△ABC∽△QBP∴＝∴＝解得：x＝故答案为：或．。

第五讲点在数轴上的运动一．解答题（共15小题）1．已知数轴上两点A，B对应的数分别为﹣1，3，P为数轴上的动点，其对应的数为x．（1）数轴上是否存在点P，使P到点A、点B的之和为5？若存在，请求出x的值；若不存在，说明理由；（2）当点P以每分钟1个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度的速度向左运动，点B以每分钟20个单位长度的速度向左运动．问，它们同时出发几分钟时点P到点A、点B的距离相等？2．已知数轴上两点A，B对应的数分别为﹣1，3，P为数轴上的动点，其对应的数为x．（1）若点P到A，B两点的距离相等，求点P对应的数；（2）数轴上是否存在点P，使点P到A，B的距离之和为5？若存在，请求出x 的值；若不存在，请说明理由；（3）当点P以每分钟1个单位长的速度从原点O向左运动时，点A以每分钟5个单位长的速度向左运动，点B以每分钟20个单位长的速度向左运动，问它们同时出发，几分钟后点P到A，B两点的距离相等？3．已知数轴上两点A、B对应的数分别是6，﹣8，M、N为数轴上两个动点，点M从A点出发向左运动，速度为每秒2个单位长度，与此同时，点N从B点出发向右运动，速度为M点的3倍，经过多长时间，点M与点N相距50个单位长度？这时点M、N所对应的数分别是多少？4．已知A、B在数轴上对应的数分别用a、b表示，且（b+10）2+|a﹣20|=0，P 是数轴上的一个动点．（1）在数轴上标出A、B的位置，并求出A、B之间的距离．（2）当P点满足PB=2PA时，求P点对应的数．（3）动点P从原点开始第一次向左移动1个单位长度，第二次向右移动3个单位长度，第三次向左移动5个单位长度，第四次向右移动7个单位长度，依此类推，…点P能够移到与A、B重合的位置吗？若能，请探索第几次移动时重合；若不能，请说明理由．5．在一条数轴上有A、B两点，点A表示数﹣4，点B表示数6，点P是该数轴上的一个动点（不与A、B重合）表示数x．点M、N分别是线段AP、BP的中点（1）如果点P在线段AB上，则点M表示的数是，则点N表示的数是（用含x的代数式表示），并计算线段MN的长；（2）如果点P在点B右侧，请你计算线段MN的长；（3）如果点P在点A左侧，则线段MN的长度会改变吗？如果改变，请说明理由；如果不变，请直接写出结果．6．如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10．动点P 从点O出发，以每秒6个单位长度的速度沿数轴向右匀速运动，设运动时间为t （t＞0）秒．（1）写出数轴上点B表示的数；当t=3时，OP=（2）动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问点R运动多少秒时追上点P？（3）动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问点R运动多少秒时PR相距2个单位长度？7．动点A、B同时从数轴上的原点出发向相反的方向运动，且A、B的速度之比是1：4（速度单位：长度单位/秒），3秒后，A、B两点相距15个单位长度．（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置．（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间？8．如图，已知数轴上的点A对应的数是a，点B对应的数是b，且满足（a+5）2+|b﹣1|=0（1）求数轴上到点A、点B距离相等的点C对应的数；（2）动点P从点A出发，以2个单位/秒的速度向右运动，设运动时间为t秒，问：是否存在某个时刻t，恰好使得P到点A的距离是点P到点B的距离的2倍？若存在，请求出t的值；若不存在，请说明理由．9．如图，数轴上的点O和A分别表示0和10，点P是线段OA上一动点，沿O→A→O 以每秒2个单位的速度往返运动1次，B是线段OA的中点，设点P运动时间为t秒（0≤t≤10）．（1）线段BA的长度为；（2）当t=3时，点P所表示的数是；（3）求动点P所表示的数（用含t的代数式表示）；（4）在运动过程中，若OP中点为Q，则QB的长度是否发生变化？若不变，请求出它的值；若变化，请直接用含t的代数式QB的长度．10．如图，数轴原点为O，A、B是数轴上的两点，点A对应的数是1，点B对应的数是﹣4，动点P、Q同时从A、B出发，分别以1个单位/秒和3个单位/秒的速度沿着数轴正方向运动，设运动时间为t秒（t＞0）．（1）AB两点间的距离是；动点P对应的数是；（用含t的代数式表示）动点Q对应的数是；（用含t的代数式表示）（2）几秒后，点O恰好为线段PQ中点？（3）几秒后，恰好有OP：OQ=1：2？11．已知数轴上A点表示数a，C点表示数c，且a、c满足|a+24|+（c﹣8）2=0，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．（1）点A表示的数为，点B表示的数为．（2）用含t的代数式表示P到点A和点C的距离：PA=，PC=．（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A．在点Q运动过程中，点P与点Q能否重合？若能，请求出点Q运动的时间．12．阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a ﹣b|；当A、B两点都不在原点时，如图2，点A、B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|；如图3，当点A、B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a﹣b|；如图4，当点A、B在原点的两边，|AB|=|OB|+|OA|=|a|+|b|=a+（﹣b）=|a﹣b|；回答下列问题：（1）数轴上表示2和5的两点之间的距离是，数轴上表示1和﹣3的两点之间的距离是；（2）数轴上若点A表示的数是x，点B表示的数是﹣2，则点A和B之间的距离是，若|AB|=2，那么x为；（3）当x是时，代数式|x+2|+|x﹣1|=5；（4）若点A表示的数﹣1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒个单位长度，求运动几秒后，点Q可以追上点P？（请写出必要的求解过程）13．去年“十•一”黄金周期间，某风景区在7天假期中每天接待游客的人数变化如下表：（正数表示比前一天多的人数，负数表示比前一天少的人数）日期10月1日10月2日10月3日10月4日10月5日10月6日10月7日人数变化（万人）+1.6+0.8+0.4﹣0.4﹣0.8+0.2﹣1.4（1）请判断七天内游客人数最多的是哪天？最少的是哪天？它们相差多少万人？（2）若9月30日游客人数为3万人，门票每人次200元，2%的游客符合免费条件，8%的游客符合减半收费条件，求该风景区7天门票总收入是多少万元？14．小王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接下来的一周交易日内，小王记下该股票每日收盘价格相比前一天的涨跌情况：（单位：元）星期一二三四五每股涨跌（元）+2﹣0.5+1.5﹣1.8+0.8根据上表回答问题：（1）星期二收盘时，该股票每股多少元？（2）本周内该股票收盘时的最高价，最低价分别是多少？（3）已知买入股票与卖出股票均需支付成交金额的千分之五的交易费．若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？15．从2016年1月1日开始，北京市居民生活用气阶梯价格制度正式实施，一般生活用气收费标准如下表所示，比如6口以下的户年天然气用量在第二档时，其中350立方米按2.28元/m3收费，超过350立方米的部分按2.5元/m3收费．小锋一家有五口人，他想帮父母计算一下实行阶梯价后，家里天然气费的支出情况．（1）如果他家2017年全年使用200立方米天然气，那么需要交多少元天然气费？（2）如果他家2017年全年使用400立方米天然气，那么需要交多少元天然气费？（3）如果他家2016年需要交1563元天然气费，他家2016年用了多少立方米天然气？参考答案与试题解析一．解答题（共15小题）1．已知数轴上两点A，B对应的数分别为﹣1，3，P为数轴上的动点，其对应的数为x．（1）数轴上是否存在点P，使P到点A、点B的之和为5？若存在，请求出x的值；若不存在，说明理由；（2）当点P以每分钟1个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度的速度向左运动，点B以每分钟20个单位长度的速度向左运动．问，它们同时出发几分钟时点P到点A、点B的距离相等？【解答】解：（1）当P在A点左侧时：3﹣x+（﹣1﹣x）=5，解得：x=﹣；当P在B右侧时，x﹣3+x﹣（﹣1）=5，解得：x=；当P在A、B之间时，x不存在；（2）①设它们同时出发a分钟时点P到点A、点B的距离相等，此时A，B不重合，由题意得：﹣a﹣（﹣5a﹣1）=（3﹣20a）﹣（﹣a），解得：a=．②当A，B重合时，20a=5a+4，解得：a=，答：它们同时出发分钟或分钟时点P到点A、点B的距离相等．2．已知数轴上两点A，B对应的数分别为﹣1，3，P为数轴上的动点，其对应的数为x．（1）若点P到A，B两点的距离相等，求点P对应的数；（2）数轴上是否存在点P，使点P到A，B的距离之和为5？若存在，请求出x 的值；若不存在，请说明理由；（3）当点P以每分钟1个单位长的速度从原点O向左运动时，点A以每分钟5个单位长的速度向左运动，点B以每分钟20个单位长的速度向左运动，问它们同时出发，几分钟后点P到A，B两点的距离相等？【解答】解：（1）∵1﹣（﹣1）=2，2的绝对值是2，1﹣3=﹣2，﹣2的绝对值是2，∴点P对应的数是1．（2）当P在A左侧时，3﹣x+（﹣1﹣x）=5，解得：x=﹣；当P在B右侧时，x﹣3+x﹣（﹣1）=5，解得：x=；当P在A、B之间时，x不存在；综上所述，x=﹣或x=；（3））①当B未追上A时，﹣x+1+5x=3﹣20x+x，解得：x=；∴分钟时点P到点A、点B的距离相等．②B追上A时，20x=5x+4，解得：x=，∴分钟时点P到点A、点B的距离相等．答：当经过或分钟时，点P到点A，点B的距离相等．3．已知数轴上两点A、B对应的数分别是6，﹣8，M、N为数轴上两个动点，点M从A点出发向左运动，速度为每秒2个单位长度，与此同时，点N从B点出发向右运动，速度为M点的3倍，经过多长时间，点M与点N相距50个单位长度？这时点M、N所对应的数分别是多少？【解答】解：设经过x秒点M与点N相距50个单位．依题意可列方程为：2x+6x﹣14=50，解方程，得x=8．2x=16，16﹣6=10，即点M所对应的数是﹣10．6x=48，48﹣8=40，即点N所对应的数是40．答：经过8秒点M与点N相距50个单位，这时点M、N所对应的数分别是﹣10，40．4．已知A、B在数轴上对应的数分别用a、b表示，且（b+10）2+|a﹣20|=0，P 是数轴上的一个动点．（1）在数轴上标出A、B的位置，并求出A、B之间的距离．（2）当P点满足PB=2PA时，求P点对应的数．（3）动点P从原点开始第一次向左移动1个单位长度，第二次向右移动3个单位长度，第三次向左移动5个单位长度，第四次向右移动7个单位长度，依此类推，…点P能够移到与A、B重合的位置吗？若能，请探索第几次移动时重合；若不能，请说明理由．【解答】解：（1）∵（b+10）2+|a﹣20|=0，∴b+10=0，a﹣20=0，∴b=﹣10，a=20．A、B的位置如图所示：∴AB=|﹣10﹣20|=30；（2）设P点对应的数为x，当P点满足PB=2PA时，分三种情况讨论：①若点P在点B的左侧，则PB＜PA，与PB=2PA不符，舍去；②若点P在AB之间，则x﹣（﹣10）=2（20﹣x），解得x=10；③若点P在点A的右侧，则x﹣（﹣10）=2（x﹣20），解得x=50，综上所述，P点对应的数为10或50；（3）由题可得，第一次点P表示﹣1，第二次点P表示2，点P表示的数依次为﹣3，4，﹣5，6…，∴第n次为（﹣1）n•n，∵点A表示20，点B表示﹣10，∴当n=20时，（﹣1）n•n=20；当n=10时，（﹣1）n•n=10≠﹣10，∴第20次P与A重合；点P与点B不重合．5．在一条数轴上有A、B两点，点A表示数﹣4，点B表示数6，点P是该数轴上的一个动点（不与A、B重合）表示数x．点M、N分别是线段AP、BP的中点（1）如果点P在线段AB上，则点M表示的数是，则点N表示的数是（用含x的代数式表示），并计算线段MN的长；（2）如果点P在点B右侧，请你计算线段MN的长；（3）如果点P在点A左侧，则线段MN的长度会改变吗？如果改变，请说明理由；如果不变，请直接写出结果．【解答】解：（1）如图1所示，∵点A表示数﹣4，点B表示数6，点P表示数x，点M、N分别是线段AP、BP 的中点，∴点M表示，点N表示，∴MN=﹣=5，故答案为：，；（2）如图2所示，∵点A表示数﹣4，点B表示数6，点P表示数x，点M、N分别是线段AP、BP 的中点，∴点M表示，点N表示，∴MN=﹣﹣=5；（3）不会改变，MN=5，理由同（2）．6．如图，已知数轴上点A表示的数为6，B是数轴上一点，且AB=10．动点P 从点O出发，以每秒6个单位长度的速度沿数轴向右匀速运动，设运动时间为t （t＞0）秒．（1）写出数轴上点B表示的数﹣4；当t=3时，OP=18（2）动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问点R运动多少秒时追上点P？（3）动点R从点B出发，以每秒8个单位长度的速度沿数轴向右匀速运动，若点P，R同时出发，问点R运动多少秒时PR相距2个单位长度？【解答】解：（1）∵数轴上点A表示的数为6，B是数轴上一点，且AB=10，∴BO=4，∴数轴上点B表示的数为：﹣4，∵动点P从点O出发，以每秒6个单位长度的速度沿数轴向右匀速运动，∴当t=3时，OP=18；故答案为：﹣4，18；（2）如图1，设点R运动x秒时，在点C处追上点P，则OC=6x，BC=8x，∵BC﹣OC=OB，∴8x﹣6x=4，解得：x=2，∴点R运动2秒时，在点C处追上点P．（3）设点R运动x秒时，PR=2．分两种情况：如图2，一种情况是当点R在点P的左侧时，8x=4+6x﹣2，即x=1；如图3，另一种情况是当点R在点P的右侧时，8x=4+6x+2，即x=3．综上所述R运动1秒或3秒时PR相距2个单位．7．动点A、B同时从数轴上的原点出发向相反的方向运动，且A、B的速度之比是1：4（速度单位：长度单位/秒），3秒后，A、B两点相距15个单位长度．（1）求出两个动点运动的速度，并在数轴上标出A、B两点从原点出发运动3秒时的位置．（2）若A、B两点从（1）中的位置同时向数轴负方向运动，几秒后原点恰好处在两个动点正中间？【解答】解：（1）设动点A的速度是x单位长度/秒，根据题意得：3（x+4x）=15解得：x=1，则4x=4．答：动点A的速度是1单位长度/秒，动点B的速度是4单位长度/秒；标出A，B点如图：（2）设y秒时，原点恰好处在两个动点的正中间，根据题意得：3+y=12﹣4y解得：y=1.8，答：1.8秒时，原点恰好处在两个动点的正中间．8．如图，已知数轴上的点A对应的数是a，点B对应的数是b，且满足（a+5）2+|b﹣1|=0（1）求数轴上到点A、点B距离相等的点C对应的数；（2）动点P从点A出发，以2个单位/秒的速度向右运动，设运动时间为t秒，问：是否存在某个时刻t，恰好使得P到点A的距离是点P到点B的距离的2倍？若存在，请求出t的值；若不存在，请说明理由．【解答】解：（1）∵（a+5）2+|b﹣1|=0，∴a=﹣5，b=1．设点C对应的数为x，则BC=1﹣x，AC=x+5，∵BC=AC，∴1﹣x=x+5，解得：x=﹣2，∴点C对应的数为﹣2．（2）假设存在，点P对应的数为﹣5+2t，∴PA=2t，PB=|﹣5+2t﹣1|=|2t﹣6|，∵PA=2PB，∴2t=2×|2t﹣6|．当2t=4t﹣12时，t=6；当2t=12﹣4t时，t=2．故存在某个时刻t，恰好使得P到点A的距离是点P到点B的距离的2倍，此时t的值为2秒或6秒．9．如图，数轴上的点O和A分别表示0和10，点P是线段OA上一动点，沿O→A→O 以每秒2个单位的速度往返运动1次，B是线段OA的中点，设点P运动时间为t秒（0≤t≤10）．（1）线段BA的长度为5；（2）当t=3时，点P所表示的数是6；（3）求动点P所表示的数（用含t的代数式表示）；（4）在运动过程中，若OP中点为Q，则QB的长度是否发生变化？若不变，请求出它的值；若变化，请直接用含t的代数式QB的长度．【解答】解：（1）∵B是线段OA的中点，∴BA=OA=5；故答案为：5；（2）当t=3时，点P所表示的数是2×3=6，故答案为：6；（3）当0≤t≤5时，动点P所表示的数是2t，当5≤t≤10时，动点P所表示的数是20﹣2t；（4）QB的长度发生变化，当0≤t≤5时，QB=5﹣t，当5≤t≤10时，QB=5﹣（20﹣5t）=t﹣5．10．如图，数轴原点为O，A、B是数轴上的两点，点A对应的数是1，点B对应的数是﹣4，动点P、Q同时从A、B出发，分别以1个单位/秒和3个单位/秒的速度沿着数轴正方向运动，设运动时间为t秒（t＞0）．（1）AB两点间的距离是5；动点P对应的数是1+t；（用含t的代数式表示）动点Q对应的数是﹣4+3t；（用含t的代数式表示）（2）几秒后，点O恰好为线段PQ中点？（3）几秒后，恰好有OP：OQ=1：2？【解答】解：（1）AB两点间的距离是1﹣（﹣4）=5；动点P对应的数是1+t；（用含t的代数式表示）动点Q对应的数是﹣4+3t；（用含t的代数式表示）故答案为：5，1+t，﹣4+3t；（2）设t秒后，点O恰好为线段PQ中点，依题意有1+t+（﹣4+3t）=0，解得t=．故秒后，点O恰好为线段PQ中点；（3）P、Q在原点的两边，2（1+t）+（﹣4+3t）=0，解得t=．P、Q在原点的一边，2（1+t）=（﹣4+3t），解得t=6．故或6秒后，恰好有OP：OQ=1：2．11．已知数轴上A点表示数a，C点表示数c，且a、c满足|a+24|+（c﹣8）2=0，点C表示的数与点B表示的数互为相反数，动点P从A出发，以每秒1个单位的速度向终点C移动，设移动时间为t秒．（1）点A表示的数为﹣24，点B表示的数为﹣8．（2）用含t的代数式表示P到点A和点C的距离：PA=t，PC=32﹣t．（3）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，运动到终点A．在点Q运动过程中，点P与点Q能否重合？若能，请求出点Q运动的时间．【解答】解：（1）∵|a+24|+（c﹣8）2=0，∴a+24=0，c﹣8=0，解得：a=﹣24，c=8，∵点C表示的数与点B表示的数互为相反数，∴点B表示的数为﹣8，故答案为：﹣24，﹣8；（2）∵动点P从A出发，以每秒1个单位的速度向终点C移动，∴PA=t，∵AC=32，∴PC=32﹣t，故答案为：t，32﹣t；（3）设点Q运动x秒时，点P和点Q重合．当点Q从点A向点C运动时3x﹣x=16，解得：x=8，当点Q从点C向点A运动时，3x+x+16=32×2，x=12，答：点Q运动8秒或12秒追上．12．阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a ﹣b|；当A、B两点都不在原点时，如图2，点A、B都在原点的右边，|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|；如图3，当点A、B都在原点的左边，|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣（﹣a）=|a﹣b|；如图4，当点A、B在原点的两边，|AB|=|OB|+|OA|=|a|+|b|=a+（﹣b）=|a﹣b|；回答下列问题：（1）数轴上表示2和5的两点之间的距离是3，数轴上表示1和﹣3的两点之间的距离是4；（2）数轴上若点A表示的数是x，点B表示的数是﹣2，则点A和B之间的距离是|x+2| ，若|AB|=2，那么x为0或﹣4；（3）当x是﹣3或2时，代数式|x+2|+|x﹣1|=5；（4）若点A表示的数﹣1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒个单位长度，求运动几秒后，点Q可以追上点P？（请写出必要的求解过程）【解答】解：（1）数轴上表示2和5的两点之间的距离是|5﹣2|=3；数轴上表示1和﹣3的两点之间的距离是|﹣3﹣1|=4；故答案为：3，4；（2）∵点A表示的数是x，点B表示的数是﹣2，∴点A和B之间的距离|x﹣（﹣2）|=|x+2|；当|AB|=2时，|x+2|=2，解得x=0或﹣4；故答案为：|x+2|，0或﹣4；（3）∵|x+2|+|x﹣1|=5，∴①当x＜﹣2时，﹣x﹣2﹣x+1=5，解得x=﹣3；②当﹣2≤x≤1时，x+2﹣x+1=5，此方程无解；③当x＞1时，x+2+x﹣1=5，解得x=2；故答案为：﹣3或2；（4）设运动n秒后，点Q可以追上点P，∵点B与点A的距离是10，∴3n ﹣n=10，解得n=4，∴运动4秒后，点Q可以追上点P．13．去年“十•一”黄金周期间，某风景区在7天假期中每天接待游客的人数变化如下表：（正数表示比前一天多的人数，负数表示比前一天少的人数）日期10月1日10月2日10月3日10月4日10月5日10月6日10月7日人数变化（万人）+1.6+0.8+0.4﹣0.4﹣0.8+0.2﹣1.4（1）请判断七天内游客人数最多的是哪天？最少的是哪天？它们相差多少万人？（2）若9月30日游客人数为3万人，门票每人次200元，2%的游客符合免费条件，8%的游客符合减半收费条件，求该风景区7天门票总收入是多少万元？【解答】解：（1）根据题意，10月3日游客最多，比9月30日多：1.6+0.8+0.4=2.8（万人），10月7日游客最少，比9月30日多，1.6+0.8+0.4﹣0.4﹣0.8+0.2﹣1.4=0.4（万人），最多与最少相差：2.8﹣0.4=2.4（万人）．（2）根据题意10月1日至10月7日游客人数分别是：3+1.6=4.6（万人），4.6+0.8=5.4（万人），5.4+0.4=5.8（万人），5.8﹣0.4=5.4（万人），5.4﹣0.8=4.6（万人），4.6+0.2=4.8（万人），4.8﹣1.4=3.4（万人），7天游客的总数是：4.6+5.4+5.8+5.4+4.6+4.8+3.4=34（万人），7天门票的总收入是：100×34×8%+200×34×90%=6392（万元）．14．小王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接下来的一周交易日内，小王记下该股票每日收盘价格相比前一天的涨跌情况：（单位：元）星期一二三四五每股涨跌（元）+2﹣0.5+1.5﹣1.8+0.8根据上表回答问题：（1）星期二收盘时，该股票每股多少元？（2）本周内该股票收盘时的最高价，最低价分别是多少？（3）已知买入股票与卖出股票均需支付成交金额的千分之五的交易费．若小王在本周五以收盘价将全部股票卖出，他的收益情况如何？【解答】解：（1）星期二收盘价为25+2﹣0.5=26.5（元/股）．（2）收盘最高价为25+2﹣0.5+1.5=28（元/股），收盘最低价为25+2﹣0.5+1.5﹣1.8=26.2（元/股）．（3）小王的收益为：27×1000（1﹣5‰）﹣25×1000（1+5‰）=27000﹣135﹣25000﹣125=1740（元）．∴小王的本次收益为1740元．15．从2016年1月1日开始，北京市居民生活用气阶梯价格制度正式实施，一般生活用气收费标准如下表所示，比如6口以下的户年天然气用量在第二档时，其中350立方米按2.28元/m3收费，超过350立方米的部分按2.5元/m3收费．小锋一家有五口人，他想帮父母计算一下实行阶梯价后，家里天然气费的支出情况．（1）如果他家2017年全年使用200立方米天然气，那么需要交多少元天然气费？（2）如果他家2017年全年使用400立方米天然气，那么需要交多少元天然气费？（3）如果他家2016年需要交1563元天然气费，他家2016年用了多少立方米天然气？【解答】解：（1）如果他家2016年全年使用300立方米天然气，那么需要交天然气费2.28×200=456（元）；（2）如果他家2016年全年使用400立方米天然气，那么需要交天然气费2.28×350+2.5×（400﹣350）=798+125=923（元）；（3）∵2.28×350+2.5×（500﹣350）=1173，1173＜1563，∴小锋家2016年所用天然气超过了500立方米．设小锋家2016年用了x立方米天然气．根据题意得 2.28×350+2.5×（500﹣350）+3.9（x﹣500）=1563，即1173+3.9（x﹣500）=1563，移项，得3.9（x﹣500）=390．系数化1得x﹣500=100．移项，得x=600．答：小锋家2016年用了600立方米天然气．。

第五讲 基本盈亏问题1. 1. 老师拿来10个苹果，平均分给5个同学，每个人分几个呢？如果再来两个同学，还是每人分那么多，还差几个苹果呢？2. 2. 羊村村长给小羊们发青草丸子，每只羊分到的一样多，还剩下20个青草丸子。

后来又来了一只小羊，分给它同样多的丸子后，只剩下10个青草丸子了，请问每只小羊分到几个青草丸子？3．老师拿来一些苹果，分给5个同学，每个人分到的一样多，还剩下1个，如果又来1个同学，分给他同样多的苹果后，还差1个，那么每个同学分几个苹果呢？老师原来有几个苹果？4．老师拿来一些苹果，分给3个同学，每个人一样多，还剩下10个，又来了两个同学，分给他们同样多的苹果后，还剩下2个，每个同学分几个苹果呢？老师原来有几个苹果？例1老师拿来很多剪纸，分给5个同学，每人分到的一样多，还剩下22张，又来了两个同学，分给他们一样多的剪纸后，就只剩下6张了。

请问每个同学分几张剪纸？老师一共拿来了多少张剪纸？【练习】1.羊村村长给小羊们发青草丸子，每只羊分到的一样多，还剩下20个青草丸子。

后来又来了两只小羊，分给它同样多的丸子后，只剩下10个青草丸子了，请问每只小羊分到几个青草丸子？2.乐乐准备了一些棒棒糖发给班里的同学，开始发给7个同学，还剩下14根。

后来又来了3名同学，发给他们同样多的棒棒糖后，就只剩下5根了。

请问每个同学发几根棒棒糖？乐乐开始一共准备了多少根棒棒糖？3.老师给同学们发作业本，每个人发同样多的作业本后，还剩下20本。

后来给新来的2个同学也发了同样多的作业本，就只剩下12本，请问每个同学发几本？剩下的作业本还能发给几个同学？例2裁缝要往一些西服上缝扣子，如果每件西服缝3个扣子的，还会剩下26个扣子；如果每件缝5个，就只剩下4个扣子了。

请问：裁缝一共有多少个扣子？几件西服？【练习】1.把一些桃子分给猴子们，如果每只猴子分5个，那么还剩下12个桃子；如果每只猴子分8个，就只剩下3个桃子了，问有多少只猴子？有多少个桃子？2.某车队买回来一些新轮胎，要是把每辆车的2个前胎全部换掉，还能剩下20个轮胎；要是把每辆车的4个轮胎全部换掉，就只剩下6个轮胎了。

第五讲和差问题课前复习1.二(1)班有学生52人，二(2)班有学生48人，要使这两个班学生人数一样多，应该从二(1)班中调几个学生到二（2）班？【答案】二(1)班比二(2)班多几人?52-48=4(人)二(1)班调几人到二(2)班，使两班人数相等?4÷2=2(人)答：应该从二(1)班调2人到二(2)班，两个班学生人数才会一样多.2. 小华比小荣多12张画片，要使两人的画片一样多，小华应给小荣几张画片?【答案】12÷2=6（张），小华应给小荣6张画片.我们先来认识一下和差问题：甲乙两数的和是16，差是2，求甲乙两数各是多少?类似这样的问题，就叫做和差问题.搞清楚两个数的和与差是解决和差问题的关键，在解题过程中，有些题目往往不直接告诉我们这两个数的和或差.当我们熟悉了和差问题的特点和解法后，应当有意识地把题目中的数量关系，转化为直接已知的两个量的和与差.解题的基本公式是：(两数的和一两数的差)÷2=较小的数较小的数+两数的差=较大的数(两数的和+两数的差)÷2=较大的数较大的数一两数的差=较小的数解答完后，将得到的结果放回原题中，看是否符合题意，你就清楚自己做得对不对了.实践应用【例1】二年级一班和二班共有85人，一班比二班多3人.问一班、二班各有多少人?【分析】本题是和差问题的基本题型，已知两个数的和与两个数的差，然后求大小两个数各是多少.和差问题一般可以借助线段图来进行分析.方法一：一班人数：(85+3)÷2=44(人) ，二班人数：44-3=41（人）方法二：二班人数：(85-3)÷2=41(人) ，一班人数：41+3=44（人）【例2】王大伯家养的白兔和黑兔一共有22只，如果再买4只白兔，白兔和黑兔的只数一样多.王大伯家养的白兔和黑兔各多少只?方法一：黑兔有多少只?(22+4)÷2=13(只)白兔有多少只?22-13=9(只) 或 13-4=9(只)方法二：白兔有多少只?(22-4)÷2=9(只)黑兔有多少只?22-9=13(只) 或9+4=13(只)答：白兔有9只，黑兔有13只.【例3】图书馆的书架上、下两层共存书220本，如果从上层拿出10本放人下层，则两层书架上书数相等.求原来上、下层各存书多少本?【分析】根据从上层拿出10本放入下层后两层书架上的书同样多，可以知道上层书架上的书比下层书架上的书多2个10本，如果从上层书架中减去10×2=20(本)，就和下层书架上的书同样多，那么上、下两层书架上书的总数减少了20本，这时上、下两层书架上的书的总数就相当于下层书架上书的2倍.方法一：下层：(220-20)÷2=100(本) 上层： 220-100=120(本)方法二：上层；（220+20）÷2=120（本）下层：220-120=100（本）拓展训练1、陈红和李玲平均身高为130厘米，陈红比李玲高8厘米，陈红和李玲身高各是多少厘米?【分析】陈红和李玲平均身高为130厘米，她们身高的和为：130×2=260(厘米)方法一：陈红：(260+8)÷2 =134(厘米) 李玲：134-8=126(厘米)方法二：李玲：（260-8）÷2 =126(厘米) 陈红：126+8=134（厘米）2、二(1)班平均分成两组做游戏，如果从第一组调3人到第二组，两组的人数同样多，都是12人，原来两组各有多少人?【分析】二(1)班一共有学生12×2=24（人），如果从第一组调3人到第二组，两组的人数同样多，那么可以看出第一组比第二组多3×2=6（人），分析到这里就是一道典型的和差应用题了.方法一：一组：（24+6）÷2=15（人）二组：15-6=9（人）方法二：一组：（24-6）÷2=9（人）二组：24-9=15（人）【例4】长方形操场的长与宽相差80米，沿操场跑一周是400米，求这个操场的长与宽是多少米？【分析】一周有两个长和两个宽，由条件可知长与宽的和为400÷2=200(米)长是(200+80)÷2=140(米) 宽是(200-80)÷2=60(米)拓展训练甲、乙两人同时打字，2分钟共打了240个字，已知甲每分钟比乙多打10个字.问甲、乙两人每分钟各打多少个?【分析】2分钟共打了240个字，那么甲、乙两人一分钟就打了240÷2=120（个）.方法一：甲(240÷2+10)÷2=65(个) 乙 65-10=55(个)方法二：乙(240÷2-10)÷2=55(个) 甲 55+10=65（个）【例5】有大、小两个油桶，一共装油24千克，两个油桶都倒出同样多的油后分别还剩9千克和5千克.问：原来大、小两个油桶各装油多少千克?【分析】两个油桶都倒出同样多的油后分别还剩9千克和5千克，那么也就是说大桶比小桶多4千克的油，知道这两桶油的和，又找到了这两桶油的差，这道题就变成了典型的和差问题的应用题了.方法一：大桶：（24+4）÷2=14（千克）小桶：14-4=10（千克）方法二：小桶：（24-4）÷2=10（千克）大桶：10+4=14（千克）【例6】甲、乙两筐苹果，甲筐比乙筐多19千克，从甲筐取出多少千克放入乙筐，就可以使乙筐中的苹果比甲筐的多3千克?【分析】如果把初始状态中乙筐的苹果看作0千克，那么甲筐相当于有19千克苹果．同时相当于甲、乙两筐共有苹果19千克．重新取放后问题可改变为：甲、乙两筐共有苹果19千克，其中乙筐中的苹果比甲筐的多3千克，求乙筐中有苹果多少千克．解：根据分析，从甲筐中取出苹果：(19+3)÷2=11(千克)．【例7】甲、乙两校共有学生1262人，部分学生因搬家需要转学，已知由甲校转入乙校25人，这样甲校比乙校还多12人，求两校原来有学生多少人?【分析】由甲校转入乙校25人，这样甲校比乙校还多12人，实际上甲校比乙校多25×2+12=62(人)，乙：(1262-62)÷2=600(人) 甲：1262-600=662(人)解答和差应用题，首先要弄清两个数相差多少的不同叙述方式．有些题目明确给了两个数的差，而有些应用题把两个数的差“暗藏”起来，我们管暗藏的差叫“暗差”．本题就是经过转换变形后，成为一个基本的和差问题．拓展训练小华和小敏共有铅笔25枝，如果小华用去4枝，小敏用去3枝，那么小华还比小敏多2枝，小华和小敏原来各有多少枝铅笔？【分析】如果小华用去4枝，小敏用去3枝，那么小华还比小敏多2枝，这就说明原来小华的铅笔比小敏的铅笔多3枝.找到了这个暗差，这道题就简单了.方法一：小华：（25+3）÷2=14（枝）小敏：14-3=11（枝）方法二：小敏：（25-3）÷2=11（枝）小华：11+3=14（枝）【例8】有三块布料一共190米，第二块比第一块长20米，第三块比第二块长30米.每块布料各长多少米?【分析】先画线段图从线段图可以看出，以第一块为标准，第二块减少20(米)，第三块减少20+30=50(米)，总和减少20+50=70(米)，即190-70=120 (米).120米相当于第一块布料长的3倍，求出第一块布料的长度，第二块、第三块就可以求出.解(1)第一块布料长度的3倍是：190-(20+20+30)=120(米)(2)第一块布料的长度是：120÷3=40(米)(3)第二块布料的长度是： 40+20=60(米)(4)第三块布料的长度是： 60+30=90(米)【例9】有一个盒子里装满了球，第一次拿出1只，第二次比第一次多拿了2只，第三次比第二次多拿了2只……8次刚好拿完.这盒球共有多少只?【分析】第一次拿1只，第二次拿(1+2)只，比第一次多1个2，第三次拿(1+2+2)只，比第一次多2个2，第四次拿(1+2+2+2)只，比第一次多3个2，第八次拿(1+2+2+2+2+2+2+2)只，比第一次多7个2.解：8+2×(1+2+3+4+5+6+7)=8+2×28=8+56=64(只)答：这盒球一共有64只.知道两个数的和，以及它们的差，要求这两个数，这类和差问题的应用题可用下面的公式计算.(和+差)÷2=大数和-大数=数(和-差)÷2=小数和-小数=大数附加题（以下提供的内容，供老师参考使用）1.【例3】解答后，可将条件改为：如果从上层拿出10本放入下层后，上层比下层还多6本.问题不变.一方面是【例3】的扩展题，另一方面为【例6】的解题思路作铺垫.10×2+6=26（本）(220-26)÷2=97(本) 上层 220-97=123(本)2. 两个连续奇数的和是36，这两个数分别是多少?【分析】两个连续奇数的差是2.较小数：(36-2)÷2=17 较大数：36-17=193.某一服装厂做童装，甲乙两人共做36件，乙丙两人共做34件，甲丙两人共做38件.三人各做多少件? 评注：本题的最佳解法为解法一.【分析】：此题关键在于转化为求两个数的和与差.因此，解法较多.解法一：甲乙36件，乙丙34件，甲丙38件，共36+34+38=108(件)这正好是甲乙丙和的2倍.因此，甲乙丙和108÷2=54(件)甲：54-34=20(件) 乙：54-38=16(件) 丙：54-36=18(件)解法二：甲和丙同样与乙相加，结果甲乙和是36件，乙丙和是34件，说明甲比丙多36-34=2(件)，又知甲丙的和是38件，所以，甲：(38+2)÷2=20(件) 乙：36-20=16(件) 丙：38-20=18(件)解法三：甲乙36件加上乙丙34件，就是甲丙与乙的2倍的和，减去甲丙38件，剩下就是乙的2倍乙：(36+34-38)÷2 =32÷2=16(件) 甲：36-16=20(件) 丙：38-20=18(件)练习五1.果园共260棵桃树和梨树，其中桃树的棵数比梨树多20棵.桃树和梨树各有多少棵?【答案】方法一：桃树：（260+20）÷2=140（棵）梨树：140-20=120（棵）方法二：梨树：（260-20）÷2=120（棵）桃树：120+20=140（棵）答：桃树有140棵，梨树有120棵.2．小华和小林一起做花，小华把自己做的花送给小林5朵，两人做的花的朵数一样多，这时小林有12朵花，原来小华做了几朵花?【答案】一共的花：12×2=24（朵），小华比小林多5×2=10（朵）方法一：小华：（24+10）÷2=17（朵）小林：17-10=7（朵）方法二：小林：（24-10）÷2=7（朵）小华：7+10=17（朵）答：原来小华做了17朵花.3. 甲乙两个仓库共存大米56包，从第乙仓库调8包到甲仓库，两个仓库大米的包数就同样多了，甲、乙两个仓库原有大米各多少包?【答案】乙比甲多8×2=16（包）甲：（56-16）÷2=20（包）乙：56-20=16（包）答：甲仓库有大米20包，乙仓库有大米16包.4．书架上有故事书45本，比连环画少10本，科技书比连环画多10本，问：故事书多，还是科技书多?多几本?【答案】科技书多，多10+10=20（本）5．有一根钢管长12米，要锯成两段，使第一段比第二段短2米.每段各长多少米?【答案】第一段：(12-2)÷2=5(米) 第二段：12-5=7(米)答：第一段长5米，第二段长7米.6. 兄弟俩现在年龄和是28岁，3年前哥哥比弟弟大2岁，兄弟俩现在各多少岁?【答案】3年前哥哥比弟弟大2岁，现在哥哥仍比弟弟大2岁，他们的年龄差不变.哥哥：(28+2)÷2=15(岁) 弟弟：28-15=13(岁)答：哥哥现在15岁，弟弟现在13岁.数学故事报效祖国宏愿------ 华罗庚的故事同学们都知道，华罗庚是一位靠自学成才的世界一流的数学家.他仅有初中文凭，因一篇论文在《科学》杂志上发表，得到数学家熊庆来的赏识，从此华罗庚北上清华园，开始了他的数学生涯.1936年，经熊庆来教授推荐，华罗庚前往英国，留学剑桥.20世纪声名显赫的数学家哈代，早就听说华罗庚很有才气，他说：“你可以在两年之内获得博士学位.”可是华罗庚却说：“我不想获得博士学位，我只要求做一个访问者.”“我来剑桥是求学问的，不是为了学位.”两年中，他集中精力研究堆垒素数论，并就华林问题、他利问题、奇数哥德巴赫问题发表18篇论文，得出了著名的“华氏定理”，向全世界显示了中国数学家出众的智慧与能力.1946年，华罗庚应邀去美国讲学，并被伊利诺大学高薪聘为终身教授，他的家属也随同到美国定居，有洋房和汽车，生活十分优裕.当时，不少人认为华罗庚是不会回来了.新中国的诞生，牵动着热爱祖国的华罗庚的心.1950年，他毅然放弃在美国的优裕生活，回到了祖国，而且还给留美的中国学生写了一封公开信，动员大家回国参加社会主义建设.他在信中袒露出了一颗爱中华的赤子之心：“朋友们！梁园虽好，非久居之乡.归去来兮……为了国家民族，我们应当回去……”虽然数学没有国界，但数学家却有自己的祖国.华罗庚从海外归来，受到党和人民的热烈欢迎，他回到清华园，被委任为数学系主任，不久又被任命为中国科学院数学研究所所长.从此，开始了他数学研究真正的黄金时期.他不但连续做出了令世界瞩目的突出成绩，同时满腔热情地关心、培养了一大批数学人才.为摘取数学王冠上的明珠，为应用数学研究、试验和推广，他倾注了大量心血.据不完全统计，数十年间，华罗庚共发表了152篇重要的数学论文，出版了9部数学著作、11本数学科普著作.他还被选为科学院的国外院士和第三世界科学家的院士.从初中毕业到人民数学家，华罗庚走过了一条曲折而辉煌的人生道路，为祖国争得了极大的荣誉.。

第五讲文学常识、修辞、语法、标点符号解析卷1．（2024年广东省深圳市中考语文真题）请选出下列说法正确的一项（）A. “白发三千丈”和“黄河之水天上来”这两句诗运用了夸张的修辞手法。

B. “市民可以在手机上申请车牌摇号。

”这句话的主干是“手机申请摇号”。

C. 关联词考察：“即使……但”（原题未全）。

D. 《史记》中“世家”是用来记述平民的，陈涉出身农夫，所以记录在世家中。

【答案】A【解析】试题分析：B主干应为“市民申请摇号”；C项关联词语没有成套的运用。

改为“即使……也”或“虽然……但”。

D“世家”主要是诸侯传记，不是平民。

2.（2024年广东省深圳市中考语文真题）请选出下列说法错误的一项（）A. “荡胸生层云，决眦入归鸟”这句诗运用了对偶的修辞手法。

B. 《小石潭记》的作者是唐代的韩愈，“唐宋八大家”之一。

C. “必需说碧绿的菜畦，光滑的石井栏，高大的皂荚树……”句中的划线词都是形容词。

D. “不但……还……”这是一个递进关系的复句。

【答案】B【解析】试题分析：本题是一道基础学问综合题，考查了修辞手法、课文学问背景、词性、复句的学问。

B项中《小石潭记》是八年级下册的课文，作者是柳宗元，初中阶段语文教材中选用的韩愈的古文只有一篇《马说》。

3.（2024年广东省深圳市中考语文真题）请选出下列说法中有误的一项 ( )A.《儒林外史》是我国清代一部长篇讽刺小说，它的作者是吴敬梓。

B.阅读新闻，要留意它结构上的五个部分，即标题、导语、主体、背景、结语。

C.“苇子还是那么狠狠地往上钻，目标似乎就是天上。

”这句话运用了比方的修辞方法。

D.“在海外生活了八、九年的杨先生最终确定回国创业。

“这句话中顿号的运用是不正确的。

【答案】C【解析】 C项没有运用比方的修辞手法。

4.（2024年广东省深圳市中考语文真题）请选出下列说法正确的一项（）（2分）A．“花朵儿一串挨着一串，一朵接着一朵，彼此推着挤着，好不活泼喧闹。

第五讲差倍问题
一、同步测试题
1、四年（1）班参加合唱团的同学比四年（2）班多16人，四年（1）班合唱团的人生是四年2 班的3倍，四年2班有（）人参加合唱团？
2、有2袋大米，大袋比小袋多56千克，如果将小袋的大米吃掉4千克，这时大袋的大米刚好是小袋的4倍，这时小袋大米重（）千克
3、牧场里羊的数量是牛的5倍。

后来买出去羊200只，这是羊和牛的数量一样多，牧场有牛（）多少只。

4、小红有存款600元。

小张有存款400元，两人取出同样多的钱后，小红的存款是小张的3倍，那么小张还剩下（）钱
5甲乙两个仓库存有同样多的花生，甲仓库运出120吨后，而乙仓库存入60吨后，这时乙仓库正好是甲仓库的3倍，甲仓库原理存有（）吨花生。

课后练习题
1、一头牛的重量比一只羊重450千克，牛的重量正好是羊的10倍，那么这只羊有（）
千克
2、一头牛的重量比一匹马重240千克，牛的重量比马的2倍还多20千克，那么这匹马有（）千克
3图书柜中的故事书比文艺书多136本，如果故事书被借走16本，这时故事书是文艺书的5倍，那么图书柜中有文艺书（）本
4、两框梨的重量相等，如果从甲中拿出30千克放入乙中，那么乙的重量是甲的3倍，乙框中原来有梨（）千克。

5、便利店进了同样多的可乐和矿泉水，矿泉水买了180瓶，可乐买了100瓶后，剩下的可乐是矿泉水的5倍，便利店原来进了（）瓶矿泉水。

第五讲奇偶性分析例1．能从右表中选出5个数，使它们的和等于35吗？为什么？例2．从起点起，每隔1米种一棵树。

如果把3块“爱护树木”的小牌分别挂在三棵树上，那么不管怎样挂，至少有两棵挂牌的树，它们之间的距离数是偶然（以米为单位）。

这是为什么？例3某班同学参加学校的数学竞赛。

试题共50题。

评分标准是：答对一道给3分，不答给一分，答错倒扣1分。

请你说明该班同学得分总和一定是偶数。

例4．33个小朋友做游戏，每一次均有8个小朋友向后转，问能不能经过这样若干次的向后转，使所有的小朋友全部转过身去？例5．红、黄、篮三种色笔都有很多，混在一起合成大堆，最少要分成多少堆，才能保证找得到这样的两堆，把这两堆合并后这三种色笔的支数都是偶数。

例6．有一批文章共15篇，各篇文章的页数分别是非曲直页、2页、3页、……、14页和15页的稿纸，如果将这些文章按某种次序装订成册，并统一编上号码，那么每篇文章的第一页是奇数页码的文章最多有几页？例7．教室里有7排椅子，每排7张，每张椅子上坐着一个学生，如果一周后，每个学生都必须和他相邻（前、后、左、右）的某一个同学交换座位，问能不能换成？第五讲 奇偶性分析练习 姓名_____________ 2011.7.81．能从右表中选出5个数，使它们的和等于30吗？为什么？2．1+2+3+4++……+2000+2001+2002的和是奇数还是偶数？3．()()()()()22222222222002200120012000433221++++++++++ 的和是奇数还是偶数？4．小华买一本共96页的练习本，并并依次将每张纸的正反面编上号（即从第一页一直编到192页），小丽从这本练习本中撕下25张纸，并将写在纸上的50个编号相加。

试问：小丽所得的和数能不能为1996？5．如下图，从0点起每隔3米种一棵树。

如果把3块“爱护树木”的小林牌分别挂在3棵树上，那么不管怎样挂，至少有两棵挂牌的树之间的距离是偶然（以米为单位）。