九年级开学测试题

黑龙江省哈尔滨市虹桥初级中学校2024-2025学年九年级上学期开学测试数学试题一、单选题1．-2的倒数是（ ）A ．-2B ．12-C ．12 D ．22．下列方程是关于x 的一元二次方程的是（ ）A ．2210x y ++=B ．2112x x +=C ．20ax bx c ++=D ．23(1)2(1)x x +=+3．下列计算不正确的是（ ）A ．()339a a =B ．()362n n a a =C ．()2122n n x x ++=D ．326x x x ⋅= 4．下列图形中，是轴对称图形的是（ ）A ．B ．C ．D ． 5．一元二次方程x 2+2x+1=0的根的情况（ ）A ．有一个实数根B ．有两个相等的实数根C ．有两个不相等的实数根D ．没有实数根 6．顺次连接矩形四边中点所得的四边形一定是（ ）A ．正方形B ．矩形C ．菱形D ．等腰梯形 7．如图AD CD ⊥，AB 13=，BC 12=，CD 3=，AD 4=，则sinB ?=（ ）A ．5 13B ．1213 C ．35 D ．458．若一次函数=y ax b +的图象经过第一、二、四象限，则下列不等式一定成立的是（ ）A ．0a b +<B ．0a b ->C ．0ab >D ．0ba <9．如图，某数学兴趣小组测量一棵树CD 的高度，在点A 处测得树顶C 的仰角为45︒，在点B 处测得树顶C 的仰角为60︒，且A BD 、、三点在同一直线上，若()8AB =米，则这棵树CD 的高度是（ ）A ．B ．C ．D ．10．如图，四边形ABCD 是平行四边形，点E 在CD 边上，则下列结论错误的是（ ）A ．AF BF FE FD =B ．DE DF AB BD =C ．AF BF AE BD = D ．DE EF DC AF=二、填空题11．将数字307000用科学记数法表示为．12．在函数324x y x +=-中，自变量x 的取值范围是. 13．把多项式39x x -因式分解的结果是.14．不等式组20210x x ->⎧⎨+>⎩的解集是． 15．直线132y x =-向上平移3个单位后，所得直线的解析式为．16．某商品经过两次连续的降价，由原来的每件250元降为每件160元，则该商品平均每次降价的百分率为.17．如图，DE 为△ABC 的中位线，点F 在DE 上，且∠AFB ＝90°，若AB ＝10，BC ＝16，则EF 的长为.18．已知平行四边形ABCD 中，15AB =，13AC =，AE 为BC 边上的高，且12AE =，则平行四边形ABCD 的面积为．19．阅读材料：整体代值是数学中常用的方法．例如“已知23a b -=，求代数式631a b --的值．”可以这样解：()6313213318a b a b --=--=⨯-=．根据阅读材料，解决问题：若3x =是关于x 的一元一次方程2mx n +=的解，则代数式2296621m mn n m n ++++-的值是20．如图四边形,,ABCD AD AB BC ==30,ACD ︒∠=cos BAC ∠=2CD =，则AC =．三、解答题21．先化简，再求代数式2344111a a a a ++⎛⎫-÷ ⎪--⎝⎭的值，其中3tan304cos60a =-o o . 22．图1、图2分别是 8×10的网格，网格中的每个小正方形的边长均为1．请按要求画出下列图形，所画图形的各个顶点均在所给小正方形的顶点上．(1)在图1中画一个周长为(2)在图2 中画出有一个锐角为 45°，面积为9的平行四边形，并直接写出平行四边形的周长．23．为迎接2019年中考，某中学对全校九年级学生进行了一次数学期末模拟考试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成了如下两幅不完整的统计图，请你根据统计图中提供的信息解答下列问题：(1)这次调查共抽取了多少名同学？(2)将条形统计图补充完整；(3)若该中学九年级共有1000人参加了这次数学考试，估计该校九年级共有多少名学生的数学成绩可以达到优秀？24．已知矩形ABCD 的对角线,AC BD 相交于点O ，点E 是边AD 上一点，连接,,BE CE OE ，且BE CE =．(1)如图1，求证：BEO CEO △≌△；(2)如图2，设BE 与AC 相交于点F ，CE 与BD 相交于点H ，过点D 作AC 的平行线交BE 的延长线于点G ，在不添加任何辅助线的情况下，请直接写出图2中的四个三角形（AEF △除外），使写出的每个三角形的面积都与AEF △的面积相等．25．某粮食生产基地为了落实习近平总书记的重要讲话精神，积极扩大粮食生产规模，计划投入一笔资金购买甲、乙两种农机具，已知1件甲种农机具比1件乙种农机具多1万元，用15万元购买甲种农机具的数量和用10万元购买乙种农机具的数量相同．(1)求购买1件甲种农机具和1件乙种农机具各需多少万元？(2)若该粮食生产基地计划购买甲、乙两种农机具共20件，且购买的总费用不超过48万元，则甲种农机具最多能购买多少件26．如图，在ABC V 中，90ABC ∠=︒，()045ACB αα∠=︒<<︒．将线段CA 绕点C 顺时针旋转90︒得到线段CD ，过点D 作DE BC ⊥，垂足为E ．(1)如图1，求证：ABC CED ≅V V ．(2)如图2，ACD ∠的平分线与AB 的延长线相交于点F ，连接DF ，DF 的延长线与CB 的延长线相交于点P ，猜想PC 与PD 的数量关系，并加以证明．(3)如图3，在（2）的条件下，将BFP △沿AF 折叠，在α变化过程中，当点P 落在点E 的位置时，连接EF ．若20CD =，求CEF △的面积．27．如图1，在平面直角坐标系中AOB V 的顶点A 在x 轴负半轴上，点B 在y 轴正半轴上，1sin ,2BAO B ∠=点坐标(0,3)．(1)求直线AB 的解析式；(2)如图2，点P 从A 点出发沿射线AB 方向以每秒2个单位长度的速度运动，运动时间为t ，连接OP ．设BOP △的面积为S ，试用含t 的代数式表示S ．（不要求写出t 的取值范围）．(3)如图3，在（2）的条件下，当S =P 作PG x ⊥轴于点G ，连接BG ．E 为第一象限内一点，连接,PE BE 交PG 于点F ，点Q 在PE 的延长线上，GF GQ =，GQ BP ∥，在线段BF 上取点,M MG 交BQ 于点N ．当,3BM PE BQ BN ==时，求BPQ V 的面积和Q 点坐标．。

2024-2025学年黑龙江省哈尔滨市九年级上学期开学测试语文试题一、基础·运用(15分)阅读下面文字，回答1--4题。

通过上学期的学习，我们感受到了语文课本中的各种风采：在艺术方面，表演安塞腰鼓的后生们精彩绝伦的舞姿，展现了一种震 (hàn)人心的生命力，；在文学方面，庄子时常驰骋想象，遨游宇宙。

他想到北冥里的那尾叫“鲲”的大鱼，一夜之间，它化为鹏鸟，展翼高飞，；在革命方面，闻一多先生在李公朴先生追悼会上，面对敌人的卑鄙行为，他悲愤地痛斥台下那些企图狡(biàn)、挑(bō)离间的反动派特务，；在科研方面，丁壁中先生重视实验在科学中的重要性，发扬并继承了真正的格物 (zhì)知精神。

，成为名副其实的物理学大师。

1.(3分) 语段中加点字的注音不正确的一项是 )A. 驰骋(chěng)B. 卑鄙(bì)C. 悲愤(fèn)D. 名副(fù) 其实2.(3分) 括号处依次填入汉字书写正确的一项是 ( )A. 憾B. 辨C. 拔D. 致3.(3分) 文章划波浪线句有语病，下列选项修改正确的一项是( )A.把“发扬”和“继承“调换位置B.将“重视”改为“注重”C.把“科研方面”调至“丁肇中先生”后面D.将“真正”改为“纯粹”4.(3分) 填入文中横线处的语句，与上下文衔、恰当的一项是 ( )①他通过孜孜不倦的努力获得诺贝尔物理学奖②进行了一场激动人心的演讲③我们感受到磅礴的力量之美④于是他写下瑰丽之作——《逍遥游》A. ①②③④B. ③④②①C. ④③①②D. ②①③④5.(3分)新学期的号角已经吹响，你的朋友小明还沉浸在假期的轻松散漫中，为此，作为好友你应该如何规劝他及早收心，尽快加入到紧张忙碌的毕业班的学习生活中?下列表述最准确、最得体的一项是 ( )A. 小明，毕业学年是初中生活里最关键的一年，我们应该以学习为主，那些令人着迷的游戏和网络小视频可以放学以后再玩。

黑龙江省哈尔滨美佳外国语学校2024-2025学年九年级上学期开学测试数学试题一、单选题1．﹣5的绝对值是（ ） A ．5B ．﹣5C ．15-D ．152．下列计算正确的是（ ） A ．224426a a a += B ．5210a a a ⋅= C ．623a a a ÷=D ．()224a a -=3．下列四种化学仪器的示意图中，是轴对称图形的是（ ）A ．B ．C ．D ．4．已知点()3,2-在反比例函数()0ky k x=≠的图象上，则k 的值为（ ） A ．3-B ．3C ． 6-D ．65．二次函数22(1)3y x =--+的顶点坐标是（ ） A ．(1,3)-B ．(1,3)C ．(0,1)D ．(0,3)6．一种药品原价每盒48元，经过两次降价后每盒27元，两次降价的百分率相同，则每次降价的百分率为（ ） A ．20%B ．22%C ．25%D ．28%7．如图，在平行四边形ABCD 中，EF AB P ，:2:3DE AE =，BD 的长为5，则BF 的长为（ ）A ．2B ．3C ．52D ．48．通过平移2y x =-的图象，可得到2(1)2y x =-+-的图象，下列平移方法正确的是（ ） A ．向左移动1个单位，向上移动2个单位 B ．向右移动1个单位，向上移动2个单位C ．向左移动1个单位，向下移动2个单位D ．向右移动1个单位，向下移动2个单位9．定义一种新的运算：如果0a ≠，则有2a b a b =+▲，那么722⎛⎫- ⎪⎝⎭▲的值（ ）A ．34B ．32- C ．152 D ．1210．在矩形ABCD 中，4AB =，3BC =，动点P 从D 出发（不与点D 重合），向点C 运动，连接AP 交射线BC 于点Q ，若D P x =，BQ y =，则在下面函数图象中，大致能反映y 与x 之间函数关系的是（ ）A ．B ．C ．D ．二、填空题11．中国的领水面积约为370 000 km 2，将数370 000用科学记数法表示为：．12．若式子13x -有意义，则实数x 的取值范围是．13=． 14．因式分解：394a a -=． 15．不等式组2130x x ≤⎧⎨+>⎩的解集为．16．如图，是二次函数2y ax bx c =++图象的一部分，其对称轴为直线1x =，若与x 轴的其中一个交点为(3,0)A ，则由图象可知，与x 轴的另一个交点坐标是．17．如图，A ，B 是双曲线(0)ky x x=>上的两点，连接OA ，.OB 过点A 作AC x ⊥轴于点C ，交OB 于点.D 若D 为AC 的中点，AOD △的面积为3，点B 的坐标为(),2m ，则m 的值为．18．如图是由一些同样大小的三角形按照一定规律所组成的图形，第1个图有4个三角形，第2个图有7个三角形，第3个图有10个三角形…按照此规律排列下去，第23个图中三角形的个数是．19．矩形ABCD 中，对角线交于点O ，点E 在对角线BD 上，若6AB =，BC =，2OE =，则AE 的长度为．20．如图，四边形ABCD ，连接对角线AC 、BD ，=90ACD ∠︒，且AC CD =，若90ABC ∠=︒，1AB =，5BD =，则AD 的长为．三、解答题21．先化简，再求值231122x x x -⎛⎫-÷⎪++⎝⎭的值，其中1x =． 22．图a 、图b 是两张形状、大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，点A 、B 在小正方形的顶点上．(1)在图a 中画出ABC V （点C 在小正方形的顶点上），使ABC V 为轴对称图形；(2)在图b 中画出四边形ABDE （点D 、E 都在小正方形的顶点上），使四边形ABDE 为轴对称图形且面积为4．23．某校为丰富学生的课余生活，开展了多姿多彩的体育活动，开设了五种球类运动项目：A 篮球，B 足球，C 排球，D 羽毛球，E 乒乓球．为了解学生最喜欢以上哪种球类运动项目，随机抽取部分学生进行调查（每位学生仅选一种），并绘制了统计图．某同学不小心将图中部分数据丢失，请结合统计图，完成下列问题：(1)本次调查的样本容量是______，扇形统计图中D 对应圆心角的度数为______︒； (2)请通过计算，补全条形统计图；(3)若该校共有2000名学生，请你估计该校最喜欢“E 乒乓球”的学生人数． 24．如图，四边形ABCD 是菱形，点E 在BD 延长线上，ADB BCE ∠=∠．(1)求证：BCD BEC ∽△△．(2)当6,4BC BD ==时，求DE 的长．25．为推进“书香社区”建设，某社区计划购进一批图书．已知购买2本科技类图书和3本文学类图书需156元，购买4本科技类图书和5本文学类图书需284元． (1)每本科技类图书与每本文学类图书的价格分别为多少元?(2)社区计划购进科技类图书和文学类图书共60本，且总费用不超过2000元，那么最多购进科技类图书多少本26．已知，在正方形ABCD 中，点E 、F 分别在边CD 和AD 上，连接AE 、BF 交于点G ，AF DE =．(1)如图1，求证：90AGF ∠=︒；(2)如图2，若点E 为CD 的中点，求证：2AG GF =；(3)如图3，在（2）的条件下，连接BD 交AE 于点H ，BGE ∠的平分线交BD 于点M ，过点M 作MN AE ∥交CD 于点N ，若6AB =，求MN 的长．27．在平面直角坐标系中，O 为坐标原点，抛物线22y ax bx =++分别交x 轴于(1,0)A -、(4,0)B 两点，交y 轴于点C ．(1)如图1，求抛物线的解析式；(2)如图2，点P 为第四象限抛物线上一点，连接AP 、BP ，设点P 的横坐标为t ，ABP V 的面积为S ，求S 与t 的函数关系式（不要求写出自变量t 的取值范围）； (3)如图3，在（2）的条件下，当252S =时，Q 为抛物线第三象限上一点，连接PQ 、AC 、BC ，若2ACB APQ ∠=∠，求点Q 的横坐标．。

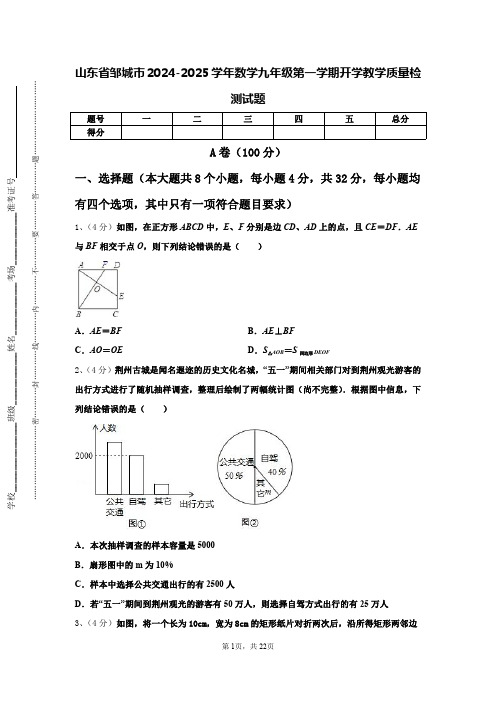
山东省邹城市2024-2025学年数学九年级第一学期开学教学质量检测试题题号一二三四五总分得分A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）如图，在正方形ABCD 中，E 、F 分别是边CD 、AD 上的点，且CE ＝DF ．AE 与BF 相交于点O ，则下列结论错误的是（）A ．AE ＝BF B ．AE ⊥BF C ．AO ＝OE D ．S △AOB ＝S 四边形DEOF 2、（4分）荆州古城是闻名遐迩的历史文化名城，“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查，整理后绘制了两幅统计图（尚不完整）．根据图中信息，下列结论错误的是（）A ．本次抽样调查的样本容量是5000B ．扇形图中的m 为10%C ．样本中选择公共交通出行的有2500人D ．若“五一”期间到荆州观光的游客有50万人，则选择自驾方式出行的有25万人3、（4分）如图，将一个长为10cm，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（）．A ．210cm B ．220cm C ．240cm D ．280cm 4、（4分）二次根式中字母x 的取值范围是（）A ．x≠﹣3B ．x≥﹣3C ．x ＞﹣3D ．全体实数5、（4分）如图，将边长为8㎝的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ，则线段CN 的长是（）A ．3cm B ．4cm C ．5cm D ．6cm 6、（4分）如图，已知四边形ABCD 是平行四边形，下列结论中不正确．．．的是（）．A ．当AB ＝BC 时，它是菱形B ．当AC ＝BD 时，它是正方形C ．当∠ABC ＝90º时，它是矩形D ．当AC ⊥BD 时，它是菱形7、（4分）已知M 、N 是线段AB 上的两点，AM ＝MN ＝2，NB ＝1，以点A 为圆心，AN 长为半径画弧；再以点B 为圆心，BM 长为半径画弧，两弧交于点C ，连接AC ，BC ，则△ABC 一定是()A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形8、（4分）下列说法正确的是（）A ．410x +=是二项方程B ．22x y y -=是二元二次方程C ．132x x -=是分式方程D 210-=是无理方程二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）甲、乙两人进行射击比赛，在相同条件下各射击12次，他们的平均成绩各为8环，12次射击成绩的方差分别是：S 甲＝3，S 乙＝2.5，成绩较为稳定的是__________．（填“甲”或“乙”）10、（4分）如图，平行四边形ABCD 的对角线AC ，BD 交于O ，EF 过点O 与AD ，BC 分别交于E ，F ，若AB ＝4，BC ＝5，OE ＝1.5，则四边形EFCD 的周长_____．11、（4分）如图，直线AB 与反比例函数()4 0y x x ＝＞的图象交于点A(u ，p)和点B(v ，q)，与x 轴交于点C ，已知∠ACO=45°，若13＜u ＜2，则v 的取值范围是__________．12、（4分）如图，50ABC AD ∠=，垂直平分线段BC 于点D ABC ∠，的平分线BE 交AD于点E ，连结EC ，则∠AEC 的度数是．13、（4分）分解因式：m 2-9m=______．三、解答题（本大题共5个小题，共48分）14、（12分）为了对某市区全民阅读状况进行调查和评估，有关部门随机抽取了部分市民进行每天阅读时间情况的调查，并根据调查结果制做了如下尚不完整的频数分布表（被调查者每天的阅读时间均在0﹣120分钟之内）阅读时间x （分钟）0≤x ＜3030≤x ＜6060≤x ＜9090≤x ≤120频数450400m 50频率0.450.40.1n （1）被调查的市民人数为多少，表格中，m ，n 为多少；（2）补全频数分布直方图；（3）某市区目前的常住人口约有118万人，请估计该市区每天阅读时间在60～120分钟的市民大约有多少万人？15、（8分）在平行四边形ABCD 中，C ∠和D ∠的平分线交于,M DM 的延长线交AD 于E ，是猜想：（1）CM 与DE 的位置关系？（2）M 在DE 的什么位置上？并证明你的猜想.（3）若24,5DE CM ==，则点M 到BC 距离是多少？16、（8分）（1）解不等式组：32112(1)2x x x x +>+⎧⎪⎨+<-⎪⎩①②（2）化简：252111a a a a a a -⎛⎫-⋅ ⎪+-⎝⎭．17、（10分）已知：△AOB 和△COD 均为等腰直角三角形，∠AOB =∠COD =90°．连接AD ，BC ，点H 为BC 中点，连接OH ．（1）如图1所示，求证：1 OH AD 2=且OH AD ⊥（2）将△COD 绕点O 旋转到图2、图3所示位置时，线段OH 与AD 又有怎样的关系，并选择一个图形证明你的结论18、（10分）解方程：(1)x 2+2x =0(2)x 2-4x-7=0.B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）某n 边形的每个外角都等于它相邻内角的14，则n ＝_____．20、（4分）如果点A (1，n )在一次函数y ＝3x ﹣2的图象上，那么n ＝_____．21、（4分）如图,菱形ABCD 的对角线AC 、BD 相交于点O,E 、F 分别是AB 、BC 边的中点,连接EF,若,BD=4,则菱形ABCD 的边长为__________.22、（4分）已知直线y kx b =+经过点（－2，2），并且与直线21y x =+平行，那么b =________.23、（4分）在一频数分布直方图中共有9个小长方形，已知中间一个长方形的高等于其它8个小长方形的高的和的17，且这组数据的总个数为120，则中间一组的频数为_______．二、解答题（本大题共3个小题，共30分）24、（8分）已知关于x 的一元二次方程x 1﹣3x+k ＝0方程有两实根x 1和x 1．(1)求实数k 的取值范围；(1)当x 1和x 1是一个矩形两邻边的长且矩形的对角线长为k 的值．25、（10分）益群精品店以转件21元的价格购进一批商品，该商品可以白行定价，若每件商B 品位价a 元，可卖出（350-10a ）件，但物价局限定每件商品的利润率不得超过20%，商店计划要盈利400元，求每件商品应定价多少元？26、（12分）（1）在图中以正方形的格点为顶点，画一个三角形，、；（2）求此三角形的面积及最长边上的高.参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、C 【解析】试题解析：A 、∵在正方形ABCD 中，AB BC CD AD ∴===，又CE DF ，=AF DE ∴=，90D BAF ∠=∠=︒，∴BAF ≌ADE ，AE BF ，∴=故此选项正确；B 、∵BAF ≌ADE ，BFA AED ∴∠=∠，90AED EAD ∠+∠=︒，90BFA EAD ∴∠+∠=︒，90AOF ∴∠=︒，AE BF ∴⊥，故此选项正确；C 、连接BE ，假设AO=OE ，BF AE ，⊥∴90AOB BOE ∠=∠=︒，BO BO =，∴ABO ≌EBO ，AB BE ∴=，又AB BC ，=BC BE <，∴AB 不可能等于BE ，∴假设AO OE =不成立，即AO OE ≠，故此选项错误；D 、∵BAF ≌ADE ， BAF ADE S S ∴=， ,BAF AOF ADE AOF S S S S ∴-=-∴S △AOB =S 四边形DEOF ，故此选项正确．故选C ．2、D 【解析】【分析】结合条形图和扇形图，求出样本人数，进而进行解答．【详解】A 、本次抽样调查的样本容量是200040%=5000，正确；B 、扇形图中的m 为10%，正确；C 、样本中选择公共交通出行的有5000×50%=2500人，正确；D 、若“五一”期间到荆州观光的游客有50万人，则选择自驾方式出行的有50×40%=20万人，错误，故选D ．【点睛】本题考查了条形统计图、扇形统计图，熟悉样本、用样本估计总体等知识是解题的关键，另外注意学会分析图表．3、A 【解析】根据题意可得菱形的两对角线长分别为4cm ，5cm ，根据面积公式求出菱形的面积．【详解】由题意知，AC 的一半为2cm ，BD 的一半为2.5cm ，则AC=4cm ，BD=5cm ，∴菱形的面积为4×5÷2=10cm²．故选A ．本题考查了菱形的性质，解题的关键是掌握对角线平分且垂直的菱形的面积等于对角线积的一半．4、D【解析】根据任何实数的平方是非负数，可得答案．【详解】二次根式中字母x的取值范围是x+3任意实数，x是任意实数.故选：D.此题考查二次根式有意义的条件，解题关键在于掌握其定义.5、A【解析】分析：根据折叠的性质，只要求出DN就可以求出NE，在直角△CEN中，若设CN=x，则DN=NE=8﹣x，CE=4cm，根据勾股定理就可以列出方程，从而解出CN的长．详解：设CN=xcm，则DN=（8﹣x）cm，由折叠的性质知EN=DN=（8﹣x）cm，而EC=12BC=4cm，在Rt△ECN中，由勾股定理可知EN2=EC2+CN2，即（8﹣x）2=16+x2，整理得16x=48，所以x=1．故选：A．点睛：此题主要考查了折叠问题，明确折叠问题其实质是轴对称，对应线段相等，对应角相等，通常用勾股定理解决折叠问题．6、B【解析】分析：A、根据菱形的判定方法判断，B、根据正方形的判定方法判断，C、根据矩形的判定方法判断，D、根据菱形的判定方法判断.详解：A、菱形的判定定理，“一组邻边相等的平行四边形是菱形”，故A项正确；B、由正方形的判定定理，“对角线互相垂直且相等的平行四边形是正方形”可知，对角线仅相等的平行四边形是矩形，故B 项错误；C 、矩形的判定定理，“一个角是直角的平行四边形是矩形”，故C 项正确；D 、菱形的判定定理，“对角线互相垂直的平行四边形是菱形”，故D 项正确。

福建省2024年数学九上开学质量检测试题题号一二三四五总分得分A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）某校八（5）班为筹备班级端午节纪念爱国诗人屈原联谊会，班长对全班学生爱吃哪几种水果作了民意调查，最终决定买哪些水果．下面的调查数据中您认为最值得关注的是（）A ．中位数B ．平均数C ．众数D ．方差2、（4分）如图，△ABC 的周长为17，点D ,E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为点N ，∠ACB 的平分线垂直于AD ，垂足为点M ，若BC =6，则MN 的长度为（）A ．32B ．2C ．52D ．33、（4分）代数式2x ，3a b +，x+3y ，1x y -中分式有（）A ．1个B ．2个C ．3个D ．4个4、（4分）如图所示的四边形，与选项中的四边形一定相似的是（）A ．B ．C ．D ．5、（4分）在平面直角坐标系中，点M （﹣2，1）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6、（4分）一个正多边形每个外角都是30°，则这个多边形边数为（）A ．10B ．11C ．12D ．137、（4分）已知一组数据a .b .c 的平均数为5，方差为4，那么数据2a -，2b -，2c -的平均数和方差分别是（）A ．3，2B ．3，4C ．5，2D ．108、（4分）下列调查中，最适合采用抽样调查的是（）A ．对某地区现有的16名百岁以上老人睡眠时间的调查B ．对“神舟十一号”运载火箭发射前零部件质量情况的调查C ．对某校九年级三班学生视力情况的调查D ．对某市场上某一品牌电脑使用寿命的调查二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）甲、乙两人进行射击测试，每人10次射击成绩的平均数都是8.5环，方差分别是：S 甲2=2，S 乙2=1.5，则射击成绩较稳定的是（填“甲”或“乙“）．10、（4分）一次函数y=kx+b 的图象如图所示，若点A(3，m)在图象上，则m 的值是__________.11、（4分）定义运算“★”：对于任意实数,a b ，都有2a b a b =+å，如：224248=+=å．若(1)37x -=å，则实数x 的值是_____．12、（4分）勾股定理，是几何学中一颗光彩夺目的明珠，被称为“几何学的基石”．中国是发现和研究勾股定理最古老的国家之一．中国古代数学家称直角三角形为勾股形，较短的直角边称为勾，另一直角边称为股，斜边称为弦，所以勾股定理也称为勾股弦定理．三国时期吴国赵爽创制了“勾股圆方图”（如图）证明了勾股定理．在这幅“勾股圆方图”中，大正方形ABCD 是由4个全等的直角三角形再加上中间的那个小正方形EFGH 组成的．若小正方形的边长是1，每个直角三角形的短的直角边长是3，则大正方形ABCD 的面积是_____．13、（4分）．三、解答题（本大题共5个小题，共48分）14、（12分）（1）﹣3|+2sin45（﹣12）﹣1（2）（1122x x +-+）÷2244x x x -+15、（8分）在ABCD 中，60D ∠=︒，4AD DC ==，动点M 以每秒1个单位的速度从点A 出发运动到点B ，点N 以相同的速度从点B 出发运动到点C ，两点同时出发，过点M 作MP CD ⊥交直线CD 于点P ，连接NM 、NP ，设运动时间为t 秒.(1)当2t =和3t =时，请你分别在备用图1，备用图2中画出．．符合题意的图形；(2)当点P 在线段CD 上时，求t 为何值时，以A 、M 、C 、P 为顶点的四边形是平行四边形；(3)当点P 在线段DC 的延长线上时，是否存在某一时刻t 使90PMC ∠=︒，若存在，请求出t 的值；若不存在，请说明理由.16、（8分）如图，在△ABC 中，点D 是AB 的中点，点F 是BC 延长线上一点，连接DF ，交AC 于点E ，连接BE ，∠A=∠ABE ．（1）求证：DF 是线段AB 的垂直平分线；（2）当AB=AC ，∠A=46°时，求∠EBC 及∠F 的度数．17、（10分）为了预防流感，某学校在休息日用药熏消毒法对教室进行消毒.已知药物释放过程中，室内每立方米空气中的含药量y（mg）与时间t（h）成正比；药物释放完毕后，y 与t 之间的函数解析式为y=（a 为常数），如图所示.根据图中提供的信息，解答下列问题：（1）写出从释放药物开始，y 与t 之间的两个函数解析式及相应的自变量取值范围；（2）据测定，当空气中每立方米的含药量降低到0.25mg 以下时，学生方可进入教室，那么药物释放开始，至少需要经过多少小时，学生才能进入教室？18、（10分）已知y ＋6与x 成正比例，且当x ＝3时，y ＝－12，求y 与x 的函数关系式．B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）某鞋店试销一种新款女鞋，销售情况如下表所示：型号2222.52323.52424.525数量（双）351015832鞋店经理最关心的是哪种型号的鞋销量最大．对他来说，下列统计量中最重要的是（）A ．平均数B ．众数C ．中位数D ．方差20、（4分）如图，一次函数 2 4y x =-+的图象交x 轴于点A ，交y 轴于点B ，点P 在线段AB 上，过点P 分别作PD x ⊥轴于点D ，PC y ⊥轴于点C ．若矩形OCPD 的面积为32，则P 点的坐标为______．21、（4分）如图，在Rt △ABC 中，∠ACB=90°，AC=5cm ，BC=12cm ，将△ABC 绕点B 顺时针旋转60°，得到△BDE ，连接DC 交AB 于点F ，则△ACF 与△BDF 的周长之和为_______cm ．22、（4分）因式分解：3222x x y xy +=﹣__________．23、（4分）观察：①)231-=，②25-=-，③(272-=-，…，请你根据以上各式呈现的规律，写出第6个等式：__________．二、解答题（本大题共3个小题，共30分）24、（8分）菱形ABCD 中,两条对角线AC 、BD 相交于点O,点E 和点F 分别是BC 和CD上一动点,且∠EOF+∠BCD=180°，连接EF.(1)如图2,当∠ABC=60°时，猜想三条线段CE 、CF 、AB 之间的数量关系___；(2)如图1,当∠ABC=90°时,若AC=4,BE=，求线段EF 的长；(3)如图3,当∠ABC=90°,将∠EOF 的顶点移到AO 上任意一点O ′处,∠EO ′F 绕点O ′旋转,仍满足∠EO ′F+∠BCD=180°,O ′E 交BC 的延长线一点E,射线O ′F 交CD 的延长线上一点F,连接EF 探究在整个运动变化过程中,线段CE 、CF,O ′C 之间满足的数量关系，请直接写出你的结论.25、（10分）在△ABC 中，∠C ＝90°，AC ＝6，BC ＝8，D 、E 分别是斜边AB 和直角边CB 上的点，把△ABC 沿着直线DE 折叠，顶点B 的对应点是B ′．（1）如图（1），如果点B ′和顶点A 重合，求CE 的长；（2）如图（2），如果点B ′和落在AC 的中点上，求CE 的长．26、（12分）如图，已知双曲线ky x ，经过点D （6，1），点C 是双曲线第三象限上的动点，过C 作CA ⊥x 轴，过D 作DB ⊥y 轴，垂足分别为A ，B ，连接AB ，BC ．（1）求k 的值；（2）若△BCD 的面积为12，求直线CD 的解析式；（3）判断AB 与CD 的位置关系，并说明理由．参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、C 【解析】根据平均数、中位数、众数、方差的意义进行分析选择．【详解】解：平均数、中位数、众数是描述一组数据集中程度的统计量；方差、标准差是描述一组数据离散程度的统计量．既然是为筹备班级端午节纪念爱国诗人屈原联谊会做准备，那么买的水果肯定是大多数人爱吃的才行，故最值得关注的是众数．故选：C ．此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的平均数、中位数、众数各有局限性，因此要对统计量进行合理的选择和恰当的运用．2、C 【解析】证明BNA BNE ≅，得到BA BE =，即BAE △是等腰三角形，同理CAD 是等腰三角形，根据题意求出DE ，根据三角形中位线定理计算即可.【详解】BN 平分ABC ∠，BN AE ⊥，ABN EBN ∴∠=∠，ANB ENB ∠=∠，在BNA 和BNE 中，ABN EBNBN BN ANB ENB∠=∠⎧⎪=⎨⎪∠=∠⎩，BNA BNE ∴≅，BA BE ∴=，BAE ∴是等腰三角形，同理CAD 是等腰三角形，∴点N 是AE 中点，点M 是AD 中点（三线合一），MN ∴是ADE 的中位线，17611BE CD AB AC +=+=-=，1165DE BE CD BC ∴=+-=-=，1522MN DE ∴==.故选C .本题考查的是三角形中位线定理、等腰三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键.3、A 【解析】直接利用分式的定义分析得出答案．【详解】解：代数式2x ，3a b+，x+3y ，1x y -中分式有：1x y -．故选A ．本题考查了分式的定义，正确把握定义是解题关键．4、D 【解析】根据勾股定理求出四边形ABCD 的四条边之比，根据相似多边形的判定方法判断即可．【详解】作AE ⊥BC 于E ，则四边形AECD 为矩形，∴EC ＝AD ＝1，AE ＝CD ＝3，∴BE ＝4，由勾股定理得，AB ＝5，∴四边形ABCD 的四条边之比为1：3：5：5，D 选项中，四条边之比为1：3：5：5，且对应角相等，故选：D ．此题考查相似多边形的判定定理，两个多边形的对应角相等，对应边成比例，则这两个多边形相似，此题求出多边形的剩余边长是解题的关键，利用矩形的性质定理，勾股定理求出边长.5、B 【解析】∵点P 的横坐标为负，纵坐标为正，∴该点在第二象限．故选B ．6、C 【解析】根据多边形的边数等于360°除以每一个外角的度数列式计算即可得解．解答：360°÷30°=1．故选Ｃ．“点睛”本题考查了多边形的内角与外角，熟练掌握多边形的外角和、多边形的每一个外角的度数、多边形的边数三者之间的关系是解题的关键．7、B 【解析】根据数据a,b,c 的平均数以及方差即可求出a-2,b-2,c-2的平均数和方差.【详解】∵数据a,b,c 的平均数是5，∴()153a b c ++=，∴()()11222252333a b c a b c -+-+-=++-=-=，∴数据a-2,b-2,c-2的平均数是3，∵数据a,b,c 的方差为4，∴()()()222155543a b c ⎡⎤-+-+-=⎣⎦∴a-2,b-2,c-2的方差()()()222123232343a b c ⎡⎤=--+--+--=⎣⎦所以B 选项正确.主要考查平均数和方差的公式计算以及灵活运用.8、D 【解析】试题分析：A ．人数不多，容易调查，适合普查．B ．对“神舟十一号”运载火箭发射前零部件质量情况的调查必须准确，故必须普查；C ．班内的同学人数不多，很容易调查，因而采用普查合适；D ．数量较大，适合抽样调查；故选D ．考点：全面调查与抽样调查．二、填空题（本大题共5个小题，每小题4分，共20分）9、乙【解析】解：∵S 甲2=2，S 乙2=1.5，∴S 甲2＞S 乙2，∴乙的射击成绩较稳定．故答案为乙．本题考查了方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．方差通常用s 2来表示，计算公式是：s 2=1n [（x 1﹣x¯）2+（x 2﹣x¯）2+…+（x n ﹣x¯）2]；方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．10、2.5【解析】先用待定系数法求出直线解析式，再将点A 代入求解可得．【详解】解：将（-2，0）、（0，1）代入y=kx+b，得：201k bb-+⎧⎨⎩＝＝，解得：121 kb⎧⎪⎨⎪⎩＝＝∴y=12x+1，将点A（3，m）代入，得：312m +=即 2.5m=故答案为：2.5本题主要考查直线上点的坐标特点，熟练掌握待定系数法求函数解析式是解题的关键．11、3或﹣1．【解析】根据新定义运算法则得到关于x的方程，通过解方程来求x的值．【详解】解：依题意得：（x﹣1）2+3=7，整理，得（x﹣1）2=4，直接开平方，得x﹣1=±2，解得x1=3，x2=﹣1．故答案是：3或﹣1．本题主要考查了直接开平方法解一元二次方程的知识，解答本题的关键是掌握新定义a★b=a2+b，此题难度不大．12、25【解析】由BF=BE+EF结合“小正方形的边长是1，每个直角三角形的短的直角边长是3”即可得出直角三角形较长直角边的长度，结合三角形的面积公式以及正方形面积公式即可得出结论．【详解】∵EF=1，BE=3，∴BF=BE+EF=4，∴S 正方形ABCD=4⋅S △BCF+S 正方形EFGH=4×12×4×3+1×1=25.故答案为：25.此题考查勾股定理的证明，解题关键在于掌握勾股定理的应用13、【解析】==．三、解答题（本大题共5个小题，共48分）14、（1）-1（2）22x x -+【解析】（1）根据实数混合运算顺序和运算法则计算可得；（2）先计算括号内分式的加法、除法转化为乘法，再约分即可得．【详解】解：（1）原式＝3+2×2﹣2﹣2＝3﹣4＝﹣1；（2）原式＝222(2)(2)(2)2x x x x x x ++--⋅+-，＝22(2)(2)(2)2x x x x x -⋅+-，＝22x x -+．本题主要考查分式的混合运算与实数的混合运算，解题的关键是熟练掌握分式的混合运算顺序和运算法则．15、(1)见解析；(2)当1t =时，以A M C P 、、、为顶点的四边形是平行四边形；(3)103t =时，90PNC ∠=︒.【解析】(1)根据AM ＝t ⨯1可得，再根据题意过点过点M 作MP CD ⊥交直线CD 于点P ，连接NM 、NP 即可;(2)过A 作AE CD ⊥于E ，先证明四边形AMPE 是平行四边形，从而得到AM＝PE，在Rt△ADE 中法求得DE=2，再求出PC＝2-t,根据要使以A M C P 、、、为顶点的四边形是平行四边形则AM＝PC，得到关于t 的方程，解方程即可;(3)当P 在线段DC 延长线上时,可得())24,4BG t MG t =-=-，()2438GN t t t =--=-，()383GP t =-，再根据MG GP +得到关于t 的方程，解方程即可.【详解】(1)如备用图1、2所示；(2)若点P 在线段CD 上时，过A 作AE CD ⊥于E ，如图∵MP CD⊥∴MP AE∕∕又在平行四边形ABCD 中，AB CD ∕∕，即AM PE∕∕∴四边形AMPE 是平行四边形，∴AM PE=由运动可知AM t=∴PE t =，在Rt DEA ∆中60,4D AD ∠=︒=∴12,2DE AD AE ===2PC DC DE PE t =--=-，要使四边形AMCP 为平行四边形，则只需AM PC =，即2t t =-，解得，1t =,当1t =时，以A M C P 、、、为顶点的四边形是平行四边形；(3)当P 在线段DC 延长线上时，假设时，如图易知())24,4BG t MG t =-=-，()2438GN t t t =--=-，()383GP t =-，∵PM =，∴MG GP +=，)()4383t t -+-=，解得103t =，故103t =时，90PNC ∠=︒.考查了平行四边形的动点问题，解题关键是灵活运用勾股定理、平行四边形的性质等知识，认真分析题意．16、（1）见解析；（2）∠EBC =21°，∠F=23°．试题分析：(1)、根据题意得出AE=BE ，然后结合AD=BD 得出答案；(2)、根据等腰三角形的性质得出∠ABC=∠ACB=67°，根据∠EBC=∠ABC ﹣∠ABE 和∠F=90°﹣∠ABC 得出角度．试题解析：(1)、证明：∵∠A=∠ABE ，∴EA=EB ，∵AD=DB ，∴DF 是线段AB 的垂直平分线；(2)、解：∵∠A=46°，∴∠ABE=∠A=46°，∵AB=AC ，∴∠ABC=∠ACB=67°，∴∠EBC=∠ABC ﹣∠ABE=21°，∠F=90°﹣∠ABC=23°．17、(1)y ＝t （0≤t≤）(2)6小时【解析】(1)将点代入函数关系式,解得,有将代入,得,所以所求反比例函数关系式为;再将代入,得,所以所求正比例函数关系式为.(2)解不等式,解得,所以至少需要经过6小时后，学生才能进入教室.18、y=﹣2x ﹣1．【解析】试题分析：先根据y+1与x 成正比例关系，假设函数解析式，再根据已知的一对对应值，求得系数k 即可．解：∵y+1与x 成正比例，∴设y+1=kx （k≠0），∵当x=3时，y=﹣12，∴﹣12+1=3k ，解得k=﹣2∴y+1=﹣2x ，∴函数关系式为y=﹣2x ﹣1．一、填空题（本大题共5个小题，每小题4分，共20分）19、B根据题意可得：鞋店经理最关心的是，哪种型号的鞋销量最大，即各型号的鞋的众数．【详解】鞋店经理最关心的是，哪种型号的鞋销量最大，而众数是数据中出现次数最多的数，故鞋店经理关心的是这组数据的众数．故选：B．20、（32，1）或（12，3）【解析】由点P在一次函数y＝﹣2x+4的图象上，可设P（x，﹣2x+4），由矩形OCPD的面积是3 2可求解．【详解】解：∵点P在一次函数y＝﹣2x+4的图象上，∴设P（x，﹣2x+4），∴x（﹣2x+4）＝3 2，解得：x1＝32，x2＝12，∴P（32，1）或（12，3）．故答案是：（32，1）或（12，3）本题运用了一次函数的点的特征的知识点，关键是运用了数形结合的数学思想．21、1．【解析】∵将△ABC绕点B顺时针旋转60°，得到△BDE，∴△ABC≌△BDE，∠CBD=60°，∴BD=BC=12cm，∴△BCD为等边三角形，∴CD=BC=BD=12cm，在Rt△ACB中，=13，△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=1故答案为1．考点：旋转的性质．22、()2x x y -【解析】先提取公因式x ，再对余下的多项式利用完全平方公式继续分解．【详解】解：原式()()2222x x xy y x x y =-+=-，故答案为：()2x x y -本题考查提公因式，熟练掌握运算法则是解题关键.23、213-=【解析】第n 个等式左边的第1个数为2n+1，根号下的数为n （n+1），利用完全平方公式得到第n 个等式右边的式子为2（n ≥1的整数），直接利用已知数据得出数字变化规律，进而得出答案．【详解】解：∵①232111)-=⨯+-=，②25221-=⨯+-=，③7231-=⨯+-=-，……∴第n 个式子为：221n +-=，∴第6个等式为：213-=故答案为：213-=．本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．二、解答题（本大题共3个小题，共30分）24、（1）CE+CF=AB ；（2）；（3）CF−CE =O`C.【解析】（1）如图1中，连接EF ，在CO 上截取CN=CF ，只要证明△OFN ≌△EFC ，即可推出CE+CF=OC ，再证明OC=AB 即可．（2）先证明△OBE ≌△OCF 得到BE=CF ，在Rt △CEF 中，根据CE +CF =EF 即可解决问题．（3）结论：CF-CE=O`C ，过点O`作O`H ⊥AC 交CF 于H ，只要证明△FO`H ≌△EO C ，推出FH=CE ，再根据等腰直角三角形性质即可解决问题．【详解】(1)结论CE+CF=AB.理由：如图1中，连接EF ，在CO 上截取CN=CF.∵∠EOF+∠ECF=180°，∴O 、E.C.F 四点共圆,∵∠ABC=60°，四边形ABCD 是菱形，∴∠BCD=180°−∠ABC=120°，∴∠ACB=∠ACD=60°，∴∠OEF=∠OCF ，∠OFE=∠OCE ，∴∠OEF=∠OFE=60°，∴△OEF 是等边三角形，∴OF=FE ，∵CN=CF,∠FCN=60°，∴△CFN 是等边三角形，∴FN=FC ，∠OFE=∠CFN ，∴∠OFN=∠EFC ，在△OFN 和△EFC 中，，∴△OFN ≌△EFC ，∴ON=EC ，∴CE+CF=CN+ON=OC ，∵四边形ABCD 是菱形,∠ABC=60°，∴∠CBO=30°，AC ⊥BD ，在RT △BOC 中,∵∠BOC=90°,∠OBC=30°，∴OC=BC=AB,∴CE+CF=AB.(2)连接EF∵在菱形ABCD 中,∠ABC=90°，∴菱形ABCD 是正方形，∴∠BOC=90°,OB=OC,AB=AC,∠OBE=∠OCF=45°,∠BCD=90°∵∠EOF+∠BCD=180°，∴∠EOF=90°，∴∠BOE=∠COF ∴△OBE ≌△OCF ，∴BE=CF ，∵BE=，∴CF=，在Rt △ABC 中,AB +BC =AC ,AC=4∴BC=4，∴CE=，在Rt △CEF 中,CE +CF =EF ，∴EF=答：线段EF 的长为，(3)结论：CF−CE=O`C.理由：过点O`作O`H ⊥AC 交CF 于H ，∵∠O`CH=∠O`HC=45°，∴O`H=O`C ，∵∠FO`E=∠HO`C,∴∠FO`H=∠CO`E ，∵∠EO`F=∠ECF=90°，∴O`.C.F.E 四点共圆，∴∠O`EF=∠OCF=45°，∴∠O`FE=∠O`EF=45°，∴O`E=O`F ，在△FO`H 和△EO`C 中，，∴△FO`H ≌△EO C ，∴FH=CE ，∴CF−CE=CF−FH=CH=O`C.本题考查正方形的性质、全等三角形的判定和性质、勾股定理、四点共圆等知识，解题的关键是发现四点共圆，添加辅助线构造全等三角形，属于中考压轴题．25、(1);(2)【解析】（1）如图（1），设CE ＝x ，则BE ＝8﹣x ；根据勾股定理列出关于x 的方程，解方程即可解决问题．（2）如图（2），首先求出CB ′＝3；类比（1）中的解法，设出未知数，列出方程即可解决问题．【详解】（1）如图（1），设CE ＝x ，则BE ＝8﹣x ；由题意得：AE ＝BE ＝8﹣x ，由勾股定理得：x 2+62＝（8﹣x ）2，解得：x ＝，即CE 的长为：．（2）如图（2），∵点B ′落在AC 的中点，∴CB ′＝AC ＝3；设CE ＝x ，类比（1）中的解法，可列出方程：x 2+32＝（8﹣x ）2解得：x ＝．即CE 的长为：．该题主要考查了翻折变换的性质及其应用问题；解题的关键是灵活运用翻折变换的性质，找出图形中隐含的等量关系；借助勾股定理等几何知识点来分析、判断、推理或解答．26、（1）k=6；（2）直线CD 的解析式为1y x 22=-；（3）AB ∥CD ，理由见解析.【解析】（1）把点D 的坐标代入双曲线解析式，进行计算即可得解.（2）先根据点D 的坐标求出BD 的长度，再根据三角形的面积公式求出点C 到BD 的距离，然后求出点C 的纵坐标，再代入反比例函数解析式求出点C 的坐标，然后利用待定系数法求一次函数解析式解答.（3）根据题意求出点A 、B 的坐标，然后利用待定系数法求出直线AB 的解析式，可知与直线CD 的解析式k 值相等，所以AB 、CD 平行.【详解】解：（1）∵双曲线k y x =经过点D （6，1），∴k16=，解得k=6.（2）设点C 到BD 的距离为h ，∵点D 的坐标为（6，1），DB ⊥y 轴，∴BD=6，∴S △BCD =12×6•h=12，解得h=4.∵点C 是双曲线第三象限上的动点，点D 的纵坐标为1，∴点C 的纵坐标为1－4=－3.∴63x =，解得x=－2.∴点C 的坐标为（－2，－3）.设直线CD 的解析式为y=kx ＋b ，则2k b 3{6k b 1-+=-+=，解得1k {2b 2==-.∴直线CD 的解析式为1y x 22=-.（3）AB ∥CD.理由如下：∵CA ⊥x 轴，DB ⊥y 轴，点C 的坐标为（－2，－3），点D 的坐标为（6，1），∴点A 、B 的坐标分别为A （－2，0），B （0，1）.设直线AB 的解析式为y=mx+n ，则2m n 0{n 1-+==，解得1m {2n 1==.∴直线AB 的解析式为1y x 12=+.∵AB 、CD 的解析式k 都等于12相等.∴AB 与CD 的位置关系是AB ∥CD.。

山东省济南市实验中学2024-2025学年数学九年级第一学期开学检测试题题号一二三四五总分得分A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）下列图形中，是中心对称图形的是（）A ．B ．C ．D ．2、（4分）下列各组数不能作为直角三角形三边长的是（）A ．3，4，5B C ．0.3，0.4，0.5D ．30，40，503、（4分）（2016广西贵港市）则x 的取值范围是（）A ．x ＜1B ．x ≤1C ．x ＞1D ．x ≥14、（4分））A ．3B ．3-C ．3±D ．95、（4分）甲、乙、丙、丁四位同学在一次数学测验中的平均成绩是90分，而甲、乙、丙三人的平均成绩是88分，下列说法一定正确的是（）A ．丁同学的成绩比其他三个同学的成绩都好B ．四位同学成绩的中位数一定是其中一位同学的成绩C ．四位同学成绩的众数一定是90分D ．丁同学成绩是96分6、（4分）如图，直线1y x =+与y 轴交于点1A ，依次作正方形111A B C O 、正方形2221A B C C 、…正方形1n n n n A B C C -使得点1A 、2A 、…，n A 在直线1x +上，点1C 、2C 、…，n C 在x 轴上，则点n B 的坐标是（）A ．(21,21)n n --B ．(21,)n n -C ．()1121,2n n --+D ．()121,2n n --7、（4分）的值在（）A ．0与1之间B ．1与2之间C ．2与3之间D ．3与4之间8、（4分）如图，四边形ABCD 是边长为5cm 的菱形，其中对角线BD 与AC 交于点O ，BD ＝6cm ，则对角线AC 的长度是（）A ．8cm B ．4cm C ．3cm D ．6cm 二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）若1mn =，2m n -=，则22m n mn -的值是__________.10、（4分）端午节那天，“味美早餐店”的粽子打9折出售，小红的妈妈去该店买粽子花了54元钱，比平时多买了3个，则平时每个粽子卖_____元．11、（4分）如图，在菱形ABCD 中，4AB =，菱形的面积为15，则菱形的对角线之和为__．12、（4分）如图，将矩形ABCD 绕点B 顺时针旋转α度(0360)α︒<<︒，得到矩形BEFG ．若AG DG =，则此时α的值是_____．13、（4分）若m 的小数部分，则221m m ++的值是______．三、解答题（本大题共5个小题，共48分）14、（12分）如图，小明用自制的直角三角形纸板DEF 测量树的高度1B .他调整自己的位置，设法使斜边DF 保持水平，并且边DE 与点B 在同一直线上，已知纸板的两条直角边DE =40cm .EF =30cm ，测得边DF 离地面的高度AC =1.5m ，CD =10m ，求树高AB .15、（8分）如图，直线l 1的函数表达式为y ＝﹣3x +3，且l 1与x 轴交于点D ，直线l 2经过点A ，B ，直线l 1，l 2交于点C ．(1)求点D 的坐标；(2)求直线l 2的解析表达式；(3)求△ADC 的面积．16、（8分）某市举行“行动起来，对抗雾霾”为主题的植树活动，某街道积极响应，决定对该街道进行绿化改造，共购进甲、乙两种树共50棵，已知甲树每棵800元，乙树每棵1200元．（1）若购买两种树的总金额为56000元，求甲、乙两种树各购买了多少棵？（2）若购买甲树的金额不少于购买乙树的金额，至少应购买甲树多少棵？17、（10分）解一元二次方程：（1）()21412x x x -=-；（2）2523x x +=.18、（10分）小东拿着一根长竹竿进一个宽为5米的矩形城门，他先横着拿但进不去；又竖起来拿，结果竹竿比城门还高1米，当他把竹竿左右斜着拿时，两端刚好顶着城门的对角，问竹竿长多少米？B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）0)x >=___________.20、（4分）若关于x 的分式方程3122x a x -=-的解是非负数，则a 的取值范围是__________．21、（4分）如图，已知四边形ABCD 是平行四边形，对角线AC 、BD 交于点O ，E 是BC 的中点，若AB ＝6，则OE ＝_____．22、（4分）数据5，5，6，6，6，7，7的众数为_____23、（4分）如图，在Rt ABC ∆中90BAC ∠=︒，4BC =，E 、F 分别是BC 、AC 的中点，延长BA 到点D ，使12AD AB =，则DF =_____________．二、解答题（本大题共3个小题，共30分）24、（8分）先化简，再求值：2321121x x x x x -⎛⎫--÷ ⎪--+⎝⎭，其中x 是13x -≤≤中的一个正整数解．25、（10分）如图，在矩形ABCD 中，8AB =，16BC =，点P 从点D 出发向点A 运动，运动到点A 停止，同时，点Q 从点B 出发向点C 运动，运动到点C 即停止，点P 、Q 的速度都是每秒1个单位，连接PQ 、AQ 、CP ．设点P 、Q 运动的时间为t 秒（1）当t 为何值时，四边形ABQP 是矩形；（2）当6t =时，判断四边形AQCP 的形状，并说明理由；26、（12分）如图，一次函数1y mx n =+的图象与x 轴、y 轴分别交于A 、B 两点，与反比例函数2(0)k y x x =<交于点C ，过点C 分别作x 轴、y 轴的垂线，垂足分别为点E 、F ．若2OB =，6CF =，13OA OE =．（1）求点A 的坐标；（2）求一次函数和反比例函数的表达式．参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、C 【解析】根据中心对称图形的概念对各选项分析判断即可得解．【详解】解：A 、不是中心对称图形，故本选项错误；B 、不是中心对称图形，故本选项错误；C 、是中心对称图形，故本选项正确；D 、不是中心对称图形，故本选项错误．故选：C ．本题考查了中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后两部分重合．2、B 【解析】选项A ，222345+=，三角形是直角三角形；选项B ，222+≠，三角形不是直角三角形；选项C ，2220.30.40.5+=，三角形是直角三角形；选项D ，222304050+=，三角形是直角三角形；故选B ．3、C 【解析】依题意得：100x -≥⎧⎪≠，解得x ＞1，故选C ．4、A【解析】a =进行计算即可．【详解】=-=；故选：A.本题考查了二次根式的计算与化简，解题的关键是熟练掌握二次根式的运算法则.5、D【解析】根据算术平均数的定义，中位数的定义以及众数的定义对各选项分析判断利用排除法求解．【详解】.解：A、丁同学的成绩为90×4﹣88×3＝96（分），而由甲、乙、丙三人的平均成绩是88分无法判断三人的具体成绩，无法比较，此选项错误；B、四位同学成绩的中位数可能是四个数据中的一个，也可能不在所列数据中，此选项错误；C、由于不清楚四位同学的各自成绩，所以不能判断众数，此选项错误；D、丁同学的成绩为90×4﹣88×3＝96（分），此选项正确；故选D．本题考查了算术平均数的定义，中位数的定义，以及众数的定义，是基础题，熟记各概念是解题的关键．6、D【解析】先求出直线y＝x＋1与y轴的交点坐标即可得出A1的坐标，故可得出OA1的长，根据四边形A1B1C1O是正方形即可得出B1的坐标，再把B1的横坐标代入直线y＝x＋1即可得出A1的坐标，同理可得出B2，B3的坐标，可以得到规律：B n（2n−1，2n−1），据此即可求解．【详解】解：∵令x＝0，则y＝1，∴A1（0，1），∴OA1＝1．∵四边形A1B1C1O是正方形，∴A1B1＝1，∴B1（1，1）．∵当x＝1时，y＝1＋1＝2，∴B2（3，2）；同理可得，B 3（7，4）；∴B 1的纵坐标是：1＝20，B 1的横坐标是：1＝21−1，∴B 2的纵坐标是：2＝21，B 2的横坐标是：3＝22−1，∴B 3的纵坐标是：4＝22，B 3的横坐标是：7＝23−1，∴Bn 的纵坐标是：2n−1，横坐标是：2n −1，则B n ()121,2n n --故选：D ．本题考查了一次函数图象上点的坐标特征、正方形的性质和坐标的变化规律．此题难度较大，注意正确得到点的坐标的规律是解题的关键．7、B 【解析】1，即可得出结果．【详解】解：∵1，1与2之间．故选：B ．此题主要考查了估算无理数大小，正确得出接近的有理数是解题关键．8、A 【解析】首先根据菱形的性质可得BO ＝DO ，AC ⊥DB ，AO ＝CO ，然后再根据勾股定理计算出AO 长，进而得到答案．【详解】解：∵四边形ABCD 是菱形，∴BO ＝DO ，AC ⊥DB ，AO ＝CO ，∵BD ＝6cm ，∴BO ＝3cm ，∵AB ＝5cm ，∴AO ＝4（cm ），∴AC ＝2AO =8cm ．故选：A ．本题考查菱形的性质，要注意菱形的对角线互相垂直，有直角即可用勾股定理求某些边的长.二、填空题（本大题共5个小题，每小题4分，共20分）9、2【解析】提取公因式因式分解后整体代入即可求解．【详解】22()122m n mn mn m n -=-=⨯=.故答案为：2.此题考查因式分解的应用，解题关键在于分解因式.10、2【解析】设平时每个粽子卖x 元，根据题意列出分式方程，解之并检验得出结论．【详解】设平时每个粽子卖x 元．根据题意得：解得：x ＝2经检验x ＝2是分式方程的解故答案为2.本题考查了分式方程的应用，解题的关键是找准等量关系，列出分式方程．11、【解析】由菱形的性质得出12OA OC AC ==，12OB OD BD ==，AC BD ⊥，由勾股定理和良宵美景得出OA 2+OB 2=16①，2OB×OB=15②，①+②得：（OA+OB ）2=31，即可得出结果．【详解】解：四边形ABCD 是菱形，12OA OC AC ∴==，12OB OD BD ==，AC BD ⊥，4AB =，菱形的面积为15，2216OA OB ∴+=①，1152AC BD ⨯=，215OA OB ∴⨯=②，①+②得：()231OA OB +=，OA OB ∴+=，AC BD ∴+=；故答案为：．本题考查了菱形的性质、勾股定理、完全平方公式；熟练掌握菱形的性质是解题的关键．12、60°或300°【解析】由“SAS”可证△DCG ≌△ABG ，可得CG=BG ，由旋转的性质可得BG=BC ，可得△BCG 是等边三角形，即可求解．【详解】解：如图，连接CG ，∵四边形ABCD 是矩形，∴CD=AB ，∠DAB=∠ADC=90°，∵DG=AG ，∴∠ADG=∠DAG ，∴∠CDG=∠GAB ，且CD=AB ，DG=AG ，∴△DCG ≌△ABG （SAS ），∴CG=BG ，∵将矩形ABCD 绕点B 顺时针旋转α度（0°＜α＜360°），得到矩形BEFG ，∴BC=BG ，∠CBG=α，∴BC=BG=CG ，∴△BCG 是等边三角形，∴∠CBG=α=60°，同理当G 点在AD 的左侧时，△BCG 仍是等边三角形，Α=300°故答案为60°或300°.本题考查了旋转的性质，全等三角形的判定和性质，等边三角形的判定和性质，证明△BCG 是等边三角形是本题的关键．13、1【解析】根据题意知1m ，而()2221=1m m m +++，将m 代入，即可求解．【详解】解：∵m 1.414...≈，∴1m ，∴())222221=1=11==2m m m ++++．故答案为1．本题目是二次根式的变型题，难度不大，正确理解题干并表示出来，是顺利解题的关键．三、解答题（本大题共5个小题，共48分）14、9米【解析】利用直角三角形DEF 和直角三角形BCD 相似求得BC 的长后加上小明同学的身高即可求得树高AB ．【详解】解：∵∠DEF=∠BCD=90°∠D=∠D∴△DEF ∽△DCB ∴BC DC EF DE =，∵DE=40cm=0.4m ，EF=30cm=0.3m ，AC=1.5m ，CD=10m ，∴BC 100.30.4=，∴BC=7.5米，∴AB=AC+BC=1.5+7.5=9米．本题考查了相似三角形的应用，解题的关键是从实际问题中整理出相似三角形的模型．15、(1)D （1,0）(2)y=32x-6(3)可求得点C(2,-3),则S △ADC =92【解析】解：（1）因为D 是1L ：33y x =-+与x 轴的交点，所以当0y =时，1x =，所以点(1,0)D ；（2）因为3(4,0),(3,2A B -在直线2L 上，设2L 的解析式为403{{23362k b k y kx b k b b +===+∴∴+=-=-，所以直线2L 的函数表达式362y x =-；（3）由326{{2333x y x y y x ==-∴=-=-+，所以点C 的坐标为(2,3)-，所以ADC ∆的底413,AD =-=高为C 的纵坐标的绝对值为3，所以193322ADC S ∆=⨯⨯=；此题考查一次函数解析式的求法，一次函数与坐标轴交点的求.和二元一次方程组的解法，两条直线交点的求法，即把两个一次函数对应的解析式构成二元一次方程组，求出方程组的解就是两条直线的交点坐标，也考查了三角形面积的求法；16、（1）购买了甲树10棵、乙树40棵；（2）至少应购买甲树30棵．【解析】（1）首先设甲种树购买了x 棵，乙种数购买了y 棵，由题意得等量关系：①进甲、乙两种树共50棵；②购买两种树总金额为56000元，根据等量关系列出方程组，再解即可；（2）首先设应购买甲树x 棵，则购买乙种树（50﹣a ）棵，由题意得不等关系：购买甲树的金额≥购买乙树的金额，再列出不等式，求解即可．【详解】解：（1）设购买了甲树x 棵、乙树y 棵，根据题意得50800120056000x y x y +=⎧⎨+=⎩解得：1040x y =⎧⎨=⎩答：购买了甲树10棵、乙树40棵；（2）设应购买甲树a 棵，根据题意得：800a ≥1200（50﹣a ）解得：a ≥30答：至少应购买甲树30棵．此题主要考查了二元一次方程组和一元一次不等式的应用，关键是正确理解题意，找出题目中的等量关系和不等关系，列出方程组和不等式．17、（1）112x =，214x =-；（2）12x =或213x =-【解析】(1)先变形为4x （2x-1）+2x-1=0，然后利用因式分解法解方程；(2)先把方程化为一般式，然后利用求根公式法解方程；【详解】解：（1）4x （2x-1）+2x-1=0，（2x-1）（4x+1）=0，2x-1=0或4x+1=0，所以112x =，214x =-；（2）2523x x +=.3x 2-5x-2=0，△=（-5）2-4×3×(-2)=49，523x ±=⨯所以12x =或213x =-；本题考查了解一元二次方程-因式分解法：就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了配方法解一元二次方程．18、12米【解析】可设竹竿长为x ，再根据竹竿比城门高1米，竹竿左右斜着拿时，两端刚好顶着城门的对角，利用勾股定理可得结果.【详解】解：设竹竿长x 米，x 2=（x -1）2+52；，解得x =12，答：竹竿长为12米.本题考查勾股定理的应用，学生需要掌握勾股定理的定义即可求解.一、填空题（本大题共5个小题，每小题4分，共20分）19、3x y 【解析】根据二次根式的乘法，可得第二个空的答案；【详解】0)x >=3=；故答案为：3x y .此题考查二次根式的性质与化简，解题关键在于掌握运算法则.20、1a ≥且6a ≠【解析】分式方程去分母转化为整式方程，由分式方程的解是非负数，确定出a 的范围即可．【详解】去分母得：622x a x -=-，即225a x -=，由分式方程的解为非负数，得到225a -≥0，且225a -≠2，解得：1a ≥且6a ≠，故答案为：1a ≥且6a ≠．此题考查了分式方程的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．21、3【解析】根据平行四边形的对角线互相平分可得OA ＝OC ，然后判断出OE 是三角形的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半可得OE ＝12AB ．【详解】解：在▱ABCD 中，OA ＝OC ，∵点E 是BC 的中点，∴OE 是三角形的中位线，∴OE ＝12AB ＝3故答案为3本题考查了平行四边形的性质和三角形中位线定理，平行四边形对角线互相平分的性质，三角形的中位线平行于第三边并且等于第三边的一半，熟记性质与定理是解题的关键．22、6【解析】根据众数的定义可得结论．【详解】解：数据5，5，6，6，6，7，7，其中数字5出现2次，数字6出现3次，数字7出现2次，所以众数为6.故答案为：6本题主要考查众数的定义，解题的关键是掌握众数的定义：一组数据中出现次数最多的数据叫做众数．23、2【解析】连接EF 、AE ，证四边形AEFD 是平行四边形，注意应用直角三角形斜边上的中线等于斜边的一半和平行四边形的性质：平行四边形的对边相等，求得AE 长即可．【详解】连接EF ，AE .∵点E ，F 分别为BC ，AC 的中点，∴EF ∥AB ,EF =12AB .又∵AD =12AB ，∴EF =AD .又∵EF ∥AD ，∴四边形AEFD 是平行四边形.在Rt △ABC 中，∵E 为BC 的中点，BC =4，∴AE =12BC =2.又∵四边形AEFD 是平行四边形，∴DF =AE =2.本题主要考查了平行四边形判定，有中点时需考虑运用三角形的中位线定理或则直角三角形斜边上的中线等于斜边的一半.二、解答题（本大题共3个小题，共30分）24、化简为22x x --+，当x=3时，此时的值为-10.【解析】先根据分式混合运算的法则把原式进行化简，再把x 的值代入进行计算即可，【详解】解：原式=()()211311112x x x x x x x x --⎡⎤---⨯⎢⎥----⎣⎦=()()()2311112x x x x x x -----⎡⎤⨯⎢⎥--⎣⎦=()221412x x x x -⎛⎫-+⨯ ⎪--⎝⎭=22x x --+，当x=3时，代入原式=2332=10--+-；本题主要考查了分式的化简求值，掌握分式的化简求值是解题的关键.25、（1）8t =；（2）当6t =时，四边形AQCP 为菱形,理由见解析．【解析】（1）由矩形性质得出16BC AD ==，8AB CD ==，由已知可得，BQ DP t ==，16AP CQ t ==-，当BQ AP =时，四边形ABQP 为矩形，得出方程，解方程即可；（2）6t =时，BQ 6=，6DP =，得出16610CQ =-=，16610AP =-=，AP CQ =，//AP CQ ，四边形AQCP 为平行四边形，在Rt ABQ ∆中，与勾股定理求出10AQ ==，得出AQ CQ =，即可得出结论．【详解】解：（1）在矩形ABCD 中，8AB =，16BC =，16BC AD ∴==，8AB CD ==，由已知可得，BQ DP t ==，16AP CQ t ==-，在矩形ABCD 中，90B ∠=︒，//AD BC ，当BQ AP =时，四边形ABQP 为矩形，16t t ∴=-，解得：8t =，∴当8t s =时，四边形ABQP 为矩形；（2）四边形AQCP 为菱形；理由如下：6t =，6BQ ∴=，6DP =，16610CQ ∴=-=，16610AP =-=，AP CQ ∴=，//AP CQ ，∴四边形AQCP 为平行四边形，在Rt ABQ ∆中，10AQ ===，AQ CQ ∴=，∴平行四边形AQCP 为菱形，∴当6t =时，四边形AQCP 为菱形；本题考查了矩形的判定与性质、菱形的判定、勾股定理、平行四边形的判定等知识；熟练掌握判定与性质是解题的关键．26、（1）(2,0)-；（2）224y x =-.【解析】（1）利用13OA OE =，6OE CF ==可以就可以求出A 点的坐标（2）利用A，B 的坐标求出一次函数的解析式，然后利用C 点坐标求出反比例函数的表达式。

深实验中学部 2025 届九年级开学考测试英语试卷考试时间：90分钟试卷满分：100分说明：请考生在答题卷指定区域按要求规范作答，考试结束上交答题卷。

听力部分(15分)一、根据你在录音里听到的句子，从下面每小题的A、B、C三个选项中选择最佳答句，每小题念一遍：(共5分, 10小题, 每小题0.5分)1. A. Yes, it's lost. B. Sure, here you are. C. No, you mustn't.2. A. Yes, I'm afraid so. B. I hope not. C. Yes, it is.3. A. For two hours. B. In half an hour. C. Three times a day.4. A. Every morning. B. At 7:30. C. Some bread.5. A. All right. B. Not at all. C. Never mind.6. A. It's great. B. Our English teacher. C. I don't think so.7. A. That's all right. B. Thank you. C. The same to you.8. A. At the school gate. B. At 10:30 a. m. C. By taxi.9. A. Music is great. B. Nothing at all. C. Pop music.10. A. It was my aunt. B. It was my aunt's. C. It was for my aunt.二、下面各组对话后均有一个与对话内容相关的问题，从下面每小题的 A、B、C三个选择中找出能回答这个问题的最佳答案，每小题念两遍：(共5分，5小题，每小题1分)11. Where are the two speakers?A. In an office.B. In a classroom.C. In a shop.12. Where does the man come from?A. America.B. Canada.C. China.13. Who wants to have a glass of milk?A. The woman.B. Tom.C. John.14. What does the woman mind the man doing?A. Smoking.B. Sitting there.C. Talking to her.15. When will Lily arrive?A. At 5:55.B. At 5:30.C. At 5:40.三、听短文，从下面每小题的A、B、C三个选项中选择最佳答案，每小题念两遍：(共5分5小题，每小题1分)16. Who buys a robot as a birthday present for the speaker?A. His mother.B. His father.C. His brother.17. What does the robot look like?A. It has two arms, two legs, a body and a head.B. It has two legs and a head, but no arms.C. It has a head, a body and two wheels.18. What can the robot do in the morning?A. It can make breakfast.B. It can take a walk with him.C. It can wake him up.19. How often does the speaker need to change its battery?A. Every day.B. Every two days.C. Every three days.20. Which of the following statements is TRUE?A. The robot isn't happy when I call it Eric.B. The robot's program has to be upgraded(使升级) every week.C. The robot can talk.笔试部分(85分)客观题四、选择填空(共5分，10小题，每小题0.5分)从下面每小题的A、B、C、D四个选项中选出可以填入空白处的最佳选项。

怀化市重点中学2024年九年级数学第一学期开学综合测试试题题号一二三四五总分得分批阅人A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）在一次统考中，从甲、乙两所中学初二学生中各抽取50名学生进行成绩分析，甲校的平均分和方差分别是82分和245分，乙校的平均分和方差分别是82分和190分，根据抽样可以粗略估计成绩较为整齐的学校是（）A ．甲校B ．乙校C ．两校一样整齐D ．不好确定哪校更整齐2、（4分）下列式子中，是二次根式的是（）A ．B ．πC D ．3、（4分）矩形各内角的平分线能围成一个（）A ．矩形B ．菱形C ．等腰梯形D ．正方形4、（4分）关于数据－4，1，2，－1，2，下面结果中，错误的是()A ．中位数为1B ．方差为26C ．众数为2D ．平均数为05、（4分）下列图形，可以看作中心对称图形的是（）A ．B ．C ．D ．6、（4分）下列代数式中，属于最简二次根式的是()A ．B ．C ．D ．7、（4分）若关于x 的不等式组11x a x -<⎧⎨≥⎩的整数解有3个，则a 的取值范围是（）A ．3＜a ≤4B ．2＜a ≤3C ．2≤a ＜3D ．3≤a ＜48、（4分）一次统计八（2）班若干名学生每分跳绳次数的频数分布直方图的次数（结果精确到个位）是（）A ．数据不全无法计算B ．103C ．104D ．105二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）某校为了提升初中学生学习数学的兴趣，培养学生的创新精神，举办了“玩转数学”比赛．评委从研究报告、小组展示、答辩三个方面为每个参赛小组打分，按照研究报告占40%，小组展示占30%，答辩占30%计算各小组的成绩，各项成绩均按百分制记录．甲小组的研究报告得85分，小组展示得90分，答辩得80分，则甲小组的参赛成绩为_____．10、（4分）已知△ABC 的周长为4，顺次连接△ABC 三边的中点构成的新三角形的周长为__________．11、（4分）如图，梯形ABCD 中，AB∥CD，点E、F、G 分别是BD、AC、DC 的中点．已知两底差是6，两腰和是12，则△EFG 的周长是．12、（4分）菱形ABCD 中，60B ∠=，5AB =，以AC 为边长作正方形ACFE ，则点D 到EF 的距离为_________．13、（4分）的正方形ABCD 中，C （0，5），点A 在x 轴上，点B 在反比例函数y =m x （x ＞0，m ＞0）的图象上，点D 在反比例函数y =n x （x ＜0，n ＜0）的图象上，那么m +n =______．三、解答题（本大题共5个小题，共48分）14、（12分）如图，AD 是△ABC 的边BC 上的高，∠B ＝60°，∠C ＝45°，AC ＝6.求：(1)AD 的长；(2)△ABC 的面积．15、（8分）某住宅小区有一块草坪如图所示．已知AB ＝3米，BC ＝4米，CD ＝12米，DA ＝13米，且AB ⊥BC ，求这块草坪的面积．16、（8分）如图，四边形ABCD 是正方形，点G 是BC 上一点，DE ⊥AG 于点E ，BF ∥DE 且交AG 于点F.（1）求证：AE=BF ；（2）当∠BAG=30°，且AB=2时，求EF-FG 的值.17、（10分）先化简，再求值：（3m-6m m 1+）÷22m -2m 1m -1+，其中m ＝2019－18、（10分）某游泳池有900立方米水，每次换水前后水的体积保持不变．设放水的平均速度为v 立方米/小时，将池内的水放完需t 小时，（1）求v 关于t 的函数表达式，并写出自变量t 的取值范围；（2）若要求在2.5小时至3小时内（包括2.5小时与3小时）把游泳池内的水放完，求放水速度的范围．B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）如图,在ABC ∆中,ABC ∠和ACB ∠的角平分线相交于O 点,若125BOC ∠=︒,则A ∠的度数为______.20、（4分）关于x 的一元二次方程x 2﹣2x+k ﹣1=0没有实数根，则k 的取值范围是_____．21、（4分）如图，把Rt △ABC (∠ABC ＝90°)沿着射线BC 方向平移得到Rt △DEF ，AB ＝8，BE ＝5，则四边形ACFD 的面积是________．22、（4分）将正比例函数y=﹣2x 的图象沿y 轴向上平移5个单位，则平移后所得图象的解析式是_____．23、（4分）小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，根据图中的信息，成绩较稳定的是____．二、解答题（本大题共3个小题，共30分）24、（8分）已知一次函数y=kx+b，当x=2时y 的值是﹣1，当x=﹣1时y 的值是1．（1）求此一次函数的解析式；（2）若点P（m，n）是此函数图象上的一点，﹣3≤m≤2，求n 的最大值．25、（10分）我市劲威乡A 、B 两村盛产柑橘，A 村有柑橘200吨，B 村有柑橘300吨，现将这些柑橘运到C 、D 两个冷藏仓库，已知C 仓库可储存240吨，D 仓库可储存260吨，从A 村运往C 、D 两处的费用分别为每吨20元和25元，从B 村运往C 、D 两处的费用分别为每吨15元和18元．设从A 村运往C 仓库的柑橘重量为x 吨，设A 、B 两村运往两仓库的柑橘运输费用分别为y A 元和y B 元．（1）请填写下表（2）求出y A 、y B 与x 之间的函数解析式；（3）试讨论A 、B 两村中，哪个村的运费最少；（4）考虑B 村的经济承受能力，B 村的柑橘运费不得超过4830元，在这种情况下，请问怎样调运才能使两村运费之和最小？求出这个最小值．26、（12分）某超市预测某饮料会畅销、先用1800元购进一批这种饮料，面市后果然供不应求，又用8100元购进这种饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元．（1）第一批饮料进货单价多少元？（2）若两次进饮料都按同一价格销售，两批全部售完后，获利不少于2700元，那么销售单价至少为多少元？参考答案与详细解析一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、B【解析】根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．【详解】∵甲校和乙校的平均数是相等的，甲校的方差大于乙校的方差，∴成绩较为整齐的学校是乙校．故选B．本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．2、D【解析】根据二次根式的定义分别进行判定即可．【详解】解：A、根指数为3，属于三次根式，故本选项错误；B、π不是根式，故本选项错误；C、无意义，故本选项错误；D符合二次根式的定义，故本选项正确．故选：D．（a≥0）叫二次根式．3、D【解析】根据矩形的性质及角平分线的性质进行分析即可．【详解】矩形的四个角平分线将矩形的四个角分成8个45°的角，因此形成的四边形每个角是90°又知两条角平分线与矩形的一边构成等腰直角三角形，所以这个四边形邻边相等，根据有一组邻边相等的矩形是正方形，得到该四边形是正方形．故选D．此题是考查正方形的判别方法，判别一个四边形为正方形主要根据正方形的概念，途经有两种：①先说明它是矩形，再说明有一组邻边相等；②先说明它是菱形，再说明它有一个角为直角4、B【解析】A．∵从小到大排序为-4，-1，，1，2，2，∴中位数为1，故正确；B．4121205x-++-+==，()()()()222224010102022655s--+--+-+-⨯==，故不正确；C．∵众数是2，故正确；D．4121205x-++-+==，故正确；故选B.5、B【解析】根据中心对称图形的概念对各选项分析判断即可得解．【详解】A、不是中心对称图形，故本选项不符合题意；B、是中心对称图形，故本选项符合题意；C、不是中心对称图形，故本选项不符合题意；D、不是中心对称图形，故本选项不符合题意．故选：B．本题考查了中心对称图形的概念，解题关键在于中心对称图形是要寻找对称中心，旋转180度后两部分重合．6、A【解析】最简二次根式满足下列两个条件：(1)被开方数的因数是整数,因式是整式；(2)被开方数中不含能开得尽方的因数或因式，再对各选项逐一判断即可.【详解】解：A 、是最简二次根式，故A 符合题意；B 、，故不是最简二次根式，故B 不符合题意；C 、，故不是最简二次根式，故C 不符合题意；D 、，故不是最简二次根式，故D 不符合题意；故答案为：A 本题考查二次根式，解题的关键是熟练运用最简二次根式的定义，本题属于基础题型．7、B 【解析】解第一个不等式可得x ＜a+1，因关于x 的不等式组11x a x -<⎧⎨≥⎩有解，即1≤x ＜a+1，又因不等式组11x a x -<⎧⎨≥⎩的整数解有3个，可得3＜a+1≤4，即可得2＜a ≤3，故选B.点睛：本题考查了不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．8、C 【解析】根据频数分布直方图可知本次随机抽查的学生人数为：2+4+6+3=15（人）；然后取每一小组中间的数值近似地作为该组内每位学生的每分钟跳绳次数，再用加权平均数求解即可.【详解】解：根据频数分布直方图可知本次随机抽查的学生人数为：2+4+6+3=15（人）；所以这若干名学生每分钟跳绳次数的平均数=（62×2+87×4+112×6+137×2）÷15≈103.67≈104，故选C.本题考查学生读取频数分布直方图的能力和利用统计图获取信息的能力.对此类问题，必须认真观察题目所给的统计图并认真的思考分析，才能作出正确的判断，从而解决问题.二、填空题（本大题共5个小题，每小题4分，共20分）9、85分【解析】根据加权平均数的定义计算可得．【详解】根据题意知，甲小组的参赛成绩为85×40%+90×30%+80×30%=85（分），故答案为：85分．本题考查的是加权平均数的求法，根据某方面的需要选拔时往往利用加权平均数更合适．10、2【解析】抓住三角形的中位线定理进行分析解答，根据题意的分析可以知道三角形的中位线平行于第三边，并且等于它的一半.【详解】根据题意可知：三角形的中位线平行于第三边，并且等于它的一半，所以三条中位线组成的三角形的周长为故答案为：2.考查三角形的中位线定理，三角形的中位线平行于第三边而且等于第三边的一半.11、1．【解析】试题分析：延长EF交BC于点H，可知EF，FH，FG、EG分别为△BDC、△ABC、△BDC和△ACD 的中位线，由三角形中位线定理结合条件可求得EF+FG+EG，可求得答案．解：连接AE，并延长交CD于K，∵AB∥CD，∴∠BAE=∠DKE，∠ABD=∠EDK，∵点E、F、G分别是BD、AC、DC的中点．∴BE=DE，在△AEB和△KED中，，∴△AEB≌△KED（AAS），∴DK=AB，AE=EK，EF 为△ACK 的中位线，∴EF=CK=（DC﹣DK）=（DC﹣AB），∵EG 为△BCD 的中位线，∴EG=BC，又FG 为△ACD 的中位线，∴FG=AD，∴EG+GF=（AD+BC），∵两腰和是12，即AD+BC=12，两底差是6，即DC﹣AB=6，∴EG+GF=6，FE=3，∴△EFG 的周长是6+3=1．故答案为：1．点评：此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．12、．【解析】分两种情况讨论：①当正方形ACFE 边EF 在AC 左侧时，②当正方形ACFE 边EF 在AC 右侧时．【详解】解：∵四边形ABCD 是菱形，∠B=60°，∴△ACD 是等边三角形，且DO ⊥AC ．∵菱形的边长为5，∴DO==2分两种情况讨论：①当正方形ACFE 边EF 在AC 左侧时，过D 点作DH 2⊥EF ，DH 2长度表示点D 到EF 的距离，DH 2；②当正方形ACFE 边EF 在AC 右侧时，过D 点作DH 1⊥EF ，DH 1长度表示点D 到EF 的距离，DH 1．故答案为：5+2或5-2．本题考查菱形的性质、正方形的性质、等边三角形的判定和性质，同时考查了分类讨论思想．解决此类问题要借助画图分析求解．13、±5【解析】由勾股定理可求点A 坐标，分两种情况讨论，利用全等三角形的判定和性质求出B 、D 的坐标，即可求解．【详解】解：设点A （x ，0）∴AC 2=OA 2+OC 2，∴26=25+OA 2，∴OA=1∴点A （1，0），或（-1，0）当点A （1，0）时，如图，过点B 作BF ⊥x 轴，过点C 作CE ⊥y 轴，与BF 交于点E ，过点D 作DH ⊥x 轴，交CE 于点G ，∵∠CBE+∠ABF=90°，且∠CBE+∠ECB=90°∴∠ECB=∠ABF，且BC=AB，∠E=∠AFB=90°∴△ABF≌△BCE（AAS）∴BE=AF，BF=CE∵OF=OA+AF∴CE=OF=1+BE=BF∴BF+BE=1+BE+BE=5∴BE=2，∴BF=3∴点B坐标（3，3）∴m=3×3=9，∵A（1，0）,C（0，5）,B（3，3）,∴点D(1+0-3，0+5-3)，即（-2，2）∴n=-2×2=-4∴m+n=5若点A（-1，0）时，同理可得：B（2，2）,D（-3，3）,∴m=4，n=-9∴m+n=-5故答案为：±5本题考查了反比例函数图象上点的坐标特征，正方形的性质，全等三角形的判定和性质，利用分类讨论思想解决问题和利用方程思想解决问题是本题的关键．三、解答题（本大题共5个小题，共48分）14、（1）AD＝；（2）S△ABC＝9＋.【解析】试题分析：（1）根据三角形内角和可得∠DAC=45°，根据等角对等边可得AD=CD，然后再根据勾股定理可计算出AD的长；（2）根据三角形内角和可得∠BAD=30°，再根据直角三角形的性质可得AB=2BD，然后利用勾股定理计算出BD的长，进而可得BC的长，然后利用三角形的面积公式计算即可．解：(1)∵∠C＝45°，AD是△ABC的边BC上的高，∴∠DAC＝45°，∴AD＝CD.∵AC2＝AD2＋CD2，∴62＝2AD2，∴AD＝(2)在Rt△ADB中，∵∠B＝60°，∴∠BAD＝30°，∴AB＝2BD.∵AB2＝BD2＋AD2，∴(2BD)2＝BD2＋AD2，BD.∴S△ABC＝12BC·AD＝12(BD＋DC)·AD＝12＋＝9＋15、36平方米【解析】连接AC，根据勾股定理，求得AC，再根据勾股定理的逆定理，判断三角形ACD是直角三角形．这块草坪的面积等于两个直角三角形的面积之和．【详解】连接AC，如图，∵AB⊥BC，∴∠ABC=90°．∵AB=3米，BC=4米，∴AC=5米．∵CD=12米，DA=13米，∴CD2+AC2=144+25=169=132=DA2，∴∠ACD=90°，∴△ACD为直角三角形，∴草坪的面积等于=S△ABC+S△ACD=3×4÷2+5×12÷2=6+30=36（米2）．本题考查了勾股定理和勾股定理的逆定理．16、（1）证明见解析；（2）EF-FG=233-1.【解析】分析：（1）首先根据角与角之间的等量代换得到∠ABF =∠DAE ，结合AB =AD ，∠AED =∠BFA ，利用AAS 证明△ABF ≌△DAE ，即可得到AE =BF ；（2）首先求出BF 和AE 的长度，然后在Rt △BFG 中求出BG =2FG ，利用勾股定理得到BG 2=FG 2+BF 2，进而求出FG 的长，于是可得EF ﹣FG 的值．详解：（1）∵四边形ABCD 是正方形，∴AB =AD ，∠BAF +∠DAE =∠BAD =90°．又∵DE ⊥AG ，BF ∥DE ，∴∠AED =∠BFA =90°．∵∠BAF +∠ABF =90°，∴∠ABF =∠DAE．在△ABF 和△DAE中，AB AD ABF DAE AED BFA =⎧⎪∠=∠⎨⎪∠=∠⎩，∴△ABF ≌△DAE （AAS），∴AE =BF ；（2）∵∠BAG =30°，AB =2，∠BEA =90°，∴BF =12AB =1，AF=，∴EF =AF ﹣AE =AF ﹣BF﹣1．∵BF ⊥AG ，∠ABG =90°，∠BAG=30°，∴∠FBC =30°，∴BG =2FG ，由BG 2=FG 2+BF 2，∴4FG 2=FG 2+1，∴FG =3，∴EF ﹣FG 1﹣3=3﹣1．点睛：本题主要考查了正方形的性质、全等三角形的判定与性质以及勾股定理等知识，解答本题的关键是根据AAS 证明△ABF ≌△DAE ，此题难度一般．17、3m ，【解析】先根据分式混合运算的法则把原式进行化简，再把m 的值代入进行计算即可．【详解】解：原式=()()()221133611m m m m m m m +-+⨯-+-=3m ，当时，原式．本题考查分式的化简求值，解题的关键是熟练运用分式混合运算的法则，本题属于基础题型．18、（1）v 关于t 的函数表达式为v ＝900t ，自变量的取值范围为t ＞0；（2）放水速度的范围为300≤x ≤360立方米/小时．【解析】（1）由题意得vt ＝900，即v ＝900t ，自变量的取值范围为t ＞0，（2）把t ＝2.5，t ＝3代入求出相应的v 的值，即可求出放水速度的范围．【详解】（1）由题意得：vt ＝900，即：v ＝900t ，答：（2）当t ＝2.5时，v ＝9002.5＝360，当t ＝3时，v ＝9003＝300，所以放水速度的范围为300≤v ≤360立方米/小时，答：所以放水速度的范围为300≤x ≤360立方米/小时．考查求反比例函数的关系式以及反比例函数图象上点的坐标特点，解题关键在于根据常用的数量关系得出函数关系式．一、填空题（本大题共5个小题，每小题4分，共20分）19、70°【解析】根据三角形的内角和等于180°，求出∠OBC+∠OCB ，再根据角平分线的定义求出∠ABC+∠ACB ，然后利用三角形的内角和等于180°，列式计算即可得解．【详解】解：∵125BOC ∠=︒，∴∠OBC+∠OCB=180°-125°=55°，∵BO 平分∠ABC ，CO 平分∠ACB ，∴∠ABC=2∠OBC ，∠ACB=2∠OCB ，∴∠A=180°-110°=70°；故答案为：70°.此题考查了三角形的内角和定理，角平分线的定义，整体思想的利用是解题的关键．20、k＞1【解析】∵关于x的一元二次方程x1﹣1x+k﹣1=0没有实数根，∴△＜0，即（﹣1）1﹣4（k﹣1）＜0，解得k＞1，故答案为k＞1．21、40【解析】根据平移的性质可得CF=BE=5，然后根据平行四边形的面积公式即可解答.【详解】由平移的性质可得：CF=BE=5,∵AB⊥BF，∴四边形ACFD的面积为：AB·CF=8×5=40，故答案为40.本题考查了平移的性质和平行四边形面积公式，掌握平移的性质和平行四边形面积公式是解题的关键.22、y＝－2x+1【解析】根据上下平移时只需让b的值加减即可，进而得出答案即可．解：原直线的k=-2，b=0；向上平移1个单位得到了新直线，那么新直线的k=-2，b=0+1=1．故新直线的解析式为：y=-2x+1．故答案为y=-2x+1．“点睛”此题主要考查了一次函数图象与几何变换，求直线平移后的解析式时要注意平移时k的值不变，只有b发生变化．23、小明【解析】观察图象可得：小明的成绩较集中，波动较小，即方差较小，故小明的成绩较为稳定．【详解】解：根据图象可直接看出小明的成绩波动不大，根据方差的意义知，波动越小，成绩越稳定，故答案为：小明．此题主要考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．二、解答题（本大题共3个小题，共30分）24、（1）一次函数的解析式为23y x =-+；（2）n 的最大值是9.【解析】试题分析：（1）把x=2，y=-1代入函数y=kx+b ，得出方程组，求出方程组的解即可；（2）把P 点的坐标代入函数y=-2x+3，求出m 的值，根据已知得出不等式组，求出不等式组的解集即可．试题解析：（1）依题意得：21,5.k b k b +=-⎧⎨-+=⎩解得，2,3.k b =-⎧⎨=⎩∴一次函数的解析式为y 2x 3=-+.(2)由（1）可得，y 2x 3=-+.∵点P (m ,n )是此函数图象上的一点,∴n 2m 3=-+即3nm 2-=，又∵3m 2-≤≤，∴3n322--≤≤解得，1n 9-≤≤.25、（1）200-x，240-x，x+60；（2）y A＝－5x＋5000，y B＝3x＋4680；（3）40＜x≤200时，y A＜y B，A村运费较少，x＝40时，y A＝y B，,两村运费一样，x＜40时，B村运费较少（4）由A村运往C库50吨，运D库150吨，而B村运往C库190吨，运D库110吨则两村运费之和最小，为9580元【解析】（1）结合题意用含x的代数式表示填写即可;（2）利用运送的吨数×每吨运输费用=总费用，列出函数解析式即可解答；（3）由（1）中的函数解析式联立方程与不等式解答即可；（4）首先由B村的荔枝运费不得超过4830元得出不等式，再由两个函数和，根据自变量的取值范围，求得最值．【详解】解：（1）A，B两村运输荔枝情况如表，收收地地运运地地C D总计A x吨200-x200吨B240-x x+60300吨总计240吨260吨500吨（2）y A=20x+25（200-x）=5000-5x，y B=15（240-x）+18（x+60）=3x+4680；（3）①当y A=y B，即5000-5x=3x+4680，解得x=40，当x=40，两村的运费一样多，②当y A＞y B，即5000-5x＞3x+4680，解得x＜40，当0＜x＜40时，A村运费较高，③当y A＜y B，即5000-5x＜3x+4680，解得x＞40，当40＜x≤200时，B村运费较高；（4）B村的荔枝运费不得超过4830元，y B=3x+4680≤4830，解得x≤50，两村运费之和为y A+y B=5000-5x+3x+4680=9680-2x，要使两村运费之和最小，所以x的值取最大时，运费之和最小，故当x=50时，最小费用是9680-2×50=9580（元）．26、(1)4元/瓶．(2)销售单价至少为1元/瓶．【解析】（1）设第一批饮料进货单价为x元/瓶，则第二批饮料进货单价为（x+2）元/瓶，根据数量＝总价÷单价结合第二批购进饮料的数量是第一批的3倍，即可得出关于x的分式方程，解之经检验后即可得出结论；（2）由数量＝总价÷单价可得出第一、二批购进饮料的数量，设销售单价为y元/瓶，根据利润＝销售单价×销售数量﹣进货总价结合获利不少于2100元，即可得出关于y的一元一次不等式，解之取其最小值即可得出结论．【详解】（1）设第一批饮料进货单价为x元/瓶，则第二批饮料进货单价为（x+2）元/瓶，依题意，得：81002x ＝3×1800x，解得：x＝4，经检验，x＝4是原方程的解，且符合题意．答：第一批饮料进货单价是4元/瓶；（2）由（1）可知：第一批购进该种饮料450瓶，第二批购进该种饮料1350瓶．设销售单价为y元/瓶，依题意，得：（450+1350）y﹣1800﹣8100≥2100，解得：y≥1．答：销售单价至少为1元/瓶．正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式．。

河南省郑州市郑州外国语学校2024-2025学年数学九年级第一学期开学综合测试试题题号一二三四五总分得分批阅人A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）已知一组数据共有20个数，前面14个数的平均数是10，后面6个数的平均数是15，则这20个数的平均数是（）A ．23B ．1.15C ．11.5D ．12.52、（4分）如图，将ABC 绕点A 顺时针旋转70°后，得到ADE ，下列说法正确的是（）A ．点B 的对应点是点E B ．∠CAD=70°C ．AB=DE D ．∠B=∠D 3、（4分）以下列各组数为边长，能组成直角三角形的是（）A ．1，2，3B ．2，3，4C ．3，4，6D ．124、（4分）a 的取值范围是（）A ．a ＜1B ．a≤1C ．a≥1D ．a ＞15、（4分）七巧板是我国祖先的一项卓越创造．下列四幅图中有三幅是小明用如图所示的七巧板拼成的，则不是小明拼成的那副图是（）A ．B ．C ．D ．6、（4分）有意义，那么x 的范围在数轴上表示为（）A ．B ．C ．D ．7、（4分）湖州是“两山”理论的发源地，在一次学校组织的以“学习两山理论，建设生态文明”为主题的知识竞赛中，某班6名同学的成绩如下（单位：分）：97,99,95,92,92,93，则这6名同学的成绩的中位数和众数分别为（）A ．93分，92分B ．94分，92分C ．94分，93分D ．95分，95分8、（4分）x 的取值范围是（）A ．2x ≠B ．2x ≥C ．2x >D ．0x ≥二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）已知点A （a ,b ）是一次函数3y x =-+的图像与反比例函数1y x =的图像的一个交点，则11a b +=___．10、（4分）若1x =，则代数式221x x ++的值为__________．11、（4分）如图，在矩形ABCD 中，AD=9cm ，AB=3cm ，将其折叠，使点D 与点B 重合，则重叠部分(△BEF)的面积为_________cm 2.12、（4分）将直线y=2x-3向上平移5个单位可得______直线．13、（4分）若方程组2x y b x y a +=⎧⎨-=⎩的解是13x y =-⎧⎨=⎩，则直线y ＝﹣2x+b 与直线y ＝x ﹣a 的交点坐标是_____．三、解答题（本大题共5个小题，共48分）14、（12分）某蛋糕店为了吸引顾客，在A 、B 两种蛋糕中，轮流降低其中一种蛋糕价格，这样形成两种盈利模式，模式一：A 种蛋糕利润每盒8元，B 种蛋糕利润每盒15元；模式二：A 种蛋糕利润每盒14元，B 种蛋糕利润每盒11元每天限定销售A 、B 两种蛋糕共40盒，且都能售完，设每天销售A 种蛋糕x 盒（1）设按模式一销售A 、B 两种蛋糕所获利润为y 1元，按模式二销售A 、B 两种蛋糕所获利润为y 2元，分别求出y 1、y 2关于x 的函数解析式；（2）在同一个坐标系内分别画出(1)题中的两个函数的图象；（3）若y 始终表示y 1、y 2中较大的值，请问y 是否为x 的函数，并说说你的理由，并直接写出y 的最小值．15、（8分）四边形ABCD 是正方形，E 、F 分别是DC 和CB 的延长线上的点，且DE=BF ，连接AE 、AF 、EF ．（1）求证：△ADE ≌△ABF ；（2）填空：△ABF 可以由△ADE 绕旋转中心点，按顺时针方向旋转度得到；（3）若BC=8，DE=6，求△AEF 的面积．16、（8分）如图，在△ABC 中，CF ⊥AB 于点F ，BE ⊥AC 于点E ，M 为BC 的中点连接ME 、MF 、EF ．（1）求证：△MEF 是等腰三角形；（2）若∠A=70 ，∠ABC=50°，求∠EMF 的度数．17、（10分）嘉淇同学要证明命“两相对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图的四边形ABCD ，并写出了如下不完整的已知和求证．已知：如图，在四边形ABCD 中，BC ＝AD ，AB ＝____．求证：四边形ABCD 是____四过形．（1）在方框中填空，以补全已知和求证；（2）按嘉淇的想法写出证明：证明：（3）用文宇叙述所证命题的逆命题为____________________．18、（10分）在平面直角坐标系xOy 中，点P 在函数的图象上，过P 作直线轴于点A ，交直线于点M ，过M 作直线轴于点B .交函数的图象于点Q 。

安徽省亳州市蒙城中学2024-2025学年数学九年级第一学期开学检测试题题号一二三四五总分得分A 卷（100分）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、（4分）下列各式不能用平方差公式法分解因式的是（）A ．x 2﹣4B ．﹣x 2﹣y 2C ．m 2n 2﹣1D ．a 2﹣4b 22、（4分）▱ABCD 中，对角线AC 与BD 相交于点E ，将△ABC 沿AC 所在直线翻折至△AB ′C ，若点B 的落点记为B ′，连接B ′D 、B ′C ，其中B ′C 与AD 相交于点G ．①△AGC 是等腰三角形；②△B ′ED 是等腰三角形；③△B ′GD 是等腰三角形；④AC ∥B ′D ；⑤若∠AEB ＝45°，BD ＝2，则DB ′；其中正确的有（）个．A ．2B ．3C ．4D ．53、（4分）若a 为有理数，且满足|a |+a=0，则（）A ．a ＞0B ．a ≥0C ．a ＜0D ．a ≤04、（4分）图中两直线L 1，L 2的交点坐标可以看作方程组()的解．A ．121x y x y -=⎧⎨-=-⎩B ．121x y x y -=-⎧⎨-=⎩C ．321x y x y -=⎧⎨-=⎩D ．321x y x y -=⎧⎨-=-⎩5、（4分）小明坐滴滴打车前去火车高铁站，小明可以选择两条不同路线：路线A 的全程是25千米，但交通比较拥堵，路线B 的全程比路线A 的全程多7千米，但平均车速比走路线A 时能提高60%，若走路线B 的全程能比走路线A 少用15分钟．若设走路线A 时的平均速度为x 千米/小时，根据题意，可列分式方程()A ．25321.6x x -＝15B ．3225151.6x x -=C ．322511.64x x -=D ．253211.64x x -=6、（4分）下列函数的图象经过()0,1，且y 随x 的增大而减小的是（）A ．y x=-B ．1y x =-C ．21y x =+D ．1y x =-+7、（4分）在平面直角坐标系中，点A 坐标为（2，2），点P 在x 轴上运动，当以点A ，P 、O 为顶点的三角形为等腰三角形时，点P 的个数为（）A ．2个B ．3个C ．4个D ．5个8、（4分）如图，天平右盘中的每个砝码的质量都是1g ，则物体A 的质量m(g)的取值范围，在数轴上可表示为（）A ．B ．C ．D ．二、填空题（本大题共5个小题，每小题4分，共20分）9、（4分）写出在抛物线244y x x =--上的一个点________．10、（4分）实数,a b 在数轴上的对应点的位置如图所示，则__________．11、（4分）如图，两个完全相同的三角尺ABC 和DEF 在直线l 上滑动．要使四边形CBFE 为菱形，还需添加的一个条件是____(写出一个即可)．12、（4分）若代数式241x x +-的值比232x x -的值大3，则x 的值为______.13、（4分）如图，在菱形ABCD 中，点E 是AD 的中点，对角线AC ，BD 交于点F ，若菱形ABCD 的周长是24，则EF=______.三、解答题（本大题共5个小题，共48分）14、（12分）A 、B 两种机器人都被用来搬运化工原料，A 型机器人比B 型机器人每小时多搬运30kg ，A 型机器人搬运900kg 与B 型机器人搬运600kg 所用时间相等，两种机器人每小时分别搬运多少化工原料？15、（8分）经销店为厂家代销一种新型环保水泥，当每吨售价为260元时，月销售量为45吨，每售出1吨这种水泥共需支付厂家费用和其他费用共100元．该经销店为扩大销售量、提高经营利润，计划采取降价的方式进行促销，经市场调查发现，当每吨售价每下降10元时，月销售量就会增加7.5吨．（1）当每吨售价是240元时，此时的月销售量是多少吨.（2）该经销店计划月利润为9000元而且尽可能地扩大销售量，则售价应定为每吨多少元？16、（8分）如图，在ABC 中，100BAC ∠=︒，将ABC 绕点A 逆时针旋转150︒，得到ADE ，使得点B 、C 、D 恰好在同一条直线上，求E ∠的度数．17、（10分）我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单，为了尽快交货，增开了一条生产线，实际每月生产能力比原计划提高了50%，结果比原计划提前5个月完成交货，求每月实际生产智能手机多少万部．18、（10分）2018年5月，某城遭遇暴雨水灾，武警战士乘一冲锋舟从A 地逆流而上，前往C 地营救受困群众，途经B 地时，由所携带的救生艇将B 地受困群众运回A 地，冲锋舟继续前进，到C 地接到群众后立刻返回A 地，途中曾与救生艇相遇，冲锋舟和救生艇距A 地的距离y （千米）和冲锋舟出发后所用时间x （分）之间的函数图象如图所示，假设群众上下冲锋舟和救生艇的时间忽略不计，水流速度和冲锋舟在静水中的速度不变．（1）冲锋舟从A 地到C 地的时间为分钟，冲锋舟在静水中的速度为千米/分，水流的速度为千米/分．（2）冲锋舟将C 地群众安全送到A 地后，又立即去接应救生艇，已知救生艇与A 地的距离y （千米）和冲锋舟出发后所用时间x （分钟）之间的函数关系式为y ＝kx+b ，若冲锋舟在距离A 地203千米处与救生艇第二次相遇，求k 、b 的值．B 卷（50分）一、填空题（本大题共5个小题，每小题4分，共20分）19、（4分）若一个正多边形的内角和是其外角和的3倍，则这个多边形的边数是______．20、（4分）如图，在等腰梯形ABCD 中，AB ∥CD ，AD AB =，BD ⊥BC ，则∠C =________．21、（4分）观察下列各式：112⨯，123⨯，134⨯，……请利用你所发现的规律，+…+，其结果为_______．22、（4分）如图，在正方形ABCD 中，边长为2的等边三角形AEF 的顶点E 、F 分别在BC 和CD 上，下列结论：①CE=CF ；②∠AEB=75°；③BE+DF=EF ；④S 正方形ABCD =2+．其中正确的序号是（把你认为正确的都填上）．23、（4分）顺次连接等腰梯形各边中点所得的四边形是_____．二、解答题（本大题共3个小题，共30分）24、（8分）如图，AD 是△ABC 边BC 上的高，用尺规在线段AD 上找一点E ，使E 到AB 的距离等于ED (不写作法，保留作图痕迹)25、（10分）计算：-(2)34(3)()21-26、（12分）如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC 的长为13米，此人以0.5米/秒的速度收绳，6秒后船移动到点D 的位置，问船向岸边移动了大约多少米？（假设绳子是直的，结果精确到0.1米， 1.414≈ 1.732≈）一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）1、B【解析】利用平方差公式的结构特征判断即可．【详解】解：下列各式不能用平方差公式法分解因式的是-x2-y2，故选：B．本题考查了用平方差公式进行因式分解，熟练掌握是解题的关键.2、D【解析】利用平行四边形的性质、翻折不变性一一判断即可解决问题；【详解】解：∵四边形ABCD是平行四边形，∴BE＝DE，AD∥BC，AD＝BC，∴∠GAC＝∠ACB，由翻折可知：BE＝EB′＝DE，∠ACB＝∠ACG，CB＝CB′，∴∠GAC＝∠ACG，∴△AGC，△B′ED是等腰三角形，故①②正确，∵AB′＝AB＝DC，CB′＝AD，DB′＝B′D，∴△ADB′≌△CB′D，∴∠ADB′＝∠CB′D，∴GD＝GB′，∴△B′GD是等腰三角形，故③正确，∵∠GAC＝∠GCA，∠AGC＝∠DGB′，∴∠GAC＝∠GDB′，∴AC∥DB′，故④正确．∵∠AEB＝45°，BD＝2，∴∠BEB ′＝∠DEB ′＝90°，∵DE ＝EB ′＝1，∴DB ′，故⑤正确．故选：D ．本题考查翻折变换、等腰三角形的性质、平行四边形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．3、D 【解析】试题解析：0a a +=，a a ，∴=-0a ∴≤，即a 为负数或1．故选D ．4、B 【解析】分析：根据图中信息分别求出直线l 1和l 2的解析式即可作出判断.详解：设直线l 1和l 2的解析式分别为1122 y k x b y k x b ，=+=+，根据图中信息可得：111231k b b +=⎧⎨=-⎩，2222230k b k b +=⎧⎨-+=⎩，解得：1121k b =⎧⎨=-⎩，2211k b =⎧⎨=⎩，∴l 1和l 2的解析式分别为211y x y x =-=+，，即21x y -=，1x y -=-，∴直线l 1和l 2的交点坐标可以看作方程121x y x y -=-⎧⎨-=⎩的交点坐标.故选B.点睛：根据图象中的信息由待定系数法求得直线l 1和l 2的解析式是解答本题的关键.5、D 【解析】解：设走路线A 时的平均速度为x 千米/小时，根据题意得：25x ﹣321.6x =14．故选D ．6、D 【解析】根据一次函数的性质，k ＜0，y 随x 的增大而减小，找出各选项中k 值小于0的选项即可．再把点()0,1代入，符合的函数解析式即为答案.【详解】A.y x =-，当x=0时，y=0，图象不经过()0,1，不符合题意;B.,1y x =-，当x=0时，y=-1，图象不经过()0,1，不符合题意;C.21y x =+，k=2>0，y 随x 的增大而增大,不符合题意;D.y=-x+1，当x=0时，y=1，图象经过()0,1,k=-1<0，y 随x 的增大而减小本题考查了一次函数图像的性质，判断函数图像是否经过点，把点的x 坐标代入求y 坐标，如果y 值相等则函数图像经过点，如不相等则不经过，当k>o,y 随x 的增大而增大，,当k<0，y 随x 的增大而减小.7、C 【解析】先分别以点O 、点A 为圆心画圆，圆与x 轴的交点就是满足条件的点P ，再作OA 的垂直平分线，与x 轴的交点也是满足条件的点P ，由此即可求得答案.【详解】如图，当OA=OP 时，可得P 1、P 2满足条件，当OA=AP 时，可得P 3满足条件，当AP=OP 时，可得P 4满足条件，故选C.本题考查了等腰三角形的判定和坐标与图形的性质，正确的分类并画出图形是解题的关键.8、A 【解析】∵由图可知，1g<m<2g ，∴在数轴上表示为：。