=90°→ kmax
a b
E
于是 kmax=d /l=10
p
缺级:
k d k 4k 4,8 a
o 屏上实际呈现: 0,±1,±2,±3,±5,±6, ±7,±9共8级,15条亮纹(±10在 无穷远处,看不见)。
f
例:一光栅的光栅常数d=2.1×10-6m,透光缝宽a=0.7×10-6, 用波长l=5000Å的光、以i=30°的入射角照射,求能看见几级、 几条谱线。
§14.1光的衍射现象和惠更斯-菲涅耳原理
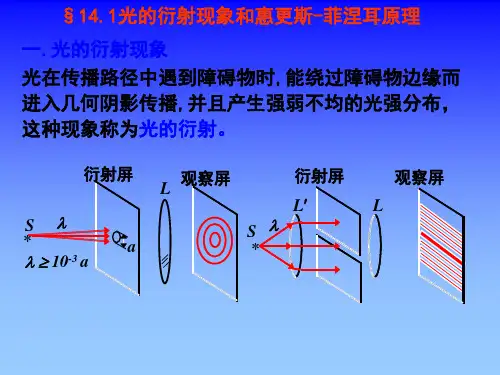
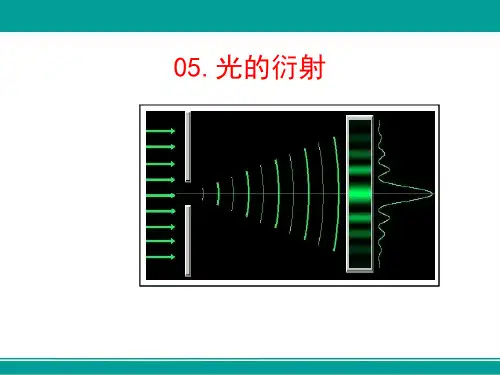
一.光的衍射现象 光在传播路径中遇到障碍物时,能绕过障碍物边缘而 进入几何阴影传播,并且产生强弱不均的光强分布, 这种现象称为光的衍射。
衍射屏
Sl
*
a
l10-3 a
观察屏 L
衍射屏
L
Sl
*
观察屏 L
二.惠更斯-菲涅耳原理
惠更斯原理:媒质中波所传到的各点都可看作是发射子波的波
例:(1)b=a, d=a+b=2a,则 k=2k =±2,4,6,…级缺。
(2)b=2a, d=a+b=3a, 则 k=3k =±3,6,9,…级缺。
讨论d和l 对衍射图样的影响
d sin kl (k 0,1,2,)
k 1,
s in k 1
sink
l
d
光栅常数越小,明纹越窄,明纹间相隔越远.
2
a sinθ (2k 1) l 亮纹 (k=1,2,3,…)
2
θ 0 零级(中央)亮纹
波带数
S
*
A
a
C B
p
注意:
1.k=1...
2.明暗…
o
3. ...
4.波带数