粒子滤波的公式和matlab
- 格式:doc
- 大小:204.50 KB
- 文档页数:5

MATLAB粒子滤波重采样1. 简介粒子滤波(Particle Filter)是一种基于蒙特卡洛方法的滤波算法,用于在非线性和非高斯系统中进行状态估计。
粒子滤波通过使用一组粒子来近似系统的后验概率分布,从而实现对系统状态的估计。
重采样是粒子滤波算法中的一个重要步骤,用于根据粒子的权重对粒子进行重新采样,以提高估计的准确性。
在本文中,我们将使用MATLAB编写粒子滤波算法,并实现重采样步骤。
2. 粒子滤波算法步骤粒子滤波算法通常包括以下步骤:1.初始化粒子集合:根据先验分布或已知信息,生成一组随机粒子,表示系统的可能状态。
2.预测步骤:根据系统的动力学模型,对粒子进行状态预测。
3.更新步骤:使用测量模型和观测值对粒子进行权重更新。
4.规范化权重:对粒子的权重进行规范化,使其总和等于1。
5.重采样步骤:根据粒子的权重,对粒子进行重新采样,以提高估计的准确性。
6.重复步骤2-5,直到达到停止条件。
在本文中,我们将重点关注重采样步骤的实现。
3. 粒子滤波重采样算法重采样步骤的目标是根据粒子的权重,从当前粒子集合中生成新的粒子集合,以便更好地表示后验概率分布。
常用的重采样方法包括多项式重采样和系统性重采样。
下面是系统性重采样算法的伪代码:1. 初始化:给定粒子集合P和对应的权重W。
2. 计算累积权重:计算累积权重C,其中C(i) = sum(W(1:i)),i为粒子的索引。
3. 生成随机数:生成一个均匀分布的随机数r,取值范围为[0, 1]。
4. 重采样:对于每个粒子i,找到满足C(j) > r且C(j-1) <= r的最小索引j,将粒子j 添加到新的粒子集合中。
5. 返回新的粒子集合。
下面是MATLAB代码实现粒子滤波重采样的函数:numParticles = size(particles, 2);newParticles = zeros(size(particles));cumulativeWeights = cumsum(weights);r = rand(1) / numParticles;index = 1;for i = 1:numParticlesu = r + (i - 1) / numParticles;while cumulativeWeights(index) < uindex = index + 1;endnewParticles(:, i) = particles(:, index);endend4. 示例应用为了演示粒子滤波重采样算法的应用,我们将使用一个简单的二维机器人定位问题。

粒子滤波(PF)MATLAB实现程序x = 0; % 初始状态R = input('请输入过程噪声方差R的值: ');; % 测量噪声协方差Q = input('请输入观测噪声方差Q的值: '); % 过程状态协方差tf = 100; % 模拟长度N = 100; % 粒子滤波器中的粒子个数xhat = x;P = 2;xhatPart = x;%粒子滤波器初期for i = 1 : Nxpart(i) = x + sqrt(P) * randn;endxArr = [x];yArr = [x^2 / 20 + sqrt(R) * randn];xhatArr = [x];PArr = [P];xhatPartArr = [xhatPart];close all;for k = 1 : tf% 模拟系统x = 0.5 * x + 25 * x / (1 + x^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;y = x^2 / 20 + sqrt(R) * randn;% 粒子滤波器for i = 1 : Nxpartminus(i) = 0.5 * xpart(i) + 25 * xpart(i) / (1 + xpart(i)^2) + 8 * cos(1.2*(k-1)) + sqrt(Q) * randn;ypart = xpartminus(i)^2 / 20;vhat = y - ypart;% 观测和预测的差q(i) = (1 / sqrt(R) / sqrt(2*pi)) * exp(-vhat^2 / 2 / R); end% 平均每一个估计的可能性qsum = sum(q);for i = 1 : Nq(i) = q(i) / qsum;%归一化权值end% 重采样for i = 1 : Nu = rand;qtempsum = 0;for j = 1 : Nqtempsum = qtempsum + q(j);if qtempsum >= uxpart(i) = xpartminus(j);break;endendendxhatPart = mean(xpart);% 在图片中表示出数据xArr = [xArr x];yArr = [yArr y];xhatArr = [xhatArr xhat];PArr = [PArr P];xhatPartArr = [xhatPartArr xhatPart];endt = 0 : tf;figure;plot(t, xArr, 'b.', t, xhatPartArr, 'k-');set(gca,'FontSize',10); set(gcf,'Color','yellow'); xlabel('time step'); ylabel('state');legend('真实值', 'PF估计值');xhatRMS = sqrt((norm(xArr - xhatArr))^2 / tf); xhatPartRMS = sqrt((norm(xArr - xhatPartArr))^2 / tf); disp(['PF估计误差均方值= ', num2str(xhatPartRMS)]);。

以下是一个简单的 MATLAB 粒子滤波器的代码示例:```matlab% 初始化参数N = 100; % 粒子数量dt = 0.1; % 时间步长x = [0 0]; % 初始位置P = eye(2); % 初始协方差矩阵Q = eye(2); % 过程噪声协方差矩阵R = eye(2); % 观测噪声协方差矩阵G = [0.9 0.1; 0.1 0.9]; % 转换矩阵N_particles = size(Q,1); % 粒子数量particles = zeros(N_particles,2); % 初始化粒子particles(:,1) = x(1); % 设置粒子的 x 分量particles(:,2) = x(2); % 设置粒子的 y 分量weights = ones(N_particles,1) / N_particles; % 初始化权重% 模拟观测数据z = [1.2 0.5]; % 观测位置R_inv = inv(R); % 观测噪声协方差矩阵的逆H = [z(1) -z(2); z(2) z(1)]; % 观测矩阵y = H * x; % 预测的观测值% 粒子滤波步骤for t = 1:100% 重采样步骤weights = weights / sum(weights);index = randsample(1:N_particles, N, true, weights); particles = particles(index,:);% 预测步骤x_pred = particles;P_pred = Q;x_pred = G * x_pred;P_pred = P_pred + dt * G * P_pred;P_pred = P_pred + P_pred * G' + R;% 更新步骤y_pred = H * x_pred;S = H * P_pred * H' + R_inv;K = P_pred * H' * inv(S);x = x_pred + K * (z - y_pred);P = P_pred - P_pred * K * H';end```在这个代码示例中,我们使用了两个步骤:重采样步骤和预测/更新步骤。


一、介绍粒子滤波算法粒子滤波算法是一种基于蒙特卡洛方法的非线性、非高斯滤波算法,它通过一组随机产生的粒子来近似表示系统的后验概率分布,从而实现对非线性、非高斯系统的状态估计。
在实际应用中,粒子滤波算法被广泛应用于目标跟踪、导航、机器人定位等领域。
本文将以matlab 实例的形式介绍粒子滤波算法的基本原理和应用。
二、粒子滤波算法的原理及步骤粒子滤波算法的主要原理是基于贝叶斯滤波理论,通过一组随机产生的粒子来近似表示系统的后验概率分布。
其具体步骤如下:1. 初始化:随机生成一组粒子,对于状态变量的初始值和方差的估计,通过随机抽样得到一组粒子。
2. 预测:根据系统模型,对每个粒子进行状态预测,得到预测状态。
3. 更新:根据测量信息,对每个预测状态进行权重更新,得到更新后的状态。
4. 重采样:根据更新后的权重,对粒子进行重采样,以满足后验概率分布的表示。
5. 输出:根据重采样后的粒子,得到对系统状态的估计。
三、粒子滤波算法的matlab实例下面以一个简单的目标跟踪问题为例,介绍粒子滤波算法在matlab中的实现。
假设存在一个目标在二维空间中运动,我们需要通过一系列测量得到目标的状态。
我们初始化一组粒子来近似表示目标的状态分布。
我们根据目标的运动模型,预测每个粒子的状态。
根据测量信息,对每个预测状态进行权重更新。
根据更新后的权重,对粒子进行重采样,并输出对目标状态的估计。
在matlab中,我们可以通过编写一段简单的代码来实现粒子滤波算法。
我们需要定义目标的运动模型和测量模型,然后初始化一组粒子。
我们通过循环来进行预测、更新、重采样的步骤,最终得到目标状态的估计。
四、总结粒子滤波算法是一种非线性、非高斯滤波算法,通过一组随机产生的粒子来近似表示系统的后验概率分布。
在实际应用中,粒子滤波算法被广泛应用于目标跟踪、导航、机器人定位等领域。
本文以matlab实例的形式介绍了粒子滤波算法的基本原理和应用,并通过一个简单的目标跟踪问题,展示了粒子滤波算法在matlab中的实现过程。

pf算法举例及其matlab实现-概述说明以及解释1.引言1.1 概述PF算法(Particle Filter Algorithm),又称为粒子滤波算法,是一种基于蒙特卡洛方法的非线性滤波算法。
与传统的滤波算法相比,PF算法具有更大的灵活性和鲁棒性,在估计复杂非线性系统状态的过程中表现出良好的性能。
PF算法基于一种随机采样的思想,通过对系统状态进行一系列粒子的采样,再通过对这些粒子的权重进行重要性重采样,最终获得对状态估计的准确性更高的结果。
在PF算法中,粒子的数量决定了滤波算法的精度,粒子越多,估计结果越准确,但也会增加计算复杂度。
因此,在实际应用中需要根据实际情况灵活选择粒子数量。
作为一种高效的滤波算法,PF算法在众多领域都有广泛的应用。
例如,粒子滤波算法在目标跟踪、传感器网络定位、机器人定位与导航等领域都有着重要的作用。
其在目标跟踪领域的应用尤为突出,由于PF算法可以处理非线性和非高斯分布的情况,使得目标跟踪更加准确和稳定。
在Matlab中,PF算法也得到了广泛的应用和实现。
Matlab提供了丰富的函数和工具箱,可以便捷地实现PF算法。
借助Matlab的强大数据处理和可视化功能,我们可以更加便捷地进行粒子滤波算法的实现和结果分析。
本文将从PF算法的基本概念出发,介绍其应用举例和在Matlab中的具体实现。
通过对PF算法的研究和实践,我们可以更好地理解和应用这一强大的滤波算法,为实际问题的解决提供有效的手段。
通过对Matlab 的使用,我们还可以更加高效地实现和验证粒子滤波算法的性能,为进一步的研究和应用奠定基础。
在接下来的章节中,我们将详细介绍PF算法的原理及其在现实应用中的具体案例。
随后,我们将展示如何使用Matlab实现PF算法,并通过实验结果对其性能进行评估和分析。
最后,我们将总结PF算法和Matlab 实现的主要特点,并对未来的发展进行展望。
文章结构的设定在撰写一篇长文时非常重要,它能够为读者提供一个整体的概览,帮助他们更好地理解文章的内容安排。

在MATLAB中使用粒子滤波进行状态估计Introduction:在许多实时系统或者控制系统中,状态估计是至关重要的一环。
状态估计涉及通过测量数据来推断或估计系统的当前状态。
而粒子滤波(Particle filter)作为一种无模型非线性滤波器,被广泛应用于状态估计问题中。
在本文中,我们将重点介绍如何在MATLAB中使用粒子滤波进行状态估计。
Particle filter基本原理:粒子滤波基于贝叶斯滤波理论,并通过一系列随机样本表示系统的可能状态。
它的基本原理是通过一个粒子集合来近似表示系统状态的概率密度函数。
粒子滤波的核心思想是通过对每个状态进行加权采样来逼近概率密度函数。
粒子的数量越多,逼近的精度就越高,但同时计算量也会增加。
在粒子滤波算法中,每个粒子表示系统的一个假设状态,粒子的权重表示此假设状态的似然度。
而粒子的更新则通过重采样和预测两个步骤来实现。
重采样过程会根据粒子的权重来决定哪些粒子要留下来,而预测过程则通过系统动力学方程来生成新的粒子。
在状态估计问题中,粒子滤波可以通过将传感器测量数据与系统模型相结合,来估计系统的状态。
在MATLAB中使用粒子滤波:使用MATLAB进行粒子滤波非常方便,因为MATLAB提供了强大的工具箱和函数来支持粒子滤波算法,比如Statistics and Machine Learning Toolbox和Sensor Fusion and Tracking Toolbox。
在这里,我们将使用Statistics and Machine Learning Toolbox来进行演示。
步骤一: 初始化粒子集合首先,我们需要根据系统的先验信息,生成一组初始化的粒子。
我们可以根据先验概率密度函数来对粒子赋初值。
```MATLABnumParticles = 1000; % 粒子的数量particleSet = rand(numParticles, 2); % 初始化粒子集合```步骤二: 测量更新接下来,我们需要使用传感器测量数据来对粒子进行加权更新。

% 二维直线运动模型:%X=FX+V 状态模型%Z=[z1;z2] 观测模型clc;clear all;%%N1=300; %粒子数time=60;x_state(1)=1;vx(1)=5;y_state(1)=1;vy(1)=7;%%Process Noise Covariance%%%%%%%% 都是标准差xstate_noise=10; %没有用的参数Vx_noise=1;%%Measurement Noise Covariance%%%% 都是标准差theta_noise=0.1; %3/180*pidistance1_noise=3;xobs = [];yobs = [];theta1(1)=0;%%Ture State%%%%%%%%for i=2:time%% State model%%%%%%%%%%%accx = normrnd(0,Vx_noise,1,1);x_state(i)=x_state(i-1)+vx(i-1)+0.5*accx;vx(i)=vx(i-1)+accx;accy = normrnd(0,Vx_noise,1,1);y_state(i)=y_state(i-1)+vy(i-1)+0.5*accy;vy(i)=vy(i-1)+accy;end%%Measurement Value%%%%%for i=1:time%%Measure model%%%%%%%%%distance1(i)=sqrt(x_state(i)^2+y_state(i)^2)+distance1_noise*randn(1);%theta1(i)=atan(y_state(i)/x_state(i))+theta_noise*randn(1);%使用下面增加了象限判断的角度计算方式[-pi,pi]if x_state(i)>0 && y_state(i)>=0theta1(i) = atan(y_state(i)/x_state(i))+theta_noise*randn(1) ; %观测方程endif x_state(i)<0 && y_state(i)>=0theta1(i) = (atan(y_state(i)/x_state(i))+pi) +theta_noise*randn(1); %观测方程endif x_state(i)<0 && y_state(i)<=0theta1(i) = (atan(y_state(i)/x_state(i))-pi) +theta_noise*randn(1); %观测方程endif x_state(i)>0 && y_state(i)<=0theta1(i) = atan(y_state(i)/x_state(i)) +theta_noise*randn(1); %观测方程endxobs = [xobs distance1(i)*cos(theta1(i))];yobs = [yobs distance1(i)*sin(theta1(i))];end%%%Particle Filtering%%%%%%%%%%%%%%x_pf(1)=x_state(1);vx_pf(1)=vx(1);y_pf(1)=y_state(1);vy_pf(1)=vy(1);xp1=zeros(1,N1);xp2=zeros(1,N1);xp3=zeros(1,N1);xp4=zeros(1,N1); %%%%%Initial particles 得到初始化的粒子群%%%%%%%%for n=1:N1;%M1=[delta1*randn(1),delta2*randn(1),delta3*randn(1),delta4*randn(1)];%M1=diag(M1);xp1(n)=x_pf(1)+normrnd(0,Vx_noise,1,1);xp2(n)=vx_pf(1)+normrnd(0,Vx_noise,1,1);xp3(n)=y_pf(1)+normrnd(0,Vx_noise,1,1);xp4(n)=vy_pf(1)+normrnd(0,Vx_noise,1,1);end%**filter process*** angel and distance**************** for t=2:time%%%Prediction Process%%%%for n=1:N1accx = normrnd(0,Vx_noise,1,1);xpre_pf(n)=xp1(n)+xp2(n)+0.5*accx;vxpre_pf(n)=xp2(n)+accx;accy = normrnd(0,Vx_noise,1,1);ypre_pf(n)=xp3(n)+xp4(n)+0.5*accy;vypre_pf(n)=xp4(n)+accy;end%%%Calculate Weight Particles%%%%for n=1:N1vhat1=sqrt(xpre_pf(n)^2+ypre_pf(n)^2)-distance1(t);%vhat2=atan(ypre_pf(n)/xpre_pf(n))-theta1(t);%使用下面增加了象限判断的角度计算方式if xpre_pf(n)>0 && ypre_pf(n)>=0ag = atan(ypre_pf(n)/xpre_pf(n)) ; %观测方程endif xpre_pf(n)<0 && ypre_pf(n)>=0ag = (atan(ypre_pf(n)/xpre_pf(n))+pi); %观测方程endif xpre_pf(n)<0 && ypre_pf(n)<=0ag = (atan(ypre_pf(n)/xpre_pf(n))-pi) ; %观测方程endif xpre_pf(n)>0 && ypre_pf(n)<=0ag = atan(ypre_pf(n)/xpre_pf(n)); %观测方程endvhat2=ag-theta1(t);q1=(1/distance1_noise/sqrt(2*pi))*exp(-vhat1^2/2/distance1_noise^2);q2=(1/theta_noise/sqrt(2*pi))*exp(-vhat2^2/2/theta_noise^2);q(n)=q1*q2+1e-99;endq = q./sum(q);P_pf = cumsum(q);%%Resampling Process 这是一种均匀的重采样方法,随机数的产生不再是从[0,1]上任意产生,而是使这个随机数渐进式的增大,与权重累加和一样,都是交替上升,这样的比较更有规律性,更周到%%%%%%%%%%%%%%ut(1)=rand(1)/N1;k = 1;hp = zeros(1,N1);for j = 1:N1ut(j)=ut(1)+(j-1)/N1;while(P_pf(k)<ut(j));k = k + 1;end;hp(j) = k;q(j)=1/N1;end;xp1 = xpre_pf(hp); xp2 = vxpre_pf(hp); % The new particles xp3 = ypre_pf(hp); xp4 = vypre_pf(hp);%% Compute the estimate%%%%%%%%%%%%%x_pf(t)=mean(xp1);y_pf(t)=mean(xp3);end%%%%Result of Tracking%%%%%%%%%%%%% figure;plot(x_state,y_state,'r-*',x_pf,y_pf,'b-o',xobs,yobs,'g-d') xlabel('x state'); ylabel('y state');legend('实际轨迹','滤波轨迹','观测轨迹');set(gcf,'Color','White');%figure;%plot(1:time,distance_error,'r');%legend('distance error');。

粒子滤波matlab粒子滤波(Particle Filter)是一种基于蒙特卡洛方法的非线性贝叶斯滤波算法,广泛应用于目标跟踪、定位和状态估计等领域。
它在一些特定的问题中,如非线性、非高斯、非线性动态模型和非线性观测模型的情况下,表现出了良好的适应性和准确性。
本文将以MATLAB为例,一步一步介绍粒子滤波(Particle Filter)的原理和实现。
1. 粒子滤波的基本原理:粒子滤波是通过随机样本(粒子)来对目标状态进行估计的一种方法。
它通过构建一个粒子集合来代表目标状态空间上的概率密度函数,并按照贝叶斯滤波的理论进行权重更新和重采样,从而实现对目标状态的估计。
2. 粒子滤波的实现步骤:a) 初始化:根据已知的先验知识,初始化粒子集合。
粒子的初始状态可以根据先验分布随机生成,通常可以使用高斯分布进行初始化。
b) 预测/更新:根据系统的动态模型进行粒子的状态预测,然后根据观测模型,计算每个粒子与观测数据的相似度/权重。
c) 权重归一化:计算出所有粒子的权重之后,对权重进行归一化,使得所有权重之和等于1。
d) 重采样:根据权重对粒子进行重采样,即以一定的概率选取粒子,从而减少粒子集合中的多样性,提高粒子集合的估计准确性。
e) 重复以上步骤:重复预测/更新、权重归一化和重采样的步骤,直到满足终止条件(如达到最大迭代次数)或目标状态已被准确估计。
3. MATLAB中的粒子滤波实现:在MATLAB中,可以使用`particlefilter`函数来实现粒子滤波。
以下是一个简单的例子,演示如何使用MATLAB实现粒子滤波。
MATLAB% 设置粒子滤波参数numParticles = 1000; % 粒子数量maxIterations = 100; % 最大迭代次数% 初始化粒子集合initialParticles = initializeParticles(numParticles);% 初始化权重initialWeights = ones(numParticles, 1) / numParticles;% 创建粒子滤波对象pf = particlefilter(@predictionFcn, @observationFcn, initialParticles, initialWeights);pf.ResamplingMethod = 'systematic'; % 设置重采样方法% 遍历迭代for iteration = 1:maxIterations% 提取当前迭代的观测数据observation = getObservation(iteration);% 预测粒子的状态predictedParticles = predict(pf);% 更新粒子权重updatedWeights = update(pf, observation);% 完成一次迭代的粒子滤波estimate = estimate(pf);% 显示估计结果displayEstimate(estimate);end4. 粒子滤波的应用:粒子滤波广泛应用于目标跟踪、定位和状态估计等领域。

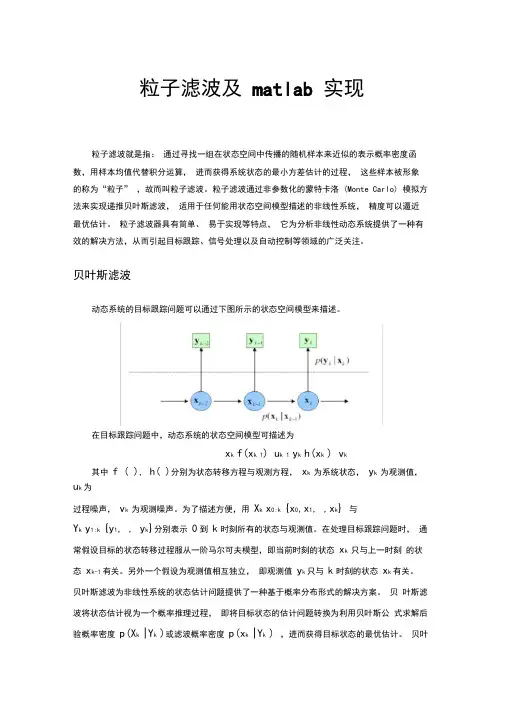
粒子滤波及matlab 实现粒子滤波就是指:通过寻找一组在状态空间中传播的随机样本来近似的表示概率密度函数,用样本均值代替积分运算,进而获得系统状态的最小方差估计的过程,这些样本被形象的称为“粒子” ,故而叫粒子滤波。
粒子滤波通过非参数化的蒙特卡洛 (Monte Carlo) 模拟方法来实现递推贝叶斯滤波,适用于任何能用状态空间模型描述的非线性系统,精度可以逼近最优估计。
粒子滤波器具有简单、易于实现等特点,它为分析非线性动态系统提供了一种有效的解决方法,从而引起目标跟踪、信号处理以及自动控制等领域的广泛关注。
贝叶斯滤波动态系统的目标跟踪问题可以通过下图所示的状态空间模型来描述。
在目标跟踪问题中,动态系统的状态空间模型可描述为x k f(x k 1) u k 1 y k h(x k ) v k其中f ( ), h( )分别为状态转移方程与观测方程,x k 为系统状态,y k 为观测值,u k为过程噪声,v k 为观测噪声。
为了描述方便,用X k x0:k {x0,x1, ,x k} 与Y k y1:k {y1, , y k}分别表示0到k时刻所有的状态与观测值。
在处理目标跟踪问题时,通常假设目标的状态转移过程服从一阶马尔可夫模型,即当前时刻的状态x k 只与上一时刻的状态x k-1有关。
另外一个假设为观测值相互独立,即观测值y k只与k时刻的状态x k有关。
贝叶斯滤波为非线性系统的状态估计问题提供了一种基于概率分布形式的解决方案。
贝叶斯滤波将状态估计视为一个概率推理过程,即将目标状态的估计问题转换为利用贝叶斯公式求解后验概率密度p(X k |Y k )或滤波概率密度p(x k |Y k ) ,进而获得目标状态的最优估计。
贝叶斯滤波包含预测和更新两个阶段, 预测过程利用系统模型预测状态的先验概率密度, 新过程则利用最新的测量值对先验概率密度进行修正,得到后验概率密度。
假设已知 k 1时刻的概率密度函数为 p(x k 1|Y k 1 ) ,贝叶斯滤波的具体过程如下:(1)预测过程,由 p(x k 1|Y k 1) 得到 p(x k |Y k 1):p( x k , x k 1|Y k 1) p(x k | x k 1,Y k 1)p(x k 1|Y k 1)当给定 x k 1时,状态 x k 与 Y k 1相互独立,因此p(x k ,x k 1|Y k 1) p(x k |x k 1)p(x k1|Y k 1)上式两端对 x k 1 积分,可得 Chapman-Komolgorov 方程p(x k |Y k 1) p(x k |x k 1)p(x k 1|Y k 1)dx k 1(2)更新过程,由 p(x k |Y k 1)得到 p(x k |Y k ):获取 k 时刻的测量 y k 后,利用贝叶斯公式对先验概率密度进行更新,得到后验概率p(y k |x k ,Y k 1)p(x k |Y k 1) p( y k |Y k 1) 假设 y k 只由 x k 决定,即p(y k |x k ,Y k 1) p(y k |x k )因此p(y k |x k )p(x k |Y k 1) p(y k |Y k 1)其中, p(y k |Y k 1) 为归一化常数 p(y k |Y k 1) p(y k |x k )p(x k |Y k 1)dx k贝叶斯滤波以递推的形式给出后验 (或滤波 ) 概率密度函数的最优解。
matlab11种数字信号滤波去噪算法Matlab是一种强大的数学软件,广泛应用于信号处理领域。
在数字信号处理中,滤波去噪是一个重要的任务,可以提高信号的质量和准确性。
本文将介绍Matlab中的11种数字信号滤波去噪算法。
1. 均值滤波:该算法通过计算信号中一定窗口内的像素平均值来去除噪声。
它适用于高斯噪声和椒盐噪声的去除。
2. 中值滤波:该算法通过计算信号中一定窗口内的像素中值来去除噪声。
它适用于椒盐噪声的去除。
3. 高斯滤波:该算法通过对信号进行高斯模糊来去除噪声。
它适用于高斯噪声的去除。
4. 维纳滤波:该算法通过最小均方误差准则来估计信号的真实值,并去除噪声。
它适用于高斯噪声的去除。
5. 自适应滤波:该算法通过根据信号的局部特性来调整滤波器的参数,从而去除噪声。
它适用于非线性噪声的去除。
6. 小波去噪:该算法通过将信号分解为不同频率的小波系数,并对系数进行阈值处理来去除噪声。
它适用于各种类型的噪声的去除。
7. Kalman滤波:该算法通过对信号进行状态估计和观测更新来去除噪声。
它适用于线性系统的去噪。
8. 粒子滤波:该算法通过使用一组粒子来估计信号的状态,并通过重采样来去除噪声。
它适用于非线性系统的去噪。
9. 线性预测滤波:该算法通过使用线性预测模型来估计信号的未来值,并去除噪声。
它适用于平稳信号的去噪。
10. 自适应线性组合滤波:该算法通过对信号进行线性组合来估计信号的真实值,并去除噪声。
它适用于各种类型的噪声的去除。
11. 稀疏表示滤波:该算法通过使用稀疏表示模型来估计信号的真实值,并去除噪声。
它适用于各种类型的噪声的去除。
以上是Matlab中的11种数字信号滤波去噪算法。
每种算法都有其适用的场景和优缺点,根据具体的信号和噪声类型选择合适的算法进行去噪处理。
Matlab提供了丰富的函数和工具箱,可以方便地实现这些算法,并对信号进行滤波去噪。
通过合理选择和组合这些算法,可以有效提高信号的质量和准确性,为后续的信号处理任务提供更好的基础。
粒子滤波作者-niewei120——nuaaBayes法则:贝叶斯定理由英国数学家贝叶斯( Thomas Bayes 1702-1763 ) 发展,用来描述两个条件概率之间的关系,比如P(A|B) 和P(B|A)。
按照乘法法则:P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B),可以立刻导出贝叶斯定理公式:P(A|B)=P(B|A)*P(A)/P(B)。
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A的条件下的概率是不一样的;然而,这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。
Pr(A)是A的先验概率或边缘概率。
之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
先验概率的计算比较简单,没有使用贝叶斯公式;而后验概率的计算,要使用贝叶斯公式。
若用Pr(B|A)/Pr(B)表示标准似然度,则后验概率= 标准似然度* 先验概率。
例子:一座别墅在过去的20 年里一共发生过 2 次被盗,别墅的主人有一条狗,狗平均每周晚上叫 3 次,在盗贼入侵时狗叫的概率被估计为0.9,问题是:在狗叫的时候发生入侵的概率是多少?我们假设A 事件为狗在晚上叫,B 为盗贼入侵,则P(A) = 3 / 7,P(B)=2/(20·365)=2/7300,P(A | B) = 0.9,按照公式很容易得出结果:P(B|A)=0.9*(2/7300)/(3/7)=0.00058贝叶斯决策理论方法基本思想是:1、已知类条件概率密度参数表达式和先验概率。
2、利用贝叶斯公式转换成后验概率。
3、根据后验概率大小进行决策分类。
贝叶斯滤波的核心思想就是利用已知的信息来判断状态变量的后验概率,在目标跟踪中也就是对所有观测值Z1:Zk={Z1,Z2…Zk}已知的情况下,计算出后验概率P(Xk|Z1:k),其计算的方法具体分为预测和更新。
matlab粒子滤波中,请问状态方程的x(t)和观测方程的y(t)表达什么意思?x(t)=f(x(t-1),u(t),w(t)) (1) 状态转移方程,u(t)为控制量,w(t) 为模型噪声y(t)=h(x(t),e(t)) (2) 观测方程,e(t)为观测噪声1,2,0,3,1,1,这些粒子中肯定1出现的概率是最大的,对每个粒子初始权值1/N; 假设现有一个状态转移方程X(t)=X(t-1)+1+W,于是将这N个粒子通过状态转移方程求得了X(1)时刻的粒子状态,2,3,1,4,2,2(这里没有加上噪声W,为了看着方便,W一般是高斯噪声) 得到状态后通过观测方程踪,那这个观测方程就是颜色直方图的似然度函数,于是得到了每个粒子的似然度匹配值,假设X(1)i(iX(1)=SUM(X(1)i*w(1)i); i=1~N来求得,或者也可以取w最大的一点的X值也就是说在粒子滤波器中状态转移方程求的是粒子在下一个时刻的状态,观测方程是对粒子在这一状态的评价,即这个状态与最优的状态相比好不好,好,则这一点所占的权重就大,不好,则占的权重就小粒子滤波算法源于Montecarlo的思想,即以某事件出现的频率来指代该事件的概率。
因此在滤波过程中,需要用到概率如P(x)的地方,一概对变量x采样,以大量采样的分布近似来表示P(x)。
因此,采用此一思想,在滤波过程中粒子滤波可以处理任意形式的概率,而不像Kalman滤波只能处理高斯分布的概率问题。
他的一大优势也在于此。
再来看对任意如下的状态方程x(t)=f(x(t-1),u(t),w(t)) (1)y(t)=h(x(t),e(t)) (2)其中的x(t)为t时刻状态,u(t)为控制量,w(t) 和e(t)分别为模型噪声和观测噪声。
(1)当然是状态转移方程,(2)是观测方程。
那么对于这么一个问题粒子滤波怎么来从观测y(t),和x(t-1),u(t) 滤出真实状态x(t)呢?看看滤波的预估阶段:粒子滤波首先根据x(t-1) 和他的概率分布生成大量的采样,这些采样就称之为粒子。
粒子滤波原理及Matlab应用粒子滤波(Particle Filter)是一种基于蒙特卡洛方法的滤波算法,用于解决非线性非高斯系统的状态估计问题。
相比于传统的卡尔曼滤波和扩展卡尔曼滤波,粒子滤波更适用于非线性系统和非高斯噪声。
粒子滤波的原理是通过一组粒子来近似表示系统的状态概率分布。
每个粒子都代表了系统的一个可能的状态。
粒子的数量越多,越能准确地表示系统的状态分布。
粒子在每个时刻根据系统动态模型进行状态的演化,并根据观测数据和测量模型进行状态的更新。
最后,根据粒子的权重对状态进行估计。
粒子滤波的步骤如下:1. 初始化粒子:根据先验的状态分布,生成一组初始的粒子,每个粒子的状态服从先验分布。
2. 粒子演化:根据动态模型,对每个粒子的状态进行预测计算。
通常使用随机扰动模型来考虑系统的不确定性。
3. 更新权重:根据观测数据和测量模型,计算每个粒子的权重。
权重反映了粒子与观测数据的吻合程度。
观测数据越能解释粒子的状态,权重越高。
4. 重采样:根据粒子的权重,进行重采样,选择得分高的粒子,代表系统的更可能状态。
重采样操作消除了粒子之间的权重差异,保持粒子的多样性。
5. 估计状态:根据重采样得到的粒子集合,计算估计的状态值。
可以是粒子的平均值、加权平均值、最大权重对应的状态等。
粒子滤波在Matlab中的应用可以通过以下步骤实现:1. 初始化粒子:根据先验的状态分布,生成一组初始的粒子。
可以使用rand函数生成符合先验分布的随机数,然后根据状态的取值范围进行线性变换得到初始粒子集合。
2. 粒子演化:根据系统的动态方程,对每个粒子的状态进行演化计算。
可以使用for循环对每个粒子进行状态更新,并添加一定的随机扰动来模拟系统的不确定性。
3. 更新权重:根据观测数据和测量模型,计算每个粒子的权重。
可以使用权重的计算公式根据观测数据和测量模型计算后验概率,并对权重进行归一化处理。
4. 重采样:根据粒子的权重,进行重采样操作。
粒子滤波原理及应用matlab仿真一、引言粒子滤波(Particle Filter)是贝叶斯滤波(Bayesian Filter)的一种扩展,用于解决非线性和非高斯问题。
它是一种基于蒙特卡罗方法的状态估计算法,可以用于目标跟踪、机器人定位、信号处理等领域。
本文将详细介绍粒子滤波的原理及其在matlab中的应用。
二、贝叶斯滤波贝叶斯滤波是一种基于贝叶斯定理的概率推断方法,用于估计状态变量在给定观测值下的后验概率分布。
其核心思想是将先验概率分布和观测数据结合起来,得到后验概率分布。
具体地,在时间步k时刻,假设状态变量为x(k),观测变量为y(k),则根据贝叶斯定理:P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中,P(x(k)|y(1:k))表示在已知前k个观测值下x(k)的后验概率分布;P(y(k)|x(k))表示在已知x(k)时y(k)的条件概率分布,也称为似然函数;P(x(k)|y(1:k-1))表示在已知前k-1个观测值下x(k)的先验概率分布;P(y(k)|y(1:k-1))表示前k-1个观测值的边缘概率分布。
三、粒子滤波基本原理粒子滤波是一种基于贝叶斯滤波的蒙特卡罗方法,它通过在状态空间中随机采样一组粒子来近似表示后验概率分布。
每个粒子都代表一个可能的状态变量,其权重反映了该状态变量与观测值之间的匹配程度。
具体地,在时间步k时刻,假设有N个粒子{ x(1), x(2), ..., x(N) },则每个粒子都有一个对应的权重w(i),且满足:∑ w(i) = 1根据贝叶斯定理可得:P(x(k)|y(1:k)) = P(y(k)|x(k)) * P(x(k)|y(1:k-1)) / P(y(k)|y(1:k-1))其中,P(y(k)|x(k))和P(x(k)|y(1:k-1))可以通过系统模型和观测模型计算得到。
姓名:朱林富 学号:08120361 研究方向:粒子滤波基于粒子滤波实现的目标被动跟踪1.1被动定位系统是一个仅有角测量的系统,通常对于目标距离是不可测的。
由于实时处理和计算存储量的需求,通常选用递推滤波算法来实现。
由于系统本身的弱观测性,状态空间模型非线性强,导致滤波算法的收敛精度和收敛时间满足不了要求。
处理这种非线性、非高斯问题,粒子滤波算法有很好的表现。
粒子滤波的基本思想是:首先依据系统状态向量的经验条件分布,在状态空间抽样产生一组随机样本集合,这些样本集合称为粒子;然后根据观测值不断调整粒子的权重大小和样本位置;最后通过调整后的粒子信息修正最初的的经验条件分布,估计出系统状态和参数。
该算法是一种递推滤波算法,可以用来估计任意非线性非高斯随机系统的状态和参数。
粒子滤波主要有三步基本操作:采样(从不含观察值的状态空间产生新的粒子)、权值计算(根据观察值计算各个粒子的权值)、重采样(抛弃权值小的粒子,使用权值大的粒子代替),这三步构成了粒子滤波的基本算法。
SIRF(Sample Importance Resampling Filter)算法是粒子滤波的一种基本算法。
1.2被动定位系统中二维纯方位目标跟踪模型如上图所示。
以观测站为原点,建立二维直角坐标系,图中标出了目标在k 时刻、k-1时刻的位置,目标到观测站的距离R 不可测。
系统状态模型为:11,1,2,...,k k k x x u k n --=Φ+Γ= (1.1) 系统观测模型为:1tan (/)k k k k z y x v -=+ (1.2)其中[,,,]k k Tk k x k y x x V y V =为系统的k 时刻状态值(目标在坐标系x,y 方向上的位置和速度),11k-1u [,]k k Tx y u u --=为k-1时刻x,y 方向上的系统噪声,k v 为k 时刻的观测噪声。
k z 为k 时刻的观测角度。
1100010000110001⎡⎤⎢⎥⎢⎥Φ=⎢⎥⎢⎥⎣⎦ 100.500100.5⎡⎤⎢⎥⎢⎥Γ=⎢⎥⎢⎥⎣⎦为了实现方便,设定系统噪声为一零均值高斯白噪声。
初始状态x 描述了被跟踪目标的初始状态。
传感器测量目标的角度,会产生测量误差和受到测量噪声的污染,测量方程式如1.2所示。
为了简便,其中测量噪声设定为一零均值高斯白噪声v k ~N (0,r )1.3在被动定位系统的二维纯方位目标跟踪中,SIRF 算法的步骤如下:1)采样:根据系统状态方程式(1.1)采样得到k 时刻粒子集{}()1,1,2,...,N i k i x i N ==11111111()()()1()()()()()1()()0.50.5k k k k k k k k k k i i i i k k x x i i i x x x i i i i kk y y i i i y y y x x V V V yyVV V --------()-()()-()=++μ=+μ=++μ=+μ(1.3)2)权值计算:选取先验概率密度函数()1()i k k p x x -|为重要性函数,意味着权值更新为()()1()i i ik k k k p z x -ω∝ω|,且由观测方程式( 1.2)得1k v t a n (/)k k k z y x -=- (1.4)由于观测噪声与系统状态相互独立,根据式(1.4)得()()1()()()1()()()()((tan (/)))(tan (/))i i i i i i i x k k v k k v k k k k v k k k p z x p v x p z y x x p z y x --|=|=-|=- 假设观测噪声为一零均值高斯白噪声,则权值计算为:式1.5*()()1()()1()()21()(tan (/))exp (tan (/))2i i i i i i k x k k v k k k k k k p z x p z y x z y x --2⎡⎤ω=|=-=--⎢⎥δ⎣⎦ 3)权值归一化:当各个粒子权值计算完成后进行权值归一化()*()*()1/Ni i i k kk i =ω=ωω∑ 4)重采样:采用RSR 重采样算法,获得新粒子集{}()()1,Ni i k k i x =ω----------------重采样程序------------------------------------------------------------indr=1;indd=rN; %设置指针的初始值 K=rN/W; %计算中间变量KU=rand(1,1); %随机生成一个随机阈值 for i=1:rN; %主循环temp=K.*w_buffer(i,1)-U; %添加一个中间变量temp r_buffer(indr,1)=quzheng(temp); %U=r_buffer(indr,1)-temp; %更新阈值 if r_buffer(indr,1)>0 %i_buffer(indr,1)=i; %存储被复制粒子的地址 indr=indr+1; elsei_buffer(indd,1)=i; % 存储被抛弃粒子的地址 indd=indd-1; end; iR=indr-1;-------------------------------------------------------------------------------------------------- 5)状态值输出:()()1()()1()()1()()1ˆˆˆˆˆk kk kNi i k k k i Ni i x k x i Ni i k k k i Ni i y k y i xx V V yy V V =====ω=ω=ω=ω∑∑∑∑----------------状态输出程序---------------------------------------------------------- X=0;Vx=0;Y=0;Vy=0; for i=1:rN;X=X+w_buffer(i,1).*x_buffer(i,1); % 计算x 方位值Vx=Vx+w_buffer(i,1).*Vx_buffer(i,1); % 计算x 方向速度值 Y=Y+w_buffer(i,1).*y_buffer(i,1); % 计算y 方位值 Vy=Vy+w_buffer(i,1).*Vy_buffer(i,1); % 计算y 方向速度值 end;rX(t,1)=X/W; % 输出值归一化 rVx(t,1)=Vx/W;rY(t,1)=Y/W; rVy(t,1)=Vy/W;-------------------------------------------------------------------------------------------------- SIRF 算法功能框图如下图所示:每输入一个观测值k z 都将经过5步产生一个状态值输出ˆk x,这5步是:采样、权值计算、权值归一化、重采样、状态值输出。
1.4在MATLAB 中仿真目标跟踪过程,取粒子数N=1024,为实现简便设系统噪声和测量噪声均为零均值高斯白噪声。
采样粒子位置和速度的初始分布分别为:00202022()(4.5,0.2)()(4,0.3)()(0.2,0.01)()(0.15,0.02)x y p x N p y N p V N p V N ====设真实的轨迹初始位置和速度为:00004.5; 4.5;0.2;0.2x y x y V V ====--------------------------------系统参数初始化程序--------------------------------------------xMEAN=4.5;xSIGMA=0.2; %初始化采样粒子的位置和速度 yMEAN=4;ySIGMA=0.3; VxMEAN=0.2;VxSIGMA=0.01; VyMEAN=0.15;VySIGMA=0.02;UxMEAN=0;UxSIGMA=0.015625; % 初始化x 方向和y 方向噪声,均% 为零均值高斯白噪声UyMEAN=0;UySIGMA=0.015625; % 标准差 为 0.015625 UzMEAN=0;UzSIGMA=0.001;为了便于比较,用一段程序描述目标的真实运动轨迹。
-----------------------------真实运动轨迹程序-------------------------------------------------- x0=4.5;y0=4.5;Vx0=0.2;Vy0=0.2; % 初始化真实状态的初值tX(1,1)=x0;tY(1,1)=y0;tVx(1,1)=Vx0;tVy(1,1)=Vy0;w0=gauss(UxMEAN,UxSIGMA,rSTEP); %噪声w1=gauss(UyMEAN,UySIGMA,rSTEP);w2=gauss(UzMEAN,UzSIGMA,rSTEP);tZ(1,1)=atan(tY(1,1)./tX(1,1))+w2(1,1); %初始测量角for t=2:rSTEPtX(t,1)=tX(t-1,1)+tVx(t-1,1)+w0(t,1); % tX(t,1)存储目标x方向的真实坐标值tY(t,1)=tY(t-1,1)+tVy(t-1,1)+w1(t,1); % tY(t,1)存储目标y方向的真实坐标值tVx(t,1)=tVx(t-1,1)+0.5.*w0(t,1); % tVx(t,1)存储目标x方向的真实速度值tVy(t,1)=tVy(t-1,1)+0.5.*w1(t,1); % tVy(t,1)存储目标y方向的真实速度值tZ(t,1)=atan(tY(t,1)./tX(t,1))+w2(t,1); % tZ(t,1)用来存储每一时刻的测量角end;初始化和真实轨迹描述完成后,用1.2中讲到的SIRF算法实现被动跟踪。
具体步骤分为:1)采样2)权值计算3)权值归一化4)重采样5)状态值输出。
详细程序及注释见附件中particle.m文件仿真结果如下图所示,虚线为目标实际运动轨迹,实线为估计的目标运动轨迹。