信息论中关于互信息的三种不同理解的统一性
- 格式:pdf
- 大小:169.03 KB
- 文档页数:2

互信息物理含义摘要:1.互信息的定义和概念2.互信息在信息论中的应用3.互信息在机器学习中的应用4.互信息在实际生活中的应用5.提高互信息的方法和技巧6.总结:互信息的重要性正文:互信息(Mutual Information,简称MI)是一种用于衡量两个随机变量之间相关性的度量指标。
它在信息论、机器学习以及实际生活中都有广泛的应用。
本文将介绍互信息的物理含义、应用场景以及提高互信息的方法。
1.互信息的定义和概念互信息是由信息论学家香农(Claude Shannon)首次提出的。
它是一种衡量两个随机变量之间相互依赖程度的度量。
互信息的计算公式为:MI(X, Y) = I(X; Y) = H(X) - H(X|Y)其中,X和Y是两个随机变量,H(X)表示X的熵,H(X|Y)表示在已知Y的情况下X的熵。
MI(X, Y)的值范围在0到无穷大之间。
当X和Y相互独立时,MI(X, Y)等于0;当X和Y完全相同时,MI(X, Y)达到最大值。
2.互信息在信息论中的应用在信息论中,互信息常用于衡量通信系统中的信源编码、信道编码等问题。
通过计算互信息,可以评估信息传输的效率以及信道的可靠性。
3.互信息在机器学习中的应用在机器学习中,互信息被广泛应用于特征选择、模型评估以及异常检测等方面。
通过计算不同特征之间的互信息,可以找到关联性较强的特征,从而降低特征维度,提高模型性能。
同时,互信息还可以用于评估模型预测的准确性,为超参数调优提供依据。
4.互信息在实际生活中的应用在实际生活中,互信息也有着广泛的应用。
例如,在金融领域,可以通过计算股票间的历史互信息来发现潜在的投资机会;在医学领域,可以利用互信息分析不同生理指标之间的关联性,为疾病诊断提供依据。
5.提高互信息的方法和技巧要提高互信息,可以尝试以下方法:- 增加数据量:数据量越大,互信息通常越高。
- 优化特征选择:选择关联性较强的特征,有助于提高互信息。
- 数据预处理:对数据进行归一化、标准化等预处理,可以提高互信息。


自信息、互信息、信息熵、平均互信息,定义、公式(1)自信息:一个事件(消息)本身所包含的信息量,它是由事件的不确定性决定的。
比如抛掷一枚硬币的结果是正面这个消息所包含的信息量。
随机事件的自信息量定义为该事件发生概率的对数的负值。
设事件 的概率为 ,则它的自信息定义为 (2)互信息:一个事件所给出关于另一个事件的信息量,比如今天下雨所给出关于明天下雨的信息量。
一个事件 所给出关于另一个事件 的信息定义为互信息,用 表示。
(3)平均自信息(信息熵):事件集(用随机变量表示)所包含的平均信息量,它表示信源的平均不确定性。
比如抛掷一枚硬币的试验所包含的信息量。
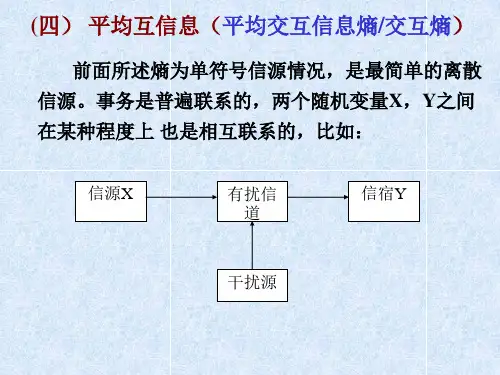
随机变量X 的每一个可能取值的自信息 的统计平均值定义为随机变量X 的平均自信息量: (4)平均互信息:一个事件集所给出关于另一个事件集的平均信息量,比如今天的天气所给出关于明天的天气的信息量。
为了从整体上表示从一个随机变量Y 所给出关于另一个随机变量 X 的信息量,我们定义互信息 在的XY 联合概率空间中的统计平均值为随机变量X 和Y 间的平均互信息画出各种熵关系图。
并作简要说明I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(XY)当X,Y 统计独立时,I(X;Y)=0实际信源往往是有记忆信源。
对于相互间有依赖关系的N 维随机变量的联合熵存在以下关系(熵函数的链规则) :定理3.1 对于离散平稳信源,有以下几个结论: (1)条件熵 随N 的增加是递减的;(2)N 给定时平均符号熵大于等于条件熵 (3)平均符号熵 随N 的增加是递减的;(4)如果 ,则 存在,并且分组与非分组码,奇异与非奇异码,唯一可译码与非唯一可译码。
即时码与非即时码1. 分组码和非分组码将信源符号集中的每个信源符号固定地映射成一个码字 Si ,这样的码称为分组码W i 。
用分组码对信源符号进行编码时,为了使接收端能够迅速准确地将码译出,分组码必须具有一些直观属性。

信息论中的信息熵与互信息信息论是一门研究信息传输和处理的学科,它的核心概念包括信息熵和互信息。
信息熵是衡量信息的不确定性和随机性的度量,而互信息则是衡量两个随机变量之间的相关性。
本文将从信息熵和互信息的定义、计算方法以及实际应用等方面进行探讨。
一、信息熵的定义与计算方法信息熵是信息论中的一个重要概念,它衡量了一个随机变量的平均不确定性。
在信息论中,我们通常用离散概率分布来表示随机变量的不确定性。
对于一个离散随机变量X,其概率分布为P(X),则其信息熵H(X)的定义如下:H(X) = -ΣP(x)log2P(x)其中,x表示随机变量X的取值,P(x)表示该取值出现的概率。
信息熵的单位通常用比特(bit)来表示。
信息熵的计算方法非常直观,我们只需要计算每个取值的概率乘以其对应的对数,并求和即可。
信息熵越大,表示随机变量的不确定性越高;反之,信息熵越小,表示随机变量的不确定性越低。
二、互信息的定义与计算方法互信息是衡量两个随机变量之间相关性的度量。
对于两个离散随机变量X和Y,其互信息I(X;Y)的定义如下:I(X;Y) = ΣΣP(x,y)log2(P(x,y)/(P(x)P(y)))其中,P(x,y)表示随机变量X和Y同时取值x和y的概率,P(x)和P(y)分别表示随机变量X和Y的边缘概率分布。
互信息的计算方法与信息熵类似,我们只需要计算每个取值同时出现的概率乘以其对应的对数,并求和即可。
互信息越大,表示两个随机变量之间的相关性越强;反之,互信息越小,表示两个随机变量之间的相关性越弱。
三、信息熵与互信息的实际应用信息熵和互信息在信息论中有广泛的应用,并且在许多领域中也得到了广泛的应用。
在通信领域中,信息熵被用来衡量信源的不确定性,从而确定数据传输的最佳编码方式。
互信息则可以用来衡量信道的容量,从而确定数据传输的最大速率。
在机器学习领域中,信息熵被用来衡量决策树的不确定性,从而确定最佳的划分属性。
互信息则可以用来衡量特征与标签之间的相关性,从而确定最佳的特征选择方法。

基尼系数信息增益互信息概述及解释说明1. 引言1.1 概述本文主要介绍了三个与数据分析相关的重要指标,包括基尼系数、信息增益和互信息。
这些指标在数据挖掘、机器学习和统计分析等领域中被广泛应用,可以帮助我们理解和解释数据中的关联、相关性以及变量的重要性。
1.2 文章结构本文将按照以下结构进行阐述:首先,我们将详细介绍基尼系数,包括其定义与原理、计算方法以及常见应用场景。
接着,我们将深入讲解信息增益的概念,并探讨其与熵的关系以及在特征选择算法中的具体应用。
最后,我们将详细解释互信息的基本概念与定义,并讨论它与条件熵之间的关系,同时还将涉及到互信息在实际案例中的应用领域。
1.3 目的通过本文对基尼系数、信息增益和互信息进行全面介绍,旨在提供读者们一个清晰而全面的认识。
读者可以了解到这些指标在数据分析中发挥的作用和意义,并且能够辨别适合使用哪种指标来解决不同类型的问题。
此外,我们还将对各个指标的特点、优缺点进行总结,以及展望这些指标未来发展的方向。
以上就是“1. 引言”部分的详细内容。
2. 基尼系数2.1 定义与原理基尼系数是衡量数据集纯度或不确定性的指标之一。
在决策树算法中,基尼系数用于衡量一个特征的分类能力,即该特征将数据集划分为不同类别的能力。
基尼系数越小,表示使用该特征进行分类时纯度越高。
基尼系数的计算公式如下:$$Gini(p) = 1 - \sum_{i=1}^{J}{(p_i)^2}$$其中,$J$ 表示类别的个数,$p_i$ 表示第$i$ 个类别占总样本的比例。
2.2 计算方法在实际应用中,计算基尼系数可以分为以下几个步骤:步骤1: 统计每个类别在数据集中出现的次数,并计算各个类别所占比例;步骤2: 对于每个特征,按照不同取值对数据集进行划分,并计算划分后子集合的基尼系数;步骤3: 根据依据某一特征划分后子集合的基尼系数大小选择最优划分点(即使得基尼系数最小)。
常见的情况是,在构建决策树时,基尼系数用于比较不同特征进行特征选择的优劣。

信息论与编码第二版答案《信息论与编码(第二版)》是Claude Elwood Shannon所撰写的经典著作,该书于1948年首次出版,至今被广泛认可为信息论领域的权威指南。
本书通过数学模型和理论阐述了信息的量化、传输、存储以及编码等相关概念和原理。
深入浅出的阐述方式使得本书具备了普适性和可读性,成为信息论领域学习者和研究者的必备参考。
信息论是研究信息的传输、处理和应用的科学,其最初来源于通信工程领域。
而编码作为信息论的一个重要分支,旨在寻求一种有效的方式将信息转化为符号或信号,以便能够高效地传输和存储。
编码的主要目标是通过减少冗余或利用统计特征来压缩信息,并提高信号传输过程中的容错性。
在信息论中,最重要的概念之一是“信息熵”。
信息熵是信息的不确定性度量,也可以看作是信息的平均编码长度。
当一个事件出现的可能性均匀时,信息熵达到最大值,表示信息的不确定度最高;而当事件的概率趋于一个时,信息熵达到最小值,表示事件的确定性最高。
例如,抛一枚公正的硬币,其正反面出现的概率均为0.5,那么信息熵将达到最大值,即1比特。
如果硬币是正面朝上或者反面朝上,那么信息熵将达到最小值,即0比特。
除了信息熵,信息论中还有许多重要的概念,如条件熵、相对熵和互信息等。
其中,条件熵表示给定某些信息后的不确定性,相对熵则用于比较两个概率分布之间的差异,而互信息则度量了两个随机变量之间的相关性。
编码是信息论中的关键技术之一,其目的是将信息通过某种规则进行转换,使其适于传输或存储。
常见的编码方法有哈夫曼编码、香农-费诺编码和算术编码等。
其中,哈夫曼编码常用于无损压缩,通过根据字符频率设计不等长的编码,使得频率高的字符用较短的编码表示,而频率低的字符用较长的编码表示,从而达到压缩的效果。
算术编码则通过将整个信息序列映射为一个实数,从而实现更高的压缩比。
信息论与编码的研究对众多领域都具有重要意义。
在通信领域中,信息论的结果对于提高信道容量和降低误差率具有指导意义。

一、判断题1、信息论主要研究目的是找到信息传输过程的共同规律,提高信息传输的可靠性、有效性、保密性和认证性,以达到信息传输系统的最优化。
(√)2、同一信息,可以采用不同的信号形式来载荷;同一信号形式可以表达不同形式的信息。
(√)3、通信中的可靠性是指使信源发出的消息准确不失真地在信道中传输;(√)4、有效性是指用尽量短的时间和尽量少的设备来传送一定量的信息。
(√)5、保密性是指隐蔽和保护通信系统中传送的消息,使它只能被授权接收者获取,而不能被未授权者接收和理解。
(√)6、认证性是指接收者能正确判断所接收的消息的正确性,验证消息的完整性,而不是伪造的和被窜改的。
(√)7、在香农信息的定义中,信息的大小与事件发生的概率成正比,概率越大事件所包含的信息量越大。
(×)8、通信中获得的信息量等于通信过程中不确定性的消除或者减少量。
(√)9、离散信道的信道容量与信源的概率分布有关,与信道的统计特性也有关。
(×)10、连续信道的信道容量与信道带宽成正比,带宽越宽,信道容量越大。
(×)11、信源熵是信号符号集合中,所有符号的自信息的算术平均值。
(×)12、信源熵具有极值性,是信源概率分布P的下凸函数,当信源概率分布为等概率分布时取得最大值。
(×)13、离散无记忆信源的N次扩展信源,其熵值为扩展前信源熵值的N倍。
(√)14、互信息的统计平均为平均互信息量,都具有非负性。
(×)15、信源剩余度越大,通信效率越高,抗干扰能力越强。
(×)16、信道剩余度越大,信道利用率越低,信道的信息传输速率越低。
(×)17、信道输入与输出之间的平均互信息是输入概率分布的下凸函数。
(×)18、在信息处理过程中,熵是不会增加的。
(√)19、熵函数是严格上凸的。
(√)20、信道疑义度永远是非负的。
(√)21、对于离散平稳信源,其极限熵等于最小平均符号熵。

信息熵互信息-回复信息熵和互信息(mutual information)是信息论中常用的概念,用于衡量信息的不确定性和两个随机变量之间的相关性。
在本文中,我们将逐步探讨这两个概念的含义、计算方法以及在实际应用中的意义和应用场景。
第一部分:信息熵信息熵是由信息论奠基人克劳德·香农(Claude Shannon)在1948年提出的概念,它是对随机变量不确定性的度量。
如果一个事件的发生是非常确定的,即我们已经知道该事件发生了或者不发生了,那么它的信息熵就是0;如果一个事件的发生是非常不确定的,即我们对该事件发生与否一无所知,那么它的信息熵就是最大值,通常用最大熵H(X)来表示。
信息熵的计算公式如下:H(X) = -Σp(x)log₂p(x)其中,X表示随机变量,p(x)表示事件x发生的概率。
信息熵可以理解为对所有可能事件的加权平均信息量。
当事件的概率分布趋于均匀时,信息熵取得最大值,反映了最大的不确定性;而当事件的概率分布趋于偏向某一个事件时,信息熵趋于0,反映了最小的不确定性。
信息熵的应用非常广泛,特别是在信息论、通信系统以及机器学习等领域中起着重要的作用。
在信息论中,信息熵可以衡量信息源的不确定性,概率分布的熵越大,表示信息源越不确定,携带的信息量也就越大。
在通信系统中,可以通过信息熵来评估信道的容量,即信道可以传输的最大的信息量。
在机器学习中,信息熵常被用于构建决策树模型,通过信息熵对特征进行选择,从而实现对数据的分类和预测。
第二部分:互信息互信息是衡量两个随机变量之间的相关性的度量指标。
它表示了一个随机变量通过观测另一个随机变量能够提供的信息量,或者说一个随机变量的信息熵减去它在给定另一随机变量的条件下的信息熵。
互信息可以用于特征选择、聚类分析、异常检测等领域。
互信息的计算公式如下:I(X;Y) = ΣΣp(x,y)log₂(p(x,y)/(p(x)p(y)))其中,X和Y是两个随机变量,p(x)和p(y)分别代表X和Y的概率分布,p(x,y)表示X和Y联合分布的概率。


互信息是一种在信息论和统计学中用于描述随机变量之间相关性的度量。
在信息理论中,互信息是两个随机变量X和Y之间的“信息交换量”,它可以用来衡量X和Y的信息量有多大程度的不确定性减少。
具体来说,假设我们有两个随机变量X和Y,它们可以取任何可能的值。
互信息是X和Y的联合概率分布与两个独立随机变量的联合概率分布之间的差异。
换句话说,互信息是描述X 和Y之间的相关性或依赖性的量。
在实践中,互信息通常通过计算两个变量之间的互相关函数来获得。
如果X和Y之间的互相关函数接近零,那么我们可以说X和Y是独立的,也就是说它们之间的相关性非常小。
相反,如果互相关函数接近1,那么我们可以说X和Y高度相关,也就是说它们之间的相关性非常大。
互信息在许多领域都有应用,包括信号处理、数据压缩、机器学习和生物信息学等。
在信号处理中,互信息可以用于衡量两个信号之间的相似性或差异。
在数据压缩中,互信息可以帮助确定哪些数据可以丢弃而不显著降低信息量。
在机器学习中,互信息可以用于衡量特征之间的关系,这有助于选择最有用的特征和优化模型性能。
此外,互信息还可以用于生物信息学中,例如在基因表达数据分析中。
在这种情况下,互信息可以帮助研究人员理解不同基因表达之间的相关性,从而有助于理解生物系统的复杂性。
总的来说,互信息是一种描述随机变量之间相关性的度量。
它可以帮助我们了解两个变量之间的依赖关系,并应用于各种领域,如信号处理、数据压缩、机器学习和生物信息学。
作为一种有用的工具,互信息在许多实际应用中发挥着至关重要的作用。
互信息互信息是信息论中的一个重要概念,它用来描述两个随机变量之间的相关性。
在信息论中,信息量是表示一个事件的不确定性的度量,而互信息则表示两个随机变量之间的相关性程度。
在这篇文章中,我们将深入探讨互信息的概念、计算方法以及在实际应用中的意义。
互信息的概念互信息是用来衡量两个随机变量之间相互依赖程度的指标。
在信息论中,两个随机变量X和Y的互信息I(X;Y)定义为它们联合概率分布与各自边缘概率分布之间的差异。
换句话说,互信息衡量了当我们知道一个随机变量的取值时,另一个随机变量的不确定性减少了多少。
互信息可以被看作是信息熵的补集,即I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X),这里H(X)和H(Y)分别表示X和Y的边缘熵,H(X|Y)和H(Y|X)分别表示在已知条件下的条件熵。
互信息的计算互信息的计算通常涉及到对联合概率分布、边缘概率分布以及条件概率分布的计算。
假设X和Y都是离散随机变量,其联合概率分布为P(X,Y),边缘概率分布分别为P(X)和P(Y),则互信息可以通过以下公式计算:I(X;Y) = ΣΣ P(X,Y) * log(P(X,Y) / (P(X) * P(Y)))在实际应用中,可以通过样本数据的统计信息来估计概率分布,从而计算互信息。
互信息的意义互信息在模式识别、数据挖掘和机器学习等领域中有着广泛的应用。
在特征选择和特征提取中,互信息被用来评估特征与目标变量之间的相关性,从而选择最具有代表性的特征。
在聚类分析中,互信息可以帮助评估聚类结果的质量和稳定性。
此外,互信息还可以用于半监督学习和异常检测等任务中。
总的来说,互信息作为一个重要的信息度量指标,在各个领域都有着重要的作用,可以帮助我们理解数据之间的关系,从而更好地进行数据分析和处理。
结语通过本文的介绍,我们了解了互信息的概念、计算方法以及在实际应用中的意义。
互信息作为一个重要的信息度量指标,在信息论和机器学习领域都有着重要的应用价值。
互信息(MutualInformation) 本⽂根据以下参考资料进⾏整理: 1.维基百科: 2.新浪博客: 在概率论和信息论中,两个随机变量的互信息(Mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。
不同于相关系数,互信息并不局限于实值随机变量,它更加⼀般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。
互信息(Mutual Information)是度量两个事件集合之间的相关性(mutual dependence)。
互信息是点间互信息(PMI)的期望值。
互信息最常⽤的单位是bit。
1.互信息的定义 正式地,两个离散随机变量 X 和 Y 的互信息可以定义为: 其中 p(x,y) 是 X 和 Y 的,⽽p(x)和p(y)分别是 X 和 Y 的分布函数。
在的情形下,求和被替换成了: 其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数,⽽p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。
互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。
平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为⼀个确定的量。
如果对数以 2 为基底,互信息的单位是。
直观上,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中⼀个,对另⼀个不确定度减少的程度。
例如,如果 X 和 Y 相互独⽴,则知道 X 不对 Y 提供任何信息,反之亦然,所以它们的互信息为零。
在另⼀个极端,如果 X 是 Y 的⼀个确定性函数,且 Y 也是 X 的⼀个确定性函数,那么传递的所有信息被 X 和 Y 共享:知道 X 决定 Y 的值,反之亦然。
因此,在此情形互信息与 Y(或 X)单独包含的不确定度相同,称作 Y(或 X)的。
⽽且,这个互信息与 X 的熵和 Y 的熵相同。
(这种情形的⼀个⾮常特殊的情况是当 X 和 Y 为相同随机变量时。
万方数据
信息论中关于互信息的三种不同理解的统一性
作者:艾科拜尔·艾合麦提
作者单位:西北民族大学计算机与信息工程学院
刊名:
中小企业管理与科技
英文刊名:MANAGEMENT & TECHNOLOGY OF SME
年,卷(期):2009(6)
1.张正言.黄炜嘉.张冰.ZHANG Zheng-yan.HUANG Wei-jia.ZHANG Bing《信息论与编码》实验教学平台的设计[期刊论文]-现代电子技术2011,34(3)
2.项世军数字水印在"信息论"教学中的一点体会[期刊论文]-科教文汇2009(33)
3.王世鹏德雷斯基对意向性自然化的说明及其对马克思主义哲学的启示[学位论文]2009
4.雷义川信息与信息化[期刊论文]-中国职业技术教育2005(14)
5.朱月明.朱云.ZHU Yue-ming.ZHU Yun信息量与信息获取量的关系[期刊论文]-辽宁工程技术大学学报(社会科学版)2006,8(5)
6.吴造林.WU Zao-Lin拉格朗日乘子法在信息论中的应用[期刊论文]-科技情报开发与经济2008,18(23)
7.阳东升.张维明.刘忠.黄金才信息时代的体系——概念与定义[期刊论文]-国防科技2009(3)
8.刘瑞英.LIU Rui-ying对数和不等式在信息论中的应用[期刊论文]-保定学院学报2008,21(2)
9.燕善俊信息论与编码课程教学探讨[期刊论文]-高等函授学报(自然科学版)2011(2)
10.苗东升.MIAO Dong-sheng信息研究对人文科学的意义[期刊论文]-华中科技大学学报(社会科学版)
2006,20(2)
引用本文格式:艾科拜尔·艾合麦提信息论中关于互信息的三种不同理解的统一性[期刊论文]-中小企业管理与科技 2009(6)。