轴对称中考练习题精选(含答案)一

2021中考数学专题训练轴对称与中心对称一、选择题1. 下列四个交通标志图中，为轴对称图形的是()2. 点(－1，2)关于原点的对称点坐标是()A．(－1，－2) B．(1，－2)C．(1，2) D．(2，－1)3. 如图，在4×4的正方形网格中，已有四个小正方形被涂黑.若将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形，则该小正方形的位置可以是()A.(一，2)B.(二，4)C.(三，2)D.(四，4)4. 2018·达州下列图形中是中心对称图形的是()5. 如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为()A．40°B．45°C．50°D．60°6. 如图，在RtABC 中，90ACB ∠=︒，分别以点B 和点C 为圆心，大于12BC 的长为半径作弧，两弧相交于D E ，两点，作直线DE 交AB 于点F ，交BC 于点G ，连接CF ．若3AC =，2CG =，则CF 的长为A ．52B ．3C ．2D ．727. 如图，线段AB 外有C ，D 两点(在AB 同侧)，且CA=CB ，DA=DB ，∠ADB=80°，∠CAD=10°，则∠ACB 的度数为( )A .80°B .90°C .100°D .110°8. 如图，∠AOB=60°，点P 是∠AOB 内的定点且OP=，若点M ，N 分别是射线OA ，OB 上异于点O 的动点，则△PMN 周长的最小值是 ( ) A .B .C .6D .3二、填空题9. 如图，已知BC 为等腰三角形纸片ABC 的底边，AD ⊥BC ，∠BAC ≠90°.将此三角形纸片沿AD 剪开，得到两个三角形，若把这两个三角形拼成一个四边形，则能拼出______个中心对称图形．10. 如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时，阴影部分的面积为.11. 如图，在△ABC中，AB，AC的垂直平分线分别交BC于点E，F.若△AEF的周长为10 cm，则BC的长为cm.12. 数学活动课上，两名同学围绕作图问题:“如图①，已知直线l和直线l外一点P，用直尺和圆规作直线PQ，使PQ⊥直线l于点Q.”分别作出了如图②③所示的两个图形，其中作法正确的为图(填“②”或“③”).13. 现要在三角地带ABC内(如图)建一座中心医院，使医院到A，B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请你确定这座中心医院的位置.14. 如图，在△ABC中，AC=BC=2，AB=1，将它沿AB翻折得到△ABD，则四边形ADBC的形状是形，点P，E，F分别为线段AB，AD，DB上的任意一点，则PE+PF的最小值是.三、作图题15. 如图，在对R t△OAB依次进行位似、轴对称和平移变换后得到R t△O′A′B′.(1)在坐标纸上画出这几次变换相应的图形；(2)设P(x，y)为△OAB边上任一点，依次写出这几次变换后点P对应点的坐标．16. 如图，1O，2O，3O，4O为四个等圆的圆心，A，B，C，D为切点，请你在图中画出一条直线，将这四个圆分成面积相等的两部分，并说明这条直线经过的两个点是；如图，1O，2O，3O，4O，5O为五个等圆的圆心，A，B，C，D，E为切点，请你在图中画出一条直线，将这五个圆．．．分成面积相等的两部分，并说明这条直线经过的两个点是．DCBAO4O3O2O1EDCBAO5O4O3O2O1四、解答题17. 如图，Rt△ABC的顶点A，B，C关于直线MN的对称点分别为A'，B'，C'，其中∠A=90°，AC=8 cm，点C，B，A'在同一条直线上，且A'C=12 cm.(1)求△A'B'C'的周长; (2)求△A'CC'的面积.18. 如图，在△ABC中，AB 边的垂直平分线DE 分别与AB 边和AC 边交于点D和点E ，BC 边的垂直平分线FG 分别与BC 边和AC 边交于点F 和点G ，若△BEG 的周长为16，GE=3，求AC 的长.19. [材料阅读]在平面直角坐标系中，以任意两点P (x 1，y 1)，Q (x 2，y 2)为端点的线段的中点坐标为⎝ ⎛⎭⎪⎫x 1＋x 22，y 1＋y 22.[运用](1)已知点A (－2，1)和点B (4，－3)，则线段AB 的中点坐标是________；已知点M (2，3)，线段MN 的中点坐标是(－2，－1)，则点N 的坐标是________． (2)已知平面上四点A (0，0)，B (10，0)，C (10，6)，D (0，6)．直线y ＝mx －3m ＋2将四边形ABCD 分成面积相等的两部分，则m 的值为________．(3)在平面直角坐标系中，有A (－1，2)，B (3，1)，C (1，4)三点，另有一点D ，可使以点A ，B ，C ，D 为顶点的四边形为平行四边形，求点D 的坐标．20. 如图1，将△ABC 纸片沿中位线EH 折叠，使点A 的对称点D 落在BC 边上，再将纸片分别沿等腰△BED 和等腰△DHC 的底边上的高线EF 、HG 折叠，折叠后的三个三角形拼合形成一个矩形．类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．(1)将▱ABCD 纸片按图2的方式折叠成一个叠合矩形AEFG ，则操作形成的折痕分别是线段________，________；S 矩形AEFG ∶S ▱ABCD ＝________．(2)▱ABCD 纸片还可以按图3的方式折叠成一个叠合矩形EFGH ，若EF ＝5，EH ＝12，求AD 的长．(3)如图4，四边形ABCD 纸片满足AD ∥BC ，AD <BC ，AB ⊥BC ，AB ＝8，CD ＝10.小明把该纸片折叠，得到叠合正方形．．．，请你帮助画出叠合正方形的示意图，并求出AD ，BC 的长．图1 图2 图3 图42021中考数学 专题训练 轴对称与中心对称-答案一、选择题 1. 【答案】B2. 【答案】B3. 【答案】B [解析] 如图，把(二，4)位置的小正方形涂黑，则整个图案构成一个以直线AB 为对称轴的轴对称图形.4. 【答案】B5. 【答案】C[解析] 由作法得CG ⊥AB.∵AC ＝BC ，∴CG 平分∠ACB ，∠A ＝∠B ＝40°. ∵∠ACB ＝180°－∠A －∠B ＝100°， ∴∠BCG ＝12∠ACB ＝50°.6. 【答案】A【解析】由作法得GF 垂直平分BC ，∴FB FC =，2CG BG ==，FG BC ⊥， ∵90ACB ∠=︒，∴FG AC ∥，∴BF CF =， ∴CF 为斜边AB 上的中线， ∵22345AB =+=， ∴1522CF AB ==．故选A ．7. 【答案】C8. 【答案】D[解析]分别以OB ，OA 为对称轴作点P 的对称点P 1，P 2，连接OP 1，OP 2，P 1P 2，P 1P 2交射线OA ，OB 于点M ，N ，则此时△PMN 的周长有最小值，△PMN 的周长=PN +PM +MN=P 1N +P 2M +MN=P 1P 2，根据轴对称的性质可知OP 1=OP 2=OP=，∠P 1OP 2=120°，∴∠OP 1M=30°，过点O 作MN 的垂线段，垂足为Q ，在Rt △OP 1Q 中，可知P 1Q=，所以P 1P 2=2P 1Q=3，故△PMN 周长的最小值为3.二、填空题9. 【答案】3 [解析] 在这里具有中心对称图形特征的是平行四边形，所以两个三角形中对应相等的两条边重合只能拼一个．因为三角形只有三条边，所以只有三种情况．10. 【答案】12[解析]∵菱形的两条对角线的长分别为6和8，∴菱形的面积=×6×8=24.∵点O 是菱形两条对角线的交点， ∴阴影部分的面积=×24=12.11. 【答案】10[解析] ∵AB ，AC 的垂直平分线分别交BC 于点E ，F ，∴AE=BE ，AF=CF .∴BC=BE+EF+CF=AE+EF+AF=10 cm .12. 【答案】③13. 【答案】解:作线段AB的垂直平分线EF，作∠BAC的平分线AM，EF与AM 相交于点P，则点P处即为这座中心医院的位置.14. 【答案】菱[解析]∵AC=BC，∴△ABC是等腰三角形.将△ABC沿AB翻折得到△ABD，∴AC=BC=AD=BD，∴四边形ADBC是菱形.∵△ABC沿AB翻折得到△ABD，∴△ABC与△ABD关于AB成轴对称.如图所示，作点E关于AB的对称点E'，连接PE'，根据轴对称的性质知AB垂直平分EE'，∴PE=PE'，∴PE+PF=PE'+PF，当E'，P，F三点共线，且E'F⊥AC时，PE+PF有最小值，该最小值即为平行线AC与BD间的距离.作CM⊥AB于M，BG⊥AD于G，由题知AC=BC=2，AB=1，∠CAB=∠BAD，∴cos∠CAB=cos∠BAD，即=，∴AG=，在Rt△ABG中，BG===，由对称性可知BG长即为平行线AC，BD间的距离，∴PE+PF的最小值=.三、作图题15. 【答案】解：(1)解图(2)设坐标纸中方格边长为单位1.则P(x ，y )――→以O 为位似中心放大为原来的2倍(2x ，2y )――→沿y 轴翻折(－2x ，2y )――→向右平移4个单位(－2x ＋4，2y )――→向上平移5个单位(－2x ＋4，2y ＋5).16. 【答案】1O ，3O 如图（提示：答案不惟一，过13O O 与24O O 交点O 的任意直线都能将四个圆分成面积相等的两部分）；5O ，O ，如图（提示：答案不惟一，如4AO ，3DO ，2EO ，1CO 等均可）．O DCBAO 4O 3O 2O 1EO DCBAO 5O 4O 3O 2O 1四、解答题17. 【答案】解:(1)∵Rt △ABC 的顶点A ，B ，C 关于直线MN 的对称点分别为A'，B'，C'，AC=8 cm ，A'C=8cm ，∴AB=A'B'，AC=A'C'，∠A'=∠A=90°.∴△A'B'C'的周长为A'C'+B'C'+A'B'=AC+A'C=12+8=20(cm). (2)由(1)得A'C'=AC=8 cm ，∠A'=90°，∴△A'CC'的面积为A'C ·A'C'=×12×8=48(cm 2).18. 【答案】解:∵DE 垂直平分线段AB ，GF 垂直平分线段BC ，∴EB=EA ，GB=GC. ∵△BEG 的周长为16， ∴EB+GB+GE=16. ∴EA+GC+GE=16.∴GA+GE+GE+GE+EC=16. ∴AC+2GE=16. ∵GE=3， ∴AC=10.19. 【答案】解：(1)(1，－1) (－6，－5) (2)12(3)设点D 的坐标为(x ，y)．若以AB 为对角线，AC ，BC 为邻边的四边形为平行四边形，则AB ，CD 的中点重合，∴⎩⎪⎨⎪⎧1＋x 2＝－1＋32，4＋y 2＝2＋12，解得⎩⎨⎧x ＝1，y ＝－1；若以BC 为对角线，AB ，AC 为邻边的四边形为平行四边形，则AD ，BC 的中点重合，∴⎩⎪⎨⎪⎧－1＋x 2＝3＋12，2＋y 2＝1＋42，解得⎩⎨⎧x ＝5，y ＝3；若以AC 为对角线，AB ，BC 为邻边的四边形为平行四边形，则BD ，AC 的中点重合，∴⎩⎪⎨⎪⎧3＋x 2＝－1＋12，1＋y 2＝2＋42，解得⎩⎨⎧x ＝－3，y ＝5. 综上可知，点D 的坐标为(1，－1)或(5，3)或(－3，5)．20. 【答案】【思维教练】(2)AD ＝DH ＋AH ，由折叠性质和全等三角形得出DH ＝HN ，FN ＝AH ，即AD ＝FH ，由叠合矩形的概念可知∠FEH ＝90°，利用勾股定理求出AD ；(3)观察图形的特点，可以考虑从CD 的中点横向和竖向折叠或从分别从每个角的位置向内折叠构成矩形，利用构成的直角三角形求解得出结果．解：(1)AE ，GF ；1∶2(2分)(2)∵四边形EFGH 是叠合矩形，∠FEH ＝90°，又EF ＝5，EH ＝12.∴FH ＝EF 2＋EH 2＝52＋122＝13.(4分)由折叠的轴对称性可知，DH ＝HN ，AH ＝HM ，CF ＝FN.易证△AEH ≌△OGF ，∴CF ＝AH.(5分)∴AD ＝DH ＋AH ＝HN ＋FN ＝FH ＝13.(6分)(3)本题有以下两种基本折法，如解图1，解图2所示．(作出一种即可)1 2 按解图1的折法，则AD ＝1，BC ＝7；按解图2的折法，则AD ＝134，BC ＝374.(10分)。

2024年中考备考：初二数学上册：画轴对称图形经典例题（含答案）一、单选题1. 下列剪纸图案中，能通过轴对称变换得到的有（ C ）2. 下列说法错误的是（B ）A．关于某直线对称的两个图形一定能完全重合B．全等的两个三角形一定关于某直线对称C．轴对称图形的对称轴至少有一条D．线段是轴对称图形3.如图是一个台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出（球可以经过多次反射），则该球最后将落入的球袋是（B ）A．1 号袋 B．2 号袋 C．3 号袋 D．4 号袋4.如图所示，在3×3的正方形网格中已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形的办法有( C )A．3种 B．4种 C．5种 D．6种解析：试题分析：如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，选择的位置有以下几种：1处，3处，7处，6处，5处，选择的位置共有5处故选C.考点：利用轴对称设计图案点评：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．5.在如上图由5个小正方形组成的图形中，再补上一个小正方形，使它成为轴对称图形，你有几种不同的方法( C )A．2种 B．3种 C．4种 D．5种6. 小强将一张正方形纸片按如图所示对折两次，并在如图位置上剪去一个小正方形，然后把纸片展开，得到的图形应是（B ）7. 如图，直线l1与直线l2相交，∠α＝60°，点P在∠α内（不在l1 ，l2上）。

小明用下面的方法作P的对称点：先以l1为对称轴作点P关于l1的对称点P1 ，再以l2为对称轴作P1关于l2的对称点P2 ，然后再以l1为对称轴作P2关于l1的对称点P3 ，以l2为对称轴作P3关于l2的对称点P4 ，……，如此继续，得到一系列点P1 ，P2 ，P3 ，…，。

第13章复习与中考演练一、选择题1.[2020·宜昌]下面四幅图是摄影爱好者抢拍的一组照片.从对称美的角度看,拍得最成功的是()2.[2020·枣庄]如图图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=6,AC=5,则△ACE的周长为()A.8B.11C.16D.173.[2020·兰州]若点A(-4,m-3),B(2n,1)关于x轴对称,则()A.m=2,n=0B.m=2,n=-2C.m=4,n=2D.m=4,n=-24.[2020·长春]如图图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:①分别以点B和点C为圆心,大于BC长的一半为半径作圆弧,两弧相交于点M和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是()A.∠BDN=∠CDNB.∠ADC=2∠BC.∠ACD=∠DCBD.2∠B+∠ACD=90°5.[2020·成都]如图图,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于1BC的长2为半径作弧,两弧相交于点M,N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为()A.2B.3C.4D.66.[2020·临沂]如图图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD的度数为()A.40°B.50°C.60°D.70°7.[2019·南宁]如图图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG 的度数为()A.40°B.45°C.50°D.60°8.[2020·哈尔滨]如图图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为()A.10°B.20°C.30°D.40°9.[2019·衢州]“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在点O相连并可绕点O转动,点C固定,OC=CD=DE,点D,E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是()A.60°B.65°C.75°D.80°二、填空题10.[2020·齐齐哈尔]若等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是.11.[2020·黄冈]已知:如图图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=度.12.[2020·达州]如图图,点P(-2,1)与点Q(a,b)关于直线l(y=-1)对称,则a+b=.13.[2020·宜昌]如图图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC=米.14.[2020·台州]如图图,等边三角形纸片ABC的边长为6,E,F是边BC的三等分点.分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是.三、解答题15.[2019·南宁]如图图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别是A(2,-1),B(1,-2),C(3,-3).(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1;(2)请画出与△ABC关于y轴对称的△A2B2C2;(3)请写出点A1,A2的坐标.16.[2020·吉林]①②③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点.在给定的网格中,按下列要求画图:(1)在图①中,画一条不与AB重合的线段MN,使MN与AB 关于某条直线对称,且M,N为格点;(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点;(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.17.[2020·绍兴]问题:如图图,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.答案:∠DAC=45°.思考:(1)如图图果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗?说明理由;(2)如图图果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“∠BAE=n°”,其余条件不变,求∠DAC的度数.答案1.B2.B∵DE垂直平分AB,∴AE=BE.∴△ACE的周长=AC+CE+AE=AC+CE+BE=AC+BC=11.3.B4.C由作图可知,MN垂直平分线段BC,∴DB=DC,MN⊥BC.∴∠BDN=∠CDN,∠B=∠DCB.∴∠ADC=∠B+∠DCB=2∠B.∵∠A=90°,∴∠ADC+∠ACD=90°.∴2∠B+∠ACD=90°.5.C由作图知,MN是线段BC的垂直平分线,∴BD=CD.∵AC=6,AD=2,∴BD=CD=4.6.D∵在△ABC中,AB=AC,∠A=40°,∴∠B=70°.∵CD∥AB,∴∠BCD=∠B=70°.7.C由尺规作图的痕迹得CG⊥AB.∵AC=BC,∴CG平分∠ACB,∠A=∠B=40°.∵∠∠ACB=50°.ACB=180°-∠A-∠B=100°,∴∠BCG=128.A∵∠BAC=90°,∠B=50°,∴∠C=40°.∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',∴∠AB'B=∠B=50°.∴∠CAB'=∠AB'B-∠C=10°.9.D∵OC=CD=DE,∴∠O=∠ODC,∠DCE=∠DEC.∴∠DEC=∠DCE=∠O+∠ODC=2∠ODC.∵∠O+∠OED=3∠ODC=∠BDE=75°,∴∠ODC=25°.∵∠CDE+∠ODC=180°-∠BDE=105°,∴∠CDE=105°-∠ODC=80°.10.10或11①当3是腰长时,三角形的三边长分别为3,3,4,此时能组成三角形,∴周长=3+3+4=10;②当3是底边长时,三角形的三边长分别为3,4,4,此时能组成三角形,∴周长=3+4+4=11.综上所述,这个等腰三角形的周长是10或11.11.40∵AD=DC,∴∠DAC=∠C=35°.∴∠ADB=∠DAC+∠C=70°.∵AB=AD,∴∠B=∠ADB=70°.∴∠BAD=180°-∠B-∠ADB=180°-70°-70°=40°.12.-5∵点P(-2,1)与点Q(a,b)关于直线l(y=-1)对称,∴a=-2,b=-3.∴a+b=-2-3=-5.13.48∵∠ABC=60°,∠ACB=60°,∴∠BAC=60°.∴△ABC是等边三角形.∵BC=48米,∴AC=48米.14.6∵等边三角形纸片ABC的边长为6,E,F是边BC的三等分点,∴EF=2.∵△ABC是等边三角形,∴∠B=∠C=60°.∵DE∥AB,DF∥AC,∴∠DEF=∠B=60°,∠DFE=∠C=60°.∴△DEF是等边三角形.∴△DEF的周长是2×3=6.15.解:(1)如图图图所示,△A1B1C1即为所求.(2)如图图图所示,△A2B2C2即为所求.(3)A1(2,3),A2(-2,-1).16.解:(1)如图图图①,MN即为所求.(答案不唯一)(2)如图图图②,PQ即为所求.(答案不唯一)(3)如图图图③,△DEF即为所求.(答案不唯一)17.解:(1)∠DAC的度数不会改变.理由:∵EA=EC ,∴∠EAC=∠C.① ∴∠AED=∠EAC+∠C=2∠C. ∵BA=BD ,∴∠BAD=∠BDA. ∵∠BAE=90°,∴∠B=90°-∠AED=90°-2∠C.∴∠BAD=12(180°-∠B )=12[180°-(90°-2∠C )]=45°+∠C.∴∠DAE=90°-∠BAD=90°-(45°+∠C )=45°-∠C.② 由①②得,∠DAC=∠DAE+∠EAC=45°-∠C+∠C=45°. (2)设∠B=m °,则∠BAD=12(180°-m °)=90°-12m °,∠AEB=180°-n °-m °.∴∠DAE=n °-∠BAD=n °-90°+12m °.∵EA=EC ,∴∠CAE=12∠AEB=90°-12n °-12m °.∴∠DAC=∠DAE+∠CAE=n °-90°+12m °+90°-12n °-12m °=12n °.。

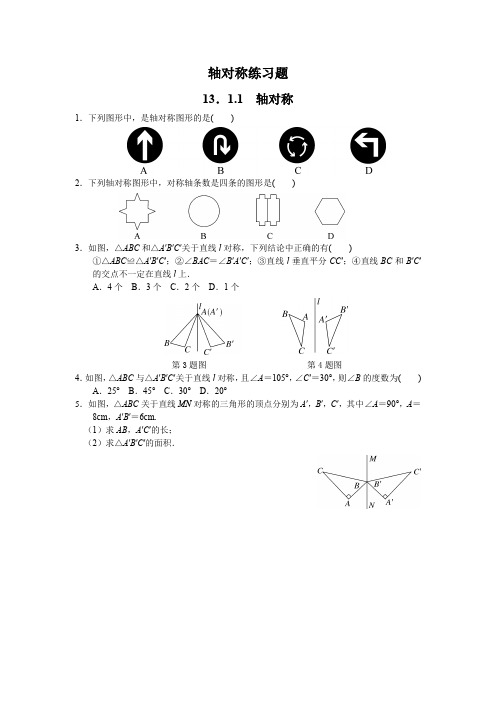
轴对称练习题13．1.1轴对称1．下列图形中，是轴对称图形的是()2．下列轴对称图形中，对称轴条数是四条的图形是()3．如图，△ABC和△A′B′C′关于直线l对称，下列结论中正确的有()①△ABC≌△A′B′C′；②∠BAC＝∠B′A′C′；③直线l垂直平分CC′；④直线BC和B′C′的交点不一定在直线l上．A．4个B．3个C．2个D．1个第3题图第4题图4．如图，△ABC与△A′B′C′关于直线l对称，且∠A＝105°，∠C′＝30°，则∠B的度数为() A．25° B．45° C．30° D．20°5．如图，△ABC关于直线MN对称的三角形的顶点分别为A′，B′，C′，其中∠A＝90°，A＝8cm，A′B′＝6cm.（1）求AB，A′C′的长；（2）求△A′B′C′的面积．13．1.2线段的垂直平分线的性质第1课时线段垂直平分线的性质和判定1．如图，在△ABC中，AB的垂直平分线交AC于点P，P A＝5，则线段PB的长度为() A．3 B．4 C．5 D．6第1题图第2题图2．如图，AC＝AD，BC＝BD，则有()A．AB与CD互相垂直平分B．CD垂直平分ABC．AB垂直平分CD D．CD平分∠ACB3．如图，在△ABC中，D为BC上一点，且BC＝BD＋AD，则点D在线段________的垂直平分线上．第3题图第4题图4．如图，在Rt△ABC中，斜边AB的垂直平分线交边AC于点D，交边AB于点E，且∠CBD ＝∠ABD，则∠A＝________°.5．如图，在△ABC中，AB的垂直平分线交AB于E，交BC于D，连接AD.若AC＝4cm，△ADC的周长为11cm，求BC的长．第2课时 线段垂直平分线的有关作图1．如图，已知线段AB ，分别以点A ，点B 为圆心，以大于12AB 的长为半径画弧，两弧交于点C 和点D ，作直线CD ，在CD 上取两点P ，M ，连接P A ，PB ，MA ，MB ，则下列结论一定正确的是( ) A ．P A ＝MA B ．MA ＝PE C ．PE ＝BE D ．P A ＝PB2．已知图中的图形都是轴对称图形，请你画出它们全部的对称轴．3．已知下列两个图形关于直线l 成轴对称．(1)画出它们的对称轴直线l ； (2)填空：两个图形成轴对称，确定它们的对称轴有两种常用方法，经过两对对称点所连线段的________画直线；或者画出一对对称点所连线段的____________．4．如图，在某条河l 的同侧有两个村庄A 、B ，现要在河道上建一个水泵站，这个水泵站建在什么位置，能使两个村庄到水泵站的距离相等？13．2画轴对称图形第1课时画轴对称图形1．已知直线AB和△DEF，作△DEF关于直线AB的轴对称图形，将作图步骤补充完整(如图所示)．(1)分别过点D，E，F作直线AB的垂线，垂足分别是点________；(2)分别延长DM，EP，FN至________，使________＝________，________＝________，________＝________；(3)顺次连接________，________，________，得△DEF关于直线AB的对称图形△GHI. 2．如图，请画出已知图形关于直线MN对称的部分．3．如图，以AB为对称轴，画出已知△CDE的轴对称图形．第2课时用坐标表示轴对称1．在平面直角坐标系中，点P(－2，3)关于x轴对称的点的坐标是()A．(2，3) B．(2，－3)C．(－2，－3) D．(3，－2)2．在平面直角坐标系中，点P(－3，4)关于y轴的对称点的坐标为()A．(4，－3) B．(3，－4)C．(3，4) D．(－3，－4)3．平面内点A(－2，2)和点B(－2，－2)的对称轴是()A．x轴B．y轴C．直线y＝4 D．直线x＝－24．已知△ABC在直角坐标系中的位置如图所示，若△A′B′C′与△ABC关于y轴对称，则点A的对称点A′的坐标是()A．(－3，2) B．(3，2)C．(－3，－2) D．(3，－2)第4题图第5题图5．如图，点A关于x轴的对称点的坐标是________．6．已知点M(a，1)和点N(－2，b)关于y轴对称，则a＝________，b＝________．7．如图，在平面直角坐标系中有三点A(－1，5)，B(－1，0)，C(－4，3)．(1)在图中作出△ABC关于y轴的对称图形△A1B1C1；(2)写出点A1，B1，C1的坐标；(3)△A1B1C1的面积是________．轴对称13．1.1轴对称1．A 2.A 3.B 4.B5．解：(1)∵AB与A′B′是对应线段，∴AB＝A′B′＝6cm.又∵AC与A′C′是对应线段，∴A′C′＝AC＝8cm.(2)∵∠A′与∠A是对应角，∴∠A′＝∠A＝90°，∴S△A′B′C′＝A′B′·A′C′÷2＝24(cm2)．13．1.2线段的垂直平分线的性质第1课时线段垂直平分线的性质和判定1．C 2.C 3.AC 4.305．解：∵AB的垂直平分线交AB于E，交BC于D，∴AD＝BD.∵△ADC的周长为11cm，∴AC＋CD＋AD＝AC＋CD＋BD＝AC＋BC＝11cm.∵AC＝4cm，∴BC＝7cm.第2课时线段垂直平分线的有关作图1．D2．解：如图所示．3．解：(1)图略．(2)中点垂直平分线4．解：连接AB，作线段AB的垂直平分线MN交直线l于点P，则点P即为所求位置．图略．13．2画轴对称图形第1课时画轴对称图形1．(1)M，P，N(2)G，H，I GM DM HP EP IN FN(3)GH HI IG2．解：如图所示．3．解：如图所示．第2课时用坐标表示轴对称1．C 2.C 3.A 4.B 5.(－5，－3) 6.217．解：(1)如图．(2)A1(1，5)，B1(1，0)，C1(4，3)．(3)7.5。

中考数学复习图形的轴对称一、选择题1．下列图形中，既是轴对称又是中心对称图形的是( A )A．菱形B．等边三角形C．平行四边形D．等腰梯形2．如图，若要添加一条线段，使之既是轴对称图形又是中心对称图形，正确的添加位置是( A )3．如图，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是(－2，3)，先把△ABC向右平移4个单位长度得到△A1B1C1，再作与△A1B1C1关于x轴对称的△A2B2C2，则点A的对应点A2的坐标是( B )A．(－3，2) B．(2，－3) C．(1，－2) D．(－1，2)4．如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为( C ) A．30°B．45°C．60°D．75°,第4题图),第5题图) 5．如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l 对称，D为线段BC′上一动点，则AD＋CD的最小值是( A )A．4 B．3 2 C．2 3 D．2＋ 3【解析】如图，作点A关于直线BC′的对称点A1，连结A1C交直线BC′于点D.由图可知当点D 在C′B的延长线上时，AD＋CD最小，而点D为线段BC′上一动点，∴当点D与点B重合时AD＋CD值最小，此时AD＋CD＝AB＋CB＝2＋2＝4.故选A.二、填空题6．如图，已知正方形的边长为4 cm ，则图中阴影部分的面积是__8_cm 2__． 【解析】阴影部分面积恰好为正方形面积的一半． 7．如图，将⊙O 沿弦AB 折叠，点C 在AmB ︵上，点D 在AB ︵上，若∠ACB ＝70°，则∠ADB＝__110°__．,第7题图) ,第8题图)8．如图，将矩形ABCD 沿GH 对折，点C 落在Q 处，点D 落在AB 边上的E 处，EQ 与BC 相交于点F .若AD ＝8，AB ＝6，AE ＝4，则△EBF 的周长为__8__．【解析】设DH ＝x ，则AH ＝8－x ，由折叠的对称性，可知EH ＝DH ＝x ，在Rt △AEH 中，应用勾股定理，得AE 2＋AH 2＝EH 2，即42＋(8－x )2＝x 2，解得x ＝5.由∠QEH ＝90°，可证明△AHE ∽△BEF ，因此AE BF ＝AH BE ＝EH EF ，即4BF ＝32＝5EF ，可以求得BF ＝83，EF ＝103，所以△EBF 周长为83＋103＋2＝8. 9．如图，在边长为2的菱形ABCD 中，∠A ＝60°，点M 是AD 边的中点，连结MC ，将菱形ABCD 翻折，使点A 落在线段CM 上的点E 处，折痕交AB 于点N ，则线段EC 的长为__7－1__．【解析】如图，过点M 作MF ⊥DC 于点F ，∵在边长为2的菱形ABCD 中，∠A ＝60°，M 为AD 中点，∴2MD ＝AD ＝CD ＝2，∠FDM ＝60°，∴∠FMD ＝30°，∴FD ＝12MD ＝12，∴FM ＝DM ×cos30°＝32，∴MC ＝FM 2＋CF 2＝7，∴EC ＝MC －ME ＝7－1. ,第9题图) ,第10题图)10．如图，∠AOB ＝60°，点P 是∠AOB 的平分线OC 上的动点，点M 在边OA 上，且OM ＝4，则点P 到点M 与到边OA 的距离之和的最小值是__23__．【解析】过M 作MN ′⊥OB 于N ′，交OC 于P ，则MN ′的长度等于PM ＋PN 的最小值，即MN ′的长度等于点P 到点M 与到边OA 的距离之和的最小值，∵∠ON ′M ＝90°，OM ＝4，∴MN ′＝OM ·sin60°＝23，∴点P 到点M 与到边OA 的距离之和的最小值为2 3.三、解答题11．如图，在菱形ABCD 中，∠ABC ＝45°，点P 是对角线BD 上的任一点，点P 关于直线AB ，AD ，CD ，BC 的对称点分别是点E ，F ，G ，H ，BE 与DF 相交于点M ，DG 与BH相交于点N，求证：四边形BMDN是正方形．解：∵四边形ABCD是菱形，∴∠ABD＝∠DBC＝∠ADB＝∠BDC.∵∠ABC＝45°，点P关于直线AB，AD，CD，BC的对称点分别是点E，F，G，H，∴∠MBN＝∠MDN＝90°，∠MBD＝∠MDB＝45°.∴△BDM是等腰直角三角形．∴∠BMD＝90°，BM＝DM.∴四边形BMDN是正方形12．在3×3的正方形网格中，有一个以格点为顶点的三角形(阴影部分)如图所示，请你在图①，图②，图③中，分别画出一个与该三角形成轴对称且以格点为顶点的三角形，并将所画三角形涂上阴影．(注：所画的三个图不能重复．)解：如图所示：13．如图，在每个小正方形的边长均为1个单位长度的方格纸中，有线段AB和直线MN，点A，B，M，N均在小正方形的顶点上．(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上)，使四边形ABCD是以直线MN为对称轴的轴对称图形，点A的对称点为D，点B的对称点为点C；(2)请直接写出四边形ABCD的周长．解：(1)图略(2)四边形ABCD的周长为AB＋BC＋CD＋DA＝5＋22＋5＋32＝25＋52如图，在边长为1个单位的小正方形所组成的网格中，△ABC 的顶点均在网格上．(1)sin B 的值是__35__； (2)画出△ABC 关于直线l 对称的△A 1B 1C 1(A 与A 1，B 与B 1，C 与C 1相对应)，连结AA 1，BB 1，并计算梯形AA 1B 1B 的面积．解：(2)画图略，由轴对称的性质可得AA 1＝2，BB 1＝8，高BC ＝4，S 梯形AA 1B 1B ＝12(AA 1＋B 1B )·BC ＝12(2＋8)×4＝20。

参考答案1. D2. C3. C4. D5. A6. A7. B8. C9. C 10. C11. 3：40 12. 68° 13. 75° 14. 12cm 15. 6 16. 4 17. 6 18. 819. 解：∵在Rt △ABC 中，∠ACB ＝90°，∠A ＝26°，∴∠B ＝64°. ∵将△CBD 沿CD 折叠，使点B 恰好落在AC 边上的点E 处，且∠ACB ＝90°，∴∠BCD ＝∠ECD ＝45°，∠CED ＝∠B ＝64°. ∴∠CDE ＝180°－∠ECD －∠CED ＝71°.20. 解：∵∠ACB ＝90°，∴∠B ＋∠BAC ＝90°. ∵CD ⊥AB ，∴∠CAD ＋∠ACD ＝90°.∴∠ACD ＝∠B . ∵AE 是∠BAC 的平分线，∴∠CAE ＝∠EAB . ∵∠EAB ＋∠B ＝∠CEA ，∠CAE ＋∠ACD ＝∠CFE ，∴∠CFE ＝∠CEF .∴CF ＝CE . ∴△CEF 是等腰三角形．21. 解：∵△ACD 的周长是14 cm ，∴AD ＋DC ＋AC ＝14 cm. 又∵DE 是BC 的垂直平分线，∴BD ＝DC . ∴AD ＋DC ＝AD ＋BD ＝AB . ∴AB ＋AC ＝14 cm. ∵AB 比AC 长3 cm ，∴AB －AC ＝3 cm. ∴AB ＝8.5 cm ，AC ＝5.5 cm.22. 解：设∠A ，∠B ，∠C 是该等腰三角形的三个内角，且∠A ＝12∠B . 设∠A ＝x °，则∠B ＝2x °.①若∠B 是顶角，则∠A ，∠C 是底角，于是有∠C ＝∠A ＝x °. ∵∠A ＋∠B ＋∠C ＝180°，∴x ＋2x ＋x ＝180. 解得x ＝45，故∠A ＝∠C ＝45°，∠B ＝90°； ②若∠B 是底角，∵∠A ≠∠B ，∴∠A 是顶角，∠C ＝∠B ＝2x °. ∵∠A ＋∠B ＋∠C ＝180°，∴x ＋2x ＋2x ＝180. 解得x ＝36，故∠A ＝36°，∠B ＝∠C ＝72°. 综上所述，等腰三角形的各内角分别为45°，45°，90°或36°，72°，72°.23. 证明：(1)∵AD ∥BC ，∴∠ADE ＝∠FCE . ∵E 是CD 的中点，∴DE ＝CE . 又∵∠AED ＝∠FEC ，∴△ADE ≌△FCE (ASA)．∴FC ＝AD .(2)∵△ADE ≌△FCE ，∴AE ＝EF ，AD ＝CF . 又∵BE ⊥AE ，∴BE 是线段AF 的垂直平分线．∴AB ＝BF ＝BC ＋CF . ∵AD ＝CF ，∴AB ＝BC ＋AD .24. 解：OI ⊥BC . 证明：连接AO ，延长OI 交BC 于点M . ∵OE ，OF 分别为AB ，AC 的中垂线，∴OA ＝OB ，OA ＝OC .∴OB ＝OC . 又∵BI ，CI 分别为∠OBC ，∠OCB 的平分线，∴点I 必在∠BOC 的平分线上．∴∠BOI ＝∠COI . 在△BOM 和△COM 中，⎩⎨⎧OB ＝OC ，∠BOM ＝∠COM ，OM ＝OM ，∴△BOM ≌△COM (SAS)．∴∠BMO ＝∠CMO . 又∵∠BMO ＋∠CMO ＝180°. ∴∠BMO ＝∠CMO ＝90°. ∴OI ⊥BC .25. 证明：(1)∵△ACD 和△BCE 都是等边三角形，∴AC ＝DC ，BC ＝EC ，∠ACD ＝∠BCE ＝60°. ∵∠ACD ＋∠DCE ＋∠ECB ＝180°，∴∠DCE ＝60°. ∴∠ACE ＝∠DCB ＝120°. 在△ACE 和△DCB中，⎩⎨⎧AC ＝DC ，∠ACE ＝∠DCB ，CE ＝CB ，∴△ACE ≌△DCB (SAS)．∴∠EAC ＝∠BDC .。

一、选择题1．若a ，b 是等腰ABC 的两边长，且满足()2370a b -+-=，此三角形的周长是（ ）A ．13B ．13或17C ．17D ．202．以下尺规作图中，点D 为线段BC 边上一点，一定能得到线段AD BD =的是（ ） A ． B ．C ．D ．3．如图，已知ABC ∆中，,AB AC =点,D E 是射线AB 上的两个动点(点D 在点E 的右侧)．且,CE DE =连结CD ，若ACE x ∠=，BCD y ∠=．则y 关于x 的函数关系式是（ ）A ．()900180y x x =-<<︒B ．()101802y x x =<<︒C ．()39001802y x x =-<<︒D ．()201803y x x =<<︒ 4．如图，在ABC ∆中，90,30C B ︒︒∠=∠= ，以A 为圆心，任意长为半径画弧分别交AB AC 、于点M 和N ，再分别以M N 、为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP ，并延长交BC 于点D ，则下列说法中正确的个数是（ ）①AD 是BAC ∠的平分线；②60ADC ︒∠=；③点D 在AB 的垂直平分线上﹔④若2AD =，则点D 到AB 的距离是1，:1:2DAC ABC S S ∆∆=A ．2B ．3C ．4D ．55．如图，等边ABC 的顶点(1,1)A ，(3,1)B ，规定把等边ABC “先沿x 轴翻折，再向左平移1个单位”为一次变换，这样连续经过2021次变换后，ABC 顶点C 的坐标为（ ）A ．(2020,13)-+B ．(2020,13)---C ．(2019,13)-+D ．(2019,13)--- 6．如图，在△ABC 中，∠BAC ＝90°，AD 是高，BE 是中线，CF 是角平分线，CF 交AD 于点G ，交BE 于点H ，下面说法：①△ABE 的面积＝△BCE 的面积；②∠AFG ＝∠AGF ；③∠FAG ＝2∠ACF ；④BH ＝CH ．其中正确的是（ ）A ．①②③④B ．①②③C ．②④D ．①③7．如图，在△ABC 纸片中，AB=9cm ，BC=5cm ，AC=7cm ，沿过点B 的直线折叠这个三角形，使点C 落在AB 边上的点E 处，折痕为BD ，则△ADE 的周长为是（ ）A ．9cmB ．11cmC ．12cmD ．14cm 8．下列推理中，不能判断ABC 是等边三角形的是（ ） A ．A B C ∠=∠=∠ B ．,60AB AC B =∠=︒C ．60,60A B ∠=︒∠=︒D ．AB AC =，且B C ∠=∠ 9．如图，C 是线段AB 上的一点，ACD △和BCE 都是等边三角形，AE 交CD 于M ，BD 交CE 于N ，交AE 于O ，则①DB AE =；②AMC DNC ∠=∠；③60AOB ∠=︒；④DN AM =；⑤CMN △是等边三角形．其中，正确的有（ ）A ．2个B ．3个C ．4个D ．5个10．如图，是一个 3×4 的网格（由 12 个小正方形组成，虚线交点称之格点）图中有一个三角形，三个顶点都在格点上，在网格中可以画出（ ）个与此三角形关于某直线对称的格点三角形．A ．6B ．7C ．8D ．911．如图，AC AD =，BC BD =，则有（ ）A ．AB 与CD 互相垂直平分B ．CD 垂直平分ABC ．CD 平分ACB ∠ D ．AB 垂直平分CD12．如图，在等腰ABC 中，118ABC ︒∠=，AB 垂直平分线DE 交AB 于点D ，交AC 于点E ，BC 的垂直平分线PQ 交BC 于点P ，交AC 于点Q ，连接BE ，BQ ，则EBQ ∠=（ ）A ．65︒B ．60︒C ．56︒D ．50︒二、填空题13．如图，已知60AOB ︒∠=，点P 在边OA 上， 10OP =，点,M N 在边OB 上， PM PN =，若3,MN =则OM 的长是__________．14．如图，在平面直角坐标系中，直线l 与x 轴交于点1B ，与y 轴交点于D ，且111,60OB ODB =∠=︒，以1OB 为边长作等边三角形11AOB ，过点1A 作12A B 平行于x 轴，交直线l 于点2B ，以12A B 为边长作等边三角形212A A B ，过点2A 作23A B 平行于x 轴，交直线l 于点3B ，以23A B 为边长作等边三角形323A A B ，…，按此规律进行下去，则点6A 的横坐标是______．15．如图，ABC 中，AB BC =，点D 在线段BC 上（不与点,B C 重合）． 作法如下：①连接AD ，作AD 的垂直平分线分别交直线,AB AC 于点,P Q ，连接,DP DQ ，则APQ DPQ △≌△；②过点D 作AC 的平行线交AB 于点P ，在线段AC 上截取AQ ，使AQ DP =，连接,PQ DQ ，则APQ DQP △≌△；③过点D 作AC 的平行线交AB 于点P ，过点D 作AB 的平行线交AC 于点Q ，连接PQ ，则APQ DQP △≌△；④过点D 作AB 的平行线交AC 于点Q ，在直线AB 上取一点P ，连接DP ，使DP AQ =，连接PQ ，则APQ DPQ △≌△．以上说法一定成立的是__________．（填写正确的序号）16．如图，在ABC 中，D 是BC 上一点，,105AC AD DB BAC ==∠=︒，则B ∠=________°．17．如图在钝角△ABC 中，已知∠BAC=135°，边AB 、AC 的垂直平分线分别交BC 于点D 、E ，连接AD 、AE ，则∠DAE=_____18．如图，在锐角△ABC 中，AB ＝62 ，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M ，N 分别是AD 和AB 上的动点，则BM ＋MN 的最小值是_____________．19．如图，∠AOB ＝45°，OC 平分∠AOB ，点M 为OB 上一定点，P 为OC 上的一动点，N 为OB 上一动点，当PM ＋PN 最小时，则∠PMO 的度数为___________．20．如图，在等边三角形ABC 中，CM 平分ACB ∠交AB 于点M ．（1）ACM ∠的大小=__________（度）；（2）AMC ∠的大小=__________（度）；（3）已知4AB =，点D 为射线CM 上一点，作∠DCE=60︒，()CE CD CD AB =≠，连接DE 交射线CB 于点F ，连接BD ，BE 当以B ，D ，M 为顶点的三角形与BEF 全等时，线段CF 的长为__________．三、解答题21．如图，,A B AE BE ∠=∠=，点D 在AC 边上，12,AE ∠=∠和BD 相交于点O ． （1）求证：AEC BED ∆≅∆（2）若70BDE ︒∠=，求1∠的度数．22．如图，已知∠A ＝∠D ＝90°，E 、F 在线段BC 上，DE 与AF 交于点O ，且AB ＝CD ，BE ＝CF ．求证：（1）Rt △ABF ≌Rt △DCE ；（2）OE ＝OF ．23．如图：已知ABC 中AB AC =：（1）尺规作图：过A 点作//AE BC （不写作法，保留作图痕迹）；（2）求证：AE 是ABC 的一个外角角平分线．24．已知ABC 是等边三角形，点D 是AC 的中点，点P 在射线BC 上，点Q 在线段AB 上，120PDQ ∠=︒．（1）如图1，若点Q 与点B 重合，求证：DB DP =；（2）如图2，若点P 在线段BC 上，8AC =，求AQ PC +的值．25．已知：90,A D AB DC ︒∠=∠==，点,E F 在直线BC 上，位置如图所示，且BE CF =．（1）求证：AF DE =；（2）若PO 平分EPF ∠，求证：PO 垂直平分线段BC ．26．（1）如图①，已知：在ABC 中，90BAC ∠=︒，AB AC =，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．求证：DE BD CE =+．（2）如图②，将（1）中的条件改为：在ABC 中，AB AC =，D 、A 、E 三点都在直线m 上，并且有BDA AEC BAC a ∠=∠=∠=，其中a 为任意锐角或钝角．请问结论DE BD CE =+是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图③，D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合），点F 为BAC ∠平分线上的一点，且ABF 和ACF 均为等边三角形，连接BD 、CE ，若BDA AEC BAC ∠=∠=∠，试判断DEF 的形状．（不需要说明理由）【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据绝对值非负性的性质以及平方的非负性可知a和b的值，然后根据等腰三角形的性质分情况计算即可；【详解】∵()2-+-=，a b370∴ a=3，b=7，若腰为3时，3+3＜7，三角形不成立；若腰为7时，则周长为7+7+3=17，故选：C．【点睛】本题考查了非负性的性质以及等腰三角形的性质，熟练掌握知识点是解题的关键；．2．D解析：D【分析】点D到点A、点B的距离相等可知点D在线段AB的垂直平分线上，据此可得答案．【详解】解：∵点D到点A、点B的距离AD=BD，∴点D在线段AB的垂直平分线上，故选择：D．【点睛】本题主要考查作图−复杂作图，解题的关键是掌握线段中垂线的性质与尺规作图．3．B解析：B【分析】根据等腰三角形的性质得出∠ACB=∠ABC=x+∠BCE和∠D=∠DCE=y+∠BCE，由三角形的外角性质得出∠ABC=∠D+∠BCD ，即x+∠BCE= y+∠BCE+ y ，即x=2y ，得出y 关于x 的函数关系式．【详解】解：∵AB AC =，ACE x ∠=，∴ ∠ACB=∠ABC=x+∠BCE ，∵CE DE =，BCD y ∠=∴∠D=∠DCE=y+∠BCE ，∵ ∠ABC 是△BCD 的一个外角，∴∠ABC=∠D+∠BCD ，即 x+∠BCE= y+∠BCE+ y ，即x=2y ， ∴()101802y x x =<<︒， 故选：B ．【点睛】 本题主要考查了等腰三角形的性质，三角形的外角性质，三角形的外角等于它不相邻的两个内角和．熟练掌握并运用各性质是解题的关键．4．B解析：B【分析】先根据三角形内角和计算出∠BAC=60°，再利用基本作图对①进行判断；利用∠BAD=∠CAD=30°得到∠ADC=60°，则可对②进行判断；利用∠B=∠BAD 得到DA=DB ，根据线段垂直平分线的性质定理的逆定理可对③进行判断．利用30度角所对的直角边是斜边的一半、三角形的面积计算公式即可得出两个三角形的面积之比．【详解】解：由作法得，AD 平分∠BAC ，所以①正确；∵∠C=90°，∠B=30°，∴∠BAC=60°，∴∠BAD=∠CAD=12×60°=30°， ∴∠ADC=90°-∠CAD=60°，所以②正确；∵∠B=∠BAD ，∴DA=DB ，∴点D 在AB 的垂直平分线上，所以③正确；在直角△ACD 中，∠CAD=30°，∴CD=12AD ， ∴BC=CD+BD=12AD+AD=32AD ，1124DAC S AC CD AC AD ∆=⋅=⋅．∴11332224ABC S AC BC AC AD AC AD ∆=⋅=⋅=⋅， ∴13::1:344DAC ABC S S AC AD AC AD ∆∆=⋅⋅=，故④错误． 所以，正确的结论有3个故选：B ．【点睛】 本题考查了角平分线的性质、线段垂直平分线的性质以及作图-基本作图．解题时需要熟悉等腰三角形的判定与性质．5．D解析：D【分析】先求出点C 坐标，第一次变换，根据轴对称判断出点C 变换后在x 轴下方然后求出点C 纵坐标，再根据平移的距离求出点C 变换后的横坐标，最后写出第一次变换后点C 坐标，同理可以求出第二次变换后点C 坐标，以此类推可求出第n 次变化后点C 坐标．【详解】∵△ABC 是等边三角形AB=3-1=2∴点C 到x 轴的距离为1+21=+2 ∴C(2，1+由题意可得:第1次变换后点C 的坐标变为(2-1，1)，即(1，1-，第2次变换后点C 的坐标变为(2-21)，即(0，1+第3次变换后点C 的坐标变为(2-3，1)，即(-1，1--第n 次变换后点C 的坐标变为(2-n ，1)(n 为奇数)或(2-n ，1+为偶数)， ∴连续经过2021次变换后，等边ABC 的顶点C 的坐标为(-2019，1-， 故选：D ．【点睛】本题考查了利用轴对称变换（即翻折）和平移的特点求解点的坐标，在求解过程中找到规律是关键． 6．B解析：B【分析】根据等底等高的三角形的面积相等即可判断①；根据三角形内角和定理求出∠ABC ＝∠CAD ，根据三角形的外角性质即可推出②；根据三角形内角和定理求出∠FAG ＝∠ACD ，根据角平分线定义即可判断③；根据等腰三角形的判定判断④即可．【详解】∵BE 是中线，∴AE＝CE，∴△ABE的面积＝△BCE的面积（等底等高的三角形的面积相等），故①正确；∵CF是角平分线，∴∠ACF＝∠BCF，∵AD为高，∴∠ADC＝90°，∵∠BAC＝90°，∴∠ABC＋∠ACB＝90°，∠ACB＋∠CAD＝90°，∴∠ABC＝∠CAD，∵∠AFG＝∠ABC＋∠BCF，∠AGF＝∠CAD＋∠ACF，∴∠AFG＝∠AGF，故②正确；∵AD为高，∴∠ADB＝90°，∵∠BAC＝90°，∴∠ABC＋∠ACB＝90°，∠ABC＋∠BAD＝90°，∴∠ACB＝∠BAD，∵CF是∠ACB的平分线，∴∠ACB＝2∠ACF，∴∠BAD＝2∠ACF，即∠FAG＝2∠ACF，故③正确；根据已知条件不能推出∠HBC＝∠HCB，即不能推出BH＝CH，故④错误；故选：B．【点睛】本题考查了三角形内角和定理，三角形的外角性质，三角形的角平分线、中线、高，等腰三角形的判定等知识点，能综合运用定理进行推理是解此题的关键，题目比较好，属于中考题型．7．B解析：B【分析】根据折叠的性质得到：DE=CD，BE=BC=5cm，求出AE=4cm，根据△ADE的周长为AD+DE+AE=AC+AE代入数值计算即可得解．【详解】由折叠得：DE=CD，BE=BC=5cm，∵AB=9cm，∴AE=AB-BE=9cm-5cm=4cm，∴△ADE的周长为AD+DE+AE=AC+AE=7cm+4cm=11cm，故选：B．【点睛】此题考查折叠的性质：折叠前后对应边相等，正确理解折叠的性质是解题的关键．8．D解析：D【分析】根据等边三角形的定义、判定定理以及三角形内角和定理进行判断．【详解】A 、由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；B 、由“有一个角是60°的等腰三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；C 、由“∠A ＝60°，∠B ＝60°”可以得到“∠A ＝∠B ＝∠C ＝60°”，则由“三个角都相等的三角形是等边三角形”可以判断△ABC 是等边三角形，故本选项不符合题意；D 、由“AB ＝AC ，且∠B ＝∠C”只能判定△ABC 是等腰三角形，故本选项符合题意． 故选：D ．【点睛】本题主要考查了等边三角形的判定和三角形内角和定理，属于基础题．（1）由定义判定：三条边都相等的三角形是等边三角形．（2）判定定理1：三个角都相等的三角形是等边三角形．（3）判定定理2：有一个角是60°的等腰三角形是等边三角形．9．C解析：C【分析】易证△ACE ≌△DCB ，可得①正确；即可求得∠AOB ＝120°，可得③错误；再证明△ACM ≌△DCN ，可得②④正确和CM ＝CN ，即可证明⑤正确；即可解题．【详解】解：∵ACD △和BCE 都是等边三角形∵∠ACD ＝∠BCE ＝60°，∴∠DCE ＝60°，在△ACE 和△DCB 中，AC DC ACE DCB CB CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△DCB （SAS ），∴∠BDC ＝∠EAC ，DB ＝AE ，①正确；∠CBD ＝∠AEC ，∵∠AOB ＝180°−∠OAB−∠DBC ，∴∠AOB ＝180°−∠AEC−∠OAB ＝120°，③错误；在△ACM 和△DCN 中，60BDC EAC DC ACACD DCN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ∴△ACM ≌△DCN （ASA ），∴AM ＝DN ，④正确；∠AMC ＝∠DNC ，②正确；CM ＝CN ，∵∠ACD ＝∠BCE ＝60°，∴∠MCN ＝180°-∠ACD-∠BCE =60°，∴△CMN 是等边三角形，⑤正确；故有①②④⑤正确．故选：C ．【点睛】本题考查了全等三角形的判定和全等三角形对应边、对应角相等的性质，本题中求证△ACE ≌△DCB 和△ACM ≌△DCN 是解题的关键．10．B解析：B【分析】先确定对称轴，再找到对称点进而可以找到符合题意的对称三角形即可．【详解】解：如图，左右对称的有4个，如图，上下对称的有1个，如图，关于正方形的对角线对称的有2个，∴一共有7个与原三角形关于某直线对称的格点三角形，故选：B ．【点睛】本题考查了轴对称图形的性质，找到正确的对称轴，画出相应的对称三角形是解决本题的关键．11．D解析：D【分析】根据线段垂直平分线的判定定理解答．【详解】∵AC AD =，BC BD =，∴AB 垂直平分CD ，故D 正确，A 、B 错误，OC 不平分∠ACB ，故C 错误，故选：D ．【点睛】此题考查线段垂直平分线的判定：到线段两个端点距离相等的点在这条线段的垂直平分线上．12．C解析：C【分析】根据等腰ABC ，118ABC ︒∠=，得到AB=CB ，∠A=∠C=1(180)312ABC ︒︒-∠=，由DE 垂直平分AB ，求得∠ABE=31A ∠=︒，同理：31QBC C ∠=∠=︒，根据∠EBQ=∠ABC-∠ABE-∠QBC 计算得出答案．【详解】在等腰ABC 中，118ABC ︒∠=，∴AB=CB ，∠A=∠C=1(180)312ABC ︒︒-∠=， ∵DE 垂直平分AB ，∴AE=BE ，∴∠ABE=31A ∠=︒，同理：31QBC C ∠=∠=︒，∴∠EBQ=∠ABC-∠ABE-∠QBC=56︒，故选：C．【点睛】此题考查等腰三角形的性质，线段垂直平分线的性质，三角形的内角和定理，熟记线段垂直平分线的性质是解题的关键．二、填空题13．5【分析】作PH⊥MN于H如图根据等腰三角形的性质得MH=NH=MN=15在Rt△POH中由∠POH=60°得到∠OPH=30°则根据在直角三角形中30°角所对的直角边等于斜边的一半可得OH=OP=解析：5【分析】作PH⊥MN于H，如图，根据等腰三角形的性质得MH=NH=12MN=1.5，在Rt△POH中由∠POH=60°得到∠OPH=30°，则根据在直角三角形中，30°角所对的直角边等于斜边的一半可得OH=12OP=5，然后计算OH-MH即可．【详解】作PH⊥MN于H，如图，∵PM=PN，∴MH=NH=12MN=1.5，在Rt△POH中，∵∠POH=60°，∴∠OPH=30°，∴OH=12OP=12×10=5，∴OM=OH-MH=5-1.5=3.5．故答案为：3.5．【点睛】本题考查了含30度角的直角三角形的性质：在直角三角形中，30°角所对的直角边等于斜边的一半．也考查了等腰三角形的性质．14．5【分析】过A1作A1A⊥OB1于A过A2作A2B⊥A1B2于B过A3作A3C⊥A2B3于C根据等边三角形的性质以及含30°角的直角三角形的性质分别求得A1的横坐标为A2的横坐标为A3的横坐标为进而解析：5【分析】过A1作A1A⊥OB1于A，过A2作A2B⊥A1B2于B，过A3作A3C⊥A2B3于C，根据等边三角形的性质以及含30°角的直角三角形的性质，分别求得A1的横坐标为1212-，，A2的横坐标为2212-，A3的横坐标为3212-，进而得到A n的横坐标为212n-，据此可得点A6的横坐标．【详解】解：如图所示,过A1作A1A⊥OB1于A,则OA=12OB1=12，即A1的横坐标为12=1212-，∵160ODB∠=°，∴∠OB1D=30°，∵A1B2//x轴，∴∠A1B2B1=∠OB1D=30°，∠B2A1B1=∠A1B1O=60°，∴∠A1B1B2=90°，∴A1B2=2A1B1=2，过A2作A2B⊥A1B2于B,则A1B=12A1B2=1，即A2的横坐标为12+1=2212-，过A3作A3C⊥A2B3于C，同理可得,A2B3=2A2B2=4,A2C=12A2B3=2，即A3的横坐标为12+1+2=3212-，同理可得,A4的横坐标为12+1+2+4=4212-，由此可得,A n的横坐标为212n-，∴点A6的横坐标是62163==31.522-，故答案为31.5．【点睛】本题是一道找规律问题，涉及到等边三角形的性质、含30度角的直角三角形，解题的关键要利用等边三角形的性质总结出关于点A的系列点的规律．15．①②③【分析】根据题意画出图形再根据垂直平分线的性质平行线的性质和三角形全等的判定可以得证【详解】解：①如图∵PQ为AD的垂直平分线∴PA=PDQA=QD∴在△APQ和△DPQ中∴△APQ≌△DPQ解析：①②③【分析】根据题意画出图形，再根据垂直平分线的性质，平行线的性质和三角形全等的判定可以得证．【详解】解：①如图，∵PQ为AD的垂直平分线，∴PA=PD，QA=QD，∴在△APQ和△DPQ中，PA PDPQ PQQA QD=⎧⎪=⎨⎪=⎩，∴△APQ≌△DPQ（SSS），①正确；②如图，∵PD ∥AC ，∴∠DPQ=∠AQP ，∴在△APQ 和△DQP 中，AQ DP AQP DPQ QP PQ =⎧⎪∠=∠⎨⎪=⎩，∴△APQ ≌△DQP （SAS ），②正确 ；③如图，∵PD ∥AC ，∴∠DPQ=∠AQP ，同理∠DQP=∠APQ ，∴在△APQ 和△DQP 中，DPQ AQP PQ PQDQP APQ ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△APQ ≌△DQP （ASA ），③正确 ；④如图，△APQ ≌△DPQ 不成立，④错误；故答案为①②③．【点睛】本题考查三角形与平行线的综合应用，熟练掌握垂直平分线的性质，平行线的性质和三角形全等的判定是解题关键．16．25【分析】设∠ADC ＝α然后根据AC ＝AD ＝DB ∠BAC ＝105°表示出∠B 和∠BAD 的度数最后根据三角形的内角和定理求出∠ADC 的度数进而求得∠B 的度数即可【详解】解：∵AC ＝AD ＝DB ∴∠B ＝解析：25【分析】设∠ADC ＝α，然后根据AC ＝AD ＝DB ，∠BAC ＝105°，表示出∠B 和∠BAD 的度数，最后根据三角形的内角和定理求出∠ADC 的度数，进而求得∠B 的度数即可．【详解】解：∵AC ＝AD ＝DB ，∴∠B ＝∠BAD ，∠ADC ＝∠C ，设∠ADC ＝α，∴∠B ＝∠BAD ＝2α ， ∵∠BAC ＝105°，∴∠DAC ＝105°﹣2α， 在△ADC 中， ∵∠ADC +∠C +∠DAC ＝180°，∴2α+105°﹣2α＝180°， 解得：α＝50°，∴∠B ＝∠BAD ＝2α＝25°， 故答案为：25．【点睛】 本题考查了等腰三角形的性质：①等腰三角形的两腰相等；②等腰三角形的两个底角相等，熟练掌握等腰三角形的性质是解题的关键．17．90°【分析】根据等腰三角形的性质和线段垂直平分线的性质即可得到结论【详解】解：连接DAEA 如图∵∠BAC=135°∴∠B+∠C=180°-135°=45°∵DF 是AB 的垂直平分线EG 是AC 的垂直平解析：90°【分析】根据等腰三角形的性质和线段垂直平分线的性质即可得到结论．【详解】解：连接DA、EA，如图，∵∠BAC=135°，∴∠B+∠C=180°-135°=45°，∵DF是AB的垂直平分线，EG是AC的垂直平分线，∴DA=DB，EA=EC，∴∠B=∠DAB，∠C=∠EAC，∴∠DAB +∠EAC =∠B+∠C=45°，∴∠DAE=∠BAC –(∠DAB +∠EAC)=135°-45°=90°．故答案为：90°．【点睛】本题考查线段的垂直平分线的性质，解题的关键是熟练掌握线段的垂直平分线的性质．18．6【分析】作BH⊥AC垂足为H交AD于M′点过M′点作M′N′⊥AB垂足为N′则BM′+M′N′为所求的最小值再根据AD是∠BAC的平分线可知M′H=M′N′再由锐角三角函数的定义即可得出结论【详解解析：6【分析】作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值，再根据AD是∠BAC的平分线可知M′H=M′N′，再由锐角三角函数的定义即可得出结论．【详解】解：如图，作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值．∵AD是∠BAC的平分线，∴M′H=M′N′，∴BH是点B到直线AC的最短距离（垂线段最短），∵AB=2∠BAC=45°，∴BH=AH∴222+=AH BH AB∴BH=6．∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=6．故答案为6．【点睛】本题考查的是轴对称-最短路线问题，解答此类问题时要从已知条件结合图形认真思考，通过角平分线性质，垂线段最短，确定线段和的最小值．19．45°【分析】找到点M关于OC对称点M′过点M′作M′N⊥OB于点N交OC 于点P则此时PM+PN的值最小再根据角平分线的性质及三角形内角和即可得出答案【详解】解：如图找到点M关于OC对称点M′过点M解析：45°【分析】找到点M关于OC对称点M′，过点M′作M′N⊥OB于点N，交OC于点P，则此时PM+PN 的值最小，再根据角平分线的性质及三角形内角和即可得出答案．【详解】解：如图，找到点M关于OC对称点M′，过点M′作M′N⊥OB于点N，交OC于点P，则此时PM+PN 的值最小．∵PM=PM′，∴此时PM+PN=PM′+PN′=M′N′，∵点M与点M′关于OC对称，OC平分∠AOB，∴OM=OM′，∵∠AOB=45°，∴∠PM'O=∠AOB=45°，∴∠PMO=∠PM'O=45°，故答案为：45°．【点睛】本题考查了利用轴对称的知识寻找最短路径的知识，涉及到两点之间线段最短、垂线段最短的知识，有一定难度，正确确定点P及点N的位置是关键．20．2或6或【分析】（1）根据等边三角形的性质及角平分线的性质求解；（2）根据等边三角形的三线合一的性质解答；（3）根据题意分两种情况：当点D在线段CM上时当点D在线段CM的延长线上时分别画出图形利用全解析：3090 2或6或23【分析】（1）根据等边三角形的性质及角平分线的性质求解；（2）根据等边三角形的三线合一的性质解答；（3）根据题意分两种情况：当点D在线段CM上时，当点D在线段CM的延长线上时，分别画出图形，利用全等三角形的性质解答．【详解】（1）∵△ABC是等边三角形，∴∠ACB=60︒，∵CM平分ACB∠，∠ACB=30，∴∠ACM=12故答案为：30；∠，（2）∵△ABC是等边三角形，CM平分ACB∴CM⊥AB，∴∠AMC=90︒，故答案为：90︒；（3）∵∠DCE=60︒，CD=CE，∴△CDE是等边三角形，∴DE=CE=CD，∵∠BCM=∠ACM=30，∴∠BCE=30，∴CF平分∠DCE，∵CD=CE，∴CB垂直平分DE，①当点D在线段CM上时，当△BDM≌△BEF时，如图1，∴BF=BM=2，∴CF=CB-BF=4-2=2；当△BDM≌△EBF时，如图1，则EF=BM=2，∴CD=DE=4，,∵AB=4，CD<CM<4,∴此种情况不成立，舍去；②当点D在线段CM的延长线上时，当△BDM≌△BEF时，如图2，∴BF=BM=2，∴CF=BC+BF=4+2=6,；当△BDM≌△EBF时，如图3，则EF=BM=2，∴CE=2EF=4，∴2223CF CE EF =-=，故答案为： 2或6或23．．【点睛】此题考查等边三角形的性质，利用三线合一的性质进行证明，全等三角形的性质，熟记等边三角形的性质是解题的关键．三、解答题21．（1）见解析；（2）40°【分析】（1）由12∠=∠得到BED AEC ∠=∠，然后根据ASA 即可证明AEC BED ∆≅∆； （2）由（1）得DE=CE ，70C BDE ∠=∠=︒，由三角形内角和即可求出1∠的度数．【详解】解：()11=2∠∠，BED AEC ∠=∠∴又,A B AE BE ∠=∠=()AEC BED ASA ∴∆≅∆；()2AEC BED ∆≅∆70,BDE C DE CE ∴∠=∠=︒=70C EDC ︒∴∠=∠=118027040︒︒︒∴∠=-⨯=；【点睛】本题考查了等腰三角形的性质，全等三角形的判定和性质，三角形的内角和定理，解题的关键是掌握全等三角形的判定和性质进行解题．22．（1）见解析；（2）见解析【分析】（1）由于△ABF 与△DCE 是直角三角形，根据直角三角形全等的判定的方法即可证明； （2）先根据三角形全等的性质得出∠AFB ＝∠DEC ，再根据等腰三角形的性质得出结论．【详解】证明：（1）∵BE ＝CF ，∴BE＋EF＝CF＋EF，即BF＝CE，∵∠A＝∠D＝90°，∴△ABF与△DCE都为直角三角形，在Rt△ABF和Rt△DCE中∵BF CE AB CD=⎧⎨=⎩，∴Rt△ABF≌Rt△DCE（HL）；（2）∵Rt△ABF≌Rt△DCE（已证），∴∠AFB＝∠DEC，∴OE＝OF．【点睛】本题主要考查全等三角形的判定和性质以及等腰三角形的判定定理，掌握HL判断两个直角三角形全等，是解题的关键．23．（1）见解析；（2）见解析．【分析】（1）作∠CAE=∠C即可；（2）延长BA，根据两直线平行，同位角相等，有∠EAF=∠B，由（1）可知∠CAE=∠C，再根据AB=AC，可得∠B=∠C，等量替换之后即可得证．【详解】（1）射线AE为所求；（2）证明：如图所示，延长BA，∵//AE BC，∴∠EAF=∠B，∠CAE=∠C，∵AB=AC，∴∠B=∠C，∴∠EAF=∠CAE，∴AE是ABC的一个外角角平分线．【点睛】本题考查了平行线的性质和判定，等腰三角形的性质和角平分线的判定等知识，掌握相关知识是解题的关键．24．（1）证明见解析；（2）4．【分析】（1）由等边三角形的性质证明30DBC ∠=︒，再利用三角形的内角和定理求解30DPB ∠=︒，从而可得结论； （2）过点D 作//DE BC 交AB 于点E ，先证明ADE 为等边三角形，再证明QDE PDC ≌，可得QE PC =， 从而可得答案．【详解】证明：（1）∵ABC 为等边三角形，∴,60BA BC ABC =∠=︒∵D 为AC 的中点，∴DB 平分ABC ∠，∴30DBC ∠=︒． ∵120PDB ∠=︒，∴1801203030DPB ∠=︒-︒-︒=︒，∴DBC DPB ∠=∠，∴DB DP =．（2）过点D 作//DE BC 交AB 于点E ．∵ABC 为等边三角形，8AC =，点D 是AC 的中点，∴4,60AD CD ABC ACB A ==∠=∠=∠=︒．∵//DE BC ，∴60AED B ∠=∠=︒．60ADE C ∠=∠=︒，∴ADE 为等边三角形，120EDC ∠=︒，∴4AD ED AE ===，∴ED CD 4==．∵120QDP EDC ∠=∠=︒，,QDE EDP EDP PDC ∴∠+∠=∠+∠∴QDE PDC ∠=∠．∵,60ED CD AED C =∠=∠=︒，∴QDE PDC ≌，∴EQ PC =，∴4AQ PC AQ QE AE +=+==．【点睛】本题考查的是等腰三角形的判定，等边三角形的性质与判定，三角形的全等的判定与性质，掌握以上知识是解题的关键．25．（1）证明见解析；（2）证明见解析．【分析】(1)根据已知条件证明Rt △ABF ≌Rt △DCE(HL)即可得出结论；(2)根据Rt △ABF ≌Rt △DCE 可得出∠E=∠F ，即△PEF 为等腰三角形，又因为PO 平分∠EPF ，根据三线合一可知PO 垂直平分EF ，从而得出PO 垂直平分BC ．【详解】（1）证明:∵BE=CF ，BC=CB∴BF=CE ，在Rt △ABF 与Rt △DCE 中，BF CE AB DC =⎧⎨=⎩∴Rt △ABF ≌Rt △DCE(HL)，∴AF=DE ；（2）∵Rt △ABF ≌Rt △DCE ，∴∠E=∠F∴△PEF 为等腰三角形,又∵PO 平分∠EPF∴PO ⊥BC(三线合一)，EO=FO(三线合一)又∵EB=FC∴BO=CO ，∴PO 垂直平分线段BC.【点睛】本题考查的知识点是全等三角形的判定及性质、垂直平分线的判定、等腰三角形的性质，角平分线的性质，难度不大，但综合性较强，考验了学生综合分析问题的能力. 26．（1）见解析；（2）成立，证明见解析；（3）DEF 为等边三角形【分析】（1）根据BD ⊥直线m ，CE ⊥直线m 得∠BDA=∠CEA=90°，而∠BAC=90°，根据等角的余角相等得∠CAE=∠ABD ，然后根据“AAS”可判断△ADB ≌△CEA ，则AE=BD ，AD=CE ，于是DE=AE+AD=BD+CE ；（2）由∠BDA=∠AEC=∠BAC ，就可以求出∠BAD=∠ACE ，进而由AAS 就可以得出△BAD ≌△ACE ，就可以得出BD=AE ，DA=CE ，即可得出结论；（3）由等边三角形的性质，可以求出∠BAC=120°，就可以得出△BAD ≌△ACE ，就有BD=AE ，进而得出△BDF ≌△AEF ，得出DF=EF ，∠BFD=∠AFE ，而得出∠DFE=60°，即可推出△DEF 为等边三角形．【详解】（1）证明：∵BD ⊥直线m ，CE ⊥直线m ，∴90BDA CEA ∠=∠=︒∵90BAC ∠=︒，∴90BAD CAE ∠+∠=︒∵90BAD ABD ∠+∠=︒，∴CAE ABD ∠=∠．在ADB △和CEA 中：CAE ABD BDA CEA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ADB CEA AAS ≌（）△△． ∴AE BD =，AD CE =．∴DE AE AD BD CE =+=+．（2）成立．证明如下：∵∠BDA=∠BAC=α，又∵DBA ADB BAC CAE ∠+∠=∠+∠∴∠DBA=∠CAE ，在ADB △和CEA 中：DBA CAE BDA AEC AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ADB CEA AAS ≌△△． ∴AE BD =，AD CE =，∴DE AE AD BD CE =+=+．（3）DEF 为等边三角形．证明：∵△ABF 和△ACF 均为等边三角形，∴AB=AF=AC ，∠ABF=∠CAF=60°，BF=AF,∴由（2）可知，△ADB ≌△CEA ，∴BD=AE ，∠DBA=∠CAE ，∴∠DBA+∠ABF=∠CAE+∠CAF ，∴∠DBF=∠FAE ，∵在△DBF 和△EAF 中，BD AE DBF FAE BF AF ⎧⎪∠∠⎨⎪⎩＝＝＝ ∴△DBF ≌△EAF （SAS ），∴DF=EF ，∠BFD=∠AFE ，∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF 为等边三角形．【点睛】本题属于三角形综合题，主要考查了全等三角形与等边三角形的综合应用，解题的关键是熟练掌握全等三角形的判定与性质以及等边三角形的判定与性质并灵活运用，属于中考常考题型．。

轴对称经典中考试题及答案解析一知识点1：轴对称图形定义：如果一个图形沿一条折叠，直线两旁的部分能够互相，这个图形就叫做轴对称图形.这条直线就是它的 .这时我们就说这个图形关于这条直线（或轴）对称.如图12-2所示，△ABC是轴对称图形.【答案】直线、对称轴、1.（2006广东深圳）下列图形中，是．轴对称图形的为（ D ）ＡＢＣＤ知识点2：两个图形成轴对称：把一个图形沿着某一条直线折叠，如果它能够及重合，那么就是说这两个图形关于这条直线对称（也叫轴对称），这条直线叫做，折叠后的点是对应点，叫做对称点.如图12-3所示，△ABC及△A′B′C′关于直线l对称，直线l叫做对称轴.A和A′,B和B′，C和C′是对称点.【答案】另一个图形、对称轴、互相重合2.如图12－8所示，它们都是对称图形，请观察并指出哪些是轴对称图形，哪些图形成轴对称.【答案】图（1）（3）（4）（6）（8）（10）是轴对称图形；图（2）（5）（7）（9）成轴对称.知识点3：轴对称的性质：（1）如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的 .类似地，轴对称图形的对称轴，是任何一对对应点所连线段的 .（2）成轴对称的两个图形，如果把一个轴对称图形沿对称轴分成两个图形，那么这两个图形，这两个图形。

3.（2006扬州）如图，这是小亮制作的风筝，为了平衡做成轴对称图形，已知 OC是对称轴，∠A=35°，∠ACO=30°，那么∠BOC=°．【提示】由轴对称图形的性质可知：ACO BCO∆≅∆,得∠BOC＝∠AO C=180°－∠A－∠ACO=115°知识点4：线段的垂直平分线定义和性质及判定定义：经过线段并且于这条线段的直线叫做这条线段的垂直平分线.性质：线段垂直平分线上的点及这条线段两个端点的距离 .判定:及一条线段两个端点距离相等的点在这条线段的上.【答案】中点、垂直、相等、垂直平分线4.（2006淮安）如图，平行四边形ABCD中，AB=3，BC=5，AC的垂直平分线交AD于E，则△CDE的周长是（ B ）A．6 B．8 C．9 D．10【答案】由垂直平分线的性质可知：EA EC,所以△CDE的周长＝CD+DE+EC=CD+DE+EA=CD+DA=AB+BC=3+5=8,选B。

中考数学复习《轴对称》专项练习题-带含有答案一、单选题1．下列平面图形中，不是轴对称图形的是（）A．B．C．D．2．若点与关于x轴对称，则点的坐标为（）A．B．C．D．3．在中，和的度数如下，能判定是等腰三角形的是（）A．B．C．D．4．如图，PD垂直平分AB，PE垂直平分BC，若PA的长为7，则PC的长为（）A．5 B．6 C．7 D．85．如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC＝6，AC＝5，则△ACE的周长为（）A．8 B．11 C．16 D．176．如图，在等边△ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC＝45°，则下列结论不正确的是（）A．B．BC＝2DE C．∠ABE＝15°D．DE＝2AE7．如图，矩形中，对角线的垂直平分线分别交，于点，若AM=1，BN=2，则的长为（）A．B．C．D．8．如图，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM、MC下列结论：①DF=DN；②ABE≌△MBN；③△CMN 是等腰三角形；④AE=CN；，其中正确的结论个数是（）A．1个B．2个C．3个D．4个二、填空题9．如图，在△ABC中，AB＝AC，AD⊥BC于点D，若BC＝6，则CD＝．10．已知等腰三角形ABC，其中两边，满足，则ABC的周长为．11．在中，点D为斜边上的一点，若为等腰三角形，那么的度数为．12．如图，在中AB=AC，∠A=120°，AB的垂直平分线分别交，于D，E，BE=3，则的长为.13．如图，在中，∠ACB=90°，∠A=30°，将绕点C逆时针旋转得到，点M是的中点，点N是的中点，连接，若，则线段的最大值是．三、解答题14．如图,在正方形网格上的一个△ABC．(其中点A． B． C均在网格上)①作△ABC关于直线MN的轴对称图形△A′B′C′；②以P点为一个顶点作一个与△ABC全等的△EPF(规定点P与点B对应,另两顶点都在图中网格交点处).③在MN上画出点Q，使得QA+QC最小。

2021中考数学分类集训：轴对称与中心对称一、选择题1. 下列图形中，既是轴对称图形又是中心对称图形的是()2. 如图所示的图案中，是中心对称图形的是()3. 如图所示的尺规作图是作 ()A.一条线段的垂直平分线B.一个角的平分线C.一条直线的平行线D.一个角等于已知角4. 图中的四个图形，对称轴的条数为4的图形有()A.1个B.2个C.3个D.4个5. 如图，将△ABC以点O为旋转中心旋转180°后得到△A′B′C′.ED是△ABC的中位线，经旋转后变为线段E′D′.已知BC＝4，则线段E′D′的长度为()A．2 B．3 C．4 D．1.56. 在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1对称，再作△B2A3B3与△B2A2B1关于点B2对称……如此作下去，则△B2n A2n＋1B2n＋1(n是正整数)的顶点A2n＋1的坐标是()A．(4n－1，3) B．(2n－1，3)C．(4n＋1，3) D．(2n＋1，3)7. 把一张长方形纸片按图2①②所示的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是图3中的()8. 2020·河北模拟如图所示，A1(1，3)，A2(32，32)，A3(2，3)，A4(3，0)．作折线OA1A2A3A4关于点A4中心对称的图形，得折线A8A7A6A5A4，再作折线A8A7A6A5A4关于点A8中心对称的图形……以此类推，得到一个大的折线．现有一动点P从原点O出发，沿着折线以每秒1个单位长度的速度运动，设运动时间为t秒．当t＝2020时，点P的坐标为()A．(1010，3) B．(2020，3 2)C．(2016，0) D．(1010，3 2)二、填空题9. 将一张矩形纸片折叠成如图所示的图形，若AB=10 cm，则AC=cm.10. 等腰三角形的两边长分别为6 cm，13 cm，其周长为________ cm.11. 如图，直线a∥b，△ABC的顶点C在直线b上，边AB与直线b相交于点D.若△BCD是等边三角形，∠A＝20°，则∠1＝________．12. 在平面直角坐标系中，点P(4，2)关于直线x＝1的对称点的坐标是________．13. 如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，AD恰好平分∠BAC.若DE＝1，则BC的长是________．14. 如图，在△ABC中，AB，AC的垂直平分线分别交BC于点E，F.若△AEF的周长为10 cm，则BC的长为cm.15. 画图:试画出下列正多边形的所有对称轴，并完成表格.根据上表，猜想正n 边形有 条对称轴.16. (2019•黄冈)如图，AC BD ，在AB 的同侧，288AC BD AB ===，，，点M为AB 的中点，若120CMD ∠=︒，则CD 的最大值是__________．三、解答题17. 如图，正方形ABCD 与正方形A 1B 1C 1D 1关于某点中心对称．已知A ，D 1，D三点的坐标分别是(0，4)，(0，3)，(0，2)． (1)求对称中心的坐标；(2)写出顶点B ，C ，B 1，C 1的坐标．18. 如图，在正方形网格中，△ABC 的三个顶点都在格点上，点A ，B ，C 的坐标分别为(－2，4)，(－2，0)，(－4，1)，结合所给的平面直角坐标系解答下列问题：(1)画出△ABC关于原点O对称的△A1B1C1；(2)平移△ABC，使点A移动到点A2(0，2)的位置，画出平移后的△A2B2C2，并写出点B2，C2的坐标；(3)在△ABC，△A1B1C1中，△A2B2C2与________成中心对称，其对称中心的坐标为________.19. 请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹．(1)如图①，四边形ABCD中，AB＝AD，∠B＝∠D，画出四边形ABCD的对称轴m；(2)如图②，四边形ABCD中，AD∥BC，∠A＝∠D，画出BC边的垂直平分线n.20. 如图，在平面直角坐标系中，△ABC各顶点的坐标分别为A(－2，－2)，B(－4，－1)，C(－4，－4)．(1)作出△ABC关于原点O成中心对称的△A1B1C1.(2)作出点A关于x轴的对称点A′.若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界)，求a的取值范围．21. 如图，已知一个直角三角形纸片ACB，其中∠ACB＝90°，AC＝4，BC＝3，E、F分别是AC、AB边上的点，连接EF.(1)如图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S四边形ECBF ＝3S△EDF，求AE的长；(2)如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M 处，且使MF∥CA.①试判断四边形AEMF的形状，并证明你的结论；②求EF的长．轴对称与中心对称-答案一、选择题1. 【答案】B2. 【答案】D3. 【答案】A4. 【答案】B[解析] 图①是轴对称图形，有6条对称轴;图②是轴对称图形，有4条对称轴;图③是轴对称图形，有2条对称轴;图④是轴对称图形，有4条对称轴.故对称轴的条数为4的图形有2个.5. 【答案】A [解析] ∵ED 是△ABC 的中位线，BC ＝4，∴ED ＝2.又∵△A ′B ′C ′和△ABC 关于点O 中心对称，∴E ′D ′＝ED ＝2.6. 【答案】C[解析] A 1(1，3)，A 2(3，－3)，A 3(5，3)，A 4(7，－3)，…，∴点A n 的坐标为⎩⎨⎧（2n －1，3）（n 为奇数），（2n －1，－3）（n 为偶数）.∵2n ＋1是奇数，∴点A 2n ＋1的坐标是(4n ＋1，3)．故选C.7. 【答案】C8. 【答案】A二、填空题9. 【答案】10 [解析]如图，∵矩形的对边平行， ∴∠1=∠ACB ，由翻折变换的性质，得∠1=∠ABC ， ∴∠ABC=∠ACB ， ∴AC=AB ，∵AB=10 cm ，∴AC=10 cm . 故答案为10.10. 【答案】32[解析] 由题意知，应分两种情况：(1)当腰长为6 cm 时，三角形的三边长为6 cm ，6 cm ，13 cm ，6＋6＜13，不能构成三角形；(2)当腰长为13 cm 时，三角形的三边长为6 cm ，13 cm ，13 cm ，能构成三角形，周长＝2×13＋6＝32(cm)．11. 【答案】40°[解析] 如图．∵△BCD 是等边三角形，∴∠BDC＝60°.∵a∥b，∴∠2＝∠BDC＝60°.由三角形的外角性质和对顶角的性质可知，∠1＝∠2－∠A＝40°.12. 【答案】(－2，2)[解析] ∵点P(4，2)，∴点P到直线x＝1的距离为4－1＝3.∴点P关于直线x＝1的对称点P′到直线x＝1的距离为3.∴点P′的横坐标为1－3＝－2.∴对称点P′的坐标为(－2，2)．13. 【答案】3[解析] ∵AD平分∠BAC，且DE⊥AB，∠C＝90°，∴CD＝DE ＝1.∵DE是AB的垂直平分线，∴AD＝BD.∴∠B＝∠DAB.∵∠DAB＝∠CAD，∴∠CAD＝∠DAB＝∠B.∵∠C＝90°，∴∠CAD＋∠DAB＋∠B＝90°.∴∠B＝30°.∴BD＝2DE＝2.∴BC＝BD＋CD＝2＋1＝3.14. 【答案】10[解析] ∵AB，AC的垂直平分线分别交BC于点E，F，∴AE=BE，AF=CF.∴BC=BE+EF+CF=AE+EF+AF=10 cm.15. 【答案】解:如图.故填3，4，5，6，n.16. 【答案】14【解析】如图，作点A 关于CM 的对称点A'，点B 关于DM 的对称点B'．∵120CMD ∠=︒，∴60AMC DMB ∠+∠=︒， ∴60CMA'DMB'∠+∠=︒， ∴60A'MB'∠=︒， ∵MA'MB'=，∴A'MB'△为等边三角形，∵14CD CA'A'B'B'D CA AM BD ≤++=++=， ∴CD 的最大值为14，故答案为：14．三、解答题17. 【答案】解：(1)∵点D 和点D 1是对称点， ∴对称中心是线段DD 1的中点， ∴对称中心的坐标是(0，52)．(2)B(－2，4)，C(－2，2)，B 1(2，1)，C 1(2，3)．18. 【答案】解：(1)△ABC 关于原点O 对称的△A 1B 1C 1如图所示．(2)平移后的△A 2B 2C 2如图所示，其中点B 2的坐标为(0，－2)，点C 2的坐标为(－2，－1)．(3)△A1B1C1(1，－1)19. 【答案】解：(1)如图①，直线m即为所求．(2)如图②，直线n即为所求．20. 【答案】【思维教练】要作△ABC关于点O的中心对称图形，可先分别求出点A，B，C 关于点O 中心对称点，再顺次连接即可；(2)先作出点A′，再根据点A′在ΔA1B1C1，从而得出平移距离a满足A′A1<a<A′D(其中点D是A′A1与B1C1的交点)．解：(1)如解图，△A1B1C1就是所求作的图形：(2分)(2)A′如图所示；(4分)a的取值范围是4＜a＜6.(6分)21. 【答案】(1)如解图①，∵折叠后点A落在AB边上的点D处，解图①∴EF ⊥AB ，△AEF ≌△DEF ，∴S △AEF ＝S △DEF ，∵S 四边形ECBF ＝3S △EDF ，∴S 四边形ECBF ＝3S △AEF ，∵S △ACB ＝S △AEF ＋S 四边形ECBF ，∴S △ACB ＝S △AEF ＋3S △AEF ＝4S △AEF ， ∴14△△AEF ACB S S =， ∵∠EAF ＝∠BAC ，∠AFE ＝∠ACB ＝90°，∴△AEF ∽△ABC ， ∴2△△（）AEF ACB S AE ABS =， ∴214（）=，AE AB 在Rt △ACB 中，∠ACB ＝90°，AC ＝4，BC ＝3，∴AB 2＝AC 2＋BC 2，即AB ＝42＋32＝5，∴(AE 5)2＝14，∴AE ＝52；(2)①四边形AEMF 是菱形．证明：如解图②，∵折叠后点A 落在BC 边上的点M 处，∴∠CAB ＝∠EMF ，AE ＝ME ，又∵MF ∥CA ，∴∠CEM ＝∠EMF ，∴∠CAB ＝∠CEM ，∴EM ∥AF ，∴四边形AEMF 是平行四边形，而AE ＝ME ，∴四边形AEMF 是菱形，解图②②如解图②，连接AM ，与EF 交于点O ，设AE ＝x ，则AE ＝ME ＝x ，EC ＝4－x ， ∵∠CEM ＝∠CAB ，∠ECM ＝∠ACB ＝90°，∴Rt △ECM ∽Rt △ACB ，∴EC AC ＝EM AB ，∵AB ＝5， ∴445-，x x =解得x ＝209， ∴AE ＝ME ＝209，EC ＝169，在Rt △ECM 中，∵∠ECM ＝90°，∴CM 2＝EM 2－EC 2，即CM 22EM EC -＝（209）2－（169）2＝43，∵四边形AEMF 是菱形，∴OE ＝OF ，OA ＝OM ，AM ⊥EF ，∴S AEMF 菱形＝4S △AOE ＝2OE ·AO ，在Rt △AOE 和Rt △ACM 中，∵tan ∠EAO ＝tan ∠CAM ，∴OE AO ＝CM AC ，∵CM ＝43，AC ＝4，∴AO ＝3OE ，∴S AEMF 菱形＝6OE 2，又∵S AEMF 菱形＝AE ·CM ，∴6OE 2＝209×43，解得OE ＝2109，∴EF ＝2OE ＝4109.。