2018-2019 NBA美国职业篮球联赛

2018nba常规赛开始时间安排什么时候开赛2018nba常规赛什么时候开始打开赛时间具体日期是几号？2017-2018NBA赛季即将打响，2018nba常规赛赛程怎么安排的？怎么对阵的？2018nba常规赛开始及结束时间是什么时候？下面小编整理的2018nba常规赛时间日程安排相关资料，一起来看看吧。

2018nba常规赛什么时候开赛_2018nba常规赛开始时间_2018nba 常规赛比赛日程2018年4月左右NBA常规赛NBA比赛分为：季前赛、常规赛和季后赛三大部分。

NBA的季前赛为各球队的热身赛，常规赛比赛采用主、客场制，30支球队在常规赛赛季共要进行1230场比赛，每个球队在常规赛中参加的比赛场次数都是82场。

不过常规赛中各球队相互间的比赛场数不等。

同一联盟且同一赛区的球队之间进行两主、两客，共4场比赛;不同联盟间的球队之间进行一主、一客，共两场比赛;同一联盟不同赛区的两支球队间进行3到4场比赛，这一比赛数目各队不同，但可保证各队参加常规赛的总场次是82场比赛。

当NBA出现劳资纠纷等情况的时候比赛场次数会发生变化，变为50场，称为缩水赛季。

常规赛结束之后，东、西联盟排前八位的球队进入季后赛争夺，东西两个联盟中各个赛区的冠军加上成绩最好的赛区的第二名组成前四号种子，剩余四支球队则按成绩依次排为五到八号种子。

季后赛是淘汰赛制，第一轮是东、西部联盟的第一名对第八名，第二名对第七名，第三名对第六名，第四名对第五名。

淘汰赛直到决出东、西部冠军为止，然后由东、西部冠军队进行总决赛。

季后赛和总决赛都采用7场4 胜制，常规赛胜率较高的球队获得多一个主场的优势。

季后赛主客场按2，2，1，1，1原则进行(其中NBA总决赛主客场自2014年开始由2-2-1-1-1取代之前的2-3-2)。

比赛规则NBA比赛分为：常规赛和季后赛两大部分。

常规赛自每年的10月底11月初开始，至次年的4月20日左右结束。

季后赛从4月下旬开始进行，直到6月中旬决出总冠军为止。

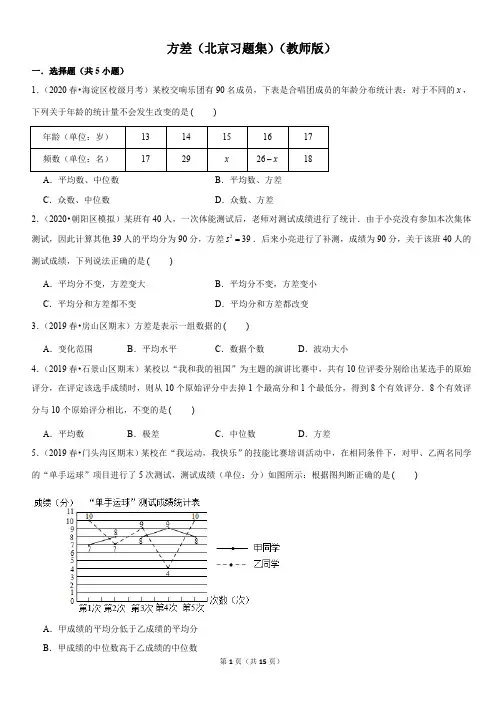
方差（北京习题集）（教师版）一．选择题（共5小题）1．（2020春•海淀区校级月考）某校交响乐团有90名成员，下表是合唱团成员的年龄分布统计表：对于不同的，下列关于年龄的统计量不会发生改变的是 年龄（单位：岁） 13 14 15 16 17 频数（单位：名） 172918 A ．平均数、中位数 B ．平均数、方差C ．众数、中位数D ．众数、方差2．（2020•朝阳区模拟）某班有40人，一次体能测试后，老师对测试成绩进行了统计．由于小亮没有参加本次集体测试，因此计算其他39人的平均分为90分，方差．后来小亮进行了补测，成绩为90分，关于该班40人的测试成绩，下列说法正确的是 A ．平均分不变，方差变大 B ．平均分不变，方差变小C ．平均分和方差都不变D ．平均分和方差都改变3．（2019春•房山区期末）方差是表示一组数据的 A ．变化范围B ．平均水平C ．数据个数D ．波动大小4．（2019春•石景山区期末）某校以“我和我的祖国”为主题的演讲比赛中，共有10位评委分别给出某选手的原始评分，在评定该选手成绩时，则从10个原始评分中去掉1个最高分和1个最低分，得到8个有效评分．8个有效评分与10个原始评分相比，不变的是 A ．平均数B ．极差C ．中位数D ．方差5．（2019春•门头沟区期末）某校在“我运动，我快乐”的技能比赛培训活动中，在相同条件下，对甲、乙两名同学的“单手运球”项目进行了5次测试，测试成绩（单位：分）如图所示：根据图判断正确的是 A ．甲成绩的平均分低于乙成绩的平均分B ．甲成绩的中位数高于乙成绩的中位数x ()x 26x -239s =()()()()C ．甲成绩的众数高于乙成绩的众数D ．甲成绩的方差低于乙成绩的方差 二．填空题（共8小题）6．（2020•北京模拟）如果一组数据，，，，的方差是1，那么数，，，，的方差是 ．7．（2019秋•栾城区期末）一中和二中举行数学知识竞赛，参赛学生的竞赛得分统计结果如表： 学校 参赛人数 平均数 中位数 方差 一中 45 83 86 82 二中458384135某同学分析上表后得到如下结论： ①一中和二中学生的平均成绩相同；②一中优秀的人数多于二中优秀的人数（竞赛得分分为优秀）； ③二中成绩的波动比一中小．上述结论中正确的是 ．（填写所有正确结论的序号）8．（2020春•海淀区校级月考）如果一组数据，，，，的方差是．把这组数据中每个数都减去同一个非零常数，得到一组新数：；，，，记这组新数据的方差为，则 ．（填“”，“ ”或“”9．（2020•丰台区模拟）已知一组数据，，的平均数为5，方差为3，那么数据，，的平均数和方差分别是 、 ．10．（2019春•海淀区期末）八年级（1）班甲、乙两个小组的10名学生进行飞镖训练，某次训练成绩如下甲组成绩（环 8 7 8 8 9 乙组成绩（环98797由上表可知，甲、乙两组成绩更稳定的是 ．11．（2019•平谷区一模）某商场甲、乙、丙三名业务员5个月的销售额（单位：万元）如下表：销售额 业务员 第1月 第2月 第3月 第4月 第5月甲 7.2 9.6 9.6 8.0 9.3 乙7.89.79.85.89.91x 2x 3x 4x 5x 110x -210x -310x -410x -510x -85…1x 2x 3x ⋯⋯n x 20S k 1x k -2x k -3x k -n x k ⋯⋯-21S 21S 20S >=<)a b c 2a +2b +2c +))丙 9.2 5.8 8.5 9.9 9.9则甲、乙、丙三名业务员中销售额最稳定的是 ．12．（2019•北京）小天想要计算一组数据92，90，94，86，99，85的方差，在计算平均数的过程中，将这组数据中的每一个数都减去90，得到一组新数据2，0，4，，9，，记这组新数据的方差为，则 （填“”，“ ”或” ”13．（2019春•昌平区期末）有两名学员小林和小明练习飞镖，第一轮10枚飞镖掷完后两人命中的环数如图所示，已知新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是 ；这名选手的10次成绩的极差是 ．三．解答题（共2小题）14．（2019•朝阳区二模）某部门为新的生产线研发了一款机器人，为了了解它的操作技能情况，在相同条件下与人工操作进行了抽样对比．过程如下，请补充完整．收集数据对同一个生产动作，机器人和人工各操作20次，测试成绩（十分制）如下： 机器人 8.0 8.1 8.1 8.1 8.2 8.2 8.3 8.4 8.4 9.0 9.0 9.0 9.1 9.1 9.4 9.5 9.5 9.5 9.5 9.6 人工 6.1 6.2 6.67.2 7.2 7.5 8.0 8.2 8.3 8.59.19.69.89.99.99.910101010整理、描述数据按如下分段整理、描述这两组样本数据：成绩 人数 生产方式机器人 0 0 9 11 人工（说明：成绩在9.0分及以上为操作技能优秀，分为操作技能良好，分为操作技能合格，6.0分以下为操作技能不合格）20s 4-5-21s 21s 20s >=<)x 67x <…78x <…89x <…910x ……8.0~8.9 6.0~7.9分析数据两组样本数据的平均数、中位数、众数和方差如下表所示：平均数 中位数 众数 方差 机器人 8.8 9.5 0.333 人工 8.6101.868得出结论（1）如果生产出一个产品，需要完成同样的操作200次，估计机器人生产这个产品达到操作技能优秀的次数为 ； （2）请结合数据分析机器人和人工在操作技能方面各自的优势： ．15．（2019春•海淀区校级月考）在美国职业篮球联赛赛季常规赛结束后，某球迷为了比较、两名球员的表现，在官网上找到了他们整个常规赛季的数据如下图所示，其中，得分和助攻的数据可以反映球员的进攻表现，盖帽和抢断则可以反映球员的防守表现，篮板数既可以反映进攻表现，又可以反映防守表现．数据值越高，说明球员在该项上表现越好（1）在这两名球员整个常规赛季的比赛中总得分较高的一位是 （填或（2）根据统计图判断，这两位球员中，哪一位在常规赛季的防守表现更好，并说明理由；（3）两位球员所在的球队都进入了季后赛，该球迷为了进一步比较两人在季后赛前的状态，对两人常规赛季最后10场比赛的数据进行了分析，所得的数据如下：得分助攻平均数方差平均数方差 球员 29.3 37.05 2.6 1.10 球员29.4116.5210.210.42请根据上述数据，分别从得分和助攻两个角度比较、两位球员在季后赛前的表()2018NBA A B A )B A B A B现．方差（北京习题集）（教师版）参考答案与试题解析一．选择题（共5小题）1．（2020春•海淀区校级月考）某校交响乐团有90名成员，下表是合唱团成员的年龄分布统计表：对于不同的，下列关于年龄的统计量不会发生改变的是 年龄（单位：岁） 13 14 15 16 17 频数（单位：名） 172918 A ．平均数、中位数 B ．平均数、方差C ．众数、中位数D ．众数、方差【分析】由频数分布表可知年龄15岁和年龄16岁的两组的频数和为26，即可得知总人数，结合前两组的频数知出现次数最多的数据及第45、46个数据的平均数，可得答案．【解答】解：由表可知，年龄为15岁与年龄为16岁的频数和为， 则总人数为：， 故该组数据的众数为14岁， 中位数为：（岁．即对于不同的，关于年龄的统计量不会发生改变的是众数和中位数． 故选：．【点评】本题主要考查频数分布表及统计量的选择，由表中数据得出数据的总数是根本，熟练掌握平均数、中位数、众数及方差的定义和计算方法是解题的关键．2．（2020•朝阳区模拟）某班有40人，一次体能测试后，老师对测试成绩进行了统计．由于小亮没有参加本次集体测试，因此计算其他39人的平均分为90分，方差．后来小亮进行了补测，成绩为90分，关于该班40人的测试成绩，下列说法正确的是 A ．平均分不变，方差变大 B ．平均分不变，方差变小C ．平均分和方差都不变D ．平均分和方差都改变【分析】根据平均数，方差的定义计算即可．【解答】解：小亮的成绩和其他39人的平均数相同，都是90分， 该班40人的测试成绩的平均分为90分，方差变小，故选：．【点评】本题考查方差，算术平均数等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考x ()x 26x -2626x x +-=1729261890+++=(1414)214+÷=)x C 239s =()Q ∴B题型．3．（2019春•房山区期末）方差是表示一组数据的 A ．变化范围B ．平均水平C ．数据个数D ．波动大小【分析】根据方差的意义选择正确的选项即可．【解答】解：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好． 故选：．【点评】本题主要考查了方差的定义，解题的关键是掌握方差是反映一组数据的波动大小的一个量．4．（2019春•石景山区期末）某校以“我和我的祖国”为主题的演讲比赛中，共有10位评委分别给出某选手的原始评分，在评定该选手成绩时，则从10个原始评分中去掉1个最高分和1个最低分，得到8个有效评分．8个有效评分与10个原始评分相比，不变的是 A ．平均数B ．极差C ．中位数D ．方差【分析】根据平均数、极差、中位数、方差的意义即可求解．【解答】解：根据题意，从10个原始评分中去掉1个最高分和1个最低分，得到8个有效评分．8个有效评分与10个原始评分相比，不变的是中位数． 故选：．【点评】本题考查了平均数、中位数、众数、方差的意义．平均数是指在一组数据中所有数据之和再除以数据的个数；中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）；一组数据中出现次数最多的数据叫做众数；一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差．5．（2019春•门头沟区期末）某校在“我运动，我快乐”的技能比赛培训活动中，在相同条件下，对甲、乙两名同学的“单手运球”项目进行了5次测试，测试成绩（单位：分）如图所示：根据图判断正确的是 A ．甲成绩的平均分低于乙成绩的平均分B ．甲成绩的中位数高于乙成绩的中位数()D ()C ()C ．甲成绩的众数高于乙成绩的众数D ．甲成绩的方差低于乙成绩的方差【分析】通过计算甲、乙的平均数可对进行判断；利用中位数的定义对进行判断；利用众数的定义对进行判断；根据方差公式计算出甲、乙的方差，则可对进行判断．【解答】解：、甲的平均数（分，乙的平均数（分，所以选项错误；、甲的中位数为8（分，乙的中位数为9（分，所以选项错误； 、甲的众数为8（分，乙的众数为10，所以选项错误；、甲的方差；乙的方差，所以选项正确． 故选：．【点评】本题考查了方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．也考查了中位数和众数． 二．填空题（共8小题）6．（2020•北京模拟）如果一组数据，，，，的方差是1，那么数，，，，的方差是　1　．【分析】根据题意得；数据，，，，的平均数设为，则数据，，，，的平均数为，在根据方差公式进行计算：即可得到答案．【解答】解：根据题意得；数据，，，，的平均数设为，则数据，，，，的平均数为，根据方差公式：．则：，， ， 故答案为：1【点评】此题主要考查了方差公式的运用，关键是根据题意得到平均数的变化，再正确运用方差公式进行计算即可．A B C D A 1(78898)85=++++=)1(1079410)85=++++=)A B ))B C )C D 22212[(78)3(88)(98)]55=-+-+-=2222126[2(108)(78)(48)(98)]55=-+-+-+-=D D 1x 2x 3x 4x 5x 110x -210x -310x -410x -510x -1x 2x 3x 4x 5x a 110x -210x -310x -410x -510x -10a -222221251[()()(]5S x x x x x x =-+-+⋯-1x 2x 3x 4x 5x a 110x -210x -310x -410x -510x -10a -222211251[()()()]15S x a x a x a =-+-+⋯-=222221251{[(10)(10)][(10)(10)](10)(10)]}5S x a x a x a =---+---+⋯---2221251[()()()]5x a x a x a =-+-+⋯-1=7．（2019秋•栾城区期末）一中和二中举行数学知识竞赛，参赛学生的竞赛得分统计结果如表： 学校 参赛人数 平均数 中位数 方差 一中 45 83 86 82 二中458384135某同学分析上表后得到如下结论： ①一中和二中学生的平均成绩相同；②一中优秀的人数多于二中优秀的人数（竞赛得分分为优秀）； ③二中成绩的波动比一中小．上述结论中正确的是　①②　．（填写所有正确结论的序号） 【分析】根据平均数、中位数、方差的定义即可判断．【解答】解：由表格可知，一中和二中学生的成绩平均成绩相同，故此选项正确； 根据中位数可以确定，一中优秀的人数多于二中优秀的人数，故此选项正确； 根据方差可知，一中成绩的波动性比二中小，故此选项错误． 故①②正确， 故答案为：①②．【点评】本题考查平均数、中位数、方差等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．8．（2020春•海淀区校级月考）如果一组数据，，，，的方差是．把这组数据中每个数都减去同一个非零常数，得到一组新数：；，，，记这组新数据的方差为，则 ．（填“”，“ ”或“”【分析】根据题目中的数据可以求得变化后的数据的方差，从而可以解答本题． 【解答】解：新数的方差是：，所以． 故答案为：【点评】本题考查方差，解答本题的关键是明确题意，会计算一组数据的方差．9．（2020•丰台区模拟）已知一组数据，，的平均数为5，方差为3，那么数据，，的平均数和方差分别是　7　、 ．【分析】根据数据，，的平均数为5可知，据此可得出的值；再由方差为3可得出数据，，的方差． 【解答】解：数据，，的平均数为5，85…1x 2x 3x ⋯⋯n x 20S k 1x k -2x k -3x k -n x k ⋯⋯-21S 21S =20S >=<)222212()()()n x k x k x k x k x k x k S n--++--++--+=2210S S ==a b c 2a +2b +2c +a b c 1()53a b c ++=1(222)3a b c +++++2a +2b +2c +Q a b c， ， 数据，，的平均数是3；数据，，的方差为3， ， ，，的方差．故答案为：7、3．【点评】本题考查的是方差，熟记方差的定义是解答此题的关键．10．（2019春•海淀区期末）八年级（1）班甲、乙两个小组的10名学生进行飞镖训练，某次训练成绩如下甲组成绩（环 8 7 8 8 9 乙组成绩（环98797由上表可知，甲、乙两组成绩更稳定的是　甲　．【分析】根据方差计算公式，进行计算，然后比较方差，小的稳定，在计算方差之前还需先计算平均数． 【解答】解：，，， 甲组成绩更稳定．故答案为：甲．【点评】考查平均数、方差的计算方法，理解方差是反映一组数据的波动大小的统计量，方差越小，数据越稳定． 11．（2019•平谷区一模）某商场甲、乙、丙三名业务员5个月的销售额（单位：万元）如下表：销售额 业务员 第1月第2月第3月第4月第5月甲 7.2 9.6 9.6 8.0 9.3 乙 7.8 9.7 9.8 5.8 9.9 丙9.25.88.59.99.9则甲、乙、丙三名业务员中销售额最稳定的是　甲　．∴1()53a b c ++=∴11(222)()252733a b c a b c +++++=+++=+=∴2a +2b +2c +Q a b c ∴2221[(5)(5)(5)]33a b c -+-+-=2a ∴+2b +2c +22222211[(27)(27)(27)]5)(5)(5)]333a b c a b c =+-++-++-=-+-+-=))8788985x ++++==甲9879785x ++++==乙(2222221[(88)(78)(88)(88)98)0.45S ⎤=-+-+-+-+-=⎦甲(2222221[(98)(88)(78)(98)78)0.85S ⎤=-+-+-+-+-=⎦乙Q 22S S <乙甲∴【分析】方差越小．方差越小的越稳定，方差越大的波动越大，从而越不稳定，从数据的集中趋势可以看出哪个更集中，哪个更分散，从而得解．【解答】解：将甲乙丙三组数据按照从小到大排列： 甲 7.2 8.0 9.3 9.6 9.6 乙 5.8 7.8 9.7 9.8 9.9 丙5.8 8.5 9.2 9.9 9.9可以看出甲组数据更集中一些，乙丙的数据较为分散，而数据越分散则方差越大，数据越集中，则方差越小．方差越小的越稳定，则本题甲、乙、丙三名业务员中销售额最稳定的是甲． 故答案为：甲．【点评】方差是反映数据波动大小的统计量，在可以观察出波动大小，从而知道方差大小的情况下，可以不用具体计算每组数据的方差值．12．（2019•北京）小天想要计算一组数据92，90，94，86，99，85的方差，在计算平均数的过程中，将这组数据中的每一个数都减去90，得到一组新数据2，0，4，，9，，记这组新数据的方差为，则 （填“”，“ ”或” ”【分析】根据一组数据中的每一个数据都加上或减去同一个非零常数，那么这组数据的波动情况不变，即方差不变，即可得出答案．【解答】解：一组数据中的每一个数据都加上（或都减去）同一个常数后，它的平均数都加上（或都减去）这一个常数，两数进行相减，方差不变， 则．故答案为．【点评】本题考查方差的意义：一般地设个数据，，，的平均数为，则方差，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立，关键是掌握一组数据都加上同一个非零常数，方差不变．13．（2019春•昌平区期末）有两名学员小林和小明练习飞镖，第一轮10枚飞镖掷完后两人命中的环数如图所示，已知新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是　小林　；这名选手的10次成绩的极差是 ．20s 4-5-21s 21s =20s >=<)Q ∴2210s S ==n 1x 2x n x ⋯x 2222121[(()()]n S x x x x x x n=-+-+⋯+-【分析】方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．极差是指一组数据中最大数据与最小数据的差．极差最大值最小值．【解答】解：根据折线统计图，可知小林是新手， 小林10次成绩的极差是 故答案为：小林，9．【点评】本题考查了方差与极差，正确理解方差与极差的意义是解题的关键． 三．解答题（共2小题）14．（2019•朝阳区二模）某部门为新的生产线研发了一款机器人，为了了解它的操作技能情况，在相同条件下与人工操作进行了抽样对比．过程如下，请补充完整．收集数据对同一个生产动作，机器人和人工各操作20次，测试成绩（十分制）如下： 机器人 8.0 8.1 8.1 8.1 8.2 8.2 8.3 8.4 8.4 9.0 9.0 9.0 9.1 9.1 9.4 9.5 9.5 9.5 9.5 9.6 人工 6.1 6.2 6.6 7.2 7.27.5 8.0 8.2 8.3 8.59.19.69.89.99.99.910101010整理、描述数据按如下分段整理、描述这两组样本数据：成绩 人数 生产方式机器人 0 0 9 11 人工　3　（说明：成绩在9.0分及以上为操作技能优秀，分为操作技能良好，分为操作技能合格，6.0分以下为操作技能不合格）分析数据两组样本数据的平均数、中位数、众数和方差如下表所示：=-1019-=x 67x <…78x <…89x <…910x ……8.0~8.9 6.0~7.9平均数 中位数 众数 方差 机器人 8.8 9.5 0.333 人工 8.6101.868得出结论（1）如果生产出一个产品，需要完成同样的操作200次，估计机器人生产这个产品达到操作技能优秀的次数为 ； （2）请结合数据分析机器人和人工在操作技能方面各自的优势： ． 【分析】（1）根据三数定义和方差计算公式分别计算得出答案； （2）计算出抽测的20次的优秀所占比例，再乘以200即可； （3）根据（1）中所得数据进行全面分析即可． 【解答】解：补全表格如下：机器人 0 0 9 11 人工 33410平均数 中位数 众数 方差 机器人 8.8 9.0 9.5 0.333 人工 8.68.8101.868（1）；（2）机器人的样本数据的平均数和中位数都明显高于人工，方差较小，可以推断其优势在于操作技能水平较高的同时还能保持稳定．人工的样本数据的众数为10，机器人的样本数据的最大值为9.6，可以推断人工的优势在于能完成一些最高水平的操作．【点评】此题主要考查了方差和众数、中位数、平均数，关键是掌握三数定义和方差的计算公式．15．（2019春•海淀区校级月考）在美国职业篮球联赛赛季常规赛结束后，某球迷为了比较、两名球员的表现，在官网上找到了他们整个常规赛季的数据如下图所示，其中，得分和助攻的数据可以反映球员的进攻表现，盖帽和抢断则可以反映球员的防守表现，篮板数既可以反映进攻表现，又可以反映防守表现．数据值越高，说明球员在该项上表现越好（1）在这两名球员整个常规赛季的比赛中总得分较高的一位是 （填或 （2）根据统计图判断，这两位球员中，哪一位在常规赛季的防守表现更好，并说明理由；67x <...78x <...89x <...910x (11)20011020⨯=()2018NBA A B B A )B（3）两位球员所在的球队都进入了季后赛，该球迷为了进一步比较两人在季后赛前的状态，对两人常规赛季最后10场比赛的数据进行了分析，所得的数据如下：得分助攻平均数方差平均数方差 球员 29.3 37.05 2.6 1.10 球员29.4116.5210.210.42请根据上述数据，分别从得分和助攻两个角度比较、两位球员在季后赛前的表现．【分析】（1）在图中直接可以看到，两名球员整个常规赛季的比赛中的总得分较高；（2）防守情况看盖帽，抢断，篮板情况来分析，从图中可以看到球员的各项成绩都要好于球员；（3）从得分角度看，球员的平均得分高于球员的平均得分，但是从方差角度看，球员的平均得分比球员稳定；从助攻角度看，球员助攻得分远高于球员，但从方差角度看，球员助攻得分比球员稳定； 【解答】解：（1）从图中看到球员的场均得分是分，运动员是分，因此两名球员整个常规赛季的比赛中总得分较高的一位是， 故答案为：．（2）防守情况看盖帽，抢断，篮板情况，从图中看到，球员均场盖帽2.6大于球员的0.9，球员均场抢断1.5大于 球员均场抢断1.4，球员均场篮板11.1大于球员均场篮板8.6，综合比较球员的防守明显好于球员，因此球员在常规赛季的防守表现更好．（3）从得分角度看，球员的平均得分高于球员的平均得分，但是从方差角度看，球员的平均得分比球员A B A B B A B B A A B B A A B A 7.528.1210.75⨯=B 8.227.5225.5⨯=B B A B A B A B A B A B A A B稳定；从助攻角度看，球员助攻得分远高于球员，但从方差角度看，球员助攻得分比球员稳定； 因此，综合看，球员得分和助攻的表现都很稳定，而球员在季后赛前整体状况优于球员．【点评】考查知识点：从统计图中获取信息；从不同角度进行数据的分析；方差的意义．能够综合运用统计的知识进行数据分析处理，做出合情的推理是解题的关键．B A A B A B A。

nba 排名NBA排名引言：NBA作为全球最受欢迎的职业篮球联赛，每个赛季都吸引着数以百万计的观众。

而NBA排名则是球迷们最感兴趣的话题之一。

排名显示了各支球队在赛季中的竞争力和表现。

本文将深入探讨NBA排名的计算方法、重要性以及过去几个赛季中的一些例子。

一、NBA排名的计算方法在NBA赛季中，排名是根据各支球队的胜负比率来确定的。

胜利次数越多的球队排名越靠前，而输掉比赛次数越多的球队则排名较低。

如果两支球队的胜负比率相同，那么可以通过两队之间的战绩、净胜分以及其他各种具体的统计数据来进行进一步的比较。

最终，根据这些因素，NBA将球队进行排名，以决定季后赛的资格和球队的种子排名。

二、NBA排名的重要性1. 季后赛资格：每个赛季结束后，NBA排名最好的八支球队将晋级季后赛。

对于球队来说，争夺一个季后赛的资格是他们每个赛季的首要目标之一。

只有获得季后赛资格，球队才有机会争夺总冠军。

2. 种子排名：在季后赛中，种子排名决定了球队在比赛中的对手。

排名越高的球队将与排名较低的球队比赛，这通常给排名高的球队带来了更大的竞争优势和更好的机会进一步晋级。

3. 球队声誉和荣誉：排名高的球队通常被视为强队，并获得更多的关注和尊重。

球队在联盟中的声誉和荣誉也与他们的排名紧密相关。

三、过去几个赛季的NBA排名例子1. 2016-2017赛季：在这个赛季中，克利夫兰骑士队以51胜31负的战绩排名第一。

他们在东部联盟中表现出色，并最终成功晋级总决赛。

2. 2017-2018赛季：休斯顿火箭队以65胜17负的战绩排名第一。

他们在西部联盟中取得了最佳战绩，并在季后赛中一路领先。

3. 2018-2019赛季：密尔沃基雄鹿队以60胜22负的战绩排名第一。

他们在东部联盟中表现出色，但最终在东部决赛中失利。

总结：NBA排名是衡量球队在赛季中竞争力的重要指标。

球队们渴望通过战胜其他对手来提高自己的排名，以获得更好的竞争优势和更多的荣誉。

nba老鹰NBA老鹰：历史、成就和未来展望介绍NBA老鹰队是美国职业篮球联赛（NBA）中的一支篮球队，总部位于乔治亚州亚特兰大市。

老鹰队成立于1946年，是NBA历史上较为悠久的球队之一。

随着多年的发展和壮大，老鹰队在NBA赛场上积累了丰富的历史和众多的成就。

本文将重点回顾老鹰队的历史，探讨他们的成就，并对未来的发展进行展望。

历史老鹰队的历史可以追溯到1946年，当时该队还被称为特里中心霍克斯队。

随后几年，球队在一个新的地理位置建立了他们的主场，并改名为亚特兰大鹰队。

从那时起，老鹰队在亚特兰大市内积极发展，逐渐成为南部地区一支备受瞩目的篮球队。

成就老鹰队在过去的几十年里收获了许多令人瞩目的成就。

在1950年代，球队取得了五个东部联盟冠军，并在1958年夺得了他们职业生涯中唯一的一座NBA总冠军。

这个辉煌的时代培养了许多重要的球队成员，其中包括传奇球员波勒里德、克里夫哈根斯和鲍勃佩蒂特等。

随后的几十年里，老鹰队虽然没有再赢得总冠军，但他们在季后赛中仍然表现出色，并拥有很多令人难以忘怀的球员。

近年来，老鹰队在2018-2019赛季重建了球队，并重新设定了目标。

他们签下了年轻有潜力的球员，并通过选秀获得了一些有前途的新秀。

这些努力在2020-2021赛季中得到了回报，老鹰队成功进入了季后赛，并凭借理查德·强森、特雷·扬和德昆·亨特等球员的出色表现，打进了东部决赛。

未来展望老鹰队的未来看起来非常光明。

他们的现有阵容中拥有年轻有实力的球员，这使得他们在未来几年可以成为一支竞争力很强的球队。

此外，球队还在贸易和签约市场上保持积极性，以增强阵容实力。

老鹰队的教练组和管理层也非常注重球队的发展，他们将尽最大的努力打造一个具有实力和团队精神的球队，为球迷们带来更多的成功。

老鹰队还从社区和球迷群体中得到了广泛的支持。

亚特兰大市对于篮球的热爱和对老鹰队的热情支持为球队的发展提供了不可估量的力量。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==NBA新赛季实力排行_NBA新赛季排行榜201X_201Xnba新赛季MVPNBA新赛季实力排行整合，201Xnba新赛季MVP会是谁呢?上赛季的勇士在杜兰特加盟后，常规赛经过短暂的磨合，在赛季初便展现了凶猛的火力，季后赛他们更是凭借16-1的惊人战绩碾压对手夺得总冠军。

下面是学习啦小编为大家整理NBA新赛季排行榜201X的相关资料，供大家参考!NBA新赛季实力排行_NBA新赛季排行榜201X_201Xnba新赛季MVP第一、金州勇士勇士队在夺得总冠军后，并未因自由球员的续约金额问题而分崩离析，相反，在杜兰特做出约950万美元的降薪后，他们留下了伊戈达拉、利文斯顿、帕楚里亚，还引进了尼克扬、卡西比，以及选中新秀乔丹贝尔。

这样的操作无疑让勇士队在新赛季的进攻火力变得更加强大，而经过一赛季的磨合之后，超级四巨会让新赛季的勇士变得更加恐怖!第二、休斯顿火箭上赛季常规赛夺得55胜排名第三的好成绩，季后赛第二轮败给常规赛夺得61胜排名第二的马刺，被淘汰并不算爆冷。

休赛期火箭队通过交易得到克里斯保罗，哈登在关键时刻将得到一位全明星帮手，他也不用再担心会被对手针对性的包夹防守。

随后莫雷在自由市场上出手引进PJ塔克、卢克巴莫特两位出色的防守球员，续约了内内，签下就将布莱克，确保了内线的轮转和深度。

新赛季的火箭将会比上赛季更加难对付。

第三、圣安东尼奥马刺马刺走了戴德蒙和西蒙斯两名主要替补球员，但他们签下了鲁迪盖伊和洛文吉，续约了米尔斯，迎回了老妖刀吉诺比利，而加索尔的合同也即将敲定，在伦纳德和阿尔德里奇的带领下，新赛季的马刺仍然是联盟顶级球队之一，只要波波维奇在，他们就不会被排除在强队的行列。

而伦纳德的出色攻防能力加上波波老辣的战术，他们仍然会是勇士最忌惮的球队。

第四、克利夫兰骑士骑士队休赛期非常努力的想要引进保罗乔治和吉米巴特勒，但都以失败告终，失去了与詹姆斯关系密切的总经理大卫格里芬，让他们在后期的引援上并没有太多大的动静，签下老将卡尔德隆代替德隆威廉姆斯，引进实力前锋杰夫格林，签下土耳其新人奥斯曼，这份引援名单不禁让人担心新赛季的骑士已经难以继续跟勇士抗衡，但只要有詹姆斯在，骑士仍然是东部最顶级的球队，仍然是最有希望晋级总决赛的球队。

美国职业篮球联赛
Ruth Devlin
【期刊名称】《空中英语教室(初级版.大家说英语)》
【年(卷),期】2024()2
【摘要】篮球是世界上最受欢迎的运动之一。

人们爱打篮球,也爱看篮球赛,特别是NBA球赛。

NBA的球员可谓是世界上最顶尖的球员,他们可以跳得很高,能从很远的地方投篮。

他们拥有数百万的球迷,球迷们有最爱的球队,像是湖人队或火箭队。

他们会穿戴支持球队的球衣去看比赛,并为球员们大声加油喝彩。

每个人都希望自己支持的球队获胜。

【总页数】4页(P32-34)
【作者】Ruth Devlin
【作者单位】不详
【正文语种】中文
【中图分类】G84
【相关文献】
1.欧洲职业足球联赛与美国职业篮球联赛运营模式比较研究
2.美国职业篮球联赛对中国职业篮球联赛的冲击和影响
3.美国职业篮球联赛运营策略对中国职业篮球联赛的启示
4.音乐在对抗性体育运动中的应用——以美国职业篮球联赛和美国职业橄榄球大联盟为例
5.美国职业篮球联赛队员“位置模糊化”分析及其启示
因版权原因，仅展示原文概要，查看原文内容请购买。

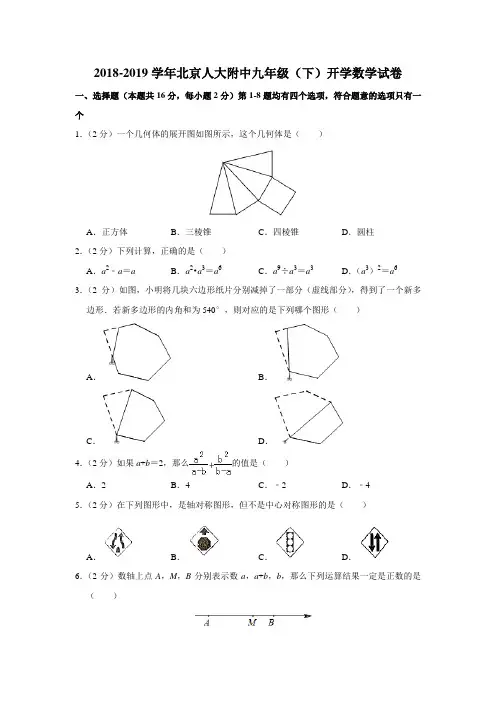
2018-2019学年北京人大附中九年级（下）开学数学试卷一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个1．（2分）一个几何体的展开图如图所示，这个几何体是（）A．正方体B．三棱锥C．四棱锥D．圆柱2．（2分）下列计算，正确的是（）A．a2﹣a＝a B．a2•a3＝a6C．a9÷a3＝a3D．（a3）2＝a6 3．（2分）如图，小明将几块六边形纸片分别减掉了一部分（虚线部分），得到了一个新多边形．若新多边形的内角和为540°，则对应的是下列哪个图形（）A．B．C．D．4．（2分）如果a+b＝2，那么的值是（）A．2B．4C．﹣2D．﹣45．（2分）在下列图形中，是轴对称图形，但不是中心对称图形的是（）A．B．C．D．6．（2分）数轴上点A，M，B分别表示数a，a+b，b，那么下列运算结果一定是正数的是（）A．a+b B．a﹣b C．ab D．|a|﹣b7．（2分）下面的统计图反映了我国2013年到2017年国内生产总值情况．（以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》，其中国内生产总值绝对数按现价计算，增长速度按不变价格计算）根据统计图提供的信息，下列推断合理的是（）A．从2013﹣2016年，我国国内生产总值逐年下降B．从2013﹣2017年，我国国内生产总值的增长率逐年下降：C．从2013﹣2017年，我国国内生产总值的平均增长率约为6.7%D．计算同上年相比的增量，2017年我国国内生产总值的增量为近几年最多8．（2分）如图是一个无理数生成器的工作流程图，根据该流程图，下面说法①当输入值x为16时，输出值y为②当输出值y为时，输入值x为3或9③存在这样的正整数x，输入x之后，该生成器能够一直运行，但始终不能输出y值．④对于任意的正无理数y，都存在正整数x，使得输入x后能够输出y．其中正确的是（）A．①②B．①③C．①④D．②③二、填空题（本题共16分，每小题2分）9．（2分）使分式有意义的x的取值范围是．10．（2分）如图，BD平分∠ABC，点E为BA上一点，EG∥BC交BD于点F．若∠1＝35°，则∠ABC的度数为．11．（2分）1月21日，2019年春运拉开了帷幕，2月3日腊月二十八当天，北京西站迎来春运高峰，单日发送旅客达到2622000人，将262000用科学记数法表示为．12．（2分）如图，DE分别是△ABC边AC，BC的中点，若△CDE的面积为2，则四边形ABED的面积为．13．（2分）春节假期，小陈驾车从珠海出发到香港，去时在港珠澳大桥上用了40分钟，返回时平均速度提高了25千米/小时，在港珠澳大桥上的用时比去时少了10分钟，求小陈去时的平均速度，设他去时驾车的平均速度为x千米/小时，则可列方程为．14．（2分）如图，⊙O是△ABC的外接圆，若∠ACO＝40°，则∠B的度数为．15．（2分）图1是甲、乙两个圆柱形水槽的轴截面示意图，乙槽中有一圆柱体铁块立放其中（圆柱形铁块的下底面完全落在乙槽底面上）．现将甲槽中的水匀速注入乙槽，甲、乙两个水槽中水的深度y（厘米）与注水时间x（分钟）之间的关系如图2所示．①图2中折线ABC表示槽中水的深度与注水时间之间的关系（选填“甲”或“乙”）；②点B的纵坐标表示的实际意义是．16．（2分）某水果公司以2.2元/千克的成本价购进10000kg苹果．公司想知道苹果的损坏率，从所有随机拙取若干进行统计，部分结果如表：（结果估计这批苹果损坏的概率为精确到0.1），据此，若公司希望这批苹果能获得利润23000元，则销售时（去掉损坏的苹果）售价应至少定为元/千克．三、解答题（本题共68分，第17-21题，每小题5分，第22题6分，第23题5分，第24-26题，每小题5分，第27、28题，每小题5分）17．（5分）计算：18．（5分）解不等式组19．（5分）下面是小星同学设计的“过直线外一点作已知直线的平行线”的尺规作图过程：已知：如图，直线l和直线l外一点A求作：直线AP，使得AP∥l作法：如图①在直线l上任取一点B（AB与l不垂直），以点A为圆心，AB为半径作圆，与直线l交于点C．②连接AC，AB，延长BA到点D；③作∠DAC的平分线AP．所以直线AP就是所求作的直线根据小星同学设计的尺规作图过程，（1）使用直尺和圆规，补全图形（保留作图痕迹）（2）完成下面的证明证明：∵AB＝AC，∴∠ABC＝∠ACB（填推理的依据）∵∠DAC是△ABC的外角，∴∠DAC＝∠ABC+∠ACB（填推理的依据）∴∠DAC＝2∠ABC∵AP平分∠DAC，∴∠DAC＝2∠DAP∴∠DAP＝∠ABC∴AP∥l（填推理的依据）20．（5分）已知关于x的方程x2﹣6x+k+7＝0有两个不相等的实数根．（1）求k的取值范围；（2）当k为正整数时，求方程的根．21．（5分）如图，矩形ABCD中，对角线AC，BD交于点O，以AD，OD为邻边作平行四边形ADOE，连接BE．（1）求证：四边形AOBE是菱形；（2）若∠EAO+∠DCO＝180°，DC＝2，求四边形ADOE的面积．22．（6分）在美国职业篮球联赛（NBA）2018赛季常规赛结束后，某球迷为了比较A、B 两名球员的表现以反映球员的防守表现，篮板数既可以反映进攻表现，又可以反映防守表现．数据值越高，说明球员在该项上表现越好（1）在这两名球员整个常规赛季的比赛中总得分较高的一位是（填A或B）（2）根据统计图判断，这两位球员中，哪一位在常规赛季的防守表现更好，并说明理由；（3）两位球员所在的球队都进入了季后赛，该球迷为了进一步比较两人在季后赛前的状态，对两人常规赛季最后10场比赛的数据进行了分析，所得的数据如下：请根据上述数据，分别从得分和助攻两个角度比较A、B两位球员在季后赛前的表现．23．（5分）在平面直角坐标系xOy中，反比例函数（x＞0）的图象G经过点A（，4）．（1）求k的值：（2）横、纵坐标都是整数的点叫做整点，点B的坐标为（﹣1，﹣1），点C的坐标为（0，t），点D的坐标为（t，0）（其中t＞0），直线BC，BD分别交图象G于点P，Q．将图象G在点P，Q之间的部分与线段BP，BQ围成的区域（不含边界）记为W①当点P恰好与A重合时，求出此时t的值和区域W内的整点个数：②若区域内恰好有5个整点，结合函数图象，直接写出t的取值范围．24．（6分）如图，AB为⊙O的直径，弦CD⊥AB，过点D作⊙O的切线DN，且有DN∥AC．（1）求证：△ACD是等边三角形．（2）连接并延长CB，交DN于E，连接AE，交CD于点F，若⊙O的半径为2，求EF 的长．25．（6分）有这样一个问题如图1，在等边△ABC中，AB＝4，D为BC的中点，E，F分别是边AB，AC上的动点，且∠EDF＝60°，若BE+AF＝3，试求BE的长．爱钻研的小峰同学发现，可以通过几何与函数相结合的方法来解决这个问题，下面是他的探究思路，请帮他补充完整．（1）注意到△ABC为等边三角形，且∠EDF＝60°，可得∠BED＝∠CDF，于是可证△BED∽△CDF，进而可得，注意到D为BC中点，BD＝CD＝2，因此BE和CF 满足的等量关系为．（2）设BE＝x，AF＝y，则x的取值范围是．结合（1）可得y与x的函数关系为．（3）在平面直角坐标系xOy中，根据已有的经验画出y与x的函数图象，请在图2中完成画图．（4）回到原问题，要使BE+AF＝3，即为x+y＝3，利用（3）中的图象，通过测量，可以得到原问题的近似解为BE＝（精确到0.1）．问题的精确解，则可以通过解方程组求得．26．（6分）已知抛物线y＝ax2﹣2ax+3（a≠0）（1）抛物线的对称轴为x＝．（2）若抛物线与x轴交于P，Q两点，且PQ＝4，①求抛物线的表达式；②将该抛物线在0≤x≤4间的部分记为图象G，将图象G在直线y＝t（上方的部分沿y＝t翻折，其余部分保持不变，得到个新函数的图象，记这个函数的最大值为M，最小值为m，若M﹣m≤6，求t的取值范围．27．（7分）在Rt△ABC中，∠ACB＝90°，D为BC边上一点（不与B，C重合），延长DC 到点E，使得CE＝CD，过点E作AB的平行线，与AC的延长线交于点F，直线FD与AB交于点G，设∠ABC＝α．对于一般的情况，如图1，（1）直接写出∠AFD＝．用含α的代式表示；（2）取AB的中点M，求证：DF＝2MG；对于α＝45°的特殊情况，如图2，（3）连接EG，若EG⊥AD，求的值．28．（7分）在平面直角坐标系xOy中，对于点A（a，b），若某函数在a﹣1≤x≤a+1内有定义，且对此范围内的任意x的值，对应的y都满足b﹣1≤y≤b+1，就称这个函数是点A的“限定函数”．（1）以下函数：①y＝﹣x②y＝③y＝2x2﹣1④y＝﹣（x﹣1）2原点O的限定函数是（填序号）；（2）如图1，点A（m，n）是函数y＝﹣上的动点，若函数y＝﹣是点A的限定函数”，求m的取值范围．（3）如图2，半圆为以O为圆心，为半径的圆在x轴上方的部分，在x轴负半轴上有一动点M，过M作半圆的切线，切点为P，点P关于y轴对称点为Q．将射线PM、劣弧、射线OQ在半圆外的部分组合成一个新函数的图象（图中实线），若这个函数是原点O的“限定函数”，写出tan∠MOP的取值范围．2018-2019学年北京人大附中九年级（下）开学数学试卷参考答案与试题解析一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个1．【解答】解：由图可得，这个几何体是四棱锥，故选：C．2．【解答】解：A、a2﹣a，不能合并，故A错误；B、a2•a3＝a5，故B错误；C、a9÷a3＝a6，故C错误；D、（a3）2＝a6，故D正确；故选：D．3．【解答】解：设这个新多边形的边数是n，则（n﹣2）•180°＝540°，解得：n＝5，故选：C．4．【解答】解：当a+b＝2时，原式＝﹣＝＝＝a+b＝2，故选：A．5．【解答】解：A、不是轴对称图形，也不是中心对称图形，故此选项错误；B、是轴对称图形，不是中心对称图形，故此选项正确；C、是轴对称图形，也是中心对称图形，故此选项错误；D、不是轴对称图形，是中心对称图形，故此选项错误；故选：B．6．【解答】解：数轴上点A，M，B分别表示数a，a+b，b，由它们的位置可得a＜0，a+b ＞0，b＞0且|a|＜|b|，则a﹣b＜0，ab＜0，|a|﹣b＜0，故运算结果一定是正数的是a+b．故选：A．7．【解答】解：A．从2013﹣2016年，我国国内生产总值逐年增长，此选项错误；B．∵7.8%＞7.3%＞6.9%＞6.7%，∴2013﹣2016年，我国国内生产总值的增长率逐年降低，但2016﹣2017年增长率上升，此选项错误；C．∵×（7.8%+7.3%+6.9%+6.7%+6.9%）＝7.12%，∴2013﹣2017年，我国国内生产总值的平均增长率约为7.12%，此选项错误；D．2016﹣2017年我国国内生产总值增长的最多，此选项正确．故选：D．8．【解答】解：①输入值x为16时，，，即，故①正确；②x的值不唯一．x＝3或x＝9或81等，故②不正确；③当x＝0，1时，始终输不出y值．因为0，1的算术平方根是0，1，一定是有理数；故③正确；④对于任意的正无理数y，都存在正整数x，使得输入x后能够输出y，如输入π2，故④不正确；故选：B．二、填空题（本题共16分，每小题2分）9．【解答】解：当分母x﹣1≠0，即x≠1时，分式有意义．故答案是：x≠1．10．【解答】解：∵EG∥BC，∠1＝35°，∴∠DBC＝35°，∵BD平分∠ABC，∴∠ABC＝70°．故答案为：70°11．【解答】解：将2622000用科学记数法表示为：2.622×106．故答案为：2.622×106．12．【解答】解：∵D、E分别是△ABC边AC，BC的中点，∴DE∥AB，DE＝AB，∴△CDE∽△CAB，∴＝（）2，即＝，解得，S△ABC＝8，∴四边形ABED的面积＝8﹣2＝6，故答案为：6．13．【解答】解：设他去时驾车的平均速度为x千米/小时，则返回时驾车的平均速度为（x+25）千米/小时，依题意，得：x＝（x+25）．故答案为：x＝（x+25）．14．【解答】解：连接OA，如图，∵∠ACO＝40°，OA＝OC，∴∠CAO＝∠ACO＝40°，∴∠AOC＝100°，∴∠B＝50°．故答案为：50°．15．【解答】解：①图2中折线ABC表示乙槽中水的深度与注水时间之间的关系；②点B的纵坐标表示的实际意义是乙槽内液面恰好与圆柱形铁块顶端相平（或铁块的高度）；故答案为：乙；乙槽内液面恰好与圆柱形铁块顶端相平（或铁块的高度）；16．【解答】解：根据表中的损坏的频率，当实验次数的增多时，苹果损坏的频率越来越稳定在0.1左右，所以苹果的损坏概率为0.1．根据估计的概率可以知道，在10000千克苹果中完好苹果的质量为10000×0.9＝9000千克．设每千克苹果的销售价为x元，则应有9000x＝2.2×10000+23000，解得x＝5．答：出售苹果时每千克大约定价为5元可获利润23000元．故答案为：0.1，5．三、解答题（本题共68分，第17-21题，每小题5分，第22题6分，第23题5分，第24-26题，每小题5分，第27、28题，每小题5分）17．【解答】解：原式＝2×+﹣1﹣2+1＝+﹣1﹣2+1＝0．18．【解答】解：∵解不等式①得：x≤3，解不等式②得：x＜1，∴不等式组的解集是x＜1．19．【解答】解：（1）如图所示，直线AP即为所求．（2）证明：∵AB＝AC，∴∠ABC＝∠ACB（等边对等角），∵∠DAC是△ABC的外角，∴∠DAC＝∠ABC+∠ACB（三角形外角性质），∴∠DAC＝2∠ABC，∵AP平分∠DAC，∴∠DAC＝2∠DAP，∴∠DAP＝∠ABC，∴AP∥l（同位角相等，两直线平行），故答案为：（等边对等角），（三角形外角性质），（同位角相等，两直线平行）．20．【解答】解：（1）由已知得：△＝b2﹣4ac＝（﹣6）2﹣4（k+7）＝8﹣4k＞0，解得：k＜2．（2）∵k＜2，且k为正整数，∴k＝1．将k＝1代入到方程x2﹣6x+k+7＝0中，得x2﹣6x+8＝0，∵x2﹣6x+8＝（x﹣4）（x﹣2）＝0，解得：x1＝4，x2＝2．21．【解答】解：（1）∵四边形ABCD是矩形，∴DO＝BO．∵四边形ADOE是平行四边形，∴AE∥DO，AE＝DO，AD∥OE．∴AE∥BO，AE＝BO，∴四边形AOBE是平行四边形．∵AD⊥AB，AD∥OE，∴AB⊥OE．∴四边形AOBE是菱形；（2）设AB与EO交点为M．∵AB∥CD，∴∠DCO＝∠BAO．∵四边形AOBE是菱形，∴∠EAO＝2∠BAO．∵∠EAO+∠DCO＝180°，∴∠BAO＝120°，∠EAM＝60°．又AM＝AB＝1，∴BM＝．∴EO＝2，∴△AEO面积为×2×1＝，∴四边形ADOE面积＝2．22．【解答】解：（1）从图中看到A球员的场均得分是7.5×28.1＝210.75分，B运动员是8.3×27.5＝225.5分，因此两名球员整个常规赛季的比赛中总得分较高的一位是B，故答案为：B．（2）防守情况看盖帽，抢断，篮板情况，从图中看到，A球员均场盖帽2.6大于B球员的0.9，A球员均场抢断1.5大于B球员均场抢断1.4，A球员均场篮板11.1大于B球员均场篮板8.6，综合比较A球员的防守明显好于B球员，因此A球员在常规赛季的防守表现更好．（3）从得分角度看，B球员的平均得分高于A球员的平均得分，但是从方差角度看，A 球员的平均得分比B球员稳定；从助攻角度看，B球员助攻得分远高于A球员，但从方差角度看，A球员助攻得分比B 球员稳定；因此，综合看，A球员得分和助攻的表现都很稳定，而B球员在季后赛前整体状况优于A 球员．23．【解答】解：（1）点A（，4）代入，∴k＝6，（2）①∵点P恰好与A重合，∴设AB直线解析式为y＝kx+b，将A（，4）和B（﹣1，﹣1）代入，，∴，∴y＝2x+1，点C（0，t）代入y＝2x+1，∴t＝1，∴D（1，0），设直线BD的解析式为y＝mx+n，将点B（﹣1，﹣1），D（1，0）代入，，∴，∴y＝x﹣，∵点（0，1），（1，3），（3，1）在W区域的边界上，∴区域W内的整点有5个；如图：②由①可知t＝1刚好有5个点，即点（0，0），（1.1），（2，1），（1，2），（2，2），当点（1，2）在直线BC上时，此时解析式为y＝x+，C（0，t）在y＝x+上，t＝，此时D（，0），BD的解析式为y＝x﹣，点（2，1）在BD直线上，∴t＝时，W区域内有3个整数点，∴＜t≤1时，区域内恰好有5个整点；24．【解答】（1）证明：连OD，并反向延长交AC于点G，∵DN是⊙O的切线，∴OD⊥DN，由切线的性质，可证∵DN∥AC，∴OG⊥AC，∴AD＝DC，∵CD⊥AB，∴AC＝AD，∴△ACD是等边三角形；（2）解：∵CD⊥AB，∠CAD＝60°，∴∠CAB＝30°，∴，∴，∴，BC＝2，∵AB为⊙O的直径，∴∠ACB＝90°，由（1）知DG⊥AC，OD⊥DN，∴四边形GDCE是矩形，∴CE＝DG＝OG+OD＝1+2＝3，DE＝CG＝，∴＝，∵AC∥DE，∴△ACF∽△EDF，∴，设EF＝x，则AF＝，∴，解得x＝．25．【解答】解：（1）由△BED∽△CDF，可得，∵BD＝CD＝2，∴BE•CF＝4，故答案为BE•CF＝4．（2）由题意：1≤x≤4．∵由△BED∽△CDF，可得，∵BD＝CD＝2，BE＝x，CF＝4﹣y，∴x（4﹣y）＝4，∴y＝4﹣．故答案为1≤x≤4，y＝4﹣．（3）函数图象如图所示：（4）观察图象可知两个函数的交点P的横坐标约为1.6，故BE＝1.6故答案为1.6．26．【解答】解：（1）x＝﹣＝1，故答案是1；（2）①令y＝0，则x＝1±，则PQ＝2＝2，解得：a＝﹣1，故抛物线的表达式为：y＝﹣x2+2x+3；②图象翻折前后如下图所示，点M坐标为（1，4），则MS＝4﹣t，则点M′纵坐标为t﹣（4﹣t）＝2t﹣4，当点M′在点H上时，即2t﹣4≥﹣5，即：t≥，此时M＝t，m＝﹣5，t+5≤6，解得：t≤1，即：﹣≤t≤1；当点M′在点H下方时，t＜﹣，M＝t，m＝2t﹣4，则t﹣2t+4≤6，解得：t≥﹣2，即：﹣2≤t＜﹣；故：t的取值范围为即：﹣≤t≤1或﹣2≤t＜﹣．27．【解答】解：（1）∵AB∥EF∴∠ABC＝∠E＝α，∵CD＝CE，CF⊥DE∴DF＝EF，∴∠FDC＝∠E＝α∵CF⊥DE∴∠AFD＝90°﹣∠CDF＝90°﹣α故答案为：90°﹣α（2）设BG＝a，GM＝b，∴BM＝a+b，∵点M是AB中点，∴AM＝BM＝a+b，∴AG＝AM+GM＝a+b+b＝a+2b，∵DF＝EF∴∠E＝∠FDE，∵AB∥EF∴∠E＝∠B，∴∠B＝∠EDF＝∠GDB∴BG＝GD＝a，∵AC⊥BC∴∠A＝90°﹣∠B，∠DFC＝90°﹣∠EDF∴∠A＝∠DFC∴AG＝GF＝a+2b∴DF＝GF﹣GD＝2b，∴DF＝2GM，（3）由（2）可知：设BG＝GD＝a，GM＝b，则DF＝2b＝EF，AG＝a+2b＝GF，∵∠ABC＝45°∴∠GDB＝45°∴∠AGD＝90°＝∠BGD＝∠DFE∴BD＝a，DE＝2b，DC＝CE＝b，∠AGH+∠DGH＝90°，∵AH⊥GE∴∠GAH+∠AGH＝90°∴∠GAH＝∠DGH，且∠AHG＝∠DHG＝90°∴△AGH∽△GDH∴∵∠GAH＝∠DGH，∠AHG＝∠EFG＝90°∴△AGH∽△GEF∴∴∴∴a＝2b∴BC＝BD+CD＝a+b＝3b∴＝＝328．【解答】解：（1）原点O的限定函数满足的条件是：﹣1≤x≤1内有定义，且对此范围内的任意x的值，对应的y都满足﹣1≤y≤1，对于函数③y＝2x2﹣1，图象如下图1所示，满足﹣1≤x≤1内有定义，且对此范围内的任意x的值，对应的y都满足﹣1≤y≤1；同理函数①也满足条件；故答案是①③；（2）点A坐标（m，n），则m﹣1≤x≤m+1，n﹣1≤y≤n+1，①当点A在y轴右侧时，且m﹣1≥0，n＝﹣m2，由题意得：，其中n＝﹣m2，解得：，即m≤，此时m的值符合图中虚线所示的位置；②当点A在y轴左侧时，且m﹣1＜0，同理可得：m≥﹣，综合①②可得：﹣≤m≤；（3）如图2，用边长为2的正方形框定x、y的取值范围，交PM于点N交x轴于点K、H，交OQ于点S，此时的情况是临界点的情况．①射线PM部分的情况，在临界点时，KN＝1，设：OM＝x，则KM＝1﹣x，tan∠KMN＝＝＝tan∠PMO＝＝，解得：x＝，tan∠MOP＝＝；②射线OQ部分的情况，射线OQ为第一象限角平分线，则直线OQ与y轴的夹角为45°，则直线OP与y轴的夹角也为45°，故此时tan∠MOP＝1，故：≤tan∠MOP≤1．。

DOI：10.16655/ki.2095-2813.2005-5659-9026基于多元回归的NBA球员薪金与技术数据分析①罗舜(福州大学经济与管理学院 福建福州 350108)摘要：该文运用文献资料法、数理统计法、比较研究法，对2018—2019赛季美国男子职业篮球联赛常规赛场均得分前50名的球员的赛季薪金与各项技术数据进行分析与比对，将球员数据进行分类，对球员各类技术数据进行相关分析，并将得出的结果可视化，最后得出每个因素对球员工资的影响程度，为中国职业篮球联赛球员的挑选提供理论性的参考。

结果表明：2018—2019赛季美国男子职业篮球联赛常规赛顶尖球员的技术数据中，在满足t检验的显著性水平Sig＜0.05的情况下，场均篮板、场均助攻和场均得分对球员赛季薪金有显著性影响并且呈正相关，其中场均助攻的影响程度最高；场均失误对球员赛季薪金有显著性影响并且呈负相关。

关键词：美国职业篮球联赛 篮球技术数据 多元回归分析 薪金中图分类号：G841 文献标识码：A 文章编号：2095-2813(2021)02(a)-0229-04 Analysis of NBA Players Salaries and Technical Data Based onMultiple RegressionLUO Shun(School of Economics and Management Fuzhou University, Fuzhou, Fujian Province, 350108 China) Abstract: This paper uses the methods of literature, mathematical statistics and comparative research to analyze and compare the season salary and various technical data of the top 50 players with average score in each game in the regular field of the 2018—2019 NBA, classify the player data, make relevant analysis on all kinds of technical data of the players, and visualize the results, and finally get each of them. The inf luence of the factors on the player's salary can provide theoretical reference for the selection of players in the CBA. The results show that: in the technical data of the top players in the regular season of the 2018—2019 NBA, under the condition of meeting the significance level sig<0.05 of the t-test, the average rebounds, assists and scores have a significant and positive impact on the players' season salary, of which the average assists have the highest impact. The average mistakes havea significant impact on the players' season salary. It also has negative correlation.Key Words: American professional basketball league; Basketball technical data; Multiple regression analysis; Salary伴随世界经济的不断发展，如今竞技体育项目发展趋势是体育赛事的规范化、产业化。