第08讲 归纳、猜想、证明

半角模型三个条件 ①共顶点 ②小角是大角一半 ③大角边相等模型一：90°夹45°半角模型【例】如图，等腰ABC Rt ∆中，AC AB BAC ==∠,90，点D E ,是BC 边上两点，若45=∠EAD ，则线段DE EC BD ,,之间有怎样的数量关系，并说明理由解答：把三角形进行旋转写法尽量不用【旋转（两小角变大角）】得证：222DE EC BD =+模型二：120°夹60°半角模型【例】如图，ABC ∆是边长为1的等边三角形，BDC ∆是等腰三角形，且120=∠BDC ，以D 为顶点作一个60角，使其两边分别交AB 于M 交AC 于点N ，连接MN ，求AMN ∆的周长解答：把三角形进行旋转写法尽量不用【旋转（两小角变大角）】得证：2模型三：半角模型与正方形【例】如图，F E ,分别是正方形ABCD 的边CD BC ,上的点，且45=∠EAF ，EF AH ⊥，H为垂足（1）求证：EF DF BE =+ （2）求证：BC AH =（3）若2,3==DF BE ，求AB 的长（4）当点F E ,分别在DC CB ,的延长线上时，线段DF BE ,和EF 之间有怎样的数量关系？请写出你的猜想，并证明解答：（1）同理可证 （2）可证 （3）得证6=AB（4）图略，得证DF EF BE =+模型四：半角模型与对角互补模型【例】问题1：如图1，在等腰梯形ABCD 中，BC AD //，CD BC AB ==，点N M ,分别在CD AD ,上，若ABC MBN ∠=∠21，试探究线段CN AM MN ,,有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD 中，180,=∠+∠=ADC ABC BC AB ，点N M ,分别在CD DA ,的延长线上，若ABC MBN ∠=∠21仍然成立，请你进一步探究线段AM MN ,， CN 又有怎样的数量关系，写出你的猜想，并给予证明解答：（1）得证MN CN AM =+ （2）得证CN AM MN =+模型五：对角模型与矩形【例】如图，在矩形ABCD 中，4,2==BC AB ，点F E ,分别在CD BC ,上，若,5=AE45=∠EAF ，则AF 的长为解法：①方法一：半角模型（2种）【构造使其满足半角模型三个条件】 ②方法二：K 型三垂直（3种）【构造等腰直角三角形】 ③方法三：构造相似三角形（1种）【构造135°角】④方法四：12345模型（最快）【和角公式（两角和45°，一个正切值是21，另一个正切值是31）】 得证1034=AF。

归纳—猜想—证明归纳法是由一系列有限的特殊事例得出一般结论的推理方法。

归纳法分为不完全归纳法与完全归纳法，数学归纳法是“完全归纳”的一种科学方法，对于无穷尽的事例，常用不完全归纳法去发现规律，得出结论，并设法予以证明，这就是“归纳—猜想—证明”的思想方法，1．什么是归纳法在初中学习平面几何时，常会遇到如下推理：三角形内角和为180°，直角三角形是三角形，所以直角三角形内角和为180°。

这种由一般命题推出特殊命题的推理方法，我们称为演绎法。

但很多时候，往往需要从特殊的事例推出一般的原理，例如，一个人通过若干天的观察，看到“太阳从东方升起”， 就推出一般结论：“今后的每一天太阳都从东方升起”，这种推理方法叫做归纳法。

归纳法在科学发展和社会生活中起着重要作用，如气象工作者、水文工作者根据积累的历史资料作气象预测、水文预测，用的就是归纳法归纳法有什么特点？来看两个问题。

问题1：这里有一袋球共10个，要判断这袋球的颜色是白色，还是其他颜色，请问怎么办？学生：一个个拿出来看一看。

教师：这一袋球都是白色的。

问题2：数列的通项公式()2255n a n n =-+，计算1234,,,a a a a 的值，可以得到什么结论？学生：该数列的前四项都是1，猜测该数列的所有项都是1教师：这是错误的结论，该数列第五项是25。

解决以上两个问题用的都是归纳法——用一些特殊事例推出一般结论。

为什么问题1的结论正确，问题2的结论错误呢？这是因为问题1中，一共10个球，全部看了一遍，结论当然正确。

问题2中，根据前4 项为1，推测到所有项都是1，由于自然数有无数多个，因此得出的结论不一定正确。

实际上在这两个问题中运用的归纳法是有区别的，问题1中把研究对象都一一考察到了，这样推出结论的归纳法称为完全归纳法（通过验证一切可能的特殊事例，从而得出一般性结论，这种归纳推理称为完全归纳法）。

问题2中，根据部分事实推出了更加一般的事实，这种推理方法称为不完全归纳法（通过验证有限的特殊事例，从中推断出一般性的结论，这种归纳推理称为不完全归纳法）。

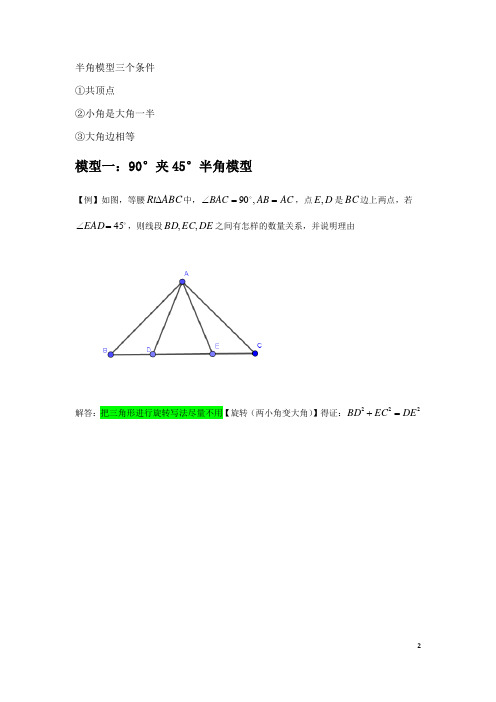
半角模型三个条件①共顶点②小角是大角一半③大角边相等模型一：90°夹45°半角模型【例】如图，等腰ABC Rt ∆中，AC AB BAC ==∠,90，点D E ,是BC 边上两点，若 45=∠EAD ，则线段DE EC BD ,,之间有怎样的数量关系，并说明理由解答：把三角形进行旋转写法尽量不用【旋转（两小角变大角）】得证：222DE EC BD =+模型二：120°夹60°半角模型【例】如图，ABC ∆是边长为1的等边三角形，BDC ∆是等腰三角形，且 120=∠BDC ，以D 为顶点作一个 60角，使其两边分别交AB 于M 交AC 于点N ，连接MN ，求AMN ∆的周长解答：把三角形进行旋转写法尽量不用【旋转（两小角变大角）】得证：2模型三：半角模型与正方形【例】如图，F E ,分别是正方形ABCD 的边CD BC ,上的点，且45=∠EAF ，EF AH ⊥，H 为垂足（1）求证：EF DF BE =+（2）求证：BC AH =（3）若2,3==DF BE ，求AB 的长（4）当点F E ,分别在DC CB ,的延长线上时，线段DF BE ,和EF 之间有怎样的数量关系？请写出你的猜想，并证明解答：（1）同理可证（2）可证（3）得证6=AB（4）图略，得证DF EF BE =+模型四：半角模型与对角互补模型【例】问题1：如图1，在等腰梯形ABCD 中，BC AD //，CD BC AB ==，点N M ,分别在CD AD ,上，若ABC MBN ∠=∠21，试探究线段CN AM MN ,,有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD 中， 180,=∠+∠=ADC ABC BC AB ，点N M ,分别在CD DA ,的延长线上，若ABC MBN ∠=∠21仍然成立，请你进一步探究线段AM MN ,， CN 又有怎样的数量关系，写出你的猜想，并给予证明解答：（1）得证MN CN AM =+（2）得证CN AM MN =+模型五：对角模型与矩形【例】如图，在矩形ABCD 中，4,2==BC AB ，点F E ,分别在CD BC ,上，若,5=AE 45=∠EAF ，则AF 的长为解法：①方法一：半角模型（2种）【构造使其满足半角模型三个条件】 ②方法二：K 型三垂直（3种）【构造等腰直角三角形】③方法三：构造相似三角形（1种）【构造135°角】④方法四：12345模型（最快）【和角公式（两角和45°，一个正切值是21，另一个正切值是31）】 得证1034AF。

高二数学归纳 猜想 证明（一）知识归纳：由事物的部分特殊事例猜想出事物的一般结论，这种方法人们称为“不完全归纳法”，用不完全归纳法得出的结论需要经过证明，因此全部过程可以小结为下面程序：①计算命题取特殊值时的结论；②对这些结果进行分析，探索数据的变化规律，并猜想命题的一般结论；③证明所猜想的结论. （二）学习要点：在中学数学内，“归纳—猜想—证明”的推理方法一般只局限于数列的内容，而且与正整数n 有关，其它内容中很少有要求，解决问题时要注意以下几点，①计算特例时，不仅仅是简单的算数过程，有时要通过计算过程发现数据的变化规律；②猜想必须准确，绝对不能猜错，否则将徒劳无功；③如果猜想出来的结论与正整数n 有关，一般用数学归纳法证明.【例1】已知数列{}n a 满足关系式∈≥+=>=--n a a a a a a a n n n ,2(12),0(111N +），（Ⅰ）用a 表法a 2，a 3，a 4；（Ⅱ）猜想a n 的表达式（用a 和n 表示），并证明你的结论.[解析]（Ⅰ）;7183141314212,31412112212,23342232a a aa a aa a a a a a a a a a a a a a a a +=+++⨯=+=+=+++⨯=+=+= （Ⅱ）（ ,)12(12,)12(12111001a a a a a a a -+=-+==） 猜想,)12(1211a aa n n n -+=--下面用数学归纳法证明：1°．当n=1时，∴-+==,)12(12001a aa a 当n=1结论正确； 2°．假设当n=k 时结论正确，即aaa k k k )12(1211-+=--，∴当n=k+1时 a a aa a a k k k k k k 1112)12(1212--++-+=+= =,)12(1222121aa a a a kk k k -+=-⨯+-当n=k+1时结论也正确； 根据1°与2°命题对一切n ∈N*都正确.[评析]“归纳—猜想—证明”是解决数列的某些问题的一种重要方法，对于一些变换技巧比较高的问题，如果能通过这种方法解答成功，则解答过程比较其它方法更容易.【例2】已知数列{}n a 满足：,232,1111-+⨯+==n n n a a a 计算a 2，a 3，a 4的值，由此归纳出a n 的公式，并证明你的结论.[解析]很容易算出a 2=5，a 3=16，a 4=44，但由此猜想出结论显然是非常困难的，下面作一些探索. ∵a 2=2 a 1+3×2°=2×1+3×2°，a 3=2（2×1+3×2°）+3×21=22×1+2×3×21， a 4=2（22×1+2×3×21）+3×22=23×1+3×3×22；猜想a n =2n －1+（n －1）×3×2n －2=2n －2（3n －1）；用数学归纳法证明：1°．当n=1时，a 1=2－1×=1，结论正确； 2°．假设n=k 时，a k =2k －2（3k －1）正确，∴当n=k+1时，111123)13(2232---+⨯+-=⨯+=k k k k k k a a =)23(21+-k k ],1)1(3[21)1(-+=-+k k 结论正确；由1°、2°知对n ∈N*有).13(22-=-n a n n[评析]如果计算出来的数据很难猜出结论时，应考虑整理计算过程，探索数据的变化规律，看看能否猜想成功. 【例3】已知等差数列{}n a 中，a 2=8，前10项的和S 10=185， （Ⅰ）求数列{}n a 的通项公式a n ；（Ⅱ）若从数列{}n a 中依次取出第2，4，8， (2)，…项，按原来的顺序排成一个新数列，试求新数列的前n 项和A n ；（Ⅲ）设 B n =n （5+3 a n ），试比较A n 和B n 的大小，并说明理由. [解析]（Ⅰ）设公差为d ，∴;23)1(35,5345101858111+=-⨯+=∴⎩⎨⎧==⇒⎩⎨⎧+=-=n n a a d da d a n （Ⅱ）设新数列为{}nb ，∴2232+⨯==nn n a b∴A n =3×（2+22+23+ (2)）+2n=3×2n ＋1+2n －6；（Ⅲ）∵,48163,22283,8443,119)119(3212=⨯==-⨯==-⨯=∴+=+=A A A n n n n B n A 4=3×32+2=98，A 5=3×64+4=196，A 6=3×128+6=390，A 7=3×256+8=776，…… 而B 1=20，B 2=58，B 3=114，B 4=188，B 5=280，B 6=390，B 7=518，…… ①当n=1，2，3，4，5时，B n >A n ； ②当n=6时，B 6=A 6；③当n ≥7，且n ∈N*时，猜想A n >B n ，用数学归纳法证明： 1°．当n=7时，A 7=766>518=B 7，结论正确；2°．假设当n=k （k ≥7）时，A k >B k ，即3×2k+1+2k －6>9k 2+11k ⇒2k+1>3k 2+3k+2，∴n=k+1时，)]1(11)1(9[]6)1(223[2211+++--++⨯=-+++k k k B A k k k =6×2k+2－9k 2－27k －24=6×[2 k+1－（3k 2+3k+2）]+6×（3k 2+3k+2）－9k 2－27k －24 =6×[2k+1－（3k 2+3k+2）]+9k 2－9k －12>9k 2－9k －12=9k （k －1）－12≥9×7×（7－1）－12>0 ∴A k+1>B k+1，即n=k+1时，结论也正确； 根据1°、2°知当n ≥7且n ∈N*时，有A n >B n .[评析]从上面例子可以看出，归纳猜想不仅仅是要有对数据的观察能力，还需要有一定的经验，否则很难作出上述准确的猜想.【例4】已知数列{}n a 满足：,2121221nn n a a a a a +===++且问是否存在常数p 、q ，使得对一切n ∈N*都有,12n n n qa pa a +=++并说明理由.[解析] ∵,112,3222341223=+==+=a a a a a a 设存在这样的常数p 、q ，∴,141133234123⎩⎨⎧-==⇒⎩⎨⎧=+=+⇒⎩⎨⎧+=+=q p q p q p qa pa a qa pa a 由此猜想，对n ∈N*，有,412n n n a a a -=++ 下面用数学归纳法证明这个结论：1°．当n=1时，12343a a a -==，结论正确；2°．假设当n=k 时结论正确，即,412k n k a a a -=++ ∴当n=k+1时，,42)2(4242)4(21212121221121223++++++++++++++-=-+-=--=+-=+=k k k k k k k k k k k k k k k k a a a a a a a a a a a a a a a a ∴当n=k+1时结论正确，故当n ∈N*时，n n n a a a -=++124成立.[评析]例4是一类探索题型，由条件直接推出结论是非常困难的，通过归纳—猜想—证明的方法，难度不大.。

数学高考综合能力题选讲8归纳、猜想、证明题型预测观察、归纳、猜想、证明是解决探索性问题的重要思维方法，也是高考考查的热点.范例选讲例1 .已知数列t a j满足a1 =2，对于任意的n € N,都有a. > 0，且(n +1 h n2+a n a n+ - na n/ =0.又知数列满足：b n =2n」+1.(I)求数列i a j的通项a n以及它的前n项和S n !(n )求数列妃｝的前n项和Tn!(m )猜想S n和T n的大小关系，并说明理由.讲解：(n +1 b n2+a n a n卅-nan/ =0是关于a.和的二次齐次式，故可利用求根公式得到a n与a n十的更为明显的关系式，从而求出a(1 ) ••• a n >0 (n€ N,且(n + 畑2+••• ( n +1)(斗2+(禹-n=0 • a n+ a n十T a n > 0 ( n€ N),a n _ n an+ n +1即丑an+ n+12a n a n+l 一na n+l = 0，a n a n十-1 ±J1 +4n(n +1)2(n+1)-1 ±(2n +1) _-2(n+1)—n一nan a n an」a n_2 …a 3 a 2n n—1 n —2— *=a 1 a n」an_2 a n_3a 2 a 1n —1 n —23又 a 1 =2,所以，a n =2 n .S n = a 1 + a 2 +…+ a n = 2(1 + 2 +…+ n )= n 2 + n (n) V b n =2n」+1 f二 T n =bi +b 2 +…+b n =(2° +21十•• +2n」)+ n = 2n+ n-1(rn)T n -S n =2n— n 2-1 I1°当n=5时，前面已验证成立;2°假设n =k(k>5)时命题成立，即2k：>k 2+1成立，那么当n=k+1(k>5) 时』 2k + =2 ”2k A2 -(k 2 +1 A k 2 +k2 + 2 >k 2 +5k + 2 :>k 2+2k + 2 =(k +1 丫 +1 .即n=k+1(k>5)时命题也成立.由以上1°、2°可知，当nA5时，有T n 》S n ;综上可知：当n=1时，T i =S i ;当2<门v5时，T n <S n ，当n 》5时，有T^ S n . 点评：注意到2n的增长速度大于n 2+1的增长速度，所以，在观察与归纳的 过程中，不能因为从n=1到n=4都有T^S n 就得出T^ S n 的结论，而应该坚信: 必存在n ，使得2n>n 2+1，从而使得观察的过程继续下去.当n=1时, 当n=2时, 当n=3时, 当n=4时, 当n=5时, 当n=6时,猜想：当n J 1 -12-1 =0 ,T1 = S1; =22 -22 -1 = -1 ’:* T2 € S2; =23 -32 -1 = —2 T，* T3 V S3;=24 -42 -1 = -1 ’ * * T^ S4;=Q 5 — 52 — 1 = 6 T< * T 5 > S5 ;=26 -62 -1 =27 ,* * T 6》S6 ;T n >S n .即 2n》n 2十1 .下用数学丁2 - S2 T3 —S3T 4 -S 4 T6 — S 6>5时, T i -S i T 5 —S5P,使得当n> P 时，总有a 2+a计wa n ? 2讲解：(I)首先考虑能否化简已知条件a n 屮，但事实上这一条路7 —a n走不通，于是，我们转而考虑通过计算一些 a k 的值来寻找规律.不难得到:16 … c 4 c 4 a8 =— , a 9 =12 , a 10 = —8 , a11=- - , a 12=0, a13 =-,3 37可以看出：a 8, a 9均大于2,从a 10到a 13均小于2,但能否由此断定当 也有a n €2 ?这就引导我们去思考这样一个问题： 若a ^2 ,能否得出为此，我们考查a n 卅-2与a n -2的关系，易得a n 卄 2=汗-2 =—7 -a n 7 - a n必有a n <2 .(I)，我们还需验证当n= 1,2，…，9时，是否均有a n A 2 . 验证.即通过已知条件解出：an =7办十—4 .由此，我们可 a n41 中3以从37出发，计算出这个数列的第6项到第1项，从而得出结论.另外，得益于上述解法，我们也可以考虑这样的问题：“若a n 中>2，能否得 出 a n >2”？由an-2=7an+~4_2=5(an+-2)不难得知：上述结论是正确的.an + +3 a ^1 +3所以，存在m =10，使得当n Am 时，a n 吒2 ；当n c m 时，a n 》2 .例2已知数列l a j 中,a 7 =4,an41 = +47 —a n (I)是否存在自然数m,使得当n >m 时,an c 2;当 n c m 时，an a 2 ?(n)是否存在自然数nAl3 时,可以看出：当 3^2时，必有an+<2 .于是，我们可以确定：当nW 时,为了解决问题 方法之一是（n ）问题等价于：是否存在自然数P,使得当n>p 时，总有a n 二 +an 卡一2a n ■<0 .由（I ）可得：an/ +a n 出—2a n3 _ 2(an-2) "(7-an 13+an ) 我们已经知道：当n>i0时，a n £2，于是但.-23<0, （7-a n ）<0，所以, 我们只需考虑：是否存在不小于10的自然数P ，使得当n > P 时，总有a n >-3 ? 观察前面计算的结果，可以看出: a io 吒—3 ， a ii ,a i2,a i3均大于-3，可以猜 想：P =11即可满足条件. 这样的猜想是否正确？我们只需考查 +3与a n +3的关系: 由 an 十 +3 =3a n +4+3 7 -a n an + 25 =上二可知：上述结论正确. 7 -a n另外，如果我们注意到从 a ii 到a i3，数列的项呈递增的趋势，贝U 也可以考虑a n+ -a n - 比少〉0,从而得出结论. 出 3a n 中4 田 a n 卅一 an—an = 「7-a n7-a n点评：（i ）归纳、猜想是建立在细致的观察和缜密的分析基础上的，并非 无源之水、无本之木.（2） 上述分析的过程如果用数学归纳法写出，则相当简 洁，但同时也掩盖了思维的过程.。

数学归纳法数学归纳法一般地，证明一个与正整数n 有关的命题，可按下列步骤进行： (1)(归纳奠基)证明当n 取第一个值n 0 (n 0∈N *)时命题成立；(2)(归纳递推)假设n ＝k (k ≥n 0，k ∈N *)时命题成立，证明当n ＝k ＋1时命题也成立．只要完成这两个步骤，就可以断定命题对从n 0开始的所有正整数n 都成立．上述证明方法叫做数学归纳法． [难点正本 疑点清源]1．数学归纳法是一种重要的数学思想方法，主要用于解决与正整数有关的数学问题．证明时步骤(1)和(2)缺一不可，步骤(1)是步骤(2)的基础，步骤(2)是递推的依据．2．在用数学归纳法证明时，第(1)步验算n ＝n 0的n 0不一定为1，而是根据题目要求，选择合适的起始值．第(2)步，证明n ＝k ＋1时命题也成立的过程，一定要用到归纳假设，否则就不是数学归纳法．1． 凸k 边形内角和为f (k )，则凸k ＋1边形的内角和为f (k ＋1)＝f (k )＋________.2． 用数学归纳法证明：“1＋12＋13＋…＋12n －1<n (n >1)”，由n ＝k (k >1)不等式成立，推证n ＝k ＋1时，左边应增加的项的项数是________． 3． 用数学归纳法证明1＋a ＋a 2＋…＋a n ＋1＝1－a n ＋21－a (a ≠1，n ∈N ＋)，在验证n ＝1成立时，左边需计算的项是( )A ．1B ．1＋aC ．1＋a ＋a 2D ．1＋a ＋a 2＋a 34． 已知n 为正偶数，用数学归纳法证明1－12＋13－14＋…－1n ＝2⎝⎛⎭⎫1n ＋2＋1n ＋4＋…＋12n 时，若已假设n ＝k (k ≥2且k 为偶数)时命题为真，则还需要用归纳假设再证( )A ．n ＝k ＋1时等式成立B ．n ＝k ＋2时等式成立C ．n ＝2k ＋2时等式成立D ．n ＝2(k ＋2)时等式成立5． 已知f (n )＝1n ＋1n ＋1＋1n ＋2＋…＋1n2，则( )A ．f (n )中共有n 项，当n ＝2时，f (2)＝12＋13B ．f (n )中共有n ＋1项，当n ＝2时，f (2)＝12＋13＋14C ．f (n )中共有n 2－n 项，当n ＝2时，f (2)＝12＋13D ．f (n )中共有n 2－n ＋1项，当n ＝2时，f (2)＝12＋13＋14题型一 用数学归纳法证明等式例1 已知n ∈N *，证明：1－12＋13－14＋…＋12n －1－12n ＝1n ＋1＋1n ＋2＋…＋12n .探究提高 (1)用数学归纳法证明等式问题是常见题型，其关键点在于弄清等式两边的构成规律，等式两边各有多少项，初始值n 0是几；(2)由n ＝k 到n ＝k ＋1时，除等式两边变化的项外还要充分利用n ＝k 时的式子，即充分利用假设，正确写出归纳证明的步骤，从而使问题得以证明．用数学归纳法证明：对任意的n ∈N *，11×3＋13×5＋…＋1(2n －1)(2n ＋1)＝n2n ＋1.题型二 用数学归纳法证明不等式例2 用数学归纳法证明：1＋n 2≤1＋12＋13＋…＋12n ≤12＋n (n ∈N *)．探究提高 (1)用数学归纳法证明与n 有关的不等式一般有两种具体形式：一是直接给出不等式，按要求进行证明；二是给出两个式子，按要求比较它们的大小，对第二类形式往往要先对n 取前几个值的情况分别验证比较，以免出现判断失误，最后猜出从某个n 值开始都成立的结论，常用数学归纳法证明．(2)用数学归纳法证明不等式的关键是由n ＝k 时成立得n ＝k ＋1时成立，主要方法有①放缩法；②利用基本不等式法；③作差比较法等．用数学归纳法证明：对一切大于1的自然数，不等式⎝⎛⎭⎫1＋13⎝⎛⎭⎫1＋15·…·⎝⎛⎭⎫1＋12n －1>2n ＋12均成立．题型三 用数学归纳法证明整除性问题 例3 用数学归纳法证明42n ＋1＋3n＋2能被13整除，其中n 为正整数．探究提高 用数学归纳法证明整除问题，P (k )⇒P (k ＋1)的整式变形是个难点，找出它们之间的差异，然后将P (k ＋1)进行分拆、配凑成P (k )的形式，也可运用结论：“P (k )能被p 整除且P (k ＋1)－P (k )能被p 整除⇒P (k ＋1)能被p 整除．”已知n 为正整数，a ∈Z ，用数学归纳法证明：a n ＋1＋(a ＋1)2n－1能被a 2＋a ＋1整除．归纳、猜想、证明典例：(12分)在各项为正的数列{a n }中，数列的前n 项和S n 满足S n ＝12⎝⎛⎭⎫a n ＋1a n . (1)求a 1，a 2，a 3；(2)由(1)猜想数列{a n }的通项公式，并且用数学归纳法证明你的猜想．审题视角 (1)数列{a n }的各项均为正数，且S n ＝12⎝⎛⎭⎫a n ＋1a n ，所以可根据解方程求出a 1，a 2，a 3；(2)观察a 1，a 2，a 3猜想出{a n }的通项公式a n ，然后再证明． 规范解答温馨提醒 (1)本题运用了从特殊到一般的探索、归纳、猜想及证明的思维方式去探索和发现问题，并证明所得结论的正确性，这是非常重要的一种思维能力．(2)本题易错原因是，第(1)问求a 1，a 2，a 3的值时，易计算错误或归纳不出a n 的一般表达式．第(2)问想不到再次利用解方程的方法求解，找不到解决问题的突破口.方法与技巧1． 在数学归纳法中，归纳奠基和归纳递推缺一不可．在较复杂的式子中，注意由n ＝k 到n ＝k ＋1时，式子中项数的变化，应仔细分析，观察通项．同时还应注意，不用假设的证法不是数学归纳法．2． 对于证明等式问题，在证n ＝k ＋1等式也成立时，应及时把结论和推导过程对比，以减少计算时的复杂程度；对于整除性问题，关键是凑假设；证明不等式时，一般要运用放缩法．3． 归纳—猜想—证明属于探索性问题的一种，一般经过计算、观察、归纳，然后猜想出结论，再用数学归纳法证明．由于“猜想”是“证明”的前提和“对象”，务必保证猜想的正确性，同时必须注意数学归纳法步骤的书写． 失误与防范1． 数学归纳法仅适用于与正整数有关的数学命题．2． 严格按照数学归纳法的三个步骤书写，特别是对初始值的验证不可省略，有时要取两个(或两个以上)初始值进行验证；初始值的验证是归纳假设的基础． 3． 注意n ＝k ＋1时命题的正确性．4． 在进行n ＝k ＋1命题证明时，一定要用n ＝k 时的命题，没有用到该命题而推理证明的方法不是数学归纳法．A 组 专项基础训练(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1． 用数学归纳法证明“1＋2＋22＋…＋2n ＋2＝2n ＋3－1”，在验证n ＝1时，左边计算所得的式子为( )A ．1B ．1＋2C ．1＋2＋22D ．1＋2＋22＋232． 用数学归纳法证明“2n >n 2＋1对于n ≥n 0的正整数n 都成立”时，第一步证明中的起始值n 0应取( ) A ．2B ．3C ．5D ．63． 用数学归纳法证明1＋2＋3＋…＋n 2＝n 4＋n 22，则当n ＝k ＋1时左端应在n ＝k 的基础上加上( )A ．k 2＋1B ．(k ＋1)2 C.(k ＋1)4＋(k ＋1)22D ．(k 2＋1)＋(k 2＋2)＋…＋(k ＋1)24． 用数学归纳法证明：“(n ＋1)·(n ＋2)·…·(n ＋n )＝2n ·1·3·…·(2n －1)”，从“k 到k ＋1”左端需增乘的代数式为( )A ．2k ＋1B ．2(2k ＋1) C.2k ＋1k ＋1D.2k ＋3k ＋1二、填空题(每小题5分，共15分)5． 用数学归纳法证明“2n ＋1≥n 2＋n ＋2(n ∈N ＋)”时，第一步验证为________． 6． 若f (n )＝12＋22＋32＋…＋(2n )2，则f (k ＋1)与f (k )的递推关系式是__________．7． 用数学归纳法证明“当n 为正奇数时，x n ＋y n 能被x ＋y 整除”，当第二步假设n ＝2k －1(k ∈N ＋)命题为真时，进而需证n ＝________时，命题亦真． 三、解答题(共22分)8． (10分)若n 为大于1的自然数，求证：1n ＋1＋1n ＋2＋…＋12n >1324.。

2019-2020年高二数学归纳 猜想 证明 新课标（一）知识归纳：由事物的部分特殊事例猜想出事物的一般结论，这种方法人们称为“不完全归纳法”，用不完全归纳法得出的结论需要经过证明，因此全部过程可以小结为下面程序：①计算命题取特殊值时的结论；②对这些结果进行分析，探索数据的变化规律，并猜想命题的一般结论；③证明所猜想的结论.（二）学习要点：在中学数学内，“归纳—猜想—证明”的推理方法一般只局限于数列的内容，而且与正整数n 有关，其它内容中很少有要求，解决问题时要注意以下几点，①计算特例时，不仅仅是简单的算数过程，有时要通过计算过程发现数据的变化规律；②猜想必须准确，绝对不能猜错，否则将徒劳无功；③如果猜想出来的结论与正整数n 有关，一般用数学归纳法证明.【例1】已知数列满足关系式∈≥+=>=--n a a a a a a a n n n ,2(12),0(111N +）， （Ⅰ）用a 表法a 2，a 3，a 4；（Ⅱ）猜想a n 的表达式（用a 和n 表示），并证明你的结论.[解析]（Ⅰ）;7183141314212,31412112212,23342232a a a a a a a a a a a a a a a a a a a a a a +=+++⨯=+=+=+++⨯=+=+= （Ⅱ）（ ,)12(12,)12(12111001aa a a a a a -+=-+==） 猜想下面用数学归纳法证明： 1°．当n=1时，∴-+==,)12(12001aa a a 当n=1结论正确； 2°．假设当n=k 时结论正确，即，∴当n=k+1时 aa a a a a k k k k k k 1112)12(1212--++-+=+= =,)12(1222121aa a a a k k k k -+=-⨯+-当n=k+1时结论也正确； 根据1°与2°命题对一切n ∈N*都正确.[评析]“归纳—猜想—证明”是解决数列的某些问题的一种重要方法，对于一些变换技巧比较高的问题，如果能通过这种方法解答成功，则解答过程比较其它方法更容易.【例2】已知数列满足：,232,1111-+⨯+==n n n a a a 计算a 2，a 3，a 4的值，由此归纳出a n 的公式，并证明你的结论.[解析]很容易算出a 2=5，a 3=16，a 4=44，但由此猜想出结论显然是非常困难的，下面作一些探索. ∵a 2=2 a 1+3×2°=2×1+3×2°，a 3=2（2×1+3×2°）+3×21=22×1+2×3×21，a 4=2（22×1+2×3×21）+3×22=23×1+3×3×22；猜想a n =2n －1+（n －1）×3×2n －2=2n －2（3n －1）；用数学归纳法证明：1°．当n=1时，a 1=2－1×=1，结论正确；2°．假设n=k 时，a k =2k －2（3k －1）正确，∴当n=k+1时，111123)13(2232---+⨯+-=⨯+=k k k k k k a a = 结论正确；由1°、2°知对n ∈N*有[评析]如果计算出来的数据很难猜出结论时，应考虑整理计算过程，探索数据的变化规律，看看能否猜想成功.【例3】已知等差数列中，a 2=8，前10项的和S 10=185，（Ⅰ）求数列的通项公式a n ；（Ⅱ）若从数列中依次取出第2，4，8，…，2n ，…项，按原来的顺序排成一个新数列，试求新数列的前n 项和A n ；（Ⅲ）设 B n =n （5+3 a n ），试比较A n 和B n 的大小，并说明理由.[解析]（Ⅰ）设公差为d ，∴;23)1(35,5345101858111+=-⨯+=∴⎩⎨⎧==⇒⎩⎨⎧+=-=n n a a d d a d a n （Ⅱ）设新数列为，∴∴A n =3×（2+22+23+…+2n ）+2n=3×2n ＋1+2n －6；（Ⅲ）∵,48163,22283,8443,119)119(3212=⨯==-⨯==-⨯=∴+=+=A A A n n n n B n A 4=3×32+2=98，A 5=3×64+4=196，A 6=3×128+6=390，A 7=3×256+8=776，……而B 1=20，B 2=58，B 3=114，B 4=188，B 5=280，B 6=390，B 7=518，……①当n=1，2，3，4，5时，B n >A n ；②当n=6时，B 6=A 6；③当n ≥7，且n ∈N*时，猜想A n >B n ，用数学归纳法证明：1°．当n=7时，A 7=766>518=B 7，结论正确；2°．假设当n=k （k ≥7）时，A k >B k ，即3×2k+1+2k －6>9k 2+11k2k+1>3k 2+3k+2，∴n=k+1时，)]1(11)1(9[]6)1(223[2211+++--++⨯=-+++k k k B A k k k =6×2 k+2－9k 2－27k －24=6×[2 k+1－（3k 2+3k+2）]+6×（3k 2+3k+2）－9k 2－27k －24=6×[2 k+1－（3k 2+3k+2）]+9k 2－9k －12>9k 2－9k －12=9k （k －1）－12≥9×7×（7－1）－12>0∴A k+1>B k+1，即n=k+1时，结论也正确；根据1°、2°知当n ≥7且n ∈N*时，有A n >B n .[评析]从上面例子可以看出，归纳猜想不仅仅是要有对数据的观察能力，还需要有一定的经验，否则很难作出上述准确的猜想.【例4】已知数列满足：,2121221nn n a a a a a +===++且问是否存在常数p 、q ，使得对一切n ∈N*都有并说明理由.[解析] ∵,112,3222341223=+==+=a a a a a a 设存在这样的常数p 、q ， ∴,141133234123⎩⎨⎧-==⇒⎩⎨⎧=+=+⇒⎩⎨⎧+=+=q p q p q p qa pa a qa pa a 由此猜想，对n ∈N*，有 下面用数学归纳法证明这个结论：1°．当n=1时，，结论正确；2°．假设当n=k 时结论正确，即 ∴当n=k+1时，,42)2(4242)4(21212121221121223++++++++++++++-=-+-=--=+-=+=k k k k k k k k k k k k k k k k a a a a a a a a a a a a a a a a ∴当n=k+1时结论正确，故当n ∈N*时，成立.[评析]例4是一类探索题型，由条件直接推出结论是非常困难的，通过归纳—猜想—证明的方法，难度不大.。