下载文档原格式
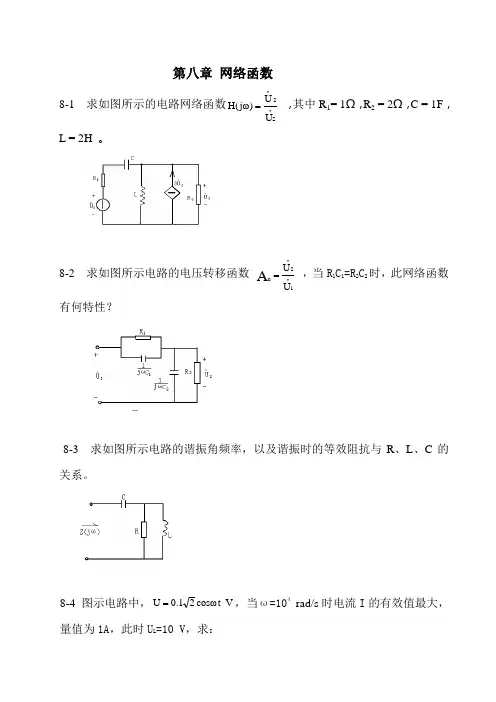
第八章 网络函数8-1 求如图所示的电路网络函数∙∙=S2U U )ωj (H ，其中R 1= 1Ω，R 2 = 2Ω，C = 1F ，L = 2H 。
8-2 求如图所示电路的电压转移函数 ∙∙=12u U U A ，当R 1C 1=R 2C 2时，此网络函数有何特性？8-3 求如图所示电路的谐振角频率，以及谐振时的等效阻抗与R 、L 、C 的关系。
8-4 图示电路中，V t ωcos 21.0U =，当ω=104 rad/s 时电流I 的有效值最大，量值为1A ，此时U L =10 V ，求：（1） R 、L 、C 及品质因数Q ，（2） 电压U C 。
8-5 RLC 串联电路中，已知电源电压U S =1mV ，f =1.59MHz ，调整电容C 使电路达到谐振，此时测得电路电流I 0=0.1mA ，电容上的电压U co =50 mV ，求电路元件参数R 、L 、C 及品质因数Q 和通频带B f 。
8-6 图示电路中，L 1=0.01H ，L 2=0.02H ，M= 0.01H ，R 1=5Ω，R 2=10Ω，C=20μF ，试求电路的谐振角频率，若外加电压 V 06U ∠=∙，求谐振时两电感上的电压1U ∙和2U ∙。
8-7 图示电路中，正弦电压有效值U=210 V ，电流有效值I=3 A ，且电流与电压同相，容抗X C =15Ω，求R 2和X L 。
8-8图示电路中，设R=10Ω，L=1H ，C=0.1F ， V )ψt ωcos(210U S +=。
（1）ω为何值时电路发生谐振？（2）求谐振时的电流i 。
（3）求谐振时RC 并联部分的复功率。
8-9 图示正弦电路中，R=1Ω，L=1H ，A )30t cos(2i S -= ，试问可变电容C 为多大时U c 最大？并求其最大值。
8-10 图示正弦电路中U s =12V ，R i = 60K Ω,L = 54μH ，C=100 pF ，R=9Ω,R L = 60 K Ω, 电路处于谐振状态，求谐振角频率和R L 两端的电压U L 。
Python中的数据分析和统计方法Python是一门功能强大的编程语言，广泛应用于数据分析和统计方法。
本文将详细介绍Python中常用的数据分析和统计方法，并按类进行章节划分，深入探讨每个章节的具体内容。
第一章：数据预处理在进行数据分析之前，通常需要对原始数据进行清洗和预处理。
Python提供了很多用于数据预处理的库和方法。
其中，pandas是最常用的库之一。
pandas可以用于数据的读取、清洗、转换和合并等操作。
另外，NumPy库也提供了许多用于数组操作和数值运算的函数，可用于数据预处理过程中的一些计算。
第二章：数据可视化数据可视化是数据分析的重要环节，它可以使得数据更加直观和易于理解。
Python中有多个可视化库可以使用，如Matplotlib、Seaborn和Plotly等。
这些库可以生成各种类型的图表，如线图、散点图、柱状图和饼图等。
通过合理选择和使用可视化方法，可以更好地展示数据的分布和趋势。
第三章：统计描述统计描述是对数据进行摘要和概括的过程。
在Python中，可以使用pandas库的describe()函数来计算数据的基本统计量，如均值、标准差、最大值和最小值等。
此外，还可以使用scipy库中的一些函数来计算概率分布、置信区间和假设检验等统计指标。
第四章：回归分析回归分析是数据分析中常用的一种方法，用于探究变量之间的关系和预测未来趋势。
Python中的statsmodels库提供了许多回归分析的方法，如线性回归、逻辑回归和多元回归等。
通过回归分析，可以得到模型的参数估计和拟合优度等指标，进而对未知数据进行预测和推测。
第五章：聚类分析聚类分析是将数据按照相似性进行分组的一种方法。
在Python 中，可以使用scikit-learn库中的KMeans算法来进行聚类分析。
KMeans算法通过迭代计算将数据划分为K个簇，使得同一簇内的数据相似度最高，不同簇之间的相似度最低。
聚类分析可以帮助我们发现数据中潜在的模式和规律。
