自动控制原理 实验报告3

一、实训目的本次实训旨在通过实际操作和实验，加深对自动控制原理的理解，掌握控制系统分析和设计的基本方法，提高动手能力和分析问题、解决问题的能力。

通过实训，使学生能够：1. 理解自动控制系统的基本组成和原理；2. 掌握典型控制系统的时域响应和频域响应分析方法；3. 学会使用实验设备进行控制系统实验，并能够分析实验结果；4. 培养团队协作和沟通能力。

二、实训仪器与设备1. 自动控制原理实验台；2. 信号发生器；3. 数据采集器；4. 计算机；5. 控制系统模拟软件。

三、实训内容1. 控制系统结构分析通过实验台搭建一个典型的控制系统，分析其结构，包括各个环节的功能和相互关系。

2. 时域响应实验对搭建的控制系统进行阶跃响应实验，记录并分析系统的输出波形，计算超调量、上升时间、调节时间等性能指标。

3. 频域响应实验对搭建的控制系统进行频率特性实验，记录并分析系统的幅频特性、相频特性，绘制Bode图。

4. 控制系统设计根据实验结果，对控制系统进行设计，包括PID参数整定、控制器设计等。

四、实验过程1. 搭建控制系统根据实验要求，搭建一个典型的控制系统，包括控制器、执行器、被控对象等环节。

2. 进行阶跃响应实验使用信号发生器产生阶跃信号，输入到控制系统中，记录输出波形，并计算超调量、上升时间、调节时间等性能指标。

3. 进行频率特性实验使用信号发生器产生不同频率的正弦信号，输入到控制系统中，记录输出波形，并绘制Bode图。

4. 控制系统设计根据实验结果，对控制系统进行设计，包括PID参数整定、控制器设计等。

五、实验结果与分析1. 阶跃响应实验通过阶跃响应实验，可以分析系统的稳定性和动态性能。

例如，超调量反映了系统的振荡程度，上升时间反映了系统的响应速度，调节时间反映了系统达到稳态所需的时间。

2. 频率特性实验通过频率特性实验，可以分析系统的频率响应特性。

例如，幅频特性反映了系统对不同频率信号的放大倍数，相频特性反映了系统对不同频率信号的相位延迟。

《自动控制原理》自动控制PID实验报告课程名称自动控制原理实验类型：实验项目名称：自动控制PID一、实验目的和要求1、学习并掌握利用MATLAB 编程平台进行控制系统复数域和频率域仿真的方法。

2、通过仿真实验研究并总结PID 控制规律及参数对系统特性影响的规律。

3、实验研究并总结PID 控制规律及参数对系统根轨迹、频率特性影响的规律，并总结系统特定性能指标下根据根轨迹图、频率响应图选择PID 控制规律和参数的规则。

二、实验内容和原理一）任务设计如图所示系统，进行实验及仿真程序，研究在控制器分别采用比例（P）、比例积分（PI）、比例微分（PD）及比例积分微分（PID）控制规律和控制器参数（Kp、Ki、Kd）不同取值时，控制系统根轨迹和阶跃响应的变化，总结pid 控制规律及参数变化对系统性能、系统根轨迹、系统阶跃响应影响的规律。

具体实验容如下：1、比例（P）控制，设计参数Kp 使得系统处于过阻尼、临界阻尼、欠阻尼三种状态，并在根轨迹图上选择三种阻尼情况的Kp 值，同时绘制对应的阶跃响应曲线，确定三种情况下系统性能指标随参数Kp 的变化情况。

总结比例（P）控制的规律。

2、比例积分（PI）控制，设计参数Kp、Ki 使得由控制器引入的开环零点分别处于：1）被控对象两个极点的左侧；2）被控对象两个极点之间；3）被控对象两个极点的右侧（不进入右半平面）。

分别绘制三种情况下的根轨迹图，在根轨迹图上确定主导极点及控制器的相应参数；通过绘制对应的系统阶跃响应曲线，确定三种情况下系统性能指标随参数Kp 和Ki 的变化情况。

总结比例积分（PI）控制的规律。

3、比例微分（PD）控制，设计参数Kp、Kd 使得由控制器引入的开环零点分别处于：1）被控对象两个极点的左侧；2）被控对象两个极点之间；66 3）被控对象两个极点的右侧（不进入右半平面）。

分别绘制三种情况下的根轨迹图，在根轨迹图上确定控制器的相应参数；通过绘制对应的系统阶跃响应曲线，确定三种情况下系统性能指标随参数Kp 和Kd 的变化情况。

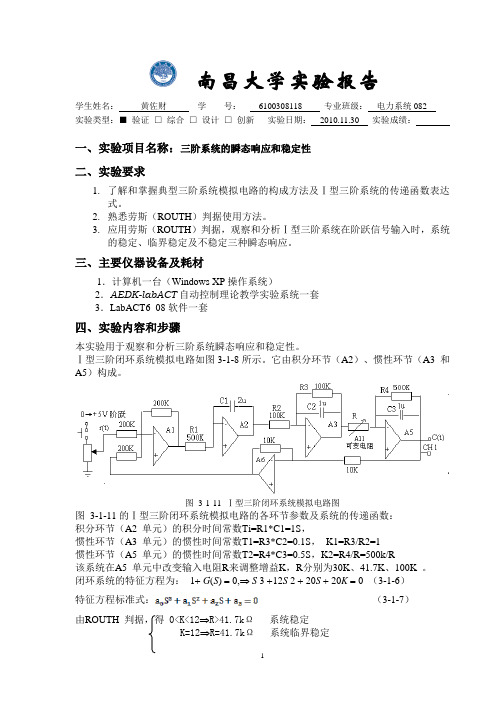
南昌大学实验报告学生姓名：黄佐财学号：6100308118 专业班级：电力系统082实验类型：■验证□综合□设计□创新实验日期：2010.11.30 实验成绩：一、实验项目名称：三阶系统的瞬态响应和稳定性二、实验要求1.了解和掌握典型三阶系统模拟电路的构成方法及Ⅰ型三阶系统的传递函数表达式。

2.熟悉劳斯（ROUTH）判据使用方法。

3.应用劳斯（ROUTH）判据，观察和分析Ⅰ型三阶系统在阶跃信号输入时，系统的稳定、临界稳定及不稳定三种瞬态响应。

三、主要仪器设备及耗材1．计算机一台（Windows XP操作系统）2．AEDK-labACT自动控制理论教学实验系统一套3．LabACT6_08软件一套四、实验内容和步骤本实验用于观察和分析三阶系统瞬态响应和稳定性。

Ⅰ型三阶闭环系统模拟电路如图3-1-8所示。

它由积分环节（A2）、惯性环节（A3 和A5）构成。

图3-1-11 Ⅰ型三阶闭环系统模拟电路图图3-1-11的Ⅰ型三阶闭环系统模拟电路的各环节参数及系统的传递函数：积分环节（A2 单元）的积分时间常数Ti=R1*C1=1S，惯性环节（A3 单元）的惯性时间常数T1=R3*C2=0.1S，K1=R3/R2=1惯性环节（A5 单元）的惯性时间常数T2=R4*C3=0.5S，K2=R4/R=500k/R该系统在A5 单元中改变输入电阻R来调整增益K，R分别为30K、41.7K、100K 。

闭环系统的特征方程为：1+ G(S) = 0,⇒ S 3 +12S 2 + 20S + 20K = 0 （3-1-6）特征方程标准式：（3-1-7）由ROUTH 判据，得 0<K<12⇒R>41.7kΩ系统稳定K=12⇒R=41.7kΩ系统临界稳定K>12 R<41.7k Ω 系统不稳定Ⅰ型三阶闭环系统模拟电路图见图3-1-11，分别将（A11）中的直读式可变电阻调整到30K 、41.7K 、100K ，跨接到A5 单元（H1）和（IN ）之间，改变系统开环增益进行实验。

⾃动控制原理实验报告实验名称：实验⼀控制系统建模的Matlab ⽅法实验时间：实验地点：实验⽬的：1.了解Matlab 软件的基本使⽤⽅法 2.掌握常⽤的系统建模命令实验内容：1.⽤Matlab 描述6852)(232++++=s ss ss G⽅法⼀： fenzi=[1 0 2]; fenmu=[1 5 8 6]; g=tf(fenzi,fenmu) ⽅法⼆：g=tf([1 0 2],[1 5 8 6])2.已知某系统的传递函数为6852)(23++++=s ss s s G ，绘制系统的零极点分布图。

运⾏程序并记录结果。

num=[1 2]; den=[1 5 8 6];[z,p,k]=tf2zp(num,den) pzmap(p,z) 3.已知441)(221+++=s ss s G ，61)(2+=s s G ，101)(++=s s s H ，求化简结果。

g1=tf([1 0 1],[1 4 4]); g2=tf([1],[1 6]); sys1=series(g1,g2)sys2=parallel(g1,g2)h=tf([1 1],[1 10]); sys3=feedback(sys1,h)实验名称：实验⼆线性系统时域分析的Matlab ⽅法实验时间：实验地点：实验⽬的：1.掌握线性系统时域分析的常⽤命令 2.能编程实现系统时域分析3.进⼀步熟悉Matlab 软件的使⽤实验内容：1.已知系统的特征⽅程为05432234=++++s s s s ，求系统特征根 p=[1 2 3 4 5]; r=roots(p)2.某⼆阶系统的闭环传递函数为222)(nn nw s w sw s G ++=ξ，其中s rad w n /5=，编程实现不同阻尼⽐情况下⼆阶系统单位阶跃响应的仿真。

写出对语句的注释。

fenzi=[25]; k1=-0.5; k2=0; k3=0.7; k4=1.0; k5=1.2; fenmu1=[1 2*k1*5 25]; fenmu2=[1 2*k2*5 25]; fenmu3=[1 2*k3*5 25]; fenmu4=[1 2*k4*5 25]; fenmu5=[1 2*k5*5 25];t=0:0.1:10;c1=step(fenzi,fenmu1,t); c2=step(fenzi,fenmu2,t); c3=step(fenzi,fenmu3,t); c4=step(fenzi,fenmu4,t); c5=step(fenzi,fenmu5,t); figure plot(t,c1)title('阻尼⽐-0.5') gridfigure plot(t,c2)title('阻尼⽐0')gridfigureplot(t,c3,t,c4,t,c5); xlabel('时间') ylabel('输出') grid实验名称：实验三线性系统根轨迹分析的Matlab ⽅法实验时间：实验地点：实验⽬的：1.掌握线性系统根轨迹分析的Matlab ⽅法 2.能编程绘制已知系统的根轨迹 3.掌握分析仿真结果的⽅法实验内容：1.已知单位负反馈系统的开环传递函数为)15.0)(12.0()(1++=s s s Ks G ，)12()1()(2++=s s s K s G，)3)(2()5()(1+++=s s s s K s G ，分别编程绘制系统根轨迹，并记录仿真结果。

自动控制原理实验报告课程名称 自动控制原理 成 绩 实验项目 控制系统的根轨迹作图 指导教师 王春玲 学生姓名 张利国 学号 200800804010 班级专业 08电科本 实验地点 综合楼205 实验日期 2010 年 11 月 24 日一、实验目的1.利用计算机完成控制系统的根轨迹作图；2.了解控制系统根轨迹图的一般规律；3.利用根轨迹进行系统分析及校正。

二、实验步骤1.在Windows 界面上用鼠标双击matlab 图标，即可打开MATLAB 命令平台。

2.练习相关M 函数根轨迹作图函数：格式1：rlocus(sys) 格式2：rlocus(sys,k)格式3：r=rlocus(sys) 格式4：[r,k]=rlocus(sys)函数功能：绘制系统根轨迹图或者计算绘图变量。

格式1：控制系统的结构图如图所示。

输入变量sys 为LTI 模型对象，k 为机器自适应产生的从0→∞的增益向量，绘制闭环系统的根轨迹图。

格式2：k 为人工给定的增益向量。

格式3：返回变量格式，不作图。

r 为返回的闭环根向量。

格式4：返回变量r 为根向量，k 为增益向量，不作图。

三、实验内容给定如下各系统的开环传递函数，作出它们的根轨迹图，并完成给定要求。

1. )2)(1()(01++=s s s k s G g程序：k=1; %零极点模型的增益值z=[]; %零点p=[0,-1,-2]; %极点sys=zpk(z,p,k); rlocus(sys)根轨迹图：要求： （1）准确记录根轨迹的起点.终点与根轨迹的条数共三条；（2）确定根轨迹的分离点与相应的根轨迹增益分离点：-0.423+7.65e-009i ；根轨迹增益为0.385。

（3）确定临界稳定时的根轨迹增益k gL上下的根轨迹增益都一样，都是6.02。

2. )164)(1()1()(202++-+=s s s s s k s G g要求： 确定根轨迹与虚轴交点并确定系统稳定的根轨迹k g 增益范围。

实验三 线性定常系统的稳态误差一、实验目的1. 通过本实验，理解系统的跟踪误差与其结构、参数与输入信号的形式、幅值大小之间的关系；2. 研究系统的开环增益K 对稳态误差的影响。

二、实验设备同实验一。

三、实验内容1. 观测0型二阶系统的单位阶跃响应和单位斜坡响应，并实测它们的稳态误差；2. 观测I 型二阶系统的单位阶跃响应和单位斜坡响应，并实测它们的稳态误差；3. 观测II 型二阶系统的单位斜坡响应和单位抛物坡，并实测它们的稳态误差。

四、实验原理通常控制系统的方框图如图4-1所示。

其中G(S)为系统前向通道的传递函数，H(S)为其反馈通道的传递函数。

图4-1由图4-1求得)()()(11)(S R S H S G S E +=（1）由上式可知，系统的误差E(S)不仅与其结构和参数有关，而且也与输入信号R(S)的形式和大小有关。

如果系统稳定，且误差的终值存在，则可用下列的终值定理求取系统的稳态误差：)(lim 0S SE e s ss →=（2）本实验就是研究系统的稳态误差与上述因素间的关系。

下面叙述0型、I 型、II 型系统对三种不同输入信号所产生的稳态误差ss e 。

1．0型二阶系统设0型二阶系统的方框图如图4-2所示。

根据式（2），可以计算出该系统对阶跃和斜坡输入时的稳态误差：图4-2 0型二阶系统的方框图1） 单位阶跃输入（sS R 1)(=） 3112)1.01)(2.01()1.01)(2.01(lim 0=⨯+++++⨯=→S S S S S S e S ss图表 1仿真结果中可以看到，读到的误差值为324.506mV ，基本符合理论的推算结果。

Matlab 仿真2） 单位斜坡输入（21)(s S R =） ∞=⨯+++++⨯=→2012)1.01)(2.01()1.01)(2.01(lim SS S S S S e S ss上述结果表明0型系统只能跟踪阶跃输入，但有稳态误差存在，其计算公式为：Pss K R e +=10其中)()(lim 0S S H S G K p →≅，R 0为阶跃信号的幅值。

第1篇一、实验目的1. 理解自控制原理的基本概念和基本方法。

2. 掌握典型控制系统的组成和基本工作原理。

3. 学习使用实验仪器，进行控制系统模拟实验。

4. 分析和评估控制系统的性能指标，提高对控制系统设计和优化的认识。

二、实验仪器与设备1. EL-AT-III型自动控制系统实验箱一台2. 计算机一台3. 万用表一个三、实验原理1. 自控制原理基本概念：自控制原理是研究如何利用反馈信息来控制系统的行为，使其达到预定的目标。

其基本原理是：通过将系统的输出信号反馈到输入端，与输入信号进行比较，产生误差信号，然后根据误差信号调整系统的控制策略，以达到控制目标。

2. 典型控制系统组成：典型控制系统通常由控制器、被控对象、反馈环节和执行机构组成。

3. 控制系统模拟实验：利用实验箱和计算机，通过模拟电路搭建典型控制系统，进行实验研究。

四、实验内容1. 实验一：典型环节及其阶跃响应- 实验目的：掌握控制模拟实验的基本原理和一般方法，掌握控制系统时域性能指标的测量方法。

- 实验步骤：1. 搭建一阶系统的模拟电路。

2. 通过计算机等测量仪器，测量系统的输出，得到系统的动态响应曲线及性能指标。

3. 改变系统的参数，分析参数对系统性能的影响。

2. 实验二：二阶系统阶跃响应- 实验目的：了解二阶系统的阶跃响应特性，掌握二阶系统的性能指标。

- 实验步骤：1. 搭建二阶系统的模拟电路。

2. 通过计算机等测量仪器，测量系统的输出，得到系统的阶跃响应曲线及性能指标。

3. 分析二阶系统的性能指标，如上升时间、超调量、调节时间等。

3. 实验三：连续系统串联校正- 实验目的：学习连续系统串联校正方法，提高控制系统的性能。

- 实验步骤：1. 搭建连续系统的模拟电路。

2. 分析系统的性能指标，确定校正方法。

3. 通过计算机等测量仪器，测量校正后的系统输出，评估校正效果。

五、实验结果与分析1. 实验一：通过搭建一阶系统的模拟电路，测量系统的输出，得到系统的动态响应曲线及性能指标。

实验三 线性系统的频域分析一、实验目的1．掌握用MATLAB 语句绘制各种频域曲线。

2．掌握控制系统的频域分析方法。

三、实验内容 四、实验报告1．根据内容要求，写出调试好的MATLAB 语言程序，及对应的结果。

2. 记录显示的图形，根据实验结果与各典型环节的频率曲线对比分析。

3. 记录并分析ζ对二阶系统bode 图的影响。

4．根据频域分析方法分析系统，说明频域法分析系统的优点。

5．写出实验的心得与体会。

1．典型二阶系统2222)(nn ns s s G ωζωω++=绘制出6=n ω，1.0=ζ，0.3，0.5，0.8，2的bode 图，记录并分析ζ对系统bode 图的影响。

num =[0 0 36]; den1=[1 1.2 36]; den2=[1 3.6 36]; den3=[1 6.0 36]; den4=[1 9.6 36]; den5=[1 24 36]; w=logspace(-2,3,100); bode(num,den1,w); gridtext (4.2,-15,'¦Î=0.1') holdbode(num,den2,w); text (2.5,-22,'¦Î=0.3') bode(num,den3,w); text (13.5,-150,'¦Î=0.5') bode(num,den4,w); text (24,-157,'¦Î=0.8')bode(num,den5,w); text (1.4,-45,'¦Î=2.0')-100-80-60-40-20020M a g n i t u d e (d B)10-210-110101102103P h a s e (d e g )Bode DiagramFrequency (rad/sec)结果分析:从图中可看出ζ越小,中频段振荡越剧烈。