第四章 集中趋势测量法习题_社会统计学1

社会研究的统计应用 李沛良第二篇 统计叙述：单变项与双变项 2~3 简化一个、两个变项之分布1.关于数值中小数的取舍问题。

“四舍五入”之“四舍”没有问题，同时结合“前单五入”，即“五”前面是单数就进位，若是双数则舍掉（0算双数）。

2.所谓集中趋势测量法，就是找出一个数值来代表变项的分布，以反映资料的集结情况。

此法的意义在于，可以根据这个代表值（或称典型值）来估计或预测每个研究对象（即个案）的数值。

这样的估计或预测，当然会有错误，但由于所根据的数值最有代表性，故所发生之错误的总和理应是最小的。

众值 （Mo ）：次数最多的值。

中位值（Md ）：在一个序列的中央位置之值。

均值 （）：变项的各个数值之和，求取一个平均数。

3.离散趋势测量法，是要求出一个值来表示个案与个案之间的差异情况。

该法与集中趋势测量法具有互相补充的作用。

集中趋势测量法所求出的是一个最能代表变项所有资料的值，但其代表性的高度却要视乎各个个案之间的差异情况。

如果个案之间的差异很大，则众值、中位值、均值的代表性就会甚低；此时以这三个值作估计或预测，所犯的错误就会很大。

离异比率（V ）：非众值的次数与全部个案数目的比率。

质异指数（IQV ）：其作用是求出各个类别之间在理论上最多的可能差异中实际上出现了多少差异。

（k=变项的类别数目，f=每个类别的实际次数）四分位差（Q ）：将个案由低至高排列后分为四个等分，第一个四分位置的值Q1与第三个四分位置的值Q3的差异。

标准差（S ）：将各数值（x ）与其均值（）之差的平方和除以全部个案数目，然后取其平方根。

公式中x 与相差，就是表示以均值作为代表值时会引起的偏差或错误。

总之，集中趋势测量法与离散趋势测量法并用，可以一方面知道资料的代表值，有助于估计或预测的工作，另一方面可以知道资料的差异情况，反映估计或预测时会犯的错误。

正态分布与标准值？ 简化两个变项之分布 统计相关交互分类与百分表简化相关与消减误差相关测量与假设检定相关测量法，目的是要理解两个变项在“样本”（随机与非随机样本均可）中的相关“强弱”程度及方向。

社会统计学试题及答案一、单项选择题（每题2分，共20分）1. 社会统计学中，用来描述一组数据集中趋势的指标是（）。

A. 众数B. 中位数C. 均值D. 方差答案：C2. 以下哪个选项不属于描述统计学的内容？（）A. 数据收集B. 数据整理C. 数据分析D. 数据预测答案：D3. 在统计学中，用来衡量数据离散程度的指标是（）。

A. 标准差B. 均值C. 众数D. 中位数答案：A4. 以下哪个概念不是社会统计学的研究对象？（）A. 人口数量B. 收入水平C. 股票价格D. 家庭结构答案：C5. 社会统计学中，用来衡量两个变量之间相关关系的强度的指标是（）。

A. 相关系数B. 回归系数C. 标准差D. 方差答案：A6. 以下哪个选项不是社会统计学中常用的数据收集方法？（）A. 问卷调查B. 观察法C. 实验法D. 文献分析答案：C7. 在统计学中，用来衡量数据集中程度的指标是（）。

A. 标准差B. 均值C. 众数D. 中位数答案：B8. 以下哪个选项是社会统计学中常用的数据整理方法？（）A. 频数分布表B. 回归分析C. 假设检验D. 相关分析答案：A9. 社会统计学中，用来描述一组数据分布形态的指标是（）。

A. 偏度B. 峰度C. 均值D. 方差答案：A10. 以下哪个概念是社会统计学中用来描述数据的离散程度的？（）A. 标准差B. 均值C. 众数D. 中位数答案：A二、多项选择题（每题3分，共15分）1. 社会统计学中，用来描述一组数据的指标包括（）。

A. 均值B. 众数C. 方差D. 标准差E. 中位数答案：ABDE2. 以下哪些是社会统计学中常用的数据分析方法？（）A. 描述性分析B. 推断性分析C. 回归分析D. 假设检验E. 相关分析答案：ABCDE3. 社会统计学中，用来衡量数据离散程度的指标包括（）。

A. 标准差B. 方差C. 偏度D. 峰度E. 极差答案：ABE4. 以下哪些是社会统计学中常用的数据收集方法？（）A. 问卷调查B. 观察法C. 实验法D. 文献分析E. 访谈法答案：ABDE5. 社会统计学中，用来描述一组数据分布形态的指标包括（）。

社会统计学试卷社会工作与管理（本）专业一、单项选择题（每小题1分，共15分）1．在下列两两组合的平均指标中，哪一组的两个平均数完全不受极端数值的影响？ 【 】A ．算术平均数和调和平均数B ．几何平均数和众数C ．调和平均数和众数D ．众数和中位数2．抽样推断的目的是 【 】A ．以样本指标推断总体指标B ．取得样本指标C ．以总体指标估计样本指标D ．以样本的某一指标推断另一指标3．下列哪两个变量之间的相关程度高 【 】A ．商品销售额和商品销售量的相关系数是0.9；B ．商品销售额与商业利润率的相关系数是0.84；C ．平均流通费用率与商业利润率的相关系数是-0.94；D ．商品销售价格与销售量的相关系数是-0.91。

4． 在抽样推断中，可以计算和控制的误差是 【 】A ．抽样实际误差B ．抽样标准误差C ．非随机误差D ．系统性误差5．不重复抽样的抽样标准误公式比重复抽样多了一个系数 【 】A ．n N N --1B ．1++N nNC ．1--N n ND ．n N N ++16．估计标准误说明回归直线的代表性，因此 【 】A ．估计标准误数值越大，说明回归直线的代表性越大；B ．估计标准误数值越大，说明回归直线的代表性越小；C ．估计标准误数值越小，说明回归直线的代表性越小；D ．估计标准误数值越小，说明回归直线的实用价值越小。

7．平均差与标准差的主要区别是 【 】A ．意义有本质的不同B ．适用条件不同C ．对离差的数学处理方法不同D ．反映的变异程度不同8．“统计”一词的含义可以包括的是 【 】A ．统计工作、统计资料、统计学B ．统计工作、统计资料、统计方法C ．统计资料、统计学、统计方法D ．统计工作、统计学、统计方法9．已知甲数列的算术平均数为100，标准差为20；乙数列的算术平均数为50，标准差为9。

由此可以认为 【 】A ．甲数列算术平均数的代表性好于乙数列B ．乙数列算术平均数的代表性好于甲数列C ．两数列算术平均数的代表性相同D ．两数列算术平均数的代表性无法比较10．变量x 与y 之间的负相关是指 【 】A. x 数值增大时y 也随之增大B. x 数值减少时y 也随之减少C. x 数值增大时y 随之减少D. y 的取值几乎不受x 取值的影响11．次数数列各组变量值都增加2倍，每组次数减少2倍，中位数 【 】A ．减少2倍B ．增加2倍C ．减少1倍D ．不变12．第一类错误是在下列条件下发生 论 【 】A. 原假设为真B. 原假设为假C. 显著性水平较小D. 显著性水平较大13．设()2,~σμN X ，b aX Y -=，其中a 、b 为常数，且0≠a ，则~Y 【 】A. ()222,b a b a N +-σμB.()222,b a b a N -+σμC.()22,σμa b a N +D. ()22,σμa b a N -14．设随机变量),(~2σμN X ，则随σ增大，{}σμ<-X P 【 】A.单调增大B.单调减小C.保持不变D.增减不定15．设随机变量,X Y 相互独立，)1,0(~N X ,)1,1(~N Y ，则 【 】A.2/1)0(=≤+Y X PB.2/1)1(=≤+Y X PC.2/1)0(=≤-Y X PD.2/1)1(=≤-Y X P二、填空题（每空1分，共10分）1．社会调查资料有 、统计规律性的特点。

社会心理统计学考试试题一、单选题（每题 3 分，共 30 分）1、下列哪个不是描述数据集中趋势的统计量？（）A 均值B 中位数C 众数D 方差2、在正态分布中，均值和中位数的关系是（）A 均值大于中位数B 均值小于中位数C 均值等于中位数D 无法确定3、样本标准差的计算公式为（）A √∑（X X）²／ nB √∑（X X）²／（n 1)C ∑（X X）²／ nD ∑（X X）²／（n 1)4、进行假设检验时，若 p 值小于显著性水平α，则（）A 拒绝原假设B 接受原假设C 无法确定D 以上都不对5、相关系数的取值范围是（）A －1, 1B 0, 1C （∞，＋∞）D 0, ＋∞）6、对于两个独立样本的均值差异检验，应采用（）A t 检验B z 检验C F 检验D 卡方检验7、在方差分析中，用于衡量不同组之间变异的统计量是（）A 组内方差B 组间方差C 总方差D 误差方差8、下列哪种抽样方法不是概率抽样？（）A 简单随机抽样B 分层抽样C 整群抽样D 方便抽样9、以下哪个图形最适合展示分类数据的分布情况？（）A 直方图B 折线图C 饼图D 箱线图10、回归分析中，判定系数 R²的取值范围是（）A 0, 1B －1, 1C 0, ＋∞）D （∞，＋∞）二、多选题（每题 4 分，共 20 分）1、以下哪些是描述数据离散程度的统计量？（）A 极差B 四分位差C 方差D 标准差2、假设检验中可能犯的错误有（）A 第一类错误B 第二类错误C 抽样误差D 非抽样误差3、影响样本容量大小的因素有（）A 总体方差B 允许误差C 置信水平D 抽样方法4、方差分析的基本假定包括（）A 正态性B 方差齐性C 独立性D 随机性5、下列哪些是相关分析和回归分析的区别？（）A 变量的地位不同B 分析的目的不同C 对变量的要求不同D 计算方法不同三、简答题（每题 10 分，共 30 分）1、请简述中心极限定理的内容及其在统计学中的作用。

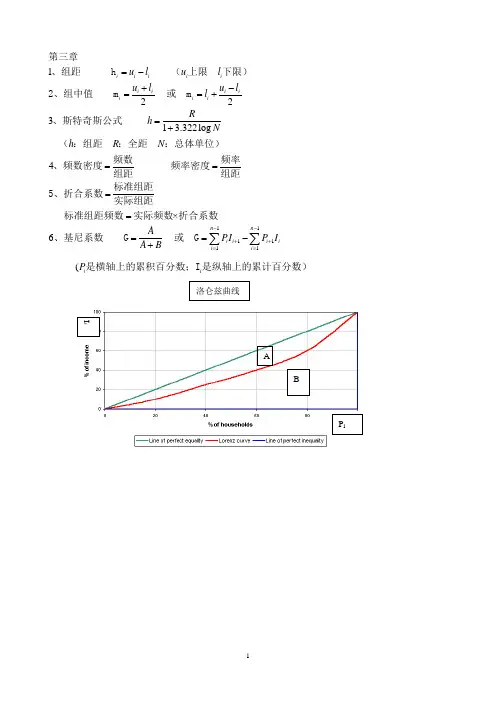
12231 3.322log 4×6i i i i i i i i i i i i u l u l u l u ll Rh N h R N AA B =-+-==+=+=====+第三章、组距 h （上限 下限）2、组中值 m 或 m 、斯特奇斯公式 （：组距 ：全距 ：总体单位）频数频率、频数密度 频率密度组距组距标准组距5、折合系数实际组距标准组距频数实际频数折合系数、基尼系数 G 111111n n i i i ii i PI P I --++===-∑∑ 或 G(i i P 是横轴上的累积百分数；I 是纵轴上的累计百分数）洛仑兹曲线P iI iAB1(2))(1)1221222d d X X X N fXX fN NN NN F L ==++-=+∑∑∑第四章1、算术平均数（）（）未分组资料 分组资料 注：对于单项数列分组，X即为变量值，若为组距式分组，则X为组中值 f:各组频数2、中位数（M 未分组资料 若N为奇数，则取第位上的变量值为中位数，若为偶数，则取第 位和第位上的两个变量值的平均数作为中位数（）分组资料 M 112h h L : 2m m d m m m m m N F U f f f F F N---⨯=-⨯或 M 中位数所在组的下限： 中位数所在组的频数： 小于中位数所在组的各组频数之和（向上累计） h ： 中位数所在组的组距 U: 中位数所在组的上限： 包括中位数所在组的各组频数之和（向上累计） 注： 中位数所在组由确定11111111133333334h :h 34h :N F l f F l f NF l f F l -=+⨯-=+⨯3、四分位数（1）第一四分位数 Q ：小于第一四分位数所在组的各组累计频数（向上累计） 第一四分位数所在组的下限 ：第一四分位数所在组的组距 ：第一四分位数所在组的组距（2）第三四分位数 Q ：小于第三四分位数所在组的各组累计频数（向上累计） 第三四分位数所在组的3311212h 1h :h 5o o o oo o f L L ∆=+⨯∆+∆∆∆下限 ：第三四分位数所在组的组距 ：第三四分位数所在组的组距4、众数（M ）（）未分组资料 先将所有数据顺序排列，观察某些变量值出现的次数最多，这些变量值就 是众数（2）分组资料 M 众数所在组的下限：众数所在组频数与前一组频数之差 ：众数所在组频数与后一组频数之差 ：众数所在组的组距、几何平均数11lg lg anti(lg )(2)1lg lg anti(lg )g g g g g gg g g X Nf X NX ========∑∑（M ）（）简单几何平均数 M 或 M M M 加权几何平均数M 或 M M M 注：若为组距式分组，则为组中值3112316)(1)111111...(2):312=23h h N h d o g h N Q Q NX X X X XNNf XX f X X -==++++==-≥≥-⋅∑∑、调和平均数（M 简单调和平均数（未分组） M 加权调和平均数（分组）M 注：若为组距式分组，为组中值 各组频数7、各种平均数的关系2M M M M 第五章、全距 R=X X 、四分位差 Q D、平均差=2=::X X Nf X XfX f X f -⋅-⋅∑∑（1）未分组资料 A D （）分组资料 A D 注：若为组距式分组，为组中值 各组频数4、标准差（S）（1）未分组资料(2)分组资料 注：若为组距式分组，为组中值 各组X X S-频数5、标准分 Z=社会统计学复习整理一、变量的测量层次61(2)37=1:83(o o oR R M M M o d o R X X SXN f f NNf X M X M X M S Sαα⋅⋅=-⋅=----==A D 、变异系数（）全距系数 V =A D平均差系数 V =（）标准差系数 V 、异众比率（非众数的频数与总体单位数的比值） V R 众数的频数、偏态系数())偏态=二、判断变量层次的技巧1.首先所有的变量都是定类变量。

社会统计学试题及答案社会统计学是一门研究社会现象数量特征和规律性的科学，它在社会科学领域中占有重要的地位。

以下是一套社会统计学的模拟试题及答案，供学生参考和练习。

社会统计学模拟试题一、选择题（每题2分，共20分）1. 社会统计学研究的主要对象是：A. 个体行为B. 社会现象的数量特征C. 社会现象的质的属性D. 社会现象的因果关系答案：B2. 下列哪一项不是统计数据的类型？A. 定类数据B. 定序数据C. 定距数据D. 定性数据答案：D3. 在统计分析中，中位数是：A. 数据集中的最小值B. 数据集中的中间值C. 数据集中的平均值D. 数据集中的最大值答案：B4. 标准差是衡量数据：A. 中心趋势的指标B. 离散程度的指标C. 相关程度的指标D. 偏态的指标答案：B5. 以下哪个是参数估计的步骤？A. 收集数据B. 计算样本统计量C. 确定置信区间D. 所有以上答案：D二、简答题（每题10分，共30分）6. 简述社会统计学与数理统计学的区别。

答案：社会统计学与数理统计学的主要区别在于研究对象和应用领域。

数理统计学主要研究的是概率论在统计推断中的应用，它更侧重于数学理论和方法。

而社会统计学则侧重于社会现象的量化分析，它将数理统计的方法应用于社会科学研究中，以揭示社会现象的数量特征和规律。

7. 解释什么是抽样误差，并举例说明。

答案：抽样误差是指由于从总体中随机抽取样本进行研究，而导致样本统计量与总体参数之间存在差异的情况。

例如，在一项关于城市居民收入水平的研究中，如果只抽取了高收入区域的居民作为样本，那么得到的样本均值可能会高于整个城市居民的实际平均收入，这就是抽样误差的一个例子。

8. 描述相关系数的计算方法及其意义。

答案：相关系数是用来衡量两个变量之间线性关系强度和方向的统计量。

最常用的相关系数是皮尔逊相关系数，其计算公式为：\[ r =\frac{\sum (X_i - \overline{X})(Y_i -\overline{Y})}{\sqrt{\sum (X_i - \overline{X})^2 \sum (Y_i - \overline{Y})^2}} \] 其中，\( X_i \) 和 \( Y_i \) 分别是变量X 和Y的观测值，\( \overline{X} \) 和 \( \overline{Y} \) 是它们的平均值。

社会统计学讲义第一章导论一、社会统计学1、社会统计学是运用统计的一般原理，对社会各种静态结构与动态趋势进行定量描述或推断的一种专门方法和技术。

研究对象：概括而言是指社会现象的数量方面。

2、选择统计分析方法的原则是根据研究目的和资料本身的特点选择。

3、统计分析的作用：(1)可对资料进行简化和描述；(2)可对变量间的关系进行描述和深入地分析（统计分析通过事后解释使得探讨变量间复杂的因果联系成为可能）；(3)可通过样本资料推断总体（通过参数估计和假设检验，将样本推论到总体并指出这种推论的误差及做出这种推论的把握有多大）。

4、社会统计的基本程序（1）制定计划；（2）统计调查；（3）统计整理；（4）统计分析；（5）统计报告。

5、几个基本概念（1）总体与单位总体又称母体，是作为统计研究对象的、由许多具有共性的单位构成的整体。

构成总体的每一个个体称为总体单位，简称单位或个体。

3个基本特征：大量性、同质性和变异性。

（2）标志与变量总体的每个单位都具有许多属性和特性，说明总体单位属性或数量特征的名称在统计上称为标志，分为数量标志和品质标志。

可变的品质标志无法用数值表示，我们称之为变项；可变的数量标志能够用数值表示，我们称之为变量。

（3）指标与指标体系统计指标是反映总体(或样本总体)的数量特征的概念或范畴。

一个完整的统计指标由两部分构成：指标名称和指标数值。

在社会统计中，如要全面把握对象总体情况，就不能单凭一个指标，而要靠一组相互联系的并与之相适应的指标来完整地反映对象总体。

指标体系就是一系列有内在联系的统计指标的集合体。

二、社会调查研究的程序社会学研究之阶段与步骤（1）确定课题：来源与社会学理论、当前社会现实和要解决的实际问题；具有强烈的时代感、为国家现代化服务；（2）了解情况：查阅文献和向有经验、有知识的人了解，运用个案调查、典型调查进行探索性研究；（3）提出一定的想法和建立假设：差异式、函数式；（4）建立概念和测量方法：采用适当的术语和概念；操作化定义；概念的表现形式往往具有多值性；（5）设计问卷：内容包括事实、态度与看法、行为趋向、理由；方式有固定答题式和自由答题式；（6）试填问卷：发现不周或遗漏之处在试填阶段予以纠正；（7）调查实施（抽样调查）：从局部推论到全体（8）校核与登录（9）统计分析与命题的检验：检验最初研究阶段的命题或假设是否得到证实或部分证实，在此基础上对研究内容提出建议和确定进一步的研究方案。

第四章 集中趋势测量法一、填空1．某班级中男生人数所占比重是66.7%，则男生和女生的比例关系是（ ）。

2．在频数分布图中，（ ）标示为曲线的最高点所对应的变量值。

3．在频数呈偏态分布时，（ ）必居于X 和M 0之中。

4．算术平均数、调和平均数、几何平均数又称为（ ）平均数，众数、中位数又称为（ ）平均数，其中（ ）平均数不受极端变量值得影响。

5．调和平均数是根据（ ）来计算的，所以又称为（ ）平均数。

6．加权算术平均数是以（ ）为权数，加权调和平均数是以（ ）为权数的。

7．对于未分组资料，如总体单位数是偶数，则中间位置的两个标志值的算术平均数就是（ ）。

二、单项选择1．分析统计资料，可能不存在的平均指标是（ ）。

A 众数B 算术平均数C 中位数D 几何平均数2．对于同一资料，算术平均数，调和平均数和几何平均数在数量级上一般存在如下关系（ ）。

A g M ≥h M ≥XB h M ≥X ≥g MC h M ≥g M ≥XD X ≥g M ≥h M3．下面四个平均数中，只有（ ）是位置平均数。

A 算术平均数B 中位数C 调和平均数D 几何平均数 4．从计算方法上看，PK Q P Q P /1111∑∑是（ ）。

A 算术平均数B 调和平均数C 中位数D 几何平均数 5．由右边的变量数列可知：（ ）。

A 0M >d M ； B d M >0M ； C 0M >30 D d M >306．某车间三个小组，生产同种产品，其劳动生产率某月分别为150，160，165（件/工日），产量分别为4500，4800，5775（件），则该车间平均劳动生产率计算式为（ ）。

A33.1583165160150=++（件/工日）完成生产定额数 工人数 10－2020－30 30－40 40－50 50－6035 20 25 10 15B 53.158577548004500577516548001604500150=⨯+⨯+⨯＋＋（件/工日）C 68.158165577516048001504500577548004500=++++（件/工日）D21.1581651601503＝⨯⨯（件/工日）7．关于算术平均数的性质，不正确的描述是（ ）。